Abstract
Cooling devices grounded in solid-state physics are promising candidates for integrated-chip nanocooling applications. These devices are modeled by coupling the quantum non-equilibirum Green’s function for electrons with the heat equation (NEGF+H), which allows to accurately describe the energetic and thermal properties. We propose a novel machine learning (ML) workflow to accelerate the design optimization process of these cooling devices, alleviating the high computational demands of NEGF+H. This methodology, trained with NEGF+H data, obtains the optimum heterostructure designs that provide the best trade-off between the cooling power of the lattice (CP) and the electron temperature ( ). Using a vast search space of
). Using a vast search space of 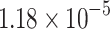 different device configurations, we obtained a set of optimum devices with prediction relative errors lower than
different device configurations, we obtained a set of optimum devices with prediction relative errors lower than 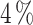 for CP and
for CP and 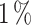 for Te. The ML workflow reduces the computational resources needed, from two days for a single NEGF+H simulation to 10 s to find the optimum designs.
for Te. The ML workflow reduces the computational resources needed, from two days for a single NEGF+H simulation to 10 s to find the optimum designs.
Subject terms: Electrical and electronic engineering, Semiconductors, Electronic devices
Introduction
The drastic rise in chip power consumption, due to its miniaturization and high-density packaging, is a significant issue that leads to local hot spots in nanoelectronic devices 1,2. These hot spots degrade the performance, reliability and lifetime of the devices, making it crucial to manage and mitigate thermal effects effectively 3,4. Traditional techniques to reduce this issue, such as liquid cooling 5 or fan-based systems 6, involve the cooling of the entire chip, a procedure recognized for its substantial power consumption 7. It is noteworthy that approximately 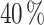 of the energy utilized by data centers is dedicated to cooling 8. Then, the challenge of managing self-induced heat 9 entails the exploration of innovative cooling solutions, as the ones grounded in solid-state physics 10–12. In this context, this study focus on one of the most promising solid-state cooling devices, the asymmetric double-barrier heterostructures based on semiconductors, which had been validated as an effective integrated-chip cooling solution 13,14. To capture the physics involved in these heterostructures, and, specifically, to evaluate the energy transfer between the semiconductor lattice and the conduction electrons, the performed simulations self-consistently couple the quantum non-equilibrium Green’s function formalism for electrons with the heat equation (NEGF+H) 15,16. To assess the amount of heat removed from the device, we calculate the cooling power (CP) which is defined as the energy transfer between the lattice and the electrons via phonon absorption. In addition, a virtual probe technique is used to calculate the electron temperature in the quantum well (
of the energy utilized by data centers is dedicated to cooling 8. Then, the challenge of managing self-induced heat 9 entails the exploration of innovative cooling solutions, as the ones grounded in solid-state physics 10–12. In this context, this study focus on one of the most promising solid-state cooling devices, the asymmetric double-barrier heterostructures based on semiconductors, which had been validated as an effective integrated-chip cooling solution 13,14. To capture the physics involved in these heterostructures, and, specifically, to evaluate the energy transfer between the semiconductor lattice and the conduction electrons, the performed simulations self-consistently couple the quantum non-equilibrium Green’s function formalism for electrons with the heat equation (NEGF+H) 15,16. To assess the amount of heat removed from the device, we calculate the cooling power (CP) which is defined as the energy transfer between the lattice and the electrons via phonon absorption. In addition, a virtual probe technique is used to calculate the electron temperature in the quantum well (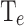 ) and the electrochemical potential inside the device 17,18. The overall cooling performance in this work is evaluated as a trade-off between CP and
) and the electrochemical potential inside the device 17,18. The overall cooling performance in this work is evaluated as a trade-off between CP and 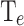 , depending on the targeted application.
, depending on the targeted application.
However, the high computational requirements make it essential to address a critical aspect of the implementation of the accurate NEGF+H methodology. Performing a simulation of one double-barrier heterostructure configuration can extend for a couple of days when executed on a single CPU core. Hence, the optimization of these devices is challenging for several reasons: (i) the high computational resources required for each accurate NEGF+H simulation; (ii) the number of design parameters to optimize; iii) the non-linear dependence between the design parameters and the cooling performance. These challenges highlight the need to explore complementary methods, such as those based on machine learning (ML), which can provide trend information to accelerate the device design process. Drawing on the success of these ML-based techniques in other nanoelectronic studies 19–22, we present a novel methodology using two neural network (NN). This approach aims to identify heterostructures with optimal cooling performance while minimizing computational cost. Therefore, the combination of NEGF+H with the proposed ML-based methodology, not only accelerates nanoelectronic device design but also unveils crucial insights for optimizing cooling performance, marking a significant advancement in the searching for an integrated-circuit cooling solution.
The contents of this work are distributed as follows. Section “Device description” shows the asymmetric double barrier heterostructure description with the explanation of how these devices operate. Then, the section “Results” presents the main results of this work, starting with the ML workflow and the validation against NEGF+H (section “Machine learning workflow and validation”), together with the structure optimization of the devices (section “Structure optimization”). The discussion is presented in section “Discussion” and the details of the methods used in this work are presented in section “Methods” distributed in: the NEGF+H simulation methodology (section “NEGF+H simulation methodology”), dataset description and pre-processing (section “Dataset description and pre-processing”), ML methodology (section “Machine learning methodology”), and metrics definition (section “Metrics”). Finally, after data (Data availability) and code (Code availability) availability, the main conclusions of this work are summarized in section “Conclusions”.
Device description
Although the workflow presented in this work can be applied globally to a large number of nanoelectronic or cooling devices based on solid-state physics, as a proof of concept, we focus on the asymmetric double-barrier heterostructures.
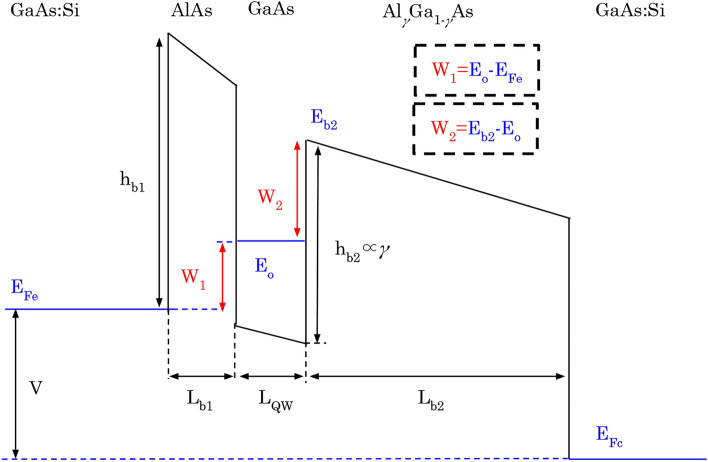
These heterostructures are designed to contain a GaAs quantum well (QW) separated by two barriers from the GaAs:Si emitter and collector, whose electrostatic potential profile is shown in Fig. 1. The GaAs:Si emitter and collector have donor concentrations of 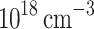 . The AlAs first barrier (b1) is defined by its length
. The AlAs first barrier (b1) is defined by its length 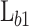 , fixed to a constant value of
, fixed to a constant value of 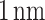 , and its height
, and its height 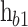 , determined from the band offset between AlAs and the emitter. The QW GaAs is placed between the two barriers defined by the QW length
, determined from the band offset between AlAs and the emitter. The QW GaAs is placed between the two barriers defined by the QW length 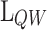 . The second barrier (b2) is made of
. The second barrier (b2) is made of 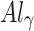
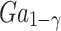 As with varying fraction of Al concentration
As with varying fraction of Al concentration 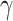 . The e height of the b2
. The e height of the b2 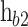 is proportional to
is proportional to 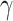 depending on the material band gap, defined as
depending on the material band gap, defined as 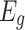 (
(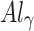
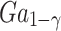 As)=
As)=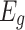 (GaAs)+1.247
(GaAs)+1.247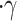 for
for 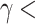 0.45 23. The b2 is defined by the length
0.45 23. The b2 is defined by the length 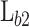 , being a thicker barrier to prevent tunneling of electrons. Applying a bias (V) between the two contacts leads to the resonant tunnelling injection of electrons in the QW from the emitter, and subsequently, the extraction of electrons via thermionic emission above the b2. The design parameters chosen for the optimization in this study are the
, being a thicker barrier to prevent tunneling of electrons. Applying a bias (V) between the two contacts leads to the resonant tunnelling injection of electrons in the QW from the emitter, and subsequently, the extraction of electrons via thermionic emission above the b2. The design parameters chosen for the optimization in this study are the 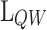 ,
, 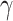 , and
, and 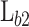 , together with V.
, together with V.
Fig. 1.
Potential profile of the double-barrier heterostructure based on AlGaAs. 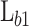 ,
, 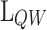 , and
, and 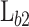 , are the lengths of the b1, QW, and the b2, respectively. The height of the first barrier (
, are the lengths of the b1, QW, and the b2, respectively. The height of the first barrier (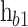 ) is determined from the band offset between AlAs and the emitter, and the height of the second barrier (
) is determined from the band offset between AlAs and the emitter, and the height of the second barrier (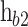 ) is proportional to
) is proportional to 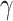 , which is the fraction of aluminium in the alloy. V is the bias between the Fermi energy of the emitter
, which is the fraction of aluminium in the alloy. V is the bias between the Fermi energy of the emitter 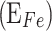 and the Fermi level of the collector (
and the Fermi level of the collector (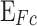 ),
),  is the energy interval between the (E0) and
is the energy interval between the (E0) and 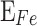 . The
. The 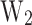 is the energy interval between E0 and the conduction band edge of the b2 (
is the energy interval between E0 and the conduction band edge of the b2 (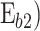 .
.
These design parameters, combined with the bias, determine the energetic properties of the devices by defining the activation energies 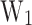 and
and 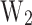 shown in Fig. 1. The first corresponds to the energy interval between the QW ground state energy (E0) and the Fermi energy of the emitter
shown in Fig. 1. The first corresponds to the energy interval between the QW ground state energy (E0) and the Fermi energy of the emitter 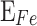 , and the latter is equal to the energy interval between the E0 and the conduction band edge of the b2
, and the latter is equal to the energy interval between the E0 and the conduction band edge of the b2 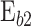 .
. 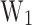 and
and 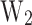 are very relevant since they represent the energy required for an electron to be transmitted from the emitter to the collector. Cooling in this structure relies on two related effects, the evaporative cooling of electrons 13, lowering the
are very relevant since they represent the energy required for an electron to be transmitted from the emitter to the collector. Cooling in this structure relies on two related effects, the evaporative cooling of electrons 13, lowering the 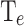 , and the absorption of phonons by the electrons 24, cooling the lattice, which is measured with the CP. These two mechanisms are linked through the electron-phonon coupling 15.
, and the absorption of phonons by the electrons 24, cooling the lattice, which is measured with the CP. These two mechanisms are linked through the electron-phonon coupling 15.
Results
The selected cooling devices rooted in solid-state physics, the double-barrier heterostructures, are simulated using NEGF+H (described in section “NEGF+H simulation methodology”), which allows to accurately determine the electrical and thermal properties of the device. The search for the optimal cooling device is highly computational demanding due to the large execution times required for these simulations (a few days each), and the large number of combinations of design parameters that influence its performance. To speed up this process, we propose a novel optimization workflow based on two ML models, which is agnostic and can be applied to the study of different nanoelectronic devices.
Machine learning workflow and validation
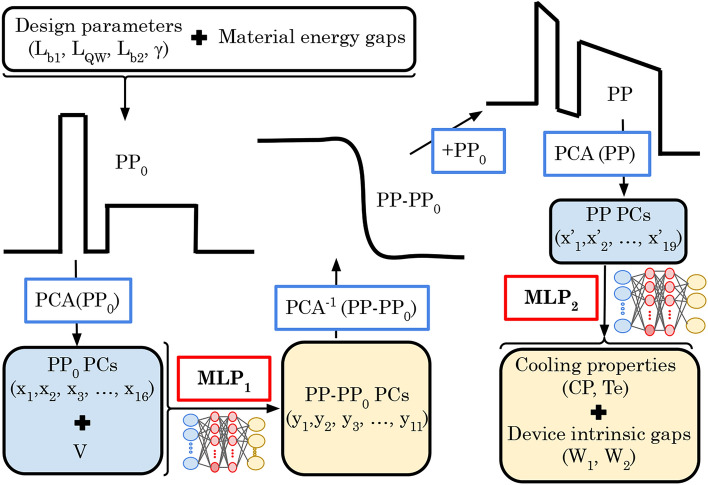
The presented methodology combines two ML-based models trained with data from simulations performed with the accurate NEGF+H. This ML workflow is proposed to optimize the thermionic cooling heterostructures, significantly decreasing the computational cost and speeding up the search process for the optimum device. As an intermediate step, this methodology is capable of obtaining the electrostatic potential profile (PP) to make a realistic evaluation of the thermal and energetic properties.This intermediate step provides additional information about the different device configurations and helps to improve the subsequent prediction of the thermal and electrical properties of the devices.
The ML workflow is shown in Fig. 2, whereas the design specifications are exhaustively described in section “Machine learning methodology”. In order to improve the accuracy of the results and to reduce the complexity of the NN models, various data processing operations were carried out, which are described below. The first step is to generate the first solution of the potential profile (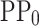 ) from the design parameters (
) from the design parameters (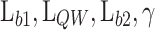 ) and the energy intervals of the different materials that form the heterostructure. Subsequently, the principal component analysis (PCA) 25 is applied to reduce the features of the
) and the energy intervals of the different materials that form the heterostructure. Subsequently, the principal component analysis (PCA) 25 is applied to reduce the features of the 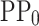 , drastically decreasing the number of significant features used in the first multi-layer perceptron (MLP1) NN. This feature reduction implies a decrease of the computational complexity of MLP1. An extended PCA criterion is to set the number of principal components (
, drastically decreasing the number of significant features used in the first multi-layer perceptron (MLP1) NN. This feature reduction implies a decrease of the computational complexity of MLP1. An extended PCA criterion is to set the number of principal components (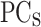 ) to retain the
) to retain the 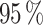 of the cumulative variance 22, but in our case this criterion does not provide enough resolution for the perfect reconstruction of the potential profile (the sharpness of the profile is essential to correlate electronic and thermal properties). Then, to store the maximum amount of variance, the number of
of the cumulative variance 22, but in our case this criterion does not provide enough resolution for the perfect reconstruction of the potential profile (the sharpness of the profile is essential to correlate electronic and thermal properties). Then, to store the maximum amount of variance, the number of 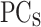 is calculated to retain the
is calculated to retain the 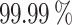 of the cumulative variance, thus reducing the number of features that reproduce the
of the cumulative variance, thus reducing the number of features that reproduce the 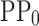 from 1200 to 16. The combination of the
from 1200 to 16. The combination of the 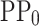
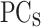 (
(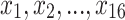 ) with the applied bias (V) constitute the input of the MLP1 NN described in section “Machine learning methodology” below.
) with the applied bias (V) constitute the input of the MLP1 NN described in section “Machine learning methodology” below.
Fig. 2.
Machine learning procedure. From the combination of the design parameters (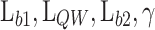 ) and the material energy gaps, the first solution of the potential profile (
) and the material energy gaps, the first solution of the potential profile (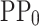 ) is constructed, and its features are reduced by applying the principal component analysis (PCA(PP0)) to obtain the
) is constructed, and its features are reduced by applying the principal component analysis (PCA(PP0)) to obtain the  principal components (
principal components (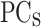 ). The
). The 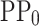
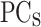 combined with the V are the inputs of the first multi-layer perceptron (MLP1), which gives the difference between potential profile (PP) and
combined with the V are the inputs of the first multi-layer perceptron (MLP1), which gives the difference between potential profile (PP) and 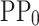 (PP-PP0)
(PP-PP0) 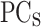 as the output. The PP of the device is obtained by applying the inverse principal component analysis (PCA) (
as the output. The PP of the device is obtained by applying the inverse principal component analysis (PCA) (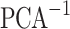 (PP-PP0) and adding the PP0. The inputs of the second multi-layer perceptron (MLP2) are the PP
(PP-PP0) and adding the PP0. The inputs of the second multi-layer perceptron (MLP2) are the PP 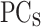 obtained from the application of PCA(PP) to the PP. Finally, the MLP2 provides, as output the information about the cooling properties (CP,
obtained from the application of PCA(PP) to the PP. Finally, the MLP2 provides, as output the information about the cooling properties (CP, 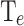 ) and the device activation energies (
) and the device activation energies (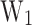 ,
, 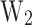 ).
).
The MLP1 model provides, as shown in Fig. 2, the difference between electrostatic potential profile (PP) for the applied bias and 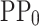 (PP-PP0)
(PP-PP0) 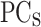 (
(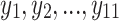 ) as output. From the PP-PP0
) as output. From the PP-PP0
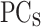 , the PP is reconstructed using the inverse transformation of the PCA (
, the PP is reconstructed using the inverse transformation of the PCA (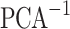 (PP-PP0)) and adding the
(PP-PP0)) and adding the 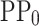 (see Fig. 2). The training process for the MLP1 model takes just
(see Fig. 2). The training process for the MLP1 model takes just 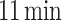 , contrasting with the runtime of a couple of days (depending on the applied bias) required for one simulation with the NEGF+H methodology. This highlights the remarkable reduction in computational time between these two approaches.
, contrasting with the runtime of a couple of days (depending on the applied bias) required for one simulation with the NEGF+H methodology. This highlights the remarkable reduction in computational time between these two approaches.
The features of the PP are then reduced with the above-mentioned PCA criteria, thus defining the PP with 19 features (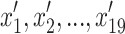 ) instead of 1200. Note that, the number of
) instead of 1200. Note that, the number of 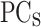 corresponding to PP are larger than for
corresponding to PP are larger than for 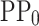 because of the higher complexity of its shape (see Fig. 2). The PP
because of the higher complexity of its shape (see Fig. 2). The PP 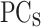 are the input of the second multi-layer perceptron (MLP2) whose specifications are shown in section “Machine learning methodology”. The MLP2 gives as output the CP and the
are the input of the second multi-layer perceptron (MLP2) whose specifications are shown in section “Machine learning methodology”. The MLP2 gives as output the CP and the 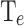 that assess the device’s performance in managing thermal characteristics. Additionally, the
that assess the device’s performance in managing thermal characteristics. Additionally, the 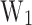 is predicted with the MLP2 and the
is predicted with the MLP2 and the 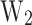 can be calculated from other variables, as seen in Fig. 1:
can be calculated from other variables, as seen in Fig. 1:
 |
1 |
where  , therefore,
, therefore,  can be defined from known variables as
can be defined from known variables as 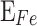 and
and 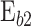 are extracted from the shape of the predicted PP (see Fig. 1):
are extracted from the shape of the predicted PP (see Fig. 1):
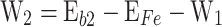 |
2 |
The total training time for MLP2 amounts to just 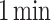 , emphasizing its efficiency in swiftly generating essential insights for device optimization.
, emphasizing its efficiency in swiftly generating essential insights for device optimization.
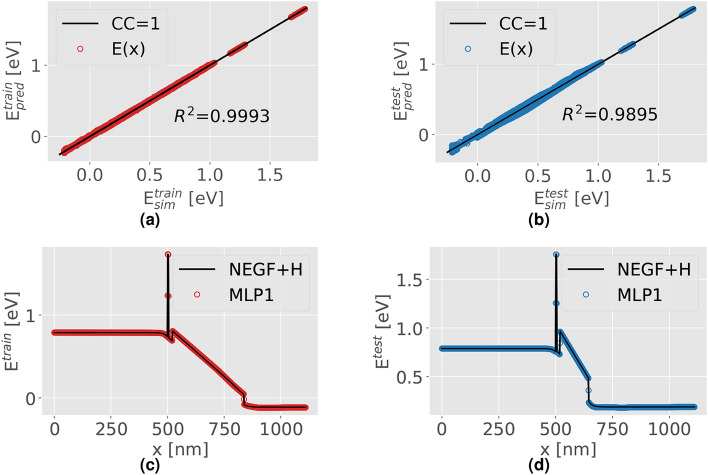
In Fig. 3, there are shown the outcomes of MLP1 due to the training and testing NN processes. It is noteworthy to observe in the top figures a significant correlation for each point of the PP, denoted as E, between the NEGF+H simulations (x-axis) and the predictions generated by MLP1 (y-axis). This correlation is illustrated in Fig. 3a,b for both the training (a) and testing (b) subsets. The presented correlation in Fig. 3a,b highlights the accuracy of the PP predictions with our model. As an example of the quality of the prediction, Fig. 3c,d present the comparison between the simulated (NEGF+H) and the predicted (MLP1) PP for two randomly selected profiles, where the vertical axis is E and the horizontal axis is the distance from the start of the emitter contact. This bottom figures correspond to two different PP from the training (Fig. 3c) and the testing (Fig. 3d) subsets.
Fig. 3.
The correlation for each point of the PP, denoted as E, between the NEGF+H simulations and MLP1 predictions is depicted in the top figures for the training (a) and test (b). The Pearson’s coefficient (CC) equal to 1 shows the perfect correlation line between prediction and simulation. An example of the reconstructed PP of MLP1 predictions in comparison to NEGF+H simulations, for randomly selected profiles, is illustrated in the bottom figures from both the training subset (c) and the test subset (d). The variable x is the distance from the start of the emitter contact.
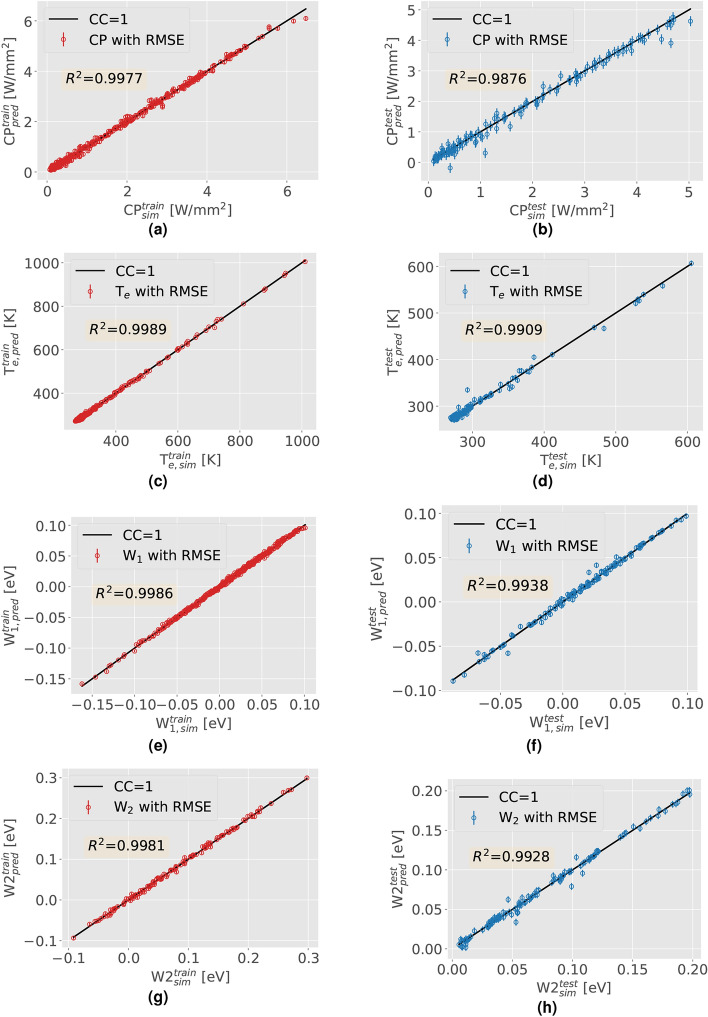
To assess the performance of MLP2, Fig. 4 shows the comparison between simulated and predicted CP (a–b), 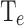 (c–d),
(c–d), 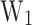 (e–f), and
(e–f), and 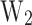 (g–h) for the training (left) and test (right) subsets. The correlations of all the outputs have coefficient of determination (
(g–h) for the training (left) and test (right) subsets. The correlations of all the outputs have coefficient of determination (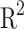 ) (see definition in section “Metrics”) higher than 0.9977, and 0.9876 for training and test subsets, respectively. Considering the possible sources of error propagated by the prediction of
) (see definition in section “Metrics”) higher than 0.9977, and 0.9876 for training and test subsets, respectively. Considering the possible sources of error propagated by the prediction of 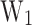 with MLP2, the PP with MLP1 and the extraction of
with MLP2, the PP with MLP1 and the extraction of  and
and 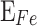 from this PP, the
from this PP, the 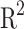 of 0.9928 highlights the good prediction of
of 0.9928 highlights the good prediction of 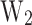 values.
values.
Fig. 4.
Performance of MLP2 on training (left) and test (right) subsets for the output variables CP (a–b), 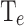 (c–d),
(c–d), 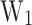 (e–f), and
(e–f), and 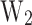 (g–h). The black line (CC=1) is the line of perfect correlation, and y-axis error bars correspond to the root-mean-square error (RMSE).
(g–h). The black line (CC=1) is the line of perfect correlation, and y-axis error bars correspond to the root-mean-square error (RMSE).
The performance metrics (RMSE, and 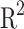 defined in section “Metrics”) for each NN (MLP1 and MLP2) outputs are shown in the Table 1. These RMSE and
defined in section “Metrics”) for each NN (MLP1 and MLP2) outputs are shown in the Table 1. These RMSE and 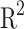 values are a clear indicative of the prediction accuracy of the ML workflow when trying to predict the energetic and thermal properties of this cooling heterostructures. As expected, due to possible features not included in the training set selection, the accuracy of the subset test is slightly lower. Then, once the accuracy of the models has been proved, it is important to take into account the clear advantage of using our ML procedure, the computational savings. Whereas one single NEGF+H simulation takes a couple of days, the total training time for the two NN models (MLP1, and MLP2) is
values are a clear indicative of the prediction accuracy of the ML workflow when trying to predict the energetic and thermal properties of this cooling heterostructures. As expected, due to possible features not included in the training set selection, the accuracy of the subset test is slightly lower. Then, once the accuracy of the models has been proved, it is important to take into account the clear advantage of using our ML procedure, the computational savings. Whereas one single NEGF+H simulation takes a couple of days, the total training time for the two NN models (MLP1, and MLP2) is 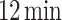 .
.
Table 1.
Train and Test root-mean-square error (RMSE) and coefficient of determination 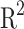 metrics for MLP1 and MLP2.
metrics for MLP1 and MLP2.
| Model | MLP1 | MLP2 | ||||
|---|---|---|---|---|---|---|
| Magnitude | PP [meV] | CP [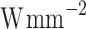 ] ] |
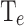 [K] [K] |
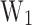 [meV] [meV] |
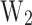 [meV] [meV] |
|
| Train | RMSE | 4.10 | 0.06 | 3.26 | 1.49 | 3.36 |
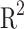 |
0.9993 | 0.9986 | 0.9992 | 0.9991 | 0.9984 | |
| Test | RMSE | 7.26 | 0.10 | 6.12 | 3.13 | 4.34 |
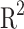 |
0.9895 | 0.9876 | 0.9909 | 0.9938 | 0.9928 | |
Structure optimization
Once the ML procedure was correctly calibrated and validated, the next step is to perform the prediction of the energetic and thermal properties of the asymmetric double-barrier heterostructure. To predict the optimum heterostructure, a search space is generated from the simulated dataset boundaries: 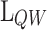 between 3.2 and
between 3.2 and 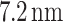 ,
, 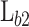 between 50 and
between 50 and 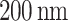 ,
, 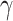 between 0.05 and 0.30, and V between 0.1 and
between 0.05 and 0.30, and V between 0.1 and 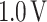 . The dataset from NEGF+H simulations, composed by 630 different device configurations, is increased 188 times generating for the ML predictions a search space of
. The dataset from NEGF+H simulations, composed by 630 different device configurations, is increased 188 times generating for the ML predictions a search space of 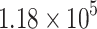 configurations of design parameters.
configurations of design parameters.
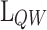 and
and 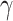 impact on electrostatic properties
impact on electrostatic properties
To analyze the physical insights of the presented heterostructures, the relation between two crucial design parameters (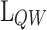 and
and 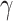 ) and the electrostatic properties of the devices (
) and the electrostatic properties of the devices (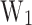 and
and 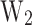 ) is studied. To simplify the multidimensional analysis, the predicted data was filtered to select the best CP performance device depending on
) is studied. To simplify the multidimensional analysis, the predicted data was filtered to select the best CP performance device depending on 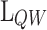 and
and 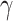 values.
values.
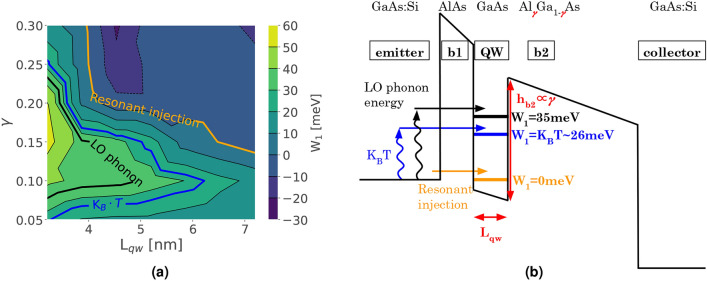
In Fig. 5a a colour map for 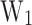 is shown as a function of
is shown as a function of 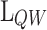 and
and 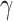 . It can be seen that increasing the
. It can be seen that increasing the 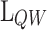 lowers
lowers 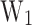 due to the decrease of
due to the decrease of 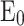 . The relation between
. The relation between 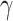 and
and 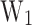 is not linear, with a maximum at
is not linear, with a maximum at 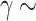 0.15 and two local minimums at
0.15 and two local minimums at 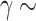 0.05 and
0.05 and 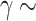 0.30. Note that, for
0.30. Note that, for 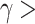 0.15 and
0.15 and 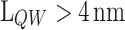 , there is a region with negative
, there is a region with negative 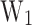 values because
values because 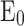 is below the
is below the 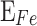 . In this figure, the highlighted contour levels for the main injection mechanisms of electrons in the QW correspond to: the resonant tunnel injection
. In this figure, the highlighted contour levels for the main injection mechanisms of electrons in the QW correspond to: the resonant tunnel injection 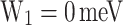 , the thermalization energy at room temperature
, the thermalization energy at room temperature 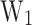 =
=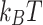
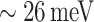 , and the polar optical phonon (LO phonon) absorption energy
, and the polar optical phonon (LO phonon) absorption energy 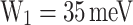 26. Fig. 5b shows a schematic explanation for each injection mechanism of electrons in the QW, depending on
26. Fig. 5b shows a schematic explanation for each injection mechanism of electrons in the QW, depending on 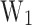 . One of these presented mechanisms, the LO phonon absorption in the emitter, is the first contribution to the cooling process inside the device 13.
. One of these presented mechanisms, the LO phonon absorption in the emitter, is the first contribution to the cooling process inside the device 13.
Fig. 5.
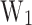 dependence with design parameters
dependence with design parameters 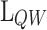 and
and 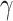 a. Diagram of the main mechanisms for electron tunnel injection in the QW b.
a. Diagram of the main mechanisms for electron tunnel injection in the QW b.
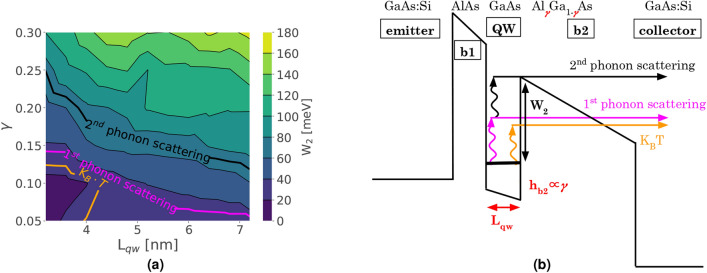
Figure 6a shows a colour map representing the linear increase of 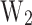 with
with 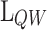 and
and 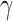 . This linear grow is explained by two reasons: (i) increasing
. This linear grow is explained by two reasons: (i) increasing 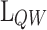 decreases
decreases 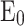 because the QW is widening; (ii)
because the QW is widening; (ii) 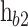 is directly proportional to
is directly proportional to 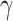 (aluminium concentration). Fig. 6b presents the mechanisms that lead to the cooling of the device via phonon absorption, and electron thermionic emission from the QW. These mechanisms are the electron-phonon scattering, the electron thermal excitation at room temperature of the electrons, and the tunnelling through the b2. Taking into account the cooling mechanisms for the lattice,
(aluminium concentration). Fig. 6b presents the mechanisms that lead to the cooling of the device via phonon absorption, and electron thermionic emission from the QW. These mechanisms are the electron-phonon scattering, the electron thermal excitation at room temperature of the electrons, and the tunnelling through the b2. Taking into account the cooling mechanisms for the lattice, 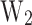 will be the most relevant parameter to evaluate the cooling performance of the device (CP) and the temperature of the remaining electrons in the QW (
will be the most relevant parameter to evaluate the cooling performance of the device (CP) and the temperature of the remaining electrons in the QW (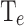 ).
).
Fig. 6.
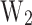 dependence with design parameters
dependence with design parameters 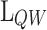 and
and 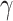 a. Diagram of the main electron mechanisms for thermionic emission from the QW b.
a. Diagram of the main electron mechanisms for thermionic emission from the QW b.
Device optimization
The best performing device is determined by the impact of the activation energies on the cooling properties. It becomes clear that the cooling is primarily influenced by 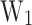 , and
, and 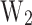 within the device. Furthermore, the sharpness of b2, defined by
within the device. Furthermore, the sharpness of b2, defined by 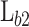 and V, facilitates tunnelling through b2, influencing the overall cooling efficiency of the system.
and V, facilitates tunnelling through b2, influencing the overall cooling efficiency of the system.
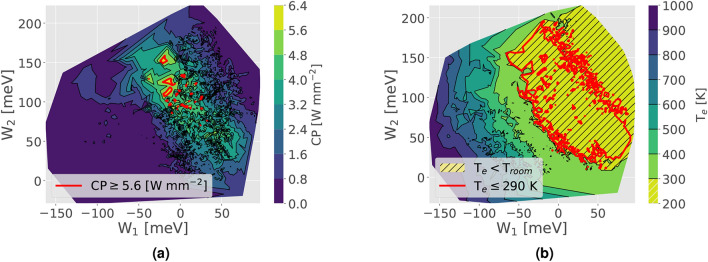
Figure 7 presents the CP (a) and 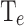 (b) dependence on
(b) dependence on 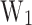 , and
, and 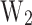 . Figure 7a shows that the devices reaching the highest CP are clustered around the resonance injection point (
. Figure 7a shows that the devices reaching the highest CP are clustered around the resonance injection point (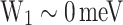 ), and the
), and the 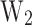 values exceed the second phonon absorption in the QW (
values exceed the second phonon absorption in the QW (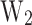
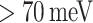 ). Then, most of the thermionic emission occurs through b2 tunnelling. The benchmark criterion chosen to filter the best-performing devices is CP
). Then, most of the thermionic emission occurs through b2 tunnelling. The benchmark criterion chosen to filter the best-performing devices is CP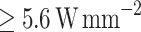 .
.
Fig. 7.
Colour maps for CP a and 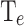 b as a function of the activation energies
b as a function of the activation energies 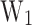 and
and 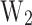 . The red contour serves as a benchmark criterion for the highest performance devices. The hatched area delimits the region where
. The red contour serves as a benchmark criterion for the highest performance devices. The hatched area delimits the region where 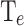 falls below the
falls below the 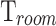 .
.
In Fig. 7b the hatched area delimits the region where 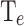 falls below the room temperature
falls below the room temperature 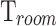 . A substantial number of devices, characterized by
. A substantial number of devices, characterized by 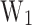
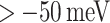 and
and 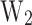
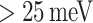 , exhibit
, exhibit 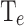 lower than
lower than 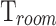 . Consequently, the benchmark criterion utilized for selecting the best-performing devices is
. Consequently, the benchmark criterion utilized for selecting the best-performing devices is 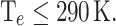
These results show that CP and 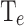 are not directly correlated due to their distinct underlying mechanisms: CP is influenced by phonon absorption, while
are not directly correlated due to their distinct underlying mechanisms: CP is influenced by phonon absorption, while 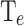 depends on the allowed energy levels in the QW.
depends on the allowed energy levels in the QW.
Nevertheless, certain cases exhibit a favourable trade-off between both cooling performance magnitudes (CP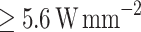 , and
, and 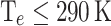 ). The details of these optimal devices are presented in Table 2. Additionally, we conducted subsequent NEGF+H simulations for these devices to validate the obtained results that are also shown in the Table 2, together with the relative error (
). The details of these optimal devices are presented in Table 2. Additionally, we conducted subsequent NEGF+H simulations for these devices to validate the obtained results that are also shown in the Table 2, together with the relative error (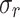 ) between both values. The
) between both values. The 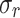 values (see section: Metrics) show the accuracy of the double multi-layer perceptron (MLP) workflow to optimize the cooling heterostructures. Note that, all
values (see section: Metrics) show the accuracy of the double multi-layer perceptron (MLP) workflow to optimize the cooling heterostructures. Note that, all 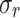 are lower than the
are lower than the 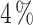 when predicting the CP, and lower than the
when predicting the CP, and lower than the 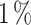 for
for 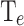 , demonstrating the precision of the model predictions.
, demonstrating the precision of the model predictions.
Table 2.
Details of the three predicted optimal device configurations, validated through posterior NEGF+H simulations. The relative error (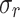 ) between the predicted and simulated properties is provided to compare the results.
) between the predicted and simulated properties is provided to compare the results.
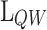 [nm] [nm] |
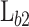 [nm] [nm] |
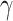 |
Dev. | V [V] | CP [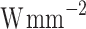 ] ] |
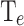 [K] [K] |
|
|---|---|---|---|---|---|---|---|
| 3.2 | 50 | 0.30 | (1) | 0.7 | Pred. | 6.16 | 284.7 |
| Val. | 6.16 | 286.4 | |||||
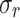 [%] [%] |
0.0 | 0.6 | |||||
| 0.8 | Pred. | 6.40 | 287.0 | ||||
| Val. | 6.65 | 285.6 | |||||
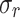 [%] [%] |
3.7 | 0.5 | |||||
| 3.6 | 50 | 0.28 | (2) | 0.7 | Pred. | 6.49 | 287.2 |
| Val. | 6.29 | 286.6 | |||||
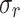 [%] [%] |
3.2 | 0.2 | |||||
| 0.29 | (3) | 0.7 | Pred. | 6.45 | 285.0 | ||
| Val. | 6.48 | 288.0 | |||||
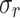 [%] [%] |
0.5 | 1.0 | |||||
| 0.8 | Pred. | 6.29 | 289.5 | ||||
| Val. | 6.36 | 289.9 | |||||
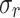 [%] [%] |
1.1 | 0.1 |
Discussion
The presented ML workflow exhibits remarkable accuracy in predicting various critical parameters to optimize thermionic cooling heterostructures. The high correlation coefficients and low RMSE observed in both MLP1 and MLP2 validate the reliability of the predictions. This suggests that the ML models successfully capture the intricate relationships within the dataset, enabling an accurate estimation of key device properties.
The efficiency demonstrated in optimizing thermionic cooling heterostructures implies that the ML approach could be extended to tackle the complexities of advanced devices. The adaptability of the presented methodology, based in the relation between the design parameters, the PP and the cooling properties, suggests its viability in addressing the challenges posed by more complex nanoelectronic and cooling devices. This double NN workflow is agnostic and could be applied to a wide range of different devices, as it is independent of the internal structure or physical system mechanisms. It operates by extracting the relevant features of an analyzed system, and accelerates the search of the optimal solution for a set of input design parameters. In addition, the application of transfer learning techniques 27 were previously demonstrated to be effective to update and adapt the trained models by adding new features to them 20. The implementation of these techniques could be used to increase the number of design parameters (length or height of the first barrier) or to evaluate more complex heterostructures such as the quantum cascade cooler 28 (a greater number of potential barriers). In addition, as it is an agnostic tool depending on the relationship between the design parameters and the potential profile, it could easily be applied to other types of material-based cooling heterostructures or to semiconductor devices for other applications.
This approach, which combines ML with complex and accurate simulation techniques (NEGF+H), has demonstrated that is capable to accelerate the development of a new-generation of circuit-integrated cooling devices.
Methods
In this section, the methods used in this work are presented. It includes: the NEGF+H simulation methodology (section “NEGF+H simulation methodology”), the dataset description (section “Dataset description and pre-processing”), the ML methodology (section “Machine learning methodology”), and the definition of the metrics used in this work (section “Metrics”).
NEGF+H simulation methodology
To investigate the electron and heat transport in these semiconductor heterostructures, we use an in-house built simulation software 29 that couples self-consistently the non-equilibrium Green’s function formalism for electrons 30,31 with heat and Poisson equations (NEGF+H) 32. This methodology is able to reproduce key aspects of the physics, taking into account thermal, and quantum effects, and the electron transport formalism.
This method relies on the self-consistent calculation of the retarded Green’s function at energy E and transverse wavevector 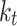 that reads:
that reads:
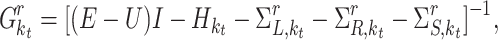 |
3 |
where U is the electrostatic potential energy, I is the identity matrix, and 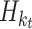 is the effective mass Hamiltonian.
is the effective mass Hamiltonian. 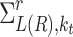 are the self-energies for the left (L) and right (R) semi-infinite device contacts 33,
are the self-energies for the left (L) and right (R) semi-infinite device contacts 33, 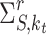 is the self-energy calculated within the self-consistent Born approximation (SCBA) 34–36 that accounts for the interaction between electrons and both the acoustic phonons and polar optical phonons.
is the self-energy calculated within the self-consistent Born approximation (SCBA) 34–36 that accounts for the interaction between electrons and both the acoustic phonons and polar optical phonons.
The lesser/greater Green’s functions are then obtained using the following identities:
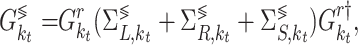 |
4 |
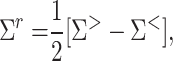 |
5 |
where the total scattering energy for a given transverse mode 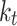 can be decomposed into
can be decomposed into
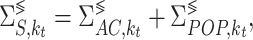 |
6 |
where 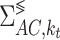 is the self-energy for acoustic phonons calculated within the elastic assumption at position j along the transport axis that can be expressed as 37,38
is the self-energy for acoustic phonons calculated within the elastic assumption at position j along the transport axis that can be expressed as 37,38
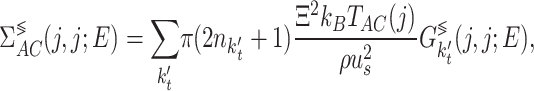 |
7 |
where 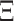 is the deformation potential,
is the deformation potential, 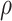 is the mass density,
is the mass density, 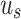 is the sound velocity and
is the sound velocity and 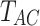 is the temperature of acoustic phonons. We assume interactions with acoustic phonons to be local, and therefore only consider the diagonal part of the Green’s function39.
is the temperature of acoustic phonons. We assume interactions with acoustic phonons to be local, and therefore only consider the diagonal part of the Green’s function39.
The scattering self-energy for polar optical-phonons (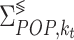 ) is defined in Eq. (8) and we use the diagonal expression that have been proposed in previous work by Moussavou et al. to effectively describe their long range interactions40. For a given wavevector
) is defined in Eq. (8) and we use the diagonal expression that have been proposed in previous work by Moussavou et al. to effectively describe their long range interactions40. For a given wavevector 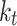 , we have :
, we have :
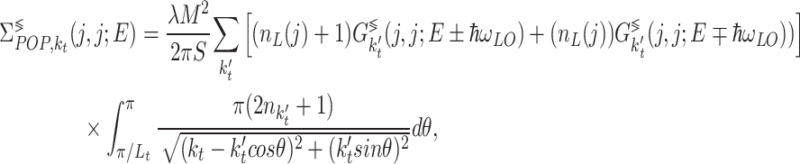 |
8 |
where 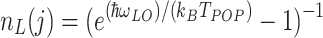 with
with 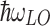 the LO phonon energy and
the LO phonon energy and 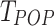 their temperature, M is the Fröhlich factor,
their temperature, M is the Fröhlich factor, 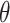 is the angle between
is the angle between 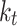 and
and 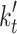 .
. 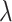 is a scaling factor correcting for the reduced strength emerging from the diagonal approximation. The value
is a scaling factor correcting for the reduced strength emerging from the diagonal approximation. The value 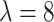 used in this paper has been obtained using the physically-based analytical model developed in 40.
used in this paper has been obtained using the physically-based analytical model developed in 40.
Obtaining the Green’s function then yields many physical properties such as the electron current density spectrum (in 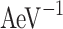
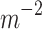 )
) 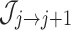 from position j to
from position j to  :
:
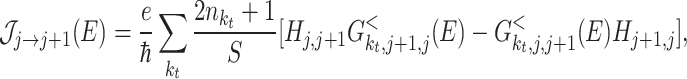 |
9 |
where 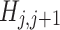 corresponds to the nearest-neighbour hopping term in the discretized tight-binding-like Hamiltonian. From this expression we can deduce the electronic energy current 41:
corresponds to the nearest-neighbour hopping term in the discretized tight-binding-like Hamiltonian. From this expression we can deduce the electronic energy current 41:
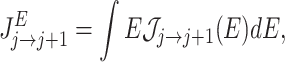 |
10 |
whose first derivative corresponds to the cooling power density (in 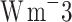 ):
):
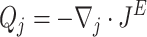 |
11 |
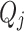 defines the energy transfers between the lattice and the electrons and serves as a source term allowing us to couple electron transport equations and heat equation. Finally, integrating the negative part of
defines the energy transfers between the lattice and the electrons and serves as a source term allowing us to couple electron transport equations and heat equation. Finally, integrating the negative part of 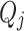 over direction of transport yields the cooling power (CP), representing the amount of heat removed from the device.
over direction of transport yields the cooling power (CP), representing the amount of heat removed from the device.
As a post-processing step, we calculate using the Büttiker probe method 42–44
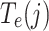 and
and 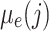 , the local electronic temperature and electrochemical potential 45. This method relies on weakly coupling the device to a simulated probe defined by the following self-energy:
, the local electronic temperature and electrochemical potential 45. This method relies on weakly coupling the device to a simulated probe defined by the following self-energy:
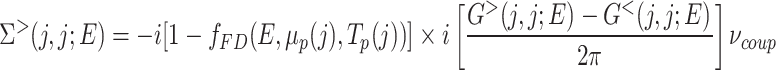 |
12 |
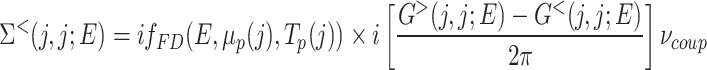 |
13 |
where 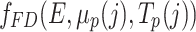 is the Fermi-Dirac distribution of the probe depending on the electrochemical potential
is the Fermi-Dirac distribution of the probe depending on the electrochemical potential 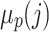 and the electronic temperature
and the electronic temperature 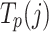 .
. 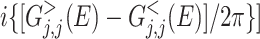 is the local density of states, common to the probe and the device, and
is the local density of states, common to the probe and the device, and 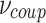 is the energy independent coupling strength between the probe and the system.
is the energy independent coupling strength between the probe and the system.
By connecting the probe to the device, a net electron and energy current is produced. It can be calculated as follows, using the previously determined Green’s functions of the device:
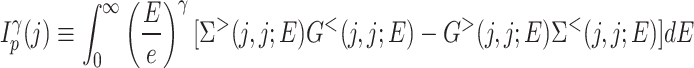 |
14 |
in which 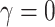 or 1 for the electron or energy current, respectively.
or 1 for the electron or energy current, respectively.
The principle is now to find 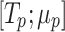 such that
such that 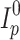 and
and  vanish. The probe is then in a local equilibrium with the device, itself arbitrarily out-of-equilibrium. The temperature and chemical potential of the probe are therefore accurate measurements of the device thermodynamic properties.
vanish. The probe is then in a local equilibrium with the device, itself arbitrarily out-of-equilibrium. The temperature and chemical potential of the probe are therefore accurate measurements of the device thermodynamic properties.
In order to find the vanishing conditions of the currents in each point of the device, we solve the two coupled non-linear Eq. (14) using a Newton-Raphson algorithm 46.
Dataset description and pre-processing
The dataset used for this work is the result of the NEGF+H simulator combined with the Büttiker probes explained in section “NEGF+H simulation methodology”. The simulated dataset includes the design parameters of the device (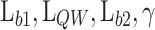 ), the V, the calculated PP, the activation energies (
), the V, the calculated PP, the activation energies (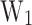 ,
, 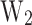 ), and the thermal properties (CP,
), and the thermal properties (CP, 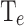 ). To generate a representative dataset, the simulated devices were selected to generate an equidistant four-dimensional mesh in the hypercube composed by four variables:
). To generate a representative dataset, the simulated devices were selected to generate an equidistant four-dimensional mesh in the hypercube composed by four variables: 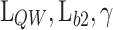 , and V. Note that,
, and V. Note that, 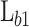 is assumed to be constant. In these conditions, the dataset comprises 630 mesh points. Before performing any pre-processing step, we calculate the
is assumed to be constant. In these conditions, the dataset comprises 630 mesh points. Before performing any pre-processing step, we calculate the 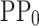 from the design parameters and the material energy gaps, which is also stored into the dataset.
from the design parameters and the material energy gaps, which is also stored into the dataset.
To use the data from simulations in the ML workflow, a pre-processing is carried out. The dataset (630) is divided in a two-step process into subsets. In the first step, an 80/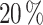 random split is employed to create a primary training set and a testing set (126). Subsequently, the training set from the initial split is further divided in the second step, using an 80/
random split is employed to create a primary training set and a testing set (126). Subsequently, the training set from the initial split is further divided in the second step, using an 80/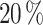 random split, resulting in the final training subset (403) and a validation subset (101). The split ratio is extremely dependant on the number of hyperparameters used in the neural networks and on the characteristics of the dataset (size of the dataset, representativity of relevant features on the dataset), and this parameter then needs to be optimized. In our case this optimization was carried by probe-essay initial tests. The first test consisted of a 90/
random split, resulting in the final training subset (403) and a validation subset (101). The split ratio is extremely dependant on the number of hyperparameters used in the neural networks and on the characteristics of the dataset (size of the dataset, representativity of relevant features on the dataset), and this parameter then needs to be optimized. In our case this optimization was carried by probe-essay initial tests. The first test consisted of a 90/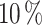 split, which resulted in the overfitting of the NNs as the dataset was not too large to use this percentage. The second test had the opposite response, when applying the 70/
split, which resulted in the overfitting of the NNs as the dataset was not too large to use this percentage. The second test had the opposite response, when applying the 70/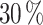 split (common for small datasets) it was found that the NNs were not capable to capture the effect of all the desired features. Hence, the two-step 80/
split (common for small datasets) it was found that the NNs were not capable to capture the effect of all the desired features. Hence, the two-step 80/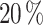 approach ensures a robust model training, while providing subsets for fine-tuning and evaluation, enhancing the reliability of our results.
approach ensures a robust model training, while providing subsets for fine-tuning and evaluation, enhancing the reliability of our results.
As the dataset is composed by variables ranging in different order of magnitudes, it is important to normalize each variable to avoid divergences in the loss function optimization process. The scaling of our dataset has been done with the Scikit-learn function MinMaxScaler 47. This tool normalizes the data to the maximum and minimum values (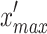 and
and 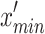 ) of each variable (
) of each variable (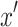 ) in a selected range [
) in a selected range [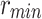 ,
, 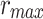 ], as follows:
], as follows:
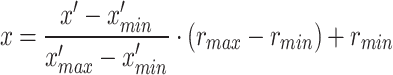 |
15 |
We assume a range between 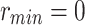 and
and 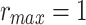 . The scaling object from MinMaxScaler is fitted to the training subset. Then, the validation and test subsets are transformed with the fitted scaling object. With this procedure, we ensure that the distributions of the test and validation subset are not collected in the training subset.
. The scaling object from MinMaxScaler is fitted to the training subset. Then, the validation and test subsets are transformed with the fitted scaling object. With this procedure, we ensure that the distributions of the test and validation subset are not collected in the training subset.
Machine learning methodology
To build both NNs we used the Pytorch 1.13.1 48 and the Scikit-learn 1.0.2 47 libraries, with Ray Tune 2.2.0 49 for the hyperparameter optimization, on Python 3.8. The process analyzed in this work is a non-linear regression problem, therefore, the architecture chosen is the MLP 50. The activation functions used in each perceptron for both MLPs is the hyperbolic tangent 51. The batch size for the train and validation subsets is 64, and the selected loss function is the mean-square error (MSE).
The MLP1 structure consists of an input layer with 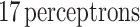 representing the
representing the 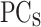 of the
of the 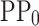 52 combined with the bias voltage (V), two hidden layers with 42 and
52 combined with the bias voltage (V), two hidden layers with 42 and 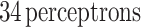 , and an output layer with
, and an output layer with 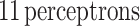 . This output layer represents the
. This output layer represents the 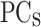 of the difference between PP and
of the difference between PP and  (PP-PP0
(PP-PP0
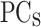 ) which allows to obtain the PP-PP0 curve. PP-PP0 as the output of the MLP allows working with a continuous and derivable function (see Fig. 2). This implies a reduction of the noise produced by the backpropagation process in the MLP1 optimization. In addition, the number of
) which allows to obtain the PP-PP0 curve. PP-PP0 as the output of the MLP allows working with a continuous and derivable function (see Fig. 2). This implies a reduction of the noise produced by the backpropagation process in the MLP1 optimization. In addition, the number of 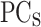 needed to reproduce PP-PP0 is smaller than for PP, improving the accuracy of our non-linear regression model as the number of input perceptrons (17) is larger than the number of output perceptrons (11). The optimization algorithm used in the minimization of the loss function for the MLP1 is the stochastic gradient descent (SGD) with momentum 0.9 53. Also, an adaptive learning rate scheduler technique 54 is applied to avoid the local minimums when using this optimization algorithm. With the described structure and the mentioned post-processing, the MLP1 has the capability to predict the PP from the
needed to reproduce PP-PP0 is smaller than for PP, improving the accuracy of our non-linear regression model as the number of input perceptrons (17) is larger than the number of output perceptrons (11). The optimization algorithm used in the minimization of the loss function for the MLP1 is the stochastic gradient descent (SGD) with momentum 0.9 53. Also, an adaptive learning rate scheduler technique 54 is applied to avoid the local minimums when using this optimization algorithm. With the described structure and the mentioned post-processing, the MLP1 has the capability to predict the PP from the 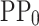 (an analogy of solving NEGF+H).
(an analogy of solving NEGF+H).
The MLP2 is designed with an input layer of 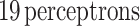 representing the
representing the 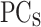 of the PP, two hidden layers both with
of the PP, two hidden layers both with 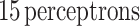 , and an output layer with
, and an output layer with 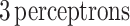 representing the output thermal parameters CP,
representing the output thermal parameters CP, 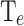 , and the energy interval
, and the energy interval 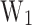 . For MLP2 the optimization algorithm used is the adaptive moment estimation (Adam) 55. Note that, the
. For MLP2 the optimization algorithm used is the adaptive moment estimation (Adam) 55. Note that, the 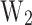 can be extracted from
can be extracted from 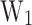 and the PP of the device.
and the PP of the device.
To a better understanding of the input and outputs of the double NN procedure, section “Machine learning workflow and validation” includes a step-by-step explanation of the ML workflow shown in Fig. 2.
Metrics
To evaluate and compare the accuracy of the model predictions, we have considered two performance metrics, the (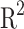 ) and the root-mean-square error (RMSE).
) and the root-mean-square error (RMSE).
(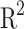 ) provides information about the quality of the model predictions, being a statistical measure of the correlation between the simulated data and the predicted one. The
) provides information about the quality of the model predictions, being a statistical measure of the correlation between the simulated data and the predicted one. The 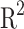 is defined as:
is defined as:
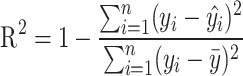 |
16 |
where 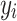 is the i-th simulated value,
is the i-th simulated value, 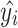 the i-th model prediction,
the i-th model prediction, 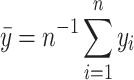 the mean of the simulated values and n the number of evaluated points. As can be seen, the shorter the gap between the simulation and prediction, the nearest the
the mean of the simulated values and n the number of evaluated points. As can be seen, the shorter the gap between the simulation and prediction, the nearest the 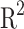 value will be to 1.
value will be to 1.
RMSE is used to evaluate the quality of the regression model (in the units of the studied variable) and it is defined as:
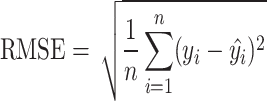 |
17 |
As the gap between simulation and prediction narrows, the RMSE also decreases, indicating that models with the lowest RMSE values exhibit superior accuracy.
Finally, the relative error 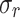 used to validate the prediction of the best configurations against the NEGF+H results, is defined as follows:
used to validate the prediction of the best configurations against the NEGF+H results, is defined as follows:
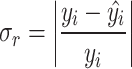 |
18 |
This metric is a relative percentage, and therefore, values closer to 0 correspond with more accurate predictions.
Conclusions
The presented workflow, based in two NN models trained with data from NEGF+H simulations, demonstrates its effectiveness in optimizing cooling devices based on solid-state physics as the thermionic cooling heterostructures. By significantly reducing computational costs and accelerating the search for optimal device configurations, the presented ML-based workflow could be a good complement to traditional simulation techniques as the NEGF+H. An additional advantage lies in the capability of our approach to derive the potential profile (PP), providing insights into the physics of the devices and enabling a realistic evaluation of thermal and energetic properties.
Evaluation metrics, including the RMSE and 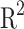 , confirm the high accuracy of both multi-layer perceptron models (MLP1 and MLP2). The correlations between simulated and predicted values for PP, cooling power (CP), electron temperature in the quantum well
, confirm the high accuracy of both multi-layer perceptron models (MLP1 and MLP2). The correlations between simulated and predicted values for PP, cooling power (CP), electron temperature in the quantum well 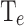 , and the activation energies (
, and the activation energies (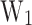 , and
, and 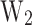 ), are robust, emphasizing the reliability of our machine learning workflow.
), are robust, emphasizing the reliability of our machine learning workflow.
Moving beyond the assessment of MLP1 and MLP2, the methodology’s efficiency is demonstrated by the fast training times (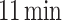 and
and 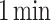 , respectively) compared to traditional NEGF+H simulations (couple of days for a single simulation). With the calibrated and validated ML procedure, a wide search space is created for predicting optimal device configurations, expanding the input simulated dataset from 630 to
, respectively) compared to traditional NEGF+H simulations (couple of days for a single simulation). With the calibrated and validated ML procedure, a wide search space is created for predicting optimal device configurations, expanding the input simulated dataset from 630 to 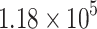 different design parameter configurations.
different design parameter configurations.
The impact of QW length 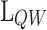 and fraction of Al concentration
and fraction of Al concentration 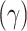 on
on 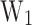 and
and 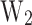 is analyzed, revealing insights into device performance.
is analyzed, revealing insights into device performance. 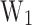 exhibits a linear relationship with
exhibits a linear relationship with 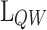 and nonlinear with
and nonlinear with 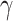 , offering information on electron injection in the quantum well (QW).
, offering information on electron injection in the quantum well (QW).  linearly increases with
linearly increases with 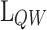 and
and 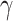 . These activation energies serve as critical indicators for optimizing device operation and understanding cooling mechanisms in the QW: the electron-phonon scattering and the electron thermionic emission.
. These activation energies serve as critical indicators for optimizing device operation and understanding cooling mechanisms in the QW: the electron-phonon scattering and the electron thermionic emission.
Additionally, the thermal characteristics of the optimal devices were confirmed through subsequent simulations using NEGF+H methodology. The obtained results show relative errors below the 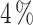 for the CP, and below the
for the CP, and below the 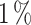 for the
for the 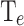 .
.
In conclusion, our machine learning methodology demonstrates exceptional accuracy, efficiency, and utility in optimizing thermionic cooling heterostructures. The ability to swiftly predict device properties and explore a vast search space, convert this approach in a valuable tool for advancing the design and the performance of complex devices like these semiconductor heterostructures.
Acknowledgements
This work was supported by the Spanish MICINN/AEI, Xunta de Galicia, and FEDER Funds under Grant RYC-2017-23312, Grant PID2019-104834GB-I00, Grant PID2022-141623NB-I00, Grant PID2022-142709OB-C21/PID2022-142709OA-C22, Grant ED431F 2020/008, Grant ED431C 2022/16 and GELATO ANR project (ANR-21-CE50-0017).
Author contributions
JGF developed the ML workflow, performed the data processing and filtering, and was the main contributor to the writing of the manuscript. GE was responsible for the NEGF+H simulation of the devices, assisted in the development of the ML workflow, and wrote the NEGF+H methodology. EC and NS managed the correct development of the ML workflow and data processing. KH helped with the correct understanding of the physics of these devices. AGL and MB are responsible for the conceptualization and supervision of the different tasks carried out in this collaboration. All authors read and approved the final manuscript.
Data availability
Part of the simulated dataset for training both neural network models and predicting the optimal asymmetric double-barrier semiconductor based heterostructures is available in the following Zenodo repository: https://doi.org/10.5281/zenodo.11032095.
Code availability
The code used for the presented ML workflow is also available at 56.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Julian G. Fernandez and Gueric Etesse
References
- 1.Gaska, R., Osinsky, A., Yang, J. & Shur, M. Self-heating in high-power AlGaN-GaN HFETs. IEEE Electron. Device Lett.19, 89–91. 10.1109/55.661174 (1998). [Google Scholar]
- 2.Pop, E. & Goodson, K. E. Thermal phenomena in nanoscale transistors. J. Electron. Packag.128, 102–108. 10.1115/1.2188950 (2006). [Google Scholar]
- 3.Bar-Cohen, A. & Wang, P. On-chip thermal management and hot-spot remediation 349–429 (Springer, 2009). [Google Scholar]
- 4.Gong, T. et al. Co-optimization of electrical-thermal-mechanical behaviors of an on-chip thermoelectric cooling system using response surface method. Appl. Therm. Eng.244, 122699. 10.1016/j.applthermaleng.2024.122699 (2024). [Google Scholar]
- 5.van Erp, R., Soleimanzadeh, R., Nela, L., Kampitsis, G. & Matioli, E. Co-designing electronics with microfluidics for more sustainable cooling. Nature585, 211–216. 10.1038/s41586-020-2666-1 (2020). [DOI] [PubMed] [Google Scholar]
- 6.Kandlikar, S. G. Review and Projections of Integrated Cooling Systems for Three-Dimensional Integrated Circuits. J. Electron. Packag.136, 02400. 10.1115/1.4027175 (2014). [Google Scholar]
- 7.Sohel Murshed, S. & Nieto de Castro, C. A critical review of traditional and emerging techniques and fluids for electronics cooling. Renew. Sustain. Energy Rev.78, 821–833. 10.1016/j.rser.2017.04.112 (2017). [Google Scholar]
- 8.Avgerinou, M., Bertoldi, P. & Castellazzi, L. Trends in data centre energy consumption under the european code of conduct for data centre energy efficiency. Energies[SPACE] 10.3390/en10101470 (2017). [Google Scholar]
- 9.Ziabari, A., Zebarjadi, M., Vashaee, D. & Shakouri, A. Nanoscale solid-state cooling: A review. Rep. Prog. Phys.79, 095901. 10.1088/0034-4885/79/9/095901 (2016). [DOI] [PubMed] [Google Scholar]
- 10.Gebrael, T. et al. High-efficiency cooling via the monolithic integration of copper on electronic devices. Nat. Electron.5, 394–402. 10.1038/s41928-022-00748-4 (2022). [Google Scholar]
- 11.Tsutsui, M. et al. Peltier cooling for thermal management in nanofluidic devices. Device2, 100188. 10.1016/j.device.2023.100188 (2024). [Google Scholar]
- 12.Bradley, D. I. et al. On-chip magnetic cooling of a nanoelectronic device. Sci. Rep.[SPACE] 10.1038/srep45566 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yangui, A., Bescond, M., Yan, T., Nagai, N. & Hirakawa, K. Evaporative electron cooling in asymmetric double barrier semiconductor heterostructures. Nat. Commun.[SPACE] 10.1038/s41467-019-12488-9 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhu, X. et al. Electron transport in double-barrier semiconductor heterostructures for thermionic cooling. Phys. Rev. Appl.[SPACE] 10.1103/physrevapplied.16.064017 (2021). [Google Scholar]
- 15.Bescond, M. et al. Thermionic cooling devices based on resonant-tunneling algaas/gaas heterostructure. J. Phys.: Condens. Matter30, 064005. 10.1088/1361-648X/aaa4cf (2018). [DOI] [PubMed] [Google Scholar]
- 16.Bescond, M. & Hirakawa, K. High-performance thermionic cooling devices based on tilted-barrier semiconductor heterostructures. Phys. Rev. Appl.14, 064022. 10.1103/PhysRevApplied.14.064022 (2020). [Google Scholar]
- 17.Stafford, C. A. Local temperature of an interacting quantum system far from equilibrium. Phys. Rev. B93, 245403. 10.1103/PhysRevB.93.245403 (2016). [Google Scholar]
- 18.Shastry, A. & Stafford, C. A. Temperature and voltage measurement in quantum systems far from equilibrium. Phys. Rev. B94, 155433. 10.1103/PhysRevB.94.155433 (2016). [Google Scholar]
- 19.Butola, R., Li, Y. & Kola, S. R. A machine learning approach to modeling intrinsic parameter fluctuation of gate-all-around si nanosheet mosfets. IEEE Access10, 71356–71369. 10.1109/access.2022.3188690 (2022). [Google Scholar]
- 20.García-Loureiro, A., Seoane, N., Fernández, J. G., Comesaña, E. & Pichel, J. C. A machine learning approach to model the impact of line edge roughness on gate-all-around nanowire fets while reducing the carbon footprint. PLoS ONE18, e0288964. 10.1371/journal.pone.0288964 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xu, H. et al. A machine learning approach for optimization of channel geometry and source/drain doping profile of stacked nanosheet transistors. IEEE Trans. Electron Devices69, 3568–3574. 10.1109/ted.2022.3175708 (2022). [Google Scholar]
- 22.Fernandez, J. G., Seoane, N., Comesaña, E., Pichel, J. C. & Garcia-Loureiro, A. An accurate machine learning model to study the impact of realistic metal grain granularity on nanosheet fets. Solid-State Electron.207, 108710. 10.1016/j.sse.2023.108710 (2023). [Google Scholar]
- 23.Adachi, S. GaAs and related materials: bulk semiconducting and superlattice properties (World Scientific, 1994). [Google Scholar]
- 24.Weng, Q. et al. Quasiadiabatic electron transport in room temperature nanoelectronic devices induced by hot-phonon bottleneck. Nat. Commun.[SPACE] 10.1038/s41467-021-25094-5 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vafakhah, M. & Janizadeh, S. Chapter 6 - application of artificial neural network and adaptive neuro-fuzzy inference system in streamflow forecasting. In Sharma, P. & Machiwal, D. (eds.) Advances in Streamflow Forecasting, 171–191, 10.1016/B978-0-12-820673-7.00002-0 (Elsevier, 2021).
- 26.Lee, N.-E., Zhou, J.-J., Chen, H.-Y. & Bernardi, M. Ab initio electron-two-phonon scattering in gaas from next-to-leading order perturbation theory. Nat. Commun.[SPACE] 10.1038/s41467-020-15339-0 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pan, J. et al. Transfer learning-based artificial intelligence-integrated physical modeling to enable failure analysis for 3 nanometer and smaller silicon-based cmos transistors. ACS Appl. Nano Mater.4, 6903–6915. 10.1021/acsanm.1c00960 (2021). [Google Scholar]
- 28.Etesse, G., Salhani, C., Zhu, X., N. Cavassilas, K. H. & Bescond, M. Selective energy filtering in multiple quantum well nanodevice: The quantum cascade cooler. Physical Review Applied (Accepted 9 of April 2024).
- 29.Bescond, M., Dangoisse, G., Zhu, X., Salhani, C. & Hirakawa, K. Comprehensive analysis of electron evaporative cooling in double-barrier semiconductor heterostructures. Phys. Rev. Appl.17, 014001. 10.1103/PhysRevApplied.17.014001 (2022). [Google Scholar]
- 30.Datta, S. Frontmatter. i-viii, Cambridge Studies in Semiconductor Physics and Microelectronic Engineering (Cambridge University Press, 1995). [Google Scholar]
- 31.Haug, H. & Jauho, A. Quantum kinetics in transport and optics of semiconductors (Springer Series in Solid-State Sciences, 2007).
- 32.Bescond, M., Dangoisse, G., Zhu, X., Salhani, C. & Hirakawa, K. Comprehensive analysis of electron evaporative cooling in double-barrier semiconductor heterostructures. Phys. Rev. Appl.17, 014001. 10.1103/PhysRevApplied.17.014001 (2022). [Google Scholar]
- 33.Ferry, D. K., Goodnick, S. M. & Bird, J. Frontmatter, i–iv 2nd edn. (Cambridge University Press, 2009). [Google Scholar]
- 34.Jin, S., Park, Y. J. & Min, H. S. A three-dimensional simulation of quantum transport in silicon nanowire transistor in the presence of electron-phonon interactions. J. Appl. Phys.[SPACE] 10.1063/1.2206885 (2006). [Google Scholar]
- 35.Lee, Y., Lannoo, M., Cavassilas, N., Luisier, M. & Bescond, M. Efficient quantum modeling of inelastic interactions in nanodevices. Phys. Rev. B93, 205411. 10.1103/PhysRevB.93.205411 (2016). [Google Scholar]
- 36.Svizhenko, A. & Anantram, M. Role of scattering in nanotransistors. IEEE Trans. Electron Devices50, 1459–1466. 10.1109/TED.2003.813503 (2003). [Google Scholar]
- 37.Jacoboni, C. & Reggiani, L. The Monte Carlo method for the solution of charge transport in semiconductors with applications to covalent materials. Rev. Mod. Phys.55, 645–705. 10.1103/RevModPhys.55.645 (1983) (Publisher: American Physical Society). [Google Scholar]
- 38.Jin, S., Park, Y. & Min, H. A three-dimensional simulation of quantum transport in silicon nanowire transistor in the presence of electron-phonon interactions. J. Appl. Phys.99, 123719–123719. 10.1063/1.2206885 (2006). [Google Scholar]
- 39.Bescond, M., Carrillo-Nuñez, H., Berrada, S., Cavassilas, N. & Lannoo, M. Size and temperature dependence of the electron-phonon scattering by donors in nanowire transistors. Solid-State Electron.122, 1–7. 10.1016/j.sse.2016.04.010 (2016). [Google Scholar]
- 40.Moussavou, M., Lannoo, M., Cavassilas, N., Logoteta, D. & Bescond, M. Physically based diagonal treatment of the self-energy of polar optical phonons: performance assessment of iii-v double-gate transistors. Phys. Rev. Appl.10, 064023. 10.1103/PhysRevApplied.10.064023 (2018). [Google Scholar]
- 41.Lake, R. & Datta, S. Energy balance and heat exchange in mesoscopic systems. Phys. Rev. B46, 4757–4763. 10.1103/PhysRevB.46.4757 (1992). [DOI] [PubMed] [Google Scholar]
- 42.Büttiker, M. Role of quantum coherence in series resistors. Phys. Rev. B33, 3020–3026. 10.1103/PhysRevB.33.3020 (1986). [DOI] [PubMed] [Google Scholar]
- 43.Romano, G., Gagliardi, A., Pecchia, A. & Di Carlo, A. Heating and cooling mechanisms in single-molecule junctions. Phys. Rev. B81, 115438. 10.1103/PhysRevB.81.115438 (2010). [Google Scholar]
- 44.Rhyner, R. & Luisier, M. Atomistic modeling of coupled electron-phonon transport in nanowire transistors. Phys. Rev. B89, 235311. 10.1103/PhysRevB.89.235311 (2014). [Google Scholar]
- 45.Meair, J., Bergfield, J. P., Stafford, C. A. & Jacquod, P. Local temperature of out-of-equilibrium quantum electron systems. Phys. Rev. B90, 035407. 10.1103/PhysRevB.90.035407 (2014). [Google Scholar]
- 46.Venugopal, R., Paulsson, M., Goasguen, S., Datta, S. & Lundstrom, M. S. A simple quantum mechanical treatment of scattering in nanoscale transistors. J. Appl. Phys.93, 5613–5625. 10.1063/1.1563298 (2003). [Google Scholar]
- 47.Pedregosa, F. et al. Scikit-learn: machine learning in python. J. Mach. Learn. Res.12, 2825–2830 (2011). [Google Scholar]
- 48.Paszke, A. et al. Pytorch: An imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems 32, 8024–8035 (Curran Associates, Inc., 2019).
- 49.Liaw, R. et al. Tune: A research platform for distributed model selection and training (2018). arXiv:1807.05118.
- 50.Subasi, A. Chapter 3 - machine learning techniques. In Subasi, A. (ed.) Practical Machine Learning for Data Analysis Using Python, 91–202, 10.1016/B978-0-12-821379-7.00003-5 (Academic Press, 2020).
- 51.Goodfellow, I. J., Bengio, Y. & Courville, A. Deep Learning (MIT Press, Cambridge, MA, USA, 2016). http://www.deeplearningbook.org.
- 52.Holland, S. M. Principal components analysis (pca ) (2008).
- 53.Ketkar, N. Stochastic Gradient Descent, 113–132 (Apress, Berkeley, CA, 2017).
- 54.Xu, Z., Dai, A. M., Kemp, J. & Metz, L. Learning an adaptive learning rate schedule (2019). arXiv:1909.09712.
- 55.Kingma, D. P. & Ba, J. Adam: A method for stochastic optimization (2017). arXiv:1412.6980.
- 56.Fernandez, J. G. et al. CoolML. https://gitlab.citius.usc.es/modev/coolML (2024). [Online].
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Part of the simulated dataset for training both neural network models and predicting the optimal asymmetric double-barrier semiconductor based heterostructures is available in the following Zenodo repository: https://doi.org/10.5281/zenodo.11032095.
The code used for the presented ML workflow is also available at 56.