Understanding tumour growth variability in breast cancer xenograft models identifies PARP inhibition resistance biomarkers

Abstract

Understanding the mechanisms of resistance to PARP inhibitors (PARPi) is a clinical priority, especially in breast cancer. We developed a novel mathematical framework accounting for intrinsic resistance to olaparib, identified by fitting the model to tumour growth metrics from breast cancer patient-derived xenograft (PDX) data. Pre-treatment transcriptomic profiles were used with the calculated resistance to identify baseline biomarkers of resistance, including potential combination targets. The model provided both a classification of responses, as well as a continuous description of resistance, allowing for more robust biomarker associations and capturing the observed variability. Thirty-six resistance gene markers were identified, including multiple homologous recombination repair (HRR) pathway genes. High WEE1 expression was also linked to resistance, highlighting an opportunity for combining PARP and WEE1 inhibitors. This framework facilitates a fully automated way of capturing intrinsic resistance, and accounts for the pharmacological response variability captured within PDX studies and hence provides a precision medicine approach.

Introduction

Resistance to targeted therapy is one of the major factors that renders a multitude of cancer treatments ineffective. A number of underlying reasons for resistance have been identified, including mutation and expression level changes to the drug’s target, an increase in DNA-damage repair, increased anti-apoptotic pathways, and changes in drug metabolism or the tumour microenvironment, to name a few^1,2. These complex arrays of factors contribute to the challenges of understanding the mechanism(s) of resistance to a particular targeted therapy and how to circumvent it.

Resistance can be grouped into two broad categories, intrinsic and acquired². Resistance that is classified as intrinsic or innate means that there is a pre-treatment subpopulation of cells in the tumour that is insensitive to the treatment. As a result of treatment, the population of sensitive cells will then decrease leading to a tumour that is primarily composed of resistant cells and, hence, to a resistance phenotype². In contrast, acquired resistance refers to drug resistance occurring during the duration of the treatment in an otherwise sensitive population of cells. This can be further divided into spontaneous and drug-induced resistance³. These parallel mechanisms together contribute towards the critical need to rationalise and address drug resistance to targeted cancer therapies.

There is a large body of modelling work on quantifying and elucidating the mechanisms of resistance that span multiple fields^4–6. Well-studied and published are the classical differential equation-based models that try to capture the macroscale dynamics of the tumour and its response to treatment, as well as the signalling network involved in the drug action process and the cellular population dynamics (including the effect of the microenvironment with varying complexity) that can incorporate stochastic or spatiotemporal effects^1,7–9. On the other hand, we have data-oriented approaches that utilise the plethora of information available on the structure and network of biological processes, as well as the large scale of ‘omics’ data available to extract key biomarkers of resistance and sensitivity to a treatment^10,11. Rarely have these approaches been combined into a single framework that utilises both mathematical modelling techniques together with ‘omics’ data.

Olaparib was the first PARP inhibitor (PARPi) to be approved¹² and is one of four now used to treat a number of different cancers, namely ovarian, breast, pancreatic and prostate cancers¹³: https://www.ema.europa.eu/en/medicines/human/EPAR/lynparza¹⁴: https://www.accessdata.fda.gov/drugsatfda_docs/label/2020/208558s014lbl.pdf.

PARP binds to DNA single-strand breaks (SSBs), utilising NAD+ to initiate repair by generating poly [ADP-ribose] (PAR) chain modifications¹⁵ that remodel chromatin to allow recruitment of repair factors as well as modifying PARP itself to allow chromatin dissociation, enabling the binding of additional repair proteins¹⁶. PARP inhibitors prevent auto-PARylation and result in PARP trapping onto the DNA, which, during replication, leads to the formation of DNA double-strand breaks (DSBs)¹⁷. When Homologous Recombination Repair (HRR) is functional, these DNA DSBs are accurately repaired, but in cells deficient in HRR, such as those with loss-of-function BRCA1/2 mutations, the error-prone non-homologous end joining (NHEJ) pathway is employed¹⁸ leading to genomic instability and cancer cell death. HRR is a complex repair process¹⁹, so PARPi sensitivity extends beyond the loss of BRCA1 and BRCA2 function to additional HRR proteins, including RAD51, ATR, CHK1, PALB2 and other Fanconi anaemia-associated repair factors²⁰.

Despite the effectiveness of PARPi, the appearance of resistance is well documented and often associated with the recovery of HRR pathway functionality through reversion mutations, dysregulation of the DNA-end resection pathway, protection of stalled DNA replication forks and epigenetic modifications^21–24.

Multiple mechanisms predicting the response to olaparib have been well studied. Characterisation of the HRR status through the detection of HRR-related gene mutations (HRRm gene panel), HRR deficiency (HRD) genomic scar score, BRCA1 gene promoter hypermethylation and detection of RAD51 nuclear foci are some of the main methods being used to predict response^{20,21,24–26}. Despite these insights, the lack of response of some HRR-deficient tumours, as well as the response in BRCA wild-type tumours to PARPi, cannot always be explained. Hence, a critical step towards personalised medicine is understanding the intrinsic (baseline) mechanisms of response to olaparib by moving beyond HRR status alone.

One of the primary aims of the study was to formulate a computational framework that captures the dynamics of tumour growth and treatment effect, including resistance, offering a continuous description of drug response and finally integrating the model output with ‘omics’ data to extract markers of resistance. This framework builds upon a recently published study by the authors that performs a comprehensive assessment of tumour growth models applied to untreated PDX and CDX (cell line-derived Xenograft) models²⁷. While here it is applied to olaparib in triple-negative breast cancer (TNBC) PDX models, the framework itself can be generalised and is sufficiently robust to be applied for different treatments as well as various tumour types. This study is a follow up to²³ where the primary data have been presented.

This framework offers a complementary and more comprehensive approach to traditional methods of classification, such as mRECIST criteria, which make use of particular timepoints/events to classify a tumour^28,29. In contrast, this methodology is built around fitting all data and timepoints together, which allows for more informative decisions on the behaviour of each tumour and the ‘personal’ dynamics each tumour displays as part of its growth/drug response. Additionally, a continuous scale of response has multiple benefits, including a much finer separation between different behaviours, even within tumours that would have been grouped in the same class. In addition, this approach provides an understanding of the underlying variability in studies with replicates and robust identification of biomarkers by correlating the whole range of their expression to a similarly continuous output.

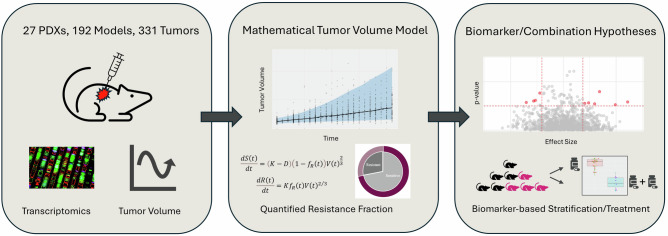
Towards validation, the mathematical model was fitted to the olaparib and adavosertib (WEE1i) in vivo combination data in addition to performing pathway enrichment analysis and differential survival analysis. This framework capturing dynamic tumour growth metrics and ‘omics’ integration to predict resistance biomarkers, provides an opportunity to learn from variability within PDX studies, helping reduce the inference gap between preclinical and clinical studies, thus is more likely to drive early-stage clinical success. A visual representation of the framework is shown in Fig. 1.

Fig. 1. A visual demonstration of the typical workflow for the developed framework.

The fitting of the data using nonlinear mixed effects (see Methods) calculates the resistance fraction ($f_R$) that is used to predict markers of resistance and response to a particular drug. This is followed by in silico and in vitro validation studies across pathway analysis, preclinical efficacy screens. The framework can easily be adapted to different tumour types and treatments.

Results

Resistance fraction, classification of PDXs and comparison to mRECIST

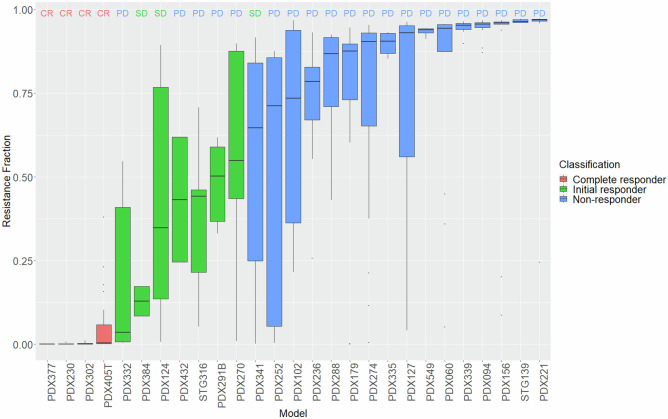
The output of the model is the resistance fraction for each individual mouse. The classification of each PDX is derived from a consensus of the classifications of the replicates within that PDX and the resistance fraction value from the median of the resistance fraction values of the replicates. There are two main observations from Fig. 2. The first is the large inter-mouse variability seen within each PDX. This variability stems from the diversity in behaviour in the replicates of each PDX, which makes it exceptionally difficult to summarise the tumour dynamics of each PDX using a simple categorical classification³⁰. In contrast to the classification, the resistance fraction as a continuous value offers a much more robust way of capturing both the average behaviour as well as its variability. The second is the difference between the mRECIST criteria classification and the model classification for the 27 PDXs (4 CR, 3 SD and 20 PD). Most disagreements are found in the category we defined as initial responders. mRECIST only partially captures that behaviour through the SD category. Identifying early responders is key towards therapeutic intervention strategies as this group might benefit from a different treatment compared to non-responders, for example drug combinations. Supplementary Figs. 7 show these differences in full detail, clearly demonstrating their difference from non-responders.

Fig. 2. Continuous and discrete olaparib 100 mg/kg response of TNBC PDXs.

Resistance fraction boxplots with median, min, max and upper and lower quartiles. mRECIST classification is found at the top of each boxplot representing three distinct categories: complete responders (CR), stable disease (SD) and progressive disease (PD) and colours represent the mathematical model classification into complete responders (red), initial responders (green) and non-responders (blue).

The diagnostic plots, parameter estimates and errors as well as the variability of the individual parameter estimates can be found in Supplementary Figs. 1–5, Supplementary Table 1 and demonstrate a good fitting of the model to the data. Supplementary Fig. 13 shows the model fit to individual tumours together with the respective resistance fraction. Supplementary Fig. 6 is the Fig. 2 equivalent for 50 mg/kg.

Markers of response to olaparib

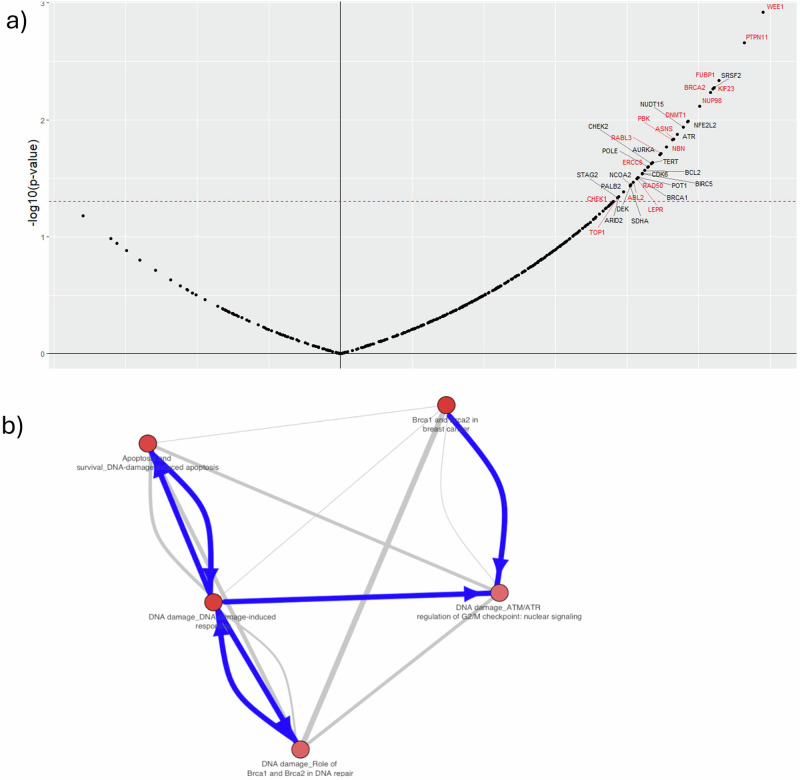
In order to identify biomarkers of resistance to olaparib, baseline transcriptomics was correlated with model-derived resistance fractions ($f_R$) at baseline for each PDX (see “Materials and methods”) treated with olaparib 100 mg/kg. Predicted gene markers of olaparib resistance are shown in Fig. 4. There are 36 positively correlating biomarkers with resistance fraction. Figure 3A shows the volcano plots of the correlation between mRNA expression of the CIVIC genes and the resistance fraction. “Non-significant” gene names are excluded from the plot.

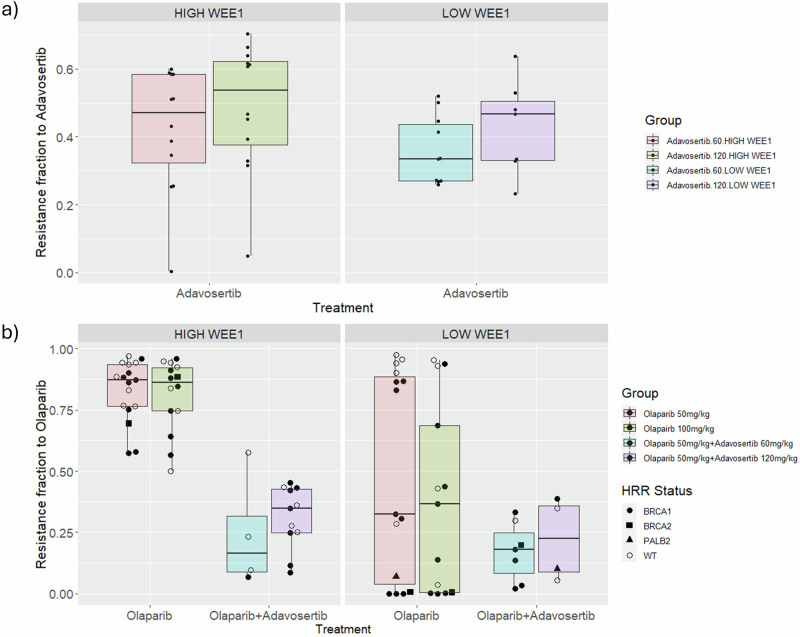
Fig. 4. Effect of WEE1 expression on olaparib and adavosertib resistance fractions.

Facets represent expression levels of WEE1 with respect to the median expression value in the cohort of PDXs. Individual point colour specifies the HRR status of PDX. Non wild type (WT) PDXs indicate either a mutation (BRCA1, BRCA2m, PALB2) or hypermethylation of BRCA1 promoter (Supplementary Table 5). A Resistance fraction of adavosertib is stratified with respect to WEE1 expression levels for adavosertib single agent. B Resistance fraction of olaparib is stratified with respect to WEE1 expression levels for olaparib single agent and adavosertib combination. Also separated by dose for either drug.

Fig. 3. Resistance correlation markers and enriched ontology terms.

A Olaparib 100 mg/kg markers where y-axis is the log-transformed p-value with the threshold at p = 0.05. The x-axis is the Pearson’s correlation ρ with a threshold of 0.03 and −0.03. Highlighted in red are the markers found in both doses. B Crosstalk analysis of olaparib 100 mg/kg hits: The network of the top five ontology terms from pathway enrichment analysis is depicted. Nodes represent top terms, and edges represent significant similarities (as measured by hypergeometric test) between these entities. The edge thickness depends on the size of the intersection between two ontology terms, while the colour of the node corresponds to the enrichment z-score.

WEE1 and ATR are particularly interesting as inhibitors targeting these genes have been explored in combination with olaparib^31,32. Seven genes were identified (ATR, BRCA1, BRCA2, CHEK1, CHEK2, PALB2 and NBN) that have been linked to the HRR pathway, which is directly associated with the mechanism of action of olaparib²². Pathway enrichment analysis was performed using MetaCore, where the probability of a random intersection between a set of IDs the size of a target list with ontology entities is estimated in the p-value of hypergeometric intersection (Source: Clarivate; Fig. 3B). This analysis highlighted key pathways known to be associated with DNA damage repair, including: ‘BRCA1 and BRCA2 in cancer’, ‘Apoptosis and survival_DNA damage-induced apoptosis’, ‘DNA damage_ATM/ATR regulation of G2/M checkpoint: nuclear signalling’. Top enriched pathway maps are shown in Supplementary Table 3. In addition to the enrichment analysis, the selected genes were annotated with OncoKB³³ and checked against published independent studies (Supplementary Table 9). In OncoKB the genes are annotated using five categories: therapeutic, prognostic, diagnostic, resistance, and FDA-levels. Finally, the same analysis was performed for 50 mg/kg, which showed many similarities in the results, including 17 common markers (highlighted in red in Fig. 4A) and many common pathways. These can be found in Supplementary Fig. 8a, b and Supplementary Table 4.

Additionally, we assessed the ability of the feature set to predict response by training machine learning models to predict Resistance Fraction (regression) and RECIST binary response (classification). For the latter, we binarized RECIST values such that the non-response “0” class was covered by “Progressive Disease” (PD), and the “1” class by everything else. The models trained were Gradient Boosting Machines, Random Forests and Linear/Logistic Regression; they were limited by the small dataset size (n = 27 training samples) and imbalanced class distribution (e.g. 20/27 classed as PD), which resulted in relatively low metrics (e.g. 0.65 AUC for logistic regression, RMSE of 0.33 for linear regression).

Feature importances were extracted using in-built metrics from all models that revealed a common set of features driving predictions across model types. Suppl Fig. 21 shows the comparison of extracted important features from ML models with the statistically derived features proposed as core resistance-driving biomarkers as part of this study. Thirty-six markers were identified as significant using the linear correlation, and to that end, for each ML feature selection method, we kept the top 36 markers based on weight/importance. Many markers are shared between the simple correlation and the ML methods, with markers such as BIRC5, KIF23, DNMT1 and POLE being common in all methods and WEE1 included as one of the top features in 4/6 ML methods. Random Forest methods and methods that use the continuous metric of Resistance Fraction (FR) as output share more common markers with the correlation (15–17 common) compared to logistic regression and gradient boost (7–10 common) (see Supplementary Fig. 21). Finally, we have implemented a train-test split across our dataset to map consistency of identified markers as a way of validation. We have included the results of this in Supplementary Fig. 22, with WEE1 being identified as the most consistent marker along with other key resistance markers identified, such as PTPN11, SRSF2, BRCA2 and others. We note and recognise that the statistical significance derived from such a small ‘n’ restricts interpretation and confidence in the observations made.

Survival analysis, including selected markers

To assess the clinical significance of the 36 biomarkers identified, these were analysed using Kaplan–Meier survival plots, stratified by expression, and hazard ratios calculated to further deconvolute their association to olaparib resistance. This process was done not to find new markers but to try and understand the effect of the identified markers on the overall survival of both treated and untreated cases. Survival analysis was performed on the baseline mRNA data for both the treated and untreated tumours (331 samples for 100 mg/kg and 563 samples for untreated). Table 1 shows the markers and each category.

Table 1.

Markers grouped by survival analysis category

Markers	Category
ABL2, ASNS, ATR, BRCA2, CDK6, CHEK2, ERCC5, KIF23, NBN, NFE2L2, NUP98, PALB2, PBK, PTPN11, RABL3, STAG3, TERT, TOP1, WEE1	Differential survival in both groups—same trend
BCL2, BIRC5, CHECK1, DEK, LEPR, NCOA2, NUDT15, POLE, POT1, SDHA, SRSF2	Differential survival only in treated group
AURKA	Differential survival only in untreated groups
ARID2, BRCA1, DNMT1, FUBP1, FUBP1, RAD50	No differential survival in either group

The four categories offer an interesting perspective on the identified markers. The first and biggest category are markers that show a differential survival in both treated and untreated of the same kind, meaning that in both groups, lower expression leads to higher survival. The fact that these markers show differential survival in the untreated might be an indication that these are associated with disease progression. A closer inspection of the hazard ratios found in Supplementary Table 8 reveals that for most cases, there is a greater separation (higher hazard ratio) of these markers in the treated group and hence implies that they are not only disease progression but also resistance markers. The second category shows only differential survival in the treated group, which might highlight features that are closer to true resistance markers. The third and fourth groups, with markers that do not show any differential survival in the treated group or no differential survival in either group despite being correlated to the resistance fraction, indicate that these few markers lose their significance when variability is introduced through the use of the individual tumours (as was done for the Kaplan–Meier analysis). Selected cases of the Kaplan–Meier curves are found in Supplementary Figs. 9–11.

High WEE1 expression as a marker of resistance to olaparib

High expression of the gene encoding the cell cycle checkpoint regulator WEE1 kinase was identified by the model as the strongest marker of resistance to both doses of olaparib treatment. WEE1 regulates cell cycle progression and aids DNA repair, which aids tumour cell replication. To validate this finding, an independent dataset is used that includes adavosertib³⁴ single agent and the combination with olaparib PDX data (the fitted model in “Methods”—Mathematical model and parameters in Supplementary Table 2.

If high WEE1 expression is a marker of resistance to olaparib, then we could expect the resistance fraction to olaparib in the combination-treated PDXs to be, on average, lower than the resistance fraction found in the PDXs treated with single-agent olaparib. The reasoning behind this is that if high WEE1 expression is a true marker of resistance to olaparib, then inhibiting the activity of its protein product from the onset could lead to higher treatment efficacy of olaparib. Since the treatment effects of both drugs are fixed to their respective single agent data, the only way in which the mathematical model will interpret this increased treatment efficacy of olaparib is from a decreased olaparib resistance fraction. Figure 4 shows the differences in the olaparib resistance fraction in PDXs treated with single-agent olaparib and with the adavosertib combination, as well as the effect on the adavosertib resistance fraction. All cases are stratified by LOW and HIGH WEE1 expression with respect to the median expression value.

When comparing olaparib single agent response to that of the combination, there are two key observations from Fig. 4B. Firstly, there is a clear correlation between the resistance fraction and WEE1 expression in the case of olaparib single agent versus the combination with resistance significantly decreased in the combination group. Secondly, the combination group has a markedly lower olaparib resistance fraction than the single agent olaparib group (Mann–Whitney rank test p-value « 0.05, effect size = 0.79) that becomes less prominent for LOW WEE1 expression (Mann–Whitney rank test p-value = 0.31). Both observations are consistent with high WEE1 expression being a marker of resistance to olaparib. Finally, as seen in Fig. 4B HRR status seems not to correlate with the resistance fraction differences between HIGH and LOW WEE1, further supporting the importance of WEE1 levels as a marker. A survival analysis (Kaplan–Meier) of single-agent versus combination and of LOW WEE1 vs HIGH WEE1 can be found in Supplementary Fig. 16 demonstrating the increase in survival when WEE1 is intrinsically low or inhibited. Also, Supplementary Fig. 17 shows the decrease in resistance fraction for olaparib 50 mg/kg monotherapy to the combination of olaparib 50 mg/kg with either adavosertib 60 or 120 mg/kg. That decrease appears in both high and low WEE1 groups, which points towards a combination effect in addition to the sensitisation of the tumours to olaparib.

Finally, high variability in resistance fraction was observed for the low-WEE1 PDXs treated with olaparib monotherapy. This could be attributed to the expression of other markers identified as markers of resistance to olaparib. To explore this further, we split these PDXs into two groups. The low olaparib resistance group (less than the median) and the high group (higher and equal to the median). A Kolmogorov–Smirnov test was then performed on the expression of the 40 (excluding WEE1) identified markers to check for statistical differential expression. 12 markers had a significant differential expression LEPR, DNMT1, PBK, RABL3, BCL2, BIRC5, DEK, NUDT15, RBM15, KF23 and STAG2. These markers, individually or in combination, could potentially explain the variability observed. Results are summarised in Supplementary Fig. 18.

RAD51 foci

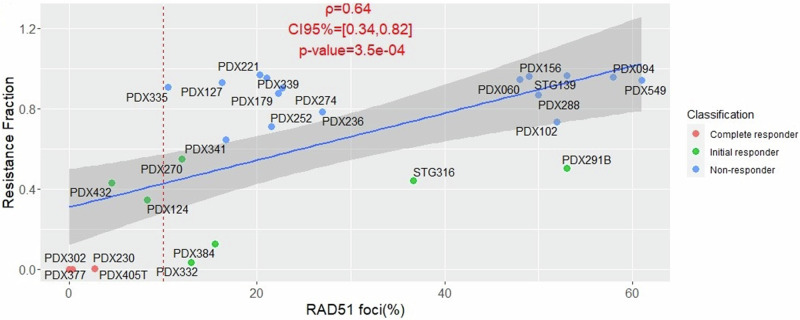
RAD51 foci have been shown to provide an accurate prediction of response to PARPi that extends beyond BRCA mutation status^23,24. A statistically significant correlation was found between RAD51 foci score and tumour volume change for olaparib-treated PDXs²¹. While this offers an implicit association between RAD51 foci and resistance, using the current model and the quantification of intrinsic resistance a more explicit correlation is performed. Figure 5 shows the correlation between the resistance fraction and (pre-treatment) RAD51 foci score for both doses.

Fig. 5. Pearson’s correlation of resistance fraction to RAD51 foci scores for Olaparib 100 mg/kg.

Colour is assigned by classification using the resistance model. Pearson’s ρ value, 95% confidence intervals and p-value are included. The red dotted line corresponds to the 10% threshold for differentiating PARPi‐sensitive from PARPi‐resistant¹⁹.

A high correlation (ρ = 0.64) is observed, indicating that the RAD51 foci score is not only capable of classifying into responders and non-responders but also provides a good continuous description of intrinsic resistance/response to olaparib. The correlation becomes even stronger (ρ = 0.75), when we consider only PDXs which are HRD but does remain to similarly high levels for non-HRD (see Supplementary Table 5). Correlation with olaparib 50 mg/kg is also very strong (ρ = 0.74) and can be found in Supplementary Fig. 19.

Discussion

This manuscript builds upon the data and methodology of two papers^23,27. The data of ref. ²³ are fitted using an extended version of the NLME Maynord model used in ref. ²⁷ is expanded beyond control data to include not only a treatment effect that is dependent on the dose but also two subpopulations, a resistant and a sensitive. This is done in order to estimate the Resistance Fraction at baseline and use it a means of characterising response and identifying biomarkers.

This manuscript showcases a robust mathematical model for assessing tumour growth, treatment response and intrinsic resistance. Formulated as part of the nonlinear mixed-effect statistical framework, it allowed us to fit pre-clinical data for olaparib-treated TNBC PDX tumours. Quantifying accurately and confidently the resistance fraction intrinsic to the tumours has led to its use as the basis for further statistical modelling, which, when combined with transcriptomics data, was able to identify potentially important biomarkers of resistance to the PARPi olaparib.

The work presented here is a combination of statistics and mathematical modelling with the addition of biomarker statistics separately. The reasoning for that separation was the complexity of including so many markers as inputs to the NLME model. Significant efforts need to be made to reduce the number of markers as much as possible before including them as covariates to the mathematical model, and that is a potential future extension for this framework. Nevertheless, the important gap that is being filled is the lack of such an integrated approach where a mathematical model of tumour growth is used as a means of filtering and ranking biomarkers.

One of the findings of particular interest was the high level of WEE1 expression associated with olaparib resistance. Olaparib treatment and the resulting PARP trapping have been reported to induce increased replication stress and replication fork stalling³⁵. Stalled forks can, in turn, ‘collapse’ following nuclease cleavage to form DNA DSBs. This increased S-phase DNA damage would be predicted to generate an increased dependency on a G2/M checkpoint to allow repair before the cells enter mitosis. So one possible explanation for higher levels of WEE1 associated with olaparib resistance could be a need for a more effective G2/M checkpoint. This is unlikely to provide a complete explanation, however, since PMYT1, another important G2/M checkpoint gene was not found to be over-expressed in olaparib resistant models. Unlike PMYT1, WEE1 also plays important roles in S-phase dealing with replication stress and stalled replication forks. These roles include the inhibition of nucleases that can induce stalled replication fork collapse and the formation of DNA DSBs. The data presented here, indicating high WEE1 expression as a PARPi resistance factor, therefore suggests WEE1’s role in PARPi resistance may also include a greater ability to deal with stalled replication forks following PARP trapping. Consistent with this idea, is that two other genes whose proteins play dual roles at both the G2/M checkpoint and in the S-phase replication stress response, namely ATR and CHK1, were also identified as being associated with olaparib resistance when expressed at higher levels (Fig. 4). Moreover, the EFFORT Phase 2 clinical trial assessed the combination efficacy of adavosertib (WEE1i) and Olaparib in patients³⁶, as well as a dose escalation study in solid tumours³⁷. In addition, some preclinical studies have also reported the potential combination benefit of Olaparib with WEE1i as well as other small molecule inhibitors categorised as DNA damage repair agents^38,39.

Other markers identified in Fig. 3, were also associated with the DNA damage response and the mechanism of action of olaparib, including those associated with HRR, namely BRCA1, BRCA2, CHEK2, PALB2 and NBN, as well as STAG2 that is part of the cohesion complex necessary for the use of the sister chromatid, an undamaged template during HRR⁴⁰. Additional confidence in the mathematical modelling used here to identify factors associated with olaparib resistance also comes from the pathway enrichment analysis that identified five top pathways associated with olaparib resistance that can all be linked to the PARPi mechanism of action; namely, three DDR-associated pathways, the BRCA1/2 breast cancer pathway and the DNA damage apoptosis and survival associated pathways.

One additional, but clinically relevant finding from this study, was that the more accurate use of resistance fractions to classify preclinical olaparib response (compared to the more traditional mRECIST approach), could effectively be predicted using the RAD51 foci assay (Fig. 5). It is now possible to assess basal levels of RAD51 foci to predict HRR functionality⁴¹ and current efforts are underway to generate diagnostics based on the RAD51 assay⁴². The data presented here are consistent with the goal of using RAD51 foci to predict PARPi sensitivity or resistance. RAD51 has been established as a key resistance marker in several other studies previously, however also acknowledging that the biological mechanisms underpinning this activity is not straightforward/consistent or fully understood yet. RAD51 plays a critical role within the Homologous Recombination Repair pathway (HRR), and its upregulation has been observed in resistance to PARP inhibition in BRCAm cells in vitro⁴³. Recent studies have also explored the potential of RAD51 as a potential drug target within the context of BRCAm TNBC, showing synergistic efficacy with dual PARP-RAD51 conjugates in breast cancer cells⁴⁴. Whilst this and similar studies exploring the synthetic lethality of olaparib with RAD51i have shown promise, this field needs further in-depth studies to confirm and establish therapeutic potential.

While intrinsic resistance is a major contributor to treatment failure, there are other ways resistance can occur that are not considered in this framework. Quantifying all potential types of resistance is challenging and requires specific types of experimental protocols to provide the data in order to separate them⁴⁵. To model acquired resistance, we would need to measure mRNA expression not only at baseline but also post-treatment. That would allow us to quantify and correlate the changes we see in gene expression to the tumour growth dynamics observed. In the data used for this study, only baseline transcriptomics were available. Trying to include and quantify acquired resistance using the data in this paper led to parameter identifiability issues with respect to resistance parameter estimates. Both the equations and the general framework of the approach presented here, are flexible enough to include additional terms and data.

Although the simple Pearson’s correlation does provide relevant markers, more complex statistical and machine-learning methods could also be used to extract features. This includes nonlinear models that do not assume a linear relationship between the expression and the resistance fraction. An initial test was performed using ML models such as Random Forest and Gradient Boost but struggled due to the limited dataset and the imbalances in the class distribution. Further parameter reduction methods might need to be implemented to decrease the parameter space. A further limitation of the model is that $f_R$ is treatment-specific parameter based on efficacy and hence cannot differentiate between non-response and resistance. In practical terms, what that means is that this parameter will attain a high value (close to 1) if the tumour does not respond because of resistance but because of the wrong (non-efficacious) treatment being given. In the case of our data and any case where the treatment is the right one for a particular indication then $f_R$ should emulate true resistance.

Mathematical modelling of resistance to cancer treatments offers a unique opportunity for new metrics to characterise resistance as well as sensitivity and the degree of response. These new metrics, such as the resistance fraction used in this manuscript, offer a continuous description of the behaviours seen, can account for variability, and can very naturally be summed up for each individual (PDX) model. We believe that these metrics can, in turn, provide a very viable and robust input to bioinformatic and statistical models including, but not limited to, regression, differential gene expression and random forest models, consequently enriching their descriptive and predictive capabilities. The goal of the resistance fraction is not to replace the mRECIST criteria or other classification methods but rather to supplement them. For example, in the identification of interesting subcategories, such as the initial responders defined here. All the above can be particularly useful in generating early intervention strategies for TNBC patients and, by extension, other tumour types, discovering potential combination targets and validating existing biomarkers (as was shown here for the RAD51 foci assay). With further validation in the clinic, this methodology could make an important contribution to the future practises of precision medicine.

Methods

Patient-derived xenograft (PDX) models and in vivo treatment experiments

Fresh tumour samples from TNBC patients were collected for implantation into nude mice under an institutional review board (IRB)-approved protocol. Experiments were conducted following the European Union’s animal care directive (2010/63/EU) and were approved by the Ethical Committee of Animal Experimentation of the Vall d’Hebron Research Institute. Informed consent was collected from all patients.

Surgical or biopsy specimens from primary tumours or metastatic lesions were immediately implanted in mice as described in ref. ²². Our cohort is composed of 33 patient-derived xenografts (PDX) treated with olaparib as a single agent, and 27 PDX treated with adavosertib (WEE1 inhibitor, WEE1i) as a single agent and the combination with olaparib. To evaluate drug sensitivity, tumour-bearing mice were equally distributed into treatment groups once tumours reached sizes ranging from 100 to 300 mm³. As a single agent, olaparib is administered orally six times per week unless otherwise specified (in 10%v/v DMSO/10%w/v Kleptose [HP-β-CD]) at 50 or 100 mg/kg. For the 50 mg/kg there are 32 PDX, 240 mice, 161 of which have two tumours grafted on either side, giving a total of 402 tumours. For 100 mg/kg, there are 27 PDXs (4 CR, 3 SD and 20 PD). PDX and 192 mice (139 with two tumours), diving 331 tumours overall. Similarly, as a single agent, adavosertib is administered orally five times per week unless otherwise specified (in 0.5%v/v Methylcellulose) at 60 mg/kg or 120 mg/kg, with 24 and 20 PDX, respectively. The combination is given with either dose of adavosertib, but only with 50 mg/kg of olaparib. Experiments with different doses are analysed separately.

Tumour growth is measured with calliper bi-weekly from the first day of treatment. To generate PDX models with acquired resistance to PARPi, olaparib treatment was maintained for up to 150 days in olaparib-sensitive tumours until individual tumours regrew. In all experiments, mouse weight was recorded twice weekly. The tumour volume was calculated as V = 4/3/L × l², “L” being the largest diameter and “l” the smallest. Mice were euthanized when tumours reached 1500 mm³ or in case of severe weight loss, in accordance with institutional guidelines. Baseline (pre-treatment) transcriptomics were obtained for each of the 33 PDX.

Only the olaparib single agent data are used for the development of the framework and 100 mg/kg dose for the biomarker discovery pipeline. The combination, adavosertib and olaparib 50 mg/kg data are then used for validation checks for a particular marker. This choice was based on the fact that 100 mg/kg is the clinically relevant dose and hence more relevant biomarkers associated with resistance to that dose instead of 50 mg/kg.

Mathematical model

As can be seen from the data, there is a wide spectrum of different dynamics, from the simple response and non-response curves to the more complex relapse dynamics. In order to be able to capture the diverse dynamics of these data sets, it is necessary to account for the differences in response using resistance. The inclusion of resistance is particularly essential when it comes to modelling the U-shaped regression/relapse pattern seen in many cases, which points towards a change in the responsiveness of the tumour occurring throughout the duration of the study. The Mayneord model^46,47 is an empirical model of tumour growth where the rate of change of the volume is proportional to the surface of the tumour. The basic assumption of this model is that the rate of growth of the radius of the tumour is constant which gives rise to the proportionality of the tumour volume change to the surface. Since modelling resistance will add further complexity, the goal was for the base model to remain as simple as possible while being adequate at describing tumour growth at the same time. By introducing two compartments, one for the sensitive and one for the resistant part of the tumour, the model changes as follows:

$$\frac{\mathit{dS}\left(t\right)}{\mathit{dt}}=\left(K-D\right)\left(1-f_R\left(t\right)\right){V\left(t\right)}^{\frac{2}{3}},S\left(t\right)=V\left(t\right)\left(1{-f}_R\left(t\right)\right)$$ 1

$$\frac{dR\left(t\right)}{dt}=K{f}_R\left(t\right){V\left(t\right)}^{2/3}.R\left(t\right)=V\left(t\right)f_R\left(t\right)$$ 2

Where $S$ is the sensitive tumour volume, $R$ is the resistance tumour volume, $\mathit{V}$ is the total tumour volume, $K$ is the growth rate of the tumour, $D$ is the treatment effect and the total volume is given by $S+R$. $f_R$ is the resistance fraction of the tumour at time $t$ given by $R\left(t\right)/\left(R\right(t)+S(t\left)\right)$. $f_R\left(0\right)$ is the resistance fraction at time zero and the main parameter being fitted, needed for the initial conditions of the two subpopulations. It ranges from 0 to 1 with 0 being a completely sensitive tumour and 1 being completely resistant.

In addition to olaparib single agent data, the adavosertib single agent and combination with olaparib data are fitted using the aforementioned model for subsequent analysis. For that purpose, the core model remains the same, with the only difference being that instead of two compartments, there are four: sensitive to both treatments, sensitive to olaparib but resistant to adavosertib; resistant to olaparib but sensitive to adavosertib and resistant to both.

Model development

Fitting was performed using non-linear mixed effects (NLME)⁴⁸, NLME is a statistical framework that can incorporate mechanistic and semi-mechanistic models such as the tumour growth and allows for a more complete capturing of the data by taking into account all individual data, inter-individual variability, dependence of measurements and ignoring missing values.

Volume time-series data were fitted on the logarithmic scale with an additive error, no covariance between different parameters and the first order conditional estimation (FOCE)⁴⁹ method in NONMEM [ICON plc Ireland]. Both doses were fitted together to get an accurate estimation of their difference in efficacy.

The growth rate population and random effects were fixed to values estimated using the untreated data from our dataset. That was done to decrease the number of parameters that we needed to fit in order to keep the values and model more reproducible. The fitting process was performed 100 times using the ‘retries’ functionality of PSN with varying initial estimates. The purpose being to assess the stability of the model as well as derive a consensus for the discrete classification of the growth curves.

The classification of the growth curves into complete responders, initial responders and non-responders is done in two steps. First, we separate complete responders from the rest by setting a cut-off to the resistance fraction below, which we assume is practically zero. Having extracted the complete responders, the initial and non-responders are separated using a mathematical inequality that determines the sign of the volume derivative at time zero. Adding (1) and (2) gives $\mathit{dV}/\mathit{dt}$ and solving for $\frac{dV}{dt{\mid }_{t=0}}>0$ gives:

$$f_R\left(0\right)-\frac{D-K}{D}>0.$$ 3

Inequality (3) shows that if the resistance fraction is higher than the $D-K/D$ the tumour volume will start increasing from the beginning of the experiment. The opposite yields a tumour volume that initially decreases (negative derivative) before eventually increasing again (relapse).

Regarding the choice of time zero, with PARPi, there is a delay between administration and effect due to the build-up of the DNA damage over a few cell cycles; this was not included in the mathematical model. So, the simulated tumour from the model immediately demonstrates the effect of the drug. While this might not capture the initial timepoints perfectly, it does capture the overall dynamics and curve of the tumour growth. Since then, there has been no delay in the model. The fraction at time zero is the one that will determine if the tumour shows no response or some response before relapsing. If the delay was accounted for in the model, the choice of time zero as the time point against which the above inequality is checked would be incorrect as the effect of the drug wouldn’t be evident until a later timepoint. Then the choice of the timepoint would have been non-trivial and subject to variability.

Based on the above tumours are initially assigned a classification. Since the parameter estimation is run 100 times that classification is subject to variation. As a result, to derive the final classification a consensus is used of the classification in all 100 runs, i.e. the most popular classification is the final. Similarly, the classification in the level of the PDX is derived. Having acquired the final classification of the mice (replicates) for a particular PDX we assign to it a classification based on the most common classification of the mice that comprise it.

Mathematical model assumptions, nonlinear mixed effects formulation and parameter values

• While the tumour growths are different and there is evidence to suggest that the growth rate of the sensitive is faster than the resistant in this paper we will assume they are the same due to potential identifiability issues.

• There can potentially be a number of sources of resistance to treatment, which include intrinsic, acquired as well as drug-induced resistance. Because we have only pre-treatment transcriptomic data there is no meaningful way to associate any markers with acquired resistance, which would require access to measurements of mRNA expression throughout the duration of the treatment. Due to that fact it was decided to keep the model as simple as possible by only considering an intrinsic resistance parameter which could be associated with the mRNA data to derive potential markers of resistance.

• No random effect was associated with the treatment fixed effect parameter $D$. That was done, without loss of generality, in order to enhance the idea that any variation in the mean response to the treatment stems from the resistance parameter. Further test including a random effect for the treatment parameter showed no significant differences.

• An essential assumption for the stability of the parameter estimation was the restriction of the treatment effect to be always larger than the growth rate (both fixed and random effect included). Failure to satisfy that condition led to the estimation of the parameters varying widely between the multiple runs and being very sensitive to initial estimates. That was undesirable as in order to identify the biomarkers we want the parameter quantification to be as stable and accurate as possible. To enforce the restriction we assume the treatment is always proportional to the growth following the formula $K(1+{\mathit{THETA}}_D)$ where ${\mathit{THETA}}_D$ is the fixed effect of the treatment. Similar formulas can be used such as the additive $K+{\mathit{THETA}}_D$ which yield similar results.

• The resistance fraction $f_R$ was fitted as a logistic function to restrict it between zero and 1. For that reason an exact zero value is almost never attained. That makes it necessary to introduce a cut-off value below which we assume that the resistance fraction is practically zero.

• Olaparib requires a few cell cycles before it’s full effect can take place. That leads to a delay in the full effect which cause the tumour to initially grow before regression can occur in the mice that do respond to the drug. While a delay can be included in the mathematical model it causes identifiability issues with the treatment effect leading to very prolonged delay periods and unrealistically high treatment effects. The only remedy is a precise and realistic range restriction on the values the delay can take which won’t allow the treatment effect to assume very large values. Since there are no references as to what this range might the delay was not included. The model can get around that initial delay by varying the initial tumour volume. A higher tumour volume smooths out that behaviour in the simulated curves and allows the model to be fitted to a much better degree in the cases where the delay is observed. Of course that leads to a higher initial tumour volumes for these particular mice by we believe without loss of generality and correct characterization of the curves.

• Continuous dose instead of intervals.

• To account for both doses fitted together an additional parameter was added on top of the parameter for the 50 mg/kg dose. The sign of the effect was left unrestricted to access whether the fitting process will naturally show that the 100 mg/kg dose is more efficacious:

$$D_{olap}=K\left(1+e^{\left({THETA}_{50}+{THETA}_{extra}\left(DOSE-50\right)/50\right)}\right)$$

The diagnostic plots found in the Supplementary Figs. 1–4 demonstrate a good fitting of the model to the data. The residual errors are centred around zero with no visible deviation from normality and the individual predictions (IPRED) demonstrate a very close fit to the raw data. The final fitted parameter values and errors are in Supplementary Table 1. These represent the values from the best out of the 100 runs of the method.

It is worth mentioning that the 100 iterations revealed minimal differences between them with regards to the resistance fraction of each individual tumour. Supplementary Fig. 5 demonstrates the variability per individual tumour for the 100 runs. The same behaviour is observed in all PDXs and both doses but only specific PDXs are shown for clarity reasons. mRECIST criteria are included at the top of each boxplot for comparison.

Combination model

The model used to fit the adavosertib monotherapy and combination data is based on (1) and (2) we the addition of two extra compartments to account for resistance to either and both treatments. The model is as follows:

$$\frac{dS1\left(t\right)}{dt}=\left(K-D_{\mathrm{olap}}-D_{\mathrm{Adav}}\right)\left(1-f_R^1\left(t\right)\right){\left({1-f}_R^2\left(t\right)\right)V\left(t\right)}^{\frac{2}{3}},S1\left(0\right)=V\left(0\right)\left(1-f_R^1\left(0\right)\right)\left(1-f_R^2\left(0\right)\right)$$

$$\frac{dS2\left(t\right)}{dt}=\left(K-D_{\mathrm{olap}}\right)\left(1-f_R^1\left(t\right)\right){f_R^2\left(t\right)V\left(t\right)}^{\frac{2}{3}},S2\left(0\right)=V\left(0\right)\left(1-f_R^1\left(0\right)\right)f_R^2\left(0\right)$$

$$\frac{dS3\left(t\right)}{dt}=\left(K-D_{\mathrm{Adav}}\right)f_R^1\left(t\right){\left({1-f}_R^2\left(t\right)\right)V\left(t\right)}^{\frac{2}{3}},S3\left(0\right)=V\left(0\right)f_R^1\left(0\right)\left(1-f_R^2\left(0\right)\right)$$

$$\frac{dR\left(t\right)}{dt}=K{f}_R^1\left(t\right)f_R^2\left(t\right){V\left(t\right)}^{2/3}.R\left(0\right)=V\left(0\right)f_R^1\left(0\right)f_R^2\left(0\right)$$

Where $S1-S3$ are the sensitive tumour volumes to both, Olaparib only and adavosertib only respectively, $R$ is the resistance tumour volume to both. $f_R^1,f_R^2$ are the resistance fractions of the tumour at time $t$ given for Olaparib and adavosertib, respectively. Finally, $D_{\mathit{olap}},D_{\mathit{Adav}}$ are the treatment effect of Olaparib and adavosertib.

Modified mouse RECIST

Given that the PDX data utilised in this study was obtained from Serra et al. ²³, we followed the criteria defined in that study. In order to capture the response of the subcutaneous implants, a modified Response Evaluation Criteria in Solid Tumours (RECIST) criteria was used which was based on the % tumour volume change: complete response (CR), best response ← 95%; partial response (PR), best response ← 30%; stable disease (SD), −30% < best response < +20%; progressive disease (PD), best response > +20%.

Transcriptomic features

Having fitted the data, various measures of response and resistance can be used in order to identify biomarkers of resistance to olaparib. A typical approach would be to use the classification of the PDXs to separate them into responders (complete responders, initial responders) and non-responders and then perform a differential gene expression using the pre-treatment mRNA expression to see what genes are deferentially expressed between the two groups⁵⁰. While this can be accomplished using both the mRECIST criteria and the classification of our model we believe that the most informative way is to use the continuous description of resistance (resistance fraction) that has been acquired. That offers the identification of genes that potentially show a more rigorous correlation throughout the range of the resistance/response spectrum in contrast to the dichotomy of a classification. To that end a linear correlation (Pearson’s correlation) was performed between the resistance fraction, in the PDX level (median of the resistance fractions of the individual tumours originating from that PDX, 27 unique PDXs for olaparib 100 mg/kg), and the pre-treatment processed mRNA expression values (see “Methods”—Processed mRNA data) of certain genes. The correlation was performed for the resistance fraction estimated in the olaparib 100 mg/kg dosing group. In order to decrease the number of genes we are exploring we primarily focused on a list of genes called CIViC (clinical interpretation of variants in cancer) which is comprised of 440 genes (at the time of investigation) that have been identified by manual curation to be clinically relevant to cancer⁵¹ (see Supplementary Table 6).

A threshold needs to be established that separate significant and non-significant correlations. A p-value less than or equal to 0.05 was used for that purpose. Due to the p-value and the correlation strength being related to each other in the case of simple linear correlations we did not use the latter as a threshold. The full list of correlation values for the CIViC genes can be found in the Supplementary Table 7.

Finally, we have implemented a train-test split across our dataset to map consistency of identified markers as a way of validation. We divided the 27 PDX models into 2/3:1/3 train:test split iterated over 100-fold (small ‘n’ required a large number of folds to identify any signal with identifying consistent markers) (Suppl. Fig. 22).

Pathway enrichment analysis and cross-talk

We used MetaCore (Source: Clarivate) to perform enrichment analysis. Genes were matched to possible targets in functional ontologies of MetaCore. The probability of a random intersection between a set of IDs the size of target list with ontology entities is estimated in p-value of hypergeometric intersection. The lower p-value means higher relevance of the entity to the dataset. Canonical pathway maps represent a set of signalling and metabolic maps for human. All maps are created by expert PhD scientists from Clarivate Analytics relying on published peer-reviewed literature.

To adjust enrichment results we additionally performed crosstalk analysis. The network of the top 10 ontology terms from pathway enrichment analysis. Nodes represent top terms and edges represent significant similarities (as measured by hypergeometric test) between these entities. The edge thickness depends on the size of intersection between two ontology terms while the colour of the node corresponds to the enrichment z-score.

Survival analysis

After identifying key genes, Kaplan–Meier survival analysis was performed on treated and control data stratified by HIGH (≧mean expression value) and LOW (<mean expression value) expression for each of the genes. For this analysis, individual tumour survival endpoints were utilised as opposed to a PDX-level given the potential uncertainty that could be introduced by aggregating survival endpoints at the PDX-level. Markers were then separated into four categories depending on which groups they demonstrated a differential survival for. The stratified survival curves were compared using the hazard ratio (HR) using the Cox proportional-hazard model. Analysis was performed in R using survival 3.6–4 package^52,53.

Processed mRNA data

The available RNAseq data are TPM (Transcripts Per Kilobase Million) normalised. The data originate from two different batches marked as “old” and “new”. Supplementary Fig. 12 demonstrates through a UMAP a separation of the expression profiles between samples which is highly correlated to the batch. This is also seen in the expression distribution plot in Supplementary Fig. 13a. To correct for that ComBat batch correction was applied to the LOG(x + 1) transformed data smoothing the differences between the clusters as seen in Supplementary Fig. 13b.

Inclusion and ethics statement

This study was performed by a team of collaborative scientists with a diverse background across gender, nationalities, scientific and technical capabilities etc. All in vivo data analysed as part of this study were published previously (Serra et al., Clin Cancer Res. (2022) 28 (20): 4536–4550 and aligned with established ethical protocols. All animal procedures were approved by the Ethics Committee of Animal Research of the Vall d’Hebron Institute of Oncology and by the Catalan Government and were conformed to the principles of the WMA Declaration of Helsinki, the Department of Health and Human Services Belmont Report, and following the European Union’s animal care directive (2010/63/EU).

Author contributions

D. Voulgarelis: Conceptualisation, data curation, software, formal analysis, investigation, visualisation, writing—original draft, writing—review and editing. J.V. Forment: Conceptualisation, data provision, formal analysis, investigation, writing—original draft, writing—review and editing. A. Herencia Ropero: Data provision, formal analysis, investigation, writing—original draft, writing—review and editing. D. Polychronopoulos: Formal analysis, investigation, writing—original draft, writing—review and editing. J. Cohen-Setton: Formal analysis, investigation, writing—review and editing. A. Bender: Supervision. V. Serra: Data provision, supervision. M.J. O’Connor: Conceptualisation, supervision, writing–original draft, writing—review and editing. J.W.T. Yates: Conceptualisation, resources, supervision, funding acquisition, visualisation, writing–original draft, project administration, writing—review and editing. K.C. Bulusu: Conceptualisation, resources, supervision, funding acquisition, visualisation, writing—original draft, project administration, writing—review and editing.

Data availability

PDX tumour volume data is included in the GitHub repository. Baseline transcriptomics data are available upon request from our academic collaborators at Vall d’Hebron Institute of Oncology (VHIO) who are also authors on this paper. Combination pharmacology data used in this study has been included in another study from these authors (Serra et al., Clin Cancer Res (2022) 28 (20): 4536–4550).

Single agent timeseries data have been published in “Cruz C, Castroviejo-Bermejo M, Gutiérrez-Enríquez S, Llop-Guevara A, Ibrahim YH, Gris-Oliver A, Bonache S, Morancho B, Bruna A, Rueda OM, Lai Z. RAD51 foci as a functional biomarker of homologous recombination repair and PARP inhibitor resistance in germline BRCA-mutated breast cancer. Annals of Oncology (2018)”.

All other data used and results generated are included in the submission as supplementary data.

Code Availability

All code (NONMEM model, jupyter notebook for ML models) is included in GitHub repository.

Competing interests

D.V., J.V.F., M.J.O, J.C.-S. and K.C.B. are full-time employees and shareholders of AstraZeneca. D.V. was a PostDoc fellow of the AstraZeneca PostDoc programme. D.P., J.W.T.Y. and A.B. were employees of AstraZeneca and J.W.T.Y. is an AZ shareholder. The remaining authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41698-024-00702-x.