ABSTRACT
With the increasing availability of large‐scale multimodal neuroimaging datasets, it is necessary to develop data fusion methods which can extract cross‐modal features. A general framework, multidataset independent subspace analysis (MISA), has been developed to encompass multiple blind source separation approaches and identify linked cross‐modal sources in multiple datasets. In this work, we utilized the multimodal independent vector analysis (MMIVA) model in MISA to directly identify meaningful linked features across three neuroimaging modalities—structural magnetic resonance imaging (MRI), resting state functional MRI and diffusion MRI—in two large independent datasets, one comprising of control subjects and the other including patients with schizophrenia. Results show several linked subject profiles (sources) that capture age‐associated decline, schizophrenia‐related biomarkers, sex effects, and cognitive performance. For sources associated with age, both shared and modality‐specific brain‐age deltas were evaluated for association with non‐imaging variables. In addition, each set of linked sources reveals a corresponding set of cross‐modal spatial patterns that can be studied jointly. We demonstrate that the MMIVA fusion model can identify linked sources across multiple modalities, and that at least one set of linked, age‐related sources replicates across two independent and separately analyzed datasets. The same set also presented age‐adjusted group differences, with schizophrenia patients indicating lower multimodal source levels. Linked sets associated with sex and cognition are also reported for the UK Biobank dataset.
Keywords: biomarker, fusion, independent vector analysis, multimodal, schizophrenia
MMIVA fusion of GM, mALFF, and FA features by treating each modality as one of M datasets in an IVA model and without requiring linked expression levels to be identical for all modalities. Such flexibility permits even strongly linked sources to capture modality‐specific variability, as supported by the data.
Summary.
Multimodal data fusion based on independent vector analysis (MMIVA) detects linked multimodal subject expression levels (here, the sources) which do not have to be identical for all modalities, so that even strongly linked sources may also capture unique modality‐specific variability.
MMIVA learns separate loading/mixing parameters for each modality and for each source, so the detected links may better reflect what the data supports.
Multimodal, multi‐mode brain‐age delta analysis of discovered age‐associated sets of subject expression levels from MMIVA enables investigations about aging in terms of both shared and unique (per modality) contributions in the UK Biobank study.
In a schizophrenia dataset, the multimodal spatial maps from one age‐related linked set largely replicated one of the key age‐related sets from the UK Biobank dataset. The same set also presented age‐adjusted group differences, with schizophrenia patients indicating lower multimodal source levels.
1. Introduction
Multimodal neuroimaging data can provide rich information to better understand brain structures and functions, and boost biomarker detection (Uludag and Roebroeck 2014). Although analysis of each data modality separately can yield important insights into the structural or functional integrity of the brain, the relationship between different views from multimodal neuroimaging data is often complex and unknown. Data‐driven approaches are ideal for such cases, leveraging naturally occurring associations across modalities to discover structure–function relationships, which may not occur in the same regions and may covary among subjects in complex ways. As more research institutions participate in open science data sharing practices, large‐scale neuroimaging datasets ( 1000 subjects) with multimodal data are becoming widely available, giving researchers opportunities to develop novel approaches to multimodal fusion analysis that can offer insights into cross‐modal (joint) associations and identify important missing links in brain development and mental disorders (Calhoun and Sui 2016).
Blind source separation (BSS) techniques, in particular independent component analysis (ICA) (Comon 1994; Bell and Sejnowski 1995), have gained popularity in neuroimaging analysis because they make minimal assumptions about the latent sources, are readily available, and yield interpretable results. However, ICA is only suitable for single modality data. Several other methods have been developed to extract multimodal features, including canonical correlation analysis (Hotelling 1936), extensions of ICA such as joint ICA (Calhoun et al. 2006) and parallel ICA (Liu, Demirci, and Calhoun 2008), as well as independent vector analysis (IVA) (Adalı, Anderson, and Fu 2014; Kim, Eltoft, and Lee 2006), which generalizes ICA to multiple datasets. Recently, we proposed a data‐driven blind source separation model called multidataset independent subspace analysis (MISA) (Silva et al. 2021) that generalizes many basic BSS techniques, such as ICA and IVA, to recover subspaces (i.e., a collection of linked latent sources) within and across multiple datasets simultaneously. MISA utilizes the Kotz distribution (Kotz 1974) to model source distributions, thus leveraging all‐order statistics (second‐ and higher‐order) to model the underlying latent subspaces. Another advantage of MISA is that it allows comparison across many different types of BSS because they are special cases of the general model it implements. In this work, we use MISA to implement the multimodal IVA (MMIVA) model described in Section 2.4 and demonstrate its utility on two large neuroimaging datasets: one including typical older adults from the UK Biobank enhanced imaging study, and the other including pooled data from multiple studies/sites that investigate psychosis and age‐matched controls.
We evaluated MMIVA on standard derivative data from three neuroimaging modalities: (1) gray matter tissue probability segmentation (GM) maps from structural MRI (sMRI) data, which markedly convey regional variations in gray matter concentration with age, sex and other neurobiological factors, (2) amplitude of low frequency fluctuations (ALFF) maps computed from resting state functional MRI (rs‐fMRI) scans, which inform about the strength of local connectivity as well as potential for long‐range associations, and (3) fractional anisotropy (FA) maps obtained from diffusion MRI (dMRI) scans, which characterize the degree of directional water diffusion in white matter bundles. In the two independent datasets we considered, the results show several cross‐modal associations are present. Moreover, we observed covariation of these linked sources with factors such as age, sex, and cognition, as well as group label (patients with psychosis vs. control subjects).
In the following, Section 2 describes the data, preprocessing, and methodology utilized in this work. Section 3 presents our results, which are further discussed in Section 4 before presenting our final conclusions.
2. Methods
2.1. Imaging Data
We used two large independent multisite datasets to evaluate the MMIVA model. For the first dataset, we utilized imaging data from a subset of 3497 subjects participating in the UK Biobank study (Miller et al. 2016), a prospective epidemiological study with a large imaging database. Specifically, we utilized multivariate features (Calhoun and Adali 2008) extracted from each subject and each data modality. All data included in our analysis were collected in two of the participating locations in the United Kingdom. 1
The second dataset includes pooled data of 999 subjects from four studies that collected imaging data from patients with schizophrenia, schizo‐affective disorder, bipolar disorder and age‐matched healthy controls. These studies are Center of Biomedical Research Excellence in brain function and mental illness (COBRE 2 ) (Aine et al. 2017), function biomedical informatics network (fBIRN 3 ) (Keator et al. 2016), Maryland Psychiatric Research Center (MPRC 4 ), and Bipolar and Schizophrenia Network for Intermediate Phenotypes (BSNIP 4 ) (Tamminga et al. 2014). The demographics information is summarized in Table 1.
TABLE 1.
Dataset demographics information.
| Dataset | Site |
|
|
|
|
|
Mean age (SD) (years) | Age range (years) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| UK Biobank dataset | |||||||||||||
| UKB | 1 | 2379 | 1201 | 1178 | 2379 | N/A | 63.1 (7.2) | 48–79 | |||||
| UKB | 2 | 528 | 251 | 277 | 528 | N/A | 61.8 (7.3) | 46–79 | |||||
| Patient datasets | |||||||||||||
| COBRE | 1 | 160 | 123 | 37 | 85 | 75 | 37.79 (12.8) | 18–65 | |||||
| MPRC | 1 | 60 | 44 | 16 | 26 | 34 | 38.67 (13.2) | 16–62 | |||||
| MPRC | 2 | 106 | 43 | 63 | 62 | 44 | 40.28 (13.1) | 16–64 | |||||
| MPRC | 3 | 1 | 1 | 0 | 0 | 1 | 55.00 (0.0) | 55–55 | |||||
| BSNIP | 1 | 237 | 133 | 104 | 137 | 100 | 37.62 (14.7) | 16–65 | |||||
| BSNIP | 2 | 192 | 103 | 89 | 99 | 93 | 40.13 (13.2) | 15–65 | |||||
| FBIRN | 1 | 24 | 19 | 5 | 16 | 8 | 36.00 (9.9) | 22–51 | |||||
| FBIRN | 2 | 17 | 14 | 3 | 8 | 9 | 40.88 (9.9) | 23–57 | |||||
| FBIRN | 3 | 53 | 41 | 12 | 27 | 26 | 42.81 (12.5) | 19–60 | |||||
| FBIRN | 4 | 54 | 44 | 10 | 27 | 27 | 36.04 (11.4) | 20–58 | |||||
| FBIRN | 5 | 16 | 9 | 7 | 7 | 9 | 38.62 (9.4) | 22–53 | |||||
| FBIRN | 6 | 44 | 21 | 23 | 24 | 20 | 34.93 (10.6) | 19–58 | |||||
| FBIRN | 7 | 35 | 30 | 5 | 20 | 15 | 37.91 (10.2) | 18–60 | |||||
Note: Demographics in the UK Biobank dataset and the patient datasets are shown in the table.
Abbreviations: , number of controls; , number of female subjects; , number of male subjects; , number of patients.
All participants provided informed consent from their respective institutional review boards.
The image acquisition parameters for each study and modality are available as Section S1.1.
2.2. Subject Measures Data
UK Biobank provides extensive phenotype information for each subject, including age, sex, lifestyle measures, cognitive scores, and so forth. We used a subset of the subject measures (SM) reported in (Miller et al. 2016) to identify associations between the subject demographics and the multivariate source component vectors (SCVs) obtained from MMIVA. Following the approach in Smith et al. (2015), we dropped subjects with more than 4% missing data. This resulted in (out of 3497) subject scores for MANCOVA analysis (see Section 2.6). Of 64 SMs, we dropped 10 measures which had extreme values. Extreme values are identified in two steps. First, the sum of squared absolute median deviations (ssqamdn) for each SM is computed. Second, if there is any SM with max(ssqamdn) > 100 × mean(ssqamdn), then that SM has subjects with extreme outliers which can influence statistical analysis and, thus, that SM is dropped. This resulted in 54 phenotypes including age, sex, fluid intelligence, a set of measures covering amount and duration of physical activity, frequency of alcohol intake, cognitive test scores, time spent watching TV, and sleep duration (see Table S2 for details). For the measures that were retained, any missing values were imputed utilizing the K‐Nearest Neighborhood method implemented in MATLAB's knnimpute() (Cunningham and Delany 2021).
The SMs in the patient dataset include only age, sex, and diagnosis information.
2.3. Preprocessing
We processed each of the three imaging data modalities to obtain GM, ALFF, and FA feature maps, which were then used for multimodal fusion analysis. Preprocessing details are available as Section S1.3. In summary, all modalities were Gaussian smoothed (with filter FWHM = 10 mm (GM), 6 mm (mALFF), 6 mm (FA)) and resampled to 3 3 3 mm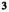 resolution. The same masks defined for UK Biobank were used in the patient datasets.
resolution. The same masks defined for UK Biobank were used in the patient datasets.
Prior to running our fusion model, we verified that none of the included voxels contained invalid values, such as NaN or Inf. For each modality, we also performed variance normalization of the subject‐specific spatial maps (mean removed, then divided by standard deviation), followed by mean removal per voxel (across subjects). Finally, site effects were regressed out voxelwise from the datasets (separately for UK Biobank analysis, and for patient dataset analysis) to account for mean differences in spatial maps due to scanner effects as follows:
| (1) |
where is the data matrix from each modality, , with being a column vector of ones and being one‐hot encoded vectors containing the site labels. Other heterogeneities, such as age and sex, were not accounted for until after MMIVA, at which point we assessed their effect by means of an age‐delta analysis and effect size measures.
2.4. Multimodal IVA (MMIVA) Fusion Model
Here we present a general IVA approach for direct analysis of heterogeneous multimodal data. We assume that the underlying feature expression levels across subjects will contain patterns that are, to an extent, similar across modalities. This assumption is not unlike the underlying assumption of shared expression levels in popular joint ICA methods (Calhoun et al. 2006; Groves et al. 2011), but by assuming only similarity, we remove a strong limitation, allowing for differences in the subject expression levels of each modality to occur, which is more realistic and flexible. Furthermore, independent vector analysis is a natural extension of independent component analysis. While ICA operates on a single dataset to obtain statistically independent source signals via estimation of one linear unmixing matrix, IVA performs joint estimation of many unmixing matrices simultaneously across multiple datasets (Kim, Eltoft, and Lee 2006; Anderson et al. 2014).
2.4.1. Review of ICA and IVA
Briefly, ICA is a blind source separation model that assumes linear mixing of statistically independent sources , yielding the observed data :
| (2) |
where is the invertible mixing matrix, and is the number of observations (here, the number of subjects). The ICA algorithm seeks to identify the sources by estimating an unmixing matrix , according to certain properties of the sources such as higher‐order statistics and non‐Gaussianity. Another typical strategy for solving the ICA problem involves minimizing the mutual information among the sources:
| (3) |
where is the differential entropy of the ‐th source, given by .
IVA extends the ICA model to multiple () datasets, assuming a linear mixture of independent sources for each dataset:
| (4) |
and, additionally, taking into account the statistical dependence (i.e., linkage) among corresponding sources, that is, those with same index . Each ‐th collection of linked sources is called a source component vector (SCV) and defined as . Here, , such that each SCV spans across the three modalities.
Solving the IVA problem involves minimizing the following mutual information loss function:
| (5) |
where , and the terms in the big parentheses correspond to the joint entropy of the ‐th SCV, . The joint entropy not only captures unique information from each modality (in the sum portion) but also the shared information across modalities (i.e., the mutual information). Thus, minimizing the joint entropy entails learning the mutual information linkage as well. This shows that IVA will seek independence among SCVs while capturing multimodal dependence within SCVs; the mutual information indicates dependence among sources in the ‐th SCV (Adalı, Anderson, and Fu 2014). In this article, the terms SCV and subspace are used interchangeably to describe a collection of linked (or dependent) multimodal sources.
2.4.2. Implementing MMIVA
Since both ICA and IVA are unified under the more general MISA, we take advantage our flexible MISA implementation (Silva et al. 2021) to estimate the multimodal IVA fusion model described above, leveraging both second‐ and higher‐order statistics. This implementation enables direct data fusion even when is a tall matrix and has a different number of rows (the modality's intrinsic dimensionality) in each modality (Silva et al. 2014a). The utility of this “transposed IVA” approach was also demonstrated in the sample‐poor (low ) regime using only second‐order statistics (Adali, Levin‐Schwartz, and Calhoun 2015a, 2015b). A broader discussion with comparisons to other BSS approaches in data fusion is also available (Silva and Plis 2019).
As depicted in Figure 1, we performed MMIVA fusion of the GM, mALFF, and FA features by treating each modality as one of the datasets in the IVA model described above. Following initialization of the unmixing weights, MMIVA was then estimated directly from the full data by configuring and running MISA as an IVA model, yielding our final joint decompositions . Spatial maps were then estimated using least squares as , where is the source matrix from each modality.
FIGURE 1.
Multimodal IVA (MMIVA) fusion. First, we opted for cross‐modality co‐registration and masking to select the features used in this 3‐way fusion analysis. Second, we pursued a multimodal group PCA (MGPCA) preprocessing strategy that accounts for the total variance of each modality, ensuring they contribute equally to the estimation of common directions. Third, the proposed MGPCA+ICA initialization of the unmixing weights serves to “pre‐align” the latent subspaces. Nevertheless, learning of the final unmixing is still done with the full 30‐by‐voxels matrices, that is, MMIVA leverages the full dimensionality of the spatial features (no data reduction), allowing for full interaction between modalities. Fourth, the choice of Kotz parameters (, , ) is such that it addresses potential limitations of the zero‐mean Laplace distribution typically employed in IVA literature, namely that its derivative at 0 is not well‐defined (discontinuous), thus eliminating certain risks for numerical instability. Fifth, unlike typical IVA methods, the choice of Kotz distribution is sensitive to all‐order statistics, not just second‐order (also known as linear dependence). Sixth, sources are expression levels, meaning that the patterns in the expression levels over subjects (not the spatial maps) are statistically independent of one another and linked across modalities. This is a sensible choice because it treats subjects as the observations, which is atypical of blind source separation in neuroimaging due to the often low sample sizes (i.e., sample‐poor regimes, low ). Finally, MMIVA is the first mature application of MISA on real multimodal datasets (although a preliminary version that did not account for site effects and did not include the study on patients appeared at the IEEE EMBC 2021 conference (Damaraju et al. 2021)).
As discussed earlier, MMIVA accounts for dependence (as subject covariation) among corresponding sources across modalities. For both MISA and MMIVA models, the SCV distributions are assumed to take a multivariate Kotz distribution (Nadarajah 2003; Kotz 1974):
| (6) |
where is the SCV dimensionality, controls the shape of the distribution, controls the kurtosis, and controls the hole size, while and are defined for brevity. denotes the gamma function. The positive definite dispersion matrix is related to the SCV covariance matrix by . The multivariate Kotz distribution has been shown to generalize well across multivariate Gaussian, multivariate Laplace, and multivariate power exponential distributions (Anderson et al. 2013). For MMIVA, the Kotz parameters were set to , , to produce a distribution shape slightly less peaked than a Laplace distribution and yield (the standard deviation of the successful Logistic distribution in Infomax). Note that increasing flattens the distribution peak and might be appropriate for sub‐Gaussian source estimation. Also, makes the distribution more peaked, while induces a “doughnut” shape. Here, we opted for a more conservative choice, deferring further experimentation to future work.
A common heuristic was used to select the model order (i.e., the number of sources ): identify a range of stable model order values and select a number in or slightly above that range. This practice tends to enhance the spatial distinctiveness of the results, often producing smaller networks/patterns that can be combined to approximate lower model order solutions, suggesting that not much is lost by choosing a higher model order (Rachakonda, Du, and Calhoun 2017). The stable range of Akaike's information criterion (AIC) based on the singular values of MGPCA was found between 27 and 34 sources, and we opted for a round number in that range, specifically = 30.
2.4.3. MGPCA + ICA Initialization
In order to initialize and “pre‐align” the SCVs, the multimodal data matrices were reduced to 30 principal directions using multimodal group principal component analysis (MGPCA). Unlike standard PCA that finds orthogonal directions of maximal variation for each modality separately, MGPCA finds directions of maximal common variation, that is, eigenvectors are computed based on the average of the scaled covariance matrices:
| (7) |
where , is the expectation operator, and indicates the Frobenius norm. The scaling factor we used is , which is the ratio of the variance in the modality to the number of observations (subjects), to ensure that each modality contributes equally to the common covariance structure. Letting and be the top 30 eigenvalues (with largest absolute value) and eigenvectors of , respectively, we define the reduced joint dataset and corresponding whitening matrices as follows:
| (8) |
| (9) |
| (10) |
where , and . Following, the MGPCA‐reduced data underwent an ICA estimation using the Infomax objective (Bell and Sejnowski 1995) to obtain 30 common independent sources .
We improved upon the Infomax estimate by configuring and running MISA as an ICA model initialized with , but now assuming source distributions to follow a univariate Kotz distribution with parameters , , , thus yielding . The final combined MGPCA + ICA estimate was utilized to initialize the MMIVA model and make sure the initial estimates align with the common space. The MISA methods were implemented using the MISA toolbox (Silva et al. 2021). Analysis code can be found at https://github.com/trendscenter/MMIVA.git.
2.5. Design Considerations
The following summarizes the key design considerations of MMIVA:
We opted for cross‐modality co‐registration and masking to select the features used in this 3‐way fusion analysis.
We pursued a multimodal group PCA (MGPCA) preprocessing strategy that accounts for the total variance of each modality, ensuring they contribute equally to the estimation of common directions.
The proposed MGPCA+ICA initialization of the unmixing weights serves to “pre‐align” the latent subspaces. Nevertheless, learning of the final unmixing is still done with the full 30‐by‐voxels matrices, that is, MMIVA leverages the full dimensionality of the spatial features (no data reduction), allowing for full interaction between modalities.
The choice of Kotz parameters (, , ) is such that it addresses potential limitations of the zero‐mean Laplace distribution typically employed in IVA literature, namely that its derivative at 0 is not well‐defined (discontinuous), thus eliminating certain risks for numerical instability.
Unlike typical IVA methods, the choice of Kotz distribution is sensitive to all‐order statistics, not just second‐order (also known as linear dependence).
Sources are expression levels, meaning that the patterns in the expression levels over subjects (not the spatial maps) are statistically independent of one another and linked across modalities. This is a sensible choice because it treats subjects as the observations, which is atypical of blind source separation in neuroimaging due to the often low sample sizes (i.e., sample‐poor regimes, low ).
2.6. Statistics
2.6.1. Multivariate Tests
We used the MANCOVAN toolbox to identify associations between the subject measures (SM) and the multivariate source component vectors (SCVs) obtained from MMIVA. The MANCOVAN Toolbox evaluates multivariate MANCOVA models and implements multivariate stepwise regression (backward selection mode) to identify associations between SM (predictors) and MMIVA sources (multivariate response) for each modality separately (one MANCOVA model per modality, each with sources/responses). The stepwise regression approach eliminated insignificant SM terms at the level at each step using the multivariate Lawley–Hotelling trace test.
2.6.2. Univariate Tests
Subsequently, univariate tests with the surviving SM terms are reported for each of the 30 sources within each modality. Initial model selection based on multivariate tests significantly reduces the total number of tests performed. The univariate tests were performed and corrected for multiple comparisons at Bonferroni threshold (0.05/30, for 30 sources).
In addition to the SMs, the following nuisance covariates were included prior to stepwise regression:
sMRI: correlation of warped subject GM segmentation map to mean GM segmentation map,
dMRI: correlation of warped subject FA map to mean FA map, and
rs‐fMRI: correlation of warped subject mALFF map to mean mALFF map, and mean framewise displacement (mFD) computed from rigid body movement estimates from resting fMRI scan realignment step.
Any variables with fewer than eight levels were modeled as categorical variables and the rest were modeled as continuous variables. Only age by sex interaction was considered.
2.6.3. Effect Size
Eta‐squared () was used to measure the strength of the relationship between the predictors and the SCVs. is defined as the ratio of variance explained (the sums‐of‐squares, or ) in the dependent variable by a predictor while controlling for other predictors:
In the implementation, we calculated the unbiased estimator of the population's , epsilon‐squared (). The reason we chose epsilon‐squared () is that it has been found to be less biased compared to omega‐squared () (Carroll and Nordholm 1975). Detailed explanation of effect size indices can be found in Albers and Lakens (2018). Both Type II and Type III sum‐of‐squares are used to evaluate effect sizes. In general, we prioritize Type II statistics because Type II is more statistically powerful than Type III when no interactions are present (Langsrud 2003). For those SCVs where an interaction term has significant value (), we replaced Type II by Type III effect sizes. We then identified SCVs with effect sizes (Cohen 1992) for each predictor in each modality. SCVs are selected if the same SM meets this effect size criterion on at least two of the three modalities. The univariate tests are reported alongside effect sizes for completeness, but do not play a role in SCV selection (see Sections S1.8 and S1.9).
2.7. Brain‐Age Delta Modeling on UK Biobank Data
To further evaluate the significant age‐related UK Biobank SCVs identified with MANCOVA, we evaluated the difference between the predicted brain age and the chronological age (the brain‐age delta) in two steps, similar to that described in Smith et al. (2020). In a brain age model, there are two main components: chronological age, which carries a normative essence to it, and deviations. 5 Then, building a model that approximates brain age will partially (since it is an approximation) capture variability from each of the two components. Our interest is then on the physiological effects that explain the deviations from the expected (chronological) age. In that sense, when predicting brain age from imaging features, the interesting portion of the captured variability is associated with the deviations because we want to understand what (non‐imaging) factors associate with these deviations.
With that in mind, we estimated source‐specific brain‐age deltas for each SCV as follows. First, we conducted a partialling step in order to determine each source's unique contribution. To that end, we regressed out all other sources from each source. 6 , 7 Inspection of these partialled sources revealed that partialled sMRI and dMRI features were highly anti‐correlated. Thus, we chose to include only the partialled sMRI feature in this brain‐age analysis (an analysis including partialled dMRI instead of sMRI is included as Section S1.5). We also noticed that, given the high correlation within SCVs, partialling by‐and‐large removed the shared (and the largest) portion of the variability within SCVs. Thus, we evaluated the top singular vector of each SCV to capture the shared information between modalities, based on the singular value decomposition (SVD) of the 3‐column matrix containing all three sources from the same SCV, each normalized to have unit standard deviation. These shared‐SVD features are naturally independent across SCVs because the SCVs from which they were derived are statistically independent from each other to begin with. Since partialled terms have the shared information removed, the shared‐SVD features are also at most only weakly correlated with partiallized terms. We verified that the correlation among the SVD‐shared features and partialled sMRI, fMRI, and dMRI sources is low. Therefore, we selected the SVD‐shared features, partialled sMRI, and partialled fMRI expression levels for the following brain‐age analysis. As mentioned previously, we included an analysis with SVD‐shared features, partialled dMRI, and partialled fMRI expression levels as Section S1.5. In all analyses, we then evaluated the Pearson correlations between subject measures and the final source‐specific 2‐stage brain‐age delta , and between the subject measures and partialled . A step‐by‐step description of the brain‐age delta modeling and estimation is available as Section S1.5.1.
3. Results
Following SCV estimation by the proposed multimodal IVA approach, the MANCOVA procedures revealed significant predictors for each modality, including age, psychosis, sex, and prospective memory to name a few. Then, for each modality, we fit a univariate multiple regression model between each individual source in that modality and all significant predictors in order to measure effect sizes.
For the UK Biobank dataset, after MANCOVA stepwise regression, we fit linear models using the surviving variables as follows:
Nine variables (sex, time spent watching tv, age first had sexual intercourse, time to answer, fluid intelligence, age, physical exercise principal component 1, spatial normalization, interaction between sex and age) to predict each sMRI source.
Eleven variables (alcohol, sex, sleep duration, age first had sexual intercourse, time to answer, fluid intelligence, age, physical exercise principal component 3, spatial normalization, mean framewise displacement, interaction between sex and age) to predict each fMRI source.
Eight variables (sex, time spent watching TV, time to answer, fluid intelligence, mean time to correctly identify matches, age, spatial normalization, interaction between sex and age) to predict each dMRI source.
The instances where Type III effect sizes were reported for the UK Biobank dataset are listed in Section S1.8 (see also Figure S8).
For the patient dataset, we fit linear models using the same seven predictors (age, sex, diagnosis, the interaction between age and sex, the interaction between age and diagnosis, the interaction between sex and diagnosis, the interaction among age, sex and diagnosis) to predict unimodal sources for each of the three modalities. No interaction terms were significant, so only Type II effect sizes are reported (except for dMRI of SCV 5; see Figure S9).
The effect size measure indicated five age‐related SCVs (3, 5, 8, 16, 17), five sex‐related SCVs (9, 10, 16, 17, 22) and one SCV (22) associated with time to answer in the UKB dataset. In the patient dataset, two schizophrenia‐related SCVs (14, 19) and six age‐related SCVs (2, 4, 6, 18, 19, 20) were identified.
Next, we report the cross‐modal Pearson correlations captured within the aforementioned SCVs. These reflect the degree of similarity between patterns of expression level across subjects. Table 2 below summarizes the strength of multimodal pairwise links recovered by MMIVA, indicating high similarity in expression levels between modalities, particularly between fMRI and dMRI. This is indicative of strong multimodal linkages (i.e., for the reported SCVs, the corresponding spatial maps of each modality are expressed at relatively similar levels in each subject). It supports the idea that the same underlying brain process may be driving the expression of the linked multimodal sources in an SCV. This observation also supports the joint interpretation of the corresponding multimodal spatial maps of an SCV.
TABLE 2.
Cross‐modal Pearson correlations within SCVs.
| SCV | sMRI‐fMRI | fMRI‐dMRI | sMRI‐dMRI |
|---|---|---|---|
| SCVs in the UK Biobank dataset | |||
| 3 | 0.720 | 0.840 | 0.667 |
| 5 | 0.639 | 0.764 | 0.613 |
| 8 | 0.643 | 0.920 | 0.634 |
| 9 | 0.692 | 0.873 | 0.663 |
| 10 | 0.740 | 0.700 | 0.703 |
| 16 | 0.773 | 0.908 | 0.746 |
| 17 | 0.728 | 0.785 | 0.693 |
| 22 | 0.642 | 0.539 | 0.692 |
| SCVs in the patient dataset | |||
| 2 | 0.705 | 0.634 | 0.603 |
| 4 | 0.649 | −0.666 | −0.637 |
| 6 | 0.758 | 0.807 | 0.709 |
| 14 | 0.623 | 0.699 | 0.549 |
| 18 | 0.7 | 0.722 | 0.595 |
| 19 | 0.742 | 0.884 | 0.768 |
| 20 | 0.67 | 0.788 | 0.675 |
Note: SCVs are highly similar between modalities, particularly between fMRI and dMRI.
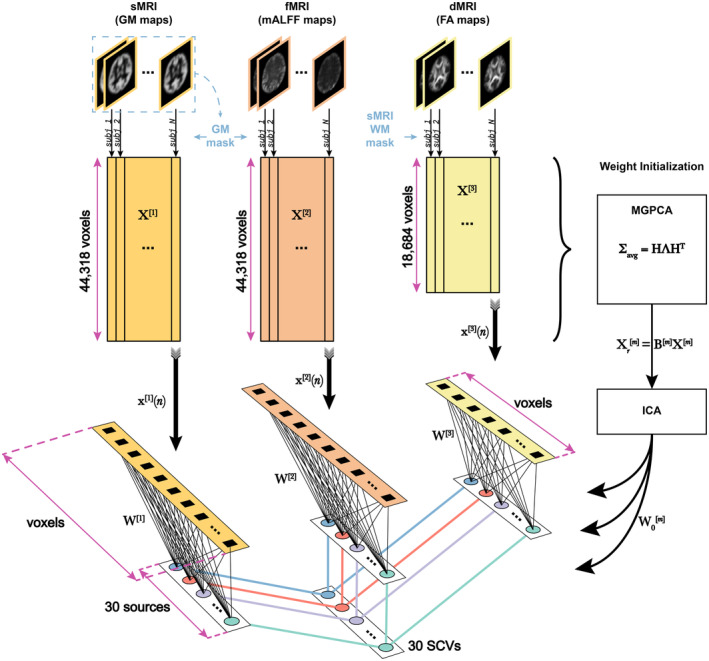
Following, we show Pearson correlations between spatial maps of the two datasets for each modality. In Figure 2, the SCVs from the patient dataset were sorted from highest to lowest spatial correlation in the sMRI modality since that modality showed the largest evidence of cross‐dataset similarities. Notice how the spatial map of the age‐related SCV 8 in the UK Biobank dataset (Figure 3) is highly correlated with the spatial map of the age‐ and schizophrenia‐related SCV 19 in the patient dataset (Figure 6), in both sMRI and dMRI modalities, indicating replication of the multimodal link identified by MMIVA. Detailed descriptions of UK Biobank SCV 8 and patient SCV 19 are presented in Sections 3.1 and 3.2, respectively.
FIGURE 2.
Pearson correlations between the spatial maps of the two datasets for each modality. Absolute values of Pearson correlations between spatial maps from the two datasets were evaluated for each modality. Both datasets were processed separately, with no cross‐contamination. The sMRI correlations showed the largest evidence of cross‐dataset similarities. Thus, SCVs were matched across datasets based on sMRI correlations using the Jonker–Volgenant algorithm (Jonker and Volgenant 2005) for the linear sum assignment problem. The best‐matched sMRI correlations were then sorted in descending order. The resulting optimal permutation of patient SCVs was then applied to the other modalities.
FIGURE 3.
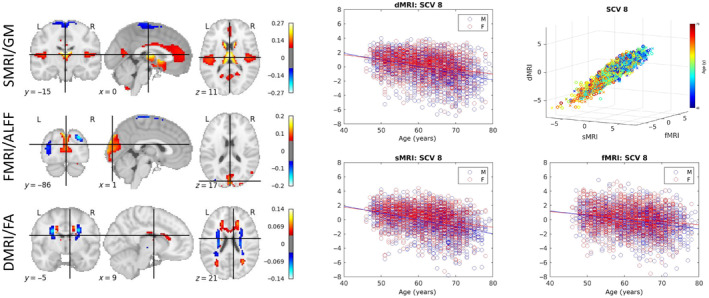
Age‐related SCV. Left: The spatial maps corresponding to the mixing weights for each modality. Right: A 3D scatter plot of SCV 8 illustrates the strong association between multimodal subject expression levels, as well as their relationship to age, for the UK Biobank data. Each point represents a subject, color coded by the age (circles indicate males; crosses indicate females). The same data as in the top right panel is depicted separately for each modality on the other panels, plotted against subject age.
FIGURE 6.
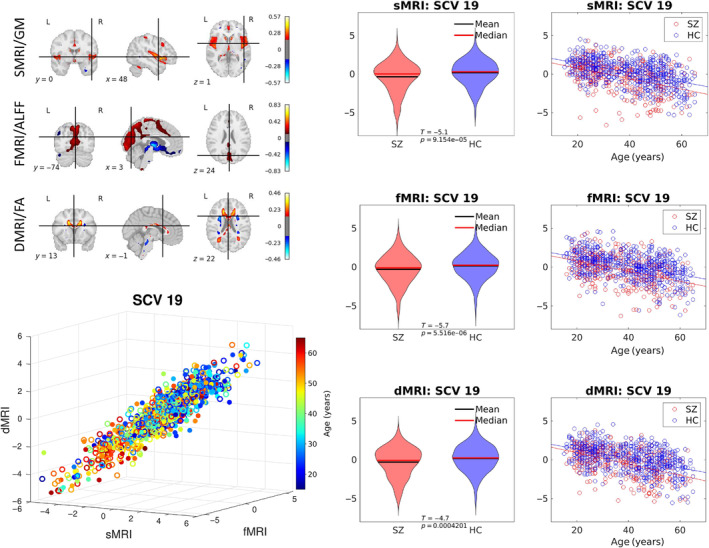
Schizophrenia‐related SCV. Top left: The spatial maps correspond to the mixing weights for each modality. Bottom left: A 3D scatter plot of SCV 19 illustrates the association between the identified multimodal subject expression levels and age for patient data color coded by subject age (circles indicate females; filled circles indicate males). Right: The SCVs are also plotted by control (HC) and schizophrenia patient group (SZ) as violin plots and by age as scatter plots to demonstrate consistent reduction in source intensities in SZ patients across all ages.
3.1. Associations With Aging in UK Biobank
Five SCVs (3, 5, 8, 16, and 17) showed age effects consistently for all three modalities for the UK Biobank data. The sources from all SCVs with age effects had their sign oriented in the direction of decline with age. The 3D scatter‐plot of linked subject expression profiles (sources) in SCV 8, which is the SCV carrying the most significant age association, is presented in Figure 3. Consistent with Table 2, a strong linear association can be observed between modalities. The corresponding mixing weights (spatial maps) are also presented and depict in hot colors the regions expressing larger values at younger age (likewise, expressing lower values at older age) for each of the three modalities. In sMRI (gray matter), age‐associated reductions were observed in the dorsal and ventral caudate, nucleus accumbens, rostral and caudal temporal thalamus, caudal hippocampus, ventro‐ and dorso‐medial parieto‐occipital sulci, several areas of the anterior and posterior cingulate gyrus, and several areas by the sylvian fissure (mainly in the superior temporal and dorsal insular gyri), with age‐related increases in sensorimotor areas, visuomotor area 7, lateral occipital gyrus, as well as the inferior frontal junction and parts of the nucleus accumbens and putamen. Similar levels of subject‐specific age‐associated reductions were observed in fMRI (ALFF), in areas such as the dorsal prefrontal cortex, Broca's area, the caudal angular and supramarginal gyri, the extreme part of inferior temporal gyrus adjacent to the fusiform gyrus, and portions of the visual cortex including the cuneus, the ventro‐medial part of the parieto‐occipital sulcus, and the superior part of the occipital polar cortex, with age‐related increases in sensorimotor, thalamus, and parietal/occipital areas including the angular gyrus, visuomotor area 7, the lateral superior occipital gyrus, the middle occipital gyrus, and the inferior part of the occipital polar cortex. In dMRI (FA), analogous subject‐specific age‐related reductions occurred in the anterior portion of the corpus callosum, forceps minor, superior longitudinal fasciculus II, the anterior thalamic radiation, and the optic radiation, with age‐related increases in the corticospinal tract, superior thalamic radiation, caudal parts of the arcuate fasciculus, and the middle longitudinal fasciculus. The remaining age‐associated sources are shown in Figure S1.
The subject expression level sources from the SVD‐shared information, sMRI and fMRI modalities in these five SCVs (15 sources in total) were subsequently used to predict the brain age (using chronological age as a surrogate) and estimate the brain‐age delta. The mean absolute error of the overall brain‐age delta estimation is 2.70 years when using the SVD‐shared information from each SCV, plus the sMRI and fMRI sources (partialled over all 15 sources) in one model. The mean absolute errors are 2.58, 0.41 and 0.61 years for models including only SVD‐shared, partialled sMRI‐only, partialled fMRI‐only, respectively. Figure 4 (from top to bottom) shows (1) the predicted expression levels of each source as a function of a cubic age model (i.e., with linear, quadratic, and cubic age terms); (2) the correlation between age and the expression levels of SVD‐shared features, sMRI and fMRI sources (and their partialled versions), as well as the regression coefficient and regression significance at the first stage; (3) the standard deviation of the estimated brain‐age delta (and its partialled version) at the second stage, its mean absolute error, and the standard deviation of predicted age at the first stage. Ten out of the fifteen features have a coefficient with significant age dependence ( < 0.05/15, Bonferroni correction). The bottom panel indicates that the SVD‐shared features explain the largest amount of the age variance, with smaller but significant unique contributions from sMRI (SCVs 8, 16, 3, 17) and fMRI (SCV 5). In the same panel, the close agreement between standard deviations from predicted age and second stage brain‐age delta suggests that the patterns extracted from the imaging data are largely descriptive of brain age, rather than chronological age.
FIGURE 4.
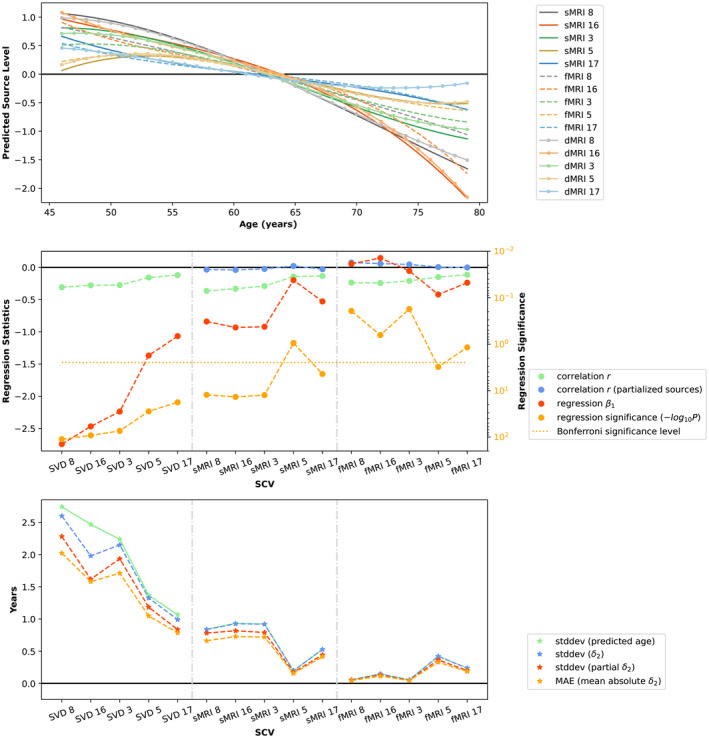
Brain‐age delta modeling. Top: Predicted source levels as a function of chronological age using a cubic model. Middle: Regression statistics at Stage 1 of brain‐age delta modeling (see Equation 11 in Supporting Information). Bottom: Standard deviation of predicted age, standard deviation of Stage 2 brain‐age delta (see Equation 12 in Supporting Information) and its partialled version, and mean absolute error in Stage 2 brain‐age model. SCVs are sorted according to the correlation between their SVD‐shared features and age. The close agreement between standard deviations from predicted age and second stage brain‐age delta suggests that the patterns extracted from the imaging data are largely descriptive of brain age, rather than chronological age.
As presented in Figure 5, positive correlations between age delta and non‐imaging variables indicate accelerated age decline. After FDR correction with q value 0.05, a handful of statistically significant associations were identified between source‐specific brain‐age deltas and non‐imaging phenotypes. Most associations were with time to answer in a prospective memory test, namely SCVs 5 (shared + sMRI), 17 (shared), and 8 (fMRI). Shared 5 and 17, as well as fMRI 8, indicate decelerated age decline with higher time to answer. sMRI 5 indicates accelerated age decline with higher time to answer. Only shared 5 and 17 associations seem to replicate significantly within males and females. Also, higher frequency of exercise in last 4 weeks associated with accelerated age decline in fMRI 17. See Figure S3 for partialled sMRI correlations.
FIGURE 5.
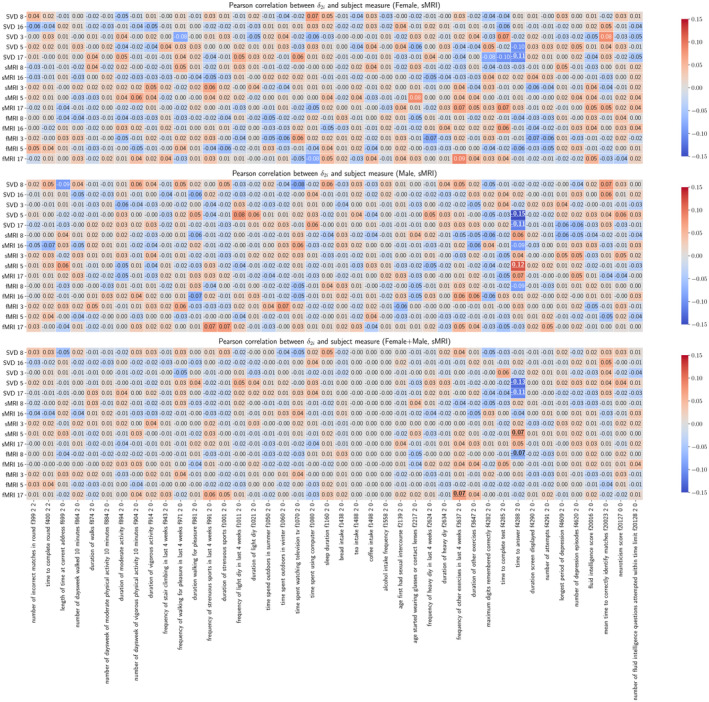
Pearson correlations between vectors and subject measures. Pearson correlations are calculated between vectors and variables for each gender and for all subjects. The underscored correlations are significant.
Analysis results including dMRI instead of sMRI are also available as Supporting Information: dMRI age delta modeling (Figure S2), dMRI age delta correlations (Figure S4), and partialled dMRI age delta correlations (Figure S5).
3.2. Associations With Schizophrenia
Linked subject expression levels were also identified in the patient dataset. In particular, SCV 19 (see Figure 6) not only shows association with age, but also provides evidence of age‐adjusted group differences between controls and patients with schizophrenia. Specifically, patients show lower source levels in all three modalities. Moreover, SCV 19 remarkably replicates the spatial patterns of UKB SCV 8 described in Section 3.1, indicating linked sources are identified across two independent datasets.
In addition, SCV 14 (see Figure S7) is also identified as a schizophrenia‐related source. In SCV 14, patients have higher source intensities in all three modalities. In sMRI, positive weights, which indicate decline with aging, are shown in the temporal lobe, the occipital lobe, the lingual gyrus and the orbital part of inferior frontal gyrus, while negative weights can be found in the insula and the frontal inferior operculum. In fMRI, the superior frontal cortex and the superior parietal cortex have positive activation. In dMRI, positive weights can be seen in the superior longitudinal fasciculus while negative weights can be found in the corpus calossum.
3.3. Associations With Sex Effects in UK Biobank
Five SCVs (9, 10, 16, 17, and 22) show significant sex effects in UK Biobank data. Females show significantly higher source intensities than males in SCV 9 and 16 (see Figure 7 for SCV 16) while males show significantly higher source intensities than females in SCVs 10, 17, and 22 (see Figure S6).
FIGURE 7.
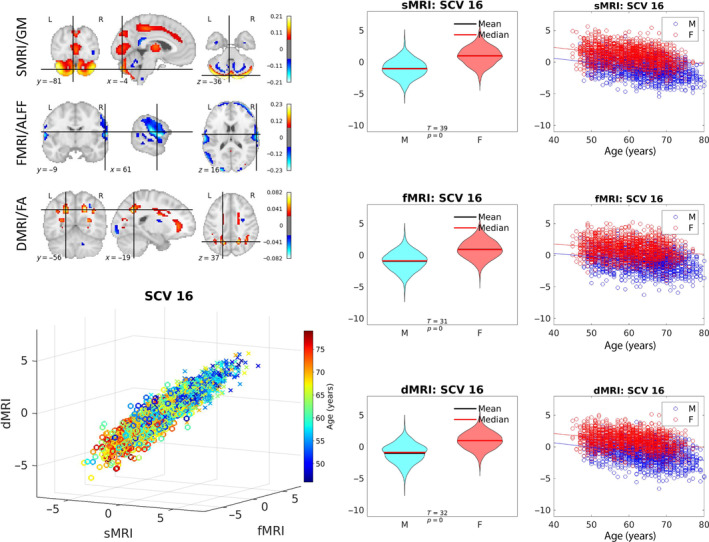
Sex‐related SCV. Illustration of SCV 16. Top left: The spatial maps correspond to the mixing weights for each modality. Bottom left: Multimodal subject expression level sources, depicting all subjects (colored by age; circles indicate females while crosses indicate males). Right: Source intensity differences related to sex effects.
For SCV 16, in both sexes, notice the linear covariation with age and similar trajectory of decline with age observed in cerebellar regions (sMRI/GM) and superior longitudinal fasciculus I plus forceps minor (dMRI/FA), as well as increase with age in temporo‐parietal cortex (fMRI/ALFF).
In sMRI, SCVs 10 and 17 show negative weights (increase with age) in the parietal lobe and the cerebellum, respectively. SCV 9 shows slight increase with age in the temporal lobe, and slight decrease with age in the angular gyrus. SCV 22 shows both positive and negative weights in the cerebellum. In fMRI, SCVs 10 and 17 show positive weights in the frontal lobe. SCV 9 shows slight increase with age in the cuneus (occipital lobe). SCV 22 shows positive weights in the olfactory cortex. In dMRI, SCV 10 has positive weights in forceps minor, while SCV 17 shows negative weights in the posterior end of the superior longitudinal fasciculus II. SCV 9 shows slight decline with age in the vertical occipital fasciculus, and SCV 22 shows positive weights in the brain stem. Except for SCV 9, as the age increases, regions with positive weights experience decline (conversely, increase, in regions with negative weights).
3.4. Associations With Cognitive Performance in UK Biobank
As shown in Figure 8, the SCV 22 shows significant linear association with time to answer (TTA) in a prospective memory test across all three modalities. Subjects with faster responses have higher source intensities. Males have slightly higher source intensities than females in all three modalities. The spatial maps highlight the cerebellum in sMRI, the olfactory cortex in fMRI, and the brain stem in dMRI.
FIGURE 8.
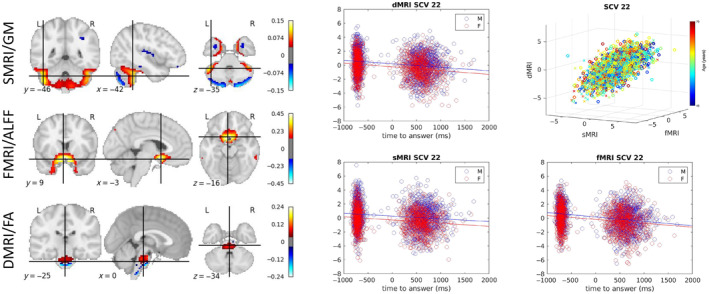
Time to answer‐related SCV. Left: The spatial maps corresponding to the mixing weights for each modality are shown. Right: A 3D scatter plot of SCV 22 illustrates the association between the identified multimodal subject expression levels and age for UK Biobank data. 2D scatter plots illustrate the relationship between the time to answer and the source intensities for each of the three modalities.
4. Discussion
In this work, we demonstrate that the proposed multimodal IVA model, initialized with a multimodal group projection (see Section 2.4), can extract independent multimodal subspaces that show significant covariation with subject phenotypes. The proposed approach directly leverages multimodal associations and is applied to two large datasets independently. The results highlight several linked multimodal patterns of expression over subjects that are significantly associated with aging, sex, cognition, and psychosis indicators. Five SCVs (SCVs 3, 5, 8, 16, 17) were identified that were significantly associated with age based on effect size (). The aging curves for UK Biobank reported in Figure 4 show ample evidence on nonlinear aging effects in the recovered SCVs, particularly for SCVs 3 and 5. The strongest acceleration in age‐related decline was observed in SCV 16, although this may be a result of the strong sex differences present in that SCV (see aging plots in Figure 7).
As presented in Figure 3, for the UK Biobank dataset, age‐associated decline in gray matter density (hot spatial areas of sMRI SCV 8 weights) was primarily seen in caudate, thalamus, insular regions, anterior and posterior cingulate cortex, and lingual gyrus, consistent with earlier findings (Brickman et al. 2007; Hu et al. 2014). The ALFF maps corresponding to SCV 8 suggest reductions in visual, parietal, and dorsal prefrontal regions, which covary with the structural changes, also consistent with prior literature (Hu et al. 2014). In dMRI, FA intensity reductions observed in the identified spatial map weights of SCV 8 are associated with age and occur in the anterior corpus callosum, forceps minor, superior longitudinal fasciculus II, the anterior thalamic radiation, and the optic radiation.
In UKB SCV 8, the GM nonlinear decline with age in the caudate and hippocampus agrees with cross‐sectional studies from multiple sites on adult development (Walhovd et al. 2011; Ziegler et al. 2012; Fjell et al. 2013) though here the nonlinear effect is more prominent at younger age and seems to become more linear at older age. In the thalamus and nucleus accumbens, the more linear decline at old age also aligns with prior findings (Walhovd et al. 2011; Ziegler et al. 2012; Fjell et al. 2013). Accelerated decline has been observed previously in temporal and occipital areas (Storsve et al. 2014), while we observed such effect more prominently at younger age. Slightly deviating from our observation of roughly linear decline at older age, deceleration at older age has been reported for anterior cingulate, prefrontal, and temporal areas (Storsve et al. 2014; Rast et al. 2018). On the other hand, the observed increase in the occipital lobe has been previously associated with longitudinally decreased cognition (Leong et al. 2017). In general, nonlinear average trajectories of structural change are supportive of increased individual variability with higher age due to the potential presence of maintenance and growth trajectories, assuming plasticity remains into higher age (Oschwald et al. 2020). From a multimodal perspective, Jirsaraie et al. (2023) have reported that certain gray and white matter areas are of high importance for brain age prediction (many of which are also present in UKB SCV8), especially for chronic brain disorders such as Alzheimer's disease and schizophrenia, which supports our replication result in patients' SCV 19 below. Considering that the population included in our UKB analysis consists of only unaffected adults with ‘healthy’ cognition, some scaffolding theories of aging, such as STAC (Spreng and Turner 2019), predict that such individuals “should be able to compensate for age‐related atrophy and, thus, maintain cognitive performance” (Oschwald et al. 2020), which may help explain why no significant cognitive effects were found relating to any of the five age‐related SCVs we identified for this dataset. Brain‐age delta was estimated using shared‐SVD source features, partialled sMRI sources and partialled fMRI sources. Each individual source from each of the three modalities within an SCV describes a pattern of subject‐specific expression levels that is linked (covaries) between modalities within that SCV, while being statistically independent from sources in other SCVs. The mean absolute error (MAE) of overall age prediction is 2.70 years, and the mean absolute errors are 2.58, 0.41, and 0.61 years when using only the five individual sources from each feature type (shared‐SVD, partialled sMRI, and partialled fMRI, respectively)—all cases based on the same multimodal IVA decomposition. The high MAE of shared‐SVD features indicates the largest portion of variability associated with deviations is captured by the shared aspects of the linked sources. The association between each individual source and age for each subject was also computed. As shown in Figure 4, all five SVD‐shared features, four sMRI sources (SCVs 3, 8, 16, 17), and one fMRI source (SCV 5) show significant age regression beta weights. Though the unique variability of the partialled sMRI source from SCV 5 does not contribute significantly to the age regression model, the corresponding partialled fMRI source from SCV 5 does show significant contribution. Thus, all five SCVs display significant age regression coefficients in at least one modality, and we conclude that each modality contributes complementary information not captured in other modalities. Moreover, the brain‐age delta result using only the five sources from shared‐SVD features supports that each modality is valuable and largely predictive of brain age, which is largely a consequence of the inherent multimodal link (correlation) among expression levels within SCVs. The advantage of such multimodal analysis is not only that it leverages hidden covariation across modalities to recover linked subject expression patterns, but also that it captures unique information from each modality by allowing these patterns to differ across modalities. Note that in our brain‐age delta analysis, confound variables head size, scanner table position and scan‐date‐related slow drifts described in Smith et al. (2020) were not included.
Two SCVs (SCVs 14, 19) in the patient dataset are associated with schizophrenia effects. SCV 19 revealed schizophrenia effects as sMRI gray matter intensity reduction in the temporal lobe, consistent with previous findings (Karlsgodt, Sun, and Cannon 2010). Schizophrenia‐associated reductions can also be observed in the medial parietal lobe, including the posterior cingulate cortex in fMRI ALFF maps, also aligned with previous literature (Venkataraman et al. 2012). The dMRI spatial map shows decreased FA values in the anterior thalamic radiation and forceps minor tracts, which is close to the superior longitudinal fasciculus and cingulate bundle reported in Kyriakopoulos et al. (2008). As is the nature of the proposed multimodal IVA approach, all of these regional changes covary at similar levels over subjects across all three modalities. Interestingly, the high spatial correlation between age‐related SCV 8 in the UK Biobank dataset and schizophrenia‐related SCV 19 in the patient dataset, in both sMRI and dMRI modalities, suggests that some source linkages recovered by MMIVA replicate very well across two independent datasets analyzed separately. While this study was not primarily targeted at schizophrenia and rather aimed at demonstrating the richness and relevance of linked latent multimodal patterns, it was highly encouraging to observe the replication of (unaffected) UKB SCV 8 as patients' SCV 19 across modalities, especially considering that both datasets are very different from one another. Such evidence supports the generalizability of the proposed approach. In addition, it also demonstrates its applicability to the study of schizophrenia by corroborating known findings from previous schizophrenia research (Gupta et al. 2015; Bora et al. 2011), in particular the lower gray matter expression patterns in the thalamus, superior temporal, anterior cingulate, and dorsal insular gyri (likewise for the lower ALFF in the occipital cortex (Turner et al. 2013) and FA in the fronto‐striatal circuit (Bora et al. 2011)). Besides automatically connecting these findings, the results produced by MMIVA also suggest a connection with higher ALFF thalamic activity in SZ, which may be compensatory for the aforementioned gray matter reduction. Lastly, some differences in the spatial extent and sign of regional patterns can be observed between UKB SCV 8 and patients' SCV 19, which could, in part, be attributed to differences in data quality, acquisition sequence, and population included in each study. Schizophrenia patients tend to be less still and scanner distortions from differences in TR, susceptibility, and overall SNR may be present. The effects of these differences tend to be more pronounced in ALFF than in GM or FA features. Sex differences were mainly reflected in SCVs 9, 10, 16, 17, and 22 for the UK Biobank dataset. Females show significantly higher source intensities than males in SCVs 9, and 16, while males show higher intensities than females in SCVs 10, 17, and 22. Consistent with previous studies (Liu et al. 2020; Ritchie et al. 2018), males have significantly higher source intensities than females in the parietal lobe (SCV 10) and the cerebellum (SCV 17) from sMRI/GM, the frontal lobe in both SCV 10 and 17 from fMRI/ALFF, the forceps minor (SCV 10) and the superior longitudinal fasciculus II (SCV 17) from dMRI/FA. As shown in Figure 7 for SCV 16, females have higher intensities than males in the cerebellum from sMRI/GM, the temporo‐parietal lobe from fMRI/ALFF as well as the superior longitudinal fasciculus I and forceps minor from dMRI/FA. In SCV 16, decline with aging can be found in the sMRI and dMRI modalities while increase with aging can be observed in fMRI/ALFF maps.
One SCV (SCV 22) has associations with time to answer in a prospective memory test. As presented in Figure 8, the cerebellum identified by the sMRI source has been found to relate to the biological basis of time perception and fast response (Grondin 2010), and prospective memory (Cona et al. 2016).
In terms of limitations of the current study, we consider the following aspects: model assumptions, biases, generalizability, and miscellaneous, which are addressed separately below.
4.1. Assumptions
Statistical dependence within SCVs: A key assumption of the MMIVA approach is that there is one (or more) underlying process at the subject level that modulates the expression of spatial patterns in a similar way for all modalities. This underlying process establishes a link between imaging modalities, which implies statistical dependence between them.
Statistical independence between SCVs: Another key assumption of the MMIVA model is that the process(es) underlying the joint modulation of expressions (i.e., the SCV) are entirely independent and unrelated to each other, inducing statistical independence between SCVs. Numerous studies (using mCCA (Qi et al. 2018), PLS (Sui et al. 2012), IVA‐G (Adali, Levin‐Schwartz, and Calhoun 2015a)) have explored this concept but have been largely limited to simple statistical uncorrelation (i.e., second‐order statistics, SOS), not independence. We believe the latter is more meaningful since it accounts for both second‐ and higher‐order statistics (HOS). As such, it also delivers uncorrelation, but with potential for better decoupling of the SCVs and, thus, improved interpretability.
Stationarity (or identical distribution): Naturally, the strength of the link may be different for each modality pair, but it is assumed that it stays constant/consistent across subjects. This implies that each subject must follow the same (i.e., stationary) population‐level distribution of linked multimodal expression levels. For the UK Biobank dataset used here, it is reasonable to expect all unaffected subjects were sampled from the same distribution. This is less true for the patients dataset, since two populations are combined (typical controls and schizophrenia patients) and their multimodal expression level distributions are expected to differ. That said, evidence from ICA‐based fusion literature supports that such changes are less detrimental to performance if the mixings (here, spatial patterns) are shared among both populations. In particular, this is analogous to the observation in joint ICA that differences in the shared mixings are more detrimental to performance than differences in source distribution (Silva et al. 2014b). Since in MMIVA neither sources nor mixings are shared across modalities, we expect even less effects from violations of stationarity, especially with only a few subject groups included. However, site effects could cause multiple deviations from the population distribution, which we tried to mitigate by removing all site‐effects before MMIVA in both of our experiments. Although we did not investigate it, removal of site‐effects in this fashion could lead to loss of interesting information and may not address differences in the latent (SCV) space because removal is carried out at the input data level, not the output (see Adeli et al. (2021)).
Sample independence: Here, each subject is treated as an independent sample drawn from the population. This is fairly true, especially for the UK Biobank dataset since it is a very large prospective study (though it is restricted to adults in the UK who are more than 40 years old, i.e., a mild conditional sampling). For the patient dataset, this assumption is reasonable considering the data comes from different studies, each with their own recruitment policies (also inducing some negligible conditional sampling).
Linearity: the MMIVA model assumes that the data of each modality is a linear mixture of the sources (subject expression levels), where the mixings are the spatial maps. In other words, the voxel‐wise data values across subjects are a linear combination of latent independent sources. It is possible that nonlinear effects are present in the data. These could be from the true mixing process being nonlinear (Abrol et al. 2021), or because of residual artifacts of the data collection and preprocessing. During data collection, for example, MR field inhomogeneities may exist. For preprocessing, subject‐ and site‐level artifact corrections may induce or leave behind unwanted nonlinearities. Notably, all datasets were spatially normalized into the MNI template, which is an imperfect nonlinear operation meant to warp brains of different shapes into a common grid. Although nonlinear mixings are considered out of scope and, thus, a limitation of this work, we note the ample evidence for nonlinear aging curves across the various SCVs (Figure 4).
4.2. Bias
Modality specific noise: The sources of noise can be quite different per modality. While we do not conduct noise modeling directly, we believe that random noise sources from one modality are likely statistically independent from noise in a different modality. Since MMIVA seeks linkage between modalities (SCVs) it is unlikely to recover (and therefore averts) noise within SCVs. Still, certain physiological and behavioral confounds (such as head motion and heart beat) may induce some level of association between noise sources across modalities. We leave an assessment of potentially linked multimodal noise in our results as future work, although confounding factors were accounted for in both MANOVA and age‐delta analyses.
Conditional sampling: our results are limited to the subject populations studied (typical middle‐ and old‐aged adults in the UK, as well as multisite patients screened for schizophrenia). This means that data bias may occur and the trained model may not produce the same results if used on data from, say, underrepresented populations. In the UK Biobank study, there is a concerted effort to ensure the sample is representative of the population, which mitigates some of this bias. The patient dataset has some built‐in variability due to the combination of several studies, which can mitigate some of the data bias from the individual studies, especially those with small N.
Implicit weighting: In every fusion model, there is a risk that one modality may eclipse or overwhelm the other. To somewhat mitigate this issue, we opted to resample all modalities to the same mm MNI space. Still, the number of GM voxels is considerably higher than WM, meaning GM and ALFF modalities have much more voxels (and weight parameters W) than FA. We approached this issue in two different ways, as follows. MGPCA: For initialization of the weight parameters W, we put forward an approach for modality weighting based on the total variance of each modality. This approach is called multimodal group PCA (MGPCA) and aims to find a projection for each modality that equally accounts for the variance contribution of each modality and captures a common subspace among all modalities. Scale control: While initialization of the weight parameters with MGPCA ensures projection to a balanced common subspace before MMIVA training starts, it is still possible that the weighting will become unbalanced during training and cause one or more modalities to overwhelmingly influence the results. To counter that, we leverage the scale‐controlled loss in MISA (Silva et al. 2021), which ensures stability and consistency of the source variances across modalities throughout the training procedure.
MNI space. Still, the number of GM voxels is considerably higher than WM, meaning GM and ALFF modalities have much more voxels (and weight parameters W) than FA. We approached this issue in two different ways, as follows. MGPCA: For initialization of the weight parameters W, we put forward an approach for modality weighting based on the total variance of each modality. This approach is called multimodal group PCA (MGPCA) and aims to find a projection for each modality that equally accounts for the variance contribution of each modality and captures a common subspace among all modalities. Scale control: While initialization of the weight parameters with MGPCA ensures projection to a balanced common subspace before MMIVA training starts, it is still possible that the weighting will become unbalanced during training and cause one or more modalities to overwhelmingly influence the results. To counter that, we leverage the scale‐controlled loss in MISA (Silva et al. 2021), which ensures stability and consistency of the source variances across modalities throughout the training procedure.
4.3. Generalization
Our results are limited to the subject populations studied. It is possible that the results would change if a more diverse population was considered. However, comparing results between the two (unrelated) datasets analyzed revealed that at least one SCV replicated very well across both datasets (both datasets were analyzed completely separate from each other). Therefore, this provides some evidence in support of the replicability of our main finding for aging, suggesting MMIVA may generalize well. Also, this observation is, at least partially, a result of the large number of subjects analyzed in each dataset.
4.4. Miscellaneous
Data features: this work only leverages GM, FA, and ALFF features, but many other types of features are available which bear useful information for data fusion. Some noteworthy examples include network connectivity matrices (Wu et al. 2015), functional (static or dynamic) and structural (from tractography and diffusion weighted imaging), metabolomic uptake imaging (such as positron emission tomography (Zaidi and Becker 2016)), and vasculature/circulation information (such as cerebral blood flow and arterial spin labeling (Baller et al. 2022)). Inclusion/substitution of these modalities has potential to yield meaningful discoveries about underlying mechanisms in the brain. Moreover, the choice to use ALFF features means the current work does not leverage dynamic information from the fMRI datasets.
Number of sources: the current work sets the number of sources empirically, broadly based on the literature. Current trends suggest high‐order models are useful for studying functional dynamics, yet typical multimodal analysis is limited to low‐order. We opted for a C = 30 as a comparatively high number in the context of multimodal fusion.
Presence of subspaces and fixed spatial maps: this work limits the analysis to linkage of single unimodal components across modalities, but it is possible, and quite reasonable, that multiple components from one modality would be simultaneously linked to the same source in another modality. In general, groups of sources from each modality could be linked across modalities. Estimation of such multidimensional structures is very challenging and demands additional research. One limitation of not accounting for multidimensional structures is the inability to detect changes in spatial configuration (as in “blob shapes”) across groups of subjects from different populations. This is because each subspace only contains exactly one source from each modality. Consequently, the spatial configuration of the identified spatial maps is rigid across all subjects, modulating only according to a scalar value (the subject expression level in the SCVs). As such, any direct assessment of spatial map conformity with current theories of compensatory dedifferentiation (Spreng and Turner 2019) in older adults (e.g., Hemispheric Reduction Asymmetry in Older Adults (HAROLD), Compensation‐Related Utilization of Neural Circuits Hypothesis (CRUNCH), Scaffolding Theory of Aging Cognition (STAC)) is quite limited. However, note that this is a limitation shared with other data fusion methods, which circumvent this issue post hoc by estimating approximate subgroup spatial maps via back‐reconstruction (Silva and Plis 2019). While we do not carry out such analysis here, work is currently underway to address this limitation and accommodate direct estimation of unimodal groups of sources linked across modalities (Li et al. 2024).
5. Conclusion
We demonstrated the ability of multimodal independent vector analysis (MMIVA) to extract linked multimodal modes of subject variations that capture different aspects of phenotypical information including aging effects, schizophrenia‐related biomarkers, sex effects, and cognitive performance across two large independent datasets. With the increasing demand of multimodal neuroimaging data analysis, the MMIVA fusion model shows a promising ability to identify linked sources with associated phenotypes across multiple neuroimaging modalities and multiple datasets.
Conflicts of Interest
The authors declare no conflicts of interest.
Supporting information
Data S1.
Acknowledgments
This work was supported by NIH grant R01MH118695 and NSF grant #2112455. Judith M. Ford is the recipient of a Distinguished Research Career Scientist award (#IK6CX002519) from the Department of Veterans Affairs. This research has been conducted using the UK Biobank Resource under Application Number 34175. We also acknowledge the FBIRN team who coordinated and performed the data acquisition, including Aysenil Belger, Juan R. Bustillo, Kelvin O. Lim, Daniel S. O'Leary, Bryon A. Mueller, Adrian Preda, and Steven G. Potkin.
Funding: This work was supported by U.S. Department of Veterans Affairs (IK6CX002519), National Science Foundation (2112455), and National Institutes of Health (R01MH118695).
Endnotes
Data from UK Biobank is available directly from UK Biobank.
COBRE data is available from COINS, https://coins.trendscenter.org/.
Due to IRB restrictions, the fBIRN phase III data cannot be shared directly, but individuals interested in requesting access can contact Theo Van Erp, tvanerp@hs.uci.edu.
MPRC and BSNIP data are available through the NIMH Data Archive (NDA), https://nda.nih.gov/.
Including those due to known and unknown confounds.
Mean removal is performed before and after partialling. Partialled variances are adjusted to .
Strictly speaking, we could have regressed out only the sources within the same SCV since all others are independent by the definition of SCVs. Results were nearly identical with such approach.
Data Availability Statement
The data that support the findings of this study are available from the UK Biobank, COBRE, fBIRN, MPRC, and BSNIP studies. Restrictions apply to the availability of these data, which were used under license for this study. Data are available from https://www.ukbiobank.ac.uk/ with the permission of the UK Biobank, COBRE, fBIRN, MPRC, and BSNIP studies.
References
- Abrol, A. , Fu Z., Salman M., et al. 2021. “Deep Learning Encodes Robust Discriminative Neuroimaging Representations to Outperform Standard Machine Learning.” Nature Communications 12, no. 1: 353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adalı, T. , Anderson M., and Fu G.‐S.. 2014. “Diversity in Independent Component and Vector Analyses: Identifiability, Algorithms, and Applications in Medical Imaging.” IEEE Signal Processing Magazine 31, no. 3: 18–33. [Google Scholar]
- Adali, T. , Levin‐Schwartz Y., and Calhoun V. D.. 2015a. “Multimodal Data Fusion Using Source Separation: Application to Medical Imaging.” Proceedings of the IEEE 103, no. 9: 1494–1506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adali, T. , Levin‐Schwartz Y., and Calhoun V. D.. 2015b. “Multimodal Data Fusion Using Source Separation: Two Effective Models Based on ICA and IVA and Their Properties.” Proceedings of the IEEE 103, no. 9: 1478–1493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adeli, E. , Zhao Q., Pfefferbaum A., et al. 2021. “Representation Learning With Statistical Independence to Mitigate Bias.” In 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), 2512–2522. Waikoloa, USA: IEEE. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aine, C. , Bockholt H. J., Bustillo J. R., et al. 2017. “Multimodal neuroimaging in schizophrenia: description and dissemination.” Neuroinformatics 15, no. 4: 343–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albers, C. , and Lakens D.. 2018. “When Power Analyses Based on Pilot Data Are Biased: Inaccurate Effect Size Estimators and Follow‐Up Bias.” Journal of Experimental Social Psychology 74: 187–195. [Google Scholar]
- Anderson, M. , Fu G., Phlypo R., and Adalı T.. 2014. “Independent Vector Analysis: Identification Conditions and Performance Bounds.” IEEE Transactions on Signal Processing 62, no. 17: 4399–4410. [Google Scholar]
- Anderson, M. , Fu G.‐S., Phlypo R., and Adali T.. 2013. “Independent Vector Analysis, the Kotz Distribution, and Performance Bounds.” In 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, 3243–3247. Vancouver, Canada: IEEE. [Google Scholar]
- Baller, E. B. , Valcarcel A. M., Adebimpe A., et al. 2022. “Developmental Coupling of Cerebral Blood Flow and fMRI Fluctuations in Youth.” Cell Reports 38, no. 13: 110576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell, A. J. , and Sejnowski T. J.. 1995. “An Information‐Maximization Approach to Blind Separation and Blind Deconvolution.” Neural Computation 7, no. 6: 1129–1159. [DOI] [PubMed] [Google Scholar]
- Bora, E. , Fornito A., Radua J., et al. 2011. “Neuroanatomical Abnormalities in Schizophrenia: A Multimodal Voxelwise Meta‐Analysis and Meta‐Regression Analysis.” Schizophrenia Research 127, no. 1: 46–57. [DOI] [PubMed] [Google Scholar]
- Brickman, A. M. , Habeck C., Zarahn E., Flynn J., and Stern Y.. 2007. “Structural Mri Covariance Patterns Associated With Normal Aging and Neuropsychological Functioning.” Neurobiology of Aging 28, no. 2: 284–295. [DOI] [PubMed] [Google Scholar]
- Calhoun, V. D. , and Adali T.. 2008. “Feature‐Based Fusion of Medical Imaging Data.” IEEE Transactions on Information Technology in Biomedicine 13, no. 5: 711–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun, V. D. , Adalı T., Kiehl K. A., Astur R., Pekar J. J., and Pearlson G. D.. 2006. “A Method for Multitask fMRI Data Fusion Applied to Schizophrenia.” Human Brain Mapping 27, no. 7: 598–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun, V. D. , and Sui J.. 2016. “Multimodal Fusion of Brain Imaging Data: A Key to Finding the Missing Link(s) in Complex Mental Illness.” Biological Psychiatry: Cognitive Neuroscience and Neuroimaging 1, no. 3: 230–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll, R. M. , and Nordholm L. A.. 1975. “Sampling Characteristics of Kelley's and Hays' .” Educational and Psychological Measurement 35, no. 3: 541–554. [Google Scholar]
- Cohen, J. 1992. “Statistical Power Analysis.” Current Directions in Psychological Science 1, no. 3: 98–101. [Google Scholar]
- Comon, P. 1994. “Independent Component Analysis, a New Concept?” Signal Processing 36, no. 3: 287–314. [Google Scholar]
- Cona, G. , Bisiacchi P. S., Sartori G., and Scarpazza C.. 2016. “Effects of Cue Focality on the Neural Mechanisms of Prospective Memory: A Meta‐Analysis of Neuroimaging Studies.” Scientific Reports 6, no. 1: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham, P. , and Delany S. J.. 2021. “K‐Nearest Neighbour Classifiers—A Tutorial.” ACM Computing Surveys (CSUR) 54, no. 6: 1–25. [Google Scholar]
- Damaraju, E. , Silva R. F., Adali T., and Calhoun V. D.. 2021. “A Multimodal IVA Fusion Approach to Identify Linked Neuroimaging Markers.” In 43rd IEEE EMBC, 3928–3932. Mexico: IEEE. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fjell, A. M. , Westlye L. T., Grydeland H., et al. 2013. “Critical Ages in the Life Course of the Adult Brain: Nonlinear Subcortical Aging.” Neurobiology of Aging 34, no. 10: 2239–2247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grondin, S. 2010. “Timing and Time Perception: A Review of Recent Behavioral and Neuroscience Findings and Theoretical Directions.” Attention, Perception, & Psychophysics 72, no. 3: 561–582. [DOI] [PubMed] [Google Scholar]
- Groves, A. R. , Beckmann C. F., Smith S. M., and Woolrich M. W.. 2011. “Linked Independent Component Analysis for Multimodal Data Fusion.” NeuroImage 54, no. 3: 2198–2217. [DOI] [PubMed] [Google Scholar]
- Gupta, C. N. , Calhoun V. D., Rachakonda S., et al. 2015. “Patterns of Gray Matter Abnormalities in Schizophrenia Based on an International Mega‐Analysis.” Schizophrenia Bulletin 41, no. 5: 1133–1142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hotelling, H. 1936. “Relations Between Two Sets of Variates.” Biometrika 28: 321–377. [Google Scholar]
- Hu, S. , Chao H. H.‐A., Zhang S., Ide J. S., and Li C.‐S. R.. 2014. “Changes in Cerebral Morphometry and Amplitude of Low‐Frequency Fluctuations of Bold Signals During Healthy Aging: Correlation With Inhibitory Control.” Brain Structure & Function 219, no. 1: 983–994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jirsaraie, R. J. , Gorelik A. J., Gatavins M. M., et al. 2023. “A Systematic Review of Multimodal Brain Age Studies: Uncovering a Divergence Between Model Accuracy and Utility.” Patterns 4, no. 4: 100712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonker, R. , and Volgenant A.. 2005. “A Shortest Augmenting Path Algorithm for Dense and Sparse Linear Assignment Problems.” Computing 38: 325–340. [Google Scholar]
- Karlsgodt, K. H. , Sun D., and Cannon T. D.. 2010. “Structural and Functional Brain Abnormalities in Schizophrenia.” Current Directions in Psychological Science 19, no. 4: 226–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keator, D. B. , van Erp T. G., Turner J. A., et al. 2016. “The Function Biomedical Informatics Research Network Data Repository.” NeuroImage 124: 1074–1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, T. , Eltoft T., and Lee T.‐W.. 2006. “Independent Vector Analysis: An Extension of ICA to Multivariate Components.” In International Conference on Independent Component Analysis and Signal Separation, 165–172. Charleston, South Carolina: Springer. [Google Scholar]
- Kotz, S. 1974. “Multivariate Distributions at a Cross Road.” In Proceedings of the NATO Advanced Study Institute, Statistical Distributions in Scientific Work, 247–270. Calgary, Canada: Springer. [Google Scholar]
- Kyriakopoulos, M. , Vyas N. S., Barker G. J., Chitnis X. A., and Frangou S.. 2008. “A Diffusion Tensor Imaging Study of White Matter in Early‐Onset Schizophrenia.” Biological Psychiatry 63, no. 5: 519–523. [DOI] [PubMed] [Google Scholar]
- Langsrud, Ø. 2003. “ANOVA for Unbalanced Data: Use Type II Instead of Type III Sums of Squares.” Statistics and Computing 13, no. 2: 163–167. [Google Scholar]
- Leong, R. L. F. , Lo J. C., Sim S. K. Y., et al. 2017. “Longitudinal Brain Structure and Cognitive Changes Over 8 Years in an East Asian Cohort.” NeuroImage 147: 852–860. [DOI] [PubMed] [Google Scholar]
- Li, X. , Kochunov P., Adali T., Silva R. F., and Calhoun V. D.. 2024. “Multimodal Subspace Independent Vector Analysis Effectively Captures the Latent Relationships Between Brain Structure and Function.” bioRxiv 2023: 2023.09.17.558092. [Google Scholar]
- Liu, J. , Demirci O., and Calhoun V. D.. 2008. “A Parallel Independent Component Analysis Approach to Investigate Genomic Influence on Brain Function.” IEEE Signal Processing Letters 15: 413–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, S. , Seidlitz J., Blumenthal J. D., Clasen L. S., and Raznahan A.. 2020. “Integrative Structural, Functional, and Transcriptomic Analyses of Sex‐Biased Brain Organization in Humans.” Proceedings of the National Academy of Sciences 117, no. 31: 18788–18798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller, K. L. , Alfaro‐Almagro F., Bangerter N. K., et al. 2016. “Multimodal Population Brain Imaging in the UK Biobank Prospective Epidemiological Study.” Nature Neuroscience 19, no. 11: 1523–1536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadarajah, S. 2003. “The Kotz‐Type Distribution With Applications.” Statistics 37, no. 4: 341–358. [Google Scholar]
- Oschwald, J. , Guye S., Liem F., et al. 2020. “Brain Structure and Cognitive Ability in Healthy Aging: A Review on Longitudinal Correlated Change.” Reviews in the Neurosciences 31, no. 1: 1–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kotz, S. 1974. “Multivariate Distributions at a Cross Road.” In Statistical Distributions in Scientific Work, 247–270. Calgary, Canada: Springer. [Google Scholar]
- Qi, S. , Calhoun V. D., van Erp T. G. M., et al. 2018. “Multimodal Fusion With Reference: Searching for Joint Neuromarkers of Working Memory Deficits in Schizophrenia.” IEEE Transactions on Medical Imaging 37, no. 1: 93–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rachakonda, S. , Du Y., and Calhoun V. D.. 2017. Model Order Prediction in ICA. Vancouver, Canada: OHBM. [Google Scholar]
- Rast, P. , Kennedy K. M., Rodrigue K. M., et al. 2018. “APOE4 Genotype and Hypertension Modify 8‐Year Cortical Thinning: Five Occasion Evidence From the Seattle Longitudinal Study.” Cerebral Cortex 28, no. 6: 1934–1945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritchie, S. J. , Cox S. R., Shen X., et al. 2018. “Sex Differences in the Adult Human Brain: Evidence From 5216 UK Biobank Participants.” Cerebral Cortex 28, no. 8: 2959–2975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva, R. F. , and Plis S. M.. 2019. “How to Integrate Data From Multiple Biological Layers in Mental Health?” In Personalized Psychiatry: Big Data Analytics in Mental Health, edited by Passos I. C., Mwangi B., and Kapczinski F., 135–159. Cham, Switzerland: Springer. [Google Scholar]
- Silva, R. F. , Plis S. M., Adalı T., and Calhoun V. D.. 2014a. “Multidataset Independent Subspace Analysis Extends Independent Vector Analysis.” In Proceedings of the IEEE ICIP 2014, 2864–2868. France: IEEE. [Google Scholar]
- Silva, R. F. , Plis S. M., Adali T., and Calhoun V. D.. 2014b. “A Statistically Motivated Framework for Simulation of Stochastic Data Fusion Models Applied to Multimodal Neuroimaging.” NeuroImage 102, no. pt. 1: 92–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva, R. F. , Plis S. M., Adali T., Pattichis M. S., and Calhoun V. D.. 2021. “Multidataset Independent Subspace Analysis With Application to Multimodal Fusion.” IEEE Transactions on Image Processing 30: 588–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, S. M. , Elliott L. T., Alfaro‐Almagro F., et al. 2020. “Brain Aging Comprises Many Modes of Structural and Functional Change With Distinct Genetic and Biophysical Associations.” eLife 9: e52677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, S. M. , Nichols T. E., Vidaurre D., et al. 2015. “A Positive‐Negative Mode of Population Covariation Links Brain Connectivity, Demographics and Behavior.” Nature Neuroscience 18, no. 11: 1565–1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spreng, R. N. , and Turner G. R.. 2019. “Structure and Function of the Aging Brain.” In The Aging Brain: Functional Adaptation Across Adulthood, 9–43. Washington, DC: American Psychological Association. [Google Scholar]
- Storsve, A. B. , Fjell A. M., Tamnes C. K., et al. 2014. “Differential Longitudinal Changes in Cortical Thickness, Surface Area and Volume Across the Adult Life Span: Regions of Accelerating and Decelerating Change.” Journal of Neuroscience 34, no. 25: 8488–8498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sui, J. , Adali T., Yu Q., Chen J., and Calhoun V. D.. 2012. “A Review of Multivariate Methods for Multimodal Fusion of Brain Imaging Data.” Journal of Neuroscience Methods 204, no. 1: 68–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamminga, C. A. , Pearlson G., Keshavan M., Sweeney J., Clementz B., and Thaker G.. 2014. “Bipolar and Schizophrenia Network for Intermediate Phenotypes: Outcomes Across the Psychosis Continuum.” Schizophrenia Bulletin 40, no. Suppl_2: S131–S137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner, J. , Damaraju E., Van Erp T., et al. 2013. “A Multi‐Site Resting State fMRI Study on the Amplitude of Low Frequency Fluctuations in Schizophrenia.” Frontiers in Neuroscience 7: 137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uludag, K. , and Roebroeck A.. 2014. “General Overview on the Merits of Multimodal Neuroimaging Data Fusion.” NeuroImage 102: 3–10. [DOI] [PubMed] [Google Scholar]
- Venkataraman, A. , Whitford T. J., Westin C.‐F., Golland P., and Kubicki M.. 2012. “Whole Brain Resting State Functional Connectivity Abnormalities in Schizophrenia.” Schizophrenia Research 139, no. 1–3: 7–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walhovd, K. B. , Westlye L. T., Amlien I., et al. 2011. “Consistent Neuroanatomical Age‐Related Volume Differences Across Multiple Samples.” Neurobiology of Aging 32, no. 5: 916–932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, L. , Calhoun V. D., Jung R. E., and Caprihan A.. 2015. “Connectivity‐Based Whole Brain Dual Parcellation by Group ICA Reveals Tract Structures and Decreased Connectivity in Schizophrenia.” Human Brain Mapping 36, no. 11: 4681–4701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaidi, H. , and Becker M.. 2016. “The Promise of Hybrid PET/MRI: Technical Advances and Clinical Applications.” IEEE Signal Processing Magazine 33, no. 3: 67–85. [Google Scholar]
- Ziegler, G. , Dahnke R., Jancke L., Yotter R. A., May A., and Gaser C.. 2012. “Brain Structural Trajectories Over the Adult Lifespan.” Human Brain Mapping 33, no. 10: 2377–2389. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1.
Data Availability Statement
The data that support the findings of this study are available from the UK Biobank, COBRE, fBIRN, MPRC, and BSNIP studies. Restrictions apply to the availability of these data, which were used under license for this study. Data are available from https://www.ukbiobank.ac.uk/ with the permission of the UK Biobank, COBRE, fBIRN, MPRC, and BSNIP studies.


