Skip to main content
NCBI home page
Chemical Science logoLink to Chemical Science
. 2024 Oct 30;15(48):20328–20337. doi: 10.1039/d4sc05304d

Probing decoherence in molecular 4f qubits†

Steen H Hansen a,‡, Christian D Buch a,‡, Jonatan B Petersen b, Michelle Rix a, Marc Ubach I Cervera a, Asger Strandfelt a, Richard E P Winpenny b, Eric J L McInnes b, Stergios Piligkos a,✉
PMCID: PMC11575486  PMID: 39568949

Abstract

We probe herein the fundamental factors that induce decoherence in ensembles of molecular magnetic materials. This is done by pulse Electron Paramagnetic Resonance measurements at X-band (∼9.6 GHz) on single crystals of Gd@Y(trensal) at 0.5, 10−1, 10−2 and 10−3% doping levels, using Hahn echo, partial refocusing and CPMG sequences. The phase memory time, Tm, obtained by the Hahn echo sequence at X-band is compared to the one previously determined at higher frequency/magnetic field (∼240 GHz). The combined information from these experiments allows to gain insight into the contributions to decoherence originating from various relaxation mechanisms such as spin–lattice relaxation, electron and nuclear spin diffusion and instantaneous diffusion. We show that while at high magnetic fields Tm is limited by spin–lattice relaxation seemingly attributed to a direct process, at lower fields the limiting factor is spectral diffusion. At X-band, for Gd@Y(trensal) we determine a Tm in the range 1–12 μs, at 5 K, depending on the magnetic field and concentration of Gd(trensal) in the isostructural diamagnetic host Y(trensal). Importantly, Gd@Y(trensal) displays measurable coherence at temperatures above liquid nitrogen ones, with 125 K being the upper limit. At the lowest dilution level of 10−3% and under dynamic decoupling conditions, the ratio of Tmversus the time it takes to implement a quantum gate, TG, reaches the order of 104, in the example of a single qubit π-rotation, which corresponds to an upper limit of gate fidelity of the order of 99.99%, reaching thus the lower limit of qubit figure of merit required for implementations in quantum information technologies.

We probe herein the fundamental factors that induce decoherence in ensembles of molecular magnetic materials.graphic file with name d4sc05304d-ga.jpg

Introduction

Coherent superposition and entanglement of quantum mechanical states are fundamental properties of matter the exploitation of which forms the basis for a variety of emerging new technologies, collectively referred to as quantum technologies,1–3 such as quantum computing,4–8 simulators,9 communications,10 sensing,11–16 metrology,10 cryptography17 and imaging.18 Two-dimensional or higher dimensionality quantum systems (qubits or qudits, respectively) such as superconducting nanostructures,19,20 photons,21,22 nitrogen vacancies in diamonds,23–25 single atoms in silicon,26–28 trapped ions,29,30 photo excited states,31–33 atoms on surfaces34 and metal complexes35–57 can be used as quantum hardware. Unlike many other candidates, molecular magnetic materials routinely display many low energy states compatible with the encoding of multiple qubits and qudits.57–62 Importantly, the multilevel structure of their eigenspectrum provides an expanded computational space dimension, as compared to individual qubits, and offers the capability to implement quantum algorithms at the single molecule level,47,48,63 efficiently encode quantum error correction algorithms54,57,64 or the first example of a quantum simulation using a molecular system.53 Implementation of single and entangled quantum gates on molecular magnetic materials is performed by coherent manipulation of individual or entangled electronic or electronuclear angular momenta.65,66 Such coherent manipulations are achieved by electromagnetic pulse excitations, usually within an applied external magnetic field. The phase memory time, Tm, reflects the time for which the information encoding state retains its phase coherence.67 According to the DiVincenzo criteria,68 the fidelity with which such states are created depends on the relative magnitude of Tm and the time it takes to implement a quantum gate, TG, with the ratio Tm/TG required to be of the order of at least 104 to achieve a satisfactory fidelity. Thus, Tm and TG are critical parameters determining the suitability of a given material as quantum hardware. Decoherence,69 the loss of coherence, is due to the interaction of the quantum system with its environment and results in loss of superposition collapsing the dynamic state of the quantum system to its thermal equilibrium eigenstates. Decoherence is due to fluctuations of the resonance frequency of the quantum system, partly induced by local magnetic field fluctuations generated by the dynamics of environmental angular momenta, such as electronic or nuclear spins. Such fluctuations can be induced by the electromagnetic pulse excitation, resulting in instantaneous diffusion or by the intrinsic dynamics of the environment resulting in spectral diffusion. The main factors to which spectral diffusion is usually attributed to are electron and nuclear spin diffusion. However, the relative contributions of such local magnetic field fluctuations diminish with increasing resonance frequency. Thus, the phase memory time should increase at higher resonance frequencies, which in the case of real or effective spin-half systems translates to higher applied magnetic fields. However, spin–lattice relaxation, reflecting the longitudinal relaxation induced to the quantum system by exchange of angular momentum with the lattice phonons, parametrised by the inverse of the longitudinal relaxation time, T1, which is the upper limit for Tmvia the dependence Tm ≤ 2T1, increases with increasing external magnetic field, especially when determined by a direct process.70,71

We probe herein the relative importance of these different decoherence mechanisms to Tm. We have previously studied Gd@Y(trensal) at the 0.5% doping level in the isostructural diamagnetic host Y(trensal) (0.5%, Gd0.005Y0.995(trensal)), with H3trensal = 2,2′,2′′-tris(salicylideneimino)triethylamine)), by pulse Electron Paramagnetic Resonance (EPR) at high frequency (240 GHz, 9 T). These studies revealed one of the highest Tm (12 μs at 3 K) amongst the to date proposed 4f molecular qubits.56 However, under these conditions Tm is limited by a T1 of the order of 30 μs at 3 K, by what appears to be a direct process.56 SQUID magnetometry of 0.5% at 0.3 T revealed a T1 of the order of 20 ms at 1.9 K (Fig. S1, S2 and Tables S1, S2†). Other derivatives of Gd(trensal) have been found to have a T1 of hundreds of ms in the magnetic field regime of 1000–5000 G.72,73 Thus, at magnetic fields of the order of the ones involved at X-band EPR (∼9.6 GHz), T1 increases by about 3 orders of magnitude with respect to the one observed at 9 T and so does the upper limit imposed to Tm by T1. We study herein, Tm and T1 of single crystals of Gd@Y(trensal) at 0.5%, 10−1%, 10−2% and 10−3% doping levels by X-band pulse EPR at magnetic fields in the range 0 to 0.7 T, to probe Tm, and the factors that determine it, under these conditions.

Experimental

Sample preparation

Single crystals of Gd0.005Y0.995(trensal) (0.5%), Gd0.001Y0.999(trensal) (10−1%), Gd0.0001Y0.9999(trensal) (10−2%) and Gd0.00001Y0.99999(trensal) (10−3%) were grown according to the literature.74 All chemicals and solvents for the synthesis were obtained from commercial sources except for Gd(OTf)3·9H2O and Y(OTf)3·9H2O which were prepared from the corresponding oxide and triflic acid as described in the literature.75

Electron paramagnetic resonance (EPR)

All pulse EPR measurements were performed on single crystals of Gd(trensal) doped into the isostructural diamagnetic host Y(trensal).

Measurements on 0.5%

Pulse EPR spectra were recorded at X-band on a Bruker Elexsys 580 spectrometer fitted with a Bruker ER 4118X-MD5 dielectric resonator. The setup was cooled with a Bruker Flexline Cryogen-free system and the temperature controlled with an Oxford Instruments Mercury ITC. A single crystal of 0.5% was placed with the unique axis parallel to the magnetic field (B0 ∥ C3). The crystal alignment was checked by comparing echo-detected field-sweep (EDFS) measurements to a simulated spectrum (Fig. 2, top) based on the crystal field (CF) parameters determined in our previous study (Table S3†).56

Fig. 2. EDFS (blue) of 0.5% with B0 ∥ C3 (top) and of 10−3% with B0 ⊥ C3 (bottom) at 5.5 K, compared to simulations (black) using previously determined CF parameters (Table S3†).

Fig. 2

Open in a new tab

Measurements on 10−1%, 10−2% and 10−3%

Pulse EPR spectra were recorded at X-band on a Bruker Elexsys 580 spectrometer fitted with a Bruker ER 4118X-MD5W dielectric resonator. The setup was cooled by an oxford instruments flow cryostat and the temperature controlled with an Oxford Instruments Mercury ITC. Because of their larger than 3 mm length, single crystals of 10−3% were placed with the unique axis vertical, thus perpendicular to the magnetic field (B0 ⊥ C3), which is applied in the horizontal plane. EDFS spectra (Fig. 2, bottom for 10−3%) were measured using a standard Hahn echo sequence π/2–τ–π–τ–echo with π-pulses of 32 ns and τ of 300 ns.

T 1 and Tm measurements

T 1 and Tm were measured using inversion recovery and Hahn-echo decay pulse sequences π–t–π/2–τ–π–τ–echo and π/2–τ–π–τ–echo, respectively. In the case of Tm measurements, a large degree of ESEEM was observed with a frequency of ω ≈ 1 MHz. At low temperatures, the ESEEM effect was suppressed by use of long pulses. Due to the decrease in Tm with increasing temperature, this was not possible at temperatures above 20 K. Tm decays were modelled as mono-exponential ones. T1 decays of 10−3% were also modelled as mono-exponential ones, while those of 0.5% required use of bi-exponential functions.

Partial refocusing pulses

Instantaneous diffusion was probed by use of a π/2–τ–Θ–τ–echo sequence,67,76,77 with 80 ns π/2 pulses and Θ pulses of 40, 80, 120 and 160 ns.

Carr-Purcell-Meiboom-Gill (CPMG) sequence

Relaxation traces using CPMG dynamic refocusing,67,78,79 consisting of the sequence: πx/2–[τ–πy–τ]n–echo, with n up to 120, were measured using π/2 pulse lengths of 16 ns.

Results and discussion

Gd(trensal), as other members of the Ln(trensal) family,80–82 crystallises in the trigonal space group P3̄c1. The Gd(iii) centre is hepta-coordinated by the trensal ligand, with the ligand forming a three-armed chiral screw around the metal centre (Fig. 1). In the crystal structure, the crystallographic and molecular C3 axes coincide. They also coincide with the hexagonal axis of the macroscopic crystal. A single crystal of Gd(trensal) was oriented parallel or perpendicular to the magnetic field, B0. The EDFS spectrum of 0.5% with B0 ∥ C3 shows the expected seven allowed EPR transitions of the 8S7/2 term at the same magnetic fields as predicted by the simulation (Fig. 2, top, S3 and S4†). For 10−3% and B0 ⊥ C3, only 6 transitions were observed as the transitions between levels 1–2, (1 ↔ 2)⊥, and 2–3, (2 ↔ 3)⊥, overlap (Fig. 2, bottom and S5).

Fig. 1. Molecular structure of Gd(trensal) (a) seen along the threefold symmetry axis and (b) seen from the side. Colour code: C, gray; H, white; N, nitrogen; O, oxygen; Gd, cyan.

Fig. 1

Open in a new tab

Relaxation

Longitudinal (T1) and transverse (Tm) relaxation measurements were performed on each of the above-mentioned observed lines (Fig. S6–S32†), as described in previous sections. The measured T1 values for the various investigated EPR transitions are significantly different. For 0.5% and B0 ∥ C3, an increase of T1 with magnetic field is observed (Fig. 3, top), where T1 increases from the lowest value of 863 μs for the (1 ↔ 2)∥ transition to the highest value at 3.5 ms for the (4 ↔ 5)∥ transition (Fig. 3, top), a fourfold increase. Qualitatively similar results are obtained for 0.5% and B0 ⊥ C3 (Fig. S43†). In contrast, for 10−3% and B0 ⊥ C3, the longest T1 is observed for transition (7 ↔ 8)⊥ with the (5 ↔ 6)⊥ transition having the shortest T1 (Fig. 3, bottom). This indicates that both the magnetic field and the nature of the eigenvectors involved in the particular EPR transition influence T1, both doing so via the magnetoelastic coupling terms 〈f|∂Ĥ/∂R|i〉, with |i〉 and |f〉 the eigenvectors involved in the transition and ∂Ĥ/∂R the derivative of the Hamiltonian due to the ∂R displacement.70,71 Furthermore, as previously discussed, a very large increase in T1 was observed going from high field/frequency measurements to lower field/frequency ones. For 0.5% and B0 ∥ C3, the T1 of the (7 ↔ 8)∥ transition (Fig. 3, top) increases by two orders of magnitude with respect to the one determined at 240 GHz, from 24 μs at 240 GHz to 2.5 ms at 9.7 GHz at 5.5 K, hence, accordingly lifting the upper Tm limit. However, the observed Tm does not follow this increase in T1. In contrast, the (7 ↔ 8)∥ transition has a significantly lower Tm at X-band than at 240 GHz (1.6 μs versus 4.3 μs, respectively). As previously mentioned, the relative contributions to decoherence (Δω/ω, with Δω the dephasing) induced from local magnetic field fluctuations due to environmental dynamics decrease with increasing transition frequency, ω. This results in a progressive insensitivity of the dynamic state towards decoherence with increasing transition frequency. For 0.5% and B0 ∥ C3 a slight increase of Tm with field is observed while for 10−3% and B0 ⊥ C3, Tm shows non-monotonic behaviour with the central line (4 ↔ 5)⊥ transition (Fig. 3, bottom) displaying the shortest Tm. Again, as for T1, both the magnetic field and the composition of the involved eigenstates influence Tm. Qualitatively similar results are obtained for 0.5% and B0 ⊥ C3 (Fig. S43†).

Fig. 3. Field dependence of T1 and Tm for 0.5% with B0 ∥ C3 (top) and for 10−3% with B0 ⊥ C3 (bottom) at 5.5 K.

Fig. 3

Open in a new tab

With respect to the temperature, T, dependence of the relaxation dynamics, as anticipated, T1 of all investigated resonances is highly temperature dependent, decreasing by three to four orders of magnitude from 5 to 125 K (Fig. 4). At X-band, a T1 ∝ T−2.9 dependence is observed in this T range, which is a higher exponent dependence than what observed at 240 GHz (T1 ∝ T−0.44) reflecting the increasing dominance with magnetic field of the direct process as compared to Raman ones. Dynamic susceptibility thermodynamic SQUID measurements of 0.5% between 4.9 and 1.9 K (Fig. 4, S1, S2 and Tables S1, S2†) revealed a T1 ∝ T−1.8 dependence indicating that longitudinal relaxation is determined by a combination of processes, likely direct and Raman ones, as determined in previous studies.65,80T1 values obtained by pulse EPR measurements below 5 K deviate from the T1 ∝ T−2.9 behaviour and are closer to the T1 ∝ T−1.8 dependence.

Fig. 4. Temperature dependence of T1 and Tm obtained by EPR measurements of 0.5% and 10−3% with B0 ∥ C3 and B0 ⊥ C3. The dashed lines are linear fits to log(T1) vs. log(T) as described in the main text.

Fig. 4

Open in a new tab

Sources of decoherence

Given that at low temperatures the determined Tm of Gd(trensal) at X-band is about two to three orders of magnitude lower than the corresponding T1 (Fig. 4), we now investigate the factors that limit it under these experimental conditions. In contrast to T1, Tm shows little temperature dependence up to about 40 K (Fig. 4). Above this temperature, Tm becomes limited by T1 and hence decreases accordingly, ultimately reaching the lowest detectable by our instrument level at about 100 K for B0 ⊥ C3 and 125 K for B0 ∥ C3.

Magnetic dipole interactions between Gd(trensal) moieties distributed within the diamagnetic Y(trensal) lattice induce decoherence via dipolar magnetic field fluctuations due to indirect spin flip-flops involving neighbouring Gd(trensal) sites. The local magnetic field, Bloc, generated by a magnetic dipole at distance r from the dipole is inversely proportional to the cube of r (Bloc ∝ r−3). Thus, magnetic field fluctuations due to dipolar interactions should also scale accordingly. Under these conditions, one would expect an inverse linear dependence of Tm to the concentration of paramagnetic sites in the host lattice until indirect electron–electron dipolar interactions cease to constitute the limiting factor. However, it has been shown that deviations from this simple behaviour can be observed when the coupling of the paramagnet to the spin bath, as well as the dynamics of the spin bath, are explicitly taken into account.83 To determine the dependence of Tm on the concentration, C, of Gd(trensal) sites in the Y(trensal) lattice, we studied samples diluted between 0.5 and 10−3% (0.5%, 10−1%, 10−2% and 10−3%). For B0 ⊥ C3, we observe that while Tm initially increases fast with inverse concentration, at doping levels between 10−2% and 10−3%Tm increases only marginally with C−1, thus shows signs of saturation (Fig. 5). This indicates that at the lowest studied doping level of 10−3%, corresponding to a 30 μM molarity for Gd(trensal), dipolar interactions cease to be the dominating limiting factor for Tm (Fig. 5). Given that the typical volume of a herein measured Gd(trensal) crystal is of the order of 50 mm3, this corresponds to about 1015 measured spins at a doping level of 10−3%, which corresponds to the lowest limit of number of spins that can be measured within a convenient amount of time (few minutes) with our experimental setup at X-band. Thus, while diluting from 0.5% to 10−3% led roughly to an increase of an order of magnitude in Tm, further dilution is not expected to lead to a further substantial increase in Tm. In addition, the paramagnetic ion content of samples more dilute than 10−3 reaches the detection limit of our setup at X-band, estimated to be roughly 1012 to 1013 spins, and would require much longer measurement times to achieve satisfactory signal to noise ratios.

Fig. 5. Inverse concentration dependence of Tm with B0 ⊥ C3 at 5 (10−1% and 10−2%) and 5.5 (0.5% and 10−3%) K. The solid lines are guides for the eye.

Fig. 5

Open in a new tab

Instantaneous diffusion contributions to decoherence occur as a consequence of neighbouring spins to the observed one being excited by the electromagnetic excitation pulse, hence causing a variation of the local field at the observed site. Instantaneous diffusion is often the limiting factor for impurities or defects in spin-free solid state materials such as silicon or diamond.76,77 The occurrence of this decoherence mechanism can be investigated by varying the macroscopic turning angle, Θ, of the refocusing pulses employed in a Hahn echo sequence, hence addressing fewer spins at the microscopic level. The dependence of Tm to Θ is expected to follow:67,76graphic file with name d4sc05304d-t1.jpgwith T2(id), T2(dff) and T2(iff) being the instantaneous diffusion, direct flip flop and indirect flip flop contributions to Tm, respectively. T2(dff) is often small compared to the other terms. Both T2(id) and T2(dff) scale as sin2(Θ/2), while T2(iff) is independent of Θ. Thus, extrapolation to Θ = 0 corresponds to a decoherence regime where complete suppression of the instantaneous diffusion and direct flip flop contributions occurs, leaving only the one from indirect flip flops (T−12(iff)) which is also called spectral diffusion. The experimental realisation of this regime is achieved by either reducing the amplitude of the magnetic field component (B1), either the length, of the refocusing pulse (Θ pulse in Fig. 6) with respect to what required for a π pulse. Herein we investigate resolved resonances from single crystals probing unique molecular orientations. Thus, we chose to vary the length of the refocusing pulse as the change in the excitation profile related to the variation of the pulse length is not expected to result in different orientational sub-populations being probed. Negligible variation of Tm with Θ was observed for all the investigated transitions (Fig. 6 and S33–S36†) suggesting that direct flip-flops and instantaneous diffusion are not dominant decoherence mechanisms under these experimental conditions. This is also expected as the sample is relatively highly magnetically dilute. Furthermore, the thermal population distribution of the mS sublevels of Gd(iii) results in only a single sublevel being resonantly addressed out of 8 possible, effectively resulting in a smaller fraction of the spins being in resonance with the microwave pulse.

Fig. 6. T m of 10−3% with B0 ⊥ C3 at 5.5 K measured via a Hahn echo sequence with variable length of the refocusing pulse at 4367, 3817, 3249 and 2917 Gauss, showing no angle dependence. The solid lines are guides for the eye.

Fig. 6

Open in a new tab

Decoherence originating from indirect flip flops (spectral diffusion) occurs as a consequence of the stochastic noise of nearby spin pairs flipping during the Hahn echo sequence. Spectral diffusion effects can be remediated for by dynamic decoupling,67,84,85 for example by employing the CPMG pulse sequence where a π-pulse-train refocuses the transverse magnetization.67,78,79 This effectively acts as a frequency filter for magnetic noise, giving rise to much longer transverse relaxation time. Application of the CPMG pulse sequence for 10−3% with B0 ⊥ C3 and varying length of the pulse train revealed a substantial increase of Tm (Fig. 7 and S37–S39 and Table S6†). In particular, for the (6 ↔ 7)⊥ transition at 4367 Gauss, Tm increases from about 10.8 μs for n = 0 (Hahn echo) to around 180 μs for n = 180, thus by a factor of 16.4. The linear dependence of Tm on the length of the pulse train indicates that the dominant decoherence mechanism under these experimental conditions is spectral diffusion, which is also expected given the large number of nuclear spin bearing atoms present in the studied crystals. In particular, hydrogen atoms of the lattice are expected to heavily induce decoherence.41 Thus, we show herein that repetitive refocusing of the transverse magnetisation can substantially increase Tm in nuclear spin-rich media, by dynamically suppressing nuclear spectral diffusion.

Fig. 7. T m of 10−3% with B0 ⊥ C3 at 5.5 K as a function of the number of refocusing CPMG pulses at 4367, 3817, 3249 and 2917 Gauss. The solid lines are guides for the eye.

Fig. 7

Open in a new tab

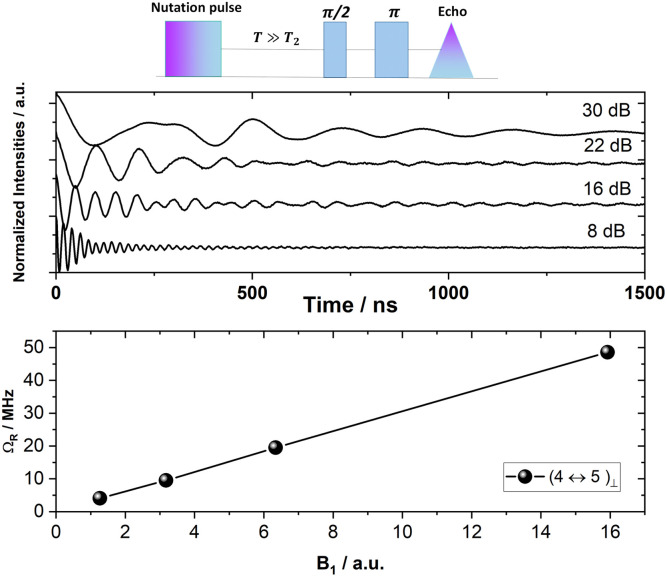
The multilevel structure of molecular magnetic materials has been proposed for the implementation of quantum error correction algorithms or of multiple qubits. For this purpose, the ability to place in a coherent superposition any two arbitrary eigenstates, say |i〉 and |j〉, of the system is required. However, it has been shown that this universality can also be achieved by sequentially addressing several allowed transitions connecting the two eigenstates of interest, |i〉 and |j〉, with other eigenstates of the Hilbert space, say |k〉. Thus a coherent superposition of |i〉 and |j〉 can be achieved via the |k〉 states (|i〉↔|k〉↔|j〉).86 To demonstrate that the spin eigenstates of Gd(trensal) can be placed in coherent superposition, we performed transient nutation experiments (θ–T–π/2–τ–π–τ–echo, Fig. 8 and S40–S42†). Using a Fourier transform of the time trace of the echo evolution, the Rabi frequency, ΩR, at each power level for the different allowed transitions was obtained. For Rabi oscillations, ΩR scales linearly with microwave power, as:graphic file with name d4sc05304d-t2.jpgwith g the g-factor, μB the Bohr magneton, B1 the magnetic field of the microwave pulse, ℏ the reduced Planck constant and S and mS the spin angular momentum and its projection on the quantisation axis, respectively. A linear fit to the Rabi oscillation frequency as a function of B1 shows that the oscillations observed in the nutation experiment are indeed Rabi oscillations (Fig. 8 and S42†).

Fig. 8. (Top): Schematic of the transient nutation pulse sequence and associated Rabi oscillations of 10−3% with B0 ⊥ C3 at 5.5 K for the central (4 ↔ 5)⊥ transition. (Bottom): Rabi frequencies plotted against the relative magnitude of the magnetic field component of the microwave pulse (B1).

Fig. 8

Open in a new tab

The above described Rabi-nutation experiments also provide the timescale, TG, for single qubit gates, for example π or π/2 rotations. It can for example be seen from Fig. 8, that the duration of a π rotation is of the order of 10 ns at the highest power investigated (9 dB). This time duration for a π gate combined with the long coherence times achieved via CPMG, results in a Tm/TG ratio of the order of 104 (Table 1), which is the desired order of magnitude for the figure of merit of a qubit. This demonstrates that quantum gates implemented on molecular materials can reach fidelities of 99.99% or above.

π-Rotation gate durations, TG, associated phase memory times, Tm and Tm/Tg ratios for four different allowed transitions of Gd(trensal) 10−3% with B0 ⊥ C3.

Transition T G (π-rotation)/ns T m/μs T m/TG
(3 ↔ 4)⊥ 12 109 9083
(4 ↔ 5)⊥ 12 64 5333
(5 ↔ 6)⊥ 10 124 12 400
(6 ↔ 7)⊥ 12 178 14 833
Open in a new tab

Conclusions

We undertook herein a systematic investigation of the mechanisms that induce decoherence in qubits implemented in molecular magnetic materials. We show that in the case that these processes are probed by pulse EPR under the most usual experimental conditions (X-band), nuclear spin spectral diffusion is the dominant process determining decoherence. However, spectral diffusion effects can be remediated for by dynamic refocusing sequences, such as CPMG, even in such dense nuclear spin environments. For the materials investigated herein, the bulk concentration is of 3 M which, for example, corresponds to a concentration of proton nuclear spins of the order of 80 M, given that each molecule has 27 protons. This is a relatively large concentration of nuclear spins that dynamic refocusing is able to remediate for. Thus, it is not absolutely necessary to utilise nuclear spin free environments, such as frozen solution in solvents devoid of nuclear spins, to study the coherent properties of these materials. Furthermore, use of dynamic decoupling allowed Tm of the investigated materials to be increased by two orders of magnitude. This resulted in reaching 180 μs for 120 refocusing pulses with the increase in Tm being linear to the number of refocusing pulses, thus without showing signs of saturation. The obtained Tm's combined with TG's of the order of 10 ns leads to qubit figure of merit ratios of the order of 104. This demonstrates the suitability of molecular magnetic materials for use as hardware for quantum technologies. Chemical engineering of organic scaffolds where protons are exchanged for deuterium that has a significantly lower magnetic moment than protons would allow use of pulse sequences not including dynamic refocusing. Detection of an echo at relatively high temperatures (125 K) indicates that further tuning of the dynamic magnetic properties of lanthanide-based molecular materials can lead to coherent magnetic properties at even higher temperatures, as has been demonstrated in the case of transition metal complexes. Finally, we provide herein detailed solid state relaxation data of lanthanide coordination complexes, obtained on magnetically dilute single crystals of trigonal symmetry.

Data availability

Data for this article, including pulsed EPR data are available as ESI.†

Author contributions

The project was jointly conceived by CDB, SHH and SP. CDB and AS prepared the samples. JBP, MUIC, MR and SHH performed the measurements. CDB, JBP and SHH performed the data analysis, supervised by SP, REPW and EJLM. The manuscript was written jointly by all authors, who all have read and agreed to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

SC-015-D4SC05304D-s001
SC-015-D4SC05304D-s002

Acknowledgments

We thank the Novo Nordisk Foundation for research grant: NNF21OC0070832 Exploratory Interdisciplinary Synergy Programme, NNF20OC0065610 Project Grants in the Natural and Technical Sciences 2020 and NNF21OC0068806 Research Infrastructure – Large equipment and facilities 2021 financing the Copenhagen Pulse-EPR Facility and the EPSRC for grants EP/R011079/1 (Established Career Fellowship to R. E. P. W.), EP/W014521/1 and EP/X034623 (EPR National Research Facility).

†

Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc05304d

Notes and references

  1. Riedel M. F. Bloch I. Debuisschert T. Wilhelm-Mauch F. Pruneri V. Vitanov N. V. Wehner S. Calarco T. Europe's Quantum Flagship is taking off. Europhys. News. 2018;49:30–34. doi: 10.1051/epn/2018506. [DOI] [Google Scholar]
  2. Atzori M. Sessoli R. The Second Quantum Revolution: Role and Challenges of Molecular Chemistry. J. Am. Chem. Soc. 2019;141:11339–11352. doi: 10.1021/jacs.9b00984. [DOI] [PubMed] [Google Scholar]
  3. MacFarlane A. G. J. Dowling J. P. Milburn G. J. Quantum technology: the second quantum revolution. Philos. Trans. R. Soc. London, Ser. A. 2003;361:1655–1674. doi: 10.1098/rsta.2003.1227. [DOI] [PubMed] [Google Scholar]
  4. Awschalom D., Samarth N. and Loss D., Semiconductor Spintronics and Quantum Computation, Springer, Berlin, 2002 [Google Scholar]
  5. Barnett S. M., Quantum information, Oxford University Press, Oxford, 2009 [Google Scholar]
  6. Thiele S. Balestro F. Ballou R. Klyatskaya S. Ruben M. Wernsdorfer W. Electrically driven nuclear spin resonance in single-molecule magnets. Science. 2014;344:1135–1138. doi: 10.1126/science.1249802. [DOI] [PubMed] [Google Scholar]
  7. Ekert A. Jozsa R. Quantum computation and Shor's factoring algorithm. Rev. Mod. Phys. 1996;68:733–753. doi: 10.1103/RevModPhys.68.733. [DOI] [Google Scholar]
  8. Shor P. W., Algorithms for quantum computation: discrete logarithms and factoring, in Proceedings 35th Annual Symposium on Foundations of Computer Science, 1994, pp. 124–134 [Google Scholar]
  9. Daley A. J. Bloch I. Kokail C. Flannigan S. Pearson N. Troyer M. Zoller P. Practical quantum advantage in quantum simulation. Nature. 2022;607:667–676. doi: 10.1038/s41586-022-04940-6. [DOI] [PubMed] [Google Scholar]
  10. Giovannetti V. Lloyd S. Maccone L. Advances in quantum metrology. Nat. Photonics. 2011;5:222–229. doi: 10.1038/nphoton.2011.35. [DOI] [Google Scholar]
  11. Dovzhenko Y. Casola F. Schlotter S. Zhou T. X. Büttner F. Walsworth R. L. Beach G. S. D. Yacoby A. Magnetostatic twists in room-temperature skyrmions explored by nitrogen-vacancy center spin texture reconstruction. Nat. Commun. 2018;9:2712. doi: 10.1038/s41467-018-05158-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lovchinsky I. Sushkov A. O. Urbach E. de Leon N. P. Choi S. De Greve K. Evans R. Gertner R. Bersin E. Müller C. McGuinness L. Jelezko F. Walsworth R. L. Park H. Lukin M. D. Nuclear magnetic resonance detection and spectroscopy of single proteins using quantum logic. Science. 2016;351:836–841. doi: 10.1126/science.aad8022. [DOI] [PubMed] [Google Scholar]
  13. Shi F. Zhang Q. Wang P. Sun H. Wang J. Rong X. Chen M. Ju C. Reinhard F. Chen H. Wrachtrup J. Wang J. Du J. Single-protein spin resonance spectroscopy under ambient conditions. Science. 2015;347:1135–1138. doi: 10.1126/science.aaa2253. [DOI] [PubMed] [Google Scholar]
  14. Barry J. F. Turner M. J. Schloss J. M. Glenn D. R. Song Y. Lukin M. D. Park H. Walsworth R. L. Optical magnetic detection of single-neuron action potentials using quantum defects in diamond. Proc. Natl. Acad. Sci. U. S. A. 2016;113:14133–14138. doi: 10.1073/pnas.1601513113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Yu C.-J. von Kugelgen S. Laorenza D. W. Freedman D. E. A Molecular Approach to Quantum Sensing. ACS Cent. Sci. 2021;7:712–723. doi: 10.1021/acscentsci.0c00737. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Aslam N. Zhou H. Urbach E. K. Turner M. J. Walsworth R. L. Lukin M. D. Park H. Quantum sensors for biomedical applications. Nat. Rev. Phys. 2023;5:157–169. doi: 10.1038/s42254-023-00558-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Zapatero V. van Leent T. Arnon-Friedman R. Liu W.-Z. Zhang Q. Weinfurter H. Curty M. Advances in device-independent quantum key distribution. Npj Quantum Inf. 2023;9:10. doi: 10.1038/s41534-023-00684-x. [DOI] [Google Scholar]
  18. Moreau P.-A. Toninelli E. Gregory T. Padgett M. J. Imaging with quantum states of light. Nat. Rev. Phys. 2019;1:367–380. doi: 10.1038/s42254-019-0056-0. [DOI] [Google Scholar]
  19. Arute F. Arya K. Babbush R. Bacon D. Bardin J. C. Barends R. Biswas R. Boixo S. Brandao F. Buell D. A. Burkett B. Chen Y. Chen Z. Chiaro B. Collins R. Courtney W. Dunsworth A. Farhi E. Foxen B. Fowler A. Gidney C. Giustina M. Graff R. Guerin K. Habegger S. Harrigan M. P. Hartmann M. J. Ho A. Hoffmann M. Huang T. Humble T. S. Isakov S. V. Jeffrey E. Jiang Z. Kafri D. Kechedzhi K. Kelly J. Klimov P. V. Knysh S. Korotkov A. Kostritsa F. Landhuis D. Lindmark M. Lucero E. Lyakh D. Mandra S. McClean J. R. McEwen M. Megrant A. Mi X. Michielsen K. Mohseni M. Mutus J. Naaman O. Neeley M. Neill C. Niu M. Y. Ostby E. Petukhov A. Platt J. C. Quintana C. Rieffel E. G. Roushan P. Rubin N. C. Sank D. Satzinger K. J. Smelyanskiy V. Sung K. J. Trevithick M. D. Vainsencher A. Villalonga B. White T. Yao Z. J. Yeh P. Zalcman A. Neven H. Martinis J. M. Quantum supremacy using a programmable superconducting processor. Nature. 2019;574:505–510. doi: 10.1038/s41586-019-1666-5. [DOI] [PubMed] [Google Scholar]
  20. Kjaergaard M. Schwartz M. E. Braumüller J. Krantz P. Wang J. I. J. Gustavsson S. Oliver W. D. Superconducting Qubits: Current State of Play. Annu. Rev. Condens. Matter Phys. 2020;11:369–395. doi: 10.1146/annurev-conmatphys-031119-050605. [DOI] [Google Scholar]
  21. Knill E. Laflamme R. Milburn G. J. A scheme for efficient quantum computation with linear optics. Nature. 2001;409:46–52. doi: 10.1038/35051009. [DOI] [PubMed] [Google Scholar]
  22. Madsen L. S. Laudenbach F. Askarani M. F. Rortais F. Vincent T. Bulmer J. F. F. Miatto F. M. Neuhaus L. Helt L. G. Collins M. J. Lita A. E. Gerrits T. Nam S. W. Vaidya V. D. Menotti M. Dhand I. Vernon Z. Quesada N. Lavoie J. Quantum computational advantage with a programmable photonic processor. Nature. 2022;606:75–81. doi: 10.1038/s41586-022-04725-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Dutt M. V. Childress L. Jiang L. Togan E. Maze J. Jelezko F. Zibrov A. S. Hemmer P. R. Lukin M. D. Quantum register based on individual electronic and nuclear spin qubits in diamond. Science. 2007;316:1312–1316. doi: 10.1126/science.1139831. [DOI] [PubMed] [Google Scholar]
  24. Maurer P. C. Kucsko G. Latta C. Jiang L. Yao N. Y. Bennett S. D. Pastawski F. Hunger D. Chisholm N. Markham M. Twitchen D. J. Cirac J. I. Lukin M. D. Room-temperature quantum bit memory exceeding one second. Science. 2012;336:1283–1286. doi: 10.1126/science.1220513. [DOI] [PubMed] [Google Scholar]
  25. Gulka M. Wirtitsch D. Ivady V. Vodnik J. Hruby J. Magchiels G. Bourgeois E. Gali A. Trupke M. Nesladek M. Room-temperature control and electrical readout of individual nitrogen-vacancy nuclear spins. Nat. Commun. 2021;12:4421. doi: 10.1038/s41467-021-24494-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Pla J. J. Tan K. Y. Dehollain J. P. Lim W. H. Morton J. J. Jamieson D. N. Dzurak A. S. Morello A. A single-atom electron spin qubit in silicon. Nature. 2012;489:541–545. doi: 10.1038/nature11449. [DOI] [PubMed] [Google Scholar]
  27. Steger M. Saeedi K. Thewalt M. L. Morton J. J. Riemann H. Abrosimov N. V. Becker P. Pohl H. J. Quantum information storage for over 180 s using donor spins in a 28Si “semiconductor vacuum”. Science. 2012;336:1280–1283. doi: 10.1126/science.1217635. [DOI] [PubMed] [Google Scholar]
  28. Morley G. W. Warner M. Stoneham A. M. Greenland P. T. van Tol J. Kay C. W. Aeppli G. The initialization and manipulation of quantum information stored in silicon by bismuth dopants. Nat. Mater. 2010;9:725–729. doi: 10.1038/nmat2828. [DOI] [PubMed] [Google Scholar]
  29. Schafer V. M. Ballance C. J. Thirumalai K. Stephenson L. J. Ballance T. G. Steane A. M. Lucas D. M. Fast quantum logic gates with trapped-ion qubits. Nature. 2018;555:75–78. doi: 10.1038/nature25737. [DOI] [PubMed] [Google Scholar]
  30. Blatt R. Wineland D. Entangled states of trapped atomic ions. Nature. 2008;453:1008–1015. doi: 10.1038/nature07125. [DOI] [PubMed] [Google Scholar]
  31. Maylander M. Chen S. Lorenzo E. R. Wasielewski M. R. Richert S. Exploring Photogenerated Molecular Quartet States as Spin Qubits and Qudits. J. Am. Chem. Soc. 2021;143:7050–7058. doi: 10.1021/jacs.1c01620. [DOI] [PubMed] [Google Scholar]
  32. Olshansky J. H. Krzyaniak M. D. Young R. M. Wasielewski M. R. Photogenerated Spin-Entangled Qubit (Radical) Pairs in DNA Hairpins: Observation of Spin Delocalization and Coherence. J. Am. Chem. Soc. 2019;141:2152–2160. doi: 10.1021/jacs.8b13155. [DOI] [PubMed] [Google Scholar]
  33. Maylander M. Kopp K. Nolden O. Franz M. Thielert P. Vargas Jentzsch A. Gilch P. Schiemann O. Richert S. PDI-trityl dyads as photogenerated molecular spin qubit candidates. Chem. Sci. 2023;14:10727–10735. doi: 10.1039/D3SC04375D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hanson R. Awschalom D. D. Coherent manipulation of single spins in semiconductors. Nature. 2008;453:1043–1049. doi: 10.1038/nature07129. [DOI] [PubMed] [Google Scholar]
  35. Atzori M. Tesi L. Morra E. Chiesa M. Sorace L. Sessoli R. Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits. J. Am. Chem. Soc. 2016;138:2154–2157. doi: 10.1021/jacs.5b13408. [DOI] [PubMed] [Google Scholar]
  36. Atzori M. Benci S. Morra E. Tesi L. Chiesa M. Torre R. Sorace L. Sessoli R. Structural Effects on the Spin Dynamics of Potential Molecular Qubits. Inorg. Chem. 2018;57:731–740. doi: 10.1021/acs.inorgchem.7b02616. [DOI] [PubMed] [Google Scholar]
  37. Gaita-Arino A. Luis F. Hill S. Coronado E. Molecular spins for quantum computation. Nat. Chem. 2019;11:301–309. doi: 10.1038/s41557-019-0232-y. [DOI] [PubMed] [Google Scholar]
  38. Zadrozny J. M. Niklas J. Poluektov O. G. Freedman D. E. Multiple quantum coherences from hyperfine transitions in a vanadium(IV) complex. J. Am. Chem. Soc. 2014;136:15841–15844. doi: 10.1021/ja507846k. [DOI] [PubMed] [Google Scholar]
  39. Zadrozny J. M. Niklas J. Poluektov O. G. Freedman D. E. Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit. ACS Cent. Sci. 2015;1:488–492. doi: 10.1021/acscentsci.5b00338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Yu C. J. Graham M. J. Zadrozny J. M. Niklas J. Krzyaniak M. D. Wasielewski M. R. Poluektov O. G. Freedman D. E. Long Coherence Times in Nuclear Spin-Free Vanadyl Qubits. J. Am. Chem. Soc. 2016;138:14678–14685. doi: 10.1021/jacs.6b08467. [DOI] [PubMed] [Google Scholar]
  41. Graham M. J. Yu C. J. Krzyaniak M. D. Wasielewski M. R. Freedman D. E. Synthetic Approach To Determine the Effect of Nuclear Spin Distance on Electronic Spin Decoherence. J. Am. Chem. Soc. 2017;139:3196–3201. doi: 10.1021/jacs.6b13030. [DOI] [PubMed] [Google Scholar]
  42. Bader K. Dengler D. Lenz S. Endeward B. Jiang S. D. Neugebauer P. van Slageren J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014;5:5304. doi: 10.1038/ncomms6304. [DOI] [PubMed] [Google Scholar]
  43. Ardavan A. Rival O. Morton J. J. Blundell S. J. Tyryshkin A. M. Timco G. A. Winpenny R. E. Will spin-relaxation times in molecular magnets permit quantum information processing? Phys. Rev. Lett. 2007;98:057201. doi: 10.1103/PhysRevLett.98.057201. [DOI] [PubMed] [Google Scholar]
  44. Lenz S. Bamberger H. Hallmen P. P. Thiebes Y. Otto S. Heinze K. van Slageren J. Chromium(iii)-based potential molecular quantum bits with long coherence times. Phys. Chem. Chem. Phys. 2019;21:6976–6983. doi: 10.1039/C9CP00745H. [DOI] [PubMed] [Google Scholar]
  45. Fataftah M. S. Zadrozny J. M. Coste S. C. Graham M. J. Rogers D. M. Freedman D. E. Employing Forbidden Transitions as Qubits in a Nuclear Spin-Free Chromium Complex. J. Am. Chem. Soc. 2016;138:1344–1348. doi: 10.1021/jacs.5b11802. [DOI] [PubMed] [Google Scholar]
  46. Wojnar M. K. Laorenza D. W. Schaller R. D. Freedman D. E. Nickel(II) Metal Complexes as Optically Addressable Qubit Candidates. J. Am. Chem. Soc. 2020;142:14826–14830. doi: 10.1021/jacs.0c06909. [DOI] [PubMed] [Google Scholar]
  47. Vincent R. Klyatskaya S. Ruben M. Wernsdorfer W. Balestro F. Electronic read-out of a single nuclear spin using a molecular spin transistor. Nature. 2012;488:357–360. doi: 10.1038/nature11341. [DOI] [PubMed] [Google Scholar]
  48. Thiele S. Balestro F. Ballou R. Klyatskaya S. Ruben M. Wernsdorfer W. Electrically driven nuclear spin resonance in single-molecule magnets. Science. 2014;344:1135–1138. doi: 10.1126/science.1249802. [DOI] [PubMed] [Google Scholar]
  49. Shiddiq M. Komijani D. Duan Y. Gaita-Arino A. Coronado E. Hill S. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature. 2016;531:348–351. doi: 10.1038/nature16984. [DOI] [PubMed] [Google Scholar]
  50. Pedersen K. S. Ariciu A. M. McAdams S. Weihe H. Bendix J. Tuna F. Piligkos S. Toward Molecular 4f Single-Ion Magnet Qubits. J. Am. Chem. Soc. 2016;138:5801–5804. doi: 10.1021/jacs.6b02702. [DOI] [PubMed] [Google Scholar]
  51. Handzlik G. Magott M. Arczyński M. Sheveleva A. M. Tuna F. Sarewicz M. Osyczka A. Rams M. Vieru V. Chibotaru L. F. Pinkowicz D. Magnetization Dynamics and Coherent Spin Manipulation of a Propeller Gd(III) Complex with the Smallest Helicene Ligand. J. Phys. Chem. Lett. 2020;11:1508–1515. doi: 10.1021/acs.jpclett.9b03275. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Ariciu A. M. Woen D. H. Huh D. N. Nodaraki L. E. Kostopoulos A. K. Goodwin C. A. P. Chilton N. F. McInnes E. J. L. Winpenny R. E. P. Evans W. J. Tuna F. Engineering electronic structure to prolong relaxation times in molecular qubits by minimising orbital angular momentum. Nat. Commun. 2019;10:3330. doi: 10.1038/s41467-019-11309-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Chicco S. Allodi G. Chiesa A. Garlatti E. Buch C. D. Santini P. De Renzi R. Piligkos S. Carretta S. Proof-of-Concept Quantum Simulator Based on Molecular Spin Qudits. J. Am. Chem. Soc. 2024;146:1053–1061. doi: 10.1021/jacs.3c12008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Carretta S. Zueco D. Chiesa A. Gómez-León Á. Luis F. A perspective on scaling up quantum computation with molecular spins. Appl. Phys. Lett. 2021;118:240501. doi: 10.1063/5.0053378. [DOI] [Google Scholar]
  55. Martínez-Pérez M. J. Cardona-Serra S. Schlegel C. Moro F. Alonso P. J. Prima-García H. Clemente-Juan J. M. Evangelisti M. Gaita-Ariño A. Sesé J. van Slageren J. Coronado E. Luis F. Gd-Based Single-Ion Magnets with Tunable Magnetic Anisotropy: Molecular Design of Spin Qubits. Phys. Rev. Lett. 2012;108:247213. doi: 10.1103/PhysRevLett.108.247213. [DOI] [PubMed] [Google Scholar]
  56. Buch C. D. Kundu K. Marbey J. J. van Tol J. Weihe H. Hill S. Piligkos S. Spin-Lattice Relaxation Decoherence Suppression in Vanishing Orbital Angular Momentum Qubits. J. Am. Chem. Soc. 2022;144:17597–17603. doi: 10.1021/jacs.2c07057. [DOI] [PubMed] [Google Scholar]
  57. Hussain R. Allodi G. Chiesa A. Garlatti E. Mitcov D. Konstantatos A. Pedersen K. S. De Renzi R. Piligkos S. Carretta S. Coherent Manipulation of a Molecular Ln-Based Nuclear Qudit Coupled to an Electron Qubit. J. Am. Chem. Soc. 2018;140:9814–9818. doi: 10.1021/jacs.8b05934. [DOI] [PubMed] [Google Scholar]
  58. Lockyer S. J. Chiesa A. Brookfield A. Timco G. A. Whitehead G. F. S. McInnes E. J. L. Carretta S. Winpenny R. E. P. Five-Spin Supramolecule for Simulating Quantum Decoherence of Bell States. J. Am. Chem. Soc. 2022;144:16086–16092. doi: 10.1021/jacs.2c06384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Lockyer S. J. Chiesa A. Timco G. A. McInnes E. J. L. Bennett T. S. Vitorica-Yrezebal I. J. Carretta S. Winpenny R. E. P. Targeting molecular quantum memory with embedded error correction. Chem. Sci. 2021;12:9104–9113. doi: 10.1039/D1SC01506K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Jenkins M. D. Duan Y. Diosdado B. García-Ripoll J. J. Gaita-Ariño A. Giménez-Saiz C. Alonso P. J. Coronado E. Luis F. Coherent manipulation of three-qubit states in a molecular single-ion magnet. Phys. Rev. B. 2017;95:064423. doi: 10.1103/PhysRevB.95.064423. [DOI] [Google Scholar]
  61. Gimeno I. Urtizberea A. Román-Roche J. Zueco D. Camón A. Alonso P. J. Roubeau O. Luis F. Broad-band spectroscopy of a vanadyl porphyrin: a model electronuclear spin qudit. Chem. Sci. 2021;12:5621–5630. doi: 10.1039/D1SC00564B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Aguilà D. Barrios L. A. Velasco V. Roubeau O. Repollés A. Alonso P. J. Sesé J. Teat S. J. Luis F. Aromí G. Heterodimetallic [LnLn'] Lanthanide Complexes: Toward a Chemical Design of Two-Qubit Molecular Spin Quantum Gates. J. Am. Chem. Soc. 2014;136:14215–14222. doi: 10.1021/ja507809w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Godfrin C. Ferhat A. Ballou R. Klyatskaya S. Ruben M. Wernsdorfer W. Balestro F. Operating Quantum States in Single Magnetic Molecules: Implementation of Grover's Quantum Algorithm. Phys. Rev. Lett. 2017;119:187702. doi: 10.1103/PhysRevLett.119.187702. [DOI] [PubMed] [Google Scholar]
  64. Chiesa A. Petiziol F. Macaluso E. Wimberger S. Santini P. Carretta S. Embedded quantum-error correction and controlled-phase gate for molecular spin qubits. AIP Adv. 2021;11:025134. doi: 10.1063/9.0000166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Bode B. E. Fusco E. Nixon R. Buch C. D. Weihe H. Piligkos S. Dipolar-Coupled Entangled Molecular 4f Qubits. J. Am. Chem. Soc. 2023;145:2877–2883. doi: 10.1021/jacs.2c10902. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Little E. J. Mrozek J. Rogers C. J. Liu J. McInnes E. J. L. Bowen A. M. Ardavan A. Winpenny R. E. P. Experimental realisation of multi-qubit gates using electron paramagnetic resonance. Nat. Commun. 2023;14:7029. doi: 10.1038/s41467-023-42169-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Goldfarb D. and Stoll S., EPR Spectroscopy: Fundamentals and Methods, Wiley, 2018 [Google Scholar]
  68. DiVincenzo D. P. The Physical Implementation of Quantum Computation. Fortschr. Phys. 2000;48:771–783. doi: 10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E. [DOI] [Google Scholar]
  69. Takahashi S. Tupitsyn I. S. van Tol J. Beedle C. C. Hendrickson D. N. Stamp P. C. E. Decoherence in crystals of quantum molecular magnets. Nature. 2011;476:76–79. doi: 10.1038/nature10314. [DOI] [PubMed] [Google Scholar]
  70. Shrivastava K. N. Theory of Spin–Lattice Relaxation. Phys. Status Solidi B. 1983;117:437–458. doi: 10.1002/pssb.2221170202. [DOI] [Google Scholar]
  71. Abragam A. and Bleaney B., Electron Paramagnetic Resonance of Transition Ions, Dover, New York, 1986 [Google Scholar]
  72. Lucaccini E. Baldovi J. J. Chelazzi L. Barra A. L. Grepioni F. Costes J. P. Sorace L. Electronic Structure and Magnetic Anisotropy in Lanthanoid Single-Ion Magnets with C(3) Symmetry: The Ln(trenovan) Series. Inorg. Chem. 2017;56:4729–4739. doi: 10.1021/acs.inorgchem.7b00413. [DOI] [PubMed] [Google Scholar]
  73. Buch C. D. Hansen S. H. Tram C. M. Mitcov D. Piligkos S. Functionalized Trigonal Lanthanide Complexes: A New Family of 4f Single-Ion Magnets. Inorg. Chem. 2020;59:16328–16340. doi: 10.1021/acs.inorgchem.0c02121. [DOI] [PubMed] [Google Scholar]
  74. Pedersen K. S. Ungur L. Sigrist M. Sundt A. Schau-Magnussen M. Vieru V. Mutka H. Rols S. Weihe H. Waldmann O. Chibotaru L. F. Bendix J. Dreiser J. Modifying the properties of 4f single-ion magnets by peripheral ligand functionalisation. Chem. Sci. 2014;5:1650–1660. doi: 10.1039/C3SC53044B. [DOI] [Google Scholar]
  75. Vesborg P. C. K. Chorkendorff I. Brock-Nannestad T. Dethlefsen J. R. Bendix J. Note: Simple means for selective removal of the 365 nm line from the Hg spectrum using Dy. Rev. Sci. Instrum. 2011;82:096102. doi: 10.1063/1.3639128. [DOI] [PubMed] [Google Scholar]
  76. Dikarov E. Zgadzai O. Artzi Y. Blank A. Direct Measurement of the Flip-Flop Rate of Electron Spins in the Solid State. Phys. Rev. Appl. 2016;6:044001. doi: 10.1103/PhysRevApplied.6.044001. [DOI] [Google Scholar]
  77. Tyryshkin A. M. Tojo S. Morton J. J. L. Riemann H. Abrosimov N. V. Becker P. Pohl H.-J. Schenkel T. Thewalt M. L. W. Itoh K. M. Lyon S. A. Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater. 2012;11:143–147. doi: 10.1038/nmat3182. [DOI] [PubMed] [Google Scholar]
  78. Carr H. Y. Purcell E. M. Effects of Diffusion on Free Precession in Nuclear Magnetic Resonance Experiments. Phys. Rev. 1954;94:630–638. doi: 10.1103/PhysRev.94.630. [DOI] [Google Scholar]
  79. Meiboom S. Gill D. Modified Spin-Echo Method for Measuring Nuclear Relaxation Times. Rev. Sci. Instrum. 1958;29:688–691. doi: 10.1063/1.1716296. [DOI] [Google Scholar]
  80. Pedersen K. S. Dreiser J. Weihe H. Sibille R. Johannesen H. V. Sørensen M. A. Nielsen B. E. Sigrist M. Mutka H. Rols S. Bendix J. Piligkos S. Design of Single-Molecule Magnets: Insufficiency of the Anisotropy Barrier as the Sole Criterion. Inorg. Chem. 2015;54:7600–7606. doi: 10.1021/acs.inorgchem.5b01209. [DOI] [PubMed] [Google Scholar]
  81. Bernhardt P. V. Flanagan B. M. Riley M. J. Completion of the isomorphous Ln(trensal) series. Aust. J. Chem. 2001;54:229–232. doi: 10.1071/CH01076. [DOI] [Google Scholar]
  82. Kanesato M. Yokoyama T. Synthesis and structural characterization of Ln(III) complexes (Ln = Eu, Gd, Tb, Er, Tm, Lu) of tripodal tris[2-(salicylideneamino)ethyl]amine. Chem. Lett. 1999:137–138. doi: 10.1246/cl.1999.137. https://dx.doi.org/10.1246/cl.1999.137 [DOI] [Google Scholar]
  83. Maze J. R. Taylor J. M. Lukin M. D. Electron spin decoherence of single nitrogen-vacancy defects in diamond. Phys. Rev. B. 2008;78:094303. doi: 10.1103/PhysRevB.78.094303. [DOI] [Google Scholar]
  84. Stoll S. Schweiger A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006;178:42–55. doi: 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
  85. Bar-Gill N. Pham L. M. Jarmola A. Budker D. Walsworth R. L. Solid-state electronic spin coherence time approaching one second. Nat. Commun. 2013;4:1743. doi: 10.1038/ncomms2771. [DOI] [PubMed] [Google Scholar]
  86. Luis F. Alonso P. J. Roubeau O. Velasco V. Zueco D. Aguila D. Martinez J. I. Barrios L. A. Aromi G. A dissymmetric [Gd(2)] coordination molecular dimer hosting six addressable spin qubits. Commun. Chem. 2020;3:176. doi: 10.1038/s42004-020-00422-w. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SC-015-D4SC05304D-s001
SC-015-D4SC05304D-s001.zip (3.3MB, zip)
SC-015-D4SC05304D-s002
SC-015-D4SC05304D-s002.pdf (44.8MB, pdf)

Data Availability Statement

Data for this article, including pulsed EPR data are available as ESI.†

Articles from Chemical Science are provided here courtesy of Royal Society of Chemistry

RESOURCES