Binding kinetics of quaternary ammonium ions in Kcv potassium channels

ABSTRACT

Kcv channels from plant viruses represent the autonomous pore module of potassium channels, devoid of any regulatory domains. These small proteins show very reproducible single-channel behavior in planar lipid bilayers. Thus, they are an optimum system for the study of the biophysics of ion transport and gating. Structural models based on homology modeling have been used successfully, but experimental structural data are currently not available. Here we determine the size of the cytosolic pore entrance by studying the blocker kinetics. Blocker binding and dissociation rate constants ranging from 0.01 to 1000 ms⁻¹ were determined for different quaternary ammonium ions. We found that the cytosolic pore entrance of Kcv_NTS must be at least 11 Å wide. The results further indicate that the residues controlling a cytosolic gate in one of the Kcv isoforms influence blocker binding/dissociation as well as a second gate even when the cytosolic gate is in the open state. The voltage dependence of the rate constant of blocker release is used to test, which blockers bind to the same binding site.

Introduction

Viral Kcv (K⁺ channel from chlorella virus) channels are optimum candidates for the study of conduction and gating mechanisms in the pore of potassium channels. Their small size prevents the interference from regulatory domains and provides results of high reproducibility [1]. There are up to five gating processes already described in these autonomous pores in the range of hundreds of milliseconds to microseconds, which can be kinetically well separated [2,3]. The existence of >80 isoforms in the Kcv family with different properties can serve as a guideline for mutational studies [1,2,4–6]. These benefits of Kcv channels greatly facilitate the determination of molecular parameters such as voltage-dependent ion distribution in the selectivity filter [3,7] and an unusual mechanism for the cytosolic gate in Kcv_S [2].

Currently, no experimental structures for Kcv channels are available. Successful MD (Molecular Dynamics) simulation studies and 3D RISM (3D reference interaction site model) calculations have been done with structural models based on homology modeling and extensive refinements [2,7–9]. The selectivity filter of Kcv channels conforms with the canonical filter structure of the K⁺ channel family, while the cytosolic gate does not. Therefore, it is desirable to have independent experimental structural constraints for this region. Thus, one issue of this work is the determination of the diameter of the cytosolic pore entrance (CPE).

To this end, we use small molecules binding inside ion channel pores and blocking their conductance. The study of this process has often been used for several purposes. In pharmacologically motivated studies, the understanding of the blocking mechanism supports the development of more specific and more effective drugs. Blocker accessibility studies are often used to identify the gate of a channel. In MthK channels, it has been verified in this way that the voltage- and calcium-controlled gate is in the selectivity filter [10,11]. Also for K2P channels, the absence of a cytosolic bundle-crossing gate has been demonstrated with blockers [12].

Here we use the kinetics of blocking by six different quaternary ammonium blockers (QAs) applied to Kcv_NTS for the determination of the accessible diameter of the CPE. In addition, the comparison with Kcv_S was used for the question whether the cytosolic gate in this isoform influences blocker access also in the open state. Kcv_S is less suitable for the determination of the diameter of the CPE because the blocking effect is too small for the reliable determination of the rate constants of blocking at higher negative voltages.

QAs of different sizes are often used to map the diameter of the cytosolic pore entrance (CPE) and the cavity. Due to their physical similarity to hydrated alkali metal ions, QAs ubiquitously block potassium (K⁺) channels from the cytosolic side [13,14] by binding in the aqueous cavity at or near the dehydration site, where the K⁺ ions strip off their water shell prior to entering the selectivity filter [15]. Early studies concluded that the path between the cytosol and the binding site in the squid axon K⁺ channel must be at least 9 Å [13] or 12 Å [16] wide. Studies considering the individual on- and off-rates of the blockers as an alternative or in addition to the apparent dissociation constant provide a more detailed picture on the pore accessibility [17]. In some of these studies, a sudden steep drop (by about a factor of 30) in the on-rate between two QAs of different sizes was interpreted as an indirect measure for the diameter of the CPE [18].

For Kcv_NTS in this study, the accessibility of blockers to their binding site shows that the diameter is more than 11 Å, similar to values found also for other channels with an open bundle crossing [12,17,19].

The second question deals with the kind of mechanisms influencing blocking kinetics. Kcv_S and Kcv_NTS share about 90% sequence identity but differ in the presence (Kcv_S) or absence (Kcv_NTS) of the aforementioned cytosolic gate, which in Kcv_S involves the movement of a phenylalanine side chain [2]. We found that there is a significant difference in the binding and release kinetics for QAs even in the open state between the two channel isoforms. Via mutations at the cytosolic gate, we disprove the assumption that the decrease in the rate constant of blocker binding occurring also in the open state of the inner gate in Kcv_S is caused by diffusion limitation due to narrowing of the pathway by the side chain of F78. In the case of blocker release, the hypothesis of trapping is at least weakened. Instead, it is concluded that the hydrophobicity and/or conformation of the microenvironment at the binding is modified by the residues controlling the gate. This is supported by the finding that part of this microenvironment also influences a second component of the intrinsic sub-millisecond gating at positive voltages.

This topic is of general importance since also other channels have aromatic side chains, which are facing the channel cavity such as the NaK2K channel [20] and Eag1 [21]. In CNG channels, narrowing of the central gate in the cavity is controlled by cGMP binding and also involves a phenylalanine [22].

Materials and methods

Mutagenesis, protein expression, and purification

The genes encoding for Kcv_NTS and Kcv_S were cloned into the pEXP5-CT/TOPO vector (Invitrogen) in previous works [2,23]. A stop codon inserted directly upstream of the coding sequence for the 6×His-tag in the plasmid allows for expression of the native channel proteins. Point mutations were introduced by site-directed mutagenesis using a protocol based on the method described in [24]. All constructs were sequenced by Microsynth Seqlab prior to expression.

For channel expression, an in vitro reaction (Expressway™ Mini Cell-Free Expression System, Invitrogen) was used. MSP1D1-His DMPC nanodiscs (16 µM, Cube Biotech), containing multiple His tags, were added to the expression mixture. Purification was done on a 0.2 mL HisPur^TM Ni-NTA spin column (ThermoFisher Scientific) following the manufacturer’s instructions with one change in the protocol: Neither the washing nor the elution solutions contained salts, only imidazole. This improves the reconstitution efficiency into the bilayer [25].

Lipid bilayer experiments

Vertical planar lipid bilayer experiments were performed at room temperature (20–25°C) as described previously [23]. Briefly, 1,2-diphytanoyl-sn-glycero-3-phosphocholine (DPhPC, Avanti Polar Lipids) membranes were formed using the pseudo-painting/air bubble technique [26] or the monolayer folding technique [27]. The purified channel-nanodisc complexes were diluted with 250 mM imidazole by a factor of 10⁴ to 10⁵, and 1–3 µl of the dilution was added directly to the bilayer in the trans compartment with a bent microliter syringe.

Recordings were done in symmetrical 100 mM KCl, 10 mM HEPES, adjusted to pH 7.0 with KOH. Channel orientation was verified utilizing the known asymmetry of the apparent IV curves of Kcv channels [28]. The trans compartment was grounded, and voltages were applied to the cis compartment. Positive currents in the graphs correspond to outward currents in the in vivo situation.

Constant voltages between +160 mV and −160 mV in steps of 20 mV were applied for 1 to 5 minutes. Currents were measured in voltage-clamp mode via Ag/AgCl electrodes connected to a patch-clamp amplifier (L/M-EPC-7, List-Medical, or Axopatch 200B, Molecular Devices), filtered with a 1-kHz 4-pole Bessel filter and digitized with a sampling frequency of 5 kHz (LIH 1600, HEKA Elektronik). The software Patchmaster (HEKA Elektronik) was used to control voltage protocols and record the currents. Currents recorded at constant voltage after the capacitive artifact following each voltage jump were analyzed. Blocker concentration was changed by replacing an appropriate amount of the solution with a stock solution of the respective QA-chloride in the cis (= cytosolic) chamber and gentle but thorough mixing with a 1 mL pipette. All blocker stock solutions contained 100 mM KCl and 10 mM HEPES. pH was adjusted to 7.0 with KOH.

Abbreviation of blocker names: TMA = tetramethylammonium, TEA = tetraethylammonium, TPrA = tetrapropylammonium, TBA = tetrabutylammonium, TPeA = tetrapentylammonium and THxA = tetrahexylammonium.

Different versions of the same Markov model for the determination of the rate constants of blocking

Figure 1a shows the complete Markov model including blocking and intrinsic gating, which holds for all experiments. From previous investigations [2,7,29], four (Kcv_NTS) to five (Kcv_S) closed states (F (“fast”), M (“medium”), C₁-C₃) and one open state (O) of intrinsic gating are known. C₃ occurs only in Kcv_S, but not in Kcv_NTS. The connection of the blocked state B solely to the open state is justified by the fact that in our steady-state recordings we can measure only those rate constants of blocking during the open state of the channel. Note that we do not exclude an additional closed-state block, however this would not be observable in our experiments. Further details on this argument and a discussion that a closed-state block is unlikely to significantly distort the results for the open-channel block are provided in a previous paper [7]. The wide temporal range of blocking kinetics for the different blockers requires two different methods of analysis (dwell-time analysis and fitting of current amplitude histograms) with different temporal resolution. Consequently, different versions of the full Markov model are used to account for the limitations of the two methods.

Figure 1.

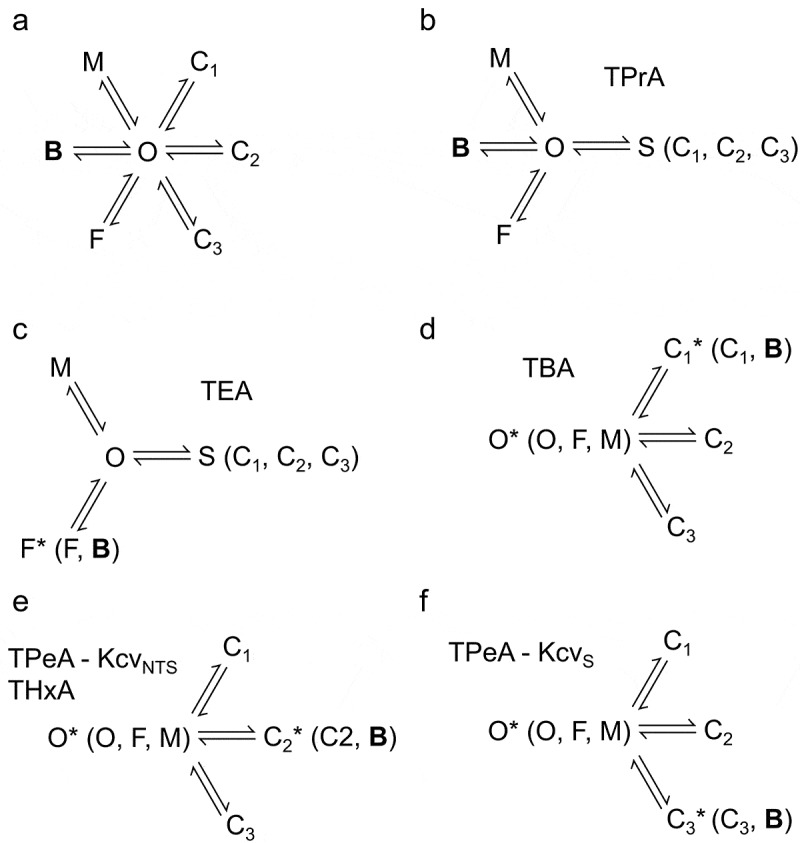
Markov models used for the fitting of the blocking kinetics. (a) The full Markov model with all states as known so far from previous studies [2,3,29] supplemented by the blocked state B. The states C₁, C₂ and C₃ belong to slow gating with dwell times longer than a millisecond, with C₃ occurring only in Kcv_S due to its cytosolic gate [2]. These states can be analyzed by a jump detector and dwell time analysis. F and M belong to fast gating (dwell-time in F about 5 µs) and medium gating (dwell-time in M is voltage-dependent ranging between 150 µs to 40 µs) [3]. (b, c) The models used for the analysis of fast blockers. C₁ - C₃ cannot be resolved by the beta distribution analysis and are merged into S (“slow”). (c) For TEA, B has a similar dwell time as F, so the two states cannot be kinetically separated. (b) for TPrA, this separation is possible [7]. (d,e,f) in the experiments with slow blockers, the dwell time in B coincides with one of the slow states C₁ - C₃. Thus, only two (Kcv_NTS) or three (Kcv_S) closed states are detected in the dwell time histograms. The inclusion of B is identified by concentration dependence. O,F,M are merged into an apparent open state O*. Definition: The rate constant of the transition from a state X to a state Y is called k_XY. k_BO as the rate constant of blocker dissociation is also called k_off.

For the analysis of individual blockers, some of the states in Figure 1a are merged into a representative state to avoid overfitting when the data analysis cannot kinetically separate them. If the blocking events are so fast that they cannot be resolved by full open-closed transitions, they cause excess noise [30–32] of the open-channel current (Figure 3a, below). In this case, they have to be evaluated by fits of amplitude histograms with extended beta distributions (Figure S1 [32,33]). This method cannot distinguish between the slow intrinsic closed states since the related gating events cause equal contributions to the shape of the amplitude histograms. Thus, C₁ – C₃ are merged into one representative slow state S, resulting in the 5-state model used for TPrA (Figure 1b) already previously described [7]. In addition, extended beta distribution analysis faces the same principal problem as dwell-time analysis: If two states have the same average dwell time, they cannot be distinguished. Therefore, state B of the TEA data is furthermore merged with the very short closed state F (Figure 1c) since their dwell times are similar (i.e. k_off is in a similar range as k_FO (Figure S3). For the definition of the rate constants, see legend of Figure 1).

Figure 3.

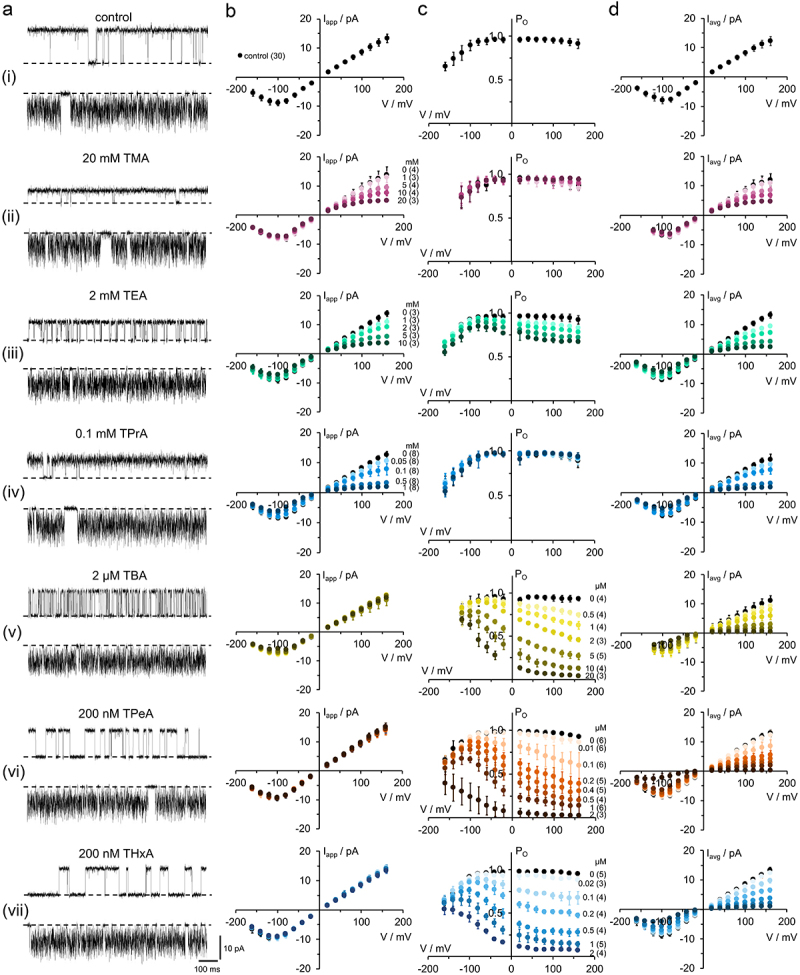
Blocking properties of Kcv_NTS by cytosolic QAs. (a) Single-channel fluctuations in DPhPC bilayers in symmetric 100 mM KCl without and with different QAs recorded at +120 mV (upper traces) and −120 mV (lower traces). The closed channel is indicated by a dashed line. The blocker concentrations are given above the traces. (b) Apparent single-channel channel I_app/V-relations without (black) and with (colored) blocker, concentrations indicated at the curves in either (b) or (c). (c) Apparent open probabilities and (d) time averaged I_avg/V relations with I_avg = I_app·P₀. Mean ± s.D., number of independent recordings is indicated in brackets.

For the slow blockers, we use dwell time analysis. Thus, C₁–C₃ remain separated in the model. Instead, the short closed states M and F and the open state O are merged into an apparent open state O* (Figure 1d–f), since they cannot be distinguished by this method. Furthermore, for each slow blocker, the dwell time of the blocked state B overlaps with one of the closed states, depending on the blocker and channel isoform. When B is merged with one of the closed states, this leads to a state C₁*, C₂* or C₃*. The decision, which one includes B, is made by inspecting the dependency of the individual state occupancies on blocker concentration (Figures 6 to 8, below and Figure S4).

Figure 6.

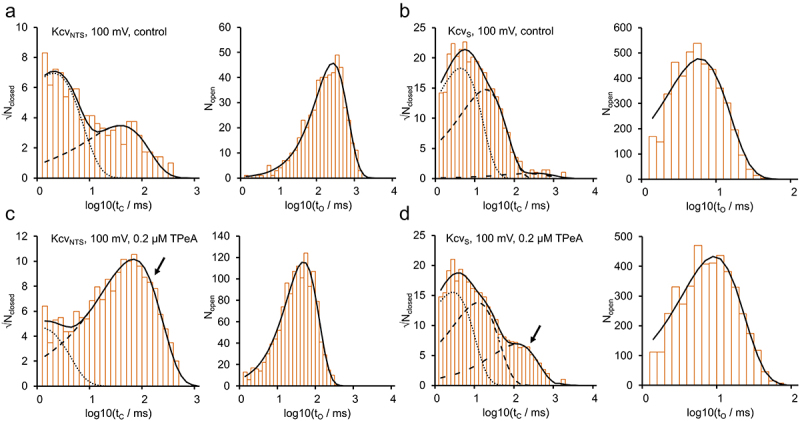
Dwell-time histograms of (a,c) Kcv_NTS and (b,d) Kcv_S under control conditions and blocked by TPeA. Exemplary closed- and open-time histograms at +100 mV for the control (a,b) and 200 nM TPeA (c,d). Open histograms (right hand side in each panel) were fitted by Eq. 1 (black) with a single exponential. Closed time histograms were fitted with a sum (black, continuous line) of two exponentials for Kcv_NTS or three exponentials for Kcv_S. Individual components: C₁ = dotted, C₂ = dashed, C₃ = dash-dot. Inclusion of state B in one of the closed states is indicated by the arrows.

Figure 7.

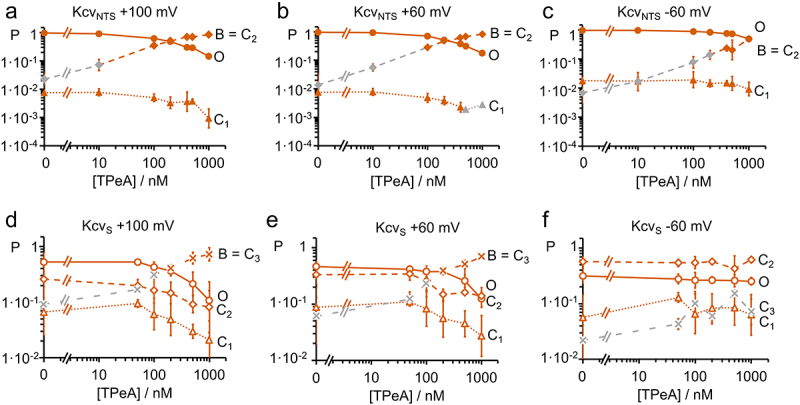
Dependence of occupation probabilities P of the states in the Markov models of Figure 1e or f on TPeA concentration. Association of the blocked state B to C₂ (diamonds in (a-c)) or C₃ (crosses in (d-f) is based on the dependence of their occupation probabilities on blocker concentration. The occupation probabilities of the open state (P_O, circles) and of the two or three closed states (P_C1, triangles, P_C2, diamonds, and P_C3, crosses) are shown for (a,b,c) Kcv_NTS (filled symbols) and for (d,e,f) Kcv_S (open symbols) at different TPeA concentrations at (a,d) +100 mV, (b,e) +60 mV and (c,f) −60 mV. Averages ± sd of three experiments each. Orange symbols in the curves related to B mark the concentrations, where the occupation probability of the respective state exceeds 10 times that of the control value and are therefore dominated by B. Grey symbols indicate that this probability is too small for the identification of B. for Kcv_S at −60 mV, and for both channels at −100 mV (not shown), this threshold was not reached (only gray symbols). The two additional gray triangles in B are data points, where due to the low probability of C₁, n = 3 could not be achieved for this state. This did not affect the determination of C₂.

Figure 8.

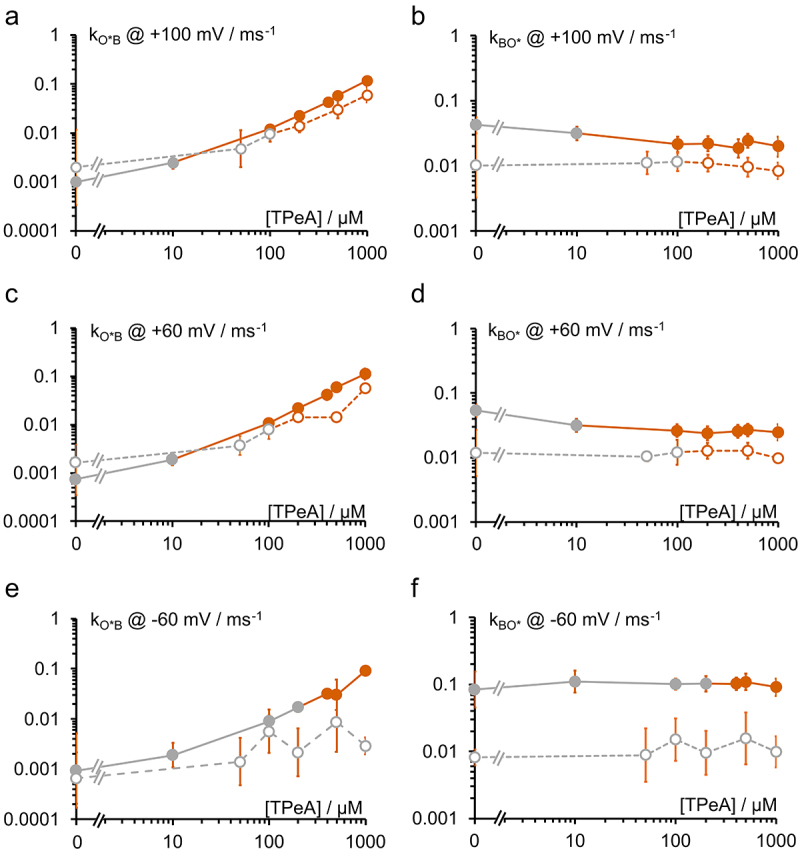
Rate constants of blocking of the open channel (a,c,e) k_OB and (b,d,f) k_BO as obtained from the dwell time histograms in Figure 6 by means of Eqs. 1 and 3 at −60 mV, +60 mV and +100 mV. Filled symbols: Kcv_NTS, open symbols; Kcv_S. Orange symbols are those where the blocked state B dominates the intrinsic closed state, and the rate constants can be taken as a good approximation of the rate constants of blocking. Grey symbols: this condition was not met; the rate constant was not used for further analysis. Mean ± sd of three experiments each.

Analysis of fast blockers by extended beta distributions

As mentioned above, kinetics and blocking faster than the bandwidth of the recording set-up and the associated true open channel current I_true, which is also obscured by the filtering, have to be analyzed by fitting amplitude histograms with extended beta distributions [29,32] exploiting the open-channel excess noise [30,31]. Briefly, the program generates simulated time series [33,34] of single-channel current for the generation of the theoretical amplitude histogram, which is then fitted to the measured one by a simplex algorithm [35] by varying I_true and the rate constants of the Markov model (Figure 1b,c). The simulation and fitting algorithms and fitting strategies have been published elsewhere [32–34,36]. It is important to note that the simulation is done in continuous time and includes Gaussian noise of the same magnitude as the experiment and a digital representation of the jump-response of the 4^th-order Bessel filter used for the experiments. A more detailed description of the fit algorithm and examples of fits (Figure S1) are given in the Supplement.

Since this algorithm does not detect individual events, no precise minimal event length can be given. We estimated previously that gating about 100–500-fold faster as the filter frequency (1kHz in this work) can still reliably be quantified at SNR comparable to those in this study [32]. The temporal resolution depends on the deviation of the open peak from the Gaussian distribution of the baseline noise [37].

Analysis of slow blockers with dwell-time histograms

Open and closed dwell-time histograms of the single-channel recordings with slow blockers were calculated with an 8th-order Hinkley detector [38]. Briefly, the experimenter sets the current values for the baseline and the open channel, and the algorithm calculates a cumulative test value g_t from the raw data, counting only those data points which cross the halfway line between the closed and open level. When g_t reaches the threshold, which is set according to the noise level, a jump is detected [38]. Not considering filtering of the data, the approximate minimal detectable event length in sampling intervals is about t_res = 22/SNR² = 4.4 ms/SNR² (Figure 5 in [38]), where SNR is the signal-to-noise-ratio. For dwell time analysis, only ±60 and ±100 mV were used; the SNR was at least 10. Consequently, the limiting factor for the event length is here the four-pole Bessel filter of 1 kHz, which has a rise time of about 400 µs. During the subsequent analysis of the resulting dwell-time histograms, we consider only events longer than 1 ms. For a more detailed description of these estimations, see [38,39]. Blockers that are faster than 1 ms are analyzed with extended beta distributions.

Figure 5.

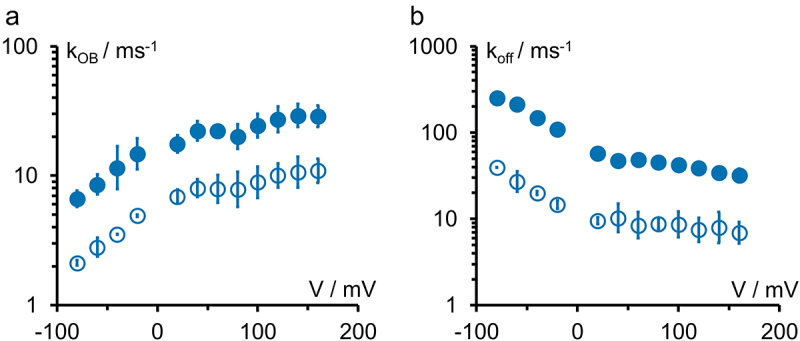
Kinetics of the open-state block with TPrA for the two channel isoforms Kcv_NTS (filled symbols, no cytosolic gate) and Kcv_S open symbols, with cytosolic gate) (Figure 2a,c). (a) Rate constant k_OB of blocker binding and (b) rate constant k_BO = k_off of blocker release for 0.1 mM cytosolic TPrA. Averages ± sd of three experiments each. The small errors are a typical benefit of Kcv channels.

The resulting lifetimes were grouped into bins with exponentially increasing width. The theoretical probability density function of the open and closed lifetimes can be expressed as a sum of exponential functions, converted to match the exponential binning. The expected number N_i of events in the i-th bin with bin width Δt_i is

$$Ni=\mathit{N}\cdot \left(\sum _{\mathit{j}=1}^{n}aj\cdot e^{-\frac{ti}{\tau j}}\left(e^{\frac{\mathrm{\Delta }ti}{\tau j}}-1\right)\right).$$ (1)

For open-time histograms n = 1 was used, for closed-time histograms n = 2 or 3. The time constants τ_j and the amplitude factors a_j describe the rate constants of the employed Markov model [40]. N denotes the total number of events. Due to the limited temporal resolution of the experimental setup, a notable number of short closed events associated with C₁ were missed by the jump detector. This results in an overestimation of the mean open lifetime τ_O. Therefore, a simple missed events correction was applied as described in [2].

Individual probabilities of the closed states C_j and the open state O were calculated by

$$\mathit{P}\left(Cj\right)=\frac{aCj\cdot \tau Cj}{\tau O+{\sum }_{j=1}^{n}aCj\cdot \tau Cj}\mathrm{and}\mathit{P}\left(\mathit{O}\right)=\frac{\mathit{\tau }\mathit{O}\mathit{\hspace{0.17em}}}{\tau O+{\sum }_{j=1}^{n}aCj\cdot \tau Cj}$$ 2a,b)

Since all closed states are directly connected to the open state (Figure 1), the rate constants could be calculated directly from the time constants and amplitude factors:

$$kCj\mathit{O}=\frac{1}{\tau Cj}\mathrm{and}kOCj=\frac{aCj}{\tau O}$$ 3a,b)

Dwell time fits were done with Matlab (MathWorks).

Supplementary material

The Supplementary Material contains additional figures and two tables. Figure S1: Fits of amplitude histograms with and without blocker. Figure S2: Example of time series, IV curves and open probabilities for the blocking experiments on Kcv_S. Figure S3: Blocking kinetics for TEA. Figure S4: Identification of the blocked state for TBA and THxA. Figure S5: Block by TPrA does not affect the OM-gating k_OM in all investigated constructs. Figure S6: Block by TBA does not affect the k_OM in Kcv_NTS. Figure S7: No effect of mutations on I_true. Table S1: Rate constants for the example fits in Figure S1. Table S2: Products of rate constants.

Results and discussion

Dependence of current and open probability on blocker size in Kcv_NTS

To measure the effect of blockers with different sizes, mono-cationic quaternary ammonium ions (QAs) with increasing size from TMA to THxA (Figure 2b) were applied to the cytosolic side of the viral K⁺ channel Kcv_NTS.

Figure 2.

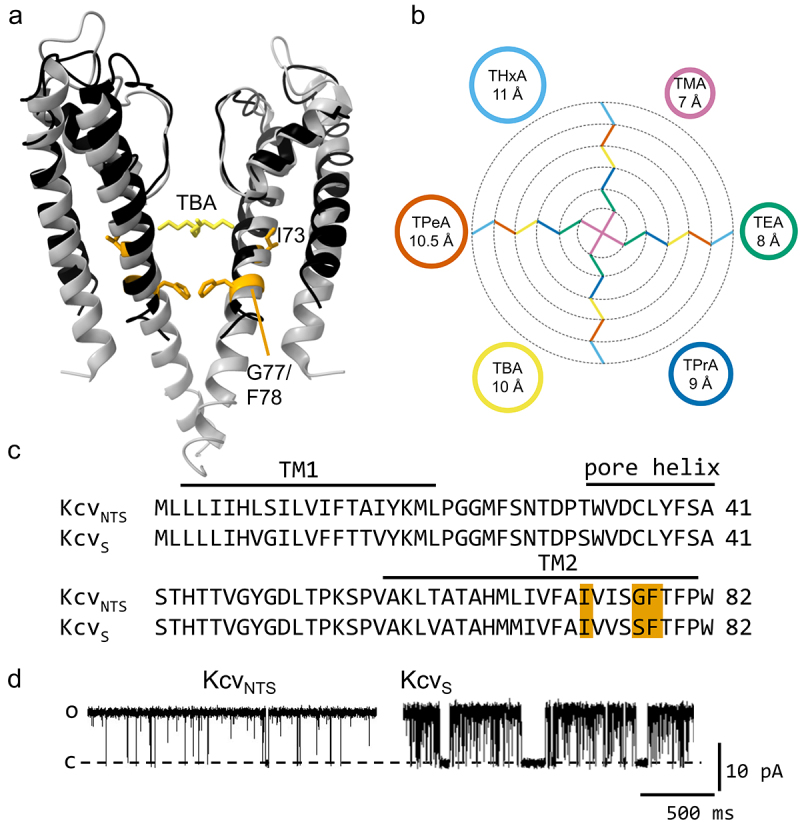
(a) Comparison of the structure of a homology model for Kcv_NTS and the structure of the TBA@KcsA complex (pdb code 2HVK), which is used as an illustration of the location of the blocker [41]. Two monomers of the KcsA channel are shown in gray, the TBA ion (yellow) is located inside the cavity. The homology model of Kcv_NTS on the template structure of KirBac1.1 (1P7B) calculated with Swissmodel [42] is shown in black with the amino acids discussed in this work highlighted in orange. Structures drawn with UCSF chimera [43]. (b) size of quaternary ammonium blockers (QAs), as estimated by [44]. The colors of the alkyl chains refer to the circles with the same color. The same accessible color palette ([45] and https://www.accessiblecolorpalette.com/, accessed June 2024) for the blockers is used in all figures in this work. (c) Sequence alignment of Kcv_NTS and Kcv_S. Residues I73, G/S77 and F78 are highlighted in orange. (d) Representative single-channel traces of Kcv_NTS and Kcv_S at +120 mV in a DPhPC membrane in 100 mM KCl.

Figure 3a shows representative single-channel recordings from Kcv_NTS in DPhPC bilayers in symmetric 100 mM KCl at blocker concentrations close to the respective apparent K_Ds. All blockers show an increasing effect at positive voltages. The blocking kinetics become slower with increasing blocker size, as illustrated in Figure 3a.

The small blockers (TMA, TEA, and TPrA) cause a block, which is faster than the bandwidth of the recording. Averaging over the fast events by the 1-kHz low-pass filter leads to a reduction of the apparent current I_app (Figure 3bii–iv). The larger QAs (TBA, TPeA, and THxA) block slower, leading to a decrease in P_O (Figure 3cv–vii). An exception is TEA, which has two effects, one on I_app and one on P₀ (Figure 3biii,ciii). The increase in open-channel noise caused by the small blockers is easier to see in the time series at positive voltages in Figure 3a, since at negative voltages, it is mixed with the noise originating from fast intrinsic gating [3] seen in the control (Figure 3ai). The decrease in P_O caused by the larger blockers is indicated by the long sojourns at the baseline at positive voltages. Fast and slow blockers have similar effects on I_avg, the current obtained from averaging over the whole time series (Figure 3d).

To study the influence of the inner gate region on the block, the same experiments as in Figure 3 were also performed with the closely related channel Kcv_S and selected blockers (TEA, TPrA, TBA, TPeA, Figure S2). Fewer blockers were applied here, because Kcv_S was used only for studying the effect of the cytosolic gate (Figure 2a,c) and not the determination of the diameter of the CPE. Qualitatively, the results with Kcv_S were very similar to those of Kcv_NTS with a voltage-dependent block whose kinetics slow down with the size of the blocker.

The dependence of K_D on blocker size in Kcv_NTS and Kcv_S

For a more quantitative description, the apparent dissociation constants K_D were determined from concentration response curves (Figure 4a–d). Depending on the kinetics, the inhibition (Inh_exp) was calculated from the ratio of I_app (TMA, TPrA), I_avg (TEA) or P_O (TBA, TPeA, and THxA) with and without blocker (Eq. 4):

Figure 4.

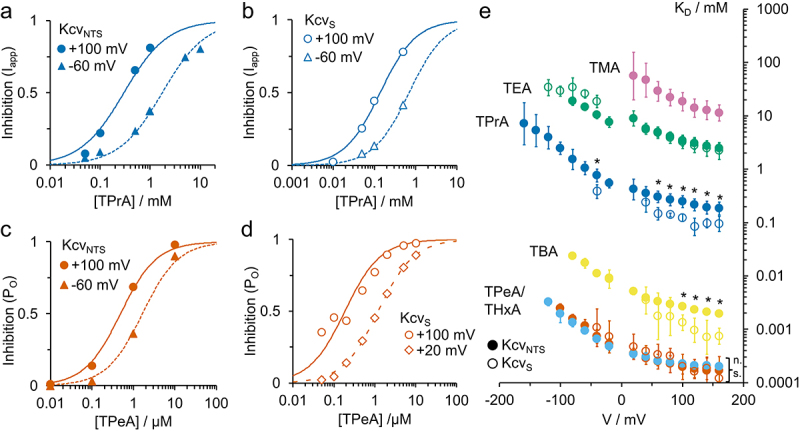
Representative concentration response curves of inhibition Inh_exp for (a,b) TPrA (9 Å diameter) and (c,d) TPeA (10.5 Å) in (a,c) Kcv_NTS and in (b,d) Kcv_S as obtained from the data in Figure 3 and Figure S2, respectively. Fit with Eq. 5. (e) Voltage dependence of apparent K_D (as obtained from fits like those in Figure 4a–d) for the different blockers in Kcv_NTS (filled circles) and Kcv_S (open circles). TMA: purple, TEA: green, TPrA: dark blue, TBA: yellow, TPeA: light blue, THxA: orange. *: At these voltages, the K_D for TPrA and TBA differ significantly from each other in Kcv_NTS and Kcv_S. “n.s.:” The K_D for TPeA (Kcv_NTS and Kcv_S) and TPeA (Kcv_NTS) do not differ significantly at any voltage. One-parameter ANOVA with threshold p = 0.05.

$$\mathit{In}h\mathit{exp}=1-\frac{\mathit{I}\mathit{app},\mathit{B}}{I\mathit{app}},\mathit{In}h\mathit{exp}=1-\frac{\mathit{P}\mathit{O},\mathit{B}}{PO},\mathit{In}h\mathit{exp}=1-\frac{\mathit{I}\mathit{avg},\mathit{B}}{I\mathit{avg}}$$ (4a,b,c)

The subscript B indicates the experimental parameters determined with the blocker, the absence of this notation the control without blocker. The Hill equation (Eq. 5) with a fixed Hill coefficient of 1 leads to a satisfactory fit in all cases (Figure 4a–d).

$$\mathit{Inh}=\frac{c}{KD+\mathit{c}}$$ (5)

with c = concentration of the blocker. Not all experiments reached saturation, but the range is sufficient to determine the apparent dissociation constant K_D, assuming maximum inhibition Inh_max = 1. K_D values for both channel isoforms at various voltages are shown in Figure 4e.

The K_D strongly declines with blocker size. For the largest two blockers (TPeA and THxA), K_D becomes independent of blocker size, as confirmed by a one-way ANOVA test for p < 0.05. All apparent K_D curves (Figure 4e) show a roughly exponential increase with negative voltages. This results from the voltage dependence of both blocker binding and dissociation [7], which was also observed in other channels [17,18,46]. For TPrA, we recently demonstrated that the cause of the voltage dependency of k_off is electrostatic repulsion of the blocker by the ion occupation in binding site S4 in the selectivity filter [7].

For TPrA and TBA, the apparent K_D for Kcv_S is significantly smaller (= higher affinity) than that for Kcv_NTS (Figure 4e), especially at positive voltages. This result is surprising since it was expected that the additional cytosolic gate in Kcv_S [2] might hinder the access of QAs to their binding site, which would result in a lower apparent affinity. The fact that we still detect differences in blocking in the open channel means that structural differences between the two isoforms must cause additional changes at the cytosolic pore mouth and/or the cavity, which also affect the open channel. For a better characterization of such differences, the individual rate constants of blocker binding (k_on) and of release (k_off) were determined in addition to K_D = k_off/k_on. TPeA is the largest blocker that was tested with both isoforms. There is no significant difference in the K_D between Kcv_NTS and Kcv_S.

Kinetic analysis of the fast blockers in Kcv_NTS and Kcv_S

The reduced Markov model in Figure 1b is used to determine the rate constants of TPrA binding, k_OB (Figure 5a), and of blocker release, k_BO = k_off (Figure 5b), for the open-state block. 0.1 mM TPrA has been applied to the cytosolic side of Kcv_NTS (filled circles) and Kcv_S (open circles), and the data are analyzed with extended beta distributions [32]. Regular (non-extended) beta distributions [47,48] have been used [17] for the block by TEA. In that study and in our previous work [7] as well as in Figure 5, both rate constants are voltage dependent.

The voltage dependency of k_off is somewhat stronger (factor of about 10 between −80 mV and +160 mV) than that of k_on (factor of about 5). The voltage dependence of k_off arises from the increase of K⁺ occupancy at the binding site S4 in the selectivity filter in the blocked state [7] at negative voltages. k_on decreases at negative voltages, presumably because the blocker has to move against the inward flow of ions in the unblocked state.

An interesting finding in Figure 5 is the parallel shift of the curves of k_OB (binding) and k_off (release) between those from Kcv_NTS and Kcv_S. This may indicate a change of the Eyring barriers for k_on and k_off as discussed below. Both rate constants are faster in Kcv_NTS than in Kcv_S at all voltages with a factor of about 3 for k_OB and about 5–8 for k_off. The larger influence of the channel isoform on k_off explains the difference in the apparent K_D in Figure 4e. A possible role of the residues involved in the cytosolic gate of Kcv_S [2] is investigated by the mutational studies below.

The fact that TEA affects both I_app and P_O (Figure 3) indicates a more complex blocking mechanism than for the other blockers. In contrast to all other phenomena observed in this work, the effect of TEA on P_O seems to be mostly voltage independent. Here, we only determine the kinetics of the fast TEA block, which is more comparable with that of the other blockers. The rate constants for TEA block were only determined for Kcv_NTS and are given in Figure S3.

Kinetic analysis of the slow blockers in Kcv_NTS and Kcv_S

For the slower blockers, TBA, TPeA, and THxA, dwell time analysis using the models in Figure 1d–f is employed, as illustrated in Figures 6–8. Representative dwell time histograms without blocker (control) and for the block of Kcv_NTS and Kcv_S by TPeA are shown in Figure 6 for +100 mV. The apparent open state O* is fitted by a single exponential function, the closed histograms with two (Kcv_NTS) or three (Kcv_S) exponential functions (Eq. 1, Figure 6). For Kcv_NTS, the blocked state B coincides with C₂ (Figure 6c), as obvious from the strong increase of the apparent C₂ with TPeA (dashed line); C₁ decreases because of mass conservation. In contrast, for Kcv_S, B coincides with C₃ (Figure 6d, dash-dotted line). Due to the increased number of “closed” events with the blocker, the mean duration of the open state is shifted leftwards for Kcv_NTS (Figure 6a,c right-hand side). Because the blocking events are longer, but rarer in Kcv_S, the mean open duration is dominated by the intrinsic gating and not visibly affected by the blocker (Figure 6b,d right-hand side).

The voltage dependence of the occupation probabilities P is obtained from the time constants and amplitude factors of the individual exponential components in Figure 6 (Eq. 1) by means of Eq. 2. They are plotted in Figure 7. The TPeA-induced increases in C₂ in Kcv_NTS (Figure 7a–c) and in C₃ in Kcv_S (Figure 7d,e) are obvious. At negative voltages in Kcv_S, the effect of TPeA is too small to be detected (Figure 7f). Note that the respective C state (intrinsic gating) and state B (blocking) are not assumed to be mechanistically related, they have to be merged in the analysis because their dwell-times happen to coincide. They can be distinguished only by their concentration dependence.

Figures 6 and 7 show that at higher concentrations the TPeA block dominates either the C₂ (Kcv_NTS) or the C₃-component (Kcv_S). Thus, the rate constants for the respective closed state at concentrations higher than 100 nM (Kcv_NTS) and 200 nM (Kcv_S) were used as an approximation for the rate constants of open-state blocking (Figure 8). The threshold was set to a value at which the combined probability of B and the intrinsic closed state exceeds 10 times the probability of the closed state under control conditions. The same analysis was also done for TBA and THxA (Figure S4).

Whereas the ratio between Kcv_NTS and Kcv_S for both rate constants is in the order of 3 to 8 for TPrA (Figure 5), this difference decreases to a factor of 2 to 3 for TPeA (orange symbols in Figure 8). Since TPeA is larger than TPrA, this argues against the hypothesis that the causative difference between the two channels is a difference in pore diameter thus weakening the argument that the gate in Kcv_S decreases the pore diameter even in the open state. Further conclusions from the experiments in Figures 5–8 are discussed in the next section together with the data from the other blockers.

Role of blocker size in Kcv_NTS

To assess the kinetic origin of the size dependence of the apparent K_D in Figure 4e, we determine k_on and k_off for all blockers (except for TMA, which is too fast to be analyzed even with extended beta distributions). Since k_on is defined as a concentration-independent parameter, it was calculated from k_OB by Eq. 6 with c being the blocker concentration.

$$k\mathrm{on}=\frac{\mathit{k}\mathrm{OB}}{\mathit{c}}\mathrm{or}k\mathrm{O}\ast \mathrm{B}=k\mathrm{on}\text{cdotc}+\mathrm{offset}$$ 6a,b)

For TEA and TPrA, Eq. 6a is applied to each individual experiment with subsequent averaging over all analyzed concentrations. In the case of TBA, TPeA, and THxA, state B is merged with one of the slow closed states of intrinsic gating resulting in C₁*, C₂* or C₃*. Thus, the dependence of k_O*B on concentration is fitted with a linear equation (Eq. 6b); the offset accounts for the control values without blocker (Figures 8a–e, leftmost data points). Merging the fast intrinsic states into O* (Figure 1d–f) does not influence the results of slow gating analysis. k_on determining the steepness of k_O*B of the graph in Figure 8 is averaged over all analyzed experiments. Also k_off is concentration-independent and is calculated by simply averaging k_BO or k_BO* over all experiments and concentrations; limited to those concentrations and voltages where blocker dissociation can be reliably determined (e.g. orange data points in Figure 8b–f for TPeA).

Because of the voltage dependence of the block, a single concentration is often not enough to analyze the full voltage range. At negative voltages and low concentrations, the block is too weak, and at high concentrations at positive voltages, the block is nearly complete, and not enough events can be detected. Since both k_on (Eq. 6a) and k_off are concentration-independent, pooling their values from different concentrations allows covering a larger voltage range [7].

Similar to Figure 5, the voltage dependence of k_off (Figure 9b) is slightly stronger than that of k_on (Figure 9a), particularly at negative voltages (Figure 9b) (Note that Figure 9a,c have a linear scale and Figure 9b,d a logarithmic scale). Figure 9b,d show that k_off changes exponentially by more than 4 orders of magnitude when the blocker size increases from 8 Å to 11 Å. This phenomenon originates in the higher hydrophobicity of the larger QAs [13,15,17] and causes the decrease of K_D with blocker size (Figure 4e).

Figure 9.

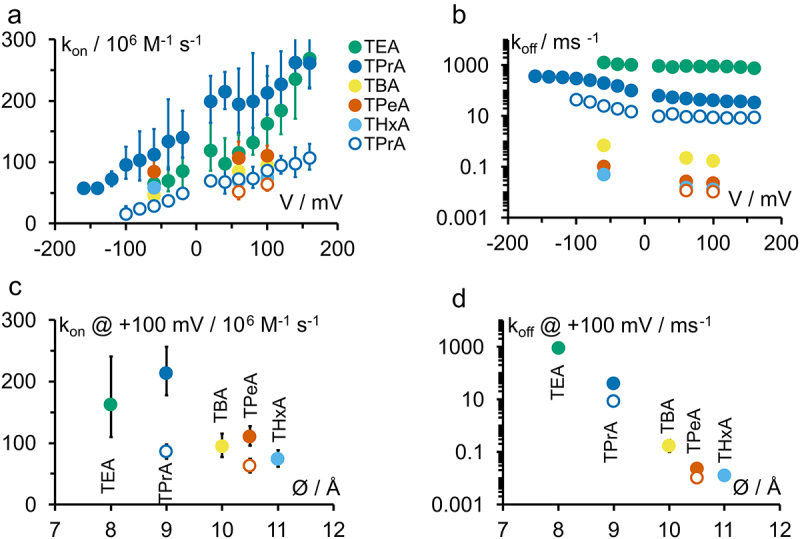
(a,b) Voltage dependence of the rate constants of open-state block (A) k_on as calculated by Eq. 6 and (B) k_off for different QAs. (c,d) Dependence of (C) k_on and (D) k_off at +100 mV on blocker diameter estimated by Robinson and Stokes [46]. Filled symbols: Kcv_NTS, open symbols: Kcv_S. Colors are defined in (A). Averages +/- sd of three experiments each.

k_on has been used to determine the accessible diameter of pores in other studies. In IRK1 and ROMK1 [18], the drop in k_on from TPrA to TBA was a factor of about 30, indicating that TBA was too large to properly enter. In contrast, we only observe a factor of 2 to 3 between TEA and TPrA or TBA and TPeA here, comparable with the drop between the small TEA and TPrA in IRK1 and ROMK1 [18]. This indicates that the cytosolic pore entrance (CPE) of Kcv_NTS is at least 11 Å wide. Note that the diameters given in Figure 9 are approximations since the exact flexibility of the blockers [49,50] and of the protein is not known. For the sake of comparability, here we use the diameters as given in Figure 2b [44] as also used by other publications.

From the dependence of k_on on blocker size, a CPE diameter of ca. 9 Å was estimated for the inward rectifying K⁺ channels IRK1 and ROMK1 [18]. Larger diameters of about 12 Å were reported for BK-like channels from rat muscle [17]. The closest bacterial homologue of BK channels, MthK also exhibits a very wide CPE of ca. 12 Å diameter, similar to the open-pore conformation of KcsA [19]; and K2P channels are still blocked by molecules as big as THxA (11 Å) [51]. Hence, the structure of the open CPE in Kcv appears to be more similar to that of channels cited in this second group.

Test of whether the blockers bind to the same binding site

The voltage dependence for k_off is very similar in both Kcv_NTS and Kcv_S for all blockers (parallel shift in Figure 9b). This voltage dependence is used to address the question of whether the different blockers all bind to the same binding site in Kcv_NTS. First, for the comparison with other investigations in the literature, we fitted k_off with an exponential curve k_off = k_off,0·exp(-zδ·FV/RT) (Figure 10a) even though k_off in this study is clearly not strictly exponential (Figures 9b, 10a). The resulting values of the effective valence zδ (TEA: 0.03 ± 0.04, TPrA: 0.23 ± 0.09, TBA: 0.16 ± 0.07, TPeA: 0.14 ± 0.12, THxA: 0.36 ± 0.05) are comparable to those in the literature (e.g. approx. 0.5 for TEA, TPrA, TBA, and TPeA in IRK1 and ROMK1 [18]). An ANOVA test shows that the effective valences zδ for TPrA, TBA, and TPeA in Kcv_NTS are indeed identical. The deviation of TEA can be explained by the unusual occurrence of two time constants. The deviation of THxA should not be overinterpreted, it might as well originate in the non-exponential shape of k_off and the different availability of sufficiently strong blocking effects at negative voltages for the different blockers.

Figure 10.

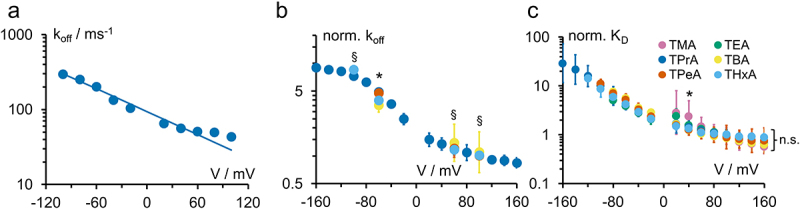
(a) Exemplary fit of k_off on an Kcv_NTS data set with 0.5 mM cytosolic TPrA with the equation k_off = k_off,0·exp(-zδ·FV/RT), zδ = 0.28, k_off,0 = 1.05·10⁵ s^−1. (b) Overlay of the normalized (see text) k_off for TPrA (dark blue), TBA (yellow), TPrA (orange) and THxA (light blue) in Kcv_NTS. §: No significant difference between the data points at this voltage. *: at least one data point is significantly different from the others. (c) Normalized (see text) K_D of all blockers in Kcv_NTS. A significant difference for at least one of the data points from the others is only found at +40 mV. One-parameter ANOVA with threshold p = 0.05.

In a previous work, we determined the correct equation of the voltage dependence of k_off for TPrA in Kcv_NTS [7]. The blocker is removed from its binding site by electrostatic repulsion by the K⁺ ion at the S4 binding site. Importantly, the presence of the blocker does not disturb the K⁺ distribution in the selectivity filter [7]. The curve shape is given by the ion occupation of binding site S4 in the 5-state model of ion hopping [52]. The equation for k_off includes the 10 rate constants of the 5-state ion hopping model [52], four of them being voltage-dependent. To decide whether this mechanism, including the location of the binding site also holds for the other blockers, it is not necessary to repeat this intricate analysis. Instead, we compare the voltage dependence of the different k_off directly. The k_off-curve of TPrA was used as reference and normalized to the mean value at +100 mV. All other curves were then shifted by an adequate factor. This factor was determined by calculating the ratio of the mean values (k_{off,other blocker}/k_off,TPrA) for each voltage and then averaging over all voltages. Figure 10b shows a good coincidence of the shifted k_off. An ANOVA test reveals that the curves of TPrA, TBA, TPeA, and THxA coincide at +100 mV and +60 mV. For TPrA and THxA this is also true at −100 mV. Since TPrA and THxA are the blockers with the largest difference in diameter, we take these results as an indication that there is no serious difference of the voltage dependence of k_off for all four blockers, even though TBA and TPeA did not reach −100 mV. This is because the overlap of blocked and closed states makes dwell time analysis of the slow blockers challenging. This could also explain the minor deviation at −60 mV. TEA is not considered here because it has two different blocking mechanisms (Figure 3).

On a more “macroscopic” scale, the K_D values of all blockers for Kcv_NTS coincide when shifted in the same way. ANOVA indicates a high reliability of this coincidence (Figure 10c). In conclusion, it is very likely that the binding site is the same for TPrA, TBA, TPeA, and THxA and also the coupling between the K⁺ ions at S4 and blocker dissociation k_off is the same.

Influence of the residues on positions 77 and 78 on open-state blocking kinetics

Kcv_S possesses a cytosolic gate, which is absent in Kcv_NTS (Figure 2a,c) [2]. This gate consists of an unusual mechanism. It does not form a bundle crossing; instead, a hydrogen bond between the S77 side chain on TM2 and the backbone carbonyl of I73 controls the positioning of the side chain of F78, which can occlude the pathway for ions at the CPE. The phenylalanine is also present in Kcv_NTS, but a glycine at position 77 instead of the serine causes the gate to be constitutively open. The S77G/G77S mutations switch the gating phenotypes of the two channels, both for the slow cytosolic gate (state C₃ [2]) and the second component of O-M gating (state M in the Markov models, Figure 1) visible only at positive voltages. The voltage-dependent component at negative voltages is identical in both isoforms (Figure S5). The single-channel current is not affected (Figure S7).

In order to investigate whether the residues forming the cytosolic gate are responsible for the differences in the TPrA block in Kcv_NTS and Kcv_S, we determined the rate constants k_on and k_off of the open state block in Kcv_NTS, Kcv_S and for several mutations at the cytosolic gate.

Compared to Kcv_NTS, k_on and k_off are decreased both in Kcv_S (Figure 5) and in the mutant Kcv_NTS G77S (which introduces the gate into Kcv_NTS) (Figure 11a,d open circles). The decrease of k_off is stronger than that of k_on thus leading to a decrease in K_D. In the reverse case, the mutant Kcv_S S77G shows the same blocking rate constants as Kcv_NTS (Figure 11a,d filled circles). This result seems to support the hypothesis that the bulky side chain of F78 also in the open state is in a position where it hinders access and release of the blocker, as long as the second component of the gate, S77, is also present.

Figure 11.

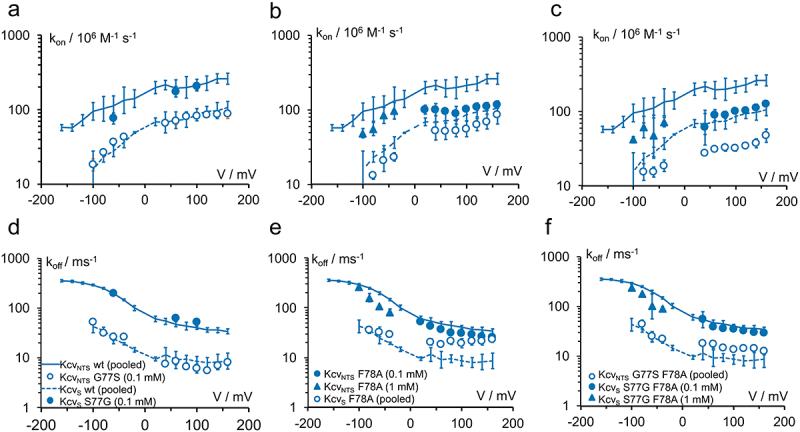
Block by TPrA. Influence of the residues at positions 77 and 78 on the rate constants of (a, b, c) blocker binding k_on = k_OB/[TPrA] and (d,e,f) release (k_BO = k_off) in different mutants of Kcv_NTS and of Kcv_S. Lines show the wild-type data (Kcv_NTS: continuous, Kcv_S: dashed), the symbols indicate the residue at locations 77: G = filled, S = open for the mutants (a,d) S77G and G77S (b,e) F78A and (c,f) the double mutants. “pooled:” wt data averaged over TPrA concentration from 0.05 – 5 mM (Kcv_NTS) and 0.1 – 1 mM (Kcv_S), data for Kcv_NTS S77G F78A averaged over 0.1 & 1 mM. All other blocker concentrations are indicated in the legends. All data points: mean ± sd of at least three experiments each. Because of the decrease of the signal with higher negative voltages, rate constants could not be determined from fitting amplitude histograms for voltages more negative than −80 mV or −60 mV for all mutants and Kcv_S.

However, this simple picture is destroyed when the mutation F78A comes into play. The side chain of alanine is too small to hinder blocker access or release. Therefore, the elimination of the phenylalanine side chain by replacing F with A “should” increase k_on and k_off. However, Figure 11b,c show that even the opposite effect occurs in the case of k_on. With both serine (Kcv_NTS G77S F78A and Kcv_S F78A) and glycine (Kcv_NTS F78A and Kcv_S S77G F78A), k_on is reduced by the F78A mutation.

In the case of k_off, the elimination of the phenylalanine side chain in Kcv_S leads to a small increase, which even reaches the k_off of Kcv_NTS at high positive voltages (Figure 11e). The increase of k_off with S on position 77 is much smaller in the double mutant Kcv_NTS G77S F78A (Figure 11f).

Conclusion

The accessibility studies above with blockers of different size have determined a lower bound for the width of the path from the cytosol to the entrance of the selectivity filter in Kcv_NTS: at least 11 Å (Figure 9). In previous electrophysiological studies on ion dynamics in the selectivity filter of Kcv_NTS diffusion limitation at the cytosolic pore entrance was neglected without any experimental evidence [3,7]. Now, the experimentally determined minimal CPE diameter verifies that the CPE is wide enough not to pose any significant diffusion limitation for K⁺ ions. This information can also provide a useful additional constraint for future structural models in addition to those that have been already used successfully [2,7–9].

Aside from being a good model system, Kcv channels are a possible future target for molecules preventing virus spreading in alga cultures. This work investigates the cytosolic pore mouth, which is not easily accessible (assuming the channels are oriented in the virus in the same way as in heterologous expression systems). However, any biophysical information about a potential drug target might be useful someday. Kcv_PBCV-1 from a different chlorella virus has an external binding site for TEA [53] and might be an even more interesting target.

Diffusion limitations and/or pore diameter restrictions by bulky amino acids have been studied in different channels [20,21]. Kopec and colleagues [54] found that changes in the diameter of the CPE of MthK did not prohibit K⁺ movement. Similarly, in Kcv_NTS, in the case of k_on in this study, the results in Figure 11b,c clearly rule out the involvement of diffusion limitation by the phenylalanine on position 78, since its replacement by alanine decreases and does not increase k_on.

The increase of k_off in the mutant F227A (roughly corresponding to F78A in Kcv here) in the bacterial Na⁺ channel has been called trapping [55], i.e. the phenylalanine hinders the dissociation of the blocker. This trapping (or lack thereof) has often been used to identify the location of a gate [10,11]. However, in Figure 11d,e, the increase of k_off in F78A is zero or very small at negative voltages (Figure 11e) or strongly voltage-dependent at positive voltages (Figure 11d). Thus, a minor participation of trapping cannot be excluded, but another mechanism not based on the phenylalanine is the alternative or at least the dominating origin of the effect of the mutants on k_off.

Such a hypothetical mechanism could be a change in conformation or hydrophobicity near the binding site of the blocker. It is well documented, that the binding of QAs to the potassium channel pore is mostly due to hydrophobic interactions, e.g [15]. The aforementioned hypothesis is supported by the fact that, also the voltage-independent component of k_OM of intrinsic gating at positive voltages, called k_OM,2 is influenced by the S-G mutations, but not by mutations at position 78 (Figure S5). Thus, the binding site for blocker and the (currently still unknown) site controlling k_OM,2 seem to be in nearby positions of the protein but are not identical. Even though the mutations at position 77 influence both blocking and k_OM,2 (Figure 11 and Figure S5) the blockers have no influence on voltage-dependent O-M gating at negative voltages (Figure S5 for TPrA and Figure S6 for TBA). This supports our previous findings that the blocker does not disturb the ion occupation in the selectivity filter, as verified by 3D reference interaction site model (3D RISM) calculation [7].

If the mutations at positions 77 and 78 both influence the binding kinetics, then the question comes up of whether they act on the same Eyring barrier for the blocking kinetics. Such a concerted action on an Eyring barrier for channel gating has been found to influence the number of subunits with the mutation S42T on k_OM [56]. In Table S2, an additive contribution of both mutations in Figure 11 to the height of the energy barrier (as indicated by the product of the ratios of the rate constants) for the rate constants of blocker kinetics is found only for k_on and only when Kcv_NTS wt provides the protein background. In all other cases, the double mutations do not contribute in such an additive manner to the energy barrier, indicating that the effects caused by the single mutations in these three cases are energetically not independent [57] or act on different parts of the protein.

Funding Statement

The work has been supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), research grant HA 712/14-3 to U.P.H. and Heisenberg Fellowship SCHR 1467/4-1 and FOR 2518 (DynIon, SCHR 1467/6-1) to I. S.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Author contributions

TK, TSG, OR, and ND performed experiments and analyzed data. UPH analyzed the data and wrote the manuscript. IS designed research, analyzed data, and wrote the manuscript. All authors edited the manuscript.

Data availability statement

Materials and data created in this work as well as the program bownhill are available upon reasonable request.

Supplementary material

Supplemental data for this article can be accessed online at https://doi.org/10.1080/19336950.2024.2402749