Imaging‐genomic spatial‐modality attentive fusion for studying neuropsychiatric disorders

Abstract

Multimodal learning has emerged as a powerful technique that leverages diverse data sources to enhance learning and decision‐making processes. Adapting this approach to analyzing data collected from different biological domains is intuitive, especially for studying neuropsychiatric disorders. A complex neuropsychiatric disorder like schizophrenia (SZ) can affect multiple aspects of the brain and biologies. These biological sources each present distinct yet correlated expressions of subjects' underlying physiological processes. Joint learning from these data sources can improve our understanding of the disorder. However, combining these biological sources is challenging for several reasons: (i) observations are domain specific, leading to data being represented in dissimilar subspaces, and (ii) fused data are often noisy and high‐dimensional, making it challenging to identify relevant information. To address these challenges, we propose a multimodal artificial intelligence model with a novel fusion module inspired by a bottleneck attention module. We use deep neural networks to learn latent space representations of the input streams. Next, we introduce a two‐dimensional (spatio‐modality) attention module to regulate the intermediate fusion for SZ classification. We implement spatial attention via a dilated convolutional neural network that creates large receptive fields for extracting significant contextual patterns. The resulting joint learning framework maximizes complementarity allowing us to explore the correspondence among the modalities. We test our model on a multimodal imaging‐genetic dataset and achieve an SZ prediction accuracy of 94.10% (p < .0001), outperforming state‐of‐the‐art unimodal and multimodal models for the task. Moreover, the model provides inherent interpretability that helps identify concepts significant for the neural network's decision and explains the underlying physiopathology of the disorder. Results also show that functional connectivity among subcortical, sensorimotor, and cognitive control domains plays an important role in characterizing SZ. Analysis of the spatio‐modality attention scores suggests that structural components like the supplementary motor area, caudate, and insula play a significant role in SZ. Biclustering the attention scores discover a multimodal cluster that includes genes CSMD1, ATK3, MOB4, and HSPE1, all of which have been identified as relevant to SZ. In summary, feature attribution appears to be especially useful for probing the transient and confined but decisive patterns of complex disorders, and it shows promise for extensive applicability in future studies.

Attentive fusion of neuroimaging and genomics data classify schizophrenia (SZ) with high precision. The attention scores provide the most contributing imaging‐genetics features for characterizing the disorder. The proposed fusion module is self‐explaining; interprets how each biological sources complement the other and leverage their combination to better understand SZ.

1. INTRODUCTION

Our brain processes multimodal signals from the outer world to understand real events and respond accordingly (Bayoudh et al., 2021; Guo et al., 2019; Kosslyn et al., 2010; Nanay, 2018; Summaira et al., 2021). Leveraging information from diverse sources allows for a better understanding of a given phenomenon. Likewise, multimodal learning enables researchers and practitioners to benefit from the unique strengths of each modality, leading to improved performance, enhanced accuracy, and richer insights (Ngiam et al., 2011; Sohn et al., 2014). Applications of multimodal learning models are wide‐ranging and include fields such as computer vision (Hosseinzadeh & Wang, 2021; Liu et al., 2021; Xi et al., 2020), healthcare (Huang, Pareek, Seyyedi, et al., 2020; Menon & Krishnamurthy, 2021; Naderi et al., 2019), and speech recognition (Palaskar et al., 2018; Yuhas et al., 1989), among others (Sengupta et al., 2020). Moreover, the potential applications of multimodal learning in studying mental disorders are vast and continue to expand (Calhoun & Sui, 2016; Rahaman et al., 2021; Rahaman et al., 2023; Shi et al., 2017; Venugopalan et al., 2021; Zhang et al., 2022). The rationale lies in multiple biological domains that are affected by the underlying physical conditions. Therefore, maximizing the complementarity among these sources can potentially lead to a more comprehensive understanding of the data.

Research indicates that useful biological information is encoded across different sources. Neuroimaging provides structural and functional information about the brain through various imaging modalities (Calhoun & Sui, 2016; Zhang et al., 2022). Genetic data provide another source of information regarding disease‐related aberrations (Hardoon et al., 2009; Le Floch et al., 2012). The integration of data from different modalities and sources can offer a richer and more nuanced understanding of complex mental disorders. Data from multiple modalities are not mutually exclusive but complement each other in describing brain processes (Zhang et al., 2022). Particularly, neuroimaging modalities, when combined, can achieve enhanced temporal and spatial resolution and bridge the gap between physiological and cognitive representations (Liu, Sun, & Zhang, 2018). Hence, multimodal learning frameworks have emerged as effective tools for analyzing data from multiple sources, including neuroimaging (Aine et al., 2017; Calhoun & Sui, 2016; Shi et al., 2017; Tulay et al., 2019) and genetic data (Bogdan et al., 2017; Rahaman et al., 2021). Past research has demonstrated significant correlations between structural and functional changes in the brain and mental disorders (Salgado‐Pineda et al., 2011; Segall et al., 2012). Moreover, existing scientific literature points to a promising area of exploration: the correlation between genetic variants and neural activity concerning neuropsychiatric disease‐related degeneration (Hardoon et al., 2009; Le Floch et al., 2012; Liu & Calhoun, 2014). Such a disorder schizophrenia (SZ) is genetically complex and affects the brain's structure and function (MacDonald III et al., 2009; Meyer‐Lindenberg, 2010; Rahaman et al., 2021). Nevertheless, significant challenges arise in the joint analysis of genetic, structural, and functional data, as they often carry information at different scales and formats. A perceptive fusion module is necessary for enhancing the model's performance as it ensures the judicious use of the most informative sources in subsequent tasks. A bottleneck strategy might facilitate the integration of these diverse knowledge domains, overcoming the obstacles posed by differing data scales and formats. The bottleneck in a neural network (NN) is a layer with fewer neurons than the layer below or above it (He et al., 2016; Park et al., 2018). It helps to learn representations better and emphasize salient features for the target variable. Thus, our intuition is to operate fusion in this layer with bottleneck attention.

Research has provided a thorough classification of fusion methodologies (Huang, Pareek, Zamanian, et al., 2020; Poria et al., 2017). These fusion strategies are broadly divided into three subcategories: early fusion, mid/intermediate fusion, and late fusion, depending on the phase of the model where the integration takes place. The mid‐fusion approach is particularly notable due to its wide range of applications. In this scheme, fusion occurs after feature extraction from different input modes (Huang, Pareek, Zamanian, et al., 2020). However, integrating multiple sources in the intermediate phase presents a challenge, as differences in data types, collection methods, scales, and preprocessing can lead to inconsistencies in data representations. To address this issue, modality‐specific NNs are used to first learn the hidden space representations of the inputs. These networks translate the multimodal inputs into a uniform embedding space, after which the mid‐fusion module is used for the integration (Poria et al., 2017; Roitberg et al., 2019). It is important to note that even when employing latent space fusion, the resulting fused feature map can be high‐dimensional, with each unit's contribution to the subsequent task potentially varying in importance. Consequently, simply connecting the fused tensor to the predictor may limit the model's performance. This problem is especially pronounced when data modalities are unevenly informative about the downstream task, a common occurrence in medical data collection. Neuroimaging and genomics datasets often contain weak descriptors of the underlying biology for a few samples. Therefore, the fusion module needs to enhance the synergies between these data sources. Previous research has proposed various embedding fusion techniques, including attention‐based (Hazarika et al., 2018; Vaswani et al., 2021), multiplicative combination layer (Liu, Li, et al., 2018), and transformer (Nagrani et al., 2021). An early adaptation of the bottleneck attention module (BAM) (Park et al., 2018) known as the mBAM (Rahaman et al., 2022) examined both spatial and modality dimensions. It employed a fully connected (FC) layer with compression to learn spatial attention from the fused two‐dimensional tensor.

In this study, we present a fusion module called spatio‐modality fusion using bottleneck attention, which carefully examines the amalgamation. We use dilated convolutional (Yu & Koltun, 2015) methods to learn the contextual pattern. The module explores spatial dimensions using a convolutional neural network (CNN) (Gu et al., 2018) augmented by a larger receptive field (RF), a feature known as dilated convolution. Using dilated convolutions significantly expands the RF, facilitating the collection of contextual patterns from the combined data (Park et al., 2018). These contextual patterns play a crucial role in the downstream tasks. Our study shows that the dilated convolutional layer performs better than the FC layers (Figure 3). In earlier studies, the FC layers lost considerable spatial information while downsampling from the combined tensor to a one‐dimensional vector (Rahaman et al., 2022). Furthermore, the subsequent attention operation performed on the compressed version produced a low‐dimensional (vector) mask. Our method, on the other hand, implements spatial attention on the original version of the fused tensor, generating a two‐dimensional attention mask. Simultaneously, the module learns to apply attention across the modalities to select the best source, and in spatial dimensions to mask the compressed feature vectors, fostering a richer knowledge extraction. The attention mask delineates the significance of each feature on classification, in our case identifying SZ. Therefore, the mask can also be utilized to generate other analytics of the test samples, for example, subgrouping based on disease relevance.

FIGURE 3.

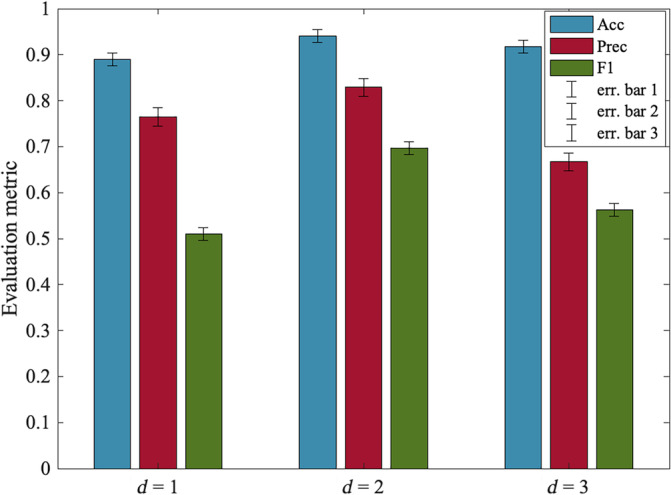
Model's performance for various dilation rates (d). The error bars stand for the confidence interval for the metrics accuracy (ACC), precision (Prec), and F1‐score. The dilation rate indicates the expansion of the convolution kernel. Optimal performance is achieved at d = 2. The d = 1 represents the standard convolution. As the dilation rate increases beyond 2, we can see the performance start to decline.

The modalities we use for the classification are structural and functional neuroimaging data and genome‐wide polymorphism data. We test the model on a dataset comprising 437 subjects, including individuals with SZ (162) and controls (275), intending to classify SZ. Our proposed method produces a multidimensional attention mask to elucidate the model's decisions and underlying neurobiological basis. This attention mask encodes the relative importance of each modality and spatial significance. The spatio‐modality attention identifies structural magnetic resonance imaging (sMRI) components—such as the supplementary motor area (SMA), left insula, caudate, and temporal pole—of high importance for detecting SZ (Figure 4). The attention scores on static functional connectivity suggest that several connections among the sensorimotor (SM), subcortical (SC), and cognitive control (CC) are particularly salient in SZ. Biclustering the attention scores from three modalities discovers a multimodal cluster that includes a subset of relevant structural components, functional connections, and genes. The implicated genes, CSMD1, ATK3, MOB4, and HSPE1, have been previously recognized as relevant to SZ. The primary features of our method are as follows:

1. A fusion module capable of encoding both modality and spatial attention.

2. A dilated convolution to extract spatial patterns with a large RF.

3. A two‐dimensional spatio‐modality attention mask, enabling further data analytics such as subgroup identification.

4. A self‐explainable model via the attention scores for modality and contextual dimension.

FIGURE 4.

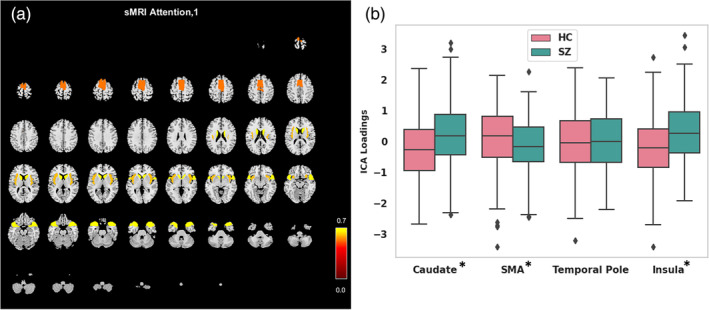
The spatio‐modality attention‐based sMRI features analysis. (a) Attention scores are computed on all sMRI components, and the significant ones are visualized on a structural montage. The components are supplementary motor area (SMA), caudate, temporal pole, and insula. (b) The ICA loadings for the most contributing components in HC and SZ groups. The error bars represent the standard deviation (SD). The asterisk sign on component name stands for the statistical significance of the difference between HC and SZ. We run two‐sample t‐test to validate the differences. We use p‐value <.05 to mark the significant differences.

2. DATA PREPROCESSING

2.1. Structural MRI

We preprocessed sMRI scans using statistical parametric mapping (SPM12, http://www.fil.ion.ucl.ac.uk/spm/). The preprocessing steps include unified segmentation and normalization of sMRI scans into gray matter, white matter, and CSF. During the segmentation step, we use a modulated normalization algorithm to generate gray matter volume. Following this, we use a Gaussian kernel with a full width at half maximum (FWHM) of 6 mm to smooth the gray matter densities.

2.2. Functional MRI

We use the SPM12 toolbox for preprocessing functional MRI data. To ensure steady‐state magnetization, we remove the first five time points of the fMRI. Next, we carry out rigid body motion correction using the INRI‐Align robust M‐estimation approach and apply the slice‐timing correction. We then spatially normalized fMRI images into the Montreal Neurological Institute standard space, using an echo‐planar imaging template, and resampled to 3 × 3 × 3 mm³ isotropic voxels. The images are then smoothed with a Gaussian kernel with FWHM = 6 mm, similar to the sMRI data.

2.3. Genomics

The preprocessing steps for the genetic data are described in our prior work (Adhikari et al., 2019; Chen et al., 2013). There are several standard preprocessing tools for genomics data, and we use Plink (Purcell et al., 2007) for both preprocessing and imputation. Linkage disequilibrium (LD) pruning was administered at r ² < .9. We use the Psychiatric Genomics Consortium (PGC) for SZ suggested genome‐wide association study (GWAS) (Purcell et al., 2007) score to select the features. The analysis selects 1280 single‐nucleotide polymorphisms (SNPs) distributed across 108 risk loci. The PGC study (He et al., 2015) reveals these SNPs express statistically significant associations with SZ at p < 1 × 10⁻⁴. The datasets verify the test retest experiment for MRI acquisitions by recording multiple repetitive scans for each subject and also account for the stable MRI signal.

More details about preprocessing and quality control are described in these studies (Fu, Iraji, et al., 2021; Iraji et al., 2022).

3. OUR PROPOSED MULTIMODAL ARCHITECTURE

Figure 1 demonstrates our proposed architecture for multimodal learning. The model incorporates three modality‐specific NNs, referred to as subnetworks, which are used for learning the latent space embedding from each input source. These NNs are selected based on their effectiveness given the type of input data, and we empirically validate their efficacy. The subnetworks conduct dimensionality reduction and account for missing entries and other discrepancies to effectively learn the representations from each incoming modality. The latent embeddings from all modalities are concatenated into a multidimensional tensor. This tensor goes through a novel spatio‐modality attention‐based fusion module, which is described in Figure 2. Once this is completed, the two‐dimensionally attended fused embedding is used as input to a multilayer perceptron (MLP). This is followed by a SoftMax layer for classification. This approach allows us to extract rich features from multiple modalities and harness the power of NNs to classify complex data effectively.

FIGURE 1.

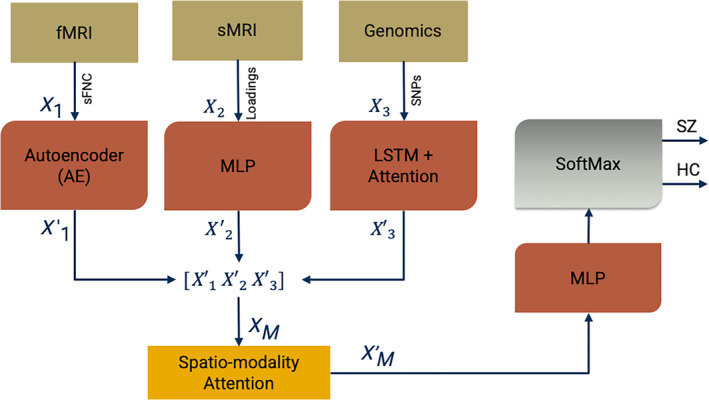
Our proposed multimodal framework with spatio‐modality temporal attention. These models incorporate three major processing steps: Imaging‐genomics preprocessing and dimensionality reduction, neural subnetworks for learning latent space embedding, and the predictor. We run group ICA on sMRI and fMRI data. We generate static functional network connectivity (sFNC) among the ICNs extracted from fMRI decomposition. We select the ICA loading parameter as the input feature for sMRI modality. The GWAS‐based genetic variable selection is carried out for genetic modality. The subnetworks are deep neural networks for learning the modality‐wise representation. Subnetwork 1 is an autoencoder (AE) for learning sFNC, subnetwork 2 is a multilayered perceptron (MLP) for sMRI loadings, and subnetwork 3 is a bi‐directional long short‐term memory (LSTM) unit with attention for learning SNPs. The combined embedding is attended in spatial and modality direction and sent through an MLP followed by a SoftMax layer for the classification. The architecture is jointly trained using an Adam optimizer.

FIGURE 2.

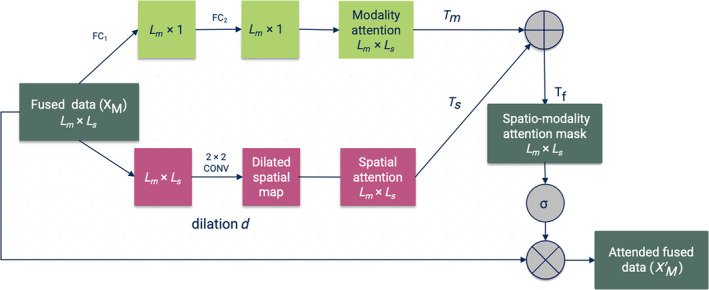
Our proposed spatio‐modality attention module for multimodal fusion. The concatenated embeddings are sent through two different branches. (i) The modality branch that learns the cross‐modality interactions and mounts it into $T_m$ attention mask and (ii) the spatial branch ($T_s$) captures the relevant context from each biological site. These two masks are merged into a final attention mask $T_f.$ The spatial branch uses dilated convolution for learning the contextual understanding of the multimodal tensor and fully connected layer for modality attention.

3.1. Input features quantification

This phase of the framework includes a few processing units for refining and performing the initial decomposition of the data collected from multiple biological domains. We execute a fully automated spatially constrained group ICA (GICA) using the Group ICA of fMRI Toolbox (GIFT) available at this link: (http://trendscenter.org/software/gift) (Iraji et al., 2021) and the NeuroMark (Adhikari et al., 2019) template on the combined subjects from three datasets, which include FBIRN (Keator et al., 2016), COBRE (Aine et al., 2017), and MPRC (Adhikari et al., 2019). The selection of intrinsic component networks (ICNs) in this study is based on the NeuroMark template. We selected 53 pairs of ICNs and arranged them into seven functional networks based on prior anatomical and functional knowledge fields (Fu, Iraji, et al., 2021; Iraji et al., 2022). The total number of connectivity networks extracted was 53, covering the whole brain. These ICNs were distributed into seven functional domains (Fu, Iraji, et al., 2021; Fu, Sui, et al., 2021): sub‐cortical (SC), auditory, SM, visual (VS), cognitive‐control (CC), default‐mode, and cerebellar domain. After estimating subject‐specific networks, we compute the subject‐wise static functional network connectivity (sFNC). The square matrix (53 × 53) represents the Pearson correlation between the time course of ICNs. We vectorize the sFNC matrix using the upper diagonal entries to ease the encoder's training process. A similar approach was used for structural MRI source‐based morphometry (ICA on gray matter maps) (Gupta et al., 2019; Saha et al., 2022), resulting in 30 structural components along with their loading values. The provided ICA priors are estimated from the 6500 subjects used in the referred study (Abrol et al., 2017). The ICA on sMRI yields individual‐level structural networks and corresponding loadings. For the sMRI modality, we used the loadings of the structural networks as the structural features. The third modality includes the set of SNPs selected from genomic data based on GWAS‐significant SZ risk SNPs identified by the large PGC study.

3.2. Deep neural networks

We employ distinct deep neural networks (DNNs) for extracting modality‐wise features. The design choices are explained in the following subsections, and their efficacy is tested on the dataset. We use an autoencoder (AE) (Goodfellow et al., 2016) to learn the representation of sFNC. It follows an encoder and decoder architecture, with each submodule consisting of five linear layers. The encoder compresses the input and generates a compressed embedding. The decoder reconstructs the input from the encoded features map. The loss function computes the reconstruction loss as the mean square error (MSE). We use the sFNC matrix as an input from the fMRI modality and employ an AE with rectified linear unit activation for learning the representations. AE is effective for learning semantic meanings and compressed abstraction of input data with successful applications in diverse fields of study (Chen et al., 2017; Hong et al., 2015). We use Xavier initialization (Kumar, 2017) from Pytorch to set the initial values of the layers in the network. We applied a dropout strategy with a probability p of 0.2 to minimize overfitting. Overfitting refers to a situation where a model performs well on the training data but fails to generalize to unseen data. Dropout is a regularization technique that helps to mitigate this issue by randomly ignoring a subset of features during training, reducing the complexity of the model and promoting generalization. For the sMRI subnetwork, we use the loading parameters from GICA. The feature vector has a length of 30, where each value represents the expression level of a subject on a group structural independent component. In general, loadings are just betas/coefficients of the variance mixture linear equations (Calhoun & Allen, 2013). The loading value corresponds to how much variance a subject contributes to a given group component. As the loadings are the vector of discrete values, for simplicity, we deployed an MLP to efficiently learn the sMRI features. An MLP is a type of artificial NN that consists of multiple layers of nodes in a directed graph, with each layer FC to the next one. It can model complex, nonlinear relationships between input and output data, making it a suitable choice for feature extraction in this context. Each layer of the MLP takes the output of the previous layer (or the input data for the first layer), applies a set of weights (learned during training), and then applies an activation function, producing the output for that layer. By adjusting the weights during training, the MLP can learn to extract salient features from the input data that are informative for the task at hand, which in this case, is the classification of SZ. The subnetwork is FC since the data dimension (30) is lower than the other modalities. In the final layer of our network, we dilated the embeddings to 100 to ensure consistency with the size of latent features derived from different modalities. We implemented a bi‐directional long short‐term memory (bi‐LSTM) network with an attention mechanism (Ashish, 2017) to extract features from SNPs. The use of a bi‐LSTM was informed by its anticipated ability to capture contextual information from a sequence (Li et al., 2019; Melamud et al., 2016). We assume that neighboring SNPs may show LD with one other, potentially forming a neighborhood substructure. The bi‐LSTM is designed to capture the localized semantics of genomic data, which might help differentiate between cases of the disorder and controls. In addition, the attention scores signify contributing neighbors to the context, further enhancing the DNN's discriminative power.

3.3. Spatio‐modality attention

We propose a fusion module that takes a multimodal joint embedding and probes the concatenated tensor in both modality and spatial dimensions. The architecture is demonstrated in Figure 2. The architecture is inspired by the BAM (Park et al., 2018), which has been implemented for learning channels and spatial attention in classification and prediction tasks (Tang et al., 2021; Woo et al., 2018; Yaseen et al., 2022). We adapt the module for fusing different modalities. The module is integrated with a mid/intermediate fusion (Boulahia et al., 2021) in a multimodal learning framework. In mid‐fusion, the modality‐specific DNNs generate compressed representations of input streams (bottleneck layers) from each source. Our intuition is to run two‐dimensional attention on these bottleneck layers. Our module uses two simultaneous attention branches that forage significant bits from the fused tensor. These branches can be treated as two distinct scoring functions across modality and spatial dimensions. We use FC linear layers in modality dimensions to learn the attention weights per modality. FC layer, is a type of layer used in NNs where all neurons in the previous layer are connected to the neurons in the next layer. The FC operation is defined in the following Equation (2).

$$\mathrm{FC}\left(x\right)=W^{T}x+b$$ (1)

where $W\in {ℝ}^{N\times 1}$ and $b\in {ℝ}^{N\times 1}$ are the weight matrix and bias, respectively, and N is the input dimension. x is the input to the FC operation, in the context of Equation (1), and b is the bias vector in the FC layer.

For another branch, the module employs dilated convolution layers for extracting the relevant spatial patterns. The dilated convolutional filters arbitrate a large RF for collecting contextual information. In our study, we are using only three modalities, so we skip the reduction. However, the reduction ratio in modality direction could potentially help in combining a large number of modalities in further studies.

3.3.1. Modality attention scoring (T _m )

The modality attention branch assigns scores to the modality dimension to signify the most informative and discriminative source for the downstream task. The modality attentions mask (T _m ) gathers importance scores that characterize the contribution of input modality to the classification of SZ. Figure 2 illustrates the attention‐weighting architecture. An FC linear layer (FC₁) is applied to the input tensor, $X_M$ (L _m × L _s) to reduce the dimension to the number of modalities (L _m). Here, L _s is defined as the latent embedding size consistent across the modalities. The compressed data are then passed through another FC layer (FC₂) to compute the attention weights for each modality. We also use batch normalization (BN) (Ioffe & Szegedy, 2015) to adjust the scale with the spatial branch. Moreover, BN improves the speed, performance, and stability of the NNs. Then, the tensor is expanded to the shape of the input tensor L _m × L _s. We can formulate the operation as follows:

$$T_m=\mathrm{BN}({\mathrm{FC}}_2\left({\mathrm{FC}}_1\left(X_M\right))\right)$$ (2)

Here, T _m refers to the transformed tensor after the application of BN and two FC layers.

3.3.2. Spatial attention branch (T _s )

We opt for capturing the context from the aggregated multimodal embedding tensor, which extracts contextual information in the form of spatial patterns. For spatial attention, the submodule uses a CNN. We use dilated convolution (Yu & Koltun, 2015) to create a large RF that assists in apprehending the context. The dilated convolution inflates the kernel by inserting holes between the kernel elements (Yu & Koltun, 2015). An additional parameter, dilation ratio (d), indicates the extent to which the kernel is widened. There are usually d‐1 spaces inserted between kernel entries. We use an empirically validated convolutional filter of dimension 2 × 2 with a dilation ratio (d) = 2 on the combined tensor. Figure 2 shows the dilated convolution for spatial significance. The branch weighs the fused data for identifying salient loci relevant to downstream tasks. The spatial attention mask is also expanded to a shape of L _m × L _s. Equation 3 is the operation for spatial attention and illustrates the overall processing in the spatial branch.

$$T_s=\mathrm{BN}(d^{2\times 2}\left(d^{2\times 2}\left(X_M\right))\right)$$ (3)

Here, $T_s$ represents the spatial attention mask. The operation helps to create a large RF that captures the context or spatial pattern in the input data. We merge the spatial attention mask, $T_s$ and the modality attention mask, $T_m$ to generate the final mask, $T_f$ (see Equations 4).

$$T_f=\mathrm{\sigma }\left(T_s+T_m\right)$$ (4)

The operation in Equation (4) is an element‐wise summation between $T_s$ and $T_m$ to compute the final fused attention mask, $T_f$. We apply a sigmoid function ($\sigma$) to bind the values of $T_f$ between 0 and 1. The sigmoid function is commonly used in NNs to introduce nonlinearity and to map any input to a value between 0 and 1, making it especially suitable for models where we have to predict probabilities.

Next, we use element‐wise multiplication operation (⊗) to fuse the attention mask $T_f$ and the input tensor X (Equation 5).

$$X_{△}=X\otimes T_f$$ (5)

This operation highlights the important features in the input tensor according to the attention mask. The result is a new tensor matrix, which emphasizes the regions of the input that are most informative for the task at hand. We use $X_{△}$ as the input to the MLP followed by a SoftMax layer to classify the samples (Figure 1). Together, these operations help to guide the model to focus on the most informative features across different modalities and spatial locations when performing the downstream task, such as classification or regression.

3.4. Multimodal joint training

We split the dataset into two primary categories: 80% for training and 20% for evaluation. The evaluation data are then further divided equally into testing and validation sets. We train the joint model for 450 training epochs and validate its performance on the validation set. For the training phase, we use the Adam optimizer from Pytorch with a learning rate of 10⁻⁴ and a batch size of 32. The loss terms include MSE for the AE subnetwork reconstruction loss and binary cross‐entropy for the model's classification loss. We implement early stopping to balance the training and validation loss, which eventually regularizes the model. Our training scheme optimizes for accuracy and saves the best‐performing model. For the validation phase, we used the k‐fold cross‐validation (Bengio & Grandvalet, 2003) technique for k = 10. The cross‐validation method randomly divides the datasets into 10 equal partitions and uses 9 of them to train the model and the remaining one for testing the performance. The technique interchanges the training and testing set and repeats the process 10 times. In the testing phase, we utilize the best‐performing model saved from the validation phase and apply it to the testing samples. Our performance metrics, which include accuracy, precision, recall, and F1 score, are computed in this phase. We report the final performance on the held‐out test dataset. To empirically validate the results and other architectural specifications, we run the model 50 times and report average results across these repetitions with corresponding standard deviations. We also introduced multiple random initializations (Thimm & Fiesler, 1995) of the NN to ensure the agnosticism of the model to different initial conditions. The resulting metrics in Table 1 are summarized across distinct initializations. The joint training of all three modalities allows the sources to interact and helps modality‐specific subnetworks to optimally converge by leveraging learning from the other subnetworks. Moreover, we implement a multimodal regularization technique for the completeness of the experiments. This technique aims to eliminate bias by maximizing the functional entropies (Gat et al., 2020). We designed our implementation based on the existing regularizer and utilities.

TABLE 1.

Performance comparison of our proposed model with several baselines (unimodal, bi‐modal, and tri‐modal) and the state‐of‐the‐art models for a similar task.

Models	Modalities	Data	Accuracy	Precision	Recall	F1 score
Autoencoder	Unimodal	fMRI	0.811 ± 0.15	0.587 ± 0.11	0.451 ± 0.05	0.510 ± 0.11
Multilayer perceptron		sMRI	0.782 ± 0.13	0.439 ± 0.12	0.477 ± 0.04	0.443 ± 0.09
bi‐LSTM with attention		SNPs	0.673 ± 0.15	0.338 ± 0.13	0.498 ± 0.04	0.403 ± 0.08
Mid fusion	Bi‐modal	sMRI + fMRI	0.835 ± 0.14	0.577 ± 0.09	0.478 ± 0.03	0.523 ± 0.01
Mid fusion		SNPs + sMRI	0.784 ± 0.18	0.397 ± 0.08	0.455 ± 0.03	0.424 ± 0.15
Mid fusion		SNPs + fMRI	0.813 ± 0.14	0.501 ± 0.05	0.443 ± 0.03	0.470 ± 0.01
Early fusion	Multimodal	sMRI + fMRI + SNPs	0.701 ± 0.11	0.575 ± 0.12	0.460 ± 0.03	0.511 ± 0.02
Late fusion		sMRI + fMRI + SNPs	0.781 ± 0.08	0.615 ± 0.12	0.400 ± 0.04	0.485 ± 0.03
Mid‐fusion (Rahaman et al., 2021)		sMRI + fMRI + SNPs	0.876 ± 0.06	0.640 ± 0.07	0.501 ± 0.04	0.562 ± 0.04
Mid‐fusion with attention (Rahaman et al., 2023)		sMRI + fMRI + SNPs	0.921 ± 0.02	0.798 ± 0.07	0.522 ± 0.04	0.631 ± 0.05
Mid‐fusion with mBAM (Rahaman et al., 2022)		sMRI + fMRI + SNPs	0.932 ± 0.04	0.903 ± 0.06	0.561 ± 0.05	0.692 ± 0.04
Spatio‐modality mid fusion		sMRI + fMRI + SNPs	0.941 ± 0.05	0.829 ± 0.06	0.601 ± 0.06	0.697 ± 0.05

Note: The performance metrics are presented as (mean ± standard deviation) across 50 repetitive runs.

4. EXPERIMENTAL RESULTS & DISCUSSION

We analyzed three datasets, COBRE (Mayer et al., 2013), fBIRN (Keator et al., 2016), and MPRC (Adhikari et al., 2019). The merged dataset consists of 437 subjects, with 275 healthy controls (HCs) and 162 subjects with SZ. The performance of our proposed model is benchmarked against several other models, including unimodal and multimodal baselines using imaging‐genetics datasets. The performance comparison is detailed in Table 1. In early fusion, input data from all modalities are merged at the first step, and the resultant vector is then processed through an NN. For late fusion, we use different networks for distinct modalities. Each network classifies a sample based on the data it receives, and a max voting scheme (Morvant et al., 2014) is used to determine the final label for each instance. Our proposed spatio‐modality attentive fusion model outperforms the comparing methods (Table 1), achieving an accuracy of 94.1% in differentiating SZ. Other performance metrics are either superior or comparable to the benchmark models. Since our dataset is slightly imbalanced, we used the harmonic mean of precision and recall given by the F1 score (Goutte & Gaussier, 2005) for the classification performance evaluation. Our proposed model achieves an F1 of 0.697 with a reasonable balance between precision and recalls expected in a biological population. Substantial performance improvements are achieved when the BAM is used for fusion (as shown in the last two rows of Table 1), highlighting the utility of BAM in multimodal fusion. The performance of the model using only genetic data is consistently low. This suggests that genomic data is solely an insufficient descriptor of phenomena, that is, discriminating SZ. However, the noteworthy observation is the ability of the genomic data to complement other modalities in multimodal settings, especially when spatio‐modality fusion is employed. This underscores the capacity of the fusion module to leverage the contributions from various modalities with greater precision. Our model can suppress the features from less informative sources while prioritizing those from more informative ones, a desirable characteristic to effectively learn the multimodal representation of input data.

4.1. Reproducibility and reliability of the results

Reproducibility is a fundamental aspect that speaks to the reliability and validity of the computational findings (Adali & Calhoun, 2022; Klapwijk et al., 2021). The crucial medical research domain such as neuroimaging signifies the utility of replication most. It allows for the independent verification of results across analytical frameworks, enhancing the adaptability of vital neurobiological outcomes. In this study, we evaluate the reproducibility of the model's performance on the neuroimaging population by employing cross‐validation strategies to assess the generalizability and stability of the results across different subsets of the data. We combine three datasets in this study COBRE, fBIRN, and MPRC, and preprocess them under the same imaging protocols. Rationally, we create three parts of the combined dataset and we check the reproducibility of each subpopulation separately. For recording performance on each dataset, we train the model on two other datasets. For instance, COBRE performance is computed using the COBRE sample as held‐out test data, and the model is trained on only samples from fBIRN and MPRC. Additionally, these experiments aid in eradicating the acquisition bias and explore the model's efficacy on a smaller population. Furthermore, we generate two random splits of the data for the completeness of the experiments. It utilizes randomization training/validation and testing cohort selection. In the first random split (RDS 1), we select 40% of held‐out data for testing and the remaining for training and validation. In the second one (RDS 2), we randomly select another 30% for the held‐out and the remaining for training and validation. Table 2 shows the model performance on these diverse randomizations of the dataset to provide a comprehensive understanding of the efficiency of such a framework in disease prediction. We observe the performances are reasonably reproducible from different settings of input data. Three parts of the combined dataset yield comparable results with the final performance of the proposed framework. Two random splits also exhibit proportionate metrics validating the reliability of the model in the downstream task, which is classification in our case. However, with more data for training (RSD 2 in Table 2), the model achieves slightly better performance—standard in data‐driven approaches. We also validate the extracted salient attributes of the data contributing to the SZ characterization across these splits. The spatio‐modality attention‐based feature analysis in the following subsection is carried out on the summarized set of features stable through independent segments of the dataset. To evaluate the impact of dilation on contextual learning, we conducted experiments using distinct dilatation d values. These also contribute to the verification of the model's robustness on specific choice configurations. Figure 3 presents the results for three performance metrics: accuracy, precision, and F1‐score. The bar graph showing the evaluation metrics also includes the confidence interval. It indicates a lower and upper bound of the data that describes a range or a corridor in which 95% of the predictions would fall given the actual true value. We employed dilated convolution to extract contextual information. The dilation rate d = 1 represents the standard convolution, while d greater than 1 denotes the dilated version. The model demonstrates superior performance with a dilation value of 2 and experiences a performance drop for higher values. These findings suggest that dilation helps in extracting contextual information through a larger RF and is beneficial for accurate prediction. Nevertheless, because our multimodal fused tensor has limited dimensions, larger dilation might skip important transient patterns in the data by adding more holes in the RF. Due to the limited dimensions of the concatenated tensor, we are unable to explore the sensitivity beyond a dilation ratio of 3.

TABLE 2.

Reproducible performance of the proposed method for diverse subsets of the data.

Dataset/Split	Training and validation	Held‐out test data	Accuracy	Precision	Recall	F1‐score
COBRE	fBIRN + MPRC	COBRE	0.920 ± 0.08	0.802 ± 0.07	0.575 ± 0.05	0.68 ± 0.06
fBIRN	COBRE + MPRC	fBIRN	0.931 ± 0.09	0.801 ± 0.06	0.586 ± 0.05	0.67 ± 0.05
MPRC	COBRE + fBIRN	MPRC	0.901 ± 0.12	0.787 ± 0.09	0.589 ± 0.07	0.674 ± 0.07
RDS 1	60% of total data	40% of total data	0.932 ± 0.08	0.801 ± 0.01	0.608 ± 0.05	0.691 ± 0.03
RDS 2	70% of total data	30% of total data	0.937 ± 0.07	0.854 ± 0.03	0.583 ± 0.04	0.693 ± 0.03

Note: The first three rows represent the performance on the independent dataset and the bottom two rows stand for random splits.

4.2. Spatio‐modality attention for features attribution

In this experiment, we explore the feature's (from all modalities) contribution toward the disease classification. The proposed spatio‐modality attention inscribes these significance scores. Thus, for feature attribution, we refine the attention values. However, to summarize the scores, averaging over multiple dimensions might drastically suppress the data, hence weakly depicting the tangible statistics. Here, we compute spatio‐modality attention scores on a trained model by constraining multiple criteria. The values are summarized across the subjects and input feature dimensions. Furthermore, we compute scores feature‐wise from all three modalities and determine a threshold representing the global mean throughout all the attention masks. We select the significant contributions by passing attention scores greater than the threshold only. Then, we filter the influential features by selecting significant contributions across at least 10% of the total population. The attention from all the settings mentioned in the reproducibility section is scrutinized to find a stable set of features. Therefore, we determine a contributing feature by their significant contribution toward classification across a reasonable number of samples. We avoid the features that are highly contributing to a few samples but are inconsistent across the population. As these sources are unstable and spurious, they are not reliable for neurological interpretation. Figure 4a shows the sMRI feature analysis based on spatio‐modality attention values. By thresholding the attention score, we observe four components to be significantly contributing to differentiating SZ. These components are the caudate, SMA, temporal pole, and insula. These components are the caudate, SMA, temporal pole, and insula. Moreover, we examine their ICA loadings on both HC and SZ groups and visualize the group‐level statistics in Figure 4b. The HC loadings group mean is higher than the SZ mean, which indicates that HC subjects have higher gray matter density in the SMA region than SZ subjects. Alternatively, the SZ subjects are more heavily expressed in the insula and caudate than the HC group. Of note, the structural components differentiated through our method are associated with SZ, for example, caudate (Crespo‐Facorro et al., 2007; Mueller et al., 2015) and temporal pole (John, 2009). Prior research also reported that aberrant motor behavior in SZ is associated with SMA volume (Schröder et al., 1995; Stegmayer et al., 2014). Also, insula activation has been associated with the processing of emotional facial expressions, which is deficient in individuals with SZ (Sheffield et al., 2020; Wylie & Tregellas, 2010). The differences in gray matter density patterns between these groups aid in understanding the brain's structural alterations associated with SZ. We also run the two‐sample t‐test on the loading values from both subject groups (HC/SZ) to verify the statistical significance of the group differences. We found three of the salient features (Caudate, SMA, and Insula) show statistically substantial differences between control and individuals with SZ at a level of p < .05. Furthermore, we analyze the attention computed from fMRI features. The static functional connections are shown in the connectograms of Figure 5. The connections are weighted by the attention scores in Figure 5a. The connections among SM, CC, and SC are identified as most salient for classification. We further analyze the static functional connectivity of these edges between distinct brain components. Figure 5b shows average connectivity strengths are mostly negative (blue) and a few are positive (yellow). That demonstrates that most components are inversely correlated. The HC connectograms in Figure 5c show a connection with positive connectivity strength between IC 3 of SC to IC 10 of SM, whereas a positive connection in SZ dynamic is visible between IC 1 from SC to IC 30 of the CC domain. The HC dynamics are more strongly connected in the SC and SM regions than the dynamics of SZ subjects. The average functional connectivity strength between the components of these two regions is higher for HC subjects than for SZ. The visual (VS) domain also shows connectedness with other domains in HC dynamics where the SZ connections are comparatively weaker. The weaker connectivity in SZ might create functional impairments and dysfunction (Kaufmann et al., 2015; Koshiyama et al., 2018). Moreover, these connectivities also symbolize the communication between different parts of the brain for carrying out neural activities. Further study of these connections is required to assess their roles in overall cognition and information processing within these subject groups.

FIGURE 5.

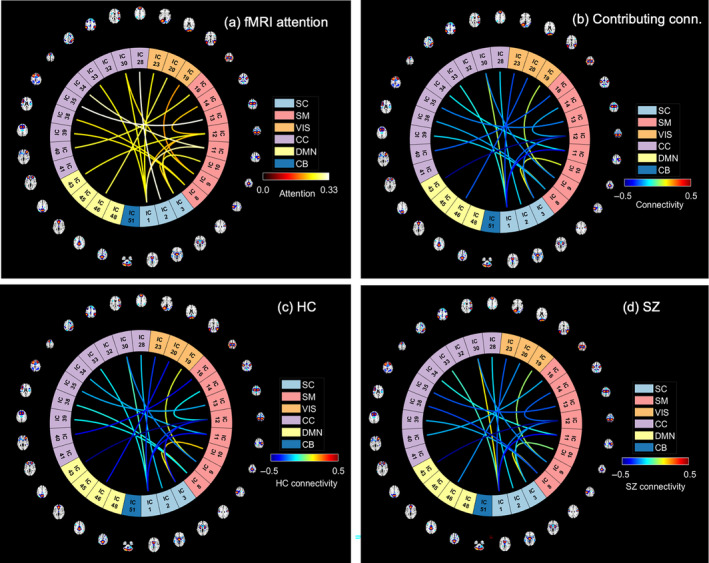
The spatio‐modality attention scores computed from fMRI features (static functional connectivity (sFNC)). (a) The sFNC connections are weighted by their corresponding attention score. After thresholding, we show the connections that are effective for predicting schizophrenia at all different configurations of the model executions. The warm‐colored connections are the significant ones; highly contributing to (a). We observe several contributing connections among sensorimotor (SM), cognitive control (CC), and subcortical (SC) regions. (b) The connections are weighted with the mean connectivity across the subject group. (c) Connections are weighted by the mean connectivity strength computed across the HC group. (d) SZ group's connectivity.

4.3. Biclustering using spatio‐modality attention scores

The spatio‐modality attention masks provide the significance scores for the features from all modalities. In this experiment, we run biclustering of these scores across modalities to examine the subgrouping of subjects and features based on their association with SZ. Another rationale behind this experiment is to visualize the relation among distinct biological domains and their coregulation in diseased conditions. To run the analysis, first, we concatenate the feature's attention from sMRI, fMRI, and genomics modality, which is a two‐dimensional matrix of (subject × features). Then, we run the N‐BiC biclustering (Rahaman et al., 2020) for clustering the attention scores in both dimensions. We choose N‐BiC because it allows clustering without specifying the expected number of biclusters and regulates the overlap between clusters. For two‐dimensional data, it requires a heuristic to represent attributes from one variable as a function of attributes from another variable. It then exhaustively searches for all intrinsic subgroups and conditionally merges along the way. We sort features based on their consistently significant contributions to the classification. We select a subset of subjects for each feature where the attention values are higher than the global mean – the average attention across all the subjects and features. We choose features that exhibit this higher value across at least 10% of the total subjects. Initially, N‐BiC yielded four biclusters then merged into two to regulate overlap. We repeat the run 10 times to stabilize the results. The outcomes show one multimodal and one unimodal bicluster (Table 3). The multimodal bicluster includes the following sMRI components: the anterior cingulate cortex, the medial prefrontal cortex, the caudate, the temporal pole, and the Frontal. It groups three SNPs including four genes CSMD1, ATK3, MOB4, HSPE1, and 26 static functional connections among several brain regions. AKT3 provides instructions for making a protein that is mostly active in the nervous system. The gene creates learning and memory‐related deficits, and the SNP is identified as an associated genome‐wide significant locus for SZ (Howell et al., 2017; Howell & Law, 2020). CSMD1 is known as a complement regulatory gene and has also been associated with SZ (Athanasiu et al., 2017; Liu et al., 2019). Figure 6 visualizes the sFNC connections through HC, SZ, and HC‐SZ connectograms, respectively. In general, HC and SZ connections appear homogenous and rational since they are clustered into a single subgroup. However, one connection emerged with a strong HC‐SZ difference between the CC (IC 28) and SM network (IC 12) even with the maximized homogeneity. These multimodal features analogously contributed to characterizing SZ; therefore, it potentially provides a link among these physiologies for disease‐related deficits. These strong homogenous associations with SZ suggest potential co‐aberration of these physiologies (genomics and brain) suggesting that further exploration of their coupling and progression may help improve our understanding of the disorder. Further analysis of these features would be productive to infer their joint modulation in SZ conditions. Also, a tri‐modal feature set can potentially help explain the behavioral deficits from multiple biological perspectives.

TABLE 3.

The clusters extracted from biclustering on the attention values from all three modalities.

Bicluster	SZ subjects	HC subjects	sMRI features. (components loadings)	fMRI features (sFNC connections)	Genomics features (SNPs)
1	30	21	ACC + mpFC, Caudate, Temporal Pole, Frontal	# connections: 26	SNP IDs: rs10927041, rs10108628, rs10931784 Associated genes: AKT3, CSMD1 MOB4, HSPE1‐MOB4
2	23	18	‐	# connections: 73	‐

Note: The N‐BiC primarily extracts four biclusters that are merged into two due to higher overlaps with the earlier ones. Bicluster 1 is multimodal and bicluster 2 is unimodal consisting of 73 sFNC connections.

Abbreviation: ACC, anterior cingulate cortex.

FIGURE 6.

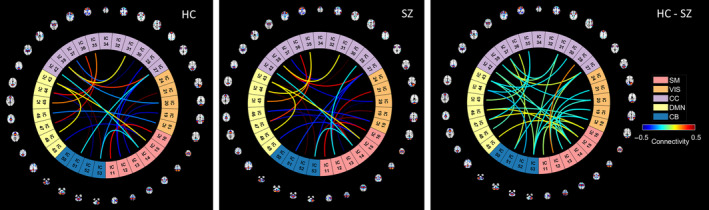
Connectograms generated from sFNC connections included in the multimodal bicluster (bicluster 1). There are HC/SZ group differences in the strength of static functional connectivity in cognitive control (CO) to sensorimotor (SM), and visual (VS) regions.

5. CONCLUSION

Our proposed fusion model attentively probes the dimensions of the fused latent space and provides a more rational synthesis of multiple biological sources. The spatio‐modality attention module boosts the classification performance and achieves an accuracy of 94.1% with a 0.697 F1 score. The noteworthy performance of the classifier with spatio‐modality attentive fusion evidences the utility of such a technique in multimodal learning. Moreover, the spatio‐modality attention scores are potentially self‐explaining for the feature attributions toward the downstream task and provide an avenue for running further experiments, for example, subgrouping, and illustrating group differences. Our model learns spatial patterns through a large (dilated) RF for a better representation. The usage of dilated convolution for spatial scoring is potentially effective for foraging contextual information. In multimodal settings, the dilation is shown to be providing a comprehensive view of the available modes of data. The modality submodule signifies each source and generates modality‐wise contributions. As such, the controlled scoring also interprets the model's decision and offers insights into the neurobiological relevance. This relevance can potentially explain the underlying substrate of the disorder under investigation, SZ. In all, the model seeks relevant patterns in the brain's structural features, functional mechanisms, and genomic pathways that lead to a coherent deciphering of SZ. Additionally, the analysis of modality‐specific contributions helps discriminate SZ‐affected physiologies with limited availability. The subgrouping of subjects and multimodal features based on the attention scores can potentially manifest the co‐regulation of multiple biological domains in diseased conditions. The proposed fusion module can discover reliable biomarkers for the disorder, and the preceding interpretation recommends features that can help explain the underlying mechanism of the disease.

AUTHOR CONTRIBUTIONS

Md Abdur Rahaman and Yash Garg instantiated a bottleneck attention module for multimodal data fusion. Md Abdur Rahaman and Vince Calhoun designed the spatio‐modality multisource fusion applied on neuroimaging genetics data. Md Abdur Rahaman ran the experiments and drafted the manuscript. Zening Fu, Armin Iraji, and Jiayu Chen helped to preprocess the datasets and edited the manuscript. Peter Kochunov, L. Elliot Hong, Theo G. M. Van Erp, and Adrian Preda collaborated in data collection and edited the manuscript. Vince Calhoun supervised all aspects of the project, thoroughly edited the paper, and gave valuable feedback on the results. All authors have approved the final version of the submission.

CONFLICT OF INTEREST STATEMENT

The authors declare no conflicts of interest.

Rahaman, M. A. , Garg, Y. , Iraji, A. , Fu, Z. , Kochunov, P. , Hong, L. E. , Van Erp, T. G. M. , Preda, A. , Chen, J. , & Calhoun, V. (2024). Imaging‐genomic spatial‐modality attentive fusion for studying neuropsychiatric disorders. Human Brain Mapping, 45(17), e26799. 10.1002/hbm.26799

DATA AVAILABILITY STATEMENT

According to the IRB data privacy agreement, we are restricted to share any subject‐specific data. However, the datasets are available online following the referred studies and also available from the corresponding authors on request. The preprocessing pipeline is public, as referred in the manuscript. All the preprocessing tools are available online at http://trendscenter.org/software, and the model's architectural details are available from the corresponding author.