Abstract
A major goal in synthetic development is to build gene regulatory circuits that control patterning. In natural development, an interplay between mechanical and chemical communication shapes the dynamics of multicellular gene regulatory circuits. For synthetic circuits, how non-genetic properties of the growth environment impact circuit behavior remains poorly explored. Here, we first describe an occurrence of mechano-chemical coupling in synthetic Notch (synNotch) patterning circuits: high cell density decreases synNotch-gated gene expression in different cellular systems in vitro. We then construct, both in vitro and in silico, a synNotch-based signal propagation circuit whose outcome can be regulated by cell density. Spatial and temporal patterning outcomes of this circuit can be predicted and controlled via modulation of cell proliferation, initial cell density, and/or spatial distribution of cell density. Our work demonstrates that synthetic patterning circuit outcome can be controlled via cellular growth, providing a means for programming multicellular circuit patterning outcomes.
Subject terms: Synthetic biology, Pattern formation, Genetic circuit engineering
A major goal in synthetic development is to build gene regulatory circuits that control patterning. Here the authors discover that elevated cell density dampens SynNotch signaling, enabling the design of density-dependent synNotch patterning circuits where multicellular patterning outcomes are programmed by controlled cell proliferation in time and space.
Introduction
During embryonic development, morphogenesis emerges through the interplay between chemical and mechanical processes that occur simultaneously to generate the architecture of the embryo1. At least in part, this is due to the tremendous growth and cell proliferation that occurs to bring a single cell to generate a multicellular organism. For example, in the zebrafish model, the embryo goes from 256 cell stage to around 22,000 in around 14 h, during which the body plan patterning and morphogenesis is established2. It has been shown that, during natural development chemical and mechanical processes can proceed in sequence, with patterning providing a template for mechanical regulation3–6. The information can flow in the other direction too, whereby mechanical inputs like substrate stiffness or cell shape can affect signaling and patterning7–11. Finally, the two aspects (mechanics and chemical) can be intertwined in so-called mechano-chemical systems; these mechano-chemical systems seem to abound in developmental transitions12–22. Despite emerging examples, many principles remain obscure regarding how information flows between mechanical processes and chemical circuits in general, and how this contributes to expand, constrain, or regulate patterning and morphogenetic outcomes. This lack is due at least in part to the complexity of the embryo which presents inherent challenges to studying and controlling developmental transitions in general, and ones where mechanical properties and gene circuit signaling dynamics are intertwined in particular.
One particular effector of mechanical input into signaling, patterning and morphogenesis is cell density and its origin through cell growth and proliferation. Since at least the publication of D’arcy’s “On Growth and Form”1, cell growth and proliferation have been recognized as playing an important role in shaping multicellular morphogenesis. More recently, cell proliferation is starting to be implicated as an input for patterning: as a recent example in vivo, a mechanically induced organizing center was seen to be induced via proliferation-driven compression in the development of rodent incisors23. When cultivating cells in vitro, it is well known that cell density significantly impacts growth and differentiation of cells, so much that cell density is a parameter that needs to be extensively optimized both for cell line maintenance and directed differentiation protocols24–43.
A major emerging theme in the field of synthetic development is the development of gene circuits that enable controlled morphogenesis of patterned tissues19,44–52; building self-organized systems through biological circuits could become the basis for a new approach to the engineering of resilient, self-healing and self-forming structures of multiple scales. Highly simplified engineered systems have been generated in this fashion that provide controlled and defined experimental systems in which to analyze gene circuits within the context of a multicellular structure53–60. Comparatively less is known whether or how density impacts synthetic gene circuits and synthetic signaling pathways, and so whether density can be manipulated to control signaling mediated patterning outcomes is not currently known. Engineered systems provide an ideal setting to study mechano-chemical coupling where signaling and mechanical phenomena can be isolated, measured and modulated. Additionally, introducing mechanical-chemical coupling in synthetic gene circuits could uncover novel strategies for engineering multicellular systems to achieve patterning and morphogenesis goals.
Synthetic circuits based on Notch signaling, or so-called synNotch circuits, have emerged as a modular and flexible strategy for engineering multicellular mammalian systems53–55. The synNotch system uses engineered receptors modeled after the endogenous developmental signaling pathway Notch/Delta. This endogenous pathway is contact-dependent and is used extensively during development to generate cell-scale patterns61–63. In the synthetic version, synNotch, both the input and output of the pathway have been rendered user-definable and, as such, are orthogonal to the endogenous Notch pathway. Using this system, developmental circuits have been engineered in 2D culture as well as in 3D fibroblast aggregates where a synthetic signal affects multicellular signaling and mechanics by driving expression of key adhesion proteins53–55. In these synNotch circuits though, information flows from engineered signaling proteins to downstream effects, for example on mechanical properties of the cell through changes in cell-cell adhesion. To achieve a complete synthetic mechano-chemical system with reciprocal information flow between both modalities, mechanical inputs to signaling must also be characterized. Insights that synNotch could be a good candidate to develop such a system are emerging. First, although the specific mechanisms may differ based on the cellular context and the endogenous or synthetic nature of the receptors (e.g., ref. 64), the proposed general mechanism of activation for Notch and synNotch signaling involve a mechanical “pulling force” that exposes the protease cleavage site for further signal transduction64–69. Second, cellular mechanical tension, shear stress, ECM stiffness, and cell density have been shown to play a role in Notch signaling in certain contexts70–76. Third, synNotch has been engineered to respond to different degrees of pulling force77. Whether these inputs can be used to create a system where mechanics or cell proliferation affects not only signaling, but also patterning outcomes has not been explored.
Mathematical models have been an important tool for understanding morphogenesis in natural systems78–80 and thus provide a potential strategy for the design and analysis of synthetic systems that incorporate mechanical-chemical coupling. Cell-based models of Notch-mediated signaling81 have uncovered key insights into the self-organization of regular spatial patterns82, the regulation of cell fate bifurcation by receptor-ligand interactions and cell geometry63,83,84, and the important roles of ligand expression levels and competition in robust patterning61,83,85. This tool has also been used to catalyze the discovery and design of novel circuits for morphogenesis86,87. Such models have been used to study natural cases of mechano-chemical coupling84,88–90 but have not yet been applied to synthetic cell systems.
Here, we first identify cell density as a non-genetic parameter of cell culture that affects synNotch signaling, through a screening of mechanical inputs in a murine fibroblast cell line (L929) and in mouse embryonic stem cells (mES). Cell density above a critical threshold robustly dampens synNotch signaling, not only in 2D, but also in 3D and with multiple synNotch receptor/ligand pairs. This is due, at least in part, to a transcriptional repression at high density, which particularly affects membrane-bound signaling partners (ligands and receptors). We then build, both in vitro and in silico, a synNotch-based patterning circuit to study the effects of cell density on patterning outcomes. We construct a spatial-propagation multicellular synNotch circuit, which contains a local relay circuit with a sender (signal-originating) cell type and a transceiver (signal-propagating) cell type that both receives and propagates a fluorescent signal. With this simple genetic circuit, we show that cell density and proliferation can affect patterning outcomes, such that the same genetically identical cells can generate spatial and temporally distinct patterns depending on how cell density is regulated in time and/or in space. We finally discuss how our work could provide insight in mechano-chemical patterning circuits, and how cell density can be used as a control point for programming multicellular circuit patterning outcomes.
Results
Cell density impacts SynNotch signal transduction
With the goal of integrating mechano-chemical control in synNotch-based multicellular synthetic gene circuits, we first decided to evaluate the impact of non-genetic factors such as tissue mechanics and cell density on synNotch signal transduction. To quantify the impact of individual perturbations to the physical environment on synNotch signaling, we employed a previously reported in vitro assay for synNotch activation based on a sender-receiver cell signaling paradigm in the mouse fibroblast cell line L929 (Figs. 1A, B and S1). Briefly, two L929 mouse fibroblast cell lines, a sender cell line and a receiver cell line, are engineered such that signaling between a sender cell and receiver cell can be assessed by the presence of a red fluorescent reporter in receiver cells. Sender cells constitutively express membrane-bound green fluorescent protein (GFP), which acts as the ligand for an anti-GFP synNotch receptor on receiver cells (anti-GFP synNotch, Fig. 1A). The intracellular portion of the anti-GFP synNotch receptor contains a tetracycline-controlled transactivator (tTA) which is freed from the membrane upon contact-dependent activation and translocates to the nucleus where it activates expression of cytosolic mCherry. To assay synNotch activity, sender and receiver fibroblasts are co-cultured in a 1:1 ratio for 24 h, by which time mCherry fluorescence in alive activated receiver cells can be assayed via a fluorescence activated cell sorter (FACS) machine (see Fig. S1 for FACS gating scheme).
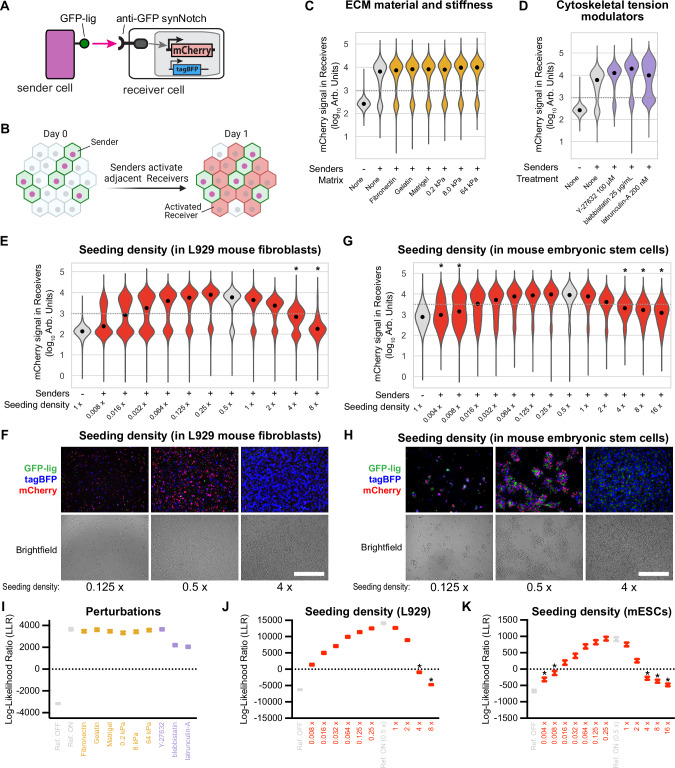
Fig. 1. Screening of mechanical perturbations reveals cell density-dependence of synNotch receptor activation.
A Schematic of Sender-Receiver synNotch signaling. Membrane-bound GFP-ligand in Senders binds synNotch in Receivers cleaving synNotch, freeing the intracellular domain (tTA-VP64) to translocate to the nucleus and activate mCherry reporter. B Schematic of synNotch signaling assay. Senders and Receivers are co-cultured at a 1:1 ratio and mCherry activation in receivers is measured at 24 h. C–E Violin plots depict the distributions of mCherry fluorescence (log10 scale) measured via FACS in L929 Receiver cells (n = 4660–6733 cells) cultured in the indicated conditions for 24 h, seeded at an overall density of “1x” (1250 cells/mm2, counting Senders and Receivers), except where indicated otherwise. In (C), SynNotch signaling assay is performed with cells on different growth substrate materials and stiffnesses, in (D) with chemical modulators of cytoskeletal tension, in (E) with different initial cell densities at the same Senders:Receivers ratio 1:1. mCherry signal is specifically measured in Receiver cells (Fig. S1 shows gating scheme). Gray violin plots are reference samples for OFF and ON Receiver states. Black dots indicate medians. Dashed gray lines indicate the separation between ON and OFF populations. * indicates the sample is more likely OFF than ON, as determined by the log-likelihood ratio (LLR). Representative bright field and fluorescent micrographs of L929 (F) and mES (H) sender/receiver co-culture after 24 h of culture at the indicated densities. GFP-lig is expressed in senders, tagBFP in the receivers. Scale bars 500 µm. G Violin plots of mCherry fluorescence in mESCs Receivers after 24 h of coculture with mESCs Senders at the indicated densities, 1x is 6000 c/mm2. Dashed gray lines and * as in (E). I–K Plots of the LLR calculated for each sample. The circle represents the LLR of the measured data and the error bars denote 95% CI with n = 1e6, calculated by bootstrapping. Points above zero indicate the sample resembles the ON state more than the OFF state. Error bars represent 95% confidence intervals (see “Methods”). All experiments were repeated at least 3 times with similar results. Source data are provided as Source Data file.
In this experimental setup, we varied extracellular matrix (ECM) composition, substrate stiffness, cytoskeletal tension, and cell density, then evaluated via FACS their impact on synNotch activation of the reporter gene mCherry. Cells grown on different substrates or at varying stiffnesses exhibited similar mCherry activation as the reference condition (Figs. 1C and S2A). Cytoskeletal tension modulation, modulated by the addition of three drugs known to affect cytoskeletal contractility and actin polymerization (Y-27632 (ROCK-inhibitor)91, blebbistatin92, and latrunculin-A93,94), affected cellular morphology (Fig. S2B, C), but did not affect signaling activity in the presence of sender cells (Fig. 1D and Supplementary Fig. S2D). The absence of a difference of signaling with these treatments was confirmed with a statistical test (Fig. 1I).
In contrast, when cells were grown across a range of cell densities from 0.008x − 8x confluency (1x = 1250 cells/mm2), signal outcome followed a bell-shaped curve going from lower to medium to higher densities. Densities outside a central optimal window between 0.125X and 2X exhibited significant and reproducible signal inhibition in receivers (Fig. 1E, F and Supplementary Fig. 3). Signaling was significantly compromised above the critical threshold density of 4x (Fig. 1J). Although not significant, signaling was reduced at lower densities, presumably because of less frequent cell-cell contacts. Importantly, we exclude that at high densities the cells are not signaling because they are dead, since in our gating structure we only evaluate signaling from the non-dead cells (see Fig. S1). Cells at high densities do seem to become “stressed” (see more below, in the “Mechanistic insights” section). We then tested if the reduction of synNotch signaling at high density is restricted to a GFP/anti-GFP synNotch pathway or extends to other pairs of ligand-receptor. To do so, we co-cultured an alternative pair of L929 Senders and Receivers which express mCherry-ligand (a fusion of mCherry with a PDGFR transmembrane domain) as the ligand and anti-mCherry/GAL4-VP64 synNotch55 as the receptor that induces the expression of tagBFP in activated receiver cells. We found that a similar bell-shaped curve of synNotch activation is obtained in this system; we noted a shift in the optimal culture density, which ranges from 0.5x to 4x in this system (Supplementary Fig. S3C), meaning that although qualitatively the phenomenon is replicated, the exact quantitative impact of cell density on synNotch activation may be different for different pairs and/or ligand-receptor affinities.
We then asked if density-dependency of synNotch signaling is a feature of the specific cell line, or a phenomenon that would apply to other cellular contexts; to do so, we tested cell density effects on synNotch signaling in mouse embryonic stem cells. We co-cultured mouse embryonic stem cells (mESCs) Senders and Receivers expressing the ligand-receptor system of GFP-lig (PDGFR-GFP) and anti-GFP synNotch95. synNotch signaling in mESCs is similarly affected by initial seeding density, with a bell-shaped curve of activation of alive receiver cells at increasing cell densities; the optimal signaling occurs here in a central window between 0.064x and 1x (where 1x is 6000 c/mm2; see Fig. 1G, H and Supplementary Figs. S3D and S4). Alive receiver cells coming from densities below 0.008x and above 4x showed statistically significant compromised signaling (Fig. 1K).
Based on the density-dependent changes in synNotch signaling in 2D cultures, we wondered if similar effects would arise in 3D cultures. To test this, we seeded L929 Senders:Receivers 3D spheroids of different sizes, and found that, similar to the 2D setting, increasing cell numbers (hence potentially cellular crowding) dampens synNotch signaling in 3D systems, with a critical threshold of around 8000 cells, which corresponds to approximately 700,000c/mm3 (Supplementary Fig. S5A–D). Interestingly, when we repeated the same experiment in 3D structures that are elongated and not spherical, activation seems to be restricted in localized domains at the tip of the structures (Supplementary Fig. S5E).
In sum, these results expose a previously unreported effect of cell density on synNotch signaling, such that signaling is supported in a system-specific cell density window.
Mechanistic insights on the sensitivity of synNotch signaling to density
After discovering that synNotch signaling was decreased at high cell culture densities, we sought to understand how different factors were contributing to this phenomenon.
We first asked if the nature of the mechanism is through a secreted molecule in the media, by performing conditioned-media experiments: media conditioned by L929 cells cultured at high densities applied on an L929 Senders:Receivers co-culture did not recapitulate the impact of high culture densities on signaling, making a soluble-molecule mediated mechanism less likely (Supplementary Fig. S6A). We then asked if the mechanism was through a classical YAP-mediated mechanotransduction11, by visualizing YAP nuclear localization at different densities; Supplementary Fig. S6B shows that YAP localization is mainly cytoplasmic both at the 1x density and at the 4x density used here in L929 cells, making it less likely that synNotch inhibition at high cellular densities is due to a YAP-dependent mechanism.
It has been suggested that cellular crowding causes reduced proliferation, cell movement and an overall reduction in transcription, a phenomenon sometimes referred to as “contact-inhibition”96. To test if this was at play in our system, we measured total RNA content per cell at different densities 24 h after seeding. We found that total mRNA levels decreased substantially at higher seeding densities in L929 cultures (Fig. 2A). We confirmed this phenomenon by showing that, at high densities, the induction of reporter gene expression from the dox-inducible tTA-VP64 transcription factor is strongly reduced (Supplementary Fig. S6C). Additionally, L929 cell motility was decreased at higher densities (Supplementary Fig. S6D), and both L929 and mESCs have reduced cell sizes at high densities (Supplementary Fig. S6E, F). We also measured cell death percentage in the cultures at high densities and found that: L929 cells display a low baseline cell death that increases to around 10% at 8X densities (equal to 10,000 c/mm2, Fig. S6G); mES cells display a basal cell death percentage of around 10–20% at low confluency, which increases with increasing confluence up to 80% at 16X (equal to 96,000 c/mm2, Fig. S6H), again indicating a progressive increase in cell stress at higher confluency. (We remind here that for the synNotch signaling experiments of Fig. 1, we only measure synNotch reporter induction in non-dead cells, both for L929 and mES cells). These data suggest that cells at the high densities used here are in a general state of reduced activity.
Fig. 2. High cell density represses global mRNA production and reduces the expression level of membrane-associated synNotch signaling proteins which have short half-lives.
A Average of total RNA amount per L929 cell after 24 h of culture at the indicated densities as measured by spectrophotometer (Nanodrop). Lighter dots indicate individual experiment medians, darker dots the average of those. n = 3 experiments. B Fluorescence intensity levels read via FACS of different proteins at increasing cell density. L929 fibroblasts were analyzed by FACS 24 h after seeding at the indicated densities (1 x is 1250 cells/mm2). parental: unmodified L929; receivers: anti-GFP synNotch driving mCherry cells; sender: L929 cells expressing GFP-lig (PDGFR-GFP) on their surface; cytoplasmic GFP cells: L929 cells engineered to overexpress cytoplasmic GFP. SynNotch levels are measured via immunofluorescence with an antibody that recognizes a small peptide tag at the N-terminus of the synNotch protein (anti-myc-tag). 4000 or more cells per distribution are displayed, black dots indicate the medians of each distribution. Fluorescence levels were normalized as fold changes from the negative control, and plotted with a log10 scale. Lighter dots: individual experiment medians; darker and larger dots: average of those. n = 3 experiments. C Representative micrograph pictures of bright field and green fluorescence of L929 cells expressing GFP-lig, 24 h after being seeded at the indicated densities. 1x is 1250 cells/mm2. Scale bar 500 µm. See Supplementary Fig. S7 for results of similar experiments in mES cells. D, E Degradation kinetics of cytoplasmic GFP versus membrane-bound GFP-lig (see section “Measure of GFP and PDGFR-GFP half-life” in the “Methods”). L929 (D) and mES cells (E) are engineered to express cytoplasmic or membrane-bound GFP in a dox-controllable manner. The graphs report expression values for GFP over time measured via FACS after its expression is repressed via the small molecule Doxycycline at day 0. Normalized experimental means ± s.e.m. are reported. n = 3 experiments. Dark green: GFP levels; Light green: GFP-lig. Black horizontal dotted line: half maximum fluorescence. Colored vertical dotted lines were traced to infer proteins’ half-lives. Vertical error bars: s.e.m. Solid lines are normalized averages of 3 medians from 3 individual experiments. All experiments were repeated at least 3 times with similar results. Source data are provided as Source Data file.
We then asked whether high cell density specifically affects synNotch signaling components. To address this question, we evaluated expression levels of synNotch ligand GFP and anti-GFP synNotch receptors via FACS; we found that both in L929 (Figs. 2B, C and S8) and mES cells (Figs. S7A, B and S8), synNotch ligand GFP and anti-GFP receptor protein abundance decreased after 24 h of culture at high densities, whereas cytoplasmic GFP protein expression was not affected. We confirmed that other overexpressed cytoplasmic or nuclear proteins, both in L929 and mESCs, are not affected by 24 h culture at high cell densities (Supplementary Figs. S7C–E and S8).
For some signaling receptors, receptor-ligand complexes clustering is relevant for signaling. We set out to assess if ligands of the synNotch family are affected in their abundance and/or localization by the presence of their cognate receptors and at different densities. We first assessed the levels of GFP-ligand in presence of receiver cells at different densities (Fig. S9A), and we confirmed that GFP-ligands in sender cells decrease at the increase of cell density. We noted that the decrease of the levels of GFP ligand seem to be more pronounced when the sender cells are cultivated with receiver cells; this prompted us to assess the microscope localization of GFP ligand in presence or absence of neighbor cells with an anti-GFP synNotch receptor. To do so, we cultivated a mixed culture of sender cells and parental cells on one case, and a mixture of sender cells with receiver cells on a different well; in both cases we evaluated GFP localization via confocal microscopy. As shown in Fig. S9B, C, localization of GFP ligand changes dramatically in conditions where senders have parental neighbors, where GFP localization is diffuse, to strongly punctuated localization when senders are cultivated alongside receiver cells. We repeated a similar setup where we evaluate synNotch receptor localization, and observed a similar, although less dramatic, differences (Fig. S9E). Finally, the area of these receptor-induced punctae of ligands decrease with increasing cell density (Fig. S9D), suggesting that these punctae could be active signaling components that become limited at high density.
The results so far suggests that GFP ligands and synNotch receptors may be specifically reduced at high density. Given that these are both membrane proteins, and that membrane proteins may present lower stability97, we measured the half-life of synNotch ligand GFP and compared it to a simple cytoplasmic GFP: we discovered that synNotch ligand GFP half-life is indeed shorter compared to cytoplasmic GFP, being estimated at respectively 19 h (membrane GFP) vs. 28 h (cytoplasmic GFP) in L929, and 7.5 h vs. 16.5 h in mESCs (Fig. 2D, E).
We then asked if, from a quantitative standpoint, the observed reduction in GFP-ligand levels at high density could participate in the reduction of the signaling output at high densities. To address this question, we constructed L929 sender cell lines expressing GFP at different levels via FACS sorting; with these, we stimulated receiver cells, and showed that indeed the activation of receivers is dampened in proportion to the reduction of the expression of ligand on sender cells (Fig. S10A–C). As synNotch activation by its ligand depends on ligand levels as well as synNotch expression levels53 their reduced levels may contribute to decreasing signaling strength at high density.
Taken together, these results suggest that high cell culture densities induce a global cell stress state that include transcriptional slowdown, reduced motility and cell rounding; this results in a decrease in the expression of membrane proteins with shorter half-lives. These factors contribute to explain the reduction of synNotch signaling at high densities. Does this phenomenon give us a way to control patterning outcomes via controlling cell proliferation or cell density?
Signal propagation circuit exhibits density-dependency patterning outcome
We next sought to investigate the impact of density-dependent signal attenuation on the behavior of a multicellular synNotch patterning circuit. We focused on the “lateral propagation” circuit, a paradigmatic example of emergent patterning wherein a signal is relayed from cell to cell via contact-dependent signaling between neighboring cells62. This system has not been used for synthetic patterning, though it has been engineered before in a semi-synthetic manner56. The circuit relies on “Transceiver” cells that can both receive and send a cell-surface signal (membrane-bound PDGFR-GFP, “GFPlig”) (Fig. 3A, B). When in contact with a ligand, transceivers become activated and can propagate the signal to neighboring transceivers, triggering a propagating wave of signaling by relay.
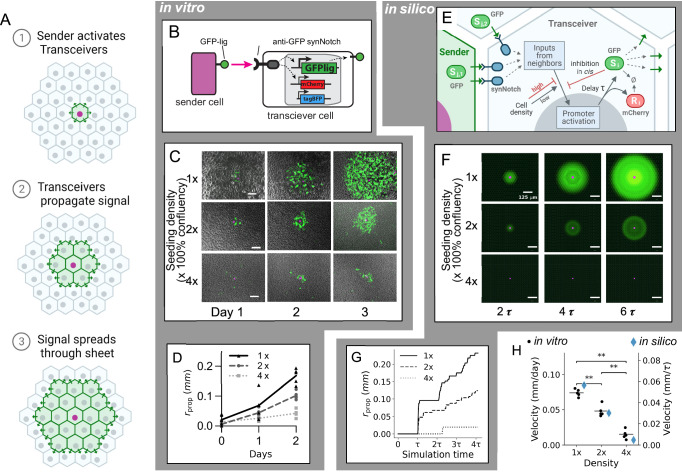
Fig. 3. Cell density tunes the velocity of signal propagation in a synNotch-based spatial propagation circuit.
A Schematic of signaling wave propagation (green) in a monolayer of transceiver cells (gray) initiated by a sender cell (purple nucleus). B–D The in vitro Transceiver circuit propagation. B Membrane-bound GFP-ligand in Senders binds synNotch in Transceiver cells, cleaving synNotch, freeing the intracellular domain to translocate to the nucleus and activate its target genes: a GFP-ligand cassette, and an mCherry reporter cassette. Receiver cells also constitutively express a tagBFP marker. C Signal propagation over time. Micrograph images of propagation assays in vitro centered around a representative sender cell (purple) at the indicated time points and at the indicated initial density (1x is 1250 cells/mm2). Bright field (grayscale) is overlaid with GFP signal (green) and nuclear infrared fluorescent marker expressed in sender cells (purple). Scale bar 100 μm. See Supplementary Movies 1–3 for time-lapses. D Graph of propagation radius rprop over time for three cell densities (n = 5 foci). E–G A computational model of Transceiver signaling. E Schematic of the model. A sender cell (left) presents GFP ligand s (green ellipsoid and triangles) to a Transceiver cell (center, “i”). Ligand from cell i’s neighbors (“j”) activates SynNotch receptors (blue). Activated SynNotch stimulates production of ligand and a reporter r (red ellipsoid) after a time delay τ. The production rate depends on cell density. The ligand s also inhibits its production (“cis-inhibition”). Ø indicates degradation. F In silico simulation of transceiver signaling, where green is GFP ligand, purple is a sender cell at the indicated times and cell densities of 1x, 2x, and 4x (without cell growth). Scale bar 125 μm. See Supplementary Movie 4 for time-lapse. G Propagation velocity (rprop) in silico for densities of 1x, 2x, and 4x. H Strip plot of propagation velocity in vitro (black dots; horizontal line indicates mean) and in silico (blue diamonds) at indicated cell densities. n = 5 foci. **p < 0.01 (p = 7.937e−03 for all pairwise comparisons), two-sided Mann–Whitney–Wilcoxon test. All experiments were repeated at least 3 times with similar results. Source data are provided as a Source Data file.
We implemented this circuit in vitro in a mouse L929 fibroblast cell line. Transceiver cells were generated that express an anti-GFP receptor activating transcription of the GFP ligand. To do so, three transgenes were stably integrated (Fig. 2B): one constitutively expresses a synNotch receptor with an anti-GFP nanobody as the extracellular domain and the transcription factor tetracycline transactivator (tTA) as the intracellular domain. A second expresses membrane bound GFP (synNotch cognate ligand) under control of the tetracycline responsive element (TRE) promoter. A third expresses cytosolic mCherry driven by TRE as a reporter of synNotch activation and constitutively expresses the blue fluorescent protein tagBFP to mark transceivers. We generated several clones of L929 cells where these transgenes were all integrated into the genome. Transceiver clone function was evaluated by co-culturing with sparse sender cells and performing high-magnification time-lapse imaging centered on individual sender cell foci, and imaging and measuring the area of GFP fluorescence using a semi-automated image analysis workflow (see section “Image analysis” in the “Methods”).
Once this assay was set up, we tested the signal propagation outcome at different densities. At a cell density of 1250 cells/mm2 (100% confluent, or “1x”), a propagating wave of transceiver signaling travels outward through the cell monolayer (Fig. 3C and Supplementary Videos 1–3). The mean velocity of propagation was mm/day. When we plated the same cells at higher density of 2x and 4x, this velocity was reduced to mm/day and mm/day respectively (Fig. 3D). Similar trends were observed for all clones generated (Fig. S11). Thus, this synthetic lateral propagation circuit can generate signaling waves whose velocity is responsive to seeding cell density.
These results show that the signaling dynamics of the signal-propagation synNotch circuit can be modulated via cell density. They further suggest that cell density could be used as a mechano-chemical control mechanism to dynamically pattern synthetic tissues without requiring the engineering of additional biochemical circuit components.
To explore the space of patterns that could arise when initial cell density and proliferation rate are modulated, we decided to develop a computational model of the multicellular synNotch signaling with density-dependent attenuation, and to use it to study the impact of density-dependent signal transduction on signal propagation in a multicellular sheet.
First, we constructed a computational model of synNotch signaling with parametrized density-dependent attenuation (see “Methods”, Fig. 3E and Supplementary Fig. S12). To do so, we initialized a hexagonal lattice of transceiver cells with a single sender cell. At time the sender cell begins expressing the signal and chemical reaction equations are integrated forward in time (see section “Mathematical modeling” in the “Methods”; Eq. (2) and Supplementary Text). Changes in cell density are modeled by changing the size of all cells equally. At a higher density, for example, cell size is reduced to occupy less area while preserving the hexagonal lattice (Fig. S12C, inset images). The density-dependence of signaling is modeled by multiplying the amount of ligand involved in signaling by a coefficient that encodes the efficiency of signaling. This coefficient decays exponentially as cell density increases above 1x density (Fig. S12C, blue curve) or decreases below 1x and was parameterized by comparison with the propagation data in Fig. 3.
With this in silico model of density-dependent, signal-propagation circuit, we sought to simulate propagation on a monolayer lattice at different densities. We perform the simulation of the signal propagation patterning circuit at cell densities of 1x, 2x, and 4x confluence. In the simulations, a wave of activation begins propagating outwards at a speed that depends on density (Fig. 3F and Supplementary Video 4). Propagation area begins to increase after a time delay and then continually rises, with a wave velocity of , and at 1x, 2x and 4x densities, respectively, recapitulating the slower speed of Transceiver propagation at higher cell densities (Fig. 3G and Supplementary Movie 4). Simulation time is shown in units of “tau” to provide an intuitive scale for dimensionless time. Figure 3H shows the quantitative dependence of propagation speed on density for experimental and simulated circuits together. These results showed that the computational model can recapitulate the phenotypic patterning behavior of the in vitro counterpart.
Signal propagation reaches limiting regimes due to cell population growth
Given that cell density changes over time as cells proliferate in cell culture, we wondered if the patterns of gene expression generated by the multicellular signal propagation system would display non-linear dynamical behavior as a function of cell proliferation and initial cell density. Figure 4A shows an example of a 7-day time course in which transceivers were co-cultured with senders at a plating density of 1250 cells/mm2 (1x). As shown in the GFP channel images, transceivers begin propagating signal by Day 1 of growth, and the signaling wave propagates outwards over the first 3 days. By Day 4–5, however, propagation speed and overall signal intensity start to decline, and by Day 7 GFP expression is almost fully suppressed. This resulted in self-limiting propagation with a characteristic diameter of 0.5 mm (see also Supplementary Movies 5 and 6 for time-lapse movies). This suggests that the transceiver cells, over time, cross the cell density regime where the signaling becomes inhibited. Notably, transceivers that express and then down-regulate GFP signal continue to express the mCherry reporter at Day 7 (mCherry channel), suggesting slower degradation kinetics of cytoplasmic mCherry compared to membrane GFP. Importantly, cells re-plated at 1x density after a 7-day time course are still capable of propagation after re-plating, suggesting that signaling down-regulation is a reversible phenomenon (Fig. S13).
Fig. 4. Cell population growth over time leads to self-limiting activation of the synNotch-based spatial propagation circuit.
A Propagation and attenuation of signal over a 7-day time-course. Fluorescence micrographs of an isolated propagation focus from a 1:100 sender:transceiver co-culture plated at a density of 1250 cells/mm2 (1x) at the indicated time point (days). GFP-lig (PDGFR-GFP) produced by senders and activated transceivers is shown in green, and mCherry (reporter for synNotch activation in transceivers, see schematic in Fig. 3B) is shown in red. Scale bar 100 μm. See Supplementary Movies 5 and 6 for time-lapse movies. B Cell density measured over time. Black dots indicate cell density of sender-transceiver co-cultures (n = 2–4 technical replicates, mean ± s.d.), measured by automated cell counting. The thick light blue line shows the best-fit logistic growth curve (thinner blue lines: 80% CI). C Quantification of the signaling area over time for in vitro and simulated Transceivers (black circles and blue curve, respectively). In vitro co-culture (1:100 ratio) was performed as in (A); n = 2–4 technical replicates, mean ± s.d. In silico simulation with growth was performed with one Sender on an 80 × 80 Transceiver lattice with an initial density of 1x, using the best-fit logistic growth curve from (B). D Renderings of GFP and mCherry levels in the Transceiver simulation at daily time-points. The mCherry reporter (second row, red), given a 10x slower degradation rate, persists for many days after attenuation, similarly to the in vitro time-course (A). See Supplementary Movie 7 for time-lapse. All experiments were repeated at least 3 times with similar results. Source data are provided as a Source Data file.
Given the negative correlation between cell density and signaling, we hypothesized that the decrease in GFP signaling at later times is due to an increase in cell density secondary to cell proliferation. To test this hypothesis, we counted cell numbers over the time course in culture.
The resulting growth curve is sigmoidal, plateauing by 4–5 days. Importantly, the drop in GFP expression around day 4–5 (Fig. 4A, C) coincides with the culture growing to a density of ≥5000 cells/mm2 (4x), which was found to be inhibitory to sender-receiver signaling (Fig. 1E). With this in vitro dataset, we were also able to parametrize the computational system with the in vitro cell proliferation rate by fitting the cell number dynamics into the logistic equation (see sections “Statistical analysis”, “Mathematical modeling” in the “Methods” and Fig. S14 for detailed parameter estimation procedure and results). When added to the computational model, cell proliferation led to an inhibition of signaling by day 3–4 (Fig. 4D, blue curve), similar to the in vitro data. Additionally, when mCherry is given a 10x longer half-life than GFP in simulation, mCherry levels remain elevated for the entire time-course (Fig. 4D and Supplementary Movie 7).
Thus, density-induced attenuation of signaling is a plausible explanation of the observed signaling shutdown during long-term culture.
Overall, we show using in vitro experimentation and mathematical modeling that signal propagation through a proliferating transceiver population can have a transient, self-limiting nature consistent with a density-induced attenuation of synNotch activity. In other words, cell proliferation can shut off signaling in previously activated transceivers if the culture achieves cell densities that are not conducive to cell-cell signaling.
In silico exploration of growth parameters reveals distinct phases of activation explained by a critical density
Having demonstrated the accuracy of the computational model in reproducing patterning outcomes in presence of cell proliferation, we could, then, apply the model to explore the generative possibilities of the signal-propagation circuit for a wide range of initial cell density conditions and cell proliferation rates.
In order to define the space of achievable qualitative and quantitative phenotypes for the density-modulated transceiver signaling circuit, we simulated circuit behavior for different values of the initial density and proliferation rate and generated a phase diagram of signaling phenotypes (Fig. 5A, B). For each parameter combination, a 50 X 50 lattice of transceiver cells and one Sender were simulated for 8.0 days. We observe signaling behavior that falls into three categories, or phases, which lead to activation regions of different quantitative sizes: above a critical threshold of initial density, Transceivers are “attenuated” and do not activate. Transceivers that are initially below this threshold will activate and may either become inhibited due to population growth (activation area is “limited”) or stay activated until the end of simulation time (“unlimited”) (Figs. 5C and S15). The boundary between the latter two phases is determined by the time at which the population density crosses (Fig. 5D, E), plus the time it takes for fluorescence to fully decay. Thus, our model predicts that Transceiver activation and the size of individual activation spots can be controlled by manipulating the parameters of cell proliferation.
Fig. 5. In silico screening of regimes of initial density and growth rate reveals a morphospace of signal propagation behaviors.
Theoretical dependence of qualitative (A) and quantitative (B) Transceiver activation on the parameters of cell proliferation. A A phase diagram showing distinct qualitative behaviors as a function of the intrinsic proliferation rate (g) and initial cell density (ρ0). The carrying capacity ρmax is held constant to its best-fit value in Fig. 4 (see “Methods” for more details, and Supplementary Fig. S15 for a 3D phase diagram including ρmax). Each simulation contains a 50 × 50 lattice of Transceivers with one Sender cell. After simulation, dynamics were classified into distinct phases of attenuated (gray), limited (light blue), or unlimited (dark blue) propagation (see “Methods” for details of classification). Black squares highlight exemplary parameter sets shown in (C). B The maximum area achieved by the propagation disc, superimposed on the phase diagram in (A) as white circles of diameter proportional to the area of signaling, see legend on the graph. C Example time-courses and simulation renderings for each phase of (A), corresponding to the black squares in (A). See Supplementary Movie 8 for time-lapse. D, E Illustrative graphs highlighting how the timing of Transceiver (de)activation depends on the parameters of growth. D The logistic growth equation, with parameters g, ρ0, ρmax. E Growth curves for the parameter sets in (C). Above ρchigh (indicated as ρcrit above the dotted line), signaling shuts down. Simulations in the limited phase cross the threshold during the time-course, while those in the other phases remain on either side of ρchigh.
In sum, with the computational exploration we identified three dynamical behaviors in silico that can emerge in cells harboring the same genetic circuit, and these behaviors can be accessed by manipulating parameters linked to cell density, such as intrinsic proliferation rate and initial cell density.
Growth rate-modulating drugs push transceivers into different phase regimes
We wanted now to see if, in the in vitro system, we could control patterning outcomes by controlling cell proliferation and initial cell densities to access the different phenotypes observed in silico. According to the computational model, decreasing the intrinsic rate of proliferation (g) should greatly extend the amount of time spent at densities permissive to signaling and therefore shift our system from a regime of self-limited propagation into a regime where propagation is virtually unlimited (from the light blue region to the dark blue region in the Fig. 5A phase diagram). Conversely, increasing the proliferation rate within the self-limited region should decrease the radius of propagation (light blue region in Fig. 5B). Finally, increasing the initial plating density of the culture greater than 1250 cells/mm2 (1x) should reduce the size of propagation foci.
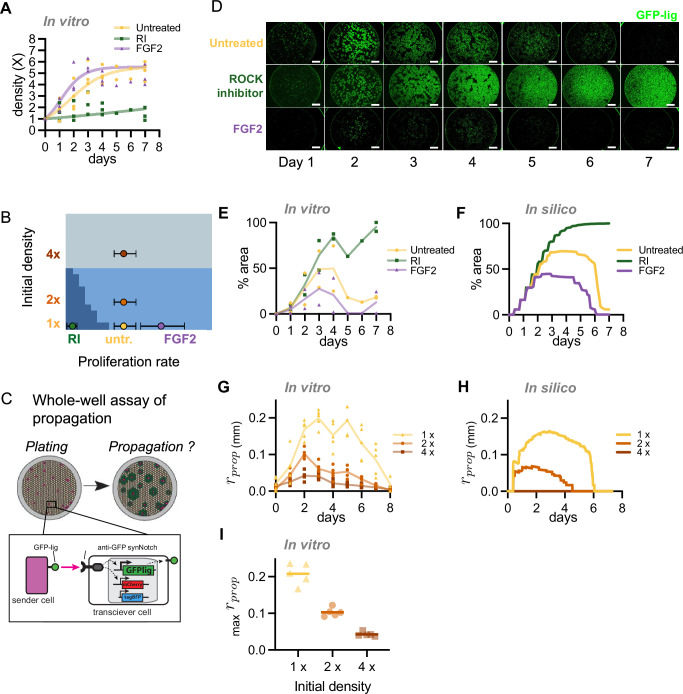
To test whether modulating proliferation and seeding cell density produces different activation phenotypes in vitro, we performed propagation experiments in conditions that perturb cell proliferation, namely small molecule inhibitors of proliferation (Y-2763298, a small molecule ROCK inhibitor (RI) that limits proliferation99–101, or mitomycin C, an alkylating agent that suppresses cell proliferation), or growth factors to increase proliferation (FGF2 Refs. 102–104 and growth factors in the FBS increasing FBS concentration in the culture medium). We first calculated the effect of these treatments on the proliferation rate of transceiver cells (Fig. 6A and Supplementary Fig. S16A). When we placed those values in the phase diagram obtained computationally (Fig. S17), the signaling regime is predicted to go into new sections of the phase diagram (Fig. 6B).
Fig. 6. Control of Transceiver activation area by manipulating cell proliferation rate and initial cell density.
A Time-course of cell density measures for cells grown in presence of growth-modulating drug as indicated: Untreated (yellow circles), FGF2 (violet triangles), or ROCK-inhibitor (RI; green squares). Automated cell counting was used to measure density (symbols: experimental means from n = 3 experiments) and parametrize the logistic growth equation (solid lines of corresponding color). “Untreated” sample reproduced from Fig. 3B. For similar experiments with other treatments see Fig. S16A. B Theoretical phase diagram of Transceiver propagation behavior as a function of proliferation rate (g) and initial cell density (ρ0) (see Fig. 4A), with markers indicating the fitted parameters of different experimental conditions. The circle represents the best-fit growth rate based on growth curve data and the error bars denote 90% CI with n = 1e6, calculated by bootstrapping. C Schematic of the whole-well propagation assay. A co-culture of senders (purple) and transceivers (brown) is plated in a culture well at time t = 0. Each sender acts as a propagation focus (inset diagram), and the distribution of ligand produced in the well (green) over time is assessed by fluorescence imaging. This assay allows quantification of propagation without isolation of single propagation foci. D Time-series micrographs of 1:100 sender:transceiver co-cultures plated at 1x density (1250 cells/mm2) under various drug treatments. Senders and activated transceivers produce GFP (green). Scale bar 1 mm. Note the plastic well border produces a circular green artifact. E Percent of the well in (D) covered by GFP fluorescence over time (experimental means from n = 2 experiments). For similar experiments with other treatments see Fig. S16B, C. F Simulated results for propagation area over time in the conditions of in vitro parameters of (D). G in vitro propagation of single foci over time for different initial densities. Y-axis is propagation radius (rprop) (symbols: radii of 5 individual foci). H Simulated results corresponding to in vitro conditions of (G). I Peak propagation radius in vitro for different initial densities (n = 5 foci, bars indicates mean). See also Fig. S16. Source data are provided as Source Data file.
To test these predictions, we devised a “whole well” assay of signal propagation. Figure 6C shows a schematic of this assay in which senders (purple) and transceivers (brown) are initially plated in a 1:100 ratio (top left diagram). Each sender (inset diagram, bottom) locally triggers a wave of GFP signaling (green), and in permissive conditions, these foci expand and fuse over time to occupy a significant percentage of the surface area of the culture well (top right diagram). This assay allows us to quantify transceiver propagation in cases where isolation of individual propagation foci is challenging, such as when propagation is so efficient that adjacent foci in the well rapidly fuse.
To test the outcome of signal propagation upon changes in cell proliferation (moving on the X axis of the phase diagram), we run the whole well signal-propagation assay in presence of the proliferation-modulating treatments (Figs. 6D, E and S16B, C). In the absence of drug treatment, transceivers initially produce GFP ligand and subsequently shut off expression by day 6–7 (first row, “untreated”), as in the single-foci experiments (Fig. 4A). In conditions where cell proliferation is increased, activation is limited in the first days and is followed by rapid GFP signal depletion (e.g., FGF2 row in Fig. 6D). Conversely, in conditions that reduce proliferation rates, GFP ligand propagation proceeds virtually indefinitely and fills the entire culture well (e.g., ROCK-inhibitor row in Fig. 6D). The same trends are observed in the computational simulations carried out with the parametrized proliferation values (Fig. 6F).
Alternatively, the Y-axis of the phase diagram can be traversed by changing the initial cell density. Single-foci propagation assays were performed as described above, in vitro and in silico, starting from initial densities of 1x, 2x, or 4x confluent cell density. Figures 6G–I and S18A, B show that the behavior of the propagation follows the predictions of the model. In Fig. 6G (in vitro; mean ± s.d.) and Fig. 6H (in silico), the propagation disc is smaller and deactivates faster at an initial density of 2x. At an initial density of 4x, there is no activation in silico and very little activation above baseline in vitro. Thus, as initial density increases, the critical attenuation density is reached more quickly and there is less time for the signal to spread. Due to the persistence of mCherry after transceiver deactivation (see Fig. 3A), an important property of transceiver patterning is the maximum size of the activation disc before deactivation. As shown in Fig. 6I, the initial density determines the maximum area of the propagation disc. Signal propagation in vitro followed the predictions of the model, with less signal propagation at higher densities, and smaller maximum radius of the foci before GFP attenuation. Finally, selected perturbations of proliferation rate coupled with cell density also followed computational predictions, as shown in Supplementary Fig. S18C, D.
Altogether, these observations demonstrate that spatiotemporal patterning with the signal-propagation circuit based on synNotch can be modulated with initial seeding density and proliferation rate. Can these results be exploited to generate spatial patterns over a whole culture well?
Tissue-scale cell density distributions generate spatial signaling activation distributions and kinematic waves
In order to define distinct regions of differentiation, embryonic tissues regulate the spatial distribution of chemical morphogens78,105,106. Recently, chemical distributions have been engineered to direct spatial differentiation using exogenous morphogens55,107. Here, we instead set out to engineer spatial information in a non-genetic fashion in the form of cell density distributions, which can be decoded by transceivers into distinct spatial domains. We hypothesized that a spatial distribution of cell density can elicit a distribution of GFP ligands, as signaling occurs when density is within the optimal range (). Figure 7A shows a computational example where a spatial gradient of initial density causes distinct regions of GFPlig expression (see “Methods”).
Fig. 7. Spatial patterns of cell density produce millimeter-scale activation patterns and kinematic waves.
A Left—phase diagram of qualitative behaviors of transceiver activation as a function of intrinsic proliferation rate (g) and initial cell density (r0) for t = 2.7 days. Top right—Schematic of spatial pattern of density in a culture well, S = signaling, NS = non signaling. Bottom right—signal propagation simulation with initial condition of patterned cell density. Green represents the GFP concentration at steady-state [GFP]SS. B, C In vitro density and signaling patterns. B Stitched epifluorescence micrographs of a culture well seeded with a sender:transceiver co-culture (1:100 ratio) in a spatial pattern of initial density (average of 2x) and imaged at 64 h of culture. Scale bar 2 mm. DAPI staining was used as a cell density readout (see Fig. S19B). Yellow box quantified in (C). C Fluorescence profiles showing the anti-correlated DAPI and GFP patterns, n = 1 profile shown. See Fig. S19 for the cell density pattern method. D, E In silico modeling predicts long-range kinematic waves over time. D Phase diagrams at three time-points with logarithmic y-axes. The density range between ρclow and ρchigh (white dotted and dashed lines) is optimal for signaling. E Modeling results of signal propagation in a non-uniform cell density field. Green is [GFP]SS. Between ρclow and ρchigh (white dotted and dashed lines) is optimal for signaling. F, G Synthetic kinematic wave generated by a density pattern in vitro. F Epifluorescence micrographs of a culture well seeded with 1:100 senders:transceivers in a spatial pattern of density (average of 1x, i.e., 1250 c/mm2) and imaged daily. Green indicates activated transceivers, blue is correlated to cell number. Scale bar 2 mm. The yellow box region is quantified in (G). See Supplementary Movies 9–12 for time-lapse movie of this dataset, and Figs. S19 and 20 for more examples and details. G Spatial profile of GFP fluorescence in (F) over time. White dots show the mean wavefront position, which has a velocity of 0.67 ± 0.18 mm/day (mean ± s.d.). All experiments were repeated at least 3 times with similar results. Source data are provided as a Source Data file.
To test this prediction, we established an in vitro system where a 1:100 mixture of senders and transceivers was seeded in a tissue culture well. Based on the number of seeded cells, the density was 2x confluence (2500 cells/mm2) on average, but the initial seeding was biased towards one end of the well, forming a gradient of cell density. We then imaged a nuclear stain (DAPI) and GFP as a proxy of cell density and signaling activation, respectively (see also Fig. S19). As shown in Fig. 7B, C, at 3 days of culture the GFP output of the transceivers is patterned along the well in a way that recapitulates the cell density pattern. Thus, spatial patterns of gene expression can be established with this circuit given the cell-density dependency, via establishing cell density patterns.
We also hypothesized that we could obtain kinematic wave-like behaviors with the appropriate initial cell density gradients. We first explored this hypothesis in the computational model. The hypothesis follows the idea that, as is the case with uniform cell density, gradients of cell density could produce rich signaling behavior over time due to the dynamics of cell population growth. In particular, because signaling activation occurs in our system within an optimal range of density (see Fig. 1E), we hypothesized that at lower densities, a spatial gradient of cell density could cause a virtual wave of activation across the well. Due to population growth, a region of the culture well that begins the time-course too sparse for activation over time will enter the optimal range and eventually exit this range. In Fig. 7D, phase diagrams at three consecutive time-points of simulation are annotated with the critical densities, plotted dotted lines. Over time, regions of the well with different initial densities (shown on a logarithmic Y-axis) should enter the optimal range between the two lines at different times. As shown using an example gradient in Fig. 7E, this staggered activation creates the appearance of a large wave spreading through the well. However, this wave is in fact only virtual, or “kinematic,” meaning each region is turning on and off independently based on its local cell density.
We then sought to exploit cell proliferation to generate a kinematic wave of activation across the culture well in vitro. We found that indeed, a region of the well that begins the time-course too sparse for activation over time will enter the optimal range and eventually exit this range. This staggered activation creates the appearance of a large wave spreading through the well (Fig. 7F, Supplementary Figs. S19, S20 and Supplementary Movies 9–12). However, this wave seems in fact only virtual, or “kinematic”, meaning each region is turning on and off independently based on its local cell density. We found the wave velocity to be 0.67 ± 0.18 mm/day (mean ± s.d.) (Fig. 7G), 5.1 times faster than the speed of direct cell-to-cell propagation measured at 1x confluent density (Fig. 2H) and roughly twice the speed of directed fibroblast motility108. Collectively, these results show that we can create spatio-temporal patterns of signal activation through biased distributions of cell density coupled with population growth.
Discussion
The astonishing diversity of tissue patterning and morphology in our own bodies, compared to the relative uniformity of the starting material (fertilized oocyte), underscore a challenge of how the genetic circuits for patterning achieve precision in an ever-changing mechanical environment. In particular, patterning of cell growth (proliferation) generates complex inhomogeneities in cell density over space and time in all growing tissues. This observation provokes the fundamental question of whether and how mechano-chemical circuits expand achievable patterning behaviors, compared to chemical only circuits, to achieve some of the organization that we see in multicellular shapes and patterns. We report here a first example of a realization of synthetic patterning circuit based on synNotch signaling, which we find to be sensitive to cell density, and how this can be used to increase patterning outcome via control of cell proliferation and cell density.
We first here discovered that cell-density inhibits SynNotch activation of target genes, which was previously unreported. We demonstrate density-dependency of gene induction via synNotch with two different synNotch signal/receptor pairs, and in two different cell lines, a mouse fibroblast and in mouse embryonic stem cells; and we also show it both in 2D and in 3D environments. The data collected points to a mechanism whereby high cell density induces a transcriptionally repressed state that particularly decreases transmembrane protein abundance at the plasma membrane, consequently generating a signaling-depressed state as well. Other mechanisms could contribute, including decreased cell migration at higher densities.
When cultivating cells in vitro it has been shown that, in several non-synthetic systems, cell density significantly impacts the growth and differentiation of cells, so much that cell density is a parameter that needs to be extensively optimized both for cell line maintenance and directed differentiation protocols24–43. The density ranges that we investigate here in 2D and in 3D are comparable to the range of values recorded for developing embryos (sea star embryo between 500 and 4000 c/mm2, Xenopus mesoderm—between 1 and 2000 c/mm2, avian presomitic mesoderm has an antero-posterior gradient of cell density from 10,000 to 6000 cells/mm2)41. Moreover, examples of cell-density mediated effects are starting to emerge in in vivo settings: a recent study reported the identification of an organizing center induced via proliferation-driven increase of cell density in the development of rodent incisors23. Mechanistically, these effects have been described as due to mechanotransduction, or metabolic effects, or cell shape effects. It remains to be seen if, in these natural systems, phenomena like the one described in the synthetic system in this manuscript are at play. The mechanism that we observe here, linked to a transcriptional slow down, might extend to other signaling proteins, both natural and synthetic; and even non-signaling proteins, e.g., metabolic enzymes and short-lived transcription factors. Our data points the interested reader to consider this phenomenon especially for short-lived proteins.
Secondly, we designed and constructed in vitro and in silico an orthogonal synthetic patterning system based on synNotch lateral propagation signaling cells we termed transceivers. This system enables activated transceiver cells to activate their neighbors leading to signal propagation waves initiated by sender cells. When this circuit is implemented in a cellular system that does operate in a cell-density dependent regime, it generates signal propagation waves from sender cells (as was previously shown is a semi-synthetic system with a similar logic57). The fact that, in our system, signaling is coupled with cell density significantly increases the control points, and ultimately also the possible patterning outcomes. We see this for example with the capacity of controlling propagation velocity with different static densities. When the cell density is increasing over time, the propagation becomes self-limiting; when cell density is non-uniform in space, spatial patterns are observed. Finally, when cell density is non-uniform both in space and in time, we observe kinematic wave patterns. This remarkable increase of patterning outcomes from the same genetic circuit, highlights a key feature of mechano-chemical circuits in general, i.e., that they can achieve increased control and phenotypic diversity compared to the chemical-only components. It is possible that these systems emerged as a necessity during evolution as a need to achieve patterning in a proliferating mass of cells; they may also have significantly contributed to increasing the diversity of patterning that were possible, without changes in the underlying genetics.
A feature of the work presented here that we want to highlight is the integration of computational and in vitro work. Thanks to the computational system, built and parametrized with an in vitro initial dataset, and despite a lack of quantitative parameter estimation for many of the molecular interactions, it was possible to enumerate the qualitative behaviors possible with this density-dependent multicellular circuit, and explain them from simple properties of the components and their interactions. This computational analogue was helpful to characterization of the possible patterning outcomes of the system for a wide range of initial conditions of density and proliferation and was helpful to guide further the in vitro realization. Integration of computational design is a trend in synthetic biology, is very well developed for circuits in bacteria109 and is been deployed for multicellular systems58–60,86 and is being discussed for complex synthetic developmental pattern generation. The example of integration presented here provides an example of how to integrate computational design into Synthetic Development (synDev) efforts. Although for some applications it may not be required to have a precise parametrization, we do note that in some specific instances the overlap between in silico simulations and in vitro results is not complete. For example, the experimental propagation area was found to be smaller than predicted by modeling in Fig. 6E, F. Such a deviation could be a result of imaging pipeline thresholding, or of effects of the drugs that are not taken into account in the model, such as drug induced changes in the production rate of ligand, cell motility, or the process of fusion between adjacent signaling foci. Increasing parametrization of more variables in the model could potentially increase agreement between model and data.
The features of the propagation circuit described above point to systems that would benefit from this type of circuit in general, and this specific circuit in particular. Systems that display differences in cell density either in time (i.e., all 2D and 3D growing cell cultures), or in space (e.g., developing organoids or even embryos), could embed a synNotch circuit of this kind to read on these cell density differences, and produce localized responses, for example growth factors for localized delivery of signals, or cell autonomous differentiation. The self-limiting feature of the circuit to circles of controllable radii, could be used to generate cell state domains of controlled size, for example to produce specific signaling or structural molecules, or even for differentiation of placode-like structures in epithelia, or smart signaling centers in feeder layers.
The current implementation of the propagation circuit is limited to a one-directional control of signaling via cell density. The result is an open loop circuit that displays controllability from the outside as we described above. One outstanding feature of endogenous genetic circuits is their capacity to autonomously close the loop and control back the mechanical properties via the circuit output itself. Exciting future directions for extension of this work in this direction would include generating transceiver cell line that activate proliferation control genes, either cell autonomously or non cell-autonomously, to generate a closed-loop circuit architecture for autonomous control of patterning outcomes. Mechano-chemical coupling phenomena could provide a route towards constructing synthetic circuits that can modulate progression through morphogenesis in a stepwise fashion, for example, executing new gene expression programs sequentially following the completion of a morphogenetic program, towards the construction and control of circuits of complexity similar to the ones observed in vivo.
Altogether, we described a way to study and control synthetic patterning circuits based on synNotch through modification of cellular growth in vitro and in silico; we believe this mechano-chemical feedback on signaling could provide a valuable addition to the toolbox of the engineer of synthetic morphogenetic systems.
Methods
Constructs
Constructs design
The pHR_SFFV_LaG17_synNotch_TetRVP64 (Addgene #79128). The pHR_SFFV_GFPligand (Addgene #79129) were provided by AddGene, whereas the pHR_TRE3G_mCherry_PGK_BFP was obtained as described in this reference53. The rest of the constructs were cloned via In-Fusion cloning (Clontech #ST0345). Specifically, the plasmids used for engineering fibroblasts were cloned in the pHR plasmid for lentivirus production.
Lentivirus production
Lentivirus was produced by co-transfecting the transfer plasmids (pHR) and vectors encoding packaging proteins (pMD2.G and pCMV-dR8.91). Plasmids were transfected by lipofectamine LTX transfection reagent (Thermo Fisher Scientific) in HEK293-T cells (Takara 632180) plated the day before in 6-well plates at approximately 70% confluence (800,000 cells/well). Supernatant containing viral particles was collected 2 days after transfection and filtered to eliminate dead cells and cellular debris (cut-off 0.45 μm).
Cell lines—L929
L929 mouse fibroblast cells (ATCC# CCL-1) and HEK293 cells (Takara 632180) were cultured in DMEM high glucose, [+] L-Glutamine, [−] Sodium Pyruvate (Invitrogen) containing 10% fetal bovine serum (Laguna Scientific), 1% penicillin-streptomycin (Sigma-Aldrich P4333) and tetracycline (100 ng/ml) when indicated.
We generated engineered cell lines that we call “Senders” in the manuscript. The L929 Senders were obtained by transduced to stably express surface GFP (GFP fused to the PDGFR transmembrane domain, Addgene construct #79129), with or without the addition of a nuclear infrared fluorescent marker (H2B-miRFP703, Addgene plasmid #112853) under control of the SFFV promoter.
We generated engineered cell lines that we call “Transceivers” in the manuscript. L929 transceivers were obtained via transduction with three different virions. The first virion constitutively expresses an anti-GFP antibody (Lag17) fused to a syn-Notch receptor with the transcription factor tetracycline Trans-Activator (tTA) as its intracellular domain, under the control of the SFFV promoter. This receptor harbors a myc-tag on its extracellular domain that can be visualized by immunostaining (Addgene #79128). A second virion expresses both the mCherry reporter and BFP, respectively under control of the Tetracycline responsive element (TRE-3G) promoter (cloned with the Infusion kit from the Addgene plasmid #133805) and the constitutive PGK promoter (cloned with Infusion from Addgene plasmid #79120). The third virion expresses surface GFP ligand (PDGFR-GFP, chimeric protein made of the PDGFRB transmembrane domain plus 63 bp serving as a “natural linker” and GFP combined with the proper secretion signal peptide) under transcriptional control of the TRE-3G promoter. Cells were sorted based on tagBFP expression, myc staining (SynNotch has a myc tag) (Cell Signaling, clone 9B11) and GFP signal (transceivers have some leaky expression). Monoclonal lines 25A2, 5CC and T2 were generated by expanding cultures from single cells, which were then screened for signal propagation efficiency.
“Receiver” cells were obtained from the Lim Lab, and were produced as previously described53. Briefly, they contain the LaG17 synNotch TetRVP64 (Addgene #79128) anti-GFP synNotch receptor, and a TRE–>mCherry reporter for synNotch induction visualization.
“Senders hi / med / medlo / lo” lines were obtained by transducing L929 fibroblasts with a vector encoding PDGFR-GFP under the control of the SFFV promoter, followed by gating 4 populations exhibiting different levels of GFP signal intensity via FACS.
“Dox - cytoplasmic GFP” cells were engineered by transduction of parental L929 cells with 2 virions. The first encoded tTA-VP64 and tagBFP, separated by an IRES sequence and under the control of the SFFV promoter. The second expressed GFP under the control of the TRE-3G promoter. Cells were sorted based on tagBFP expression and GFP signal in the absence of doxycycline. Addition of 1 mg/mL doxycyline (Sigma-Aldrich #D3447) led to GFP signal extinction.
“dox-Sender” cells were generated by transduction of L929 cells with 2 virions. The first encoded tTA-VP64 and tagBFP, separated by an IRES sequence and under the control of the SFFV promoter. The second expressed PDGFR-GFP under the control of the TRE-3G promoter. Cells were sorted based on tagBFP expression and GFP signal in the absence of doxycycline. Addition of 1 mg/mL doxycycline led to maximal GFP signal extinction.
“mCherrylig Senders” were generated with a vector driving the expression of PDGFR-mCherry (chimeric protein made of the PDGFRB transmembrane domain plus 63 bp serving as a “natural linker” and mCherry, combined with the proper secretion signal peptide) (Addgene #216668) under the control of the SFFV promoter. Cells were sorted based on mCherry signal positivity. “tagBFP Receivers” were generated with 2 vectors, the first for expressing the anti-mCherry SynNotch receptor FLAG-LaM4-Notch-GAL4VP64 under the control of the ELf1a promoter (Addgene #216669), and the second placing the expression of tagBFP under the control of a 5xUAS promoter and the expression of the Hygromycin Resistance gene under the control of the PGK promoter (Addgene #216665). Cells were selected with 0.4 mg/mL hygromycin until a parallel culture of control non-transduced cells completely died. They were then sorted based on staining of the FLAG peptide with an anti-flag antibody (R&D Systems, clone 1042E used at 1:100 dilution).
Cultures were maintained in a 37 °C incubator with 5% CO2 and relative humidity (VWR). For viral transduction, cells were plated in 6-well dishes to achieve approximately 10% confluence at the time of infection. For lentiviral transduction, 10–100 ml of each virus supernatant was added directly to cells, with 1 μl of polybrene (Millipore Sigma) also added to increase infection efficiency. Viral media was replaced with normal growth media 48 h post-infection. Cells were sorted for co-expression of each component of the pathways via fluorescence-activated cell sorting (FACS) on a FacsAria2 (Beckton-Dickinson) and by staining for the appropriate myc-tag with fluorescence-tagged antibody where needed. A bulk-sorted population consisting of fluorescence-positive cells was established for “sender” cells. For single-cell clonal population establishment of transceivers, single cells were sorted by FACS into 96-well plates starting from populations of cells infected with lentiviral particles for the relevant expression constructs. After sorting, monoclonal population were expanded and screened for the activation of the GFP ligand after stimulation with anti-myc antibodies (Cell Signaling Technology) bound to an A/G plate (Thermo Scientific).
Cell lines—ESC
Mouse embryonic stem cells were cultured in DMEM high glucose, [+] L-Glutamine, [−] Sodium Pyruvate (Invitrogen) containing 15% fetal bovine serum (Laguna Scientific), 1% GlutaMax (Thermo Fisher Scientific #35050061), 1% non-essential amino acids (Thermo Fisher Scientific #11140050), 2 mM Sodium Pyruvate (Thermo Fisher Scientific #11360070), 7 ppm 2-mercaptoethanol, 1% penicillin-streptomycin (Sigma-Aldrich P4333).
ESC Sender (SyNPL CmGP1GH1) and Receiver (SyNPL STCA1) cultures were obtained from the Lowell lab95. The GFP and membrane GFP dox-inducible ESC lines were generated from the ZX1 cell line, which we obtained from Michael Kyba’s group110.
To generate doxycycline-inducible GFP and PDGFR-GFP ESC lines, we took advantage of the inducible cassette exchange system described previously110. Briefly, the ORF of GFP with or without a signal sequence and a transmembrane domain were cloned into a vector containing 2 asymmetric loxP sites via In-Fusion cloning. The ZX1 ESC line was used for transfection, which contains corresponding loxP sites in the HPRT locus flanking a CRE recombinase coding sequence, an upstream TRE and a downstream promoterless Neomycin resistance cassette. One day before the transfection, the expression of the CRE was induced in ZX1 ESCs by adding 500 ng/mL of doxycycline to the medium. Transfection was performed using lipofectamine 2000 (Invitrogen), then Neomycin was added the next day to the medium at a concentration of 300 ug/mL to select for the cells with the correct site-specific insertion of the plasmid. After 7 to 10 days of Neomycin selection, dox-inducible GFP or GFPlig ESCs were further purified by FACS-sorting GFP+ cells after 24 h of dox induction at 500 ng/mL.
3D cell culture
Agarose micromolds were prepared as indicated by the provider (Microtissues, Sigma-Aldrich). Briefly, agarose was dissolved in saline water. Melted agarose was poured in silicon molds encoding either single spheroids circular wells or rectangular wells for generating rods. L929 Senders:Receivers 1:1 cell suspensions were prepared as indicated in the provider’s documentation to seed spheroids and rods of desired sizes. Cultures were imaged 24 h post seeding with a Keyence BZ-X710 microscope.
Experiments
Signaling modulation assay
Senders and receivers L929 cells were co-cultured in a 1:1 ratio in DMEM + 10% for 24 h. Then, cells were detached and analyzed by FACSAria2 (Becton-Dickinson). The mCherry signal is specifically measured in Receiver cells, which can be gated out thanks to constitutive tagBFP expression (Supplementary Fig. 1). The control activation is performed on tissue-culture treated plastic dishes, at a 100% confluent cell density, in the absence of drug treatment. In the positive and negative controls (gray violin plots) sender cells are present and absent, respectively. We report and refer to the density of the cell culture as a multiple of the density at 100% confluence (cells cover 100% of the surface). We estimated by visual inspection that the confluent density is 1250 cells/mm2 for L929, and refer to it as 1x confluence or simply “1x”.
The experiments where ECM composition is modulated (fibronectin, matrigel, gelatin), the procedure used Fibronectin (Corning via VWR, VWR catalog #47743-728) was used without dilution and incubated for 1 h at 37 °C; matrigel (Corning via VWR, VWR catalog #47743-720) 10 ul of Matrigel were diluted in 1 ml of DMEM in ice and then incubated at 37 °C for 45 min for the coating; gelatin (Sigma-Aldrich, catalog #G1890) at is provided ready to use and incubated for 1 h at room temperature to prepare the plate before cell seeding at 1X density.
For the stiffness modulation, experiments were performed at 1x density on a commercial plate with FN coating on the silicone bottom (CytoSoft 6-well Plates, Advanced Biomatrix).
The set of experiment done in the presence of cytoskeletal modulators, the drugs Y-27632 to inhibit Rock (Stem Cell Technologies, #72304), used at 100 uM; latrunculin (Sigma-Aldrich, Catalog #L5163) at 200 uM; blebbistatin (Sigma-Aldrich Catalog #B0560) at 25 ug/ml. All the drug treatments were done on tissue treated plastic dishes at 1X plating density.
The set of experiments with modulated cell density at plating were done on standard tissue culture plastic, at the indicated densities, where 1x = 1250 cells/mm2 for L929, and 1x = 6000 cells/mm2 for mESCs. 2x density would then be 2500 cells/mm2 for L929 and 12,000 cells/mm2 for mESCs. Cell numbers were evaluated with a Countess II cell counter (Thermo Fisher Scientific). To note, it is known that the outcome of cell counting varies from user to user and method to method, and we thus recommend to visually compare experiments to assess which density is considered as 100% confluency, and to ultimately perform a dose-response curve like the ones depicted in Fig. 1E–G for a specific cell line and a specific user.
Measurement of various signals via FACS
For all experiments, except where indicated otherwise, cells were cultured 24 h after seeding at indicated plating density. Cells were then detached with TrypLE Select (Thermo Fisher Scientific #12563029), resuspended in FACS buffer (5 % FBS in DPBS). Cells were then stained if necessary for 30 min at 4 °C before washing. anti-GFP antibody: Thermo Fisher Scientific clone 5F12.4, anti-myc antibody: Cell Signaling clone 9B11. Cells were then processed in a Becton Dickinson FACSAria II and data processed with FlowJo and Python. When signal is reported as «normalized fluorescence (log10 arb. units)», signal from individual cells were divided by the mean signal in control cells, before being transformed with the Numpy log10 function. As this function generate inf values for some rows, those were removed before plotting.
All the antibody are used at 1:100 dilution unless otherwise noticed.
Imaging
To measure the GFP aggregates via microscopy (S9D), we did as follow: we plated sender + transceiver cells at 1:100 density at the indicated densities of 1X, 2X or 4X. We then fixed the cells with 4% PFA for 10 min, and performed immunostaining for anti-GFP synNotch receptor with an anti-myc antibody Alexa 647-conjugated (Cell Signaling Technology, Catalog #2233S). Fluorescent microscopy images were captured with a Keyence BZ-X710 digital microscope machine. To measure the aggregates surface area, the green fluorescent channel was isolated and analyzed by itself; a mask was obtained and the surface individual GFP aggregates was calculated in ImageJ with the function “Analyze Particles”.
For analysis of YAP localization (Fig. S6B), L929 parental cells were plated at the indicated densities of 1X or 4X for 24 h, fixed in 4% PFA and stained with an anti-YAP/TAZ mouse antibody (Santa Cruz Biotechnology, Catalog #sc-376830 AF647, used at 1:200 dilution), and imaged after DAPI counterstaining with a Keyence digital microscope.
Actin staining was performed by incubating cells in conditioned media + 1/1000 SPY555-actin (Cytoskeleton, Inc.) for 1 h before live imaging.
For imaging of the membrane-bound fraction of PDGFR-GFP and SynNotch in L929 Senders and Receivers, cells were fixed 24 h after being seeded with a 4% PFA solution in DPBS, but not permeabilized. They were then stained with either an anti-GFP antibody (Thermo Fisher Scientific clone 5F12.4) or an anti-myc antibody (Cell Signaling clone 9B11) directly coupled to a far-red fluorophore. Multiple z-slices of different fields of the cultures were then imaged with a Leica inverted SP8 confocal microscope. Z-slices were then combined with the Z-project Add algorithm of Fiji, and representative fields selected for figure generation.
For evaluating cell density distribution in kinematic wave experiments, cells were cultured with a “0.01X” DAPI concentration, where “1X” corresponds to 2 drops of NucBlue (Thermo Fisher Scientific) per mL of media.
All the antibody are used at 1:100 dilution unless otherwise noticed.
Conditioned media
For the conditioned media experiment (Fig. S6A), sender and transceiver cells were plated at 1X or 4X density for 1 day, after 24 h the media was harvested; in another plate, sender + transceiver cells at 1:1 ratio were plated at either 1X or 4X densities; plating media was conditioned media from either 1X or 4X densities.
Propagation experiments
The L929 Sender and Transceiver cells are passaged in presence of tetracycline (100 ng/ml); for the propagation experiments, sender and receivers are co-plated at a ratio of 1:1000 in absence of tetracycline. Cells were imaged by automated inverted epifluorescence microscope (Keyence BZ-X710) at a magnification of 2X for the image acquisition of the whole well and at 20X for the image acquisition of the single spots.
Growth curves
Proliferation rate was tuned with the addition of 50 µM ROCK inhibitor (Y-27632, RI, Stem Cell Technologies, #72304), 1 µM mitomycin-C (Stem Cell Technologies, #73274), 250 ng/mL FGF2 or a concentration of 25% of FBS. Cells were plated at a 1x initial seeding density, and 3 wells were dissociated at each timepoint for cell counting with a Countess II device (Thermo Fisher Scientific). The counts in each well were averaged to generate an experimental mean.
Measure of GFP and PDGFR-GFP half-life
To measure the stability (half-life) of cytoplasmic GFP and PDGFR-GFP, we used cell lines where the expression of those proteins was controlled by the presence of doxycycline.
In Fig. 2D, for L929 cells, cell lines “dox-cytoplasmic GFP” and “dox-sender” were engineered such that the addition of 1 mg/mL doxycycline would lead to complete shutdown of GFP signal down to baseline (see section “Cell lines—L929” in the “Methods”). These cells were cultured without doxycycline for a minimum of 7 days, and multiple wells were then seeded at a density of 0.125x in media containing 1 mg/mL doxycycline. GFP signal was then measured at regular intervals by dissociating the cells and measuring fluorescence with a FACS machine (BD). This experiment was performed 3 times, with the plot showing the average of experimental medians and s.e.m. In the graphs of Fig. 2D, the GFP values are normalized so that 0 corresponds to fluorescence levels in cells kept in doxycycline (dox) for more than a week, and 1 to the fluorescence in the cells at the start of the experiment.
In Fig. 2E, for ESC lines, cell lines “dox-cytoplasmic GFP” and “dox-sender” were engineered such that the addition of 1 mg/mL doxycycline would lead to maximum induction of GFP expression, and absence of doxycycline would lead to GFP expression shutdown (see section “Cell lines—mESC” in the “Methods”). Cells were cultured with 1 mg/mL doxycycline for a minimum of 7 days before being plated at a density of 0.06x at the same time that doxycycline was removed. GFP signal was then measured at regular intervals by dissociating the cells and measuring fluorescence with a FACS machine (BD). This experiment was performed 3 times, with the plot showing the average of experimental medians and error bars: s.e.m. For Fig. 2E, solid lines were generated from the average of 3 medians from 3 individual experiments, normalized so that 0 corresponds to fluorescence levels in cells kept without doxycycline (dox) for more than a week, and 1 to the fluorescence in the cells cultured with dox for more than a week at the start of the experiment (for details, see “Methods”).
For both L929 and ESC lines, the signal in each experiment was normalized so that the maximum GFP fluorescence would be set at 1, and the baseline (minimum) GFP fluorescence at 0. This was achieved by subtracting the minimum measure GFP signal before dividing by (maximum GFP signal minus minimum GFP signal) for each signal.
Death index
Cell death was estimated by quantifying the percentage of all ungated FACS events above a threshold of DAPI signal. The death index is calculated as the percentage of all events above a DAPI positivity threshold. We note that this index encompasses both intact cells with compromised membrane permeability and nuclei debris in the FACS events.
Induction of protein expression at different densities
To evaluate how seeding density affected the efficiency of protein expression induction, we cultured L929 “cytoplasmic GFP”, i.e., cells that were engineered such that the addition of doxycycline (or tetracycline) would lead to complete shutdown of GFP signal down to baseline (see section “Cell lines—L929” in the “Methods”). Cells either with (OFF) or without (ON) tetracycline at 1 mg/mL for a minimum of 7 days to maximize gene expression. Cells were then plated at a range of densities, with (OFF-OFF, ON-OFF) or without (ON-ON) doxycycline 1 mg/mL to maximize target gene shut down. Twenty-four hours after plating, cells were dissociated and fluorescence measured with a FACS machine (BD). This experiment was performed 2 times, with the plot showing individual experimental medians and the average of experimental medians.
Kinematic wave
To seed cells unevenly in a 96-well plate, 40,000 cells were seeded in 2 steps: 27,000 cells were seeded in 20 µL on the side of the plate while it was tilted 45°, and given 30 min to adhere at room temperature without moving the plate. The plate was then laid flat, and 13,000 cells were seeded in 180 µL injected in the center of the well. Cells were once again given 30 min at room temperature to adhere without perturbations, before returning the plate to a culture incubator. Wells were then imaged with a 2X objective fitted on a Keyence BZ-X710 every day for the duration of the experiment.
Quantification of total RNA levels
After removal of the media, RNA lysis buffer was added directly to the culture wells. Extraction of total RNA from cells was performed with the Quick-RNA miniprep kit (Zymo) according to the manufacturer’s instructions. RNA concentration was measured using Nanodrop and total quantity was estimated for each sample by multiplying this concentration by the total volume of RNA. Total RNA content per cell was estimated by dividing this amount by the number of cells initially seeded.
Image analysis
Processing of fluorescence images
To quantify the profiles of fluorescence intensity in microscope images, analysis was performed by Fiji-ImageJ. Background was subtracted and binary masks for fluorescent signals were generated to automatically segment propagation spots and quantify the area of fluorescence.
The Subtract Background algorithm of ImageJ was routinely used to even out the background signal in fluorescence channels. The Turbo look-up table sometimes used to show single-channel fluorescence fields was obtained from: https://github.com/cleterrier/ChrisLUTs/blob/master/Turbo.lut.
Cell shape analysis
We sought to quantify the change in projected cell shape. In the absence of a membrane marker, zoomed-in fields of view were selected at random from bright field images taken before FACS analysis (1:1 Sender:Receiver ratio, imaged at 24 h of co-culture). Using Python, outlines of a subset of cells in the field of view were drawn manually and their area and perimeter were calculated. Both Senders and Receivers were counted and not distinguished. The circularity index was calculated as. The index ranges from 0 to 1, where is a perfect circle.
Inference of cell motility
Cell motility speed in Supplementary Fig. S6D was inferred by particle image velocimetry (PIV) applied to brightfield images. In each density condition, bright field images of three regions of interest (ROIs) were taken hourly for 160 h using an automated inverted epifluorescence microscope (Keyence BZ-X710) at 20X magnification. Every ten frames, the flow field was measured by comparing the locations of “particles” (cell fragments) in adjacent frames (i.e., 0 h to 1 h, 10 h to 11 h, etc.). Particle velocities were then grouped within a 64 × 64 pixel window to generate a vector field of velocities. Outlier velocities were replaced with the local mean in a 3 × 3 window kernel, and the mean velocity in the ROI was measured.
Data analysis and plotting
Data were analyzed and plotted using Python with the Seaborn, Numpy and Pandas plugins; Excel; GraphPad Prism 10.
FACS signals normalization
We normalized some FACS signals, especially when we plotted multiple experiments on the same figure, to account for variability in signal intensity from day to day. We either (1) divided the fluorescence intensity in the conditions of interest by the median intensity of a negative control (unactivated Receivers, parental cells, etc.); (2) bound the intensities between 0 and 1, with the following formula, where is the highest signal in the dataset to be set at 1, the signal in the negative control to be set at 0, S the signal to normalize and the normalized signal .
Statistical analysis
Comparison of fluorescence measurements by FACS
We use two samples as reference distributions for the ON and OFF signaling phenotypes and determine whether each experimental sample resembles the ON distribution more than the OFF distribution using a likelihood ratio test. Specifically, each reference sample was converted to a probability distribution by binning the data into a histogram with 1000 bins and dividing each bin’s quantity by the total. Before division, a small quantity is added to each bin to avoid division by zero. Then, for each experimental sample consisting of fluorescence measurements , the log-likelihood ratio (LLR) was calculated as . A sample with LLR < 0 more likely originated from the OFF distribution than the ON distribution and was considered to have attenuated signaling. This procedure was found to be robust to the number of bins used for the histograms (Supplementary Figs. S8 for L929, and S10 for mES cells).
Estimation of population growth parameters
To model the dynamics of cell density in culture, we use the logistic equation, a differential equation that describes how population density evolves over time according to:
| 1 |
At low densities , there is exponential growth at the intrinsic growth rate . As density increases further, however, population density saturates as it asymptotically approaches the carrying capacity . Observed data are assumed to be normally distributed about the curve with constant standard deviation σ. First, we used MLE to infer , , and σ using data from co-cultures with starting densities of 1x, 2x, and 4x, and confidence intervals were determined using the residual bootstrapping method. We then studied the effects of ROCK-i and FGF2 on growth by estimating and and from treated co-cultures with a starting density of 1x. During this second fitting, the carrying capacity was held constant in order to alleviate parameter degeneracies. Specifically, when treated with ROCK-i, density dynamics are near-constant, and the data can be explained equally well by either very slow growth (low g) or very low carrying capacity (). Note that because signaling in our model only depends on the density itself, both of these explanations produce the same predicted behavior. Thus, fixing during parameter inference for ROCK-i- and FGF2-treated samples removes the ambiguity of fitting without affecting signaling behavior in silico.
Mathematical modeling
Computational modeling of transceiver signaling
To model the multicellular sheet, we use a fixed lattice of cells, a framework used extensively to study Notch-mediated patterning63,81–85,111. In our model, each cell occupies a region on a hexagonal lattice. For a given density, the area of each hexagon on the lattice is set equal to the average area of cells in a confluent monolayer in vitro. As depicted in Fig. 3E, each cell contains a system of chemical reactions that model synNotch signal transduction (see “Methods”). A given cell (i) in direct contact with its neighbors (j) can express both the signaling ligand (s) and the reporter protein (r). To model cytoplasmic projections, which are known to affect Notch-mediated patterning systems81,112,113, contact strength is weighted by cell-cell distance on the lattice (Supplementary Fig. 12A). Using a standard dimensional analysis procedure, all variables, including time, are modeled as dimensionless (see Supplementary Information for variable definitions).
Following ligand-induced receptor activation, the recipient transceiver cell responds by expressing ligand s after a time delay, corresponding to transcription, translation, and membrane trafficking of the ligand. Finally, a transceiver cell expressing the ligand on its surface (in cis) has a reduced capacity for sensing ligand in trans, a phenomenon termed cis-inhibition that is observed to regulate endogenous and synthetic Notch signaling63. Please see Supplementary Fig. 12B for an example of sender, receiver, and transceiver activation dynamics in silico. Lattices of size 50x50 and 150x150 were used for phase diagram simulations and whole-well propagation simulations, respectively. Otherwise, all simulations use a 80×80 lattice.
Changes in cell density are modeled by changing the size of all cells equally. At a higher density, for example, cell size is reduced to occupy less area while preserving the hexagonal lattice (Supplementary Fig. 12C, inset images). The density-dependence of signaling is modeled by multiplying the amount of ligand-receptor complex by a coefficient that decays exponentially as cell density deviates from the baseline confluent density, 1x (Supplementary Fig. 12C, blue curve). The dependence on density was parameterized by comparison with data shown in Figs. 3 and 4.
The area of propagation was quantified as the area occupied by Transceivers expressing ligand at a level greater than the threshold k (see Table 1 for values of all parameters used in simulation). Wave velocity was calculated similarly to the in vitro case.
Table 1.
Modeling parameters
| Parameter | Meaning | Value used |
|---|---|---|
| α | Ligand production rate when induced | 3.0 |
| k | Inducible promoter threshold | 0.02 |
| p | Cooperativity (ultrasensitivity) of promoter | 2.0 |
| ε | Strength of ligand-receptor inhibition in cis | 1.0 |
| τ | Time delay for ligand production | 0.30a |
| γ | Decay rate of reporter relative to ligand | 0.1 |
| m | Sensitivity of synNotch signaling to density | 1.0 |
| r_int | Maximum distance for cell-cell contacts | 3 cell diametersb |
| v_thresh | Ligand production rate threshold for phase calculation | 0.5 |
aExpressed in dimensionless time-units; corresponds to 0.43 times the generation time of the cell line.
br_int = 1 was used for whole-well simulations.
Introducing growth in the model
Changes in cell density are modeled spatially by changing the size of individual cells while preserving the hexagonal structure of the lattice (Supplementary Fig. 12C, inset images). At a density of 2x, for example, cell size is reduced by half. To create density-dependent signaling, the amount of ligand-receptor complex produced during signaling is multiplied by a coefficient that decays exponentially as cell density deviates from 1x (Supplementary Fig. 12C, blue curve). The exponential function was parameterized by comparison with the propagation data in Figs. 3 and 4. The effect of growth dynamics on signaling was simulated by updating the density at each time-point according to the parameterized logistic growth equation.
Classification of propagation dynamics into phases
For classification, signaling dynamics at early and late time points are used. Parameter sets are labeled “attenuated” if the initial signal production rate (where i indexes transceiver cells) is below a chosen threshold (Supplementary Fig. 15B). If the initial production rate is above this value, they were labeled “limited” if all Transceivers become inactivated by the end of the time-course and “unlimited” otherwise. As above, a transceiver was considered activated based on the amount of expressed ligand (; see Table 1).
Each of the three behavioral phases corresponds to a discrete region of the phase diagram. In the dark blue region of Fig. 5A, Transceiver activation persists throughout the time-course and propagation is unlimited. In the blue region of limited propagation, the wave of activation initiates but becomes fully attenuated at some point during the time-course. In this regime, Transceiver activation is limited in time and space, and the maximum area achieved during the time-course depends on both (Fig. 5B). Finally, in the gray region, no activation occurs and signaling has been fully turned off above a critical density that does not depend on other growth parameters (Supplementary Fig. 12; see “Methods” for details of calculation). Therefore, these phases represent different collective signaling dynamics (Fig. 4C and Supplementary Movie 8). Furthermore, the monotonic nature of the logistic equation (plotted in Fig. 4D) helps explain the three observed phases as outcomes of three types of growth curves: density stays below , density crosses during the time-course, or density stays above (Fig. 5E). In particular, the attenuated propagation phenotype can be accessed above a specific initial cell density, regardless of proliferation; for the other 2 phenotypes where propagation is observed, whether the systems displays a limiting behavior or propagates in an unlimited fashion can be controlled via controlling proliferation even for cells plated at the same initial density. Note that a similar critical density determines the density at which signaling turns on.
Measuring signaling in different growth regimes
Whole-well propagation assays were simulated by randomly seeding a 150 × 150 hexagonal lattice with senders and transceivers in a 1:100 ratio (n = 10 replicates) and numerically integrating over 7 days of simulation time. Density dynamics were updated using the fitted population growth parameters, and a shorter cell-cell contact distance was used.
Dynamical equations for receiver and transceiver signaling
Following a procedure of dynamical modeling and dimensional analysis (see Supplementary Text), we model the dynamical response of a Transceiver cell using a system of delay differential equations:
| 2 |
| 3 |
Here, and denote the amounts of ligand (“signal”) and reporter, respectively, present in cell . The maximum protein production rate is equal for both species after non-dimensionalization. The parameter γ represents the reporter’s degradation rate as a fraction of the ligand’s degradation rate, and τ represents the time delay between activation and expression, during which proteins are being manufactured and trafficked. Production rates for both species depend non-linearly on , the total amount of ligand sensed by the cell, based on a Hill-like function.
| 4 |
Here, and are the threshold and Hill coefficient (ultrasensitivity) of activation. A Hill-like activation function was chosen to represent a cooperative transcription factor assembly, such as the dimerization of tTA-VP16. Given a cell and its neighbors , the total amount of input ligand is , where is a weighted matrix of cell-cell contacts, described in the next section. Meanwhile, and represent different mechanisms of inhibition. Notch family receptors are known to be inhibited by ligand proteins expressed in cis (on the same membrane), and the strength of this interaction is represented by the dimensionless parameter . We find that activation depends on the cell density, with the most efficient activation occurring at ~100% confluence (). To model the decay in signaling sensitivity at higher and lower densities, we introduce a density sensitivity factor:
| 5 |
Note that , and at densities lower or higher than , decays at a rate in a log-symmetric fashion (i.e., ). Table 1 shows the parameter values used for all simulations.
When , and at lower or higher densities, β decays to zero in a log-symmetric fashion (i.e., doubling the density has the same effect as halving it). Table 1 shows the parameter values used for all simulations. , and at lower or higher densities, β decays to zero in a log-symmetric fashion (i.e., doubling the density has the same effect as halving it). Table 1 shows the parameter values used for all simulations.
The cell-cell contact matrix
The matrix represents the extent of cell-cell contact between the signal-sending cell and signal-receiving cell . This matrix is used to map the amount of signal presented to each cell as a function of the amount expressed by each other cell. Accordingly, encodes the signal-sending “flux” between each cell and thus conserves mass. Because of this property, is a Markov matrix (), and thus the signaling input to a cell is a weighted mean of the ligand expressed by its neighbors. Weights were calculated by evaluating a Gaussian kernel centered on cell i at each neighbor , truncating the kernel at a maximum contact radius , and normalizing to satisfy the Markov constraint. Supplementary Fig. 5A shows an example of these calculated weights.
Integration of delay differential equations
Equations were integrated over time using a forward-Euler integration scheme with fixed time-step of . Time delays were represented as an integer number of time-steps and resolved using the method of steps for delay differential equations, with all chemical species set to zero expression at time . Starting at time , sender cell expression of signaling ligand is set to . Simulations, as well as data analysis and plotting, were performed using a custom Python library (see “Code availability”).
Cell density and length-scale in the model
In our model, we define the area of each hexagonal cell to be equal to the average area at the given density. For instance, at a density of 1250 cells/mm2 the cell area is 1250−1 mm2 = 800 µm2. The side length of a hexagon is then calculated from the area and used to infer linear distances on the plane of the lattice (propagation distances, scale bars, etc.). To circumvent computational complexity associated with re-meshing after each cell division, density changes are modeled by re-scaling cell sizes using the area relationship above, preserving the structure of the lattice. This choice may under-estimate propagation velocity due to the contribution of cell division to signal diffusion.
Alignment of in vitro and in silico time-scales
In our chemical reaction system, the time-scale of reaction kinetics is set by the degradation rate constant of the ligand species . In practice, this rate is difficult to measure directly. Instead, we relate this time-scale to the observed in vitro system by assuming that ligand degradation and dilution occurs at a constant rate across all conditions and that this rate can be approximated by , the intrinsic growth rate of the wild-type cell line. For example, we assume that during the exponential phase of growth ligand decay is primarily due to dilution by growth and division rather than by active proteasomal degradation. Thus, we were able to relate the time units of the computational and in vitro systems.
Simulation of GFP at steady-state
Steady-state concentrations of GFP () in transceivers were measured by simulation of senders and transceivers randomly seeded on a 40 × 40 hexagonal lattice in a 1:100 ratio (n = 5 replicates). Cell lattices were simulated for 8 days at 1000 different densities ranging from to , with no population growth (constant density). At the final time-point, the mean concentration of GFP in transceiver cells was used as an estimate for .
Identification of critical densities
The critical densities and were calculated by simulating the steady-state ligand concentration in transceivers at different (constant) densities (see above section “Simulation of GFP at steady-state”). At both ends, the critical density is the density at which steady-state ligand expression crosses the promoter threshold .
Statistics and reproducibility
All experiments were replicated at least twice to assess reproducibility, independently from the number of technical replicates in those experiments.
FACS experiments violin plots were generated from at least 4000 cells from a single technical replicate. Each experimental mean from FACS data was generated from at least 4000 cells from a single technical replicate. Each experimental mean from cell counting and image analysis data was generated from at least two technical replicates.
Statistical comparisons pertaining to single cell data from FACS experiments in Fig. 1 were performed with the log-likelihood ratio (LLR) method. Statistical comparisons in Fig. 3H were assessed with a two-sided Mann–Whitney–Wilcoxon test.
No statistical method was used to predetermine sample size. No data were excluded from the analyses. The experiments were not randomized. The Investigators were not blinded to allocation during experiments and outcomes assessment.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Description of Additional Supplementary Files
Source data
Acknowledgements
We thank D. Carra and Z. Shappell from the Morsut lab for sharing the L929 mCherry Senders and tagBFP Receivers line; the Flow Cytometry Facility and Optical Imaging Facility of the Eli and Edith Broad CIRM Center; M. Johnson for her critical review of this manuscript and valuable feedback; A. Subramanian for critical scientific discussions; J. Bois and M. Elowitz for sharing teaching materials for mathematical modeling; S.O. for coding advice; and the Morsut and Thomson labs for their scientific input and support. The authors acknowledge their family and friends that support them always and in particular for the times of this work that took place during the COVID-19 pandemic. This work was partially funded by the Human Frontier Science Program (HFSP) Organisation, funding M.S. with Long Term Fellowship (LT000469/2019-L); the CIRM-Bridges internship fellowship (A.K. and K.P.); a Belgian American Educational Foundation (BAEF) postdoctoral fellowship (B.S.); the National Institute of General Medicine of the NIH award number R35 GM138256 (L.M.); the National Science Foundation award number CBET-2034495 RECODE and CBET-2145528 Faculty Early Career Development Program (L.M.); grant 2023-332386 from the Chan Zuckerberg Initiative Donor Advised Fund, CZI DAF, an advised fund of the Silicon Valley Community Foundation (L.M., M.T.); the Heritage Medical Research Institute (M.T.); and the David and Lucile Packard Foundation (M.T.). S.L. is supported by a Wellcome Trust Senior Fellowship [220298]. M.M. is supported by a University of Edinburgh School of Biological Sciences new staff start-up award. Figures 1B and 3A, E are created with BioRender.com.
Author contributions
L.M. and M.T. directed the research and acquired funding; M.S. discovered the phenomenon of density dependent signaling and initiated the experimental branch, with help from A.K., V.A.M., and T.S.; G.Q. and L.M. co-mentored M.S. for his fellowship acquisition; P.S.B. led the computational branch, and together with M.S. developed the material for the first submission; J.C. led the revision work, focusing on investigating the mechanisms of density dependence; B.S., N.J., and K.P. supported the experimental work in revision; D.S. supported the computational work; M.M. and S.L. provided the mES cells material and directions.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Data availability
A partial dataset for computational simulations is available at the following URL: https://data.caltech.edu/records/q8n10-tsk03. Source data are provided with this paper. And are also available at this link 10.6084/m9.figshare.26932366.
Code availability
Code used to perform mathematical simulations, parameter fitting, and statistical tests is available at 10.5281/zenodo.11560530.
Competing interests
L.M. is an inventor on a synNotch patent for applications in cancer cell therapy licensed to Gilead. The remaining authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Marco Santorelli, Pranav S. Bhamidipati, Josquin Courte.
Contributor Information
Matt Thomson, Email: mthomson@caltech.edu.
Leonardo Morsut, Email: leonardo.morsut@med.usc.edu.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-53078-8.
References
- 1.Thompson, D. W. On Growth and Form (Dover publication, New York, 1917).
- 2.Kobitski, A. Y. et al. An ensemble-averaged, cell density-based digital model of zebrafish embryo development derived from light-sheet microscopy data with single-cell resolution. Sci. Rep.5, 8601 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Feroze, R., Shawky, J. H., von Dassow, M. & Davidson, L. A. Mechanics of blastopore closure during amphibian gastrulation. Dev. Biol.398, 57–67 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zallen, J. A. & Goldstein, B. Cellular mechanisms of morphogenesis. Semin. Cell Dev. Biol.67, 101–102 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fukaya, T. Dynamic regulation of anterior-posterior patterning genes in living Drosophila embryos. Curr. Biol.31, 2227–2236.e6 (2021). [DOI] [PubMed] [Google Scholar]
- 6.Ko, C. S. & Martin, A. C. The cellular and molecular mechanisms that establish the mechanics of Drosophila gastrulation. in Current Topics in Developmental Biology, Vol. 136 (ed. Solnica-Krezel, L.) 141–165 (Academic Press, 2020). [DOI] [PubMed]
- 7.Chanet, S. & Martin, A. C. Chapter thirteen—Mechanical force sensing in tissues. in Progress in Molecular Biology and Translational Science, Vol. 126 (eds. Engler, A. J. & Kumar, S.) 317–352 (Academic Press, 2014). [DOI] [PMC free article] [PubMed]
- 8.Tschumperlin, D. J. Mechanotransduction. in Comprehensive Physiology (ed Prakash, Y. S.) 1057–1073 (John Wiley & Sons, Ltd, 2011). [DOI] [PubMed]
- 9.Heisenberg, C.-P. & Bellaïche, Y. Forces in tissue morphogenesis and patterning. Cell153, 948–962 (2013). [DOI] [PubMed] [Google Scholar]
- 10.Cai, X., Wang, K.-C. & Meng, Z. Mechanoregulation of YAP and TAZ in cellular homeostasis and disease progression. Front. Cell Dev. Biol. 9, 673599 (2021). [DOI] [PMC free article] [PubMed]
- 11.Dupont, S. et al. Role of YAP/TAZ in mechanotransduction. Nature474, 179–183 (2011). [DOI] [PubMed] [Google Scholar]
- 12.Veerman, F., Mercker, M. & Marciniak-Czochra, A. Beyond turing: far-from-equilibrium patterns and mechano-chemical feedback. Philos. Trans. R. Soc. Math. Phys. Eng. Sci379, 20200278 (2021). [DOI] [PubMed] [Google Scholar]
- 13.Urdy, S. On the evolution of morphogenetic models: mechano-chemical interactions and an integrated view of cell differentiation, growth, pattern formation and morphogenesis. Biol. Rev.87, 786–803 (2012). [DOI] [PubMed] [Google Scholar]
- 14.Hannezo, E. & Heisenberg, C.-P. Mechanochemical feedback loops in development and disease. Cell178, 12–25 (2019). [DOI] [PubMed] [Google Scholar]
- 15.Chan, C. J., Heisenberg, C.-P. & Hiiragi, T. Coordination of morphogenesis and cell-fate specification in development. Curr. Biol.27, R1024–R1035 (2017). [DOI] [PubMed] [Google Scholar]
- 16.Schiffhauer, E. S. & Robinson, D. N. Mechanochemical signaling directs cell-shape change. Biophys. J.112, 207–214 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Scott, L. E., Weinberg, S. H. & Lemmon, C. A. Mechanochemical signaling of the extracellular matrix in epithelial-mesenchymal transition. Front. Cell Dev. Biol. 7, 135 (2019). [DOI] [PMC free article] [PubMed]
- 18.Goehring, N. W. & Grill, S. W. Cell polarity: mechanochemical patterning. Trends Cell Biol.23, 72–80 (2013). [DOI] [PubMed] [Google Scholar]
- 19.Ebrahimkhani, M. R. & Ebisuya, M. Synthetic developmental biology: build and control multicellular systems. Curr. Opin. Chem. Biol.52, 9–15 (2019). [DOI] [PubMed] [Google Scholar]
- 20.Le Roux, A.-L., Quiroga, X., Walani, N., Arroyo, M. & Roca-Cusachs, P. The plasma membrane as a mechanochemical transducer. Philos. Trans. R. Soc. B Biol. Sci374, 20180221 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mao, Q. & Lecuit, T. Chapter thirty-seven—Mechanochemical interplay drives polarization in cellular and developmental systems. in Current Topics in Developmental Biology, Vol. 116 (ed. Wassarman, P. M.) 633–657 (Academic Press, 2016). [DOI] [PubMed]
- 22.Howard, J., Grill, S. W. & Bois, J. S. Turing’s next steps: the mechanochemical basis of morphogenesis. Nat. Rev. Mol. Cell Biol.12, 392–398 (2011). [DOI] [PubMed] [Google Scholar]
- 23.Shroff, N. P. et al. Proliferation-driven mechanical compression induces signalling centre formation during mammalian organ development. Nat. Cell Biol.26, 519–529 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sharma, R. K. et al. Quorum sensing by gelsolin regulates programmed cell death 4 expression and a density-dependent phenotype in macrophages. J. Immunol.207, 1250–1264 (2021). [DOI] [PubMed] [Google Scholar]
- 25.Memon, B., Karam, M., Al-Khawaga, S. & Abdelalim, E. M. Enhanced differentiation of human pluripotent stem cells into pancreatic progenitors co-expressing PDX1 and NKX6.1. Stem Cell Res. Ther.9, 15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kim, D. S. et al. Cell culture density affects the stemness gene expression of adipose tissue-derived mesenchymal stem cells. Biomed. Rep.6, 300–306 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wilson, H. K., Canfield, S. G., Hjortness, M. K., Palecek, S. P. & Shusta, E. V. Exploring the effects of cell seeding density on the differentiation of human pluripotent stem cells to brain microvascular endothelial cells. Fluids Barriers CNS12, 13 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.LeBlanc, L. et al. β-catenin links cell seeding density to global gene expression during mouse embryonic stem cell differentiation. iScience25, 103541 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chang, S.-Y. et al. Enhanced inner-ear organoid formation from mouse embryonic stem cells by photobiomodulation. Mol. Ther. Methods Clin. Dev.17, 556–567 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kempf, H. et al. Bulk cell density and Wnt/TGFbeta signalling regulate mesendodermal patterning of human pluripotent stem cells. Nat. Commun.7, 13602 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Mori, M. et al. Hippo signaling regulates microprocessor and links cell-density-dependent miRNA biogenesis to cancer. Cell156, 893–906 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Guo, M. et al. Proteomic analysis of the effects of cell culture density on the metastasis of breast cancer cells. Cell Biochem. Funct.37, 72–83 (2019). [DOI] [PubMed] [Google Scholar]
- 33.Xue, R., Li, J. Y., Yeh, Y., Yang, L. & Chien, S. Effects of matrix elasticity and cell density on human mesenchymal stem cells differentiation. J. Orthop. Res.31, 1360–1365 (2013). [DOI] [PubMed] [Google Scholar]
- 34.Srimasorn, S. et al. Increased neuronal differentiation efficiency in high cell density-derived induced pluripotent stem cells. Stem Cells Int.2019, 1–8 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sukho, P. et al. Effect of cell seeding density and inflammatory cytokines on adipose tissue-derived stem cells: an in vitro study. Stem Cell Rev. Rep.13, 267–277 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Singh, S. J., Turner, W., Glaser, D. E., McCloskey, K. E. & Filipp, F. V. Metabolic shift in density-dependent stem cell differentiation. Cell Commun. Signal.15, 44 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Venugopal, B., Mogha, P., Dhawan, J. & Majumder, A. Cell density overrides the effect of substrate stiffness on human mesenchymal stem cells’ morphology and proliferation. Biomater. Sci.6, 1109–1119 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Noda, S. et al. Effect of cell culture density on dental pulp-derived mesenchymal stem cells with reference to osteogenic differentiation. Sci. Rep.9, 5430 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lu, H. et al. Effect of cell density on adipogenic differentiation of mesenchymal stem cells. Biochem. Biophys. Res. Commun.381, 322–327 (2009). [DOI] [PubMed] [Google Scholar]
- 40.Najafabadi, M. M., Bayati, V., Orazizadeh, M., Hashemitabar, M. & Absalan, F. Impact of cell density on differentiation efficiency of rat adipose-derived stem cells into Schwann-like cells. Int. J. Stem Cells9, 213–220 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Barone, V. et al. Local and global changes in cell density induce reorganisation of 3D packing in a proliferating epithelium. Development151, dev202362 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Moreira, S., Espina, J. A., Saraiva, J. E. & Barriga, E. H. A toolbox to study tissue mechanics in vivo and ex vivo. in Cell Polarity Signaling, Vol. 2438 (eds. Chang, C. & Wang, J.) 495–515 (Springer, 2022). [DOI] [PubMed]
- 43.Xiong, F., Ma, W., Bénazéraf, B., Mahadevan, L. & Pourquié, O. Mechanical coupling coordinates the co-elongation of axial and paraxial tissues in avian embryos. Dev. Cell55, 354–366.e5 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Santorelli, M., Lam, C. & Morsut, L. Synthetic development: building mammalian multicellular structures with artificial genetic programs. Curr. Opin. Biotechnol.59, 130–140 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ho, C. & Morsut, L. Novel synthetic biology approaches for developmental systems. Stem Cell Rep.16, 1051–1064 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Davies, J. Using synthetic biology to explore principles of development. Development144, 1146 LP–1141158 (2017). [DOI] [PubMed] [Google Scholar]
- 47.Schlissel, G. & Li, P. Synthetic developmental biology: understanding through reconstitution. Annu. Rev. Cell Dev. Biol.36, 339–357 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Toda, S., Frankel, N. W. & Lim, W. A. Engineering cell-cell communication networks: programming multicellular behaviors. Curr. Opin. Chem. Biol.52, 31–38 (2019). [DOI] [PubMed] [Google Scholar]
- 49.Ebrahimkhani, M. R. & Levin, M. Synthetic living machines: a new window on life. iScience24, 102505 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Velazquez, J. J., Su, E., Cahan, P. & Ebrahimkhani, M. R. Programming morphogenesis through systems and synthetic biology. Trends Biotechnol.36, 415–429 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zarkesh, I. et al. Synthetic developmental biology: engineering approaches to guide multicellular organization. Stem Cell Rep.17, 715–733 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Teague, B. P., Guye, P. & Weiss, R. Synthetic morphogenesis. Cold Spring Harb. Perspect. Biol.8, a023929 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Morsut, L. et al. Engineering customized cell sensing and response behaviors using synthetic notch receptors. Cell164, 780–791 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Toda, S., Blauch, L. R., Tang, S. K. Y., Morsut, L. & Lim, W. A. Programming self-organizing multicellular structures with synthetic cell-cell signaling. Science361, 156–162 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Toda, S. et al. Engineering synthetic morphogen systems that can program multicellular patterning. Science370, 327–331 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Matsuda, M., Koga, M., Nishida, E. & Ebisuya, M. Synthetic signal propagation through direct cell-cell interaction. Sci. Signal.5, ra31–ra31 (2012). [DOI] [PubMed] [Google Scholar]
- 57.Matsuda, M., Koga, M., Woltjen, K., Nishida, E. & Ebisuya, M. Synthetic lateral inhibition governs cell-type bifurcation with robust ratios. Nat. Commun.6, 6195 (2015). [DOI] [PubMed] [Google Scholar]
- 58.Li, P. et al. Morphogen gradient reconstitution reveals Hedgehog pathway design principles. Science360, 543–548 (2018). [DOI] [PMC free article] [PubMed]
- 59.Ma, Y. et al. Synthetic mammalian signaling circuits for robust cell population control. http://biorxiv.org/lookup/doi/10.1101/2020.09.02.278564 (2020). [DOI] [PMC free article] [PubMed]
- 60.Zhu, R., Del Rio-Salgado, J. M., Garcia-Ojalvo, J. & Elowitz, M. B. Synthetic multistability in mammalian cells. Science375, eabg9765 (2022). [DOI] [PubMed] [Google Scholar]
- 61.Petrovic, J. et al. Ligand-dependent Notch signaling strength orchestrates lateral induction and lateral inhibition in the developing inner ear. Development141, 2313–2324 (2014). [DOI] [PubMed] [Google Scholar]
- 62.Sjöqvist, M. & Andersson, E. R. Do as I say, Not(ch) as I do: lateral control of cell fate. Dev. Biol.447, 58–70 (2019). [DOI] [PubMed] [Google Scholar]
- 63.Sprinzak, D. et al. Cis Interactions between notch and delta generate mutually exclusive signaling states. Nature465, 86–90 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Khamaisi, B., Luca, V. C., Blacklow, S. C. & Sprinzak, D. Functional comparison between endogenous and synthetic notch systems. ACS Synth. Biol.11, 3343–3353 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kopan, R. & Ilagan, M. X. G. The canonical notch signaling pathway: unfolding the activation mechanism. Cell137, 216–233 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Gordon, W. R., Arnett, K. L. & Blacklow, S. C. The molecular logic of Notch signaling—a structural and biochemical perspective. J. Cell Sci121, 3109–3119 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Sprinzak, D. & Blacklow, S. C. Biophysics of notch signaling. Annu. Rev. Biophys.50, 157–189 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Lovendahl, K. N., Blacklow, S. C. & Gordon, W. R. The molecular mechanism of notch activation. in Molecular Mechanisms of Notch Signaling (eds. Borggrefe, T. & Giaimo, B. D.) 47–58 (Springer International Publishing, 2018). [DOI] [PubMed]
- 69.Stassen, O. M. J. A., Ristori, T. & Sahlgren, C. M. Notch in mechanotransduction—from molecular mechanosensitivity to tissue mechanostasis. J. Cell Sci.133, jcs250738 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Mack, J. J. et al. NOTCH1 is a mechanosensor in adult arteries. Nat. Commun.8, 1620 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Hunter, G. L. et al. A role for actomyosin contractility in Notch signaling. BMC Biol.17, 12 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Matsuo, E. et al. Substrate stiffness modulates endothelial cell function via the YAP-Dll4-Notch1 pathway. Exp. Cell Res.408, 112835 (2021). [DOI] [PubMed] [Google Scholar]
- 73.Weijts, B. et al. Blood flow-induced Notch activation and endothelial migration enable vascular remodeling in zebrafish embryos. Nat. Commun.9, 5314 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Meloty-Kapella, L., Shergill, B., Kuon, J., Botvinick, E. & Weinmaster, G. Notch ligand endocytosis generates mechanical pulling force dependent on dynamin, epsins, and actin. Dev. Cell22, 1299–1312 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Theodoris, C. V. et al. Human disease modeling reveals integrated transcriptional and epigenetic mechanisms of NOTCH1 haploinsufficiency. Cell160, 1072–1086 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Matsuno, Y. et al. Notch signaling regulates cell density-dependent apoptosis of NIH 3T3 through an IL-6/STAT3 dependent mechanism. Eur. J. Cell Biol.97, 512–522 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Sloas, D. C., Tran, J. C., Marzilli, A. M. & Ngo, J. T. Tension-tuned receptors for synthetic mechanotransduction and intercellular force detection. Nat Biotechnol. 41, 1287–1295 (2023). [DOI] [PMC free article] [PubMed]
- 78.Turing, A. M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B. Biol. Sci.237, 37–72 (1997). [Google Scholar]
- 79.Gierer, A. & Meinhardt, H. A theory of biological pattern formation. Kybernetik12, 30–39 (1972). [DOI] [PubMed] [Google Scholar]
- 80.Murray, J. D. Mathematical Biology (Springer-Verlag, London, 2002).
- 81.Binshtok, U. & Sprinzak, D. Modeling the Notch response. Adv. Exp. Med. Biol.1066, 79–98 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Collier, J. R., Monk, N. A. M., Maini, P. K. & Lewis, J. H. Pattern formation by lateral inhibition with feedback: a mathematical model of delta-notch intercellular signalling. J. Theor. Biol.183, 429–446 (1996). [DOI] [PubMed] [Google Scholar]
- 83.Sprinzak, D., Lakhanpal, A., LeBon, L., Garcia-Ojalvo, J. & Elowitz, M. B. Mutual inactivation of notch receptors and ligands facilitates developmental patterning. PLoS Comput. Biol.7, e1002069 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Shaya, O. et al. Cell-cell contact area affects notch signaling and notch-dependent patterning. Dev. Cell40, 505–511.e6 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Formosa-Jordan, P., Ibañes, M., Ares, S. & Frade, J. M. Regulation of neuronal differentiation at the neurogenic wavefront. Development139, 2321–2329 (2012). [DOI] [PubMed] [Google Scholar]
- 86.Lam, C. et al. Parameterized computational framework for the description and design of genetic circuits of morphogenesis based on contact-dependent signaling and changes in cell–cell adhesion. ACS Synth. Biol.11, 1417–1439 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Mulberry, N. & Edelstein-Keshet, L. Self-organized multicellular structures from simple cell signaling: a computational model. Phys. Biol.17, 066003 (2020). [DOI] [PubMed] [Google Scholar]
- 88.Cohen, R. & Sprinzak, D. Mechanical forces shaping the development of the inner ear. Biophys. J.120, 4142–4148 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Hufnagel, L., Teleman, A. A., Rouault, H., Cohen, S. M. & Shraiman, B. I. On the mechanism of wing size determination in fly development. Proc. Natl. Acad. Sci. USA104, 3835–3840 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Pan, Y., Heemskerk, I., Ibar, C., Shraiman, B. I. & Irvine, K. D. Differential growth triggers mechanical feedback that elevates Hippo signaling. Proc. Natl. Acad. Sci. USA113, E6974–E6983 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Amano, M., Nakayama, M. & Kaibuchi, K. Rho-Kinase/ROCK: a key regulator of the cytoskeleton and cell polarity. Cytoskeleton67, 545–554 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Straight, A. F. et al. Dissecting temporal and spatial control of cytokinesis with a myosin II inhibitor. Science299, 1743–1747 (2003). [DOI] [PubMed] [Google Scholar]
- 93.Spector, I., Shochet, N. R., Kashman, Y. & Groweiss, A. Latrunculins: novel marine toxins that disrupt microfilament organization in cultured cells. Science219, 493–495 (1983). [DOI] [PubMed] [Google Scholar]
- 94.Yarmola, E. G., Somasundaram, T., Boring, T. A., Spector, I. & Bubb, M. R. Actin-Latrunculin A structure and function: differential modulation of actin-binding protein function by latrunculin A *. J. Biol. Chem.275, 28120–28127 (2000). [DOI] [PubMed] [Google Scholar]
- 95.Malaguti, M. et al. SyNPL: synthetic notch pluripotent cell lines to monitor and manipulate cell interactions in vitro and in vivo. Development149, dev200226 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Puliafito, A. et al. Collective and single cell behavior in epithelial contact inhibition. Proc. Natl. Acad. Sci. USA109, 739–744 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Yen, H.-C. S., Xu, Q., Chou, D. M., Zhao, Z. & Elledge, S. J. Global protein stability profiling in mammalian cells. Science322, 918–923 (2008). [DOI] [PubMed] [Google Scholar]
- 98.Uehata, M. et al. Calcium sensitization of smooth muscle mediated by a Rho-associated protein kinase in hypertension. Nature389, 990–994 (1997). [DOI] [PubMed] [Google Scholar]
- 99.Kosako, H. et al. Rho-kinase/ROCK is involved in cytokinesis through the phosphorylation of myosin light chain and not ezrin/radixin/moesin proteins at the cleavage furrow. Oncogene19, 6059–6064 (2000). [DOI] [PubMed] [Google Scholar]
- 100.Pitha, I. et al. Rho-kinase inhibition reduces myofibroblast differentiation and proliferation of scleral fibroblasts induced by transforming growth factor β and experimental glaucoma. Transl. Vis. Sci. Technol.7, 6 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Santos, G. L., Hartmann, S., Zimmermann, W.-H., Ridley, A. & Lutz, S. Inhibition of Rho-associated kinases suppresses cardiac myofibroblast function in engineered connective and heart muscle tissues. J. Mol. Cell. Cardiol.134, 13–28 (2019). [DOI] [PubMed] [Google Scholar]
- 102.Detillieux, K. A., Sheikh, F., Kardami, E. & Cattini, P. A. Biological activities of fibroblast growth factor-2 in the adult myocardium. Cardiovasc. Res.57, 8–19 (2003). [DOI] [PubMed] [Google Scholar]
- 103.Raballo, R. et al. Basic fibroblast growth factor (Fgf2) is necessary for cell proliferation and neurogenesis in the developing cerebral cortex. J. Neurosci.20, 5012–5023 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Dupree, M. A., Pollack, S. R., Levine, E. M. & Laurencin, C. T. Fibroblast growth factor 2 induced proliferation in osteoblasts and bone marrow stromal cells: a whole cell model. Biophys. J.91, 3097–3112 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Wolpert, L. Positional information and the spatial pattern of cellular differentiation. J. Theor. Biol.25, 1–47 (1969). [DOI] [PubMed] [Google Scholar]
- 106.Ashe, H. L. & Briscoe, J. The interpretation of morphogen gradients. Development133, 385–394 (2006). [DOI] [PubMed] [Google Scholar]
- 107.Stapornwongkul, K. S., de Gennes, M., Cocconi, L., Salbreux, G. & Vincent, J.-P. Patterning and growth control in vivo by an engineered GFP gradient. Science370, 321–327 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Cornwell, K. G. & Pins, G. D. Enhanced proliferation and migration of fibroblasts on the surface of fibroblast growth factor-2-loaded fibrin microthreads. Tissue Eng. Part A16, 3669–3677 (2010). [DOI] [PubMed] [Google Scholar]
- 109.Jones, T. S., Oliveira, S. M. D., Myers, C. J., Voigt, C. A. & Densmore, D. Genetic circuit design automation with Cello 2.0. Nat. Protoc.17, 1097–1113 (2022). [DOI] [PubMed] [Google Scholar]
- 110.Iacovino, M. et al. Inducible cassette exchange: a rapid and efficient system enabling conditional gene expression in embryonic stem and primary cells. Stem Cells29, 1580–1588 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Formosa-Jordan, P. & Ibañes, M. Competition in notch signaling with cis enriches cell fate decisions. PLoS ONE9, e95744 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Vasilopoulos, G. & Painter, K. J. Pattern formation in discrete cell tissues under long range filopodia-based direct cell to cell contact. Math. Biosci.273, 1–15 (2016). [DOI] [PubMed] [Google Scholar]
- 113.Hadjivasiliou, Z., Hunter, G. L. & Baum, B. A new mechanism for spatial pattern formation via lateral and protrusion-mediated lateral signalling. J. R. Soc. Interface13, 20160484 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Description of Additional Supplementary Files
Data Availability Statement
A partial dataset for computational simulations is available at the following URL: https://data.caltech.edu/records/q8n10-tsk03. Source data are provided with this paper. And are also available at this link 10.6084/m9.figshare.26932366.
Code used to perform mathematical simulations, parameter fitting, and statistical tests is available at 10.5281/zenodo.11560530.