The TWW Growth Model and Its Application in the Analysis of Quantitative Polymerase Chain Reaction

Abstract

It is necessary to accurately capture the growth trajectory of fluorescence where the best fit, precision, and relative efficiency are essential. Having this in mind, a new family of growth functions called TWW (Tabatabai, Wilus, Wallace) was introduced. This model is capable of accurately analyzing quantitative polymerase chain reaction (qPCR). This new family provides a reproducible quantitation of gene copies and is less labor-intensive than current quantitative methods. A new cycle threshold based on TWW that does not need the assumption of equal reaction efficiency was introduced. The performance of TWW was compared with 3 classical models (Gompertz, logistic, and Richard) using qPCR data. TWW models the relationship between the cycle number and fluorescence intensity, outperforming some state-of-the-art models in performance measures. The 3-parameter TWW model had the best model fit in 68.57% of all cases, followed by the Richard model (28.57%) and the logistic (2.86%). Gompertz had the worst fit in 88.57% of all cases. It had the best precision in 85.71% of all cases followed by Richard (14.29%). For all cases, Gompertz had the worst precision. TWW had the best relative efficiency in 54.29% of all cases, while the logistic model was best in 17.14% of all cases. Richard and Gompertz tied for the best relative efficiency in 14.29% of all cases. The results indicate that TWW is a good competitor when considering model fit, precision, and efficiency. The 3-parameter TWW model has fewer parameters when compared to the Richard model in analyzing qPCR data, which makes it less challenging to reach convergence.

Introduction

Mathematical modeling of growth dynamics using observational or experimental data has been a major tool in computational biology for many years. The purpose of this article is to introduce a new mathematical growth model capable of accurately modeling biological, medical, socioeconomic, and engineering data. These models can be applied to tumor growth (either measured as the number of cells or as the volume of a multicellular sphere), human and animal growth, plant growth, and both adult and embryonic stem cell proliferation.^1-3 In 1798, the exponential growth model was introduced by Thomas Robert Malthus manifesting his concept of population growth. ⁴ In 1838, the logistic growth model was introduced by Pierre Francois Verhulst by modifying the exponential growth and imposing a constraint based on the limited availability of resources. ⁴ In 1825, Benjamin Gompertz proposed the Gompertz growth model which has been frequently applied to biomedical data. ⁵ Around 1957, Ludwig von Bertalanffy introduced a model for animal growth. In his model, he explains the animal growth while taking into consideration the growth of the animal as the result of anabolism and catabolism of body materials. ⁶ The Richard growth model was introduced in 1959 as a generalization of the logistic growth model. ⁷ In 1981, Jon Schnute introduced his growth model which can represent logistic, Gompertz, Bertalanffy, and Richard models as its special cases.^7,8 Tumor spheroids were used to characterize the growth dynamics and response to different treatments. ⁹

Mathematical modeling is a key process to describe the behavior of biological networks. The purpose is to build a model that predicts the state of a biological phenomenon as a function of one or more predictor variables. According to Ghisletta et al, ¹⁰ rather than solely using linear or quadratic growth models, one should consider appropriate nonlinear alternatives.

Modeling growth dynamics of biological and clinical data, which include both experimental and control groups, would have provided invaluable information regarding disease progression and regression. It will also shed light on the study of biological systems from molecules to organism and the population level.^11-13

These quantitative models, alongside stem cell research, may possibly lead to novel treatments. ¹⁴ The sigmoidal growth models such as logistic, Gompertz, Bertalanffy, and Richard have been extensively used to model self-limited population growth in fields such as biology, economics, sociology, fishery, forestry, animal science, agriculture, and medical sciences.^15-20 Initially, the rate of growth increases at the early stage and then gradually decreases to zero when the biomass of the organism reaches its carrying capacity. The logistic growth model has a symmetric curve with a fixed inflection point, which is at half of its carrying capacity, while the Gompertz growth rate is asymmetric. On the contrary, the Richard growth has flexible point of inflection.^5,7,21 The Richard equation generalizes the logistic and Gompertz equations.^22,23 The Hill model is widely used in pharmacodynamics, pharmacokinetics, and pharmacology for analyzing dose-response data. ²⁴ The pharmacologist normally compares samples of treated and untreated cells at different levels of drug concentrations. Special cases of these growth functions can also serve as an activation function in machine learning. ²⁵

In 2005, Tabatabai et al ¹ introduced the hyperbolastic models of types I, II, and III, in the context of developing models with more versatility in representing actual growth rates from experimental data. The models have proven to have high precision in the representation of biological growth data, with close approximations to experimental results. These models have been particularly accurate in representation of cellular growth, such as growth of tumor cells ²⁶ or growth of stem cells.^27-29

In this article, a new growth model named TWW (Tabatabai, Wilus, Wallace) is introduced. This new model is used to analyze the well-known method of multiplying genetic sequences, polymerase chain reaction (PCR), which may be operated in a real-time calibrated mode known as quantitative PCR (qPCR). Quantitative polymerase chain reaction is a type of PCR that allows quantification of specific DNA and RNA targets. The qPCR method measures the intensity of stimulated emission released by the fluorescence probe at each end of a thermal heat cycle. A qPCR cycle curve has an exponential phase and a plateau phase. Quantitative polymerase chain reaction can amplify, detect, and quantify nucleic acids. The quantification can be absolute or relative.^30-32 Applications of qPCR include, but not limited to, the measurement and analysis of gene expression data, identification of the genetic building that is present within a set of genotyped entities, pathogen detection, the genomic link between disease and single-nucleotide polymorphism (SNP) markers and forensic sciences.^33,34

The cycle threshold (Ct) is a PCR cycle which represents the number of cycles required for the fluorescent signal to cross the threshold. The Ct values are inversely related to the volume of nucleic acid in the sample. ³⁵ The qPCR is grounded on the fact that at each cycle, the number of PCR products doubles. The Ct value is typically defined as 5 to 10 standard deviations (SDs) in the noise floor and may lie in the range of 20 to 30 PCR cycles. Ct values are related to the number of nucleic acid molecules in the sample as reported by the fluorescence signal.

A higher Ct value may indicate a lower initial messenger ribonucleic acid (mRNA) molecular count. A gene which is highly expressed would typically have a lower Ct value needed. For example, a higher DNA/RNA molecular count in the initial sample would support a lower Ct value. ³⁶

Guescini et al proposed a new method called ${\mathrm{C}}_{y_0}$ that does not assume equal reaction efficiency between unknowns and standard curve. This method is based on the fit of the Richard function to 420 independent runs of PCR reaction parameters to obtain the best-fit estimators. ³⁵

Method

The models commonly used in literature to analyze qPCR data are Richard, logistic, and Gompertz. For comparative purposes, a 5-parameter Richard model defined as

$$F(x)=\frac{\psi }{{\left(1+e^{\frac{-(x-\lambda )}{\theta }}\right)}^{\gamma }}+\delta$$

was used throughout this study. The fluorescence intensity at cycle number $x$ is denoted by $F(x)$ and $\psi ,\lambda ,\theta ,\gamma ,\mathrm{and}\delta$ are the 5 parameters of the Richard model. The 3-parameter logistic function of the form

$$F(x)=\frac{\psi }{1+\xi e^{-\rho x}}$$

and the 3-parameter Gompertz model with the following equation

$$F(x)=\psi e^{-\xi e^{-\rho x}}$$

were used throughout this article.

TWW growth model

The 3-parameter TWW growth model $F(x)$ , which is the solution of the differential equation of the form

$$f(x)=\frac{dF(x)}{dx}=\frac{\alpha \theta \beta e^{-\beta x-ArcSinh\left(\theta e^{-\beta x}\right)}}{\sqrt{1+{\theta }^2{e}^{-2\beta x}}}$$ (1)

is equal to

$$F(x)=\alpha e^{-ArcSinh\left(\theta e^{-\beta x}\right)}$$ (2)

Alternatively, the growth rate equation (1) can be written as

$$\frac{dF(x)}{dx}=r(x)F(x)$$

where the relative growth rate $r(x)=\frac{\theta \beta e^{-\beta x}}{\sqrt{1+{\theta }^2{e}^{-2\beta x}}}.$ $\alpha$ represents the carrying capacity, $\theta >0,\mathrm{and}\beta$ signifies the model parameters, while $-\infty <x<\infty$ and $ArcSinh(•)$ denotes the inverse hyperbolic sine function.

When the parameter $\beta >0,$ the function $F(x)$ grows, and when $\beta <0,$ it decays. In addition, the function $F(x)$ will form the TWW cumulative distribution function with probability density function $f(x)$ when $\alpha =1$ and $\beta >0.$

The point of inflection for the graph of equation (2) is $(x_{inf},F(x_{inf}))$ where

$$\begin{array}{l}{x}_{inf}=\frac{ln\left({\theta }^2(1+\sqrt{5})/2\right)}{2\beta }\mathrm{and}\\ F(x_{inf})=\alpha e^{-ArcSinh\left(\frac{\sqrt{2}}{\sqrt{1+\sqrt{5}}}\right)}\end{array}$$

with $ln(•)$ as natural logarithm.

The slope of the tangent line to the graph of $F(x)$ at the point of inflection is equal to

$$Slope=\sqrt{\frac{2}{3+\sqrt{5}}}{e}^{-ArcSinh\left(\sqrt{\frac{2}{1+\sqrt{5}}}\right)}\alpha \beta$$

which can be approximated as

$$Slope=0.3002831\alpha \beta$$

If one desires to calculate the point $x$ where the population reaches a fraction $K$ of its carrying capacity $\alpha ,$ then one can solve the equation $F(x)=K\alpha$ for $x,$ with $0<K<1.$ The resulting solution is

$$x=-\frac{ln\left(\frac{-Sinh(ln(k))}{\theta }\right)}{\beta }$$

An alternative but equivalent form of the 3-parameter growth function $F(x)$ is given by

$$F(x)=\alpha e^{-ArcSinh(e^{-(x-\gamma )/\delta })}$$ (3)

and the growth rate $f(x)$ is

$$f(x)=\frac{\alpha e^{-(x-\gamma )/\delta -ArcSinh\left(e^{-(x-\gamma )/\delta }\right)}}{\delta \sqrt{1+e^{-2(x-\gamma )/\delta }}}$$ (4)

Equation (3) is equivalent to equation (2) when $\theta =e^{\gamma /\delta }$ and $\beta =\frac{1}{\delta }.$

A third form of a 3-parameter TWW growth function $F(x)$ is

$$F(x)=\alpha e^{-ArcSinh\left(e^{-({\beta }_0+{\beta }_{1}x)}\right)}$$ (5)

Equation (5) is also equivalent to equation (2) when $\theta =e^{-{\beta }_0}$ and $\beta ={\beta }_1.$

The corresponding growth rate function using equation (5) is

$$f(x)=\frac{\alpha {\beta }_1{e}^{-({\beta }_0+{\beta }_{1}x)-ArcSinh\left(e^{-({\beta }_0+{\beta }_{1}x)}\right)}}{\sqrt{1+e^{-2({\beta }_0+{\beta }_{1}x)}}}$$

In the event that a 3-parameter TWW did not fit the data adequately well, we recommend that one should try the 4-parameter TWW model of the form

$$F(x)=\alpha e^{-ArcSinh\left(\theta e^{-\beta x}\right)}+\delta$$

where $\delta$ represents the vertical shift for the graph of the TWW function.

A 5-parameter TWW model has the form

$$F(x)=\alpha e^{-\phi ArcSinh\left(\theta e^{-\beta x}\right)}+\delta$$

where $\alpha ,\phi ,\theta ,\beta ,and\delta$ are model parameters with $\phi >0\mathrm{and}\theta >0.$

In some cases of fluorescence of bacterial cultures or microbial data, it may be more appropriate to use a 4- or 5-parameter TWW model if the 3-parameter does not fit the data adequately enough. ³⁷

Multivariable TWW growth model

If the function F depends on a set of independent variables $\{x_1,x_2,\dots ,x_k\},$ then the multivariable TWW growth equation of the form (equation (2)) can be written as

$$F(x_1,x_2,\dots ,x_k)=\alpha e^{-ArcSinh\left(e^{-({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_k{x}_k)}\right)}$$ (6)

where $\alpha ,{\beta }_0,{\beta }_1,{\beta }_2,\dots {\beta }_k$ are model parameters. One can notice that equation (6) is the generalization of equation (5).

For $j=1,2,\dots ,k,$ the partial rate of growth with respect to $x_j$ is

$$\frac{\partial F(x_1,x_2,\dots ,x_k)}{\partial x_j}=\frac{\alpha {\beta }_j{e}^{\begin{array}{l}-({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_k{x}_k)-\\ ArcSinh\left(e^{-({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_{12}+\dots +{\beta }_k{x}_k)}\right)\end{array}}}{\sqrt{1+e^{-2({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_k{x}_k)}}}$$ (7)

Partial elasticity

The partial elasticity of growth with respect to independent variable $x_j$ is denoted by $E_{x_j}(x_1,x_2,\dots ,x_k)$ and is given by

$$\begin{array}{l}{E}_{x_j}(x_1,x_2,\dots ,x_k)=\frac{\partial F(x_1,x_2,\dots ,x_k)}{\partial x_j}\\ \frac{x_j}{F(x_1,x_2,\dots ,x_k)}\mathrm{,}j=1,2,\dots ,k\end{array}$$

For discrete variables, the partial elasticity is calculated using

$$E_{x_j}(x_1,x_2,\dots ,x_k)=\frac{\Delta F(x_1,x_2,\dots ,x_k)}{F(x_1,x_2,\dots ,x_k)}/\frac{\Delta x_j}{x_j}$$

For TWW growth model using equation (7), the partial elasticity is given by

$$E_{x_j}(x_1,x_2,\dots ,x_k)=\frac{{\beta }_j{x}_j{e}^{-({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_k{x}_k)}}{\sqrt{1+e^{-2({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_k{x}_k)}}}$$

This partial elasticity approximates the percentage change in growth divided by percentage change in the independent variable $x_j.$ If the absolute value of partial elasticity is greater than one, then the growth is elastic; if it is less than one, it is inelastic; and if it is one, it is unit elastic. When there is only a single predictor variable, the partial elasticity is called elasticity. The cycle elasticity of fluorescence is a measure of sensitivity of fluorescence to a change in cycle number which is denoted here by $E_x$ and is equal to

$$E_x=\frac{{\beta }_{1}x{e}^{-({\beta }_0+{\beta }_{1}x)}}{\sqrt{1+e^{-2({\beta }_0+{\beta }_{1}x)}}}$$

where $x$ represents the cycle number.

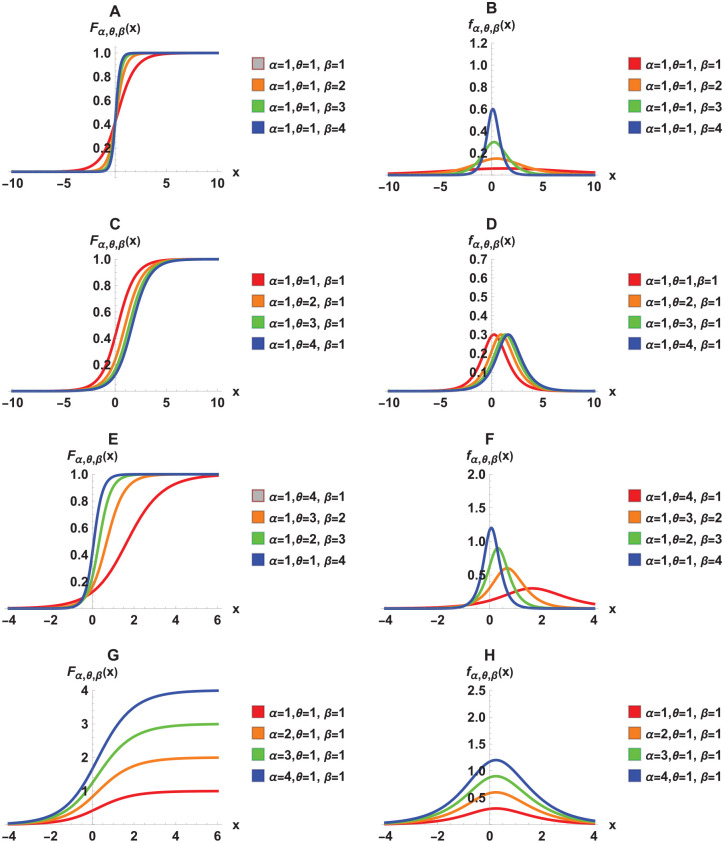
Figure 1 illustrates the growth functions as well as their respective growth rate functions for different combinations of parameters. The graphs show the flexibility of the 3-parameter TWW growth models with respect to change in parameter values.

Figure 1.

TWW growth and growth rate functions using different parameter values.

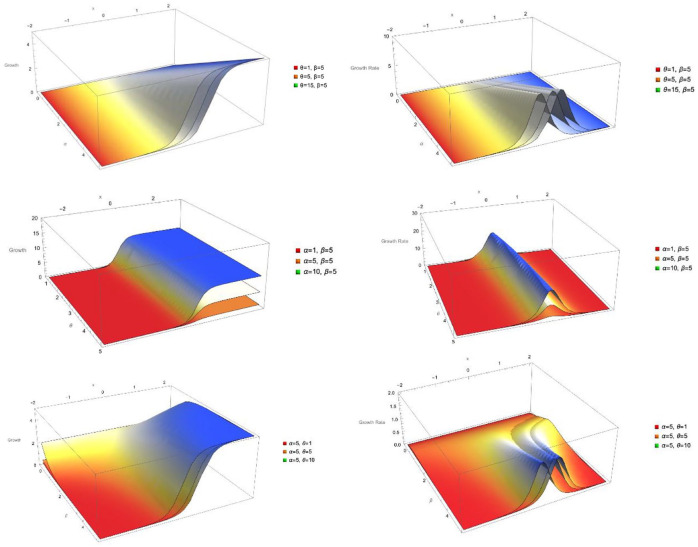
Figure 2 shows 3D graphs of growth and growth rate as a function of independent variables and a single parameter while holding the remaining parameters at a fixed level.

Figure 2.

3D graphs of growth and growth rate functions under different conditions.

Evaluation of TWW cycle threshold $(C_{TWW})$

For the 3-parameter TWW model, the first step in calculating $C_{TWW}$ is predicting the parameters of fluorescence intensities $F(x)$ as a function of cycle number $x$ using equation (2), where $\alpha$ is the maximal fluorescence intensity, $\beta$ is the fluorescence intensity intrinsic growth rate, and $\theta$ sets the fluorescent intensity displacement along the horizontal axis.

The next step is to calculate the slope of the tangent line to the graph of the 3-parameter function $F(x)$ at the point of inflection, which results in

$$Slope=\sqrt{\frac{2}{3+\sqrt{5}}}{e}^{-ArcSinh\left(\sqrt{\frac{2}{1+\sqrt{5}}}\right)}\alpha \beta$$

and can be approximated as

$$Slope=0.3002831\alpha \beta$$

As shown in Figure 3, the cycle number $C_{TWW}$ is the ordinate value at the intersection of the tangent line to the graph of fluorescence curve $F(x)$ at the point of inflection. The $C_{TWW}$ for 3-parameter TWW is

Figure 3.

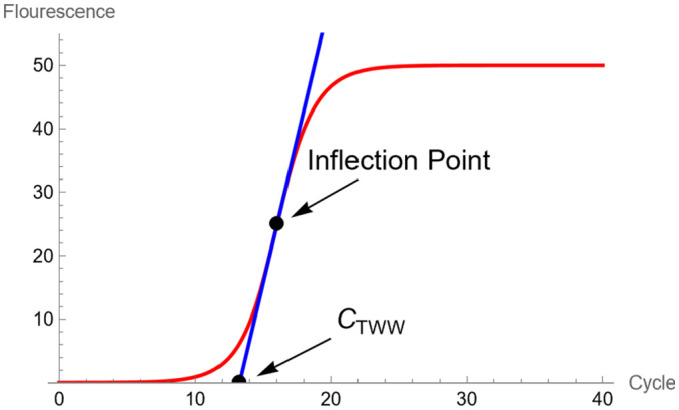
Shows the fluorescence intensity and the tangent line crossing the horizontal axis, creating the $C_{TWW}$ cycle.

$$C_{TWW}=\frac{-\sqrt{2\left(3+\sqrt{5}\right)}+ln\left(\frac{1+\sqrt{5}}{2}\right)+2ln\left(\theta \right)}{2\beta }$$

which can be approximated as

$$C_{TWW}=\frac{-2.75486+2ln\left(\theta \right)}{2\beta }$$

If one uses a 4-parameter TWW function, then the point of inflection $(x_{inf},F(x_{inf}))$ has

$$x_{inf}=\frac{ln\left(\frac{\sqrt{{\theta }^2(1+\sqrt{5})}}{\sqrt{2}}\right)}{\beta }$$

and

$$F(x_{inf})=\alpha {\mathrm{e}}^{-ArcSinh\left(\frac{\sqrt{2}}{\sqrt{1+\sqrt{5}}}\right)}+\delta$$

The slope of the tangent line to the graph of $F(x)$ at the point of inflection is equal to

$$Slope=\frac{\sqrt{2}\alpha \beta {\mathrm{e}}^{-ArcSinh\left(\frac{\sqrt{2}}{\sqrt{1+\sqrt{5}}}\right)}}{\sqrt{3+\sqrt{5}}}$$

The $C_{TWW}$ for the 4-parameter model is

$$C_{TWW}=\frac{-\sqrt{\frac{3+\sqrt{5}}{2}}\left(\alpha +\delta {\mathrm{e}}^{ArcSinh\left(\sqrt{\frac{2}{1+\sqrt{5}}}\right)}\right)+\alpha ln\left(\frac{1+\sqrt{5}}{2}\theta \right)}{\alpha \beta }$$

with an approximate value of

$$C_{TWW}=\frac{-1.37743\alpha -3.33019\delta +\alpha ln(\theta )}{\alpha \beta }$$

The 5-parameter TWW model has its point of inflection at $(x_{inf},F(x_{inf}))$ where

$$x_{inf}=\frac{ln\left(\frac{\sqrt{{\phi }^2{\theta }^2+\phi \sqrt{4+{\phi }^2}{\theta }^2}}{\sqrt{2}}\right)}{\beta }$$

and

$$F(x_{inf})=\alpha {\mathrm{e}}^{-\phi ArcSinh\left(\frac{\sqrt{2}}{\sqrt{\phi \left(\phi +\sqrt{4+{\phi }^2}\right)}}\right)}+\delta$$

The slope of the tangent line to the graph of the 5-parameter $F(x)$ at the point of inflection is equal to

$$Slope=\frac{\sqrt{2}\alpha \phi \beta {\mathrm{e}}^{-\phi ArcSinh\left(\frac{\sqrt{2}}{\sqrt{\phi \left(\phi +\sqrt{4+{\phi }^2}\right)}}\right)}}{\sqrt{2+{\phi }^2+\phi \sqrt{4+{\phi }^2}}}$$

and the $C_{TWW}$ for a 5-parameter TWW model is

$$\begin{array}{l}{C}_{TWW}=-\frac{\sqrt{2+{\phi }^2+\phi \sqrt{4+{\phi }^2}}\left(\alpha +\delta {\mathrm{e}}^{\phi ArcSinh\left(\frac{\sqrt{2}}{\sqrt{\phi \left(\phi +\sqrt{4+{\phi }^2}\right)}}\right)}\right)}{\sqrt{2}\alpha \phi \beta }+\\ \frac{ln\left(\frac{\sqrt{\phi {\theta }^2\left(\phi +\sqrt{4+{\phi }^2}\right)}}{\sqrt{2}}\right)}{\beta }\end{array}$$

Measures of fit, precision, and relative efficiency

Using PCR data of Guescini et al ³⁵ and for each combination of input molecular number and amplification mix, the average fluorescence sample over the 12 runs was calculated. Then, the 3-parameter TWW growth function, the 3-parameter Gompertz, the 3-parameter logistic, and the 5-parameter Richard functions were used to estimate the fluorescence intensity as a function of cycle number for all 4 models using the PROC NLIN function in SAS software version 9.4 with the Gauss-Newton method. To assess the fit performances of the 4 models, qPCR data were used to calculate Akaike information criterion (AIC) and Bayesian information criterion (BIC) which have been defined as

$$AIC=nln\left(\frac{SSE}{n}\right)+2K$$

and

$$BIC=nln\left(\frac{SSE}{n}\right)+Kln(n)$$

where n is the sample size, $SSE$ is the sum of squares error, and $K$ is the number of model parameters.

A model with a lower AIC and BIC provides a reasonable fit and would be selected. For each combination of input molecular number and amplification mix, AIC and BIC for all 4 models were calculated.

Additional performance measures considered are precision and relative efficiency metrics. For each combination of input molecular number and amplification mix, the precision (Pre) was calculated using the following equation:

$$Pre=\frac{S_{\widehat{F}}}{\overline{\widehat{F}}}$$

where $\overline{\widehat{F}}$ and $S_{\widehat{F}}$ are mean and SD for the estimated fluorescence, respectively. The relative efficiency (Eff) is defined as

$$Eff=\sum _{i=1}^n\left(\frac{\widehat{F_i}}{F_i}-1\right)$$

where $F_i$ and $\widehat{F_i}$ are true and estimated fluorescence intensities, respectively.

Results

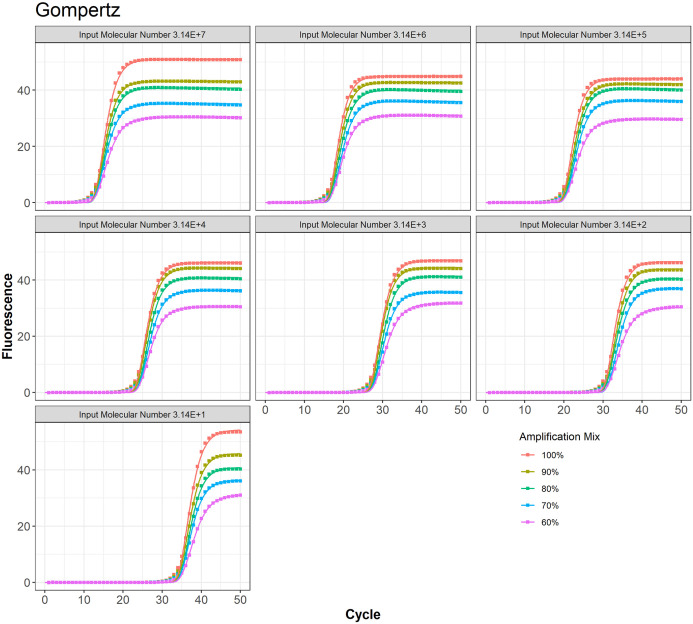
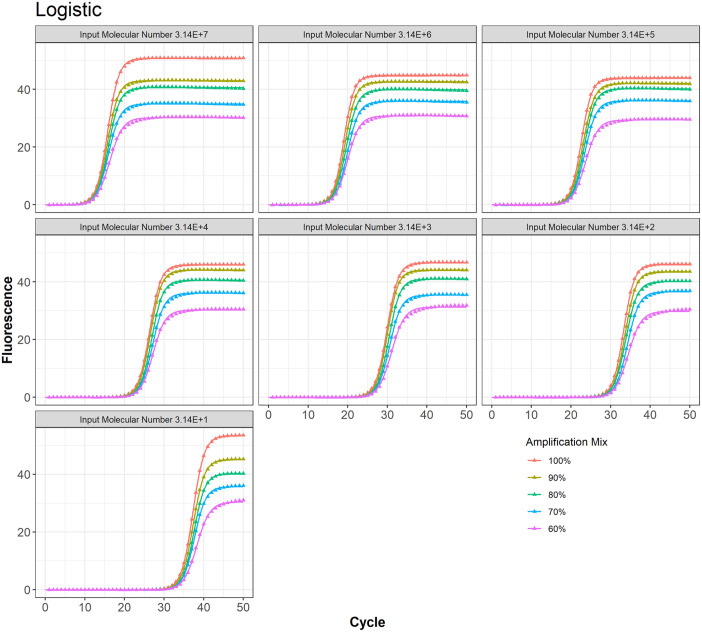
Table 1 provides the AIC and BIC values for all 4 models. For 68.57% of combination of input molecular number and amplification mix cases, the 3-parameter TWW model had the least values for AIC and BIC, indicating the best model fit among all models considered in this study. The Richard model was the best fit only in 28.57% of all cases, and the logistic was best in 2.86% of all cases. The Gompertz was the worst fit for 88.57% of all cases.

Table 1.

Values of AIC and BIC for TWW, Gompertz, logistic, and Richard models.

Amplification mixed Molecular number	100%	90%	80%	70%	60%
3.14E + 7	TWW
	AIC = −240.38 BIC = −234.64	AIC = −194.13 BIC = −188.39	AIC = −175.34 BIC = −169.60	AIC = −146.43 BIC = −140.69	AIC = −113.15 BIC = −107.42
	Gompertz
	AIC = −31.16 BIC = −25.42	AIC = −47.65 BIC = −41.92	AIC = −55.47 BIC = −49.73	AIC = −82.94 BIC = −77.20	AIC = −115.44 BIC = −109.70
	Logistic
	AIC = −191.85 BIC = −186.12	AIC = −163.09 BIC = −157.35	AIC = −157.25 BIC = −151.52	AIC = −126.90 BIC = −121.16	AIC = −98.31 BIC = −92.58
	Richard
	AIC = −189.38 BIC = −179.82	AIC = −160.50 BIC = −150.94	AIC = −158.01 BIC = −148.45	AIC = −142.86 BIC = −133.30	AIC = −136.40 BIC = −126.84
3.14E + 6	TWW
	AIC = −162.89 BIC = −157.15	AIC = −223.25 BIC = −217.51	AIC = −174.23 BIC = −168.50	AIC = −169.21 BIC = −163.47	AIC = −137.61 BIC = −131.88
	Gompertz
	AIC = −26.00 BIC = −20.26	AIC = −41.74 BIC = −36.01	AIC = −59.37 BIC = −53.63	AIC = −73.14 BIC = −67.40	AIC = −105.41 BIC = −99.68
	Logistic
	AIC = −176.56 BIC = −170.82	AIC = −219.60 BIC = −213.87	AIC = −155.89 BIC = −150.15	AIC = −148.03 BIC = −142.30	AIC = −118.78 BIC = −113.01
	Richard
	AIC = −233.34 BIC = −223.78	AIC = −223.23 BIC = −214.37	AIC = −159.03 BIC = −149.46	AIC = −154.35 BIC = −144.79	AIC = −144.86 BIC = −135.30
3.14E + 5	TWW
	AIC = −179.40 BIC = −173.67	AIC = −241.16 BIC = −235.42	AIC = −200.73 BIC = −194.99	AIC = −165.12 BIC = −159.38	AIC = −120.63 BIC = −114.90
	Gompertz
	AIC = −31.57 BIC = −25.83	AIC = −56.57 BIC = −50.82	AIC = −61.24 BIC = −55.51	AIC = −82.86 BIC = −77.12	AIC = −117.53 BIC = −111.79
	Logistic
	AIC = −189.04 BIC = −183.31	AIC = −198.61 BIC = −192.88	AIC = −169.45 BIC = −163.72	AIC = −138.19 BIC = −132.46	AIC = −105.14 BIC = −99.41
	Richard
	AIC = −223.52 BIC = −213.96	AIC = −207.67 BIC = −198.11	AIC = −174.85 BIC = −165.29	AIC = −155.55 BIC = −145.99	AIC = −139.41 BIC = −129.85
3.14E + 4	TWW
	AIC = −259.62 BIC = −253.89	AIC = −251.46 BIC = −245.72	AIC = −237.25 BIC = −231.51	AIC = −152.39 BIC = −146.65	AIC = −129.75 BIC = −124.02
	Gompertz
	AIC = −44.12 BIC = −38.39	AIC = −48.66 BIC = −42.92	AIC = −59.33 BIC = −53.59	AIC = −87.10 BIC = −81.37	AIC = −111.65 BIC = −105.92
	Logistic
	AIC = −212.42 BIC = −206.68	AIC = −199.32 BIC = −193.58	AIC = −190.23 BIC = −184.49	AIC = −127.77 BIC = −122.03	AIC = −112.65 BIC = −106.92
	Richard
	AIC = −211.98 BIC = −202.42	AIC = −198.96 BIC = −189.40	AIC = −192.21 BIC = −182.67	AIC = −148.89 BIC = −139.33	AIC = −141.36 BIC = −131.80
3.14E + 3	TWW
	AIC = −262.52 BIC = −256.79	AIC = −229.43 BIC = −223.69	AIC = −249.45 BIC = −243.72	AIC = −174.91 BIC = −169.18	AIC = −102.61 BIC = −96.88
	Gompertz
	AIC = −43.24 BIC = −37.50	AIC = −39.47 BIC = −33.73	AIC = −58.39 BIC = −52.65	AIC = −85.18 BIC = −79.44	AIC = −115.23 BIC = −109.49
	Logistic
	AIC = −206.05 BIC = −200.31	AIC = −210.86 BIC = −205.12	AIC = −191.91 BIC = −186.17	AIC = −145.38 BIC = −139.65	AIC = −89.87 BIC = −84.14
	Richard
	AIC = −205.48 BIC = −195.92	AIC = −215.76 BIC = −206.20	AIC = −192.80 BIC = −183.24	AIC = −160.87 BIC = −151.31	AIC = −127.83 BIC = −118.27
3.14E + 2	TWW
	AIC = −197.95 BIC = −192.22	AIC = −255.44 BIC = −249.70	AIC = −206.73 BIC = −201.00	AIC = −173.50 BIC = −167.77	AIC = −112.91 BIC = −107.17
	Gompertz
	AIC = −31.25 BIC = −25.52	AIC = −43.47 BIC = −37.74	AIC = −69.82 BIC = −64.08	AIC = −84.27 BIC = −78.54	AIC = −123.01 BIC = −117.27
	Logistic
	AIC = −202.86 BIC = −197.12	AIC = −233.66 BIC = −227.92	AIC = −165.22 BIC = −159.48	AIC = −145.26 BIC = −139.52	AIC = −100.45 BIC = −94.71
	Richard
	AIC = −231.48 BIC = −221.92	AIC = −237.17 BIC = −227.61	AIC = −178.07 BIC = −168.51	AIC = −161.95 BIC = −152.39	AIC = −138.60 BIC = −129.04
3.14E + 1	TWW
	AIC = −274.54 BIC = −268.81	AIC = −318.92 BIC = −313.18	AIC = −274.54 BIC = −268.81	AIC = −222.07 BIC = −216.33	AIC = −152.22 BIC = −146.49
	Gompertz
	AIC = −31.43 BIC = −25.69	AIC = −50.07 BIC = −44.34	AIC = −57.64 BIC = −51.90	AIC = −84.17 BIC = −78.44	AIC = −126.51 BIC = −120.78
	Logistic
	AIC = −273.94 BIC = −268.21	AIC = −248.63 BIC = −242.89	AIC = −279.33 BIC = −273.59	AIC = −185.62 BIC = −179.49	AIC = −140.23 BIC = −134.49
	Richard
	AIC = −272.81 BIC = −263.25	AIC = −248.67 BIC = −239.09	AIC = −276.55 BIC = −266.98	AIC = −198.42 BIC = −188.86	AIC = −185.73 BIC = −176.17

Table 2 shows the computed values for precision and relative efficiencies. TWW had the best precision 85.71% of all cases while the Richard model had the highest precision with only 14.29%. For all cases, Gompertz had the worst precision when compared with other models. TWW had the best relative efficiency 54.29% of all cases, while logistic relative efficiency was the best in only 17.14%. Richard and Gompertz tied for best relative efficiency each with approximately 14.29% of all cases.

Table 2.

Precision and relative efficiency for TWW, Gompertz, logistic, and Richard models.

Amplification mixed Molecular number	100%	90%	80%	70%	60%
3.14E + 7	TWW
	Pre = 62.22 Eff = −0.08	Pre = 62.17 Eff = −2.62	Pre = 62.81 Eff = −1.52	Pre = 62.50 Eff = 0.99	Pre = 63.09 Eff = 5.19
	Gompertz
	Pre = 63.07 Eff = −11.88	Pre = 63.02 Eff = −11.88	Pre = 63.69 Eff = −12.04	Pre = 63.43 Eff = −11.77	Pre = 64.12 Eff = −11.60
	Logistic
	Pre = 62.28 Eff = −3.42	Pre = 62.23 Eff = −4.89	Pre = 62.87 Eff = −4.14	Pre = 62.57 Eff = −2.15	Pre = 63.18 Eff = 1.40
	Richard
	Pre = 62.28 Eff = −4.68	Pre = 62.23 Eff = −8.31	Pre = 62.92 Eff = −8.88	Pre = 62.75 Eff = −13.24	Pre = 63.57 Eff = −21.78
3.14E + 6	TWW
	Pre = 72.87 Eff = 4.61	Pre = 73.70 Eff = −14.71	Pre = 74.41 Eff = −540.72	Pre = 75.29 Eff = −7.46	Pre = 75.11 Eff = −64.61
	Gompertz
	Pre = 73.69 Eff = −15.45	Pre = 74.56 Eff = −15.59	Pre = 75.34 Eff = −15.67	Pre = 76.23 Eff = −15.90	Pre = 76.12 Eff = −15.60
	Logistic
	Pre = 72.92 Eff = −5.18	Pre = 73.75 Eff = −12.26	Pre = 74.47 Eff = 232.04	Pre = 75.36 Eff = −8.40	Pre = 75.19 Eff = −36.91
	Richard
	Pre = 72.74 Eff = −10.93	Pre = 73.67 Eff = −33.21	Pre = 74.51 Eff =−2821.43	Pre = 75.43 Eff = −66.69	Pre = 75.45 Eff =−265.57
3.14E + 5	TWW
	Pre = 84.91 Eff = −2.33	Pre = 85.90 Eff = −8.81	Pre = 86.96 Eff = 6.67	Pre = 87.40 Eff = −3.71	Pre = 87.57 Eff = −1.52
	Gompertz
	Pre = 85.81 Eff = −19.00	Pre = 86.90 Eff = −19.06	Pre = 87.97 Eff = −19.37	Pre = 88.45 Eff = −19.38	Pre = 88.71 Eff = −19.11
	Logistic
	Pre = 84.97 Eff = −9.57	Pre = 85.97 Eff = −8.34	Pre = 87.03 Eff = −4.26	Pre = 87.48 Eff = −8.13	Pre = 87.67 Eff = −5.16
	Richard
	Pre = 84.81 Eff = −7.56	Pre = 86.02 Eff =−942.16	Pre = 87.08 Eff = −199.63	Pre = 87.64 Eff = −63.68	Pre = 88.08 Eff =−115.76
3.14E + 4	TWW
	Pre = 98.24 Eff =−177.96	Pre = 99.10 Eff = −9.58	Pre = 100.36 Eff = −14.82	Pre = 100.86 Eff = 53.64	Pre = 101.12 Eff = 47.68
	Gompertz
	Pre = 99.34 Eff = −22.42	Pre = 100.21 Eff = −22.66	Pre = 101.48 Eff = −22.97	Pre = 102.06 Eff = −22.89	Pre = 102.38 Eff = −22.79
	Logistic
	Pre = 98.32 Eff = −91.36	Pre = 99.18 Eff = −13.42	Pre = 100.44 Eff = −16.08	Pre = 100.96 Eff = 21.36	Pre = 101.22 Eff = 22.36
	Richard
	Pre = 98.34 Eff =−226.03	Pre = 99.20 Eff = 14.72	Pre = 100.48 Eff = −104.09	Pre = 101.2 Eff = −0.83	Pre = 101.65 Eff = −32.21
3.14E + 3	TWW
	Pre = 113.21 Eff = −13.58	Pre = 114.14 Eff = −16.96	Pre = 115.63 Eff = 289.53	Pre = 116.09 Eff = −20.20	Pre = 117.46 Eff = −19.29
	Gompertz
	Pre = 114.50 Eff = −25.96	Pre = 115.38 Eff = −26.29	Pre = 116.96 Eff = −26.49	Pre = 117.48 Eff = −26.45	Pre = 119.08 Eff = −26.28
	Logistic
	Pre = 113.31 Eff = −16.99	Pre = 114.23 Eff = −19.48	Pre = 115.73 Eff = 133.89	Pre = 116.20 Eff = −20.53	Pre = 117.61 Eff = −19.00
	Richard
	Pre = 113.35 Eff = −27.67	Pre = 114.12 Eff = −22.25	Pre = 115.77 Eff = 257.65	Pre = 116.43 Eff =−135.97	Pre = 118.36 Eff = −11.44
3.14E + 2	TWW
	Pre = 130.63 Eff = 2.83	Pre = 132.40 Eff = −47.90	Pre = 133.02 Eff = 10.10	Pre = 135.35 Eff = −18.62	Pre = 135.44 Eff = 11.01
	Gompertz
	Pre = 132.12 Eff = −29.56	Pre = 133.97 Eff = −29.81	Pre = 134.71 Eff = −29.75	Pre = 137.11 Eff = −30.09	Pre = 137.42 Eff = −29.69
	Logistic
	Pre = 130.74 Eff = −13.98	Pre = 132.52 Eff = −32.86	Pre = 133.16 Eff = −10.01	Pre = 135.51 Eff = −21.42	Pre = 135.63 Eff = −3.49
	Richard
	Pre = 130.53 Eff = −96.44	Pre = 132.37 Eff =−121.85	Pre = 133.31 Eff = 8.56	Pre = 135.80 Eff = −61.67	Pre = 136.51 Eff = −67.68
3.14E + 1	TWW
	Pre = 155.00 Eff = −23.88	Pre = 155.78 Eff = −20.13	Pre = 157.53 Eff = −27.64	Pre = 157.81 Eff = −7.99	Pre = 160.53 Eff = −12.75
	Gompertz
	Pre = 157.14 Eff = −33.18	Pre = 157.92 Eff = −33.31	Pre = 159.68 Eff = −33.59	Pre = 160.05 Eff = −33.50	Pre = 163.15 Eff = −33.41
	Logistic
	Pre = 155.19 Eff = −25.92	Pre = 155.97 Eff = −24.29	Pre = 157.72 Eff = −28.20	Pre = 158.02 Eff = −17.39	Pre = 160.81 Eff = −18.04
	Richard
	Pre = 155.29 Eff = 1.25	Pre = 156.09 Eff = −15.03	Pre = 157.80 Eff = 36.93	Pre = 158.39 Eff = −25.11	Pre = 162.01 Eff = −58.60

Table 3 shows the values of $C_{TWW}$ and ${\mathrm{C}}_{{\mathrm{y}}_0}.$ Figures 4 to 7 show the graphs of estimated fluorescence intensity as well as plots of the true fluorescence intensity values versus cycle number for different combinations of input molecular number and amplification mix using TWW, Gompertz, logistic, and Richard models.

Table 3.

Values of $C_{TWW}$ and $C_{y_0}.$

Molecular number Amplification mixed	$C_{TWW}$
	3.14E + 7	3.14E + 6	3.14E + 5	3.14E + 4	3.14E + 3	3.14E + 2	3.14E + 1
100%	13.0094	16.4675	22.6253	23.5800	27.1323	30.6586	34.4415
90%	13.0132	16.6750	20.2343	23.8180	27.3848	30.9522	34.5602
80%	13.1889	16.8337	20.5438	24.1314	27.6683	31.0145	34.8124
70%	13.0353	17.0964	20.6379	24.1929	27.7852	31.4055	34.8160
60%	13.1062	16.9670	20.5907	24.2137	27.8883	31.3127	30.8955
Molecular Number Amplification Mixed	$C_{y_0}$
	3.14E + 7	3.14E + 6	3.14E + 5	3.14E + 4	3.14E + 3	3.14E + 2	3.14E + 1
100%	13.0443	16.4053	19.9986	23.5293	27.0548	30.6088	34.3042
90%	13.1002	16.6658	20.2373	23.7784	27.3283	30.9217	34.4331
80%	13.2602	16.9188	20.5744	24.0867	27.6141	30.9796	34.6755
70%	13.2754	17.2086	20.6991	24.1974	27.6739	31.3350	34.6730
60%	13.5391	17.1482	20.6716	24.1851	27.8264	31.2026	34.7794

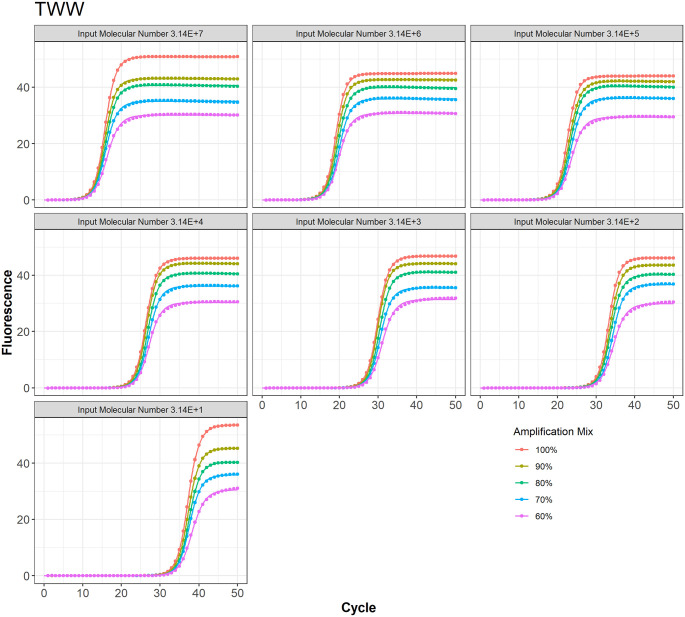
Figure 4.

TWW model fit to the PCR data at different amplification mix for all 7 input molecular numbers.

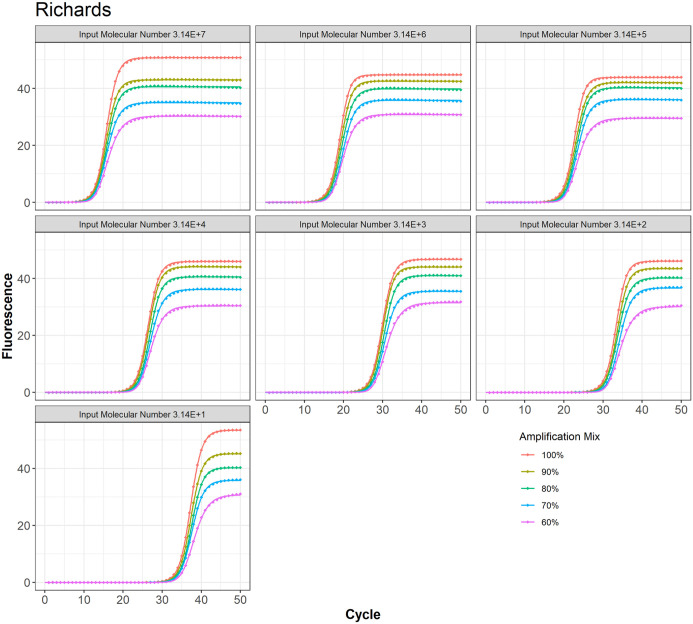
Figure 7.

Richard model fit to the PCR data at different amplification mix for all 7 input molecular numbers.

Figure 5.

Gompertz model fit to the PCR data at different amplification mix for all 7 input molecular numbers.

Figure 6.

Logistic model fit to the PCR data at different amplification mix for all 7 input molecular numbers

For each combination of fluorescence intensity and input molecular number, the cycle elasticities of fluorescence using the 3-parameter TWW method have been given in Table 4. For instance, for the molecular number 3.14E + 7 using amplification mix of 100%, the cycle elasticity evaluated at the point of inflection is 5.91%. This indicates that at the point of inflection, a 1% increase in cycle number would increase the fluorescence intensity by 5.91%. When the cycle threshold $C_{TWW}\mathrm{is}\mathrm{equal}\mathrm{to}13.0094,$ the elasticity is 7.71%, meaning that a 1% increase in cycle number would increase the fluorescence intensity by 7.71%. Figure 8 shows the graph of cycle elasticity of fluorescence for input molecular number of 3.14E + 7 and amplification mix of 100%.

Table 4.

Values of elasticities at the point of inflection and at cycle $C_{TWW}.$

$ElasticitiesforTWWmode$ at inflection point (%)
Molecular number Amplification mixed	3.14E + 7	3.14E + 6	3.14E + 5	3.14E + 4	3.14E + 3	3.14E + 2	3.14E + 1
100%	5.9142	7.7283	9.0920	9.8358	11.1669	13.0832	13.6460
90%	5.9920	7.5256	8.4833	10.0294	11.7794	12.9215	13.8733
80%	5.9356	7.2589	8.6739	10.1512	11.4720	12.3685	14.163
70%	5.6622	7.3165	8.5063	9.6916	11.0923	12.3508	13.7384
60%	5.2769	6.8838	7.9228	9.3639	10.0781	11.2238	12.3073
$ElasticitiesforTWWmodel$ at Cycle =  $C_{TWW}$ (%)
Molecular number Amplification mixed	3.14E + 7	3.14E + 6	3.14E + 5	3.14E + 4	3.14E + 3	3.14E + 2	3.14E + 1
100%	7.7099	10.5560	12.6957	13.8624	15.9508	18.9573	19.8403
90%	7.8320	10.2380	11.7405	14.1662	16.9117	18.7037	20.1969
80%	7.4334	9.8196	12.0396	14.3573	16.4295	17.8361	20.6514
70%	7.3145	9.9099	11.7766	13.6363	15.8353	17.8082	19.9852
60%	6.7099	9.2311	10.8612	13.1221	14.2427	16.0402	17.7401

Figure 8.

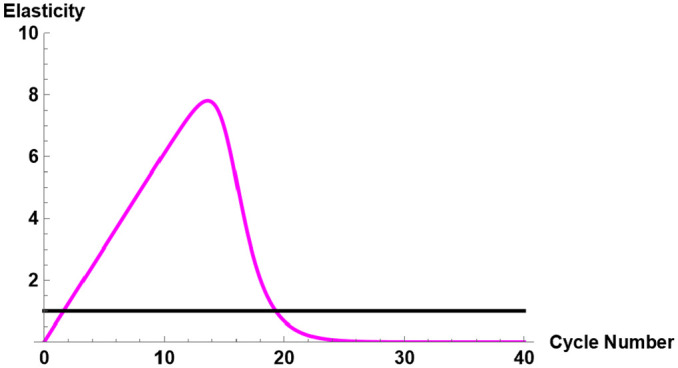
Cycle elasticity for molecular number 3.14E + 7 with amplification mix of 100%.

Table 5 shows the mean, SD, and 95% confidence interval for the fluorescence intensity for all 35 combinations of amplification mix and molecular number. The minimum value for the mean was 7.41, which belonged to 60% amplification mix and molecular number 3.14E + 1. The maximum was 35.32, which was associated with 100% amplification mix and molecular number 3.14 + 7.

Table 5.

Mean, standard deviation (SD), and 95% confidence interval (CI) for fluorescence.

Molecular number Amplification mixed	3.14E + 7	3.14E + 6	3.14E + 5	3.14E + 4	3.14E + 3	3.14E + 2	3.14E + 1
100%	35.32 (21.99) [29.07, 41.57]	28.28 (20.57) [22.44, 34.13]	24.53 (20.80) [18.62, 30.44]	22.20 (21.83) [16.00, 28.40]	19.24 (21.81) [13.04, 25.44]	15.90 (20.75) [10.00, 21.79]	14.16 (21.98) [7.91, 20.40]
90%	29.93 (18.63) [24.64, 35.23]	26.59 (19.59) [21.02, 32.15]	23.09 (19.86) [17.45, 28.74]	21.13 (20.96) [15.17, 27.09]	18.07 (20.62) [12.21, 23.93]	14.69 (19.44) [9.16, 20.21]	11.89 (18.56) [6.62, 17.17]
80%	28.05 (17.65) [23.03, 33.07]	24.62 (18.34) [19.40, 29.83]	21.87 (19.04) [16.45, 27.28]	19.17 (19.26) [13.69, 24.64]	16.47 (19.07) [11.05, 21.89]	13.36 (17.81) [8.30, 18.42]	10.44 (16.47) [5.76, 15.12]
70%	24.17 (15.17) [19.86, 28.48]	21.92 (16.53) [17.22, 26.61]	19.45 (17.05) [14.60, 24.30]	16.88 (17.09) [12.03, 21.74]	14.10 (16.42) [9.44, 18.77]	11.86 (16.11) [7.28, 16.44]	9.18 (14.55) [5.05, 13.32]
60%	20.63 (13.12) [16.90, 24.36]	18.80 (14.19) [14.77, 22.83]	15.75 (13.88) [11.81, 19.70]	14.06 (14.30) [10.00, 18.13]	12.11 (14.34) [8.04, 16.19]	9.51 (12.98) [5.82, 13.20]	7.41 (12.01) [4.00, 10.82]

In addition, a second set of publicly available qPCR data was analyzed using a 3-parameter TWW. ³⁸ The results are given as a supplemental material. The fluorescence readings used were constructed for K1/K2 amplification for the average of 5 runs at 6 molecular numbers ranging from 4.17E + 7 to 4.17E + 2.

Discussion

In this article, we introduced a new 3-, 4-, and 5-parameter TWW growth model and applied the 3-parameter TWW model to analyze the qPCR data. The performance of this new model was then compared with Gompertz, logistic, and Richard models regarding model fit, precision, and efficiency. One advantage of the TWW model, when compared with the Richard model, is the capability of its 3 parameters to adequately estimate parameters with high efficiency and accuracy. The fewer the number of parameters used, the easier convergence is when using nonlinear regression fit. If the 3-parameter TWW model does not adequately fit the data, then one can try using the 4- or 5-parameter TWW model. In the analysis of the qPCR data used in this article, the 3-parameter TWW model showed a very high level of precision and relative efficiency as well as model fit when compared to the other models. A reliable estimate of cycle threshold has an utmost importance in diagnostic testing for detection of diseases, especially when monitoring infectious diseases.

A lack of consensus exists on how best to perform, interpret, and validate qPCR experiments. The problem is exacerbated by a lack of sufficient experimental detail in many publications, which impedes a reader’s ability to evaluate critically the quality of the results presented or to repeat the experiments. Following these guidelines would result in better experimental practice, allowing more reliable and unequivocal interpretation of qPCR results.^39,40

To minimize the risk of errors and guarantee the reliability of laboratory results, quality control safeguards should be put in place. These measures may include regular tuning and upkeep of laboratory facilities, strict adherence to the laboratory standard protocol and procedures, and documentation of all processes. Following these measures will help reduce variability as well as increase precision, accuracy, and reliability. In addition, if the data quality control points toward the presence of outlier(s) or influential observation(s) in the data, one should not use the statistical method of least squares to estimate the model parameters. Instead, the usage of a robust nonlinear minimizer such as the method introduced by Tabatabai et al ⁴¹ should be used to estimate the model parameters.

Given the results shown herein, it may be feasible in a future study to use the $C_{TWW}$ model discussed as a predictor for accelerated qPCR when the method is performed primarily for the purpose of a molecular titration diagnostic that is either a qualitative or quantitative laboratory testing process. The reader may consider a case where trace RNA or DNA is to be detected subject to set limits on the number of thermal cycles. Table 4 results on elasticity may provide a guide for optimal stopping cycle determination and laboratory standardization.

When applied for the purpose of amplification of molecular constituents and subsequent processing, such as DNA and mRNA production in preparation of a molecular candidate for nucleotide sequencing, the results suggest a feasible calibration and predictive capability to reach maximum yield given initial and final PCR target conditions. The reader may consider a case where a whole genome is to be sequenced or multiple fragments of RNA are to be sequenced for viral pandemic tracking.

The close agreement of the results to the model also suggests a means of detecting signal and cycle losses when comparing to a calibrated qPCR system using the TWW growth model, such as when inhibitors are present in biological samples as mentioned by Guescini. ³⁵ A future work might include qPCR experiments for detection of various DNA/RNA of specific antigens of interest with controls.

Conclusions

We developed a family of 3-, 4-, and 5-parameter TWW growth models and compared the 3-parameter model with the classical models currently used in the analysis of qPCR. For the qPCR data that were analyzed in this article, we showed that the TWW model is a competitive model outperforming the Gompertz, logistic, and Richard models in model fit, precision, and relative efficiency and can be used as an alternative model in analyzing qPCR data. Supplementary R and Mathematica codes were included that would calculate the $C_{TWW}$ for the 3-parameter TWW model. An R package named “TWW” is publicly available to perform all necessary computations for 3-, 4-, and 5-parameter models and give their corresponding $C_{TWW}.$