Abstract
We compare ESA PROBA‐V observations of electron flux at LEO with those from the NASA Van Allen Probes mostly at MEO for October 2013. Dropouts are visible at all energy during four storms from both satellites. Equatorially trapped electron fluxes are higher than at LEO by 102 (<1 MeV) to 105 (>2.5 MeV). We observe a quite isotropic structure of the outer belt during quiet times, contrary to the inner belt, and pitch angle dependence of high energy injection. We find a very good overlap of the outer belt at MEO and LEO at ∼0.5 MeV. We use test‐particle simulations of the energetic electrons trapped in the terrestrial magnetic field to study the outer radiation belt electron flux changes during geomagnetic storms. We show that the Dst (Disturbance storm time) effect during the main phase of a geomagnetic storm results in a betatron mechanism causing outward radial drift and a deceleration of the electrons. This outward drift motion is energy independent, pitch angle‐dependent, and represents a significant distance (∼1 L‐shell at L = 5 for moderate storms). At fixed L‐shell, this causes a decay of the LEO precipitating flux (adiabatic outward motion), followed by a return to the normal state (adiabatic inward motion) during main and recovery phases. Dst effect, associated with magnetopause shadowing and radial diffusion can explain the main characteristics of outer radiation belt electron dropouts in October 2013. We also use Fokker‐Planck simulations with event‐driven diffusion coefficients at high temporal resolution, to distinguish instantaneous loss from the gradual scattering that depopulates the slot region and the outer belt after storms. Simulations reproduce the slot formation and the gradual loss in the outer belt. The typical energy dependence of these losses leads to the absence of scattering for relativistic and ultra‐relativistic electrons in the outer belt, oppositely to dropouts.
Keywords: energetic particles, geomagnetic storms, radiation belts, relativistic electrons
Key Points
Simulations reproduce effects of magnetic field modification on the motion of electrons during geomagnetic storms
The simulations help to understand the comparison of electron fluxes measured by EPT at LEO with those of MagEIS close to the equator
The data indicate that the dropouts are due to magnetopause shadowing while other flux variations are associated to waves
1. Introduction
In this study, we propose an analysis of a month period in October 2013 during which four geomagnetic storms occurred in the Earth’s magnetosphere. The electron flux in Van Allen’s radiation belts presented a wide range of variations during these storms and recovery times in between. The observations are originally provided from two different satellite sources: the NASA Van Allen Probes evolving at almost equatorial orbit (covering a Medium Earth Orbit [MEO] to geostationary GEO range) and the ESA PROBA‐V satellite evolving at Low Earth Orbit (LEO) orbit. The goal is to improve our understanding of the observed particle flux variations with respect to latitude.
The period of October 2013 is well‐known in the literature, particularly for two storms which occurred on October 2 and 8, both initiated by coronal mass ejection (CME)‐shocks impacting the magnetosphere (e.g. Hudson et al., 2015).
During the October 2, 2013 shock event, both parallel and perpendicular flux enhancements lasted more than 20 min with larger fluxes observed in the perpendicular direction (Yue et al., 2016). Yue et al. (2016) show that the initially enhanced cold plasma (<100 eV) energy flux triggered by the impact of interplanetary (IP) shock is the plasmaspheric population. The induced electric field as well as the compression of the magnetic field due to the impact of the IP shock cause rapidly accelerated low‐energy ions. Ferradas et al. (2018) studied the ion spectral structures observed of 1–50 keV ions throughout this storm, with an ion structure determined by the intensity of the convection electric field. They found the ion energy spread is limited by the presence of single noses or multiple noses spectral structures during the recovery times but by the absence of nose structure during the storm main phase. They used a model of ion drift and losses due to charge exchange to simulate the ion spectra and gain insight into the main observed features of the 1–50 keV ions for this storm. Su, Zhu, et al. (2014) reported an event of intense equatorial dusk side lower band chorus waves (with power spectral density up to 10−3 nT2 ∕Hz) observed by Van Allen Probes on October 2, 2013. During this event, the substorm injection caused several orders of magnitude enhancement in the suprathermal electron fluxes near the equatorial regions (λ < 15°) outside of L = 5. Su, Zhu, et al. (2014) computed the corresponding quasi‐linear bounce‐averaged diffusion coefficients of radiation belt energetic electrons using the STEERB code to explain the enhancements. This was done in the plasma trough for L > 5.5 and an electron plasma density between 1 and 10 #/cc. The recovery phase of the storm on October 3 is studied by Joshi et al. (2015) with observations from the Super Dual Auroral Radar Network (SuperDARN). These authors report that the neutrals drive the ion convection, with strong ion‐neutral coupling, consistent with the disturbance dynamo persisting well into the late recovery phase. The geomagnetic storm of October 2, 2013 has also caused a strong response of the ionosphere, with a large amount of energy deposition implying an ionospheric storm (e.g. Buonsanto, 1999) with dramatic changes in the polar upper atmosphere (e.g. Lu et al., 1995; Prölss, 1995). The nighttime ionospheric F2 layer was uplifted by more than 150 km during this storm (Lei et al., 2016; Ren & Lei, 2017). Ren and Lei (2017) made use of the Thermosphere Ionosphere Electrodynamics General Circulation Model (TIEGCM) to explore the possible responsible physical mechanisms and show that the motion can be attributed to the variations of vertical drift associated with zonal electric fields, with some effects found from the meridional winds and thermospheric expansion.
The observations of the shock‐induced acceleration of relativistic electrons during the storms of the October 8, 2013 are discussed in Foster et al. (2015). The solar wind shock produced an increase of the 3–4 MeV flux by two orders of magnitude successively observed by the two Van Allen Probes spacecraft. Characteristic drift echoes due to rapid radial transport in less than an electron drift period were observed through the bipolar azimuthal electric field impulse, which is a signature of solar wind shock compression of the dayside magnetopause (Foster et al., 2015; Hudson et al., 2015). Cervantes et al. (2020) carried a long‐term quasilinear computation with the full Fokker‐Planck VERB‐3D code (4 years from October 2012 to 2016) that includes our period of interest. This study and its results will be used later for qualitative comparisons (cf. Section 7). The CME‐shock‐driven storms of the October 8, 2013 have also been modeled with magnetohydrodynamic (MHD) test particle simulations, using local measurements of the inductive electric field by the Van Allen Probes located in the night sector (Hudson et al., 2015). The simulation uses the Lyon Fedder Mobarry‐Rice Convection Model (LFM‐RCM) (Pembroke et al., 2012) and follows 1.6 million electron test particles. An abrupt decrease in the outer boundary of outer zone electrons, that is, a magnetopause dropout, coincided with inward motion of the magnetopause for the October 8, 2013 storm. Hudson et al. (2015) found a complex role that ultra‐low frequency (ULF) waves play in radial transport during such events, including prompt acceleration and injection mechanisms. For the particular case of the October 8, 2013, these effects are favored by a preexisting energetic (multi‐MeV) outer zone electron source population, because of the presence of prior MeV electron enhancements associated with the previous storm on October 2. The fundamental role of the magnetic field topology found in Hudson et al. (2015) will be developed in our paper through the study of the Dst effect (cf. Sections 2 and 3). We note the wave system during the October 8 and 9 period was also complex. During the shock, Doppler‐shifted kinetic ULF Alfvén waves, with a broadband ULF spectrum up to approximately 100 Hz reported by Malaspina et al. (2015), suggesting that magnetospheric compression by IP shocks can induce wave‐particle interactions over large portions of the inner magnetosphere. The IP shock triggered a strong substorm (with maximum AE ≈ 1,400 nT), which simultaneously produced the disappearance of plasmaspheric hiss for about 5 h (Su et al., 2015) (further discussion is provided in Section 6). Yuan et al. (2019) found a typical case on October 9 where electromagnetic ion cyclotron (EMIC) waves and magnetosonic waves were modulated by the background plasma. They suggested that the plasma density structures would be favorable for simultaneous trapping of EMIC and magnetosonic waves (cf. Section 6 for a discussion on the plasmasphere and its filamentary structure in October 2013). A complex magnetic field structure has also been found by He et al. (2017), with magnetic dip event during the substorm on October 10, 2013, propagating from 15 to 19 magnetic local time (MLT) at L = 6 (He et al., 2017). The magnetic dip is suggested to be caused by ring current ion and to drift with the energetic ions. It can have an effect on trapped energetic electrons as a magnetic dip seems favorable to the formation of EMIC waves (from linear theory), which are indeed observed (He et al., 2017). Using calculated quasi‐linear diffusion coefficients for protons, these authors show that the observed EMIC waves can lead to the pitch angle scattering of ring current ions, which in turn partially relax the observed magnetic dip. Finally, on October 17, 2013, both the European Incoherent Scatter Radar (EISCAT) and a global positioning system (GPS) scintillation monitor observed an auroral E region ionization enhancement which occurred with associated phase scintillations. These auroral scintillations are discussed and modeled in three dimensions in Chartier et al. (2016) with the SIGMA scintillation model (Deshpande et al., 2014).
In our study, we focus especially on electron loss, especially on the two main kinds of processes that are observed in October 2013: sudden flux dropout as observed during geomagnetic storms and gradual electron loss in between storms. Flux dropout is a depletion of outer radiation belt electrons which can reach several orders of magnitude at the onset of most geomagnetic storms (e.g., Turner et al., 2012). The temporal magnetic field change, which occurs during geomagnetic storms, is usually studied using the Dst index, and that is why the terminology “Dst effect” was introduced by X. Li et al. (1997) to designate a physical effect of the variation of the magnetic field that causes particle motion. The Dst effect is thus a process by which the time‐varying magnetic field as well as its induced electric field affect the charged particle trajectory (Kim & Chan, 1997). The Dst effect falls in the category of betatron mechanism and of adiabatic effects. While the Dst effect is not the only physical process acting during a geomagnetic storm, it is an important process (e.g., Tu et al., 2009). In particular, when this process is associated to magnetopause shadowing, that is, a presence of the magnetopause in near‐Earth region where particles are trapped, this can cause sudden and intense loss, called dropouts. Information about drift loss to the magnetopause and outward radial diffusion are described in, for example, Shprits et al. (2006), Mann et al. (2016), and Ozeke et al. (2020). Adiabatic and magnetopause loss are reviewed in more detail by Turner and Ukhorskiy (2020).
The second type of significant loss observed in October 2013, though not reported in the aforementioned studies (with an exception for Cervantes et al. [2020]) is a gradual loss of electrons that occurred in the slot region as well as in the outer belt following the storm, during moderate to quiet times. This loss is due to pitch angle scattering as a consequence of plasma waves causing precipitation in the atmosphere (e.g., Summers & Thorne, 2003). Early computations of plasmaspheric loss were based on the integration of the Combined Release and Radiation Effects Satellite (CRRES) wave data in the pitch angle diffusion coefficients (e.g., Abel & Thorne, 1998a, 1998b, 1999; Kim et al., 2011; Meredith et al., 2009, 2007; Ripoll et al., 2014). Successive and recent tests and validations of the various Fokker‐Planck codes used to simulate gradual loss in the plasmasphere are based on the Van Allen Probes data (Mauk et al., 2013), which provides an extensive set of data of the wave environment, the plasma density, and the electron flux. Among the great variety of research studies, the ones relevant to gradual loss include the computation of nonstorm time and quiet dynamics of electron radiation belts with STEERB (e.g., Su, Xiao, et al., 2014), UCLA (e.g., Ma, Li, Thorne, Bortnik, et al., 2016; Ma, Li, Thorne, Ni, et al., 2015), and the CEVA (e.g., Ripoll et al., 2016, 2019) Fokker‐Planck codes as well as early storm recovery phases with the UCLA code (e.g., Ma, Li, Bortnik, et al., 2018; Ma, Li, Thorne, Nishimura, et al., 2016). Long periods of radiation belt dynamics have also been successful with DREAM 3‐D (Tu et al., 2013), VERB 3‐D (Cervantes et al., 2020; Drozdov et al., 2017), and the BAS code (Glauert et al., 2018). The mechanisms involved in intense losses of radiation belt electrons are reviewed in Ripoll, Claudepierre, et al. (2020), Ripoll, Denton, Hartley, et al. (2020), and Ripoll, Denton, Loridan, et al. (2020), and more information about modern computational tools and their applications can be found in Section 5 of the latter review.
To perform our analysis of the physical mechanisms that are active in the radiation belts, we use a full relativistic test‐particle code developed at BIRA‐IASB allowing us to simulate the trajectories of individual particles launched with different energies ranging from 1 eV like plasmaspheric particles to hundreds of MeV particles like radiation belt protons (e.g., Lemaire et al., 2005; Lemaire & Pierrard, 2008). With these simulations, we are able to analyze trajectories of test particles, as, for instance, the relativistic gyromotion spiraling around field lines or particles being lost, and related physical quantities, like the adiabatic invariants. This numerical code will be used for idealized and simplified storm conditions to illustrate how the Dst effect can contribute to temporally move outward MeV electrons by a large distance, thus, contributing to sudden magnetopause loss for the storms of October 2013 for which the magnetopause was pushed inward down to within the radiation belts.
To analyze the second type of loss observed in October 2013, that is, gradual loss, we use a different method and code. We perform dedicated quasi‐linear Fokker‐Planck simulations of pitch angle scattering by wave‐particle interactions (e.g., Ripoll et al., 2017, 2019). These simulations integrate all the main characteristics of the whistler‐mode waves (in the <2 kHz band) observed at a high temporal resolution in October 2013 by RBSP. We will show this way how to explain the observed energy structure of the loss at both MEO and LEO orbits and discuss how they differ from dropouts.
The article is organized as follows. Sections 2 and 3 are dedicated to the test particle method and simulations used for the data analysis. PROBA‐V and Van Allen Probes electron flux observations are presented and analyzed in October 2013 in Section 4. The modeled position of the magnetopause in October 2013 is presented in Section 5. Section 6 is dedicated to the observations of the plasmasphere and of whistler‐mode waves. Gradual plasmaspheric losses are computed in Section 7. Further discussions and limits of the study are gathered in Section 8.
2. Simulation Method for the Dynamics of Storm Times
2.1. Test‐Particle Simulations
The motion of particles in the terrestrial magnetic field can be decomposed into three superposed movements (Roederer, 1970):
-
‐
a gyromotion perpendicular to the magnetic field lines,
-
‐
a bounce motion along the magnetic field line corresponding to an oscillation between two mirror points located in each hemisphere, and
-
‐
a slower azimuthal drift of the guiding center path around the Earth to East for electrons and West for protons and other positively charged particles.
The code developed by Lemaire et al. (2005) simulates the motion of charged test particles trapped in the terrestrial magnetic field. Figure 1 (left) illustrates an example of such a simulation for 1 MeV protons.
Figure 1.
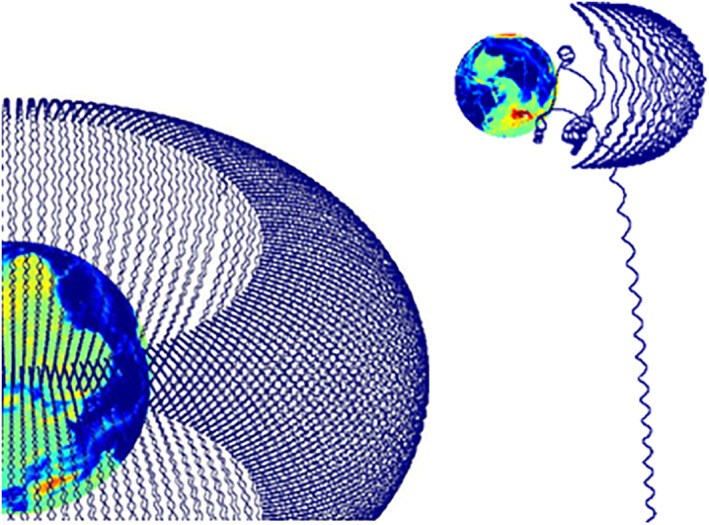
(Left) Simulation of the trajectory of a 1 MeV proton trapped in the magnetic field of the Earth. The motion can be decomposed in three superposed motions: gyration around the field line, oscillation between two mirror points in each hemisphere, and azimuthal drift. (Right) The trajectory of a particle that is lost when the magnetic field is disturbed during a geomagnetic storm.
The spiraling motion along the field lines is illustrated in Figure 1 for energetic protons because their higher mass leads to a much larger gyroradius than for electrons. Indeed, the radius ρ G of gyration perpendicular to the magnetic field is proportional to the mass m of the particles (Roederer, 1970):
It is also proportional to the perpendicular velocity, v ⊥ , of the particles, and inversely proportional to the electric charge, q, and the magnetic field intensity, B, leading, thus, to a larger radius in the equatorial plane than at higher latitudes closer to the Earth.
Three adiabatic invariants are associated with the three periodic movements, which are constant of motion as long as the temporal variations of external forces are slow compared with their respective periods of motion. The timescales associated with the adiabatic invariants are largely separated and depend on the particle energy and the magnetic field intensity at a particular location in the geomagnetic field. For instance, for a 1 MeV electron at a distance of 1.5 Earth radius (Re = 6,378 km), in the inner belt, the rotation periods corresponding to gyromotion, bouncing, and drift motion are of the order of 10−5 s, 10−1 s, and 45 min, respectively.
If the Earth’s magnetic field is completely static, the adiabatic invariants are conserved and the particle experiences an infinitely long trapping. However, the violation of one or more adiabatic invariants can lead to particle de‐trapping. Specifically, the violation of the first two invariants (associated with gyromotion and bouncing) is responsible for variations in particle energy and pitch‐angle (i.e., the angle between the velocity and the local magnetic field vector). The violation of the third adiabatic invariant (associated with the drift motion) leads to radial transport. Inward transport under the conservation of the first invariant causes particle acceleration. Since the timescale associated with the drift motion is the longest, the third adiabatic invariant is the easiest to be violated.
When the magnetic field is disturbed during a geomagnetic storm generated by a solar wind event, the particle can be lost, as illustrated in the right‐hand panel of Figure 1, or accelerated to higher energies. Test‐particle simulations allow us to determine how their trajectories are modified.
It is also possible to simulate low‐energy particles trapped in the magnetic field of the Earth, like those of the plasmasphere (typically 1 eV) (Lemaire & Pierrard, 2008; Pierrard & Lemaire, 2004). However, the low‐energy particles from the plasmasphere co‐rotate with Earth independently of their charge (electrons and protons in the same direction), so that they do not contribute to the ring current, which is due to the westward drift of protons and eastward drift of electrons. The drift motion of plasmaspheric particles is dominated by the electric field, contrary to the more energetic particles of the ring current and of the radiation belts for which the Lorentz force dominates.
2.2. Relativistic Gyromotion Test Particle Simulations
To calculate the trajectory of a relativistic test particle during a geomagnetic storm, we use the code fully described in Lemaire et al. (2005), where the generalized gyromotion equation is numerically solved using a Runge‐Kutta and Bulirsch‐Stoer method (Press et al., 1992). The differential equations for the acceleration vector components together with the differential equations for the velocity vector components form a 6D initial value problem. The initial conditions correspond to the launch of the electron.
In case of relativistic electrons (i.e., with E > 511 keV), the simulations take into account that their mass, m = γm0, depends on their speed, where γ is the Lorentz factor and m 0 is the rest mass. Usually, the gyromotion of electrons is calculated using a particle rest mass that is 20 m 0 for CPU reasons (Ukhorskiy & Sitnov, 2013), but in the present study, we use the actual rest mass of electrons. Instead of performing guiding center approximation simulations, we fully simulate the gyromotion and deduce from the trajectory of the electron the guiding center properties, such as the gyroradius, gyrofrequency, and first adiabatic invariant. With gyromotion simulations, we can investigate adiabatic behavior without assuming the guiding center approximation.
Full test‐particle simulations provide more information than simple guiding center approximation (Roederer & Zhang, 2014) since the gyration motion is also taken into account. This is particularly interesting for heavy particles such as protons, because their gyro‐resolved trajectory can be very far from the field line as the field is perturbed by the storm. The altitude of the mirror point, for instance, is not that of the guiding center, but it is rather the altitude of the spiraling particle, allowing us to explain the “East‐West effect” at low altitude when the density scale height is close to the gyration radius of the particles (Lemaire et al., 2005).
To study the adiabatic Dst effect of geomagnetic storms onto the outer radiation belt electron flux, and to quantify the contribution of the Dst effect to the observed electron dropout, we perform relativistic gyromotion test particle simulations using a modified dipole magnetic field described in the following section.
2.3. The Modified Dipole Magnetic Field Model
To simulate a geomagnetic storm, we use a time‐dependent modified dipole and its induced electric field. The modified dipole model is driven by a simulated Dst index, and is the Earth’s dipole magnetic vector field in 3D decreased by a uniform southward magnetic field whose magnitude is equal to the Dst index. This model was also used in studies of McIlwain (1996), Selesnick and Kanekal (2009), Lemaire et al. (2005), and Tu and Li (2011).
This analytic modified dipole field is well adapted to modeling adiabatic variations. More complex magnetic field models such as the TS04c magnetic field model (Tsyganenko & Sitnov, 2005) are not only dependent on Dst but also induce complex trajectories that are not necessarily due to the Dst effect, making it hard to separate the various involved processes.
The local magnetic field change in the outer radiation belt region and the simulated Dst change are the same, using this model. We present in the next section particle simulations during a synthetic Dst event with a Dst minimum of −60 nT.
3. Results of the Simulations: Ultra‐Relativistic Electrons in the Outer Radiation Belt During a Storm with Dst = −60 nT
3.1. Launching a 5 MeV Electron With a Pitch Angle of 90°
Figure 2 shows the trajectory of a 90° pitch angle electron which is launched with a relativistic kinetic energy of 5 MeV. Note that in Figure 2, we look from above Antarctica (South Pole) and the electron drifts azimuthally eastwards (i.e., clockwise in this figure). We show the electron gyromotion trajectory during a geomagnetic storm with a Dst minimum of −60 nT. This means that using our modified dipole magnetic field model, the magnetic field in the outer radiation belt region decreases by 60 nT. We analyze the full trajectory of the simulated electron motion to estimate the gyroradius and gyroperiod of the motion and unidimensional quantities of interest are presented in Figure 3.
Figure 2.
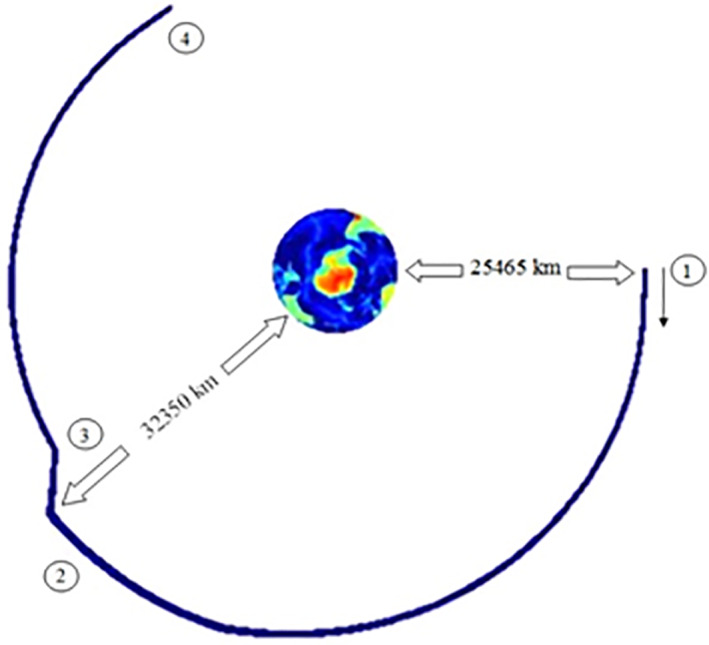
Trajectory of a 5 MeV electron with a pitch angle of 90° in the equatorial plane calculated with a relativistic gyromotion test particle simulation during a simulated geomagnetic storm reaching a minimum Dst of −60 nT and coming back to its initial altitude after the recovery phase.
Figure 3.
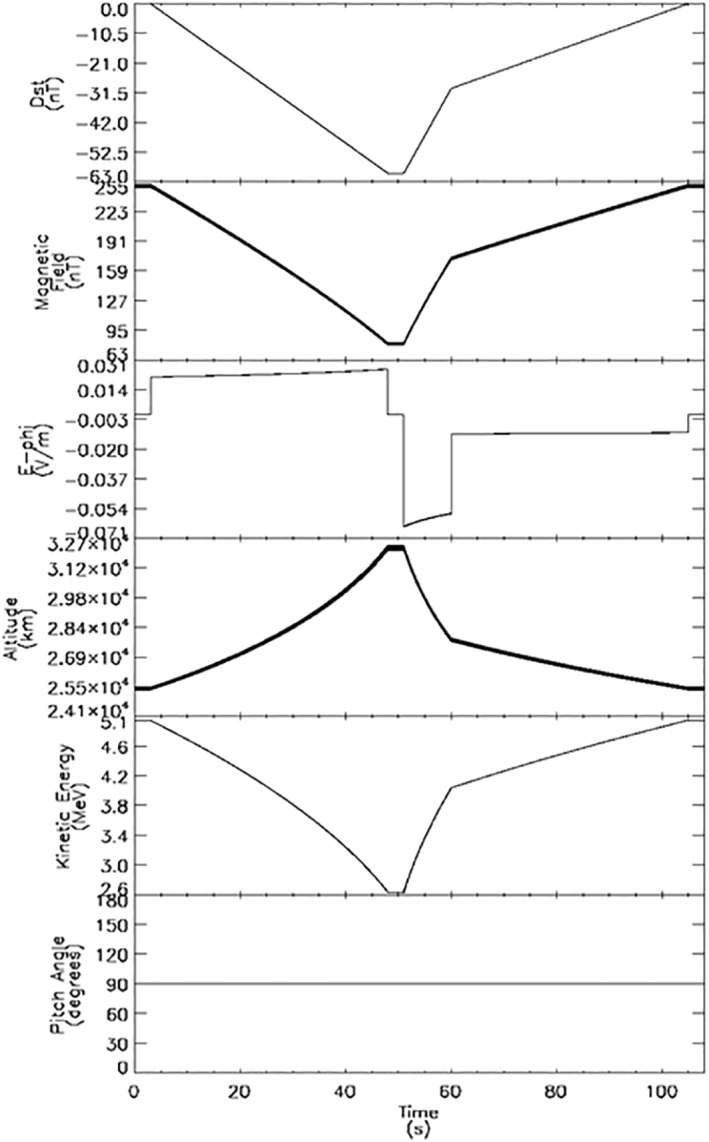
The simulated electron of Figure 2 with a pitch angle of 90°. From top to bottom: (a) the simulated Dst, (b) the magnetic field at the location of the electron, (c) the induced electric field, (d) the altitude of the electron shows the radial drift outwards during the main phase, and the radial drift inwards during the recovery phase, (e) the kinetic energy of the electron shows the deceleration during the main phase, and the acceleration during the recovery phase, (f) the instantaneous pitch angle of the electron.
The 5 MeV electron is launched at an altitude of about 25,465 km (L = 5 R e ) with a pitch angle of 90° at location (1). The magnetic field strength (at the guiding center) is about 254 nT (B1). We simulate a magnetic storm with a Dst minimum of −60 nT. The electron experiences a gradual weakening of the magnetic field strength during 50 s (Figures 3a and 3b). The Dst decrease causes the electron to drift radially outward up to an altitude of about 32,350 km (L = 6.08 Re) at location (2), about 1 L‐shell further away than the initial position. At location (2), the Dst minimum of −60 nT is reached, and the radially outward drifted electron has decelerated to 2.6 MeV (T2), half its initial energy. The magnetic field strength (at the guiding center) is about 84 nT (B2), a third of the initial magnetic field strength. The first two adiabatic invariants are conserved during the simulation.
After the main phase of the storm, a recovery phase is simulated with two steps: first a steep increase of the magnetic field followed by a return of the magnetic field to its initial state. The magnetic field increase causes the electron to accelerate and drift radially inwards, reaching location (3). When the simulated magnetic field is completely recovered, the electron is at location (4), and the adiabatic process is completely reversed, which means the electron is back located at 25,465 km (L = 5) with an energy of 5 MeV. Note that in the present example, the relatively fast (50 s) dynamics of the Dst perturbation could break the first and second adiabatic invariants if the magnetic field was not azimuthally symmetric and/or if the perturbation was not symmetric.
3.2. Outward Radial Drift of Electrons
The simulation shows that during the main phase, ultra‐relativistic outer radiation belt electrons drift radially outwards, away from the Earth. This transports the electron 1 L‐shell away for a moderate (−60 nT) storm, with some probability to cross the magnetopause position. Thus, test particles launched at a given distance from the Earth will move during the main phase of a geomagnetic storm to a higher altitude. On the contrary, during the recovery phase the electrons drift radially inwards, toward the Earth. Simulations performed for different energies show that the outward radial drift does not depend on the kinetic energy of the launched electrons, and neither does it depend on the equatorial pitch angle of the electron in the simulations using an azimuthally symmetric background field (dipole), and an azimuthally symmetric perturbation (constant Southward vector). This is confirmed by the simulations of Kim et al. (2010) who provided numerical estimates of drift loss and Dst effect for outer radiation belt relativistic electrons with arbitrary pitch angle.
The outward drift motion depends on the Dst minimum and on the launched particle’s L shell. Thus, the entire spectrum will drift away during the main phase of the storm from McIlwain shell L1 to L2. In a more complex magnetic field, like with the TS04 model, then the drift‐shells L* depend on the second invariant, K, and, therefore, on the pitch angle. The interest of this simplified simulation is to demonstrate a radial motion of ∼7,000 km (∼1 L) with (E,α) conserved after the Dst effect if the magnetic field geometry and its perturbation are not too asymmetric.
Note that if the particles drift up to the magnetopause, they will be lost. Magnetopause shadowing is the removal of the outer radiation belt electrons from the inner magnetosphere when the solar wind pushes the magnetopause closer to the Earth. When electrons drifting around the Earth encounter the magnetopause, their gyroradius becomes larger than the magnetopause thickness and consequently they escape the magnetosphere (e.g., Saito et al., 2010; Ukhorskiy et al., 2015). This has important implications for the position of the outer belt during storms (Matsamura et al., 2011). The simulations show that the electrons will radially drift outwards away from the Earth and toward the magnetopause, enhancing the dropout resulting from magnetopause shadowing.
3.3. Kinetic Energy Decrease During the Main Phase of the Storm
The simulations show that during the main phase of a geomagnetic storm, the electrons decelerate. This kinetic energy loss of the electron is due to the conservation of the first adiabatic invariant. Note that the magnetic field decreases by 60 nT, but the magnetic field that the electron experiences decreases from 254 nT (B1) to 84 nT (B2). The magnetic field decrease that the particle encounters is larger than the Dst change—about 2.5 times Dst—and this is caused by the outward radial drift of the electron. Conversely, during the recovery phase of a geomagnetic storm, the radial drift and the kinetic energy loss are reversed, with the electron moving closer to the Earth and accelerating.
In Figure 2, we show the trajectory of an electron during a time period that is less than one azimuthal drift period. Simulations can be performed over longer time periods, but we show only a segment to avoid the overplotting of the trajectory while the electron is drifting around the Earth several times. Within these conditions, the Dst effect is computed to be adiabatic and reversible, so only the initial and final situations are important.
3.4. Launching a 5 MeV Electron With a Pitch Angle of 28°
To make the link between what a satellite observes in the equatorial plane, such as the Van Allen Probes spacecraft, and a satellite located at higher latitude, such as PROBA‐V, we make the same simulation as in Figures 2 and 3 but for an electron with an equatorial pitch angle of 28°, at location (1). The electron is similarly launched at an altitude of 25,465 km (L = 5 RE) with an initial relativistic kinetic energy of 5 MeV (T1). The magnetic field strength at the guiding center is ∼250 nT (B1). Figures 4 and 5 present the results of a fully gyro‐resolved test particle simulation where the electron gyrates around the magnetic field lines. The apparently radially directed lines in Figure 4 correspond to the bounce motion of the electron. The electron experiences a weakening of the magnetic field strength. The Dst decrease to −60 nT causes the electron to drift radially outward up to an altitude of about 32,350 km (L = 6.08 Re) at location (2), similarly to the 90° electron.
Figure 4.
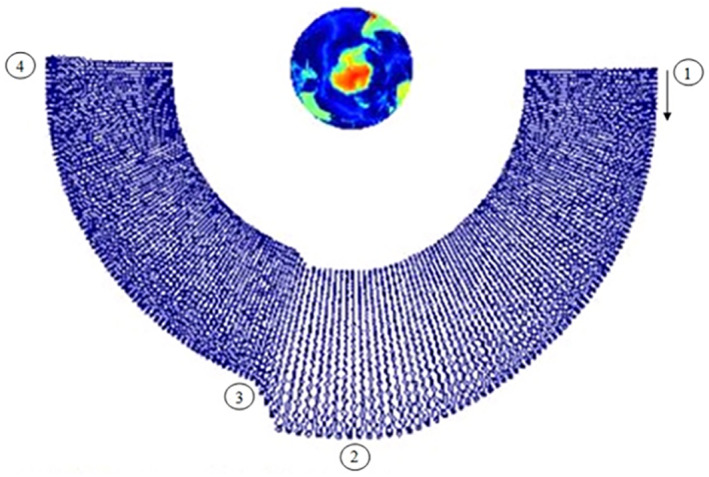
Trajectory of an electron with a pitch angle of 28° calculated with a relativistic gyromotion test particle simulation during a simulated geomagnetic storm with Dst = −60 nT. The perspective of this image shows that the electron is mirroring at higher latitude than in Figure 2. The change in L‐shell is visible looking at the external (internal) envelop that represents the drift trajectory at the equator (mirror point).
Figure 5.
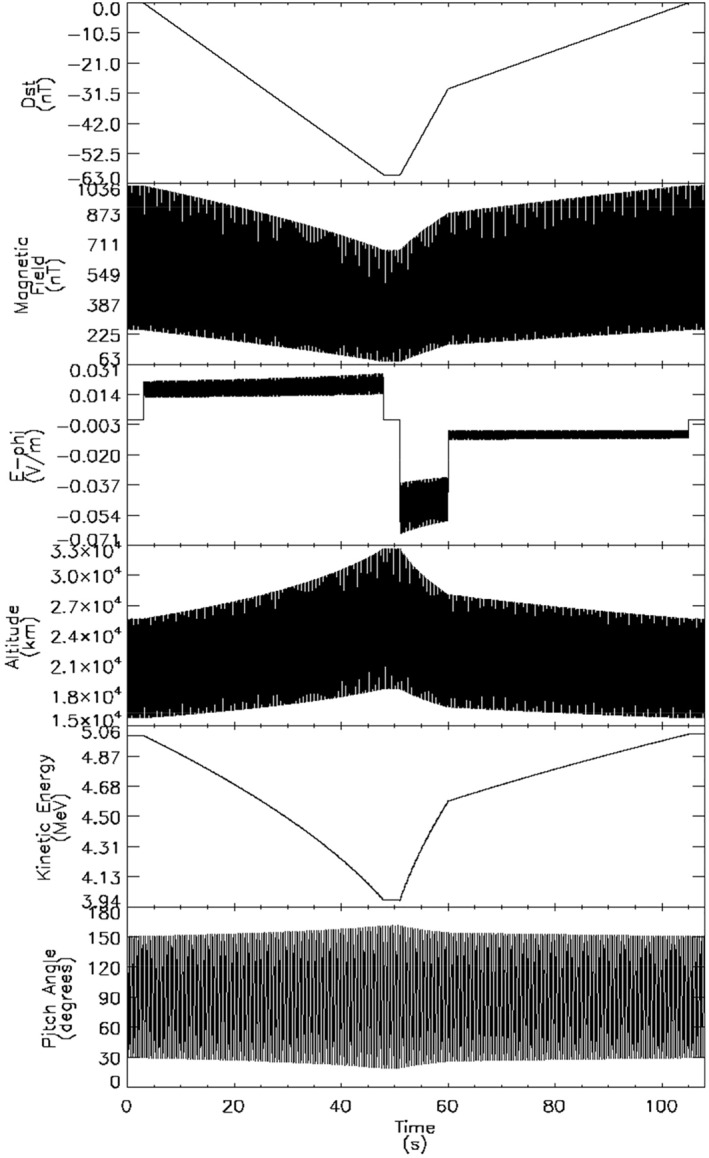
The simulated electron with a pitch angle of 28°. From top to bottom: (a) the simulated Dst, (b) the magnetic field at the location of the electron, (c) the induced electric field, (d) the altitude of the electron shows the uplift of the mirror point during the main phase, (e) the kinetic energy of the electron shows the deceleration during the main phase, (f) the instantaneous pitch angle of the electron shows that the equatorial pitch angle decreases during the main phase. The vertical lines correspond to the bounce motion of the electron.
At location (2) of the Dst minimum, the radially outward drifted electron has decelerated to 3.94 MeV (T2). The magnetic field strength (at the guiding center) is about 79 nT (B2). The relativistic first adiabatic invariant is again conserved during the simulation.
The main difference with the simulation in Figure 2 is that this electron has lost less kinetic energy, 20% of its initial energy (vs. 50% for a 90° pitch angle electron). During the recovery phase, the magnetic field increase causes the electron to accelerate and drift radially inwards, reaching location (3). When the simulated magnetic field is completely recovered, the electron is at location (4), and the adiabatic process is again completely reversed. As previously noted, the symmetry of the field and of the perturbation contribute to recover the same state.
The simulation shows that the altitude of the mirror points increases during the simulation of the main phase of the geomagnetic storm. But the change of the mirror point is only caused by the change in L‐shell of the electron, with conservation of first and second invariants. Assuming no scattering from any wave‐particle interactions, the Dst effect does not result in more losses to the atmosphere during the main phase. The relativistic electron gyromotion simulations show that the mirror points are uplifted to higher altitudes during the main phase, reducing momentarily the loss of electrons to the atmosphere at the lowest L‐shells, where the electrons are not present anymore. Atmospheric loss is shifted at higher L‐shell where the electrons have been temporally transported by the storm main phase. Dropouts are then the consequence of the outward drift motion combined with magnetopause shadowing. Conversely, after the storm and during the recovery, the position of the mirror points of the particles decreases following the particles drifting inward. Losses due to atmospheric interactions increase again at the fixed lowest L‐shell, which the electrons are populating again. Therefore, at fixed L‐shell, one can observe first a decay of the precipitating flux at LEO, followed by a return to the normal state, which is due to the temporal motion outward, then, inward, of the particles during the storm main and recovery phases. These changes in flux will be shown in the LEO observations in the next section.
While the distance of the radial drift outwards does not depend on the initial equatorial pitch angle of the launched particle in these simulations with azimuthally symmetric background magnetic field and perturbation, the kinetic energy loss does depend on the initial equatorial pitch angle. Electrons mirroring at mid‐latitudes will decelerate less than equatorial mirroring particles. If this occurs in the presence of wave‐particle interactions, which are themselves energy and pitch angle dependent, this can change the electron spectrum in a complex manner. More realistic azimuthally asymmetric fields, either for the background or the perturbation, would not conserve both energy and pitch angle. This might result in butterfly pitch angle distributions during dropouts (e.g., Albert et al., 2016).
4. Comparison With Storm Observations in the Radiation Belts
4.1. LEO Observations
The ESA satellite PROBA‐V provides observations on an LEO polar orbit at an altitude of 820 km. The inclination is 98.73°, the orbital rotation period has a duration of 101.21 min and 10:30 a.m. is the nominal local time at the descending node (Pierrard et al., 2014). The Energetic Particle Telescope (EPT) is a detector developed to measure the electron differential fluxes in seven virtual channels for E > 500 keV (Cyamukungu et al., 2014). It was launched on board PROBA‐V on May 7, 2013.
Figure 6 shows the electron fluxes observed by EPT for the month of October 2013, during which 4 moderate storms with −45 nT > Dst > −68 nT are observed on October 2, 9, 15, and 30, 2013. Dropouts, corresponding to flux depletions at L > 4 (Pierrard et al., 2020), are clearly visible at all energy ranges during all these storms. These dropouts can be understood by the outward motion associated with the Dst event, as explained by the simulations. After the dropout, the flux is generally different from what was observed before the storm, indicating non‐adiabatic behavior such as loss at the magnetopause. The refilling is progressive and depends on Dst and on L, starting from low L‐shell and progressing to higher L‐shells. For the strongest storms, the flux enhancement penetrates a low L in the slot region.
Figure 6.
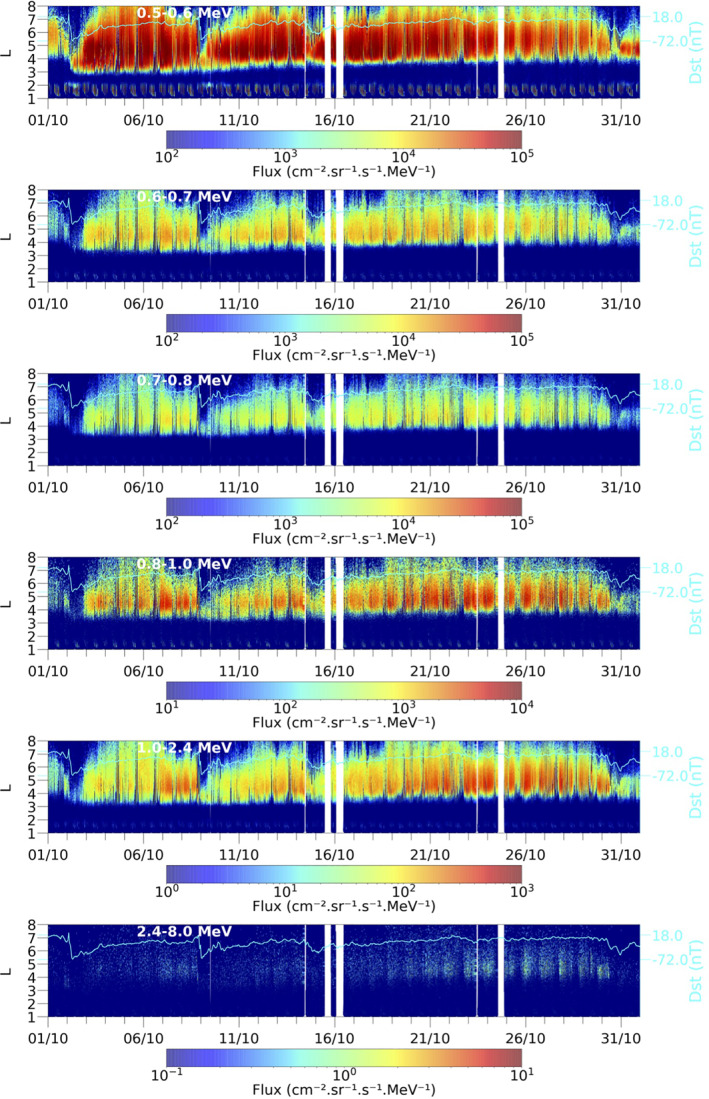
Electron fluxes observed by EPT from September 30, 2013 up to November 2, 2013, as a function of the McIlwain parameter L (vertical axis) and time (horizontal axis) for each energy channel, from top to bottom: channel 1 (500–600 keV), channel 2 (600–700 keV), channel 3 (700–800 keV), channel 4 (800–1,000 keV), channel 5 (1,200–2,400 keV), and channel 6 (2,400–8,000 keV). The observed Dst (Disturbed Storm Time) index is superposed in each panel (right scale). EPT, energetic particle telescope.
While a dropout appears for all Dst events, flux increase in the slot region is only observed for the storm of October 2, 2013, during this 1‐month period, especially visible in Ch 1 (upper panel of Figure 6). The inner edge of the outer belt is then located closer to the Earth after the storm. We can note also during this month that the slot region becomes broader with time after the injection in the slot, giving to the inner edge of the outer belt a slow outward radial motion due to the erosion of the inner edge electrons by loss from wave‐particle interactions. This erosion of the particles at the inner edge of the outer belt after the storm is especially visible at 0.5–0.6 MeV (Ch 1) and goes from L = 3 to around L = 3.8 after 1 month for Ch 1. We will come back on this physical aspect that will be simulated in Sections 6 and 7.
The omnidirectional electron flux measured at low altitude is always lower than the omnidirectional flux at the equator, since, as illustrated in Figure 4, the loss cone angle increases as you go up in latitude. Electrons with a pitch angle close to 90° mirror close to the magnetic equator and never reach low altitudes. If their pitch angle is on the contrary close to 0°, the mirror points are located at altitudes lower than 100 km and the particles are lost in the atmosphere. This altitude defines the loss cone, that is, the minimum pitch angle at which the particles are lost in the atmosphere. At the equator, the electron flux at 90° can be an order of magnitude higher than that near the loss cone, depending on the level of scattering by wave‐particle interactions. Low altitude measurements can drastically be lower than the electron flux in MEO, as we will show in the next section, and direct cross‐correlation between the observations at different latitudes can inform us on the physical mechanisms implicated in the radiation belts.
4.2. Van Allen Probes Observations
The NASA Van Allen Probes mission, formerly called RBSP (Radiation Belt Storm Probes A and B) (Mauk et al., 2013) was launched in 2012 and operated simultaneously with EPT from 2013 to 2019, enabling unprecedented studies of the electron radiation belt variability in response to solar activity. RBSP flew on a low inclination (<20°) elliptical orbit ranging from 600 to 30,600 km. We make use of energetic electron measurements from the MagEIS (Magnetic Electron Ion Spectrometer) instrument observed electrons in the energy range from 30 keV to 4 MeV (Blake et al., 2013). MagEIS is part of the Energetic particle Composition and Thermal plasma suite (ECT) instrument (Spence et al., 2013).
4.2.1. L2 Spin‐Averaged Flux Observations at the Equator
Observations of the L2 spin‐averaged flux measured by MagEIS on board Probe B of the Van Allen Probes are presented in Figure 7 for energy channels that are comparable with the EPT channels at LEO shown in Figure 6. These measurements are made within ±20° of the magnetic equator and are background corrected (Claudepierre et al., 2015). Spin‐averaged fluxes have been shown to accurately represent the omnidirectional flux (Ripoll et al., 2019). The four storms on October 2, 9, 15, and 30 are well associated with the minimum Dst. Dropouts are clearly seen on October 2, 9, and 30 at all energies. On October 15, the dropout is brief enough that either it does not remove all drifting electrons or that incoming new electrons already generate a low flux. Equatorial trapped electron fluxes are higher than at LEO as introduced previously. Below 1 MeV, maximal fluxes differ by ∼2 orders of magnitude. However, the EPT ultra‐relativistic flux (>2.4 MeV) is much lower than the RBSP flux at 2.33 MeV, with 4–5 orders of magnitude of difference between the two spacecraft, as already mentioned in Pierrard et al. (2019). Each of these fluxes are respectively consistent with previous observations such as Pierrard and Lopez Rosson (2016) for EPT and Kanekal et al. (2016) for high‐energy observations from the Relativistic Electron Proton Telescope (REPT) instrument (Baker et al., 2012). From October 1 to 31, the outer belt inner boundary is eroded from L ∼ 3 to L ∼ 4.5, following the gradual removal of slot electrons. This seems slightly further away than what is observed at LEO, for which the outer belt inner boundary moves from L ∼ 3 to L ∼ 4. This requires closer inspection of pitch angle dependent flux, as is done next, for explaining such differences.
Figure 7.
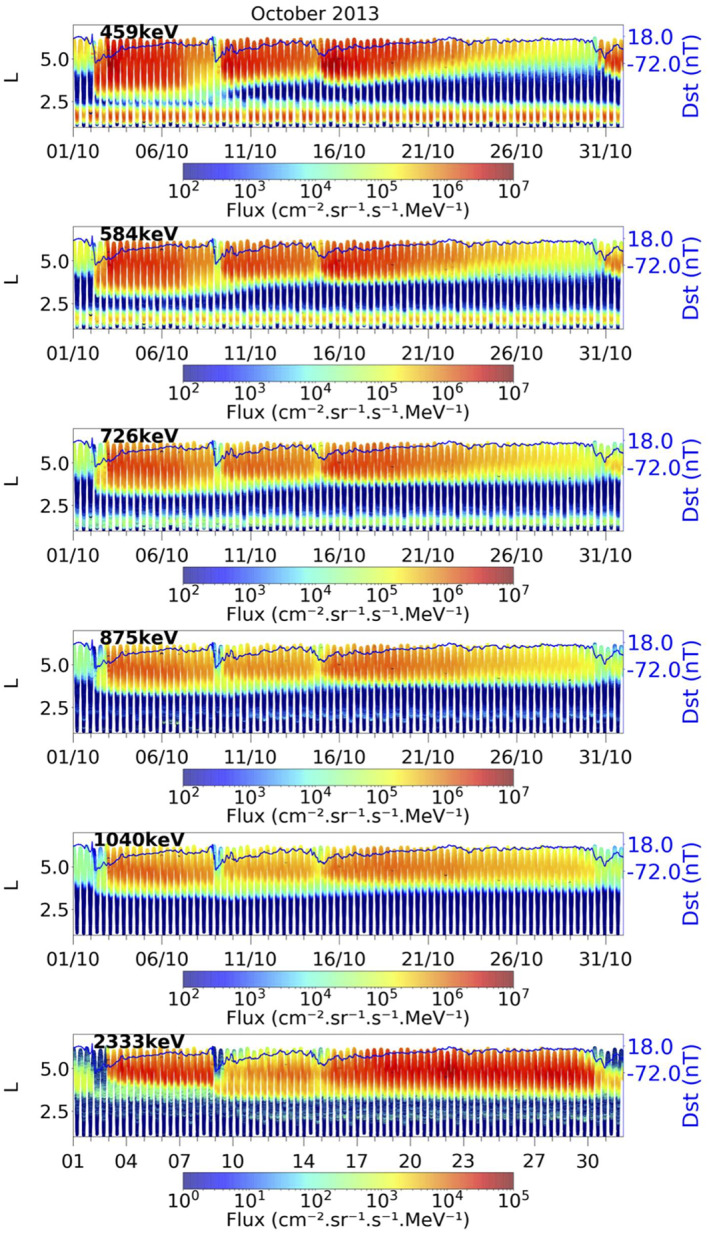
RBSP‐B/MagEIS L2 electron spin‐averaged flux in October 2013 at (from top to bottom) 459, 584, 726, 875, 1,040, and 2,333 keV plotted versus McIlwain L‐shell evaluated for a 90° pitch angle. The Dst index is superposed (blue line).
4.2.2. L3 Pitch Angle Dependent Flux at the Equator
Observations of the flux measured by MagEIS on board Probe B of the Van Allen Probes are presented in Figure 8 versus L* at 24, 41, and 90° pitch angle where L* is the Roederer parameter also evaluated for 24°, 41°, and 90° pitch angle (see Roederer and Lejosne (2018) for a review on the differences with the McIlwain parameter L). Figure 8 shows the flux intensification as pitch angle increases at all times. We do not see any change in the inner boundary of the outer belt as pitch angle changes. This is in agreement with Ripoll et al. (2019) who found the outer belt for quiet times is rather isotropic, with variation in flux of less than ∼×2 with respect to pitch angle. Conversely, the inner belt consists mostly of high pitch angle electrons (Ripoll et al., 2019).
Figure 8.
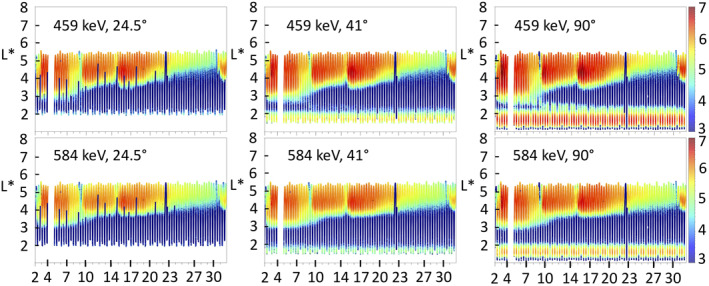
RBSP‐B/MagEIS L3 electron flux in cm−2 sr−1 s−1 MeV−1 in October 2013 at (left) low (24.5°), (center) intermediate (40°), and (right) high (90°) pitch angle plotted against L* itself computed at the corresponding pitch angle. The color bar is in log10 scale.
Figure 9 shows the same L3 flux but plotted now versus the McIlwain L‐shell evaluated at 90° to show how the L‐shell computation method influences the results as well as to be more directly comparable with EPT observations. We see the maximum McIlwain L reaches ∼6, which is larger than the maximum L*, which reaches ∼5, keeping in mind both values represent the same physical location. The outer belt inner edge being the same for both L and L*, this gives an outer belt spread over ∼3 McIlwain L‐shell or, equivalently, ∼2 L* on October 1. The inner boundary of the outer belt does not change as pitch angle changes and pitch angle isotropy of the outer belt is confirmed. Both Figures 8 and 9 also show an injection that penetrates the inner belt on October 2. This injection is observed in the 459 keV energy channel but is absent in the next RBSP energy channel centered at 584 keV, which suggests that the injection is limited to below ∼500 keV. In comparison, the energy of common substorm electron injections is ∼250 keV (Turner et al., 2012). At LEO, the 0.5–0.6 MeV EPT channel does not (and cannot) observe this injection. Interestingly, this injection is also limited to high pitch angle, being well marked for 90° electrons and with some particle traces barely visible for 41° electrons and only a few points for 25° electrons.
Figure 9.
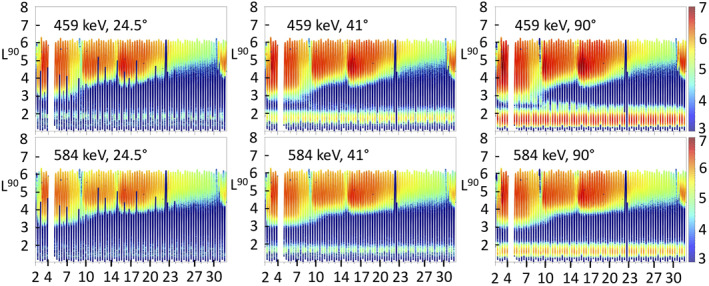
RBSP‐B/MagEIS L3 electron flux in cm−2 sr−1 s−1 MeV−1 in October 2013 at (left) low (24.5°), (center) intermediate (40°), and (right) high (90°) pitch angle plotted against L McIlwain computed at 90°. The color bar is in log10 scale.
4.3. Comparing EPT With Low Pitch Angle RBSP Flux
Figure 10 shows the RBSP‐B/MagEIS L3 electron flux in October 2013 at low pitch angle (24.5°) using L* (left panel) compared with EPT Ch 1 using the same format (right panel). Using L* at 25° for RBSP, we obtain a very good overlap of the outer belt observed at LEO by EPT and in the equatorial plane by RBSP at low pitch angle. The EPT flux is much lower than the RBSP flux. One reason is that 24° is already likely too high in pitch angle to reach PROBA‐V and match the EPT flux. It could also be that the MagEIS aperture and time integration window will accept larger pitch‐angles where the flux is larger. The energy range is also lower for RBSP, leading thus also to higher fluxes. Inter‐calibration would also help to improve the absolute value of the observed fluxes and will be undertaken in the next study. Changing L* by L_90 (McIlwain, 1966; Roederer & Lejosne, 2018) affects the upper limit of the outer belt by ∼1 L in spreading the outer belt to higher L‐shells, but does not change the lower limit.
Figure 10.
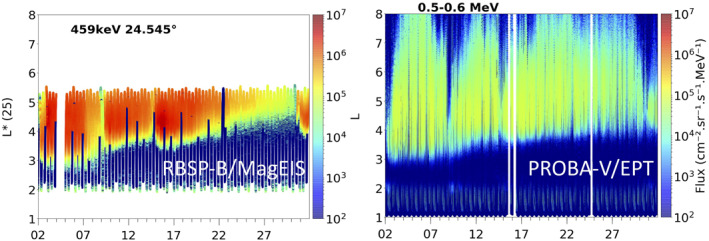
RBSP‐B/MagEIS L3 electron flux in October 2013 at low (24.5°) using L* (left panel) compared with EPT Ch 1 using the same format (right panel).
5. Magnetopause Position
The Shue et al. (1997) magnetopause standoff model is a straightforward function of the solar wind. Figure 11 (upper panel, magenta solid line) represents the magnetopause evaluated by Equation 12 in Shue et al. (1997), using Interplanetary Magnetic Field (IMF) Bz and dynamic pressure with a 5‐min sampling period. One can see that the main dropouts on October 4 and 9 observed by EPT (here for Ch 5) can directly be associated to the magnetopause shadowing. The closest positions of the magnetopause correspond to the inverted peaks of Dst and to the dropouts. Nevertheless, the modeled magnetopause is further away from Earth than the lowest L‐shell of the dropout. For the first event (October 2), the magnetopause penetrates deeper, down to L ∼ 5, but the dropout observed by EPT goes down to L ∼ 4. This could be due to the outward motion of the particles that can cause electrons to diffuse and be lost from lower L values. Note also that dropouts often start before the Dst decrease and before the lowest position of the magnetopause. This is for instance visible for the event of October 2, 2013 (see blue line in Figure 11 for the Dst index).
Figure 11.
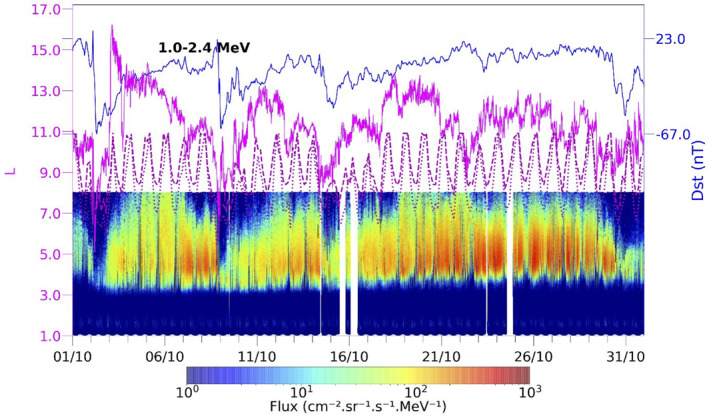
Electron fluxes observed by EPT in October 2013 in Ch 5 (1–2.4 MeV). The magnetopause position is superposed on the upper panel (magenta solid line), as well as the last closed drift shell (LCDS) for October 2013 for K ∼ 0 (magenta dotted line) and the largest K that mirrors above 100 km everywhere around the orbit (magenta dashed line). The Dst index is also superposed (upper blue line).
Figure 11 also illustrates the last closed drift shell (LCDS) as a function of time for equatorially mirroring electrons K ∼ 0 (magenta dotted line) and the largest K that mirrors above 100 km everywhere around the orbit (magenta dashed line). The LCDS is calculated with 3‐h resolution in UT, centered at the middle of the 3‐h bins. The drift shells are resampled with a resolution of 0.1 in L* to find the largest L* at a given K. The difference in the LCDS between the small and large K is about 1 Re during active times, with a higher LCDS for the larger K. The lowest value of the LCDS appears L* = 5.3 during the second storm for K ∼ 0. It reaches L* = 6 during the other storms while it is above L* = 7 during the quiet periods, in good agreement with the observed outer edge of the outer belt.
The LCDS is calculated using the Tsyganenko (1989) (T89) magnetic field model. The method used to calculate the LCDS is to compute all possible closed drift shells using the numerical discretization method in Cunningham (2016), and select the one at K ∼ 0 that has the largest value of L*. The LCDS is larger for larger values of K (smaller pitch angle). We include field lines in the drift‐shell construction for which there is more than one minimum along the field line, but only if the mirror‐point magnetic field strength for the drift shell exceeds the field strength at all other points along that field line. The diurnal variation in the LCDS is due to the variation in the angle of the dipole field with respect to the sun‐Earth line, which, along with the value of Kp, defines the closed drift shells for T89. The diurnal variation in the LCDS would not repeat exactly for each day even if Kp were fixed (which is not the case here). This is because we compute the LCDS with the same eight samples in UT each day, but Earth’s rotation around the Sun changes the UT at which a given orientation of the dipole with respect to the Sun‐Earth line is reached by a few minutes each day. Note that Cunningham (2016) has shown that radial diffusion coefficients computed in the T89 background field can be substantially larger than those computed using the dipole field as the background during active times. This would further contribute to loss from outward radial diffusion during active times.
The magnetopause position can thus directly be related to dropout events. Slower decay decreasing the flux after storms seems more related to waves, and thus to the density of the plasmaspheric background plasma, as we explain in the following sections.
6. On the Role of the Plasmasphere and Plasmaspheric Waves
Figure 12 (left) illustrates the October 2013 plasma density that is directly derived from the upper hybrid resonance frequency (Kurth et al., 2015) measured by the Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) (Kletzing et al., 2013) onboard the Van Allen Probes spacecraft. When EMFISIS density is unavailable, the density is derived from spacecraft floating potential data, which has been calibrated against previous plasma densities determined from the upper hybrid resonance frequency (Thaller et al., 2015). Spacecraft floating potential is measured by the Electric Fields and Waves (EFWs) instrument (Wygant et al., 2013). Here, Probe B is used and density values are averaged by bins of 8 h. The plasmapause location (Figure 12, right) is then defined from the first minimum L‐shell at which the density drops below the 100 cm−3 level within a 4‐h temporal bin (see also Ripoll, Denton, Hartley et al., 2020; Ripoll, Denton, Loridan et al., 2020).
Figure 12.
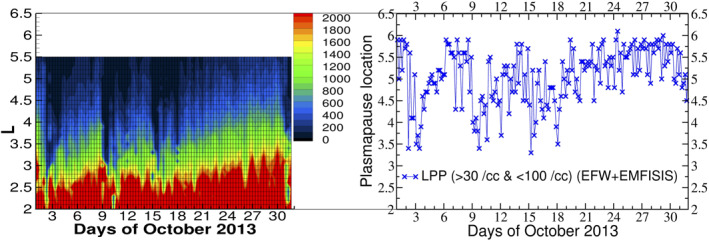
Plasma density (left) and the plasmapause position (right) observed in October 2013.
The plasma density in Figure 12 (left) shows the compression of the plasmasphere on October 2, 9, 15, and 31 associated with the small storms discussed previously. Accurate observations of the plasmasphere are essential to determine what type of waves can contribute to the observed gradual loss. During these storms, the plasmapause in Figure 12 (right) is eroded down to L ∼ 3.5. The plasmasphere recovers then rapidly in 1–2 days after these small storms and extends up back to L ∼ 5.5. This configuration is ideal for the development of plasmaspheric waves.
Plasmaspheric waves such as whistler mode hiss waves are widely present throughout the plasmasphere (e.g., Hartley et al., 2018; Malaspina et al., 2017). Figure 13 (left) shows the characteristic magnetic field amplitudes of whistler‐mode waves obtained using the trace of the magnetic‐field power‐spectral matrix calculated onboard Van Allen Probe A from 3D measurements of the EMFISIS search coil antennas. The data were further processed into the Level 4 WNA data set (Kletzing et al., 2013) which serves as a basis for our analysis. We make sure that the waves propagate in the whistler mode and we select right‐hand polarized waves with ellipticity above 0.2 (Santolik et al., 2002). We restrict the analysis to a frequency range typical for plasmaspheric hiss from 50 Hz to 2 kHz (e.g., W. Li et al., 2013; Santolik et al., 2001; Thorne et al., 1973). The total power spectral density is therefore integrated over this frequency band and rescaled with the MLT dependence of plasmaspheric hiss (Spasojevic et al., 2015) to obtain, based on local measurements, the drift‐average power of hiss in all MLT sectors of October 2013. We then accumulate the power in the bins of 8 h UT and 0.1 L and show it as the rms amplitude in Figure 13. During the storm main phase, hiss wave power is concentrated within the compressed plasmasphere. This causes loss from pitch angle diffusion at low L‐shells, between L = 2 and L = 3.5 during the first 12–24 h of the small storms on October 2, 9, and 15. Conversely, during quiet times, hiss wave power is more spread over the plasmasphere and extends up to L ∼ 5.5. Both plasmasphere density and hiss wave power are strongly coupled together (Malaspina et al., 2018). As Figure 13 is not limited to the plasmasphere only, the ∼1,000–2,000 kHz band can also contain some contribution from the lowest frequency part of whistler‐mode chorus or exohiss waves (Santolik, Macúsová, et al., 2014). We note that the 8 h binning resolution does not allow to represent the sudden disappearance of hiss waves during 5 h on October 8, 2013, as reported by Su et al. (2015). However, there is a low to mild whistler wave activity before the 8 October 2013 storm in Figure 13 (left), which may be favorable to the full disappearance of hiss waves reported by Su et al. (2015).
Figure 13.
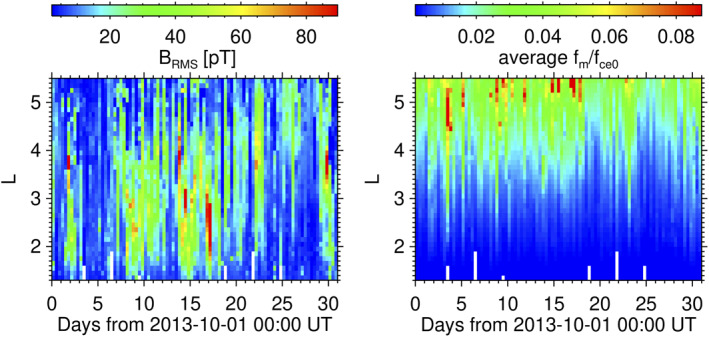
Left: Characteristic magnetic field amplitude of whistler‐mode waves (in pT) derived from measurements of Van Allen Probes A in the 50–2,000 hertz band for October 2013. Right: logarithmic mean frequency of the whistler‐mode wave normalized by the electron gyrofrequency at the equator. Values ∼0.1 (e.g. on the 4th and 17th) show the 1–2 kHz band of chorus/exohiss waves.
Figure 13 (right) shows the bin averaged quantity f m /f ce0, with the logarithmic mean frequency, f m , and the electron gyrofrequency at the equator, f ce0. The logarithmic mean frequency is obtained from the measured magnetic power spectral densities assuming their log‐normal model as a function of frequency. f m /f ce0 < ∼0.1 likely represents hiss waves and f m /f ce0 > ∼0.1 outside the plasmasphere can be considered as the lower frequency part of chorus or exohiss waves with an increased ratio f m /f ce0. Figure 13 (right) shows a very limited region (e.g., on the 4th and 17th) of these waves in the analyzed frequency range. Although chorus is known for its complex time‐frequency structure (Santolik, Kletzing, et al., 2014) resulting from nonlinear interactions, the quasilinear model of diffusion coefficients is based on averaged parameters of the whistler‐mode waves. The possible presence of low‐frequency chorus (W. Li et al., 2013; Meredith et al., 2014; Su, Zhu, et al., 2014; Xiao et al., 2017) thus do not contaminate this analysis.
The expansion of the slot region, from L = 3 on October 1 up to L ∼ 4 on October 31, due to a gradual removal of slot electrons, as well as the gradual depletion of outer belt electrons in the plasmasphere, will be both explained by wave‐particle interactions with whistler‐mode hiss waves in the next section.
7. Explaining Gradual Loss Based on Fokker‐Planck Simulations
In this section, we investigate the role of wave‐particle interactions to produce the gradual scattering occurring daily in the slot and in the outer belt. To do this, event‐driven pitch angle diffusion coefficients, D α0α0, are computed from the properties of whistler‐mode hiss waves including wave amplitude (Figure 13, left), mean frequency, mean frequency width, mean wave normal angle, mean wave‐normal‐angle width as well as plasma density (Figure 12, left). Diffusion coefficients are computed with the CEVA code originally developed by Réveillé et al. (2001). Verifications by comparisons with diffusion coefficients computed with the codes from the US AFRL and BAS (e.g., Albert, 1994, 2008; Meredith et al., 2007) have been performed in Ripoll and Mourenas (2012). Validation studies include Ripoll et al. (2016, 2017, 2019), Ripoll, Denton, Hartley et al. (2020), Ripoll, Denton, Loridan et al. (2020), and Loridan et al. (2019).
Event‐driven pitch angle diffusion coefficients are computed with an 8‐h time resolution as previously discussed. This is done for two time periods (October 3–9 and October 16–25) outside of the 2 October 2 and 9, 2013 main storms. Each period has a storm injection occurring the previous day (on October 2 and 15) and is composed of a short recovery period. This type of simulation conserves the coupling between the plasma density and the whistler‐mode wave properties, as both became available with the Van Allen Probe mission (e.g., Ripoll et al., 2019; Thorne et al., 2013; Tu et al., 2014). Computations are carried out for 39 L‐shells between L = 2 and L = 5.5, 60 energies between 50 keV and 64 MeV, and 256 pitch angles, following the method of Ripoll et al. (2017, 2019). This generates a set of 30.5 million of bounce‐averaged diffusion coefficients, D α0α0 (t, L, E, α0). Diffusion coefficients are then averaged over time for each of the two periods, L‐shell, and energy and shown for four selected L‐shells in Figure 13 (1–2 columns).
The pitch angle diffusion equation is then solved with respect to pitch angle for all fixed (L, E) (2,340 simulations) using the mean event‐driven diffusion coefficients for the two time periods (similarly to Ripoll, Denton, Hartley et al., 2020). Each of the 2,340 simulations is started with an omnidirectional distribution f = 1 at t = 0 (on October 3 and 16). Each distribution function (PSD) solution of this equation is then integrated over all pitch angles to produce an omnidirectional PSD at a single L and energy. The full solution is then assembled for all (L, E) and plotted in Figure 14 (right). Figure 14 (right) shows that relativistic electrons (∼1 MeV) are unaffected by the scattering from wave‐particle interactions with whistler‐mode hiss waves in the outer belt (already above L ∼ 3.5). Interactions with ultra‐relativistic electrons (>2 MeV) can only occur below L = 3 and at a very low scattering rate. This process cannot thus compete with the Dst effect and magnetopause shadowing computed for 5 MeV electrons in Section 3 and previously discussed. Conversely, 500 keV electrons have the highest scattering rate for L‐shells between 3.5 and 4, which corresponds well to the inner boundary of the outer belt we observe in Figures 7, 8, 9. Hundreds of keV electrons are thus sensible to wave‐particle interactions from hiss waves for a wide range of L‐shells, including the entire outer belt. This justifies the choice of demonstrating the Dst effects through the motion of ultra‐relativistic electrons in Section 3.
Figure 14.
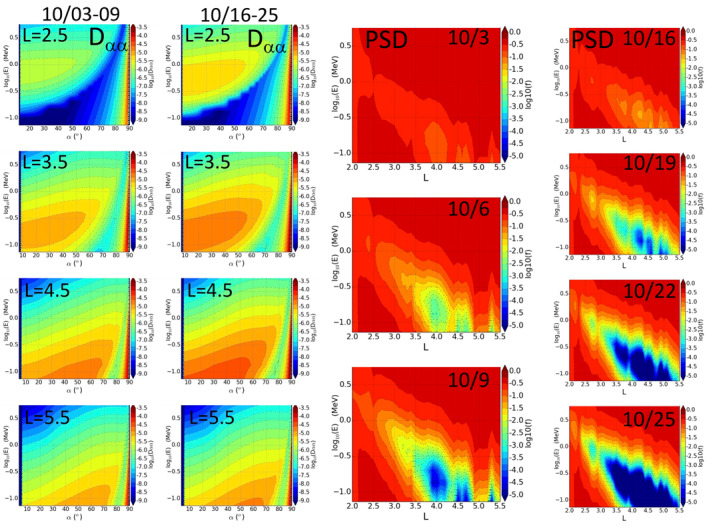
Left: Event‐driven pitch angle diffusion coefficients shown at L = 2.5, 3.5, 4.5, and 5.5 for energies between 50 keV and 6 MeV versus pitch angle (α) and computed from all wave and plasma properties (cf. Figures 12 and 13) for the period of October 3–9 (first column) and October 16–25 (second column). Right: Electron omnidirectional phase‐space density (PSD) simulated with the event‐driven pitch angle diffusion coefficients from October 3–9 (third column) and October 16–25 (fourth column) versus L and energy. The PSD decay shows the gradual decay of electrons in the slot region and in the outer belt that explains the gradual enlargement of the slot we see in the observations in Figure 6 for EPT and 7–9 for RBSP. Relativistic and ultra‐relativistic electrons (>1 MeV) are not scattered above L ∼ 3.5.
Simulated omnidirectional PSD is then normalized by the RBSP L2 flux at t = 0 (on October 3 and 16) and presented at E = 131, 447, and 630 keV in Figure 15 (right) for the two time periods. (Only 131 keV electrons are normalized with the flux of October 4 due to the very low flux on October 3). To facilitate the comparison between simulation and observation, RBSP fluxes have been binned the same way by averaging bins of 24 h (Figure 15, left). Figure 15 shows the inner boundary of the outer belt is well reproduced in the simulation, attesting of the slot formation. Gradual loss in the outer belt is also consistent with the observations. Loss of 131 keV is particularly intense in the whole outer belt such that these electrons are removed in less than a day as soon as no new substorm injections occur. Nevertheless, these simulations are not intended to produce a complete representation of the radiation belt dynamics. They remain partial as radial diffusion and local acceleration for chorus waves are absent, which is a strong limitation, for instance, during the substorm injections occurring in October 2013. This explains why our quasi‐linear simulations, limited to pitch angle diffusion, are not carried on during the storms of October 2013. The band structure visible in the simulated flux at L ∼ 5 for 447 and 630 keV electrons is inherited from the initial condition and would not exist if other processes were included.
Figure 15.
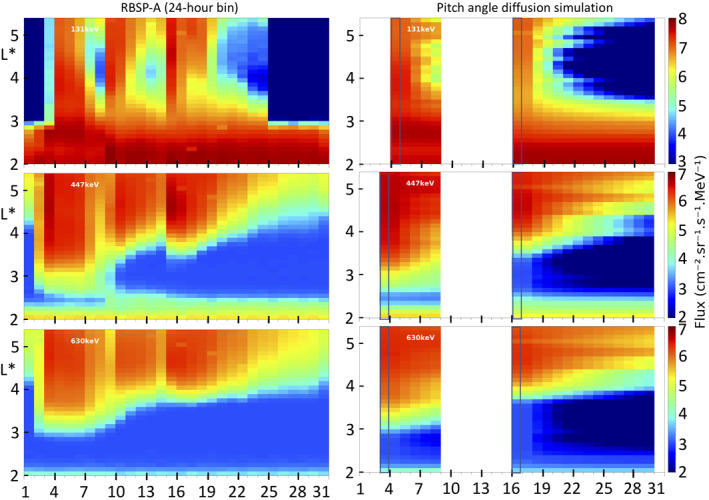
Left: RBSP‐A L2 flux observations binned by temporal bins of 24 h at (from top to bottom) E = 131, 447, and 630 keV. Right: The simulated omnidirectional flux obtained from event‐driven pitch angle diffusion simulations showing the gradual decay of radiation belt electrons in the slot region and in the outer belt. The blue frame on the right indicates the binned flux that is used to normalize the simulated flux at t = 0.
Simulation of the October 2013 period is part of the long‐term simulation (4 years from October 2012 to 2016) performed by Cervantes et al. (2020). This simulation is made with the full Fokker‐Planck VERB‐3D code (Subbotin & Shprits, 2009), which includes radial diffusion due to ULF waves, pitch angle, energy, and mixed pitch angle‐energy diffusion due to chorus and hiss waves and EMIC wave scattering and magnetopause shadowing. Diffusion coefficients are computed from statistical models. A qualitative comparison is made with their simulations, limited to the times in between the storms corresponding to our computational domain. For a first adiabatic invariant µ = 700 MeV/G, their Figure 1 shows a gradual temporal decay of outer belt electrons as in our simulation for E ∼400–600 keV and L between 4.5 and 5.5. Although our simulation does not involve as many processes, it includes the dominant loss mechanism from hiss waves, which explains why both simulations reproduce comparable gradual loss. At higher µ (their Figure 1 and their supporting information (Cervantes et al., 2020)), VERB‐3D simulations show a static behavior of the flux that is in agreement with our simulations, both showing no effect of the whistler‐mode waves for energies above ∼1 MeV (not plotted in our case).
8. Discussion on the Mechanisms Explaining Dropouts and Other Loss Processes
There are currently three types of loss mechanisms to explain the electron flux dropouts in the outer radiation belt: (i) adiabatic loss, as explained by Kim and Chan (1997), and called the “Dst effect” by X. Li et al. (1997); (ii) drift loss to the magnetopause and outward radial diffusion (e.g. Shprits et al., 2006); and (iii) pitch angle scattering due to plasma waves causing precipitation loss in the atmosphere (e.g. Summers & Thorne, 2003). Adiabatic and magnetopause loss (i and ii) are reviewed in more detail by Turner and Ukhorskiy (2020). The mechanisms involved in intense losses of outer radiation belt electrons are reviewed in Ripoll, Claudepierre, et al. (2020).
Radial diffusion is a critical process that has been shown to accelerate and decelerate particles (e.g., Mann et al., 2016; Ozeke et al., 2018, 2020). As it acts both inward and outward, radial diffusion contributes to outward loss (e.g., Hudson et al., 2015). Event‐driven radial diffusion was developed during the “Quantitative Assessment of Radiation Belt Modeling” focus group in place at Geospace Environment Modeling (Tu et al., 2009). Their use in a full 3D Fokker‐Planck code has shown promising results for other storm and non‐storm periods (e.g., Ma, Li, Bortnik, et al., 2018; Thorne et al., 2013; Tu et al., 2014). This approach coupled with the event‐driven method for scattering by whistler‐mode waves as used here is certainly one of the most promising ways to solve for the daily behavior of the radiation belts, though the modeling of dropouts and Dst effects have to be included. We note that the use of partial quasi‐linear Fokker‐Planck models is common in the literature to study dedicated effects, while a full formulation is, generally speaking, better suited, particularly for long‐term simulations (e.g., Cervantes et al., 2020) and for quantitative assessment of multi‐physical processes (e.g., Ma, Li, Bortnik, et al., 2018). There exist numerous examples of dedicated studies employing a reduced Fokker‐Planck modeling, including the absence of radial diffusion, as done here (e.g., Albert et al., 2016; Cunningham et al., 2018; Ma, Li, Thorne, Bortnik, et al., 2016; Ni et al., 2014; Ripoll, Denton, Hartley et al., 2020; Su et al., 2017; Thorne et al., 2013).
Adiabatic loss states that the electron flux dropouts during storm main phase can be attributed to the Dst effect. As the ring current develops, its diamagnetic effect slowly weakens the geomagnetic field. In this case, the time scale of this variation is larger than the drift period of electrons, so that all the three adiabatic invariants are conserved. To maintain the third adiabatic invariant, electrons move radially outward and encounter weaker geomagnetic field. To preserve the first invariant in a region of decreased magnetic field, they must lose energy, as illustrated by the simulations. If the energy spectrum is steep, then at a fixed energy and location, the electron flux is observed to decrease as Dst increases because the flux at that energy increasingly comes from higher‐energy particles originating from a more Earthward location. This process is fully adiabatic, and, thus, it is reversible.
The inflated electron drift path can encounter the magnetopause, called magnetopause shadowing (West et al., 1972), or the electrons can drift close to the magnetopause and then diffuse outward onto open field lines due to the steep phase space density gradient at the magnetopause (Shprits et al., 2006). In either case, the electrons are lost to the system.
Precipitation loss of electrons due to wave scattering is attributed to a number of wave scattering mechanisms—for example, interaction with plasmaspheric hiss (e.g., Abel & Thorne, 1998a), EMIC waves (Summers & Thorne, 2003), whistler‐mode chorus waves (e.g., Shprits et al., 2007), and lightning generated whistlers (e.g., Bortnik et al., 2006). Note that the loss time scale of whistler‐mode hiss waves is about 1–10 days according to the electron energy, so it is not likely that pitch angle scattering by hiss plays an important role in the rapid main‐phase dropout, but, as shown here in Sections 6 and 7, they contribute well to the moderate decrease of the fluxes following the storm injections. EMIC waves have been suggested to cause the MeV electron flux dropout during storm main phase (e.g., Ukhorskiy et al., 2010). If the amplitudes of EMIC waves can be as strong as 1–10 nT, these waves can result in strong ultra‐relativistic electron precipitation with energy down to about 1 MeV within several hours (e.g., Summers & Thorne, 2003). We showed that the dropout concerns also energies >1 MeV.
The effect of waves on particles is energy‐dependent, while the adiabatic loss and magnetopause shadowing is independent of the energy of the particles for the relativistic energies studied here. The fact that the observations show dropouts at all energy ranges seems to indicate that magnetopause shadowing and radial diffusion are the principal mechanisms for particle loss. The high L‐shell losses called dropouts can be attributed mainly to magnetopause shadowing, outward radial diffusion, and adiabatic losses, which affect all energies indiscriminately. However, at lower L‐shells, or in case losses are found to be energy dependent, other processes have to be proposed, like wave‐particle interactions. Even if L < 4 dropouts are difficult to explain with magnetopause shadowing, EMIC waves cannot scatter such wide range of energies and L, so that multiple waves have to play a role. The L, energy, and pitch angle characteristics of the observed dropouts are thus crucial to determine their origin. EMIC signature is visible in pitch angle distributions (PSD evolution) (Blum et al., 2019; Usanova et al., 2014).
Bortnik et al. (2006) investigated in detail a dropout event that occurred during the November 20, 2003 geomagnetic storm and reported two different dropout mechanisms dominating at high (L > 5) and lower L‐shells. At low L‐shells, losses were found to be energy dependent with <0.45 MeV electron flux losses being adiabatic whereas fluxes of 0.63 MeV electrons were not adiabatic. The nonadiabatic losses were reported to have been caused by EMIC waves in the plasmasphere.
Xiang et al. (2017) suggested recently that dropouts can be classified into distinct classes depending on the dominant loss mechanisms: magnetopause shadowing (L* > 4, dominant in June 22, 2015 event), EMIC wave scattering (L* < 4 dominant in February 27, 2014 event) leading to atmospheric losses, and combination of both mechanisms. They used the electron PSD (Phase Space Density) and calculated LCDS (Last Closed drift shell) measured by RBSP to provide this diagnostic. Other events before the launch of PROBA‐V (May 7, 2013) were also investigated. With PROBA‐V/EPT, dropouts and flux enhancements associated to geomagnetic storms have been analyzed during the 6 years of the mission, showing an impenetrable barrier for dropout L‐shells, as well as for flux injections in the slot and inner belt (Pierrard et al., 2020).
9. Conclusions
We have studied the effect of geomagnetic storms on the outer radiation belt, and especially the main loss mechanisms observed during the month of October 2013, namely dropout events and loss from wave‐particle interactions. The objective was to compare both polar LEO and MEO equatorial observations from the ESA PROBA‐V/EPT and the Van Allen Probes (RBSP) and to perform the analysis of these observations with modern numerical tools.
Dropouts, corresponding to flux depletions at L > 4 (e.g., Pierrard et al., 2020), are clearly visible at all energies during four storms occurring on October 2, 9, 15, and 30, 2013 from observations by both EPT at LEO and MagEIS at MEO. These dropouts can be understood by the outward motion associated with the Dst event. To illustrate it, we performed relativistic gyromotion test particle simulations to quantify the effect of the betatron mechanism caused by the main phase of a geomagnetic storm on the relativistic electron flux. This way, we calculated the contribution of the Dst effect on the observed electron dropout.
During the main phase of a geomagnetic storm, test‐particle simulations show that outer radiation belt particles are momentarily driven outward and decelerate, which temporally limits atmospheric scattering at both the highest latitude and the lowest L‐shells of the outer belt. Because of this outward motion, scattering is temporarily shifted to higher altitude and latitude. Conversely, during the early recovery phase, electrons drift reversibly back inward. As they do so, scattering at the lowest L‐shell and highest latitudes becomes observable again. Therefore, at fixed L‐shell, one can observe first a decay of the precipitating flux at LEO, followed by a return to the normal state, which is due to the temporal motion outward, then, inward, of the particles during the storm main and recovery phases. On top of this back and forth adiabatic motion, there can exist fast wave‐particle interactions that can modify the electron energy spectrum, but only if the characteristic time of these interactions is comparable to the fast storm timescale, itself driven by the time to reach the minimum Dst and to recover to normal Dst. When the fast and deep outward motion of the Dst effect is associated with magnetopause shadowing, this produces significant radiation belt dropout across a wide range of L and energies.
The simulations show that the kinetic energy loss of an electron caused by the Dst effect depends on its equatorial pitch angle. In azimuthally symmetric background and perturbation magnetic fields, the Dst effect is energy independent. But in reality, since equatorially mirroring electrons decelerate more than mid‐latitude mirroring electrons, and equatorial pitch angle decreases during the main phase, the dropouts could result in butterfly pitch angle distributions.
Observations of L3 MagEIS outer belt flux show a mild intensification of the flux as pitch angle increases at all times of October 2013, confirming the quite isotropic structure of the outer belt observed during quiet times by Ripoll et al. (2019). We also observe no change of the inner edge of the outer belt as pitch angle changes. Conversely, the inner belt consists mostly of high pitch angle electrons. During more active times, the pitch angle dependence of the radiation belts becomes more complex. We observe an interesting quite high energy injection of 459 keV electrons, which occurred during the October 2 storm and penetrated the inner belt. This injection is not observed at higher energies by RBSP and, thus not seen by EPT, which first channel starts at 0.5 MeV. The particularity of this injection is to have a rather strong pitch angle dependence, with the injection well observed at 90° pitch angle and hardly visible at 41° and 25°.
Comparing omnidirectional fluxes from EPT and MagEIS, we find equatorially trapped electron fluxes are higher than at LEO. Below 1 MeV, maximal fluxes differ by ∼2 orders of magnitude. However, the EPT ultra‐relativistic flux (>2.4 MeV) is much lower than the RBSP flux at 2.33 MeV, by 4–5 orders of magnitude (see also Pierrard et al., 2019). Comparing now low pitch angle (25°) electrons of 0.5 MeV measured by MagEIS at MEO with the 0.5–0.6 MeV channel of EPT at LEO, we find a very good overlap of the outer belt at all times. The EPT flux is much lower on EPT than the RBSP flux, which indicates the need of inter‐calibration. We also show that varying the L‐shell definition (i.e., the magnetic field model in use for the L‐shell calculation) affects the upper limit of the outer belt by ∼1 L in spreading the outer belt to higher L‐shells, but does not change the location of the outer belt lower edge.
From October 1 to 31, MagEIS observation shows the outer belt inner boundary is eroded from L ∼ 3 to L ∼ 4.5, with an apparent gradual removal of slot electrons. This seems slightly further away than what is observed at LEO, for which the outer belt inner boundary gradually moves from L ∼ 3 to L ∼ 4. This type of loss is the second main type of loss observed in October 2013 and is attributed to wave‐particle interactions from plasmaspheric waves. Observations of the plasmasphere from RBSP/EMFISIS and RBSP/EFW show the systematic compression/erosion of the plasmasphere for the storm of October 2, 9, 15, and 31, down to L ∼ 3.5. The plasmasphere recovers in 1–2 days after these mild storms and extends up to L ∼ 5.5, explaining why wave‐particle interactions from plasmaspheric waves are determinant for the global structure of the radiation belts. To demonstrate it further, we conducted event‐driven Fokker‐Planck simulations of pitch angle diffusion.
Diffusion coefficients are derived from all wave properties measured by RBSP/EMFISIS at a high temporal resolution of 8 h (cf. Ripoll et al., 2017, 2019). Plasmaspheric density is also fully used in the computations, which are conducted for 2 recovery periods following the storms of October 2 and October 15 at all L‐shells and energies. Comparisons between models of waves and statistical models would be highly interesting. The Fokker‐Planck simulations show the inner boundary of the outer belt is well reproduced in the simulation, attesting to the slot formation. Gradual loss in the outer belt is also consistent with the observations. The typical energy dependence of these losses leads to the absence of scattering for relativistic and ultra‐relativistic electrons in the outer belt, oppositely to dropouts. Finally, other loss processes and limitations of this study were briefly discussed. More sophisticated studies, including event‐driven radial diffusion and local acceleration from whistler‐mode chorus waves, will be needed to improve the accuracy of the simulations.
Acknowledgments
The authors thank the International Space Sciences Institute (ISSI) and the participants in a 2020 ISSI workshop for the project “Radiation belts physics”. The SafeSpace project has received funding from the European Union’s Horizon 2020 Research and Innovation Program under Grant agreement no 870437. V. Pierrard and E. Botek thank the Belgian Scientific Policy for the EPT and FEDtWIN project ENERGY. This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under Contract no. 89233218CNA000001. J.‐F. Ripoll and G. Cunningham thank an agreement between CEA/DAM and NNSA/DP on cooperation on fundamental science. G. Cunningham was supported by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under Project number 20200073DR. The research at University of Iowa was supported by JHU/APL contract 921647 under NASA prime contract NAS5‐01072. O. Santolik acknowledges additional support from Grant LTAUSA17070 for cooperation with the University of Iowa. The authors would like to thank Craig Kletzing and the EMFISIS team.
Pierrard, V. , Ripoll, J.‐F. , Cunningham, G. , Botek, E. , Santolik, O. , Thaller, S. , et al. (2021). Observations and simulations of dropout events and flux decays in October 2013: Comparing MEO equatorial with LEO polar orbit. Journal of Geophysical Research: Space Physics, 126, e2020JA028850. 10.1029/2020JA028850
Data Availability Statement
EPT data are publicly available at the ESA website http://swe.ssa.esa.int/space-radiation. All of the Levels 2 and 3 of MagEIS data used in this manuscript are in the public domain and accessible from the RBSP‐ECT website (http://www.RBSP-ect.lanl.gov/). EMFISIS data can be obtained from http://emfisis.physics.uiowa.edu. Solar wind data are from OMNI data, available from NASA GSFC’s Space Physics Data Facility (https://cdaweb.gsfc.nasa.gov/). The diffusion coefficients and simulated electron distributions are provided in the repository file http://doi.org/10.5281/zenodo.4436178.
References
- Abel, B. , & Thorne, R. M. (1998a). Electron scattering loss in Earth's inner magnetosphere: 1. Dominant physical processes. Journal of Geophysical Research, 103, 2385–2396. 10.1029/97JA02919 [DOI] [Google Scholar]
- Abel, B. , & Thorne, R. M. (1998b). Electron scattering loss in Earth's inner magnetosphere 2. Sensitivity to model parameters. Journal of Geophysical Research, 103, 2397–2407. 10.1029/97JA02920 [DOI] [Google Scholar]
- Abel, B. , & Thorne, R. M. (1999). Correction to “Electron scattering loss in the Earth's inner magnetosphere: 1, Dominant physical processes” and “Electron scattering loss in the Earth's inner magnetosphere: 2, Sensitivity to model parameters”. Journal of Geophysical Research, 104(A3), 4627–4628. 10.1029/1998JA900121 [DOI] [Google Scholar]
- Albert, J. M. (1994). Quasi‐linear pitch angle diffusion coefficients: Retaining high harmonics. Journal of Geophysical Research, 99(A12), 23741–23745. 10.1029/94JA02345 [DOI] [Google Scholar]
- Albert, J. M. (2008). Efficient approximations of quasi‐linear diffusion coefficients in the radiation belts. Journal of Geophysical Research, 113, A06208. 10.1029/2007JA012936 [DOI] [Google Scholar]
- Albert, J. M. , Starks, M. J. , Horne, R. B. , Meredith, N. P. , & Glauert, S. A. (2016). Quasi‐linear simulations of inner radiation belt electron pitch angle and energy distributions. Geophysical Research Letters, 43, 2381–2388. 10.1002/2016GL067938 [DOI] [Google Scholar]
- Baker, D. N. , Jaynes, A. N. , Hoxie, V. C. , Thorne, R. M. , Foster, J. C. , Li, X. , et al. (2012). The Relativistic Electron‐Proton Telescope (REPT) instrument on board the Radiation Belt Storm Probes (RBSP) spacecraft: Characterization of Earth's radiation belt high‐energy particle populations. Space Science Review, 179(1), 337–381. 10.1007/s11214-012-9950-9 [DOI] [Google Scholar]
- Blake, J. B. , Carranza, P. A. , Claudepierre, S. G. , Clemmons, J. H. , & Crain, W. R. (2013). The Magnetic Electron Ion Spectrometer (MagEIS) instruments aboard the Radiation Belt Storm Probes (RBSP) spacecraft. Space Science Reviews, 179, 1–4. 10.1029/10.1007/S11214-013-9991-8 [DOI] [Google Scholar]
- Blum, L. W. , Artemyev, A. , Agapitov, O. , Mourenas, D. , Boardsen, S. , & Schiller, Q. (2019). EMIC wave‐driven bounce resonance scattering of energetic electrons in the inner magnetosphere. Journal of Geophysical Research: Space Physics, 124, 2484–2496. 10.1029/2018JA026427 [DOI] [Google Scholar]
- Bortnik, J. , Thorne, R. M. , O'Brien, T. P. , Green, J. C. , Strangeway, R. J. , Shprits, Y. Y. , & Baker, D. N. (2006). Observation of two distinct, rapid loss mechanisms during the 20 November 2003 radiation belt dropout event. Journal of Geophysical Research: Space Physics, 111(A12). 10.1029/2006JA011802 [DOI] [Google Scholar]
- Buonsanto, M. J. (1999). Ionospheric storms—A review. Space Science Reviews, 88, 563–601. 10.1023/a:1005107532631 [DOI] [Google Scholar]
- Cervantes, S. , Shprits, Y. Y. , Aseev, N. A. , & Allison, H. J. (2020). Quantifying the effects of EMIC wave scattering and magnetopause shadowing in the outer electron radiation belt by means of data assimilation. Journal of Geophysical Research: Space Physics, 125, e2020JA028208. 10.1029/2020JA028208 [DOI] [Google Scholar]
- Chartier, A. , Forte, B. , Deshpande, K. , Bust, G. , & Mitchell, C. (2016). Three‐ dimensional modeling of high‐latitude scintillation observations. Radio Science, 51, 1022–1029. 10.1002/2015RS005889 [DOI] [Google Scholar]
- Claudepierre, S. G. , O'Brien, T. P. , Blake, J. B. , Fennell, J. F. , Roeder, J. L. , Clemmons, J. H. , et al. (2015). A background correction algorithm for Van Allen Probes MagEIS electron flux measurements. Journal of Geophysical Research: Space Physics, 120, 5703–5727. 10.1002/2015JA021171 [DOI] [Google Scholar]
- Cunningham, G. S. (2016). Radial diffusion of radiation belt particles in nondipolar magnetic fields. Journal of Geophysical Research: Space Physics, 121, 5149–5171. 10.1002/2015JA021981 [DOI] [Google Scholar]
- Cunningham, G. S. , Loridan, V. , Ripoll, J.‐F. , & Schulz, M. (2018). Neoclassical diffusion of radiation‐belt electrons across very low L‐shells. Journal of Geophysical Research: Space Physics, 123, 2884–2901. 10.1002/2017JA024931 [DOI] [Google Scholar]
- Cyamukungu, M. , Benck, S. , Borisov, S. , Bonnet, L. , Gh‐Grégoire, J. , Cabrera, B. , et al. (2014). The Energetic Particle Telescope (EPT) on board Proba‐V: Description of a new science‐class instrument for particle detection in space. IEEE Transactions on Nuclear Science, 61(6), 3667–3681. 10.1109/TNS.2014.2361955 [DOI] [Google Scholar]
- Deshpande, K. B. , Bust, G. S. , Clauer, C. R. , Rino, C. L. , & Carrano, C. S. (2014). Satellite‐beacon Ionospheric‐scintillation Global Model of the upper Atmosphere (SIGMA). I: High‐latitude sensitivity study of the model parameters. Journal of Geophysical Research: Space Physics, 119, 4026–4043. 10.1002/2013JA019699 [DOI] [Google Scholar]
- Drozdov, A. Y. , Shprits, Y. Y. , Aseev, N. A. , Kellerman, A. C. , & Reeves, G. D. (2017). Dependence of radiation belt simulations to assumed radial diffusion rates tested for two empirical models of radial transport. Space Weather, 15, 150–162. 10.1002/2016SW001426 [DOI] [Google Scholar]
- Ferradas, C. P. , Zhang, J.‐C. , Spence, H. E. , Kistler, L. M. , Larsen, B. A. , Reeves, G. D. , et al. (2018). Temporal evolution of ion spectral structures during a geomagnetic storm: Observations and modeling. Journal of Geophysical Research: Space Physics, 123, 179–196. 10.1002/2017JA02470210.1002/2017ja024702 [DOI] [Google Scholar]
- Foster, J. C. , Wygant, J. R. , Hudson, M. K. , Boyd, A. J. , Baker, D. N. , Erickson, P. J. , & Spence, H. E. (2015). Shock‐induced prompt relativistic electron acceleration in the inner magnetosphere. Journal of Geophysical Research: Space Physics, 120, 1661–1674. 10.1002/2014JA020642 [DOI] [Google Scholar]
- Glauert, S. A. , Horne, R. B. , & Meredith, N. P. (2018). A 30‐year simulation of the outer electron radiation belt. Space Weather, 16, 1498–1522. 10.1029/2018SW001981 [DOI] [Google Scholar]
- Hartley, D. P. , Kletzing, C. A. , Santolík, O. , Chen, L. , & Horne, R. B. (2018). Statistical properties of plasmaspheric hiss from Van Allen Probes observations. Journal of Geophysical Research: Space Physics, 123, 2605–2619. 10.1002/2017JA024593 [DOI] [Google Scholar]
- He, Z. , Chen, L. , Zhu, H. , Xia, Z. , Reeves, G. D. , Xiong, Y. , et al. (2017). Multiple‐satellite observation of magnetic dip event during the substorm on 10 October 2013. Geophysical Research Letters, 44, 9167–9175. 10.1002/2017GL074869 [DOI] [Google Scholar]
- Hudson, M. K. , Paral, J. , Kress, B. T. , Wiltberger, M. , Baker, D. N. , Foster, J. C. , et al. (2015). Modeling CME‐shock‐driven storms in 2012–2013: MHD test particle simulations. Journal of Geophysical Research: Space Physics, 120, 1168–1181. 10.1002/2014JA020833 [DOI] [Google Scholar]
- Joshi, P. P. , Baker, J. B. H. , Ruohoniemi, J. M. , Makela, J. J. , Fisher, D. J. , Harding, B. J. , et al. (2015). Observations of storm time midlatitude ion‐neutral coupling using SuperDARN radars and NATION Fabry‐Perot interferometers. Journal of Geophysical Research: Space Physics, 120, 8989–9003. 10.1002/2015JA021475 [DOI] [Google Scholar]
- Kanekal, S. G. , Baker, D. N. , Fennell, J. F. , Jones, A. , Schiller, Q. , Richardson, I. G. , et al. (2016). Prompt acceleration of magnetospheric electrons to ultrarelativistic energies by the 17 March 2015 inter‐planetary shock. Journal of Geophysical Research: Space Physics, 121, 7622–7635. 10.1002/2016JA022596 [DOI] [Google Scholar]
- Kim, H.‐J. , & Chan, A. A. (1997). Fully adiabatic changes in storm time relativistic electron fluxes. Journal of Geophysical Research, 102(A10), 22107–22116. 10.1029/97JA01814 [DOI] [Google Scholar]
- Kim, K. C. , Lee, D.‐Y. , Kim, H.‐J. , Lee, E. S. , & Choi, C. R. (2010). Numerical estimates of drift loss and Dst effect for outer radiation belt relativistic electrons with arbitrary pitch angle. Journal of Geophysical Research, 115, A03208. 10.1029/2009JA014523 [DOI] [Google Scholar]
- Kim, K.‐C. , Shprits, Y. , Subbotin, D. , & Ni, B. (2011). Understanding the dynamic evolution of the relativistic electron slot region including radial and pitch angle diffusion. Journal of Geophysical Research, 116(A10), A10214. 10.1029/2011JA016684 [DOI] [Google Scholar]
- Kletzing, C. A. , Kurth, W. S. , Acuna, M. , MacDowall, R. J. , Torbert, R. B. , Averkamp, T. , et al. (2013). The Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) on RBSP. Space Science Reviews, 179(1–4), 127–181. 10.1007/s11214-013-9993-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurth, W. S. , De Pascuale, S. , Faden, J. B. , Kletzing, C. A. , Hospodarsky, G. B. , Thaller, S. , & Wygant, J. R. (2015). Electron densities inferred from plasma wave spectra obtained by the Waves instrument on Van Allen Probes. Journal of Geophysical Research: Space Physics, 120, 904–914. 10.1002/2014JA020857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lei, J. , Zhong, J. , Mao, T. , Hu, L. , Yu, T. , Luan, X. , et al. (2016). Contrasting behavior of the F2 peak and the topside ionosphere in response to the 2 October 2013 geomagnetic storm. Journal of Geophysical Research: Space Physics, 121, 10549–10563. 10.1002/2016JA022959 [DOI] [Google Scholar]
- Lemaire, J. , Batteux, S. , & Slypen, I. (2005). The influence of a southward and northward turning of the interplanetary magnetic field on the geomagnetic cut‐off of cosmic rays, on the mirror points positions of geomagnetically trapped particles, and on their rate of precipitations in the atmosphere. Journal of Atmospheric and Solar‐Terrestrial Physics, 67(7), 719–727. 10.1016/j.jastp.2004.09.008 [DOI] [Google Scholar]
- Lemaire, J. , & Pierrard, V. (2008). Comparison between two theoretical mechanisms for the formation of the plasmapause and relevant observations. Geomagnetism and Aeronomy, 48(5), 553–570. 10.1134/S0016793208050010 [DOI] [Google Scholar]
- Li, W. , Ni, B. , Thorne, R. M. , Bortnik, J. , Green, J. C. , Kletzing, C. A. , et al. (2013). Constructing the global distribution of chorus wave intensity using measurements of electrons by the POES satellites and waves by the Van Allen Probes. Geophysical Research Letters, 40, 4526–4532. 10.1002/grl.50920 [DOI] [Google Scholar]
- Li, X. , Baker, D. , Temerin, M. , Cayton, T. , Reeves, E. , Christensen, R. , et al. (1997). Multisatellite observations of the outer zone electron variation during the November 3, 1993, magnetic storm. Journal of Geophysical Research, 102(A7). 14123–14140. 10.1029/97JA01101 [DOI] [Google Scholar]
- Loridan, V. , Ripoll, J.‐F. , Tu, W. , & Cunningham, G. (2019). On the use of different magnetic field models for the major storm of October 1990. Journal of Geophysical Research: Space Physics, 124, 6453–6486. 10.1029/2018JA026392 [DOI] [Google Scholar]
- Lu, G. , Richmond, A. D. , Emery, B. A. , & Roble, R. G. (1995). Magnetosphere‐ionosphere‐thermosphere coupling: Effect of neutral winds on energy transfer and field‐aligned current. Journal of Geophysical Research: Space Physics, 100(A10), 19643–19659. 10.1029/95JA00766 [DOI] [Google Scholar]
- Ma, Q. , Li, W. , Bortnik, J. , Thorne, R. M. , Chu, X. , Ozeke, L. G. , et al. (2018). Quantitative evaluation of radial diffusion and local acceleration processes during GEM challenge events. Journal of Geophysical Research: Space Physics, 123(3), 1938–1952. 10.1002/2017JA025114 [DOI] [Google Scholar]
- Ma, Q. , Li, W. , Thorne, R. M. , Bortnik, J. , Reeves, G. D. , Kletzing, C. A. , et al. (2016). Characteristic energy range of electron scattering due to plasmaspheric hiss. Journal of Geophysical Research: Space Physics, 121, 11737–11749. 10.1002/2016JA023311 [DOI] [Google Scholar]
- Ma, Q. , Li, W. , Thorne, R. M. , Ni, B. , Kletzing, C. A. , Kurth, W. S. , et al. (2015). Modeling inward diffusion and slow decay of energetic electrons in the Earth's outer radiation belt. Geophysical Research Letters, 42, 987–995. 10.1002/2014GL062977 [DOI] [Google Scholar]
- Ma, Q. , Li, W. , Thorne, R. M. , Nishimura, Y. , Zhang, X. J. , Reeves, G. D. , et al. (2016). Simulation of energy‐dependent electron diffusion processes in the Earth's outer radiation belt. Journal of Geophysical Research: Space Physics, 121, 4217–4231. 10.1002/2016JA022507 [DOI] [Google Scholar]
- Malaspina, D. M. , Claudepierre, S. G. , Takahashi, K. , Jaynes, A. N. , Elkington, S. R. , Ergun, R. E. , et al. (2015). Kinetic Alfvén waves and particle response associated with a shock‐induced, global ULF perturbation of the terrestrial magnetosphere. Geophysical Research Letters, 42, 9203–9212. 10.1002/2015GL065935 [DOI] [Google Scholar]
- Malaspina, D. M. , Jaynes, A. N. , Hospodarsky, G. , Bortnik, J. , Ergun, R. E. , & Wygant, J. (2017). Statistical properties of low‐frequency plasmaspheric hiss. Journal of Geophysical Research: Space Physics, 122, 8340–8352. 10.1002/2017JA024328 [DOI] [Google Scholar]
- Malaspina, D. M. , Ripoll, J.‐F. , Chu, X. , Hospodarsky, G. , & Wygant, J. (2018). Variation in plasmaspheric hiss wave power with plasma density. Geophysical Research Letters, 45, 9417–9426. 10.1029/2018GL078564 [DOI] [Google Scholar]
- Mann, I. R. , Ozeke, L. G. , Murphy, K. R. , Claudepierre, S. G. , Turner, D. L. , Baker, D. N. , et al. (2016). Explaining the dynamics of the ultra‐relativistic third Van Allen radiation belt. Nature Physics, 12(10), 978–983. 10.1038/nphys3799 [DOI] [Google Scholar]
- Matsamura, C. , Miyoshi, Y. , Seki, K. , Saito, S. , Angelopoulos, V. , & Koller, J. (2011). Outer radiation belt boundary location relative to the magnetopause: Implications for magnetopause shadowing. Journal of Geophysical Research: Space Physics, 116, A06212. 10.1029/2011JA016575 [DOI] [Google Scholar]
- Mauk, B. H. , Fox, N. J. , Kanekal, S. G. , Kessel, R. L. , Sibeck, D. G. , & Ukhorskiy, A. (2013). Science objectives and rationale for the Radiation Belt Storm Probes mission. Space Science Review, 179, 1–4. 10.1007/s11214-012-9908-y [DOI] [Google Scholar]
- McIlwain, C. E. (1966). Magnetic coordinates. Space Science Review, 5, 585–598. 10.1007/BF00167327 [DOI] [Google Scholar]
- McIlwain, C. E. (1996). Processes acting upon outer zone electrons. Geophysical Monograph, 97, 15–26. [Google Scholar]
- Meredith, N. P. , Horne, R. M. , Glauert, S. A. , & Anderson, R. R. (2007). Slot region electron loss timescales due to plasmaspheric hiss and lightning‐generated whistlers. Journal of Geophysical Research, 112, A08214. 10.1029/2007JA012413 [DOI] [Google Scholar]
- Meredith, N. P. , Horne, R. M. , Glauert, S. A. , Baker, D. N. , Kanekal, S. G. , & Albert, J. M. (2009). Relativistic electron loss time‐ scales in the slot region. Journal of Geophysical Research, 114, A03222. 10.1029/2008JA013889 [DOI] [Google Scholar]
- Meredith, N. P. , Horne, T. , Li, W. , Thorne, R. M. , & Sicard‐Piet, A. (2014). Global model of low‐frequency chorus (f LHR<f<0.1f ce) from multiple satellite observations. Geophysical Research Letters, 41(2), 280–286. 10.1002/2013GL059050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni, B. , Li, W. , Thorne, R. M. , Bortnik, J. , Ma, Q. , Chen, L. , et al. (2014). Resonant scattering of energetic electrons by unusual low‐frequency hiss. Geophysical Research Letters, 41, 1854–1861. 10.1002/2014GL059389 [DOI] [Google Scholar]
- Ozeke, L. G. , Mann, I. R. , Dufresne, S. K. Y. , Olifer, L. , Morley, S. K. , Claudepierre, S. G. , et al. (2020). Rapid outer radiation belt flux dropouts and fast acceleration during the March 2015 and 2013 storms: The role of ULF wave transport from a dynamic outer boundary. Journal of Geophysical Research: Space Physics, 125, e2019JA027179. 10.1029/2019JA027179 [DOI] [Google Scholar]
- Ozeke, L. G. , Mann, I. R. , Murphy, K. R. , Degeling, A. W. , Claudepierre, S. G. , & Spence, H. E. (2018). Explaining the apparent impenetrable barrier to ultra‐relativistic electrons in the outer Van Allen belt. Nature Communications, 9, 1844. 10.1038/s41467-018-04162-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pembroke, A. , Toffoletto, F. , Sazykin, S. , Wiltberger, M. , Lyon, J. , Merkin, V. , & Schmitt, P. (2012). Initial results from a dynamic coupled magnetosphere‐ionosphere‐ring current model. Journal of Geophysical Research: Space Physics, 117, A02211. 10.1029/2011JA016979 [DOI] [Google Scholar]
- Pierrard, V. , Botek, E. , Ripoll, J.‐F. , & Cunningham, G. S. (2020). Electron dropout events and flux enhancements associated with geomagnetic storms observed by PROBA‐V/EPT from 2013 to 2019. Journal of Geophysical Research: Space Physics, 125(12), e2020JA028487. 10.1029/2020JA028487 [DOI] [Google Scholar]
- Pierrard, V. , & Lemaire, J. (2004). Development of shoulders and plumes in the frame of the interchange instability mechanism for plasmapause formation. Geophysical Research Letters, 31(5). 10.1029/2003GL018919 [DOI] [Google Scholar]
- Pierrard, V. , & Lopez Rosson, G. (2016). The effects of the big storm events in the first half of 2015 on the radiation belts observed by EPT/PROBA‐V. Annales Geophysicae, 34, 75–84. 10.5194/angeo-34-75-2016 [DOI] [Google Scholar]
- Pierrard, V. , Lopez Rosson, G. , Borremans, K. , Lemaire, J. , Maes, J. , Bonnewijn, S. , et al. (2014). The energetic particle telescope: First results. Space Science Review, 184, 87–106. 10.1007/s11214-014-0097-8 [DOI] [Google Scholar]
- Pierrard, V. , Lopez Rosson, G. , & Botek, E. (2019). Dynamics of megaelectron volt electrons observed in the inner belt by PROBA‐V/EPT. Journal of Geophysical Research: Space Physics, 124, 1651–1659. 10.1029/2018JA026289 [DOI] [Google Scholar]
- Press, W. H. , Teukolsky, S. A. , Vetterling, W. T. , & Flannery, B. P. (1992). Numerical Recipes in FORTRAN (2nd ed.). [Google Scholar]
- Prölss, G. W. (1995). Ionospheric F‐region storms. In Volland H. (Ed.), Handbook of 1310 atmospheric electrodynamics (Vol. 2, pp. 195–248). CRC Press. [Google Scholar]
- Ren, D. , & Lei, J. (2017). A simulation study of the equatorial ionospheric response to the October 2013 geomagnetic storm. Journal of Geophysical Research: Space Physics, 122, 9696–9704. 10.1002/2017JA024286 [DOI] [Google Scholar]
- Réveillé, T. , Bertrand, P. , Ghizzo, A. , Simonet, F. , & Baussart, N. (2001). Dynamic evolution of relativistic electrons in the radiation belts. Journal of Geophysical Research, 106, 18883–18894. 10.1029/2000JA900177 [DOI] [Google Scholar]
- Ripoll, J.‐F. , Chen, Y. , Fennell, J. F. , & Friedel, R. H. W. (2014). On long decays of electrons in the vicinity of the slot region observed by HEO3 . Journal of Geophysical Research: Space Physics, 120, 460–478. 10.1002/2014JA020449 [DOI] [Google Scholar]
- Ripoll, J.‐F. , Claudepierre, S. G. , Ukhorskiy, A. Y. , Colpitts, C. , Li, X. , Fennell, J. , & Crabtree, C. (2020). Particle dynamics in the Earth's radiation belts: Review of current research and open questions. Journal of Geophysical Research: Space Physics, 125, e2019JA026735. 10.1029/2019JA026735 [DOI] [Google Scholar]
- Ripoll, J.‐F. , Denton, M. , Loridan, V. , Santolík, O. , Malaspina, D. , Hartley, D. P. , et al. (2020). How whistler mode hiss waves and the plasmasphere drive the quiet decay of radiation belts electrons following a geomagnetic storm. Journal of Physics: Conference Series. 1623, 012005. 10.1088/1742-6596/1623/1/012005 [DOI] [Google Scholar]
- Ripoll, J.‐F. , Denton, M. H. , Hartley, D. P. , Reeves, G. D. , Malaspina, D. , Cunningham, G. S. , et al (2020). Scattering by whistler‐mode waves during a quiet period perturbed by substorm activity. Journal of Atmospheric and Solar‐Terrestrial Physics. 215, 105471. 10.1016/j.jastp.2020.105471 [DOI] [Google Scholar]
- Ripoll, J.‐F. , Loridan, V. , Denton, M. H. , Cunningham, G. , Reeves, G. , Santolík, O. , et al (2019). Observations and Fokker‐Planck simulations of the L‐shell, energy, and pitch angle structure of Earth's electron radiation belts during quiet times. Journal of Geophysical Research: Space Physics, 124. 10.1029/2018ja026111 [DOI] [Google Scholar]
- Ripoll, J.‐F. , & Mourenas, D. (2012). High‐energy electron diffusion by resonant interactions with whistler mode hiss. In Dynamics of the Earth's radiation belts and inner magnetosphere. Geophysical Monograph Series (Vol. 199, pp. 281–290). 10.1029/2012GM001309 [DOI] [Google Scholar]
- Ripoll, J.‐F. , Reeves, G. D. , Cunningham, G. S. , Loridan, V. , Denton, M. , Santolik, O. , et al. (2016). Reproducing the observed energy‐dependent structure of Earth's electron radiation belts during storm recovery with an event‐specific diffusion model. Geophysical Research Letters, 43, 5616–5625. 10.1002/2016GL068869 [DOI] [Google Scholar]
- Ripoll, J.‐F. , Santolík, O. , Reeves, G. D. , Kurth, W. S. , Denton, M. H. , Loridan, V. , et al. (2017). Effects of whistler mode hiss waves in March 2013. Journal of Geophysical Research: Space Physics, 122, 7433–7462. 10.1002/2017JA024139 [DOI] [Google Scholar]
- Roederer, J. G. (1970). Dynamics of geomagnetically trapped radiation. In Roederer J. G. & Zahringer J. (Eds.), Physics and chemistry in space Vol. (2), Springer. [Google Scholar]
- Roederer, J. G. , & Lejosne, S. (2018). Coordinates for representing radiation belt particle flux. Journal of Geophysical Research: Space Physics, 123, 1381–1387. 10.1002/2017JA025053 [DOI] [Google Scholar]
- Roederer, J. G. , & Zhang, H. (2014). Dynamics of magnetically trapped particles: Foundations of the physics of radiation belts and space plasmas. Astrophysics and Space Science Library, Springer. [Google Scholar]
- Saito, S. , Miyoshi, Y. , & Seki, K. (2010). A split in the outer radiation belt by magnetopause shadowing: Test particle simulations. Journal of Geophysical Research: Space Physics, 115(A8), a08210. 10.1029/2009JA014738 [DOI] [Google Scholar]
- Santolík, O. , Kletzing, C. A. , Kurth, W. S. , Hospodarsky, G. B. , & Bounds, S. R. (2014). Fine structure of large‐amplitude chorus wave packets. Geophysical Research Letters, 41, 293–299. 10.1002/2013GL058889 [DOI] [Google Scholar]
- Santolík, O. , Macúsová, E. , Kolmasová, I. , Cornilleau‐Wehrlin, N. , & de Conchy, Y. (2014). Propagation of lower‐band whistler‐mode waves in the outer Van Allen belt: Systematic analysis of 11 years of multi‐component data from the Cluster spacecraft. Geophysical Research Letters, 41, 2729–2737. 10.1002/2014GL059815 [DOI] [Google Scholar]
- Santolik, O. , Parrot, M. , Storey, L. R. O. , Pickett, J. , & Gurnett, D. A. (2001). Propagation analysis of plasmaspheric hiss using Polar PWI measurements. Geophysical Research Letters, 28, 1127–1130. 10.1029/2000gl012239 [DOI] [Google Scholar]
- Santolik, O. , Pickett, J. S. , Gurnett, D. A. , & Storey, L. R. O. (2002). Magnetic component of narrow‐band ion cyclotron waves in the auroral zone. Journal of Geophysical Research, 107(A12), 1444. 10.1029/2001JA000146 [DOI] [Google Scholar]
- Selesnick, R. S. , & Kanekal, S. G. (2009). Variability of the total radiation belt electron content. Journal of Geophysical Research: Space Physics, 114(A2), a02203. 10.1029/2008JA013432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shprits, Y. Y. , Meredith, N. P. , & Thorne, R. M. (2007). Parameterization of radiation belt electron loss timescales due to interactions with chorus waves. Geophysical Research Letters, 34, L11110. 10.1029/2006GL029050 [DOI] [Google Scholar]
- Shprits, Y. Y. , Thorne, R. M. , Friedel, R. , Reeves, G. D. , Fennell, J. , Baker, D. N. , & Kanekal, S. G. (2006). Outward radial diffusion driven by losses at magnetopause. Journal of Geophysical Research, 111, A11214. 10.1029/2006JA011657 [DOI] [Google Scholar]
- Shue, J.‐H. , Chao, J. K. , Fu, H. C. , Russell, C. T. , Song, P. , Khurana, K.‐K. , & Singer, H. J. (1997). A new functional form to study the solar wind control of the magnetopause size and shape. Journal of Geophysical Research, 102(A5), 9497–9511. 10.1029/97JA00196 [DOI] [Google Scholar]
- Spasojevic, M. , Shprits, Y. Y. , & Orlova, K. (2015). Global empirical models of plasmaspheric hiss using Van Allen Probes. Journal of Geophysical Research: Space Physics, 120. 10370–10383. 10.1002/2015ja021803 [DOI] [Google Scholar]
- Spence, H. E. , Reeves, G. D. , Baker, D. N. , Blake, J. B. , Bolton, M. , Bourdarie, S. , et al. (2013). Science goals and overview of the radiation belt storm probes (RBSP) energetic particle, composition, and thermal plasma (ECT) suite on NASA's Van Allen Probes Mission. Space Science Reviews, 179, 1–336. 10.1007/s11214-013-0007-5 [DOI] [Google Scholar]
- Su, Z. , Gao, Z. , Zheng, H. , Wang, Y. , Wang, S. , Spence, H. E. , et al. (2017). Rapid loss of radiation belt relativistic electrons by EMIC waves. Journal of Geophysical Research: Space Physics, 122, 9880–9897. 10.1002/2017JA024169 [DOI] [Google Scholar]
- Su, Z. , Xiao, F. , Zheng, H. , He, Z. , Zhu, H. , Zhang, M. , et al. (2014). Nonstorm time dynamics of electron radiation belts observed by the Van Allen Probes. Geophysical Research Letters, 41, 229–235. 10.1002/2013GL058912 [DOI] [Google Scholar]
- Su, Z. , Zhu, H. , Xiao, F. , Zheng, H. , Wang, Y. , He, Z. , et al. (2014). Intense duskside lower band chorus waves observed by Van Allen Probes: Generation and potential acceleration effect on radiation belt electrons. Journal of Geophysical Research: Space Physics, 119, 4266–4273. 10.1002/2014JA019919 [DOI] [Google Scholar]
- Su, Z. , Zhu, H. , Xiao, F. , Zheng, H. , Wang, Y. , Shen, C. , et al. (2015). Disappearance of plasmaspheric hiss following interplanetary shock. Geophysical Research Letters, 42, 3129–3140. 10.1002/2015GL063906 [DOI] [Google Scholar]
- Subbotin, D. A. , & Shprits, Y. Y. (2009). Three‐dimensional modeling of the radiation belts using the Versatile Electron Radiation Belt (VERB) code. Space Weather, 7, S10001. 10.1029/2008SW000452 [DOI] [Google Scholar]
- Summers, D. , & Thorne, R. M. (2003). Relativistic electron pitch‐angle scattering by electromagnetic ion cyclotron waves during geomagnetic storms. Journal of Geophysical Research, 108(A4), 1143. 10.1029/2002JA009489 [DOI] [Google Scholar]
- Thaller, S. A. , Wygant, J. R. , Dai, L. , Breneman, A. W. , Kersten, K. , Cattell, C. A. , et al. (2015). Van Allen probes investigation of the large‐scale duskward electric field and its role in ring current formation and plasmasphere erosion in the 1 June 2013 storm. Journal of Geophysical Research: Space Physics, 120, 4531–4543. 10.1002/2014ja020875 [DOI] [Google Scholar]
- Thorne, R. M. , Li, W. , Ni, B. , Ma, Q. , Bortnik, J. , Chen, L. , et al. (2013). Rapid local acceleration of relativistic radiation belt electrons by magnetospheric chorus. Nature, 504(7480), 411–414. 10.1038/nature12889 [DOI] [PubMed] [Google Scholar]
- Thorne, R. M. , Smith, E. J. , Burton, R. K. , & Holzer, R. E. (1973). Plasmaspheric hiss. Journal of Geophysical Research: Space Physics, 78. 1581–1596. 10.1029/ja078i010p01581 [DOI] [Google Scholar]
- Tsyganenko, N. A. (1989). A magnetospheric magnetic field model with a warped tail current sheet. Planetary and Space Science, 37, 5–20. 10.1016/0032-0633(89)90066-4 [DOI] [Google Scholar]
- Tsyganenko, N. A. , & Sitnov, M. I. (2005). Modeling the dynamics of the inner magnetosphere during strong geomagnetic storms. Journal of Geophysical Research: Space Physics, 110(A3), a03208. 10.1029/2004JA010798 [DOI] [Google Scholar]
- Tu, W. , Cunningham, G. S. , Chen, Y. , Henderson, M. G. , Camporeale, E. , & Reeves, G. D. (2013). Modeling radiation belt electron dynamics during GEM challenge intervals with the DREAM3D diffusion model. Journal of Geophysical Research: Space Physics, 118(10), 6197–6211. 10.1002/jgra.50560 [DOI] [Google Scholar]
- Tu, W. , Cunningham, G. S. , Chen, Y. , Morley, S. K. , Reeves, G. D. , Blake, J. B. , et al. (2014). Event‐specific chorus wave and electron seed population models in DREAM3D using the Van Allen Probes. Geophysical Research Letters, 41, 1359–1366. 10.1002/2013GL058819 [DOI] [Google Scholar]
- Tu, W. , & Li, X. (2011). Adiabatic effects on radiation belt electrons at low altitude. Journal of Geophysical Research: Space Physics, 116(A9), a09201. 10.1029/2011JA016468 [DOI] [Google Scholar]
- Tu, W. , Li, X. , Chen, Y. , Reeves, G. D. , & Temerin, M. (2009). Storm‐dependent radiation belt electron dynamics. Journal of Geophysical Research: Space Physics, 114(A2), a02217. 10.1029/2008JA013480 [DOI] [Google Scholar]
- Turner, D. L. , Shprits, Y. Y. , Hartinger, M. D. , & Angelopoulos, V. (2012). Explaining sudden losses of outer radiation belt electrons during geomagnetic storms. Nature Physics, 8(3), 208–212. 10.1038/NPHYS21810.1038/nphys2185 [DOI] [Google Scholar]
- Turner, D. L. , & Ukhorskiy, A. Y. (2020). Outer radiation belt losses by magnetopause incursions and outward radial transport: New insight and outstanding questions from the Van Allen Probes era. In Jaynes A. H., & Usanova M. E. (Eds.), The dynamic loss of Earth's radiation belts (pp. 1–28). Elsevier. 10.1016/B978-0-12-813371-2.00001-9 [DOI] [Google Scholar]
- Ukhorskiy, A. Y. , Shprits, Y. Y. , Anderson, B. J. , Takahashi, K. , & Thorne, R. M. (2010). Rapid scattering of radiation belt electrons by storm‐time EMIC waves. Geophysical Research Letters, 37, L09101. 10.1029/2010GL042906 [DOI] [Google Scholar]
- Ukhorskiy, A. Y. , & Sitnov, M. I. (2013). Dynamics of radiation belt particles. Space Science Reviews, 179(1), 545–578. 10.1007/s11214-012-9938-5 [DOI] [Google Scholar]
- Ukhorskiy, A. Y. , Sitnov, M. I. , Millan, R. M. , Kress, B. T. , Fennell, J. F. , Claudepierre, S. G. , & Barnes, R. J. (2015). Global storm time depletion of the outer electron belt. Journal of Geophysical Research: Space Physics, 120(4), 2543–2556. 10.1002/2014ja020645 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usanova, M. E. , Drozdov, A. , Orlova, K. , Mann, I. R. , Shprits, Y. , Robertson, M. T. , et al. (2014). Effect of EMIC waves on relativistic and ultrarelativistic electron populations: Groundbased and Van Allen Probes observations. Geophysical Research Letters, 41, 1375–1381. 10.1002/2013GL059024 [DOI] [Google Scholar]
- West, H. I. , Buck, R. M. , & Walton, J. R. (1972). Shadowing of electron azimuthal‐drift motions near the noon magnetopause. Nature Physical Sciences, 240, 6–7. 10.1038/physci240006a0 [DOI] [Google Scholar]
- Wygant, J. R. , Bonnell, J. W. , Goetz, K. , Ergun, R. E. , Mozer, F. S. , Bale, S. D. , et al. (2013). The electric field and waves instruments on the radiation belt storm probes mission. Space Science Reviews, 179(1–4), 183–220. 10.1007/s11214-013-0013-7 [DOI] [Google Scholar]
- Xiang, Z. , Tu, W. , Li, X. , Ni, B. , Morley, S. K. , & Baker, D. N. (2017). Understanding the mechanisms of radiation belt dropouts observed by Van Allen Probes. Journal of Geophysical Research: Space Physics, 122, 9858–9879. 10.1002/2017JA024487 [DOI] [Google Scholar]
- Xiao, F. , Liu, S. , Tao, X. , Su, Z. , Zhou, Q. , Yang, C. , et al. (2017). Generation of extremely low frequency chorus in Van Allen radiation belts. Journal of Geophysical Research: Space Physics, 122(3), 3201–3211. 10.1002/2016JA023561 [DOI] [Google Scholar]
- Yuan, Z. , Yu, X. , Ouyang, Z. , Yao, F. , Huang, S. , & Funsten, H. O. (2019). Simultaneous trapping of electromagnetic ion cyclotron and magnetosonic waves by background plasmas. Journal of Geophysical Research: Space Physics, 124, 1635–1643. 10.1029/2018JA026149 [DOI] [Google Scholar]
- Yue, C. , Li, W. , Nishimura, Y. , Zong, Q. , Ma, Q. , Bortnik, J. , et al. (2016). Rapid enhancement of low‐energy (<100 eV) ion flux in response to interplanetary shocks based on two Van Allen Probes case studies: Implications for source regions and heating mechanisms. Journal of Geophysical Research: Space Physics, 121, 6430–6443. 10.1002/2016JA022808 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
EPT data are publicly available at the ESA website http://swe.ssa.esa.int/space-radiation. All of the Levels 2 and 3 of MagEIS data used in this manuscript are in the public domain and accessible from the RBSP‐ECT website (http://www.RBSP-ect.lanl.gov/). EMFISIS data can be obtained from http://emfisis.physics.uiowa.edu. Solar wind data are from OMNI data, available from NASA GSFC’s Space Physics Data Facility (https://cdaweb.gsfc.nasa.gov/). The diffusion coefficients and simulated electron distributions are provided in the repository file http://doi.org/10.5281/zenodo.4436178.


