Abstract
Radiation belt flux dropout events are sudden and often significant reductions in high‐energy electrons from Earth's outer radiation belts. These losses are theorized to be due to interactions with the dayside magnetopause and possibly connected to observations of escaping magnetospheric particles. This study focuses on radiation belt losses during a moderate‐strength, nonstorm dropout event on November 21, 2016. The potential loss mechanisms and the linkage to dayside escape are investigated using combined energetic electron observations throughout the dayside magnetosphere from the Magnetospheric Multiscale and Van Allen Probes spacecraft along with global magnetohydrodynamic and test particle simulations. In particular, this nonstorm‐time event simplifies the magnetospheric conditions and removes ambiguity in the interpretation of results, allowing focus on subsequent losses from enhanced outward radial transport that can occur after initial compression and relaxation of the magnetopause boundary. The evolution of measured phase space density profiles suggest a total loss of approximately 60% of the initial radiation belt content during the event. Together the in situ observations and high‐resolution simulations help to characterize the loss by bounding the following parameters: (a) the duration of the loss, (b) the relative distribution of losses and surface area of the magnetopause over which loss occurs, and (c) the escaping flux (i.e., loss) rate across the magnetopause. In particular, this study is able to estimate the surface area of loss to less than 2.9 × 106 RE 2 and the duration of loss to greater than 6 h, while also demonstrating the magnetic local time‐dependence of the escaping flux and energy spectrum.
Keywords: radiation belt, magnetospheric escape, energetic electrons, flux dropout events, test particle simulations
Key Points
Linkage between flux dropouts and dayside escape is investigated using observations along with global magnetohydrodynamics and test particle simulations
A nonstorm event enables study of subsequent losses that might occur after initial compression and relaxation of the magnetopause boundary
Observations and simulations help characterize loss by bounding parameters such as rate, duration, and distribution across the magnetopause
1. Introduction
Greater than tens of kiloelectronvolts energetic particles are regularly observed beyond the magnetopause at significantly higher intensities than expected from the solar wind and magnetosheath. However, the debate as to whether these particles (both electrons and ions) are of magnetospheric or solar origin began with the earliest in situ observations and has continued in the literature for several decades (e.g., review by Cohen et al., 2017, and references therein). The root of this debate focuses on whether these energetic particles originate from the solar wind and are accelerated near the bow shock (e.g., shock‐drift or diffusive shock acceleration) or if they are magnetospheric particles that have escaped beyond the magnetopause (e.g., through either magnetic reconnection or escape due to finite gyroradius effects). The origin of these particles has wide implication for both heliophysics and planetary science, as similar observations have also been made at the bow shock and upstream of other magnetized (e.g., Krimigis, 1992; Krimigis et al., 1985, 1988, 2009; Zwickl et al., 1981) and unmagnetized (e.g., Bagenal et al., 2016; Russell, Raymond, et al., 2016; Yamauchi et al., 2011) planetary bodies. If they are of magnetospheric origin, such particles also have relevance to astrophysics and the “injection problem” of cosmic ray acceleration (e.g., Zank et al., 2001), since those particles would represent stellar plasma that has been processed and accelerated in a planetary magnetosphere before escaping back into interplanetary space.
However, the improved magnetic local time (MLT) coverage and high energy, angular, compositional, and temporal resolution of the observations from the Energetic Particle Detector investigation (Blake et al., 2016; Mauk, Blake, et al., 2016) aboard the Magnetospheric Multiscale (MMS) mission (Burch et al., 2016) have opened a new chapter in the study of energetic particle dynamics at the magnetopause boundary. The unexpected regularity of this mono‐hemispheric escape (i.e., “streaming”) of energetic electrons, particularly in the dayside, dusk sector, motivated the statistical analysis of MMS energetic electron escape observations by Cohen et al. (2017). That study presented a database of 238 energetic (40 keV) electron streaming events in MMS/EIS observations during Phase 1a (September 1, 2015–March 8, 2016) identified by a clearly anisotropic (≶90°) pitch angle distribution; these signatures were concluded to result from electrons streaming/escaping along recently reconnected magnetic field lines. In addition to the unexpected frequency of occurrence of energetic electron escape across all MLT at the dayside magnetopause, two additional results from the statistical analysis of Cohen et al. (2017) are specifically noteworthy. First, statistically significant pitch angle asymmetries were observed in these escape events up to ∼200 keV. The authors presented a simplistic calculation assuming conservation of the first adiabatic invariant (μ) and suggested that these ∼200 keV electrons at the magnetopause could correspond to the loss of relativistic electrons from the outer radiation belt. Second, although the results of the study most strongly supported loss via reconnection, the authors acknowledged that other loss mechanisms could not be ruled out due to the difficulty of isolating correlated parameters (such as IMF orientation and geomagnetic indices; e.g., Russell & McPherron, 1973) to identify a chain of causality.
As suggested by Cohen et al. (2017), these escaping energetic electrons may play a significant role in addressing another long‐standing debate in the literature, this one regarding radiation belt dynamics. Outer radiation belt flux “dropout” events are drastic decreases in relativistic electron flux over broad ranges of energy, pitch angle, and radial distance in only a few hours, which have a rich history in the literature and are known to occur commonly (e.g., Turner, Morley, et al., 2012, and references therein). Although originally attributed to simple adiabatic effects during the main phase of storms (Dessler & Karplus, 1961; Roederer, 1970), more recent observations strongly suggest that these dropouts are driven by true losses from the system (e.g., H.‐J. Kim & Chan, 1997; Li et al., 1997; Morley et al., 2010). Recent work has shown that producing distributions of electron phase space density (PSD) in adiabatic invariant coordinates removes most ambiguity due to adiabatic effects. However, this method still reveals outer belt dropouts, providing strong evidence for actual loss (e.g., Turner et al., 2013).
Currently, it is believed that losses during dropouts are attributable to two mechanisms (e.g., Xiang et al., 2017, 2018), both of which can act in the presence of adiabatic motion: (a) rapid scattering into the atmospheric loss cones (i.e., either the drift or bounce loss cone), in particular by electromagnetic ion cyclotron (EMIC) waves (Aseev et al., 2017; Usanova et al., 2014), and (b) magnetopause shadowing and subsequent enhanced outward radial transport (Turner & Ukhorskiy, 2020, and references therein). However, it remains unclear which are the dominant processes in storm‐ and nonstorm‐time events (e.g., Katsavrias et al., 2015; Morley et al., 2010; Su et al., 2016). Rapid losses to the atmosphere are believed to occur due to wave‐particle interactions between relativistic electrons and waves, such as EMIC waves (e.g., Summers & Thorne, 2003).
Magnetopause shadowing describes the loss of trapped particles on drift trajectories that intersect the magnetopause following sudden compressions of the magnetosphere (e.g., K. C. Kim et al., 2008). Losses at lower L‐shells than those that directly interact with the magnetopause can occur as electrons are driven toward the magnetopause boundary by outward radial transport resulting from perturbations to the PSD radial distribution by ultralow frequency wave activity that violates the third adiabatic invariant (e.g., Loto'aniu et al., 2010; Miyoshi et al., 2006; Shprits et al., 2006; Turner, Angelopoulos, et al., 2012). Rapid deceleration due to nonlinear wave‐particle interactions (e.g., Tao et al., 2012) could also contribute to dropouts, but has yet to be thoroughly investigated.
Turner et al. (2014) presented a case study of a significant flux dropout event. Using observations from multiple spacecraft (THEMIS, Van Allen Probes, GOES), the authors confirmed that losses outside of L ≳ 4 were dominated by magnetopause shadowing and outward radial transport, but suggested influence of another loss process for multi‐MeV electrons at lower L‐shells (L* ≲ 4). Building upon this idea presented by Turner, Morley, et al. (2012) and Turner, Shprits, et al. (2012) (based on Shprits et al., 2006), the authors presented a scenario where magnetopause shadowing followed by outward radial diffusion creates a flux dropout event throughout most of the outer belt. First, a solar wind pressure pulse the moves the magnetopause inward, resulting in magnetopause shadowing. As the pressure pulse passes, the magnetopause responds to the lower pressure solar wind and moves back outward, with losses from the magnetopause generally shadowing above geostationary orbit except for the largest of magnetopause compressions; this generates a very sharp PSD gradient and enables subsequent enhanced outward radial diffusion. This outward radial transport pushes electrons from the outer radiation belt, which results in further losses to the magnetopause and irreversible flux reductions throughout much of the rest of the belt, because electrons lose energy as they move outward and such transport is an irreversible process.
Previous observational (e.g., Cohen et al., 2016, 2017; Mauk et al., 2019) and modeling studies (e.g., K. C. Kim & Lee, 2014; Mauk, Cohen, et al., 2016; Sorathia et al., 2017, 2018) have shown evidence of magnetospheric loss via interactions with the magnetopause boundary. In particular, the recent simulation results from Sorathia et al. (2018) looked at the initial direct loss of energetic electrons from the outer radiation belt when their drift trajectories intersect the compressed magnetopause during a geomagnetic storm. Complementary to that, the study presented here further investigates the potential link between outer radiation belt flux dropout events and energetic electrons that are observed to escape beyond the magnetopause during a nonstorm dropout event. In particular, using energetic electron measurements from MMS and the Van Allen Probes (Mauk et al., 2013) along with global magnetohydrodynamics (MHD) and test particle simulations, from the Grid Agnostic MHD with Extended Research Applications (GAMERA) (Sorathia et al., 2020; Zhang et al., 2019) and Conservative Hamiltonian Integrator for Magnetospheric Particles (CHIMP) (Sorathia et al., 2017, 2018, 2019) frameworks, respectively, specifically for a nonstorm event allows this study to investigate the subsequent loss of energetic electrons from the inner magnetosphere via the process of enhanced outward radial diffusion in the wake of a magnetospheric compression as proposed by Turner, Morley, et al. (2012) and Turner, Shprits, et al. (2012).
2. Observations
Between November 20 and 24, 2016, both Van Allen Probes were in the near‐midnight MLT sector, when they observed an outer radiation belt flux dropout event. Figure 1 shows the configuration of the six (two Van Allen Probes and four MMS) spacecraft used in this study and their orbit tracks for the preceding 24 h. As shown in Figure 2, the dropout began late in the day on 21 November and continued well into 23 November, with the most significant reductions in intensity occurring late in the day on 21 November. Note (a) that the slower decay of the lowest energy electrons (Figure 2a) earlier in the period are independent of the sudden dropout affecting the electrons at all energies starting on the 21st, and (b) that the MeV electrons (Figure 2d) do not return to their pre‐dropout intensities in the days following the dropout. At the same time, the MMS spacecraft were in the magnetosheath in the afternoon sector on the inbound leg of their orbit. The slower decay at lower energies is likely associated with wave‐particle interactions scattering electrons into the atmospheric loss cone; loss timescales for those processes are on the order of several days.
Figure 1.
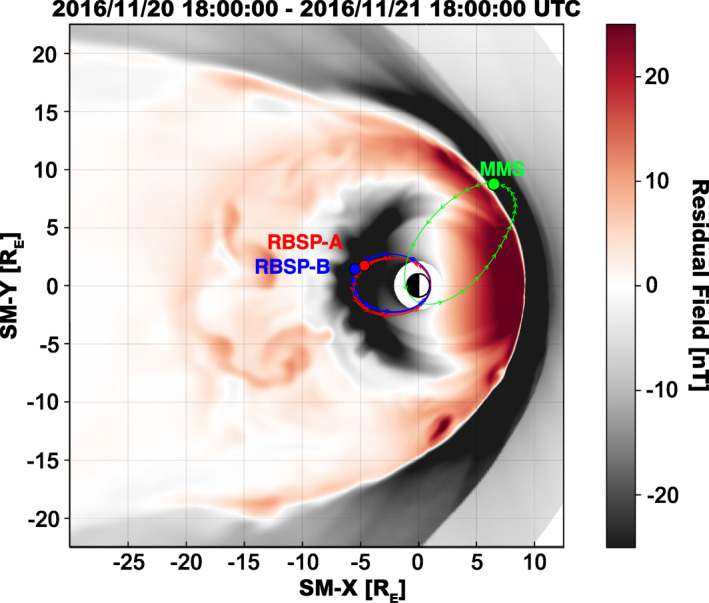
Plot showing the 24‐h orbital tracks for the Magnetospheric Multiscale and Van Allen Probes spacecraft during the November 21, 2016 dropout event studied here overlaid on a 2D slice of the SM X‐Y plane of the magnetic field at 18:00 UT from the Grid Agnostic MHD with Extended Research Applications magnetohydrodynamics simulation used in this study.
Figure 2.
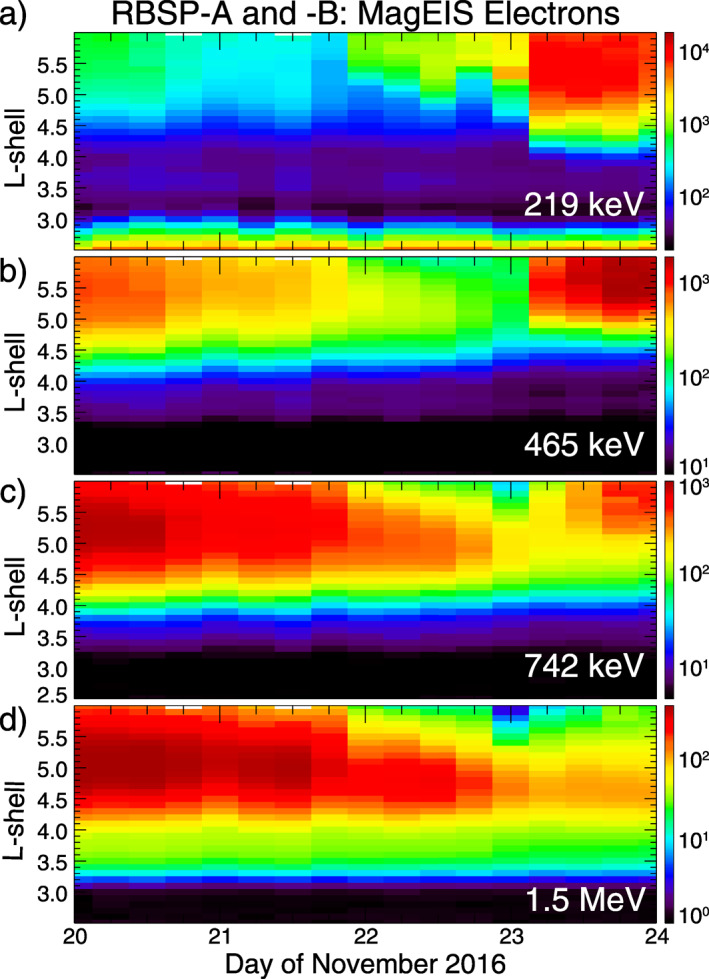
The evolution of electron intensities as observed by the Van Allen Probes/MagEIS instrument (Blake et al., 2013) at four energies sorted by L‐shell show a moderate, nonstorm flux dropout event spanning November 20–23, 2016.
Figure 3 shows an overview of the OMNI solar wind and MMS observations for this event, spanning approximately two orbits (apogee to apogee) from 12:00 UT on November 20, 2016 to 12:00 UT on November 22, 2016. MMS begins near apogee in the magnetosheath on 20 November; the spacecraft then move Earthward and encounter the magnetopause at approximately 17:30 UT at a distance of ∼10.5 R E. During the outbound leg of the orbit on 21 November, MMS flies along field lines that map to very high magnetic latitudes (and L values), as indicated by the much stronger (100 nT) field measured within the magnetosphere (compared to ∼50 nT field observed at the same L values after the magnetopause crossing on the inbound orbit on the previous day). On this outbound leg, MMS encounters the magnetopause and exits the magnetosphere at ∼07:10 UT at a distance of ∼9.0 R E. The aforementioned flux dropout event that is the focus of this study occurs while MMS is in the magnetosheath, likely driven by the solar wind dynamic pressure pulse seen in the OMNI data (Figure 3a, black line) around 12:00 UT. On the inbound leg of the second orbit (afternoon of 21 November), MMS again crossed the magnetopause and entered the magnetosphere around 19:20 UT at a distance of ∼9.4 R E. However, a surprisingly weak population of magnetospheric energetic particles is observed into ∼8 R E where an apparent dispersive injection and subsequent drift echo are encountered at ∼21:15 UT. It is believed that this magnetospheric region of low‐intensity energetic electron background is the result of the relaxation of the magnetopause boundary following its compression by the solar wind—that is, magnetospheric flux tubes largely empty of the energetic electrons processed and energized by the magnetosphere. On the outbound orbit on 22 November, MMS again flies along field lines that map to very high magnetic latitudes.
Figure 3.
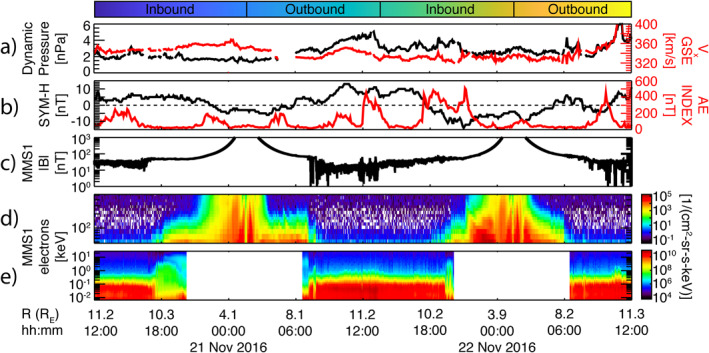
Overview plot of OMNI (King & Papitashvili, 2005) solar wind data (a) and geomagnetic indices (b) along with in situ magnetic field (c), energetic electrons (d), and lower‐energy electrons (e) from Magnetospheric Multiscale obtained by the FGM (Russell, Anderson, et al., 2016); FEEPS (Blake et al., 2016), and FPI (Pollock et al., 2016) instruments, respectively. At the top, the data are broken down by orbit legs using the same color bar used to show the temporal evolution of the phase space density profiles in Figure 4.
Together, observations from Van Allen Probes/MagEIS (Blake et al., 2013) and MMS/FEEPS (Blake et al., 2016) provide nearly continuous profiles of energetic electron PSD throughout the inner magnetosphere. Analyses from favorable conjunctions between MMS and Van Allen Probes have demonstrated that the these instruments are well cross‐calibrated, as supported by the results presented here. The loss of energetic electrons from the magnetosphere during this flux dropout event is investigated by analyzing distributions of electron PSD versus L* (which is similar to L, but inversely proportional to the third adiabatic invariant and thus also invariant) following a well‐proven approach used by multiple previous studies (e.g., Boyd et al., 2018; Chen et al., 2005; Green & Kivelson, 2004; Katsavrias et al., 2019; Turner, Angelopoulos, et al., 2012; Turner et al., 2013; Zhao et al., 2018). It should be noted that detailed error analyses for PSD calculations from THEMIS and Van Allen Probes were conducted by Turner, Angelopoulos, et al. (2012), Turner, Shprits, et al. (2012), and Morley et al. (2013), respectively, both of which found that the resulting errr was very small (6%). This is consistent with the excellent agreement between the PSD values calculated from the Van Allen Probes and MMS observations when the spacecraft crossed each other in L* and from each subsequent spacecraft passage during undisturbed geomagnetic conditions.
Figure 4 shows examples of such PSD versus L (*) distributions calculated for two different fixed values and a fixed K value of <0.1 G1/2 R E, which corresponds to only electrons with equatorial pitch angles ∼90° ± 30°. For the Van Allen Probes data, K is calculated by averaging over only equatorial pitch‐angles (restricting K < 0.1 G1/2 R E) using the Tsyganenko and Sitnov (2005) global magnetic field model. MMS PSD is calculated by averaging over local pitch‐angles ranging from 90° ± 15° when the spacecraft are at low magnetic latitudes to approximate low‐K electrons. Observations at L* 5.5 come from Van Allen Probes while those 5.5 come from MMS. It should be noted that the gap in continuity between the Van Allen Probes and MMS measurements at L*6 for the higher‐ value is a result of the relatively low upper energy (∼600 keV) limit for the FEEPS instruments. These values were selected to showcase the different responses of electrons with lower (350 MeV/G) and higher (350 MeV/G) values. In general, the losses resulting from the flux dropout events are observed only at higher values.
Figure 4.
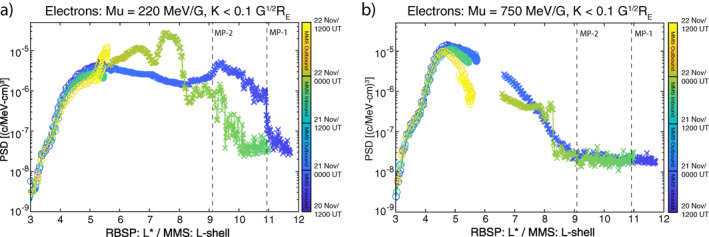
Evolution of calculated phase space density electron profiles versus radial distance for near‐equatorially‐mirroring (K < 0.1 G1/2 R E) particles as measured jointly by Van Allen Probes at L* ≲ 5.5 (circles) and Magnetospheric Multiscale (MMS) at L‐shell ≳5.5 (x's) for two different values of the first adiabatic invariant (μ). The color bar corresponds to the passage of time throughout the event. The vertical dashed lines (MP‐1, ‐2) denote the locations of the MMS magnetopause crossings.
By looking at how these profiles change over time (as indicated by color in the plots), the evolution of the magnetospheric populations can be examined. On the 20 November orbit prior to the dropout event (blue), the inbound MMS spacecraft encountered the magnetopause at just inside 11 R E, which corresponds to the sudden dropoff in = 220 MeV/G PSD distributions (4a) and denoted by the vertical dashed lines marked with “MP‐1.” The magnetopause cutoff is not as apparent in the higher, = 750 MeV/G PSD distribution (4b), which falls off much more gradually with distance. During this 20 November orbit, MMS observed a relatively robust population of energetic particles within the magnetosphere for all values shown. Notice that the PSD profiles do not include MMS observations (i.e., L 5.5) from either of the outbound legs the spacecraft's mapping to very high magnetic latitudes, as previously discussed; at such high latitudes, MMS does not observe electrons at the values of and K considered here. Though FEEPS does observe energetic electrons during this period, the very high magnetic field (latitude) from those orbits observed at these L‐shells results in very different values. However, it can be seen from Van Allen Probes data during this time that the PSD profiles at L* 5.5 change only slightly in this time, which is consistent with the loss seen in simulations conducted for a subset of this period to be discussed in later sections. The magnetopause crossing on the inbound orbit on 21 November is apparent at ∼9.4 R E in the 220 MeV/G distribution as denoted by the vertical dashed lines marked with “MP‐2”; note that the magnetopause is not nearly as apparent at 750 MeV/G. Instead, both 21 November inbound distributions are dominated by the abrupt PSD gradient arising from the injection observed at ∼8 R E. It must be noted that the dynamic injection of energetic electrons from the tail also fills the “empty” dayside flux tubes resulting from the relaxation of the magnetosphere and partially replenishes, and cannot be distinguished separately from, electron losses from enhanced outward radial transport at the L‐shells affected by the injection.
The flux dropout event, which is most evident in Van Allen Probes data in the 750 MeV/G distribution (Figure 4b), affects L 4.6 and occurs between ∼12:00 UT on 21 November and ∼12:00 UT on 22 November. Unfortunately, the lack of outer magnetospheric (L 5.5) PSD observations from MMS for the outbound leg of the orbit on 22 November inhibits our ability to calculate the total magnetospheric loss with certainty. However, the limited observations from Van Allen Probes in the inner magnetosphere can be used to estimate the loss by fitting the PSD profiles as shown in Figure 5. Here, the fit for the pre‐dropout PSD profile, including both Van Allen Probes and MMS observations, is shown in cyan and the fit for the post‐dropout partical PSD profile, from Van Allen Probes only, is in magenta. Comparing these fits using (PSDbefore − PSDafter)/PSDbefore shows that approximately 61% of the pre‐dropout electrons (total PSD loss of 0.12 c 3/cm3‐MeV3 at = 750 MeV/G) are lost from the magnetosphere. Note that (a) the vast majority of the losses (these are logarithmic y‐axes) occurred between 4.6 ≤ L < 7 (Figure 5b), and (b) this event demonstrates relatively weak loss, as simulations of storm‐time events by Sorathia et al. (2018) and an independent Van Allen Probes/MMS PSD analysis from another flux dropout event on December 14, 2015 (not shown) both resulted in >90% loss of the outer belt. As previously mentioned, it is exactly for this reason and that the magnetopause compression was not severe that this event is ideal to enable investigation of secondary losses due to enhanced outward radial transport. Figure 5b shows how the percent PSD difference (Δ%PSD) versus L‐shell for = 750 MeV/G electrons. As can be seen, the 750 MeV/G electrons in the inner magnetosphere (L 4.6) actually see enhancements (Δ%PSD > 0) after the dropout event, whereas higher (4.6) L‐shells see reductions in PSD (Δ%PSD < 0). That pattern is entirely consistent with losses due to outward radial transport following magnetopause shadowing (e.g., Turner & Ukhorskiy, 2020).
Figure 5.
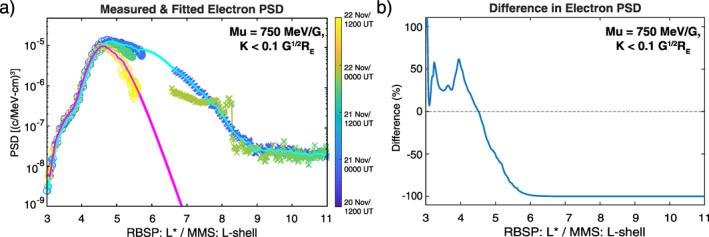
(a) Electron phase space density (PSD) versus radial distance profiles for μ = 750 MeV/G (from Figure 4b) with fits showing PSD levels before (cyan) and after (magenta) the flux dropout event. (b) Percent difference in PSD versus distance before and after the dropout calculated as (PSDbefore − PSDafter)/PSDbefore.
3. Simulations
The methodology and techniques used to model the evolution of the radiation belts in this study are described in detail by Sorathia et al. (2017, 2018); however, a brief summary is provided here. First, a global, high‐resolution MHD simulation is used to produce self‐consistent, time‐varying electromagnetic fields of the magnetosphere. The outer radiation belt is then modeled as an ensemble of test particles, chosen to match observations before the period of interest. The particle trajectories are traced through the electromagnetic fields generated by the MHD simulation to determine the dynamic evolution of the radiation belts.
The global magnetosphere model used in this study couples the newly developed GAMERA MHD model (Sorathia et al., 2020; Zhang et al., 2019), and its integrated ionospheric model, RE‐developed Magnetosphere‐Ionosphere Coupler/Solver (ReMIX), with the Rice Convection Mode (RCM; Toffoletto et al., 2003). GAMERA is the reinvention of the high‐heritage Lyon‐Fedder‐Mobarry (LFM) model (Lyon et al., 2004). GAMERA preserves the core numerical philosophy of its predecessor, which has been used extensively to study critical mesoscale structures in the magnetosphere (Cramer et al., 2017; Merkin et al., 2019; Wiltberger et al., 2015). ReMIX is a rewrite of the MIX code (Merkin & Lyon, 2010) that solves the ionospheric Ohm's law given a source of field‐aligned currents from the MHD simulation and ionospheric conductance computed using a quasi‐empirical model including both solar irradiance and precipitation contributions (Fedder & Lyon, 1995). In the GAMERA‐RCM coupled model, the diffuse electron precipitation is calculated directly from the RCM (Lin et al., 2021). The RCM provides the density and pressure in the inner magnetosphere, where energy‐dependent particle drifts dominate over plasma flows, similar to Pembroke et al. (2012).
GAMERA utilizes a warped spherical grid with higher resolution on the dayside. In this study, the grid has 192 × 192 × 256 cells in the radial, polar, and azimuthal directions, corresponding to the highest resolution LFM grid. ReMIX is coupled with GAMERA every 5 s and has a uniform grid with 0.5° resolution in both latitude and longitude and the low latitude boundary set to 45° magnetic latitude. The RCM is initialized with 115 energy channels and 180 × 181 cells in latitude and longitude, respectively. The RCM is dynamically coupled with GAMERA. The coupling frequency depends on the geomagnetic activity level, that is, quiet times correspond to a low coupling frequency. The GAMERA‐RCM model is driven solar wind data taken from the OMNI database at 1 min resolution and linearly interpolated through any data gaps. To model the dropout event, the global MHD simulation is started at 21:00 UT on November 20, 2016 and preconditioned the magnetosphere for 19 h before the period of interest between 16 UT and 18:30 UT on November 21, 2016. The three‐dimensional electromagnetic fields and plasma solution generated by the simulation are saved at a cadence of 15 s and are used to evolve the test particles during the event.
The test particle trajectories are solved using the CHIMP code (Sorathia et al., 2017, 2018, 2019). CHIMP is a 3D flexible particle integrator, fully integrated to work with the complex geometries used by GAMERA. The modeled outer radiation belt consists of 400 thousand test particles initialized in the magnetic equatorial plane, distributed between L = 3 R E and L = 9 R E. The L‐shell, pitch‐angle, and energy of each test particle are randomly chosen between the specified bounds. The initial radiation belt electrons have energies selected between 50 and 1,500 keV. The range in L‐shell and energy allows for modeling of all potential magnetospheric sources for the 75 keV electrons observed by MMS in the magnetosheath. Only the initial radiation belt was simulated. Electrons that are injected into the inner magnetosphere through mesoscale processes, as is done by Sorathia et al. (2018), are neglected in this study. The trajectories of the electrons are computed using the guiding center formalism (see Appendix A1 of Sorathia et al., 2018) and are evolved through the global electromagnetic fields between 16:00 and 18:30 UT on November 21, 2016. The test‐particle diagnostics are saved at a cadence of 0.2 s to capture the MLT and latitudinal loss profile for those electrons that are lost through the dayside magnetopause.
Finally, test particles are given a weight to be able to directly compare the simulation results to observations. The particle weight relates the number of real electrons each test‐particle represents and is calculated to match the observed PSD before the event. The pre‐event PSD is derived by combining Van Allen Probes and MMS data taken over half an orbit near midnight on November 20, 2016, analogous to the blue curves in Figure 4. A phase space grid as a function of energy and L‐shell is created, with 74 × 45 cells in each dimension, respectively, spanning energies from 50 keV to 1.5 MeV and L‐shell coverage from 3 R E to 11 R E. PSD is averaged over the measurements in each bin. MMS reaches an instrument sensitivity limit near 500 keV. PSD is extrapolated to higher energies assuming a power law for a fixed L‐shell. The data are further scaled by a factor of 0.3 for this event to ensure good agreement between MMS and Van Allen Probes near geosynchronous orbit due to the use of local pitch angles for MMS. MMS data are utilized outside of geosynchronous orbit to sample the full coverage of pitch‐angles, therefore a bivariate spline function is used to interpolate between the range of L‐shells where no data are present. To determine the pitch‐angle dependence of the PSD, Van Allen Probes data at the peak of the radiation belt flux are fit with the functional form , where n is found to be 0.8 for 500 keV electrons at L = 4.7 R E.
In order to determine when an electron is lost through the magnetopause, the local field line that the test particle is on is traced to determine the magnetic topology. The field line is defined to be closed, if both ends map to the ionosphere, open, with one end mapping to the ionosphere and the other to the outer boundary, or IMF, with both end mapping to the outer boundary, as done in Sorathia et al. (2017). The field line tracing is performed at a cadence of 0.2 s. Typical bounce periods for 75 keV electrons near the magnetopause around L‐shells of 9 R E are on the order of 2–4 s, enabling moderate latitudinal resolution. In this study, the test particle is considered to be lost through the magnetopause when the field topology transitions from an open field to the IMF, where they are then advected with the plasma and exit the simulation domain at the outer boundary. Figure 6 shows an overview of the simulation results, presenting four snapshots along the SM‐X/‐Y plane of the global MHD and test particle simulations throughout the 2.5‐h run. Contours show the residual magnetic field, with the dipole component removed, in the GAMERA simulation, with red corresponding to where the dipole field is compressed. The blue line represents the location where the vertical, B Z component, of the magnetic field is zero. The locations of the test particles are projected down to the equatorial plane, along field lines, and are shown relative to the residual magnetic field from GAMERA. The size of the test particle corresponds to the particle's weight, set to match the observed PSD distribution from RBSP and MMS before the event, shown by the blue curve in Figure 4b. The first panel shows the initialized radiation belt at the beginning of the test particle simulation, while subsequent panels show intermediary times throughout the simulation. Once a test particle resides on open magnetic field lines in the magnetosheath, it is quickly transported out of the simulation domain. Loss can be seen at the nose as well as in the flanks of the magnetosphere as the test particles approach, and cross, the magnetopause.
Figure 6.
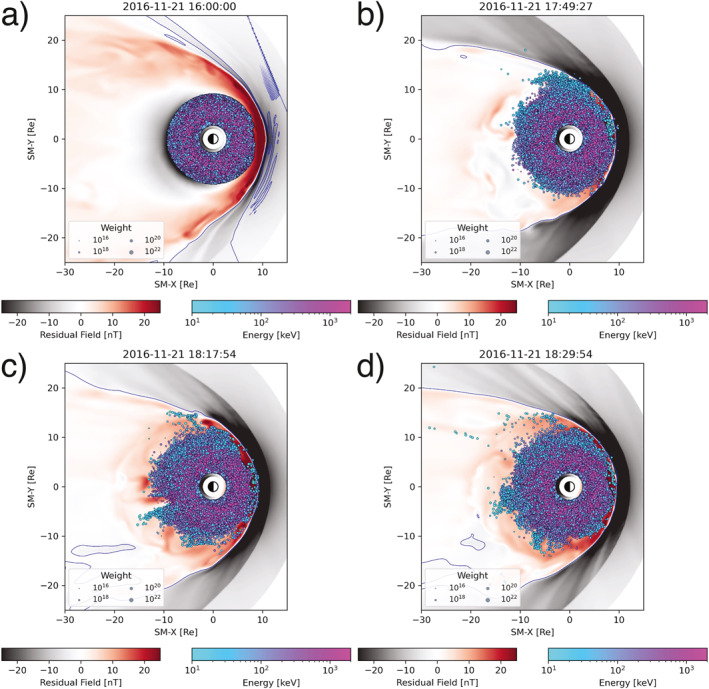
Four instantaneous slices of the SM‐X/‐Y plane showing global MHD and weighted test particle simulations performed for this study, including the initial (a) and final (d) conditions as well as intermediary phases showing losses during large‐scale structures along the magnetospheric flanks. The blue line represents the location where the vertical, B Z component, of the magnetic field is zero. The locations of the test particles are projected down to the equatorial plane, along field lines, and are shown relative to the residual magnetic field from Grid Agnostic MHD with Extended Research Applications. The size of the test particle corresponds to the particle's weight, set to match the observed phase space density distribution from RBSP and Magnetospheric Multiscale before the event, shown by the blue curve in Figure 4b.
4. Analysis: Bounding Loss Parameters
The Van Allen Probes/MMS combined observations determined that this flux dropout was much less intense than those seen during storm times (e.g., Sorathia et al., 2018) with a total loss of ∼61% of the outer radiation belt electrons. Unfortunately, definitive determination of how and where these electrons are lost would require distribution of many more spacecraft across the entirety of the dayside magnetopause. However, the study presented here benefits from in situ MMS measurements of the dayside loss (i.e., an average escaping flux rate of 2.7/cm2‐s‐sr‐keV in the 70 keV channel) and these observations and those from Van Allen Probes together with the simulations presented here can be used to bound the loss characteristics. If it is assumed that some total content of outer radiation belt electrons are lost, then the nature of the loss has three free parameters: (a) the surface area of the magnetopause over which loss occurs, (b) the duration of the loss, and (c) the escaping flux (i.e., loss) rate across the magnetopause the escaping flux (i.e., loss) rate across the magnetopause.
4.1. Area and Distribution of Dayside Magnetopause Loss
As previously alluded to, the MMS escape observations for this event can be used as a fiducial to scale the simulation results. Though outer magnetospheric coverage of the PSD profiles is sparse for this event, MMS did observe active electron escape, using the same identification criteria defined by Cohen et al. (2017), immediately upstream of the magnetopause on the inbound orbit from ∼18:10 to ∼19:15 UT on 21 November. This localized observation provides groundtruth that can be used alongside two‐dimensional estimation of escape across the dayside magnetopause obtained from the global MHD and test particle simulations described in Section 3. Figure 7 shows a map of the magnetic latitude (MLAT) versus magnetic longitude (MLON)/MLT of the escaping flux of test particle electrons within the energy range covered by the 70 keV FEEPS channel (i.e., 63–79 keV) scaled to the flux observed in situ by MMS at MLON of 54° (MLT of 15.6 h) and MLAT of −4.8° (bin outlined with green box).
Figure 7.
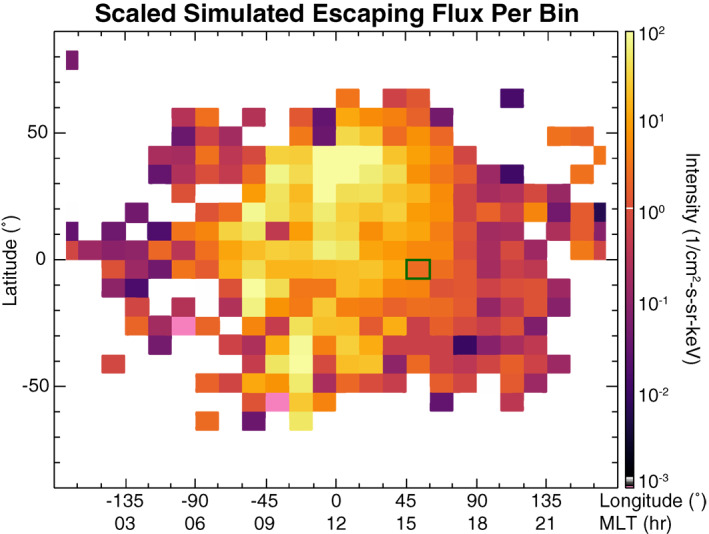
Latitude‐longitude map of the simulated escaping flux scaled to the in situ 70 keV flux level measured by Magnetospheric Multiscale during the event (green box).
The flux, in units of 1/cm2‐s‐sr‐keV, is calculated by first counting the number of test particles in a given bin and multiplying them by their PSD weighting and the electron rest mass ( = 511 keV/c 2) to calculate the total number of “real” electrons represented by the test particles. The total number of “real” electrons in each bin is then divided by , where is the average radial distance at which the electrons in the given bin encountered the magnetopause in cm, is the solid angle of a MLAT/MLON bin, addressed the half‐sphere nature of outward flow (i.e., from the magnetosphere) of the escaping electrons, is the duration of the escape (i.e., the simulation time span) in seconds, and is the width of the target energy channel in keV. This figure is similar to that presented by Sorathia et al. (2017), which showed the probability density of “escape” (i.e., last open‐closed boundary crossing) for different species for a different storm‐time event.
The total particle loss in each of the 15°‐MLON (1‐hr‐MLT) by 7.5°‐MLAT bins was determined by applying the weight of each representative test particle (e.g., Sorathia et al., 2018) to accurately capture the physical number of electrons represented. This total number of electrons in each bin was normalized to the number of representative simulated electrons in the MLT‐MLAT bin (overlaid in green in Figure 7) where the MMS observation was made and this was then scaled to the measured escaping flux rate in the 70 keV FEEPS channel. It is of particular note that the near‐equatorial region where the MMS measurement was made does not capture the region of most intense escape flux—that is, midlatitudes in the northern hemisphere near noon MLT. it is suspected that these regions of the most intense loss correspond to the most likely area for reconnection occurrence based on the IMF conditions for this event (i.e., negative and southward ). The additional dual‐peaked structure of increased loss at approximately ±40° MLAT just dawnward of the subsolar point is likely associated with the bifurcation of the electron drift paths in the dayside magnetosphere (e.g., Ukhorskiy et al., 2011). It must be noted that in comparing the MMS observations to the mapped simulation losses (Figure 7), magnetic mapping or tracing of the individual field lines was not performed; therefore it is only a rough assumption that the escaping fluxes seen in the MMS in situ observations can be correctly contributed to the corresponding MLAT/MLON bin in the simulation results.
A simplified assumption sets a reasonable upper bound on the surface area of the dayside loss as the entirety of the dayside magnetopause at a distance of ∼9.4 R E (where the inbound MMS last encountered it on 21 November)—this of course does not account for additional losses that may occur along the nightside flanks, via plasmoid escape downtail, or due to precipitation into the atmosphere. However, if this is dayside loss is assumed to be over a half‐sphere approximation of the magnetopause, which is simplest but likely an overestimation because it includes the area of the cusp, then the upper bound for the area of loss is = 2.3 × 1010 km2 = 3.6 × 106 R E 2. However, the simulation results in Figure 7 show that almost all of the escape is limited to ±70° latitude, which allows refinement of the upper bound of the surface area of loss to = 1.8 × 1010 km2 = 2.9 × 106 R E 2.
4.2. Loss Duration
The Van Allen Probes observations (Figure 4) already showed that the loss occurs in less than 24 h between 12:00 UT on 21 November and 12:00 UT on 22 November, which sets an upper bound on the loss duration. For the simulations, this study employed a shorter 2.5‐h period from 16:00 to 18:30 UT on 21 November, a period soon after the passage of the solar wind pressure pulse that overlaps with MMS observations of active electron escape, to focus computational resources on resolving boundary dynamics and the four‐dimensional phase space of the electron test particles. The results from this shortened simulation period produce only ∼5%–10% loss of the initial electron radiation belt to the magnetopause with ∼4%–5% loss to the atmosphere and significant variation in the loss over time (Figure 8); however, it must be emphasized that the simulation does not capture (a) the initial losses to the magnetopause from the magnetospheric compression, (b) additional losses from times outside of the simulation period, nor (c) nor any enhanced losses resulting from the injection of particles from tail into the magnetopause, both of which are captured in the calculation of the total percentage lost from the combined PSD profiles. In particular, losses arising from the possible dynamic injection of electrons previously discussed was not included in the simulations, therefore the amount of loss in this dropout event was actually more significant than calculated in this study. In any case, this shortened simulation period set a lower limit on the duration of the loss, providing evidence suggesting that the losses likely occur over at least 6 h (assuming 10% loss per hour). Note that the duration of the loss during this nonstorm‐time event is expectedly much more prolonged compared to the less than 2 h found previously for storm‐time dropout events (Turner et al., 2014; Ukhorskiy et al., 2015).
Figure 8.
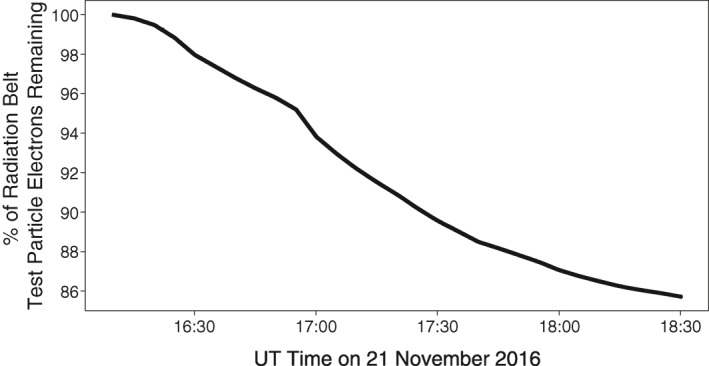
Evolution of the percentage of test particle electrons remaining from the radiation belt over the duration of the 2.5‐h simulation.
4.3. Escaping Flux Rate and Spectrum
The map of scaled escape fluxes from simulations presented in Figure 7 can also be used to estimate the escaping flux (i.e., loss) rate from the magnetosphere. Figure 7 shows the escaping flux in each bin over the 2.5‐h simulation window. Integration of the total 70 keV flux captured by the simulation can be converted into a total PSD loss of 0.04 c 3/cm3‐MeV3. This is approximately one‐third of the previously noted total PSD found to be lost during the dropout event from the combined Van Allen Probes and MMS observations. However, as noted in the previous section, the simulations only account for a 2.5‐h subset of the event and so it can easily be assumed that the full observed PSD content loss (0.12 c 3/cm3‐MeV3) could easily be accounted for in under 8 h, well within the 24 upper bound in which the observations showed the total loss to have occurred. Furthermore, Figure 7 shows that much more significant loss occurs near the beginning of the simulation than at the end when the MMS observations were obtained. This further suggests that the escaping flux rates observed by MMS are likely at the lower end of what can be expected.
The simulation results can also be used to investigate the energy‐dependence of escape across the magnetopause, expanding the localized insight provided by the in situ MMS observations. Figure 9 shows a comparison of the average escaping flux spectrum observed by FEEPS (black dashed line) versus the simulated average escaping flux spectra across all MLATs for 1‐h bins of MLT (colored solid lines), as well as the average simulated spectrum over the entire magnetopause (gray dashed line). The simulation spectra are scaled by a factor of 165 such that the intensity of the average simulation spectrum across the entire magnetopause (gray dashed line) at in the lowest energy channel matches that observed FEEPS spectrum (black dashed line). The hump in the observed FEEPS spectrum at energies 230 keV (denoted by light gray dashed line) is attributed to contamination attributed to minimum ionizing radiation from background cosmic rays that exceeds the escaping magnetospheric intensities. Note that the simulation tends to yield harder (i.e., higher intensities at higher energies) spectra than that observed by FEEPS, which is likely due to the fact that the simulations capture (a) much more intense escape early on in the simulation than at the end (see Figure 8) when the run overlaps with the FEEPS observations and (b) a much broader range of MLATs which includes the regions of highest loss near mid‐latitudes (see Figure 3). Yet again, this underscores that the localized in situ FEEPS observations capture only an instantaneous, and likely nonrepresentative, snapshot of the “typical” dayside escape rates.
Figure 9.
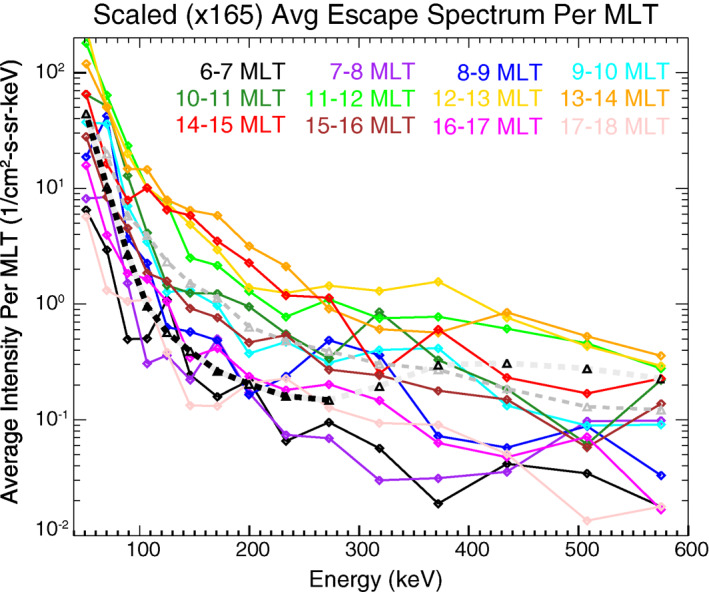
Average escaping flux spectrum measured by Magnetospheric Multiscale (black dashed line) along with the simulated average escaping flux spectra across all magnetic latitudes for 1‐h bins of magnetic local time (colored solid lines); also plotted is the average simulated spectrum over the entire dayside magnetopause (gray dashed line).
5. Conclusions
The case study presented here, of an event on November 21, 2016, provides a unique opportunity to bound the magnetopause loss due enhanced outward radial transport during a nonstorm‐time radiation belt flux dropout event using in situ measurements from the Van Allen Probes and MMS combined with global MHD and test particle simulations. The total loss from the magnetosphere determined by changes in observed PSD profiles is consistent with extrapolation of the losses generated in a shorter‐duration simulation. The simulations also demonstrate that enhanced outward radial transport can drive sustained subsequent losses from the inner magnetosphere after initial losses to the magnetopause from solar wind compression. Furthermore, the simulations provide additional evidence of the prevalence of electron loss in the dayside dusk sector, which is unexpected considering the typical theory of magnetic drift shadowing of electrons from the afternoon MLT sector. Together, the in situ observation and simulations are able to characterize the loss parameters by setting bounds on variables such as the loss duration, area and distribution of loss across the magnetopause, and the escaping flux rate.
In particular, this study's use of multi‐spacecraft measurements from MMS and Van Allen Probes to initialize test particles and subsequent use of model results to contextualize the later spacecraft measurements both enables better study of the links between radiation belt flux dropout events and magnetospheric escape as well as demonstrates an advanced symbiosis between in situ observational data and modeled data. Future studies may leverage this approach to compare these dayside magnetopause losses to those into the atmosphere, as well as the variation in radiation belt losses between storm‐ and nonstorm‐time events, and the potential correlation of dropout and escaping flux intensities with solar wind and geomagnetic parameters.
Supporting information
Supporting Information S1
Acknowledgments
The authors are grateful to the dedicated scientists and engineers of the MMS and Van Allen Probes Science, Instrument, and Operations Teams. Additional thanks are extended to Vassilis Angelopoulos, Eric Grimes, and the teams at UCLA and Berkeley for their development and support of the Space Physics Environment Data Analysis Software (SPEDAS) IDL framework (Angelopoulos et al., 2019). This work was supported by NASA MMS Guest Investigator grant 80NSSC18K1377. Work by ATM and KAS was additionally supported by NASA grants 80NSSC19K0241, 80NSSC20K1833, NNN06AA01C, and the NASA DRIVE Science Center for Geospace Storms (CGS) under Grant 80NSSC20K0601. The authors would also like to acknowledge the use of computational resources (http://doi.org/10.5065/D6RX99HX) at the NCAR‐Wyoming Supercomputing Center provided by the National Science Foundation and the State of Wyoming and supported by NCAR's Computational and Information Systems Laboratory.
Cohen, I. J. , Turner, D. L. , Michael, A. T. , Sorathia, K. A. , & Ukhorskiy, A. Y. (2021). Investigating the link between outer radiation belt losses and energetic electron escape at the magnetopause: A case study using multi‐mission observations and simulations. Journal of Geophysical Research: Space Physics, 126, e2021JA029261. 10.1029/2021JA029261
Data Availability Statement
All MMS data presented here are Level 2 and can be retrieved from the MMS Science Data Center at https://lasp.colorado.edu/mms/sdc/public/. All Van Allen Probes data presented here are Level 2 and can be retrieved from the Van Allen Probes Science Gateway at https://rbspgway.jhuapl.edu/. Additional information on the GAMERA framework can be found at http://cgs.jhuapl.edu/Models/gamera.php.
References
- Angelopoulos, V. , Cruce, P. , Drozdov, A. , Grimes, E. W. , Hatzigeorgiu, N. , King, D. A. , et al. (2019). The Space Physics Environment Data Analysis System (SPEDAS). Space Science Reviews, 215, 9. 10.1007/s11214-018-0576-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aseev, N. A. , Shprits, Y. Y. , Drozdov, A. Y. , Kellerman, A. C. , Usanova, M. E. , Wang, D. , & Zhelavskaya, I. S. (2017). Signatures of ultrarelativistic electron loss in the heart of the outer radiation belt measured by Van Allen Probes. Journal of Geophysical Research: Space Physics, 122, 102–110. 10.1002/2017JA024485 [DOI] [Google Scholar]
- Bagenal, F. , Horanyi, M. , McComas, D. J. , McNutt, R. L., Jr. , Elliott, H. A. , Hill, M. E. , et al. (2016). Pluto's interaction with its space environment: Solar wind, energetic particles, and dust. Science (6279), 351. 10.1126/science.aad9045 [DOI] [PubMed] [Google Scholar]
- Blake, J. B. , Carranza, P. A. , Claudepierre, S. G. , Clemmons, J. H. , Crain, W. R. , Dotan, Y. , et al. (2013). The Magnetic Electron Ion Spectrometer (MagEIS) instruments aboard the Radiation Belt Storm Probes (RBSP) spacecraft. Space Science Reviews, 179, 383–421. 10.1007/s11214-013-9991-8 [DOI] [Google Scholar]
- Blake, J. B. , Mauk, B. H. , Baker, D. N. , Carranza, P. , Clemmons, J. H. , Craft, J. , et al. (2016). The Fly's Eye Energetic Particle Spectrometer (FEEPS) sensors for the Magnetospheric Multiscale (MMS) mission. Space Science Reviews, 199(1), 309–329. 10.1007/s11214-015-0163-x [DOI] [Google Scholar]
- Boyd, A. J. , Turner, D. L. , Reeves, G. D. , Spence, H. E. , Baker, D. N. , & Blake, J. B. (2018). What causes radiation belt enhancements: A survey of the Van Allen Probes Era. Geophysical Research Letters, 45, 5253–5259. 10.1029/2018GL077699 [DOI] [Google Scholar]
- Burch, J. L. , Moore, T. E. , Torbert, R. B. , & Giles, B. L. (2016). Magnetospheric multiscale overview and science objectives. Space Science Reviews, 199(1–4), 5–21. 10.1007/s11214-015-01610.1007/978-94-024-0861-4_2 [DOI] [Google Scholar]
- Chen, Y. , Friedel, R. H. W. , Reeves, G. D. , Onsager, T. G. , & Thomsen, M. F. (2005). Multisatellite determination of the relativistic electron phase space density at geosynchronous orbit: Methodology and results during geomagnetically quiet times. Journal of Geophysical Research, 110, A10210. 10.1029/2004JA010895 [DOI] [Google Scholar]
- Cohen, I. J. , Mauk, B. H. , Anderson, B. J. , Westlake, J. H. , Sibeck, D. G. , Giles, B. L. , et al. (2016). Observations of energetic particle escape at the magnetopause: Early results from the MMS Energetic Ion Spectrometer (EIS). Geophysical Research Letters, 43, 5960–5968. 10.1002/2016GL068689 [DOI] [Google Scholar]
- Cohen, I. J. , Mauk, B. H. , Anderson, B. J. , Westlake, J. H. , Sibeck, D. G. , Turner, D. L. , et al. (2017). Statistical analysis of MMS observations of energetic electron escape observed at/beyond the dayside magnetopause. Journal of Geophysical Research: Space Physics, 122, 9440–9463. 10.1002/2017JA024401 [DOI] [Google Scholar]
- Cramer, W. D. , Raeder, J. , Toffoletto, F. R. , Gilson, M. , & Hu, B. (2017). Plasma sheet injections into the inner magnetosphere: Two‐way coupled OpenGGCM‐RCM model results. Journal of Geophysical Research: Space Physics, 122, 5077–5091. 10.1002/2017JA024104 [DOI] [Google Scholar]
- Dessler, A. J. , & Karplus, R. (1961). Some effects of diamagnetic ring currents on Van Allen radiation. Journal of Geophysical Research, 66(8), 2289–2295. 10.1029/jz066i008p02289 [DOI] [Google Scholar]
- Fedder, J. A. , & Lyon, J. G. (1995). The Earth's magnetosphere is 165 RElong: Self‐consistent currents, convection, magnetospheric structure, and processes for northward interplanetary magnetic field. Journal of Geophysical Research, 100(A3), 3623–3635. 10.1029/94JA02633 [DOI] [Google Scholar]
- Green, J. C. , & Kivelson, M. G. (2004). Relativistic electrons in the outer radiation belt: Differentiating between acceleration mechanisms. Journal of Geophysical Research, 109, A03213. 10.1029/2003JA010153 [DOI] [Google Scholar]
- Katsavrias, C. , Daglis, I. A. , & Li, W. (2019). On the statistics of acceleration and loss of relativistic electrons in the outer radiation belt: A superposed epoch analysis. Journal of Geophysical Research: Space Physics, 124. 10.1029/2019JA026569 [DOI] [Google Scholar]
- Katsavrias, C. , Daglis, I. A. , Turner, D. L. , Sandberg, I. , Papadimitriou, C. , Georgiou, M. , & Balasis, G. (2015). Nonstorm loss of relativistic electrons in the outer radiation belt. Geophysical Research Letters, 42, 10521–10530. 10.1002/2015GL066773 [DOI] [Google Scholar]
- Kim, H.‐J. , & Chan, A. A. (1997). Fully adiabatic changes in storm time relativistic electron fluxes. Journal of Geophysical Research, 102(A10), 22107–22116. 10.1029/97JA01814 [DOI] [Google Scholar]
- Kim, K. C. , & Lee, D.‐Y. (2014). Magnetopause structure favorable for radiation belt electron loss. Journal of Geophysical Research: Space Physics, 119. 10.1002/2014JA019880 [DOI] [Google Scholar]
- Kim, K. C. , Lee, D.‐Y. , Kim, H.‐J. , Lyons, L. R. , Lee, E. S. , Öztürk, M. K. , & Choi, C. R. (2008). Numerical calculations of relativistic electron drift loss effect. Journal of Geophysical Research, 113. 10.1029/2007JA013011 [DOI] [Google Scholar]
- King, J. H. , & Papitashvili, N. E. (2005). Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. Journal of Geophysical Research, 110, A02104. 10.1029/2004JA010649 [DOI] [Google Scholar]
- Krimigis, S. M. (1992). Voyager energetic particle observations at interplanetary shocks and upstream of planetary bow shocks: 1977–1990. Space Science Reviews, 59(1–2), 167–201. 10.1007/BF01262539 [DOI] [Google Scholar]
- Krimigis, S. M. , Keath, E. P. , Mauk, B. H. , Cheng, A. F. , Lanzerotti, L. J. , Lepping, R. P. , & Ness, N. F. (1988). Observations of energetic ion enhancements and fast neutrals upstream and downstream of Uranus' bow shock by the Voyager 2 spacecraft. Planetary and Space Science, 36(3), 311–328. 10.1016/0032-0633(88)90139-0 [DOI] [Google Scholar]
- Krimigis, S. M. , Sergis, N. , Dialynas, K. , Mitchell, D. G. , Hamilton, D. C. , Krupp, N. , et al. (2009). Analysis of a sequence of energetic ion and magnetic field events upstream from the Saturnian magnetosphere. Planetary and Space Science, 57(14–15), 1785–1794. 10.1016/j.pss.2009.02.013 [DOI] [Google Scholar]
- Krimigis, S. M. , Zwickl, R. D. , & Baker, D. N. (1985). Energetic ions upstream of Jupiter's bow shock. Journal of Geophysical Research, 90(A5), 3947–3960. 10.1029/JA090iA05p03947 [DOI] [Google Scholar]
- Li, X. , Baker, D. N. , Temerin, M. , Cayton, T. E. , Reeves, E. G. D. , Christensen, R. A. , et al. (1997). Multisatellite observations of the outer zone electron variation during the November 3‐4, 1993, magnetic storm. Journal of Geophysical Research, 102(A7), 14123–14140. 10.1029/97JA01101 [DOI] [Google Scholar]
- Lin, D. , Sorathia, K. , Wang, W. , Merkin, V. G. , Bao, S. , Pham, K. H. , et al. (2021). The role of diffuse electron precipitation in the formation of subauroral polarization streams. Earth and Space Science Open Archive. 10.1002/essoar.10505900.1 [DOI] [Google Scholar]
- Loto'aniu, T. M. , Singer, H. J. , Waters, C. L. , Angelopoulos, V. , Mann, I. R. , Elkington, S. R. , & Bonnell, J. W. (2010). Relativistic electron loss due to ultralow frequency waves and enhanced outward radial diffusion. Journal of Geophysical Research, 115, A12245. 10.1029/2010JA015755 [DOI] [Google Scholar]
- Lyon, J. G. , Fedder, J. A. , & Mobarry, C. M. (2004). The Lyon‐Fedder‐Mobarry (LFM) global MHD magnetospheric simulation code. Journal of Atmospheric and Solar‐Terrestrial Physics, 66, 1333–1350. 10.1016/j.jastp.2004.03.020 [DOI] [Google Scholar]
- Mauk, B. H. , Blake, J. B. , Baker, D. N. , Clemmons, J. H. , Reeves, G. D. , Spence, H. E. , et al. (2016). The Energetic Particle Detector (EPD) investigation and the Energetic Ion Spectrometer (EIS) for the Magnetospheric Multiscale (MMS) mission. Space Science Reviews, 199(1), 471–514. 10.1007/s11214-014-0055-5 [DOI] [Google Scholar]
- Mauk, B. H. , Cohen, I. J. , Haggerty, D. K. , Hospodarsky, G. B. , Connerney, J. E. P. , Anderson, B. J. , et al. (2019). Investigation of mass/chargedependent escape of energetic ions across the magnetopauses of Earth and Jupiter. Journal of Geophysical Research: Space Physics, 124. 10.1029/2019ja026626 [DOI] [Google Scholar]
- Mauk, B. H. , Cohen, I. J. , Westlake, J. H. , & Anderson, B. J. (2016). Modeling magnetospheric energetic particle escape across Earth's magnetopause as observed by the MMS mission. Geophysical Research Letters, 43, 4081–4088. 10.1002/2016GL068856 [DOI] [Google Scholar]
- Mauk, B. H. , Fox, N. J. , Kanekal, S. G. , Kessel, R. L. , Sibeck, D. G. , & Ukhorskiy, A. (2013). Science objectives and rationale for the Radiation Belt Storm Probes mission. Space Science Reviews, 179, 3–27. 10.1007/s11214-012-9908-y [DOI] [Google Scholar]
- Merkin, V. G. , & Lyon, J. G. (2010). Effects of the low‐latitude ionospheric boundary condition on the global magnetosphere. Journal of Geophysical Research, 115. 10.1029/2010JA015461 [DOI] [Google Scholar]
- Merkin, V. G. , Panov, E. V. , Sorathia, K. A. , & Ukhorskiy, A. Y. (2019). Contribution of bursty bulk flows to the global dipolarization of the magnetotail during an isolated substorm. Journal of Geophysical Research: Space Physics, 124, 8647–8668. 10.1029/2019JA026872 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyoshi, Y. S. , Jordanova, V. K. , Morioka, A. , Thomsen, M. F. , Reeves, G. D. , Evans, D. S. , & Green, J. C. (2006). Observations and modeling of energetic electron dynamics during the October 2001 storm. Journal of Geophysical Research, 111, A11S02. 10.1029/2005JA011351 [DOI] [Google Scholar]
- Morley, S. K. , Friedel, R. H. W. , Spanswick, E. L. , Reeves, G. D. , Steinberg, J. T. , Koller, J. , et al. (2010). Dropouts of the outer electron radiation belt in response to solar wind stream interfaces: Global positioning system observations. Proceedings of the Royal Society A, 466, 3329–3350. 10.1098/rspa.2010.0078 [DOI] [Google Scholar]
- Morley, S. K. , Henderson, M. G. , Reeves, G. D. , Friedel, R. H. W. , & Baker, D. N. (2013). Phase Space Density matching of relativistic electrons using the Van Allen Probes: REPT results. Geophysical Research Letters, 40, 4798–4802. 10.1002/grl.50909 [DOI] [Google Scholar]
- Pembroke, A. , Toffoletto, F. , Sazykin, S. , Wiltberger, M. , Lyon, J. , Merkin, V. , & Schmitt, P. (2012). Initial results from a dynamic coupled magnetosphere‐ionosphere‐ring current model. Journal of Geophysical Research, 117. 10.1029/2011JA016979 [DOI] [Google Scholar]
- Pollock, C. J. , Moore, T. , Jacques, A. , Burch, J. , Gliese, U. , Saito, Y. , et al. (2016). Fast plasma investigation for magnetospheric multiscale. Space Science Reviews, 199(1), 331–406. 10.1007/s11214-016-0245-4 [DOI] [Google Scholar]
- Roederer, J. G. (1970). Dynamics of geomagnetically trapped radiation. Springer. 10.1007/978-3-642-49300-3 [DOI] [Google Scholar]
- Russell, C. T. , Anderson, B. J. , Baumjohann, W. , Bromund, K. R. , Dearborn, D. , Fischer, D. , et al. (2016). The magnetospheric multiscale magnetometers. Space Science Reviews, 199(1), 189–256. 10.1007/s11214-014-0057-3 [DOI] [Google Scholar]
- Russell, C. T. , & McPherron, R. L. (1973). Semiannual variation of geomagnetic activity. Journal of Geophysical Research, 78(1), 92–108. 10.1029/JA078i001p00092 [DOI] [Google Scholar]
- Russell, C. T. , Raymond, C. A. , Ammannito, E. , Buczkowski, D. L. , De Sanctis, M. C. , Hiesinger, H. , et al. (2016). Dawn arrives at Ceres: Exploration of a small, volatile‐rich world. Science, 353(6303), 1008–1010. 10.1126/science.aaf4219 [DOI] [PubMed] [Google Scholar]
- Shprits, Y. Y. , Thorne, R. M. , Friedel, R. , Reeves, G. D. , Fennell, J. , Baker, D. N. , & Kanekal, S. G. (2006). Outward radial diffusion driven by losses at magnetopause. Journal of Geophysical Research, 111, A11214. 10.1029/2006JA011657 [DOI] [Google Scholar]
- Sorathia, K. A. , Merkin, V. G. , Panov, E. V. , Zhang, B. , Lyon, J. G. , Garretson, J. , et al. (2020). Ballooning‐interchange instability in the near‐earth plasma sheet and auroral beads: Global magnetospheric modeling at the limit of the MHD approximation. Geophysical Research Letters, 47(14), e2020GL088227. 10.1029/2020GL088227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorathia, K. A. , Merkin, V. G. , Ukhorskiy, A. Y. , Allen, R. C. , Nykyri, K. , & Wing, S. (2019). Solar wind ion entry into the magnetosphere during northward IMF. Journal of Geophysical Research: Space Physics, 124(7), 5461–5481. 10.1029/2019ja026728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorathia, K. A. , Merkin, V. G. , Ukhorskiy, A. Y. , Mauk, B. H. , & Sibeck, D. G. (2017). Energetic particle loss through the magnetopause: A combined global MHD and test‐particle study. Journal of Geophysical Research: Space Physics, 122, 9329–9343. 10.1002/2017JA024268 [DOI] [Google Scholar]
- Sorathia, K. A. , Ukhorskiy, A. Y. , Merkin, V. G. , Fennell, J. F. , & Claudepierre, S. G. (2018). Modeling the depletion and recovery of the outer radiation belt during a geomagnetic storm: Combined MHD and test particle simulations. Journal of Geophysical Research: Space Physics, 123, 5590–5609. 10.1029/2018JA025506 [DOI] [Google Scholar]
- Su, Z. , Gao, Z. , Zhu, H. , Li, W. , Zheng, H. , Wang, Y. , et al. (2016). Nonstorm time dropout of radiation belt electron fluxes on 24 September 2013. Journal of Geophysical Research: Space Physics, 121, 6400–6416. 10.1002/2016JA022546 [DOI] [Google Scholar]
- Summers, D. , & Thorne, R. M. (2003). Relativistic electron pitch‐angle scattering by electromagnetic ion cyclotron waves during geomagnetic storms. Journal of Geophysical Research, 108(A4), 1143. 10.1029/2002JA009489 [DOI] [Google Scholar]
- Tao, X. , Bortnik, J. , Thorne, R. M. , Albert, J. M. , & Li, W. (2012). Effects of amplitude modulation on nonlinear interactions between electrons and chorus waves. Geophysical Research Letters, 39, L06102. 10.1029/2012GL051202 [DOI] [Google Scholar]
- Toffoletto, F. , Sazykin, S. , Spiro, R. , & Wolf, R. (2003). Inner magnetospheric modeling with the Rice Convection Model. Space Science Reviews, 107(1–2), 175–196. 10.1023/a:102553200804710.1007/978-94-007-1069-6_19 [DOI] [Google Scholar]
- Tsyganenko, N. A. , & Sitnov, M. I. (2005). Modeling the dynamics of the inner magnetosphere during strong geomagnetic storms. Journal of Geophysical Research, 110, A03208. 10.1029/2004JA010798 [DOI] [Google Scholar]
- Turner, D. L. , Angelopoulos, V. , Li, W. , Hartinger, M. D. , Usanova, M. , Mann, I. R. , et al. (2013). On the storm‐time evolution of relativistic electron phase space density in Earth's outer radiation belt. Journal of Geophysical Research: Space Physics, 118, 2196–2212. 10.1002/jgra.50151 [DOI] [Google Scholar]
- Turner, D. L. , Angelopoulos, V. , Morley, S. K. , Henderson, M. G. , Reeves, G. D. , Li, W. , et al. (2014). On the cause and extent of outer radiation belt losses during the 30 September 2012 dropout event. Journal of Geophysical Research: Space Physics, 119, 1530–1540. 10.1002/2013JA019446 [DOI] [Google Scholar]
- Turner, D. L. , Angelopoulos, V. , Shprits, Y. , Kellerman, A. , Cruce, P. , & Larson, D. (2012). Radial distributions of equatorial phase space density for outer radiation belt electrons. Geophysical Research Letters, 39. 10.1029/2012GL051722 [DOI] [Google Scholar]
- Turner, D. L. , Morley, S. K. , Miyoshi, Y. , Ni, B. , & Huang, C.‐L. (2012). Outer radiation belt flux dropouts: Current understanding and unresolved questions. In Summers D., Mann I. R., Baker D. N., & Schulz M. (Eds.), Dynamics of the Earth's radiation belts and inner magnetosphere (pp. 195–212). American Geophysical Union. 10.1029/2012GM001310 [DOI] [Google Scholar]
- Turner, D. L. , Shprits, Y. , Hartinger, M. , & Angelopoulos, V. (2012). Explaining sudden losses of outer radiation belt electrons during geomagnetic storms. Nature Physics, 8, 208–212. 10.1038/NPHYS2185 [DOI] [Google Scholar]
- Turner, D. L. , & Ukhorskiy, A. Y. (2020). Outer radiation belt losses by magnetopause incursions and outward radial transport: New insight and outstanding questions from the Van Allen Probes era. In Jaynes A. N., & Usanova M. E. (Eds.), The dynamic loss of Earth's radiation belts (pp. 1–28). 10.1016/B978-0-12-813371-2.00001-9 [DOI] [Google Scholar]
- Ukhorskiy, A. Y. , Sitnov, M. I. , Millan, R. M. , & Kress, B. T. (2011). The role of drift orbit bifurcations in energization and loss of electrons in the outer radiation belt. Journal of Geophysical Research, 116. 10.1029/2011JA016623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ukhorskiy, A. Y. , Sitnov, M. I. , Millan, R. M. , Kress, B. T. , Fennell, J. F. , Claudepierre, S. G. , & Barnes, R. J. (2015). Global storm time depletion of the outer electron belt. Journal of Geophysical Research: Space Physics, 120, 2543–2556. 10.1002/2014JA020645 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usanova, M. E. , Drozdov, A. , Orlova, K. , Mann, I. R. , Shprits, Y. , Robertson, M. T. , et al. (2014). Effect of EMIC waves on relativistic and ultrarelativistic electron populations: Ground‐based and Van Allen Probes observations. Geophysical Research Letters, 41, 1375–1381. 10.1002/2013GL059024 [DOI] [Google Scholar]
- Wiltberger, M. , Merkin, V. , Lyon, J. G. , & Ohtani, S. (2015). High‐resolution global magnetohydrodynamic simulation of bursty bulk flows. Journal of Geophysical Research: Space Physics, 120, 4555–4566. 10.1002/2015JA021080 [DOI] [Google Scholar]
- Xiang, Z. , Tu, W. , Li, X. , Ni, B. , Morley, S. K. , & Baker, D. N. (2017). Understanding the mechanisms of radiation belt dropouts observed by Van Allen Probes. Journal of Geophysical Research: Space Physics, 122, 9858–9879. 10.1002/2017JA024487 [DOI] [Google Scholar]
- Xiang, Z. , Tu, W. , Ni, B. , Henderson, M. G. , & Cao, X. (2018). A statistical survey of radiation belt dropouts observed by Van Allen Probes. Geophysical Research Letters, 45, 8035–8043. 10.1029/2018GL078907 [DOI] [Google Scholar]
- Yamauchi, M. , Futaana, Y. , Fedorov, A. , Frahm, R. A. , Winningham, J. D. , Dubinin, E. , et al. (2011). Comparison of accelerated ion populations observed upstream of the bow shocks at Venus and Mars. Annales Geophysicae, 29(3), 511–528. 10.5194/angeo-29-511-2011 [DOI] [Google Scholar]
- Zank, G. P. , Rice, W. K. M. , le Roux, J. A. , & Matthaeus, W. H. (2001). The injection problem for anomalous cosmic rays. Acta Pathologica Japonica, 556, 494–500. 10.1086/322238 [DOI] [Google Scholar]
- Zhang, B. , Sorathia, K. A. , Lyon, J. G. , Merkin, V. G. , Garretson, J. S. , & Wiltberger, M. (2019). GAMERA: A three‐dimensional finite‐volume MHD solver for non‐orthogonal curvilinear geometries. The Astrophysical Journal, 244, 20. 10.3847/1538-4365/ab3a4c [DOI] [Google Scholar]
- Zhao, H. , Baker, D. N. , Li, X. , Jaynes, A. N. , & Kanekal, S. G. (2018). The acceleration of ultrarelativistic electrons during a small to moderate storm of 21 April 2017. Geophysical Research Letters, 45, 5818–5825. 10.1029/2018GL078582 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwickl, R. D. , Krimigis, S. M. , Carbary, J. F. , Keath, E. P. , Armstrong, T. P. , Hamilton, D. C. , & Gloeckler, G. (1981). Energetic particle events (≥30 keV) of Jovian origin observed by Voyager 1 and 2 in interplanetary space. Journal of Geophysical Research, 86(A10), 8125–8140. 10.1029/JA086iA10p08125 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information S1
Data Availability Statement
All MMS data presented here are Level 2 and can be retrieved from the MMS Science Data Center at https://lasp.colorado.edu/mms/sdc/public/. All Van Allen Probes data presented here are Level 2 and can be retrieved from the Van Allen Probes Science Gateway at https://rbspgway.jhuapl.edu/. Additional information on the GAMERA framework can be found at http://cgs.jhuapl.edu/Models/gamera.php.


