A general model for the demographic signatures of the transition from pandemic emergence to endemicity

A realistic age-structured model predicts plausible scenarios for future Covid-19 burden.

Abstract

Anticipating the medium- and long-term trajectory of pathogen emergence has acquired new urgency given the ongoing COVID-19 pandemic. For many human pathogens, the burden of disease depends on age and previous exposure. Understanding the intersection between human population demography and transmission dynamics is therefore critical. Here, we develop a realistic age-structured mathematical model that integrates demography, social mixing, and immunity to establish a plausible range for future age incidence and mortality. With respect to COVID-19, we identify a plausible transition in the age structure of risks once the disease reaches seasonal endemism across a range of immunity durations and relative severity of primary versus subsequent reinfections. We train the model using diverse real-world demographies and age-structured mixing to bound expectations for changing age incidence and disease burden. The mathematical framework is flexible and can help tailor mitigation strategies in countries worldwide with varying demographies and social mixing patterns.

INTRODUCTION

The unfolding pandemic caused by severe acute respiratory syndrome coronavirus-2 (SARS-CoV-2) threatens to be one of the biggest challenges of our time. Mounting evidence suggests a seemingly inevitable resurgence of disease toward endemism in the foreseeable future (1, 2). Identifying the age and burden profiles that may define the years ahead could help improve response preparedness, both for this pandemic and for future emerging pathogens.

A fundamental signature of coronavirus disease 2019 (COVID-19), the disease associated with SARS-CoV-2, is the age manifestation of the burden of infection and morbidity. Following infection by SARS-CoV-2, there is a clear signature of increasingly severe outcomes and fatality with age (3–5). Historical emergence of acute respiratory infections indicates that age-incidence patterns during virgin epidemics can be very different from endemic circulation (6, 7). This motivates efforts to bind the potential future age circulation and fatality to understand the evolving health burden.

Predicting age circulation in the near and mid future (e.g., 1 to 5 years since emergence) requires realistic age-structured (RAS) mathematical models that include characterization of immunity following (re-)infection. Empirical evidence from seasonal coronaviruses indicates that previous exposure may only confer short-term immunity to reinfection, allowing recurrent outbreaks (8, 9). Despite this, previous exposure may prime the immune system to provide protection against severe disease (8, 10, 11) and thus possibly reduce the public health burden of future recurrences. Here, we propose an age-structured multicompartmental susceptible-infectious-recovered-susceptible (SIRS) model that allows projections for future age circulation and disease burden of SARS-CoV-2 virus under various plausible scenarios. We frame our model around a balance between simplicity and flexibility and structure our analysis accordingly. First, to develop a baseline for the transition of age-dependent risk over long-term dynamics, we explore outcomes for a “rectangular demography” (where survival is complete until a maximum age, resulting in a rectangular age pyramid and constant population size) and “homogeneous mixing” (where individuals have equal probability of contact with individuals of all other ages). The purpose of this mass-action, homogeneous mixing model is to provide a baseline for thinking about transitions in age incidence over time. As per all mass-action models of virgin epidemics, the initial post-epidemic trough is unrealistically deep. Using a power-scaling law to allow spatial and social clustering as suggested by Liu et al. (12) will obviously alleviate this but add parameters that do not add to the overall take-home message. The subsequent step is to incorporate demographic and social complexities, including realistic age pyramids and assortative contacts among age groups, both derived from country-specific data.

Our general model projects age-incidence and thus age-morbidity patterns into the future according to chains of differential equations

$$\frac{d{S}_i^p}{\mathit{dt}}=\underset{\text{birth}}{\underbrace{{\mathrm{\mu }}_i\sum N_i}}+\underset{\text{aging in}}{\underbrace{a_{i-1}{S}_{i-1}^p}}-\underset{\text{primary infection}}{\underbrace{{\mathrm{\lambda }}_i{S}_i^p}}-\underset{\text{aging out}}{\underbrace{a_i{S}_i^p}}-\underset{\text{death}}{\underbrace{{\mathrm{\nu }}_i{S}_i^p}}$$ (1)

$$\frac{d{I}_i^p}{\mathit{dt}}=a_{i-1}{I}_{i-1}^p+{\mathrm{\lambda }}_i{S}_i^p-\underset{\text{recovery}}{\underbrace{\mathrm{\gamma }{I}_{\mathrm{i}}^p}}-a_i{I}_i^p-{\mathrm{\nu }}_i{I}_i^p$$ (2)

$$\frac{d{R}_i}{\mathit{dt}}=a_{i-1}{R}_{i-1}+\mathrm{\gamma }(I_i^p+I_i^{\mathit{np}})-\underset{\text{lost immunity}}{\underbrace{\mathrm{\omega }{R}_i}}-a_i{R}_i-{\mathrm{\nu }}_i{R}_i$$ (3)

$$\frac{d{S}_i^{\mathit{np}}}{\mathit{dt}}=\mathrm{\omega }{R}_i+a_{i-1}{S}_{i-1}^{\mathit{np}}-\underset{\text{nonprimary infection}}{\underbrace{{\mathrm{\lambda }}_{\mathrm{i}}{S}_i^{\mathit{np}}}}-a_i{S}_i^{\mathit{np}}-{\mathrm{\nu }}_{\mathrm{i}}{S}_i^{\mathit{np}}$$ (4)

$$\frac{d{I}_i^{\mathit{np}}}{\mathit{dt}}=a_{i-1}{I}_{i-1}^{\mathit{np}}+{\mathrm{\lambda }}_i{S}_i^{\mathit{np}}-\underset{\text{recovery}}{\underbrace{\mathrm{\gamma }{I}_i^{\mathit{np}}}}-a_i{I}_i^{\mathit{np}}-{\mathrm{\nu }}_i{I}_i^{\mathit{np}}$$ (5)

where $S_i^p$ and $I_i^p$ are the number of susceptible individuals and primary infections in age group i. The recovered individuals (R_i) may lose immunity and return to susceptibility ($S_i^{\mathit{np}}$) after an average protected period of 1/ω and subsequently be liable to reinfection; accordingly, $I_i^{\mathit{np}}$ is the number of nonprimary infections in age group i. The force of infection on susceptibles in age class, which is the rate at which any susceptible of age i will be infected, is ${\mathrm{\lambda }}_i=\mathrm{\beta }{\displaystyle {\sum }_j^n}{C}_{\mathit{ij}}(I_i^p+I_i^{\mathit{np}})/N_i$, where β is the baseline rate of transmission given by β = R₀γ and C_ij is the normalized contact rate between age groups i and j. In the below illustration, we assume an 80-year life expectancy and thus a birth rate μ_i = 1/80 year⁻¹ at which people are born to the youngest group in a population of size N_i (i.e., μ_i is 0 for all i > 1). For the baseline model, we assume that a_i is the age-specific rate of aging with a 1-year duration, ν_i is a rate of natural mortality (we assume ν_i = 0 for all i until the rectangular age end point), and 1/γ is the average duration of infection (taken to be 7 days in this analysis). To map our model to realistic demographies and social mixing patterns, we parametrize the model based on a broad range of countries. Details of model parameters are provided in Table 1.

Table 1. SIRS model parameters.

Parameter	Values	Details
Baseline reproduction number, R0	2.30	Estimated
Average duration of infection, 1/γ	7 days	(18)
Immune duration, 1/ω	Short-lived (3 months), 1 year, 10 years, permanent	Assumed
Natural birth rate, μ	1/80 for the youngest class; 0 for all the other age classes	80-year life expectancy
Natural mortality rate, ν	0 for all age classes	Assumed
Average rate of aging, a	1 for all age classes	Reverse of the 5-year age interval
Infection-fatality ratio	age-specific IFR	Estimated from (16)
Demography	age-specific proportion of population	Annualized from (23)
Social mixing pattern, C	age-structured number of contacts	Annualized from (24)

RESULTS

We first identify the broad consequences of the intersection of immunity and burden over immediate, medium, and longer terms (1, 10, and 20 years, respectively), explicitly considering immune scenarios that differ in the degree to which immunity prevents reinfections and/or attenuates severe cases, and then consider realistic demographics and social mixing for 11 different countries chosen to span diverse demographies. Across a 20-year horizon, we assess age-specific risk during a virgin epidemic, medium term, and a scenario of long-term endemic circulation.

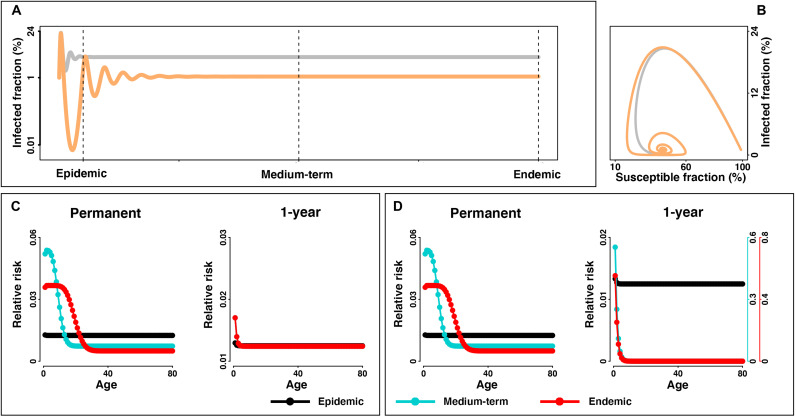
Prevalence is predicted to surge during a virgin epidemic but then recede in a diminishing wave pattern as the spread of the infection unfolds over time toward the (probably seasonally varying) endemic equilibrium (Fig. 1, A and B). Depending on immunity and demography, the virgin epidemic RAS model predicts a notably different age structure than the eventual endemic situation (Fig. 1, C and D, and fig. S1). When considering overall disease burden in the population during a probable transition from emergence to endemicity, our model highlights the importance of three main axes of variability/uncertainty: immune duration, demography, and social mixing. Over the course of emergence, the shift in the age profile of risk of infection and disease is largely dependent on the extent of infection-blocking and disease-reducing immunity. During the transition to endemism in a scenario of long-lasting immunity (assumed permanent or 10 years), the young—who for SARS-CoV-2 suffer a mild burden of disease—is predicted to have the highest rates of infection once the disease dynamics moves toward the steady state (Fig. 1C and fig. S1A), as older individuals are protected from infection by previous infection. If immunity to reinfection is brief (assumed short-lived 3 months or 1 year), changes in disease severity due to previous exposure are the main driver of changes to age-structured risk and long-term burden of mortality. The possibility of rapid reinfection and severe outcomes on reinfection would heighten long-term circulation and continued high-risk infection among adults, although it could modulate the age profile of risk over time (Fig. 1C and fig. S1A). In contrast, if disease symptoms on reinfection are attenuated, the burden of disease may decay over time even if duration of sterilizing immunity is short-lived and reinfection is frequent. In the latter scenario, the age profile of primary infections will define the shifting risk over time, and primary infection recedes to younger individuals as an emerging acute respiratory infection moves toward endemicity (Fig. 1D and fig. S1B).

Fig. 1. Trajectory of infected fraction and transitions in age structure of the risk from virgin epidemic to endemic equilibrium.

(A) Infected fraction for an outbreak is simulated with R₀ = 2.3, 1/γ = 7 days, and a short-lived (i.e., 3 months) (gray) and 1-year (orange) immunity duration over 20 years. The SIRS model is parameterized with rectangular demographic structure and homogeneous social mixing pattern. Dashed lines indicate different stages of disease dynamics. For visualization, only trajectories in scenarios of short-lasting (i.e., short-lived and 1 year) are presented. (B) Infected versus susceptible fraction. If primary and nonprimary infections have similar illness, (C) shows relative risk (i.e., age-specific infected fraction relative to the population-wide fraction) among age groups in the virgin epidemic, medium-term, and endemic stage under the scenario of permanent and 1-year immunity duration, respectively. If nonprimary infections are less severe, (D) shows relative risk from primary infections. Relative risk among age groups under the scenario of permanent, 10-year, 1-year, and short-lived immunity durations is shown in the Supplementary Materials (see fig. S1).

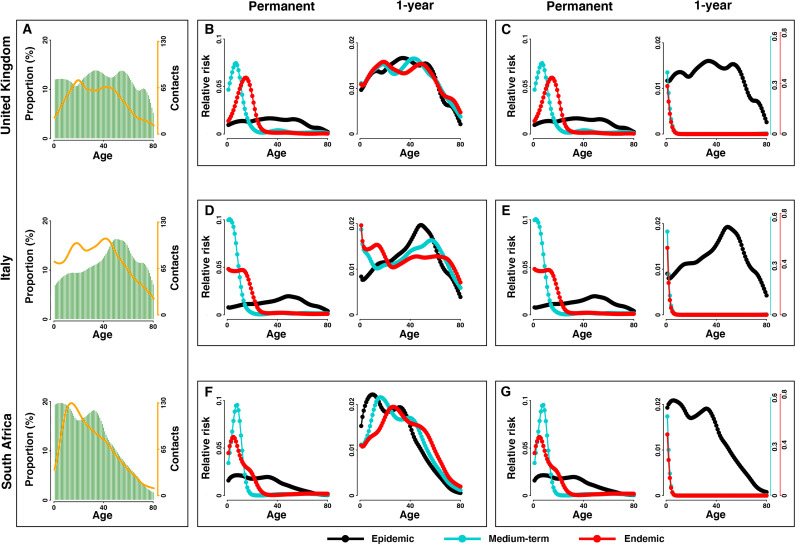
Our general model framework allows robust predictions regarding transition in the age profile of risk in the face of either short-/long-term protective immunity, reduction of severity of disease given previous exposure, and consideration of the range of countries with their different demographies and social mixing patterns (Fig. 2 and figs. S2 to S6). Broadly speaking, we find that immune scenarios are the dominant driver of transitions in age dependence and risk toward endemicity, although our framework to incorporate realistic demographies and social mixing patterns to modulate the relative risk is likely to provide a critical infrastructure for policy decision-making.

Fig. 2. Transitions in age structure of the risk in different countries.

With (A) demographic structure (greens bars) and social mixing pattern (orange lines) in United Kingdom, Italy, and South Africa, (B) to (G) show the relative risk among age groups in the virgin epidemic, medium-term, and endemic stages in the scenario of permanent and 1-year immunity durations. Risk from (B, D, and F) all infections and (C, E, and G) only primary infections is explicitly distinguished. Relative risk among age groups under the scenario of permanent, 10-year, 1-year, and short-lived immunity durations is shown in the Supplementary Materials (see fig. S2).

Assuming that previous exposure reduces severity of respiratory reinfections, the model’s projected transition is broadly consistent with those documented in several historical respiratory pandemics. In particular, the critical importance of both age and previous exposure on disease burden and mortality following the 1918 pandemic has been well characterized: The elderly were protected by immunity from previous exposure to an earlier A/H1N1-related strain, but within some years, the overall burden of mortality receded (6, 13, 14). Ongoing genomic work following on (15) tantalizes that the million-killing 1889/1890 pandemic could have been caused by the emergence of HCoV-OC43, which is now an endemic mild repeat–infecting coronavirus.

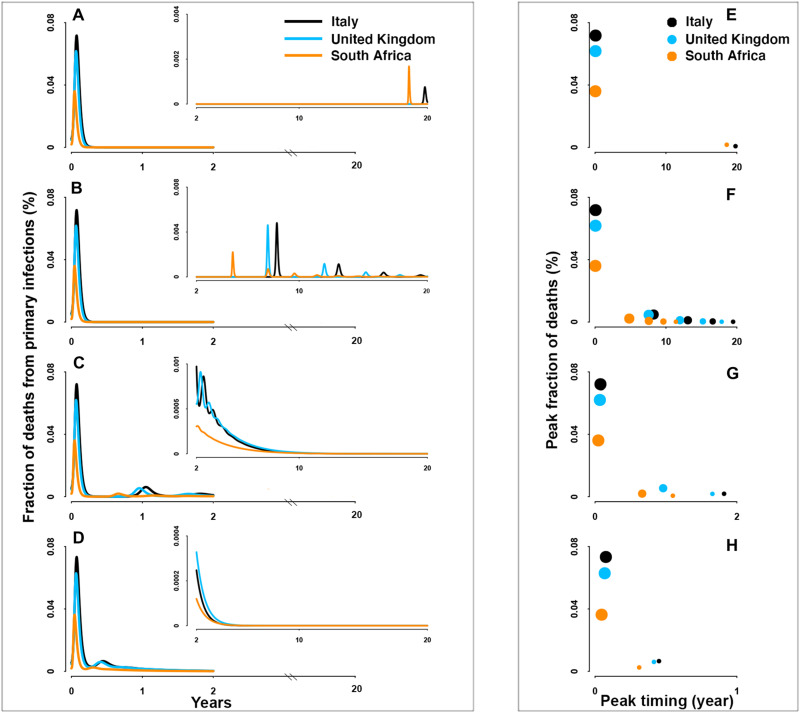
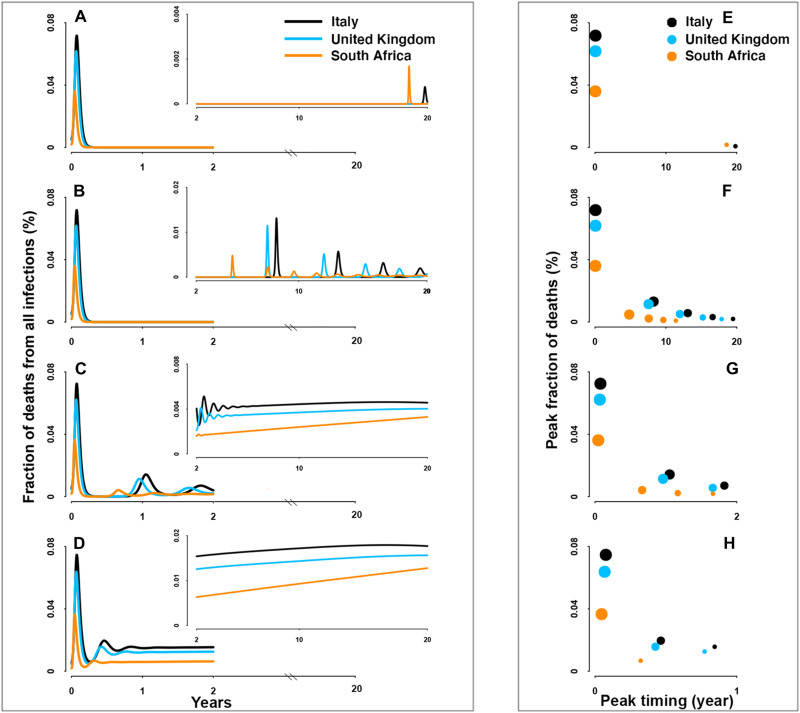
For SARS-CoV-2 preparedness, our model provides a robust framework for scenario analyses for the future. Irrespective of parametric uncertainties, the burden of mortality will peak during the virgin epidemic period (Figs. 3 and 4). The predicted magnitude of this peak is moderately affected across a plausible range of immune durations and immunity-modulated severity upon re-exposure (figs. S7 and S8). By contrast, post-pandemic burden during endemicity is shown to be strongly dependent on immune function and previous infection history as it affects infection probability and disease severity. Milder disease from reinfections (Fig. 3 and fig. S7) would give rise to decreasing mortality due to the reduction of severe cases, while burden of mortality over time may remain unchanging if primary infections do not prevent reinfections or mitigate severe disease among the elderly (Fig. 4 and fig. S8). In this bleakest scenario, excess deaths due to continual severe reinfections that result from the continuous replenishment of susceptibles via waning of immunity to reinfection will continue until effective pharmaceutical tools are available.

Fig. 3. Fraction of deaths from primary infections.

(A to D) Overall fraction of deaths over 20 years and (E to H) the timing and magnitude of consecutive peaks in the scenario of permanent, 10-year, 1-year, and short-lived (i.e., 3-month) immunity durations, respectively. Countries with different demographies and social mixing patterns are distinguished by color: Italy (black), United Kingdom (blue), and South Africa (orange). For visualization, insets show trajectories following the first 2 years.

Fig. 4. Fraction of deaths from all infections.

(A to H) Same as Fig. 3 but for deaths from both primary and nonprimary infections.

A final insight from our detailed RAS model is that regardless of immunity and mixing, the population-level burden of mortality may differ among countries because of varying demographies. Given the marked increase of infection-fatality ratio (IFR) with age, countries with older population structure would be expected to have a typically larger fraction of deaths than those with relatively younger population structure (once corrected for differences in public health infrastructure). Consistent with this, South Africa, partially due to its younger population structure, has a lower fraction of deaths as compared with older populations such as Italy. These “deaths disparities” among demographies are largely invariant over the unfolding pandemic, although young people would be predicted to contribute most to burden in the endemic era. When comparing the relative importance on the overall burden of mortality, we show that the varying demographies are a key determinant of the disparities among countries (see the “Relative effect of demographies and social mixing patterns” section in Supplementary Text; figs. S9 and S10).

DISCUSSION

Our RAS SIRS model provides a general framework to explore various scenarios for the possible unfolding of the current and future pandemic crises in the face of country-specific demographies, social mixing patterns, and the inevitable main unknowns for any emergence such as immune duration and immune mitigated reduction in severity of disease. Through the integration of age structure, social mixing, and immunity, our projections using SARS-CoV-2 as a focus for considering the broader issue, we highlight how risk will shift over time to different age classes that may suffer different burden of disease during an endemic state. Such a shift will be not only very strong if immunity is long-lived but also of great public health significance if immunity to reinfection wanes, yet previous exposure attenuates severity of disease.

By highlighting a wide range of scenarios, our model framework is a robust scaffolding to help improve preparedness and mitigation of the current and future pandemics. Furthermore, our RAS SIRS model makes critical contributions to understanding how the highly variable social context, particular demography, and age-structured mixing patterns may modulate current and future disease burden. Building upon our framework (including the detailed and documented code provided in the Supplementary Materials), health authorities will have a powerful and flexible tool to conceptualize future age circulation, strengthening context-specific preparedness and deployment of interventions. The model will handily accommodate additional uncertainties/variabilities as evidence is accumulated in the coming months and years.

Our RAS model makes several assumptions. First, we focus on the infection-blocking immunity. Incorporating realistic immunity efficacy with respect to susceptibility, transmission, and severity is an important direction for expansion. Second, we assume a general formulation for the epidemic model. This should be considered as the starting point for the extension to encompass disease-specific mechanisms. Furthermore, we assume a homogeneous susceptibility to infection, clinical fraction, and infection versus case-fatality ratio across age classes. Relaxing our assumptions by explicitly consider age-specific heterogeneities (8, 16, 17) is an important future direction. Last, we assume an exponential decay of immunity within each age class, which leads to a Gamma distributed loss over time. We believe that this is a realistic model that still needs to be further refined with the mounting clinical and empirical studies (see Supplementary Text for details of the assumptions and directions for further extensions).

MATERIALS AND METHODS

Model parameterization

Transition rates

In the base model, we assume an 80-year life expectancy and thus a birth rate μ_i = 1/80 year⁻¹ at which people are born to the youngest group in a population of size N_i (i.e., μ_i is 0 for all i > 1). We assume a_i to be the age-specific rate of aging with a 1-year duration (i.e., a_i = 1 for all i). ν_i is a rate of natural mortality, which is assumed 0 for all age classes until the rectangular age end point (i.e., ν_i = 0 for all i). 1/γ is the average duration of infection, which in the analysis is taken to be 7 days (18). We further explore its variability on epidemiological trajectories (see the “Sensitivity analyses” section). In the RAS model with country-specific population pyramid and contacts over age, we retain the assumption of zero mortality across ages below the maximum age, the same birth rate to the youngest group and the same aging rate across countries, as this will result in a broadly consistent age structure (appropriate to human demography where transients play out extremely slowly).

Estimating the reproduction number

The reproduction number is a critical parameter for our model projections. Social distancing is well documented to affect transmissibility (19), and many countries implemented such interventions during the buildup of the virgin epidemic. Given this, we assume that the effective reproduction number, i.e., the level of transmissibility, on day t, R_t, is linked to the reduced mobility on that day, m_t, via

$$\text{log}(R_t)=\text{log}(R_0)-\mathrm{\beta }{m}_t$$

where R₀ is the basic reproductive number in the absence of behavioral changes and β is the transmission rate. Reduced mobility leads to reductions in the effective reproduction number. When the reduction of mobility/mixing is 0%, R₀ provides the baseline transmissibility parameter. We use China as the reference point.

We used daily confirmed cases in China (20) and extract mobility from the Baidu database (21) in the period of 1 January to 5 March 2020. With these cases, we estimate R_t using a 14-day sliding time window using EpiEstim package (22), assuming a mean of 5.1 days and SD of 5.3 days of the serial interval (23). We then exclude estimates of R_t before 15 January 2020 in subsequent analysis, given the limited number of cases and thereby large uncertainty of R_t. We also trim the estimates of R_t after 20 February 2020 (i.e., 4 weeks after lockdown on 23 January 2020) when mobility rebounded but was not a strong correlate of reductions in R_t since then. With estimates of R_t and mobility data from 15 January to 20 February 2020 (fig. S12), we establish the transmissibility-mobility association and estimate R₀ using generalized linear model with a negative binomial link function. Note that we do not tend to explicitly fit the documented cases or optimize every transmission parameter; instead, we capture R₀ to characterize the overall basic transmissibility. The estimated R₀ is subsequently used as the baseline to simulate dynamics of COVID-19 in the age-structured SIRS model framework (see below). Furthermore, we examine how different demographies are predicted to modulate country-specific R₀’s away from the early Chinese baseline (see the “Variation of transmissibility among countries” section in Supplementary Text).

Demographics and age-structured social mixing patterns

To fully characterize the long-term age circulation across the globe, we select 11 countries across a broad range of demographic and social mixing patterns. The countries cover Asia (China, Japan, and South Korea), Europe (Spain, United Kingdom, France Germany, and Italy), North America (United States), South America (Brazil), and Africa (South Africa). For these countries, we collected age pyramids from the statistics of the United Nations (24) and country/age-specific number of contacts from Prem et al. (25). We further annualized these data to generate the finer age profile into the 1-year age brackets necessary for model predictions (fig. S13).

Age-specific IFR

Pilot studies have shown an increased IFR with age. We collect the posterior estimates of IFR from Verity et al. (17) and subsequently project them onto the 80 age groups in our study to predict burden.

Model projections

Given the RAS SIRS equations defined in Eqs. 1 to 5, we numerically integrate the model to predict dynamics of COVID-19 for the next 20 years using a variety of scenarios spanning a range of current unknowns. For each scenario, simulation was initialized with 1% infections and 0.1% recovered individuals, i.e., S^p(0) = 0.989, I^p(0) = 0.01, R = 0.001, and S^np(0) = I^np(0) = 0.

For initial insights, we studied the base model using a rectangular demography (i.e., in the absence of infection, everybody is expected to live to the age of 80, resulting in a rectangular age pyramid and constant population size) and homogeneous mixing (i.e., individuals have equal probability of contact with individuals of all other ages) under four different durations of immunity, i.e., the short-lasting immunity assumed as (i) short-lived (3 months) or (ii) 1 year and the long-lasting immunity assumed as (iii) 10 years or (iv) permanent (or lifelong). Notably, in the scenarios where reinfection is possible, functional immunity to disease may still vary (8, 10, 11). Given this, we explicitly consider two scenarios that differ in the severity of reinfections. We first assume an independence of disease severity from previous exposure, so the burden of disease depends on the sum of both primary and nonprimary infections. Alternatively, we assume that previous immunity may mitigate disease severity. In which case, milder reinfections are assumed of no contribution to shaping the epidemiological trajectories, and thus, public health burden depends on age profiles of primary infections.

Next, we contextualize the transition in age circulation for the 11 selected countries (see the “Demographics and age-structured social mixing patterns” section). We add greater demographic and social complexity to the base model, by initiating the population with country-specific age pyramids and social mixing patterns obtained as described above. We then simulate the models with a broadly consistent age structure where transients play out extremely slowly by retaining the assumption of zero mortality across ages below the maximum age and the same birth rate to the youngest group across countries (see the “Transition rates” section). This helps titrate how these variables may lead to varying patterns among countries. Relative risk among age groups is defined as the infected fraction in each age group relative to that in a population as a whole. To assess plausible transitions toward endemicity, we estimate relative risk in the 1st, 10th, and 20th year following emergence (hereafter as the virgin epidemic, medium-term, and probable endemic phases, respectively). Last, we project the trajectories of deaths in the selected countries under a variety of immune scenarios. The population-level fraction of deaths, i.e., burden of mortality, is estimated by multiplying the age-specific infected fraction with IFR. We assumed an invariant IRF for primary and nonprimary infections. Consistent with the above assessment of changing age structure, we examine the scenario with different duration of immunity and possible mitigation of illness due to previous exposure. To evaluate the relative importance of demography and social mixing pattern, we further simulate the model by using the assumed homogeneous mixing patterns (see the “Relative effect of demographies and social mixing patterns” section in Supplementary Text).

Sensitivity analyses

We validate our findings and insights by examining the uncertainty that may arise from the assumed duration of infection and model formulation. More specifically, we investigate the dynamics of disease burden by assuming an array of the average duration of infection, including 5, 9, and 11 days. In addition, we formulate a SEIRS model by explicitly incorporating the exposure (E) component and asymptomatic infections

$$\frac{d{S}_i^p}{\mathit{dt}}=\underset{\text{birth}}{\underbrace{{\mathrm{\mu }}_i\sum N_i}}+\underset{\text{aging in}}{\underbrace{a_{i-1}{S}_{i-1}^p}}-\underset{\text{primary infection}}{\underbrace{{\mathrm{\lambda }}_i{S}_i^p}}-\underset{\text{aging out}}{\underbrace{a_i{S}_i^p}}-\underset{\text{death}}{\underbrace{{\mathrm{\nu }}_i{S}_i^p}}$$ (6)

$$\frac{d{E}_i^p}{\mathit{dt}}=a_{i-1}{E}_{i-1}^p+{\mathrm{\lambda }}_i{S}_i^p-\underset{\text{latency}}{\underbrace{\mathrm{\sigma }{E}_i^p}}-a_i{E}_i^p-{\mathrm{\nu }}_i{E}_i^p$$ (7)

$$\frac{d{I}_i^{p,\mathit{sym}}}{\mathit{dt}}=a_{i-1}{I}_{i-1}^p+{\mathrm{\rho }}_2\mathrm{\sigma }{E}_i^p-\underset{\text{recovery}}{\underbrace{\mathrm{\gamma }{I}_i^{p,\mathit{sym}}}}-a_i{I}_i^{p,\mathit{sym}}-{\mathrm{\nu }}_i{I}_i^{p,\mathit{sym}}$$ (8)

$$\frac{d{I}_i^{p,\mathit{asym}}}{\mathit{dt}}=a_{i-1}{I}_{i-1}^{p,\mathit{asym}}+(1-{\mathrm{\rho }}_2)\mathrm{\sigma }{E}_i^p-\underset{\text{recovery}}{\underbrace{\mathrm{\gamma }{I}_i^{p,\mathit{asym}}}}-a_i{I}_i^{p,\mathit{asym}}-{\mathrm{\nu }}_i{I}_i^{p,\mathit{asym}}$$ (9)

$$\frac{d{R}_i}{\mathit{dt}}=a_{i-1}{R}_{i-1}+\mathrm{\gamma }(I_i^p+I_i^{\mathit{np}})-\underset{\text{lost immunity}}{\underbrace{\mathrm{\omega }{R}_i}}-a_i{R}_i-{\mathrm{\nu }}_i{R}_i$$ (10)

$$\frac{d{S}_i^{\mathit{np}}}{\mathit{dt}}=\mathrm{\omega }{R}_i+a_{i-1}{S}_{i-1}^{\mathit{np}}-\underset{\text{nonprimary infection}}{\underbrace{{\mathrm{\lambda }}_{\mathrm{i}}{S}_i^{\mathit{np}}}}-a_i{S}_i^{\mathit{np}}-{\mathrm{\nu }}_i{S}_i^{\mathit{np}}$$ (11)

$$\frac{d{E}_i^{\mathit{np}}}{\mathit{dt}}=a_{i-1}{E}_{i-1}^{\mathit{np}}+{\mathrm{\lambda }}_i{S}_i^{\mathit{np}}-\underset{\text{latency}}{\underbrace{\mathrm{\sigma }{E}_i^{\mathit{np}}}}-a_i{E}_i^{\mathit{np}}-{\mathrm{\nu }}_i{E}_i^{\mathit{np}}$$ (12)

$$\frac{d{I}_i^{\mathit{np},\mathit{sym}}}{\mathit{dt}}=a_{i-1}{I}_{i-1}^{\mathit{np}}+{\mathrm{\rho }}_2\mathrm{\sigma }{E}_i^{\mathit{np}}-\underset{\text{recovery}}{\underbrace{\mathrm{\gamma }{I}_i^{\mathit{np},\mathit{sym}}}}-a_i{I}_i^{\mathit{np},\mathit{sym}}-{\mathrm{\nu }}_i{I}_i^{\mathit{np},\mathit{sym}}$$ (13)

$$\frac{d{I}_i^{\mathit{np},\mathit{asym}}}{\mathit{dt}}=a_{i-1}{I}_{i-1}^{\mathit{np},\mathit{asym}}+(1-{\mathrm{\rho }}_2)\mathrm{\sigma }{E}_i^{\mathit{np}}-\underset{\text{recovery}}{\underbrace{\mathrm{\gamma }{I}_i^{\mathit{np},\mathit{asym}}}}-a_i{I}_i^{\mathit{np},\mathit{asym}}-{\mathrm{\nu }}_i{I}_i^{\mathit{np},\mathit{asym}}$$ (14)

For simplicity, we assume that the average duration of incubation (δ) is 6.4 days (26), the infectiousness of asymptomatic (ρ₁) is half (50%) of that of symptomatic infections, and the proportion of asymptomatic infections (ρ₂) is 40% (27). The force of infection on susceptibles in age class i is defined by ${\mathrm{\lambda }}_i=\mathrm{\beta }{\displaystyle {\sum }_j^n}{C}_{\mathit{ij}}(I_i^{p,\mathit{sym}}+I_i^{\mathit{np},\mathit{sym}}+{\mathrm{\rho }}_1(I_i^{p,\mathit{asym}}+I_i^{\mathit{np},\mathit{asym}}))/N_i$, where superscripts sym and asym denote the symptomatic and asymptomatic infections, respectively. β is the baseline rate of transmission given by β = R₀γ, and C_ij is the normalized contact rate between age groups i and j. We simulate the model and estimate the age-specific risk in the scenario of the rectangular demography and homogeneous mixing.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/33/eabf9040/DC1