Spinel oxide enables high-temperature self-lubrication in superalloys

Abstract

The ability to lubricate and resist wear at temperatures above 600 °C in an oxidative environment remains a significant challenge for metals due to their high-temperature softening, oxidation, and rapid degradation of traditional solid lubricants. Herein, we demonstrate that high-temperature lubricity can be achieved with coefficients of friction (COF) as low as 0.10-0.32 at 600-900 °C by tailoring surface oxidation in additively-manufactured Inconel superalloy. By integrating high-temperature tribological testing, advanced materials characterization, and computations, we show that the formation of spinel-based oxide layers on superalloy promotes sustained self-lubrication due to their lower shear strength and more negative formation and cohesive energy compared to other surface oxides. A reversible phase transformation between the cubic and tetragonal/monoclinic spinel was driven by stress and temperature during high temperature wear. To span Ni- and Cr-based ternary oxide compositional spaces for which little high-temperature COF data exist, we develop a computational design method to predict the lubricity of oxides, incorporating thermodynamics and density functional theory computations. Our finding demonstrates that spinel oxide can exhibit low COF values at temperatures much higher than conventional solid lubricants with 2D layered or Magnéli structures, suggesting a promising design strategy for self-lubricating high-temperature alloys.

The authors develop an approach for enhancing the wear resistance and lubricity of metals at elevated temperatures of in oxidative environments, where traditional solid lubricants fail. By engineering surface oxidation in additively manufactured Inconel, they achieve low friction coefficients, between 0.10 and 0.32 at 600-900 °C, through the formation of a spinel-based oxide layer.

Introduction

The ability to lubricate and resist wear at temperatures above 600 °C in an oxidative environment remains a significant materials challenge for metallic systems requiring high-speed and long operational life^1–3. Various liquid and solid lubricants have been developed to reduce high-temperature friction and wear on metallic surfaces. However, most of them fail at temperatures above 600 °C due to oxidation or structural decomposition. For example, graphite and molybdenum disulfide oxidize and degrade rapidly beyond 350 °C^4,5. So far, only about 20 solid lubricating phases have been identified after decades of experimental study. The structural origin of these lubricating materials is related to their 2D layered (e.g. MoS₂, WS₂, MoO₂, Re₂O₇, h-BN, graphite)⁶ or Magnéli structure (e.g. V₂O₅, Bi₂O₃, Ti₄O₇, BaS)⁷. The elastic shear constant C₄₄ for Magnéli and 2D phases is low due to the distorted metal–oxygen octahedral architecture, resulting in large inter-layer distances⁵. Density functional theory (DFT) calculations show that the decohesion energy in such structures is governed by a shielded Coulomb interaction between the interlayers, whose relatively large distance results in weak coupling and easily plastically deformable structures⁵. The low inter-layer bonding strength in these solid lubricants leads to the desired lubrication at temperatures below 600 °C, but unfortunately, such structural bonding breaks down at high temperatures, limiting their usage under extreme conditions.

To minimize the overall material loss at high temperatures, a wear-resistant and self-lubricating surface is desired. In reality, a high strength, yet abrasive surface is often achieved in refractory metals, whereas soft yet lubricious surface is often achieved in 3d transition metals^4,5. Neither is ideal. Incorporating the lubricous phases inside a strong metal matrix could be a convenient way to harness the traits of both. This is demonstrated in the temperature-adaptive chameleon lubricating systems (e.g. VN–Ag, NbN–Ag)⁵. However, the incorporation of these lubricating particles in metal matrix composites often results in a wear-friction tradeoff (i.e. reduction of friction at the cost of wear resistance) and poor fracture resistance^8,9. If the metal itself, such as widely used Ni-based superalloy Inconel 718, renowned for its exceptional mechanical stability and corrosion resistance up to 650 °C^10,11, undergoes oxidation to generate a lubricious surface layer at elevated temperatures, the addition of additional lubricating particles becomes unnecessary, thereby alleviating the previously mentioned challenges. Nevertheless, previous work showed that Inconel 718^12,13 forms an abrasive surface oxide layer (glaze layer) with COFs over 0.65 from 600 to 750 °C.

In the realm of metal manufacturing, the manufacturing process directly influences the surface properties of the metal. We hypothesize that additively manufactured Inconel 718 may exhibit distinct oxidation phases resulting in unique lubricant surface properties. By serendipitous discovery, we demonstrate that spinel-based oxides formed on the surface of additively manufactured Inconel 718 results in average COFs as low as 0.13–0.34 at 600–900 °C, promoting sustained self-lubrication. Unlike prior studies, we heat treat the as-printed (AP) Inconel 718 to allow the formation of high-density interphase boundary, which promotes the formation of lubricious spinel oxide layers to lower surface friction and reduce wear. To further promote sustained self-lubrication, we employed a small sliding speed of 0.01 m/s to allow adequate oxidation between successive wear passes using a high-temperature tribometer with temperature control up to 1000 °C (Fig. 1a, b). Through multi-scale materials characterization and computation studies, we show that during high-temperature wear, the surface oxidation of Cr and mixed transition metals lead to the formation of AB₂O₄ (A = Ni, Fe and B = Cr, Fe) spinel oxides, whose structural incommensurability between the AO₄ tetrahedra and BO₆ octahedra layers generate structural lubricity at high temperature, as opposed to abrasive Cr-rich corundum-structured oxides with only octahedra layers. Our work demonstrates that self-lubrication and high-temperature wear resistance can co-exist in spinel-covered Ni-based superalloy, which establishing a material design strategy to transform abrasive oxides to lubricous oxides beyond traditional operating temperatures via appropriate alloying.

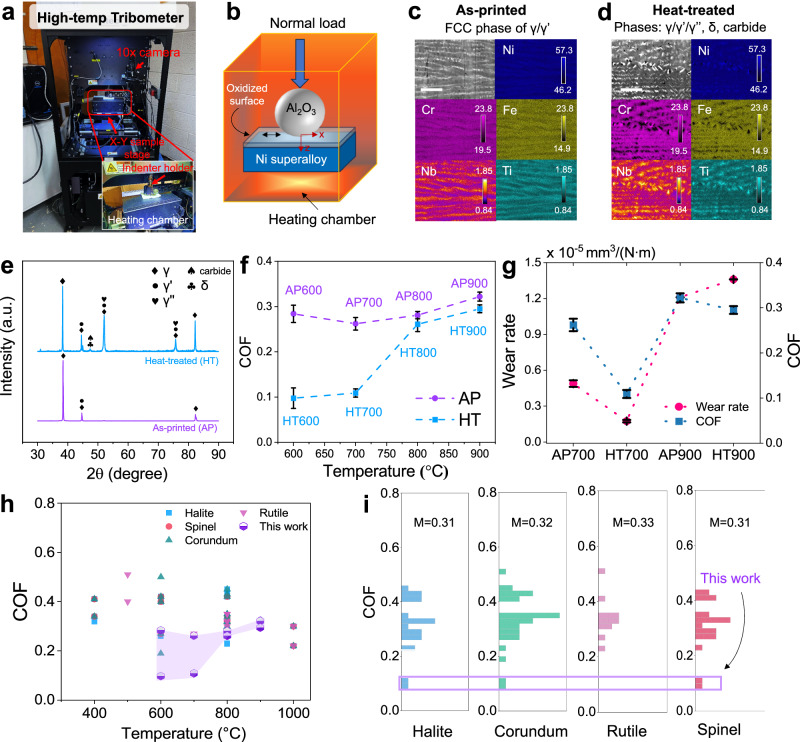
Fig. 1. Experimental setup and high-temperature tribological behavior.

a Photo and b schematic illustration of the high-temperature tribometer. x- and y- in (b) represent frictional (F_x) and normal force (F_z) directions, respectively. c, d Backscattered scanning electron microscope images and corresponding elemental maps from wavelength-dispersive spectrometer (WDS) in as-printed (AP) and heat-treated (HT) Inconel 718 samples before wear test. Scale bar: 4 µm. Compositional scale range (min, max): Ni (46.2, 57.3 at.%), Cr (19.5, 23.8 at.%), Fe (14.9, 23.8 at.%), Nb (0.84, 1.85 at.%), Ti (0.84, 1.85 at.%). e X-ray diffraction patterns of samples before wear test. f COF of AP and HT samples from 600 to 900 °C. Error bar is standard deviation from three tests. g Wear rate (defined as total volume loss divided by the sliding distance and normal load) and COF of AP and HT samples at 700 and 900 °C. Error bar is the standard deviation from nine measurements. h Summary of COF from literature and this work using Al₂O₃ as counter body. For surface with more than one oxide type, all oxides are plotted as overlapping points in (h). i COF histogram of various oxides (halite, corundum, rutile, and spinel). M in (i) represents the average value of the COF. Data used in (h) and (i) are provided in the Source Data file. AP and HT represent as-printed and heat-treated, respectively.

Results

High-temperature tribological behavior of Inconel 718

Inconel 718, a precipitation-hardened Ni–Cr alloy, consists of a Ni-rich γ matrix with three intermetallic precipitation phases: (1) γ′ with a composition of Ni₃(Al, Ti) and a face-centered cubic structure, (2) γ″ with a composition of Ni₃Nb and a body-centered tetragonal structure, and (3) δ phase with a composition of Ni₃Nb and an orthorhombic crystal structure^14,15. Conventional manufacturing of Inconel 718 is challenging due to its thermally stable precipitates, particularly when working with complex shapes when the machine parts themselves are often made of a similar material. We fabricated Inconel 718 additively via selective laser melting (SLM). In addition to the AP condition, we performed heat treatment on half of the samples based on thermodynamic calculations (calculation details in Supplementary Section 1; fabrication and heat treatment steps in the “Methods” section). Briefly, starting from ∼750 K (∼477 °C), the precipitation of γ′ phase occurs. At the two aging temperatures 894 K (∼621 °C) and 991 K (∼718 °C), Cr content in the alloy matrix were 19.05 and 20.11 wt% respectively, slightly larger than that of the AP Inconel 718 (∼19.00 wt%).

We first investigated the microstructure of the AP and heat-treated (HT) Inconel samples before the wear test (Fig. 1c–e). We found that AP samples exhibited γ and γ′ phases (Fig. 1e), which resulted in a rather uniform contrast under backscattered SEM (Fig. 1c). Upon heat treatment, additional γ″, carbide, and δ phases appeared^15,16. The Nb-enriched acicular inter-dendritic δ phases, as confirmed by the wavelength-dispersive spectrometer (WDS) mapping (Fig. 1d), were apparent as the white contrast with lath morphology (Fig. 1d). The overlap observed in the Ti map indicates a coexistence of δ and γ′ phases¹⁷. The broader Nb-rich areas surrounding the needle-like δ structures suggest the presence of the γ″ phase. Laves phase was not detected in neither AP or HT samples since the solidification rates in SLM were very high, 10³–10⁶ °C/s, unlike that from traditional casting or welding¹⁸. These results indicate that heat treatment leads to a more pronounced and ordered distribution of secondary phases, which increases the interphase boundary density compared to the AP state. Phase boundary is important for Cr diffusion due to its propensity for segregation¹⁹ and its potential to achieve a higher diffusion coefficient²⁰. More extensive phase boundary coverage in HT samples results in shortened diffusion pathway and more uniform surface distribution of Cr compared to AP samples (detailed analysis in Supplementary Information Section 1.4). We find such uniform Cr distribution promotes the formation of layered spinel oxides and minimizes the formation of spherical corundum structures (vide infra), which is essential for surface lubrication.

We then investigated the tribological behavior of Inconel 718 under different processing conditions at high temperature using a high-temperature tribometer with a ball-on-plate configuration (Fig. 1a, b). In our setup, the two bodies in contact are alumina ball (Al₂O₃, diameter of 6.35 mm) and flat Inconel 718 coupons fabricated via SLM, in reciprocal relative motion (detailed testing parameters and conditions are provided in the “Methods” section). Hereafter, AP600, AP700, AP800, and AP900 represent AP samples subjected to wear test under 600, 700, 800, and 900 °C, respectively, and likewise for HT samples. In the testing conditions from 600 to 900 °C, HT samples exhibited lower COF values, suggesting that they are more lubricious than AP samples (Fig. 1f). Unlike the temperature-adaptive chameleon lubricating composites such as VN–Ag and NbN–Ag⁵ that show a wear-friction tradeoff, we found that wear rate also tend to be lower when COF was smaller, such as those observed at 700 °C (Fig. 1g). The overall wear rate is on the order of ∼10⁻⁵ mm³/(N·m), which is one order of magnitude smaller than those reported for similar materials worn at room temperature¹⁵. Notably, at 700 °C, heat treatment results in a significant reduction in both wear and friction, yet such an effect is negligible at 900 °C. These results indicate that heat treatment after SLM leads to the formation of a more lubricious surface than that of the AP state at all temperatures studied.

In a two-body contact scenario, material transfer between the two surfaces (i.e. the Al₂O₃ ball and Inconel surface) could affect the overall tribological response. Detailed characterization of the Al₂O₃ ball after the wear test (see Supplementary Information Sections 4.5, 4.6) reveals that material was primarily transferred from the Inconel surface to the Al₂O₃ ball during high-temperature wear, with the transferred material consisting mainly of oxidized Inconel. Stott¹ suggested that low sliding speed, low load, and high oxidation rates reduce wear at 400–600 °C. However, our results indicate that increasing the temperature from 700 to 900 °C leads to a higher COF and wear rate, despite increased oxidation. This suggests that the structure and properties of the oxide layer, rather than its thickness, are crucial in determining the tribological response.

The wear track morphology on both the Al₂O₃ ball and Inconel surfaces indicates the wear mechanism changed from mild oxidational wear at 700 °C to moderate oxidational wear at 900 °C (Supplementary Information Section 4.1). Notably, the contacting surface on HT700 is even larger than that of AP700 (Supplementary Fig. 32b, c). As shown in Supplementary Fig. 5, HT700 has a higher hardness than AP700 at 700 °C, which is often assumed to result in a smaller contact area²¹, should there be no oxide layer present. These results indicate that (1) oxide reactively formed on Inconel surface is mainly affecting the frictional response and contact geometry, and (2) the low COF and wear rate of HT samples is mainly due to that lubricious oxide formed on Inconel as a result of heat treatment, while the AP samples form oxides that are more abrasive.

We conducted a literature review of high-temperature COF as a function of surface oxides formed on various metals against an Al₂O₃ counter body from room temperature to 1000 °C (Fig. 1h, i, references provided in Supplementary Section 3.2, and raw data in the Source Data file). Our HT600 and HT700 samples exhibit the lowest COF values among all reported oxides at high temperatures (purple shaded area in Fig. 1h), with average values of 0.10 (standard deviation: 0.023) for HT600 and 0.11 (standard deviation: 0.009) for HT700, respectively. This suggests the exceptional lubricating properties of the oxidized surface of SLM Inconel 718. Our analysis shows that spinel oxides are more lubricious than halite, corundum, and rutile structured oxides (Fig. 1i), which motivated us to study the surface oxide phase of AP vs. HT samples worn at 700 and 900 °C.

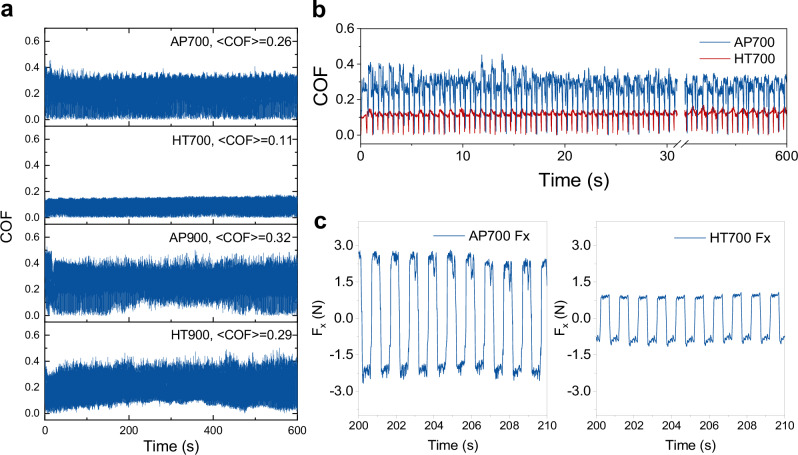
We began to study the temporal evolution of COF of AP and HT samples, which were recorded at a sampling frequency of 100 Hz, or 0.01 s per data step (Fig. 2a, b). This sampling rate is chosen because COF temporal fluctuation is a direct measurement of contact kinetics between the surface oxide and the counter body. Among the four samples (AP700, HT700, AP900, and HT900), HT700 exhibited the lowest average COF of 0.11. The large amplitude in the COF data is attributed to the reciprocal motion of the wear test, which causes periodic oscillations in the frictional force (F_x) between positive and negative values (Fig. 2c). This results in a near-zero COF every time the motion changes direction, approximately every 0.05 s (with a sliding frequency f = 1 Hz). Figure 2b shows examples of these oscillations in the COF data for AP700 and HT700. More details on the raw data for the frictional force (F_x), normal force (F_z), and power spectra of COF for all samples are provided in Supplementary Information Section 3. Briefly, increasing the testing frequency from 1 to 2 Hz results in a higher COF for HT700, similar to the behavior observed in stainless steel 316 tested under the same conditions (load, temperature, counter body). These results suggest that sufficient oxidation is necessary to achieve effective surface lubrication. However, at high scratching frequency (2 Hz), the oxide layer may not be thick enough to lubricate the entire surface.

Fig. 2. Temporal evolution of COF and friction force F_x.

a COF of AP and HT samples from 700 and 900 °C. b COF of AP700 vs. HT700, c frictional force (F_x) for AP700 and HT700 samples from 200 to 210 s. COF represents the coefficient of friction. AP and HT represent as-printed and heat-treated, respectively.

Structural origin of surface lubrication

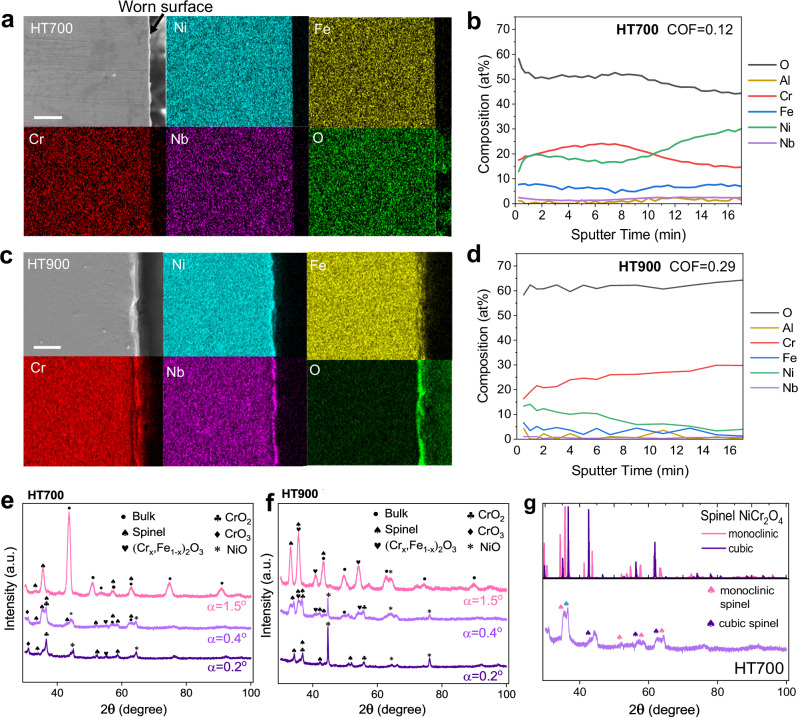
To understand the structural origin of surface lubrication in the HT sample, elemental mapping, X-ray photoelectron spectroscope (XPS), grazing incidence X-ray diffraction (GI-XRD), and TEM-based imaging and phase mapping were performed (additional worn surface characterization results in Supplementary Section 4). The average oxide thickness increased with temperature, from ∼0.5–1 µm at 700 °C to ∼2–4 µm at 900 °C, with no significant variation between the HT and AP samples. Nanomechanical measurements (see details in Supplementary Information Section 5) show higher hardness increment at 900 °C than 700 °C along the wear track due to thicker oxide formation at higher temperatures. At 700 °C, the oxide layer is thin and uniform (Fig. 3a). At 900 °C, the oxide layer becomes thicker and discontinuous, with an outermost oxide layer enriched in Cr and an inner layer enriched in Ni and Nb (Fig. 3c). XPS depth profiles show that increasing temperature from 700 to 900 °C in the HT sample mainly increases the Cr concentrations near the surface (Fig. 3b, d). Noticeably, the compositional profiles of HT700 show bi-layered oxide structures as represented by an outer layer (sputter time 0–10 min) enriched in Cr:Ni≈1:1 and an inner layer (sputter time above 10 min) enriched in Cr:Ni≈1:2. See complete XPS data for AP bulk, HT bulk, AP700, AP900, HT700, and HT900 in Supplementary Section 4.3.

Fig. 3. Worn surface chemistry and phase.

a, c SEM images and corresponding elemental maps of HT700 and HT900 cross-sectional samples. Scale bar in (a, c): 10 µm. XPS line profiles of O, Al, Cr, Fe, Ni, and Nb from the wear track region of b HT700 and d HT900 samples. Sputter time 0 corresponds to the outermost surface and higher sputter time corresponds to deeper location below the surface. GI-XRD results for e HT700 and f HT900 samples within the wear track region. The incident angle (α) is varied to probe the ultrathin surface oxide layer where the smallest α value indicates the outermost surface. g Comparison of cubic vs. monoclinic NiCr₂O₄ spinel with HT700 GI-XRD results at α = 0.4°.

The GI-XRD results for HT700 confirm the oxide structure evolution from a Cr/Ni-oxide dominated outmost layer to a spinel dominated inner layer with the increase of incident angle α from 0.2° (outmost layer) to 0.4° (Fig. 3e; here the X-ray penetration depth is estimated to be ∼2 nm for α = 0.2°, ∼39 nm for α = 0.6°, ∼79 nm for α = 1°, and ∼171 nm for α = 2° based on the literature²²). On the contrary, the oxide structure in AP700 is rather similar through its thickness, with a small amount of (Cr_x, Fe_1−x)₂O₃ and spinel, and no indication of a layered oxide structure (Fig. 3f, details in Supplementary Information Sections 4.1–4.4). Further analysis shows in HT700, both high symmetry (cubic) and low symmetry (monoclinic) spinel structures are present (Fig. 3g)²³. However, due to similar radii of Ni, Fe, and Cr that can all form spinel with close lattice constants and are indifferentiable in X-ray diffraction (XRD), high-resolution XPS spectra (see Supplementary Section 4.3) are supplemented to determine the spinel composition. The XPS results show that for Ni, the spinel compositions of NiFe₂O₄ and NiCr₂O₄ are identified; for Cr, NiCr₂O₄ spinel is identified; and for Fe, FeCr₂O₄ and NiFe₂O₄ spinel are present. Thus we conclude that the composition of spinel oxides can be written as AB₂O₄ (A = Ni, Fe, and B = Fe, Cr) or (Ni, Fe)(Fe, Cr)₂O₄, whereas the exact fraction of cation occupancy in the AO₄ tetrahedra and BO₆ octahedra sites are difficult to elucidate using existing techniques.

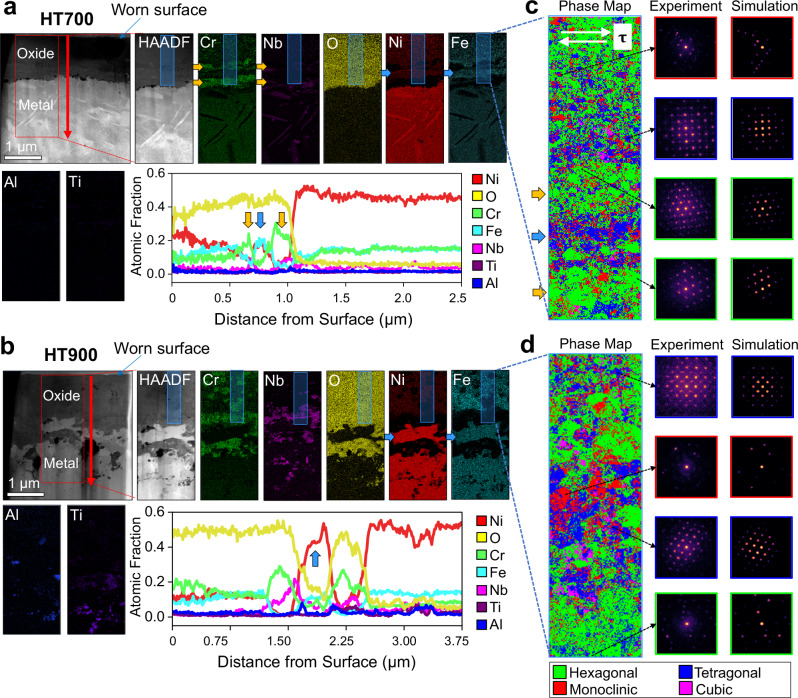
To gain a comprehensive understanding of the oxide structure, TEM-based imaging and phase mapping are performed for HT700 and HT900 samples. Representative HAADF-STEM image and elemental maps of the worn surface of HT700 sample (Fig. 4a) reveal two layers with a high concentration of Cr, accompanied by an accumulation of Nb, near the oxide/substrate interface (the orange arrows in the Cr and Nb maps in Fig. 4a). These Cr-rich oxide layers are separated by a Ni/Fe-rich oxide layer (the blue arrow in the Ni and Fe maps in Fig. 4a). Above this initial layered oxide structure, the elemental composition becomes increasing rich in Ni, and decreasing in Cr and Fe concentration. Collectively, both TEM and XPS results confirm the formation of layered oxide structure for HT700 with variational compositions from 0 to 1 µm below the surface. On the contrary, rather uniform oxide compositions are identified throughout the oxide layer in the HT900 sample (Fig. 4b). Note that a largely metallic Ni-rich phase (the blue arrow in Fig. 4b elemental maps) embedded in the surface oxide is also detected. Above this metallic particle phase (close to the surface), the oxide structure is characterized by Cr-rich oxides of ∼100–200 nm in diameter uniformly distributed inside the whole oxide. The overall Cr concentration increases only slightly toward the surface and all other elements remain in constant concentrations from 0 to 2.5 µm below the surface (apart from the metallic particle).

Fig. 4. Microstructure and phase distribution in the surface oxide.

a, b HAADF-STEM images of the HT700 and HT900 cross-sectional samples followed by elemental maps for Nb, O, Ni, Fe, Al, and Ti corresponding to the areas enclosed by the dashed red boxes and averaged elemental line profiles starting from the surface of the sample going downward in the red arrow direction. c, d Phase map analysis of the areas enclosed by the shaded blue boxes in the HT700 and HT900 sample images shown in (a) and (b), respectively. White arrows in (c) represent the sliding direction. Yellow and blue arrows in (c) represent corundum-structured and spinel-structured metal oxide layer, respectively. Hexagonal (167), tetragonal (98), monoclinic (12), and cubic (227) phases are represented by the green, blue, red, and magenta-colored regions, respectively. SG represents the space group. AP and HT represent as-printed and heat-treated, respectively. Example NBED patterns and their corresponding Bloch wave simulation matches are shown outlined with their color-coordinated phase match.

To determine the crystal structure of the surface oxide, we employ an advanced crystallographic phase mapping algorithm²⁴ that utilizes four-dimensional (4D)-STEM data to produce a series of two-dimensional (2D) electric diffraction patterns across a 2D area of the sample (Fig. 4c, d). In the phase maps, the hexagonal (space group 167), tetragonal (space group 98), monoclinic (space group 12), and cubic phases (space group 227) are represented by the green-, blue-, red-, and magenta-colored regions, respectively. Next to each phase map are a series of examples of experimentally acquired electron diffraction patterns and their respective Bloch wave simulation matches. Additional STEM images in Supplementary Fig. 27 show that the feature size in the phase maps is consistent with the grain sizes observed: the grain sizes of the HT700 and HT900 samples being on the order of 5–30 nm and 50–200 nm, respectively. Starting from the bottom of the HT700 phase map, we notice two regions (marked by the orange arrows in Fig. 4c), are heavily populated with hexagonal phase, corresponding to the two Cr-rich oxide layers seen in the HT700 elemental maps in Fig. 4a. Note that corundum structure (such as Al₂O₃ and Cr₂O₃) has hexagonal close-packed array of oxide anions with 2/3 of the octahedral holes occupied by the cation. This hexagonal phase labeled as green areas is thus determined to be corundum-structured oxide that is rich in Cr. The Ni/Fe-rich oxide layer (marked by the blue arrow in Fig. 4c) sandwiched between the two Cr-rich oxide layers is determined to be dominated by the low-symmetry tetragonal/monoclinic spinel rich in Ni, Fe, with some Cr. Above the upper Cr-rich oxide layer, it shows a mixed phase, including hexagonal, tetragonal, monoclinic, and cubic spinel until approaching the topmost surface, where the hexagonal corundum-structured phase is dominant again. This topmost corundum-structured layer is rich in Ni, Cr, and Fe. This four-dimensional scanning electron microscopy (4D-STEM) phase map result agrees well with the GI-XRD results (Fig. 3g), in which the topmost layer of HT700 is dominated by corundum-structured oxide, while the interior oxide contains both high symmetry (cubic) and low symmetry (tetragonal and monoclinic) spinel. Interestingly, more cubic spinel can be found in the HT900 than HT700 due to its better thermal stability than tetragonal and monoclinic spinel, as discussed in the next section. When the wear temperature increased from 700 to 900 °C, the oxide microstructure clearly coarsened, as shown in the phase maps (Fig. 4d) and in virtual bright field and annular dark-field images of HT700 and HT900 (Supplementary Fig. 27). The oxide structure of HT900 can be viewed as corundum-structured oxide particles of ∼50–200 nm embedded in the matrix of coarse tetragonal and monoclinic spinel oxide phases of similar sizes, whereas the oxide structure of HT700 consists of smaller ∼5–30 nm grains.

Mechanical properties of corundum- vs. spinel-structured oxide

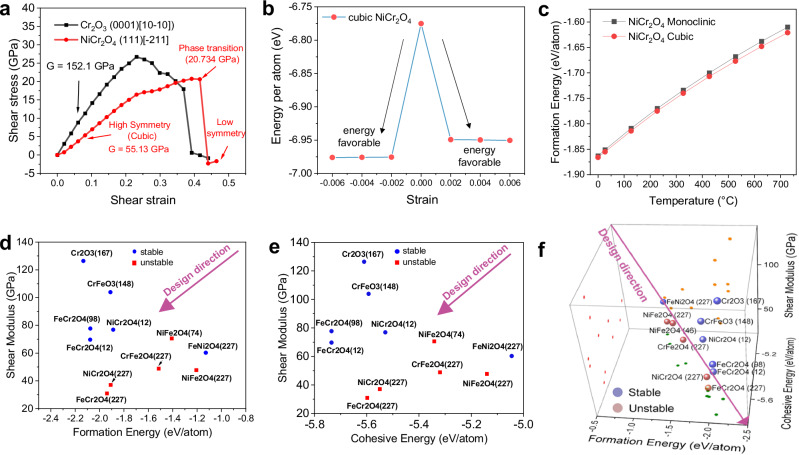
Next, we perform quantitative calculations of ideal shear strength of corundum- and spinel-structured oxide to demonstrate their different resistance to shear deformation. Figure 5a shows the DFT calculated shear stress vs. strain curve of corundum-structured Cr₂O₃ (0001)[10$\overline{1}$0] and cubic spinel NiCr₂O₄ (111)[$\overline{2}$11]. For the cubic NiCr₂O₄, calculations were performed for two different slip systems: (111)[1$\overline{1}$0] and (111)[$\overline{2}$11]. We find that the shear modulus is similar for both systems, ranging from ∼50–55 GPa at a strain of ∼0.04 strain to ∼70–72 GPa at a strain of ∼0.2. Comparing such two systems, the (111)[$\overline{2}$11] shears more easily, with a lower phase transition stress of 20.73 GPa (vs. 28.06 GPa for (111)[1$\overline{1}$0] system), after which, the high symmetry cubic spinel transforms to a lower symmetry structure. On the other hand, Cr₂O₃ (0001)[10$\overline{1}$0] exhibit a much higher shear modulus than spinel, ranging from ∼152 GPa at a strain of ∼0.04 strain to ∼125 GPa at a strain of ∼0.2. Similarly, the phase transition stress of Cr₂O₃ is 26.72 GPa, much higher than that of the cubic spinel NiCr₂O₄ (111)[$\overline{2}$11]. Thus, in the HT samples worn at 700 °C, when a spinel layer is formed inside the surface oxide, a much lower COF and wear rate can be obtained. In all other conditions, either in the AP samples or HT samples at even higher temperatures of 900 °C, the formation of a large amount of spherical corundum-structured phases makes the surface layer hard to shear, hence more abrasive with higher COF.

Fig. 5. DFT simulation and oxide lubricity design criteria.

DFT calculated a ideal shear stress vs. strain curves of cubic NiCr₂O₄ spinel and Cr₂O₃ corundum-structured oxide. b Energy per atom for cubic NiCr₂O₄ spinel under different minor shear strain. c Formation energy of NiCr₂O₄ with monoclinic and cubic structures calculated from 0 to 700 °C. DFT calculated shear modulus vs. d formation energy and e cohesive energy for metal oxides, where blue round symbols represent stable structure and red square symbols represent un/metastable structure. f Oxide lubricity design criteria combining shear modulus, formation and cohesive energies and strain-stability of oxides.

Oxide lubricity prediction

Our results show that heat treatment after SLM further improves wear resistance and lowers the COF as low as ∼0.1 by promoting the formation of a unique layered oxide structure at 700 °C (Fig. 4). To understand the surface oxidation thermodynamics, we calculated the phase fraction of all relevant oxides using Thermo-Calc software, as detailed in Supplementary Information Section 6.2. The simulation results are in great agreement with the experimental results. As temperature increases from 700 to 900 °C, the spinel volume fraction reduces, and the corundum-structured oxide content increases significantly in both AP and HT samples. At 900 °C, the formation of metal oxide is thicker, which is sometimes intuitively considered to result in lower COF. However, our results show that the COF increases when the temperature rises to 900 °C due to the increase of corundum-structured oxide volume fraction and coarser microstructure.

This work emphasizes the significant role of spinel oxide formed on HT sample at 700 °C that contributed to a record low COF. However, existing oxide lubricity models such as crystal chemical model²⁵ and polarizability model²⁶ failed to predict the lubricity of the spinel oxide in this work. To this end, we develop a computational approach to predict the oxide lubricity based on four criteria: (1) shear modulus, indicative of lubricity; (2) formation energy, indicative of thermodynamic stability and formation propensity; (3) cohesive energy, indicative of oxide’s melting point; and (4) phase stability under minor strain, which is crucial for achieving ultra-low COF, especially when considering potential friction-induced phase transitions, such as the Jahn–Teller effect²⁷.

We perform DFT calculations of these key properties of all relevant Ni-, Fe-, and Cr-based binary and ternary oxide, for which little high-temperature COF data exist in the literature (Fig. 5d, e, more details in Supplementary Section 6). The computation results show that a more negative formation energy suggests better thermal stability and a lower shear modulus suggests better lubricity (Fig. 5d); whereas materials with higher cohesive energies often have higher melting and boiling points (Fig. 5e) as more energy is needed to break their strong bonds^28,29. Therefore, to increase the operational temperature range of these solid lubricants, higher cohesive energy is preferred. Using such criteria, we propose the design direction of thermally stable, lubricious oxide with high melting point for different metal oxides, i.e. toward simultaneously lowering shear modulus, and increasing formation and cohesive energy (the absolute value), as indicated by the arrow direction in Fig. 5f. Corundum-structured Cr₂O₃ (space group 167) and CrFeO₃ (space group 227) fall in the opposite direction of the arrow, hence are not lubricious. A few selected candidates in the design direction include: FeCr₂O₄ (space group 12, monoclinic), NiCr₂O₄ (space group 12, monoclinic), FeCr₂O₄ (space group 98, tetragonal), and NiFe₂O₄ (space group 227, cubic). Experimentally, the first three compositions are indeed observed in HT700.

Note that in Fig. 5d, e, several cubic spinel phases (e.g. NiCr₂O₄, space group 227) are labeled as unstable due to stress-induced-phase transformations. Such mechanical stability of oxides was assessed by subjecting them to a shear strain of 0.0035, employing the energy-strain method^30,31. Oxides manifesting the Jahn–Teller effect under this strain were categorized as unstable, while those not displaying this effect were designated as mechanically stable in Fig. 5d–f. At high temperatures, cubic spinel is more thermally stable than its low symmetrical counterpart, as shown from our DFT calculated formation energy in Fig. 5c. However, such structures are not mechanically stable under stress by the Jahn–Teller effect²⁷: the cubic NiCr₂O₄ spinel can easily find lower energy state under a minor strain of 0.002 (Fig. 5b), which can be easily achieved from surface friction during sliding wear. Two additional stress-induced phase transformation mechanisms of NiCr₂O₄ also exist: first, the spinel is found to decompose into corundum and halite at a hydrostatic compressive stress of ∼3.88 GPa (Supplementary Fig. 35b, c); second, the cubic spinel can transform to the low-symmetry spinel at an ideal shear stress of ∼21–28 GPa (Fig. 5a). Such transformation stress is expected to be much lower for the more defective spinel structures measured experimentally. Collectively, these three stress-induced-transformation mechanisms tend to drive the cubic spinel to low-symmetry spinel. Consequently, these low-symmetry spinel oxides are anticipated to be the prevailing constituents within the wear track due to constant frictional contact. This is indeed in agreement with the phase map results in Fig. 4c for HT700 sample, where the volume fraction of tetragonal/monoclinic spinel is much higher than that of the cubic spinel. In addition, the spinel layer is parallel to the sliding direction, which is another evidence for the shear-induced phase transformation.

Discussion

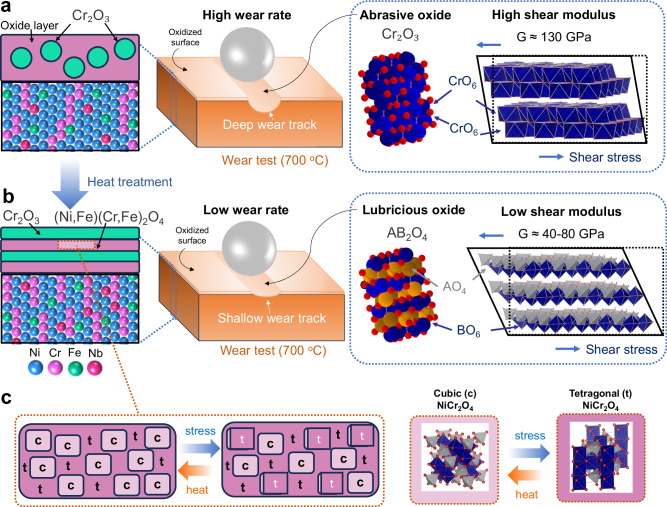
Traditional solid lubricates decompose rapidly at high temperatures due to low inter-layer bonding strength in their 2D layered or Magnéli structures. Previously, spinel (NiCr₂O₄ and NiFe₂O₄) and corundum-structured (Cr₂O₃ and Fe₂O₃) phases were observed in the wear region of Inconel 718 at 600–800 °C^32–34. However, our work is the first time that a relatively pure spinel layer, undoped by corundum-structured particles, is characterized and identified as the root cause for the sustained high-temperature lubricity. Interestingly, in geoscience, spinel is also the most widely observed oxide in earth mantle, where high shear deformation and elevated temperatures co-exist^35,36. Our proposed model in Fig. 6 shows the formation mechanism and tribological behavior of abrasive corundum-structured (Cr₂O₃, Fig. 6a) vs. lubricious spinel oxide (AB₂O₄, Fig. 6b) during high-temperature wear. An abrasive oxidized surface results in deep wear track and high wear rate (volume loss), while a lubricious surface results in shallow wear track and low wear rate. The low COF observed in HT700 sample originates from a predominantly spinel oxide layer (not doped by large corundum-structured or Ni/Cr-oxides). These spinel structures, as mentioned previously, possess low shear modulus ranging from 40 to 80 GPa, and can work as self-replenishing lubricant from oxidation.

Fig. 6. High-temperature tribological model for Inconel 718.

a, b Schematic representation of the impact of heat treatment on the formation of abrasive corundum (Cr₂O₃) vs. lubricious spinel (AB₂O₄) oxides on the surface of Inconel 718 during high-temperature wear. Abrasive oxide layer results in deep wear track and high wear rate (volume loss), while lubricious oxide layer results in shallow wear track and low wear rate. Red atom in oxide structure represents oxygen, blue and yellow atoms represent metal. c Illustration of associated phase transformation in the surface oxide layer of heat-treated Inconel at 700 °C. c and t represent cubic and tetragonal, respectively.

During high-temperature frictional contact, two competing mechanisms are at play to control the crystal structure and phase transformation of the spinel: the thermodynamic and mechanical driving forces. On the one hand, the cubic spinel tends to be more stable at higher temperatures compared to the tetragonal/monoclinic phase due to its higher symmetry, which results in a lower energy state and greater stability at elevated temperatures. On the other hand, during wear, friction-induced shear results in a phase transformation from the cubic to low-symmetry tetragonal/monoclinic spinel. These low-symmetry spinel phases then transform back to cubic structure under high temperature, as shown in Fig. 6c. TEM-based phase analysis in Fig. 4 confirms this phase transformation, where the amount and size of cubic spinel phase reduce toward the sliding surface, likely due to the sharp strain gradient in the oxide layer to favor the cubic-to-monoclinic phase transformation.

In summary, we have shown that surface oxide structure with a relatively pure spinel layer is crucial for achieving ultra-low COF from 600 to 900 °C. Their formation is promoted by appropriate heat treatment of AP Inconel to allow the formation of high-density interphase boundary. Finally, a computational framework is developed and validated to predict the lubricity of metal oxide based on shear modulus, formation energy, cohesive energy, and phase stability, providing useful tools to accelerate the discovery and design of high-temperature solid lubricants and wear-resistant metals in future study.

Methods

Additive manufacturing and heat treatment

The commercially available Inconel 718 powder from EOS company was used to fabricate the samples by an EOS M290 machine (EOS GmbH, Germany) with Yb-fiber laser. The chemical composition of the raw powder in weight percent is listed in Supplementary Section 1.1. The SLM printed coupons have a dimension of 1.25 inches in length, 0.63 inches in width, and 0.16 inches in thickness. They were built with a subplate preheating temperature of 80 °C, a layer thickness of 40 µm, a scan speed of 960 mm/s, a hatch distance of 110 µm for the applied stripes hatch strategy, at 285 W laser power. During the SLM manufacturing process, the stripes hatch pattern was rotated 90° with respect to the previous layer. In addition to the AP samples, selected samples were HT in two steps: (1) solution annealing, where the temperature was hold at 954 °C for 10 min under nitrogen, then air cooled to room temperature; (2) aging treatment, where the temperature was first hold at 718 °C for 8 h, then the furnace was cooled to and held at 621 °C for a total precipitation time of 18 h. All the heat treatments were performed under nitrogen environment.

High-temperature tribology test

The high-temperature wear tests were performed from 600 to 900 °C in air, using a multifunctional tribometer (Rtec MFT‐5000, CA, USA) with the high-temperature module. The Rtec machine is equipped with fully automated PC-based motor control and data acquisition. All tests were carried out for three repeated times in a reciprocating ball-on-plate mode using alumina ball (Al₂O₃, diameter of 6.35 mm, 96–99.8 wt% purity, sphericity of 99.9975%, Rockwell hardness of 45N 83) as the counter body, at 8 N normal load (or 1.42 GPa Hertzian contact pressure, same as¹⁵), 5 mm stroke length, 1 Hz sliding frequency (i.e. 10 mm per sec) for 10 min. The chamber was heated at 50 °C/s from room temperature to the desired wear testing temperature, and stabilized for 10 min prior to the test. The temperature controller has a resolution of 0.1 °C. After all wear tests, the worn area dimensions were measured by a Dektak D150 profilometer from nine different locations of the wear track. The total worn volume loss was then calculated by multiplying the worn cross-sectional area by the scratch length. Hereafter, we use AP to represent AP unworn samples, whereas AP600, AP700, AP800, and AP900 represent AP samples subjected to wear tests under 600, 700, 800, and 900 °C, respectively. Similarly, HT represents heat-treated unworn samples, whereas HT600-HT900 represents HT samples subjected to wear tests under 600–900 °C.

Nanomechanical test

The hardness and elastic modulus of the worn surface were measured by a MicroMaterials instrumented nano-indentation system (NanoVatnage Platform 4, MicroMaterials, UK) equipped with a diamond Berkovich tip. All worn samples were mounted onto the sample stub using Loctite® super glue. The tip shape was calibrated by a fused silica standard prior to testing according to the Oliver and Pharr method³⁷. The sample surfaces were inspected and recorded before and after indentation using the optical microscope mounted within the nanoindenter. The loading profile used is shown in Supplementary Section 4.1. The maximum load was selected to be 10 mN, with a loading–holding–unloading profile of 15 s–5 s–15 s and a thermal balance period of 30 s when unloaded to 1 mN (10% of the maximum load). On the worn samples, a 15 × 20 array of displacement-controlled indentation was performed with a spacing of 10 µm between indents. The reduced modulus (E_r) and hardness (H) were calculated from the unloading portions of the load-displacement curve using the Oliver and Pharr method³⁷. The reduced modulus is a convolution of the elastic mechanical properties of both the sample and the diamond tip, as $\frac{1}{E_r}=\frac{1-{\nu }_s^2}{E_s}+\frac{1-{\nu }_i^2}{E_i}$, where E_s and ν_s are Young’s modulus and Poisson’s ratio of the sample, respectively, and E_i and ν_i are those for the diamond tip (E_i = 1140 GPa and ν_i = 0.07).

High-temperature hardness tests were conducted using a diamond indenter with high-temperature indentation equipment (Manufacturer: Rtec-Instrument, Model: MFT5000, Serial: RTECH3010) in an argon environment. At each temperature point, four indentations were made to determine the average hardness and standard deviation. A load of 30 N was applied for 10 s during each indentation. Afterward, the samples were cooled in an argon environment. Once the samples reached room temperature, the diagonal dimensions of the indents were measured using a microscope on a separate microhardness testing device (Manufacturer: ITW Test & Measurement GmbH, Model: Tukon 2500-3).

Microstructure characterization

The phase of unworn AP and HT samples was measured by XRD (Bruker D8 Discovery) at 40 kV and 40 mA with Cu Kα (1.54 Å). A scan speed of 0.2° s/step with a step increment of 0.02° was applied for the two-theta scan. The high-resolution surface composition images were measured by WDS with a Field Emission Electron Probe Microanalyzer (JEOL JXA-iHP200F). The wear track region was characterized by an XPS (PHI Quantera SXM, USA) in a vacuum of 10⁻⁹ Torr. The sputtering depth curve was obtained by several sweeps and time steps with 3 kV argon ion. The O 1s, Cr 2p_3/2, Fe 2p_3/2, Ni 2p_3/2, and Nb 3d were used for quantitative analysis. The spectra were calibrated using C 1s at 285 eV using the Multipak analysis software. The surface morphology and composition were measured by an analytical scanning electron microscope (JEOL IT-500HR) with an Oxford Instrument Energy Dispersive X-ray Spectroscopy (EDS). The worn surface oxide was analyzed by GI-XRD and X-ray reflectometry (XRR), using a PANalytical X’Pert PRO diffractometer with Cu Kα radiation (1.5406 Å) at 45 kV and 40 mA. The incident angle (α) of GI-XRD was selected in a range of 0.2°–1.5°, based on XRR results. The size of the mask on the incident beam was 4 mm for both GI-XRD and XRR.

Transmission electron microscopy and diffraction simulation

Characterization of worn surfaces including elemental analysis and phase distribution was carried out using 4D-STEM and EDS in STEM. Cross-section specimens for STEM were made using a FEI Helios Dualbeam Nanolab 600 focused Ga ion beam. A final cleaning cycle of the cross-section specimens was conducted at 2 keV. High-angle annular dark-field (HAADF) imaging in STEM was performed using a Themis Z (Thermo Fisher Scientific) equipped with a probe aberration corrector. The accelerating voltage of the microscope was 200 kV and the semi-convergence angle of the electron probe was 25 mrad. EDS elemental maps were obtained using a four-quadrant Super-X EDS detector with a 100 pA beam current and a pixel dwell time of 20 μs.

4D-STEM data for phase mapping near the worn surface area were acquired using an electron microscope pixel array detector (EMPAD)³⁸ with an electron probe semi-convergence angle of 0.96 mrad and a full-width half-maximum probe size of 1.6 nm. 4D-STEM data are comprised of a 2D electron diffraction pattern collected at every 2D real space scan position on the sample^39,40. The scan region for both samples was 0.25 μm × 1 μm with 125 × 500 scan points and the scan step of 2 nm.

The simulation library of electron diffraction patterns was created using computationally determined structural information based on the DFT results conducted in this work. Due to the similarity between the many numbers of described phases in this paper, a single structure was used to represent each phase: hexagonal (space group 167)—Cr₂O₃, tetragonal (space group 98)—FeCr₂O₄, monoclinic (space group 12)—FeCr₂O₄, and cubic (space group 227)—NiCr₂O₄. For the electron diffraction pattern simulation, we employ dynamical diffraction simulations based on the Bloch wave method⁴¹. In this work, we used a library of 11,000 total diffraction patterns covering the full range of unique crystallographic directions with a tilting increment of 0.3° for the aforementioned crystal structures. The crystal phase for individual electron diffraction patterns was determined by the quantitative comparison via template matching between the experimental data with simulated diffraction patterns of expected crystal structure along all possible crystal orientations^42,43. The total number of simulations for each phase was: 1500 for cubic, 2000 for hexagonal, 2500 for tetragonal, and 5000 for monoclinic, resulting in 11,000 total simulated diffraction patterns. Note that higher symmetry phases require fewer simulations to cover all possible orientations.

4D-STEM phase map matching procedure

The radial intensity profile of each experimental and simulated diffraction pattern is first calculated. Each experimental profile is then compared with all the simulated profiles and ranked using normalized cross correlation (NCC), (1D radial profile to 1D radial profile). The top 50 matches for each potential simulated pattern are then directly compared using NCC, (image to image), with the experimental pattern. In-plane pattern rotation is accounted for by rotating the pattern in 1-degree increments for all the matches. The resulting phase map has a full 3D orientation match for each experimentally collected diffraction pattern. The examples shown in the paper highlight the sensitivity of our algorithm to precisely identify both low- and high-index diffraction patterns. The phase maps consistency with our elemental data additionally supports the sensitivity of our algorithm by being able to distinguish between hexagonal, tetragonal, monoclinic, and cubic, phases accurately. We would like to note that the overall thickness of the sample and overlapping grains within the sample are obstacles that can impact matching results. In this work, the best matches of experimental to simulation data were chosen for the final result.

Computational methods

Thermo-Calc software (version 2023b) was used to simulate the phase evolution of Inconel 718 with TCNI12, Ni superalloy mobility, and TCOX12 databases⁴⁴. The equilibrium phase diagram with phase volume fraction and composition was calculated as a function of temperature. Besides that, structures of metal oxides formed at different temperatures were calculated via DFT. Vienna ab initio simulation package (VASP) and projected augmented plane-wave pseudopotentials were used for all spin-polarized DFT calculations^45,46. Structure optimization was performed using the Perdew–Burke–Ernzerhof version of the generalized gradient approximation (GGA) of the exchange-correlation functional⁴⁷, with a kinetic energy cutoff of 500 eV for the plane-wave basis set. Additionally, the GGA + U correction scheme was utilized for the d orbitals of Cr and Ni, with U values set at 3.7 eV for Cr, 5.3 eV for Fe, and 6.2 eV for Ni⁴⁸.

The supercell structure was relaxed until the Hellmann–Feynman forces on each atom was <0.02 eV/Å and an energy convergence criterion of 10⁻⁶ eV was used. The Brillouin zone of the bulk was sampled with Gamma-centered 7 × 7 × 7 k-points. Mechanical properties of the oxides were calculated by the energy-strain method^30,31, which is based on the energy variation upon the application of a small elastic strain to the equilibrium lattice. VESTA software was used for structures visualization and analysis⁴⁹. Cohesive energies (E_c) per atom of A_xB_yO_z metal oxides were used to evaluate the melting point of the oxide⁵⁰, which were calculated as:

$$E_c\left(A_x{B}_y{\mathrm{O}}_z\right)=\frac{E\left(A_x{B}_y{\mathrm{O}}_z\right)-xE\left(A_{iso}\right)-yE\left(B_{iso}\right)-zE\left(O_{iso}\right)}{\left(x+y+z\right)},$$ 1

where $E_{\mathrm{c}}\left(A_x{B}_y{\mathrm{O}}_z\right)$ stands for the cohesive energy, $E\left(A_x{B}_y{\mathrm{O}}_z\right)$ is the energy of bulk in the smallest amount, $E\left(A_{iso}\right)$, $E\left(B_{iso}\right)$, and $E\left({\mathrm{O}}_{iso}\right)$ are the energies of isolated neutral free A, B, and O atoms, respectively. To compute the cohesive energy of metal oxides, we mixed GGA and GGA + U totally, which can result in the GGA/GGA + U compatibility issues. To address this, the ad hoc energy corrections for elements are exported from the Materials Project database⁵¹.

Formation energies per atom of A_xB_yO_z metal oxides were computed using the following equation,

$$E_f\left(A_x{B}_y{\mathrm{O}}_z\right)=\frac{E\left(A_x{B}_y{\mathrm{O}}_z\right)-xE\left(A\right)-yE\left(B\right)-\frac{z}{2}E\left({\mathrm{O}}_2\right)}{x+y+z},$$ 2

where $E_{\mathrm{f}}\left(A_x{B}_y{\mathrm{O}}_z\right)$ stands for formation energy, $E\left(A_x{B}_y{\mathrm{O}}_z\right)$ is the energy of bulk in smallest amount, $E\left(A\right)$ and $E\left(B\right)$ are the energies of pure metals per atom, respectively, and $E\left({\mathrm{O}}_2\right)$ is the energy of a gas phase O₂. To compute the formation energies of metal oxides, we mixed GGA and GGA + U calculations. To address the GGA/GGA + U compatibility issues, the same ad hoc energy corrections for elements exported from the Materials Project database⁵¹ were used.

The Gibbs free energy (G) of a given system is calculated as:

$$G=E+E_{ZPE}+C_{p}T+TS,$$ 3

in which G is the Gibbs free energy, and E, E_ZPE, C_p, and S are the DFT energy, zero-point energy, heat capacity, and entropy of the system. E_ZPE, C_p, and S are calculated within the harmonic approximation using the Atomic Simulation Environment⁵².

In order to obtain the ideal shear strength, we conducted ideal shear deformation on Cr₂O₃ and NiCr₂O₄ along their plausible slip systems using DFT simulations. This was achieved by maintaining a fixed shear strain and allowing the relaxation of the other five strain components at each step of shear deformation⁵³. For each strain state, the true strain was increased by 0.02. Initially, we optimized the lattice parameters of these two systems, which were based on the atomic structures sourced from Materials Project⁵¹. Subsequently, we rotated the optimized cells along the plausible slip systems prior to performing the ideal shear deformation. Specifically, for Cr₂O₃, we select the (0001)[10$\overline{1}$0] slip system, and for NiCr₂O₄, the slip systems (111)[1$\overline{1}$0] and (111)[$\overline{2}$11] were chosen. In the shear deformation studies, a sparser k-point grid was utilized. Specifically, a 7 × 7 × 3 k-points was employed for the ideal shear deformation of Cr₂O₃. In contrast, for the shear deformation of NiCr₂O₄, a more reduced 2 × 2 × 2 k-points mesh was adopted.

Author contributions

Z.Z. and W. Cai designed the experiments. Z.Z. and Z.X. conducted the wear tests. Z.Z. conducted the XPS, SEM characterizations, and Thermo-Calc simulations. E.H., G.B., and H.K. performed the TEM characterization and phase simulations. Q.A. performed the DFT-based stress–strain calculations. X.W. printed and heat treated the Inconel 718 samples. J.Z. did the GI-XRD characterization. Z.Z. and L.M. performed the WDS characterization. Z.Z., L. Liu, and Lin L. conducted DFT calculation of formation energy, cohesive energy and shear modulus guided by H.X. Z.D. and Ling L. completed the nano-indentation tests. Z.Z. and W. Wang conducted XRD characterizations. M.I., X.C., and B.C. conducted high-temperature hardness tests. Z.Z., W. Cai, Lin L., and Y.Y. completed the data analysis. Z.Z. and W. Cai prepared the manuscript and all authors revised. W. Cai supervised the research.

Peer review

Peer review information

Nature Communications thanks Jens Hardell and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

All data supporting the findings of this study are available within the article and its Supplementary files. Atomic coordinates of the optimized computational models are provided as Supplementary Data 1. Any additional requests for raw data, including the images, diffraction patterns, and other characterization results, can be directed to, and will be fulfilled by, the corresponding authors. Source data are provided with this paper.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-54482-w.