Abstract
The activity coefficient represents the deviation between an actual solution and an ideal solution, influencing the solubility and diffusion of CO2 within a saltwater layer. Consequently, it serves as a crucial parameter for numerical simulations of CO2 storage in deep saltwater layers. However, in numerical simulations of CO2 geological storage, the majority of studies rely on the Helgeson–Kirkham–Flowers (HKF) equation to compute activity coefficients, which necessitates obtaining Debye–Hückel (DH) parameters. The conventional method calculates the DH parameters via an interpolation algorithm, which requires a long computation time during the numerical simulation. Therefore, developing a method to quickly and accurately calculate activity coefficients is vital for the overall model efficiency. This study employed machine learning algorithms to train DH parameters derived from the IAPWS-95 method. It could establish empirical formulas for DH parameters as functions of temperature and pressure, which were then substituted into the HKF equation to swiftly compute activity coefficients. The results demonstrate that the activity coefficients obtained using this method exhibit a small relative deviation from experimental values, with an average coefficient of determination of 0.9463 and an average relative error of 2.28%. Furthermore, the computational speed was improved by 48%. This approach reduces the calculation time for activity coefficients in geochemical reaction modeling, enabling DH parameters to be calculated solely based on temperature and pressure, which is easy to use and has high accuracy. It facilitates rapid calculation of activity coefficients for solutions within a temperature range of 0 to 300 °C and a pressure range of 0 to 200 MPa. Ultimately, this study holds significant importance for the numerical simulation of geochemical reactions.
1. Introduction
People have recently become increasingly concerned about CO2 emissions and environmental pollution in the petrochemical industry, which has attracted widespread global attention to reducing CO2 emissions and using clean energy. As economic development progresses, China currently ranks first in the world for annual CO2 emissions.1−3 Consequently, China has actively proposed the ambitious goal of achieving peak CO2 emissions by 2030 and attaining carbon neutrality before 2060.4,5 The primary means to achieve this goal is to control the concentration of CO2 in the air. The capture, utilization, and storage of CO26,7 are the key technologies for reducing CO2 content and represent current research hotspots. Among these, CO2 storage in deep saline water8 is an effective approach. However, due to the slow physical and chemical interactions between CO2 and the surrounding water, rocks, and other formations at specific temperatures and pressures,9−11 the use of numerical simulation methods to study geochemical reaction equilibrium models12 has emerged as one of the most crucial research methods. The activity coefficient is a crucial parameter in the geochemical reaction equilibrium model13,14 and serves as a measure of the activity of substances under specific conditions. In electrolyte solutions, due to ion interactions, the total concentration of the electrolyte does not accurately represent its effective concentration. Therefore, an activity coefficient is introduced to quantify the deviation between the actual and ideal solutions. Furthermore, the calculation of activity coefficients in saline layers is intricately linked to the DH theory.15−17 However, when applying the Debye–Hückel (DH) theory to calculate activity coefficients, the DH parameter must first be determined using the interpolation method.18 Given the numerous seepage chemistry iterations required for numerical simulations of CO2 geological storage, the efficiency of the DH parameter interpolation algorithm significantly impacts the overall simulation efficiency. Consequently, rapidly calculating the activity coefficient in the geochemical reaction equilibrium model is paramount for enhancing the speed and accuracy of CO2 geological storage numerical simulations.
At present, many scholars both domestically and internationally use the DH theory correction model to calculate the activity coefficient of solutions. It adds new parameters or short-range interactions between ions based on the DH theory. Frapiccini et al.19 used the Pitzer model to calculate the activity of water and the activity coefficients of cations, anions, and neutral species in the solution, Pitzer model considered short-range interactions between ions based on DH theory and established a semiempirical Pitzer model, but due to the application trend of the Pitzer model toward multivariate systems and a wider range, there are many mixed parameters in the Pitzer model, and the physical meaning of the parameters is not clear. Hessen et al.20 applied an improved e-NRTL model21 to CO2–H2O monoethanolamine and CO2–H2O methyldiethanolamine systems. The e-NRTL model22,23 indicates that only short-range interactions are considered between ions of the same charge, therefore the model uses the Pitzer–Debye–Hückel term to explain long-range Coulomb interactions. Novikov24 improved the Helgeson–Kirkham–Flowers (HKF) equation of state for polar undissociated substances under infinite dilution conditions to describe the properties and equilibrium of As(OH)3 and H3PO4 aqueous solutions under infinite dilution conditions, and clarified the anion parameters. This equation can theoretically and consistently describe polar non charged species, and its accuracy is comparable to the classical HKF equation. The HKF model is based on the DH theory, Some parameters in the HKF model ignore the properties of the electrolyte and are determined only by pressure and temperature. The model can be used to calculate the activity coefficient of solutions under high-temperature and high-pressure conditions. Dolejš25 evaluated the extrapolation behavior and accuracy of the HKF model, and found that the solubility of quartz is insensitive to the dielectric constant of aqueous solvents, and the solubility of aqueous silica is too high under high pressure. After recalibration, the solubility of quartz at high temperatures was underestimated. The predicted solubility values of corundum and calcite differ significantly from experimental values under high temperature and high pressure. Although the HKF model is flexible and recalibratable, it is difficult to infer between hydrothermal and high temperature and high pressure conditions, and there is significant numerical uncertainty due to parameter autocorrelation and function form issues. Akinfev et al.26 proposed a novel equation of state (EoS) for describing the thermodynamic properties of aqueous non electrolytes under infinite dilution. This equation only requires three empirical parameters to fit experimental data, which are independent of temperature and pressure and can predict the entire thermodynamic properties of solutes under infinite dilution. The new EoS is compatible with Helgeson–Kirkham Flowers’ aqueous electrolyte model and is applicable to reactions of minerals, gases, and water ions. Chen27,28 used Newton–Raphson iteration29 to calculate the DH parameters and the Pitzer equation when establishing a geochemical reaction model to calculate activity coefficients. However, this calculation method has convergence issues, and the calculation process is cumbersome. Li30 used the HKF model to calculate the chemical equilibrium constant in the CO2-water-salt-ore body phase equilibrium coupling chemical equilibrium model. However, because the parameter calculation method only covers the range of temperatures and pressures from 0 to 250 °C and 0 to 100 MPa, there is a lack of data from the HKF model under most pressure and temperature conditions. Long31 used the BP neural network algorithm to train the theoretical values in the study of CO2 geological buried models to obtain empirical formulas for activity coefficients, this method has small calculation errors and improves the calculation speed.
Although various correction models can be used to calculate the activity coefficient, most of them are time-consuming in determining the DH parameters and involve numerous parameters. Given that the HKF model can overlook the complex composition of the electrolyte solution system, some parameters are independent of its properties and only require solving for the DH parameters and related ion parameters. Therefore, building on previous research, this study introduces machine learning algorithms for the first time to establish an empirical relationship between DH parameters, pressure, and temperature. By integrating this empirical formula with the HKF model, the activity coefficient of the solution can be swiftly calculated. The aim of this study is to address the issue of slow DH parameter calculation, enhance the calculation speed of activity coefficients in numerical simulations, and significantly improve the overall numerical simulation speed for CO2 sequestration in saline water layers.
2. Machine Learning Model Process
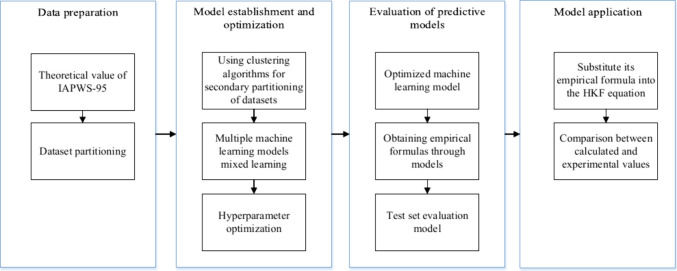
This study employs machine learning algorithms to train models for predicting DH parameters and utilizes the HKF model to calculate the activity coefficient of the solution. The entire process can be divided into four main parts, as illustrated in Figure 1.
Figure 1.
Machine learning modeling flowchart.
(1) Data preparation. Due to the large amount of data required by machine learning methods, the data are calculated using IAPWS-95 and then organized into a suitable data set, which is evenly divided into three data sets: training, validation, and testing. The training set is used to train the internal logical relationships of the model, the validation set is used for model optimization and parameter adjustment, and the test set is used only to verify the effectiveness of the model. (2) Model establishment and optimization. Different machine learning algorithms are used to process the samples, and the K-means clustering algorithm, polynomial regression algorithm, and K-NearestNeighbor (KNN) regression algorithm are applied to perform regression calculations. Hyperparameters refer to parameters manually set based on experience before training the model. These parameters are important adjustable parameters for controlling the calculations of machine learning models. Grid search techniques are used to optimize the performance of machine learning models on the validation data set. (3) Evaluation of the models. This study uses support vector machine, neural network, and K-means-KNN to compare and analyze the established model. Additionally, This study uses the mean square error (ηMSE), root-mean-square error (ηRMSE), absolute average relative deviation (ηAARD), and coefficient of determination (R2) as model evaluation indicators and selects the DH parameter prediction model with the best indicators. (4) Model application. After determining the optimal prediction model, it is combined with the HKF model, the temperature and pressure are used as input data, and then the activity coefficient of the solution is calculated. The calculated values are compared with the experimental values.
3. Training Model
3.1. Data Set Preparation
The data set for this study consists of a total of 600000 data points, all of which were obtained using the geochemical thermodynamics Python program developed by Awolayo.32 The program used the water state equation IAPWS-9532 to calculate the DH coefficient of water. However, due to the complexity and time-consuming nature of this method, it is not suitable as the method for solving DH coefficients in this paper. Nevertheless, this method can calculate a large number of theoretical DH coefficient values, which are mainly used in this study. The experimental data includes pressure, temperature, and DH parameters, some of which are shown in Table 1. The range of data usage is from 0 to 300 °C for temperature and from 0 to 200 MPa for pressure. The statistical analysis of all experimental data is shown in Table 2, where the maximum temperature in the data is 300 °C, the minimum temperature is 1 °C, and the average temperature is 150.5 °C. The maximum pressure range is 2000 bar, the minimum pressure is 1.0132 bar, and the average pressure is 1000.5 bar. the data calculated by the IAPWS-95 are divided into three parts, namely, the training set, validation set, and test set. The training set and validation set are used for model training and parameter tuning, which is the process of establishing the relationships among the DH parameters, temperature, and pressure functions. The data in the test set do not participate in the training of the model throughout the process. Its function is to evaluate the model’s generalization ability (the model’s adaptability to unknown data) after the model is established. It is calculated only once throughout the entire process, eliminating human interference. The prediction results in the test set can be used to verify the authenticity and applicability of the model.
Table 1. Experimental Data (Partial).
| Number of data | P (bar) | T (°C) | Ar | Br | bNaCl | bNa+,Cl– |
|---|---|---|---|---|---|---|
| 1 | 1.0132 | 1 | 0.4944 | 0.3254 | 2.18 × 10–06 | –0.11433 |
| 2 | 1.0132 | 2 | 0.495 | 0.3255 | 2.16 × 10–06 | –0.11406 |
| 3 | 1.0132 | 3 | 0.4956 | 0.3257 | 2.15 × 10–06 | –0.11377 |
| 4 | 1.0132 | 4 | 0.4962 | 0.3258 | 2.13 × 10–06 | –0.11345 |
| 5 | 1.0132 | 5 | 0.4968 | 0.3259 | 2.12 × 10–06 | –0.11311 |
| ··· | ··· | ··· | ··· | ··· | ··· | ··· |
| 600000 | 2000 | 300 | 0.84 | 0.3729 | –8.35 × 10–07 | 0.1366 |
Table 2. Statistical Analysis of Data.
| Parameter | Minimum value | Maximum value | Average value | Standard deviation |
|---|---|---|---|---|
| P (bar) | 1.0132 | 2000 | 1000.5 | 577.351 |
| T (°C) | 1 | 300 | 150.5 | 86.602 |
| Ar | 0.455 | 17.195 | 0.754 | 1.081 |
| Br | 0.0411 | 0.3925 | 0.349 | 0.0226 |
| bNaCl | –1.99 × 10–6 | 2.34 × 10–6 | 4.15 × 10–7 | 9.85 × 10–7 |
| bNa+,Cl– | –0.173 | 0.141 | 0.029 | 0.0751 |
3.2. Correlation Analysis of Data
There is a relationship between DH parameters with temperature and pressure. Next, the Pearson correlation coefficient33−36 will be used to study the correlation coefficient between DH parameters with temperature and pressure. Pearson correlation coefficient is a linear correlation relationship used to reflect the degree of linear correlation between two variables X and Y. According to formula 1, calculate the correlation coefficient between parameters as shown in Table 3.
| 1 |
where r is Pearson’s correlation coefficient, x̅ and y̅ are the mean values of the parameters, and xi and yi are the values of the parameters corresponding to the ith sample.
Table 3. Correlation Coefficients between Logging Parameters.
| Parameter | P (bar) | T (°C) | Ar | Br | bNaCl | bNa+,Cl– |
|---|---|---|---|---|---|---|
| P (bar) | 1 | |||||
| T (°C) | 2.7 × 10–14 | 1 | ||||
| Ar | –0.17 | –0.23 | 1 | |||
| Br | 0.028 | –0.65 | –0.37 | 1 | ||
| bNaCl | 0.11 | –0.99 | –0.27 | –0.63 | 1 | |
| bNa+,Cl– | –0.011 | –0.98 | 0.22 | 0.64 | –0.98 | 1 |
The correlation coefficients between DH parameters are presented in Table 3. In order to more intuitively display the correlation between DH parameters, a heatmap of the correlation coefficient was drawn, as shown in Figure 1. The larger the absolute value of the Person correlation coefficient, the closer it is to 1, indicating a stronger linear relationship between the two variables. The closer it is to 0, the weaker the linear relationship. Normally, we consider the Person correlation coefficient to be within the range of [0.6, 1], indicating strong correlation between two parameters, within the range of [0.4, 0.6], indicating moderate correlation, within the range of [0.2, 0.4], indicating weak correlation, and within the range of [0, 0.2], indicating weak or no correlation between two parameters. In addition, the positive and negative signs of the correlation coefficient indicate the direction of correlation, with positive numbers indicating positive correlation and negative numbers indicating negative correlation.
Observing Figure 2, The correlation between DH parameters and pressure is generally low. The correlation coefficient between bNa+,Cl– and pressure is only −0.011, and the correlation coefficient between Br and pressure is only 0.028. There is basically no correlation between bNa+,Cl– and Br with P. The correlation coefficient between Ar and pressure is −0.17, indicating a weak negative correlation between these two parameters. The correlation coefficient between bNaCl and p is 0.11, indicating a weak positive correlation between these two parameters. The correlation between DH parameters and T is high. The correlation coefficient between bNaCl and temperature reached −0.99, indicating a super strong negative correlation between these two parameters. The correlation coefficient between bNa+,Cl– and temperature is 0.98, indicating a very strong positive correlation between the two parameters. The correlation coefficients between temperature with Br and Ar are 0.65 and 0.23, respectively, indicating that both are positively correlated with temperature. The correlation between Br and temperature is strong positive, while the correlation between Ar and temperature is weak positive.
Figure 2.
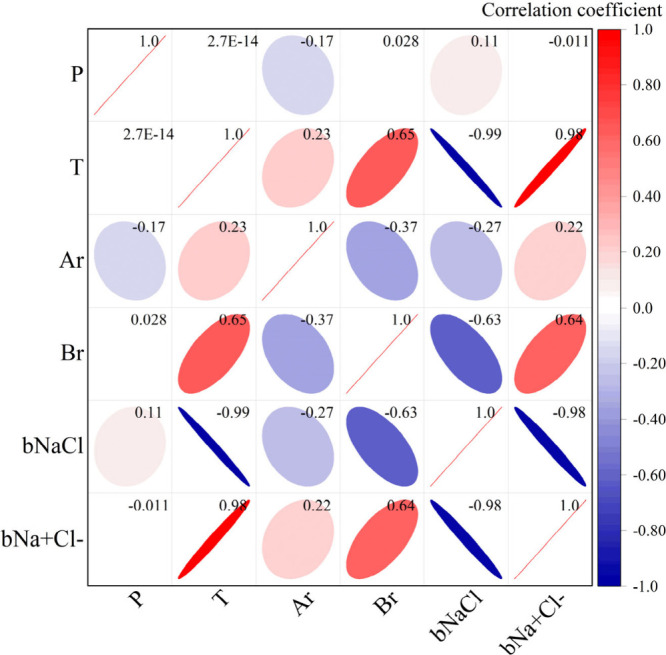
Heatmap of correlations between parameters.
3.3. Interpolation Algorithm
In the numerical simulation of CO2 deep saline geological storage, the traditional method is to use interpolation algorithm to calculate DH parameters and obtain the activity coefficient of NaCl solution. Interpolation algorithm37 is an algorithm that solves unknown data points based on the relationships between known data points using a certain function or mathematical model. The specific implementation process of the interpolation algorithm38−40 in this study is as follows:
Assuming the coordinates of a known point are (x0, y0) and (x1, y1), to calculate the value of a position y on the line connected to the known point within the interval [x0, x1], use the following formula:
| 2 |
Since the value of x is known, the value of y can be obtained according to formula 1 as follows:
| 3 |
By using eqs 2 and 3, the DH parameter can be calculated. Although interpolation algorithms are widely used in various fields, they still face significant challenges. The computational complexity of interpolation algorithms is usually high, especially when there are a large number of data points or the interpolation function is complex, which leads to longer computation time in the numerical simulation process and affects the efficiency of the model. The results of interpolation algorithms are highly dependent on the accuracy and distribution of known data points. If there are errors or uneven distribution of data points, the interpolation results may be significantly affected. Interpolation algorithms are sensitive to noise, and if there is known noise or error in the data points, the interpolation results may be significantly affected. In response to the above challenges, this study proposes a new method based on machine learning algorithms to calculate DH parameters.
3.4. Machine Learning Models
After data set preparation, the training set data are processed using the K-means clustering algorithm, polynomial regression algorithm, and K-NearestNeighbor regression algorithm (KNN).
The K-means clustering algorithm is an unsupervised machine learning algorithm based on distance measurement.41,42 K-means clustering, as a preprocessing step in this study, clusters the data and applies different classifiers to each cluster. For large-scale data sets, the K-means algorithm usually has high computational efficiency and can identify similarities and differences in the data, thereby revealing the inherent features of the data and improving the algorithm’s predictive performance.
First, the initial number of clusters k and the corresponding initial cluster center C need to be randomly specified from the training set. Then, the Euclidean distance method is used to calculate the distance from the initial cluster center to other data objects. This distance can divide the training set into k clusters, thereby achieving high similarity of data within the clusters. Finally, the model is tuned and retrained using the validation set data to achieve optimal performance. The formula is
| 4 |
In eq 4, X is the data object, Ci is the i-th cluster center, m is the dimension of the data object, and Xj and Ci are the attribute values of the j-th dimension of the data object X and cluster center C.
The polynomial regression algorithm is a special linear regression model,43,44 mainly aimed at adding new features to the model, which are the result of combining the original data features. Polynomial regression can fit data distributions of various shapes, especially nonlinear relationships. Unlike linear regression, polynomial regression can capture nonlinear trends in data by introducing higher powers of variables, providing more accurate predictions and explanations. Polynomial regression has a high degree of flexibility and can adapt to different levels of complexity by adjusting the order of the polynomial. This makes it suitable for various forms of data, including continuous and discrete data. Polynomial regression can also be combined with other techniques such as regularization, feature selection, cross validation, etc. to further improve the performance and generalization ability of the model.
First, the training set is trained into a bivariate polynomial consisting of constant and independent variables P and T that undergo finite degree multiplication and addition operations. The bivariate polynomial is transformed into a multivariate polynomial through variable substitution, and this method is used to train the original DH parameter regression model. Then, the validation set is used to optimize the polynomial coefficients of the model so that the model approximates the optimal model. The calculated value of the optimal model is used as the prediction result. The steps are as follows:
Assuming that X(t) is the n-th degree polynomial combination of the data characteristic pressure P and temperature T, the algebraic polynomial X(t) can be used:
| 5 |
Equation 5 describes a multivariate linear mathematical model, which can be expressed in its matrix form as
| 6 |
where, in eq 6, Y = (Y0, Y1, Y2, ..., Yn)T, W = (W0, W1, W2, ..., Wn)T, and
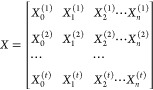 |
Solved by the least-squares method
| 7 |
By substituting eq 7 back into multiple linear regression eq 6, the predicted values at a certain temperature and pressure can be calculated using eq 6.
The KNN45−47 is an algorithm that infers the target point through the features of the k-nearest neighboring points. This method does not require assumptions about the distribution of data, nor does it require a complex model training process, making it easy to understand and implement. Unlike many other regression methods that require building complex mathematical models, KNN regression does not require explicit construction of regression equations. KNN regression can handle various types of data, including numerical, categorical, and mixed data, and does not have strict requirements for the distribution and shape of the data. It can directly use the actual values in the training data for prediction, which makes KNN regression advantageous in dealing with complex nonlinear relationships.
First, KNN identifies k adjacent points of a sample and then assigns different weights to the impact of points at different distances. The weighted average method is used in data regression, in which the weighted average of these k adjacent points is used as the prediction result. The steps are as follows:
The selected training set is Xi = (X1, X2, ..., Xn), where each training sample can be represented as Xi = (xi1, xi2, ..., xid, yi), i ∈ n, and the Euclidean distance D between the training sample Xi and the test sample Xt = (xt1, xt 2, ..., xtd, yt) can be expressed as
| 8 |
In the formula, xim and xtm are the m-th dimensions of the data object.
According to eq 8, the Euclidean distance between all training samples and test samples is calculated, and the Euclidean distances of their training samples are sorted from smallest to largest. The first k sample points Xj = (xj1, xj2, ..., xjn, yj) are removed, where j ∈ k. Then, the weight Wj of Xj on the predicted value y is defined as
| 9 |
The weights of k samples are calculated via eq 9, and the predicted value yt of the test sample Xt is subsequently calculated. The calculation method is as follows:
| 10 |
3.5. Model Evaluation Indicators
By using various machine learning algorithms to train the training data set, the K-means algorithm, polynomial regression algorithm, and KNN regression algorithm were ultimately determined to be optimal for the data set. However, the method for determining the predictive performance of the model was to use four evaluation indicators, namely, the mean square error (ηMSE), root-mean-square error (ηRMSE), absolute average relative deviation (ηAARD), and coefficient of determination (R2).
ηMSE and ηRMSE48,49 are commonly used indicators to measure the predictive ability of a model. ηMSE is the mean of the sum of the squared differences between the predicted and true values of the model. The square root of ηMSE is equal to ηRMSE. In regression models, smaller ηMSE and ηRMSE indicators are more accurate. Its expression is
| 11 |
| 12 |
ηAARD50 is the expected value of the relative error loss, which is the percentage of the absolute error to the true value. In machine learning model prediction, the smaller the ηAARD value is, the better the accuracy of the model. Its expression is
| 13 |
R2 51,52 is used to measure the proportion of changes in the dependent variable that can be determined by the independent variable. When evaluating the model, R2 is used to reflect the goodness of fit of the model to the data. The closer R2 is to 1, the more reliable the model is, the higher the prediction accuracy, and the better the prediction effect. In contrast, as R2 approaches 0, it indicates poor prediction performance. Its expression is
| 14 |
In eqs 11–14, n is the number of samples, yi is the true value, ŷi is the predicted value, and y̅i is the average value.
3.6. Activity Coefficient Calculation
Assuming that the main cation in the solution is sodium and the main anion is chlorine, after reasonably evaluating the DH parameter model, the empirical formula obtained from machine learning algorithms is substituted into the HKF53−55 equation. The HKF equation is
| 15 |
| 16 |
| 17 |
In eqs 15–17, the subscript j refers to each ion, γ is the activity coefficient of the ion, the DH parameters are Aγ, Bγ, bNaCl and bNa+,Cl–, z is the ion electric charge, I is taken as the true ionic strength of the solution, ω is the Born coefficient, η is a constant equal to 1.66027, where re, j is the effective ionic radius, and eqs 18 and 19 are the calculation methods for the parameter å.
| 18 |
| 19 |
By using machine learning algorithms, DH parameters are regressed into functions related to temperature and pressure. The effective ion radius re,j in the TOUGHREACT database is used to calculate the value of å, while the values of re, Na+ and re,Cl– are inputted from the TOUGHREACT database and can be modified as needed. The activity coefficients of NaCl solutions under various conditions can be calculated using the method of this study and then compared with the measured values in the experiment.
4. Results and Discussion
4.1. Comparison of Different Models
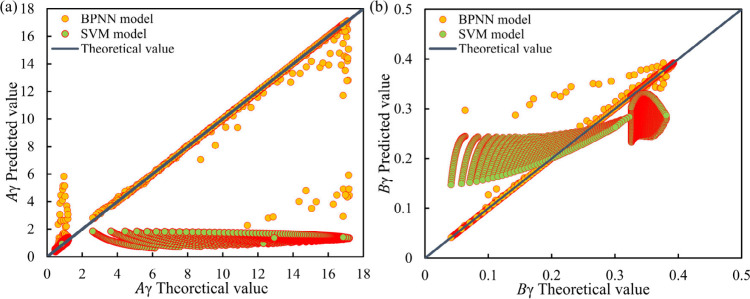
This study establishes a model using machine learning algorithms. The prediction accuracy of BP neural network (BPNN),56,57 support vector machine (SVM),58 and K-means-KNN models were compared on the data set used in this study. Conduct a comprehensive analysis based on the fitting effect diagrams of different models in the following figure. Observing subgraph a in Figure 3, most of the orange points in the SVM model are close to the blue standard line, indicating a small deviation and error range between the predicted and actual values. However, there are a few orange point data points that deviate significantly from the blue standard line and have significant differences, indicating that the SVM model has weak generalization ability and poor performance on this data set. Observing subgraph a in Figure 3, most of the green points in the BPNN model deviate significantly from the blue standard line, but there are a few green points that deviate significantly and are concentrated near the blue standard line. The model as a whole has a large error and poor performance, and the BPNN model is prone to getting stuck in local optima to some extent. It can be concluded that these two models have significant problems in training DH parameters.
Figure 3.
Fitting effect diagrams of different models. (Subfigure a presents the fitting effect on Aγ. Subfigure b presents the fitting effect of Bγ.)
Based on various performance indicators and statistical analysis results, it can be concluded that the BP neural network model and support vector machine model have significant shortcomings in fitting the DH parameters in the studied system. Their prediction accuracy and generalization ability are relatively average, and they have not achieved the expected high-level performance. This result suggests that under the current data set and problem framework, these two models may not be the optimal models. In view of this, in future research work, this paper will explore and adopt another more suitable model for fitting and predicting DH parameters, in order to obtain more accurate results.
4.2. Debye–Hückel Parameter: Empirical Formula
First, K-means clustering was used to classify Aγ, Bγ, bNaCl and bNa+,Cl– parameters under different conditions, with training data accounting for 70%, validation data accounting for 10%, and testing data accounting for 20%. Using temperature and pressure as inputs and DH parameters as outputs, DH parameter models are established based on machine learning algorithms.
Because water will transition from liquid to gas at a specific pressure and temperature, the DH parameters can be further divided using the saturated vapor pressure. The empirical formula for saturated vapor pressure is as follows:
 |
20 |
In eq 20, Psat is the saturated vapor pressure of water, bar. T is the temperature, °C. The temperature T can be substituted into eq 20 to calculate the saturated vapor pressure Psat of water.
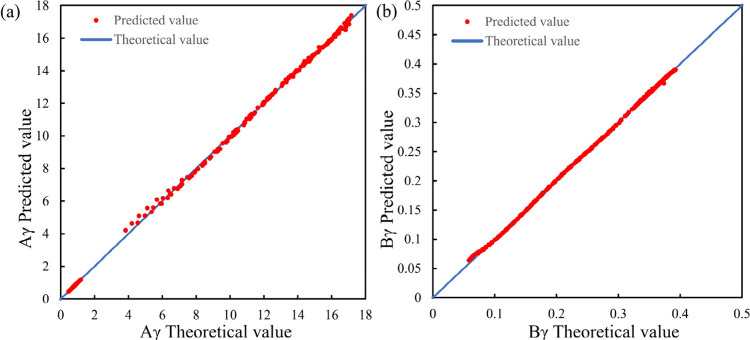
The training data for Aγ and Bγ are fed into the polynomial regression algorithm by using Python. The coefficient matrix of the polynomial is obtained through multiple sets of polynomials, and the coefficients Aγ and Bγ are obtained through the algorithm. The coefficients of the polynomial regression model are shown in Tables 4 and 5. Then, the validation data are used to optimize the initial models of Aγ and Bγ. The prediction results of the optimized polynomial regression model are shown in Figure 4.
Table 4. DH Parameters: Aγ Polynomial Coefficient Table.
| P < Psat | Psat < P < 220.6 bar | P > Psat | 700 < P < 1350 bar | 1350 < P < 2000 bar | |
|---|---|---|---|---|---|
| Coefficient | 0 < T < 300 °C | 0 < T < 300 °C | 0 < T < 300 °C | 0 < T < 300 °C | 0 < T < 300 °C |
| W0 | 8.15753657 | 0.49443726 | 0.49306613 | 0.49191262 | 0.48388707 |
| W1 | 0 | 0 | 0 | 0 | 0 |
| W2 | 4.49455454 | –1.33 × 10–05 | –2.87 × 10–05 | –2.75 × 10–05 | –2.92 × 10–05 |
| W3 | –7.37 × 10–02 | 4.54 × 10–04 | 6.34 × 10–04 | 6.88 × 10–04 | 1.08 × 10–03 |
| W4 | –3.89 × 10–02 | 1.26 × 10–07 | 1.15 × 10–08 | 9.95 × 10–09 | 7.78 × 10–09 |
| W5 | –3.65 × 10–02 | –1.02 × 10–06 | –7.16 × 10–08 | –1.17 × 10–07 | –2.44 × 10–07 |
| W6 | 5.91 × 10–04 | 8.94 × 10–06 | 4.90 × 10–06 | 4.03 × 10–06 | 2.33 × 10–06 |
| W7 | 2.42 × 10–04 | –1.12 × 10–09 | –9.57 × 10–12 | –5.59 × 10–12 | 0 |
| W8 | 1.30 × 10–04 | 7.13 × 10–10 | –2.14 × 10–10 | 1.47 × 10–10 | 0 |
| W9 | 1.22 × 10–04 | 1.01 × 10–08 | 1.55 × 10–09 | –1.88 × 10–09 | 0 |
| W10 | –2.19 × 10–06 | –3.91 × 10–08 | –1.15 × 10–08 | 2.59 × 10–09 | 0 |
| W11 | –9.17 × 10–07 | 2.53 × 10–12 | 2.20 × 10–14 | 0 | 0 |
| W12 | –2.01 × 10–07 | 1.08 × 10–13 | –3.69 × 10–13 | 0 | 0 |
| W13 | –1.61 × 10–07 | –1.23 × 10–12 | 3.87 × 10–12 | 0 | 0 |
| W14 | –1.44 × 10–07 | –3.93 × 10–11 | –2.08 × 10–11 | 0 | 0 |
| W15 | 2.80 × 10–09 | 1.06 × 10–10 | 5.09 × 10–11 | 0 | 0 |
Table 5. DH Parameters: Bγ Polynomial Coefficient Table.
| P < Psat | Psat < P < 220.6 bar | P > Psat | 700 < P < 1350 bar | 1350 < P < 2000 bar | |
|---|---|---|---|---|---|
| Coefficient | 0 < T < 300 °C | 0 < T < 300 °C | 0 < T < 300 °C | 0 < T < 300 °C | 0 < T < 300 °C |
| W0 | 0.06267438 | 0.32488912 | 0.324238567 | 0.324163605 | 0.324360463 |
| W1 | 0 | 0 | 0 | 0 | 0 |
| W2 | 4.77 × 10–02 | 2.26 × 10–06 | –1.65 × 10–07 | –1.03 × 10–06 | –1.17 × 10–06 |
| W3 | –5.92 × 10–04 | 1.47 × 10–04 | 1.66 × 10–04 | 1.78 × 10–04 | 1.81 × 10–04 |
| W4 | –3.13 × 10–03 | –4.78 × 10–09 | 1.79 × 10–09 | 8.09 × 10–10 | 4.44 × 10–10 |
| W5 | –3.69 × 10–04 | –4.22 × 10–08 | –3.85 × 10–08 | –2.44 × 10–08 | –1.73 × 10–08 |
| W6 | 6.55 × 10–06 | 2.48 × 10–07 | 1.76 × 10–07 | 1.05 × 10–07 | 6.60 × 10–08 |
| W7 | 3.53 × 10–06 | 0 | 0 | 0 | 0 |
| W8 | 4.28 × 10–07 | 0 | 0 | 0 | 0 |
| W9 | 1.27 × 10–06 | 0 | 0 | 0 | 0 |
| W10 | –2.62 × 10–08 | 0 | 0 | 0 | 0 |
| W11 | –1.31 × 10–08 | 0 | 0 | 0 | 0 |
| W12 | –2.87 × 10–09 | 0 | 0 | 0 | 0 |
| W13 | –2.39 × 10–10 | 0 | 0 | 0 | 0 |
| W14 | –1.56 × 10–09 | 0 | 0 | 0 | 0 |
| W15 | 3.43 × 10–11 | 0 | 0 | 0 | 0 |
Figure 4.
Aγ and Bγ prediction effect diagram established by the polynomial regression algorithm. (Subfigure a presents the fitting effect on Aγ. Subfigure b presents the fitting effect of Bγ.)
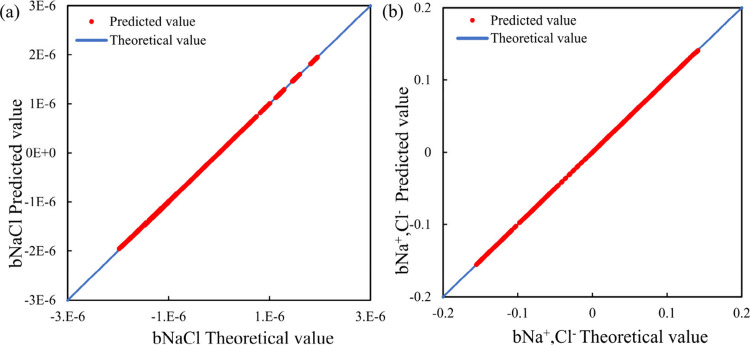
By using the KNN regression algorithm to model the training data of bNaCl and bNa+,Cl– separately, due to the large model error established by the default parameter KNN regression algorithm, the initial models of bNaCl and bNa+,Cl– were optimized using the validation data. During the parameter optimization process, the model with the best evaluation index was found. The prediction results of the optimized KNN regression model are shown in Figure 5, and the optimized KNN model parameter results are shown in Table 6.
Figure 5.
Prediction effect of bNaCl and bNa+,Cl– established by the KNN regression algorithm. (Subfigure a presents the fitting effect on bNaCl. Subfigure b presents the fitting effect of bNa+,Cl–.)
Table 6. KNN Model Parameters Table.
| Algorithm | K-value | Weight | Computing method | Metric function |
|---|---|---|---|---|
| KNN | 4 | Distance | Kd_tree | Euclidean distance |
The results of bNaCl and bNa+,Cl– predicted by the KNN model are fed into the polynomial regression algorithm, and then the polynomial empirical formulas of bNaCl and bNa+,Cl– are obtained through the predicted values of the KNN model. The model coefficients are shown in Table 7.
Table 7. DH Parameters: bNaCl and bNa+,Cl– Polynomial Coefficient Table.
|
bNaCl coefficient |
bNa+,Cl– coefficient |
|||||
|---|---|---|---|---|---|---|
| 1 < P < 700 bar | 700 < P < 1350 bar | 1350 < P < 2000 bar | 1 < P < 700 bar | 700 < P < 1350 bar | 1350 < P < 2000 bar | |
| Coefficient | 0 < T < 300 °C | 0 < T < 300 °C | 0 < T < 300 °C | 0 < T < 300 °C | 0 < T < 300 °C | 0 < T < 300 °C |
| W0 | 2.132 × 10–06 | 1.95 × 10–06 | 2.22 × 10–06 | –0.12457 | –0.12263 | –0.13261 |
| W1 | 0 | 0 | 0 | 0 | 0 | 0 |
| W2 | –5.06 × 10–11 | 4.88 × 10–10 | 1.69 × 10–11 | –6.34 × 10–06 | –1.53 × 10–05 | –3.51 × 10–06 |
| W3 | –1.28 × 10–08 | –1.41 × 10–08 | –1.44 × 10–08 | 1.43 × 10–03 | 1.46 × 10–03 | 1.43 × 10–03 |
| W4 | –6.29 × 10–17 | –2.52 × 10–13 | –1.8 × 10–16 | –1.08 × 10–17 | 6.95 × 10–09 | –4.68 × 10–17 |
| W5 | 2.14 × 10–12 | 1.37 × 10–12 | 6.1 × 10–13 | 1.78 × 10–08 | –2.64 × 10–10 | –1.82 × 10–08 |
| W6 | –6.13 × 10–13 | 5.68 × 10–12 | 9.72 × 10–12 | –1.95 × 10–06 | –1.99 × 10–06 | –1.83 × 10–06 |
4.3. Model Evaluation
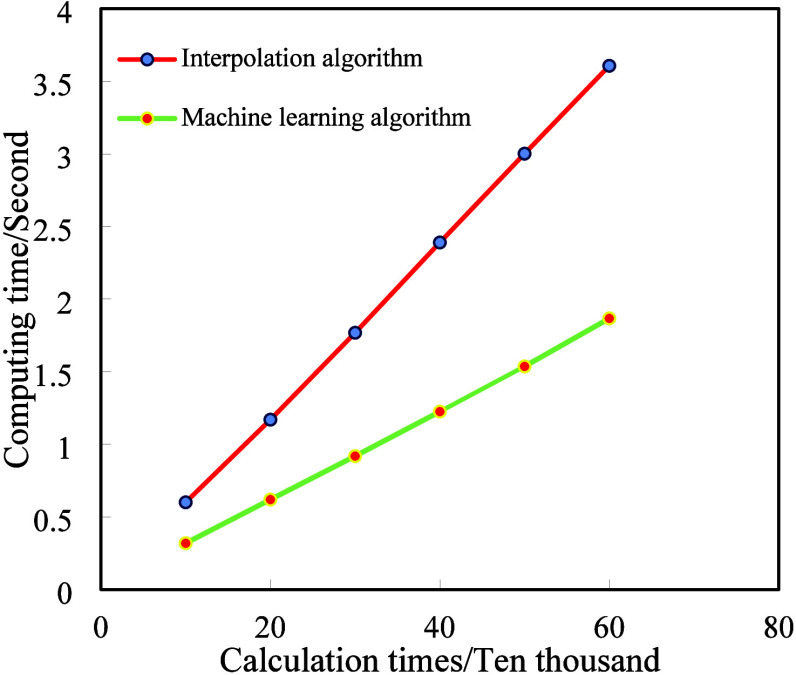
The hardware device used in this study is a laptop equipped with an i7 CPU-12490F, RTX2060s GPU, and 16GB of memory. This computer runs on the Windows 11 operating system and is configured with Python 3.6 and Anaconda environment. This study utilizes PyCharm as a compiler for writing and debugging algorithmic Python code. The data set was processed using machine learning algorithms and interpolation algorithms, and their processing times were compared. The efficiency graph is shown in Figure 6. Under the same device testing conditions, as the number of operations increases, the difference in computation time between the two algorithms gradually increases. The use of machine learning models requires less computation time, as shown in Table 8. The average computation speed of using machine learning models is 48% greater than that of interpolation algorithms (i.e., traditional calculation methods), significantly improving the computation speed of the DH parameters.
Figure 6.
Efficiency diagram of the machine learning algorithm and interpolation algorithm.
Table 8. Operation Schedule of Machine Learning and Interpolation Algorithms.
| Calculation times (Ten thousand) | Machine learning (Second) | Interpolation algorithms (Second) | Speed improvement rate (%) |
|---|---|---|---|
| 10 | 0.319 | 0.6009 | 46.91 |
| 20 | 0.62 | 1.17 | 47 |
| 30 | 0.92 | 1.7684 | 47.98 |
| 40 | 1.2255 | 2.3901 | 48.73 |
| 50 | 1.5367 | 3.0019 | 48.81 |
| 60 | 1.8673 | 3.607 | 48.23 |
Separate Aγ, Bγ and bNaCl, bNa+,Cl– test sets were input into the optimized polynomial regression model and KNN regression model, and the predicted and experimental values were evaluated. The evaluation results are shown in Table 9. The ηMSE values of the experimental and predicted values in the test set are less than 0.1, the ηRMSE values are less than 0.1, and the ηAARD values are mostly less than 1%. The model has excellent prediction accuracy, R2 is relatively large, and the value is close to 1, making it suitable for predicting DH parameters.
Table 9. DH Parameter Model Evaluation Indicators.
| Coefficient | 0 < T < 300 °C | ηMSE | ηRMSE | ηAARD | R2 |
|---|---|---|---|---|---|
| Aγ | 1 < P < 700 bar, P < Psat | 0.0179826 | 0.134099 | 11.276292 | 0.9985567 |
| 1 < P < 700 bar, Psat < P < 220.6 bar | 2.05 × 10–06 | 0.0014327 | 0.3070689 | 0.999937 | |
| 1 < P < 700 bar, P > Psat | 6.76 × 10–07 | 0.0008224 | 0.3064672 | 0.9999756 | |
| 700 < P < 1350 bar | 1.01 × 10–06 | 0.001004 | 0.3429198 | 0.9999467 | |
| 1350 < P < 2000 bar | 1.66 × 10–06 | 0.0012881 | 0.37269 | 0.9998841 | |
| Bγ | 1 < P < 700 bar, P < Psat | 9.93 × 10–07 | 0.0009965 | 0.7971206 | 0.9998352 |
| 1 < P < 700 bar, Psat < P < 220.6 bar | 7.37 × 10–08 | 0.0002714 | 0.6476086 | 0.9997761 | |
| 1 < P < 700 bar, P > Psat | 5.19 × 10–08 | 0.0002278 | 0.6472493 | 0.9998337 | |
| 700 < P < 1350 bar | 6.42 × 10–08 | 0.0002533 | 0.6497079 | 0.9997523 | |
| 1350 < P < 2000 bar | 9.98 × 10–08 | 0.0003159 | 0.6514961 | 0.9995496 | |
| bNaCl | 1 < P < 700 bar | 1.40 × 10–17 | 3.74 × 10–09 | 0.724137 | 0.9999878 |
| 700 < P < 1350 bar | 7.71 × 10–18 | 2.78 × 10–09 | 0.716769 | 0.9999915 | |
| 1350 < P < 2000 bar | 6.22 × 10–18 | 2.49 × 10–09 | 0.695731 | 0.9999924 | |
| bNa+,Cl– | 1 < P < 700 bar | 1.18 × 10–08 | 0.0001085 | 0.9671937 | 0.9999979 |
| 700 < P < 1350 bar | 6.56 × 10–09 | 8.10 × 10–05 | 0.971269 | 0.9999988 | |
| 1350 < P < 2000 bar | 5.91 × 10–09 | 7.68 × 10–05 | 0.969411 | 0.9999989 |
4.4. Solving for the Activity Coefficient of the NaCl Solution
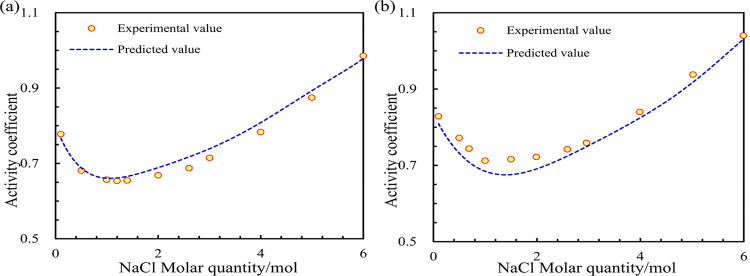
Then, machine learning models are used to calculate the DH parameter predicted values. The predicted values were substituted into the HKF equation to calculate the activity coefficients of the NaCl solutions at 25 and 110 °C. The accuracy of the machine learning model was verified by comparison with the experimental values of the activity coefficients of NaCl solutions.59,60 The relative error results were calculated using the predicted and experimental values, as shown in Table 10. The fitting effect of the model’s predicted and experimental values is shown in Figure 7.
Table 10. Comparison of NaCl Activity Coefficients and Errors in Solutions.
| Temperature (°C) | NaCl concentration (mol/kg) | Experimental value | Predicted value | R2 | Relative error (%) |
|---|---|---|---|---|---|
| 25 | 0.1 | 0.7775 | 0.7664 | 0.9716 | 1.48 |
| 25 | 1 | 0.6581 | 0.6583 | 0.22 | |
| 25 | 2 | 0.6684 | 0.6867 | 2.73 | |
| 25 | 3 | 0.7147 | 0.7393 | 3.44 | |
| 25 | 4 | 0.7832 | 0.8081 | 3.19 | |
| 25 | 5 | 0.8747 | 0.893 | 2.09 | |
| 25 | 6 | 0.9853 | 0.9786 | 0.68 | |
| 110 | 0.1 | 0.8285 | 0.8085 | 0.9209 | 2.41 |
| 110 | 1 | 0.712 | 0.676 | 5.06 | |
| 110 | 2 | 0.722 | 0.691 | 4.29 | |
| 110 | 3 | 0.759 | 0.748 | 1.45 | |
| 110 | 4 | 0.84 | 0.8248 | 1.81 | |
| 110 | 5 | 0.938 | 0.918 | 2.13 | |
| 110 | 6 | 1.04 | 1.03 | 0.96 |
Figure 7.
Fitting effect of the NaCl activity coefficients. (Subfigure a is at 25 °C. Subfigure b is at 110 °C.)
Table 10 shows that when calculating the activity coefficients of NaCl solutions at 25 and 110 °C, the average R2 of the model is 0.9463, indicating high accuracy of the fitted experimental values. The maximum relative error of the activity coefficient model value of the NaCl solution at 25 °C is 3.44%, the minimum relative error is 0.22%, and the average relative error is 1.98%. The maximum relative error of the activity coefficient model value of the NaCl solution at 110 °C is 5.06%, the minimum relative error is 0.96%, and the average relative error is 2.59%. Table 7, Figure 6 show that the activity coefficients calculated by the model are highly similar to the experimental values, and the data trends are consistent. They can be applied to the calculation of the geochemical reaction equilibrium model, indicating that the model trained by machine learning is reasonable and accurate.
Figure 8 shows a comparison of the fitting effect between the predicted values and actual values of different models. The comparison of fitting effects in Figure 8 can provide a more intuitive observation of the fluctuations and errors between the model prediction results. The figure uses dots of different colors and shapes to represent the predicted values of the machine learning model and traditional calculation methods. The two light blue dashed lines in the figure represent the 5% error line, while the dark solid line represents the true value of the activity coefficient of NaCl solution, located between the two light blue lines. It can be intuitively observed that the prediction results of the machine learning model represented by the red dots are almost entirely between the two light green 5% error lines, and are closer to the deep blue solid line. However, there is a noticeable dispersion phenomenon between the yellow dots and the red dots. The fitting effect between the predicted and actual values of the two methods indicates that the machine learning model has better accuracy and speed in calculating the activity coefficient of NaCl solution than traditional calculation methods.
Figure 8.
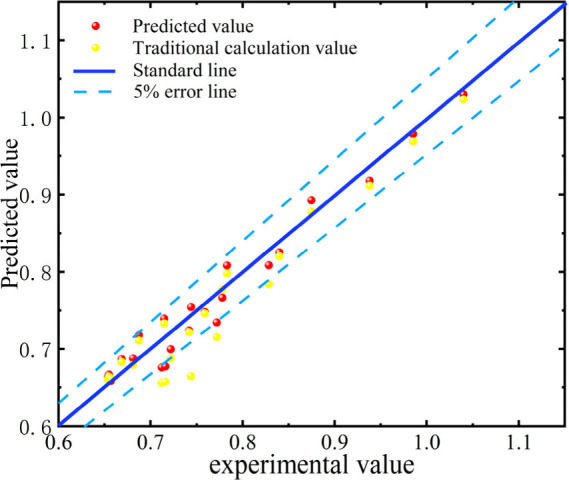
Comparison of the fitting effect between predicted values and actual values using machine learning algorithm models and interpolation methods.
Figure 9 shows the residual plot between the predicted results of the two models and the true values. Residual analysis is an effective method for determining the accuracy of model predictions, which can help determine whether the established model is suitable. The residual plots within two dashed rectangular boxes represent the machine learning model and the traditional computational method model from left to right. Observing Figure 9, it can be seen that the residuals of different models are randomly distributed without obvious patterns, indicating that all models have a certain predictive ability for the activity coefficient of NaCl solution. However, it can be observed that the residual values predicted by traditional calculation methods are relatively large, indicating that the accuracy of their prediction results is low. It is evident that the residual values of machine learning models are significantly higher than those of traditional calculation methods. It can be applied to the calculation of the geochemical reaction equilibrium model, indicating that the model trained by machine learning is reasonable and accurate.
Figure 9.
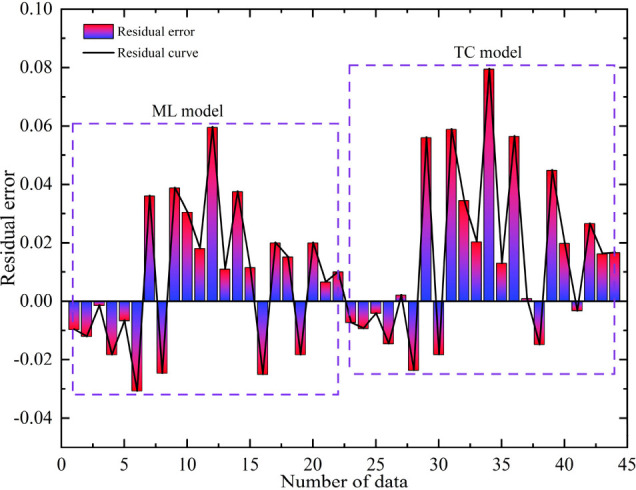
Residual plots predicted by two models.
5. Main Limitations and Future Works
The machine learning algorithm proposed in this study significantly enhances the calculation speed and accuracy of activity coefficients. However, its applicability is limited to a temperature range of 0 to 300 °C and a pressure range of 0 to 200 MPa. For geological storage conditions exceeding these limits, the accuracy and applicability of this method remain unverified, suggesting the need for further model expansion and optimization in practical applications. During the training of machine learning models, temperature and pressure are utilized as input features to predict DH parameters, with a focus solely on improving their calculation speed and accuracy. Yet, the calculation of activity coefficients may also be influenced by various other factors, such as the concentration, ion type, and ion charge of NaCl solutions, which may necessitate the use of additional relevant databases. This could potentially introduce bias in the model’s calculation results under specific conditions.
The primary objective of this study is to improve the calculation speed and accuracy of activity coefficients through the application of machine learning algorithms, indirectly enhancing the computational speed of numerical simulations for CO2 deep saltwater storage. While the numerical simulation of CO2 deep saltwater storage is not the focus of this study, it is noteworthy that computational efficiency may become a limiting factor in such simulations due to the complexity of multiple seepage coupling operations, varying geological conditions, and diverse chemical reaction types. Therefore, future research must further optimize the algorithm and consider the model’s influencing factors from multiple perspectives to improve its computational efficiency and quality.
In summary, this study has made significant progress in using machine learning algorithms to accelerate the calculation of activity coefficients in the numerical simulation of CO2 geological storage, but there are still some limitations. In order to overcome these limitations, future research needs to further explore the applicability of the model, selection of input features, validation of experimental data, interpretability of the model, optimization of computational efficiency, and numerical simulation applications.
6. Conclusions
-
(1)
Traditionally, the HKF equation is used to calculate the activity coefficient of NaCl solution in numerical simulations of CO2 deep salt water geological storage. The calculation of the HKF equation requires obtaining DH parameters, while traditional methods calculate DH parameters through interpolation algorithms, which results in longer computation time during numerical simulation. This study used machine learning algorithms to calculate DH parameters, which increased the calculation speed by 48% compared to interpolation algorithms. At the same time, machine learning algorithms can avoid many conditions and assumptions, and can only quickly calculate DH parameters based on the characteristics of the data set itself.
-
(2)
This study combines K-means clustering, polynomial regression, and KNN regression with the HKF equation to jointly train DH parameters obtained from the IAPWS-95 method, and constructs activity coefficient calculation formulas related to temperature and pressure. The activity coefficients obtained by this method have relatively small deviations from experimental values. The research results show that the average coefficient of determination between the activity coefficients calculated using machine learning algorithms and experimental values is 0.9463, with an average relative error of 2.28%.
-
(3)
This research method simplifies the calculation process of DH parameters and can quickly calculate the activity coefficient of solutions within the temperature and pressure range of 0 to 300 °C and 0 to 200 MPa, with a wide range of applications. The method proposed in this study greatly improves the efficiency of numerical simulation of CO2 geological storage. Due to its high accuracy and ease of use, this method is of great significance for numerical simulation of geochemical reactions, providing new computational methods and ideas for research in related fields.
Acknowledgments
The authors thank the editors and reviewers for their comments, which improved the quality of the manuscript. Furthermore, the authors would like to acknowledge the Cooperative Innovation Center of Unconventional Oil and Gas Resources of Yangtze University. We are grateful for the support from the National Natural Science Foundation of China (NSFC Grant No. 52004032).
Data Availability Statement
All data supporting the results of this study can be obtained in the paper or from the corresponding author. Some of the data can be obtained in the GitHub repository: https://github.com/lhlc67/DH_And_NaCl_datas
Author Contributions
B.W. Q: Conceptualization, Methodology, Software, Investigation, Formal Analysis, Writing - Original Draft. Y.Z. Z.: Conceptualization, Funding Acquisition, Resources, Supervision, Writing - Review & Editing. L.Y.: Data Curation, Formal Analysis. Y.X.Y.: Visualization, Investigation. M.L.Z.: Resources, Visualization. Y.R.Z.: Software, Validationd. Y.T.Y.: Supervision, Writing - Review & Editing.
The authors declare no competing financial interest.
References
- Lin T.; Liu X.; Sun X. Countermeasures of petrochemical industry for carbon peak and neutrality goals. Modern Chemical Industry 2023, 43 (3), 1–5. 10.16606/j.cnki.issn0253-4320.2023.03.001. [DOI] [Google Scholar]
- Zeng Y.; Wang X.; Tang H.; Liao J.; Tian M. A review on scientific connotation, realization path and challenges of peak carbon dioxide emissions and carbon neutrality strategies. Modern Chemical Industry 2022, 42 (10), 1–4. 10.16606/j.cnki.issn0253-4320.2022.10.001. [DOI] [Google Scholar]
- Gan F.; Jian X.; Chang Y.; Jin Z.; Wang H; Shi J. Exploration of carbon neutral technology path in petrochemical industry. Chemical Industry and Engineering Progress 2022, 41 (3), 1364–1375. 10.16085/j.issn.1000-6613.2021-1601. [DOI] [Google Scholar]
- Huang W.; Li Y.; Chen P. China’s CO2 pipeline development strategy under the strategy of carbon neutrality. Natural Gas Industry B 2023, 10 (5), 502–510. 10.1016/j.ngib.2023.09.008. [DOI] [Google Scholar]
- Chang Y.; Feng N. Development Countermeasures for Oil and Gas Industry Under the Background of “Carbon Peaking and Carbon Neutrality. Xinjiang Petroleum Geology 2022, 43 (2), 235–240. 10.7657/XJPG20220216. [DOI] [Google Scholar]
- Zhang L.; Cao C.; Wen S.; Zhao Y.; Peng X.; Wu J. Thoughts on the developmengt of CO2-EGR under the background of carbon peak and carbon neutrality. Natural Gas Industry B 2023, 10 (4), 383–392. 10.1016/j.ngib.2023.07.007. [DOI] [Google Scholar]
- Zhou H; Zhou Y.; Xu C. Exploration of refining and chemical integration under China’s dualcarbon target. Chemical Industry and Engineering Progress 2022, 41 (4), 2226–2230. 10.16085/j.issn.1000-6613.2022-0225. [DOI] [Google Scholar]
- Mo S.; Li Y.; Long X.; Shi X.; Zhao L.; Chen Y. Development of Numerical Simulation for CO2 mineral Sequestration. Bulletin of Geological Science and Technology 2013, 32 (6), 150–158. [Google Scholar]
- Wang T.; Yu H.; Zhu X.; Li J.; Liu R.; Kou S.; Wang J.; Liao S. Numerical simulation study on geological storage of CO2 in saline aquifers assisted by water alternating gas. China Offshore Oil and Gas 2023, 35, 198–204. 10.11935/j.issn.1673-1506.2023.04.022. [DOI] [Google Scholar]
- Cao M.; Chen J. The site selection geological evaluation of the CO2 storage of the deep saline aquifer. Acta Geologica Sinica 2022, 96, 1868–1882. 10.19762/j.cnki.dizhixuebao.2022034. [DOI] [Google Scholar]
- Mo S.; Long X.; Li Y.; Zeng F.; Shi X.; Zhang K.; Zhao L. Numerical Modeling of CO2 Sequestration in the Saline Aquifer of Yancheng Formation in Subei Basin Using TOUGHREACT-MP. Journal of Jilin University (Earth Science Edition) 2014, 44, 1647–1658. 10.13278/j.cnki.jjuese.201405208. [DOI] [Google Scholar]
- Chen J.; Bo Z. Approaches to geochemical reaction equilibrium modeling. Geological Science and Technology Information 2001, 41–46. [Google Scholar]
- Dong J.; Li Y.; Yan G.; Ke Y.; Wu R. Numerical Simulation of CO-Water-Rock Interaction Impact on Caprock Permeability. Bulletin of Geological Science and Technology 2012, 31 (1), 115–121. [Google Scholar]
- Yu B.; Lai X. Carbonic Acid Systam of Ground water and the Solubility of Calcite during Diagenesis. Acta Sedimentologica Sinica 2006, 627–635. [Google Scholar]
- Chen Z.; Anderson G.; Peng L.. Theories and Applications of Geochemical Modelling; Science Press, 2017. [Google Scholar]
- Li Y. Recent Advances in Study on Thermodynamic Models for Real Systems Including Electrolytes. Tsinghua Science and Technology 2006, 11, 181–187. 10.1016/S1007-0214(06)70173-0. [DOI] [Google Scholar]
- Li Y.; Lu J.. Electrolyte solution theory; Tsinghua University Press, 2005. [Google Scholar]
- Wang G.; Li P.. Introduction and Application of HKF Model in the Handbook of Thermodynamic Equilibrium Calculation Data; Geology Press, 1992. [Google Scholar]
- Frapiccini A.; Perez T.; Goldschmit M.; Cirimello P.; Santilli F.; Morris W. Development of a model to predict corrosion rate and flow pattern in oil and gas production. SPE/AAPG/SEG Latin America Unconventional Resources Technology Conference. URTEC 2023, D021S012R001. [Google Scholar]
- Hessen E. T.; Haug-Warberg T.; Svendsen H. F. The refined e-NRTL model applied to CO2–H2O–alkanolamine systems. Chem. Eng. Sci. 2010, 65 (11), 3638–3648. 10.1016/j.ces.2010.03.010. [DOI] [Google Scholar]
- Bollas G. M.; Chen C. C.; Barton P. I. Refined electrolyte-NRTL model: Activity coefficient expressions for application to multi-electrolyte systems. AIChE journal 2008, 54 (6), 1608–1624. 10.1002/aic.11485. [DOI] [Google Scholar]
- Shen C.; Yang S.; Li B.; Dong S.; Zhao L.; Sang Q. Research Progress of Electrolyte Solution. Guangdong Chemical Industry 2018, 45, 158–160. [Google Scholar]
- Xu J.; Zhang H.; Liu J.; Dong Z. Research progress and application of electrolyte NRTL model. Chemical Industry and Engineering Progress 2013, 32, 2023–2029. 10.3969/j.issn.1000-6613.2013.09.004. [DOI] [Google Scholar]
- Novikov A. A. Applying the Extended Helgeson–Kirkham–Flowers Equation of State to Strongly Polar Undissociated Substances: Properties of Arsenous Acid and Orthophosphoric Acids at Infinite Dilution. Russian Journal of Physical Chemistry A 2022, 96 (12), 2667–2679. 10.1134/S003602442211022X. [DOI] [Google Scholar]
- Dolejš D.; Hanková B. Mineral solubility in aqueous fluids: constraints on functionality and accuracy of equations of state for aqueous species. EGU General Assembly Conference Abstracts 2018, 10319. [Google Scholar]
- Akinfiev N. N.; Diamond L. W. Thermodynamic description of aqueous nonelectrolytes at infinite dilution over a wide range of state parameters. Geochim. Cosmochim. Acta 2003, 67 (4), 613–629. 10.1016/S0016-7037(02)01141-9. [DOI] [Google Scholar]
- Chen J.; Yang R.; Bo Z. Geochemical reaction modeling development and its application. Geological Science and Technology Information 2002, 100–104. [Google Scholar]
- Chen J.; Bo Z. Approaches to geochemical reaction equilibrium modeling. Geological Science and Technology Information 2002, 41–46. [Google Scholar]
- Gu S.; Chen J.; Tian Q. An adaptive time-step energy-preserving variational integrator for flexible multibody system dynamics. Applied Mathematical Modelling 2025, 138, 115759 10.1016/j.apm.2024.115759. [DOI] [Google Scholar]
- Li D.Gas-water-salt-rock system phase equilibrium coupling withchemical reaction equilibrium and its application in CO2 geological storage numerical simulation; University of Chinese Academy of Sciences, 2008. [Google Scholar]
- Long Y.Research on Multi-ion and Multi-component Model of Carbon Dioxide Geological Storage; Yangtze University, 2023. [Google Scholar]
- Awolayo A. N.; Tutolo B. M. PyGeochemCalc: A Python package for geochemical thermodynamic calculations from ambient to deep Earth conditions. Chem. Geol. 2022, 606, 120984 10.1016/j.chemgeo.2022.120984. [DOI] [Google Scholar]
- Jebarathinam C.; Home D.; Sinha U. Pearson correlation coefficient as a measure for certifying and quantifying high-dimensional entanglement. Phys. Rev. A 2020, 101 (2), 022112 10.1103/PhysRevA.101.022112. [DOI] [Google Scholar]
- Feng W.; Zhu Q.; Zhuang J.; Yu S. An expert recommendation algorithm based on Pearson correlation coefficient and FP-growth. Cluster Computing 2019, 22, 7401–7412. 10.1007/s10586-017-1576-y. [DOI] [Google Scholar]
- Kumar G. P.; Jena P. Pearson’s correlation coefficient for islanding detection using micro-PMU measurements. IEEE Systems Journal 2021, 15 (4), 5078–5089. 10.1109/JSYST.2020.3021922. [DOI] [Google Scholar]
- Vaferi B.; Dehbashi M.; Alibak A. H.; Yousefzadeh R. Exploring the performance of machine learning models to predict carbon monoxide solubility in underground pure/saline water. Marine and Petroleum Geology 2024, 162, 106742 10.1016/j.marpetgeo.2024.106742. [DOI] [Google Scholar]
- Maekawa T.; Matsumoto Y.; Namiki K. Interpolation by geometric algorithm. Computer-Aided Design 2007, 39 (4), 313–323. 10.1016/j.cad.2006.12.008. [DOI] [Google Scholar]
- Guo Y.; Li B.; Li Y.; Du W.; Feng W.; Feng S.; Miao G. Application of a linear interpolation algorithm in radiation therapy dosimetry for 3D dose point acquisition. Sci. Rep. 2023, 13 (1), 4539. 10.1038/s41598-023-31562-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang N.; Canini K.; Silva S.; Gupta M. Fast linear interpolation. ACM Journal on Emerging Technologies in Computing Systems (JETC) 2021, 17 (2), 1–15. 10.1145/3423184. [DOI] [Google Scholar]
- Mao J.; Wang X.; Li H. Interpolated convolutional networks for 3d point cloud understanding. Proceedings of the IEEE/CVF international conference on computer vision 2019, 1578–1587. [Google Scholar]
- Premkumar M.; Sinha G.; Ramasamy M. D.; Sahu S.; Subramanyam C. B.; Sowmya R.; Abualigah L.; Derebew B. Augmented weighted K-means grey wolf optimizer: An enhanced metaheuristic algorithm for data clustering problems. Sci. Rep. 2024, 14, 5434. 10.1038/s41598-024-55619-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J.; Yinchai W.; Siong T. C.; Li X.; Zhao L.; Wei F. A hybrid interpretable deep structure based on adaptive neuro-fuzzy inference system, decision tree, and K-means for intrusion detection. Sci. Rep. 2022, 12, 20770 10.1038/s41598-022-23765-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei J.; Chen T.; Liu G.; Yang J. Higher-order multivariable polynomial regression to estimate human affective states. Sci. Rep. 2016, 6, 23384 10.1038/srep23384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duong C.; Lim T. Use of regression models for development of a simple and effective biogas decision-support tool. Sci. Rep. 2023, 13, 4933. 10.1038/s41598-023-32121-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song Y.; Liang J.; Lu J.; Zhao X. An efficient instance selection algorithm for k nearest neighbor regression. Neurocomputing 2017, 251, 26–34. 10.1016/j.neucom.2017.04.018. [DOI] [Google Scholar]
- Qin B.; Cai X.; Ni P.; Zhang Y.; Zhang M.; Wang C. Prediction of the minimum miscibility pressure for CO2 flooding based on a physical information neural network algorithm. Measurement Science and Technology 2024, 35 (12), 126010 10.1088/1361-6501/ad6a77. [DOI] [Google Scholar]
- Shah K.; Patel H.; Sanghvi D.; Shah M. A comparative analysis of logistic regression, random forest and KNN models for the text classification. Augmented Human Research 2020, 5 (1), 12. 10.1007/s41133-020-00032-0. [DOI] [Google Scholar]
- Schubert A. L.; Hagemann D.; Voss A.; Bergmann K. Evaluating the model fit of diffusion models with the root mean square error of approximation. Journal of Mathematical Psychology 2017, 77, 29–45. 10.1016/j.jmp.2016.08.004. [DOI] [Google Scholar]
- Karunasingha D. S. K. Root mean square error or mean absolute error? Use their ratio as well. Information Sciences 2022, 585, 609–629. 10.1016/j.ins.2021.11.036. [DOI] [Google Scholar]
- Ge R.; Yu Y.; New F.; Haas S. S.; Sanford N.; Yu K.; Frangou S. Generalizability of Normative Models of Brain Morphometry Across Distinct Ethnoracial Groups. BioRxiv 2024, 10.1101/2024.10.14.618114. [DOI] [Google Scholar]
- Zhang D. A coefficient of determination for generalized linear models. American Statistician 2017, 71 (4), 310–316. 10.1080/00031305.2016.1256839. [DOI] [Google Scholar]
- Nakagawa S.; Johnson P. C.; Schielzeth H. The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. J. R. Soc., Interface 2017, 14 (134), 20170213 10.1098/rsif.2017.0213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson J.; Oelkers E.; Helgeson H. SUPCRT92: A software package for calculating the standard molal thermodynamic properties of minerals, gases, aqueous species, and reactions from 1 to 5000 bar and 0 to 1000 C. Computers & Geosciences 1992, 18, 899–947. 10.1016/0098-3004(92)90029-Q. [DOI] [Google Scholar]
- Helgeson H.; Kirkham D.; Flowers G. Theoretical prediction of the thermodynamic behavior of aqueous electrolytes by high pressures and temperatures. IV, Calculation of activity coefficients, osmotic coefficients, and apparent molal and standard and relative partial molal properties to 600 degrees C and 5kb. American journal of science 1981, 281, 1249–1516. 10.2475/ajs.281.10.1249. [DOI] [Google Scholar]
- Helgeson H. C.; Delany J.; Nesbitt H. W.; Bird D. K. Summary and critique of the thermodynamic properties of rock-forming minerals. American Journal of Science 1978, 278-A, 1–229. [Google Scholar]
- Zhao H.; Wang H.; Chang X.; Ahmad A. M.; Zhao X. Neural network-based adaptive critic control for saturated nonlinear systems with full state constraints via a novel event-triggered mechanism. Information Sciences 2024, 675, 120756 10.1016/j.ins.2024.120756. [DOI] [Google Scholar]
- Zhu B.; Zhang L.; Niu B.; Zhao N. Adaptive reinforcement learning for fault-tolerant optimal consensus control of nonlinear canonical multiagent systems with actuator loss of effectiveness. IEEE Systems Journal 2024, 18, 1681. 10.1109/JSYST.2024.3433023. [DOI] [Google Scholar]
- Zhang H.; Zou Q.; Ju Y.; Song C.; Chen D. Distance-based support vector machine to predict DNA N6-methyladenine modification. Current Bioinformatics 2022, 17 (5), 473–482. 10.2174/1574893617666220404145517. [DOI] [Google Scholar]
- Xu T.; Jin G.; Yue G.; Lei H.; Wang F. Subsurface Reactive Transport Modeling: A New Research Approach for Geo-Resources and Environments. Journal of Jilin University (Earth Science Edition) 2012, 42, 1410–1425. 10.13278/j.cnki.jjuese.2012.05.027. [DOI] [Google Scholar]
- Zhang Y.; Wang Z.; Huang S.; Liu H.; Yan Y. Electrochemical behavior and passivation film characterization of TiZrHfNb multi-principal element alloys in NaCl-containing solution. Corros. Sci. 2024, 235, 112185 10.1016/j.corsci.2024.112185. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data supporting the results of this study can be obtained in the paper or from the corresponding author. Some of the data can be obtained in the GitHub repository: https://github.com/lhlc67/DH_And_NaCl_datas