Theoretical Evaluation of Complex Dielectric Constant for Gamma Relaxation of Poly(methyl methacrylate), A Study of Quantum Chemistry and Linear Response Theory

Abstract

It is widely accepted that the γ relaxation of poly(methyl methacrylate) (PMMA) arises from the hindered rotational motion of the side chain around the C–C bond, which links to the main chain. However, the physical model to explain this process has been unknown. The hybrid density functional theory calculation showed that the PMMA intramolecular hindered rotation has an activation energy of 6.53 kcal/mol. This activation energy causes the friction coefficient to the intramolecule to hinder rotation. The qualitative value of the friction coefficient was evaluated on the basis of linear response theory by using the calculated value of the activation energy. The Lorentz model is adopted to calculate the complex dielectric constant of the γ relaxation using the calculated value of the friction coefficient. The calculated value of the complex dielectric constant agreed reasonably well with experimental results.

1. Introduction

Polymers present several relaxation processes that cause imaginary dielectric constants. These relaxation processes are usually named α, β, and γ. The terminology of α, β, and γ relaxation is somewhat vague because of the complex nature of polymers; however, the α processes are observed at lower frequencies or higher temperatures and are usually related to the dynamic glass transition, i.e., the main intermolecular internal friction mechanism due to micro Brownian translational movement of molecular chains. The typical relaxation time of α processes is in the order of pico-seconds, and many molecular dynamics (MD) studies have successfully simulated the processes both qualitatively and quantitatively. The MD methods are very suitable at simulating energy-relaxation phenomena in the relaxation time scale of pico-seconds.¹⁻⁴

Relaxation known as β processes is observed at higher frequencies or lower temperatures and is typical of local motion such as the flip motion of the phenylene group. The last and the most unexplained relaxation, known as the γ process, has its origin in the molecular fluctuations of the chain segments such as intrarotations of side chains. The relaxation time of β process is smaller than that of γ processes, and much larger than that of α processes. Therefore, molecular dynamics simulations are very difficult in the case of the β or γ processes. A nearly complete physical model for energy relaxation was given by Debye about 100 years ago for the β or γ process.^5,6 As far as the authors know, however, there are no quantitative evaluations for β or γ processes based on a clear physical model or a physical picture.

The Debye’s relaxation theory adopts the Arrhenius plot. The problem was that there were no theoretical methods to obtain quantitative values of activation energies at that time. Thus, Debye’s theory seems to have been forgotten in the field of polymer science for many years. We will get into this problem with molecular-level resolution. We study poly(methyl methacrylate) as a typical example. As shown below, we believe our arguments are not limited to this polymer only.

Poly(methyl methacrylate) (PMMA) is a polymer that has an intramolecular hindered rotational motion of the side chain around the C–C bond which links to the main chain. This intramolecular hindered rotation causes γ relaxation to PMMA. The PMMA structure is shown in Figure 1. The −C(CO)OCH₃ is the main intramolecular rotator, which rotates around the C–C bond, linking to the main chain of PMMA.

Figure 1.

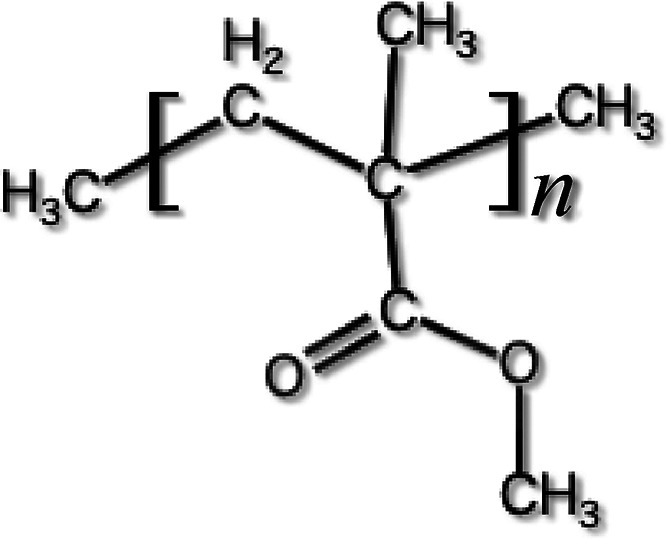
PMMA structure and main intramolecular rotator of −C(CO)OCH₃.

The imaginary part of the complex dielectric constant causes the energy loss of an external electric field as a function of its frequency and the environmental temperature. When a temperature is fixed, the imaginary part of the complex dielectric constant has a peak at a frequency f_max. Teixeira et al. measured experimentally f_max for α, β, and γ relaxations of PMMA as a function of the temperature.⁷ The f_max signals of α, β, and γ relaxations are sharply separated from each other in their experimental results.⁷ However, the molecular-level explanation for γ relaxations still has to be clarified.

In our present study, hybrid density functional theory (DFT) calculation showed that the PMMA intramolecular rotator, −C(CO)OCH₃, has an activation energy of 6.53 kcal/mol. This activation energy causes the friction coefficient to the intramolecule rotator. We used Debye’s relaxation model, almost as it is, to evaluate the value of the friction coefficient; that is, the activation energy, 6.53 kcal/mol, was used in Debye’s γ relaxation calculation. On the base of this friction coefficient, we adopted the Lorentz model to quantitatively evaluate the complex dielectric constant of the γ relaxation. The results of the calculation agreed well with the experimental results.

2. Methods

In this paper, quantum chemical calculations were carried out to analyze the intramolecular hindered rotation. All geometry optimization procedures were performed using the Gaussian16 program package⁸ with hybrid density functional theory (DFT) calculations.⁹ The exchange–correlation term was considered in the B3LYP functional.¹⁰⁻¹² The 6-31G(d) basis set^13,14 was adopted for all atoms.

3. Results and Discussion

The Activation Energy of Intramolecular Rotator

The model of the PMMA unit monomer is shown in Figure 2. Intramolecular rotator −C(CO)OCH₃ rotates around the axis C_B–C_C. The simplified version of the monomer (C_B is replaced by H) is shown in Figure 3. The moment of inertia I of the intramolecular rotator −C(CO)OCH₃ around the axis C_CH_B is obtained by calculating the distance of the O, O, CH₃ components of the rotator from the linear line (H_B–C_C), and is summed up (mass of the components)*(distance between the axis and the component).² As a result, we get the moment of inertia I of the intramolecular rotator.

1

Figure 2.

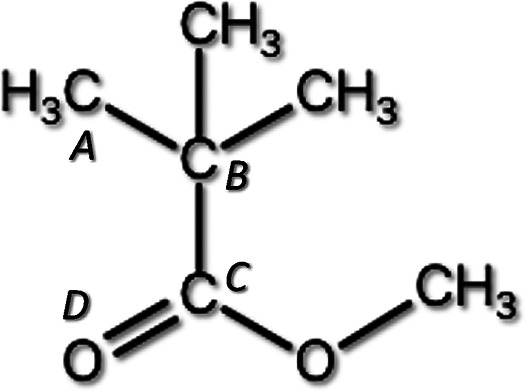
PMMA unit monomer.

Figure 3.

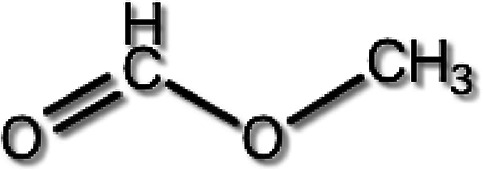
Simplified unit monomer.

The component of the dipole moment of −C(CO)OCH₃ perpendicular to C_B–C_C is calculated as 1.36147 × 10^–29 SI.

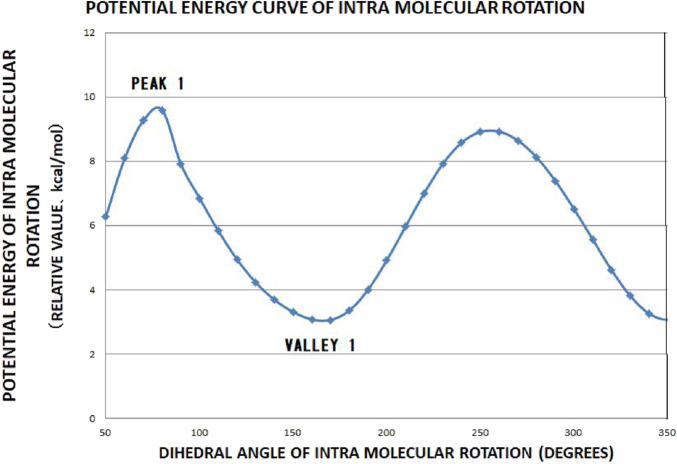
Then, we obtained the activation energy of the intramolecular hindered rotation. We performed a geometry optimization by using hybrid DFT to the trimer, as shown in Figure 4, in such a way that the dihedral angle C_A–C_B–C_C–O_D is swept by taking about 30 steps of 10 degrees. At each step, other degrees of freedom are optimized (Figure 5). The activation energy thus obtained ΔH is,

2

Figure 4.

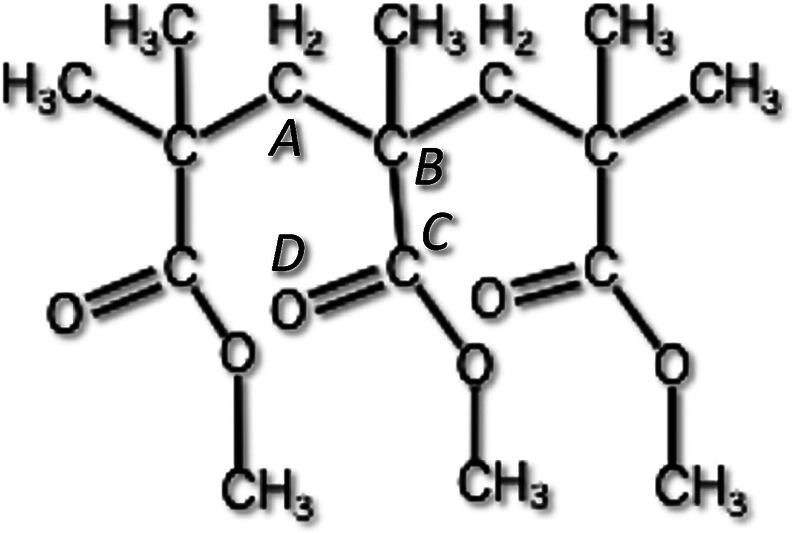
Trimer of unit of the PMMA.

Figure 5.

Potential energy curve of the intramolecular rotation calculated as a function of the dihedral angle C_A-C_B-C_C-O_D, shown in Figure 4. ΔH is calculated using PEAK 1 and VALLY 1 in this figure.

Here, we assume that the intramolecular rotator is regarded as a single mass point rotating around an axis. Let the average distance between the axis and the mass points be L. The mass m is assumed,

3

i.e., the mass m is estimated as half of the summation of the mass of O and OCH₃.

On the basis of the basic mechanics, L satisfies the following equation,

4

From eqs 1, 3, and 4, we get

5

The intramolecular rotational angular frequency, ω₀ is

6

We can regard this rotator as a harmonic oscillator¹⁵ with the spring coefficient k which satisfies

7

From eqs 3, 6, and 7, we get the force constant k,

8

4. Evaluation of Friction Coefficient on the Basis of Linear Response Theory

We introduce here the simple linear response theory¹⁶ to derive the friction coefficient from the activation energy obtained above.

In simple linear response theory, as shown in Figure 6, a particle moves parallel to the X-axis. A potential well of depth ΔH is arranged periodically with an interval distance L_well. It is assumed that a jump over a potential well is described by the mechanism of Arrhenius. Between neighboring wells, it is assumed that a particle makes a uniform linear ballistic motion without friction in the flat path between neighboring two potential wells. Under this assumption, it takes T_ballistic seconds for the particle to travel the flat path L_well. Also, we assume that it takes T_flat seconds for the particle to travel the flat path in the real system, in which a random walk may occur.

Figure 6.

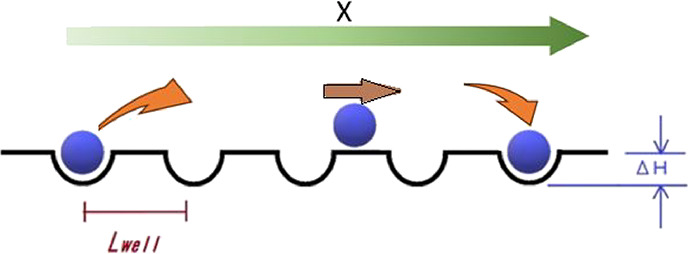
Schematic image for simple linear response theory.

In the present paper, we assume

9

We further assume that it takes T_escape seconds for the particle to escape from the potential well. We call the average time with which a particle travels one unit (one potential well plus neighboring one flat path) T_t.

10

The average velocity of the particle is

11

The friction coefficient is given by its definition,

12

where F is the external force. In the situation without any external force, the equation of Arrhenius is

13

where K_B is the Boltzmann constant, and h is the Planck constant. In the situation that right to left direction external force exists, we assume that the left potential well becomes shallower by 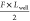, and that the right potential well becomes deeper by 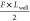. In this situation, we can assume that it takes T_{escape_L_to_R} seconds for a particle to escape from the potential well from left to right, and that it takes T_{escape_R_to_L} seconds for a particle to escape from the potential well in the opposite direction. Under these assumptions, we get right to left transition rate, R_{R_to_L}

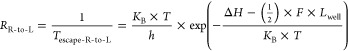14

also, left to right transition rate, R_{L_to_R}

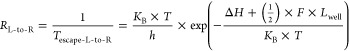15

Hereafter, we consider two cases, the low-temperature limit case and the high-temperature limit case. First, we describe a theory for low temperatures where it takes a long time for a particle to escape from a potential well,

16

When an external force F exists, and if the condition of eqs 4–8 is satisfied, (i.e., low-temperature case) the T_flat can be neglected and the following equation is valid, with T_t as the time for this process

17

By using eqs 14–16, we get

18

When eq 16 is satisfied and in addition

19

is satisfied, eq 18 is approximated by the following equation,

20

From eq 20, we get the following equations.

21

By inserting eq 21 to eq 12, we get

22

Equation 22 shows that in the low temperature case where eq 16 is satisfied, C_{fric_L_T} decreases when the temperature increases.

Next, we apply a theory for high temperature where it takes only a short time for a particle to escape from a potential well, where

23

is satisfied (high temperature case).

When temperature is high, we assume that the particle which collides with a potential well penetrates it with the probability of 50%, and is reflected by the potential well with the probability of 50%. The thermal velocity is given by

24

where m is the mass of the particle. The acceleration of the particle under the external force F is

25

In the following discussion, we assume that the velocity of the particle just after it escapes from the potential well is zero. To travel the flat path L_well, it takes L_well/v_macro seconds, where v_macro is the macroscopic velocity of the particle. After traveling the flat path L_well, the velocity of the particle will be A_acc × L_well/v_macro. The average macroscopic speed of the particle during traveling the flat path L_well is, therefore, given by,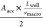. Here, we call the average macroscopic speed of the particle during traveling the flat path L_well, v_{macro_average}. Then, we can obtain the following,

26

Here, we make an approximation,

27

By inserting eq 27 to eq 26, we get

28

From eq 28, we get

29

By inserting eq 25 to eq 29, we get

30

From eq 30, we get

31

Therefore,

32

It should be noted that eqs 26 to 32 are valid only when we assume that the velocity of the particle just after escaping from the potential well is zero.

Thus, in the case of high temperature,

33

In this high temperature case, the value of the friction coefficient is independent of the temperature, contrary to the low temperature case 22.

Complex Dielectric Constant on the Basis of Lorentz Model

Let the electric charge of the oscillator q, and let the external electric field

34

The Lorents equation¹⁵ is given by

35

The static solution of eq 35 is

36

where A is given by

37

From eqs 36 and 37, we get

38

The polarizability is given by its definition as

39

where N_osc is the number of Lorentz-type oscillators in unit volume. By inserting eq 38 to eq 39, we get

40

By the definition of electric flux density,

41

where ε₀ is the permittivity of vacuum. By definition of relative permittivity,

42

Inserting eq 41 into eq 42, we get

43

Notice that relative permittivity is composed of the real part and imaginary part, as follows;

44

When we insert eq 40 into eq 43, we obtain a full description of complex relative permittivity. Then, ε_r described by eq 44 gives the full description of complex relative permittivity, if we define ε_rreal and ε_rimaginary by

45

and

46

The angular frequency ω_extmax, at which ε_rimaginary is maximum, satisfies;

47

Insering eq 46 to eq 47, we get the angular frequency

48

When

49

is satisfied, eq 5–15 is approximated as follows;

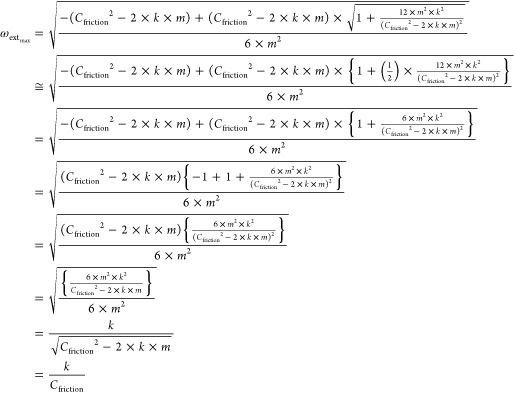50

The frequency which makes ε_rimaginary maximum is

51

By inserting eq 22 to eq 51, we get

52

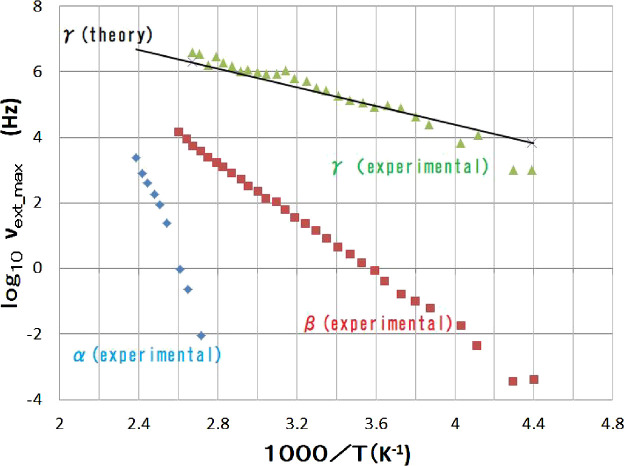
Summing up the arguments described above, we can finally show the behavior of γ relaxation as a function of the temperature. In Figure 7, the frequency giving the maximum imaginary dielectric constant is shown as a function of the temperature, where

53

is assumed. Here, π is the circle ratio, and the value of L is given by eq 5. Thus, obtained black line is plotted according to eq 52 wherein the ΔH is given by hybrid DFT calculations. Other plots in Figure 7 show data from the results of the experiment.⁷ The results obtained owing to Debye’s theory, linear response theory, Lorentz model, and the hybrid DFT calculation reasonably reproduced consistently the experimental data.⁷ Considering the complexity of the molecular level situation in polymer, this consistency justifies our arguments mentioned above. The simplified picture shown in Figure 6 reflects an essence of the complicated interactions in polymer, which is obtained in γ relaxation. Due to the complexity of the phenomenon, we are obliged to introduce many approximations onto various nontrivial processes. All of these approximations are at the zeroth or first order; however, they are not irrational. This is why we obtained the correct results.

Figure 7.

Frequency, ν_{ext_max}, gives the maximum imaginary dielectric constant. Black line shows the result of the present theoretical calculation (eqs 5–19). Other dots are the results of experiment.⁷

6. Conclusions

It is well established that MD simulations make a good theoretical analysis for α relaxation processes of polymers. As for the β relaxation, although the MD is also difficult, it is understood as a local motion. The relaxation time of γ relaxation processes, however, is usually much larger than that of α relaxation processes, and therefore, molecular dynamics simulations are very difficult in the case of γ relaxation processes. The mathematical calculations in the present paper show that the Lorentz model and Debye’s theory combined with hybrid DFT calculations on the basis of linear response theory give a good theoretical evaluation for γ relaxation processes of PMMA. We present a physical image of γ relaxation, which was ambiguous for a long time.

In the present stage of our study, it is not so clear how formula 26 should be modified if we want to expand the scheme to the other cases. Experimental and theoretical examination in the high-temperature cases will be necessary to test the validity of formula 26. In other words, the compatibility of formula 26, which seems to be based on the random walk model, should be experimentally checked at higher temperatures.

The Arrhenius equation is used to derive eq 22. This means that each atom or each functional group vibrates around a fixed point within the molecule. Those molecules would have low fluidity, which indicates similarity to a glass state. Equation 31 is derived from a simple random walk model, which suggests a ladder network model of rubber viscoelasticity, even though the present model does not include a polymer chain. It is suggested that a glass transition-like effect occurs between conditions of eq 22 and conditions of eq 31, but details are not clarified in the present study. To clarify this point, further experimental and theoretical research will need to be closely coordinated in the future.

In Figure 7, the discrepancy between the experimental value and theoretical predictions for gamma becomes more pronounced as the temperature decreases. This indicates that the calculated value underestimates the absolute value of ν_extmax, and that the plot of the experimental values shows a steep slope in the low-temperature range and a more gradual slope in the high-temperature range.

To improve the accuracy of the calculated value of ν_extmax, a more comprehensive molecular model than that shown in Figure 4 would be necessary. In addition, a more sophisticated model than the Arrhenius equation, such as absolute reaction rate theory, would also be necessary.

The experimental results show a steep slope in the low-temperature range and a more gradual slope in the high-temperature range. This suggests that the phenomenon is almost entirely explained by eq 22, which has a steep temperature dependence in the low-temperature range. However, in the high-temperature range, the influence of eq 31, which has a gradual temperature dependence, starts to mix in, causing the temperature dependence of the plot of the experimental values to begin to be more gradual.

The authors declare no competing financial interest.