Abstract
Particle picking in cryo-electron tomograms (cryo-ET) is crucial for in situ structure detection of macromolecules and protein complexes. The traditional template-matching-based approaches for particle picking suffer from template-specific biases and have low throughput. Given these problems, learning-based solutions are necessary for particle picking. However, the paucity of annotated data for training poses substantial challenges for such learning-based approaches. Moreover, preparing extensively annotated cryo-ET tomograms for particle picking is extremely time-consuming and burdensome. Addressing these challenges, we present TomoPicker, an annotation-efficient particle-picking approach that can effectively pick particles when only a minuscule portion (~ 0.3 – 0.5%) of the total particles in a cellular cryo-ET dataset is provided for training. TomoPicker regards particle picking as a voxel classification problem and solves it with two different positive-unlabeled learning approaches. We evaluated our method on a benchmark cryo-ET dataset of eukaryotic cells, where we observed about 30% improvement by TomoPicker against the most recent state-of-the-art annotation efficient learning-based picking approaches.
1. Introduction
Cryo-electron tomography (Cryo-ET) is an emerging imaging technology that has enabled in-situ 3D visualization of macromolecular structures at up to subnanometer resolution within cells in near-native contexts [1, 2]. Furthermore, cryo-ET can resolve the structures of macromolecules and protein complexes inside cells with different compositions and/or conformations. Just as importantly, mapping back molecules into their original positions within cryo-tomograms can reveal their spatial organization, providing additional potentially novel biological insights [3]. As a result, cryo-ET is emerging as a powerful new imaging approach for in situ structural biology.
Presently, the extraction of macromolecular structures from 3D cellular cryo-ET tomograms is a complex process that involves multiple steps [4, 2]. The first and most important step is locating the macromolecules in the tomograms, i.e., “particle picking” [5, 6]. However, particle picking is a challenging task for several reasons. Firstly, cryo-ET tomograms are large 3D volumes with a size ≈ 1000 × 1000 × 500 pixels, even after 4× binning [7, 8]. Secondly, these tomograms are typically possess low signal-to-noise ratios and contrast due to the complex cytoplasmic environment and low electron dosage [8, 4]. Finally, the concentration of macromolecules per image is very high (~ 500 – 1000 per cryo-tomogram) [6], making it even more difficult to locate them accurately.
Given the aforementioned challenges, manually picking particles in cryo-tomograms is extremely time-consuming and burdensome. Just as importantly, aside from ribosomes and select large macromolecular complexes (e.g., mitochondrial respiratory complexes) which can be seen by eye within cryo-tomograms due to their size and contrast, the vast majority of molecules within cells are too small to be visually detected, rendering manual picking all but impossible. To this end, automated approaches for particle picking have been developed [5, 9, 10]. A common approach is template matching (TM), which uses templates from existing data sources as references to localize similar macromolecules within the tomograms [11]. However, TM can only be applied when a reference template is available for the macromolecules to be picked and often contains reference-dependent biases [7, 12]. In addition, analogous to manual particle picking, TM is extremely time-consuming [7] and shows suboptimal performance [13]. To solve this issue, neural network-based deep learning approaches have been introduced [14, 10, 9]. These approaches provide high-throughput, fast localization of particles without reference-dependent biases. However, most of these approaches [10, 9] are based on supervised learning, which again requires manual annotation of many particles in the tomograms for training purposes. Therefore, annotation-efficient methods that can perform reliable annotations without requiring large, annotated training data are necessary.
In recent years, a few learning-based picking approaches have addressed this annotation burden [15, 16]. Huang et al. [15] developed an algorithm to detect proteins from sparse labels by regarding particle picking as a regression problem. The algorithm regards every 3D tomogram as a single sample and thus predicts particle coordinates directly at the tomogram level. This approach has two problems. First, since this method is a learning-based method and regards each tomogram as a sample, a large number of similar tomograms are required in the training set. Second, fitting tomograms as inputs to convolutional networks results in significant downsampling. This exacerbates the already serious issues associated with particle crowding within the tomogram, further diminishing signal-to-noise. Another supervised algorithm has been developed very recently, DeepETPicker [16]. Unlike the algorithm developed by Huang et al. [15], DeepETPicker can be trained on a single tomogram where several particle coordinates in the tomogram are annotated. Despite achieving success for sparse single-particle and prokaryotic tomograms, its efficacy in crowded eukaryotic tomograms has not yet been explored. Moreover, DeepETPicker [16] did not adopt any mechanism tailored to deal with the annotation-efficiency issue. Consequently, a more efficient approach for annotation in particle picking is clearly required.
In this work, we developed a novel annotation-efficient particle-picking approach called TomoPicker. Our approach only requires a small proportion (~ 0.3 – 0.5% of all particles in a tomogram dataset) of the particle’s center coordinates to be annotated beforehand. In TomoPicker, we regard particle picking as a voxel classification problem. For 3D cryo-ET tomograms, each voxel is classified as a binary value based on whether it contains particles or not. However, unlike the methodology described by Huang et al. [15], our approach can be trained on a single tomogram since we do not treat the entire tomogram as a discrete sample. Rather, we use subvolumes extracted from tomograms as samples for voxel classification. Given that only a few portions of the voxels are labeled as positive, a specific approach is necessary to deal with the large unlabeled voxels. If all unlabeled voxels are regarded as negative, it would lead to erroneous prediction and picking. To solve this problem, we introduced two positive-unlabeled (PU) learning approaches-one based on non-negative risk estimation and another based on regularization based on a prior distribution.
In this work, we developed a novel annotation-efficient particle-picking approach called TomoPicker. Our approach only requires a small proportion (~ 0.3 – 0.5% of all particles in a tomogram dataset) of the particle’s center coordinates to be annotated beforehand. In TomoPicker, we regard particle picking as a voxel classification problem. For 3D cryo-ET tomograms, each voxel is classified as a binary value based on whether it contains particles or not. However, unlike the methodology described by Huang et al. [15], our approach can be trained on a single tomogram since we do not treat the entire tomogram as a discrete sample. Rather, we use subvolumes extracted from tomograms as samples for voxel classification. Given that only a few portions of the voxels are labeled as positive, a specific approach is necessary to deal with the large unlabeled voxels. If all unlabeled voxels are regarded as negative, it would lead to erroneous prediction and picking. To solve this problem, we introduced two positive-unlabeled (PU) learning approaches-one based on non-negative risk estimation and another based on regularization based on a prior distribution.
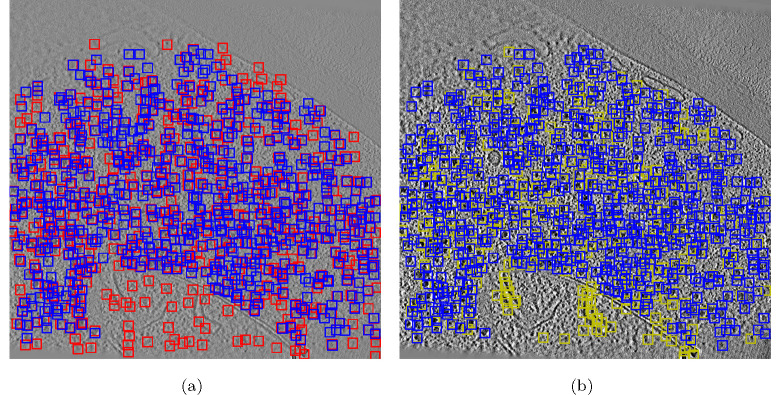
We evaluated our methods against two well-annotated benchmark datasets (one imaged with Volta-Phase-Plate (VPP) and the other imaged using Defocus-only) of eukaryotic S. Pombe cell tomograms. We also evaluated the recent and popular learning-based cryo-ET picking methods (including the state-of-the-art DeepETPicker [16]) on these datasets for the first item. Our extensive experiments demonstrate superior performance of the TomoPicker approach compared to the other earlier approaches. Our proposed KL divergence-based and non-negative risk estimator-based TomoPicker method improves the particle picking performance by ~ 30% over the DeepETPicker method in analyzing the VPP (Volta-Phase-Plate) and Defocus-only datasets, respectively. In addition, qualitatively, the TomoPicker predictions most closely resemble the ground truth when visualized (Figure 2 and Figure 4). Thus, TomoPicker shows high efficacy even when 0.4% of the total number of annotated particles in the datasets are used for training. Overall, our data suggest that TomoPicker can serve as a valuable tool for particle picking in 3D cryo-ET tomograms.
Figure 2:
Predictions vs Ground Truth for central (z = 500) xy slice of TS_0003 VPP tomogram. Blue Box = Ground Truth, Green Box = TomoPicker Predictions, Red Box = DeepETPicker Predictions, Yellow Box = CrYOLO Predictions.
Figure 4:
Predictions vs Ground Truth for central (z = 250) xy slice of TS_028 Defocus-only tomogram. Blue Box = Ground Truth, Green Box = TomoPicker Predictions, Red Box = DeepETPicker Predictions, Yellow Box = CrYOLO Predictions.
2. Related Works
Template-Matching for Particle Picking
Before the development of learning-based models, Template Matching (TM) [11, 5] was the most used approach for particle picking. In TM, structural templates from existing databases, such as the Protein Database (PDB) [17] and Electron Microscopy Data Bank (EMDB) [18], have been usually resolved through X-ray crystallography or single-particle cryo-EM. The structure of interest is first low-pass-filtered, and then randomly rotated in a fixed interval to create multiple templates. These templates are scanned throughout the cryo-ET tomograms in a sliding window manner and a cross-correlation score is calculated between the templates and each subvolume. Thus, TM determines the location of the particles and their orientations with respect to the original template. Despite being widely used, this process is extremely time-consuming given the large size of the tomograms and the large number of templates to match with. Moreover, this is prone to template-dependent biases and cannot determine any structure without known existing templates. As a result, learning-based methods have been developed for particle picking. The proposed method, TomoPicker, is also a learning-based picking method.
Supervised Learning-based Particle Picking Methods
To overcome the challenges of TM, several learning-based particle-picking methods have been developed. However, most of them [19, 20] are based on supervised learning, where a deep learning model is trained using a vast amount of manually annotated data. DeepFinder [19] and DeepiCT [20] use supervised UNet Networks to perform segmentation on cryo-ET tomograms where the predicted segmentation masks are used for particle picking. Training these models requires manual annotation of segmentation masks. DeepETPicker [16] follows a similar strategy by placing gaussian blobs in the picked location to create a ground truth segmentation map and trains a fully supervised UNet segmentation model. CrYOLO [9] performs supervised object detection using a YOLO-based object detection network. It requires the users to provide bounding box annotations instead of segmentation masks. However, CrYOLO [9] is originally developed for 2D single-particle cryo-EM images. Using this approach for 3D data requires performing 2D annotation on the 3D cryo-ET image slices and later converting the 2D predictions to 3D. Though providing boxes is easier than segmentation masks, the conversions between 2D and 3D are still a problem and successful training requires a large number of ground truth boxes to be manually annotated. Such manual annotation is also extremely time-consuming and burdensome. Unlike these methods, our method only requires providing the coordinates (approximately at the center) of a few particles to be annotated.
Weakly supervised Learning-based particle picking
A few weakly-supervised learning-based particle picking methods [15, 21] have been developed very recently that require only providing the center coordinates of a few particles in tomograms for training. These methods directly predict the center coordinate of particles given a whole 3D tomogram. However, as discussed earlier, they significantly downsampled the tomograms to treat them as a single sample. Such downsampling increases the crowding of particles, which can be tolerable only for purified or a few prokaryote tomograms with sparsely located particles but not for already crowded eukaryote tomograms. Moreover, they can be trained only on datasets containing many (≥ 50) similar tomograms. Unlike them, our method regards subvolumes from a tomogram as a sample and can be trained on a single tomogram. Since we do not require downsampling the tomograms, our method works well even on crowded eukaryote tomograms. Though we use positive-unlabeled (PU) learning similar to Huang et al. [15], our PU learning pipeline is methodologically much different from theirs.
3. Methods
Given a set of tomograms , where each tomogram is a 3D grayscale image, TomoPicker provides a set of particle coordinates for each tomogram .
TomoPicker consists of three main components for annotation-efficient particle picking in cryo-ET tomograms (Figure 1). We briefly discuss them as follows:
Figure 1: Overview of the particle picking process with TomoPicker.
First, the training tomogram is preprocessed, and a corresponding binary mask tomogram is generated, given the few manual annotations. Pairwise subvolumes and their labels are extracted from the tomogram and the binary mask tomogram, respectively, in a sliding window manner. Then, a voxel-classifier network is trained using the pairs of subvolumes and their labels using positive-unlabeled (PU) learning-based loss functions. PU learning requires the expected number of particles in the training tomogram to be provided. After training, the classifier network is applied to all subvolumes extracted from all the tomograms to infer the masks. The masks are combined for each tomogram to obtain the full binary masks. The locations of the particles are obtained from these masks through non-maximum suppression.
3.1. Preprocessing and Data Generation for Training
The tomograms in the dataset are preprocessed to enhance contrast. We load the tomograms as voxelized arrays and standardize the voxels for each tomogram to 0 mean and 1 standard deviation. Then, we clip those values that lie beyond three standard deviations from the mean (which is 0 after standardization). After clipping, we again standardized the voxels in each tomogram to 0 mean and 1 standard deviation.
A training dataset and validation dataset (optional) is selected from the dataset , where . In our experiments, we used only one tomogram for training and one for validation, keeping . For each training and validation tomograms , we create empty voxel arrays having the same shape as the corresponding tomogram. We create these empty voxel arrays to generate labels for each voxel for our voxel classification-based particle-picking network. We require a few (minuscule percent of the total particles ) particles coordinates to be provided for the training and validation tomograms. For each of the provided particle coordinates per training or validation tomogram, we put values of 1 in all the voxels around the coordinate that lie within a distance equal to the radius of that particle in the empty voxel arrays. Thus, we have a roughly spherical mask of 1 s for each labeled particle in the corresponding arrays belonging to the tomogram (Figure 1).
Given the large size of the tomograms, it is difficult to pass them directly as input to our particle-picking model. Consequently, we generate small subvolumes and submasks from the tomograms and their corresponding label arrays. To this end, we use a sliding window approach to pick subvolumes and their corresponding submasks with a given subtomogram size from the tomogram and label array , respectively. Thus, we collect subvolumes and submask pairs from the tomograms. We save all such pairs for training tomograms and use them to train our particle-picking model. For validation tomograms, we only save those pairs with submasks with at least one non-zero value. After saving the data necessary for training and validation, we move forward to the next step of model training.
3.2. Training Classifier with Positive Unlabeled (PU) Leaning
We formulate particle picking as a voxel classification problem. Our training dataset consists of pairs where serves as the voxel-wise label for the subvolume . We assume that is the set of voxels that are labeled as 1 and is the set of voxels labeled as 0. In other words, is the set of labeled particles in the training tomograms, and is the set of unlabeled particle and non-particle regions in the training dataset. Given and , we learn a classifier that distinguishes between particle and non-particle regions in the subtomograms. In other words, the classifier is our particle-picking model. We used three different strategies (two with PU learning and one without) to train the classifier, which we discuss below.
3.2.1. Positive Negative (PN) Learning
When all elements belonging to are non-particle regions, we can treat the elements in as positive samples and the elements in as negative samples. In such a scenario, we train a classifier with a standard loss minimization objective function (named PN) as shown in Equation 1.
| (1) |
Here, is the fraction of labeled and unlabeled particle regions within . The value of can be calculated as the fraction of non-zero values in the training data after the label generation process mentioned before. In other words,
| (2) |
We denote as the cost function between classifier output and labels. To implement it, we use binary cross-entropy loss defined as follows:
| (3) |
Here, is the prediction and is the ground truth label from .
However, this objective function is effective when all the particle regions in tomograms are labeled, thus belonging only to , and only non-particle regions are in , which is usually not the case. In an ideal scenario, represents only a few particles in the tomogram, whereas most of the particles belong in . As a result, PN learning provides suboptimal particle picking performance in our experiments. To this end, we introduce positive-unlabeled (PU) learning.
3.2.2. Non-negative Risk Estimator based Positive Unlabeled (PU) Leaning
We first leveraged a non-negative risk estimator-based PU Learning approach to incorporate PU learning in our cryo-ET particle picking framework. In this framework, we use as the expected average of voxel values in the label of a sample in the training tomogram. We calculate this based on the expected number of particles per training tomogram, , and the particle radius provided by the user. Based on , a fixed number of voxels are labeled as 1 in the training data generation process. If this number is denoted as , then the value of is as follows;
| (4) |
Here, is the expected total number of 1s in .
We further denote , and is implemented as Equation 3. Using these three, we denote a new quantity as follows:
| (5) |
We used a specialized version of the algorithm in [22] for training our particle-picking network. If , we update the parameters of using , where is the gradient with respect to the parameters. Otherwise, we update the parameters of using .
3.2.3. KL based Positive Unlabeled (PU) Leaning
We further introduce an alternate approach to Non-negative Risk Estimator PU learning. Instead of minimizing the positive-negative misclassification loss, a classifier can simultaneously attempt to minimize the class misclassification loss and match the expectation over . In other words, we can learn a classifier that minimizes subject to the constraint , where is the fraction of unlabeled particle regions within . We can impose such constraint through a regularization term in the objective function with a weight as shown in Equation 6.
| (6) |
In this objective, a constraint is imposed through the KL-divergence between the expectation of classifier over and the estimated fraction of unlabeled particle regions in , denoted by . This divergence is minimized when both terms are close to each other. KL divergence between two distributions and can be defined as Equation 7.
| (7) |
To calculate , we take the expected number of particles per training tomogram () as input, similar to our previous non-negative risk estimator-based approach. Given the number of voxels labeled as 1 in data generation for a particle of radius , the expected total 1 in is . Among them, is the observed number of 1. So, the expected number of unlabeled 1s that are unlabeled is . So, can be written as.
Using equation 2 and 4, can be expressed as.
| (8) |
3.3. Implementation of the classifier
To implement the classifier network , we used a MultiRes-Unet architecture [23]. Our MultiResUnet network consists of four down-sampling and four up-sampling layers. Each of the down-sampling layers consist of either ResUNet or UNet blocks, starting with an input channel of 1 and progressively increasing to 32, 64, 128, and 256 channels. The primary difference between a ResUNet block and UNet block is the use of a residual connection in the ResUNet block which adds the block’s input to its output. The UNet block, on the other hand, simply stacks two convolutional layers without any residual addition. The upsampling path mirrors this configuration, restoring spatial dimensions with transposed convolutions. Skip connections provide concatenation between the corresponding up-sampling and down-sampling layers. An optional dropout layer is used for regularization and a final 1×1 3D convolution produces the single-channel output. All the experimental results presented here use the default configuration of using ResUNet layer in the up-sampling and down-sampling networks with no additional dropout for regularization.
We train the classifier network using the losses mentioned above.—We use a mini-batch size of 8 and use Adam optimizer to optimize the parameters in . Since , we found that scaling the term and by a factor improves picking performance by picking more true positives. We set the value of as , which was found to be an optimal value in all our experiments.
3.4. Inference and Picking
After training the classifier with the above-mentioned learning strategies, we perform particle picking on all the tomograms in the dataset, including the ones we used for training and validation. For each tomogram , we use a sliding window strategy to obtain non-overlapping subvolumes of the same size as the training subtomograms. Then, we perform inference for each subvolume with our learned classifier . The inference results in a score for each voxel in the subvolumes. We merge the score outputs for each subvolume in the tomogram to a volumetric array () with the same size as the tomogram. We then apply the picking process on this merged predicted array . The process takes the required number of particles or subvolume score threshold and the particle radius as input. It operates in 4 steps. In step 1, Find the point with maximum score value in . In step 2, we append as well as the score to the extracted particle list. In step 3, we remove a roughly spherical region of particle radius around in by setting their scores to . This ensures that the same particle will not be extracted more than once. Finally, we repeat steps until particles are extracted or no prediction scores above the threshold remain.
4. Experiments & Results
4.1. Benchmarking
For benchmarking, we used well-annotated cryo-ET datasets of S. pombe cells publicly available at EMPIAR-10988 [24], which represent some of the only available well-annotated tomograms in the cellular cryo-ET domain. The dataset contains 10 Volta-Phase-Plate (VPP) tomograms and 10 Defocus-only tomograms of S. pombe cell sections (voxel spacing of 1.348 nm). Consequently, we used : 1) VPP and 2) Defocus-only tomogram sets as two different datasets in our experiments for benchmarking
4.2. Baselines
We used CrYOLO [9] and DeepETPicker [16] learning-based cryo-ET picking methods as baselines with the aim of picking ribosomal particles. Since CrYOLO [9] is a bounding box predictor method for 2D cryoEM images, it is necessary to convert 3D tomograms into 2D slices and provide 2D annotations for each slice to train CrYOLO. For slicing the tomograms, we divided them into 2D x-y slices across the z axis. If any particle fell into the th slice, we annotated all the 2D xy slices with z value in range [,] with that particle in the same (,) coordinate as the radius of ribosomes which is maximally 12 voxels (12 × 1.348 = 16 nm) in the tomograms. For DeepETPicker [16], we used their publicly available codebase with the default settings for ribosome picking.
Evaluation:
For evaluation, we calculated the number of True Positives (TP), False Positives (FP), False Negatives (FN), Precision, Recall, and F1-score predicted by the baseline models, and our proposed models. To estimate the metrics, we used the annotations of ribosome coordinates provided in the original dataset as ground truth. If any predicted coordinate is within 10 voxels of Euclidean distance from a ground truth coordinate, it is regarded as a TP. Predicted coordinates not within 10 voxels are considered FP, while ground truth coordinates without nearby predicted coordinates are considered FN. Precision and Recall are calculated as , respectively. Finally, F1 score is calculated as . By definition, precision penalizes FP but not FN. On the other hand, Recall penalizes FN, but not FP. Both FP and FN should be penalized for particle picking. Consequently, we regard F1 score as our primary evaluation criterion since it penalizes both.
4.3. Experimental setup
In our experiments for TomoPicker, we used 3D-ResUnet as the classifier network , similar to DeepETPicker [16]. We used a batch size of 8 and an initial learning rate of 2 × 10−3, which has been reduced by a factor 0.5 if validation accuracy does not improve for 5 consecutive epochs. We trained TomoPicker and CrYOLO [9] for 20 epochs, which we found to be sufficient. However, we trained DeepETPicker [16] for 100 epochs. We implemented our method in pytorch and trained the models using NVIDIA RTX A5000 GPUs.
4.4. TomoPicker (KL) performs overall best particle picking in Volta-Phase-Plate (VPP) S. Pombe cellular cryo-ET Datasets
The VPP dataset contains 10 tomograms (labeled from TS_0001 to TS_0010 consecutively) with a total of 25,311 ribosome particles. The individual tomograms from TS_0001 to TS_0010 contains 2450, 2342, 2429, 2967, 3571, 1336, 617, 2744, 3482, and 3373 ribosome particles respectively.
We trained CrYOLO, DeepETPicker, and TomoPicker with three different losses (PN, PU, and KL) on the training tomogram. For training our models, we only used 100 particle coordinates from TS_0001 for training and 100 particle coordinates from TS_0002 for validation. This accounts for only of the total particles. Since the voxel spacing is 1.348 nm and the radius of a ribosomal particle is 11–15 nm, we use voxels as the particle radius.
After training, we tested the models against all the tomograms in the dataset. We have put the precision, recall, and F1 score (up to 2 decimal places) obtained by each method against each tomogram and overall dataset in Table 1. It can be observed that TomoPicker (KL) shows the best performance in terms of F1 score - our primary criterion- in the overall evaluation. It shows 80% improvement over CrYOLO, 29% improvement over DeepETPicker, 15% improvement over TomoPicker (PN), and 12% improvement over TomoPicker (PU). While considering individual tomograms, TomoPicker (KL) performs the best in 5 out of 10 tomograms, TomoPicker (PU) performs the best in 2 out of 10 tomograms, TomoPicker (PN) performs the best in 2 out of 10 tomograms, and DeepETPicker performs the best in 1 out of 10 tomograms.
Table 1:
Precision, Recall, and F1 Score Comparison across Different Methods on VPP Ribosome Datasets with True Positives, False Positives, and False Negatives
| Dataset | Method | TP | FP | FN | Precision | Recall | F1 Score |
|---|---|---|---|---|---|---|---|
|
| |||||||
| CrYOLO | 1306 | 3322 | 1144 | 0.28 | 0.53 | 0.37 | |
| DeepETPicker | 1632 | 506 | 818 | 0.76 | 0.67 | 0.70 | |
| TS_0001 | TomoPicker (PN) | 1592 | 465 | 858 | 0.77 | 0.65 | 0.71 |
| TomoPicker (PU) | 1300 | 734 | 1150 | 0.64 | 0.53 | 0.58 | |
| TomoPicker (kl) | 1499 | 549 | 951 | 0.73 | 0.61 | 0.67 | |
|
| |||||||
| CrYOLO | 555 | 1093 | 1787 | 0.34 | 0.24 | 0.28 | |
| DeepETPicker | 323 | 87 | 2019 | 0.79 | 0.14 | 0.23 | |
| TS_0002 | TomoPicker (PN) | 51 | 46 | 1616 | 0.51 | 0.46 | 0.49 |
| TomoPicker (PU) | 1049 | 1010 | 1293 | 0.51 | 0.45 | 0.48 | |
| TomoPicker (KL) | 1222 | 858 | 1120 | 0.59 | 0.52 | 0.55 | |
|
| |||||||
| CrYOLO | 1377 | 5691 | 1052 | 0.19 | 0.57 | 0.29 | |
| DeepETPicker | 409 | 145 | 2020 | 0.74 | 0.17 | 0.27 | |
| TS_0003 | TomoPicker (PN) | 594 | 1427 | 1835 | 0.41 | 0.38 | 0.39 |
| TomoPicker (PU) | 842 | 1188 | 1587 | 0.41 | 0.35 | 0.40 | |
| TomoPicker (KL) | 1162 | 890 | 1267 | 0.57 | 0.48 | 0.52 | |
|
| |||||||
| CrYOLO | 1677 | 7016 | 1290 | 0.19 | 0.57 | 0.29 | |
| DeepETPicker | 79 | 32 | 2888 | 0.71 | 0.03 | 0.05 | |
| TS_0004 | TomoPicker (PN) | 623 | 2397 | 2344 | 0.21 | 0.21 | 0.21 |
| TomoPicker (PU) | 1142 | 1892 | 1825 | 0.38 | 0.38 | 0.38 | |
| TomoPicker (KL) | 484 | 1536 | 2483 | 0.24 | 0.16 | 0.19 | |
|
| |||||||
| CrYOLO | 800 | 2167 | 2711 | 0.27 | 0.22 | 0.24 | |
| DeepETPicker | 1353 | 276 | 2218 | 0.83 | 0.38 | 0.52 | |
| TS_0005 | TomoPicker (PN) | 1955 | 1108 | 1616 | 0.64 | 0.55 | 0.59 |
| TomoPicker (PU) | 1670 | 1378 | 1901 | 0.55 | 0.47 | 0.50 | |
| TomoPicker (KL) | 2074 | 1003 | 1497 | 0.67 | 0.58 | 0.62 | |
|
| |||||||
| CrYOLO | 210 | 1566 | 1126 | 0.12 | 0.16 | 0.13 | |
| DeepETPicker | 397 | 226 | 939 | 0.64 | 0.30 | 0.41 | |
| TS_0006 | TomoPicker (PN) | 235 | 780 | 1101 | 0.23 | 0.18 | 0.20 |
| TomoPicker (PU) | 293 | 718 | 1043 | 0.29 | 0.22 | 0.25 | |
| TomoPicker (KL) | 873 | 666 | 463 | 0.57 | 0.65 | 0.61 | |
|
| |||||||
| CrYOLO | 66 | 1133 | 551 | 0.06 | 0.11 | 0.07 | |
| DeepETPicker | 302 | 417 | 315 | 0.42 | 0.49 | 0.45 | |
| TS_0007 | TomoPicker (PN) | 247 | 771 | 370 | 0.24 | 0.40 | 0.30 |
| TomoPicker (PU) | 218 | 789 | 399 | 0.35 | 0.33 | 0.27 | |
| TomoPicker (KL) | 254 | 758 | 363 | 0.25 | 0.41 | 0.32 | |
|
| |||||||
| CrYOLO | 471 | 2273 | 2273 | 0.20 | 0.17 | 0.19 | |
| DeepETPicker | 199 | 58 | 2545 | 0.77 | 0.07 | 0.13 | |
| TS_0008 | TomoPicker (PN) | 623 | 2385 | 2121 | 0.21 | 0.23 | 0.22 |
| TomoPicker (PU) | 684 | 2326 | 2060 | 0.23 | 0.25 | 0.24 | |
| TomoPicker (KL) | 408 | 1601 | 2336 | 0.20 | 0.15 | 0.17 | |
|
| |||||||
| CrYOLO | 1158 | 4372 | 2324 | 0.21 | 0.33 | 0.26 | |
| DeepETPicker | 831 | 173 | 2651 | 0.83 | 0.24 | 0.37 | |
| TS_0009 | TomoPicker (PN) | 1690 | 1344 | 1792 | 0.56 | 0.49 | 0.52 |
| TomoPicker (PU) | 1597 | 1440 | 1885 | 0.53 | 0.46 | 0.49 | |
| TomoPicker (KL) | 675 | 1437 | 2807 | 0.33 | 0.19 | 0.25 | |
|
| |||||||
| CrYOLO | 1805 | 4289 | 1568 | 0.30 | 0.54 | 0.38 | |
| DeepETPicker | 1023 | 299 | 2350 | 0.77 | 0.30 | 0.44 | |
| TS_0010 | TomoPicker (PN) | 1561 | 1490 | 1812 | 0.51 | 0.46 | 0.49 |
| TomoPicker (PU) | 1403 | 1645 | 1970 | 0.42 | 0.40 | 0.44 | |
| TomoPicker (KL) | 1879 | 1196 | 951 | 0.61 | 0.56 | 0.58 | |
|
| |||||||
| CrYOLO | - | - | - | 0.22 | 0.34 | 0.25 | |
| DeepETPicker | - | - | - | 0.73 | 0.28 | 0.35 | |
| Overall | TomoPicker (PN) | - | - | - | 0.41 | 0.38 | 0.39 |
| TomoPicker (PU) | - | - | - | 0.42 | 0.39 | 0.40 | |
| TomoPicker (KL) | - | - | - | 0.48 | 0.43 | 0.45 | |
We further provided a qualitative analysis of the models’ particle-picking performance. We used the predicted and ground truth particle locations in TS_0003 tomograms and visualized them for a middle xy slice as bounding boxes. To convert the 3D predictions into 2D bounding boxes, we took slices across the z-axis and drew a bounding box around each predicted point (its coordinates) in the corresponding xy slice. For each z-axis value (z), we also considered neighboring slices within a [] range, as the ribosome’s radius in these tomograms is maximally 12 voxels. Given the ribosome’s diameter of 24 voxels, we center the bounding boxes on the predicted points and size them to 24 voxels. We have provided a visualization for all the model predictions and ground truth in Fig. 2. The figure shows that CrYOLO picks very few particles. DeepETPicker picks much more particles than CrYOLO, but the amount of picked particles is still very low compared to the ground truth. It can be inferred from the figure that TomoPicker (KL) predictions most resemble the ground truth.
We also provided a comparison between TomoPicker (KL) prediction and DeepETPicker prediction with respect to the ground truth for the training tomogram TS_0001 in Fig. 3. It can be observed that DeepETPicker provided prediction for many particles in the training tomogram, unlike testing tomograms where it only predicted a few (Fig. 2). On the other hand, in TomoPicker (KL) predictions, we did not observe such disparity and the predictions are consistent in both training and testing tomograms. Moreover, Fig. 3 shows that DeepETPicker predicted many particles in regions far from the ground truth, whereas TomoPicker (KL) closely resembles the ground truth. All of these observations showcase the superior performance of TomoPicker (KL) in picking particles in the VPP S. Pombe Datasets.
Figure 3:
(a) DeepETPicker vs Ground Truth for a xy slice of TS_0001 VPP tomogram which was used for training. Blue Box = Ground Truth, Red Box = DeepETPicker Predictions. (b) TomoPicker vs Ground Truth for a xy slice of TS_0001 VPP tomogram which was used for training. Blue Box = Ground Truth, Yellow Box = TomoPicker Predictions.
4.5. TomoPicker (PU) performs overall best particle picking in Defocus-only (VPP) S. Pombe cellular cryo-ET Datasets
The Defocus-only dataset consists of 10 tomograms (labeled as TS_026, TS_027, TS_028, TS_029, TS_030, TS_034, TS_037, TS_041, TS_043, TS_045) with a total of 25,901 ribosome particles. The individual tomograms on the abovementioned sequence contains 838, 1673, 5305, 2897, 2783, 3783, 1646, 2813, 1815, and 2348 ribosome particles respectively. Among them, TS_026 has a very different organization than other tomograms and contains much fewer particles. As a result, we did not use this tomogram for training, validation, or testing. We only used 100 particle coordinates from TS_029 for training and 100 particle coordinates from TS_030 for validation. This accounts for only of the total particles.
After training, the model was tested against all the tomograms (except TS_026). Table 2 describes the precision, recall, and F1 score (up to 2 decimal places) obtained by each method against each tomogram and the overall dataset. The tables show that our proposed TomoPicker strategies outperformed the baseline methods. Overall, TomoPicker (PU) outperformed DeepETPicker by 29% and CrYOLO by 131.6%. On the other hand, TomoPicker (KL) outperformed DeepETPicker 17% and CrYOLO by 115.8% in the overall dataset. TomoPicker (PU) performed 7% better than TomoPicker (KL). Moreover, for individual tomogram results, TomoPicker (PU) performed the best in 7 tomograms, and TomoPicker (KL) performed the best in 2 tomograms.
Table 2:
Precision, Recall, and F1 Score Comparison across Different Methods on Defocus Ribosome Datasets with True Positives, False Positives, and False Negatives
| Dataset | Method | TP | FP | FN | Precision | Recall | F1 Score |
|---|---|---|---|---|---|---|---|
|
| |||||||
| CrYOLO | 1296 | 16185 | 377 | 0.07 | 0.77 | 0.14 | |
| DeepETPicker | 468 | 352 | 1205 | 0.57 | 0.28 | 0.38 | |
| TS_027 | TomoPicker (PN) | 159 | 844 | 679 | 0.28 | 0.34 | 0.31 |
| TomoPicker (PU) | 905 | 1159 | 768 | 0.44 | 0.54 | 0.48 | |
| TomoPicker (KL) | 650 | 1396 | 1033 | 0.32 | 0.39 | 0.35 | |
|
| |||||||
| CrYOLO | 3495 | 28929 | 1810 | 0.11 | 0.66 | 0.19 | |
| DeepETPicker | 1005 | 192 | 4300 | 0.84 | 0.19 | 0.31 | |
| TS_028 | TomoPicker (PN) | 688 | 1340 | 1127 | 0.37 | 0.36 | 0.36 |
| TomoPicker (PU) | 2612 | 2548 | 2693 | 0.51 | 0.49 | 0.50 | |
| TomoPicker (KL) | 2947 | 2213 | 2358 | 0.57 | 0.56 | 0.56 | |
|
| |||||||
| CrYOLO | 1950 | 14039 | 947 | 0.12 | 0.67 | 0.21 | |
| DeepETPicker | 907 | 292 | 1990 | 0.76 | 0.31 | 0.44 | |
| TS_029 | TomoPicker (PN) | 1176 | 1856 | 1721 | 0.39 | 0.41 | 0.40 |
| TomoPicker (PU) | 1653 | 1411 | 1244 | 0.54 | 0.57 | 0.55 | |
| TomoPicker (KL) | 1789 | 1278 | 1108 | 0.58 | 0.62 | 0.60 | |
|
| |||||||
| CrYOLO | 1952 | 22392 | 831 | 0.08 | 0.70 | 0.14 | |
| DeepETPicker | 824 | 234 | 1959 | 0.78 | 0.30 | 0.43 | |
| TS_030 | TomoPicker (PN) | 1200 | 1827 | 1583 | 0.40 | 0.43 | 0.41 |
| TomoPicker (PU) | 1542 | 1522 | 1241 | 0.50 | 0.55 | 0.53 | |
| TomoPicker (KL) | 1439 | 1617 | 1344 | 0.47 | 0.52 | 0.49 | |
|
| |||||||
| CrYOLO | 2499 | 13838 | 1284 | 0.15 | 0.66 | 0.25 | |
| DeepETPicker | 1064 | 249 | 2719 | 0.81 | 0.28 | 0.42 | |
| TS_034 | TomoPicker (PN) | 1491 | 2557 | 2292 | 0.37 | 0.39 | 0.38 |
| TomoPicker (PU) | 2045 | 2028 | 1738 | 0.50 | 0.54 | 0.52 | |
| TomoPicker (KL) | 1871 | 2221 | 1912 | 0.46 | 0.49 | 0.48 | |
|
| |||||||
| CrYOLO | 1039 | 10805 | 607 | 0.09 | 0.63 | 0.15 | |
| DeepETPicker | 381 | 236 | 1265 | 0.62 | 0.23 | 0.34 | |
| TS_037 | TomoPicker (PN) | 498 | 1526 | 1148 | 0.25 | 0.30 | 0.27 |
| TomoPicker (PU) | 748 | 1294 | 898 | 0.37 | 0.45 | 0.41 | |
| TomoPicker (KL) | 789 | 1249 | 857 | 0.39 | 0.48 | 0.43 | |
|
| |||||||
| CrYOLO | 1637 | 6884 | 1176 | 0.19 | 0.58 | 0.29 | |
| DeepETPicker | 518 | 196 | 2295 | 0.73 | 0.18 | 0.29 | |
| TS_041 | TomoPicker (PN) | 941 | 2092 | 1872 | 0.31 | 0.33 | 0.32 |
| TomoPicker (PU) | 1165 | 1906 | 1648 | 0.38 | 0.41 | 0.40 | |
| TomoPicker (KL) | 800 | 2236 | 2013 | 0.26 | 0.28 | 0.27 | |
|
| |||||||
| CrYOLO | 788 | 16252 | 1027 | 0.05 | 0.43 | 0.08 | |
| DeepETPicker | 402 | 237 | 1413 | 0.63 | 0.22 | 0.33 | |
| TS_043 | TomoPicker (PN) | 222 | 1783 | 1593 | 0.34 | 0.38 | 0.36 |
| TomoPicker (PU) | 688 | 1351 | 1127 | 0.34 | 0.38 | 0.36 | |
| TomoPicker (KL) | 222 | 1783 | 1593 | 0.11 | 0.12 | 0.12 | |
|
| |||||||
| CrYOLO | 1294 | 5778 | 1054 | 0.18 | 0.55 | 0.27 | |
| DeepETPicker | 462 | 176 | 1886 | 0.72 | 0.20 | 0.31 | |
| TS_045 | TomoPicker (PN) | 618 | 1409 | 1730 | 0.30 | 0.26 | 0.28 |
| TomoPicker (PU) | 783 | 1253 | 1565 | 0.38 | 0.33 | 0.35 | |
| TomoPicker (KL) | 776 | 1253 | 1572 | 0.38 | 0.33 | 0.35 | |
|
| |||||||
| CrYOLO | - | - | - | 0.12 | 0.63 | 0.19 | |
| DeepETPicker | - | - | - | 0.72 | 0.24 | 0.35 | |
| Overall | TomoPicker (PN) | - | - | - | 0.32 | 0.34 | 0.33 |
| TomoPicker (PU) | - | - | - | 0.43 | 0.46 | 0.44 | |
| TomoPicker (KL) | - | - | - | 0.39 | 0.42 | 0.41 | |
Moreover, similar to VPP experiments, we provided qualitative results of CrYOLO, DeepETPicker, and TomoPicker (PN, PU, and KL) prediction compared to ground truth in Figure 4. We visualized the prediction for a middle (z = 250) xy slice in testing tomogram TS_028. The figure indicates the lower contrast in defocus-only tomograms compared to VPP tomograms. It can be observed that CrYOLO’s picking completely differs from the ground truth. In other words, CrYOLO picked particles randomly instead of recognizing actual particles. DeepETPicker predicted much fewer particles compared to ground truth. On the other hand, TomoPicker predictions best match the ground truth.
5. Conclusion
In this work, we have introduced a novel annotation-efficient particle-picking approach, TomoPicker, for 3D cellular cryo-ET images or tomograms. In TomoPicker, we regarded particle picking in 3D cryo-ET tomograms as a voxel classification problem. As such, TomoPicker can be trained on a single tomogram. Since only a few particles are annotated in the tomogram, we leveraged two different positive-unlabeled (PU) learning approaches to train the voxel classifier in TomoPicker. We trained and compared these methods against recent learning-based particle picking methods on volta-phase-plate (VPP) and defocus-only S. Pombe cell cryo-tomograms. Consequently, we are the first to rigorously evaluate learning-based picking methods on crowded eukaryotic cell tomograms. Our exhaustive experiments demonstrate the superior (~ 30% improvement of F1 score and qualitatively closer to ground truth) performance of TomoPicker over strong baseline methods when only a minuscule portion (~ 0.3 – 0.5%) of the particles in the tomograms are annotated for training. Ultimately, given these innovations, TomoPicker is poised to become a standard approach for particle picking within the complex intracellular environment of eukaryotic cells.
6. Acknowledgement
This work was supported in part by U.S. NIH grants R01GM134020 and P41GM103712, NSF grants DBI-1949629, DBI-2238093, IIS-2007595, IIS-2211597, and MCB-2205148. This work was supported in part by Oracle Cloud credits and related resources provided by Oracle for Research, and the computational resources support from AMD HPC Fund. MRU were supported in part by a fellowship from CMU CMLH.
References
- [1].Doerr Allison. Cryo-electron tomography. Nature Methods, 14(1):34–34, 2017. [Google Scholar]
- [2].Turk Martin and Baumeister Wolfgang. The promise and the challenges of cryo-electron tomography. FEBS letters, 594(20):3243–3261, 2020. [DOI] [PubMed] [Google Scholar]
- [3].Robinson Carol V, Sali Andrej, and Baumeister Wolfgang. The molecular sociology of the cell. Nature, 450(7172):973–982, 2007. [DOI] [PubMed] [Google Scholar]
- [4].Chen Muyuan, Bell James M, Shi Xiaodong, Sun Stella Y, Wang Zhao, and Ludtke Steven J. A complete data processing workflow for cryo-et and subtomogram averaging. Nature methods, 16(11):1161–1168, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Tang Guang, Peng Liwei, Baldwin Philip R, Mann Deepinder S, Jiang Wen, Rees Ian, and Ludtke Steven J. Eman2: an extensible image processing suite for electron microscopy. Journal of structural biology, 157(1):38–46, 2007. [DOI] [PubMed] [Google Scholar]
- [6].Kim Hannah Hyun-Sook, Uddin Mostofa Rafid, Xu Min, and Chang Yi-Wei. Computational methods toward unbiased pattern mining and structure determination in cryo-electron tomography data. Journal of Molecular Biology, page 168068, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Zeng Xiangrui, Kahng Anson, Xue Liang, Mahamid Julia, Chang Yi-Wei, and Xu Min. Disca: high-throughput cryo-et structural pattern mining by deep unsupervised clustering. bioRxiv, pages 2021–05, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Liu Hsuan-Fu, Zhou Ye, Huang Qinwen, Piland Jonathan, Jin Weisheng, Mandel Justin, Du Xiaochen, Martin Jeffrey, and Bartesaghi Alberto. nextpyp: a comprehensive and scalable platform for characterizing protein variability in situ using single-particle cryo-electron tomography. Nature Methods, 20(12):1909–1919, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Wagner Thorsten, Merino Felipe, Stabrin Markus, Moriya Toshio, Antoni Claudia, Apelbaum Amir, Hagel Philine, Sitsel Oleg, Raisch Tobias, Prumbaum Daniel, et al. Sphire-cryolo is a fast and accurate fully automated particle picker for cryo-em. Communications biology, 2(1):218, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Moebel Emmanuel, Martinez-Sanchez Antonio, Lamm Lorenz, Righetto Ricardo D, Wietrzynski Wojciech, Albert Sahradha, Larivière Damien, Fourmentin Ericgc, Pfeffer Stefan, Ortiz Julio, et al. Deep learning improves macromolecule identification in 3d cellular cryo-electron tomograms. Nature methods, 18(11):1386–1394, 2021. [DOI] [PubMed] [Google Scholar]
- [11].Böhm Jochen, Frangakis Achilleas S, Hegerl Reiner, Nickell Stephan, Typke Dieter, and Baumeister Wolfgang. Toward detecting and identifying macromolecules in a cellular context: template matching applied to electron tomograms. Proceedings of the National Academy of Sciences, 97(26):14245–14250, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Liu Hsuan-Fu, Zhou Ye, Huang Qinwen, Piland Jonathan, Jin Weisheng, Mandel Justin, Du Xiaochen, Martin Jeffrey, and Bartesaghi Alberto. nextpyp: a comprehensive and scalable platform for characterizing protein variability in situ using single-particle cryo-electron tomography. Nature Methods, pages 1–11, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Liu Guole, Niu Tongxin, Qiu Mengxuan, Zhu Yun, Sun Fei, and Yang Ge. Deepetpicker: Fast and accurate 3d particle picking for cryo-electron tomography using weakly supervised deep learning. Nature Communications, 15(1):2090, 2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Teresa-Trueba Irene de, Goetz Sara K, Mattausch Alexander, Stojanovska Frosina, Zimmerli Christian E, Toro-Nahuelpan Mauricio, Cheng Dorothy WC, Tollervey Fergus, Pape Constantin, Martin, et al. Convolutional networks for supervised mining of molecular patterns within cellular context. Nature Methods, 20(2):284–294, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Huang Qinwen, Zhou Ye, Liu Hsuan-Fu, and Bartesaghi Alberto. Accurate detection of proteins in cryo-electron tomograms from sparse labels. In European Conference on Computer Vision, pages 644–660. Springer, 2022. [Google Scholar]
- [16].Liu Guole, Niu Tongxin, Qiu Mengxuan, Zhu Yun, Sun Fei, and Yang Ge. Deepetpicker: Fast and accurate 3d particle picking for cryo-electron tomography using weakly supervised deep learning. Nature Communications, 15(1):2090, 2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Berman Helen, Henrick Kim, and Nakamura Haruki. Announcing the worldwide protein data bank. Nature structural & molecular biology, 10(12):980–980, 2003. [DOI] [PubMed] [Google Scholar]
- [18].Emdb—the electron microscopy data bank. Nucleic acids research, 52(D1):D456–D465, 2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Moebel Emmanuel, Martinez-Sanchez Antonio, Lamm Lorenz, Righetto Ricardo D, Wietrzynski Wojciech, Albert Sahradha, Larivière Damien, Fourmentin Eric, Pfeffer Stefan, Ortiz Julio, et al. Deep learning improves macromolecule identification in 3d cellular cryo-electron tomograms. Nature methods, 18(11):1386–1394, 2021. [DOI] [PubMed] [Google Scholar]
- [20].Teresa-Trueba Irene de, Goetz Sara K, Mattausch Alexander, Stojanovska Frosina, Zimmerli Christian E, Toro-Nahuelpan Mauricio, Cheng Dorothy WC, Tollervey Fergus, Pape Constantin, Beck Martin, et al. Convolutional networks for supervised mining of molecular patterns within cellular context. Nature Methods, 20(2):284–294, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Zhao Yizhou, Bian Hengwei, Mu Michael, Mostofa R Uddin Zhenyang Li, Li Xiang, Wang Tianyang, and Xu Min. Cryosam: Training-free cryoet tomogram segmentation with foundation models. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 124–134. Springer, 2024. [Google Scholar]
- [22].Kiryo Ryuichi, Niu Gang, Plessis Marthinus C Du, and Sugiyama Masashi. Positive-unlabeled learning with non-negative risk estimator. Advances in neural information processing systems, 30, 2017. [Google Scholar]
- [23].Ibtehaz Nabil and Rahman M Sohel. Multiresunet: Rethinking the u-net architecture for multimodal biomedical image segmentation. Neural networks, 121:74–87, 2020. [DOI] [PubMed] [Google Scholar]
- [24].European Bioinformatics Institute. Empiar-10988: Negative stain electron microscopy of nucleosome bound by engineered minimalist reader mbtd1 binding module, 2023. Accessed: 2024-09-20. [Google Scholar]