Recurrent Connectivity Shapes Spatial Coding in Hippocampal CA3 Subregions

Abstract

Stable and flexible neural representations of space in the hippocampus are crucial for navigating complex environments. However, how these distinct representations emerge from the underlying local circuit architecture remains unknown. Using two-photon imaging of CA3 subareas during active behavior, we reveal opposing coding strategies within specific CA3 subregions, with proximal neurons demonstrating stable and generalized representations and distal neurons showing dynamic and context-specific activity. We show in artificial neural network models that varying the recurrence level causes these differences in coding properties to emerge. We confirmed the contribution of recurrent connectivity to functional heterogeneity by characterizing the representational geometry of neural recordings and comparing it with theoretical predictions of neural manifold dimensionality. Our results indicate that local circuit organization, particularly recurrent connectivity among excitatory neurons, plays a key role in shaping complementary spatial representations within the hippocampus.

Introduction

Recurrent connectivity among excitatory neurons is a critical feature of the cortical microcircuit that underlies functions such as sensory processing, working memory, and decision-making^1–6. In the hippocampus, strong recurrent excitatory connections among pyramidal neurons within the CA3 region are thought to provide a basis for memory-guided behaviors^7–10. This circuitry is believed to endow CA3 with the ability to rapidly store patterns of integrated sensory information for the initial encoding of contextual representations, and to retrieve them later from partial or degraded inputs^11,12. However, the density of recurrent collaterals changes on a gradient along the transverse axis, from low recurrence in proximal CA3 (pCA3; close to the dentate gyrus) to higher recurrence in distal CA3 (dCA3; close to CA2)^13,14, mirroring distinct molecular and physiological gradients recognized along this axis^15,16. Given these differences, it is natural to ask whether CA3 subregions hold different roles in encoding and retrieving spatial information, and how these roles translate more broadly to learning and memory functions^17–25.

To address this question, we performed a detailed functional characterization of pCA3 and dCA3 neurons in mice performing a spatial navigation task in virtual reality (VR)²⁶. We characterized the dynamics of neural representations over time and across contexts, revealing prominent differences between the two subregions. Using recurrent neural network (RNN) and Hopfield network models, we confirmed that varying the level of recurrent connectivity between excitatory neurons is sufficient to explain these differences, demonstrating that distinct connectivity patterns in pCA3 and dCA3 lead to differential mechanisms of information processing.

We conclude that distinct subregions of CA3, shaped by their respective levels of recurrent connectivity, play complementary roles in spatial memory: dCA3 may be more involved in the flexible encoding of new contexts, while pCA3 may contribute to the stable retrieval of established memories, thus balancing adaptability and consistency in memory-guided behaviors^27–29.

Results

Long-term dynamics of spatial representations

To first characterize the functional dynamics of different recurrent connections within CA3 in the dorsal hippocampus, we performed in vivo two-photon calcium imaging in a VR spatial navigation task^30,31 (Fig. 1a–c, Supplementary Fig. 1a–b). We stereotactically injected Cre-dependent adeno-associated virus (AAV) into pCA3 and dCA3 regions of Grik4-Cre mice to selectively express GCaMP8s in CA3 pyramidal neurons, and implanted a chronic imaging window above the hippocampus. Mice were head-fixed and trained to perform a goal-oriented learning (GOL) task^26,31, where a spatially fixed operant reward was given in a 2-m virtual linear environment with a 2-s inter-trial interval between laps. After two weeks of training, mice successfully learned the reward zone (RZ), as reflected by anticipatory changes in animal’s velocity and licking (Fig. 1d). On each day, we observed a subset of place cells (0.13 ± 0.01 for pCA3, 0.31 ± 0.02 for dCA3), whose responses reliably tiled the entire virtual track (Supplementary Fig. 1c, g). We quantified individual place cells’ specificity, sensitivity, and spatial information and found higher proportions of place cells with lower levels of spatial information and place field specificity in dCA3 compared to pCA3 (Supplementary Fig. 1c–f).

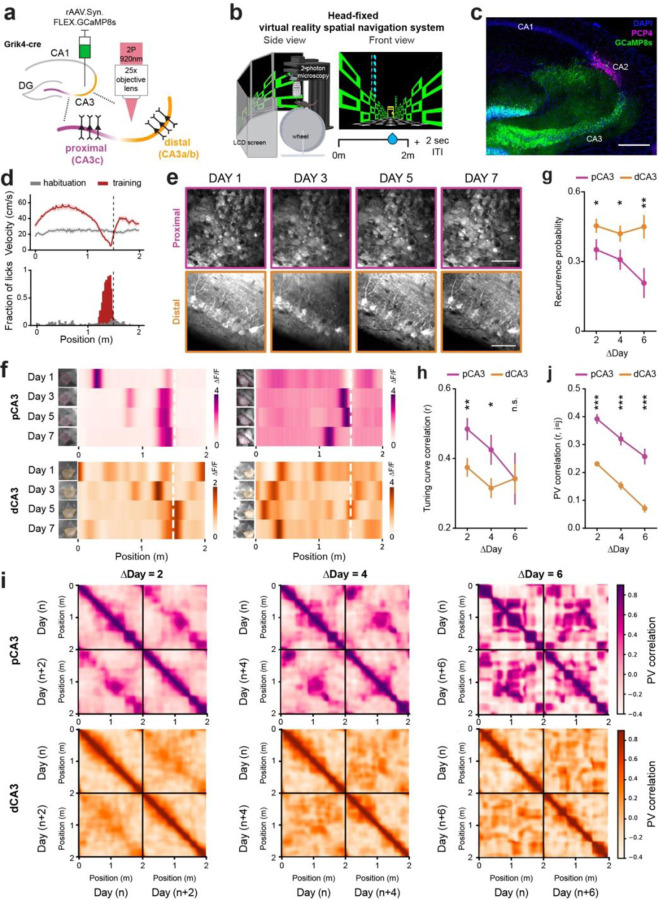
Figure 1. Dynamic and stable spatial representations by distal and proximal CA3.

a. Schematic of in vivo two-photon imaging of proximodistal CA3 neurons. Grik4-cre transgenic mice were injected with a Cre-dependent GCaMP8s virus to record the neural activities of PNs in dorsal CA3. b. Schematic of a virtual reality navigation system combined with in vivo two-photon microscopy (left) and the task structure of a goal-oriented learning (GOL) task with a fixed reward zone in a 2m virtual environment (right). ITI, intertrial interval. c. Representative confocal image showing GCaMP8s expression along the transverse axis of the CA3 region in Grik4-cre transgenic mice. Blue: DAPI, Green: GCaMP8s, Magenta: PCP4. Scale bar: 200um. d. Examples of velocity (top) and licking responses (bottom) before and after operant conditioning of the GOL task. e. Longitudinal and repetitive imaging of individual cells in proximal (top) and distal (bottom) CA3 subregions. Scale bar: 50 µm. f. Examples of cross-day registered place cells and their heatmaps of spatial tuning curves with stable place fields in pCA3 (top) and dCA3 (bottom). g. Probability of recurrence of place cells across days (mean ± SEM; two-sided unpaired t-test, p = 0.037, 0.032 and 0.0042 for ∆Day 2, 4, and 6; n = 5 and 7 mice for pCA3 and dCA3, respectively). h. Average tuning curve correlations of place cells across days (mean ± SEM; two-sided unpaired t-test, p = 0.0092, 0.029, and 0.10 for ∆Day 2, 4, and 6; n = 5 and 7 mice for pCA3 and dCA3, respectively). i. Heatmaps of population vector (PV) correlation between all pairs of positions across days for pCA3 (top) and dCA3 (bottom) place cells. The interval between days was 2 (left), 4 (middle), and 6 (right). k. PV correlation between the same position across days for pCA3 and dCA3 place cells (mean ± SEM, two-sided unpaired t-test, p = 1.06 e-14, 7.17 e-09, and 2.80 e-08 for ∆Day 2, 4, and 6, n = 5 and 7 mice for pCA3 and dCA3, respectively). Colors are matched with purple for pCA3 and orange for dCA3. n.s. = non-significant, *p < 0.05, **p < 0.01, *p < 0.001.

To investigate the long-term spatial coding properties of CA3 PNs, we tracked the same field of view every other day (Fig. 1e) as mice achieved stable behavioral performance in the GOL task. Among cross-registered cells, a subset of neurons was identified as place cells over days (Fig. 1f, Supplementary Fig. 2a, b), and we assessed whether neurons stably encoded their location over the course of the week. We found that dCA3 place cells had a higher recurrence probability (Fig. 1g), defined as the probability that a given neuron displays a significant place field across two paired sessions, irrespective of its location on the track. This result shows that dCA3 neurons overall remain more spatially selective with time compared to pCA3 neurons. To address whether place fields maintain their selectivity, we quantified the tuning curve correlations between sessions, and found that pCA3 place cells, though less numerous, are more stable over time than dCA3 place cells (Fig. 1h). At the population level, pCA3 population vectors remained highly correlated with each other across days compared to dCA3 population vectors (Fig. 1i, j, Supplementary Fig. 2c, d). In summary, these results imply that the dCA3 code is more dynamic and adaptable over time, while pCA3 implements a more stable, long-term code of spatial memory.

Generalized vs context-discriminative neural representations

Next, to investigate the neural dynamics of proximal and distal CA3 PNs in response to contextual changes, we performed a context-switching task in which animals were exposed to a (pretrained) Familiar (F) and a Novel (N) environment in 15-lap alternating blocks (Fig. 2a, b, Supplementary Fig. 3a, b) while recording from, either pCA3 or dCA3 (Fig. 2c). To quantify how contextual information is differentially processed at the single-cell level, we calculated a discrimination index (DI) of neural responses between familiar and novel contexts (Fig. 2d). We found that a significant proportion of neurons discriminated between contexts in both subregions, though a greater proportion did in dCA3 compared to pCA3 (Fig. 2e, f). Using a linear classifier with matched sample sizes, we also found that the information encoded in population activity in dCA3 discriminated between two different contexts with higher accuracy compared to that in pCA3 (Fig. 2g, h). We also evaluated the decoding performance of randomly chosen subsets of recorded neurons from pCA3 (Supplementary Fig. 3e). This analysis showed a correlation between the number of subsampled neurons and peak decoding accuracy, with the performance of the classifier being similar between all recorded pCA3 neurons and dCA3 neurons (Supplementary Fig. 3f).

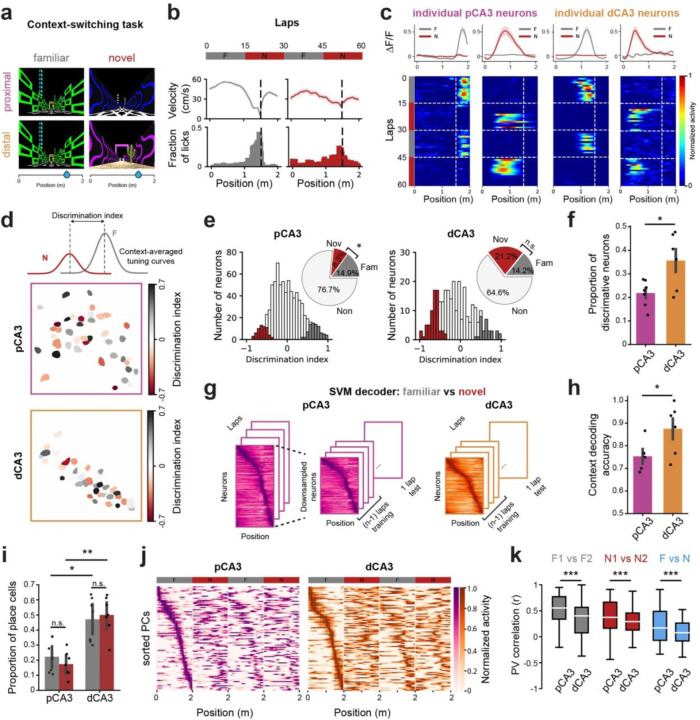
Figure 2. A generalized contextual- and spatial representation by proximal CA3 neurons.

a-b. Schematic of the context-switching task (a) and behavioral responses from an example mouse (b). Each session consisted of 60 laps with alternating blocks between familiar (gray) and novel (red) contexts. Both environments were 2m in length with the same location of operant reward. Mice showed different velocity and licking responses in familiar and novel contexts. c, Mean calcium traces (top) and heatmaps of lap-by-lap activity (bottom) for example neurons from pCA3 (b) and dCA3 (c). d. Calculation of discrimination index (DI) from context-averaged tuning curves (top) with the spatial distribution of context-discriminative PNs in pCA3 (middle) and dCA3 (bottom). e. Histogram of DI and significant DI values (colored bars, shuffling test, two-sided, p < 0.05). Inset: The fraction of neurons with significant DI in familiar (gray) and novel (red) environments. pCA3 neurons are more significantly tuned for familiar environments (p = 0.035; 7 mice), while dCA3 neurons are not significantly different between environments (p = 0.27; 7 mice). f. Proportion of neurons with significant DI value (mean ± SEM). dCA3 showed a higher level of context-discriminative neurons compared to pCA3 (p = 0.047; n = 7 mice for both pCA3 and dCA3). g. Schematic of the support vector machine (SVM) used to decode contextual information. Separate linear decoders were trained for subsampled pCA3 and dCA3 place matrices. h. SVM linear decoder performance on context discrimination (mean ± SEM). The peak decoding accuracies of dCA3 PNs in discriminating F-N contexts were higher compared to pCA3 PNs (0.61 ± 0.050 for pCA3, 0.85 ± 0.046 for dCA3; p = 0.0011; n = 7 mice for both pCA3 and dCA3). i. Proportion of place cells in familiar and novel environments. dCA3 showed a higher level of place cells in either familiar or novel environments compared to pCA3 (Kruskal-Wallis H-test, H = 16.40, p = 0.00093; post-hoc Dunn’s multiple comparison with Bonferroni correction, p = 0.015 and 0.0012 for familiar and novel context, respectively; n = 7 mice for both pCA3 and dCA3). j. Heatmaps of spatial tuning curves for pCA3 (left) and dCA3 (right) PNs during context switching. Rows are average and normalized responses for all CA3 PNs, sorted by the position of peak activity during the F1 block. k. Spatial tuning curve similarities within (F1 vs F2, N1 vs N2) and between contexts (F vs N). The population of place cells in pCA3 showed a higher level of PV correlation across conditions (p = 6.80 e-29, 4.35 e-13, 6.25 e-19 for F1 vs F2, N1 vs N2, and F vs N, respectively, n = 7 mice for both pCA3 and dCA3). Mann-Whitney U tests were used to determine statistical significance unless otherwise stated. Colors are matched as follows: purple for pCA3, orange for dCA3, gray for familiar context, and red for novel context. n.s. = non-significant, *p < 0.05, **p < 0.01, ***p < 0.001.

In addition to contextual representations, we analyzed place cell dynamics within and between environments. While both pCA3 and dCA3 neurons exhibited spatially tuned responses across context blocks (Fig. 2i, j, Supplementary Fig. 4a), pCA3 place cells showed a higher level of correlation between familiar and novel environments (Fig. 2k). In dCA3, F-N similarity increased during the second switch compared to the first switch, whereas no significant change was observed in pCA3 (Supplementary Fig. 4b, c).

Taken together, these findings suggest subregion-specific complementary roles for encoding dynamic environments, with pCA3 producing a general template for the context and dCA3 providing more specific responses (Supplementary Fig. 4d). Together, these populations might work in concert to balance flexibility and stability for encoding contextual information.

Recurrence level interpolates opposing coding strategies

Our functional imaging approach revealed dynamic and heterogeneous neural representations along the proximodistal axis of CA3 in relation to both time and context. How two subnetworks of the same hippocampal area implement opposing coding strategies remains an unanswered question. We hypothesized that these differences were driven by recurrence level as the most salient difference between these subregions. To test this hypothesis, we employed multi-level computational modeling.

First, we constructed two distinct recurrent neural network (RNN) models of CA3: a sparsely connected RNN and a densely connected RNN (Fig. 3a). The differences in recurrent connectivity of the RNNs were chosen based on earlier studies that reported recurrence level heterogeneity across the proximodistal axis of CA3^13,14 (Supplementary Fig. 5a).

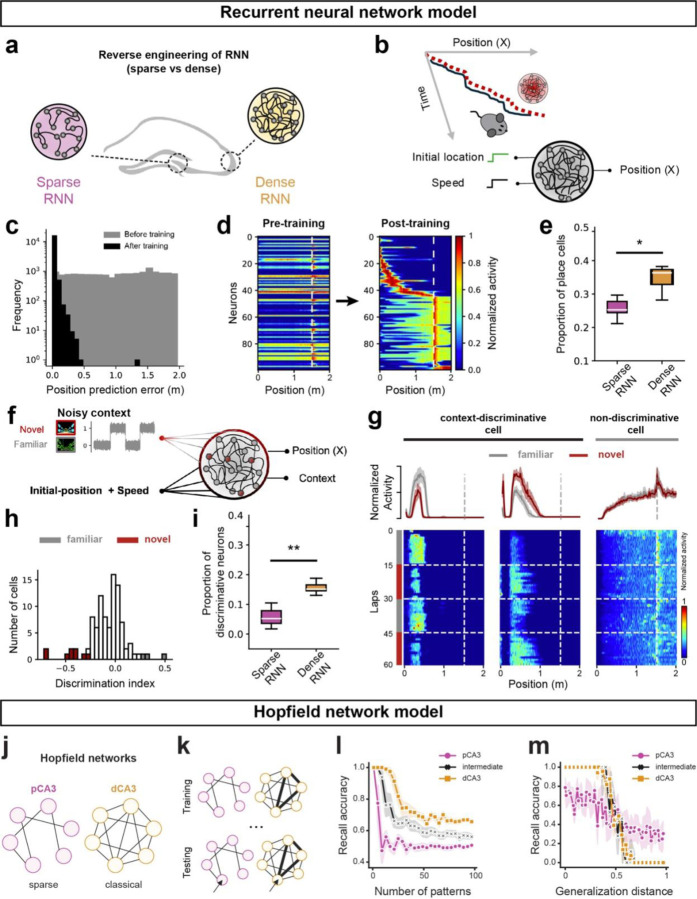
Figure 3. Distinct spatial and memory properties in sparse and dense neural networks.

a. Schematic representation of modeling proximal and distal CA3 with sparse and dense RNNs, respectively. b. Training of RNNs for a linear track navigation task using inputs of instantaneous speed and lap initiation to mimic mouse trajectory. Network connectivity and activation functions are updated during training, and post-training, activation patterns are analyzed for reverse engineering. c. Decoding accuracy of the RNNs before (gray) and after (black) training, shown by the position prediction error. d. Tuning curve evolution of RNNs with 100 cells pre- and post-training, sorted by activity levels. The tuning curves cover the spatial scale of the virtual arena. e. Proportion of spatial-tuned artificial cells in RNNs with sparse versus dense recurrence. f. Training of RNNs for context-switching tasks, where task-relevant inputs are fed to RNNs. g. Examples of artificial cell activation post-training in the context-switching task. The left shows two cells with context modulation (familiar vs. novel), while the right shows a spatially tuned cell without context-dependent activity. h. Histogram of DI and significant DI values (colored bars, shuffling test, two-sided, p<0.05) for artificial cells. i. Dependence of context-discriminative cells on recurrence level. Box plots represent the fraction of context-tuned cells for RNNs with sparse versus dense recurrence. j. Sparse (left) and classical (right) Hopfield model of associative memory, corresponding to areas pCA3 and dCA3, respectively. k. Schematic of training (storage) and testing (recall). During storage, binary patterns are sequentially presented to the network and pairwise synaptic weights are updated according to a Hebbian plasticity rule. During retrieval, corrupted patterns are presented to the network, whose dynamics recover the closest previously stored pattern. l. Dense network (dCA3) has greater discrimination capacity than the sparse (10% connectivity) network (pCA3). In repeated trials, N patterns are stored in each network and then recalled (y axis: mean bit-recall accuracy; chance level 50%). Both networks achieve 100% accuracy for small N with accuracy decreasing as N increases, but the number of patterns the sparse network is able to discriminate is much smaller than the dense network. m. Sparse network (pCA3) has greater generalization capacity than the dense network (dCA3). Each network was trained to its maximum capacity while still achieving 100% accuracy in (l). To test generalization performance, increasingly different patterns were then presented to each network (number of corrupted bits). The sparse network was able to generalize more accurately from patterns with a larger distance to the original compared to the dense network. Colors are matched as follows: purple for pCA3, orange for dCA3, gray for familiar context, and red for novel context. n.s. = non-significant, *p < 0.05, **p < 0.01, ***p < 0.001.

Informed by biological evidence showing projections from speed-selective cells in the entorhinal cortex to the hippocampus³², we designed our RNN models to receive inputs of speed and the initial location of the animal in a virtual arena (Fig. 3b). The number of training iterations was chosen to ensure both the sparse and dense RNN reached a plateau in their loss functions, ensuring a fair comparison of their performance (Fig. 3c, Supplementary Fig. 5b). Post-training analysis showed that the denser RNN model exhibited a higher proportion of place cells compared to the sparser model, consistent with our experimental observations (Fig. 1f, Fig. 3d, e).

To further explore the adaptability of place cells in the RNNs to new environments, we simultaneously provided a visual context signal and the instantaneous speed of the animal as the inputs to both network models and trained the networks to identify both location and context (Fig. 3f). Given that animals utilize visual cues to identify the context of the VR track³¹, we added noise to the context signal, representing perceptual context evidence from the visual system, to the hippocampal network. We maintained the noise level high enough to avoid a trivial scenario for the network and accordingly reinforced the engagement of a higher proportion of cells in context discrimination. As a result, the RNN model successfully learned the context-switching task with low error rates (Supplementary Fig. 5d); analysis of the hidden layer representations revealed the presence of multiple types of conjunctive and selective cells for context and place (Fig 3.g–h). A greater number of neurons in the dense RNN discriminated between familiar and novel contexts (Fig. 3i), consistent with in vivo recording data that showed higher context selectivity in dCA3 (Fig. 2f, h).

Finally, we investigated the effect of varying connectivity on memory generalization and discrimination using a Hopfield network model of CA3 subregions (Fig. 3j). Hopfield networks are widely used as models of content-addressable memory, but the classical Hopfield model requires full connectivity, which is not biologically plausible. However, we find that sparsely connected Hopfield networks, trained with the classic Hebbian rule (Fig. 3k), retain the ability to store and retrieve memories. We also find differences between memory performance in sparsely and densely connected Hopfield networks that mirror differences between pCA3 and dCA3. The dense network exhibited higher memory capacity, i.e., the ability to accurately discriminate a greater number of patterns compared to the sparse network (Fig. 3l). However, the sparse network was better at recovering patterns from significant distortions (Fig. 3m), suggesting fewer, deeper wells in its energy landscape that could aid generalization. Finally, we find that these abilities interpolate: intermediate levels of connectivity give rise to intermediate levels of discrimination and generalization (Fig. 3l, m; black line).

Dimensionality of neural manifolds altered by recurrency

Our modeling results suggest that the level of recurrence alone can account for the functional heterogeneities between pCA3 and dCA3 observed in vivo. Theoretical work has established a direct link between recurrency level and representational geometry of neurons, suggesting higher connectivity between neurons increases the mutual activity of cell populations³³, thereby constraining their representational geometry in population space (Fig. 4a).

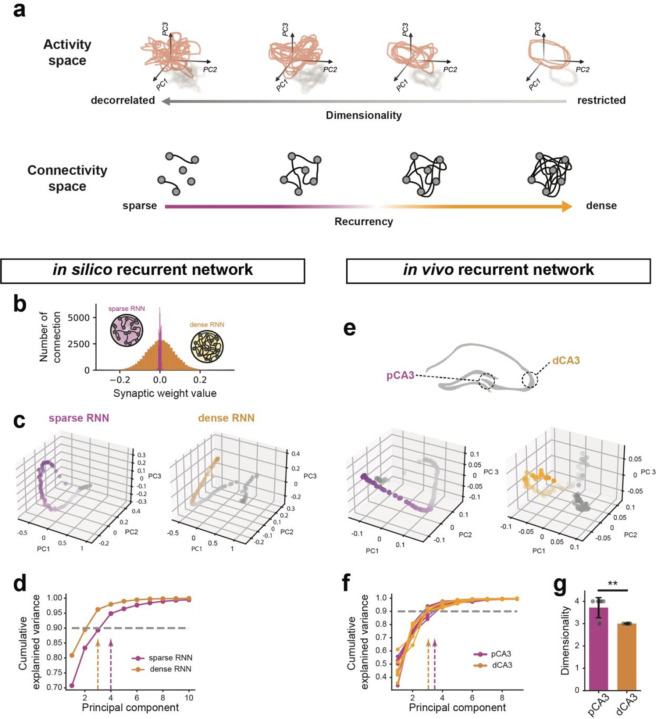
Figure 4. Neural manifold dimensionality in in vivo and in silico recurrent network.

a. Illustration of a direct link between recurrency and neuronal manifold dimensionality. b. Distribution of recurrent weights in sparse and dense RNN models. c. Principal Component Analysis (PCA) of population activities from simulated sparse (left) and dense (right) RNNs, with projections onto the top three principal components shown. d. Cumulative explained variance as a function of the number of principal components extracted from PCA with in silico simulated datasets. Dashed lines indicate the principal component at which 90% cumulative explained variance is reached. e. PCA of population activities in pCA3 and dCA3 during spatial navigation tasks, with projections onto the top three principal components shown. f. Cumulative explained variance as a function of the number of principal components extracted from PCA for in vivo neural activities. Dashed lines indicate the principal component at which 90% cumulative explained variance is reached. g. The average number of principal components required to reach 90% cumulative explained variance, as indicated by the dashed lines in f (p = 0.009). Mann-Whitney U tests were used to determine statistical significance unless otherwise stated. Colors are matched as follows: purple for pCA3 or sparse RNN, orange for dCA3 or dense RNN. n.s. = non-significant, *p < 0.05, **p < 0.01, ***p < 0.001.

We first examined this theoretical intuition in simulations of RNNs during the context-switching task. Our simulations demonstrated that altering connectivity towards sparser networks increases the dimensionality of neural manifolds, as defined by the explained variance of cumulative principal components (Fig. 4b–d). We conducted a similar analysis on the neural activities recorded during the same task to examine the neural representation geometry of proximodistal CA3 neurons (Fig. 4e). As predicted, the manifold dimensionality of representations in dCA3 was lower than that in pCA3 (Fig. 4f, g), further supporting the role of recurrent connectivity in functional heterogeneity within the CA3 circuit.

These findings underscore the critical role of recurrent connectivity in shaping the distinct functional properties of CA3 subregions. The gradient of generalization observed as a function of network sparsity highlights the importance of recurrent connectivity in the encoding and recalling of spatial and contextual information. Our computational modeling, aligned with experimental data, provides deeper insight into the mechanisms by which CA3 PNs contribute to spatial navigation and context discrimination.

Discussion

Despite extensive evidence of anatomical, molecular, and physiological heterogeneity in the CA3 along the transverse axis^{13–16,34,35}, the relationship between these differences and neural computations performed by CA3 subregions has remained largely unknown. While both stable and flexible dynamics as well as varying degrees of context generalization have been reported in CA3 using in vivo imaging^36–39, these representational features have not been systematically investigated along the proximodistal axis, nor have they been linked to CA3 subregions. In this study, we bridged these gaps by combining in vivo two-photon calcium imaging of CA3 subregions with computational modeling at multiple levels of abstraction. Our findings provide significant insights into how distinct hippocampal subcircuits differentially contribute to memory functions^36,40,41.

We found that dCA3 neurons are highly sensitive to contextual changes as well as tuned to different locations over days. This suggests that they are flexible and adaptive, possibly playing a role in learning and responding to new experiences or changes in the environment. In contrast, pCA3 neurons show more stability in their tuning over time, even though fewer neurons are tuned compared to dCA3. This stability suggests that they might be involved in encoding persistent or core aspects of the context that remain relevant across different experiences. These neurons may be essential for maintaining a stable representation of the environment, supporting consistent recall of key contextual features or stable memory traces, and could be rooted in how they integrate inputs at the subcellular level^42–44.

Consistent with recent reports on the rapid formation of place fields in the hippocampal CA1 and CA3^30,37,38,45, we also found that both pCA3 and dCA3 PNs exhibit spatially tuned neural responses that rapidly formed when the mice are exposed to novel environments. Future studies will explore the synaptic plasticity rules governing the dynamics of place field formation in CA3 along the transverse axis⁴⁶. We further observe that dCA3 PNs are more significantly tuned to novel environments compared to pCA3 PNs. It is well known that hippocampal circuits are under neuromodulatory control related to the behavioral state of animals^47–51. Correspondingly, the CA3 subregions may receive different levels of catecholaminergic input, such as dopamine and norepinephrine from the locus coeruleus, which facilitates memory formation in a new context^52–54.

It is striking that two subregions of the same hippocampal area, separated by less than a millimeter in the mouse brain and (notwithstanding the important differences we have highlighted) broadly similar in their anatomy, physiology, and development, can implement seemingly opposing computational functions. Our RNN modeling results, in which spatial and contextual representations by artificial cells corresponded closely to the empirical data in both single-cell and population level, underscore the critical role of local connectivity patterns in shaping the functional properties of neural networks. Furthermore, simulation results with dense, intermediate, and sparse Hopfield networks imply a smooth gradient between discrimination and generalization based on the level of recurrence in a subnetwork. Taken together, these findings emphasize the specific importance of recurrent connectivity in determining the computational features of neural circuits, supporting the idea that small variations in structural connectivity can lead to substantial differences in neuronal function and behavior. We further speculate that a gradient of connectivity implementing these intermediate levels exists between pCA3 and dCA3.

Our findings show that recurrent connectivity shapes the dimensionality of neural manifolds in CA3, with sparser networks yielding higher-dimensional manifolds and denser networks producing lower-dimensional ones. While an increasing body of literature associates dimensionality in neural spaces with flexibility and generalization^55–58, dimensionality alone does not fully account for a network’s computational capacity. The geometry of neural representations—encompassing factors like curvature, separation, and topology—plays a critical role in how information is processed^59–63. To fully understand flexibility and generalization, it is necessary to study the precise geometry of these representations. Previous studies have shown divergent roles in task performance are observed in networks with varying neural trajectory geometries^64,65.

Recent studies have explored how structural connectivity within networks affects their representational space, often by examining constraints such as connectivity rank^66,67. However, whether biological networks are inherently low-rank remains under debate. In our approach, we focus on binary (present-or-absent) connectivity, providing a clearer structural interpretation of how network architecture shapes representational dimensionality, complementing earlier studies that link structural biases to neuronal variability^68,69. Theory predicts that low-dimensional activity remains possible in sparse networks through fine-tuning of synaptic weights⁷⁰. Accordingly, the direct measurement of synaptic weights in vivo will be an important direction for future experimental work to dissect the synaptic basis for computational capacity.

In addition to recurrent local connectivity, subregion-specific differences in afferent inputs to CA3 can contribute to the observed differences in context-related dynamics between pCA3 and dCA3. Recent reports have highlighted a generalized neural representation by dentate gyrus granule cells, one of the main input sources to CA3³⁶, which may contribute to the more generalized contextual and spatial dynamics we observe in pCA3 PNs compared to dCA3 PNs. Similarly, subregion-specific differences in afferent inputs from the entorhinal cortex, which is also implicated in context generalization and discrimination in the CA3^71,72, may also shape context processing in CA3. Finally, the role of inhibition and subtype-specific inhibitory control of feature representations and their stability remains unknown^73–75. Future studies should investigate how external inputs modulate the cognitive flexibility of different subregions within CA3. Understanding local circuit⁷⁶ and long-range interactions will provide deeper insights into how the hippocampus supports complex behaviors, integrating contextual and spatial information to facilitate adaptive navigation and memory.

Methods

All experiments were conducted in accordance with NIH guidelines and with the approval of the Columbia University Institutional Animal Care and Use Committee. No statistical methods were used to predetermine sample sizes. The experiments were not randomized, and the investigators were not blinded to allocation during experiments and outcome assessment.

Animals

Imaging experiments were performed with healthy, 2- to 4-month-old, heterozygous adult male and female Grik4-cre mice (Jackson Laboratory, 006474) on a C57BL/6J background. Mice were group-housed under normal lighting conditions in a 12-hour light/dark cycle. Ad libitum water was provided until the beginning of training for the spatial navigation task.

Viruses

CA3 pyramidal cell imaging experiments were performed by injecting a Cre-dependent rAAV expressing GCaMP8s under the control of the synapsin promoter (rAAV9-Syn-FLEX-jGCaMP8s-WPRE-SV40; Addgene, 162377; titer, 2.3 × 10¹³ viral genomes per ml).

Surgery

All surgical procedures were performed on Grik4-cre mice (2–4 months old) under isoflurane anesthesia (4% induction, 1.5% maintenance in 95% oxygen). Mice were placed on a stereotaxic surgery instrument (Kopf Instruments), and their body temperature was maintained using a heating pad. Meloxicam and bupivacaine were administered subcutaneously to reduce discomfort. Following a skin incision, a craniotomy was performed over the right hippocampus using a drill. A sterile glass capillary loaded with rAAV was attached to a Nanoject syringe (Drummond Scientific) and slowly lowered into the right hippocampus. The proximal and distal CA3 were targeted with two x–y coordinates, each consisting of two different injection sites separated in z: AP −1.46, ML −1.75, DV −2.1, −1.9 and AP −1.46, ML −1.3, DV −2.3, −2.1 relative to bregma, with 60 nl of virus injected at each DV location. The pipette was held for 5–10 minutes after the last injection and then slowly retracted from the brain. The skin was sutured, and the mice were allowed to recover for 4 days before the window/headpost implant.

For hippocampal window and headpost implantation, as described previously^23,30,31, a 3-mm craniotomy was performed over the right anterior hippocampus, centered between the two injection coordinates. We then slowly aspirated the cortex overlying the right dorsal hippocampus and implanted a 3-mm glass-bottomed stainless-steel cannula for optical access. Subsequently, a titanium headpost with layers of dental cement was attached to the skull. The mice received 1.0 ml of saline subcutaneously and recovered in their homecage on the heating pad. All mice were monitored for 3 days of post-operative care until behavior training began.

Behavioral paradigm

After a 14-day recovery period from implant surgery, mice were water-restricted to 85–90% of their original body weight and habituated to handling and head fixation. They were then exposed to a 2-meter-long linear virtual reality (VR) corridor that remained consistent during training and recording^26,31. At the end of the environment, an inter-trial interval of 2 seconds with a blank screen was included, and the mouse was simply teleported to the next lap.

For the next 10–14 days, mice were trained to run through the virtual environment and lick for a water reward. In the habituation phase, a drop of water was given in a non-operant manner when the subject mice entered the reward zone (RZ). Additional water droplets were provided as they continued licking within a 30 cm area. In the training phase, the reward was given in an operant manner where the correct lick within the RZ could trigger the first drop of reward and subsequent droplets with additional licking. Mice were trained to run at least 30 laps in the environment. After recording during the GOL task, the context-switching task was performed the next day.

For context-switch experiments, we used a completely distinct set of visual cues along the 200 cm track as a novel environment. Each recording session consisted of four blocks: 15 laps in the Familiar context, 15 laps in the Novel context, 15 laps in the Familiar context, and 15 laps in the Novel context. The reward location remained fixed at 150 cm for both contexts. For subject mice used in both pCA3 and dCA3 imaging experiments, we used different visual cues for the novel environments, while the familiar context remained the same for both sequences.

Histology

After the completion of imaging experiments, mice were transcardially perfused with 40 ml of ice-cold PBS (Thermo Fisher), followed by 40 ml of ice-cold 4% paraformaldehyde (PFA; Electron Microscopy Sciences). The brain was then kept submerged in 4% PFA overnight at 4 °C. On the next day, coronal hippocampal sections (thickness: 100 μm) were obtained using a vibratome (VT1200-S, Leica, Germany). After brief washing with 0.3% Triton X-100 dissolved in phosphate-buffered saline (PBST), brain slices were incubated in a blocking solution (5% normal donkey serum, 0.3% PBST) for two hours at room temperature. Subsequently, slices were incubated with the primary antibody (rabbit anti-PCP4 diluted 1:500; HPA005792; Sigma-Aldrich) in a blocking solution overnight at 4 °C. After the sections were washed three times for 15 minutes with 0.3% PBST at room temperature, they were incubated with the secondary antibody (Alexa Fluor 647-conjugated donkey anti-rabbit IgG antibody diluted 1:800; 711-605-152; Jackson ImmunoResearch) in the blocking solution for 2 hours. Slices were rinsed three times for 15 minutes with 0.3% PBST, stained with DAPI (1:1000 dilution in 0.3% PBST), and then mounted on microscope slides. Fluorescence imaging was performed using a Nikon Ti-E A1R laser-scanning confocal microscope with ×10/0.45-NA Plan Apo (Nikon) or ×20/0.75-NA Plan Apo (Nikon) objective lens. 3 μm Z-stack images were processed using NIS Elements software (Nikon) or Fiji (ImageJ).

In vivo two-photon imaging

All imaging was conducted using a 2-photon 8 kHz resonant scanner (Bruker) and high-NA multiphoton objective (XLPLN25XWMP2, 25x/1-NA, Olympus). For excitation, we used a 920 nm femtosecond-pulsed laser (Chameleon Ultra II, Coherent). Pockels cells were used to regulate the power of the laser reaching the tissue. Green (GcaMP8s) fluorescence was collected through an emission cube filter set (HQ525/70 m-2p) to a GaAsP photomultiplier tube detector (Hamamatsu, 7422P-40). A custom dual-stage preamp (1.4 × 105 dB, Bruker) was used to amplify signals prior to digitization. All images were acquired with 512 × 512 pixel resolution at 30 Hz.

Calcium imaging data preprocessing

The preprocessing steps for the raw fluorescence signal have been described elsewhere^51,77. Briefly, the imaging data was motion corrected using the SIMA software package⁷⁸. The time average of each imaged cell was manually inspected, and an ROI was hand-drawn over each cell using a data visualization server program developed in the lab. The same CA3 PNs were transferred across sessions wherever possible, and identified with a unique ID, so that their activity across sessions could be tracked. Fluorescence was extracted from each ROI using the FISSA software⁷⁹ package to correct for neuropil contamination using six patches of 50% the size of the original ROI. For each resulting raw fluorescence trace, a baseline F was calculated by taking the first percentile in a rolling window of 30 s, and a ∆F/F trace was calculated. The ∆F/F trace for each cell was smoothed using an exponential filter, and all further analyses were performed on the resulting ∆F/F traces. We detected statistically significant transients as described previously⁷⁷ to use for place field calculations. All further analyses were implemented using Python using custom-written scripts.

Spatial tuning analysis

The virtual environment was divided into 100 evenly spaced bins (2 cm), which were then utilized to bin a histogram of each cell’s neuronal activity. Neuronal activity was filtered to include activity from when the animal was running above 3 cm/s and to exclude activity during the 2-sec teleportation at the end of the 2-m track. The spatial tuning curves were normalized for the animal’s occupancy and then smoothed with a Gaussian kernel (α = 6 cm) to obtain a smoothed activity estimate.

To detect place fields, we generated a baseline distribution of spatial tuning curves for each neuron by randomly and independently shifting the activity on each lap a random distance in a circular manner. Following this, we recalculated the smoothed, lap-averaged tuning curve as detailed above. We repeated this process a thousand times, determining the 95th percentile of baseline tuning values at each spatial bin, which served as the threshold for significant spatial tuning (p < 0.05). Areas of space where the true spatial tuning curve surpassed this baseline threshold were identified as potential PFs. In order to be classified as a place cell, ROIs needed to have at least 3 consecutive significant bins (6cm), but less than 25 consecutive bins (50cm). Moreover, in order to avoid spurious detection of significant bins, we set an additional criterion that there must be activity within the PF boundaries for a minimum of 20% of laps. For place cell sensitivity, representing the proportion of laps that had active events within the significant field, the number of laps that had at least 1 binarized event within the significantly detected fields was divided by the total number of laps. For place cell specificity, the total number of events within the significant field was divided by the total number of events observed within the lap. Then, it was averaged across all laps to have a single value for each ROI. If multiple fields were detected, they were computed separately and averaged across fields to have a single value for each ROI. For spatial information, it was calculated as described previously⁸⁰.

Tuning-curve correlation

To determine the level of similarity between spatial representations across different sessions for each place cell, we calculated the tuning curve correlation (Pearson correlation) for each pair of sessions imaged on different days. Only tuning curves of cells with place fields on both days were included in the analysis.

Population vector correlation

To assess the stability of spatial representations over days, we calculated the population vector (PV) correlation (Pearson correlation) between two sessions imaged on different days. Only cells defined as place cells on both days were included in the analysis. The diagonal values of the correlation matrix represent the correlation between corresponding spatial bins across different sessions. Specifically, each diagonal value indicates the correlation between the PV in a given spatial bin in one session and the PV in the same bin in another session. We averaged these diagonal correlation values across all spatial bins. This process was repeated for all pairs of sessions, and the correlation coefficient was quantified as a function of the day interval between sessions.

We also used PV correlations to quantify the similarity of the spatial code between and across contexts – F1 vs F2, N1 vs N2, and F vs N. Cells that were defined as place cells in at least one of the two blocks were included in this analysis. The same quantification process for correlation coefficients was applied

Discrimination index

As described previously⁸¹, the discrimination index (DI) was calculated for each cell to estimate the response preference toward a given context. The DI was defined by the following formula:

$$Discriminationindex=\frac{{\mu }_1-{\mu }_2}{\sqrt{\frac{1}{2}\left({\sigma }_1^2+{\sigma }_2^2\right)}}$$

where $\text{μ}$ and $\text{σ}$ represent mean and standard deviations of calcium response amplitudes across laps of each environment, respectively⁸².

To test the significance of the DI value, we generated 1,000 surrogate data sets in which laps were randomly permuted and calculated the 95th percentile of the null value per cell. If the experimentally observed DI value surpassed the top or bottom 2.5% of the distribution of surrogate DI values, we considered it context-selective. Therefore, 5% of neurons were expected to have a significant DI value in a given session by chance.

Support vector machine (SVM) analysis

To assess whether neuronal population activity patterns convey contextual information, we utilized a linear classifier support vector machine (SVM) to classify neuronal activity patterns into familiar or novel environments. For each imaging session, independent SVMs were trained and tested at each time point using a leave-one-trial-out cross-validation approach. Specifically, each decoder was trained with the neural population activity pattern from all laps except one withheld lap (n-1). We then evaluated whether the trained decoder accurately classified the held-out lap into the correct context. This process was repeated for each lap in the session, ensuring that every lap was utilized as a test lap at least once. Decoding accuracy was measured as the proportion of correct classifications. To compare the decoding efficacy between CA3 subregions, cells from proximal CA3 were subsampled to match the average detected ROI from distal CA3. The same SVM analysis procedures were then applied separately to the pCA3 and dCA3 datasets.

Neural manifold analysis

We employed Principal Component Analysis (PCA) to reduce the dimensionality of neural data and visualize neural trajectories in a low-dimensional subspace. Neural activity was represented as an N × T matrix, where N denotes the number of neurons, and T is the number of time points. To ensure comparability between pCA3 and dCA3 regions, we matched the number of recorded neurons across sessions. The data were mean-centered before PCA. The covariance matrix of the centered data, C, was calculated as:

$$C=\frac{1}{T-1}{X}_{centered}{X}_{centered,}^T$$

where $X_{centered}$ is the mean-centered data matrix. Eigenvalue decomposition was performed on C, yielding eigenvalues $\lambda i$ and corresponding eigenvectors (principal components). The neural data were projected onto the subspace spanned by the leading eigenvectors.

To determine the dimensionality of the data, we identified the minimum number of principal components k needed to explain at least 90% of the cumulative variance, calculated as:

$${\sum }_{i=1}^k\frac{{\lambda }_i}{{\sum }_{j=1}^N{\lambda }_j}\ge \mathrm{0.90.}$$

The same manifold dimensionality quantification was applied to both neuronal recordings and sparse and dense recurrent neural networks (RNNs) from simulation.

Modeling

Recurrent neural network modeling

Each subregion’s recurrent neural network (RNN) model consisted of a recurrent layer, alongside input and output layers. The network architecture and training method of our artificial neural networks was imitated from previous papers on path integrator artificial networks^83,84. The recurrent layer comprised 100 rate neurons with tanh activation functions and was implemented using the TensorFlow LSTM package⁸⁵. The output layer is a single (path integration) / two (multi-tasking network) neurons with dense connection from the recurrent layer with a linear activation function. The inputs to both the spatial imitator network and the multitasking network were the instantaneous speed and the initial position of the mice on the linear track. The initial position inputs were held constant, serving as the trial initiation signal. The network’s objective was to replicate the mice’s momentary position during each trial by integrating momentary speed and internally generated temporal signals within the network.

To stabilize network convergence, we introduced Gaussian noise as input to the network, a method shown to enhance convergence⁸⁶. In the multitasking RNN (context switching + path integration), we included a noisy input signal simulating the context visual signal encoded as a binary code, combined with Gaussian noise centered around zero with a standard deviation of 0.3. This perceptual noise was added to mimic the context-dependent visual cue noise in the virtual arena. With a noiseless context signal, we anticipated a smaller neuronal population to be involved in context identification computations. The goal of the multitasking RNN was to minimize the Euclidean distance in a two-dimensional subspace between predicted location-context pairs and actual location-context pairs.

To implement recurrent sparsity, an L1 regularization term was incorporated into the loss function, with different coefficients applied to promote either sparse $({\lambda }_{sparse}=0.1)$ or dense $\left({\lambda }_{dense}=0.001\right)$ connectivity. The total loss $L$ is defined as:

$$L=\sum {\left(X-X_{predict}\right)}^2+\lambda \sum \left|W_{recurrent}\right|$$

Where $X$ denotes the vector of momentary location and context, $X_{predict}$ is the network’s output, $W_{recurrent}$ represents the recurrent weights across hidden layer neurons, and $\lambda$ is the regularization coefficient.

Training was conducted using the Adam optimizer from the Keras package⁸⁵, with a learning rate of 1e-4 and a minimum batch size of 8. We ensured the spatiality of training by verifying the saturation of the training loss function.

To reverse-engineer network activity, we analyzed the response functions of individual neurons in the hidden layer during a feedforward epoch, where instantaneous speed and context signals were provided as inputs. Analysis of the artificial neurons, including cell selectivity and population activity, followed the same criteria used for biological neurons in this study. Additionally, we replicated the formation of place-selective cells using a network with a smaller hidden layer size (30 neurons). Population-level results were based on simulations involving 100 hidden neurons.

Hopfield networks

Hopfield networks were implemented in Python 3.8 in line with previous studies⁸⁷. In brief, a network was initialized with $N$ binary (±1) valued neurons. In the training phase, $M$ patterns $\xi$ are stored in the weight matrix according to the Hebbian rule

$$W=\sum {\xi }_j{\xi }_j^T$$

In the test phase, the trained network is initialized to a test pattern $\xi \prime$, constructed by flipping a predetermined fraction of the activities of a parent pattern $\xi$ chosen from the $M$ patterns the network was previously trained on. The network is then allowed to evolved according to the classical Hopfield dynamics

$$x\left(t\right)=sgn\left(Wx\left(t-1\right)\right)$$

where $x\left(0\right)=\xi$ until either convergence is reached (i.e., $x\left(t\right)=x\left(t-1\right)$) or a maximum number of iterations $T_{\text{max}}$ is reached.

To introduce sparsity into the Hopfield network, we choose a connection probability $p$ and sample a structural connectivity matrix $A$ where a connection exists between each pair of neurons i.i.d. with probability $p$ (equivalently, a graph is drawn from the Erdős-Rényi process parameterized by $p$). The case $p=1$ reduces to the classical Hopfield network with full connectivity, while smaller $p$ represents higher levels of sparsity. In sparse networks, weights between non-structurally connected neurons are not updated during training or used in the dynamics (which are otherwise unchanged), such that the effective weight matrix becomes

$$W_{eff}=A\odot W$$

where $\odot$ is the elementwise (Hadamard) product.

To model discrimination, we investigated how many distinct patterns networks at different levels of sparsity could store and accurately recall by drawing $M$ random binary vectors for a range of $M$ and storing them in the network. In the test phase, a fixed fraction of neurons were flipped and accuracy was read out as the similarity between the recovered pattern and the ground truth pattern.

To model generalization, we investigated perturbations to a base pattern that could still be identified with the base pattern by networks at different levels of sparsity by fixing the number of patterns $M$ and varying the fraction of flipped neurons. We again used similarity between the recovered pattern and the ground truth pattern as our accuracy metric.

Statistics

Statistical differences between means were determined by two-sided unpaired t-test and Mann-Whitney U test, Kruskal–Wallis tests with post hoc Dunn’s multiple comparison tests as mentioned in the text or figure legends. A p-value<0.05 was used as the criterion for statistical significance. Boxplots show the 25th, 50th (median), and 75th quartile ranges with the whiskers extending to 1.5 interquartile ranges below or above the 25th or 75th quartiles, respectively. All data analysis and visualization were done with custom software built on Python version 2.7.15, and 3.8.11. All data were expressed as mean ± SEM.