Fishnet mesh of centrin-Sfi1 drives ultrafast calcium-activated contraction of the giant cell Spirostomum ambiguum

Abstract

Spirostomum is a unicellular ciliate capable of contracting to a quarter of its body length in less than five milliseconds. When measured as fractional shortening, this is an order of magnitude faster than motion powered by actomyosin. Myonemes, which are protein networks found near the cortex of many protists, are believed to power Spirostomum contraction. Fast contraction, slow elongation, and calcium-triggering are hallmarks of myoneme-based motion. The biochemical basis of this motion and the molecular mechanism that supports such fast speeds are not well understood. Previous work suggests that myoneme structures in some protists are rich in centrin and Sfi1 homologs, two proteins that may underlie contraction. Centrin undergoes a significant conformational change in the presence of calcium, allowing it to bind to other centrin molecules. To understand Spirostomum contraction, we measure changes in cortical structures and model contraction of the whole cell and of the underlying protein complexes. We provide evidence that centrin/Sfi1 structures are responsible for contraction, which we propose is powered by a modulated entropic spring. Using this model, we recapitulate organismal-scale contraction in mesh simulation experiments and demonstrate the importance of structural organization of myoneme in a fishnet-like structure. These results provide a cohesive, multiscale model for the contraction of Spirostomum. Deeper understanding of how single cells can execute extreme shape changes holds potential for advancing cell biophysics, synthetically engineering contractile machinery, and cellular-inspired engineering designs.

INTRODUCTION

The giant unicellular ciliate Spirostomum has the ability to rapidly contract from a length of ~ 1 mm to 250 μm in as little as 5 ms, a speed of ~50 lengths/s. In contrast, individual muscle fibers are similar in size and can shorten by a similar fraction [1], but their typical V_max is approximately 10-fold slower [2]. Although related ciliates such as Vorticella and Stentor exhibit similar contractions, Spirostomum is notable for its speed, especially relative to its size [3]. For example, Spirostomum is 25 times larger in volume than Vorticella, but still produces three times higher velocity and acceleration [4–9]. Moreover, Spirostomum is able to quickly repeat this motion, resetting within a few seconds, unlike other fast but one-shot biological firing mechanisms such as nematocysts in jellyfish tentacles [8]. Even more interestingly, this contraction appears to be powered by a molecular mechanism distinct from conventional cytoskeletal filaments such as actin and microtubules and triggered by calcium ions, without direct association of ATP or GTP [10, 11]. Thus, Spirostomum offers a unique system for testing the physical limits of biological components to generate power, from the molecular to the organismal level. Ultimately, understanding this machinery may yield applications in the generation of mechanically robust and re-configurable cytoskeletal structures.

The unconventional cytoskeletal structures that drive the contraction of Spirostomum and related ciliates are called myonemes. Myonemes are long fibrous networks in the cortex that contract in response to calcium [12–14] and are thought to be responsible for cell shortening [15, 16]. Although they are far from fully characterized, previous observations of myonemes by electron microscopy showed fibrous bundles that change appearance and increase in density under contraction [17–19].

Although actomyosin powers many biological contractions, it has not been observed in the myoneme. Instead, myonemes are rich in centrin and large homologs of its binding partner Sfi1 [20, 21]. The presence of centrin and Sfi1 in myonemes is as surprising as the absence of actomyosin, since homologous proteins in other systems have very different known functions. In S. cerevisiae, centrin/Sfi1 filaments form a largely linear structure that may act as a molecular ruler in constructing the S. cerevisiae spindle pole body [22, 23] There is precedent for calcium-triggered contraction of centrin-based structures in algal striated flagellar roots, where centrin was first discovered [24], but despite speculation based on this earlier evidence [25], S. cerevisiae centrin-Sfi1 filaments show no evidence of kinking, bending, or sliding, even in the presence of millimolar calcium ion concentrations [22]. Thus, the molecular mechanism by which ciliate centrin and Sfi1 couple calcium influx to force generation has remained unclear.

Alongside myonemes, microtubules have been identified as a key component of the Spirostomum cortical cytoskeleton, although their potential role in contraction and/or re-elongation is not yet clear. Cortical microtubules decorate the surface of Spirostomum and form interconnected bundles along rows of basal bodies [26]. Previous models have proposed that a physical link between myonemes and microtubules could allow them to transmit forces without slipping past each other [27, 28], or that the antagonistic action of myonemes and microtubules might support repeatable contraction-elongation cycles [15, 16]. Yet the interactions between microtubules and myonemes and their mechanical contributions to changes in organismal shape remain largely unresolved.

A challenge in achieving a complete understanding of Spirostomum contraction is the range of length, time, and force scales that must be described. We have recently measured the contraction dynamics and used them to model in one dimension how the onset of contraction propagates along the entire organism [29]. However, a complete model of Spirostomum contraction would describe not only the dynamics of triggering, but also how molecular events generate force and how this force is directed to induce appropriate changes in three-dimensional organismal shape. Here, we build toward such a model with an approach that spans scales, from the molecular to the organismal. We quantitatively characterize the rearrangements within the myoneme and of the organism as a whole by light and electron microscopy. These data, in turn, inform computational models of contraction on both a coarse-grained and molecular scale. These results lead us to propose a mechanism for how centrin/Sfi1 rearrangements at the molecular level generate effective force at the organismal scale.

RESULTS

Immunofluorescence microscopy reveals organismal-scale changes in Spirostomum cortical structure under contraction

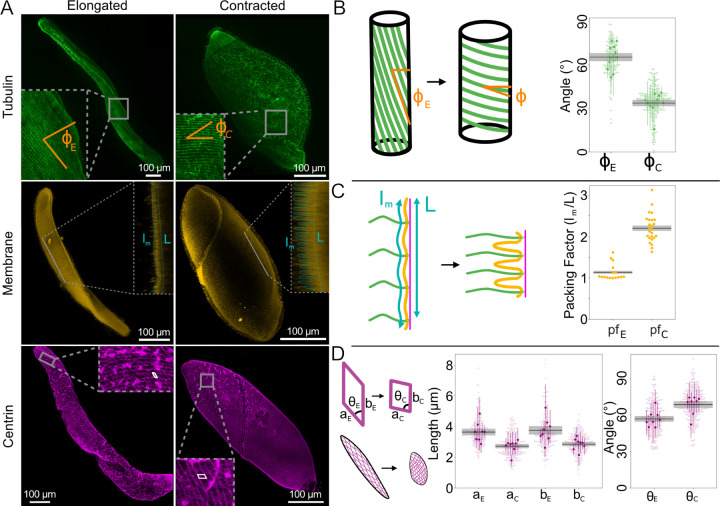
Structural changes that accompany contraction can provide information on force generation and the subsequent storage and dissipation of mechanical energy. By altering fixation conditions [30, 31] (see Supp. Materials and Methods), we can preserve cells in elongated (length = 884 ± 111 μm, N=7) or contracted (length = 306 ± 32 μm, N=12) states. This average three-fold decrease in length is accompanied by an increase in diameter from 89 ± 10 μm (N=7) to 117 ± 11 μm (N=12). Using immunofluorescence microscopy, we visualize the accompanying changes in microtubules, membrane, and centrin (Fig. 1A). Each of these structures exhibits significant, but distinct, rearrangements under contraction.

FIG. 1.

Changes in Spirostomum cortex in elongated (e) vs. contracted (c) cells quantified by immunofluorescence. A Representative example maximum intensity projections of confocal fluorescence microscopy z-stacks of Spirostomum stained via TAP952 (anti-tubulin, green, top), Cellmask Orange (membrane, yellow, middle), and 20H5 (anti-centrin, magenta, bottom). Membrane insets show single slices projected in the perpendicular plane. For space, elongated and contracted cells are shown at different scales. B-D Quantification of image features, as shown in cartoons. Black lines and gray bars show mean and SEM (over N=number of cells in each measurement). B and D Larger, darker markers show means from individual cells with standard deviation (as colored lines) and lighter, smaller markers show beeswarm plots of all individual measurements. B Microtubule pitch angle ϕ, N = 10 cells for each condition. C Packing factor due to membrane buckling, N=10 cells for each condition. D Length and angle of myoneme mesh segments, N=8 cells for each condition.

Cortical microtubules form long helical structures that change pitch under contraction (Fig. 1B). Quantification shows that the mean pitch angle (ϕ) when elongated is 64° ± 3° and, when contracted, 34° ± 2° (SEM reported on N = 10 cells, p = 1 · 10⁻⁷). However, due to the simultaneous change in diameter of the organism, these bundles in fact undergo very little change in radius of curvature despite their change in pitch. In fact, we estimate that, unlike the contribution of microtubule bending to neck elongation that has been recently reported in Lacrymaria olor [32], microtubule bending is unlikely to make a significant contribution either in opposing contraction or powering elongation in Spirostomum (see Supp. Disc. 1).

Next, we visualize the membrane organization of elongated and contracted cells using CellMask Orange (Fig. 1A). By collecting z-stacks, we observe that the membrane buckles and forms ridges under contraction (Fig. 1C). We quantify these ridges by visualizing them in cross-section (Fig. 1A, inset) and calculating their packing factor (pf), defined as the length of the contoured surface divided by the total length. We measured pf = 1.14 ± 0.03 in elongated Spirostomum and 2.20 ± 0.07 in contracted Spirostomum (SEM reported over N = 10 cells, p = 3 · 10⁻¹⁵), indicating that there is twice as much membrane per length in contracted cells compared to elongated cells. This measured packing factor is consistent with maintaining total membrane surface area under contraction. Ridges allow the effective surface area of the organism to decrease as the organism contracts, while conserving the total amount of membrane associated with the cortex. We estimate the energy stored in membrane bending during contraction (see Supp. Disc. 1) and find that it is ~ 10 fJ, which we estimate is so small as to negligibly contribute to the mechanics of the system as a whole.

Finally, we visualize the myoneme architecture in both contracted and elongated cells by staining with the centrin antibody 20H5 (Fig. 1A). In qualitative agreement with previous observations [21, 33], we observe a mesh of packed parallelogram-shaped bundles that tiles the entire surface in both elongated and contracted cells (Fig. 1A, D). Quantification of their dimensions (Fig. 1D) reveals a decrease between elongated and contracted cells in the lateral direction (a) of ~ 30%, from 3.6 ± 0.2 μm to 2.8 ± 0.1 μm in their lateral dimension (p = 0.007), and in their longitudinal direction (b) of ~ 24%, from 3.7 ± 0.3 μm to 2.8 ± 0.1 μm (p = 0.01) (SEM reported over N=8 cells). Accompanying myoneme shortening, we observe shearing of each individual parallelogram, with an increase in the angle of the vertex θ from 58.8° ± 2.9° to 68.4° ± 2.8°(p = 0.03) (SEM reported on N = 8 cells). As previously demonstrated [21], we confirm that centrin and Sfi1 colocalize in the myoneme (Fig. S1). Using the geometry we measure here and scaling previous measurements of total organismal-scale contractile force [13], we estimate that each unit of myoneme (i.e., each bundle that comprises the side of a parallelogram) must generate ∼ 10 pN of force during contraction (Supp. Disc. 1).

Coarse-grained mesh models demonstrate how myoneme fiber organization supports macro-scale contraction of the organism in 3D

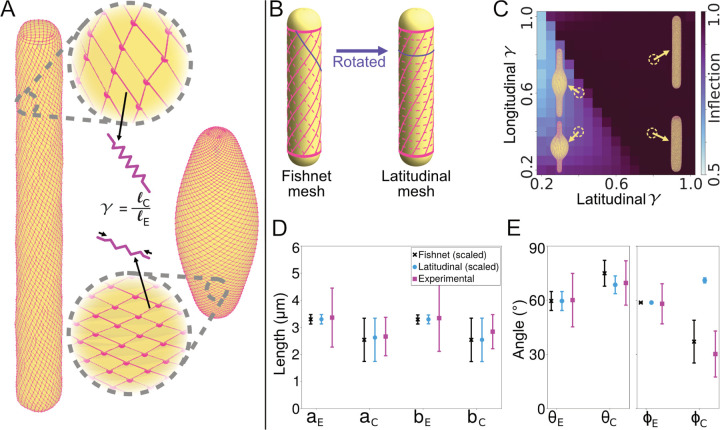
To construct a mechanical description of Spirostomum contraction at the organismal scale, we developed a coarse-grained mesh model of the cortical cytoskeleton (Fig. 2). This model helps us to understand the mechanical contributions of the cytoskeletal elements observed by immunofluorescence (Fig. 1). We modeled the myoneme system as a quadrilateral mesh which encloses a rounded cylinder (Fig. 2A). We treat the edges of the quadrilateral unit cell as harmonic springs whose rest lengths shrink by a factor (γ) during contraction. To simulate contraction, we numerically minimize the total energy objective function with respect to the configuration of the mesh under the new set of rest lengths. Since previous measurements of surrounding flows show no evidence of significant fluid emission during contraction [4], we assume conservation of total volume. To enforce this constraint, we triangulate the surface [34] by dividing each quadrangular unit cell of the mesh in two and augment the energetic objective function to include a stiff quadratic penalty against deviating from the original volume. To represent the possible mechanical contribution of microtubules, we also include an optional torsional spring term which penalizes untwisting of adjacent layers; we study whether this term is necessary to obtain the contracted shapes observed in vivo. The total energy function thus represents the balance of local elastic penalties (on the myoneme strands and microtubules) with the strict global constraint of zero volume change. See Supp. Materials and Methods for additional details and Table. S1 for model parameters.

FIG. 2.

Coarse-grained fishnet mesh model of the Spirostomum cortex recapitulates shape changes observed in vivo. A Cartoon of model, which represents myonemes as a quadrilateral mesh of springs (magenta) that surrounds a rounded cylinder (yellow). We simulate contraction by shrinking the rest lengths of the springs by a fraction γ and minimizing the total energy. B Schematic illustration of the structure of the fishnet (left) and latitudinal (right) mesh. The latitudinal mesh structure can be obtained from the fishnet mesh by rotating the dashed lines to connect opposing vertices. C Heatmap of the inflection metric (see Supp. Disc. 2 for definition) for the latitudinal mesh with varying shrinking factor γ for both edges of the mesh. Example structures are displayed near their corresponding locations on the heatmap. D and E Comparison of simulated and experimental measurements before and after contraction. Error bars represent standard deviation. D Edge lengths of the unit cells (cf. Fig. 1E). The coarse-grained simulation unit cells are scaled by a constant factor to allow comparison. E Angle of the unit cell parallelograms θ (cf. Fig. 1E) and helix twisting angle ϕ (cf. Fig. 1B).

To test the importance of the observed myoneme geometry for effective contraction, we consider two types of mesh structure: “fishnet” and “latitudinal.” In the fishnet mesh, which corresponds to the geometry found in vivo, sets of intersecting myoneme strands run along the length of the cylinder as helices with opposite handedness to each other (Fig. 2B). The initial helix angles of these strands are set to coincide with measurements of the elongated microtubule helix angles (Fig. 1B) and the angles of the myoneme unit cells (Fig. 1D). In the latitudinal mesh, which we consider as a hypothetical alternative mesh geometry, we rotate one set of strands to make it perpendicular to the long axis (dashed lines in Fig. 2B), thereby forming closed loops around the cylinder’s “lines of latitude.”

We find that the latitudinal mesh requires fine-tuning and, even with a best-fit set of parameters that includes torsional resistance, does not satisfactorily reproduce the experimentally measured changes in the mesh structure (Fig. 2C–E and Fig. S2). By contrast, we find that the contraction of the fishnet mesh structure quantitatively reproduces the experimental measurements of the changes in the side lengths of the unit cells (Fig. 1D and 2D), the angle of the unit cells (Fig. 1D and 2E) and the angle of the helix (Fig. 1B and 2E). Interestingly, we find that this agreement occurs without any torsional resistance of the microtubules. We observe that agreement occurs fairly robustly over a range of shrinking factors for the two sets of myoneme strands. Overall, the model suggests that the fishnet mesh structure is a key determinant of the experimentally observed contraction, which can explain the changes in the unit cell structure and helix angle.

TEM shows mesoscale changes in myoneme fiber from loose network to dense contracted structure

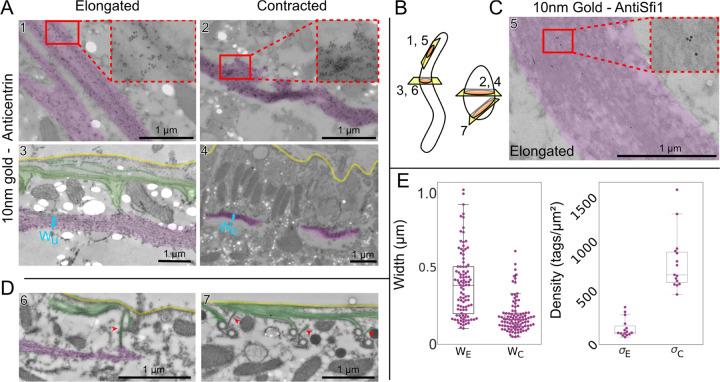
To examine the underlying structural changes in the myoneme that facilitate contraction, we performed transmission electron microscopy (TEM) on Spirostomum treated with and without EGTA, which preserves it in an elongated or contracted state, respectively (Fig. 3). Comparisons between these two states inform on the molecular and structural bases of contraction across length scales. We also performed immuno-gold labeling to verify the identity of myonemes in the TEM and to determine the localization of centrin and Sfi1 in the myoneme fibers at this scale.

FIG. 3.

Immunogold TEM reveals changes in centrin-dense myoneme fibers. Images highlighted for myoneme bundles (magenta), plasma membrane (yellow) and microtubules (green). A Representative example images immunogold labeled with 20H5 anti-centrin. In elongated cells (left, images 1 and 3), myoneme bundles appear as a loose meshwork with some long connected fibers, while in contracted cells (right, images 2 and 4), bundles appear as dense structures with no discernible fine details. There are holes present in some samples (bright white ovals) due to the fragility of the uncoated grids used to increase labeling efficiency. B Cartoon showing approximate direction of cuts. C Representative TEM image of elongated myoneme bundle labeled with Sc_25973_2 (anti-Sfi1). D Example images of connections (red arrows) between myoneme and microtubule cytoskeletons at basal bodies. The left (elongated cell) and right (contracted cell) images show perpendicular perspectives (see B) of similar structures in different cells. E Quantification of myoneme fiber width (left) measured perpendicular to the cell membrane (elongated: N=4 images with 3 preparation repeats, contracted N=5 images with 3 preparations) and tag density (right; 15 measurements shown, 3 repetitions of the preparation, measurement is average over a fiber). Each preparation contained multiple cells; it is unknown whether the images in a single preparation were of different cells.

In both elongated and contracted cells, the centrin antibody (20H5) densely and specifically labels the myoneme fibers (Fig. 3A, B). In elongated cells, we observe a loose network with fibers that run continuously throughout the section until they appear to move out of plane (Fig. 3A). In contracted cells, fibers are highly dense, and we cannot resolve their substructure in the TEM images (Fig. 3A), consistent with previous observations [19]. In both elongated and contracted cells, the centrin label is roughly uniform throughout the entire myoneme fiber, verifying it as a core myoneme component (Fig. 3 A). To label Sfi1, we used peptide antibodies raised against sequences from related ciliate Stentor (see Supp. Materials and Methods). Perhaps unsurprisingly, these Sfi1 antibodies had a lower affinity in Spirostomum, but still sparsely labeled myonemes (Fig. 3C), as expected from our own (Fig. S1) and previous observations by immunofluorescence [21].

In both elongated and contracted cells, we occasionally observe associations between microtubules and myonemes, usually near basal bodies (Fig. 3D). This direct interaction between myonemes and basal bodies has been speculated [21] and observed in a previous report [19]. Here, we newly observe that cortical microtubule bundles are also involved, and find that these interacting microtubules often show significant immunogold labeling for centrin, suggesting that centrin may play a role not only in filament structure but also in anchoring myonemes to other cortical structures (Fig. 3A3).

We quantified the width of the fibers in elongated and contracted states, finding a decrease by a factor of 3 (Fig. 3E), from a width of 0.61 ± 0.06 μm in elongated fibers to 0.20 ± 0.03 μm in contracted fibers (P = .004, SEM calculated with N=3 replicates each). Furthermore, we quantified the density of immunogold tags, observing an increase in tag density by a factor of 8 (Fig. 3E), from 116 ± 23 tags/μm² in elongated cells to 913 ± 154 tags/μm² in contracted cells (P = .04, SEM calculated with N=3 replicates each). Although both of these measurements may be subject to sources of variability, they lead to a predicted change in myoneme mesh length of 17% (assuming constant tagging efficiency and volume ≈ length × width²), which is consistent in magnitude with the shortening we observe by immunofluorescence (Fig. 1D). This consistency further suggests that most myonemal centrin remains associated throughout contraction. Thus, the structural changes we observe at the nanoscale are consistent with the organismal-scale immunofluorescence measurements, validating that these myoneme rearrangements drive contraction of the organism as a whole.

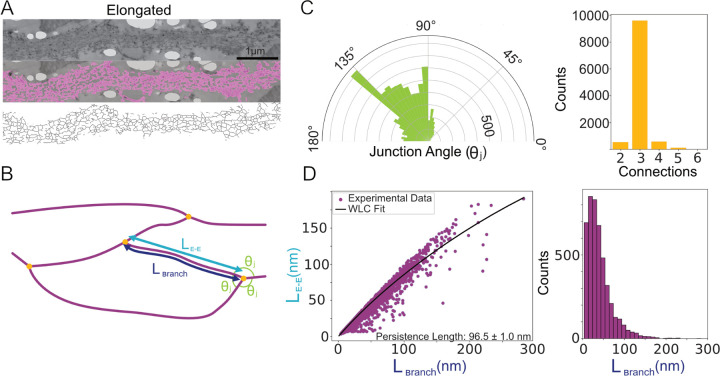
Skeletonization analysis of TEM reveals micro-scale organization of elongated myoneme fiber

The mesh-like structures we observe within myoneme bundles of elongated EGTA-treated Spirostomum show some regularity, which we characterize via semi-automated skeletonization analysis (Fig. 4A). We then process the skeletonized images to identify intersections and branches (Fig. 4B). The primary angle of the junctions is ≈ 100–135° and most junctions include 3 connections, consistent with an approximately hexagonal mesh (Fig. 4C). Amid this branching structure, we qualitatively observe many consistent, long strands traversing the long axis of the myoneme filament. Although this structure is somewhat different from that previously described by Ishida et al. [35], our preparation involved a higher concentration of EGTA for a shorter time, which may have caused the myoneme to access a more relaxed state. These long strands may be individual Sfi1 filaments, which are predicted to be up to microns long [21].

FIG. 4.

Skeletonization analysis reveals structural features of elongated myonemes. A Selected image showing segmentation analysis (magenta) and skeletonization. B Cartoon showing features quantified from the skeletonization. Branches (magenta) of segment lengths L_branch and end-to-end distances L_E−E meet at intersections (yellow dots) with junction angles θ_j. C Polar histogram of junction angles (left) and number of branches at each intersection (right) (N=5 images, 10,816 total measurements). D Left, plot of branch length versus end-to-end length, fit to a worm-like chain (WLC) model (see Methods) to estimate the persistence length. Right, histogram of branch lengths (excluding dead end branches), demonstrating notable variation.

By comparing the length of the skeletonized filaments in each branch with their end-to-end lengths, we estimate their persistence length (Fig. 4D). Assuming that there is little external force on the elongated myoneme, we apply a worm-like chain (WLC) model, which yields a fitted persistence length of 96±1 nm (SEM calculated from the covariant matrix reported by the scipy python package [36]). Notably, this estimate is similar to measurements of the calmodulin-stabilized lever arm of myosin V, which has a persistence length of ≈ 150 nm [37] and shares a gross structural similarity to centrin-bound Sfi1 helices (see below).

Molecular structural predictions suggest nano-scale mechanisms of myoneme contraction

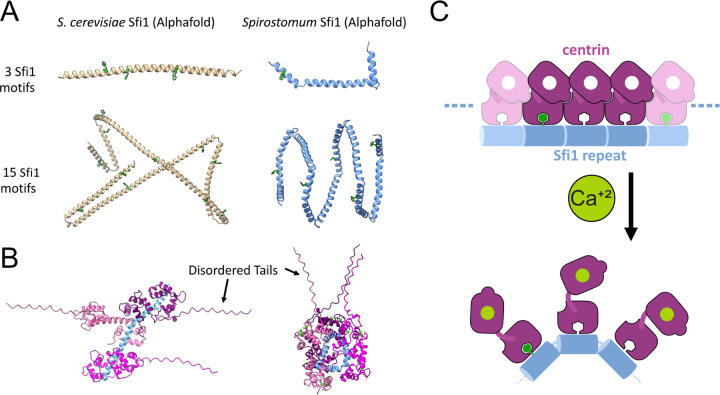
While the biochemical composition of the myoneme is not fully established, the two known components in both Spirostomum and related systems are centrin and homologs to Sfi1 [21, 38, 39]. In Saccharomyces cerevisiae, the long alpha-helical protein Sfi1 (molecular weight 110 kDa) forms a scaffold that includes as many as 24 binding sites for centrin, creating filamentous structures mediated by centrin-centrin interactions [22, 40]. To gain insight into how homologous components might have been adapted to provide a molecular basis for contraction-generating myoneme filaments in Spirostomum ambiguum, we first analyzed their sequence and then modeled their structures using AlphaFold (Fig. 5) [41–43].

FIG. 5.

Protein structures predicted by AlphaFold suggest a molecular mechanism of Sfi1-centrin mediated contraction. A Comparison between AlphaFold-predicted structures of S. cerevisiae and Spirostomum Sfi1, each pair shown at approximately the same magnification. Tryptophan residues are highlighted in green. The model predicts a large number of bending sites throughout Spirostomum Sfi1 in comparison to S. cerevisiae Sfi1 (Supp. Data 1–4). B Examples of AlphaFold-predicted structures of Spirostomum Sfi1-centrin interactions that may regulate persistence length. Predictions show two predicted states, one with a stabilized Sfi1, similar to the S. cerevisiae crystal structure, and the other with kinked Sfi1, similar to the predicted structure in the absence of centrin (Supp. Data 5 and 6). C Proposed molecular mechanism for contraction of the centrin/Sfi1 complex. In the absence of calcium, centrin may stabilizes Sfi1 in an elongated conformation. With the addition of calcium, centrin-centrin and/or centrin-Sfi1 interactions change, allowing Sfi1 to bend and shortening its end-to-end distance.

We identified putative centrin and Sfi1 protein sequences derived from Spirostomum ambiguum transcriptomics data deposited in NCBI (see Supp. Materials and Methods, Tables S2 and S3, and Supp. Data). We found several proteins that contain multiple tandem repeats of a 69 amino acid sequence similar to Sfi1-like centrin-binding proteins in Paramecium tetraurelia. While the reads we identify from deposited transcriptomics are relatively short, they still show close homology to the Giant Spasmoneme Binding Proteins GSBP1 and GSBP2 recently identified in Spirostomum minus, which contain many tandem repeats of the consensus sequence and have a very large size of up to 2000 kDa, more than 20 times larger than S. cerevisiae Sfi1 [21, 44].

Previous sequence and structural analyses in S. cerevisiae have shown that Sfi1 homologs contain up to 24 alpha-helical repeats which vary in length between approximately 23–36 amino acids (Table S4), with each repeat binding to one centrin protein [22]. Within these published crystal structures of S. cerevisiae centrin Sfi1 complexes, the individual centrins form a helical filament surrounding the central Sfi1 alpha-helix which is stabilized by head-to-tail contacts between adjacent centrins’ N-terminal and C-terminal domains [22].

In contrast, the organization of centrin-binding regions in Spirostomum Sfi1 is strikingly different. In most cases, the sequences of these Sfi1-like proteins in Spirostomum contain many consecutive 69-amino acid repeats with very few non-repeat interruptions (Table S2). Thus, the spacing of the centrin-binding sites is highly regular over a significant fraction of the protein’s length. In addition, the sequence signature of these repeats is distinct from the canonical Sfi1 repeat of S. cerevisiae and related sequences in other eukaryotes. First, each 69-amino acid repeat includes two proline residues. In contrast, there are relatively few proline residues within the S. cerevisiae Sfi1 protein. These prolines divide the 69-amino acid repeat into two sub-repeats, 36 and 33 amino acids in length. Second, a highly conserved tryptophan is observed in every Sfi1 repeat we identify in Spirostomum (Tables S2 and S3), but appears less highly conserved in S. cerevisiae Sfi1 repeats (Table S4).

To examine the structural consequences of these sequence features, we used AlphaFold to predict the structure of a 69-amino acid repeat sequences from Spirostomum ambiguum (Table S3) and a comparable sequence of three repeats from S. cerevisiae Sfi1 (PDB 2DOQ, homolog of the first 37 residues in 15 motifs) (Fig. 5A, Supp. Data 1 and 2, Table S4) [41–43]. The predicted structure for the S. cerevisiae sequence closely resembles the extended alpha-helical structure observed by crystallography (Fig. 5A, Supp. Data 1) [22]. In contrast, the AlphaFold-predicted structure of the Spirostomum ambiguum Sfi1 repeat includes two kinks within the repeat (Fig. 5A, Supp. Data 2). These interruptions to an extended alpha-helix occur near the locations of helix-breaking amino acids, such as the proline residues noted above, as well as glycines. These differences suggest a much shorter persistence length for Spirostomum ambiguum Sfi1-like repeats than for S. cerevisiae Sfi1.

We then used AlphaFold to model a more extended series of repeats for both S. cerevisiae and Spirostomum proteins (Fig. 5 A, Supp. Data 3 and 4). In this case, we analyzed a segment containing 15 Sfi1 repeats from S. cerevisiae alongside a comparable length of the Spirostomum protein containing five 69-amino acid repeats. These longer segments show an even more dramatic difference in predicted structures, with the Spirostomum ambiguum Sfi1-like protein adopting a particularly compact structure due to regular breaks that disrupt the primarily alpha-helical structure (Fig. 5A). AlphaFold predictions show a superhelical coil for a series of tandem repeats in Spirostomum ambiguum, but not in S. cerevisiae (Fig. 5A). These models support the hypothesis that Spirostomum Sfi1-like repeat proteins have an intrinsic tendency to bend or kink, promoted by the abundance of helix-breaking amino acid residues.

Finally, we used AlphaFold to predict the structure of a 69 amino acid two-repeat segment of Spirostomum ambiguum Sfi1 in complex with the C-terminal domain of Spirostomum ambiguum centrin (Fig. 5B, Supp Data 5–7). Over multiple runs, we do not see structural consensus from AlphaFold on the centrin-Sfi1 complex, but rather observe an interesting range of structures. Among the predicted structures, we see both elongated and compacted states (Fig. 5B and S3, Supp. Data 7). The elongated structure is reminiscent of the previously reported crystal structure of a comparably sized region of S. cerevisiae Sfi1 (PDB 2DOQ) in complex with centrin [22] (which, notably, was included in the training data for AlphaFold). The compacted structure is similar to the AlphaFold predicted structures of Spirostomum Sfi1 alone (Fig. 5A). In both predicted elongated and compact structures, the highly conserved Spirostomum Sfi1 tryptophan residues insert into a pocket in the C-terminal centrin domain flanked by aromatic side chains (Supp. Data 5 and 6). A similar binding mode has been observed experimentally in other systems, where the C-terminal domain of centrin binds with high affinity to alpha-helical peptides containing tryptophan, even in the absence of calcium [45–47].

Based on this analysis, we propose a molecular mechanism of myoneme contraction where centrin binding to Spirostomum repeats may prevent Sfi1 kinking in the absence of calcium, stabilizing the elongated state. Then, if calcium binding to centrin modulates this interaction, we hypothesize that it could enable these repeats to undergo the kinking we observed in the predicted AlphaFold structures when centrin is absent (Fig. 5C). We attempted to validate this model by comparing predicted AlphaFold structures in the presence and absence of calcium. Notably, however, we see both elongated and compact Sfi1 structures with and without calcium (Supp. Fig. S3), emphasizing the need for future experiments to test this model. Indeed, several molecular mechanisms might explain how calcium alters the centrin-Sfi1 interaction to favor kinking or shortening of myonemal filaments, and investigating them will be an interesting area for further study.

DISCUSSION

The data presented herein, which span from the molecular to the organismal scale, lead us to propose a new multiscale model for how structural changes at the molecular level power contraction of Spirostomum as a whole (Fig. 6). From its molecular triggering to its explanation of organismal force transduction, this proposed mechanism is notably distinct from better characterized cytoskeletal force generators, such as actomyosin contraction and microtubule sliding.

FIG. 6.

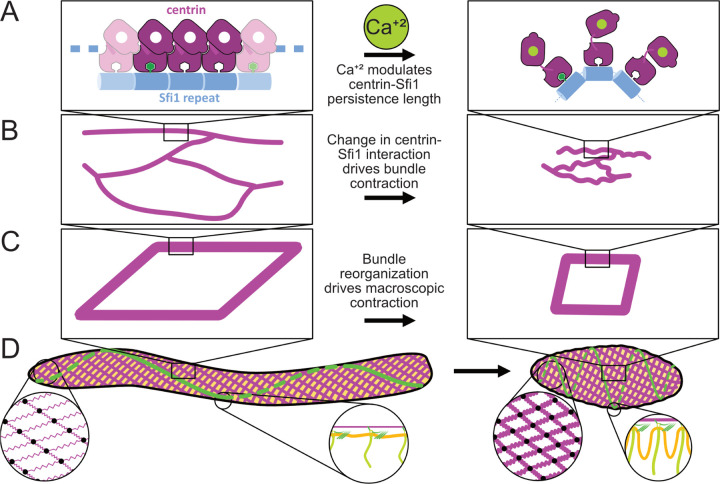
Proposed multiscale (nm-mm) hierarchical physical mechanism for Sfi1/centrin powered contraction in Spirostomum. A On the protein scale, we propose that calcium-signaled centrin modulates the stiffness of Sfi1 fibers. B At the ≈ μm scale, the change in persistence length of these fibers generates contractile force directed along the organism’s long axis. C At the mesoscale, myoneme fibers form the edges of the fishnet-like mesh, which contracts the cortex while preserving overall organismal structure. D In the organism as a whole, myonemes generate contraction. Meanwhile, membrane ridges, templated via anchorage at basal bodies to myonemes and cortical microtubule bundles, preserve overall surface area.

At the molecular level, differences in the amino acid sequences of Sfi1 in Spirostomum compared to its S. cerevisiae counterparts may explain how it achieves its distinct function. Molecular modeling predicts that the helix-breaking residues cause kinks or bends in Spirostomum Sfi1 that disrupt the otherwise largely alpha-helical structure. By coupling calcium binding to stabilization or disruption of these kinks, calcium may effectively regulate the stiffness of Spirostomum Sfi1, allowing it to behave as an entropic spring whose rest length changes in response to calcium (Fig. 6A, Supp. Disc. 1). This proposed mechanism bears some similarity to the giant protein titin, which has been proposed to act as an entropic spring to support passive relaxation and/or supplement contraction in the sarcomere [48]. However, for generating organismal scale contraction, modulating the persistence length of an Sfi1/centrin filament acting as an entropic spring would be, to our knowledge, both novel and unique in biology.

We can also now begin to understand how nanometer scale changes in the persistence length of a single filament can be coupled together in fibers that contract at the micron scale (Fig. 6B). The mesh that we see in elongated myonemes has an approximately but not precisely hexagonal network with irregular branch points. Furthermore, Spirostomum myoneme fibers appear to shorten perpendicular to contraction. These rearrangements are markedly different from other large, repeatedly contracting cellular structures such as actomyosin fibers in muscles, which include highly uniform repeating bands that maintain a constant width as they contract [49]. While irregular actomyosin networks can also contract [50], sarcomeric architecture helps them to do so more robustly and efficiently [51]. An irregular fiber formed from many filaments whose persistence lengths are modulated with calcium may allow Spirostomum to achieve efficient contraction with more structural flexibility.

Although the structure within the myoneme filaments appears somewhat random, more organization emerges at the organismal scale (Fig. 6C). The orientation of the myoneme mesh amplifies force from each individual fiber, as fibers act in parallel when they encircle the organism. Longitudinally, from head to tail, the fiber bundles act in series, which allows for a small change in size of each fiber to add up to a large change in the overall length of the organism. Furthermore, the angled, fishnet mesh ensures uniform contraction without bulges or irregularities that might lead to stress failures of organelles or the organism as a whole. Together these effects allow Spirostomum myonemes to generate large cortical forces that dramatically reshape the organism without destroying its internal structures, and to do so in a manner that is strikingly distinct from other more characterized mechanisms of biological contraction (Fig. 6D).

When myonemes contract, the immense loads accompanying their rearrangements must be effectively dissipated and productively distributed to other cellular structures to alter the shape of the organism while preserving its contents [52]. The regular structures we observe near the cell cortex in contracted cells – namely, bent microtubule bundles and membrane ridges – may help to ensure that force from contraction is directed into structures strong and flexible enough to endure it. How these structures form is not yet fully clear, but they may be patterned via mechanical coupling between myonemes and the plasma membrane. The association we observe between myonemes, cortical microtubule bundles, and basal bodies of the cilia may provide this coupling.

We have proposed here a mechanical framework that can explain Spirostomum’s rapid contraction and its molecular mechanism. However, important questions remain. First, the mechanism of elongation following Spirostomum contraction is as yet wholly uncharacterized. While we explore the idea that microtubule bundles and cell membrane may store energy from contraction, we estimate that the relevant energies are orders of magnitude apart in scale, leaving them insufficient to explain elongation. Thus, we think it is likely that as yet undescribed mechanisms allow this organism to elongate. One possible mechanism for elongation is force generated by cilia, which contributes to neck extension in Lacrymaria olor [53]. Another possibility is that active re-sequestration of calcium allows the myonemes themselves to produce elongation force.

As for contraction, while centrin and Sfi1 are key myonemal components, an in vitro assay with purified proteins would conclusively demonstrate if they are in fact sufficient for force generation, or if additional components are required. If they are sufficient, it will still be important to identify the specific interactions that drive both contraction and elongation. One possible hypothesis that merits further investigation is that calcium modulates hydrogel states of centrin, which could in turn alter its interaction with Sfi1. Centrins from various organisms have previously shown to undergo calcium-induced polymerization in vitro [54, 55], and this behavior has been proposed to in fact represent liquid-liquid phase separation, and to potentially be important in malarial infection [56]. Similar dynamics may be at play in Spirostomum contraction. Finally, both the three-branch nodes and the centrin-containing fiber that we observe near basal bodies by TEM provide important clues that additional interactions and/or biochemical components are important for myoneme organization. An in vitro assay could not only resolve these outstanding questions, but would also open the possibility of using myonemes in future applications as the basis for synthetically engineered contraction [29].