Effects of virus-induced immunogenic cues on oncolytic virotherapy

Abstract

Oncolytic virotherapy is a promising form of cancer treatment that uses viruses to infect and kill cancer cells. In addition to their direct effects on cancer cells, the viruses stimulate various immune responses partly directed against the tumour. Efforts are made to genetically engineer oncolytic viruses to enhance their immunogenic potential. However, the interplay between tumour growth, viral infection, and immune responses is complex and not fully understood, leading to variable and sometimes counterintuitive therapeutic outcomes. Here, we employ a spatio-temporal model to shed more light on this interplay. We investigate systematically how the properties of virus-induced immunogenic signals (their half-life, rate of spread, and potential to promote T-cell-mediated cytotoxicity) affect the therapeutic outcome. Our simulations reveal that strong immunogenic signals, combined with faster diffusion rates, improve the spread of immune activation, leading to better tumour eradication. However, replicate simulations suggest that the outcome of virotherapy is more stochastic than generally appreciated. Our model shows that virus-induced immune responses can interfere with virotherapy, by targeting virus-infected cancer cells and/or by impeding viral spread. In the presence of immune responses, the mode of virus introduction is important, with systemic viral delivery throughout the tumour yielding the most favourable outcomes. The timing of virus introduction also plays a critical role; depending on the efficacy of the immune response, a later start of virotherapy can be advantageous. Overall, our results emphasise that the rational design of oncolytic viruses requires optimising virus-induced immunogenic signals and strategies that balance viral spread with immune activity for improved therapeutic success.

Introduction

Oncolytic virotherapy is a promising cancer treatment that employs naturally occurring or genetically engineered viruses to preferentially target, infect and kill cancer cells¹. The subsequent activation of immune responses by infected cells can potentially further enhance the treatment outcomes^2–4. However, immune responses generated in the tumour can also work against oncolytic virus infection and undermine therapeutic efficacy^5–7. Therefore, it is important to study how virotherapy-induced immune responses in the tumour influence its efficacy and, ultimately, therapeutic outcomes.

Infection of cancer cells by oncolytic viruses leads to the production of a wide variety of immunogenic signals capable of alerting the immune system. For instance, cytokines and chemokines released by infected cells act as messenger proteins to attract and guide immune cells to the site of infection. Additionally, dying cancer cells release damage-associated molecules and stimulate the immune system to respond. Potentially, these signals lead to the recruitment and activation of immune cells in the tumour, improve the presentation of cancer antigens to T-cells, and ultimately facilitate T-cell-mediated cytotoxic killing of cancer cells^4,8,9.

The immunostimulatory nature of oncolytic viruses has led to their use in enhancing the patient’s immune responses against cancer. To this end, oncolytic viruses are being genetically engineered to improve their immunogenic potential. These modifications involve the incorporation of genes encoding for immunostimulatory signals which are released upon the infection of cancer cells^1,5,9. Such virus-encoded signals can enhance immune responses in the tumour. For instance, virus-encoded cytokines attract immune cells to the infection site, checkpoint inhibitors enhance T-cell activity by blocking inhibitory signals, and T-cell-engager proteins bring T-cells closer to cancer cells for targeted attacks. An illustrative case is T-VEC, a genetically modified herpes virus encoding GM-CSF, a cytokine boosting antigen presentation to activate T-cells^10,11. Its immunogenic properties have led to the activation of potent and durable T-cell-mediated immune responses in clinical settings, resulting in FDA and EMA regulatory approval for melanoma treatment.

While it is widely acknowledged that the release of these immunogenic signals in the tumour upon virotherapy induces immune responses, it is not completely understood how these responses influence therapeutic outcomes^12–14. If not regulated carefully, the release of immunogenic signals may hinder rather than assist in positive outcomes. Excessive or poorly regulated immune responses may damage healthy tissue, and an immune response against virotherapy may compromise its effectiveness by eliminating infected cells or neutralising the virus^5–7. Therefore, the optimal design of immunostimulatory oncolytic viruses requires an in-depth analysis of various additional factors influencing the immune response generated by virotherapy, such as the presence of antigen-specific T-cells and the tumour microenvironment.

Computational models are well-suited for studying the intricate virus-tumour-immune interplay as they enable the evaluation of specific factors while maintaining consistent conditions. For instance, a modelling approach can provide insights into crucial factors influencing treatment outcomes, such as the spatial organisation of the tumour during virotherapy^15,16, the recruitment of immune cells^16,17, and the impact of antiviral and anticancer immune responses^17–26. Unlike traditional experimental methods, modelling can facilitate the rapid exploration of different scenarios and the identification of hidden patterns that determine therapeutic outcomes to oncolytic virotherapy^19,27–29.

Previous efforts in modelling virus-tumour-immune interactions have observed that positive therapeutic outcomes are associated with the activation of anticancer immune responses^15,30–32, while poor therapeutic outcomes are linked to antiviral immune responses directed towards infected cells. The antiviral immune responses, characterised by parameters like viral clearance rates and immune-mediated killing of infected cells, have been noted to significantly undermine therapeutic efficacy^18,30,33. These findings have suggested various strategies to improve therapeutic outcomes by regulating antiviral immune responses, designing “immune-invisible” oncolytic viruses^34,35, optimising anticancer responses^30,36,37, and in improving virus delivery¹⁵.

Here, we focus on studying the relatively unexplored role of virus-induced immunogenic signals in promoting immune responses within a spatial context³⁰. In a previous study²⁹, we constructed and analysed a cell-based spatio-temporal model of tumour-virus interactions that allows to predict the outcome of oncolytic virotherapy based on cellular and viral properties. In our current model, we include the generation and spread of virus-induced immunogenic signals to assess how these signals regulate T-cell-mediated cytotoxicity. We have provided the executable version of the model (see Code availability) to aid users in their design of virus-induced immunogenic signals by conducting a spectrum of in silico experiments on a local computer. For computational efficiency, we indirectly modelled T-cell-mediated cytotoxicity and left out other aspects of the immune system. We systematically assess how the properties of virus-induced immunogenic signals, such as their half-life, rate of spread, and their potential to promote T-cell-mediated cytotoxicity can ultimately affect the therapeutic outcomes. To explore virotherapy delivery strategies, we also consider how the timing and method of virus introduction influences tumour burden reduction. Furthermore, we evaluate how tumour density influences anticancer T-cell-mediated cytotoxicity and tumour eradication. Our model shows that virus-induced immunogenic signals can spatially regulate T-cell-mediated cytotoxicity in the tumour. We demonstrate that optimal T-cell-mediated cytotoxicity can be induced by engineering immunogenic signals that are potent, have a long half-life and can rapidly diffuse in the tumour. Moreover, our findings indicate that the timing and mode of virus delivery play a critical role in shaping the therapeutic outcome. Our findings also elucidate that T-cell-mediated cytotoxicity can impede viral spread within the tumour by targeting and eliminating not only virus-infected cancer cells but, in certain scenarios, even uninfected cancer cells.

Results

Figure 1 gives an overview of the model, which considers the implication of a virus infection on a tumour that is growing in a 2D or 3D configuration. There are four different cell types: healthy stromal cells, uninfected but infection-sensitive cancer cells, infection-resistant cancer cells, and infected cancer cells. All cells can divide (if there is space for this) and die, and the birth and death rates may differ between cell types. Infection-sensitive cancer cells can become infected by an oncolytic virus, which is programmed to preferentially target and kill cancer cells while sparing stromal cells. Infection occurs systemically, but below we explore other infection variants. Via mutation, cancer cells can acquire resistance against the virus. In our previous study²⁹, we investigated how the outcome of virotherapy depends on key parameters of the model, like the rate of viral spread (b_i) and the death rate of infected cells (d_i). We showed that, due to the stochasticity of all processes in the model, alternative therapeutic outcomes (like total tumour eradication and persistence of an infection-resistant tumour) can occur for the same parameter settings. Accordingly, only probabilistic predictions can be made.

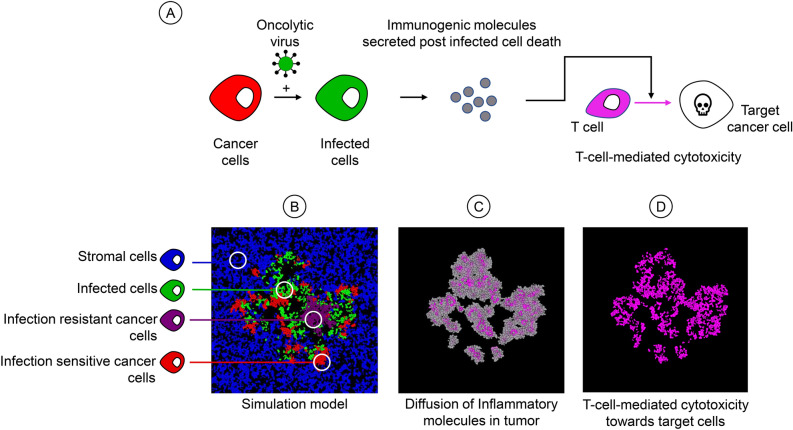
Fig. 1.

Overview of the model. (A) Crucial events in the model. An infection-sensitive cancer cell (red) can be infected by the virus, turning it into an infected cell (green). When an infected cell dies it releases immunogenic molecules. These molecules induce T-cell-mediated cytotoxicity, leading to the killing of target cells. (B) Spatial configuration of the model. The model follows the fate of four types of cells: healthy stromal cells (blue), infection-sensitive cancer cells (red), virus-infected cancer cells (green), and resistant cancer cells (purple). Cells divide or die with cell-type specific birth and death rates. Infection-sensitive cancer cells can become infected by virus that is released in the neighbourhood by infected cells. (C) Upon the death of infected cells, immunogenic molecules are released that diffuse in the tumour and eventually evaporate. (D) The local concentration of these molecules serves as a signal to induce T-cell-mediated cytotoxicity towards target cells in that area.

Here, we add a cell-specific immune response to the model to assess how virus-induced immunogenic signals regulate this response and influence therapeutic outcomes (Fig. 1A and Supplementary Figure S1). We assume that the death of an infected cancer cell results in the release and diffusion of immunogenic molecules in the tumour (Fig. 1C). These immunogenic molecules activate T-cells to be cytotoxic towards target cells in the model (e.g. infected cancer cells, but other scenarios are also considered), where the level of cytotoxicity is determined by the local concentration of the molecules (Fig. 1D). Incorporating T-cells indirectly in the model, via their cytotoxic effects on various target cells, keeps the model computationally efficient, allowing to investigate a variety of scenarios (with a sufficient number of replicates) on a normal pc.

Average effect of immune response parameters on the outcome of virotherapy

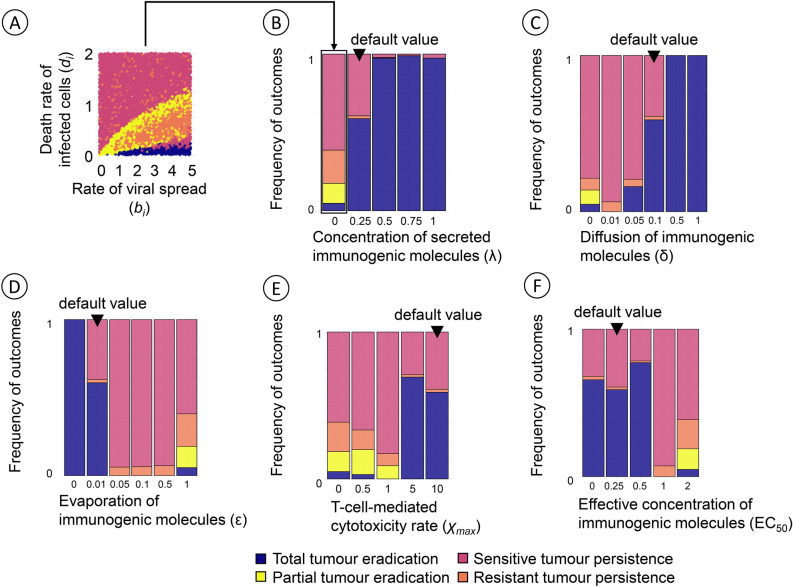
Our model can result in four therapeutic outcomes: (i) total tumour eradication, (ii) partial tumour eradication, (iii) persistence of a virus-susceptible tumour, and (iv) persistence of an infection-resistant tumour. In our previous study²⁹, we investigated how the likelihood of each outcome was affected by the properties of the virus and the various cell types and by operational parameters, such as the onset of virotherapy. Figure 2 shows how these likelihoods are modified by the key immune response parameters of our model: the concentration of immunogenic molecules released upon the death of an infected cancer cell (λ), the diffusion rate (δ) and the evaporation rate (ε) of immunogenic molecules, the maximal level of cytotoxicity (${\chi }_{max}$), and the EC₅₀ value of immunogenic molecules (the concentration of immunogenic molecules at which T-cell-mediated cytotoxicity reaches half its maximal value). For each combination of immune response parameters shown, 10,000 simulations were run, for random combinations of two other key parameters of the model: the rate of viral spread (b_i, ranging from 0 to 5) and the death rate of infected cancer cells (d_i, ranging from 0 to 2). This way, Fig. 2 indicates the effect of each immune response parameter averaged over the birth and death rates of infected cancer cells as highlighted in Fig. 2A. Figure 2 shows that for all immune parameters considered, the most typical therapeutic outcome is either total tumour eradication (blue) or the persistence of an infection-sensitive tumour (red). The other two outcomes are less prominent, as they mainly occur for specific regimes of the parameters b_i and d_i (see Bhatt et al.²⁹ or Fig. 2A). As one might have expected, the likelihood of the most positive outcome (total tumour eradication) increases with the concentration of immunogenic molecules released (Fig. 2B), the diffusion rate of these molecules (Fig. 2C), and the level of cytotoxicity induced by a given concentration of these molecules (Fig. 2E). The likelihood of total tumour eradication decreases with the evaporation rate of immunogenic molecules (Fig. 2D) and the concentration required for an effective immune response (Fig. 2F). Although the direction of these effects is not surprising, the strength of the effect is remarkable. For example, a slight increase in the evaporation rate of immunogenic molecules can shift the likelihood of total tumour eradication from above 50% to almost zero (Fig. 2D).

Fig. 2.

Average effect of the immune response parameters on the therapeutic outcome. Each panel shows how the likelihood of the four outcomes of oncolytic virotherapy is affected by one of the immune response parameters, keeping the other four parameters at their default values. In all cases, the immune response is considered to be non-specific, that is, both infected and uninfected cancer cells are potential targets of T-cell-mediated cytotoxicity. (A) Therapeutic outcome in the absence of immune effects for 10,000 simulations with varying rate of viral spread (b_i, ranging from 0 to 5) and death rate of infected cancer cells (d_i, ranging from 0 to 2). The arrow from (A) to (B) points to the corresponding frequency distribution of the 10,000 simulation outcomes, illustrating the ‘average’ outcome of virotherapy in the absence of immune effects. The frequency distributions of therapeutic outcomes in panels (B) to (F) are obtained in the same way, but now including immune effects for different values of the five immune parameters in our model. (B) The likelihood of total tumour eradication increases with the concentration λ of immunogenic molecules released upon the death of an infected cancer cell (default value: $\lambda =0.25$). The special case $\lambda =0$ corresponds to the absence of an immune response. (C) The likelihood of total tumour eradication increases with the diffusion rate δ of immunogenic molecules (default value: $\delta =0.1$). (D) The likelihood of total tumour eradication decreases with the evaporation rate ε of immunogenic molecules (default value: $\epsilon =0.01$). (E) The likelihood of total tumour eradication is small for low values of the maximal level of cytotoxicity ${\chi }_{max}$ (the maximal death rate imposed by T-cells) but relatively large once ${\chi }_{max}$ increases beyond a threshold value (default value: ${\chi }_{max}=10$). (F) The likelihood of total tumour eradication is relatively high for small values of EC₅₀ (the concentration of immunogenic molecules at which T-cell-mediated cytotoxicity reaches half its maximal value) but rapidly drops to zero in case of larger EC₅₀ values (default value: ${\text{EC}}_{50}=0.25$). The simulations employ systemic virotherapy introduction, where the virus infection occurs throughout the tumour mass.

Effect of infection site on the virotherapy outcomes

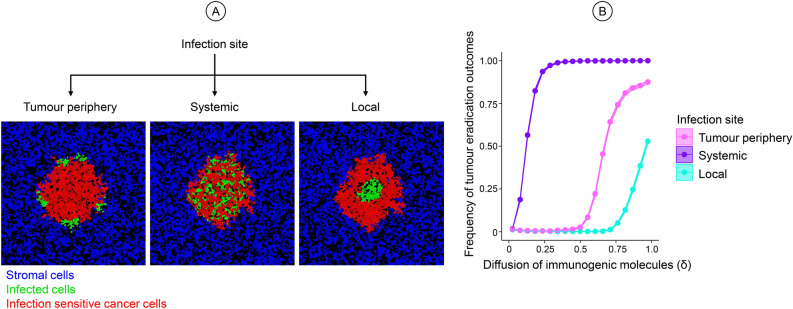
The simulations in Fig. 2 all considered systemic virotherapy, where the virus infection occurs throughout the tumour mass. In our previous study, when no immune response was involved, the therapeutic outcome did not depend on whether the virus infection was initiated locally in the centre of the tumour, at the periphery of the tumour, or systemically throughout the tumour (as illustrated in Fig. 3A). In the presence of virotherapy-induced immune responses, this is no longer the case. This is illustrated in Fig. 3B, which shows for a range or diffusion rates of immunogenic molecules (δ) how the likelihood of tumour eradication depends on the initiation of viral infection. As expected, the likelihood of tumour eradication increases with the diffusion rate. However, large diffusion rates (δ > 0.5) are required to achieve tumour eradication if the viral infection is initiated locally or at the tumour periphery. Considering that empirically estimated diffusion rates are relatively low (see Table 1), systemic viral infection in the tumour has a considerably more positive effect on the therapeutic outcome than the other methods of infection initiation. We suspect that the more localised methods of virus delivery can trigger excessive immune activity around the infection site, preventing the virus from reaching other areas of the tumour, thus hindering viral spread and reducing therapeutic efficacy. Hence, in the case of localised virus delivery, very high viral diffusion rates are required to overcome this impediment of the viral infection by the immune system. For the rest of the study, we therefore focus on the systemic delivery of the virus.

Fig. 3.

Effect of the initiation of viral infection on therapeutic outcomes. (A) Illustration of three different modes of viral infection at the tumour periphery, systemically throughout the tumour, or locally at the centre of the tumour mass. Healthy stromal cells (blue), infection-sensitive cancer cells (red), and virus-infected cancer cells (green) present in the model at the time of initiation. (B) Effect of the diffusion rate δ of immunogenic molecules on the likelihood of tumour eradication for different modes of initiating viral infection. All parameters were kept at default value except the diffusion rate (δ, ranging from 0 to 1), the rate of viral spread (b_i, ranging from 0 to 5) and the death rate of infected cancer cells (d_i, ranging from 0 to 2). 100,000 combinations were run for varying values of For each value of δ, 1000 combinations of b_i and d_i were chosen at random, and 100 replicate simulations were run per combination. Coloured lines indicate the mean value of the simulation outcomes, and coloured envelopes indicate the 95% confidence band. Mean and confidence intervals were obtained via nonparametric bootstrapping. The coloured envelopes are difficult to see due to the minimal variation in the data.

Table 1.

Parameters related to virus-induced immunogenic signals and T-cell-mediated cytotoxicity, their default values, and the range of values investigated in the simulations.

Parameter	Interpretation	Default value	Evaluated range	Reference of empirical evidence	Empirical translation
λ	Concentration of immunogenic molecules released by an infected cell upon death	0.25	0–1	Concentration ranges from 1–100 pg/ml in body fluids60, and 600 pg/ml in culture61	The λ-values from 0–1 correspond to 0–100 pg/ml
ε	Evaporation rate: fraction of molecules that disappear due to evaporation or breakdown per time interval dt	0.01	0–0.1	Half-lives of immunogenic molecules: 0.5 to 2 h for cytokines60 and 2–4 h for BiTEs/antibodies62	An ε-value of 0.01 translates to a half-life of 16 h, and a value of 0.1 translates to a half-life of 1.5 h
δ	Diffusion rate: fraction of molecules that disperse to neighbouring grid cells per time interval dt	0.1	0–0.1	Diffusion coefficient for immunogenic molecules: 600–6000 μm2/minute63–65. Tumour cells: 15–20 μm2, immune cells 8–10 μm2	600 μm2/minute translates to 30 cells per minute. In our model cells disperse 20 μm2 per 14 min
χmax	Maximum cytotoxicity (T-cell-mediated death rate of cancer cells or other target cells of the immune system)	10	0–10	11 killed target cancer cells/day by one T-cell56 and 2–16 infected cells/day by one T-cell66	A death rate of 10 corresponds to an average of 10 cells killed per day
EC50	The concentration of immunogenic molecules at which cytotoxicity reaches 50% of χmax	0.25	0–2	The EC50 value of immunogenic molecules can range from 10–3 to 103 pM for effective functions63,67	EC50 = 0.25 translates to 25 pg/ml (see λ). For an atomic mass of 14 kDa (typical for cytokines), this translates to 10–2 pM
ν	Strength of the inhibitory effect of tumour density on cytotoxicity	0	0–5	NA	NA

All other model parameters and their default values can be found in Table 1 in Bhatt et al.²⁹.

Three scenarios for the effect of immune responses on the outcome of virotherapy

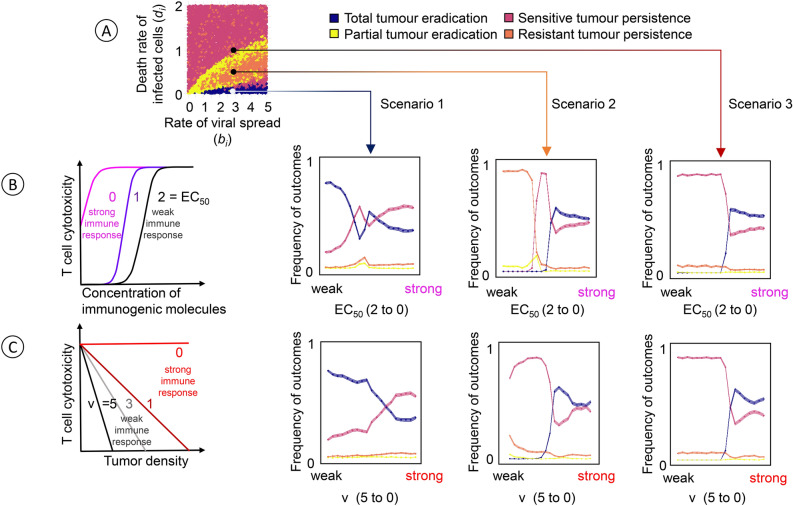
Figure 2 gives an impression of the “typical” effects of T-cell-mediated cytotoxicity on the outcome of virotherapy. To this end, each data point summarises the effects for a range of values of the parameters b_i (rate of viral spread) and d_i (death rate of virus-infected cancer cells). In Fig. 4, we zoom in and consider three specific combinations of b_i and d_i that, in the absence of an immune response, tend to lead to different therapeutic outcomes (Fig. 4A): total tumour eradication by virotherapy alone in Scenario 1, persistence of an infection-resistant tumour in Scenario 2, and persistence of an infection-sensitive tumour in Scenario 3. To these scenarios, we added an immune response. The level of T-cell-mediated cytotoxicity was systematically changed from low to high by decreasing two immune response parameters of our model (EC₅₀ in Fig. 4B; ν in Fig. 4C). As a result, the immune response is changed from ‘weak’ to ‘strong’ in the graphs of Fig. 4B and 4C. One would expect that a stronger immune response leads to a more favourable therapeutic outcome.

Fig. 4.

Effect of immune response parameters on the therapeutic outcome in three scenarios. (A) In the absence of immune responses, the likelihood of the four therapeutic outcomes depends on the rate of viral spread (b_i) and the death rate of virus-infected cancer cells (d_i). The effects of an added immune response are explored for three scenarios with an intermediate birth rate $b_i=3$ and a low, moderate, and high death rate, which in the absence of immune responses tend to result in total tumour eradication (scenario 1, $d_i=0.1$), the persistence of a resistant tumour (scenario 2, $d_i=0.5$), and the persistence of a sensitive tumour (scenario 3, $d_i=1$), respectively. For each scenario, we assessed the effect of anticancer T-cell-mediated cytotoxicity on the therapeutic outcome by systematically changing two immune response parameters. (B) Effect of the EC₅₀ value, the concentration of immunogenic molecules at which T-cell-mediated cytotoxicity reaches half its maximal value. Large EC₅₀ values indicate a ‘weak’ immune response in the sense that a high concentration of immunogenic molecules is required to trigger the response. (C) Effect of the model parameter ν, which quantifies the negative effect of local tumour density on the effectiveness of the immune response. A larger value of ν indicates a stronger inhibition of the immune response by a high density of tumour cells and, hence, a ‘weaker’ immune response. Each of the six graphs in (B) and (C) represents 100,000 simulations, where all model parameters were kept at their default values except the ones under investigation. For the parameter under investigation, 1000 combinations of b_i and d_i were chosen at random, and 100 replicate simulations were run per combination. Coloured lines indicate the mean value, and coloured envelopes indicate the 95% confidence band. Mean and confidence intervals were obtained via nonparametric bootstrapping.

The graphs for Scenario 1 show that this is not necessarily the case. In this scenario, the likelihood of total tumour eradication (blue curve) is high in the case of a weak immune response, but it drops with the strength of the immune response. In the case of a strong immune response, the likelihood of tumour eradication is even lower than the likelihood of persistence of an infection-sensitive tumour (red curve). The opposite happens in Scenario 3. Here, the likelihood of tumour persistence is almost one in the case of a weak immune response, while it is exceeded by the likelihood of tumour eradication in the case of a strong immune response. Interestingly, the transition between the two outcomes occurs quite abruptly: for both model parameters (EC₅₀ in Fig. 4B; ν in Fig. 4C), the likelihood of tumour eradication is close to zero if the parameter is above a certain threshold, while this likelihood ‘jumps’ to a value above 50% as soon as the parameter drops below the threshold. Regarding tumour eradication, Scenario 2 is very comparable to Scenario 3: the likelihood of eradication is close to zero in the case of a weak immune response (i.e. if the model parameter considered is above a threshold value), and it switches to a value slightly above 0.5 in the case of a strong immune response. Scenario 2 differs from Scenario 3 in what happens in the case of a weak immune response (no tumour eradication). This is best visible in the graph for model parameter EC₅₀ (Fig. 4B): if this parameter is close to 2, the most likely therapeutic outcome is the persistence of an infection-resistant tumour; while the most likely outcome is the persistence of an infection-sensitive tumour for a small range of EC₅₀ values around 1.0. For model parameter ν (Fig. 4C), the overall pattern is similar, but for the range of ν-values considered, we did not observe situations where the persistence of an infection-resistant tumour is the most likely outcome. This, however, happens if ν is increased beyond the value of 5 (not shown).

Interestingly, the effect of a parameter change is not necessarily monotonic. This can be seen in Scenario 1 where a decrease of EC₅₀ from 2 to 0 (Fig. 4B), the likelihood of tumour eradication (blue curve) first drops rapidly, then increases rapidly, and subsequently decreases gradually.

A detailed view on immune response effects

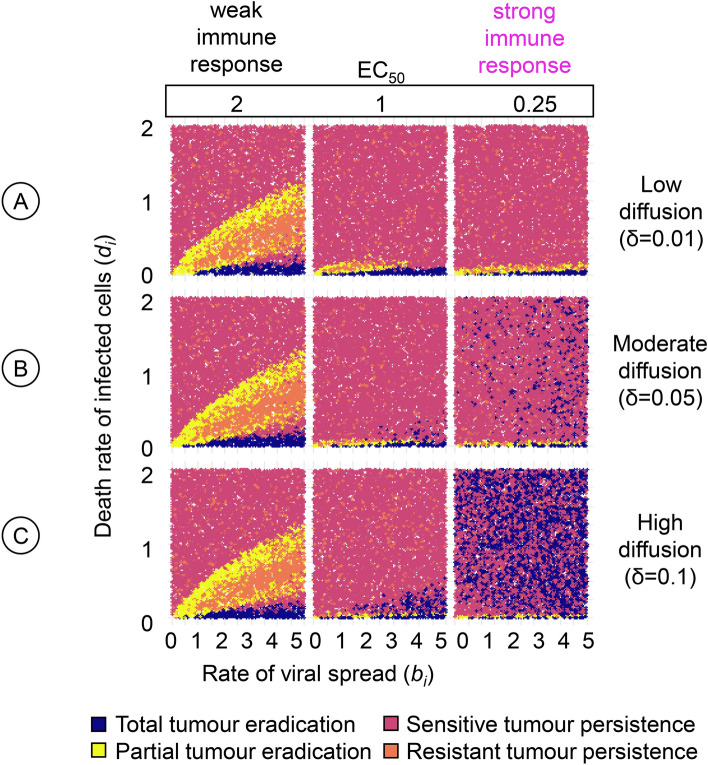
Figure 5 provides a more detailed view of immune effects on the outcome of virotherapy. Keeping all other immune-related parameters at their default values, the figure considers three values of EC₅₀, the concentration of immunogenic molecules at which T-cell-mediated cytotoxicity reaches half its maximal value, and three values of the diffusion rate δ of immunogenic molecules. For each of the nine parameter combinations, many simulations were conducted to get an overview of how the therapeutic outcome depends on the rate of viral spread (b_i) and the death rate of virus-infected cancer cells (d_i).

Fig. 5.

Detailed view of the effect of two immune parameters on the therapeutic outcome. For a range of values of the rate of viral spread (b_i) and the death rate of virus-infected cancer cells (d_i) the panels show how the outcome of oncolytic virotherapy is affected by two immune parameters: the effective concentration of immunogenic molecules (EC₅₀) and the diffusion rate (δ) of these molecules. For three diffusion rates, (A) low ($\delta =0.01$), (B) moderate ($\delta =0.05$), and (C) high ($\delta =0.1$), we assessed the effect of three EC₅₀ values, corresponding to a weak (${\text{EC}}_{50}=2$), moderate (${\text{EC}}_{50}=1$), and strong (${\text{EC}}_{50}=0.25$) immune response on therapeutic outcomes. The upper left graph resembles Fig. 2A, which depicts the corresponding graph in the absence of an immune response. For each graph in the figure, 10,000 simulations were run for parameter combinations (b_i, d_i) chosen randomly within the specified range. Each simulation is represented by a point, the colour of which indicates the therapeutic outcome. All model parameters were kept at their default values except the ones under investigation.

The three left-most graphs of Fig. 5 correspond to a high value of EC₅₀, indicating a ‘weak’ immune response (because high concentrations of immunogenic molecules are required to trigger T-cell-mediated cytotoxicity). Irrespective of the diffusion rate, the same pattern results that is characteristic of the outcome of virotherapy in the absence of an immune response (see Bhatt et al.²⁹, and Fig. 4A): the tumour tends to be eradicated (blue dots) for a wedge of parameter combinations that have in common that the death rate d_i of infected cancer cells is very low; an infection-sensitive tumour tends to persist (red dots) when d_i is very high; and the two other outcomes (yellow dots: partial tumour eradication; orange dots: persistence of an infection-resistant tumour) tend to be found for a wedge of parameter combinations for which d_i takes on intermediate values. Interestingly, a somewhat stronger immune response (middle panels, ${\text{EC}}_{50}=1$) does not lead to a more favourable therapeutic outcome. In comparison to an absent (Fig. 4A) or a weak (${\text{EC}}_{50}=2$) immune response, fewer combinations of b_i and d_i lead to total (blue) or partial (yellow) tumour eradication, while most combinations lead to the persistence of an infection-sensitive tumour. On the positive side, therapy rarely leads to the persistence of a tumour that is resistant to virotherapy (orange). Tumour eradication is only boosted if T-cell-mediated cytotoxicity does not require a high concentration of immunogenic molecules (${\text{EC}}_{50}=0.25$) and the diffusion rate of these molecules is high (Fig. 5C) or at least moderate (Fig. 5B). Under these conditions, the tumour can be eradicated even for high values of d_i. However, one needs to keep in mind that the therapeutic outcome is probabilistic and that even under these favourable immune conditions tumour eradication has a similar likelihood as the persistence of an infection-sensitive tumour.

Effect of time of therapeutic intervention

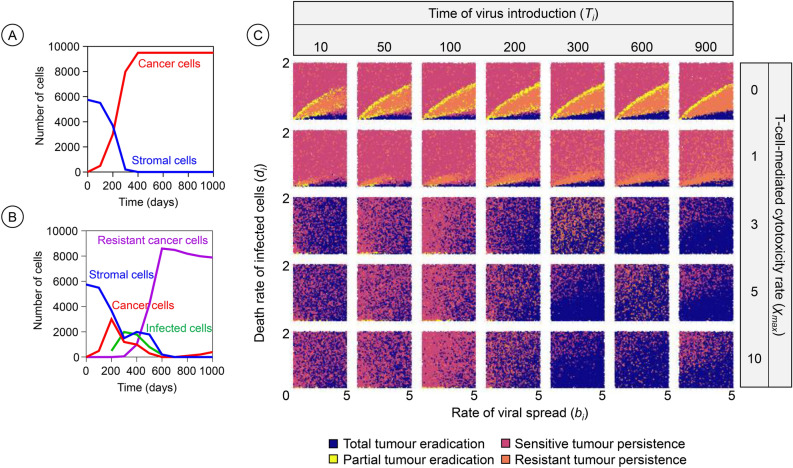
Figure 6 depicts how the therapeutic outcome depends on the time of virus introduction in the tumour. To understand the timing effects, it is helpful to consider the time change in the tumour composition in the absence of virotherapy (Fig. 6A) and the case of early-starting therapy (Fig. 6B). Figure 6C shows the pattern of therapeutic outcomes when the virus is introduced at an early or later time (time of virus introduction, T_i, organised in columns) for scenarios with different levels of anti-cancer T-cell-mediated cytotoxicity (${\chi }_{max}$ organised in rows). At early virus introduction times (T_i = 10 and 50), the tumour is small. As a result, total tumour eradication is frequent for a moderate level of T-cell-mediated cytotoxicity (${\chi }_{max}$ = 3 or 5), particularly at higher viral spread rates. Moderate T-cell-mediated cytotoxicity synergises well with virotherapy at this stage, allowing the virus to effectively spread and kill cancer cells. However, at very low (${\chi }_{max}$ = 1) or high levels of T-cell-mediated cytotoxicity (${\chi }_{max}$ = 10), total eradication is less frequent. In cases of low T-cell-mediated cytotoxicity, virotherapy alone does not eliminate the tumour, especially when the rate of viral spread is low (b_i) and the rate of infected cell death is high (d_i). Conversely, when T-cell-mediated cytotoxicity is too strong, the number of cancer cells available for viral infection is quickly reduced by anticancer T-cell-mediated killing, limiting virus spread and reducing the chance of tumour eradication. If the virus is introduced at later time points of tumour development (T_i = 100 to 300), the number of cancer cells has grown, but stromal cells, which initially act as physical barriers to viral spread, begin to decrease. The depletion of stromal cells creates a more favourable environment for viral spread and also leads to tumour eradication outcomes, particularly at moderate to high ${\chi }_{max}$ values (e.g., > 3). As the tumour progresses, however, the emergence of resistant cancer cells, particularly after time 200, begins to influence therapeutic outcomes. Resistant cancer cells impede viral spread, leading to a higher likelihood of tumour persistence or partial eradication. At time points later than 300, the tumour consists predominantly of cancer cells, of which some are resistant, and the stromal cells have been completely depleted. In these scenarios, the likelihood of total tumour eradication is reduced, particularly at low and moderate ${\chi }_{max}$ values (< 3).

Fig. 6.

Effects of time of virus introduction and T-cell-mediated cytotoxicity on the therapeutic outcome. The frequency of infection-sensitive cancer cells (in red), healthy stromal cells (blue), infected cells (green), and resistant cancer cells (purple) over time is illustrated in the absence (A) and presence (B) of virotherapy (T_i = 200, b_i = 1.2 and d_i = 0.1). (C) For a range of values of the rate of viral spread (b_i) and the death rate of virus-infected cancer cells (d_i) the panels show how the outcome of oncolytic virotherapy is affected by the introduction time of the virus (T_i , organised in columns) and the level of anticancer T-cell-mediated cytotoxicity (${\chi }_{max}$, organised in rows). The graph with T_i = 50 and ${\chi }_{max}$ = 0 corresponds to Fig. 2A, depicting the outcomes in the absence of an immune response. For each graph in the figure, 10,000 simulations were run for parameter combinations (b_i, d_i) chosen randomly within the specified range. Each simulation is represented by a point, the colour of which indicates the therapeutic outcome. All model parameters were kept at their default values except the ones under investigation.

Effects of T-cell specificity

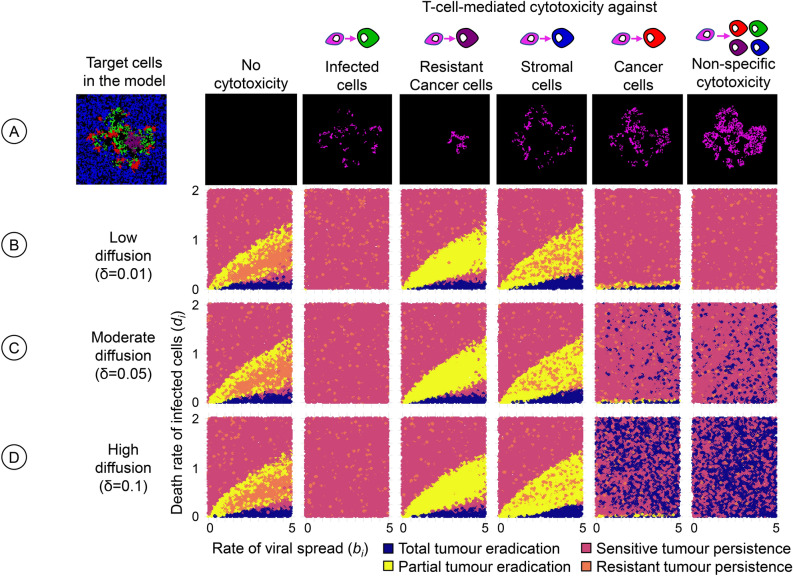
Until now, we assumed that T-cell-mediated cytotoxicity was targeted against infection-sensitive cancer cells. Figure 7 extends the investigation by assessing the therapeutic outcome for six scenarios regarding the specificity of cytotoxicity. The first scenario (no cytotoxicity) corresponds to the absence of an immune response (Bhatt et al.²⁹, and Fig. 4A) and serves as a standard of comparison. The fifth scenario (cytotoxicity targeted against infection-sensitive cancer cells) represents our default assumption and was studied above (Fig. 5, ${\text{EC}}_{50}=0.25$). If cytotoxicity is targeted against infected cells (second scenario), therapy almost always results in the persistence of the tumour. This failure of oncolytic virotherapy is not surprising as the immune system counteracts viral infection. In contrast to the second scenario, the immune response can have a positive effect on the therapeutic outcome (a higher likelihood of total or partial tumour eradication) if it is targeted against infection-resistant cancer cells (third scenario) or against healthy stromal cells (fourth scenario). Targeting stromal cells can be beneficial because these cells can prevent the effective spread of the virus by creating spatial barriers, as observed by us previously²⁹. The same applies when resistant cancer cells are targeted; here, the targeting of resistant cells can prevent the most unfavourable outcome of virotherapy: the persistence of an infection-resistant tumour. In both scenarios, the positive effect of the immune system is restricted to combinations of b_i and d_i where the death rate d_i of virus-infected cancer cells is relatively low. For those combinations of b_i and d_i where, in the absence of an immune response, virotherapy resulted in the persistence of an infection-sensitive tumour (red areas in the graphs of the left column of Fig. 7), the same outcome also resulted in the third and fourth scenario. Our model predicts that an unspecific immune response (sixth scenario) has a similar or even more favourable effect on therapeutic outcomes as a response targeted against infection-resistant cancer cells (fifth scenario). Interestingly, in both scenarios, the therapeutic outcome is typically worse than the outcome in the absence of an immune response (first scenario) if the diffusion rate of immunogenic molecules is low. This suggests that an efficient immune response throughout the tumour, facilitated by high diffusion rates, is crucial for achieving successful treatment outcomes. This was also the case when we simulated scenarios where T-cell-mediated cytotoxicity was directed towards multiple cell types simultaneously (Supplementary Figure S2) or in the setting of a 3D model (Supplementary Figure S3).

Fig. 7.

Effect of T-cell specificity on the therapeutic outcome. For three diffusion rates of immunogenic molecules, the panels show how the outcome of oncolytic virotherapy is affected if the T-cells do not target infection-sensitive cancer cells (the standard scenario) but other cells in the model. (A) The leftmost panel shows a snapshot of the potential target cells: healthy stromal cells (blue), uninfected but infection-sensitive cancer cells (red), infection-resistant cancer cells (purple), and infected cells (green). The other panels show snapshots of the distribution of immunogenic molecules for the six scenarios considered: no cytotoxicity (absence of an immune response), and T-cell-mediated cytotoxicity targeted towards either (from left to right) infected cells, infection-resistant cancer cells, stromal cells, infection-sensitive cancer cells, or all cell types present. The six scenarios were studied for three diffusion rates: (B) low ($\delta =0.01$), (C) moderate ($\delta =0.05$), and (D) high ($\delta =0.1$). For each graph in the figure, 10,000 simulations were run for parameter combinations (b_i, d_i) chosen randomly within the specified range. Each simulation is represented by a point, the colour of which indicates the therapeutic outcome. All model parameters were kept at their default values except the ones under investigation.

Discussion

In this study, we investigated the dynamics of immune responses during oncolytic virotherapy using a spatially explicit computational modelling approach. We assessed how the mode of viral delivery and the timing of virotherapy influence therapeutic outcomes, alongside exploring the effects of immunogenic molecules, target-specific immune responses, and tumour density-dependent immune inhibition. Our simulations show that for a wide range of scenarios, immune responses can aid oncolytic viruses in total tumour eradication, but only when two conditions are met: the immune response has to be cancer-specific and immunogenic molecules have to be effective and spread fast. Alternatively, strong antiviral immune responses and weak anticancer immune responses due to tumour-density effects limit the therapeutic efficacy of oncolytic viruses. Overall, our findings highlight the importance of carefully considering spatial tumour growth, viral infection dynamics, and the properties of the virus-induced immune response in the rational design of oncolytic viruses.

Various experimental and computational studies have noted the disadvantages of eliciting antiviral immune responses as they act against the tumour-killing potential of virotherapy^17–26. In our model, we replicate these findings and explain why this happens. When T-cell-mediated cytotoxicity is directed towards only infected cells, we find that even a weak cytotoxic activity leads to a rapid clearance of infected cells thus resulting in a limited spread of oncolytic viruses (Fig. 7). The elimination of infected cells reduces the persistence of the virus in the tumour and undermines favourable therapeutic outcomes. Interestingly, under some conditions, immune responses can be beneficial for the therapeutic outcome even if they are directed against infected cells. For instance, when T-cell-mediated cytotoxicity is directed towards cancer cells in addition to infected cells it leads to an increase in the likelihood of total tumour eradication (Supplementary Figure S2). However, this is only possible when immunogenic molecules diffuse at a fast rate in the tumour.

The activation of anticancer immune responses has been generally considered to be a positive factor for total tumour eradication^2,38. However, we show that T-cell-mediated cytotoxicity towards cancer cells may also lead to poor therapeutic outcomes by limiting virus spread in the tumour. We find that when T-cell-mediated cytotoxicity is directed towards infection-susceptible cancer cells surrounding infected cells, it eliminates potential target cells that could enable efficient virus spread in the tumour. The spatial barriers resulting from anticancer T-cell-mediated cytotoxicity lead to poor persistence of the virus in the tumour and thus undermine favourable therapeutic outcomes. This effect is observed to be significant for oncolytic viruses spreading at a rapid rate and infected cells dying at a slow rate (Fig. 4, scenario 1), or when infection is locally instead of systemic. Low diffusion rates of immunogenic molecules lead to similar effects, keeping the T-cell response restricted to the neighbourhood of infected cells, thereby again creating spatial barriers to local viral spread. When virotherapy alone is sufficient to eradicate cancer, T-cell killing of cancer cells may limit the spread of virus in the tumour and eventually lead to the persistence of a virus-free tumour. Thus, our model identifies potential confounding factors that could help explain therapeutic outcomes where a tumour can persist despite the activation of anticancer T-cells by oncolytic virotherapy.

Oncolytic virotherapy outcomes may depend significantly on the timing of virus introduction and the evolving tumour composition over time (Fig. 6). In practice, patients are often only considered for virotherapy after conventional therapies have failed; accordingly, the cancers of these patients have already progressed. One might think that an earlier start of virotherapy is always better, but our findings reveal that the timing effects are more nuanced. For patients with smaller tumour burdens, early intervention can indeed be advantageous. However, in later stages, when stromal cells have depleted and resistant cancer cells emerge, a later start of virotherapy may actually be more effective, depending on the level of T-cell-mediated cytotoxicity. Too strong a T-cell response can prematurely eliminate infected cancer cells, limiting viral spread. These findings thus suggest that the effect of virotherapy timing is non-monotonous; as outcomes do not consistently improve or worsen with earlier or later virus introduction but rather depend on the tumour composition and immune response at the time of therapy. Given these insights, careful consideration of the timing of virotherapy in relation to tumour stage, the presence of resistant cells, and the patient’s immune profile may help optimise strategies towards tumour eradication.

Optimal delivery strategies are being explored to improve the synergy between virotherapy and immune responses. While the finding that systemic viral infection leads to better therapeutic outcomes than localised methods is expected, our model offers novel mechanistic insights. It shows that systemic delivery reduces the concentration of T-cell-mediated cytotoxicity at infection sites, which in turn allows the virus to spread more effectively across the tumour. In contrast, localised infection triggers excessive immune responses around the injection site, limiting viral spread. To compensate for this, increasing the diffusion rates of virus-induced immunogenic signals to non-physiological levels helps spread immune activation across the tumour, improving the likelihood of tumour eradication by enhancing viral reach and immune response. This increased diffusion helps overcome spatial barriers and allows immune cells to reach and target cancer cells that lie beyond the immediate vicinity of the infection site.

The inclusion of spatial considerations in our model extends the existing work on modelling immune responses or T-cell responses to oncolytic viruses^17–26,30. Spatial modelling allows for the ability to capture the complex dynamics of oncolytic virotherapy within the tumour microenvironment. In particular, the diffusion of immunogenic molecules plays a key role in controlling the impact of T-cell-mediated cytotoxicity and, thus, affects the overall therapeutic results. High diffusion rates facilitate the extensive spread of immunogenic molecules, ensuring widespread T-cell activation and enhancing therapeutic efficacy. However, it is crucial to strike a balance, as too much diffusion, in combination with a high EC₅₀, can lead to a rapid spread of immunogenic molecules with suboptimal effects (Fig. 5). Conversely, low diffusion restricts the reach of these molecules, leading to localized T-cell activation and potential impairment of the immune response. Likewise, it is crucial to consider the diffusion rate along with the evaporation rate of immunogenic molecules, as they determine, respectively, the spatial and temporal activation of immune responses in the tumour. This observation aligns with the finding of Centofanti and colleagues that immune-mediated tumour cell clearance is spatially regulated due to the diffusion-consumption dynamics of immunogenic molecules within the tumour tissue³⁹.

Tumour density mediated regulation of immune responses has been noted as an important factor that restricts tumour eradication^40–43. However, we observe that this is not always the case. When tumour density strongly inhibits T-cell-mediated cytotoxicity towards cancer cells, we find that there is an increase in the likelihood of total tumour eradication when the oncolytic virus spreads at a faster rate and infected cells die at a slow rate (Fig. 4, scenario 1). In this case, the anticancer T-cell-mediated cytotoxicity does not limit the viral spread by targeting neighbouring infection-susceptible cells and allows efficient elimination of the tumour. Tumour density mediated suppression of T-cell-mediated cytotoxicity leads to a decrease in the likelihood of total tumour eradication only when the virus alone is unable to eliminate the tumour and requires strong activation of immune responses (Fig. 4, scenarios 2 and 3). Experimental observations so far have revealed that T-cell activity reduces with increasing tumour density due to a hypoxic microenvironment, high expression of immunosuppressive molecules and low nutrient availability^41,44–46. Therefore, for factors such as hypoxia and low nutrient availability, which also influence the properties of the virus, the activation of immune responses may prove to be critical to achieving favourable therapeutic outcomes⁴³.

The properties of the immunogenic molecules released by infected cells have a strong impact on regulating the immune responses and thereby the therapeutic outcomes. For instance, our results demonstrate that the value of the effective concentration of immunogenic molecules required to induce T-cell-mediated cytotoxicity, EC₅₀, determines if T-cell responses favour oncolytic virotherapy or not. We find that highly effective immunogenic molecules, with a low EC₅₀ value, are necessary when virotherapy alone does not yield total tumour eradication. This observation has been made numerously, where high affinity immunostimulatory molecules like cytokines or checkpoint inhibitors can improve the cytotoxicity of anticancer T-cells within the tumour, thereby improving tumour eradication^47,48. Considering the EC₅₀ of immunogenic molecules with the diffusion and evaporation rates, our findings suggest a spectrum of optimal attributes that immunogenic molecules should exhibit to effectively facilitate complete tumour eradication following virotherapy.

Knowledge about the optimal attributes of immunogenic molecules can be especially important when engineering oncolytic viruses to encode immune-stimulatory genes like cytokines, chemokines, or T-cell engager proteins. T-cell engager proteins, exemplified by Bispecific T-cell engagers (BiTEs), possess dual binding domains: one attaches to a T-cell receptor, while the other targets a cancer cell antigen. This interaction brings T-cells into direct contact with cancer cells, activating T-cells to effectively eliminate the cancer cells^49,50. Considering T-cell engager proteins as the immunogenic molecules released by infected cells⁵¹, our model provides two recommendations for improving the design of these molecules. Firstly, the effectiveness of BiTEs could be improved by restricting the specificity of the binding antigen, to avoid targeting infected cells, which we have found would greatly impair the effectiveness of the treatment. Secondly, the effectiveness of BiTEs could be improved by increasing diffusion across cells and reducing the breakdown over time of BiTEs. The breakdown of BiTEs can be improved by directed evolution and screening of BiTEs resistant to enzymatic or physiological degradation, whereas the diffusion of BiTEs can be improved by engineering smaller and low molecular weight BiTEs or by reducing the extracellular matrix density through enzymatic activity mediated by infected cells^50,52–55.

In conclusion, our study provides a deeper understanding of virotherapy-induced immunogenic signals in shaping immune responses within tumours and influencing therapeutic outcomes. We reveal the critical role of optimal immunogenic molecule diffusion in regulating T-cell-mediated cytotoxicity and identify scenarios where anticancer immune responses may paradoxically hinder therapeutic efficacy. Our findings offer practical guidance for the rational design, time of therapy, and mode of delivery of oncolytic viruses, suggesting avenues for optimising their immunogenic potential to improve therapeutic outcomes. Future research should expand upon our findings by explicitly incorporating individual T-cells and immune cells directly into our model. Exploring factors such as immune cell migration, tumour infiltration, and communication between antigen-presenting cells and T-cells could further elucidate clinical observations.

Model description

To assess the effect of immune responses on the outcome of oncolytic virotherapy, we added T-cell-mediated cytotoxicity to the model of Bhatt et al.²⁹. A flow chart of the model can be found in Supplementary Figure S1.

Brief overview of the model of Bhatt et al.²⁹

The model of Bhatt et al. (2022) considers the growth of cancer and stromal cells and the dynamics of a viral infection on a spatial grid, using an event-based time structure. The spatial grid consists of ‘grid cells’ that can either be empty or harbour cancer or stromal cells. The grid is bounded, such that cells on the boundary have fewer neighbours. Simulations were run on a 2D Voronoi grid (see Supplementary Figure S3 for 3D simulations). The model assumes that stromal and cancer cells can divide (produce a daughter that is placed into an empty neighbouring grid cell, provided that such a grid cell exists) and that cancer cells can become infected by an oncolytic virus, which is programmed to preferentially target and kill cancer cells while sparing stromal cells. By means of rare mutations, cancer cells can acquire resistance against the oncolytic virus. Hence, the model considers four different cell types: healthy stromal cells, uninfected but infection-sensitive cancer cells, infection-resistant cancer cells, and infected cancer cells. All these cells can die; and the death rate may depend on the type of cell. In the simulations reported here, all cell-type specific parameters are at their default values (Table 1 in Bhatt et al. 2022)²⁹, with the exception of the rate of viral spread (b_i) and the death rate of infected cells (d_i), which are varied as indicated in the figure legends.

In this model, each simulation results in one of the following four outcomes: complete eradication of the tumour, partial eradication of the tumour, persistence of an infection-sensitive tumour, and persistence of an infection-resistant tumour. Due to the stochasticity of all processes in the model, alternative therapeutic outcomes can occur for the same parameter settings. It is therefore important to run multiple replicate simulations for each parameter combination to get a good overview (like Fig. 2A) on how the likelihood of the various outcomes depends on the model parameters.

The model is initialised by first allowing stromal cells to cover the entire grid by naturally growing over the grid. Once a natural cover has been established, tumour cells are introduced in the centre of the grid and are allowed to grow for T_i timesteps, after which 10% of all tumour cells are infected with the oncolytic virus. We explore three different modes of infection in the model: (1) systemic infection, where the virus infects all tumour cells equally; here, 10% of all tumour cells are selected randomly for infection. (2) Local infection, where infection occurs at the centre of the tumour, and (3) Periphery infection, where only cells located on the outside of the tumour are infected. In the default set-up, the virus is introduced systemically.

Adding T cell mediated cytotoxicity to the model

We adopt an indirect approach to incorporate T-cell-mediated cytotoxicity in the model. Instead of explicitly simulating the dynamics of individual T-cells, we assume that the death of an infected cancer cell results in the release and diffusion of immunogenic molecules in the tumour. These immunogenic molecules serve as a proxy for T-cell activity, such that higher local concentrations of these molecules increase the degree of T-cell-mediated cytotoxicity, resulting in higher cell death rates. By default, we assume that cytotoxicity is targeted against uninfected-cancer cells, but other options are also considered (e.g., in Fig. 7).

To be more precise, we assume that immunogenic molecules are absent at the start of a simulation. Whenever an infected cancer cell dies, the concentration of immunogenic molecules in the corresponding grid cell is increased by λ. The immunogenic molecules do not stay indefinitely in the grid cell, but rather disperse to neighbouring grid cells following diffusion dynamics or slowly disappear due to evaporation. Diffusion is modelled by allowing a fraction δ of the local immunogenic molecules to ‘disperse away’ to the neighbouring cells at fixed time intervals dt (default value dt = 0.01 days), while at the same time new molecules are gained via dispersal from the neighbouring cells. Thus, diffusion follows similar dynamics as thermal diffusion models, using the diffusion coefficient of water. If $\eta (t)$ is the concentration of these molecules in a focal grid cell at time t and ${\eta }_j(t)$ is the concentration in the n neighbouring cells $j=1,\dots ,n$ at this time, then the concentration in the focal cell changes as follows:

$$\eta (t+dt)=(1-\delta )·\eta (t)+\delta ·\sum _j{\eta }_j(t)\left./\phantom{{\eta }_j(t)n_j}\right)n_j,$$

where $n_j$ is the number of grid cells neighbouring grid cell j. After diffusion has taken place in the whole grid, the concentration of immunogenic molecules in each grid cell is reduced due to evaporation by removing a fraction ε of these molecules (by multiplying their density by a factor 1-ε). Evaporation here combines all processes that lead to removal of the molecules, including breakdown due to cellular consumption, radiation and other processes. Concentrations below 10^–5 are set to zero.

Cytotoxicity is included in the model by increasing the mortality of the target cells by an amount $\chi (\eta ),$ which is dependent on the local concentration η of the immunogenic molecules. As a default, we assume that $\chi (\eta )$ is given by the logistic function:

$$\chi (\eta )={\chi }_{max}\left./\phantom{{\chi }_{max}(1+exp(E{C}_{50}-\eta ))}\right)(1+exp(E{C}_{50}-\eta )).$$

In other words, T-cell induced mortality increases with η in an S-shaped manner, asymptotically approaching the maximal value ${\chi }_{max}$. These assumptions are motivated by the fact that T-cells are activated in a dose-dependent manner upon stimulation with immunogenic signals such as cognate antigens, T-cell engager molecules or cytokines^56–59. The parameter ${\text{EC}}_{50}$ corresponds to that concentration η at which the T-cell-mediated cytotoxicity reaches 50% of its maximal value: $\chi ({\text{EC}}_{50})=\frac{1}{2}{\chi }_{max}$. Therefore, ${\text{EC}}_{50}$ may be viewed as the ‘effective’ concentration of immunogenic molecules, that is, the concentration required to launch an effective immune response. If ${\text{EC}}_{50}$ is small, the immune system responds to the immunogenic molecules in a highly sensitive manner; if ${\text{EC}}_{50}$ is large, an effective immune response requires a large accumulation of immunogenic molecules.

The model also includes the option that cancer cells that are located at the periphery of the tumour experience a higher T-cell-mediated mortality than cancer cells located more centrally in the tumour. The reason is that more centrally located target cells are more difficult to reach by the immune system. To model this, we expanded the expression of $\chi (\eta )$ by a density dependent term:

$$\chi (\eta ,\mathrm{\Phi })=(1-\nu \mathrm{\Phi })·{\chi }_{max}\left./\phantom{(1-\nu \mathrm{\Phi })·{\chi }_{max}(1+exp(E{C}_{50}-\eta ))}\right)(1+exp(E{C}_{50}-\eta )).$$

Here, Φ denotes the relative density of cancer cells in the neighbourhood (the fraction of neighbouring grid cells occupied by cancer cells) while ν indicates the strength of the density effect. As default, we chose $\nu =0$, corresponding to the absence of a density effect.

Author contributions

DKB, TJ, TD and FJW were involved in the conceptualisation of the study and development of the model. DKB performed the computational simulations and analysed the data. DKB, TJ, TD, and FJW interpreted the results and wrote the manuscript.

Funding

The work of FJW was supported by the European Research Council (ERC Advanced Grant No. 789240). DKB received a PhD scholarship from the Abel Tasman Talent Program (Graduate School of Medical Sciences, University of Groningen). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Data availability

The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.

Code availability

We have provided two different versions of the model compatible with all common operating systems: (1) a terminal-only version that can be used to perform demanding simulations on a high-performance computation cluster by submitting a configuration file with the required parameters and (2) an intuitive graphical user interface to visually observe the spatial interplay of the virus-cancer-immune dynamics. The code used for this work and an executable version of the Oncolytic Virus Immune simulator (OVI) can be found at www.github.com/rugtres/ovi.

Declarations

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-80542-8.