Abstract
Solar heating of the upper ocean is a primary energy input to the ocean‐atmosphere system, and the vertical heating profile is modified by the concentration of phytoplankton in the water, with consequences for sea surface temperature and upper ocean dynamics. Despite the development of increasingly complex modeling approaches for radiative transfer in the atmosphere and upper ocean, the simple parameterizations of radiant heating used in most ocean models can be significantly improved in cases of near‐surface stratification. There remains a need for a parameterization that is accurate in the upper meters and contains an explicitly spectral dependence on the concentration of biogenic material, while maintaining the computational simplicity of the parameterizations currently in use. Here, we assemble observationally‐validated physical modeling tools for the key controls on ocean radiant heating, and simplify them into a parameterization that fulfills this need. We then use observations from 64 spectroradiometer depth casts across 6 cruises in diverse water bodies, 13 surface hyperspectral radiometer deployments, and broadband albedo from 2 UAV flights to probe the accuracy and uncertainty associated with the new parameterization. A novel case study using the parameterization demonstrates the impact of chlorophyll concentration on the structure of diurnal warm layers. The parameterization presented in this work will allow for better modeling of global patterns of sea surface temperature, diurnal warming, and freshwater lenses, without a prohibitive increase in complexity.
Keywords: radiant heating, phytoplankton, bio‐physical interaction, diurnal warm layer, ocean irradiance, chlorophyll
Key Points
Using empirical physical modeling tools, we develop a bio‐physical radiant heating parameterization that remedies a gap in the literature
In situ observations of the underwater and surface solar spectrum and the surface albedo are used to probe the parameterization's accuracy
The parameterization is applied in a first‐of‐its‐kind case study of the sensitivity of diurnal warm layers to chlorophyll concentration
1. Introduction
Sunlight is the primary energy input to our planet, and with over 70% of the earth's surface covered by water, solar heating of the ocean plays a fundamental role in the behavior of the coupled ocean‐atmosphere system at small and large scales. The vertical distribution of solar heating is sensitive to the amount of absorptive material in the water, and in the open ocean where phytoplankton and their derivatives are the primary absorbing constituents (“case I waters”), the spectral absorption has been empirically shown to follow a robust power‐law relationship to the chlorophyll concentration (Morel, 1988; Morel et al., 2007; Morel & Maritorena, 2001). Consequently, spatiotemporal variability of the phytoplankton system in the surface ocean exerts a significant influence on SST, mixed‐layer heat budgets, and upper ocean dynamics (Gildor et al., 2003; Iudicone et al., 2008; Kahru et al., 1993; Kantha & Clayson, 1994; Murtugudde et al., 2002; Ohlmann et al., 1998; Sathyendranath et al., 1991; Simpson & Dickey, 1981; Zaneveld et al., 1981). Changes in the physical conditions modify phytoplankton growth in turn, and the coupling between ocean physics and biology is an important piece of the climate system that has yet to be fully untangled. In one study coupling an ocean biogeochemical model to an ocean general circulation model, Manizza et al. (2005) found that modification of light penetration by phytoplankton biomass amplified the seasonal cycles of temperature, mixed layer depth, and sea ice cover by 10%, and these physical changes caused increases in phytoplankton biomass, a positive feedback that further amplified the physical perturbations. Another study by Wetzel et al. (2006) added a marine biogeochemical model to a fully coupled atmosphere‐ocean climate model, and in addition to observing similar amplifications in the magnitude of the seasonal cycle, the timing of the seasons became more realistic, with spring starting 2 weeks earlier. It has been suggested that phytoplankton‐induced SST variability may modify the strength of the Hadley and Walker circulations (Gnanadesikan & Anderson, 2009), steer tropical cyclones away from the equator (Gnanadesikan et al., 2010), slow the meridional overturning circulation (Sweeney et al., 2005), and perhaps even play a role in Arctic Amplification (Hill, 2008).
The formation and evolution of diurnal warm layers (DWLs), which span broad areas of the tropical oceans, is especially sensitive to variability in the vertical distribution of solar heating (Bellenger & Duvel, 2009; Dickey & Simpson, 1983). These thin, stratified layers of warm surface water are a systematic feature of the equatorial Indian Ocean during the quiescent phase of the Madden‐Julian Oscillation (MJO) as well as the West Pacific Warm Pool from which the El Nino‐Southern Oscillation (ENSO) originates (Bellenger & Duvel, 2009; Thompson et al., 2019). Tantalizing evidence has been mounting for a possible coupling between phytoplankton and both the MJO and ENSO, in which wind bursts upwell nutrients and stimulate phytoplankton blooms, which subsequently trap solar radiation near the surface, increasing SST and thereby atmospheric convection during the quiescent phases of these oscillatory climate modes (Jin et al., 2013; Jochum et al., 2010; Lengaigne et al., 2007; Marzeion et al., 2005; Siegel et al., 1995; Strutton & Chavez, 2004). The tropical oceans also experience substantial precipitation, leaving stable surface layers of freshwater that can persist through periods of clear skies and intense solar heating (Shackelford et al., 2024; Thompson et al., 2019). In order to understand the role—and potential bio‐physical feedbacks—of these stratified surface layers in the tropical climate system, the solar heating profile must be accurately represented over a vertical scale of just a few meters. Yet most global models rely on simple parameterizations that are known to be inaccurate in the upper meters as their topmost ocean layer is generally ≥10 m thick. We therefore seek to build upon past work in order to develop a bio‐physical parameterization of comparable simplicity that can be relied upon throughout cases of near‐surface open ocean stratification.
This work can be conceived of as an update to the work of Morel and Antoine (1994; hereafter MA94—see Section 1.1 for further discussion), with the key improvements of (a) accuracy in the upper meters, (b) accuracy in oligotrophic waters, and (c) consistency with the standard designation of photosynthetically active radiation (PAR) wavelengths as 400:700 nm. In Section 2, we develop a Spectral Model for ocean radiant heating based on simple, observationally‐validated modeling tools. The Spectral Model is not as sophisticated as radiative transfer equation (RTE) solvers like ECOLIGHT (a simplified version of HYDROLIGHT, Mobley et al., 2009), but it is based on public‐domain tools; the complexity and cost of a commercial RTE solver is unnecessary to our goal of a simple and reliable radiant heating parameterization. In Section 3, we develop a Parameterization for ocean radiant heating by simplifying the Spectral Model to a minimum number of wavebands without sacrificing accuracy, and compare it to the existing parameterizations discussed throughout the remainder of the Introduction (for clarity, both of the above italicized terms are capitalized throughout the manuscript when referring to the specific tools developed herein). In Section 4, we undertake a discussion of the uncertainty associated with the Parameterization with respect to the Spectral Model. We then examine in situ observations of underwater irradiance profiles, spectral partitioning of surface irradiance, and surface albedo, to understand the accuracy and limitations of the Parameterization and the Spectral Model. Finally, in Section 5 we use the Parameterization to perform a case study of the sensitivity of DWLs to chlorophyll concentration, an investigation which to our knowledge has not previously been undertaken.
1.1. Foundational Work
Early research represented the underwater irradiance profile as a single exponential (e.g., Denman, 1973). While this is physically valid for a given wavelength, it is problematic when applied to the broadband solar irradiance due to spectral variability in the exponential decay rates, which span many orders of magnitude across the wavelengths in the solar spectrum. Kraus (1972) is generally credited as the first to suggest using a sum of two exponentials. Paulson and Simpson (1977; hereafter PS77) fit a double‐exponential form to Jerlov (1968, 1976)'s data for different optical water types, and this became the standard parameterization used in many mixed‐layer models even to this day (see e.g. Table 1). While the two exponentials are nominally split somewhere around the edge of the visible domain, the split is not explicitly spectral and the exponentials are simply tuned to best fit the available data. Zaneveld and Spinrad (1980) employed an alternative fitting approach to the same underlying Jerlov data, using an arc‐tangent curve to better represent the rapid extinction of irradiance in the upper 10 m. Several other parameterizations were also developed in the early 1980s to pursue specific physical research questions. Paulson and Simpson (1981; hereafter PS81) fit 9 explicitly spectral bands originally calculated by Schmidt (1908) and cataloged in Defant (1961) for the purpose of calculating solar absorption across the ocean skin—this parameterization was employed in early iterations of the COARE cool‐skin correction (Fairall, Bradley, Godfrey, et al., 1996; hereafter F96), but was shown to be inaccurate and modified for newer versions to better fit available data (Wick et al., 2005). Given that it has been shown to be inaccurate, and is built on a very small sample of laboratory data using superseded measurement techniques, PS81 likely should not be used to estimate radiant heating in the ocean. Finally, Soloviev (1982; hereafter S82) performed a three‐exponential fit to a combination of Jerlov data and a near‐surface underwater irradiance profile provided by Ivanoff (1977) to estimate a parameterization that remains in use in modern DWL studies due to its inclusion of reliable measurements in the upper meters (F96).
Table 1.
An Overview of the Radiant Heating Parameterizations Used by Most Ocean Models in CMIP6 Along With the Original Sources of Both the Underwater Attenuation Coefficients and the Partitioning of the Incident Solar Spectrum
| Model family | Radiant heating parameterization | Derived from | Reference | |
|---|---|---|---|---|
| Attenuation | Partitioning | |||
| MOM | M05 | M88 | PS77 | Griffies (2012) |
| FESOM | S05 | MA94 | MA94 | Wang et al. (2014) |
| NEMO | L07 | MM01 | PS77 | Madec et al. (2023) |
| LICOM | O03 | GM83 + M91 | SBDART | Lin et al. (2020) |
| POP | O03 | GM83 + M91 | SBDART | R. Smith et al. (2010) |
| MPAS‐Ocean | OS00 | GM83 + M91 | SBDART | Petersen et al. (2018) |
| HYCOM Ocean | PS77 | PS77 | PS77 | Wallcraft et al. (2009) |
| SIT | PS81 | PS81 | PS81 | Lan et al. (2022) |
| COCO | PS77 | PS77 | PS77 | Hasumi (2015) |
| MRI.COM | MA94 | MA94 | MA94 | Sakamoto et al. (2023) |
Note. PS77: Paulson and Simpson (1977); PS81: Paulson and Simpson (1981); GM83: Gordon and Morel (1983); M88: Morel (1988); M91: Morel (1991); MA94: Morel and Antoine (1994); OS00: Ohlmann and Siegel (2000); MM01: Morel and Maritorena (2001); O03: Ohlmann (2003); M05: Manniza et al. (2005); S05: Sweeney et al. (2005); L07: Lengaigne et al. (2007).
As the importance of biological agents in modifying visible‐wavelength attenuation became evident, chlorophyll‐dependent spectral parameterizations were developed for the visible domain as an improvement over Jerlov's qualitative water types (e.g., Siegel & Dickey, 1987; Smith & Baker, 1978). This culminated in the work of Morel (1988; hereafter M88), who combined 176 spectral downwelling irradiance measurements from 12 cruises and fitted a power‐law relationship to predict spectral attenuation from chlorophyll concentration in 5 nm bins across the 400:700 nm visible domain. MA94 then expanded the relationship to cover the full solar spectrum for use in radiant heating studies, using infrared absorption coefficients for pure water derived from Hale and Querry (1973) and extrapolating UV absorption from measurements of algae in culture. They provide a three‐exponential fit to the data that has served as the basis for many subsequent chlorophyll‐dependent parameterizations, but is acknowledged to be inaccurate in the upper meters due to the representation of the infrared wavelengths by a single exponential. Since then, the underlying data set has been updated twice—first by Morel and Maritorena (2001; hereafter MM01) and again by Morel et al. (2007; hereafter M07). In these updated publications, the power‐law fits are performed using the more accurate pure‐water absorption spectrum of Pope and Fry (1997), which is much lower in the blue‐green wavelengths than that of Smith and Baker (1981) used by M88 and MA94, yielding differences in the resulting irradiance profiles in oligotrophic waters.
With the development of increasingly powerful radiative transfer models came the opportunity to simulate a wide variety of conditions and develop parameterizations from model outputs. Ohlmann and Siegel (2000; hereafter OS00) used the HYDROLIGHT model to generate a full suite of irradiance profiles for a wide range of chlorophyll concentrations, solar zenith angles, and cloud indices, and then fit their results to a 4‐exponential form without explicit spectral partitions. In a follow‐up paper, Ohlmann (2003; hereafter O03) provides a simplification of the model dependent only on chlorophyll concentration for use in climate models, at the cost of accuracy in the upper meters. In both cases, chlorophyll‐dependent absorption was derived from the power‐law fits of M88 via Morel (1991; hereafter M91) and scattering from Gordon and Morel (1983; hereafter GM83), while the incident solar spectrum was calculated from the SBDART model (Ricchiazzi et al., 1998).
1.2. Modern Climate Modeling
Table 1 presents a non‐exhaustive summary of the radiant heating parameterizations used in most ocean models in the Coupled Model Intercomparison Project Phase 6 (CMIP6, https://wcrp‐cmip.org/cmip‐model‐and‐experiment‐documentation/#cmip6_models). All models for which documentation of the radiant heating scheme was readily available are included; of the 130 total model configurations in CMIP6, 108 contain an ocean model, 89 of which are represented by the model families cataloged in Table 1. Note that while Table 1 shows the default radiant heating configuration of each model family, specific implementations of each model in CMIP6 could have chosen a different scheme, such that Table 1 should not be interpreted as an authoritative source on the radiant heating parameterization used in every single run of a given model family. Nonetheless, Table 1 clearly displays that the foundations described in Section 1.1 continue to underpin our best climate modeling efforts, with the lifetime work of Morel and collaborators serving as the linchpin for most bio‐physical modeling, particularly at the global scale.
We note here that the combination of spectral attenuation coefficients with the non‐spectral partitioning of PS77, as in Manizza et al. (2005) and Lengaigne et al. (2007), introduces the slight inaccuracy of assigning 42% of incoming irradiance to the visible wavelengths; there is an abundance of observational evidence that the visible fraction of incident irradiance is approximately 45%–47% under clear skies (Britton & Dodd, 1976; Frouin et al., 1989; Goldberg & Klein, 1977; Howell et al., 1983; Ivanoff, 1977; Kirk, 1994; Kvifte et al., 1983; McCree, 1966; Moon, 1940; Papaioannou et al., 1993; Rao, 1984; Rodskjer, 1983; Strutton & Chavez, 2004; Weiss & Norman, 1985; Yocum et al., 1964), and increases up to ∼60% with increasing cloud cover (Blackburn & Proctor, 1983; Frouin et al., 1989; Nann & Riordan, 1991; Siegel et al., 1999; Tanre et al., 1979). Manizza et al. (2005) also performed a 50/50 split of the visible wavelengths at 530 nm with limited justification. These are small nuances and do not call the results of the studies into any serious question; we only bring the reader's attention to these decisions because of how often these formulations appear in bespoke modeling efforts to elicit key features of bio‐physical interactions (e.g., Gnanadesikan & Anderson, 2009; Holmes et al., 2019; Kim et al., 2015; Lim et al., 2019; Moeller et al., 2019; Twelves et al., 2021).
Modeling of DWLs, on the other hand, has been more seriously hampered by the limitations of the available parameterizations. For example, Prytherch et al. (2013) updated the F96 DWL model to use the chlorophyll‐dependent parameterization of O03 rather than S82. Yet O03 explicitly states that “the parameterization is not valid for depths shallower than 2 m,” making it a dubious choice for DWL modeling. Unsurprisingly, Prytherch et al. (2013) report that accurate representation of solar absorption still appears to be a primary confounding factor in modeling DWLs. Similarly, Gentemann et al. (2009) set out to improve upon the F96 DWL model by using the 9‐band spectral parameterization of PS81, the reason given being that it displays higher absorption near the surface compared to S82. PS81 developed this parameterization to estimate skin‐layer effects due to its emphasis on the very small absorption lengths in the infrared, and it has been shown to be inaccurate even in that context (see Section 1.1). In the end, Gentemann et al. (2009) had to multiply the solar absorption profile by 1.2 in order to get their model to agree well with observations.
Attempts to parameterize DWLs within global climate models often determine the radiant heating profile from the parameterization implemented in the underlying ocean model (e.g., Large & Caron, 2015). Most of the parameterizations in Table 1 work for an ocean model with 10m‐thick vertical layers, but inaccurate in the upper meters where the strongest DWLs reside. Using a different parameterization within the DWL model (specifically S82 because of its emphasis on accuracy in the upper meters) would yield more reliable DWLs, but introduces two conflicting descriptions of the underwater irradiance profile, and no possibility of including biological variability and bio‐physical feedbacks. We seek to provide here a single bio‐physical parameterization that is both accurate enough for DWL and rain layer modeling and is computationally efficient enough to be used in the underlying global model. It also must explicitly provide the photosynthetically active radiation (PAR) of the 400:700 nm domain to enable coupling to biogeochemical models.
2. Spectral Model
The purpose of this section is to develop a Spectral Model for ocean radiant heating that is conceptually and computationally accessible, and requires a minimum of input parameters. While sophisticated radiative transfer modeling tools (see e.g. Mobley, 1994; Ricchiazzi et al., 1998 as a starting point) might enable a more complete description of the process, their complexity is an impediment to our ultimate objective of a simple and reliable radiant heating parameterization. By assembling pre‐existing, observationally validated models for the solar spectrum at the ocean surface, the broadband albedo, and the spectral underwater attenuation, we create a radiant heating model for Case I waters that is both accurate and accessible, needing as inputs only the downwelling broadband irradiance, the chlorophyll concentration, and the time and location on the earth. The Spectral Model is summarized graphically in Figure 1 and as a flow‐chart in Figure 2.
Figure 1.
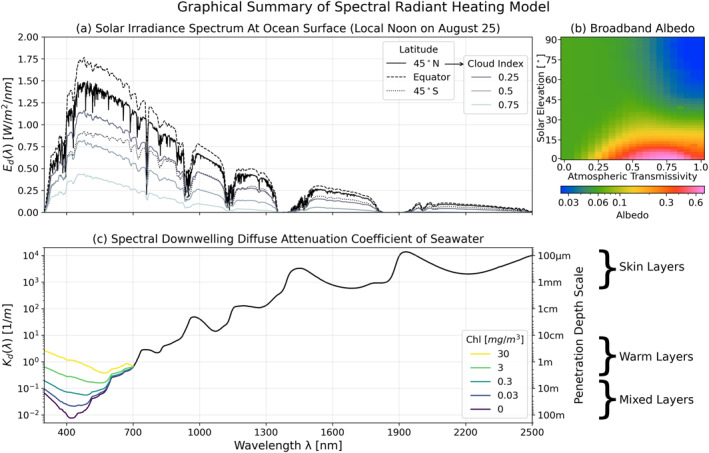
Graphical depiction of Spectral Model components. (a) Clear‐sky spectra from Diffey (2015) at three latitudes for an example date and time, differentiated by line style. For the 45N latitude, the modification of the spectrum by the cloud index model of Siegel et al. (1999) is shown with color, demonstrating the preferential transmission of shorter wavelengths through clouds. (b) Broadband albedo from Payne (1972) as a function of atmospheric transmissivity and solar elevation, shown on a logarithmic color scale. (c) Diffuse attenuation coefficients at each wavelength in the solar spectrum, with chlorophyll‐dependence in the UV and visible from Morel et al. (2007), and infrared coefficients from Bertie and Lan (1996).
Figure 2.
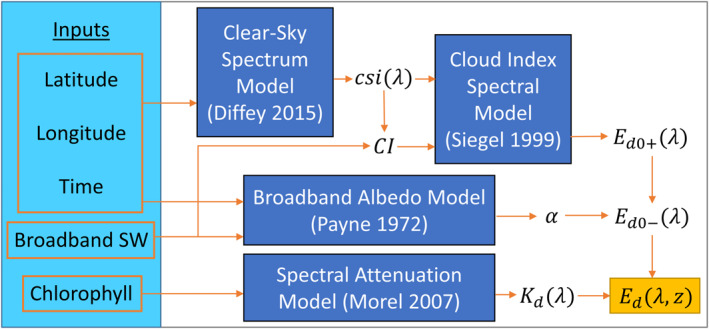
Flowchart demonstrating how the modeling tools depicted in Figure 1 and described in Section 2 can be combined for use as a Spectral Model for radiant heating.
2.1. Clear‐Sky Solar Irradiance Spectrum
To predict the solar irradiance spectrum at the ocean surface under clear skies, we employ the model of Diffey (2015), who deliberately set out to “develop a model that is as simple as it can be commensurate with delivering results of adequate accuracy.” By starting from a reference spectrum and accounting for solar angle, direct and diffuse radiation, Rayleigh scattering, aerosol scattering and absorption, and ozone absorption, Diffey (2015) demonstrate good agreement with both observations and radiative transfer modeling using nothing more complex than an Excel spreadsheet with time and position as inputs. The Excel sheet was carefully translated into Python for use in this study.
2.2. Spectral Influence of Clouds
Having predicted the solar irradiance under a clear sky, we calculate the “Cloud Index” CI of the sky in terms of the ratio between observed and predicted broadband irradiances:
| (1) |
where comes from integrating the clear‐sky spectrum predicted in Section 2.1. We then employ the empirical model of Siegel et al. (1999) to relate our broadband Cloud Index to a wavelength‐specific cloud index, scaling each wavelength in the clear‐sky spectrum by a different amount to accurately reflect the changes in spectral composition caused by clouds (namely, preferential transmission of shorter wavelengths). This leaves us with a final estimate for the solar spectrum at the ocean surface, which integrates to .
2.3. Albedo
The albedo of the sea surface does vary with wavelength, with shorter wavelengths tending to have a slightly higher albedo than red and infrared (Ohlmann et al., 2000, see Figure 12 therein). However, the magnitude of spectral variability and the absolute magnitude of the albedo are both so small that the spectral effects are second‐ or even third‐order from a radiant heating perspective, and thus we do not account for them in this model. Rather, we use the empirical model of Payne (1972), which predicts a broadband albedo as a function of the sun angle and the transmissivity of the atmosphere (equivalent to one minus the Cloud Index). This lookup table was developed from 4 months of observations at the mouth of Buzzards Bay, Massachusets, and validated against radiative transfer modeling by Ohlmann et al. (2000). The albedo may also display a small wind speed dependence at low sun angles (Katsaros et al., 1985; Payne, 1972) but low sun angles generally correspond to low absolute irradiances and are therefore of minor concern in the context of radiant heating studies outside of the high latitudes.
2.4. Underwater Attenuation
To account for the effect of biogenic substances in the water on the attenuation of UV and visible light, we use the bio‐optical parameterization originally published by M88 and most recently updated in M07. The parameterization rests on the assumption that at each wavelength, the spectral attenuation coefficient can be decomposed into two additive parts:
| (2) |
where is the attenuation due to the water itself, and is the combined attenuation due to all biogenic substances in the water (including algal cells, detritus, colored dissolved organic matter, and other associated nonalgal organisms). The “bio‐optical assumption” states that the total attenuating effect of all biogenic substances in the water co‐varies with chlorophyll in a consistent way; the Morel publications have demonstrated that this assumption is reasonable in open ocean (or “case I”) waters, with following a power‐law relationship to chlorophyll concentration:
| (3) |
where and are empirical parameters determined by a linear fit to versus observations in natural‐log space at each wavelength . M07 only published their parameterization down to 350 nm, so we follow the approach of MA94 in extrapolating the parameterization between 300:350 nm. For 700 nm, the attenuation due to the water itself is so strong that biogenic substances have negligible influence. We therefore use the “gold standard” laboratory data from Bertie and Lan (1996) for attenuation coefficients in the infrared.
3. Parameterization
Despite its simplicity, the Spectral Model derived in Section 2 is far too complex to be reasonably integrated into most ocean modeling. From large‐scale coupled climate models to 1‐D mixed‐layer models, most ocean models represent the underwater irradiance profile as the sum of just a few exponentials. Our purpose in this section is therefore to simplify our Spectral Model to just a few wavelength bands while balancing simplicity and accuracy. To do this, we first simplify the underwater attenuation coefficients, and then determine how to partition the incident irradiance between the resulting spectral bands.
3.1. Simplifying the Spectral Model to a 5‐Band Parameterization
Past work in this vein (e.g., MA94, OS00) has typically simplified the spectrum of chlorophyll‐dependent attenuation coefficients using high‐order polynomial fits, which introduce a layer of abstraction and computational complexity. We prefer to average the decay rates of M07 across spectral bands using the harmonic mean (equivalent to taking the arithmetic mean of the e‐folding depths), preserving the original form of the bio‐optical fits. Within the UV band from 300:400 nm, we improved agreement with M07 by weighting the average using a typical irradiance spectrum, which helps account for how little light there is in the 300:350 nm range compared to the 350:400 nm range. For the Visible (PAR) wavelengths from 400:700 nm, we sought to divide the spectrum into the minimum number of bands necessary to accurately reproduce the integrated spectral output of M07. To do so, we systematically tested the accuracy of representing various wavelength bands with the harmonic‐mean quantities, seeking the appropriate splits in the visible region that minimized the biases in absolute irradiance across the upper 20 m when compared to the spectral integration of M07 within the band. While just two visible‐wavelength bands have been employed in the past (e.g., Manizza et al., 2005), we found that two bands introduced too much vertical variability in the profiles compared to M07 regardless of the location of the split, while three bands, with splits at 510 and 600 nm, reproduce M07 almost perfectly. Parameters for the four resulting wavelength bands are given in Table 2. Note that while the harmonic mean is mathematically appropriate for averaging the and parameters, a rigorous manner of averaging the parameter is less obvious. However, is of relatively constant value within the spectral bands we have defined, with the exception of the 670:700 nm region in which it decreases rapidly. We therefore chose to use the arithmetic mean of the parameter, which is less sensitive to the variability in the red band, and agrees with the harmonic mean in the shorter‐wavelength bands. Given the uncertainties in at long wavelengths to begin with (see M88), and the close agreement between our simplified bands and the spectral integration of M07, this approach is adequate to the task at hand.
Table 2.
The Parameterization for Radiant Heating Developed in Section 3
| Waveband [nm] | Partition (F) | Transmission profile (multiply by 0.945 × SW) | Parameters | ||||
|---|---|---|---|---|---|---|---|
| 300:400 (UV) | 0.05 | where |
|
||||
|
| |||||||
|
| |||||||
| 400:510 (Blue) | 0.16 | where |
|
||||
|
| |||||||
|
| |||||||
| 510:600 (Yellow) | 0.14 | where |
|
||||
|
| |||||||
|
| |||||||
| 600:700 (Red) | 0.14 | where |
|
||||
|
| |||||||
|
| |||||||
| 700:2500 (IR) | 0.51 |
|
|
|
|||
|
|
|
||||||
The infrared wavelengths present a different challenge. While there is no chlorophyll‐dependence that must be preserved through the simplification, the attenuation coefficients span so many orders of magnitude between 700:2500 nm that the resulting irradiance profile in the upper meter of the ocean decreases much more rapidly than a simple exponential. In trying to fit the profile as a sum of exponentials, we found that we needed >10 exponential bands to reasonably approximate the profile, which presents a good deal of computational complexity compared to the parameterizations we intend to replace. Rather than accept a poor fit with fewer exponentials, we follow the pioneering example of Zaneveld and Spinrad (1980) in using an arctangent curve to approximate the rapid decrease near the surface. We fit Spectral Model profiles generated from a wide variety of input conditions (cloud index being varied from 0 to 0.8, in each case applied to lat/lon/time combinations yielding solar zenith angles ranging from 10° to 80° and clear‐sky irradiances from 100 to 1100 W/m2) to the form:
| (4) |
and found the fit constants (given in Table 2) that best reproduce the Spectral Model output.
Having defined five wavelength bands and produced reliable descriptions of each band's decay with depth, we must determine what fraction of the incident broadband irradiance should be assigned to each band. In a procedure analogous to that of O03 (but for spectrally defined wavebands), we initialized the Spectral Model with a range of input conditions (chlorophyll being varied from 0.01 to 10 mg/m3 and cloud index being varied from 0 to 0.8, in each case applied to lat/lon/time combinations yielding solar zenith angles ranging from 10° to 80° and clear‐sky irradiances from 100 to 1100 W/m2), and found the constant partitions between the five simplified bands that minimized the absolute difference between Spectral Model outputs and the five‐band Parameterization. The resulting partitions are 5% UV, 51% infrared, and 44% visible—subdivided into 16% blue, 14% yellow, and 14% red. These correspond to a cloud index of ∼0.2 in the Spectral Model.
Finally, the albedo of the ocean surface is generally so small that radiant heating parameterizations have historically treated it as a constant. As can be seen in Figure 1b, the Payne (1972) model yields an albedo of ∼0.055 across the majority of relevant conditions, with slightly lower albedos under very clear skies, and significantly higher albedos in conditions of very low sun angles. Because low sun angles correspond to low absolute irradiances, neglecting the variability in albedo yields very small absolute errors. We therefore follow the established literature (e.g., Fairall, Bradley, Rogers, et al., 1996) in setting a constant albedo of 0.055 for our Parameterization. The Parameterization is summarized in Table 2.
3.2. Comparison to Existing Parameterizations
Figure 3 shows depth profiles of irradiance (as a fraction of incident irradiance) from the proposed Parameterization along with the comparable chlorophyll‐dependent and constant parameterizations currently in use (as summarized in Table 1). The proposed Parameterization aligns well with the more complex formulation of OS00, particularly at high and moderate chlorophyll concentrations, with the divergence at low chlorophyll due to the implementation of a more transmissive pure‐water spectrum in M07 compared to that used by OS00. OS00 is evaluated at a cloud index of 0.2 and solar zenith angle of 20° to produce the curves in Figure 3; in general we observe comparably good agreement between the Parameterization and OS00 evaluated across a range of low cloud indices (0–0.4) and solar zenith angles (10–30°). Importantly, the complexity of OS00 allows for accuracy in the upper meters, and we observe excellent agreement between the Parameterization and OS00 at shallow depths. By contrast, MA94 agrees well with the Parameterization below a few meters deep, but is inaccurate within the upper meters. The 2‐band simplification of O03 appears to allow far too much transmission down to depths of 10s of meters before converging with the other chlorophyll‐dependent parameterizations, calling into question its applicability even at the scale of mixed‐layer heating. Among the parameterizations without chlorophyll‐dependence shown on Figure 3, S82 exhibits the best agreement with the Parameterization, including near the surface. This reveals why efforts to improve DWL modeling have struggled when switching away from S82, as PS77 and PS81 are markedly different in the upper meters. We have already suggested that PS81 should not be used; Figure 3 also calls the use of PS77 into some question even at a model layer thickness of 10 m.
Figure 3.
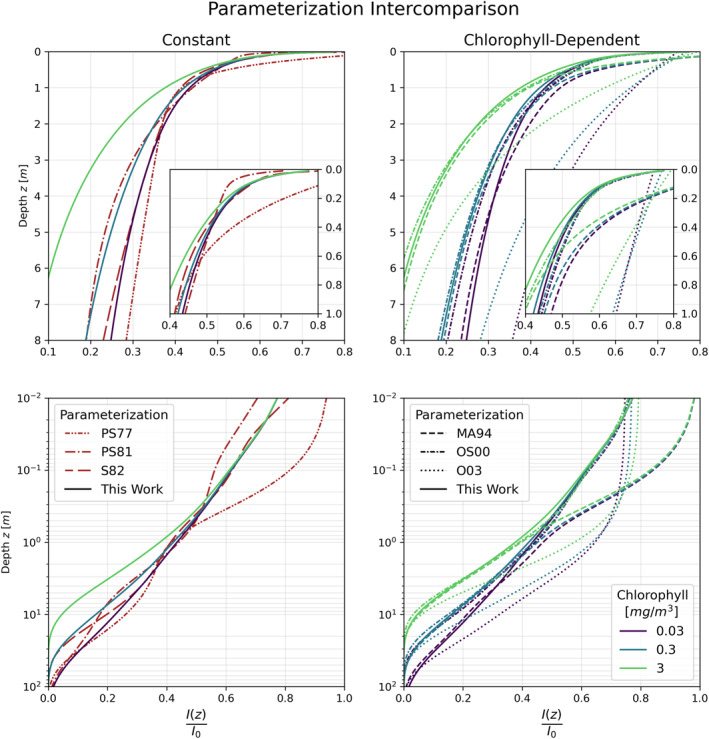
Depth profiles of irradiance (expressed as a fraction of the incident irradiance I 0 ) from the Parameterization developed in this work and the comparable existing parameterizations currently in use (see Table 1), with linear depth scale in the top row and logarithmic depth scale in the bottom row. Left panels show comparison of the proposed Parameterization to the constant parameterizations in Table 1, while right panels show comparison to the chlorophyll‐dependent parameterizations in Table 1. Inset panels show the upper meter for clarity. Parameterizations are distinguished by line style, and colored by chlorophyll concentration (constant parameterizations that do not feature chlorophyll‐dependence are colored red). The parameterizations of MA94 and OS00 are evaluated for a solar zenith angle of 20° and OS00 is evaluated for a cloud index of 0.2.
4. Uncertainty and Observations
The largest source of uncertainty in this and all preceding chlorophyll‐dependent parameterizations is the bio‐optical assumption itself. Of course, it is imperative that the relationship only be applied in case I waters, but even within these waters there is spatiotemporal variability between regions with different planktonic species distributions and environmental conditions at the same chlorophyll concentration. Nonetheless, the power‐law fits of M88 are of high quality, with correlation coefficients (R 2) > 0.9 for wavelengths from 420:550 nm. Beyond 550 nm, the quality of the fits degrades significantly and very few data points are available. The water itself plays such a large absorbing role in the red wavelengths that the relative impact of chlorophyll is much smaller, requiring a large amount of chlorophyll in the water to observe a departure from the absorption of the water alone. This is further compounded by the rapid extinction of red light even just a few meters underwater, meaning optical measurements must be made much closer to the surface in order to observe above the noise floor of the measurement device, introducing complicated boundary effects. The subsequent revisions to the parameterization in MM01 and M07 introduced substantially more measurements, but did not provide any quantification of uncertainties—95% prediction intervals at each wavelength, evaluated on the complete data set of M07, would be the ideal approach to estimating the uncertainty associated with the bio‐optical model, but would require access to the original data set.
That being said, there are several approaches available to this study to give some estimate as to the uncertainty associated with our parameterization. First, by comparing the Parameterization to the Spectral Model, we can quantify the importance of the factors neglected in the simplification process of Section 3, but cannot provide any independent evaluation of the M07 bio‐optical model itself. However, in situ observations of underwater irradiance profiles—in multiple locations with a variety of observed chlorophyll concentrations—can provide us with an independent evaluation of the Parameterization's performance in the visible wavelengths. Because our focus is on radiant heating of the ocean, we are most concerned with the absolute uncertainties (expressed in W/m2), rather than uncertainty as a percentage of the incident irradiance.
4.1. Parameterization Versus Spectral Model
The first approach to estimating the uncertainty associated with our Parameterization is to compare it to the outputs of the Spectral Model, initialized across the broad range of input conditions described in Section 3.1. The differences between them—plotted against depth in Figure 4—represent an envelope of potential uncertainty, and the colors reveal a pronounced cloud index dependence, with positive differences at low cloud indices and negative differences at high cloud indices. Line styles in Figure 4 represent different input chlorophyll concentrations. At a given cloud index, lower chlorophyll concentrations generally correspond to higher absolute differences at depth, simply because more light is able to penetrate deeper. However, the Parameterization and Spectral Model tend to agree well at a cloud index of 0.2 (red lines), and changes in chlorophyll concentration at this cloud index yield little change in the difference between Spectral Model and Parameterization. This implies that the chlorophyll‐dependence of the Spectral Model is well captured by the Parameterization, while the biggest factor that is neglected in the Parameterization is the spectral influence of clouds. The comparisons in Figure 4 would suggest an uncertainty estimate of ±30 W/m2 in the upper meters. However, although the Spectral Model is built on observationally‐validated tools, we must be cautious in interpreting it as an absolutely true representation of real‐world behavior. We therefore turn to several types of in situ observations to shed further light on the validity of both the Parameterization and the Spectral Model.
Figure 4.
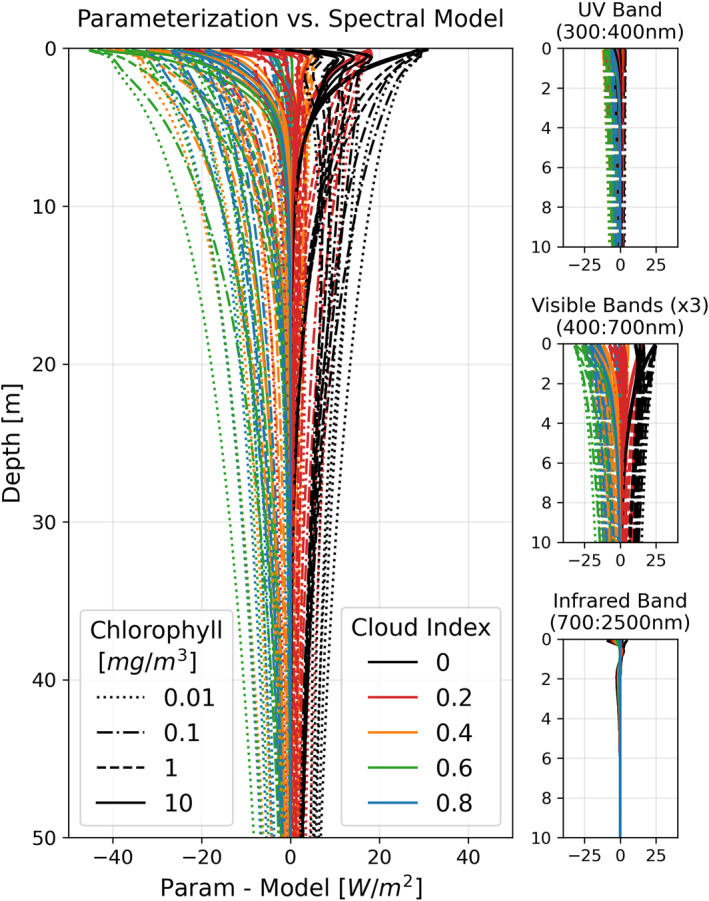
Comparison of the Parameterization to the Spectral Model in the upper 50 m across the parameter space of input conditions. The colors highlight that the differences are largely due to the inclusion/exclusion of cloud effects. The small panels show the upper 10 m split out by wavelength region, revealing the visible region to be the dominant source of variability.
4.2. Profiling Multi‐Spectral Radiometer Observations
We can test the visible‐wavelength portions of both the Spectral Model and Parameterization using a data set of 140 profiling spectroradiometer depth casts (Satlantic Profiler II equipped with 2 OCI 507 and 2 OCR 507 radiometers for a total of 14 wavelength channels spanning 380–705 nm) with coincident pyranometer and chlorophyll measurements, collected on 2 cruises in the tropical Atlantic (September 2015 and August 2016 onboard R/V Meteor), 3 cruises in the Gulf of Mexico (June 2015, August 2018, and July 2019 onboard R/V Endeavor), and one cruise in the Tropical Pacific (November 2019 onboard R/V Falkor). The casts were carefully quality‐controlled, and only included in the final data set if the standard deviation of pyranometer measurements during the cast was less than 50 W/m2 (because a single pyranometer measurement and resulting cloud index value must be assigned to each cast), resulting in a final data set of 64 casts. Figure 5c shows the distribution of parameters, demonstrating that the exclusion criteria do not introduce substantial biases compared to the overall data set, and span the ranges of input parameters reasonably well. Nonetheless the data set can only be interpreted as a reasonably representative range of potential tropical and Caribbean conditions.
Figure 5.
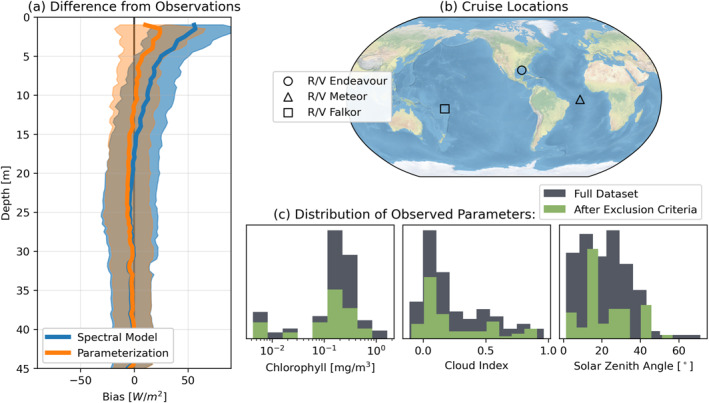
(a) Comparison of integrated visible‐wavelength irradiance profiles from 64 multi‐spectral depth casts to both the Spectral Model (blue) and the Parameterization (orange), with solid lines showing the mean bias and shaded regions spanning one standard deviation. (b) Locations of the cruises (6 total cruises undertaken onboard 3 research vessels, see Section 4.2 for further details). (c) Histograms of the observed parameters used as input conditions to the Spectral Model (and Parameterization, in the case of chlorophyll concentration), demonstrating the range of conditions sampled.
Each spectrally integrated visible irradiance profile observation was compared to the profiles predicted by both the Spectral Model and the Parameterization. Figure 5a shows the results of the comparison, revealing that the Parameterization reproduces the observations better than the Spectral Model at shallow depths. The spread in differences suggests the Parameterization is reliable to within about ±25 W/m2 in the visible wavelengths, which are the main spectral region of variability based on Figure 4. Given that cloud index dependence is the primary difference between Parameterization and Spectral Model, the superior performance of the Parameterization when compared to observations suggests the cloud index dependence of the Spectral Model may be too strong. To shed further light on this, we examine a data set of surface hyperspectral radiometer observations.
4.3. Surface Hyperspectral Radiometer Observations
While onboard R/V Falkor in the Tropical Pacific near Fiji in November 2019 (cruise FK191120), a floating hyperspectral radiometer (Seabird HyperOCR) was deployed behind the ship for 30 min near solar noon on 13 separate days to capture the downwelling spectrum in the 350–800 nm range at 3.3 nm resolution. These observations can be used to test the cloud index dependence of Spectral Model predictions for partitioning of the three visible wavelength bands used in the Parameterization. Because the pyranometer (Kipp and Zonen CMP22) mounted on the ship's mast—which is used to calculate the cloud index—was several hundred meters away from the floating radiometer, there was a temporal lag in sky conditions that is particularly evident on days with variable cloudiness, which are the most important days for filling out the cloud index parameter space. We therefore aligned the radiometer observations with the appropriate cloud index estimates by performing a lag correlation between the pyranometer and the (spectrally integrated) radiometer, with the resulting lags ranging between 19 and 72 s depending on the wind speed and direction. Figure 6 presents a comparison of observations and Spectral Model output as a function of cloud index—note the y‐axes are given as fractions of the visible irradiance rather than total solar irradiance, as the observations only span this range completely. The observations do not display any cloud index dependence until the cloud index has increased past a threshold of ∼0.2, suggesting that—at least in the visible region—clouds do not exert a spectral influence on incoming solar radiation until they are present in sufficient quantity to reduce the total incident irradiance by more than 20%. In contrast, the Spectral Model displays a linear dependence across the cloud index space, and this over‐sensitivity to low cloud indices appears to be the cause of the poor near‐surface performance of the Spectral Model in Figure 5.
Figure 6.
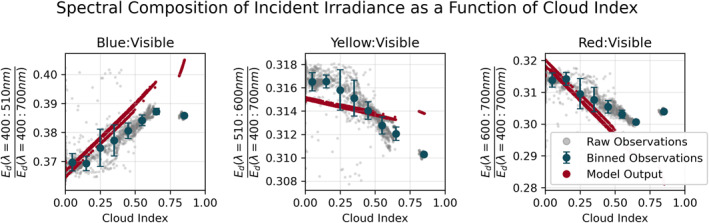
Partitioning of the three visible‐wavelength bands defined in our Parameterization as a function of cloud index. Floating hyperspectral radiometer observations are plotted in light gray and binned by cloud index in blue. Model outputs are plotted in red.
4.4. UAV Albedo Observations
While a constant albedo was chosen for simplicity in the Parameterization, the Payne (1972) model displays albedos as high as 50% or more in low sun‐angle conditions. For high‐latitude applications, therefore, a variable albedo will likely be required. For this reason, we wish to interrogate the accuracy of the Payne (1972) model to determine its suitability for future use in specific cases where low sun‐angles are prevalent. Two Uncrewed Aerial Vehicle (UAV) flights were performed during the FK191120 cruise with a payload of matched up‐ and down‐looking Hukseflux SR‐03 Pyranometers. The downwelling irradiance measurements were corrected for platform motion following the procedure outlined in Reineman et al. (2013; see also Equation 5.1 in Bannehr & Glover, 1991) with a first‐order Butterworth low‐pass filter cutoff at 1/6 Hz. After correction, the data set was subset to reject all points with roll or pitch values more than 1° from neutral, and then composited into 20‐min averages. Figure 7 shows the albedo observations from both flights compared to the Payne (1972) model (with model input parameters plotted in the lower panels). The observations and model output evolve similarly in time, but the observations are systematically lower than the model output by about 15% on average. This is unsurprising given that the Payne (1972) model is built on observations at the mouth of Buzzard's Bay, Massachusetts, a turbid coastal environment that does not provide a generalizable analog to open ocean conditions. However, it is encouraging that the temporal evolution of the model follows the observations reasonably well, suggesting that the input parameters of solar elevation and atmospheric transmissivity have been properly identified as the primary controls on albedo variability. More observations of this kind are needed in open‐ocean and high‐latitude environments to build a more robust version of this simple and potentially very powerful modeling approach. Meanwhile, for studies employing a constant albedo, the limited observations we have thus far suggest that ∼0.045 (15% lower than the current value) might be a better choice; however, more observations are needed before we advocate for implementing such a change.
Figure 7.
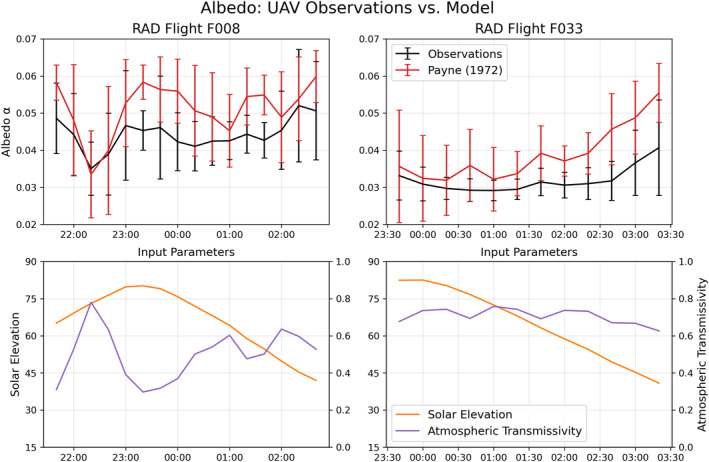
Albedo as measured directly during two UAV flights (black), compared to output of the Payne (1972) empirical model (red), with the input parameters for the model plotted in the lower panels.
5. Case Study: Sensitivity of Diurnal Warm Layers to Chlorophyll Concentration
The accuracy of the Parameterization near the surface presents an opportunity to investigate the sensitivity of DWL formation to chlorophyll concentration, a study which to our knowledge has not yet been undertaken. To quantify the impact of chlorophyll on DWL formation in a generalized way, we modified the COARE3.5 DWL algorithm (F96) to accept chlorophyll concentration as an input and use the Parameterization in its calculation of the DWL depth () and temperature increase from the base of the DWL to the ocean surface (). The modified algorithm was forced with constant inputs and an idealized sinusoidal insolation curve, and run for cases of various chlorophyll concentrations and wind speeds. The maximum and corresponding for each of these runs is shown in Figure 8, with y‐axes referenced to the output of the default COARE3.5 algorithm (which uses the S82 parameterization) run under the same conditions. Figure 8 illustrates that differences in chlorophyll concentration can change the SST of a DWL by several tenths of a degree, and its depth by several meters. Chlorophyll has the largest effect on DWL SST at low wind speeds, but the smallest effect on DWL depth, because DWLs are very thin at low wind speeds. Meanwhile, chlorophyll has a pronounced effect on DWL depth at higher wind speeds, and a non‐negligible effect on the SST.
Figure 8.
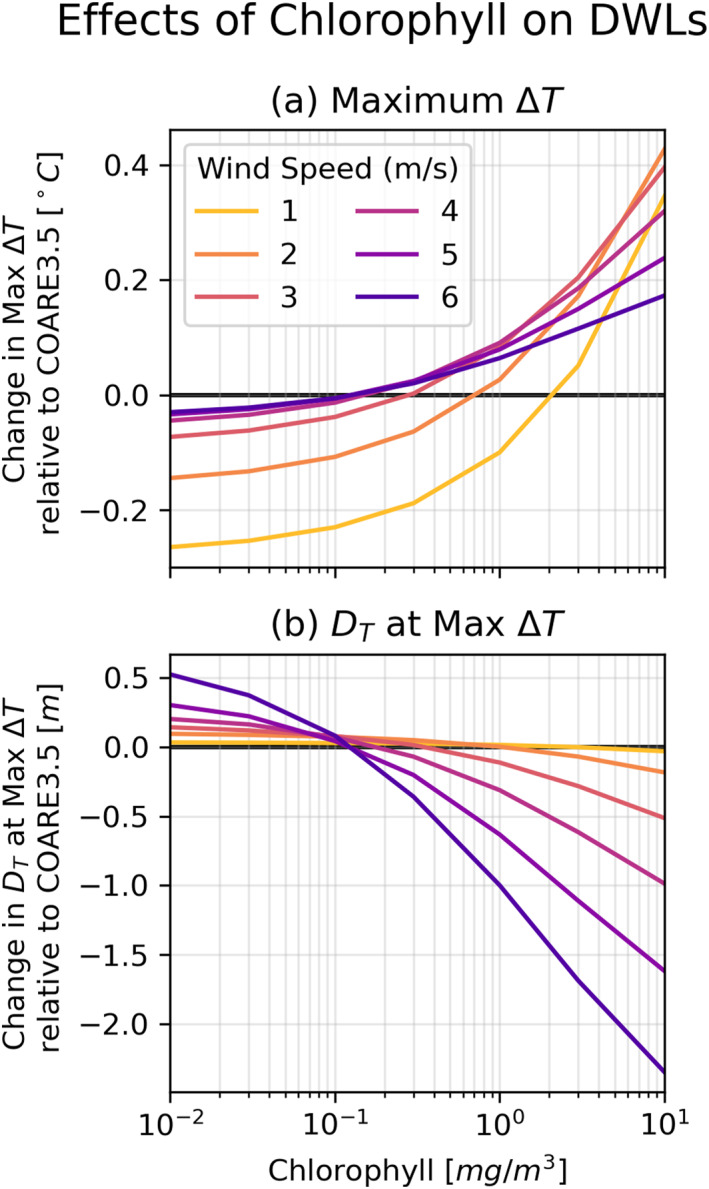
Chlorophyll‐induced changes in (a) the maximum SST change and (b) the associated depth of an idealized DWL simulated with a modified COARE3.5 using the new Parameterization, relative to the standard COARE3.5 implementation using S82.
To assess the chlorophyll effect on the temporal evolution of DWLs, Figure 9 shows a month‐long timeseries of the COARE3.5 DWL algorithm forced with shipboard observations from cruise FK191120. The black curves show the default algorithm outputs, while the colored lines underneath show the change from the default output at various chlorophyll concentrations, reinforcing the conclusions from Figure 8 that chlorophyll can modify by several tenths of a degree and by several meters. However, the effect of a given chlorophyll concentration does not always have the same sign relative to the default algorithm, due to the sensitivity of DWLs to variability in insolation and, particularly, wind speed. In summary, Figures 8 and 9 yield the generally intuitive result that more absorbing material in the water should lead to warmer and shallower DWLs as more radiant heating is trapped closer to the surface. These high‐chlorophyll warm layers simultaneously have stronger static stability and larger air‐sea temperature differences, with the consequence that more of their heat will be returned to the atmosphere via turbulent fluxes. This provides a clear mechanism by which the chlorophyll concentration could modulate the strength of atmospheric convection.
Figure 9.
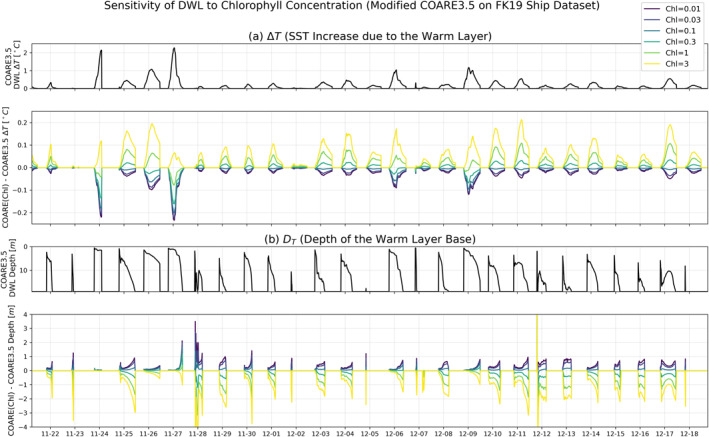
Time series of the COARE3.5 DWL model output when forced with a month of shipboard observations from the tropical Pacific. Black lines show the standard model output for (a) DWL SST change and (b) DWL depth; colored lines below show the differences from the black lines when COARE3.5 is run with the new parameterization at a variety of realistic chlorophyll concentrations.
The global ocean models in Table 1 have too coarse a vertical resolution to grow realistic DWLs, and in their default configurations DWL effects are largely ignored. We believe the COARE3.5 DWL algorithm offers one of the best options for ocean modelers interested in improving their models' representation of this important phenomenon, as it is physically grounded and computationally feasible. Whether ocean modelers choose to use the COARE DWL algorithm or another DWL parameterization (e.g., Large & Caron, 2015), the radiant heating Parameterization developed herein should be incorporated in order to yield a realistic calculation of DWL effects, especially for the largest DWLs stratified within the upper few meters. As Figures 8 and 9 make clear, the absorption of sunlight by chlorophyll has a non‐negligible impact on DWLs that must be accounted for when modeling their evolution.
6. Conclusion
We have developed a radiant heating parameterization that offers both chlorophyll dependence and accuracy in the upper meters of the ocean while maintaining a computational simplicity reasonably comparable to its predecessors. Because it explicitly calculates the profile of photosynthetically available radiation (visible light), it can be used in biological and coupled bio‐physical modeling for Case I waters as well. Using the proposed Parameterization, we demonstrate the extent to which chlorophyll concentration can affect the depth and magnitude of DWLs, providing mechanistic insight into the possible interactions between phytoplankton and atmospheric convection, and emphasizing the importance of accounting for variability in biogenic absorption when modeling DWL effects. As discussed in Section 1.2, superimposing a DWL parameterization on top of a low‐vertical‐resolution global ocean model typically requires a shared radiant heating parameterization used in both the DWL parameterization and underlying model—otherwise, conflicting descriptions of solar absorption could lead to inconsistencies in the overall heat budget of the upper ocean. The proposed Parameterization fulfills this need by offering near‐surface accuracy and chlorophyll‐dependence (key to accurate DWL modeling) without a prohibitive increase in complexity (key to global ocean modeling).
Given the uncertainties inherent to the bio‐optical assumption that we are unable to quantitatively address within this study, we have presented several lines of evidence that suggest a reasonable absolute uncertainty estimate for the proposed Parameterization of ±30 W/m2 at the surface, and ±20 W/m2 at 20 m depth. While expressing uncertainty as a percentage of the irradiance would be another valid (and depth‐independent) approach, we have focused on minimizing the absolute uncertainty in the near‐surface ocean when deriving the Parameterization, and an approximate absolute uncertainty is ultimately the most honest reflection of the tools available with which to make an uncertainty estimate. The underlying data set of M07, along with an independent global data set of full‐spectrum irradiance profiles reliable in the upper meters and paired with high‐quality chlorophyll measurements, would likely be needed in order to shed substantially more light on the uncertainties of bio‐optical parameterizations. Moving forwards, we expect the proposed Parameterization—and the discussion of other parameterizations currently in use provided herein—to enable a needed step forward in accurate bio‐physical modeling of upper ocean stratification and dynamics, particularly in the presence of DWLs and rain layers. We suggest the use of this Parameterization in any ocean modeling with vertical resolution of <2 m or parameterization of near‐surface stratification, and emphasize its applicability to all multi‐layer ocean modeling.
Acknowledgments
This research was funded by the National Science Foundation Award Number OCE 20‐49546 and Schmidt Ocean Institute Contract Number CU19‐1778 and CU19‐3241. A.S. was supported by NASA Grant 80NSSC21K0439 and by funding from the G. Unger Vetlesen Foundation and a fellowship from Columbia University's Center for Climate and Life. The authors would also like to thank the captains, officers, and crew of R/V Endeavour, R/V Meteor, and R/V Falkor.
Witte, C. R. , Subramaniam, A. , & Zappa, C. J. (2024). An improved bio‐physical parameterization for ocean radiant heating in conditions of near‐surface stratification. Journal of Geophysical Research: Oceans, 129, e2024JC021049. 10.1029/2024JC021049
Data Availability Statement
Data used in this study (Witte et al., 2024) are archived for public access on Columbia Academic Commons (https://doi.org/10.7916/wmdm‐vm51). The code used to produce the figures in this study is available for public access on GitHub (https://github.com/Zappa‐Lab/Bio‐Physical‐Radiant‐Heating‐Parameterization).
References
- Bannehr, L. , & Glover, V. (1991). Preprocessing of airborne pyranometer data. NCAR Technical Note, 45. [Google Scholar]
- Bellenger, H. , & Duvel, J.‐P. (2009). An analysis of tropical ocean diurnal warm layers. Journal of Climate, 22(13), 3629–3646. 10.1175/2008JCLI2598.1 [DOI] [Google Scholar]
- Bertie, J. E. , & Lan, Z. (1996). Infrared intensities of liquids XX: The intensity of the OH stretching band of liquid water revisited, and the best current values of the optical constants of H2O(l) at 25°C between 15,000 and 1 cm−1 . Applied Spectroscopy, 50(8), 1047–1057. [Google Scholar]
- Blackburn, W. J. , & Proctor, J. T. A. (1983). Estimating photosynthetically active radiation from measured solar irradiance. Solar Energy, 31, 2–234. 10.1016/0038-092x(83)90087-7 [DOI] [Google Scholar]
- Britton, C. M. , & Dodd, J. D. (1976). Relationships of photosynthetically active radiation and shortwave irradiance. Agricultural Meteorology, 17(1), 1–7. 10.1016/0002-1571(76)90080-7 [DOI] [Google Scholar]
- Defant, A. (1961). Physical oceanography. https://cir.nii.ac.jp/crid/1130282271105191040
- Denman, K. L. (1973). A time‐dependent model of the upper ocean. Journal of Physical Oceanography, 3(2), 173–184. [DOI] [Google Scholar]
- Dickey, T. D. , & Simpson, J. J. (1983). The influence of optical water type on the diurnal response of the upper ocean. Tellus B: Chemical and Physical Meteorology, 35B(2), 142–154. 10.1111/j.1600-0889.1983.tb00018.x [DOI] [Google Scholar]
- Diffey, B. (2015). Solar spectral irradiance and summary outputs using excel. Photochemistry and Photobiology, 91(3), 553–557. 10.1111/php.12422 [DOI] [PubMed] [Google Scholar]
- Fairall, C. W. , Bradley, E. F. , Godfrey, J. S. , Wick, G. A. , Edson, J. B. , & Young, G. S. (1996a). Cool‐skin and warm‐layer effects on sea surface temperature. Journal of Geophysical Research, 101(C1), 1295–1308. 10.1029/95JC03190 [DOI] [Google Scholar]
- Fairall, C. W. , Bradley, E. F. , Rogers, D. P. , Edson, J. B. , & Young, G. S. (1996b). Bulk parameterization of air‐sea fluxes for tropical ocean‐global atmosphere coupled‐ocean atmosphere response experiment. Journal of Geophysical Research, 101(C2), 3747–3764. 10.1029/95JC03205 [DOI] [Google Scholar]
- Frouin, R. , Lingner, D. W. , Gautier, C. , Baker, K. S. , & Smith, R. C. (1989). A simple analytical formula to compute clear sky total and photosynthetically available solar irradiance at the ocean surface. Journal of Geophysical Research, 94(C7), 9731–9742. 10.1029/JC094iC07p09731 [DOI] [Google Scholar]
- Gentemann, C. L. , Minnett, P. J. , & Ward, B. (2009). Profiles of ocean surface heating (POSH): A new model of upper ocean diurnal warming. Journal of Geophysical Research, 114(C7). 10.1029/2008JC004825 [DOI] [Google Scholar]
- Gildor, H. , Sobel, A. H. , Cane, M. A. , & Sambrotto, R. N. (2003). A role for ocean biota in tropical intraseasonal atmospheric variability. Geophysical Research Letters, 30(9), 1460. 10.1029/2002GL016759 [DOI] [Google Scholar]
- Gnanadesikan, A. , & Anderson, W. G. (2009). Ocean water clarity and the Ocean general circulation in a coupled climate model. Journal of Physical Oceanography, 39(2), 314–332. 10.1175/2008JPO3935.1 [DOI] [Google Scholar]
- Gnanadesikan, A. , Emanuel, K. , Vecchi, G. A. , Anderson, W. G. , & Hallberg, R. (2010). How ocean color can steer Pacific tropical cyclones. Geophysical Research Letters, 37(18), L18802. 10.1029/2010GL044514 [DOI] [Google Scholar]
- Goldberg, B. , & Klein, W. H. (1977). Variations in the spectral distribution of daylight at various geographical locations on the earth’s surface. Solar Energy, 19(1), 3–13. 10.1016/0038-092X(77)90083-4 [DOI] [Google Scholar]
- Gordon, H. R. , & Morel, A. Y. (1983). Physics of ocean color remote sensing. In Gordon H. R. & Morel A. Y. (Eds.), Remote assessment of ocean color for interpretation of satellite visible imagery: A review (pp. 3–23). Springer US. 10.1007/978-1-4684-6280-7_2 [DOI] [Google Scholar]
- Griffies, S. M. (2012). Elements of the modular ocean model (MOM) (2012 release with updates) (GFDL Ocean Group Technical Report 7; p. 632 + xiii). Retrieved from https://mom‐ocean.github.io/assets/pdfs/MOM5_manual.pdf [Google Scholar]
- Hale, G. M. , & Querry, M. R. (1973). Optical constants of water in the 200‐nm to 200‐μm wavelength region. Applied Optics, 12(3), 555–563. 10.1364/AO.12.000555 [DOI] [PubMed] [Google Scholar]
- Hasumi, H. (2015). CCSR ocean component model (COCO) version 4.0. Atmosphere and Ocean Research Institute, The University of Tokyo. Retrieved from http://www.jstage.jst.go.jp/article/suisan/77/1/77_1_134/_article/‐char/ja/ [Google Scholar]
- Hill, V. J. (2008). Impacts of chromophoric dissolved organic material on surface ocean heating in the Chukchi Sea. Journal of Geophysical Research, 113(C7), C07024. 10.1029/2007JC004119 [DOI] [Google Scholar]
- Holmes, R. M. , Zika, J. D. , & England, M. H. (2019). Diathermal heat transport in a global ocean model. Journal of Physical Oceanography, 49(1), 141–161. 10.1175/JPO-D-18-0098.1 [DOI] [Google Scholar]
- Howell, T. A. , Meek, D. W. , & Hatfield, J. L. (1983). Relationship of photosynthetically active radiation to shortwave radiation in the San Joaquin Valley. Agricultural Meteorology, 28(2), 157–175. 10.1016/0002-1571(83)90005-5 [DOI] [Google Scholar]
- Iudicone, D. , Madec, G. , & McDougall, T. J. (2008). Water‐mass transformations in a neutral density framework and the key role of light penetration. Journal of Physical Oceanography, 38(7), 1357–1376. 10.1175/2007JPO3464.1 [DOI] [Google Scholar]
- Ivanoff, A. (1977). Oceanic absorption of solar energy. Modelling and Prediction of the Upper Layers of the Ocean, 47–71. [Google Scholar]
- Jerlov, N. G. (1968). Optical oceanography. Elsevier Pub. Co. [Google Scholar]
- Jerlov, N. G. (1976). Marine optics. Elsevier Scientific Pub. Co. [Google Scholar]
- Jin, D. , Waliser, D. E. , Jones, C. , & Murtugudde, R. (2013). Modulation of tropical ocean surface chlorophyll by the Madden–Julian Oscillation. Climate Dynamics, 40(1–2), 39–58. 10.1007/s00382-012-1321-4 [DOI] [Google Scholar]
- Jochum, M. , Yeager, S. , Lindsay, K. , Moore, K. , & Murtugudde, R. (2010). Quantification of the feedback between phytoplankton and ENSO in the community climate system model. Journal of Climate, 23(11), 2916–2925. 10.1175/2010JCLI3254.1 [DOI] [Google Scholar]
- Kahru, M. , Leppanen, J.‐M. , & Rud, O. (1993). Cyanobacterial blooms cause heating of the sea surface. Marine Ecology Progress Series, 101(1/2), 1–7. 10.3354/meps101001 [DOI] [Google Scholar]
- Kantha, L. H. , & Clayson, C. A. (1994). An improved mixed layer model for geophysical applications. Journal of Geophysical Research, 99(C12), 25235–25266. 10.1029/94JC02257 [DOI] [Google Scholar]
- Katsaros, K. B. , McMurdie, L. A. , Lind, R. J. , & DeVault, J. E. (1985). Albedo of a water surface, spectral variation, effects of atmospheric transmittance, sun angle and wind speed. Journal of Geophysical Research, 90(C4), 7313–7321. 10.1029/JC090iC04p07313 [DOI] [Google Scholar]
- Kim, G. E. , Pradal, M.‐A. , & Gnanadesikan, A. (2015). Quantifying the biological impact of surface ocean light attenuation by colored detrital matter in an ESM using a new optical parameterization. Biogeosciences, 12(16), 5119–5132. 10.5194/bg-12-5119-2015 [DOI] [Google Scholar]
- Kirk, J. T. O. (1994). Light and photosynthesis in aquatic ecosystems (2nd ed.). Cambridge University Press. 10.1017/CBO9780511623370 [DOI] [Google Scholar]
- Kraus, E. B. (1972). Atmosphere‐ocean interaction. Clarendon. [Google Scholar]
- Kvifte, G. , Hegg, K. , & Hansen, V. (1983). Spectral distribution of solar radiation in the nordic countries. Journal of Applied Meteorology and Climatology, 22(1), 143–152. [DOI] [Google Scholar]
- Lan, Y.‐Y. , Hsu, H.‐H. , Tseng, W.‐L. , & Jiang, L.‐C. (2022). Embedding a one‐column ocean model in the community atmosphere model 5.3 to improve Madden–Julian Oscillation simulation in boreal winter. Geoscientific Model Development, 15(14), 5689–5712. 10.5194/gmd-15-5689-2022 [DOI] [Google Scholar]
- Large, W. G. , & Caron, J. M. (2015). Diurnal cycling of sea surface temperature, salinity, and current in the CESM coupled climate model. Journal of Geophysical Research: Oceans, 120(5), 3711–3729. 10.1002/2014JC010691 [DOI] [Google Scholar]
- Lengaigne, M. , Menkes, C. , Aumont, O. , Gorgues, T. , Bopp, L. , André, J.‐M. , & Madec, G. (2007). Influence of the oceanic biology on the tropical Pacific climate in a coupled general circulation model. Climate Dynamics, 28(5), 503–516. 10.1007/s00382-006-0200-2 [DOI] [Google Scholar]
- Lim, H.‐G. , Kug, J.‐S. , & Park, J.‐Y. (2019). Biogeophysical feedback of phytoplankton on Arctic climate. Part II: Arctic warming amplified by interactive chlorophyll under greenhouse warming. Climate Dynamics, 53(5), 3167–3180. 10.1007/s00382-019-04693-5 [DOI] [Google Scholar]
- Lin, P. , Yu, Z. , Liu, H. , Yu, Y. , Li, Y. , Jiang, J. , et al. (2020). LICOM model datasets for the CMIP6 ocean model intercomparison project. Advances in Atmospheric Sciences, 37(3), 239–249. 10.1007/s00376-019-9208-5 [DOI] [Google Scholar]
- Madec, G. , Bell, M. , Blaker, A. , Bricaud, C. , Bruciaferri, D. , Castrillo, M. , et al. (2023). NEMO ocean engine reference manual. 10.5281/zenodo.8167700 [DOI]
- Manizza, M. , Le Quéré, C. , Watson, A. J. , & Buitenhuis, E. T. (2005). Bio‐optical feedbacks among phytoplankton, upper ocean physics and sea‐ice in a global model. Geophysical Research Letters, 32(5), L05603. 10.1029/2004GL020778 [DOI] [Google Scholar]
- Marzeion, B. , Timmermann, A. , Murtugudde, R. , & Jin, F.‐F. (2005). Biophysical feedbacks in the tropical Pacific. Journal of Climate, 18(1), 58–70. 10.1175/JCLI3261.1 [DOI] [Google Scholar]
- McCree, K. J. (1966). A solarimeter for measuring photosynthetically active radiation. Agricultural Meteorology, 3(5), 353–366. 10.1016/0002-1571(66)90017-3 [DOI] [Google Scholar]
- Mobley, C. D. (1994). Light and water: Radiative transfer in natural waters. Retrieved from https://cir.nii.ac.jp/crid/1130282269840486656
- Mobley, C. D. , Sundman, L. K. , Bissett, W. P. , & Cahill, B. (2009). Fast and accurate irradiance calculations for ecosystem models. Biogeosciences Discussions, 6(6), 10625–10662. 10.5194/bgd-6-10625-2009 [DOI] [Google Scholar]
- Moeller, H. V. , Laufkötter, C. , Sweeney, E. M. , & Johnson, M. D. (2019). Light‐dependent grazing can drive formation and deepening of deep chlorophyll maxima. Nature Communications, 10(1), 1. 10.1038/s41467-019-09591-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moon, P. (1940). Proposed standard solar‐radiation curves for engineering use. Journal of the Franklin Institute, 230(5), 583–617. 10.1016/S0016-0032(40)90364-7 [DOI] [Google Scholar]
- Morel, A. (1988). Optical modeling of the upper ocean in relation to its biogenous matter content (case I waters). Journal of Geophysical Research, 93(C9), 10749–10768. 10.1029/JC093iC09p10749 [DOI] [Google Scholar]
- Morel, A. (1991). Light and marine photosynthesis: A spectral model with geochemical and climatological implications. Progress in Oceanography, 26(3), 263–306. 10.1016/0079-6611(91)90004-6 [DOI] [Google Scholar]
- Morel, A. , & Antoine, D. (1994). Heating rate within the upper ocean in relation to its bio–optical state. Journal of Physical Oceanography, 24(7), 1652–1665. [DOI] [Google Scholar]
- Morel, A. , Huot, Y. , Gentili, B. , Werdell, P. J. , Hooker, S. B. , & Franz, B. A. (2007). Examining the consistency of products derived from various ocean color sensors in open ocean (Case 1) waters in the perspective of a multi‐sensor approach. Remote Sensing of Environment, 111(1), 69–88. 10.1016/j.rse.2007.03.012 [DOI] [Google Scholar]
- Morel, A. , & Maritorena, S. (2001). Bio‐optical properties of oceanic waters: A reappraisal. Journal of Geophysical Research, 106(C4), 7163–7180. 10.1029/2000JC000319 [DOI] [Google Scholar]
- Murtugudde, R. , Beauchamp, J. , McClain, C. R. , Lewis, M. , & Busalacchi, A. J. (2002). Effects of penetrative radiation on the upper tropical ocean circulation. Journal of Climate, 15(5), 470–486. [DOI] [Google Scholar]
- Nann, S. , & Riordan, C. (1991). Solar spectral irradiance under clear and cloudy skies: Measurements and a semiempirical model. Journal of Applied Meteorology and Climatology, 30(4), 447–462. [DOI] [Google Scholar]
- Ohlmann, J. C. (2003). Ocean radiant heating in climate models. Journal of Climate, 16(9), 1337–1351. [DOI] [Google Scholar]
- Ohlmann, J. C. , & Siegel, D. A. (2000). Ocean radiant heating. Part II: Parameterizing solar radiation transmission through the upper ocean. Journal of Physical Oceanography, 30(8), 1849–1865. [DOI] [Google Scholar]
- Ohlmann, J. C. , Siegel, D. A. , & Mobley, C. D. (2000). Ocean radiant heating. Part I: Optical influences. Journal of Physical Oceanography, 30(8), 1833–1848. [DOI] [Google Scholar]
- Ohlmann, J. C. , Siegel, D. A. , & Washburn, L. (1998). Radiant heating of the western equatorial Pacific during TOGA‐COARE. Journal of Geophysical Research, 103(C3), 5379–5395. 10.1029/97JC03422 [DOI] [Google Scholar]
- Papaioannou, G. , Papanikolaou, N. , & Retalis, D. (1993). Relationships of photosynthetically active radiation and shortwave irradiance. Theoretical and Applied Climatology, 48(1), 23–27. 10.1007/BF00864910 [DOI] [Google Scholar]
- Paulson, C. A. , & Simpson, J. J. (1977). Irradiance measurements in the upper ocean. Journal of Physical Oceanography, 7(6), 952–956. [DOI] [Google Scholar]
- Paulson, C. A. , & Simpson, J. J. (1981). The temperature difference across the cool skin of the ocean. Journal of Geophysical Research, 86(C11), 11044–11054. 10.1029/JC086iC11p11044 [DOI] [Google Scholar]
- Payne, R. E. (1972). Albedo of the sea surface. Journal of the Atmospheric Sciences, 29(5), 959–970. [DOI] [Google Scholar]
- Petersen, M. R. , Asay‐Davis, X. S. , Jacobsen, D. W. , Maltrud, M. E. , Ringler, T. D. , Van Roekel, L. , et al. (2018). MPAS‐ocean model user’s guide version 6.0 (LA‐UR‐18‐23444). Los Alamos National Laboratory (LANL). 10.2172/1434462 [DOI] [Google Scholar]
- Pope, R. M. , & Fry, E. S. (1997). Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Applied Optics, 36(33), 8710–8723. 10.1364/AO.36.008710 [DOI] [PubMed] [Google Scholar]
- Prytherch, J. , Farrar, J. T. , & Weller, R. A. (2013). Moored surface buoy observations of the diurnal warm layer. Journal of Geophysical Research: Oceans, 118(9), 4553–4569. 10.1002/jgrc.20360 [DOI] [Google Scholar]
- Rao, C. R. N. (1984). Photosynthetically active components of global solar radiation: Measurements and model computations. Archives for Meteorology, Geophysics, and Bioclimatology Series B, 34(4), 353–364. 10.1007/bf02269448 [DOI] [Google Scholar]
- Reineman, B. D. , Lenain, L. , Statom, N. M. , & Melville, W. K. (2013). Development and testing of instrumentation for UAV‐based flux measurements within terrestrial and marine atmospheric boundary layers. Journal of Atmospheric and Oceanic Technology, 30(7), 1295–1319. 10.1175/JTECH-D-12-00176.1 [DOI] [Google Scholar]
- Ricchiazzi, P. , Yang, S. , Gautier, C. , & Sowle, D. (1998). SBDART: A research and teaching software tool for plane‐parallel radiative transfer in the Earth’s atmosphere. Bulletin of the American Meteorological Society, 79(10), 2101–2114. [DOI] [Google Scholar]
- Rodskjer, N. (1983). Spectral daily insolation at Uppsala, Sweden. Spectral Daily Insolation at Uppsala, Sweden, 33(1–2), 89–98. 10.1007/bf02273992 [DOI] [Google Scholar]
- Sakamoto, K. , Nakano, H. , Urakawa, S. , Toyoda, T. , Kawakami, Y. , Tsujino, H. , & Yamanaka, G. (2023). Reference manual for the meteorological research Institute community ocean model version 5 (technical report of the meteorological research Institute 87). Meteorological Research Institute. 10.11483/mritechrepo.87 [DOI] [Google Scholar]
- Sathyendranath, S. , Gouveia, A. D. , Shetye, S. R. , Ravindran, P. , & Platt, T. (1991). Biological control of surface temperature in the Arabian Sea. Nature, 349(6304), 6304–6356. 10.1038/349054a0 [DOI] [Google Scholar]
- Schmidt, W. (1908). Absorption der sonnenstrahlung im wasser. SB Akad. Wiss. Wien, 117, 237–253. [Google Scholar]
- Shackelford, K. , DeMott, C. A. , Jan van Leeuwen, P. , Mazloff, M. R. , & Sun, R. (2024). A cold lid on a warm ocean: Indian Ocean surface rain layers and their feedbacks to the atmosphere. Journal of Geophysical Research: Atmospheres, 129(4), e2023JD039272. 10.1029/2023JD039272 [DOI] [Google Scholar]
- Siegel, D. A. , & Dickey, T. D. (1987). On the parameterization of irradiance for open ocean photoprocesses. Journal of Geophysical Research, 92(C13), 14648–14662. 10.1029/JC092iC13p14648 [DOI] [Google Scholar]
- Siegel, D. A. , Ohlmann, J. C. , Washburn, L. , Bidigare, R. R. , Nosse, C. T. , Fields, E. , & Zhou, Y. (1995). Solar radiation, phytoplankton pigments and the radiant heating of the equatorial Pacific warm pool. Journal of Geophysical Research, 100(C3), 4885–4891. 10.1029/94JC03128 [DOI] [Google Scholar]
- Siegel, D. A. , Westberry, T. K. , & Ohlmann, J. C. (1999). Cloud color and ocean radiant heating. Journal of Climate, 12(4), 1101–1116. [DOI] [Google Scholar]
- Simpson, J. J. , & Dickey, T. D. (1981). The relationship between downward irradiance and upper ocean structure. Journal of Physical Oceanography, 11(3), 309–323. [DOI] [Google Scholar]
- Smith, R. , Jones, P. , Briegleb, B. , Bryan, F. , Danabasoglu, G. , Dennis, J. , et al. (2010). The parallel ocean program (POP) reference manual.
- Smith, R. C. , & Baker, K. S. (1978). Optical classification of natural waters 1: Optical classification. Limnology & Oceanography, 23(2), 260–267. 10.4319/lo.1978.23.2.0260 [DOI] [Google Scholar]
- Smith, R. C. , & Baker, K. S. (1981). Optical properties of the clearest natural waters (200–800 nm). Applied Optics, 20(2), 177–184. 10.1364/AO.20.000177 [DOI] [PubMed] [Google Scholar]
- Soloviev, A. (1982). On the vertical structure of the thin surface layer of the ocean during a weak wind. Izvestiya ‐ Atmospheric and Oceanic Physics, 18(7), 579–585. [Google Scholar]
- Strutton, P. G. , & Chavez, F. P. (2004). Biological heating in the equatorial Pacific: Observed variability and potential for real‐time calculation. Journal of Climate, 17(5), 1097–1109. [DOI] [Google Scholar]
- Sweeney, C. , Gnanadesikan, A. , Griffies, S. M. , Harrison, M. J. , Rosati, A. J. , & Samuels, B. L. (2005). Impacts of shortwave penetration depth on large‐scale ocean circulation and heat transport. Journal of Physical Oceanography, 35(6), 1103–1119. 10.1175/JPO2740.1 [DOI] [Google Scholar]
- Tanre, D. , Herman, M. , Deschamps, P. Y. , & de Leffe, A. (1979). Atmospheric modeling for space measurements of ground reflectances, including bidirectional properties. Applied Optics, 18(21), 3587–3594. 10.1364/AO.18.003587 [DOI] [PubMed] [Google Scholar]
- Thompson, E. J. , Moum, J. N. , Fairall, C. W. , & Rutledge, S. A. (2019). Wind limits on rain layers and diurnal warm layers. Journal of Geophysical Research: Oceans, 124(2), 897–924. 10.1029/2018JC014130 [DOI] [Google Scholar]
- Twelves, A. G. , Goldberg, D. N. , Henley, S. F. , Mazloff, M. R. , & Jones, D. C. (2021). Self‐shading and meltwater spreading control the transition from light to iron limitation in an antarctic coastal polynya. Journal of Geophysical Research: Oceans, 126(2), e2020JC016636. 10.1029/2020JC016636 [DOI] [Google Scholar]
- Wallcraft, A. J. , Metzger, E. J. , & Carroll, S. N. (2009). Software design description for the HYbrid coordinate ocean model (HYCOM), version 2.2. Defense Technical Information Center. 10.21236/ADA494779 [DOI] [Google Scholar]
- Wang, Q. , Danilov, S. , Sidorenko, D. , Timmermann, R. , Wekerle, C. , Wang, X. , et al. (2014). The finite element sea ice‐ocean model (FESOM) v.1.4: Formulation of an ocean general circulation model. Geoscientific Model Development, 7(2), 663–693. 10.5194/gmd-7-663-2014 [DOI] [Google Scholar]
- Weiss, A. , & Norman, J. M. (1985). Partitioning solar radiation into direct and diffuse, visible and near‐infrared components. Agricultural and Forest Meteorology, 34(2), 205–213. 10.1016/0168-1923(85)90020-6 [DOI] [Google Scholar]
- Wetzel, P. , Maier‐Reimer, E. , Botzet, M. , Jungclaus, J. , Keenlyside, N. , & Latif, M. (2006). Effects of ocean biology on the penetrative radiation in a coupled climate model. Journal of Climate, 19(16), 3973–3987. 10.1175/JCLI3828.1 [DOI] [Google Scholar]
- Wick, G. A. , Ohlmann, J. C. , Fairall, C. W. , & Jessup, A. T. (2005). Improved oceanic cool‐skin corrections using a refined solar penetration model. Journal of Physical Oceanography, 35(11), 1986–1996. 10.1175/JPO2803.1 [DOI] [Google Scholar]
- Witte, C. R. , Zappa, C. J. , & Subramaniam, A. S. (2024). Data for: An improved bio‐physical parameterization for radiant heating in the surface ocean [Dataset]. Columbia Academic Commons. 10.7916/wmdm-vm51 [DOI]
- Yocum, C. S. , Allen, L. H. , & Lemon, E. R. (1964). Photosynthesis under field conditions. VI. Solar radiation balance and photosynthetic efficiency. Agronomy Journal, 56(3), 249–253. 10.2134/agronj1964.00021962005600030001x [DOI] [Google Scholar]
- Zaneveld, J. R. V. , Kitchen, J. C. , & Pak, H. (1981). The influence of optical water type on the heating rate of a constant depth mixed layer. Journal of Geophysical Research, 86(C7), 6426–6428. 10.1029/JC086iC07p06426 [DOI] [Google Scholar]
- Zaneveld, J. R. V. , & Spinrad, R. W. (1980). An arc tangent model of irradiance in the sea. Journal of Geophysical Research, 85(C9), 4919–4922. 10.1029/JC085iC09p04919 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Witte, C. R. , Zappa, C. J. , & Subramaniam, A. S. (2024). Data for: An improved bio‐physical parameterization for radiant heating in the surface ocean [Dataset]. Columbia Academic Commons. 10.7916/wmdm-vm51 [DOI]
Data Availability Statement
Data used in this study (Witte et al., 2024) are archived for public access on Columbia Academic Commons (https://doi.org/10.7916/wmdm‐vm51). The code used to produce the figures in this study is available for public access on GitHub (https://github.com/Zappa‐Lab/Bio‐Physical‐Radiant‐Heating‐Parameterization).


