Theory of the Multiregional Neocortex: Large-Scale Neural Dynamics and Distributed Cognition

Abstract

The neocortex is a complex neurobiological system with many interacting regions. How these regions work together to subserve flexible behavior and cognition has become increasingly amenable to rigorous research. Here, I review recent experimental and theoretical work on the modus operandi of a multiregional cortex. These studies revealed several general principles for the neocortical interareal connectivity, low-dimensional macroscopic gradients of biological properties across cortical areas, and a hierarchy of timescales for information processing. Theoretical work suggests testable predictions regarding differential excitation and inhibition along feedforward and feedback pathways in the cortical hierarchy. Furthermore, modeling of distributed working memory and simple decision-making has given rise to a novel mathematical concept, dubbed bifurcation in space, that potentially explains how different cortical areas, with a canonical circuit organization but gradients of biological heterogeneities, are able to subserve their respective (e.g., sensory coding versus executive control) functions in a modularly organized brain.

1. INTRODUCTION

Experimental studies that falsified phrenology were pioneered by Karl Lashley a century ago. Lesioning increasingly larger portions of the brains of rats trained to carry out memory tasks, Lashley observed that behavioral performance deteriorated to a degree in proportion with the lesion size. This finding led him to propose the idea of equipotentiality: namely, outside the primary sensory areas, multiple parts of the brain work together, and when one part is damaged, its function can be assumed by another part through plasticity (Lashley 1929). In much of the twentieth century, because of technical limitations on single-cell recording from behaving animals, neuroscientists have predominantly focused on local circuits, such as place cells in the rodent hippocampus or visual motion direction and velocity tuning of neurons in the primate middle temporal visual area. As a result, our knowledge about the multiregional brain has been limited. While neural processes underlying functions are distributed, the brain is organized modularly, and subsets of brain regions are dedicated to different functions. A principled, mechanistic, and computational understanding of localized versus distributed brain functions represents a major challenge.

The situation has begun to change notably in recent years, thanks to advances in the two pillars of neuroscience: the brain connectome and neurophysiology of behaving animals. Research in brain connectomics (White et al. 1986, Sporns 2009, Seung 2012, Swanson & Lichtman 2016, Abbott et al. 2020, Wang et al. 2020) has produced quantitative connectivity data at microscopic, mesoscopic, and macroscopic scales (Hagmann et al. 2008, Bohland et al. 2009, Glasser & Van Essen 2011, Helmstaedter et al. 2013, Markov et al. 2014a, Harris et al. 2019, Xu et al. 2020, Xu et al. 2021, Foster et al. 2021, Dorkenwald et al. 2022). These anatomical findings have yielded crucial information about how specific neural circuits carry out precise computation, such as a ring network for head direction encoding (Turner-Evans et al. 2020) and vector calculations for navigation (Lyu et al. 2022) in the fruit fly Drosophila. At the same time, simultaneous recording from many neurons in multiple brain regions of behaving animals has become feasible (Dotson et al. 2017), especially with the invention of Neuropixels ( Jun et al. 2017, Steinmetz et al. 2021). Both anatomical and physiological studies are aided by transcriptomics, which provides genetic tools for classification of cell types and cell type–specific connectivity analysis (Luo et al. 2008, Tasic et al. 2018, Krienen et al. 2020).

In the following sections, I discuss new experimental and computational research that suggests provisionally general principles of structure, dynamics, and cognitive processes in a large-scale multiregional neocortex. I first summarize a particular line of connectomic analysis that has produced a directed and weighted area-to-area neocortical connectivity matrix as well as a quantification of cortical hierarchy. Then I review the developments of dynamic models that are built on the new connectivity data and incorporate the concept of macroscopic gradients of synaptic excitation and inhibition across the entire cortical mantle. Such modeling revealed a hierarchy of timescales; its empirical tests and functional implications are covered next. In simulated delayed response tasks, our model produces working memory representations that are distributed, but they engage selective subsets of cortical areas rather than indiscriminately across the whole system. Finally, in decision-making, it displays a transition from graded responses in sensory areas to an all-or-none activation in prefrontal areas, akin to the ignition phenomenon proposed in the global neuronal workspace (GNW) model of consciousness. Taken together, these results offer insights into how differential functional capabilities may emerge, by virtue of bifurcations in space, from a large-scale neocortex that is built on a canonical local circuit organization and endowed with low-dimensional heterogeneities in the form of gradients of biological properties (Wang 2020).

2. FOUR PRINCIPLES OF LARGE-SCALE NEOCORTICAL ORGANIZATION

2.1. Quantitative Characteristics of the Cortical Connectome

The advances of magnetic resonance imaging (MRI) diffusion-weighted tractography made it possible to noninvasively map out anatomical connection fibers in the brain. Functional connectivity (FC) studies have been carried out using functional MRI (fMRI), electrocorticography, electroencephalography (EEG), or magnetoencephalography (MEG). These experiments inspired and benefited from the use of graph theory, better known today as network science, applied to quantify the brain’s connectivity (Sporns 2009, Fornito et al. 2016, Bassett & Sporns 2017).

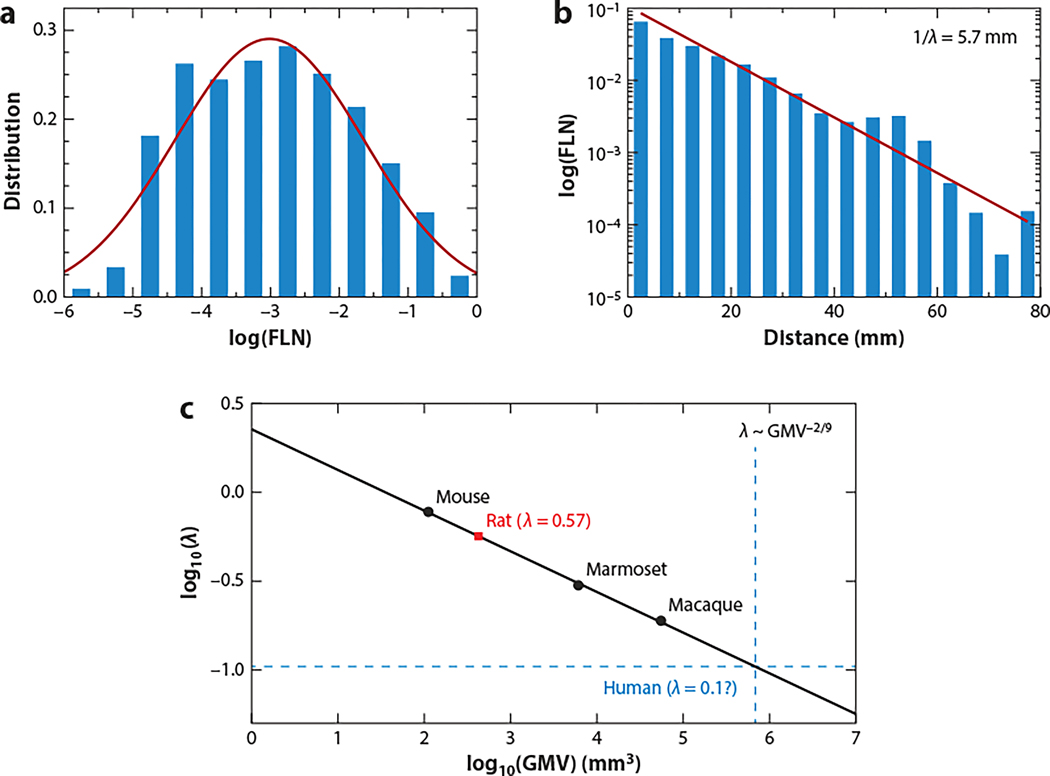
Diffusion tractography does not yield directional information: measured fibers do not distinguish projections from area A to area B or the other way around; rather, the resulting connection matrix is symmetrical. Also, due to a limited signal-to-noise ratio (Donahue et al. 2016), analysis of diffusion tractography often focuses on all-or-none binary matrix. By contrast, retrograde or anterograde tracing provides directional information as well as a reliable quantification of connection weights. The publication of a quantitative matrix of macaque cortical connectivity from the group of Henry Kennedy represents a significant recent advance (Markov et al. 2014a). In that study of a subset of cortical areas, a retrograde tracer injected in a parcellated (target) area labeled neurons in other (source) areas that project to the target area. The relative input weight of one input area, among all source areas, was quantified by the fraction of labeled neurons (FLN) found in that source area. This measure of connection weights spans five orders of magnitude (Figure 1a); some interareal inputs are strong while many others are weak. Furthermore, Markov et al. (2014a) reported that about 65% of all possible connections are present; thus, on the macroscopic scale, interareal connectivity is quite dense in macaque cortex. This is in contrast to the early collation of connectivity data on the macaque brain (CoCoMac) matrix, which contains only 15% of all possible projections. Marmoset monkey cortex displays a comparable density of interareal connectivity, as well as five orders of magnitude of FLN values (Theodoni et al. 2022). In mouse cortex, interareal connection weights measured using an anterograde tracer span three orders of magnitude (Oh et al. 2014), and the overall connection density is even higher than in monkeys (Gămănųt et al. 2018).

Figure 1.

Interareal connections of macaque monkey cortex. (a) Relative weight of connection of one among all source areas to a target area is quantified by the fraction of labeled neurons (FLN). FLNs span five orders of magnitude and are fit by a lognormal distribution. (b) The FLN between a pair of cortical areas is an exponential function of their distance (red line), with the decay rate λ = 0.175 mm⁻¹. (c) Cortical connectivity spatial length as a function of gray matter volume (GMV). Shown is the base 10 logarithm of the decay rate λ of the exponential distance rule of the mouse, marmoset, and macaque, computed in the same way in all three cases. The plot is a linear fit on these three points with a slope of −2/9. The red square is the measured value of the decay rate in the rat, and the intersection of the blue dotted lines is the predicted decay rate in the human. Panels a and b adapted from Wang & Kennedy (2016) with original data from Markov et al. (2014a) and Ercsey-Ravasz et al. (2013). Panel c adapted from Theodoni et al. (2022) (CC BY 4.0).

In primates, generally, a feedforward projection—say, from visual area V1 to V2—originates in the superficial layers, whereas a feedback projection (from V2 to V1) is mediated by neurons in the deep layers (Maunsell & Van Essen 1983). Markov et al. (2014b) introduced a parametric measure called supragranular labeled neurons (SLNs) as the fraction of all labeled neurons in a given source area that are located in the superficial layers 2 and 3, with values between 0 and 1. Using SLNs of directed projections of pairs of areas, a consistent hierarchy can be established where each area is assigned a hierarchical position. Similar hierarchy has been reported for marmoset monkeys (Theodoni et al. 2022). In mice, cortical hierarchy is also present but shallow (Gămănųt et al. 2018, Harris et al. 2019), suggesting a less hierarchical form of organization in the rodent cortex. In macaque monkeys, there is a second top-down stream originating from neurons in the supragranular layer (Markov et al. 2014b). This observation led to the proposal of a dual counterstream architecture (Vezoli et al. 2021), the functional implications of which remain to be explored.

An important finding was that the FLN of a pair of areas decreases exponentially with the wiring distance between them (Figure 1b) with a characteristic rate λ (in mm⁻¹) (Ercsey-Ravasz et al. 2013). For macaque cortex, the characteristic spatial length 1/λ_macaque = 5.7 mm. Therefore, a cortical network is not only a topological graph but spatially embedded, and the locational relationship between nodes (areas) must be taken into account in a network description. This exponential distance rule (EDR) holds for marmoset monkeys (Theodoni et al. 2022) as well as mice (Horvát et al. 2016). Across nonhuman species, the decay rate of the EDR (λ) scales with the gray matter volume following a power law with an exponent of −2/9 (Figure 1c). Using this relation, we can extrapolate the decay rate of the projection lengths in the human cortical connectome to be ∼0.1 mm⁻¹, or a characteristic spatial length of 10 mm, a prediction that can be tested experimentally. The observed new scaling remains to be explained theoretically.

Motivated by recently available data, Song et al. (2014) proposed a new class of spatially embedded random networks for the interareal cortical system. The model is generative and thus can be realized with an arbitrary number of parcellated areas. It captures the macaque data quite well, including a span of connection weights comparable to that of the macaque cortex. Interestingly, other network properties found in the model turn out to be also supported by monkey data, such as rank-ordered in-degree (number of input areas for a target area) and out-degree (number of output areas of a source area) sequences and the distribution of triad motifs (graphs made of three areas).

In summary, directed and weighted interareal connectivity of cortex displays three salient characteristics. First, it is dense and follows a lognormal distribution of connection weights spanning several orders of magnitude. Second, the classical notion of cortical hierarchy is quantified such that each area is assigned a hierarchical position and the degree of feedforwardness or feedbackness of any area-to-area projection is described parametrically. The hierarchy thus defined is steeper in sensory areas than in association areas and shallower in mice than in monkeys. In a more extended view, the cortex is organized in a two-dimensional plot defined by anatomy alone, with the radial direction corresponding to the hierarchy, whereas different modalities and sensory versus motor areas are separated along the angular direction (Mesulam 1990, Chaudhuri et al. 2015, Margulies et al. 2016, Wang 2020). Third, the cortical circuit is spatially embedded according to the EDR. Therefore, purely topological graphs are inadequate. Spatial networks (Barthélemy 2011) offer a fuller description of cortical connections that takes into consideration spatial relationships between areas. It is worth noting that the connectivity data discussed above quantify anatomical connectivity between parcellated cortical areas but not physiological strengths of synaptic connections. Future efforts are desirable to improve such quantitative brain connectome with finer spatial resolution and, importantly, cell type specificity of source and target neurons.

2.2. Macroscopic Gradients of Cortical Heterogeneities

The mammalian cortex is well known to show spatial heterogeneity of neuron density, pyramidal cell size, myelin content in the gray matter, cortical thickness, and laminar differentiation (Amunts & Zilles 2015, Barbas 2015). What are the statistical rules of cortical heterogeneity? Analysis of genomic data in humans (Burt et al. 2018) revealed low-dimensional macroscopic gradients of genomic variations across the cortical sheet, with the first principal component accounting for nearly 30% of the variance and correlating strongly with a measure of cortical hierarchy. Mice similarly display macroscopic gradients of brain-specific gene expression while showing notable differences with primates (Fulcher et al. 2019). This is also true for other measures of cortical heterogeneity. In particular, spines are small protrusions of pyramidal dendrites, with each hosting a single excitatory synapse; therefore, the spine count per pyramidal cell represents a candidate proxy for the average strength of excitation per pyramidal neuron, even though the physiological strengths of individual synapses may vary considerably. Remarkably, in macaque monkeys, the spine count per pyramidal cell displays a strong positive correlation with the hierarchical position of cortical areas (Elston 2007, Chaudhuri et al. 2015); a pyramidal cell in prefrontal areas has about 10 times more spines than one in V1 (Supplemental Figure 1a). A graded increase of spine count per pyramidal neuron has also been found in marmoset monkeys (Theodoni et al. 2022). By contrast, in mice, total spine count per pyramidal cell appears to be the same for V1 and frontal areas (Gilman et al. 2017), suggesting that the macroscopic gradient of spine counts may be a distinct feature of the primate cortex.

GABAergic inhibitory neurons subdivide into various categories (Markram et al. 2004). A disinhibitory motif was proposed theoretically (Wang et al. 2004) and supported amply by experiments (Kepecs & Fishell 2014, Tremblay et al. 2016, Cardin 2018), realized by three inhibitory subtypes defined by their projection targets: (a) to the perisomatic region of pyramidal cells and controlling spiking output of excitatory neurons, (b) to pyramidal dendrites for input control, and (c) to dendrite-targeting inhibitory cells. The ratio of input-controlling and output-controlling inhibitory cells displays a macroscopic gradient (Supplemental Figure 1b) in mice (Kim et al. 2017) and monkeys (Kondo et al. 1999, Torres-Gomez et al. 2020), with progressively fewer output-controlling and more input-controlling interneurons from early sensory areas to association areas.

In summary, macroscopic gradients represent a principle of large-scale cortical organization (Wang 2020, Bernhardt et al. 2022). The dynamic and functional implications of these macroscopic gradients across the entire cortical mantle are discussed in the remainder of this article.

3. DISTRIBUTED CORTICAL DYNAMICS AND PROCESSING

Computational modeling of information processing and behavior in a large-scale brain system has drawn attention recently (Eliasmith 2013). Structural data provide crucial information for large-scale cortical modeling (Izhikevich & Edelman 2008, Deco & Jirsa 2012, Breakspear 2017). Using FLNs (Markov et al. 2014a) and SLNs (Markov et al. 2014b), a dynamic model of the macaque cortex can be developed. How should each area be modeled? The answer depends on the scientific aim of a study. Consider first the idea of a canonical circuit valid for all cortical areas from V1 through prefrontal cortex (PFC), but in which there is a macroscopic gradient of synaptic excitation. Mathematically, a canonical architecture is implemented by an identical excitatory-inhibitory recurrent network for each local area—for instance, using a population firing rate model from Binzegger et al. (2009) or Wong & Wang (2006). Long-range area-to-area connectivity is given by measured FLNs. With the assumption that measured spine count (Elston 2007) is proportional to the synaptic excitation strength per neuron, a macroscopic gradient is introduced to vary across areas.

3.1. A Hierarchy of Timescales

Chaudhuri et al. (2015) found that a hierarchy of timescales naturally emerges from such a large-scale cortex model (Supplemental Figure 2). The hierarchy of time constants is functionally desirable. On the one hand, primary sensory areas should operate quickly to encode and process rapidly changing external stimuli. On the other hand, prefrontal and parietal cortical areas should have slow transients in the form of ramping activity required for accumulation of information in decision-making (Gold & Shadlen 2007, Wang 2008, Shadlen & Kandel 2021). The wide range of time constants emerges from the model, which depends on both a macroscopic gradient of synaptic excitation and complex feedback loops in the multiregional cortical system.

These results raise questions of how to explain a hierarchy of timescales. Consider the system in the resting state to be approximated by a linear and highly complex dynamic system (Nozari et al. 2020), for which time constants are given by the real parts of eigenvalues (Strogatz 2016). What are the system’s essential properties required for the generation of a broad range of time constants, and given the dense connectivity, why are disparate eigenmodes spatially segregated rather than intermixed throughout the system? Mathematical analyses (Chaudhuri et al. 2014, Li & Wang 2022) identified specific conditions under which a cortical circuit realizes spatial localization of time constants. A macroscopic gradient of biological properties is important for generating a broad range of time constants. Intuitively, recurrent excitation prolongs the effective time constant of a neural circuit, because a positive feedback enables neural activity to increase for a longer time than in the absence of reverberation (Seung 1996, Wang 2001). Thus, heterogeneity of synaptic excitation as well as inhibition (which shapes network dynamics) creates a broad range of time constants. Furthermore, each long-range projection pathway must be balanced, in the sense that the long-range excitatory-to-excitatory projection is counteracted by the local excitatory-to-inhibitory one (Vogels & Abbott 2009), which is aided by a larger gain of the input-output relationship for inhibitory neurons than excitatory neurons. Consequently, the net interareal input is weak relative to local recurrent dynamics. This is consistent with the observation in the tract-tracing experiments that the majority (80%) of cortical connections are part of the local circuit and originate within the injected area itself; long-range inputs from other cortical areas are relatively weak compared to local synaptic connections (Markov et al. 2014a).

3.2. Experimental Observations of a Temporal Hierarchy

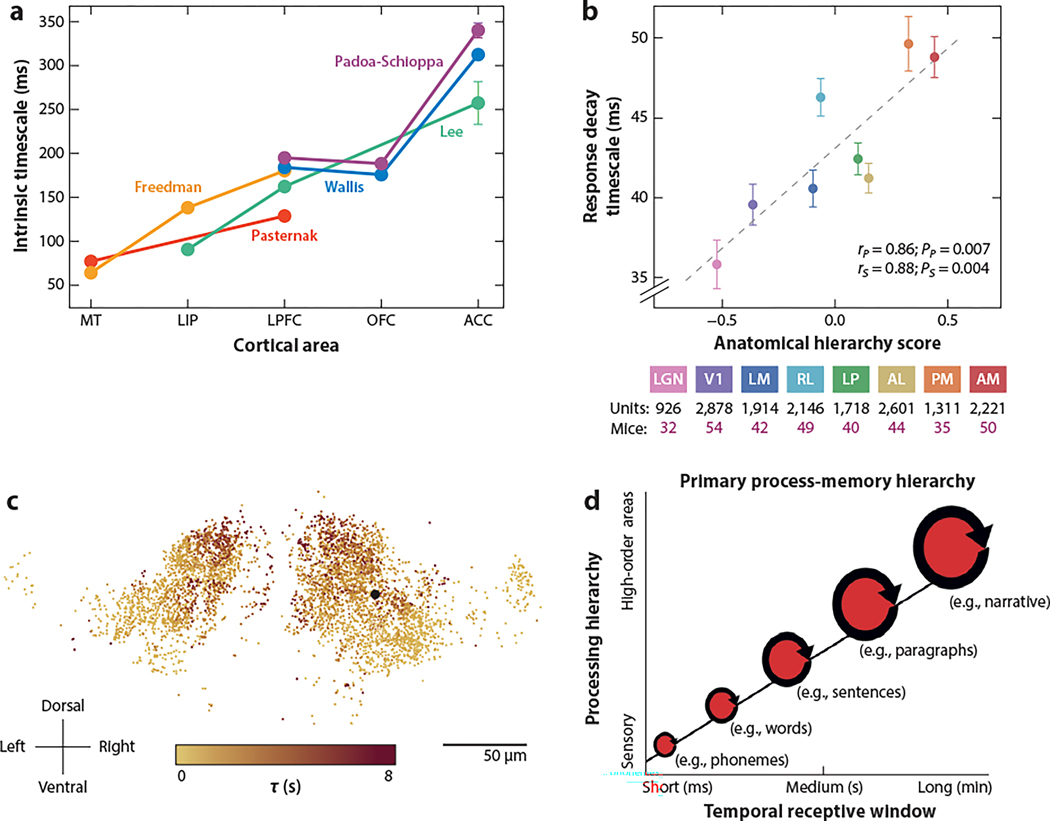
A hierarchy of temporal response windows or timescales is supported by several lines of empirical evidence. Spurred by computational findings (Chaudhuri et al. 2015), Murray et al. (2014) analyzed single-neuron data recorded from macaque monkeys performing different tasks in five laboratories. In support of the model, the characteristic time constant of neural fluctuations displayed a systematical increase along the hierarchy (Figure 2a) (see also Ogawa & Komatsu 2010, Runyan et al. 2017, Cavanagh et al. 2018, Wasmuht et al. 2018, Fascianelli et al. 2019, Spitmaan et al. 2020, Maisson et al. 2021, Manea et al. 2021). The range of the observed time constants is smaller than that in the model, possibly for several reasons. In particular, adjusting model parameter values can achieve a better quantitative comparison with data. More importantly, the biological cortex is a highly nonlinear system for which time constants are not uniquely defined but depend on its internal state; the exact range of time constants varies over the brain’s states and behaviors.

Figure 2.

Hierarchy of time constants in the neocortex. (a) Time constant extracted from autocorrelation function of neuronal spiking fluctuations during baseline of eye fixation in five cortical areas of macaque monkeys as a function of an anatomically defined hierarchical position. (b) Time constant of autocorrelation function of neuronal spiking fluctuations in thalamic LGN, the LP, V1, and five higher-order visual cortical areas (LM, AL, RL, PM, and AM) of mice as a function of their anatomically defined hierarchical positions. (c) Spatial distribution of information integration time constants in the brain of zebrafish performing a decision task. (d) Hierarchy of time constants in human cortical areas underlying language processing. A hierarchy of speech processing timescale (operationalized by measuring the temporal receptive window) in each region increases in a topographically organized manner, from milliseconds up to minutes. Abbreviations: ACC, anterior cingulate cortex; AL, anterolateral area; AM, anteromedial area; LGN, lateral geniculate nucleus; LIP, lateral intraparietal area; LM, lateromedial area; LP, visual pulvinar; LPFC, lateral prefrontal cortex; MT, middle temporal visual area; OFC, orbitofrontal cortex; PM, posteromedial area; RL, rostrolateral area. Panel a adapted from Murray et al. (2014) (CC BY 4.0). Panel b adapted with permission from Siegle et al. (2021). Panel c adapted with permission from Dragomir et al. (2020). Panel d adapted with permission from Hasson et al. (2015).

Supporting evidence was also reported for mice, from a survey of spiking activities in eight thalamic and cortical visual areas (Siegle et al. 2021). The extracted time constant from each area, as calculated using the same analysis as used by Murray et al. (2014), increases with the anatomical hierarchy (Harris et al. 2019) (Figure 2b). Siegle et al. (2021) also reported that the size of a single neuron’s spatial receptive field (RF) is progressively larger along the hierarchy in mice, as is well known in other species (Lennie 1998). Thus, along the visual cortical hierarchy, neural circuits are endowed with increased capability of integration in both space and time. Spatial integration can be achieved through convergence of projections onto neurons in one area from neurons with smaller RFs in an upstream area. The model of Chaudhuri et al. (2015) offers a mechanism for a hierarchy of temporal response windows, in parallel with the enlargement of spatial response fields in the cortical hierarchy. The hierarchy of time constants demonstrates the importance of a macroscopic gradient of circuit properties across the cortex. In zebrafish, a wide range of time constants engaged in accumulation of information for decision-making has been demonstrated and shown to be spatially segregated (Dragomir et al. 2020) (Figure 2c).

The existence of macroscopic gradients implies that cortical areas are not the same, in contrast to commonly practiced graph theoretic analysis of FC. Intuitively, one expects that FC would resemble anatomical connectivity more closely if nodes were indeed the same; therefore, the global dynamics would be predominantly determined by the interactions between nodes. This was confirmed in simulations of our multiregional macaque cortex model (Chaudhuri et al. 2015). Studies combining model simulations with fMRI data from human cortex showed that their computational model captured the measured FC significantly better when a macroscopic gradient of synaptic excitation and inhibition was incorporated into the model than in the absence of it (Demirtąs et al. 2019, Kong et al. 2021), in support of Chaudhuri et al. (2015). These works highlight the need to take macroscopic gradients into consideration in future network studies of large-scale brain dynamics, especially in the FC analysis.

A hierarchy of timescales represents a new general principle of the neocortical organization of functional importance. First, it can be deployed for representation of temporal context of stimuli from the environment (Hasson et al. 2008, Kiebel et al. 2008, Baldassano et al. 2017). Comprehension depends on temporal integration of stimuli: for instance, following the storyline when watching a movie (Hasson et al. 2008). Second, since prefrontal and posterior parietal cortices with slow dynamics mediate selective attention, their top-down signaling can instantiate proactive attention on multiple timescales (Nobre & Stokes 2019). Third, human speech is an example of information processing on multiple timescales (Poeppel 2003, Hickok & Poeppel 2007, Chien & Honey 2020, Raut et al. 2020) (Figure 2d). Presumably, perception and appreciation of music (Zatorre et al. 2002, Levitin 2006) also rely on a hierarchy of time constants in the brain.

3.3. Top-Down Processing and Gated Interareal Communication

The cortex is endowed with an abundance of feedback projections (Felleman & Van Essen 1991, Gilbert & Li 2013, Kreiman & Serre 2020). Indeed, quantification of cortical pathways shows that feedback pathways are more numerous and have a greater hierarchical reach than feedforward ones. Top-down projections play important roles, such as selective attention (Desimone & Duncan 1995, Moore & Zirnsak 2017) and predictive coding (Rao & Ballard 1999, Summerfield et al. 2006, Bastos et al. 2012). The central idea of predictive coding is that the brain is not merely a passive receiver of sensory stimulation but constantly, and actively, generates inference about the external world. Predictive coding involves a comparison between an expectation signal mediated by top-down projection and sensory stimulus from bottom-up projection. In spite of its broad appeal and potential as a general principle, up to now, predictive coding has just begun to be investigated experimentally (Keller & Mrsic-Flogel 2018). Can the emerging large-scale cortex model shed light on such top-down processes?

Since feedforward and feedback projections are layer dependent (Maunsell & Van Essen 1983, Markov et al. 2014b, Vezoli et al. 2021), to examine the interplay between bottom-up and top-down processes in a multiregional model, feedforward and feedback projections should be wired in a layer-dependent manner. Mejias et al. (2016) extended the model of Chaudhuri et al. (2015) to incorporate a laminar structure that is simple yet anatomically and physiologically constrained. The extended model is developed in three steps. First, each cortical area now consists of two layers: a superficial layer (including layer 4) and a deep layer (below layer 4). This is minimal but adequate for implementing interareal connections in a layer-dependent fashion. The synaptic connections between the two layers are informed by neurophysiology (Thomson et al. 2002, Petreanu et al. 2009, DeNardo et al. 2015, Xu et al. 2016).

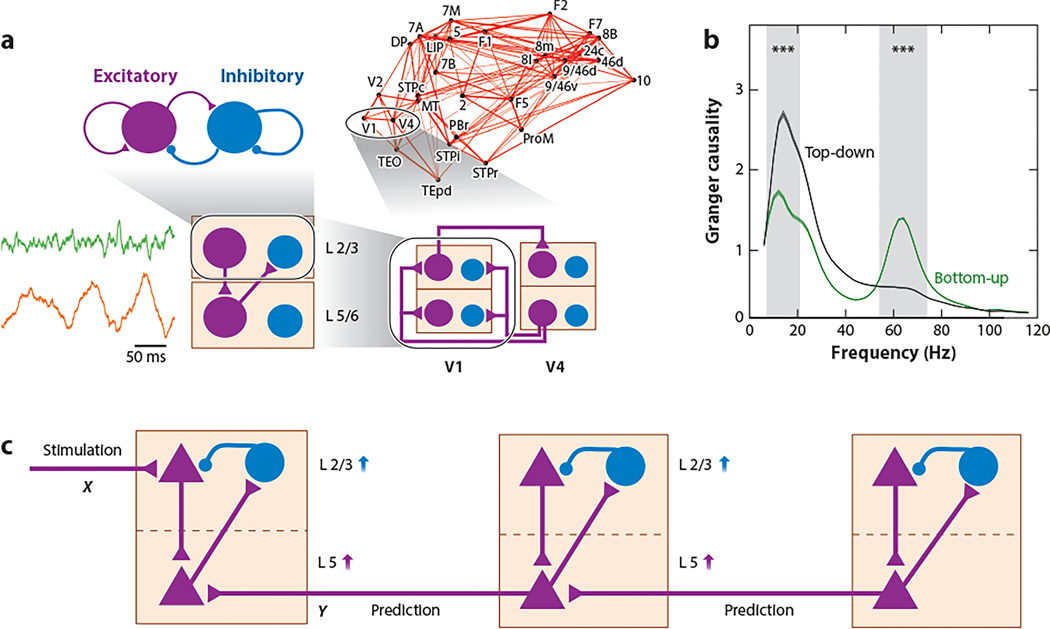
Second, numerous reports have documented that the superficial layer generates fast gamma oscillations at about 40 Hz, while the deep layer shows slower synchronous oscillations, such as alpha rhythm at about 10 Hz or beta rhythm at about 15–25 Hz (Buschman & Miller 2007, Buffalo et al. 2011, Wang 2010). In the model, neuronal populations in the deep layer show a rhythm at 10 Hz, whereas that in the superficial layer oscillates at 40 Hz (Figure 3a). Because of the synaptic interactions between the two layers, gamma oscillations in the superficial layer are modulated by alpha rhythm, as observed experimentally (Spaak et al. 2012).

Figure 3.

A multiregional model of the macaque monkey cortex endowed with a laminar structure. (a) The four levels incorporated in the model include a within-layer local microcircuit, a laminar circuit with two laminar modules, an interareal circuit with laminar-specific projections, and a large-scale network of cortical areas based on macaque anatomical connectivity. Each level is anatomically constrained. Only the connections at each level (not shown at a lower level) are plotted, for clarity. (Left) Stochastic gamma oscillations in the superficial layer (green) and alpha rhythm in the deep layer (orange). (b) Frequency-dependent Granger causality for bottom-up and top-down processes in macaque monkey cortex. ∗∗∗ denotes statistically significant difference. (c) A circuit substrate for predictive coding. Under the assumption that the dominant effect of feedback projection is excitation of infragranular pyramidal cells, which in turn project to supragranular inhibitory neurons, a top-down prediction signal Y changes the sign and is effectively inhibitory for infragranular excitatory neurons, compared with excitation X from feedforward stimulation, thereby implementing X − Y. This mechanism may apply to a chain of cortical areas in a hierarchy. Panel a adapted from Mejias et al. (2016). Panel b adapted with permission from Bastos et al. (2015).

Third, for the interareal connections, a feedforward projection originates from the superficial layer and targets the superficial layer, and a feedback projection starts with the deep layer of a source area, according to neuroanatomy. Less known are layer- and cell type–specific targets of feedback projections in macaque monkeys, although some information is available for mice (Petreanu et al. 2009, D’Souza et al. 2016, Young et al. 2021). In the model, for a feedback pathway the weights of projections into the superficial and deep layers of a target area are adjusted as free parameters.

This model reproduces salient observations from monkey experiments on feedforward versus feedback signaling (van Kerkoerle et al. 2014, Bastos et al. 2015) using a frequency-dependent Granger causality measure. For instance, a feedforward signal from V1 to V4 selectively enhances Granger causality in the gamma frequency range, whereas a feedback signal from V4 to V1 differentially increases Granger causality in the alpha frequency range (Figure 3b). These observations were reproduced by the model, provided that the feedback projection primarily targets excitatory neurons in the deep layer. Whether the latter condition is necessary remains to be further studied, both in models and experimentally.

Based on this general trend, Bastos et al. (2015) proposed a measure to deduce cortical hierarchy from frequency-dependent Granger causality analysis. Using the same analysis as in the monkey experiment, the computational model of Mejias et al. (2016) captures fairly well the hierarchy deduced from Granger causality analysis in the monkey experiment. This procedure is solely based on physiological measurements, and in the monkey experiment, these authors found that the hierarchy thus deduced correlates strongly with the anatomically deduced hierarchy. This success led Michalareas et al. (2016) to estimate cortical hierarchy based on noninvasive MEG measurements of the human cortex. Note that in humans, the cortical hierarchy has not been firmly established by purely anatomical means; therefore, a physiology-based approach is especially valuable.

The laminar model of Mejias et al. (2016) suggests a circuit substrate for predictive coding, as schematically shown in Figure 3c. Consider an area receiving a feedforward signal X onto pyramidal neurons in the superficial layer, such as external stimulation propagating along the hierarchy. A prediction signal Y from a higher area excites pyramidal neurons in the deep layers, which in turn project to supragranular inhibitory neurons, thereby changing the sign from Y to −Y, and can be compared with X as X − Y in pyramidal neurons of the superficial layers. Such a process can occur as an inverse cascade in a deep cortical network. This model prediction remains to be tested experimentally. In the real brain, a cortical area has several cell types, some of which signal expectation rather than prediction itself (Fiser et al. 2016). Moreover, multiple subclasses of inhibitory neurons are differentially targeted by feedforward and feedback projections. Therefore, there exist alternative or complementary scenarios; future work is needed to dissect brain mechanisms of predictive processing (Keller & Mrsic-Flogel 2018).

Another challenge in efforts to understand a multiregional brain system is concerned with gating of information flow, exemplified by selective attention (Olshausen et al. 1993). Gating becomes a broader challenge with the anatomical knowledge that interareal connections are dense; any given area receives inputs from several dozen source areas and projects to equally numerous target areas. “Pathway gating” (Yang et al. 2016) selectively allows inputs from particular area-to-area pathways. Currently, there are several ideas about how gating is realized (Wang & Yang 2018). First, the disinhibitory motif (Wang et al. 2004) is generalized to pathway gating, with the testable prediction that inputs from different source areas are clustered in separate parts of pyramidal dendrites, which are controlled by distinct subsets of somatostatin- or calbindin-expressing inhibitory neurons (Yang et al. 2016). Second, frequency-dependent synchronization could enhance communication to certain but not all downstream areas, thereby modulating communication differentially (Fries 2005, Buschman & Miller 2007, Wang 2010, Hahn et al. 2019). Third, information flow along a particular pathway may be encoded in a low-dimensional subspace of the source area’s population activity (Kaufman et al. 2014, Gallego et al. 2017, Semedo et al. 2019, Kohn et al. 2020, Yoo & Hayden 2020, Jazayeri & Ostojic 2021). Communication may also be flexibly reconfigured in a context-dependent manner within a target recurrent network (Mante et al. 2013). Using new tools like Neuropixels ( Jun et al. 2017), these scenarios can now be rigorously examined using simultaneous recording from multiple brain regions while animals perform rule-based task switching.

To summarize, in this section we highlighted the hierarchy of timescales as a newly established general principle of the large-scale neocortex. The connectome-based model of a multiregional cortical network opens the door for theoretical investigation of the interactions between bottom-up and top-down processes in a layer-dependent manner. Extending such modeling in the future will provide a computational platform to elucidate gated communication between cortical areas in a complex cortex-wide network.

4. DISTRIBUTED COGNITION

Brain imaging experiments and single-neuron physiology have long documented that multiple brain regions are engaged in basic cognitive processes like working memory (Baddeley 1987). For instance, in a delayed response task in which the spatial location of a briefly shown stimulus must be held in working memory across a short delay period of a few seconds, location-selective persistent neural activity during a mnemonic delay has been observed in the posterior parietal cortex (Gnadt & Andersen 1988), dorsolateral PFC (Funahashi et al. 1989), thalamus (Funahashi et al. 2004), and basal ganglia (Hikosaka & Wurtz 1983) of behaving monkeys. How can we understand the distributed nature of working memory (Christophel et al. 2017, Leavitt et al. 2017, Dotson et al. 2018)? Similarly, decision-making engages multiple brain regions (Siegel et al. 2015, Hattori et al. 2019, Pinto et al. 2019, Gallero-Salas et al. 2021), and value encoding for reward-based choice behavior is widespread in the brain (Vickery et al. 2011). In a recent study with mice performing a perceptual decision task, recording from 30,000 neurons in 40 brain regions revealed that sensory and selective choice signals are distributed differentially in distinct subsets of brain areas (Steinmetz et al. 2019). Moreover, several groups reported brain-wide activity correlated with movements (Ahrens et al. 2012, Musall et al. 2019, Steinmetz et al. 2019, Stringer et al. 2019), even in sensory areas presumably reflecting proprioceptive signals (Proske & Gandevia 2012) and/or feedback projections from motor command centers that signal corollary discharges (Sommer & Wurtz 2008, Schneider et al. 2014, Fiser et al. 2016, Schaffer et al. 2021, Zagha et al. 2022). The advances in brain connectome and neurophysiology are now spurring efforts for mechanistic and computational understanding of such distributed processes in the brain.

4.1. Distributed Working Memory: Bifurcation in Space

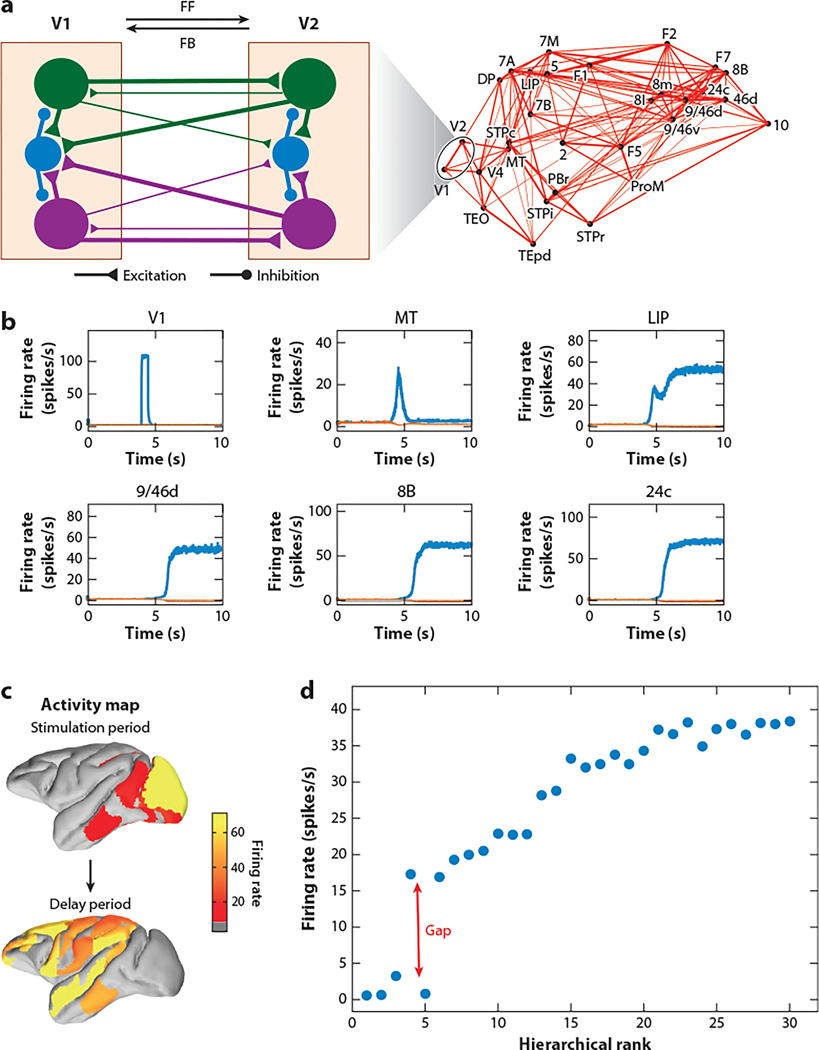
Mejias & Wang (2022) developed a large-scale model of distributed working memory using the connectivity database for macaque monkey cortex of Markov et al. (2014a). In the model, each area is described by a minimal recurrent network with two excitatory neural pools (selective for information items A and B) and an inhibitory neural pool (Wang 2002, Wong & Wang 2006). The model can be designed to explore different scenarios. For instance, when the local recurrent excitation is assumed to be insufficient to maintain persistent activity in any isolated area, the observed working memory representation in the interconnected system necessarily depends on long-distance connection loops between cortical areas, which extends the concept of synaptic reverberation to a large-scale multiregional brain system. Figure 4a–c shows model simulation of a visual delayed response task under this condition. Notably, responses to a brief input during stimulus presentation cover posterior parts of the cortex, whereas persistent activity during the delay period displays a spatial pattern involving frontal, parietal, and temporal areas. The persistent activity level of each area plotted as a function of its hierarchical position exhibits a gap in the firing rate that separates the areas with and without mnemonic activity (Figure 4d). This is reminiscent of a bifurcation in an attractor model of working memory (Amit 1995, Brunel & Wang 2001, Inagaki et al. 2019, Wang 2020). The term “bifurcation” denotes mathematically the phenomenon of the emergence of qualitatively different behavior caused by a quantitative difference in the properties (such as the strength of synaptic excitation) of a nonlinear dynamical system (Strogatz 2016). However, unlike a conventional bifurcation caused by varying an externally controlled parameter, here the abrupt transition from cortical areas not engaged in working memory to those exhibiting persistent activity occurs in the space of cortical tissue; all areas are interconnected through an abundance of long-range loops, and the transition is not sensitive to changes of parameters. I call this novel phenomenon “robust bifurcation in space” as a mechanism for distributed working memory. Similar to complex dynamic systems near a bifurcation (Nicolis & Prigogine 1977), the model predicts unusual neural fluctuations in areas at the edge of the transition (Figure 4d), which can be tested experimentally.

Figure 4.

Distributed working memory representation in a large-scale monkey cortex model in which none of the isolated areas is capable of generating persistent activity. (a) Model schema. Zooming in illustrates interareal connections between V1 and V2, each with two selective excitatory neural pools (purple and green) and an inhibitory neural pool (blue). Feedforward projection predominantly targets excitatory cells, whereas feedback projection more strongly targets inhibitory neurons (thick arrowed lines). (b) In model simulation of a visual delayed response task, activities of the two excitatory neural populations are shown for 6 sample areas. Blue lines represent activity of the neural pool selective for the shown stimulus, and orange lines represent activity of the neural pool nonselective for it. (c) The activity map is confined to the posterior part of the cortex during stimulus presentation. By contrast, persistent activity is distributed in the frontal, parietal, and temporal areas after stimulus withdrawal. Firing rate is shown in color. (d) Mnemonic firing rate of the selective neural pool in each area during the delay period is plotted as a function of its hierarchical position. Those areas displaying persistent activity are separated from those that do not by a gap in the firing rate (red arrow). Simulation results use the model from Mejias & Wang (2022). Abbreviations: 8B, frontal eye field Brodmann area 8B; 9/46d, dorsolateral prefrontal cortex Brodmann area 9 and dorsal 46; 24c, anterior cingulate cortex Brodmann area 24; FB, feedback; FF, feedforward, LIP, lateral intraparietal area; MT, middle temporal area; V1, primary visual cortex.

In the model, both local and long-range excitatory connections increase along the cortical hierarchy. To ensure network stability in spite of strong excitatory loops, the model assumes a counterstream gradient of targeting inhibitory neurons (Figure 4a). Namely, the ratio of weights of interareal inputs to excitatory and inhibitory neurons for a projection increases with its SLN value, so that for feedback projections (with small SLNs), there is a small bias in favor of targeting inhibitory neurons. This counterstream inhibitory bias not only helps to stabilize the system’s dynamics but also explains the absence of elevated persistent activity in early sensory areas where the net effect from top-down projections is inhibitory. Note that this is not necessarily inconsistent with some functional MRI studies showing working memory representation in sensory areas (reviewed in Sreenivasan et al. 2014, but see Xu 2020), because the blood-oxygen-level-dependent signal is strongly correlated with synaptic inputs (rather than spiking activity), which reflect both excitatory and inhibitory currents. At first sight, this idea seems to contradict empirical evidence that top-down signaling enhances firing of sensory neurons by selective attention, which shares a brain substrate with working memory. However, selective enhancement by attention simultaneously increases neural firing in some neurons while suppressing other neurons (Martinez-Trujillo & Treue 2004, Ardid et al. 2007), so the overall effect could be net inhibitory (Huang et al. 2019, Yoo et al. 2021). Moreover, predictive coding in its simplest form posits an overall inhibitory top-down influence (as −Y in Figure 3c). The counterstream inhibitory bias represents a new hypothesis that is experimentally testable.

To further analyze self-sustained collective dynamics of the cortex, individual areas were lesioned in model simulations (Mejias & Wang 2022). The persistent activity pattern did not disappear abruptly by such manipulations. Instead, the number of areas engaged in working memory representation gradually decreases as increasingly more randomly selected areas are lesioned, demonstrating the robustness of distributed working memory. However, certain areas are more important than others, in particular, those areas in the parietofrontal network. The model can also be used to simulate cell type–specific transient inactivation using optogenetic manipulation to fully understand the underlying network mechanism of distributed working memory. These results begin to clarify the distributed nature of working memory encoding.

Interestingly, a large-scale circuit displays a large number of distributed persistent activity patterns (attractors). Here, distinct attractor states are defined in terms of their spatial patterns, which do not depend on the number of selective excitatory neural pools per area. For instance, in a two-area network, there are at most three spatial pattern attractors (with one of the two, or both, showing persistent activity), independent of the number of selective neural pools in each area. Using a numerical approach to identify and count distinct attractors, many attractors are identified. For example, some engage the temporal lobe, others do not; a few involve the frontal polar area 10. Each of these distributed working memory attractors engages a subset of cortical areas, and frontal areas are commonly involved. Importantly, some of them are not accessible by stimulation of a primary sensory area, suggesting that they serve internal processes other than working memory of external stimulation. After all, mental processes such as thinking and reasoning, as well as emotional feelings, are largely freed from the physical world, which can be realized by various self-sustained attractor patterns of distributed brain activity.

4.2. Dopamine Modulation of the Whole Cortex

It is well known that dopamine has a major impact on working memory function (Brozoski et al. 1979). Stimulation of the D1 receptors (the most common type of dopamine receptors in the cortex) in the PFC is important to delay period activity, but either too little or too much stimulation can abolish delay period activity and impair working memory performance (Arnsten et al. 1994, Williams & Goldman-Rakic 1995, Vijayraghavan et al. 2007). In vitro studies of slices of PFC found various intricate effects of dopamine on interactions between cell types in PFC that potentially underlie this inverted U-shaped dosage dependence. D1 receptor agonists increased the slow and voltage-dependent N-methyl-d-aspartate (NMDA) component of synaptic excitation (Seamans et al. 2000). Dopamine also led to a shift from somatic to dendritic inhibition in single pyramidal cells (Gao et al. 2003) and modulation of potassium channels that contribute to neuronal adaptation (Arnsten et al. 2019).

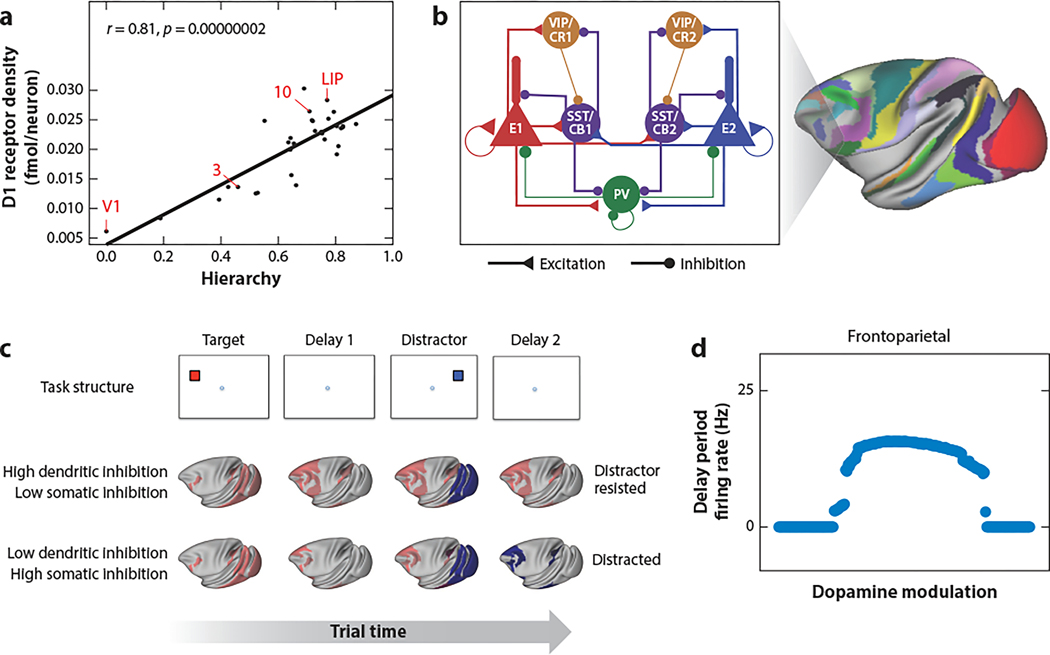
While it is known that dopamine signaling is not uniform in the cortex, there has been little quantification of how it differs throughout the cortex. Using the technique of quantitative in vitro receptor autoradiography to quantify the density of receptors across brain areas (Zilles & Palomero-Gallagher 2017), Froudist-Walsh et al. (2021) found that D1 receptor density per neuron varies in the form of a systematic gradient across the cortex. D1 receptor density increases along the cortical hierarchy, such that early sensory areas have relatively few D1 receptors per neuron, while neurons in the prefrontal and lateral parietal areas have a large amount of D1 receptors (Figure 5a). This finding demonstrates that the concept of macroscopic gradients in the cortex (Wang 2020) also holds for neuromodulation.

Figure 5.

Dopamine modulation of a multiregional cortical system. (a) The D1 receptor density per neuron increases along the anatomically defined cortical hierarchy. (b) An extended local circuit model with diverse types of inhibitory neurons. (c) Simulations of a working memory task with a distractor. With a high dendritic-somatic inhibition ratio (top row), target-selective activity (red) is maintained in the second delay in spite of the distractor that briefly causes activity in the distractor-selective neural population (blue) of visual cortical areas (middle row). With a low dendritic-somatic inhibition ratio, persistent activity becomes selective for the distractor in the second delay (bottom row). (d) Inverted U-shaped dependence on D1 modulation of persistent activity in the parietofrontal cortical areas. Abbreviations: 3, primary somatosensory cortex Brodmann area 3; 10, frontal polar cortex Brodmann area 10; E, excitatory neurons; LIP, lateral intraparietal cortex; PV, parvalbumin; SST/CB, somatostatin/calbindin; V1, primary visual cortex; VIP/CR, vasoactive intestinal peptide/calretinin-expressing inhibitory neuron. Figure adapted from Froudist-Walsh et al. (2021) (CC BY 4.0).

In an extension of our macaque cortex model to incorporate a gradient of dopamine modulation, Froudist-Walsh et al. (2021) focused on examining the hypothesis that dopamine differentially enhances dendritic inhibition and reduces somatic inhibition (Gao et al. 2003), in line with the anatomical evidence that D1 receptor expression is higher in dendrite-targeting calbindin or somatostatin-positive GABAergic cells than perisoma-targeting parvalbumin-positive ones (Mueller et al. 2020). For that purpose, the local area model is extended to include the three GABAergic cell types forming a disinhibitory motif (Figure 5b). In model simulations of a delayed visual response task, a target stimulus is first shown, which must produce a memory-guided response at the end of the trial. Following a delay, a distractor stimulus is presented, which should be ignored. A second delay period precedes the end of the trial. The activity map depicts the spatial distribution of neural firing for two selective neural populations in each cortical area included in the model (Figure 5c). When dopamine enhances dendritic inhibition and reduces somatic inhibition, the target leads to activity in the target-selective neural population spreading from the visual system to the frontal and parietal cortex. The distractor produces only transient activity in the distractor-selective neural population in the posterior areas but does not gain access to most of the frontal and parietal cortices, and behaviorally relevant memory is preserved (Figure 5c). By contrast, with low D1 activation, working memory is easily distracted, and persistent activity in the second delay becomes selective for the distractor rather than the target (Figure 5c).

Based on empirical evidence (Seamans et al. 2000, Gao et al. 2003, Arnsten et al. 2019), in our model, different targets of the D1 receptor have differential sensitivities: low-level dopamine release enhances the NMDA receptor–mediated excitation and dendritic inhibition, whereas high-level dopamine release has a net suppressive effect because of its modulation of a potassium current. Consequently, the model exhibits an inverted U-shaped dependence on the dopamine modulation of persistent activity in the parietal cortex and PFC (Figure 5d), similar to experimental observations (Arnsten 1998), now from the perspective of a large-scale cortical system. Optimality in the intermediate dopamine level can be understood by the preferential targeting of long-range connections to the distant dendrites, while local connections synapse the perisomatic region of pyramidal cells (Petreanu et al. 2009). Once a stimulus-selective persistent activity has been engaged by the initial cue, strong inhibition to the dendrites blocks distractor information in the sensory areas from entering frontal and parietal areas (with high D1 receptor density) while leaving excitatory reverberation relatively unaffected and able to maintain activity related to the behaviorally relevant cue. Furthermore, the model still works if a delayed response depends on the second stimulus rather than the first stimulus, provided that the behavioral relevance of a stimulus is learnt and correlated with phasic activity of dopamine neurons (Schultz 1998). Notably, the model captures the meta-analysis results (Leavitt et al. 2017) of mnemonic persistent activity in various cortical areas of the macaque cortex (Supplemental Figure 3).

This work illustrates a cross-level understanding that links receptors and diverse cell types to recurrent circuit dynamics and to a basic cognitive function distributed across the cortex. Such a modeling platform is valuable for addressing the current debate on precisely how distributed are working memory representations—in particular, whether sensory areas are critically involved in working memory storage (Xu 2020). On the theory side, this large-scale cortex model is suitable for exploring passive short-term memory traces (by activity-silent mechanisms) versus active working memory (Froudist-Walsh et al. 2021), a topic of current debate (Constantinidis et al. 2018, Miller et al. 2018, Wang 2021), and can be further used to elucidate the dynamical nature of working memory representation in the future. Other open questions include the following: what are the general rules that determine mechanistically which area or subnetwork of areas is essential for working memory storage? Can the concept of bifurcation in space be rigorously established mathematically?

4.3. Distributed Decision-Making and Ignition

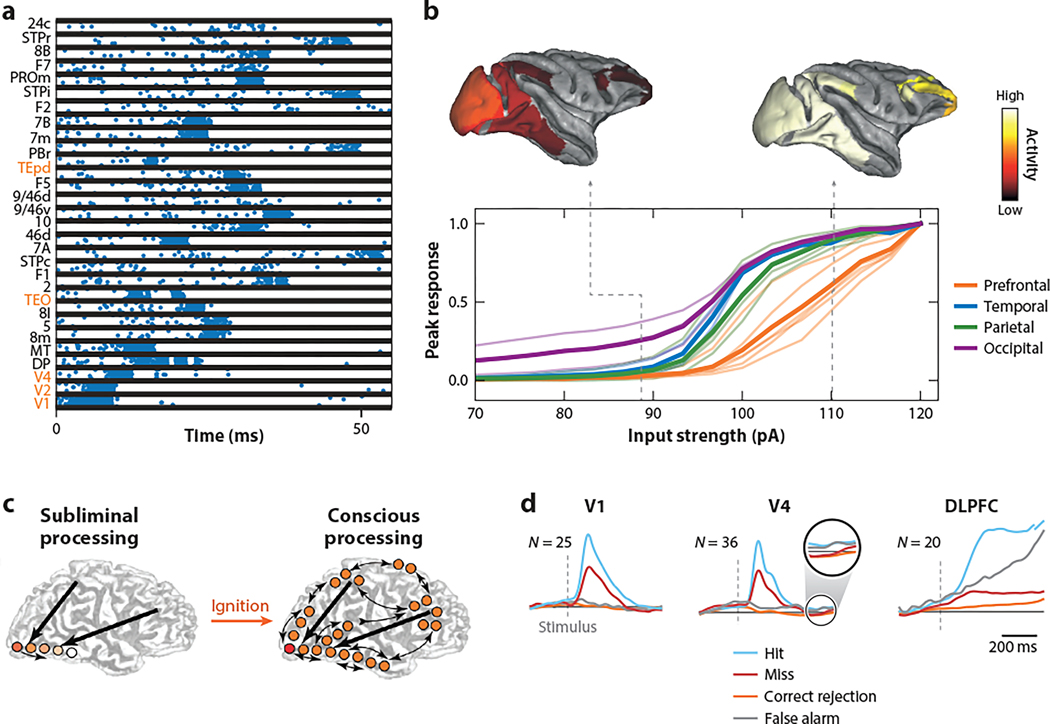
The newly available model with anatomically measured interareal connectivity provides a platform to revisit the classical problem of signal propagation (Perkel & Bullock 1968, Diesmann et al. 1999). In a spiking neuron version of the large-scale macaque cortex model endowed with highly heterogenous connection weights and an abundance of feedback loops ( Joglekar et al. 2018), in response to a brief stimulus to primary visual cortex V1, cortical areas fire a burst of spikes with various onset latencies. A few areas, such as TEO, show more than one burst, as a manifestation of complex patterns of communication across the highly recurrent cortical system (Figure 6a).

Figure 6.

Ignition in a large-scale cortex. (a) Signal propagation across some areas but not others in response to a brief input to V1 in a large-scale monkey cortex model of spiking neurons. The areas along the ventral stream showing strong response activity are indicated in orange. The list of full names of cortical areas shown is provided in Markov et al. (2014a). (b) The peak response averaged over areas in the occipital, temporal, parietal, and frontal lobes as a function of the intensity of a stimulus to V1. (c) Illustration of ignition as a physiological signature of consciousness. (d) Average normalized activity of neurons in V1, V4, and dorsolateral prefrontal cortex (DLPFC) of monkeys performing a visual detection task with intermediate contrast levels around the detection threshold. Neural signals in visual areas predominantly reflect the physical stimulus in hit and miss trials, whereas neural firing in the DLPFC displays strong responses correlated with subjective awareness in hit and false alarm trials. Panels a and b adapted from Joglekar et al. (2018). Panel c adapted with permission from Dehaene et al. (2006). Panel d adapted with permission from van Vugt et al. (2018).

The peak responses averaged over areas in each of the occipital, temporal, parietal, and frontal lobes increase with the stimulus intensity in different ways. While the dependence is graded for visual areas, the prefrontal activity displays a nonlinear thresholding effect, with virtually zero response below the input threshold ( Joglekar et al. 2018) (Figure 6b). The unexpectedly observed threshold for access to the PFC in the model resembles the so-called ignition phenomenon postulated by the theory of GNW for access consciousness (Baars 1988, Dehaene et al. 2003, Mashour et al. 2020) (Figure 6c). Access consciousness refers to subjective awareness of information. In well-controlled neuroscientific experiments, access consciousness can be studied using simple tasks (Crick & Koch 1990, Koch 2004, Dehaene 2014). For instance, in a detection task with a stimulus intensity near the detection threshold, a subject sometimes reports the presence of the stimulus but other times reports its absence, even though the physical stimulation is identical. While the activity of neurons in sensory areas reflects external inputs, neural firing in frontal areas is correlated with subjective awareness in primates (de Lafuente & Romo 2005) and rodents (Zagha et al. 2015).

Human studies using such paradigms combined with recording of event-related potential using EEG or MEG lend support to the GNW theory while revealing that the initial state of the brain biases whether a given stimulus is perceived or not (Del Cul et al. 2007, Baria et al. 2017). Specifically, conscious access corresponds to an all-or-none ignition of activity in the PFC, which in turn triggers a broadcast of information content in the brain via its extensive long-range connections. Van Vugt et al. (2018) carried out a monkey experiment with a detection task in which the contrast of a visual stimulus was varied. Simultaneous recording from neurons in V1, V4, and PFC found that firing of neurons in V1 and V4 was similar whether a near-threshold stimulus was reported in a given trial, whereas activity of neurons in PFC displayed robust differences in hit versus miss trials (Figure 6d). When no stimulus was shown, V1 and V4 neural activity was similar in false alarm and correct rejection trials. By contrast, PFC neurons ramped up their firing in false alarm but not correct rejection trials, up to a level similar to that in hit trials.

This detection experiment was simulated using our model of large-scale macaque cortex (Klatzmann et al. 2022). By varying the magnitude of an input to V1, mimicking the contrast of a visual stimulus, the model could capture the basic physiological observations and behavioral performance from the monkey experiment of van Vugt et al. (2018). There is a transition from graded dependence on input magnitude in visual areas to all-or-none activity in the PFC. A time-dependent analysis revealed a dynamic signature of the onset of ignition in the model, similar to that observed in a human experiment using an auditory detection paradigm and EEG recordings (Sergent et al. 2021). In the experiment, this stereotypical EEG signature was correlated with reports during the task as well as in the condition of passive listening when no detection was required, representing a biological marker of conscious processing independently from behavioral response (the report), an important dissociation for elucidating the role of the PFC in consciousness (Block 2019, Kapoor et al. 2020).

The global ignition phenomenon associated with access consciousness represents but one example of a variety of distributed brain processes that can now be rigorously studied experimentally and theoretically. Considerations of a complex, large brain system have brought to the fore new open questions, especially regarding the brain mechanism of interareal communication (Perich et al. 2021). Since local circuit modeling has shown that working memory and decision-making share a common brain mechanism (Wang 2002, 2008), it is likely that our large-scale cortical model capable of working memory can be generalized to account for distributed perceptual decisions (Siegel et al. 2015, Steinmetz et al. 2019, Wilming et al. 2020) and value-based choices (Vickery et al. 2011, Hattori et al. 2019).

5. SUMMARY

For arguably the first time in neuroscience, it is now possible to build a biologically based computer model of a large-scale, multiregional brain. In this review, I summarized recent progress in research going beyond local circuits toward a neuroscience of the whole brain. In contrast to previous computational modeling devoted to FC measured in resting states, here I focused on dynamics during behavior and distributed cognitive processes. I discussed findings in support of general principles about the global organization of the neocortex. First, the interareal connectivity weights obey a wide lognormal distribution (Markov et al. 2014a, Oh et al. 2014). Second, the cortical network is spatially embedded and obeys the EDR. These two characteristics are captured in a new class of random network models of the cortex (Song et al. 2014). Third, the cortical hierarchy is established quantitatively for the primate cortex (Markov et al. 2014b, Michalareas et al. 2016) as well as for mice (Harris et al. 2019, D’Souza et al. 2022). Fourth, heterogeneities of synaptic excitation and inhibition are not random among cortical areas; instead, they vary systematically along certain low-dimensional axes in the form of macroscopic gradients (Wang 2020). Fifth, there is a hierarchy of temporal integration windows in parallel with a gradual enlargement of spatial RFs of neurons along the cortical hierarchy, predicted theoretically (Chaudhuri et al. 2015) and supported by an increasing number of experiments (Murray et al. 2014, Cavanagh et al. 2018, Siegle et al. 2021, Manea et al. 2021).

Computational works have also led to falsifiable hypotheses on the organization of synaptic excitation and inhibition in the multiregional cortex. In particular, the NMDA/AMPA ratio is higher at excitatory local and feedback connections than at feedforward ones. Moreover, feedback projections tend to have a net inhibitory effect in the form of a counterstream inhibitory bias. In a laminarly organized cortex, this can be realized by a strong top-down projection to excitatory neurons in the deep layers of the recipient area, which in turn connect to inhibitory neurons in the superficial layers. This scenario constitutes a candidate anatomical substrate for predictive coding.

The emerging picture is that equipotentiality would be the wrong conclusion from recent experiments that reported whole-brain activations even during simple tasks (Musall et al. 2019, Schaffer et al. 2021). Neural processes are both distributed and localized in the brain; the challenge is to understand how. The biological macroscopic gradients combined with the mathematics of nonlinear dynamic systems give rise to the new concept of bifurcation in space, which may hold the promise for understanding cortical areas that share a canonical circuit architecture while exhibiting distinct functional capabilities such as working memory.

This review focuses on the neocortex, which closely interacts with hippocampus, thalamus, basal ganglia, cerebellum, amygdala and neuromodulatory systems through connection loops. With experimental advances in the coming years, incorporation of subcortical structures in a more comprehensive mathematical model will become possible and important for understanding how the whole brain works during cognitive processes and behavior. Plasticity in such complex large-scale brain systems underlying learning represents another widely open question in the nascent neuroscience of multiregional large-scale brain systems.

FUTURE ISSUES.

1. What are the cell type–specific targets of top-down projections and their distinctive synaptic dynamics?

2. What are the cell type–specific NMDA/AMPA ratios at feedforward, local recurrent, and feedback projections?

3. Under what conditions and in which areas is the overall impact of a top-down projection inhibitory rather than excitatory?

4. What are the salient differences in macroscopic gradients for synaptic excitation and inhibition between rodents and primates?

5. What are the computational advantages of a hierarchy of timescales?

6. How can one incorporate a rich repertoire of information representations, such as object (“What?”) and location (“Where?”) along the ventral versus dorsal pathways, in a connectome-based model of the whole cortex?

7. What would be a mathematically rigorous theory and neurophysiological tests for bifurcations in space, denoting sudden emergence of qualitatively different functional capabilities in a subset of brain regions?