Skip to main content
PMC home page
JAMA Network logoLink to JAMA Network
. 2024 Nov 22;7(11):e2429630. doi: 10.1001/jamanetworkopen.2024.29630

Data-Driven Cutoff Selection for the Patient Health Questionnaire-9 Depression Screening Tool

Brooke Levis 1,2, Parash Mani Bhandari 1, Dipika Neupane 1, Suiqiong Fan 1, Ying Sun 1, Chen He 1, Yin Wu 1, Ankur Krishnan 1, Zelalem Negeri 3, Mahrukh Imran 1, Danielle B Rice 4, Kira E Riehm 1, Marleine Azar 1, Alexander W Levis 1, Jill Boruff 5, Pim Cuijpers 6, Simon Gilbody 7, John P A Ioannidis 8,9,10,11, Lorie A Kloda 12, Scott B Patten 13, Roy C Ziegelstein 14, Daphna Harel 15, Yemisi Takwoingi 16, Sarah Markham 17, Sultan H Alamri 18, Dagmar Amtmann 19, Bruce Arroll 20, Liat Ayalon 21, Hamid R Baradaran 22, Anna Beraldi 23, Charles N Bernstein 24, Arvin Bhana 25, Charles H Bombardier 19, Ryna Imma Buji 26, Peter Butterworth 27, Gregory Carter 28, Marcos H Chagas 29, Juliana C N Chan 30, Lai Fong Chan 31, Dixon Chibanda 32, Kerrie Clover 33, Aaron Conway 34, Yeates Conwell 35, Federico M Daray 36, Janneke M de Man-van Ginkel 37, Jesse R Fann 38, Felix H Fischer 39, Sally Field 40, Jane R W Fisher 41, Daniel S S Fung 42, Bizu Gelaye 43, Leila Gholizadeh 44, Felicity Goodyear-Smith 45, Eric P Green 46, Catherine G Greeno 47, Brian J Hall 48, Liisa Hantsoo 49, Martin Härter 50, Leanne Hides 51, Stevan E Hobfoll 52, Simone Honikman 40, Thomas Hyphantis 53, Masatoshi Inagaki 54, Maria Iglesias-Gonzalez 55, Hong Jin Jeon 56, Nathalie Jetté 57, Mohammad E Khamseh 58, Kim M Kiely 59, Brandon A Kohrt 60, Yunxin Kwan 61, Maria Asunción Lara 62, Holly F Levin-Aspenson 63, Shen-Ing Liu 64, Manote Lotrakul 65, Sonia R Loureiro 66, Bernd Löwe 67, Nagendra P Luitel 68, Crick Lund 69, Ruth Ann Marrie 70, Laura Marsh 71, Brian P Marx 72, Anthony McGuire 73, Sherina Mohd Sidik 74, Tiago N Munhoz 75, Kumiko Muramatsu 76, Juliet E M Nakku 77, Laura Navarrete 78, Flávia L Osório 66, Brian W Pence 79, Philippe Persoons 80, Inge Petersen 25, Angelo Picardi 81, Stephanie L Pugh 82, Terence J Quinn 83, Elmars Rancans 83,84, Sujit D Rathod 85, Katrin Reuter 86, Alasdair G Rooney 87, Iná S Santos 75, Miranda T Schram 88, Juwita Shaaban 89, Eileen H Shinn 90, Abbey Sidebottom 91, Adam Simning 35, Lena Spangenberg 92, Lesley Stafford 93, Sharon C Sung 64, Keiko Suzuki 94, Pei Lin Lynnette Tan 61, Martin Taylor-Rowan 95, Thach D Tran 41, Alyna Turner 96, Christina M van der Feltz-Cornelis 97, Thandi van Heyningen 98, Paul A Vöhringer 99, Lynne I Wagner 100, Jian Li Wang 101, David Watson 102, Jennifer White 103, Mary A Whooley 104,105, Kirsty Winkley 106, Karen Wynter 107, Mitsuhiko Yamada 108, Qing Zhi Zeng 109, Yuying Zhang 110, Brett D Thombs 1,2,111,112,113,114, Andrea Benedetti 2,112,115,116,✉, for the Depression Screening Data (DEPRESSD) PHQ Group
PMCID: PMC11584932  PMID: 39576645

This study of cross-sectional data evaluates the cutoff selection process and sensitivity and specificity of accuracy estimation in Patient Health Questionnaire-9 screening accuracy studies.

Key Points

Question

Does data-driven optimal cutoff score selection in Patient Health Questionnaire-9 (PHQ-9) screening accuracy studies generate cutoff scores that diverge from the population-level cutoff score and overstate accuracy?

Findings

In this study of cross-sectional data from 100 primary studies including 44 503 participants, the optimal PHQ-9 scores identified varied from the population-level optimal cutoff score, and PHQ-9 screening accuracy was exaggerated. As sample size increased, overestimation of sensitivity decreased, while specificity remained within 1 percentage point.

Meaning

Findings of this study suggest that users of diagnostic accuracy evidence should evaluate studies of accuracy with caution and ensure that cutoff score recommendations are based on adequately powered research or well-conducted meta-analyses.

Abstract

Importance

Test accuracy studies often use small datasets to simultaneously select an optimal cutoff score that maximizes test accuracy and generate accuracy estimates.

Objective

To evaluate the degree to which using data-driven methods to simultaneously select an optimal Patient Health Questionnaire-9 (PHQ-9) cutoff score and estimate accuracy yields (1) optimal cutoff scores that differ from the population-level optimal cutoff score and (2) biased accuracy estimates.

Design, Setting, and Participants

This study used cross-sectional data from an existing individual participant data meta-analysis (IPDMA) database on PHQ-9 screening accuracy to represent a hypothetical population. Studies in the IPDMA database compared participant PHQ-9 scores with a major depression classification. From the IPDMA population, 1000 studies of 100, 200, 500, and 1000 participants each were resampled.

Main Outcomes and Measures

For the full IPDMA population and each simulated study, an optimal cutoff score was selected by maximizing the Youden index. Accuracy estimates for optimal cutoff scores in simulated studies were compared with accuracy in the full population.

Results

The IPDMA database included 100 primary studies with 44 503 participants (4541 [10%] cases of major depression). The population-level optimal cutoff score was 8 or higher. Optimal cutoff scores in simulated studies ranged from 2 or higher to 21 or higher in samples of 100 participants and 5 or higher to 11 or higher in samples of 1000 participants. The percentage of simulated studies that identified the true optimal cutoff score of 8 or higher was 17% for samples of 100 participants and 33% for samples of 1000 participants. Compared with estimates for a cutoff score of 8 or higher in the population, sensitivity was overestimated by 6.4 (95% CI, 5.7-7.1) percentage points in samples of 100 participants, 4.9 (95% CI, 4.3-5.5) percentage points in samples of 200 participants, 2.2 (95% CI, 1.8-2.6) percentage points in samples of 500 participants, and 1.8 (95% CI, 1.5-2.1) percentage points in samples of 1000 participants. Specificity was within 1 percentage point across sample sizes.

Conclusions and Relevance

This study of cross-sectional data found that optimal cutoff scores and accuracy estimates differed substantially from population values when data-driven methods were used to simultaneously identify an optimal cutoff score and estimate accuracy. Users of diagnostic accuracy evidence should evaluate studies of accuracy with caution and ensure that cutoff score recommendations are based on adequately powered research or well-conducted meta-analyses.

Introduction

Studies on depression screening tool accuracy often use data-driven approaches and small samples and numbers of depression cases to simultaneously establish an optimal cutoff score and estimate accuracy.1,2,3 A recent review of 172 studies found a median sample size of 194 and median number of depression cases of approximately 20.1 Seventy-six percent of the included studies identified an optimal cutoff score that diverged from a standard cutoff score, and authors of 40% of those studies recommended using their optimal cutoff score, rather than the standard cutoff, in their population.1

Previous studies on data-driven selection of test cutoff scores have reported that these methods produce overly optimistic accuracy estimates, especially in small samples.4,5,6,7,8 However, most of these studies used simulated datasets based on hypothetical test score distributions rather than real participant data. A previous study analyzed Edinburgh Postnatal Depression Scale (EPDS) data for 13 255 participants and found that in 1000 simulated or resampled studies, the cutoff score maximizing the Youden index (sensitivity + specificity – 1)9 ranged from 5 or higher to 17 or higher with resampled studies of 100 participants and from 8 or higher to 13 or higher with 1000 participants.8 Mean sensitivity overestimation was 7 percentage points for 100 participants vs 1 percentage point for resampled studies of 1000 participants, while specificity was underestimated by 1 percentage point across sample sizes.8

The standard cutoff score traditionally used to screen for major depression with the Patient Health Questionnaire-9 (PHQ-9) is 10 or higher.10,11,12,13,14 An individual participant data meta-analysis (IPDMA) of 100 primary studies (44 503 participants and 4541 cases of major depression) confirmed that a cutoff score of 10 or higher maximized combined sensitivity and specificity in studies that used a gold standard semistructured interview reference standard, although the optimal cutoff score was 8 or higher when fully structured interviews designed for lay administration were used.15,16

Many primary studies of PHQ-9 accuracy emphasize results from data-driven optimal cutoff scores.1 The degree to which accuracy is overestimated when data-driven cutoff scores are used for the PHQ-9, however, is not known. The objective of this study was to evaluate the degree to which using data-driven methods to simultaneously select an optimal PHQ-9 cutoff score and estimate accuracy yields biased estimates. We estimated, across different sample sizes, the degree to which data-driven cutoff score selection was a factor in (1) sample-specific optimal cutoff scores that differed from the population-level optimal cutoff score and (2) biased accuracy estimates. For comparison, we also estimated accuracy using the population-level optimal cutoff score in individual resampled studies and compared them with population accuracy.

Methods

The Jewish General Hospital Research Ethics Committee deemed this study of cross-sectional data exempt from ethics approval and the informed consent requirement since the study involved IPDMA of previously collected deidentified data. For each included dataset, we confirmed that the original study received ethics approval and the participants provided informed consent. We followed the Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) reporting guideline.

We used data from an IPDMA of PHQ-9 diagnostic accuracy (hereafter, main IPDMA) to represent a hypothetical population from which studies of different sizes could be resampled.16 Data in the IPDMA database were identified from a literature search covering January 1, 2000, through May 9, 2018. The main IPDMA was registered in PROSPERO (CRD42014010673), and a protocol was published.17 A protocol for the present study was published in the Open Science Framework repository prior to initiation.18 Details on the methods used to identify, obtain, and synthesize the data included in the present study are provided in eMethods 1 and 2 in Supplement 1. We used a similar methodological approach as that in the previous EPDS resampling study.8 Because of the overlap of methods in the present study and previous studies, we described the methods similarly and followed the reporting guidance from the Text Recycling Research Project.19

Statistical Analysis

For the purposes of the present study, we used the main IPDMA dataset to represent a hypothetical population and defined population sensitivity and specificity values for PHQ-9 cutoff scores to be those estimated in the hypothetical population. In the main IPDMA, we accounted for clustering of observations within each study, and we applied sampling weights to account for imbalances in participant samples when, for instance, all participants with positive PHQ-9 results but only a random portion of those with negative PHQ-9 results were administered a diagnostic interview. In the present study, we ignored clustering and sampling weights to have a defined population from which we could draw samples that represented simulated primary studies and to be able to analyze the population data and simulated primary study data with the same analytical approach. In addition, in the main IPDMA, we stratified included studies by reference standard type because previous studies have shown that different types of diagnostic interviews classify major depression differently.20,21 However, in primary analyses of the present study, we did not stratify the studies by reference standard because we were not evaluating the true screening accuracy of the PHQ-9, and combining included studies that used different reference standards allowed us to have a single hypothetical population for resampling. As a result, this procedure produced accuracy estimates that differed from those reported in the main IPDMA.16 In the present study, we calculated the population-level optimal cutoff score that maximized the Youden index in the full IPDMA dataset, which was 8 or higher.

First, we described the individual primary studies included in the main IPDMA dataset in terms of sample size, number of major depression cases, and optimal cutoff score (based on maximizing the Youden index). If there was a tie in maximum Youden index between multiple cutoff scores, we randomly selected 1 of the cutoff scores. We used the Youden index because it is by far the most common method for selecting optimal cutoff scores in depression screening accuracy studies, and our study aimed to reflect current research practices.1

Second, from the main IPDMA dataset, we sampled with replacement to generate 1000 randomly sampled studies with 100, 200, 500, and 1000 participants each to mimic what would occur in primary studies that use samples of these sizes. For each study, we defined the sample-specific optimal cutoff score as the cutoff that maximized the Youden index, with random selection in case of ties. For each sample size across the 1000 samples, we (1) graphically illustrated the variability in sample-specific optimal cutoff scores and their accuracy estimates and (2) calculated the mean difference in sensitivity and specificity estimates at the sample-specific optimal cutoff scores and at a cutoff score of 8 or higher compared with sensitivity and specificity estimates for a cutoff score of 8 or higher in the population. In additional analyses, we stratified results by optimal cutoff value.

Random selection of participants in simulated samples and averaging sensitivity and specificity across 1000 samples for each sample size were performed to balance other possible sources of divergent accuracy, such as reference standards or individual participant characteristics. Nonetheless, in sensitivity analyses, we repeated the resampling process, including only studies that used the semistructured Structured Clinical Interview for DSM (Diagnostic and Statistical Manual of Mental Disorders) Disorders as the reference standard.

For all analyses, sensitivity and specificity were estimated using 2 × 2 table counts. Analyses were performed using R, version 4.2.2 (R Project for Statistical Computing).

Results

The full IPDMA database included 100 primary studies with 44 503 participants (4541 cases [10%] of major depression), which constituted the population for the present study. eTable 1 in Supplement 1 provides the primary study characteristics. In the 100 included studies, the median (IQR) sample size was 194 (134-386) and the median (IQR) number of major depression cases was 28 (14-60). Study-specific optimal cutoff scores ranged from 3 or higher to 18 or higher (median, ≥10). Frequencies of PHQ-9 scores for cases and noncases are provided in eTable 2 in Supplement 1, with histograms in the eFigure in Supplement 1. The PHQ-9 scores were normally distributed among cases (mean [SD], 13 [6]; median [IQR], 13 [9-18]) and right-skewed among noncases (mean [SD], 4 [4]; median [IQR], 3 [1-6]). In the full IPDMA database population, unweighted sensitivity and specificity for PHQ-9 score of 8 or higher were 80.4% and 82.0%, respectively.

Variability of Sample-Specific Optimal Cutoff Scores in Simulated Samples

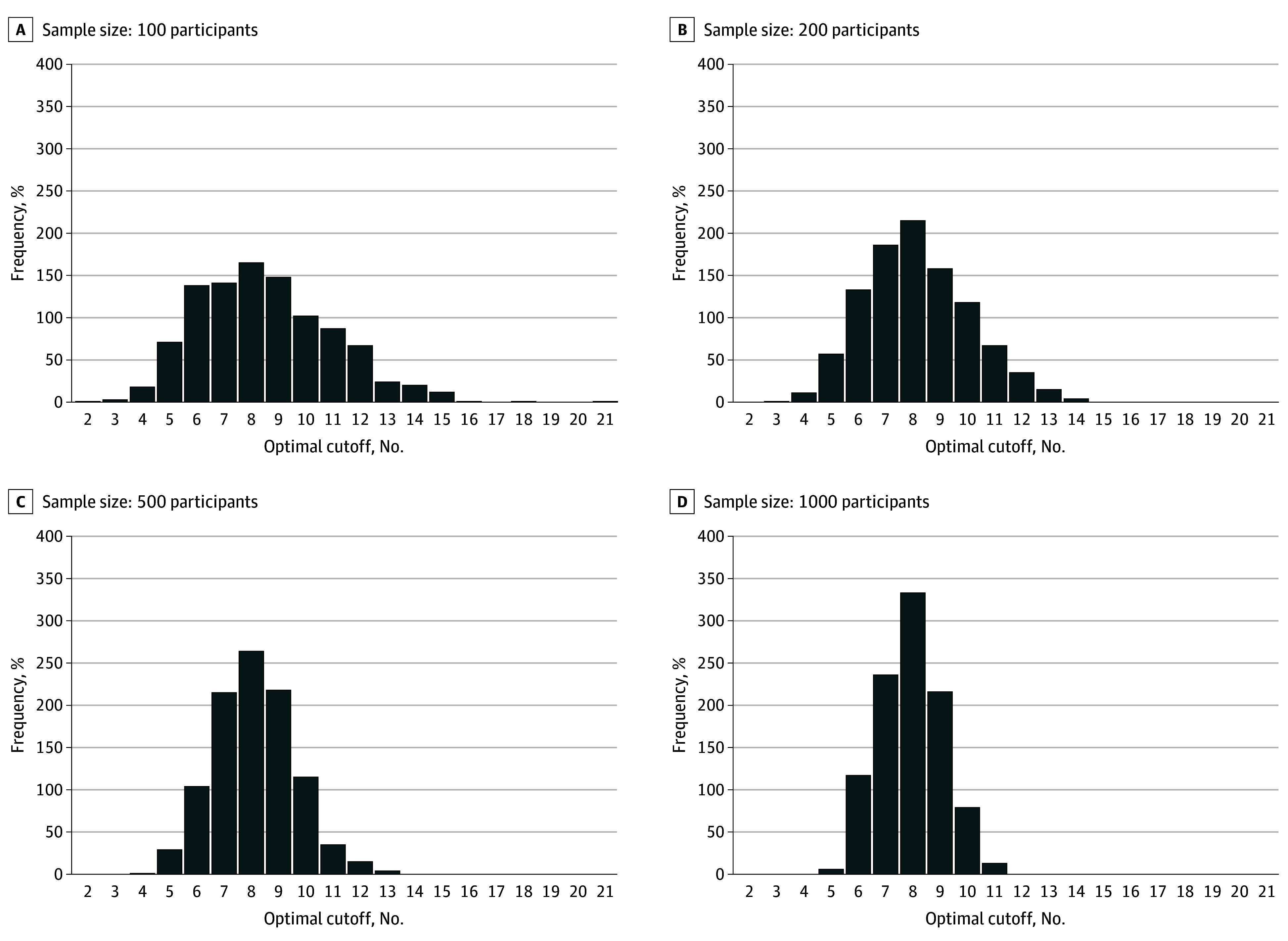
Figure 1 shows the variability of sample-specific optimal cutoff scores from 1000 resampled studies of 100, 200, 500, and 1000 participants. As sample size increased, the variability in sample-specific optimal cutoff scores decreased. Of the 1000 resampled studies of 100 participants, study-specific optimal cutoff scores ranged from 2 or higher to 21 or higher; 17% of resampled studies had an optimal cutoff score of 8 or higher, and 45% of resampled studies had an optimal cutoff score between 7 or higher and 9 or higher. When sample size of the resampled studies increased to 1000 participants per study, the range of optimal cutoff scores was 5 or higher to 11 or higher; 33% of resampled studies had an optimal cutoff score of 8 or higher, and 79% of resampled studies had an optimal cutoff score between 7 or higher and 9 or higher.

Figure 1. Variability of Data-Driven Optimal Cutoff Scores in 1000 Resampled Studies of 100, 200, 500, and 1000 Participants .

Figure 1.

Open in a new tab

Bias and Sensitivity Analyses in Simulated Samples

As shown in Figure 2, overestimation of sensitivity estimates for sample-specific optimal cutoff scores decreased with increasing sample size, whereas specificity estimates remained within 1 percentage point across sample sizes. Precision of both sensitivity and specificity estimates increased with sample size. As shown in the Table, compared with accuracy estimates for a cutoff score of 8 or higher in the full IPDMA database, study-specific optimal cutoff scores in samples of 100 participants overestimated sensitivity by a mean of 6.4 (95% CI, 5.7-7.1) percentage points and overestimated specificity by 0.6 (95% CI, 0.0-1.2) percentage points. In samples of 200 and 500 participants, sensitivity was overestimated by 4.9 (95% CI, 4.3-5.5) and 2.2 (95% CI, 1.8-2.6) percentage points, respectively, and specificity was underestimated by 0.3 percentage points (mean difference, –0.3 [95% CI, –0.8 to 0.2] percentage points) and 0.0 (95% CI, –0.4 to 0.3) percentage points, respectively. When sample size increased to 1000, study-specific optimal cutoff scores overestimated sensitivity by 1.8 (95% CI, 1.5-2.1) percentage points and underestimated specificity by 0.6 percentage points (mean difference, –0.6 [95% CI, −1.0 to −0.3] percentage points). As shown in the Table and Figure 3, when each resampled study used a prespecified cutoff score of 8 or higher, mean sample-specific sensitivity and specificity values were similar to those in the population for all sample sizes.

Figure 2. Variability in Accuracy Estimates of the Optimal Cutoff Scores in 1000 Resampled Studies of 100, 200, 500, and 1000 Participants vs Accuracy Values for a Cutoff of 8 or Higher in the Population.

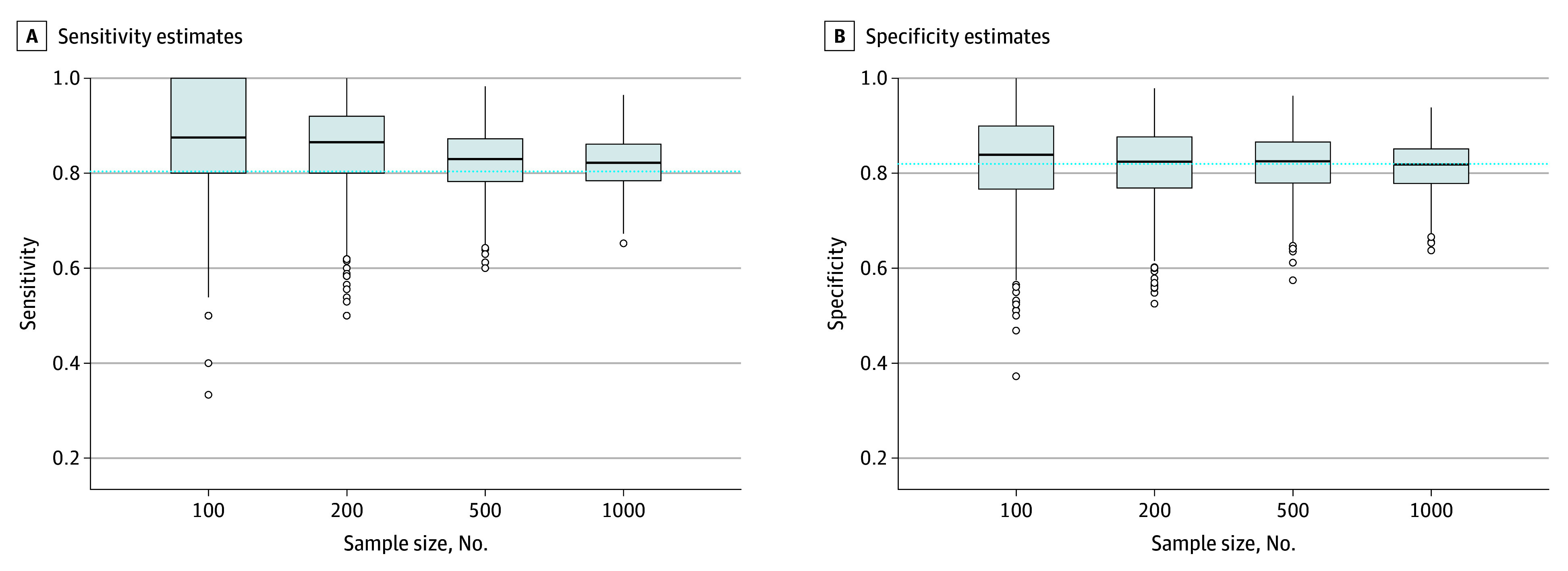
Figure 2.

Open in a new tab

Edges of boxes represent the 25th and 75th percentiles; horizontal line inside boxes represents the median; dashed horizontal line represents the accuracy of the true population-level optimal cutoff score in the full Patient Health Questionnaire-9 individual participant data meta-analysis dataset (cutoff score ≥8; sensitivity = 80.4%, specificity = 82.0%); and dots represent outliers.

Table. Mean Bias of Accuracy Estimates for 1000 Resampled Studies of 100, 200, 500, and 1000 Participants .

Mean difference (95% CI), percentage points
Sample size = 100 Sample size = 200 Sample size = 500 Sample size = 1000
Sensitivity Specificity Sensitivity Specificity Sensitivity Specificity Sensitivity Specificity
Sample-specific optimal cutoff scorea – Population-level optimal cutoff score ≥8b 6.4 (5.7 to 7.1) 0.6 (0.0 to 1.2) 4.9 (4.3 to 5.5) −0.3 (−0.8 to 0.2) 2.2 (1.8 to 2.6) 0.0 (−0.4 to 0.3) 1.8 (1.5 to 2.1) −0.6 (−1.0 to −0.3)
Sample-specific cutoff score ≥8 – Population-level optimal cutoff score ≥8 −0.8 (−1.7 to 0.0) 0.1 (−0.1 to 0.4) 0.2 (−0.3 to 0.8) −0.1 (−0.2 to 0.1) 0.1 (−0.2 to 0.4) 0.0 (−0.1 to 0.1) −0.1 (−0.4 to 0.1) 0.0 (−0.1 to 0.1)
Open in a new tab
a

Sample-specific optimal cutoff score refers to the cutoff score maximizing the Youden index in each simulated sample.

b

The optimal cutoff score in the full Patient Health Questionnaire-9 individual participant data meta-analysis dataset is 8 or higher (sensitivity = 80.4%, specificity = 82.0%).

Figure 3. Variability in Accuracy Estimates of a Cutoff Score of 8 or Higher in 1000 Resampled Studies of 100, 200, 500, and 1000 Participants vs Accuracy Values for a Cutoff of 8 or Higher in the Population.

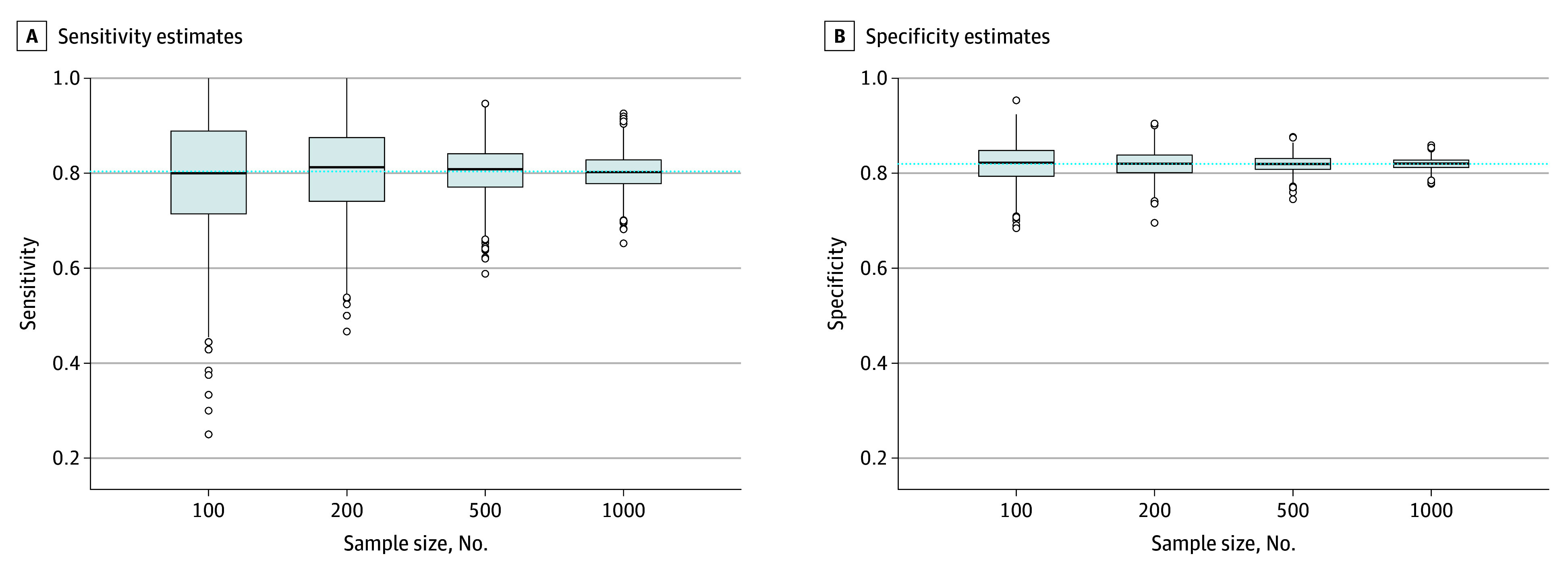
Figure 3.

Open in a new tab

Edges of boxes represent the 25th and 75th percentiles; horizontal line inside boxes represents the median; dashed horizontal line represents the accuracy of the true population-level optimal cutoff score in the full Patient Health Questionnaire-9 individual participant data meta-analysis dataset (cutoff score ≥8; sensitivity = 80.4%, specificity = 82.0%); and dots represent outliers.

As shown in eTable 3 in Supplement 1, across sample sizes, bias in estimates increased as the sample-specific optimal cutoff score diverged from 8 or higher. When the sample-specific optimal cutoff score was lower than 8, specificity was underestimated (by 6 percentage points for cutoff scores of 6 or 7 and by 16-17 percentage points for cutoff scores ≤5), whereas when the sample-specific optimal cutoff score was higher than 8, specificity was overestimated (by 5-6 percentage points for cutoff scores of 9 or 10 and by 9-11 percentage points for cutoff scores ≥11). The opposite pattern was seen for sensitivity, although there was a shift in values given that even when the sample-specific cutoff score was exactly 8 or higher, sensitivity was, on average, overestimated. As shown in eTables 4 and 5 in Supplement 1, variability in sample-specific optimal cutoff scores and bias in sensitivity and specificity were similar to the primary results when only studies that used the Structured Clinical Interview for DSM Disorders reference standard were included.

Discussion

To our knowledge, this was the first study to assess bias in PHQ-9 accuracy estimates due to data-driven optimal cutoff score selection. The main finding of this study was that data-driven optimal PHQ-9 cutoff scores often differed from the population-level optimal cutoff score, sometimes substantially, and generated biased accuracy estimates. As sample size increased from 100 to 1000 participants, variability in optimal cutoff scores decreased from a range of 2 or higher to 21 or higher to a range of 5 or higher to 11 or higher, and overestimation in sensitivity compared with the population value decreased from 6.4 to 1.8 percentage points, while specificity remained within 1 percentage point. The magnitude and direction of bias differed depending on how far the sample-specific optimal cutoff score was from the population-level optimal cutoff score of 8 or higher. When a predefined cutoff score of 8 or higher was used in resampled studies, mean accuracy estimates were consistent with overall population estimates.

Comparison With Other Studies

Previous distribution-based simulation studies have found that data-driven cutoff selection in small samples yields exaggerated accuracy estimates.4,5,6,7 Most studies on depression screening tool accuracy have small sample sizes and numbers of depression cases. Individual studies often report results from 1, several, or many cutoff scores such that there is a wide range of optimal cutoff scores and accuracy estimates across studies in the literature.1,2,3 Many researchers conclude that sample characteristics alter accuracy and that different optimal cutoff scores are needed for particular population subgroups. Results from the present study and the previous EPDS resampling study8 suggest that variability in optimal cutoff scores and accuracy estimates often occurs due to chance and imprecision in small samples even when all samples are drawn from the same population. The finding that data-driven methods and small samples may explain divergent results across studies is consistent with the results of several large IPDMA studies,15,16,22,23 which found that there were no substantive differences in depression screening tool accuracy based on participant characteristics. Additionally, the finding in the present study that accuracy estimates were similar between the full population and resampled studies when the same cutoff score was used underlines that divergences can be attributed to data-driven methods and sample size rather than to characteristics of participants in each sample.

The finding that there were larger biases in sensitivity than in specificity was not surprising given that most studies had many fewer participants with depression than without. In addition, PHQ-9 scores among cases were normally distributed, whereas scores among noncases were heavily right-skewed. Similar results were seen in the previous EPDS resampling study, which found that overestimation of sensitivity reduced from 7 percentage points in samples of 100 participants to 1 percentage point in samples of 1000 participants, while specificity was underestimated by 1 percentage point across sample sizes.8 These findings suggest that data-driven methods for cutoff score selection can allow for substantial sensitivity gains with only minor costs to specificity, although at the individual study level, sensitivity can be either overestimated or underestimated.

Implications

Clinicians and policymakers who make decisions regarding depression screening should interpret cautiously the optimal cutoff scores for the PHQ-9 and other depression screening tools identified in small single studies. Ideally, the decisions regarding what cutoff scores to use should be based on large, well-conducted meta-analyses or on multiple validations in studies with adequate sample sizes for desired precision levels. In addition, clinicians may prioritize either sensitivity or specificity in different clinical settings rather than consider them equally, as is the practice when selecting cutoff scores based on the Youden index, and select higher or lower cutoff scores depending on health and resource priorities.24 The optimal cutoff score of 8 or higher, which was identified in the hypothetical population of this study, was not derived using methods that accounted for clustering and sample weights and may reflect that participants from studies that used different reference standards were combined. PHQ-9 cutoff scores and accuracy estimates from the main IPDMA should be used clinically.16 Depression screening questionnaires are not intended to establish clinical diagnoses but can be used for screening followed by clinical evaluation of those who receive positive results. Whether screening should occur in practice requires evidence from clinical trials of screening benefit, which has not been established.25

Although the Standards for Reporting of Diagnostic Accuracy Studies reporting guideline recommends a priori sample size calculations,26 most depression screening tool accuracy studies do not conduct such calculations.2,3 Researchers conducting primary studies on accuracy should conduct sample size calculations prior to recruitment to ensure the inclusion of sufficient numbers of both cases and noncases for desired precision levels in accuracy estimates.27 In addition, selective cutoff reporting bias occurs when researchers select the cutoff scores for which to report accuracy results in their individual studies based on the relative accuracy of those cutoff scores in their sample (eg, reporting accuracy estimates for cutoff scores that maximize the Youden index but not for other cutoff scores).28,29 Selective cutoff reporting bias has been found to underestimate sensitivity for cutoff scores below a clearly defined standard and overestimate sensitivity for cutoff scores above the standard.28,29 Since summary accuracy estimates for a predefined cutoff score do not tend to be biased, researchers should report accuracy estimates for all possible cutoff scores rather than just those that are optimal in a given study or close to the optimal cutoff score.28,29 Additionally, statistical methods for estimating cutoff scores and out-of-sample performance, such as smoothing based on kernel estimation and bootstrapping, should be considered.30

Beyond variability in accuracy estimates, researchers should also consider variability in the optimal cutoff score that may be identified in individual studies. It is possible that researchers could use statistical methods to estimate uncertainty around optimal cutoff scores in their individual studies (eg, via CIs31,32) and use internal validation methods (eg, bootstrapping) to adjust for bias due to optimism.30,33 Further work to test and demonstrate such methods for the purpose of mental health screening is needed.

Strengths and Limitations

A study strength is the use of a large sample and real participant data. A limitation to consider is that we did not include datasets from recently published studies on PHQ-9 accuracy; however, we do not expect that the inclusion of more recent studies would alter the results given that newer studies would likely have similar sample sizes and heterogeneity. We included data from 100 primary studies, and we believe that the dataset used for the present study adequately represents a hypothetical population for resampling purposes. A second limitation is that we used only the Youden index to select optimal cutoff scores. Although it is by far the most common method used in depression screening accuracy studies1 and performs similarly to other indices (eg, the Euclidean distance),34 the Youden index is known to be unreliable and prone to overestimation. It is possible that results could differ slightly for an alternative method.

Conclusions

Using samples with small numbers of participants and cases to simultaneously identify an optimal cutoff score and estimate its accuracy yielded optimal cutoff scores that varied widely from study to study and exaggerated accuracy estimates. Variability in optimal cutoff scores and the extent of sensitivity exaggeration decreased as sample size increased. Researchers should conduct a priori sample size calculations to ensure the inclusion of sufficient numbers of both cases and noncases in diagnostic accuracy studies, report accuracy estimates for all cutoff scores rather than only for study-specific optimal cutoff scores, and avoid making recommendations about optimal cutoff scores and accuracy based on small single studies. Researchers also should consider using statistical methods that improve optimal cutoff score identification and estimation of accuracy outside of the study sample. Users of diagnostic accuracy evidence, including researchers, clinicians, and policymakers, should evaluate studies of PHQ-9 accuracy with caution and ensure that recommendations regarding cutoff scores are based on adequately powered and analyzed primary studies or well-conducted meta-analyses.

Supplement 1.

eMethods 1. Details on the Methodology Used to Identify, Obtain, and Synthesize the Data Included in the Present Study

eMethods 2. Search Strategies

eTable 1. Characteristics of Included Primary Studies

eTable 2. Frequencies of PHQ-9 Scores Among Participants With and Without Major Depression

eTable 3. Differences in Accuracy Estimates of the Sample Optimal Cutoffs Clustered Into Categories Based on Distance From a Cutoff of ≥8 Compared to Accuracy Estimates From a Cutoff of ≥8 in the Population

eTable 4. Variability of Data-Driven Optimal Cutoffs in 1,000 Samples of Size 100, 200, 500, and 1,000, Among Studies That Used the SCID as the Reference Standard

eTable 5. Mean Bias of Accuracy Estimates (With 95% Confidence Intervals) for 1,000 Samples of Size 100, 200, 500, and 1,000, Among Studies That Used the SCID as the Reference Standard

eFigure. Distribution of PHQ-9 Scores Among Individuals With and Without Major Depression

jamanetwopen-e2429630-s001.pdf (478KB, pdf)
Supplement 2.

Data Sharing Statement

jamanetwopen-e2429630-s002.pdf (15.1KB, pdf)

References

  • 1.Brehaut E, Neupane D, Levis B, et al. ‘Optimal’ cutoff selection in studies of depression screening tool accuracy using the PHQ-9, EPDS, or HADS-D: a meta-research study. Int J Methods Psychiatr Res. 2023;32(3):e1956. doi: 10.1002/mpr.1956 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Thombs BD, Rice DB. Sample sizes and precision of estimates of sensitivity and specificity from primary studies on the diagnostic accuracy of depression screening tools: a survey of recently published studies. Int J Methods Psychiatr Res. 2016;25(2):145-152. doi: 10.1002/mpr.1504 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Nassar EL, Levis B, Neyer MA, et al. Sample size and precision of estimates in studies of depression screening tool accuracy: a meta-research review of studies published in 2018-2021. Int J Methods Psychiatr Res. 2022;31(2):e1910. doi: 10.1002/mpr.1910 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Linnet K, Brandt E. Assessing diagnostic tests once an optimal cutoff point has been selected. Clin Chem. 1986;32(7):1341-1346. doi: 10.1093/clinchem/32.7.1341 [DOI] [PubMed] [Google Scholar]
  • 5.Ewald B. Post hoc choice of cut points introduced bias to diagnostic research. J Clin Epidemiol. 2006;59(8):798-801. doi: 10.1016/j.jclinepi.2005.11.025 [DOI] [PubMed] [Google Scholar]
  • 6.Leeflang MM, Moons KG, Reitsma JB, Zwinderman AH. Bias in sensitivity and specificity caused by data-driven selection of optimal cutoff values: mechanisms, magnitude, and solutions. Clin Chem. 2008;54(4):729-737. doi: 10.1373/clinchem.2007.096032 [DOI] [PubMed] [Google Scholar]
  • 7.Hirschfeld G, do Brasil PE. A simulation study into the performance of “optimal” diagnostic thresholds in the population: “large” effect sizes are not enough. J Clin Epidemiol. 2014;67(4):449-453. doi: 10.1016/j.jclinepi.2013.07.018 [DOI] [PubMed] [Google Scholar]
  • 8.Bhandari PM, Levis B, Neupane D, et al. ; Depression Screening Data (DEPRESSD) EPDS Group . Data-driven methods distort optimal cutoffs and accuracy estimates of depression screening tools: a simulation study using individual participant data. J Clin Epidemiol. 2021;137:137-147. doi: 10.1016/j.jclinepi.2021.03.031 [DOI] [PubMed] [Google Scholar]
  • 9.Youden WJ. Index for rating diagnostic tests. Cancer. 1950;3(1):32-35. doi: [DOI] [PubMed] [Google Scholar]
  • 10.Kroenke K, Spitzer RL, Williams JB. The PHQ-9: validity of a brief depression severity measure. J Gen Intern Med. 2001;16(9):606-613. doi: 10.1046/j.1525-1497.2001.016009606.x [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Kroenke K, Spitzer RL. The PHQ-9: a new depression diagnostic and severity measure. Psychiatr Ann. 2002;32(9):509-515. doi: 10.3928/0048-5713-20020901-06 [DOI] [Google Scholar]
  • 12.Spitzer RL, Kroenke K, Williams JB. Validation and utility of a self-report version of PRIME-MD: the PHQ primary care study.. JAMA. 1999;282(18):1737-1744. doi: 10.1001/jama.282.18.1737 [DOI] [PubMed] [Google Scholar]
  • 13.Wittkampf KA, Naeije L, Schene AH, Huyser J, van Weert HC. Diagnostic accuracy of the mood module of the Patient Health Questionnaire: a systematic review. Gen Hosp Psychiatry. 2007;29(5):388-395. doi: 10.1016/j.genhosppsych.2007.06.004 [DOI] [PubMed] [Google Scholar]
  • 14.Gilbody S, Richards D, Brealey S, Hewitt C. Screening for depression in medical settings with the Patient Health Questionnaire (PHQ): a diagnostic meta-analysis. J Gen Intern Med. 2007;22(11):1596-1602. doi: 10.1007/s11606-007-0333-y [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Levis B, Benedetti A, Thombs BD; DEPRESsion Screening Data (DEPRESSD) Collaboration . Accuracy of Patient Health Questionnaire-9 (PHQ-9) for screening to detect major depression: individual participant data meta-analysis. BMJ. 2019;365:l1476. doi: 10.1136/bmj.l1476 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Negeri ZF, Levis B, Sun Y, et al. ; Depression Screening Data (DEPRESSD) PHQ Group . Accuracy of the Patient Health Questionnaire-9 for screening to detect major depression: updated systematic review and individual participant data meta-analysis. BMJ. 2021;375:n2183. doi: 10.1136/bmj.n2183 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Thombs BD, Benedetti A, Kloda LA, et al. The diagnostic accuracy of the Patient Health Questionnaire-2 (PHQ-2), Patient Health Questionnaire-8 (PHQ-8), and Patient Health Questionnaire-9 (PHQ-9) for detecting major depression: protocol for a systematic review and individual patient data meta-analyses. Syst Rev. 2014;3:124. doi: 10.1186/2046-4053-3-124 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Levis B, Bhandari PM, Benedetti A, Thombs BD; DEPRESSD Collaboration. Evaluation of bias in diagnostic accuracy estimates due to data-driven cutoff selection: protocol for a simulation study using individual participant data from 58 studies on the diagnostic accuracy of the Patient Health Questionnaire-9 (PHQ-9). Accessed April 28, 2024. https://osf.io/pg2yc/
  • 19.Hall S, Moskovitz C, Pemberton M; Text Recycling Research Project. Best practices for researchers. V1.1. Accessed September 15, 2023. https://textrecycling.org/resources/best-practices-for-researchers/
  • 20.Levis B, Benedetti A, Riehm KE, et al. Probability of major depression diagnostic classification using semi-structured versus fully structured diagnostic interviews. Br J Psychiatry. 2018;212(6):377-385. doi: 10.1192/bjp.2018.54 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Wu Y, Levis B, Ioannidis JPA, Benedetti A, Thombs BD; DEPRESsion Screening Data (DEPRESSD) Collaboration . Probability of major depression classification based on the SCID, CIDI, and MINI diagnostic interviews: a synthesis of three individual participant data meta-analyses. Psychother Psychosom. 2021;90(1):28-40. doi: 10.1159/000509283 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Levis B, Negeri Z, Sun Y, Benedetti A, Thombs BD; DEPRESsion Screening Data (DEPRESSD) EPDS Group . Accuracy of the Edinburgh Postnatal Depression Scale (EPDS) for screening to detect major depression among pregnant and postpartum women: systematic review and meta-analysis of individual participant data. BMJ. 2020;371:m4022. doi: 10.1136/bmj.m4022 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Wu Y, Levis B, Sun Y, et al. ; DEPRESsion Screening Data (DEPRESSD) HADS Group . Accuracy of the Hospital Anxiety and Depression Scale Depression subscale (HADS-D) to screen for major depression: systematic review and individual participant data meta-analysis. BMJ. 2021;373(972):n972. doi: 10.1136/bmj.n972 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Using the PHQ-9 to screen for depression: a practice-based perspective. Accessed April 28, 2024. http://depressionscreening100.com/phq/
  • 25.Thombs BD, Markham S, Rice DB, Ziegelstein RC. Does depression screening in primary care improve mental health outcomes? BMJ. 2021;374:n1661. doi: 10.1136/bmj.n1661 [DOI] [PubMed] [Google Scholar]
  • 26.Bossuyt PM, Reitsma JB, Bruns DE, et al. ; STARD Group . STARD 2015: an updated list of essential items for reporting diagnostic accuracy studies. BMJ. 2015;351:h5527. doi: 10.1136/bmj.h5527 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Flahault A, Cadilhac M, Thomas G. Sample size calculation should be performed for design accuracy in diagnostic test studies. J Clin Epidemiol. 2005;58(8):859-862. doi: 10.1016/j.jclinepi.2004.12.009 [DOI] [PubMed] [Google Scholar]
  • 28.Levis B, Benedetti A, Levis AW, et al. Selective cutoff reporting in studies of diagnostic test accuracy: a comparison of conventional and individual-patient-data meta-analyses of the Patient Health Questionnaire-9 depression screening tool. Am J Epidemiol. 2017;185(10):954-964. doi: 10.1093/aje/kww191 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Neupane D, Levis B, Bhandari PM, Thombs BD, Benedetti A; DEPRESsion Screening Data (DEPRESSD) Collaboration . Selective cutoff reporting in studies of the accuracy of the Patient Health Questionnaire-9 and Edinburgh Postnatal Depression Scale: comparison of results based on published cutoffs versus all cutoffs using individual participant data meta-analysis. Int J Methods Psychiatr Res. 2021;30(3):e1873. doi: 10.1002/mpr.1873 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Thiele C, Hirshfeld G. cutpointr: Improved estimation and validation of optimal cutpoints in R. J Stat Softw. 2021;98(11):1-27. doi: 10.18637/jss.v098.i11 [DOI] [Google Scholar]
  • 31.Fluss R, Faraggi D, Reiser B. Estimation of the Youden index and its associated cutoff point. Biom J. 2005;47(4):458-472. doi: 10.1002/bimj.200410135 [DOI] [PubMed] [Google Scholar]
  • 32.Schisterman EF, Perkins N. Confidence intervals for the Youden index and corresponding optimal cut-point. Commun Stat Simul Comput. 2007;36(3):549-563. doi: 10.1080/03610910701212181 [DOI] [Google Scholar]
  • 33.Smith GC, Seaman SR, Wood AM, Royston P, White IR. Correcting for optimistic prediction in small data sets. Am J Epidemiol. 2014;180(3):318-324. doi: 10.1093/aje/kwu140 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Hajian-Tilaki K. The choice of methods in determining the optimal cut-off value for quantitative diagnostic test evaluation. Stat Methods Med Res. 2018;27(8):2374-2383. doi: 10.1177/0962280216680383 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplement 1.

eMethods 1. Details on the Methodology Used to Identify, Obtain, and Synthesize the Data Included in the Present Study

eMethods 2. Search Strategies

eTable 1. Characteristics of Included Primary Studies

eTable 2. Frequencies of PHQ-9 Scores Among Participants With and Without Major Depression

eTable 3. Differences in Accuracy Estimates of the Sample Optimal Cutoffs Clustered Into Categories Based on Distance From a Cutoff of ≥8 Compared to Accuracy Estimates From a Cutoff of ≥8 in the Population

eTable 4. Variability of Data-Driven Optimal Cutoffs in 1,000 Samples of Size 100, 200, 500, and 1,000, Among Studies That Used the SCID as the Reference Standard

eTable 5. Mean Bias of Accuracy Estimates (With 95% Confidence Intervals) for 1,000 Samples of Size 100, 200, 500, and 1,000, Among Studies That Used the SCID as the Reference Standard

eFigure. Distribution of PHQ-9 Scores Among Individuals With and Without Major Depression

jamanetwopen-e2429630-s001.pdf (478KB, pdf)
Supplement 2.

Data Sharing Statement

jamanetwopen-e2429630-s002.pdf (15.1KB, pdf)

Articles from JAMA Network Open are provided here courtesy of American Medical Association

RESOURCES