The allometry of brain size in Euarchontoglires: clade-specific patterns and their impact on encephalization quotients

Abstract

The timing and nature of evolutionary shifts in the relative brain size of Primates have been extensively studied. Less is known, however, about the scaling of the brain-to-body size in their closest living relatives, i.e., among other members of Euarchontoglires (Dermoptera, Scandentia, Lagomorpha, Rodentia). Ordinary least squares (OLS), reduced major axis (RMA), and phylogenetic generalized least squares (PGLS) regressions were fitted to the largest euarchontogliran data set of brain and body mass, comprising 715 species. Contrary to previous inferences, lagomorph brain sizes (PGLS slope = 0.465; OLS slope = 0.593) scale relative to body mass similarly to rodents (PGLS = 0.526; OLS = 0.638), and differently than primates (PGLS = 0.607; OLS = 0.794). There is a shift in the pattern of the scaling of the brain in Primates, with Strepsirrhini occupying an intermediate stage similar to Scandentia but different from Rodentia and Lagomorpha, while Haplorhini differ from all other groups in the OLS and RMA analyses. The unique brain–body scaling relationship of Primates among Euarchontoglires illustrates the need for clade-specific metrics for relative brain size (i.e., encephalization quotients; EQs) for more restricted taxonomic entities than Mammalia. We created clade-specific regular and phylogenetically adjusted EQ equations at superordinal, ordinal, and subordinal levels. When using fossils as test cases, our results show that generalized mammalian equations underestimate the encephalization of the stem lagomorph Megalagus turgidus in the context of lagomorphs, overestimate the encephalization of the stem primate Microsyops annectens and the early euprimate Necrolemur antiquus, but provide similar EQ values as our new strepsirrhine-specific EQ when applied to the early euprimate Adapis parisiensis.

The current work examines the scaling relationships between brain mass and body mass for one of the major mammalian clades, Euarchontoglires, the group that includes living primates, treeshrews, colugos, rodents, and lagomorphs. Previous work suggested that a similar scaling pattern of the brain was found between Lagomorpha and Primates. However, our results show that Lagomorpha scaled their brains more similarly to their closest relatives, Rodentia. One of the critical uses of brain–body size scaling equations is in calculation of metrics for relative brain size, of which the encephalization quotient (EQ) is the most familiar. Using clade-specific patterns, new EQ and phylogenetically accounted EQ equations are proposed, which should allow for effective comparison of brain sizes in analyses of euarchontoglirans at varying taxonomic scales.

One of the defining characteristics of modern primates is their relatively large brain size compared to other mammalian orders (Martin 1990). Primates have historically received significant attention with respect to the question of how their brain size scales in relation to body size (e.g., Count 1947; Gould 1975; Lande 1979; Clutton-Brock and Harvey 1980; Bronson 1981; Shea 1983; Armstrong 1985; Martin and Harvey 1985; Marino 1998; Sherwood et al. 2008; Boddy et al. 2012; Smaers et al. 2012, 2021; Holekamp et al. 2013; Burger et al. 2019). Within the order Primates, hominoids (Hominoidea) are particularly encephalized, both in the larger context of Mammalia and compared to the much less encephalized and smaller bodied strepsirrhines (Strepsirrhini). This association between body size and degree of encephalization leads to Primates having the highest slope value in ordinary least square (OLS) regression analyses of brain mass against body mass among any of the mammalian orders (Burger et al. 2019). However, to fully understand evolutionary trends that define the primate brain, it is necessary to place the scaling of the primate brain within a phylogenetic context. This exercise is 2-fold: on the one hand, it is important to explore how brain-to-body scaling relationships differ at a subordinal level within Primates, while on the other hand, it is important to put primate data into the larger context of their close, non-primate relatives.

While there is a long history of the study of relative brain size in primates, the consensus around the broader phylogenetic context within which these data should be assessed has changed relatively recently (Murphy et al. 2001). Literature from only a few decades ago treated “insectivorans” as a good model for primitive states for the primate brain—this was true, for example, with respect to the classic and oft-reanalyzed compilation of quantitative data on primate brains by Stephan et al. (1970, 1981). However, modern phylogenetic studies (e.g., Foley et al. 2023) position eulipotyphlan “insectivorans” as relatively distant to primates. Instead, Primates are broadly considered to be members of the superorder Euarchonta (together with the orders Dermoptera and Scandentia; Waddell et al. 1999), and Euarchonta is understood to be most closely related to the superorder Glires (Rodentia + Lagomorpha) within the greater grouping of Euarchontoglires (Murphy et al. 2001; Foley et al. 2023).

Recent molecular analyses have supported both Dermoptera (Mason et al. 2016; Zhang et al. 2019; Foley et al. 2023) and Sundatheria (Dermoptera + Scandentia; Olson et al. 2005; Upham et al. 2019) as the sister group of Primates. However, dermopterans are only known from 2 species, which makes it problematic to delve into the relationship between brain mass and body mass at an ordinal level. In the case of Scandentia, the present paper is the first detailed consideration of allometric relationships between brain and body mass for this group. Smaers et al. (2021) inferred a value for Scandentia from an ancestral state reconstruction analysis, but that was based on only 5 taxa, all of them tupaiines. Relative brain size has been more intensively studied in rodents (e.g., Count 1947; Mace et al. 1981; Mace and Eisenberg 1982; Pilleri et al. 1984; Hafner and Hafner 1984; Towe and Mann 1992; Bernard and Nurton 1993; Mann and Towe 2003; Matějů et al. 2016; Burger et al. 2019; Bertrand et al. 2021), but much less for lagomorphs. Burger et al. (2019) reported that the regression slope values for rodent and lagomorph regressions of brain mass on body mass were notably different. In their analysis, rodents had a slope value of 0.64, but lagomorphs were reported to have a slope value of 0.75 (Burger et al. 2019). This result implies that the brains in lagomorphs would scale more similarly to primates (slope value of 0.79; Burger et al. 2019) than they would to rodents, which would be surprising for a group that is not generally thought of as having comparatively encephalized larger members.

The calculation of allometric regressions describing brain scaling for the various euarchontogliran groups is also of particular relevance for the calculation of encephalization quotients (EQs; Jerison 1973; Supplementary Data SD1). Although sometimes criticized (e.g., Deacon 1990; Begun and Kordos 2004; Schoenemann 2006; Deaner et al. 2007; Gilbert and Jungers 2017), the calculation of metrics related to EQs for fossil taxa remains a critically important part of assessing brain size evolution through time in Primates and other orders (e.g., Boddy et al. 2012; Ni et al. 2019; Bertrand et al. 2022; Silcox et al. 2023). To date, the most commonly used equations for calculation of EQ in fossil Euarchontoglires are based on general mammalian samples (i.e., Jerison 1973; Eisenberg 1981). However, some authors have taken the approach of studying relative brain size evolution using EQs calculated from more restricted samples, which might provide a better framework for studying variation and evolution of relative brain size within the context of a particular group. For example, Pilleri et al. (1984) developed a rodent-specific equation that has recently been used for the calculation of EQs in many fossil rodent studies (Bertrand and Silcox 2016; Bertrand et al. 2016, 2017, 2018, 2019a). More recently, Grabowski et al. (2016) and Ni et al. (2019) developed primate-specific equations based on PGLS regressions of endocranial volume versus body mass, and Ni et al. (2019) coined the term “phylogenetic encephalization quotient” (PEQ). Further, Bertrand et al. (2021) developed a PEQ equation for their own sample of sciuroid rodents and extinct closest relatives, Püschel et al. (2021) also used their own equation for PEQ using extant and extinct hominoids, and Bertrand et al. (2022) conceived their own equation of PEQ for a sample of extinct placental mammals.

In the present study we aim to: (1) analyze the allometry of brain mass to body mass across Euarchontoglires and at lower taxonomic levels; (2) examine the patterns in relative brain size variation among and within major evolutionary lineages; and (3) generate clade-specific EQ equations. The goal of generating clade-specific EQ equations is to minimize error and allow authors to tailor their research questions to narrower taxonomic frameworks. The current work therefore considers patterns of allometric scaling in all euarchontogliran orders and probes the question of how best to use that information to study the evolution of relative brain size through time.

Materials and methods

The studied sample

We acquired estimates of brain size and body size for 715 species of Euarchontoglires (Supplementary Data SD2, SD4). In our analyses, we used data from previously published literature (Bertrand and Silcox 2016; Bertrand et al. 2017, 2018, 2019a, 2021; Burger et al. 2019; López-Torres et al. 2020; Smaers et al. 2021; Lang et al. 2022). In all cases, when data originated from endocranial volumes (cm³), they were converted to brain mass (g) by dividing the endocranial volume by 1.036 (Stephan et al. 1981). For details about original sources of data, see Supplementary Data SD2. In the process of combining data sets, we were careful to avoid duplicating entries. In some cases, new data for particular species were combined with data from previous literature to generate new average values. For rodents, we combined the data sets from Burger et al. (2019), Bertrand and Silcox (2016), Bertrand et al. (2018, 2021), and Lang et al. (2022). For lagomorphs, we combined the data sets from Burger et al. (2019), López-Torres et al. (2020), and Smaers et al. (2021). For primates, we combined Burger et al.’s (2019) and Lang et al.’s (2022) data sets. For scandentians, we combined Burger et al.’s (2019) and San Martin-Flores et al.’s (2018) data sets. The new scandentian sample (n = 14) allows us to generate the first regression lines for brain versus body mass for this order of mammals. The brain size data for dermopterans were obtained from Lang et al. (2022) and include both extant species; the body mass data were taken from Stafford and Szalay (2000). Although it is fundamentally uninformative to generate a regression line from only 2 points, the dermopteran species were still included in the calculations for the regression lines for Euarchonta and Euarchontoglires.

Following the total number of species in different mammalian orders by Burgin et al. (2018), the present study samples 100% of currently recognized dermopteran species (2/2), 58% of currently recognized scandentian species (14/24), 47.88% of currently recognized primate species (248/518), 31.63% of currently recognized lagomorph species (31/98), and 16.46% of currently recognized rodent species (420/2,552). Only extant taxa were included in this analysis. The main reason for the exclusion of extinct taxa is that uncertainty in body mass estimates for fossils would lead to very large amounts of error around the calculated regression lines, making it difficult to interpret any differences as being a product of relative brain size versus uncertainty in the underlying data. Also, because there is a temporal effect in brain size in several mammalian orders (Jerison 1973; Silcox et al. 2010; Orliac and Gilissen 2012; Yao et al. 2012; Bertrand et al. 2019a, 2022), simultaneously analyzing fossils with extant taxa has the potential of conflating temporal patterns with scaling relationships that exist within particular groups at a given moment in evolutionary time. However, it is a fair concern that these temporal shifts could make the scaling relationships calculated here an inaccurate representation of those that would have applied at other points in the evolution of euarchontoglirans. Investigating these complexities is beyond the scope of the current analysis.

No research was conducted on live animals.

Analysis

The scaling of brain size with body size has typically been characterized by a power law (Snell 1892; Dubois 1898; Jerison 1973), where:

$${\displaystyle \begin{array}{l}{\displaystyle (Brainmass)=\alpha {(Bodymass)}^{\beta }}\end{array}}$$

and α and β are constants representing the intercept and slope, respectively. This relationship becomes linear by log transforming both sides of the equation:

$${\displaystyle \begin{array}{l}{\displaystyle log(Brainmass)=log(\alpha )+\beta \cdot log(Bodymass)}\end{array}}$$

OLS, reduced major axis (RMA), and phylogenetic generalized least squares (PGLS) regressions were fitted to our data. We used all 3 approaches to allow for comparison to previous analyses and to enable the calculation of both regular EQs and PEQs. Bootstrapped estimates of OLS and RMA regression slopes and intercepts were generated for each taxonomic grouping based on 10,000 random resampling iterations using the Statistics101 software package (http://www.statistics101.net/). The PGLS analysis was conducted by incorporating an extensively sampled, time-scaled mammalian phylogeny (Upham et al. 2019); of the total of 715 taxa, 696 taxa could be included based on their presence in the Upham et al. (2019) analysis. All regression parameters were simultaneously estimated with phylogenetic signal in the residual error as Pagel’s lambda (Pagel 1999; Revell 2010) using the phylolm function in the R package “phylolm” (Tung Ho and Ané 2014). Regression lines of the 3 types were calculated at multiple taxonomic levels: supraordinal (Euarchonta, Glires, and Euarchontoglires), ordinal (Primates, Scandentia, Rodentia, and Lagomorpha), and subordinal (Strepsirrhini and Haplorhini).

Calculation of significance

P-values are strongly dependent on sample size and relate to an arbitrarily chosen alpha level. In this study, rather than making determinations of statistical significance using standard P-values consistent with traditional hypothesis testing, we chose to estimate what the difference in slope and intercept values is likely to be between taxonomic groups (see discussion in Smith 2020). To do this we used random resampling with replacement to generate resampling distributions of the difference between taxonomic groupings in slope and intercept values, also based on 10,000 resampling iterations. We used these resampling distributions to generate 95% confidence intervals (CIs), which is the interval that comprises 95% of the resampled differences between the 2 taxonomic groupings compared. Standard deviations and 95% CIs for the slopes, intercepts, and differences between taxonomic groupings were generated from the resampling distributions. We use standard deviation of the resampled distribution as the standard error of the bootstrap estimate (i.e., slope, intercept, or difference).

New EQ equations

In this study, we propose new clade-specific EQs (Table 1), following the model suggested by Pilleri et al. (1984) specifically for rodents, which has been previously used in studies focusing on fossil rodent endocasts (Bertrand et al. 2016; Bertrand and Silcox 2016, 2017). These equations are based on more constrained samples, instead of general mammalian samples as in Jerison (1973) or Eisenberg (1981). The new equations are derived from the OLS and the PGLS regression equations. Additionally, in this study we are using a few fossil specimens as test cases for the new EQs. In particular, we use the stem lagomorph Megalagus turgidus (FMNH UC 1642; López-Torres et al. 2020), the stem primate Microsyops annectens (UW 14559; Silcox et al. 2010), the adapoid primate Adapis parisiensis (NHM M 1345; Harrington et al. 2016), and the omomyoid primate Necrolemur antiquus (MaPhQ 289; Harrington et al. 2020) to allow us to consider the value of taxonomically constrained EQ equations. Brain mass and body mass data for these species are provided in Table 2.

Table 1.

Formulae to calculate the expected brain mass (E_c) for a given body mass (BM) for specific taxonomic groups. The EQ and PEQ are calculated by dividing the actual brain mass by the E_c given in this table. The equations are formulated the following way: 10^intercept * (body mass)^slope.

	E c for EQ	E c for PEQ
Euarchontoglires	0.045 * BM0.809	0.214 * BM0.540
Euarchonta	0.067 * BM0.805	0.189 * BM0.603
Glires	0.090 * BM0.635	0.168 * BM0.524
Rodentia	See Pilleri et al. (1984)	0.166 * BM0.526
Lagomorpha	0.117 * BM0.594	0.262 * BM0.465
Scandentia	0.151 * BM0.604	0.167 * BM0.580
Primates	0.074 * BM0.794	0.247 * BM0.607
Strepsirrhini	0.117 * BM0.679	0.206 * BM0.614
Haplorhini	0.146 * BM0.723	0.341 * BM0.578

Table 2.

Brain mass and body mass data (in grams) for selected taxa of fossil Euarchontoglires.

Order	Family	Species	Specimen number	Brain mass	Body mass	Source
Lagomorpha	Megalagidae	Megalagus turgidus	FMNH UC 1642	6.72	2,325.01	López-Torres et al. (2020)
Primates	Microsyopidae	Microsyops annectens	UW 12362	5.62	1,358 to 2,568	Silcox et al. (2010)
Primates	Adapidae	Adapis parisiensis	NHM M1345	8.39	1,103	Harrington et al. (2016)
Primates	Microchoeridae	Necrolemur antiquus	MaPhQ 289	2.36	144	Harrington et al. (2020)

Institutional abbreviations

FMNH UC—University of Chicago collection, Field Museum of Natural History, Chicago, Illinois, United States; MaPhQ—Muséum d’Histoire Naturelle Victor Brun, Montauban, France; NHM—Natural History Museum, London, United Kingdom; UW—University of Wyoming, Laramie, Wyoming, United States.

Results

Results for the OLS analysis are shown in Tables 3 and 4; the results for the PGLS analysis are shown in Tables 5 and 6; and the results for the RMA analysis are shown in the Supplementary Data SD3. The calculated regression lines are shown at the supraordinal level (Euarchonta, Glires, and Euarchontoglires; Fig. 1), ordinal level (Primates, Scandentia, Rodentia, and Lagomorpha; Fig. 2), and subordinal level (Strepsirrhini and Haplorhini; Fig. 3). Figure 4 combines different regression lines in 1 graph to better visualize the comparison between slopes and intercepts.

Table 3.

Allometries for log₁₀ brain size versus log₁₀ body size across different taxonomic levels within Euarchontoglires based on bootstrap estimates of OLS regression parameters. n = number of sampled species; r = correlation coefficient; SD = standard deviation.

Taxon	n	r	Slope	SD	95% CI		Intercept	SD	95% CI
					Lower end	Upper end			Lower end	Upper end
Euarchontoglires	715	0.959	0.809	0.009	0.791	0.826	−1.344	0.021	−1.386	−1.303
Euarchonta	264	0.963	0.805	0.011	0.783	0.827	−1.177	0.037	−1.251	−1.105
Glires	451	0.962	0.635	0.008	0.619	0.652	−1.044	0.019	−1.082	−1.008
Rodentia	420	0.959	0.638	0.010	0.619	0.657	−1.050	0.021	−1.089	−1.008
Lagomorpha	31	0.955	0.594	0.037	0.517	0.668	−0.931	0.117	−1.160	−0.693
Scandentia	14	0.964	0.604	0.048	0.502	0.692	−0.821	0.099	−1.004	−0.608
Primates	248	0.959	0.794	0.014	0.769	0.822	−1.133	0.047	−1.228	−1.044
Strepsirrhini	63	0.958	0.679	0.019	0.645	0.719	−0.932	0.053	−1.045	−0.837
Haplorhini	185	0.954	0.723	0.018	0.687	0.759	−0.834	0.066	−0.961	0.702

Table 4.

Pairwise comparisons of bootstrap estimates of differences among Euarchontoglires in OLS regression parameters. SD = standard deviation. Asterisks = likely to be different.

Taxon	Slope bootstrap difference	SD	95% CI		Intercept bootstrap difference	SD	95% CI
			Lower end	Upper end			Lower end	Upper end
Euarchonta–Glires	0.169*	0.042	0.143	0.197	−0.133*	0.042	−0.215	−0.051
Rodentia–Lagomorpha	0.044	0.039	−0.031	0.123	−0.119	0.120	−0.364	0.114
Rodentia–Scandentia	−0.034	0.102	−0.138	0.055	0.228*	0.102	0.044	0.445
Lagomorpha–Scandentia	0.010	0.153	−0.111	0.126	0.110	0.153	−0.187	0.416
Primates–Glires	0.158*	0.050	0.128	0.191	−0.088	0.050	−0.190	0.007
Primates–Rodentia	0.156*	0.050	0.125	0.189	−0.084	0.050	−0.185	0.011
Primates–Lagomorpha	0.200*	0.128	0.123	0.283	−0.204	0.128	−0.468	0.042
Primates–Scandentia	0.190*	0.108	0.103	0.294	−0.313*	0.108	−0.542	−0.114
Strepsirrhini–Haplorhini	0.044	0.085	−0.010	0.094	0.097	0.085	−0.060	0.272
Strepsirrhini–Scandentia	0.074	0.113	−0.018	0.182	−0.111	0.113	−0.348	0.093
Strepsirrhini–Rodentia	0.040*	0.056	0.002	0.083	0.117	0.056	−0.002	0.218
Strepsirrhini–Lagomorpha	0.085*	0.130	0.003	0.170	−0.002	0.130	−0.267	0.246
Haplorhini–Scandentia	0.112*	0.138	0.010	0.248	0.003	0.138	−0.302	0.246
Haplorhini–Rodentia	0.085*	0.069	0.042	0.125	0.215	0.069	0.083	0.356
Haplorhini–Lagomorpha	0.130*	0.137	0.048	0.216	0.093	0.137	−0.184	0.357

Table 5.

Allometries for log₁₀ brain size versus log₁₀ body size across different taxonomic levels within Euarchontoglires based on bootstrap estimates of PGLS regression parameters. n = number of sampled species; λ = Pagel’s lambda (tree transformation that measures phylogenetic signal); SD = standard deviation.

Taxon	n	R 2	λ	Slope	SD	95% CI		Intercept	SD	95% CI
						Lower end	Upper end			Lower end	Upper end
Euarchontoglires	696	0.766	0.898	0.540	0.011	0.518	0.561	−0.670	0.067	−0.811	−0.540
Euarchonta	254	0.779	0.882	0.603	0.022	0.561	0.644	−0.724	0.096	−0.911	−0.538
Glires	442	0.779	0.882	0.524	0.013	0.499	0.549	−0.774	0.088	−0.949	−0.611
Rodentia	413	0.784	0.875	0.526	0.013	0.501	0.550	−0.779	0.097	−0.967	−0.593
Lagomorpha	29	0.784	0.875	0.465	0.084	0.295	0.628	−0.581	0.272	−1.092	−0.083
Scandentia	14	0.784	0.875	0.580	0.114	0.364	0.803	−0.778	0.250	−1.262	−0.313
Primates	238	0.784	0.875	0.607	0.022	0.566	0.650	−0.607	0.114	−0.833	−0.385
Strepsirrhini	60	0.725	0.915	0.614	0.044	0.527	0.701	−0.687	0.193	−1.053	−0.316
Haplorhini	178	0.725	0.915	0.578	0.029	0.518	0.635	−0.468	0.162	−0.793	−0.154

Table 6.

Pairwise comparisons of bootstrap estimates of the differences in PGLS regression parameters among Euarchontoglires. SD = standard deviation. Asterisks = likely to be different.

Taxon	Slope bootstrap difference	SD	95% CI		Intercept bootstrap difference	SD	95% CI
			Lower end	Upper end			Lower end	Upper end
Euarchonta–Glires	0.079*	0.025	0.031	0.128	0.050	0.126	−0.197	0.286
Rodentia–Lagomorpha	−0.060	0.085	−0.226	0.106	0.198	0.272	−0.301	0.708
Rodentia–Scandentia	−0.054	0.115	−0.279	0.161	0.000	0.269	−0.543	0.522
Lagomorpha–Scandentia	−0.115	0.142	−0.386	0.168	0.197	0.366	−0.484	0.901
Primates–Glires	0.083*	0.026	0.031	0.132	0.167	0.144	−0.133	0.441
Primates–Rodentia	0.082*	0.026	0.034	0.134	0.172	0.147	−0.105	0.450
Primates–Lagomorpha	−0.142	0.088	−0.309	0.027	0.026	0.296	−0.534	0.616
Primates–Scandentia	0.027	0.116	−0.211	0.247	0.172	0.276	−0.365	0.708
Strepsirrhini–Haplorhini	−0.036	0.053	−0.143	0.067	0.219	0.230	−0.234	0.666
Strepsirrhini–Scandentia	−0.043	0.123	−0.281	0.197	−0.080	0.323	−0.720	0.578
Strepsirrhini–Rodentia	0.088	0.046	−0.002	0.184	0.092	0.214	−0.309	0.511
Strepsirrhini–Lagomorpha	0.149	0.091	−0.020	0.330	−0.106	0.316	−0.704	0.509
Haplorhini–Scandentia	0.007	0.118	−0.213	0.245	0.299	0.310	−0.313	0.888
Haplorhini–Rodentia	0.052	0.032	−0.012	0.117	0.311	0.188	−0.056	0.668
Haplorhini–Lagomorpha	0.113	0.090	−0.067	0.288	0.114	0.319	−0.513	0.741

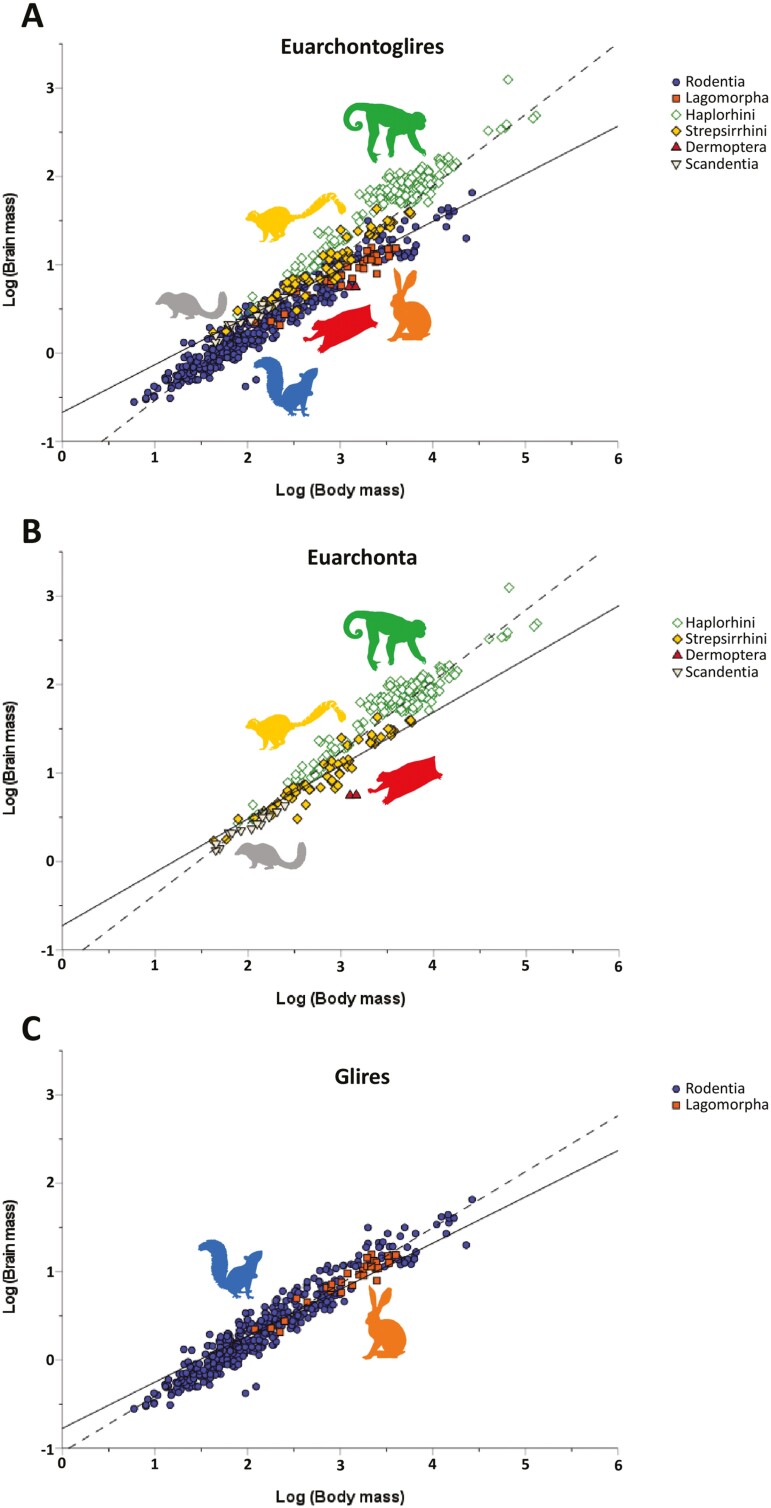
Fig. 1.

Bivariate plots of log brain mass versus log body mass for euarchontogliran species. Points are color-coded by order, except for Primates, which are divided into the suborders Haplorhini and Strepsirrhini. Best fit lines are shown for the OLS (dashed) and PGLS (solid) regressions. (A) Data for the entire sample, with the best fit line for Euarchontoglires (OLS slope = 0.809, intercept = −1.344; PGLS slope = 0.540, intercept = −0.670); (B) data for members of Euarchonta (Primates, Dermoptera, Scandentia; OLS slope = 0.805, intercept = −1.177; PGLS slope = 0.603, intercept = −0.724); (C) data for members of Glires (Rodentia, Lagomorpha; OLS slope = 0.635, intercept = −1.044; PGLS slope = 0.524, intercept = −0.774).

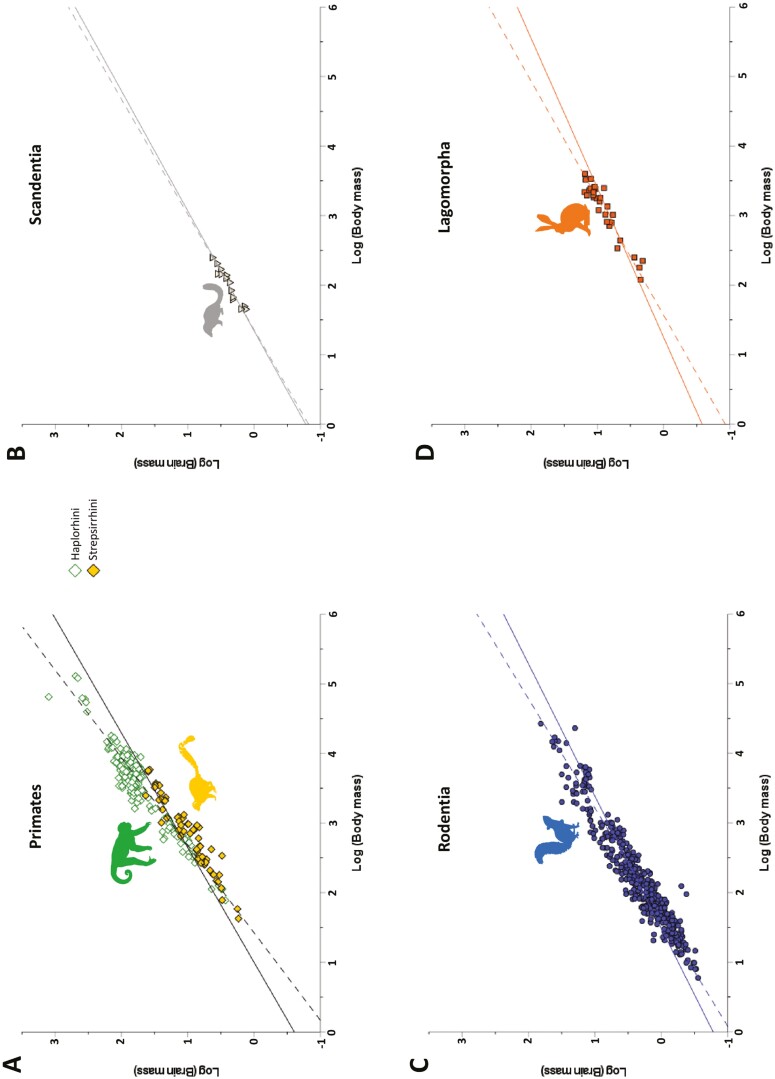
Fig. 2.

Bivariate plots of log brain mass versus log body mass for individual euarchontogliran orders. Best fit lines are shown for the OLS (dashed) and PGLS (solid) regressions. (A) Data for Primates, with points color-coded by suborder. The best fit lines are for all Primates (OLS slope = 0.794, intercept = −1.133; PGLS slope = 0.607, intercept = −0.607); (B) data for Scandentia (OLS slope = 0.604, intercept = −0.821; PGLS slope = 0.580, intercept = −0.778); (C) data for Rodentia (OLS slope = 0.638, intercept = −1.050; PGLS slope = 0.526, intercept = −0.779); (D) data for Lagomorpha (OLS slope = 0.594, intercept = −0.931; PGLS slope = 0.465, intercept = −0.581).

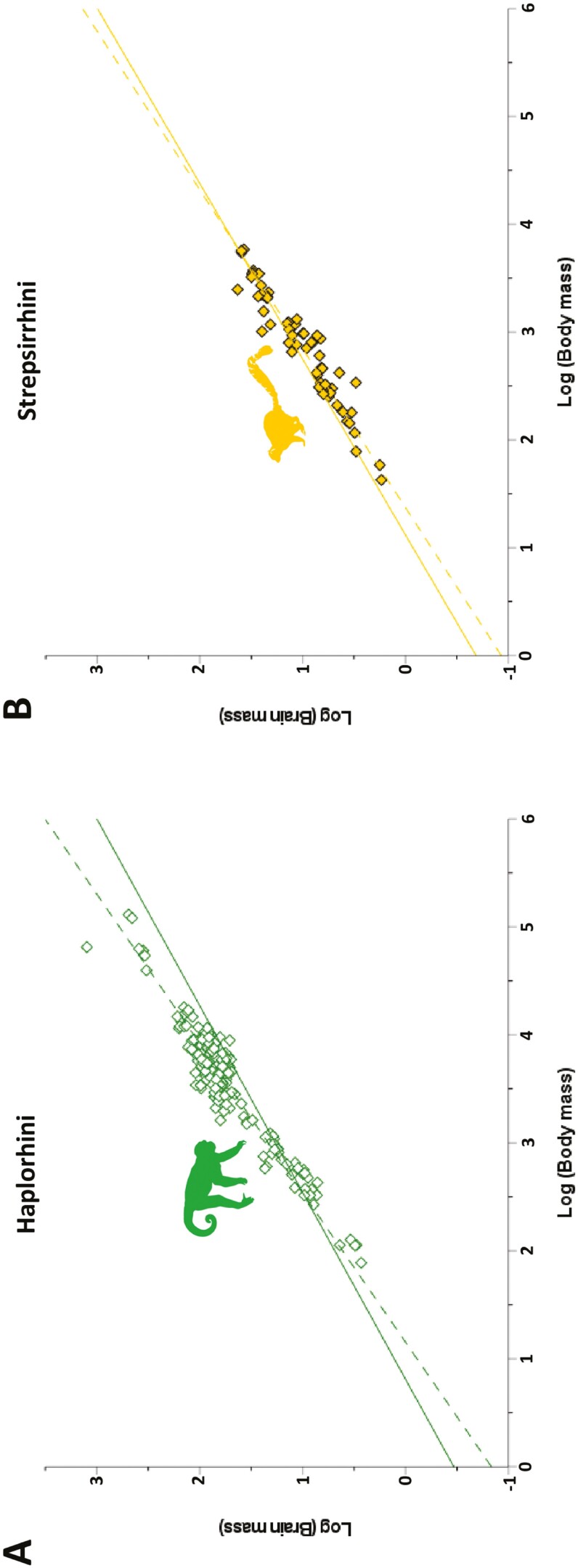
Fig. 3.

Bivariate plots of log brain mass versus log body mass for Primates by suborder. Best fit lines are shown for the OLS (dashed) and PGLS (solid) regressions. (A) Data for Haplorhini (OLS slope = 0.723, intercept = −0.834; PGLS slope = 0.578, intercept = −0.468); (B) data for Strepsirrhini (OLS slope = 0.679; intercept = −0.932; PGLS slope = 0.614, intercept = −0.687).

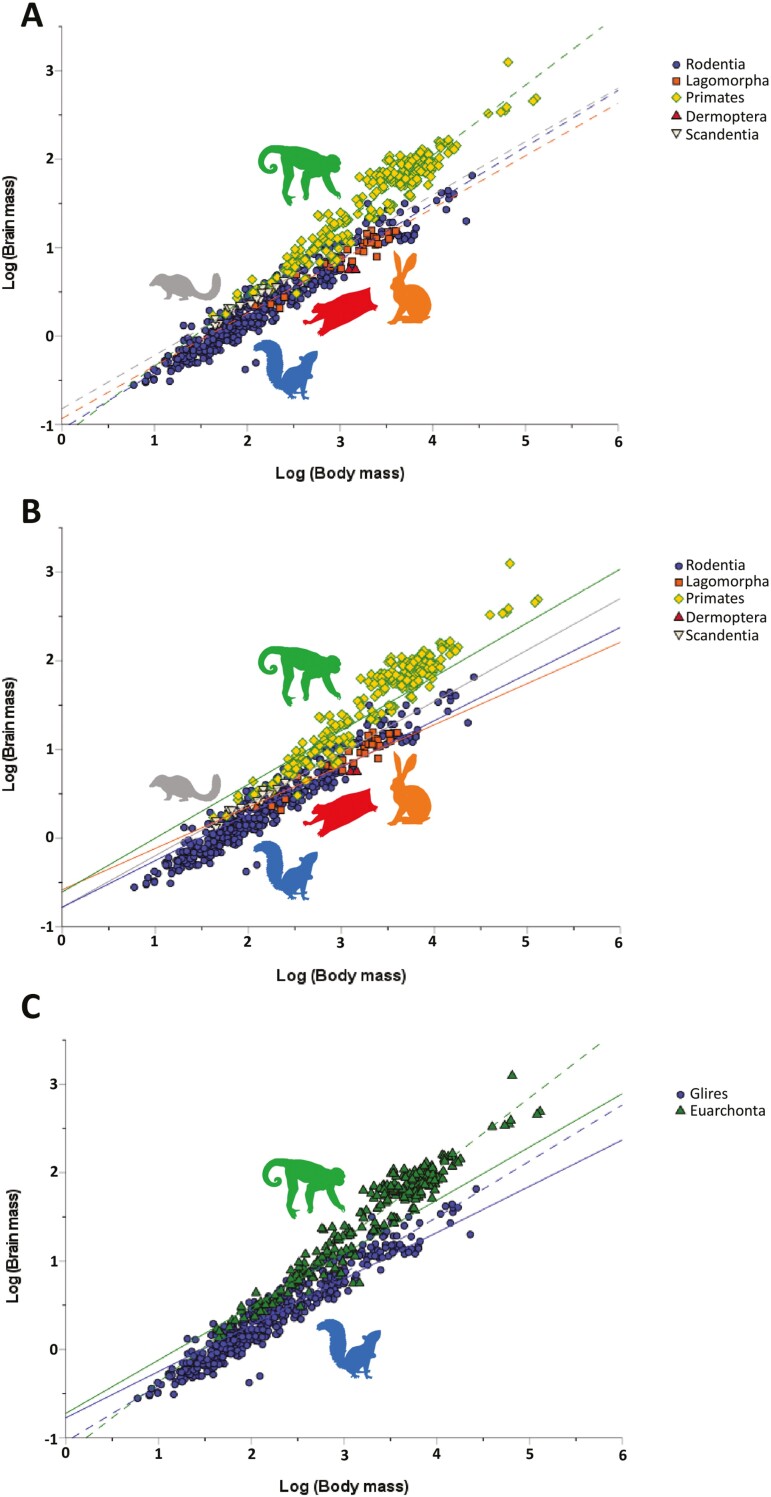
Fig. 4.

Bivariate plots of log brain mass versus log body mass for all 715 euarchontoglirans. (A) Data are color-coded by order, best fit lines are shown for the OLS regressions for each order except for Dermoptera. Primates slope = 0.794, intercept = −1.133; Scandentia slope = 0.604, intercept = −0.821; Rodentia slope = 0.638, intercept = −1.050; Lagomorpha slope = 0.594, intercept = −0.931. (B) Data are color-coded by order, best fit lines are shown for the PGLS regressions for each order except for Dermoptera. Primates slope = 0.607, intercept = −0.607; Scandentia slope = 0.580, intercept = −0.778; Rodentia slope = 0.526, intercept = −0.779; Lagomorpha slope = 0.465, intercept = −0.581. (C) Data are color-coded by superorder, best fit lines are shown for the OLS (dashed) and PGLS (solid) regressions for Euarchonta (Primates, Dermoptera, Scandentia; OLS slope = 0.805, intercept = −1.177; PGLS slope = 0.603, intercept = −0.724); and Glires (Rodentia, Lagomorpha; OLS slope = 0.635, intercept = −1.044; PGLS slope = 0.524, intercept = −0.774).

OLS analysis

Our results show that the brains of rodents, lagomorphs, and scandentians scale similarly with respect to body mass (i.e., have similar slopes; 0.638, 0.594, and 0.604, respectively; Fig. 2B–D). The 95% CIs for each of the comparisons among these 3 taxonomic groupings included zero. The bootstrap estimates of the differences in slope for the 3 comparisons ranged from −0.034 to 0.044 (Table 4). Our reanalysis of the Burger et al. (2019) data set (i.e., excluding the new data used in the present analysis) failed to recover their results with respect to lagomorphs (i.e., a slope of 0.75), suggesting that the appearance of a difference is based on an error in their analysis of their data.

When assessed at an ordinal level, the brains of primates (slope = 0.794; Fig. 2A) do show evidence of scaling differently from other euarchontogliran orders (Fig. 4A). None of the 95% CIs for any of the comparisons with Primates included zero. This same pattern was observed for Haplorhini, which exhibit a high slope value (slope = 0.723; Fig. 3A). Interestingly, the 95% CIs for comparisons of Strepsirrhini with both Rodentia and Lagomorpha excluded zero, while the comparisons with Haplorhini and Scandentia included zero. This pattern of results suggests that while the slope value for haplorhines is likely higher than other members of Euarchontoglires, strepsirrhines (slope = 0.679) occupy an intermediate scaling pattern between non-primate Euarchontoglires and haplorhines. These findings were largely mirrored by the results of RMA regression (Supplementary Data SD3), with the exception of the Strepsirrhini–Rodentia comparison.

The intercepts for these various regressions (Table 3) show that hypothetically small haplorhines would have larger brains than similarly small strepsirrhines (Fig. 3). However, the overall primate regression intersects with the y axis at a lower value (−1.133) than the haplorhine (−0.834) and the strepsirrhine (−0.932) regressions do—a byproduct of having large-brained, large-bodied anthropoids in the primate sample, which tilt the regression line in a way that increases the slope and decreases the intercept when strepsirrhines and haplorrhines are combined (Fig. 2A). Small rodents would also be expected to have smaller brains than small strepsirrhines and small haplorhines, based on the estimate of the rodent intercept (−1.050; Fig. 2C). But when looking at the general primate regression, small rodents would have larger brains than small primates (Fig. 4A)—again, is a byproduct of the high slope of the overall primate regression. The highest intercept is observed in scandentians (−0.821), with the hypothetical small scandentians having larger brains than even small haplorhines. This high intercept is probably due to the fact that scandentians have both a shallow slope (0.604; similar to the lagomorph slope, 0.594) and that they have slightly larger brains than lagomorphs of similar body mass (Fig. 4A).

PGLS analysis

The PGLS analysis showed a strong phylogenetic signal (i.e., λ ≥ 0.875 for all groupings). The main difference between the values calculated in the OLS and PGLS analyses is that PGLS gives, in the case of this study, systematically lower slope values and higher intercept values than OLS (Table 5). This contrast is particularly pronounced in primates and lagomorphs, because in these 2 groups there is a strong clade-specific pattern in body mass—for example, among haplorhines, the different major clades (i.e., tarsioids, platyrrhines, cercopithecoids, hominoids) are each fairly constrained in their size range, with only a small degree of overlap between these groups. Because this pattern is also related to relative brain mass, controlling for this pattern has the effect of substantially decreasing the slope in the regression lines generated by PGLS.

Only the comparisons between Euarchonta and Glires, Primates and Glires, and Primates and Lagomorpha excluded zero in their 95% CIs. Within primates, the slope of the regression line analyzed ordinally (0.607) is intermediate in value between the strespirrhine (0.614) and haplorrhine (0.578) slopes. Scandentians are more similar to primates in having a relatively higher slope value (0.580) than rodents (0.526) or lagomorphs (0.465; Fig. 4A and B). In comparing the PGLS and OLS slope values for the various orders the greatest similarity is observed for Scandentia (0.580 vs. 0.604, respectively), likely as a consequence of the fact that there is little phylogenetic effect on body mass in Scandentia (Fig. 2). Both the largest and smallest species of scandentians are tupaiines (Tupaia everetti, 249.5 g; Dendrogale murina, 45 g; Sargis 2002). The slope for Glires (0.524) is intermediate between the rodent (0.526) and lagomorph (0.465) slopes, although it is very similar to the rodents. It is likely that the slope for Glires is so similar to rodents because the sample of Glires is mostly composed of rodents (421 rodents vs. 31 lagomorphs). Also, the range of body mass of lagomorphs is contained within the range of body mass for rodents (Fig. 1C), so it is not expected that lagomorphs would shift the numbers substantially, as they might have if lagomorphs were clustered at one extreme or the other. The euarchontan slope (0.603) is also intermediate between the primate (0.607) and the scandentian (0.580) slopes but very close in value to the primate slope. That is a similar situation to the one seen with Glires; the euarchontan sample is largely made up of primates (248 primates, 14 scandentians, 2 dermopterans), and the scandentian and dermopteran ranges of body mass are within that of strepsirrhines (Fig. 1B). Finally, the slope for Euarchontoglires (0.540) has a value similar to those calculated for non-primate Euarchontoglires.

As in OLS, the intercepts of the PGLS regressions show that hypothetically small haplorhines would have larger brains than small strepsirrhines. However, in the PGLS analysis, the overall primate regression intersects with the y axis between the haplorhine and the strepsirrhine intercepts. Contrary to the finding in the OLS analysis, the highest intercept in PGLS, at an ordinal level, is observed for lagomorphs instead of scandentians (Fig. 4B).

Another important difference between the OLS and PGLS regressions is that in the OLS analysis there are more groups that could be considered different based on the 95% CI values in terms of scaling patterns, but PGLS fails to find most of these differences. In pairwise comparisons PGLS only finds clear differences in scaling between Euarchonta and Glires, between Primates and Glires, and between Primates and Rodentia (Table 6).

Discussion

Our results differ from the conclusion of Burger et al. (2019) that the lagomorph brain scales more similarly to primates—instead our results indicate that lagomorphs show a scaling relationship closer to that seen in rodents with respect to body mass (Fig. 4A and B). This correction highlights the uniqueness of primates in a euarchontogliran context. This is further supported in the OLS analysis, where primates are the only order of Euarchontoglires with the 95% CIs for differences in slope that do not include zero.

Strepsirrhines have similar OLS slopes to both haplorhines and scandentians, differing from those of rodents and lagomorphs. However, the scandentian slope differs from haplorhines, making strepsirrhines an apparently intermediate stage between other primates and non-primate euarchontoglirans. On the other hand, the CIs for the slope in the PGLS analysis overlap among many more ordinal groupings. However, primates stand out even in the PGLS analysis for being the only order with a CI for their slope that does not overlap with rodents. Consequently, the fact that primates appear to have a unique brain–body scaling relationship in the context of Euarchontoglires (supported by both the OLS and the PGLS analyses) further illustrates the necessity for clade-specific regular EQs and phylogenetic EQs for more restricted taxonomic entities than Mammalia.

A recent analysis (Smaers et al. 2021) examined allometric scaling relationships across Mammalia, identifying particular points in the mammalian tree where they inferred grade shifts had occurred. In their analysis, several groups analyzed here were reconstructed as part of the ancestral mammalian grade (Scandentia, Lagomorpha, Dermoptera, squirrel-related clade, Tarsioidea) based on their allometric scaling relationships not being found to have differed from the relationship calculated for the common mammalian ancestor, with a primitive PGLS slope of 0.51. However, this slope lies outside the 95% CI for Euarchontoglires, Euarchonta, Primates, and Strepsirrhini calculated here (Table 5). As such, our analysis would suggest that a grade shift might have happened earlier in the evolution of this clade than their analysis suggests. In particular, the contrast between Primates and Glires found in all analyses suggests an ordinal level shift for Primates, contrasting with inferred changes occurring only within primate subgroups in the result of Smaers et al. (2021). Possible explanations for this contrast are the notably stronger sampling of both Scandentia and Rodentia here, which allowed for a refinement of previous estimates, but also the direct inclusion of fossils in Smaers et al. (2021). However, these inferences require testing using fossil specimens that allow for a more direct window into such grade shifts.

Encephalization quotients

The EQ is a widely used index of brain size scaled to body size (Jerison 1985). As noted above, some of the most commonly used EQ equations in the field of paleoprimatology are Jerison’s (1973) and Eisenberg’s (1981), even though they are based on generalized mammalian samples. However, the use of EQs has been criticized for poorly modeling brain scaling relationships in fossil primates (Gilbert and Jungers 2017), as well as for not being a good predictor of cognitive abilities (Deaner et al. 2007). Although imperfect, no alternative has been suggested to EQs for comparing brain sizes in animals of different body masses that is not also problematic. For example, taking a narrow allometric approach (as suggested by Gilbert and Jungers 2017) is very prone to error being introduced by inconsistencies in body mass estimation, and does not offer a clear solution for making comparisons to fossil taxa outside the modern range of variation (White et al. 2023). While we agree with Smaers et al. (2021) that making comparisons between particular brain regions offers a much richer understanding of brain size evolution than looking at relative overall size (see, for example, Bertrand et al. 2019b, 2021), such an approach is limited in dealing with fossils because only certain brain regions can be isolated on endocasts. We would also argue that, in light of the high physiological cost of maintaining brain tissue, considering relative brain size has fundamental merit in discussions of brain evolution, whether or not it is an accurate proxy for measures of cognition. As such, EQs continue to serve as useful tools, and merit further work to overcome identified problems. The growing availability of brain and body mass data for Euarchontoglires allows us to elaborate subordinal, ordinal, and supraordinal EQ equations, which may allow for more meaningful comparisons relevant to some evolutionary questions than are possible with general mammalian equations, and may solve some of the problems that have been identified with EQs such as a lack of independence from body mass (Begun and Kordos 2004; Gilbert and Jungers 2017). Our results show that in the OLS regression analyses the slopes generally increase and the intercepts decrease the higher we go in taxonomic level within Euarchontoglires (see also Martin 1990). Therefore, in order to avoid overestimation and underestimation of EQs in animals with extreme body masses, it is preferable to use the most taxonomically specific EQ possible. In fact, Pilleri et al. (1984) already elaborated an OLS-based EQ equation specific to rodents that has been used in recent studies on the brain evolution of rodents (Bertrand and Silcox 2016; Bertrand et al. 2016, 2017, 2018, 2019a). Other groups within Euarchontoglires are worth exploring with respect to this approach.

López-Torres et al. (2020) described the first virtual endocast of a fossil lagomorph and provided EQs for both extant lagomorphs and a specimen of M. turgidus (FMNH UC 1642), a stem lagomorph. The body mass of M. turgidus was calculated by López-Torres et al. (2020) using the width of the occipital condyles, which is argued to be one of the most reliable measures of body mass estimation in lagomorphs (r² = 0.957; Moncunill-Solé et al. 2015). Because of the lack of a lagomorph-specific EQ, the authors used Jerison’s (1973) and Eisenberg’s (1981) equations. The present OLS-based lagomorph-specific equation (Table 1) provides a higher EQ estimate (0.53) than those calculated with generalized mammalian equations (Jerison’s EQ = 0.32; Eisenberg’s EQ = 0.40). This equation also provides higher estimates for living lagomorphs than previously calculated (i.e., López-Torres et al. 2020). Here, the critical point is that calculating the group-specific value makes it clear that in the lagomorph context Megalagus was more encephalized than previously thought (Supplementary Data SD8), with a brain only approximately half the size expected rather than approximately one-third. Our Glires-specific EQ for Megalagus gives a very similar result (0.55) to the lagomorph-specific EQ (Supplementary Data SD10). However, the Euarchontoglires-specific EQ for Megalagus drops to 0.29, even lower than the generalized mammalian EQs of Jerison (1973) and Eisenberg (1981). This is most certainly due to the effect of adding primates, and in particular highly encephalized anthropoids (Supplementary Data SD11). These differing values highlight the importance of making a choice of EQ equation that is relevant to the evolutionary question being asked, and that EQ calculations need to be put in a specific taxonomic framework.

With respect to primates, Grabowski et al. (2016) pioneered using PGLS regressions to calculate EQs instead of using the traditional OLS. They developed a primate-specific EQ, although based on endocranial volume rather than brain mass. Recently, Ni et al. (2019) expanded upon analyses of Grabowski et al. (2016) by publishing EQ equations specific for anthropoids, platyrrhines, and catarrhines based on PGLS regressions (i.e., PEQ; Ni et al. 2019). Here we complement these equations with primate-, strepsirrhine-, and haplorhine-specific equations based on OLS (regular EQ) and PGLS (phylogenetic EQ or PEQ) using brain mass (see Table 1 for the specific EQ and PEQ equations). It is worth noting that EQs and PEQs are not directly comparable, so future studies may benefit from calculating both. For example, whereas an EQ = 1 always means that the brain size of an animal is exactly the brain size expected for an animal of its size, this is not necessarily true when PEQ = 1 because the PGLS analysis corrects the position of the regression line based on phylogenetic effect (if there is one). As such, PGLS estimates have the benefit of including a metric (EQ) that allows for some degree of comparability with past analyses, while also providing information within the context of a particular analysis that reflects our understanding of phylogeny (PEQ).

Here we use 3 early primates (a plesiadapiform, an adapoid, and an omomyoid) as test cases for our new primate equations. Microsyops annectens is a microsyopid plesiadapiform from the middle Eocene of North America known from a substantively complete cranium (UW 12362; Silcox et al. 2010, 2020) with a range of EQs between 0.25 and 0.38 using Jerison’s (1973) equation, and between 0.31 and 0.49 using Eisenberg’s (1981) equation. The range of EQs is due to the fact that Silcox et al. (2010) calculated several body mass estimates, including a cranial length insectivoran equation (Thewissen and Gingerich 1989), a cranial length horizontal primate PGLS equation (Silcox et al. 2009), a cranial length generic primate equation (Martin 1990), and an upper molar area equation (Gingerich et al. 1982). Using our OLS-based primate-specific equation, Microsyops yields a lower range of EQ estimates (0.15 to 0.25) than those resulting from Jerison’s (1973) and Eisenberg’s (1981) equations. The euarchontan-specific equation gives the same EQ values as the primate-specific equation. The Euarchontoglires-specific equation provides more similar values to those of Jerison’s (1973) equation, with EQs in the range of 0.22 to 0.37. These results accentuate the fact that M. annectens had an extremely small brain for a primate (Supplementary Data SD7, SD9) but was quite similar to the stem lagomorph M. turgidus when the EQs of both are calculated using a Euarchontoglires-specific equation (Supplementary Data SD11).

Adapis parisiensis is an adapid adapoid from the late Eocene of Europe. Jerison’s (1973) equation provides an EQ of 0.65 and Eisenberg’s (1981) an EQ of 0.86 based on a very complete cranium (NHM M1345; Harrington et al. 2016). Harrington et al. (2016) calculated the body mass of A. parisiensis using the euarchontan ectal facet equation (Yapuncich et al. 2015). The relationships of adapoids are somewhat controversial, with conflicting views about whether adapoids are haplorhines (Wortman 1903; Gingerich 1973, 1984, 2012, 2015; Gingerich and Schoeninger 1977; Rasmussen and Simons 1988, 1992, 1994; Simons 1989; Simons and Rasmusen 1989; Rasmussen 1990, 1994; Bloch et al. 1997; Franzen et al. 2009) or stepsirrhines (Gregory 1920; Hoffstetter 1977; Beard et al. 1988; Dagosto 1988; Kay et al. 1997; Seiffert et al. 2009; Williams et al. 2010; Gilbert and Maiolino 2015). Current large-scale cladistic analyses tend to place adapoids in the strepsirrhine side of the primate tree (Ni et al. 2016; Gunnell et al. 2018; Seiffert et al. 2018), so the consensus leans toward considering them as most likely stem strepsirrhines. Here, we follow the current consensus and consider adapoids stem strepsirrhines and consequently apply the strepsirrhine-specific EQ equation to Adapis (Supplementary Data SD5). This equation yields an EQ of 0.62, similar to that derived from Jerison’s (1973) equation. The primate and the euarchontan-specific equations give similar results (EQ_Primates = 0.44; EQ_Euarchonta = 0.45; Supplementary Data SD7, SD9), and the Euarchontoglires-specific equation (Supplementary Data SD11) provides a similar EQ to the strepsirrhine-specific and Jerison’s (1973) equations (0.65).

Harrington et al. (2020) published a virtual endocast of the omomyoid, N. antiquus, a late Eocene European microchoerid, based on a very complete cranium (MaPhQ 289). Jerison’s (1973) equation yields an EQ of 0.68 for Necrolemur, and Eisenberg’s (1981) an EQ of 1.04. Harrington et al. (2020) calculated the body mass of N. antiquus using a cranial length equation (Martin 1990). Unlike adapoids, the phylogenetic relationships of omomyoids are much less controversial and they are mostly regarded as haplorhines, with a closer relationship to modern tarsiers (e.g., Ni et al. 2016). The haplorhine-specific equation gives a much lower EQ (0.43; Supplementary Data SD6) than that provided by the generalized mammalian equations, whereas the primate and euarchontan equations give more intermediate values (EQ_Primates = 0.59; EQ_Euarchonta = 0.62; Supplementary Data SD7, SD9). The Euarchontoglires-specific EQ yields a more similar value (0.91) to that given using Eisenberg’s (1981) equation. The results from both A. parisiensis and N. antiquus highlight the importance of selecting an EQ equation based on the research question being asked. In particular, for N. antiquus, the very low haplorhine EQ value emphasizes the contrast in relative brain size between this fossil taxon and living members of Haplorhini. So, N. antiquus was quite encephalized for an early Tertiary primate, but actually not very encephalized for a modern haplorrhine, as might be expected for a stem taxon.

To conclude, the present study explores scaling relationships between body mass and brain mass in Euarchontoglires. To our knowledge, this is the first instance that the scaling relationships between brain mass and body mass have been reported for Scandentia (Fig. 2B), a group that has been underrepresented in previous studies for lack of brain data. Our results also show that the brain of lagomorphs scales with respect to body mass similarly to rodents, and very differently than Primates (Fig. 4A and B; contra Burger et al. 2019).

Generating clade-specific EQs provides some insight into issues that have been raised with the general mammalian equations of Jerison (1973) and Eisenberg (1981). As shown by Gilbert and Jungers (2017); see also Begun and Kordos (2004), these EQ equations do an imperfect job at controlling for body mass. A critical reason for this issue is that the brain allometries in the various subgroups of mammals vary greatly, making clade-specific EQs necessary. In other words, the relationship between EQ and body mass observed by those authors stems from using a scaling equation (either Jerison’s or Eisenberg’s) that does not correctly control for body mass because it does not accurately reflect scaling relationships of the mammalian subsample of interest (i.e., Primates, Rodentia, Lagomorpha, etc.). Therefore, clade-specific EQs will be more appropriate when the research questions being asked concern a more taxonomically narrow sample. The use of Jerison’s (1973) and Eisenberg’s (1981) equations might be appropriate for research questions that concern a broad sample of mammals, particularly distantly related mammals. Choosing Jerison’s (1973) or Eisenberg’s (1981) equations for a taxonomically narrow sample (like Rodentia or Primates) will maximize the overestimations and underestimations of relative brain size for members with more extreme body sizes (either small or large, respectively). Eisenberg’s (1981) equation gives closer EQ values than Jerison’s (1973) does for rodents to those yielded by Pilleri et al.’s (1984) equation, which is a rodent-specific OLS-based equation. This makes Eisenberg’s (1981) equation a more appropriate choice for rodents over Jerison’s (1973). However, Jerison’s (1973) equation yields similar EQ values to those given by the strepsirrhine-specific EQ, making Jerison’s (1973) equation more appropriate for strepsirrhines over Eisenberg’s (1981). This contrast highlights the reality that neither is a generally preferred option across all scales of comparisons. In sum, clade-specific equations (Pilleri et al. 1984; Grabowski et al. 2016; Ni et al. 2019; Bertrand et al. 2021; this paper) should be given preference whenever the research question focuses on a particular mammalian group, and generalized mammalian equations (Jerison 1973; Eisenberg 1981) are only appropriate for broad comparative mammalian samples.

Supplementary data

Supplementary data are available at Journal of Mammalogy online.

Supplementary Data SD1. Text explaining how encephalization quotients are calculated.

Supplementary Data SD2. Body mass and brain mass data for 715 euarchontogliran species, sorted by order. Sample sizes are included as specifically as the literature allows, sometimes including ranges. Data have been extracted from the “Direct source.” Direct sources often include original sources where the data came from in the respective manuscripts. When a direct source is listed as “Combined,” it means that data from several original sources (sometimes including newly generated data) have been combined.

Supplementary Data SD3. Results from the reduced major axis (RMA) analysis. This file includes slope and intercept data for several taxonomic levels in Euarchontoglires using RMA and pairwise comparisons between regression parameters of different taxonomic groups of Euarchontoglires. Values in red denote coverage probabilities that do not include zero. N = number of species; SD = standard deviation; CI = confidence interval; CP = coverage probability.

Supplementary Data SD4. References used for tables in Supplementary Data SD2.

Supplementary Data SD5. Bivariate plots of log brain mass versus log body mass for Strepsirrhini (Fig. 3B) with Adapis parisiensis indicated with a black star. OLS regression represented as a dashed line; PGLS regression represented as a solid line. Note that the body mass and brain mass values for A. parisiensis have not been taken into account when calculating the regression lines.

Supplementary Data SD6. Bivariate plots of log brain mass versus log body mass for Strepsirrhini (Fig. 3A) with Necrolemur antiquus indicated with a black star. OLS regression represented as a dashed line; PGLS regression represented as a solid line. Note that the body mass and brain mass values for N. antiquus have not been taken into account when calculating the regression lines.

Supplementary Data SD7. Bivariate plots of log brain mass versus log body mass for Primates (Fig. 2A) with Microsyops annectens, Adapis parisiensis, and Necrolemur antiquus indicated with black stars. OLS regression represented as a dashed line; PGLS regression represented as a solid line. Note that the body mass and brain mass values for M. annectens, A. parisiensis, and N. antiquus have not been taken into account when calculating the regression lines. BM↑, high body mass estimate; BM↓, low body mass estimate.

Supplementary Data SD8. Bivariate plots of log brain mass versus log body mass for Lagomorpha (Fig. 2D) with Megalagus turgidus indicated with a black star. OLS regression represented as a dashed line; PGLS regression represented as a solid line. Note that the body mass and brain mass values for M. turgidus have not been taken into account when calculating the regression lines.

Supplementary Data SD9. Bivariate plots of log brain mass versus log body mass for Euarchonta (Fig. 1B) with Microsyops annectens, Adapis parisiensis, and Necrolemur antiquus indicated with black stars. OLS regression represented as a dashed line; PGLS regression represented as a solid line. Note that the body mass and brain mass values for M. annectens, A. parisiensis, and N. antiquus have not been taken into account when calculating the regression lines. BM↑, high body mass estimate; BM↓, low body mass estimate.

Supplementary Data SD10. Bivariate plots of log brain mass versus log body mass for Glires (Fig. 1C) with Megalagus turgidus indicated with a black star. OLS regression represented as a dashed line; PGLS regression represented as a solid line. Note that the body mass and brain mass values for M. turgidus have not been taken into account when calculating the regression lines.

Supplementary Data SD11. Bivariate plots of log brain mass versus log body mass for Euarchontoglires (Fig. 1A) with Microsyops annectens, Adapis parisiensis, Necrolemur antiquus, and Megalagus turgidus indicated with black stars. OLS regression represented as a dashed line; PGLS regression represented as a solid line. Note that the body mass and brain mass values for M. annectens, A. parisiensis, N. antiquus, and M. turgidus have not been taken into account when calculating the regression lines. BM↑, high body mass estimate; BM↓, low body mass estimate.

Author contributions

SL-T and MTS contributed to conceptualization and project administration; SL-T, OCB, ŁF-F, MML, GSM-F, and MTS to data curation; CJL and MAS to formal analysis, methodology, software, and validation; SL-T, OCB, ŁF-F, MML, CJL, and MTS to funding acquisition; MTS to supervision; SL-T and CJL to visualization; SL-T to writing—original draft; all authors contributed to investigation, resources, and writing—review & editing.

Funding

This study was supported by a National Science Centre (Cracow, Poland) grant (number 2022/45/NZ8/03585) to SL-T, a CERCA Programme/Generalitat de Catalunya, a Marie Skłodowska-Curie Actions: Individual Fellowship (H2020-MSCA-IF-2018-2020; no. 792611), and a Beatriu de Pinós 2021 BP 00042 to OCB; a National Science Centre (Cracow, Poland) grant (number 2015/18/NZ8/00637) to ŁF-F, an NSERC CGS grant to MML; National Science Foundation (DBI-1906248, DBI-2128146), a Gerstner Family Foundation Scholars Postdoctoral Fellowship, and a University of Texas Early Career Provost Fellowship to CJL; and an NSERC Discovery Grant to MTS.

Conflict of interest

None declared.

Data availability

All data are available in the Supplementary Data.