Simulation Methodologies to Determine Statistical Power in Laboratory Animal Research Studies

Abstract

Null hypothesis significance testing is a statistical tool commonly employed throughout laboratory animal research. When experimental results are reported, the reproducibility of the results is of utmost importance. Establishing standard, robust, and adequately powered statistical methodology in the analysis of laboratory animal data is critical to ensure reproducible and valid results. Simulation studies are a reliable method to assess the power of statistical tests, and biologists may not be familiar with simulation studies for power despite their efficacy and accessibility. Through an example of simulated Harlan Sprague-Dawley (HSD) rat organ weight data, we highlight the importance of conducting power analyses in laboratory animal research. Using simulations to determine statistical power prior to an experiment is a financially and ethically sound way to validate statistical tests and to help ensure reproducibility of findings in line with the 4R principles of animal welfare.

Reproducibility in Animal Research

The reproducibility crisis is a substantial barrier to performing sound research across many fields [1–3]. In laboratory animal research in particular, a study that lacks reproducibility will violate the 4R proposition of animal welfare based on the guiding principles of reduction, replacement, refinement, and responsibility to support the humane and ethical use of animals in research [4]. The use of animals in biomedical research has been widely scrutinized due to ethical concerns and a lack of confidence in clinical validity [5]. Freedman et al. [6] estimate that the cumulative irreproducibility rate in preclinical research centers around 50%, and inadequate study design and data analysis contribute to this figure. The findings of Freedman et al. are not unique; in a recent Nature survey of over 1,500 researchers, more than half the participants pointed to insufficient replication in the lab, poor oversight, or low statistical power as the greatest concerns in biological research [1]. Simulation studies can be applied to address the reproducibility gap by determining an adequate sample size required to achieve desired power for an experiment, by validating the power of statistical models, or by comparing the power between different statistical models. Although complex simulation studies should always involve consultation with a statistician, this paper aims to provide an introductory framework to enhance knowledge of simulation studies for readers no matter their background.

Statistical Power and the 4Rs

In null hypothesis significance testing, a p-value is defined as the probability of observing results at least as extreme as the sample result if the null hypothesis (${\text{H}}_0$) were true. The threshold for statistical significance is given by the significance level ($\alpha$), which is the probability of rejecting ${\text{H}}_0$ when ${\text{H}}_0$ is true; this is also known as a false positive rate or committing a “Type 1 error.” It is common to set $\alpha =.05$. When data show evidence of a statistically significant effect, ${\text{H}}_0$ is rejected in favor of an alternative hypothesis, ${\text{H}}_1$ [7]. Statistical power is defined as the probability that a hypothesis test will detect a true effect if one is present. In other words, power is the probability that a test correctly rejects ${\text{H}}_0$ when ${\text{H}}_0$ is false. Power is calculated as $1-\beta$, where $\beta$ is the probability of a false negative result, also referred to as “Type II error”, and retains an inverse relationship with $\alpha$ [7]. When the statistical test, ${\text{H}}_0$, and ${\text{H}}_1$ have been specified, the power of the test depends on multiple factors, including the sample size, significance level $\alpha$, variability in the data, and the true effect size [8].

Across many disciplines, 80% power is generally considered acceptable [7]. When a true effect is present, an underpowered study (e.g., when $1-\beta$ is much less than 80%) has a lower probability of detecting the effect and is more likely to report a false negative result. Moreover, a study that reports a statistically significant effect is less likely to be reproducible if the study has low power. If laboratory animal studies are routinely underpowered, the likelihood of observing true effects over many studies is reduced and statistically significant p-values arising from spurious findings would likely occur by chance [9].

With the 4R framework in mind, considering a study’s power is particularly relevant because the sample size should be high enough so that the study is adequately powered to detect meaningful effects, but not overpowered and wasteful of animals. If a study is underpowered and no additional animals can be utilized, the study objectives and research question should be reevaluated to keep in line with the 4R principles. Conversely, if a study is shown to have a higher power than necessary, researchers can consider reducing the number of animals used in an experimental setting to exemplify “reduction” in practice, while still maintaining an appropriate level of precision. Historically, research responsibility guidelines have been utilized for social and ethical reasons, with more limited focus on how they could improve the quality of science such as promoting more reproducible statistics [10]. Moreover, the standardization of adequately powered statistical methods is not as well-established as other research aspects (e.g., the standardization of environmental laboratory conditions) despite its potential in mitigating the reproducibility crisis [5]. While alternative methods such as closed-form equations may be sufficient to calculate power and sample size for many designs and experiments which satisfy common statistical assumptions, simulation studies are an effective and versatile tool to increase reliability in statistical results.

Simulations

Simulation studies work by creating data using computer-generated random number sampling from known probability distributions [11]. They are an advantageous method to determine the power of statistical tests and can be used for multiple study designs by modeling data to mimic real-world outcomes. Simulations can calculate the power of a test with a specified significance threshold, determine the required sample size to achieve desired power (often 80%), evaluate different effect sizes (i.e., the magnitude of a change in response or a value measuring the association between variables), and compare the power of different statistical procedures. Though many standard designs have associated closed-form power equations that are sufficient in calculating power and sample size, this approach may not be feasible for complex designs. However, simulation approaches can reproduce the estimated power from simpler tests (e.g., t-tests when parametric assumptions hold) and are efficient tools for statistical assessment in both simpler and more complex scenarios.

Simulations in practice

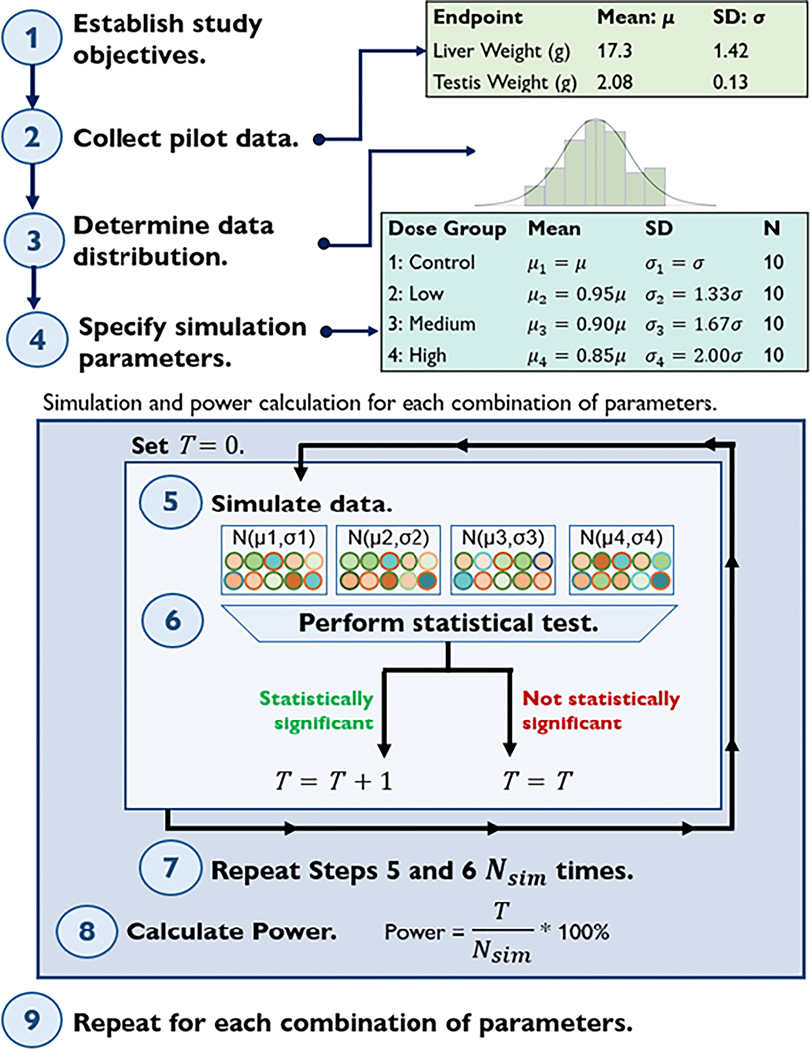
The key steps to estimate power using a simulation study are shown in Figure 1. Specific details within the steps will vary depending on the study’s objectives, design, and statistical methods.

Figure 1.

Key steps for conducting a concurrent simulation study and power analysis. $T$ is the total number of statistically significant results (e.g., p < 0.05) that occurred in $N_{sim}$ random simulations for the given effect size, sample size, and distributional assumptions. $\text{μ}$ indicates the mean, $\sigma$ indicates the standard deviation (SD), and N indicates the sample size per dose group.

To illustrate each step of a simulation study for power analysis, we use simulated data for organ weight endpoints based on reference data from the National Toxicology Program (NTP) (data not shown). Data simulation and statistical analysis was performed using R version 4.3.1.

Simulation Framework

Step 1: Establish study objectives.

A researcher should establish clear objectives prior to beginning experimentation. Null and alternative hypotheses are specified during this phase. In this example, we studied the potential toxicity of a chemical on male HSD rat liver and testis weights using Jonckheere’s trend test. Before using Jonckheere’s test on real data, we wanted to determine the power of the test to detect an effect if one truly exists. Power is calculated in reference to a specific true effect size, and our objective in this simulation study was to calculate the power of Jonckheere’s test with a 15% effect size in the high dose group, 10% effect size in the medium dose group, and a 5% effect size in the low dose group. In our example, a 15% effect size represents a 15% reduction in organ weight between the control and high dose groups. The low and medium dose groups exhibit a 5% and 10% reduction in mean when compared to the control group, respectively. Under our experimental assumptions, $H_0:{\theta }_1={\theta }_2={\theta }_3={\theta }_4$, and $H_1:{\theta }_1\ge {\theta }_2\ge {\theta }_3\ge {\theta }_4$, where ${\theta }_1$ represents the median in the control dose group, ${\theta }_2$ represents the median in the low dose group, ${\theta }_3$ represents the median in the medium dose group, and ${\theta }_4$ represents the median in the high dose group, with at least one strict inequality.

Step 2: Collect pilot data.

Once the objectives of the study have been established, collect pilot data. Biological variation is always present [5], and quality pilot data allows the researcher to sufficiently assess the endpoint of interest to formulate representative simulation parameters that account for variability. Pilot data is often collected for control animals (for example, from an online database like CEBS [12]) to determine variables such as the empirical mean, standard deviation, and distribution in the sample data. These data should be representative of the population, as summary statistics serve as the baseline for the simulation and the variability in this data influences the overall power. Control male HSD rat data from four NTP subchronic toxicology studies on post-natal day 90 were averaged and used as baseline parameters in the organ weight example, as summarized in Step 2 of Figure 1. These summary statistics are assumed to be representative of expected control group liver and testis weight values.

Step 3: Determine data distribution and verify assumptions.

After examining the empirical distribution of the control pilot data in Step 2, propose a probability distribution from which to simulate representative data. While a normal distribution may be a suitable approximation for many pilot data sets, further investigation is warranted before defaulting to any distributional choice. For brevity, we refer the reader to alternate sources that detail how to determine an appropriate distribution due to the introductory scope of this manuscript and the multipronged, intricate nature of determining a distribution dependent on the study design [11, 13, 14]. In the organ weight simulation, pilot data were approximately normally distributed.

After the distribution is determined, a statistical test is specified. Verify that the assumptions of the chosen statistical test are met by the proposed simulation distribution. Parametric statistical tests rely on certain assumptions about the distribution of the population from which the data was collected, including normality, equality of variances between experimental groups, and independent errors [7]. Parametric tests are more powerful than non-parametric tests, meaning they generally require smaller sample sizes to achieve the same statistical power. When these assumptions are violated, non-parametric approaches may be used instead, since they do not rely on assuming a specific probability distribution for the data [7]. Although assumption violations should be given due consideration, the violation of parametric assumptions does not immediately warrant the use of non-parametric tests and vice versa. Researchers should carefully assess their data in tandem with their research question to determine the best approach [8]. In the example simulation, we used Jonckheere’s trend test, the NTP standard statistical test for evaluating dose-response relationship in organ weight data. Jonckheere’s test is a non-parametric test that assumes ordinal or continuous data, independent observations, and two or more independent groups that follow the same distribution [15].

Step 4: Specify simulation parameters.

Once the simulation distribution and statistical test have been chosen, specify the simulation parameters for each of the simulated dose groups. Our pilot data were approximately normally distributed with unequal variance (heteroscedasticity) across dose groups. Therefore, each dose group was simulated from a normal distribution with unequal variances that mimicked the historical data. Simulated multi-dose group data also depends on a pre-determined effect size. In our example, the simulated high dose group data has a mean 15% lower than the control group mean (Step 4, Figure 1). Linear interpolation was used to calculate the effect size for the low (5% reduction in mean) and medium (10% reduction) dose groups.

Step 5: Simulate data.

Various statistical software packages can be used to simulate data according to the assumed distribution and parameters from Steps 3–4. Before simulating the data, it is prudent to set a seed for the software’s random number generator to ensure exact reproducibility each time the code is run. Here, liver and testis weight data were simulated with one control group and three treated dose groups. Simulated data should be plotted to ensure that it resembles the pilot data from Step 2 and to verify it follows the simulation distribution specified in Step 3. For a more comprehensive discussion of techniques for simulating data, refer to Arnold et al. [16].

Step 6: Perform statistical testing.

After simulating a data set, perform the statistical testing using the test selected in Step 3. Record whether the statistical test correctly rejects ${\text{H}}_0$ at the pre-specified significance threshold ($\text{p}<\alpha$).

Step 7: Repeat $N_{sim}$ times.

Repeat steps 5–6 (simulate data and perform statistical testing) for a total of $N_{sim}$ iterations, where $N_{sim}$ is chosen to be sizable (often ≥ 1,000 unless a large number of iterations is not computationally feasible). In the example organ weights simulation, $N_{sim}=\mathrm{10,000}$, so that a new dataset of 40 organ weight values ($N=10$ per 4 dose groups) was simulated and tested 10,000 times. The total number of the $N_{sim}$ iterations where $H_0$ is correctly rejected is denoted $T$ (see Figure 1).

Step 8: Calculate power.

Once the simulated data is analyzed, calculate power as $\frac{T}{N_{sim}}*100\%$. In our analysis, $\frac{T}{N_{sim}}*100\%=76.58\%$ power for liver weights and 93.55% power for testis weights when $N=10$ per dose group. Large-scale studies with multiple endpoints may not achieve 80% power in the analysis of each endpoint, though it is important to check that power of the statistical test is reasonable for all endpoints of interest. In this example, the power differs for liver and testis weights due to varying means and standard deviations in the empirical pilot data for those organs. With reliable levels of power, we can proceed with confidence in the statistical analysis of this data given a sample size of $N=10$ per dose group.

Step 9: Repeat for different sets of simulation parameters.

Repeat all previous steps for each desired combination of sample size, effect size, distribution, true parameter values, significance threshold, and endpoint of interest [11]. In our example, Steps 1–8 were conducted for both male liver and testis weights, with $N=10$ animals per dose group. Though the example simulation determined power based on the given sample size and distributional assumptions, researchers can conversely choose a target power (i.e., 80%) to determine an adequate sample size. Additional factors can be varied for a power analysis under this framework (Figure 1).

Limitations

Although achieving a targeted power increases the reliability of results, achieving perfect reproducibility is neither possible nor desirable [6]. A study powered at 80% would still fail to detect a true effect 20% of the time, and a study powered to detect one effect size (for example, 15% reduction in organ weight) may be underpowered to detect a smaller effect (for example, 5% reduction in organ weight). Choosing an effect size of scientific and/or clinical relevance is therefore of utmost importance. Also, while this paper is structured around determining power based on a given sample size, researchers can iterate simulations over multiple sample sizes to determine the required sample size to achieve targeted power.

This paper focuses on an example where hypothesis testing is used to test the null hypothesis of no treatment effect against an alternative hypothesis of a treatment effect. There are experimental contexts when the null hypothesis testing performed does not fall into this framework, such as testing for non-inferiority. Moreover, there is ample historical pilot data available in this paper’s example. The availability of pilot data and methods to simulate representative pilot data will vastly differ depending on the experimentation and study design. Furthermore, determining an appropriate distribution from which to simulate data is also often complex even for the simplest of designs (Step 3, Figure 1) and should be given careful attention when determining whether a simulation study is appropriate.

Discussion

Specific steps of a simulation are influenced by a myriad of factors such as the pilot data, experimental design, appropriate distribution of the data, and statistical test of choice, but the key steps described in this manuscript provide a generalized framework to conduct a simulation and power study in biological research. While there are limitations to simulation studies, simulations for power can help address the substantial reproducibility gap under the 4R framework by establishing reliability in statistical results and optimizing resources. Many of the scientific, ethical, and economic implications in laboratory animal research can be mitigated with simulation methods for power calculations.

Data Availability

R code to run the organ weight simulation outlined in this paper can be found at https://github.com/angelajeffers/simulation-power-analysis or by contacting the author.