Simulation of high-resolution test objects using non-isocentric acquisition geometries in next-generation digital tomosynthesis

Abstract

Digital breast tomosynthesis (DBT) systems utilize an isocentric acquisition geometry which introduces imaging artifacts that are deleterious to image reconstructions. The next-generation tomosynthesis (NGT) prototype was designed to incorporate various x-ray source and detector motions for the purpose of investigating alternative acquisition geometries for DBT. Non-isocentric acquisition geometries, acquisitions that vary the image magnification between projection images, are capable of ameliorating aliasing and other artifacts that are intrinsic to conventional DBT. We used virtual clinical trials (VCTs) to develop custom acquisition geometries for the NGT prototype. A high-resolution (5μm voxel size) star pattern test object was simulated to compare the high-frequency performance of isocentric with non-isocentric image reconstructions. A tilted bar pattern test object was also simulated to compare multiplanar reconstructions (MPR) of isocentric and non-isocentric acquisition geometries. Two source- and detector-motion paths were simulated to obtain super-sampled image reconstructions of the test objects. An aliasing-sensitive metric was used to evaluate spatial resolution performance for two orthogonal frequency orientations. Pairwise comparisons were made for the two frequency orientations between the isocentric and non-isocentric acquisition geometries. Non-isocentric acquisition geometries show an improvement over isocentric acquisition geometries. The greatest improvement was 75.2% for frequencies aligned perpendicular to x-ray source motion, which is the direction of frequencies for which DBT is prone to aliasing. Both frequency orientations exhibit super resolution for non-isocentric geometries. MPR of the tilted bar pattern show z- dependent degeneracies for the isocentric acquisition only, whereas MPR of the non-isocentric acquisition entirely exhibits super resolution.

1. INTRODUCTION

Digital breast tomosynthesis (DBT) acquires a three-dimensional (3D) image of a patient’s breast by acquiring multiple, two-dimensional x-ray images from serial source positions. For a conventional DBT acquisition, the x-ray projections are acquired by translating the x-ray source along an arc in the mediolateral (ML) direction. The projections are spaced equidistantly in the chest-wall plane of the patient. This acquisition geometry is isocentric, because the arc rotates about a single fulcrum in space. Such DBT systems benefit the detection of masses and low-frequency objects in the breast. That said, the detection of high-frequency objects like microcalcifications, is not benefited by DBT when compared with full- field digital mammography (FFDM)¹.

Resolution for conventional DBT is anisotropic, favoring the frequencies that are aligned parallel to x-ray source motion (${\mathit{\nu }}_{\parallel }$) with super resolution. Using super-sampled image reconstructions, resolution for ${\mathit{\nu }}_{\parallel }$ can be increased twofold, whereas the frequencies aligned perpendicular to source motion (${\mathit{\nu }}_{\perp }$) are limited to the alias frequency of the detector. Super resolution improves the resolution of periodic objects and the overall appearance and texture of breast tissue and lesions in image reconstructions.

The next-generation tomosynthesis (NGT) system is a DBT prototype that has been developed to improve the detection of microcalcifications in the breast. This prototype system investigates alternative acquisition geometries by introducing novel x-ray source and detector motions. The introduction of posteroanterior (PA) x-ray source motion has been shown to improve the spatial resolution^2–5 and volume estimation of anthropomorphic breast phantoms in image reconstructions^6,7. Non-isocentric acquisition geometries, acquisitions that increment the detector z-position between each projection, can further improve spatial sampling. Non-isocentric acquisitions can also lessen the impact of imaging artifacts like masking^8,9, spatial resolution anisotropies^10–12, and aliasing^11,13 in image reconstructions.

The primary method for validating the performance of these prototypes is through clinical trials. Clinical trials of medical imaging systems require a large number of patients, who are imaged repeatedly to compare the performance of different systems. The associated cost, duration, and radiation risk represent a significant impediment to the efficient introduction of novel imaging technologies. Virtual clinical trials (VCTs) represent an approach, based upon computer simulation of human anatomy and imaging modalities, which can help develop, optimize, and validate new and existing medical imaging methods. Fast and detailed simulations of device performance are also instrumental in prototyping clinical trials and augmenting them with simulated data, and may also assist with regulatory approval^4,14,15.

Physics VCTs, in contrast to traditional VCTs, are intended to evaluate the implementation of the novel designs using simulated image acquisitions of virtual test objects and objective metrics to evaluate device performance. We have used physics VCTs to investigate novel acquisition geometries for the NGT prototype⁴. We have shown that physics VCTs can be used to investigate novel acquisition geometries for the NGT system without exhausting resources. In this work, we use physics VCTs and high-resolution test objects to compare the performance of isocentric with non-isocentric acquisition geometries for DBT using configurations of the NGT prototype.

2. MATERIALS & METHOD

Virtual Clinical Trial pipeline

Physics VCTs are implemented using the X-ray Physics Lab’s (XPL) physics VCT pipeline. The physics VCT pipeline has been modified from the original VCT pipeline. Physics VCTs simulate the image acquisition of physical test objects and phantoms. However, rather than using a virtual reader phase of the original VCT pipeline, objective measures of physics are used to evaluate the performance of an imaging device. A tomosynthesis acquisition is simulated, in the same manner as the original pipeline, using ray-tracing methods with a dedicated graphics processing unit (GPU). The mechanical configuration of the NGT prototype is modeled using the physics VCT pipeline, where various acquisition geometries can be simulated.

Next-generation tomosynthesis prototype

Alternative acquisition geometries of the NGT prototype are achieved by creating custom x-ray source and detector motion paths for a series of x-ray projection images. The collection of projection images obtained from each custom acquisition geometry are used for tomographic reconstructions. Details of this prototype have been described in previous work^3,4,16,17. The origin of the NGT system is defined at the center of the chest-wall edge of the breast support (Figure 1). The x-y plane of the NGT system serves as an address space for the x-ray focal spot to determine an acquisition geometry. The range of the source is ±150mm in x and +180mm in y. The NGT achieves non-isocentric acquisition geometries by translating the detector in z between x-ray projections with a 44.8mm range, translating 3.2 mm between projection over 15 projections. The configuration of the NGT prototype and the two acquisition geometries that are used for the physics VCT simulations in this study are shown in Figure 1. This study is constrained to the conventional x-ray source motion only and does not include acquisition geometries with PA source motion.

Figure 1:

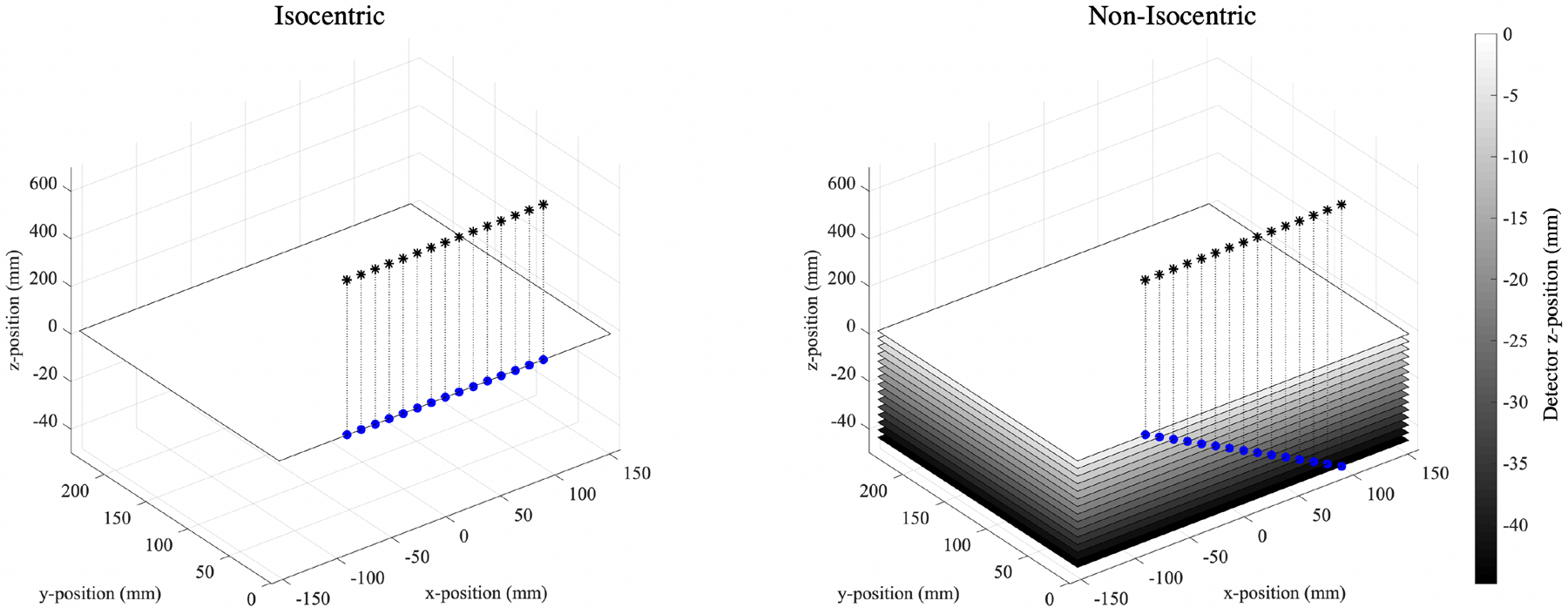
The two acquisition geometries that are used to simulate the NGT prototype. The black stars and blue dots indicate the position of the focal spot in the focal spot plane and the corresponding position of the focal spot relative to the detector position, respectively. NB: the positive and negative z-axes are scaled differently.

The geometric configuration and constraints of the NGT prototype dictate the image acquisition simulation of the physics VCTs. Physics VCTs simulate the radiographic technique for x-ray projection images that are used to render image reconstructions. Tomographic image reconstructions are created by filtered back-projection using commercial reconstruction software (Piccolo version 4.0.5, Real Time Tomography, Villanova, PA).

High-resolution test objects

A voxelized model of a star pattern test object (Model 07-542-1000, Supertech, Elkhart, IN) was created using Matlab (MathWorks, Natick, Massachusetts, version 2018a). This virtual star pattern (Figure 2) consists of 5μm isotropic voxels with three material indices: lead, acrylic, and air. The diameter of the star pattern is 45mm with a total thickness of 30μm. The range of resolution for this star pattern, from the outer edge to the innermost circle, is 1.3–20.0 line pairs per millimeter (lp/mm). The star pattern contains four quadrants, giving two possible frequency orientations for both x and y (${\mathit{\nu }}_{\parallel }$ and ${\mathit{\nu }}_{\perp }$, respectively).

Figure 2:

The virtual star pattern test object that was created to simulate the physical star pattern.

In addition to the star pattern, a bar pattern test object was created at a constant spatial resolution of 70 μm with a frequency orientation, ${\mathit{\nu }}_{\parallel }$. The bar pattern is indexed with lead and air and was created at a 45° tilt relative to the breast support (Figure 3). The tilt of the bar pattern was used to compare the spatial resolution at various depths of the image reconstruction using multiplanar reconstructions (MPR). Using the commercial reconstruction software, MPR can be achieved at arbitrary angles¹⁸. This allowed us to visualize the plane of the bar pattern test object at a plane that is oriented 45° relative to the detector plane. Conventional DBT is anisotropic in the z dimension, which degenerate periodic signals like a bar pattern or punctate calcifications in the breast, at various intervals of z. Non-isocentric acquisition geometries can reduce these degeneracies.

Figure 3:

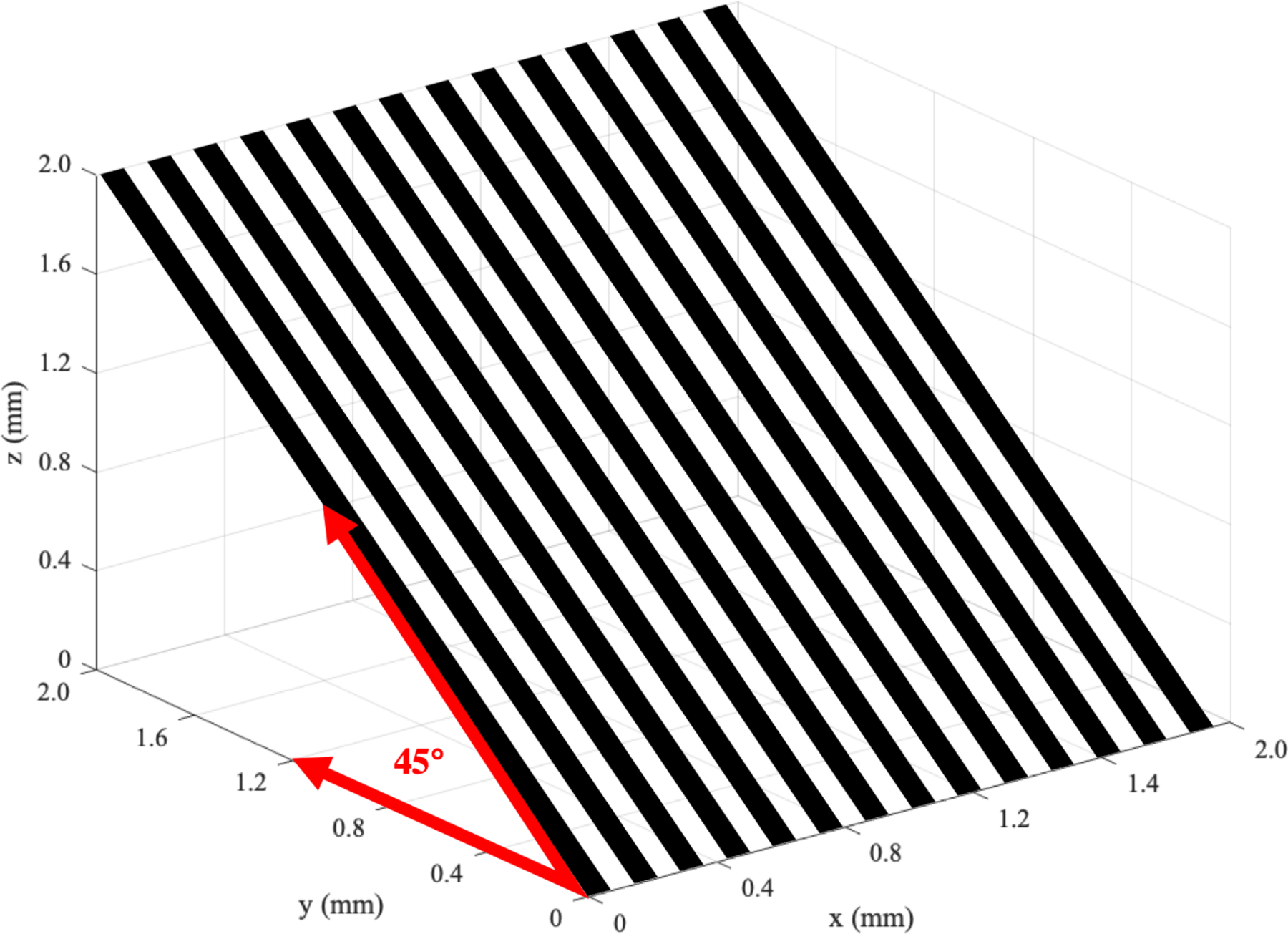
A diagram that illustrates a portion of the tilted bar pattern phantom. The spatial resolution of the phantom is 70μm (7.14 lp/mm).

Physics VCTs were used to simulate image acquisition of the virtual star pattern and tilted bar pattern using isocentric and non-isocentric configurations of the NGT prototype. The conventional x-ray source motion path (Figure 1) was simulated with and without z-direction detector motion (the z-detector position is 0 over all projections), to simulate non-isocentric and isocentric acquisition geometries, respectively. Repositioning and reproducibility of the image acquisition was simulated by perturbing the position of the phantom within 2 mm of the detector origin over 10 tomosynthesis acquisitions for each geometry. Poisson noise was also simulated for each projection image. Super-sampled image reconstructions of the star pattern test object were obtained using the simulated 2D projection images of each tomosynthesis acquisition simulation. The images were reconstructed at a 2.0x super-sampling rate (42.5 μm for the 85 μm detector element size).

The slice of the image reconstruction that contained the plane of the star pattern was used to evaluate the in-plane spatial resolution properties of the 20 image reconstructions. The radial fast Fourier transform (RFFT)¹⁹ was used to evaluate the in-plane performance of both acquisition geometries. This metric used the star pattern image as an input to produce the contrast transfer function (CTF) and RFFT graphs (e.g. Figure 4), averaged over the 10 reconstruction slices for each geometry. The CTF is analogous to the modulation transfer function (MTF) but is not normalized to unity at zero spatial frequency. The RFFT graph shows modulation of all frequencies contained in a quadrant of a star pattern image reconstruction alongside the modulation of aliased signals. The CTF was used to determine the limit of spatial resolution (LSR). Conventional DBT is spatially anisotropic¹¹; therefore, each image reconstruction is evaluated for ${\mathit{\nu }}_{\parallel }$ and ${\mathit{\nu }}_{\perp }$.

Figure 4:

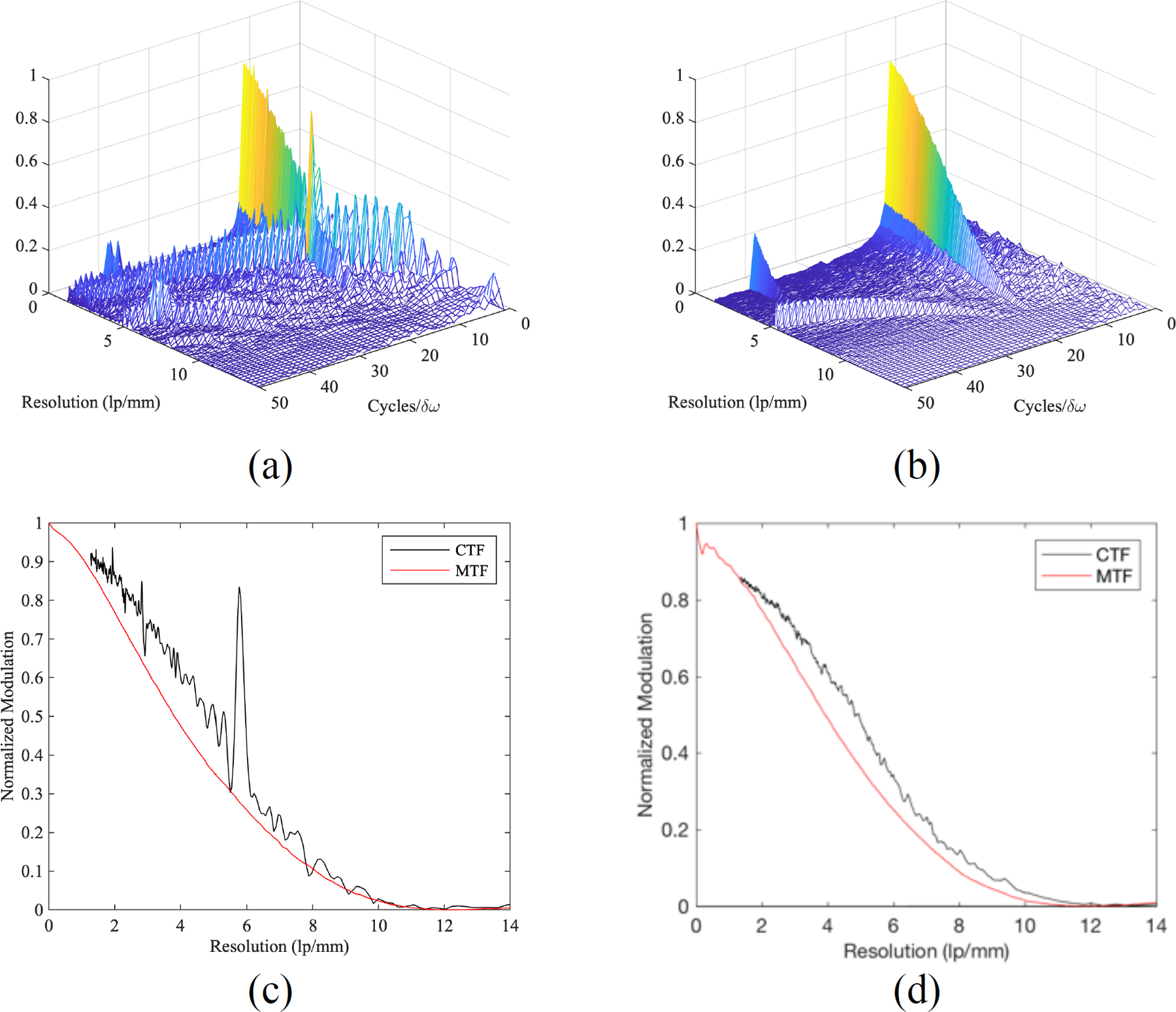
One sample of the Radial FFT for ${\mathit{\nu }}_{\parallel }$ of the conventional, isocentric geometry (a), and ${\mathit{\nu }}_{\parallel }$ of the conventional, non-isocentric geometry (b), and the corresponding MTF vs. CTF graphs (c-d).

The same acquisition geometries were used to generate an MPR of the tilted bar pattern. Images of the tilted bar pattern were reconstructed at a 2x sampling rate. The reconstruction plane was oriented at the tilt of the bar pattern. Plot profiles of a degenerate region in the image reconstruction of the isocentric acquisition geometry was produced and compared with the plot profile of the same region for the non-isocentric acquisition geometry.

3. RESULTS AND DISCUSSION

Star pattern RFFT

An example of a Radial FFT and CTF calculation is shown for a single reconstruction slice in Figure 4. The RFFT and CTF graphs of the non-isocentric acquisition geometries show a reduction of spectral leakage compared with the isocentric acquisition geometries. The Radial FFT was computed for both frequency orientations, ${\mathit{\nu }}_{\parallel }$ and ${\mathit{\nu }}_{\perp }$, and averaged over the 10 reconstruction slices for each acquisition geometry.

The non-isocentric acquisition geometry exhibits isotropic super-resolution (Figure 5), achieving a limiting spatial resolution (LSR) above the alias frequency in both ${\mathit{\nu }}_{\parallel }$ and ${\mathit{\nu }}_{\perp }$, whereas the isocentric acquisition geometry achieves super resolution for ${\mathit{\nu }}_{\parallel }$; however, resolution is limited to the alias frequency for ${\mathit{\nu }}_{\perp }$. The isocentric acquisition geometry shows more significant aliasing in the form of Moiré patterns compared with the non-isocentric acquisition geometry. The modulation contrast is higher for the isocentric acquisition geometries at the lowest spatial frequencies of the star pattern, regardless of frequency orientation.

Figure 5:

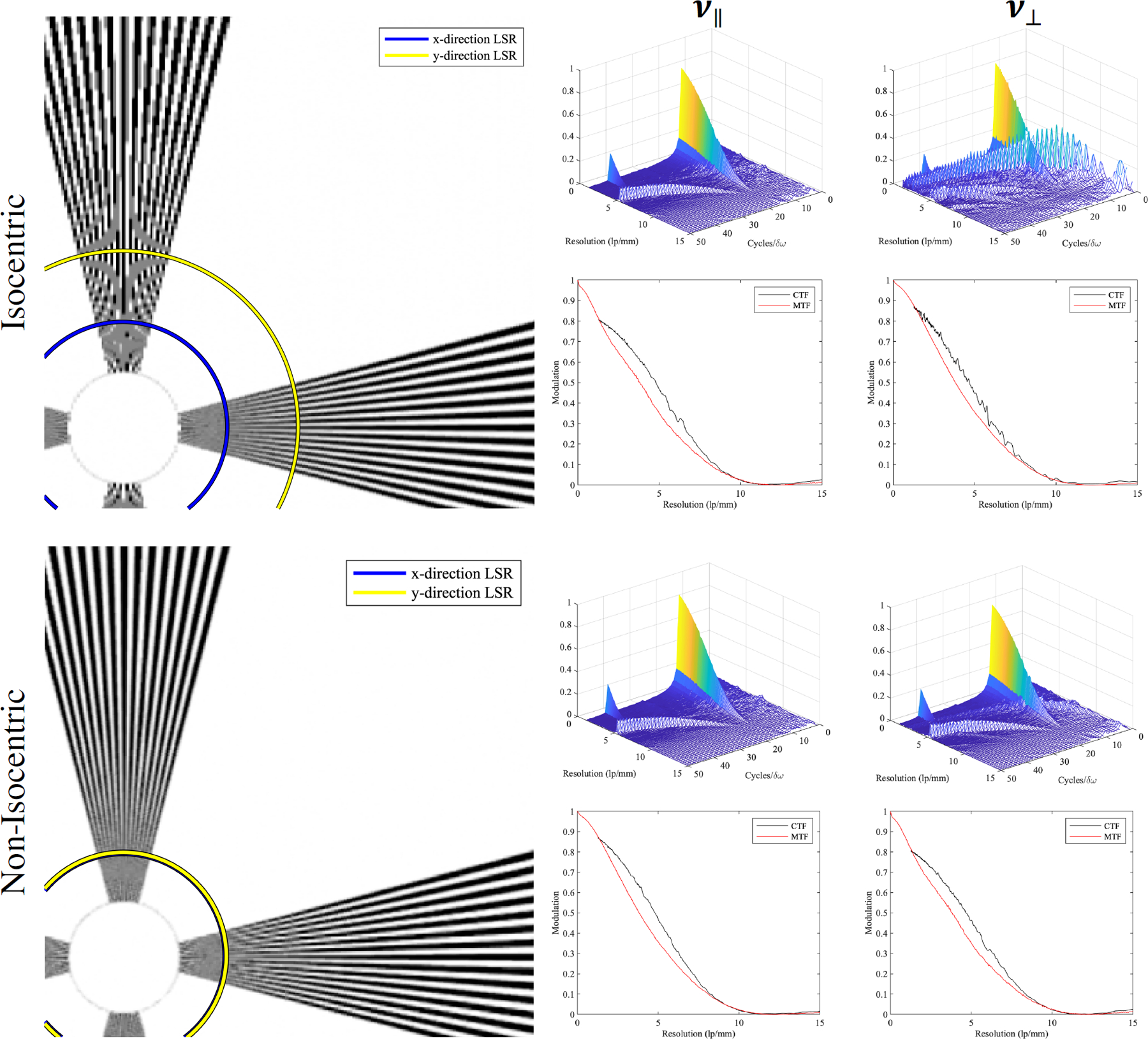
Simulated image reconstruction slices of the isocentric and non-isocentric acquisition geometry (left) and the results of the RFFT metric (right).

The LSR of the four conditions was measured using images of the star pattern and the CTF. All isocentric image reconstructions exhibited significant aliasing for ${\mathit{\nu }}_{\perp }$, and the LSR was limited to near the alias frequency of the detector (5.88 lp/mm). For reconstruction slices where super resolution was achieved, the LSR was measured at a 5% modulation of the CTF. The improvement of the LSR for the non-isocentric over the isocentric geometry was 75.2% for ${\mathit{\nu }}_{\perp }$. Both the image of the star pattern and the RFFT graph for the non-isocentric case exhibit residual aliasing artifact, but this artifact does not overcome the modulation of the input frequency.

Tilted bar pattern MPR

The tilted bar pattern was reconstructed with a roll of 45° about the x-axis for each acquisition geometry. The MPR of the isocentric acquisition geometry shows four distinct degenerate regions (e.g. the region bounded by the red box in Figure 6). Super resolution cannot be achieved at the corresponding z-locations in the image reconstruction. The MPR of the non- isocentric acquisition geometry shows multiple regions of decreased modulation, but no fully degenerate regions of the bar-pattern are seen. Super resolution is observed over the entire MPR.

Figure 6:

MPR of the tilted bar pattern for the isocentric and non-isocentric acquisition geometries with corresponding plot profiles.

4. CONCLUSION

We have shown that non-isocentric acquisition geometries can be simulated with high accuracy using physics VCTs. With 10 simulated tomosynthesis image reconstructions, we were able to measure the RFFT and LSR accurately and achieve results that are commensurate with physical experiments⁴. The LSR improved for every frequency orientation with the introduction of z-detector motion. The highest overall improvement in LSR for the non-isocentric over isocentric acquisition geometry is 75.2% for ${\mathit{\nu }}_{\perp }$. All frequency orientations of the non-isocentric reconstructions exhibit super resolution, whereas the isocentric geometry was prone to aliasing. These results suggest that non-isocentric acquisition geometries can improve the detection of high-frequency objects like microcalcifications for DBT. In the future, we will simulate additional non-isocentric acquisition geometries that include PA source motion to optimize super resolution further.