OralEpitheliumDB: A Dataset for Oral Epithelial Dysplasia Image Segmentation and Classification

Abstract

Early diagnosis of potentially malignant disorders, such as oral epithelial dysplasia, is the most reliable way to prevent oral cancer. Computational algorithms have been used as an auxiliary tool to aid specialists in this process. Usually, experiments are performed on private data, making it difficult to reproduce the results. There are several public datasets of histological images, but studies focused on oral dysplasia images use inaccessible datasets. This prevents the improvement of algorithms aimed at this lesion. This study introduces an annotated public dataset of oral epithelial dysplasia tissue images. The dataset includes 456 images acquired from 30 mouse tongues. The images were categorized among the lesion grades, with nuclear structures manually marked by a trained specialist and validated by a pathologist. Also, experiments were carried out in order to illustrate the potential of the proposed dataset in classification and segmentation processes commonly explored in the literature. Convolutional neural network (CNN) models for semantic and instance segmentation were employed on the images, which were pre-processed with stain normalization methods. Then, the segmented and non-segmented images were classified with CNN architectures and machine learning algorithms. The data obtained through these processes is available in the dataset. The segmentation stage showed the F1-score value of 0.83, obtained with the U-Net model using the ResNet-50 as a backbone. At the classification stage, the most expressive result was achieved with the Random Forest method, with an accuracy value of 94.22%. The results show that the segmentation contributed to the classification results, but studies are needed for the improvement of these stages of automated diagnosis. The original, gold standard, normalized, and segmented images are publicly available and may be used for the improvement of clinical applications of CAD methods on oral epithelial dysplasia tissue images.

Introduction

Oral cavity cancer is one of the most common types of cancer and the sixth leading cause of death in the world [1]. Histological evaluation and grading of potentially malignant disorders, such as oral epithelial dysplasia (OED), is the most reliable way for diagnosing such lesion [2].

OED is a type of abnormality that has the potential for malignant transformation and can present deformities in the size, shape, and color of cell nuclei. Traditional diagnosis for this abnormality often takes into account the thickness of epithelial tissue that is affected by the lesion along with the intensity of nuclear deformities presented, allowing its categorization in mild, moderate or severe grades [3, 4]. In recent years, nuclear segmentation and classification of histology images have been extensively employed in digital pathology [5]. In the field of histopathology, several diseases are evaluated through cell nuclei information, with nuclei segmentation being an important step for cancer diagnosis, grading and prognosis [6, 7].

Lesions of the oral mucosa exhibiting dysplasia are statistically more likely to transition into oral squamous cell carcinoma (OSCC) than non-dysplastic lesions [8]. Early diagnosis of these lesions is important so that patients can receive the appropriate treatment, avoiding their malignant transformation [9]. This histological evaluation leads to a repetitive routine that can be influenced by the specialist’s experience. This task may lead to misinterpretation and diagnosis accuracy limitations. Pathologists’ workload and experience level can influence the image analysis process.

Computational algorithms have been proposed as an auxiliary tool in decision-making by specialists [10]. With these automated approaches, computer-aided diagnosis (CAD) systems have been adopted to support specialists to accurately make better decision-making diagnoses while analyzing such abnormalities [2, 11].

The CAD systems encompass steps consisting of data preprocessing, segmentation, feature extraction, and classification. Nuclei detection and segmentation are important stages for dysplasia and cancer diagnosis and grading. Nuclei segmentation allows objects of interest to be isolated from the rest of the image, keeping only diagnostically relevant structures for analysis, ensuring robust results for classifier systems [12, 13]. This stage is often used to obtain features that are relevant for dysplasia and cancer prognosis and grading, such as shape, size and distribution [14]. Moreover, this image processing stage in CAD is used to identify tissue structures to be analyzed in subsequent steps, such as feature descriptors and classifiers [15]. However, these are complex and challenging tasks due to the irregular features of nuclei structures [16].

Considering the investigation of CAD system, different approaches have been proposed to explore the segmentation or detection of cellular structures on histological images of oral cavity tissues. Baik et al. [17] presented a method for identifying lesions with a high risk of evolving to cancer. The dataset was composed of 29 healthy tissue images, 71 mild/moderate dysplasia images, and 33 cancerous lesions, totaling 133 tissue images. The nuclei segmentation stage was performed using the random forest algorithm with different parameters associated with the number of trees. Then, another algorithm based on RF was employed to classify the nuclei between healthy and non-healthy tissues with the 10-fold cross-validation method. The proposed system obtained an accuracy rate of 86.39% and 80% at the segmentation and classification stages, respectively. This study was able to identify lesions with potentially malignant oral transformation, but there was no assessment regarding the segmentation of the structures present in these images.

Das et al. [18] proposed a method to detect keratinized regions and quantify the stage of oral squamous cell carcinoma. The image dataset was composed of 30 images of grades I, II and III of oral squamous cell carcinoma. The images were converted to the YDbDr color model and the Db channel was used in the segmentation stage since it presents a greater contrast differentiation. The intensity values from this channel were normalized and the active contour snake model was employed to segment the objects. The keratinization regions were computed based on the relation between the size of the keratinized area and the whole image. In these experiments, images with keratinization greater than 50% of the image size were classified as grade I cancer, images with information between 20 and 50% were classified as grade II cancer and images with keratinization regions between 5 and 20% were defined as grade III cancer. The method obtained an average accuracy of 95.08% for detecting these keratinized areas, but the study does not present any investigation on the features of the nuclei present in the tissues.

An OED nuclei segmentation method was shown by dos Santos et al. [14]. In this study, the image dataset consisted of 120 histological images, 30 for each class of healthy tissue and mild, moderate, and severe dysplastic lesions. Due to the low number of images, the dataset was submitted to a data augmentation stage with six transformations: horizontal flip, vertical flip, rotation, elastic transformation, grid distortion and optical distortion. Thus, an approach based on U-Net was trained with the augmented data during 500 epochs. The segmented images were refined using the Otsu threshold technique. The obtained results were compared to the gold standard marked by a pathologist and the metrics used were accuracy and Dice. The methodology presented accuracy and Dice coefficient of 0.879 and 0.820, respectively, for the OED nuclei segmentation.

A methodology for nuclei segmentation and OED grading was presented in the study of Silva et al. [19]. The Mask R-CNN model with the ResNet50 backbone was fine-tuned with 50 epochs and 150 iterations for each epoch. The model was used to segment nuclei instances for each image. Morphological operations of dilation, hole-filling and erosion were employed to improve the segmentation results and objects smaller than 30 pixels were considered background objects. The methodology achieved nuclei accuracy of 89.31% and 92.4% for the segmentation and classification stages, respectively. The methodology was capable of identifying the OED grades, but no assessment was performed regarding the impact of segmentation on the OED grading.

Shephard et al. [13] proposed a method to segment and classify nuclear instances on OED images and then assign an oral malignant transformation risk to them. The method consisted on the segmentation of nuclei within the epithelium and morphological/spatial feature extraction. The segmentation was performed using the HoVer-Net+ model, which consists of an encoder branch and four decoder branches. The encoder branch employs 50 residual layers and the decoder branches use nearest-neighbor upsampling to perform instance segmentation, nuclei classification and intra-epithelial layer segmentation. After segmentation, the images were tessellated into smaller tiles and morphological and spatial features were obtained from each of them. These features were evaluated into a multilayer perceptron to predict the malignant transformation ratio at slide level. The methodology was employed on a dataset of 116 whole-slide OED images, with 42 transitioning to malignancy. The method presented a mean Dice score of 0.691 for nuclei instance segmentation and F1-score of 0.71 in predicting OED malignant transformation. The authors highlighted that, although the method was capable of segment and classify the nuclear structures, more studies are required exploring patch-level features from pathologists.

The study of Maia et al. [20] proposed a method for automated diagnosis of oral cancer images. This task was performed using different CNN models and transformers and the obtained results were compared. The CNN models chosen were ResNet-50, VGG16, MobileNet V2 and DenseNet-121. The transformers employed were Vision Transformer (ViT), Pooling-based Vision Transformer (PiT) and Go-scale conv-attentional image Transformers (CoaT). The methodology was employed on an image dataset of oral cancer with 1930 patches of OED containing lesions, 1126 of OSCC and 707 with lesions without OED. During the experimental tests, DenseNet-121 outperformed other CNN models, presenting an F1-score of 91.93. Similarly, ViT showed highest values than other transformers, with an F1-score of 90.80. The authors highlight that histopathology images can contain various lesions and that dividing these images in smaller patches contributes to expanding the sample number while keeping relevant tissue information.

In literature, there are few datasets of oral cavity tissues, most of them consisting of lesions at advanced stages, such as OSCC or leukoplakia. In such datasets, OED cases are considered as a feature of these lesions [20]. Several studies of digital histopathology use private datasets such as Adel et al. [21] or public datasets of advanced-stage lesions such as Rahman [22]. Although there are several public datasets in the literature, such as the NuCLS [23], CryoNuSeg [24], MoNuSeg [25] and PanNuke [26], most of them consist of images of advanced-stage lesions or other regions of the body. In addition, no data presents different levels of OED progression (mild, moderate and severe).

Among the studies investigating dysplastic lesions available in the literature, a small number investigate the influence of certain stages of the CAD system on dysplasia images [13, 14, 19]. There is still a lack of research into the behavior of deep learning segmentation approaches (semantic and instance) on this type of lesion and its degrees, as well as normalization processes in segmentation and classification stages. Moreover, domain expertise is required to generate data and annotation labels [23]. Based on these characteristics, a new publicly available dataset is an important contribution to research on computational strategies for the investigation of OED grades.

Considering this overview of the literature and limitation of data availability, this study presents a fully annotated public dataset with OED grades with practical experiments commonly explored in the field of CAD systems. Thus, an investigation of CNN model approaches for nuclei segmentation and classification of OED images was detailed. The nuclei may present irregular structures, faded stains, and low contrast [16]. Then, methods for stain normalization were evaluated to normalize the colors of histological structures to enhance the contrast between the objects and minimize the dataset color variance, resulting in images that allow a more reliable analysis [27, 28]. A study was also performed to evaluate the impact of such stain normalization methods on segmentation and classification methods. The original and color-normalized images, as well as the pathologist’s gold standard annotations, are available to the scientific community.

Methodology

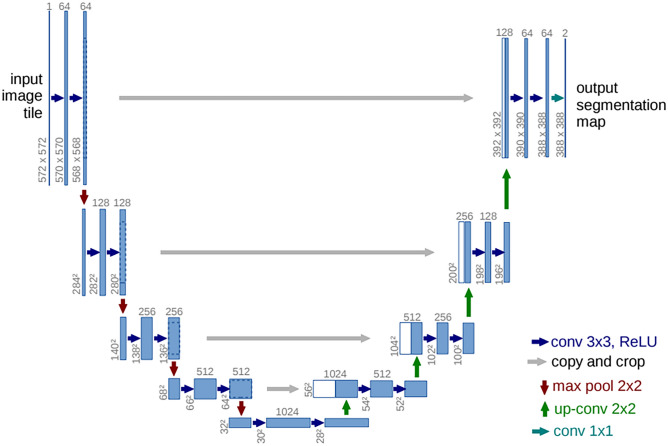
The proposed dataset was tested through the relevant experiments commonly explored in CAD systems. Thus, OED segmentation and classification tests cover the following steps: stain normalization, segmentation, post-processing, classification, and evaluation. Figure 1 shows the main steps applied to the evaluation of OED images. The system was developed using MATLAB^® and Python languages. The experiments were performed on equipment with a Ryzen 5 CPU, 64 GB of RAM and Nvidia RTX 2070 GPU with 12 GB of VRAM.

Fig. 1.

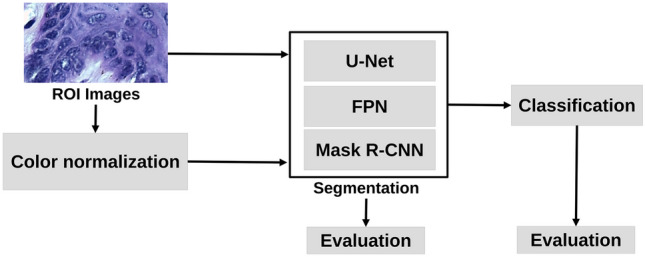
Block diagram the main steps employed to segment and classify OED lesion images

Proposed Dataset

The image dataset was built from 30 mice tongue tissue stained with H &E and previously submitted to the carcinogen 4-NQO (4-nitroquinoline-1-oxide) during two experiments carried out between 2009 and 2010. These experiments were approved by the Ethics Committee on the Use of Animals under protocol numbers 038/09 and A016/21 at the Federal University of Uberlândia, Brazil.

Mice have been widely used in the study of various human diseases due to their genetic similarities with humans [29]. In the context of oral epithelial dysplasias, the use of mice to study this condition is unique, allowing for controlled induction of oral lesions and disease progression from mild to severe. Furthermore, the use of mice reduces the need for invasive procedures in humans [30]. It also allows the study of disease progression at the cellular level, providing valuable information on nuclear cellular changes in different grades of OED [29, 31].

Lesions in histological studies can be multifocal, meaning that multiple distinct lesions may coexist within a single tissue sample and that multiple OED cases can be obtained from each slide [32]. In vivo experiments often use the three R’s (Replacement, Reduction, and Refinement) as guidelines for animal use. The goal of these guidelines is to promote the ethical use of animals in scientific research [33]. To adhere to these principles, the number of animals employed in our study was minimal, but enough to get relevant and representative data.

The histological slides were digitized with the Leica DM500 optical microscope with a magnification factor of 400$\times$ and were stored in the TIFF format with the RGB color model, 8-bit channel depth and, dimensions of 2048$\times$1536 pixels, resulting in 134 raw images, being 38, 32, 33 and 31 tissue images of healthy mucosa, mild, moderate and severe OED, respectively. Using the methodology described by [34], the images were classified among healthy epithelium tissue, mild, moderate and severe OED by one pathologist. For each class, 114 regions of interest (ROIs) of size 450 $\times$ 250 pixels were obtained, totaling 456 ROI images. Since the manual analysis can lead to misinterpretation, it is important to perform this stage with two or more specialists, reducing the divergence ratio as described in [35–37]. In the context of methodologies for histological lesions, several studies explore nuclei in premalignant and malignant lesions and assess the agreement ratio between specialists [38–40]. In this study, based on the methodology described by [41], the image nuclei were manually marked by a specialist (trained by the pathologist) and then validated and, if needed, corrected by a pathologist, defining the final gold standard annotations to be assessed by the methodology.

Stain Normalization

In order to evaluate the impact of stain normalization on cell nuclei segmentation, the images were submitted to four traditional normalization methods. The employed methods were proposed by Macenko et al. [42], Reinhard et al. [43], Tosta et al. [28] and Vahadane et al. [27]. These methods were chosen due to the relevant results shown on histological image analysis in the literature [28, 44, 45].

The method proposed by Macenko et al. [42] employs a singular value decomposition to estimate the presence of dyes across image pixels. This approach disregards pixels with low intensities in order to reduce the impact of low pigmentation. After estimating the dye presence for both the source and reference images, the values are merged to create an image with reduced color variation. The method by Reinhard et al. [43] performs color transfer between the original image and a reference image. It uses statistical correspondence between the two sets of image values to adjust the intensity values accordingly. The method by Vahadane et al. [27] uses a technique called sparse nonnegative matrix factorization to estimate dye presence across the image, effectively capturing the sparsity of dyes. These values are then combined with the stain representation of a reference image. Finally, the study of Tosta et al. [28] presented a normalization technique that involves estimating the concentration of stains in the original image and merging this information with the stain representation derived from a reference image. This combined approach results in an image that exhibits a suitable color distribution.

For this stage, three reference images were used for the investigation of the normalization methods. These images were chosen by the trained specialist and the pathologist considering the contrast between nuclei and background, shade distinction between Hematoxylin and Eosin dyes and nuclei border definition, following the criteria in the studies of Pontalba et al. [46] and Tosta et al. [47]. These images were named Ref-1, Ref-2 and Ref-3. It is noteworthy that these images were obtained from different image datasets. The Ref-1 image was obtained from a private image set of oral lesion tissues and presents a desired level of stain distribution and nuclei border definition that allows the visual identification of nuclear structures. Ref-2 is an image of a breast cancer tissue obtained from the Nuclei Segmentation dataset provided by Janowczyk and Madabhushi [48] and that presents distinguished color between the histological structures. The Ref-3 image is an image of lymph node tissue that presents high contrast between nuclear structures and was obtained from the Histopathology Classification dataset provided by Kang et al. [49].

This evaluation involved normalization methods that required a reference image for their execution. Hence, the colors of these reference images were used to align and correct the colors of the original images. Employing various reference images allowed the assessment of their impact on segmentation and classification processes. Subsequently, it is feasible to establish a correlation between the outcomes achieved in these processing steps and the selected reference image. A similar approach has been previously noted in the research conducted by Bautista and Yagi [50] and Tosta et al. [28, 47], specifically in the assessment of normalization and feature extraction methods. Although this evaluation employed only three images, this quantity was deemed adequate because of the distinctiveness of the reference images, as depicted in Fig. 2. Noticeable color distinctions among the reference images under evaluation were apparent. In a visual examination, Fig. 2(a) displays less saturated colors than the other images. Conversely, the colors in Fig. 2(b) represent both dyes with significantly different shades compared with the remaining images. Finally, Fig. 2(c) presents a significant proportion of eosin, distinguishing it from the others.

Fig. 2.

Reference images evaluated for stain normalization of histological images to be segmented and classified in further steps

Segmentation

Segmentation is a relevant task in digital image processing for other stages of CAD systems. Several methods can be used in this stage, such as thresholding, region growth, graphs and watersheds. In recent years, CNN-based image analysis models have gained significant attention in the scientific community, despite the existence of various segmentation methods. With these models, segmentation is explored as a pixel analysis problem, with pixels being labeled between object classes (semantic segmentation) or individual objects being partitioned (instance segmentation) [10]. Studies from the literature show that the segmentation is an important step for lesion grading tasks [6, 7] and that encoder (or convolutional) structures, such as CNNs, achieve relevant results for the segmentation stage [14, 51, 52].

At this stage, semantic and instance segmentation models were employed to assess how the different approaches can impact the further stages. The feature pyramid networks (FPN) and U-Net architectures were used as semantic segmentation models and the Mask R-CNN, HoVer-Net, StarDist and SOLO V2 were employed to perform nuclei instance segmentation, based on relevant results available in specialized literature [52–56]. Given a H &E image as input, the FPN model generated feature maps at multiple levels, in a fully convolutional fashion [57]. The construction of the pyramid involved a bottom-up pathway, a top-down pathway, and lateral connections. The bottom-up pathway used the feature maps generated by a backbone to create hierarchical maps at different scales. The top-down pathway generated high-resolution features through the upsample of feature maps from higher pyramid levels. Then, these features were enhanced via lateral connections that merge feature maps from the same levels of the bottom-up and the top-down pathways. An FPN model takes advantage of the multi-scale and hierarchical nature of convolutional neural networks to generate relevant features for object detection and segmentation on different scales [58]. For this model, the experiments were performed via MobileNet V2 and ResNet50, based on the results obtained in the empirical tests. For this model, the experiments were performed via MobileNet V2 and ResNet50.

Taking into account the U-Net model, the strategy consisted of convolution and deconvolution paths, using a typical CNN in the convolution stage [59] in order to extract the features from the H &E samples. The convolutional process was performed via MobileNet V2 and ResNet50 backbones. In the deconvolution path, the image was upsampled to its original size, allowing precise localization of high-resolution features. Every step of this stage was defined as an upsampling of the feature map, a concatenation with the corresponding cropped feature map from the convolution path, and two kernel convolutions, each followed by a ReLU. The cropping was applied to minimize the loss of border pixels in every convolution. Consequently, the final layer was defined with a $1\times 1$ convolution in order to map the feature vector into the desired number of classes. This network architecture is shown in Fig. 3.

Fig. 3.

Illustration model of the U-Net architecture [Source: Ronneberger et al. [59]]

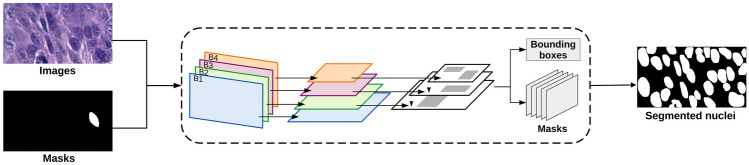
Considering the Mask R-CNN, this model was applied to obtain object detection and instance segmentation [60]. exploring bounding boxes to carry out this task [61, 62]. The Mask R-CNN model was composed of the ResNet50, feature pyramid network (FPN), and region proposal network (RPN), as shown in Fig. 4. The convolutional layers of ResNet50 were employed to build the FPN structure. The FPN features were then passed to the RPN in order to detect regions with potential objects. Each layer of the FPN employed a $3\times 3$ convolutional operation and the resulting values were processed by two fully connected layers to generate bounding boxes for each region. Then, a fully connected layer was applied to the object feature maps to determine the binary masks for each nucleus in the histological images.

Fig. 4.

Architecture illustration of the Mask R-CNN employed in the OEDs segmentation process

The HoVer-Net architecture combines object detection and instance segmentation using three decoder branches [63]. The first branch, named Nuclear Pixel branch, predicts which class a pixel belongs to. The second, called HoVer branch, computes the horizontal and vertical distances of nuclear pixels to their centroids, aiming to separate touching nuclei. Lastly, the Nuclear Classification branch is employed to determine the type of each nucleus.

The StarDist architecture consists of the object detection and instance segmentation steps [64]. Using a U-Net backbone, features are extracted from images to identify candidate objects, and their areas are determined through star-shaped polygons defined from the centroid of an object along a set of n radial directions. The second step employs a fully connected layer on feature maps and regions identified by the star-shaped distances, generating binary masks for each nucleus in the image.

SOLO v2 identifies objects through region-based processing and binary mask refinement [65]. In the first stage, the image is divided into a grid, classifying each of its cells as nuclei or background. In the second stage, mask features are extracted from FPN-generated maps, with four convolutions reducing map dimensionality, and an extra filter to generate nuclei instance masks.

To simplify the names of the models used in this study, they were renamed as follows: Model a) U-Net-Mobile, Model b) U-Net-ResNet50, Model c) FPN-Mobile, Model d) FPN-ResNet50, Model e) Mask R-CNN, Model f) Hover-Net, Model g) StarDist and Model h) SOLO V2. All models were pre-trained on the ImageNet dataset and fine-tuned to the dataset. The images were split into proportions of 60% for the training set, 10% for the validation set and 20% for the test set. In the fine-tuning stage, the same hyperparameters were employed for each model, aiming to maintain consistent training values. The models were trained with 40 epochs, 150 iterations for each epoch, a learning rate of 0.001, a momentum value of 0.9 with the Nadam optimizer and the average binary cross-entropy loss as described in [60]. In this stage, different values were evaluated to obtain the best combination between the structures and background of the investigated image.

After the segmentation, the resulting images may contain regions with noise. To address this issue, morphological operations were employed. A dilation operation was performed using a $3\times 3$ pixel kernel to enlarge the objects within the image, enhancing their edge contours. Then, a hole-filling operation was employed to eliminate holes present in the nuclei regions. Next, an erosion filter with a kernel size of $3\times 3$ pixels was used to eliminate noise and restore the nuclei regions to their original size. Finally, any objects with an area smaller than 30 pixels were removed.

Classification

In this stage, the multiclass supervised classification was employed on the image dataset. This classification was evaluated using three strategies: (1) employing CNN models, (2) a combination of handcrafted features and machine learning (ML) algorithms and (3) association of deep features and ML algorithms.

These strategies were evaluated on the non-segmented images, semantic segmented images and instance segmented images. The non-segmented images represent the ROIs obtained in the process described in the “Proposed Dataset” and “Stain Normalization” sections. The semantic segmentation step was also performed over the ROIs, allowing the obtain each image only with the nuclei but without the background region. The instance segmentation stage was employed over the ROIs resulting in individual nuclei images that were then aggregated to compose an output image.

Employing Convolutional Neural Network Models

For the first strategy, the ResNet50 and MobileNet V2 models were explored on the non-segmented images, semantic segmented images and instance segmented images, considering transfer learning to enable the use of architectures in datasets with few samples, speeding up the training process and indicating a more accurate and effective general model. These models were chosen based on relevant results of histological classification in the literature [66–69], as well as the results obtained in the semantic segmentation stages. MobileNet V2 is a CNN model designed for efficient classification with low computational costs, as introduced by Howard et al. [70]. Its architecture comprises convolutional layers, inverted residual blocks, pooling mechanisms, reduction layers, and a final classification layer. The ResNet50 model employs a residual network architecture, as proposed by He et al. [71]. This architecture features an initial input layer followed by a series of residual blocks, each containing three convolutional layers and a pooling mechanism, and a final classification layer.

For this strategy, the images were divided into proportions of 60% for the training set, 10% for the validation set, and 30% for the test set, respectively. In the fine-tuning stage, both models used the same hyperparameters. The models were trained with 40 epochs, 128 iterations for each epoch, a learning rate of 0.0001 with the Adam optimizer, and categorical cross-entropy, as shown in the studies of Laxmisagar and Hanumantharaju [72] and Bokhorst et al. [73]. As in the segmentation fine-tuning stage, different values were tested to obtain the best results.

A Combination of Handcrafted Features and Machine Learning Algorithms

The second strategy consisted of using handcrafted features as input for traditional ML classifiers. In this study, the texture features used for classification were Moran index, the entropies of Kapur, Rényi, Shannon, and Tsallis, as well as correlation, contrast, energy, and homogeneity measures, as described in previous works [74–79].

The Moran index ($M_I$) assesses the spatial autocorrelation of a pixel in comparison with the average intensity in its region. The entropies were used to quantify the level of disorder or randomness within the distribution of pixel intensities. A higher entropy value indicates a more complex and varied distribution of pixel values. Conversely, lower entropy may imply a more uniform or repetitive pattern. In this investigation, entropy features were computed for each image, offering a global measure of the image. Furthermore, Shannon entropy was applied using various sizes of sliding windows, resulting in local tissue features. Following the approach outlined in [80], seven sliding window sizes were computed, corresponding to scales of 3 $\times$ 3, 5 $\times$ 5, 7 $\times$ 7, 9 $\times$ 9, 11 $\times$ 11, 13 $\times$ 13, and 15 $\times$ 15 pixels.

A co-occurrence matrix was computed from each image and normalized by dividing each element in the matrix by the sum of all elements. The normalized matrix was used to obtain the correlation, contrast, energy, and homogeneity measures. Correlation measures the linear dependency between grayscale pixels at different positions in the image, contrast assesses the amount of local variation in the image, energy quantifies the uniformity of the texture in the image, homogeneity measures the similarity of the distribution of elements in the co-occurrence matrix to the diagonal.

The chosen traditional classifiers were the Logistic Regression (LOG), Random Forest (RF) and Support Vector Machines (SVM), based on presented results in medical images. These algorithms were chosen based on the relevant results obtained in the classification task of histological images [81–83].

The LOG classifier is a widely used algorithm for medical tasks [84]. It operates by applying a logistic function to the linear combination of input features, producing probabilities that are then used to classify instances into the nucleus or background classes. The model uses a regularization parameter to penalize large weight values, avoiding overfitting.

The RF is an ensemble learning method that builds multiple decision trees to improve the model’s accuracy and stability [85]. Each tree is independently trained on a feature subset to provide a classification, and the final prediction is determined by a majority vote. This approach reduces the model’s variance by introducing randomness to the model training process.

The SVM operates by finding an optimal hyperplane for separating instances of different classes [86]. At the training stage, SVM learns the optimal parameters, including feature weights, and defines the hyperplane. During testing, new instances are classified based on their position relative to the hyperplane, assigning them to one class if on one side and to the opposite class if on the other side.

The training and evaluation of the three classifiers were conducted using 5-fold cross-validation, a technique employed to assess ML models with a limited data sample [87]. In this approach, the dataset is partitioned into five subsets, with each subset used as the training set while the others serve as validation sets across five iterations. This process reduces bias and variations in the generated results.

Association of Deep Features and Machine Learning Algorithms

For the last strategy, the features generated by the ResNet50 CNN model, named deep features, were also applied as input for traditional ML classifiers. For this, the last convolution layer before the flattening layer was extracted from the model trained at the first strategy. A total of 1,050,624 features were obtained. Based on the studies of Ribeiro et al. [88] and Silva et al. [89], the ReliefF algorithm was used to obtain the most relevant features. It assigns weights to each feature based on how well they distinguish between instances that are close to each other [90]. These values are then normalized and sorted in descending order, where the top n features are selected as the relevant features for classification. Based on empirical experiments, the n value of 50 was chosen for this study.

These features were used to generate feature vectors to represent the images and used as input to train the ML algorithms. Similar to the classification with features from the handcraft features, the ML classifiers were trained using the 5-fold cross-validation technique.

Evaluation

The segmentation was evaluated by calculating the overlapping pixel regions of the segmented images and the images marked by the pathologist (gold standard). Evaluation of the classification was done by quantifying the number of tissue samples correctly and incorrectly classified according to dysplasia grading. Then, the following parameters were computed: true positive (TP), false positive (FP), true negative (TN) and false negative (FN). These measures were used to obtain the metrics of accuracy ($A_{\mathit{CC}}$) and F1-score (F1) to assess the methodology [91, 92].

The $A_{\mathit{CC}}$ was used to measure the ratio of pixels correctly segmented along the images and the number of ROI images correctly classified. It is defined by Eq. 1.

$$\begin{array}{c}\hfill A_{\mathit{CC}}=\frac{TP+TN}{TP+TN+FP+FN}.\end{array}$$ 1

The F1 score was used to assess the model’s performance in terms of precision and recall. It is calculated with Eq. 2.

$$\begin{array}{c}\hfill F_1=\frac{2\times TP}{2\times TP+FP+FN}.\end{array}$$ 2

In the context of segmentation, TP, TN, FP, and FN represent pixels accurately and inaccurately labeled as nuclei or background regions. For the classification stage, these metrics correspond to images correctly categorized into one of the classes.

The repeated measures ANOVA test was employed to assess the significance of differences between the different experimental conditions. This statistical test is used to analyze the effects of different variables across multiple measurements and is widely used in pathology studies [93–95]. The repeated measures ANOVA is computed using Eq. 3:

$$\begin{array}{c}\hfill F=\frac{MS_{\text{Between}}^{}}{MS_{\text{Within}}^{}},\end{array}$$ 3

where $MS_{\text{Between}}^{}$ is the mean square between groups and $MS_{\text{Within}}^{}$ is the mean square within groups.

To further explore and interpret the observed differences, post hoc tests were conducted using the Least-Squares Means approach, based on relevant results in medical applications [96–98]. This method not only provides a robust assessment of group differences but also accounts for potential confounding variables. The Least-Squares Means estimate (${\overline{Y}}_{\mathit{ij}}$) for each group i at each level of the repeated measures factor j is obtained through Eq. 4:

$$\begin{array}{c}\hfill {\overline{Y}}_{\mathit{ij}}={\beta }_0+{\beta }_{{\text{Group}}_i}+{\beta }_{{\text{Time}}_j}+{ϵ}_{\mathit{ij}},\end{array}$$ 4

where ${\beta }_0$ is the grand mean, ${\beta }_{{\text{Group}}_i}$ and ${\beta }_{{\text{Time}}_j}$ are the group and time effects, respectively, and ${ϵ}_{\mathit{ij}}$ is the residual error.

Experimental Evaluation

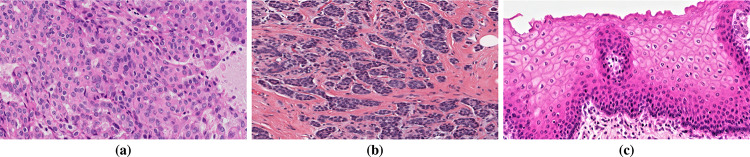
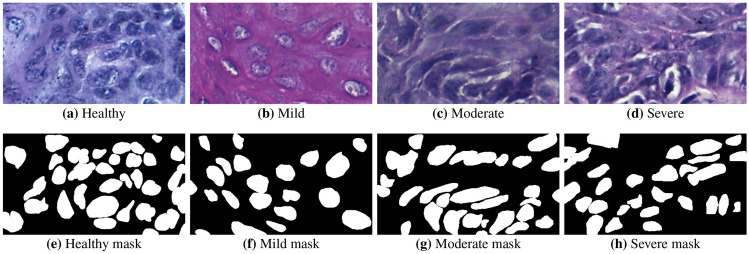
For each tissue class, digital ROIs can be seen in Fig. 5(a)–(b). The cell nuclei were manually marked by the trained specialist and the resulting labels were evaluated and validated by a pathologist, defining the gold standard annotations used to evaluate the methodology. Examples of gold standard images are depicted in Fig. 5(e)–(h).

Fig. 5.

Examples of oral histological tissues. The top row shows the ROI images and the bottom row shows the respective gold standard outlined by the pathologist

In this study, the impact of stain normalization on the segmentation and classification stages was evaluated. Examples of the application of these stain normalization methods over a moderate OED are shown in Fig. 6. The evaluation of the four normalization methods and three reference images resulted in 12 color-normalized image datasets. These images are available on the dataset repository and can be used in other studies to evaluate the impact of the normalization in segmentation or feature extraction methods. The dataset is publicly available at https://github.com/LIPAIGroup/OralEpitheliumDB.

Fig. 6.

Examples of the H &E normalization methods: a Macenko et al. [42], b Reinhard et al. [43], c Tosta et al. [28] and d Vahadane et al. [27] In this example, the methods shown were employed in the moderate OED shown in Fig. 5(c)

Segmentation CNN Model Analysis

The outputs generated by the segmentation models were compared to the gold standard marked by the pathologist. These results were evaluated visually and quantitatively for each H &E normalization method and segmentation model.

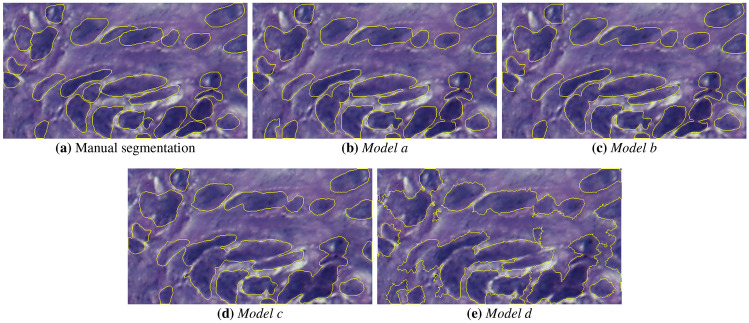
The visual comparison of the mask results for the semantic segmentation models is presented in Figs. 7 and 8, for a moderate OED without the use of H &E normalization. Figure 7 shows the binary masks generated by the models. It can be observed that there are regions of FP (indicated by regions in green color) and FN regions (in red color) close to nuclei. This may occur due to blurred borders, non-uniform shape of nuclei structures caused by the OED stage and low contrast between background and nuclei regions. Figure 8 depicts the identified nuclei regions borders over the original ROI image. From these borders, shown in yellow color, it can be seen that Models c and d present errors in the nuclei boundaries definition. Models a and b show less border irregularities, but identify clustered nuclei as one object. In general, all models detected parts of the nuclei present in the image, however, the Models c and d showed a higher number of FP regions (see Fig. 7(d) and (e)), that is, it marked nuclei regions that were not present in the expert’s marking. It can also be observed in Fig. 8(d) and (e) that the method was not able to define the shape of the objects present in the image.

Fig. 7.

Semantic segmentation masks generated by the different CNN models: a gold standard, b Model a, c Model b, d Model c and e Model d. Red and green regions indicate FN and FP regions, respectively

Fig. 8.

Semantic segmentation masks overlayed on the moderate OED image: a gold standard, b Model a, c Model b, d Model c and e Model d

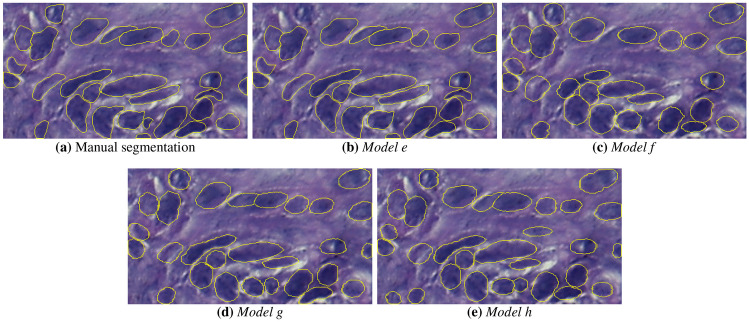
The instance segmentation masks are presented in Fig. 9. It is observed that Model e could segment the nuclear structures, showing some FN in the form of non-identified nuclei. Models f, g and h also showed satisfactory results, but failed to segment clustered objects because of the unclear nuclear boundaries. Figure 10 depicts the nuclear boundaries generated by the models. It is observed that all models defined borders close to the original image, with Models e and h showing less degradation of nuclear borders.

Fig. 9.

Instance segmentation masks generated by the CNN models: a gold standard, b Model e, c Model f, d Model g and e Model h

Fig. 10.

Contours of the instance segmentation masks over moderate OED image: a gold standard, b Model e, c Model f, d Model g and e Model h

Tables 1 and 2 display the values obtained for the semantic and instance segmentation models, respectively. Regarding non-normalized images, Models d and e achieved the highest $A_{\mathit{CC}}$ and F1 values of 90.56% and 0.81, respectively. Models c, f and g exhibited an average F1 value of 0.80, while Models a, b and h yielded $A_{\mathit{CC}}$ values close to 87%. Based on these values, it is noted that the Models d and e achieved the highest values.

Table 1.

Semantic segmentation results obtained using H &E normalization methods present in the literature using three reference images

		Model a		Model b		Model c		Model d
Method	Reference	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1
No normalization	-	87.32	0.78	87.84	0.79	89.64	0.80	90.56	0.81
Macenko et al. [42]	Ref-1	86.22	0.76	86.73	0.77	85.76	0.78	87.64	0.79
	Ref-2	86.64	0.77	86.48	0.77	87.39	0.79	87.58	0.79
	Ref-3	86.39	0.77	86.54	0.77	87.62	0.79	87.27	0.79
Reinhard et al. [43]	Ref-1	85.28	0.75	92.38	0.83	79.43	0.67	85.44	0.76
	Ref-2	84.96	0.74	85.64	0.75	81.29	0.72	86.29	0.77
	Ref-3	85.52	0.75	85.33	0.76	85.68	0.76	86.34	0.77
Tosta et al. [28]	Ref-1	85.74	0.75	84.51	0.74	86.39	0.77	87.25	0.78
	Ref-2	86.43	0.77	87.48	0.78	87.42	0.79	90.32	0.81
	Ref-3	86.66	0.77	86.13	0.77	87.25	0.79	89.44	0.80
Vahadane et al. [27]	Ref-1	86.07	0.75	85.90	0.76	85.64	0.76	85.67	0.78
	Ref-2	86.40	0.77	87.83	0.79	89.63	0.80	89.39	0.80
	Ref-3	86.78	0.77	87.35	0.78	87.48	0.79	89.66	0.80

Table 2.

$A_{\mathit{CC}}$ and F1 metrics obtained with instance segmentation models and H &E normalization methods

		Model e		Model f		Model g		Model h
Method	Reference	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1
No normalization	-	91.23	0.81	89.49	0.80	89.64	0.80	87.59	0.79
Macenko et al. [42]	Ref-1	89.68	0.80	87.80	0.79	89.48	0.80	89.33	0.80
	Ref-2	89.54	0.80	87.64	0.79	87.40	0.79	89.47	0.80
	Ref-3	89.73	0.80	87.59	0.79	87.63	0.79	87.56	0.79
Reinhard et al. [43]	Ref-1	76.34	0.59	85.42	0.78	86.28	0.77	85.28	0.78
	Ref-2	85.60	0.78	86.63	0.77	86.32	0.77	87.45	0.79
	Ref-3	87.33	0.79	85.79	0.78	85.76	0.78	87.38	0.79
Tosta et al. [28]	Ref-1	87.62	0.79	87.41	0.79	89.13	0.80	89.57	0.80
	Ref-2	90.86	0.81	89.27	0.80	87.22	0.79	89.42	0.80
	Ref-3	90.67	0.81	89.44	0.80	87.43	0.79	87.66	0.79
Vahadane et al. [27]	Ref-1	87.52	0.79	87.63	0.79	89.22	0.80	90.07	0.81
	Ref-2	90.78	0.81	85.43	0.78	85.64	0.78	89.71	0.80
	Ref-3	90.69	0.81	85.36	0.78	85.47	0.78	87.64	0.80

At this stage, four H &E normalization algorithms were employed in order to investigate their impact on the segmentation stage. The CNN models were re-trained using the H &E normalized training datasets and the same hyperparameters as specified in the “Segmentation” section.

It is noteworthy that the reference images were obtained from different image datasets. This approach allowed the evaluation of the different compositions of the histological images and their influence on normalization, segmentation and classification. This approach enabled the assessment of varying histological image compositions and their impact on the normalization, segmentation, and classification processes. Hence, it was feasible to assess the robustness of the algorithms by employing reference images with distinct tissue structures. A similar methodology was applied by [99], who assessed the presence of a substantial representation of red blood cells in various normalization techniques.

The normalization proposed by Macenko et al. [42], resulted in $A_{\mathit{CC}}$ and F1 values ranging from 85.76 to 89.73 and 0.76 to 0.80, respectively, with Models e and h achieving the highest values. Each model presented similar results for all reference images. This shows that the investigation does not bring relevant contributions to the results obtained without normalization, regardless of the segmentation model and reference image applied.

With the Reinhard et al. method [43], there is a more expressive variation among the segmentation methods. All models presented lower results compared to the baseline, except Model b, which showed $A_{\mathit{CC}}$ and F1 values of 92.38 and 0.83, respectively. In these experiments, the Model b with Ref-1 image resulted in an increase in the metric values for segmentation. However, this same image causes a F1 value degradation of 0.22 with Model e in comparison to the baseline. This reference image resulted in a greater variation among the segmentation models.

Tosta et al. [28] and Vahadane et al. [27] normalizations had close values with Models a, c, d and e. There were variations in the results among the other models, with the Tosta method allowing higher results for Models d, f and g, while the normalization of Vahadane yielding the highest results for Models b, c and h. However, it was noticed that these values were inferior or similar to the baseline results for Models a-g.

To assess the statistical significance of the segmentation and normalization methods, the repeated measures ANOVA test was performed over the obtained results. The comparison among the segmentation models resulted in a p-value of 0.058, meaning that there’s no significant difference in the results achieved by the models. Post hoc tests with the Least-Squares Means revealed statistical relevance for Model a compared with Models d, f, g and h, with p-values lower than 0.001; for Model c compared with Models d and h, with $\rho$-values lower than 0.023; and between Models g and h ($\rho$-value of 0.16). A test was performed to evaluate the statistical difference between semantic and instance segmentation approaches. At this stage, it was observed a statistical difference between the two approaches, with a $\rho$-value of 0.031.

The comparison of normalization methods resulted in a p-value of 0.015, indicating that there is a significant difference among the techniques. The post hoc tests resulted in p-values lower than 0.007 in comparison with Reinhard’s method, indicating that this technique’s results are significantly different from the baseline and the other methods.

Classification

The performance on the classification stage by ResNet50 and MobileNet V2 models is shown in Table 3. The first row of this table presents the results of the original ROI images without normalization (named baseline), and the remaining rows present the results obtained with the normalization models. The classification of non-segmented images resulted in higher values for the ResNet-50 model. The normalization by Macenko resulted in an increase in ResNet-50 values, with the highest $A_{\mathit{CC}}$ and F1 of 91.18 and 0.86, respectively. The normalization by Tosta resulted in $A_{\mathit{CC}}$ and F1 values of 86.76% and 0.84, a F1 value higher than the baseline. Other normalization methods resulted in values equal to or lower than the baseline for both classification models.

Table 3.

Results evaluation of CNN models for classification using different normalization methods

		Non-segmented				Semantic segmented				Instance segmented
		ResNet-50		MobileNet		ResNet-50		MobileNet		ResNet-50		MobileNet
Method	Reference	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1
No normalization	-	87.50	0.82	81.62	0.82	88.62	0.86	83.24	0.81	89.52	0.87	86.38	0.82
Macenko et al. [42]	Ref-1	86.76	0.81	74.26	0.76	86.94	0.81	75.92	0.77	87.33	0.81	79.29	0.77
	Ref-2	91.18	0.86	77.94	0.78	92.24	0.87	79.20	0.78	92.35	0.88	83.70	0.81
	Ref-3	90.44	0.84	76.21	0.77	91.08	0.86	79.05	0.78	91.88	0.86	83.21	0.82
Reinhard et al. [43]	Ref-1	74.26	0.76	75.74	0.76	81.22	0.81	76.62	0.71	85.20	0.81	81.22	0.80
	Ref-2	81.62	0.81	74.26	0.75	83.11	0.82	77.33	0.79	86.49	0.82	82.41	0.80
	Ref-3	80.15	0.79	75.00	0.74	83.42	0.82	77.42	0.79	84.63	0.82	82.72	0.81
Tosta et al. [28]	Ref-1	86.03	0.83	78.68	0.77	87.48	0.84	80.37	0.79	88.47	0.83	82.13	0.81
	Ref-2	86.76	0.84	86.03	0.81	88.20	0.86	87.47	0.84	87.96	0.83	88.43	0.84
	Ref-3	80.88	0.79	77.21	0.71	81.68	0.79	80.21	0.79	83.59	0.79	82.30	0.81
Vahadane et al. [27]	Ref-1	84.56	0.82	75.74	0.68	86.31	0.83	78.86	0.78	87.16	0.80	81.88	0.81
	Ref-2	86.03	0.81	84.56	0.81	86.89	0.84	85.89	0.84	88.06	0.81	88.31	0.85
	Ref-3	86.03	0.81	76.47	0.77	87.74	0.82	79.86	0.74	88.34	0.81	81.62	0.80

The semantic segmentation stage allowed an increase in the evaluation metrics for both classification models and normalization techniques. ResNet-50 showed F1 values ranging from 0.79 to 0.87, with the Macenko normalization allowing the highest value. MobileNet results ranged from 0.71 to 0.84, with the highest value being achieved with the normalization by Tosta.

The instance segmentation allowed further improvement on the classification results for both methods. The $A_{\mathit{CC}}$ values obtained with the ResNet-50 ranged from 83.59% to 92.35%, with the highest value obtained with the normalization technique by Macenko. The MobileNet model achieved results ranging from 79.29% to 88.43%, with the highest value obtained with the normalization by Tosta. The F1-score values indicate that the best result was obtained using ResNet-50 with the Macenko normalization.

Statistical tests were performed using repeated measures ANOVA to assess the significant difference between normalization methods and classification models. It was observed a significant difference between the two models, with a $\rho$-value of 0.001. The ANOVA also indicated a significant difference among the normalization methods, with a $\rho$-value of 0.029. Post hoc tests revealed the significant differences between the methods by Reinhard and the others ($\rho$-values lower than 0.039), just like between the normalization by Macenko and Tosta, with a $\rho$-value of 0.047. The test was also performed to compare the classification of the non-segmented and the segmented images, aiming to evaluate the impact of segmentation on the classification stage. This test revealed that these classification results are statistically different ($\rho$-value lower than 0.001), indicating that the segmentation allowed a significant improvement on the classification stage over the original images.

In these experiments, ResNet50 model was able to show superior performance compared to the MobileNet. The depth of ResNet50, with 50 convolutional layers, compared to the 22 layers of MobileNet, is one of the properties that directly influences the learning of more complex representations in images, a recognized issue in the specialized literature. In addition, ResNet50 considers filters of different sizes in the convolutional layers, including larger dimensions than those found in MobileNet. This fact allows the identification of global patterns in the images. For example, histological patterns contain microscopic details of cells, tissues and biological structures at different scales of observations, conditions that ResNet50 can detect. Therefore, these properties may explain the superior representation capacity of the ResNet50 against the MobileNet model in the states and images explored here, especially by identifying and quantifying more complex and subtle features commonly observed in H &E samples.

For the classification using strategy 2, the texture features were used as training data for the LOG, RF and SVM algorithms. The obtained results are shown in Tables 4 and 5. The SVM classifier achieved higher metric values than the other methods for segmented and non-segmented cases. The LOG and RF methods showed a noticeable value difference on the non-segmented images, but close values for the segmented cases. The semantic segmentation resulted in higher metric values than the non-segmented images and the instance segmentation allowed further improvement in the results. With this strategy, the normalization by Tosta combined with instance segmentation allowed the highest results, showing F1 values of 0.87, 0.90 and 0.92 for the LOG, RF and SVM classifiers, respectively.

Table 4.

Evaluation of handcrafted features combined with traditional classifiers and stain normalization on non-segmented images

		LOG		RF		SVM
Method	Reference	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1
No normalization	-	78.83	0.78	85.74	0.83	88.38	0.86
Macenko et al. [42]	Ref-1	75.44	0.74	83.28	0.82	86.84	0.86
	Ref-2	76.32	0.75	82.94	0.82	86.31	0.85
	Ref-3	77.23	0.76	83.77	0.83	87.08	0.84
Reinhard et al. [43]	Ref-1	77.44	0.76	84.12	0.83	87.29	0.83
	Ref-2	76.38	0.76	85.69	0.84	84.72	0.82
	Ref-3	77.03	0.78	85.50	0.83	83.31	0.82
Tosta et al. [28]	Ref-1	78.13	0.78	84.83	0.84	86.22	0.85
	Ref-2	77.84	0.78	85.17	0.85	86.37	0.85
	Ref-3	78.21	0.78	84.93	0.83	86.94	0.85
Vahadane et al. [27]	Ref-1	77.86	0.77	84.72	0.82	88.42	0.87
	Ref-2	79.38	0.79	85.43	0.83	87.63	0.86
	Ref-3	78.94	0.79	85.68	0.82	87.51	0.86

Table 5.

Result metrics obtained with handcrafted features combined with traditional classifiers on semantic and instance segmented images

		Semantic segmented						Instance segmented
		LOG		RF		SVM		LOG		RF		SVM
Method	Reference	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1
No normalization	-	79.10	0.81	84.66	0.83	86.77	0.84	84.18	0.82	87.39	0.84	89.38	0.87
Macenko et al. [42]	Ref-1	81.11	0.82	81.38	0.79	84.15	0.83	87.75	0.84	88.27	0.85	88.34	0.87
	Ref-2	83.50	0.82	86.30	0.84	87.76	0.85	86.72	0.84	86.09	0.84	89.27	0.88
	Ref-3	83.06	0.81	83.46	0.81	90.86	0.89	88.83	0.86	90.03	0.87	93.62	0.92
Reinhard et al. [43]	Ref-1	81.53	0.82	87.62	0.88	91.43	0.89	89.40	0.86	89.89	0.86	93.89	0.92
	Ref-2	83.82	0.84	83.91	0.81	84.28	0.83	85.61	0.83	86.18	0.83	88.21	0.86
	Ref-3	79.88	0.78	87.66	0.88	88.37	0.87	87.94	0.86	88.33	0.87	87.49	0.86
Tosta et al. [28]	Ref-1	83.75	0.83	85.11	0.84	90.36	0.89	89.32	0.86	90.44	0.88	93.94	0.92
	Ref-2	84.64	0.83	84.43	0.81	89.84	0.88	89.68	0.87	91.36	0.90	94.39	0.92
	Ref-3	83.16	0.82	85.09	0.83	86.73	0.85	85.88	0.82	88.07	0.85	88.44	0.86
Vahadane et al. [27]	Ref-1	81.99	0.81	86.95	0.84	85.39	0.82	86.14	0.82	86.38	0.85	87.83	0.84
	Ref-2	83.49	0.82	87.03	0.86	88.46	0.86	87.76	0.83	91.33	0.90	93.73	0.89
	Ref-3	83.26	0.82	87.14	0.86	90.63	0.89	88.23	0.83	91.67	0.90	94.08	0.92

A statistical evaluation was performed on the results presented in Tables 4 and 5. This assessment showed a significant difference among the classifiers, with a $\rho$-value of 0.03. The segmentation stage presented a significance compared to the non-segmented images, showing a $\rho$-value lower than 0.001. Similar to the behavior observed on the deep feature analysis, the post hoc tests indicated $\rho$-values lower than 0.05 for the LOG classifier compared to the others. It was observed a difference for the Reinhard normalization compared to the methods proposed by Tosta and Vahadane, with $\rho$-values lower than 0.05.

In addition, strategy 3 was performed using features extracted from the ResNet-50’s last convolution layer, since this CNN model achieved the highest results, as depicted in Table 3. These classification results using the LOG, RF and SVM methods are shown in Tables 6 and 7. For both segmented and non-segmented images, the RF yielded higher metric values compared to the other methods, followed by the SVM. The normalization by Macenko allowed higher values than the baseline for all algorithms, while the other methods resulted in results close to the baseline. As observed in Table 3, there was an improvement in the results when using the semantic segmentation and further improvement using the instance segmented images. The highest results were obtained on the instance segmented images using the Macenko normalization, with F1 values of 0.88, 0.92 and 0.89 for the LOG, RF, and SVM algorithms, respectively.

Table 6.

Evaluation of deep features combined with traditional algorithms from the literature and stain normalization on non-segmented images

		LOG		RF		SVM
Method	Reference	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1
No normalization	-	86.44	0.83	90.93	0.88	87.73	0.82
Macenko et al. [42]	Ref-1	86.62	0.83	91.17	0.88	89.84	0.86
	Ref-2	88.86	0.85	92.26	0.89	89.33	0.86
	Ref-3	88.94	0.85	91.23	0.88	90.42	0.88
Reinhard et al. [43]	Ref-1	80.33	0.78	83.22	0.81	82.12	0.79
	Ref-2	84.13	0.81	85.15	0.83	89.78	0.84
	Ref-3	83.28	0.81	85.83	0.84	85.34	0.81
Tosta et al. [28]	Ref-1	85.70	0.83	87.96	0.85	87.96	0.85
	Ref-2	88.53	0.85	89.34	0.86	88.73	0.85
	Ref-3	83.31	0.81	85.64	0.83	85.91	0.82
Vahadane et al. [27]	Ref-1	85.63	0.82	87.04	0.84	86.29	0.83
	Ref-2	86.07	0.84	86.92	0.84	88.12	0.85
	Ref-3	87.13	0.84	89.08	0.86	89.23	0.86

Table 7.

Result metrics obtained with deep features combined with traditional classifier algorithms on semantic and instance segmented images

		Semantic segmented						Instance segmented
		LOG		RF		SVM		LOG		RF		SVM
Method	Reference	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1	$A_{\mathit{CC}}(\%)$	F1
No normalization	-	86.51	0.84	91.22	0.88	88.62	0.86	87.32	0.84	91.74	0.89	89.17	0.87
Macenko et al. [42]	Ref-1	87.08	0.84	82.41	0.81	90.13	0.87	88.23	0.84	93.69	0.92	90.78	0.88
	Ref-2	89.05	0.86	92.74	0.89	89.73	0.87	89.84	0.85	94.22	0.92	91.26	0.89
	Ref-3	89.36	0.86	91.49	0.88	90.33	0.87	90.68	0.88	92.79	0.92	91.12	0.89
Reinhard et al. [43]	Ref-1	79.54	0.77	83.65	0.82	82.46	0.81	82.84	0.80	86.21	0.84	84.38	0.82
	Ref-2	83.39	0.81	85.44	0.83	85.04	0.83	85.39	0.83	87.64	0.84	87.41	0.84
	Ref-3	82.97	0.81	85.62	0.83	84.82	0.83	85.43	0.82	88.23	0.85	87.41	0.84
Tosta et al. [28]	Ref-1	86.12	0.83	88.23	0.86	88.31	0.86	87.39	0.84	90.17	0.88	89.42	0.85
	Ref-2	88.74	0.84	89.86	0.86	88.68	0.86	90.23	0.88	91.38	0.89	90.08	0.87
	Ref-3	82.96	0.81	85.27	0.82	85.44	0.84	86.77	0.84	87.96	0.83	86.93	0.84
Vahadane et al. [27]	Ref-1	85.96	0.84	87.28	0.83	86.74	0.84	86.44	0.84	89.33	0.86	88.44	0.83
	Ref-2	86.27	0.84	87.69	0.83	87.42	0.85	88.44	0.86	89.44	0.86	89.28	0.88
	Ref-3	86.83	0.85	89.36	0.86	88.74	0.86	88.31	0.86	90.65	0.88	89.86	0.88

Statistical evaluation with repeated measures ANOVA revealed a significant difference among the classification algorithms, with a $\rho$-value of 0.04. It also observed a relevant significance between the segmented and non-segmented images ($\rho$-value lower than 0.001) and among the normalization methods ($\rho$-value of 0.035). Post hoc tests indicated $\rho$-values lower than 0.05 for the LOG compared to the other algorithms and for the Reinhard normalization compared to the methods by Macenko and Vahadane.

These results show that the segmentation and stain normalization may impact the OED classification stage. Due to the lack of public datasets of OED images, this study brings a significant contribution to the scientific community.

Relevance of This Empirical Evaluation

The findings of this study reveal the influence of segmentation and color normalization on the OED classification stage. Given the lack of publicly available datasets for OED images, this research significantly contributes to the scientific community. This study presents a novel OED tissue section-containing image dataset derived from mice tongues, in which nuclei were meticulously labeled by a trained specialist and validated by a pathologist. Both the images and the gold standard are now accessible to the public and categorized based on the lesion’s grade.

Ethical and practical constraints often limit the availability of human tissues for research purposes. Therefore, mouse models are valuable for histologic studies [29]. By using a mouse dataset, this study contributes with relevant information on oral dysplasia and provides a tool that facilitates developing methods and experiments of digital histopathology on OED images, with potential applicability to human conditions [31].

The segmentation stage presented regions of FP and FN, primarily in areas with pigmentation granules and white tissue. At the classification stage, some combinations of stain normalization and classifiers exhibited low metric values. This variability in performance highlights the challenges of the image analysis process and the importance of robust algorithms capable of accommodating the diverse tissue characteristics.

While the methodology showed relevant results, its scalability might face constraints when extending its application to whole-slide images (WSIs). The dependence on selected ROIs may introduce biases that limit the generalizability of the methods. This indicates the importance of future researches aimed at enhancing the adaptability and scalability of the approach, ensuring its applicability in diverse image analysis scenarios.

This study offers relevant contributions, including an in-depth analysis of CNN methods for semantic and instance segmentation applied to histological OED tissue images. Moreover, the efficacy of CNN and traditional ML algorithms for the classification was investigated. Additionally, this research investigates the influence of stain normalization methods on the segmentation and classification stages. These contributions provide valuable insights for future research and clinical applications of OED cases.

Conclusion

This study introduced the first fully annotated public dataset with H &E OED images from mice tongues. These images were carefully graded and the nuclear structures were marked by a trained specialist and validated and corrected by a pathologist to generate the gold standard reference images. H &E normalization methods were employed to assess their influence on segmentation and classification tasks. The original ROIs, along with normalized and gold standard images, are publicly available in the repository. Furthermore, the dataset comprises fully marked and graded images that can be used for studying or enhancing segmentation and classification tasks. The provided ROI images, gold standard masks, and normalization and segmentation images can be used by the community for the development and study of CAD systems dedicated to OED diagnosis and grading.

Segmentation experiments revealed that the highest individual result was obtained with U-Net-ResNet-50. However, FPN-ResNet-50 and Mask R-CNN presented the best overall performance for semantic and instance segmentation, respectively. Additionally, it was observed that stain normalization degraded part of the segmentation results, suggesting that it may not be relevant for this task.

The experiments highlighted the significant role of semantic and instance segmentation methods in the classification task, leading to improved metric results. For this stage, the normalization methods showed variations in the results, with the method by Reinhard allowing values higher than those of non-normalized images. The investigation found that the H &E normalization employed was dependent on the reference image, and different combinations of normalization methods and CNN models may improve the results.

The segmentation stage presented regions of FP and FN, mainly areas with pigmentation granules and white tissue. The classification showed relevant metric results, but for some groups, these values were lower. It was observed that both stages presented variations in the result metrics. The dependence on selected ROIs for analysis may pose limitations for the methodology’s scalability, particularly when extending the application to WSIs.

In future studies, other CNN models will be employed for nuclei segmentation and OED grade classification. The stain normalization stage will explore stain augmentation, inspired by the study of Tellez et al. [100]. This will enable the investigation of the classification performance using this method and the potential enhancement of quantitative results. Additionally, methods for slide-level aggregation, such as multiple instance learning and patch-level fusion, will be explored to expand the dataset to include WSIs.

Author Contributions

Adriano Barbosa Silva: conceptualization, investigation, methodology, software, validation, formal analysis, data curation, writing, visualization. Alessandro Santana Martins: investigation, validation, writing, visualization, resources, funding acquisition. Thaína Aparecida Azevedo Tosta: methodology, software, validation, writing, resources, funding acquisition. Adriano Mota Loyola: data curation, validation, resources, writing. Sérgio Vitorino Cardoso: data curation, validation, resources, writing. Leandro Alves Neves: validation, writing, resources, funding acquisition. Paulo Rogério de Faria: conceptualization, investigation, resources, data curation, validation, writing, supervision. Marcelo Zanchetta do Nascimento: conceptualization, methodology, software, validation, formal analysis, investigation, resources, writing, supervision, project administration, funding acquisition.

Funding

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001. The authors received financial support from National Council for Scientific and Technological Development CNPq (Grants #313643/2021-0, #311404/2021-9 and #307318/2022-2), the State of Minas Gerais Research Foundation - FAPEMIG (Grant #APQ-00578-18 and Grant #APQ-01129-21) and São Paulo Research Foundation - FAPESP (Grant #2022/03020-1).

Data Availability

The data used in this study are openly available and can be used in other studies to evaluate the stages of OED analysis. The data can be acessed at: https://github.com/LIPAIGroup/OralEpitheliumDB.

Declarations

Ethics Approval

The experiments performed in this study were approved by the Ethics Committee on the Use of Animals under protocol numbers 038/09 and A016/21 at the Federal University of Uberlândia, Brazil.

Conflict of Interest

The authors declare no competing interests.