Spatial assessment of the reproducibility of Indian summer monsoon rainfall regimes in multiple gridded rainfall products

Abstract

The Indian summer monsoon (ISM) is a complex and multiscale interacting climate system, which is responsible for major contribution in India’s annual rainfall. Understanding the spatial and temporal variability of ISM rainfall is critical for managing water resources, which directly impact and regulate the functioning of India’s socio-economic conditions and subsequently, sustenance of over a billion people. This study evaluates the suitability of various gridded precipitation data products with different spatiotemporal resolutions, essential requirement for hydrologic modeling, disaster mitigation, irrigation allocation and agricultural application. Hence, we evaluate the performance of seven gridded datasets in generating time-matched characteristic event occurrences and their respective magnitudes using gauge-based Indian Meteorological Department (IMD) gridded data as reference. We observe that reanalysis datasets underperform compared to satellite and hybrid products in identifying both normal and extreme precipitation events. We develop a performance measure, called ‘rank score’ that considers deviations from IMD data in magnitude, statistical moments, and rain event detectability for a robust assessment and identifying best-suited dataset. Results indicate that APHRODITE, MSWEP, and CHIRPS (in descending order) are the most suitable data products across India. Additionally, region-specific evaluations provide valuable insights into the applicability of these datasets in different climatic and homogeneous rainfall zones.

Introduction

Precipitation is a crucial component of hydrological cycles that ultimately determines the cyclicity of water, energy, and carbon and the eventual state of the Earth system^1–3. The precipitation characteristics, such as frequency, intensity, duration, and inter-event beaks, regulate various physical processes (e.g., streamflow generation, soil moisture dynamics, functioning of an aquatic ecosystem) and socio-economic (e.g., agricultural, dam regulation) activities. With relevance to India, the summer monsoon months, i.e., June to September (JJAS) period, serve as the primal rainfall season and contribute 80% of the total annual rainfall^4,5.

The Indian landmass receives abundant insolation during summer monsoon months in response to the orbital configuration of the northern hemisphere, which causes the heating of the land^6,7. The thermal gradient between the land and ocean subsequently creates the pressure gradient towards the Indian landmass. This physical setting causes a huge influx of moisture evaporated from the oceans (primarily from the Arabian Sea and the Bay of Bengal) and move towards land from the southwest direction⁸. This incarnating moisture-laden seasonal wind flow is called the summer monsoon^9,10 and causes the Indian Summer Monsoon Rainfall (ISMR)¹¹.

The ISMR acts as the prime source of fresh water over the subcontinent, replenishing the dried soil layer, recharging the groundwater, accumulating Himalayan glacier systems, rejuvenating the river flow, and so on¹². The impacts of ISMR on physical processes eventually decide the fate of the rain-feed Indian agrarian system that ultimately regulates the proper functioning of the Indian society and economy^13–16. Hence, determining the characteristics and regimes of ISMR is fundamental cornerstone for understanding the climatic processes and variability, hydrometeorological forecasting, and assessing the imparted impacts on human lives, society, and economy^17–19. This motivates us to examine the effectiveness of the ISMR reported in the available gridded products over the Indian landmass. Here, we have selected the rainfall datasets available at 0.25° spatial resolution and daily temporal resolution or finer level, which is the desirable scale for most hydroclimatic investigations.

Gridded datasets provide precipitation estimates over continuous space, which is often a crucial requirement for using precipitation as inputs in different hydrological and climate models. Specifically, the low station density, instrumentation failure in rough weather, and difficulties in installing and maintaining over the complex terrain inhibit the applicability of the gauge-based rainfall products^20–23. Recently, Kidd et al.²⁴ have concluded that “The total area measured globally by all currently available rain gauges is surprisingly small, equivalent to less than half a football field or soccer pitch.” Therefore, the current study highlights the advantages and applicability of using the gridded datasets over a data-sparse region like India, acknowledging the respective dataset’s associated limitations.

The present study evaluates the performance of the gridded precipitation datasets in terms of their detectability and replicability of ISMR events (when daily rainfall intensity exceeds 2.5 mm^16,25) using India Meteorological Department (IMD) station-based 0.25° gridded data as the baseline²⁶. India’s large rain gauge network is utilized in developing IMD gridded data; however, the station density has varied over space and time²⁶. Past studies have indicated the effectiveness of IMD gridded data as the proxy for ground observation^27–30. However, IMD has high uncertainty over the Himalayan high mountain terrain due to the low station density. Additionally, IMD releases the whole year’s data developed based on the quality-checked observations at the end of the respective year. It hinders the real-time utilization of accurate IMD data.

Further, IMD gridded data suffers from the caveat of spatial interpolation error that relies on the density and orientation of the rain gauges^31,32. It implies that the accuracy of rain gauge-based gridded data is possibly affected over the low-density regions due to missing observations. Besides, IMD generates the gridded dataset at a somewhat coarser spatial resolution (i.e., 0.25°), even though high gauge density is observed particularly over Peninsular India²⁶. In this context, many satellite, reanalysis, and hybrid datasets are available at much finer spatial (~ 10 km) and temporal (hourly or 3-hourly) resolution and provide near real-time data^33–35. Thus, there is a dire need to assess proxies of or equally suitable to IMD data obtained from different sources (e.g., satellite, reanalysis) as the best alternative to IMD for implementing distributed hydrologic modeling and studying climate variability, and change.

We attempt to assess the performance of the seven data products through this study. In practice, a proper error correction is feasible for the examined datasets based on their known level of uncertainty and source errors. Additionally, we try to examine the quality of the data records based on the event chronology. Event chronology indicates the occurrence of an event, demarcated based on predefined thresholds, in an examined dataset at the vicinity of the actual timestamp of the event occurrence (inferred from reference dataset). It is essential to find the chronologically matched replicability of the characteristic rainfall events (at a correct timestep with accurate magnitude) in the data products, which could potentially help in implementing in early warning system.

Previous studies have also indicated that a dataset possibly has contrasting responses to different measures^36,37. By examining the results, we also note that some datasets, for example, APHRODITE, have better capability to detect rainfall events but fail to replicate the magnitude to a great extent. Additionally, past studies have found that satellite precipitation products underestimate wet events and overestimate drier events^38,39, and reanalysis data products generally tend to overestimate the rainfall magnitude^40–42. Therefore, we have proposed a new metric, namely rank score as the linear weighted combination of continuous and categorical performance measures, to comment on the overall suitability of a particular dataset.

In this study, we seek to answer two specific questions: (a) how well do the gridded rainfall datasets capture the chronologically matched different rainfall events having distinctive magnitudes, and (b) what is the overall and regional suitability (rank) of rainfall datasets for hydroclimatic applications during the summer monsoon period?

Data Products

Gridded rainfall datasets

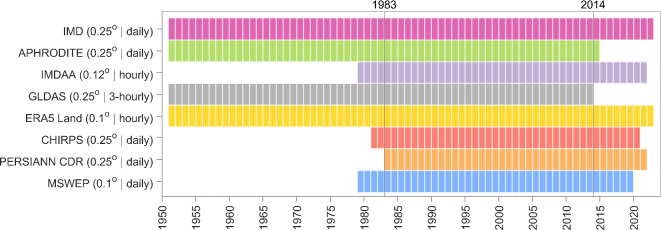
In the present study, eight gridded datasets are utilized. The data products are available at a spatial resolution of 0.25° or lower and at daily or finer temporal resolution. Primarily, the used datasets belong to four categories: (1) observational datasets (India Meteorological Department (IMD)²⁶, Asian Precipitation–Highly-Resolved Observational Data Integration Towards Evaluation of the Water Resources (APHRODITE)^43,44), (2) reanalysis datasets (Indian Monsoon Data Assimilation and Analysis reanalysis (IMDAA)^33,45,46, European ReAnalysis 5 (fifth generation)-Land (ERA5-Land)³⁵, Global Land Data Assimilation System (GLDAS)-Noah⁴⁷), (3) satellite datasets (Climate Hazards Group InfraRed Precipitation with Station (CHIRPS)⁴⁸, Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks—Climate Data Record (PERSIANN-CDR)⁴⁹) and (4) hybrid or merged dataset (Multi-Source Weighted-Ensemble Precipitation (MSWEP)^34,50). Among the considered datasets, IMD, IMDAA, and APHRODITE are regional datasets that cover the southeast Asia monsoon domain and the other five data products are global datasets. Figure 1 enumerates the specifications and details of the used datasets. All datasets are resampled to IMD 0.25° grid system using bilinear interpolation^51,52 and hourly data is aggregated at a daily timescale.

Fig. 1.

Summary of used gridded data products in this study. The length of the horizontal bars indicates the temporal extent of data availability. Spatial and temporal resolution are indicated in the braces. In this study, data is used between 1983 and 2014 (32 years) for consistent comparison across all datasets.

Homogenous hydroclimatic regions

To comment on the regional suitability and performance of precipitation datasets, ten hydroclimatic regions are considered here, belonging to (a) five Köppen-Geiger Climate zones (tropical monsoon (Am), tropical savannah (Aw), hot desert (BWh), hot steppe (BSh), and temperate with dry winter (Cwa))⁵³ and (b) five Homogenous rainfall regions (Northwest, Central Northeast, Northeast, West Central, and South Peninsular regions)^54,55 (Fig. S1). This study does not consider the hilly and polar tundra (ET) region, which primarily encompasses the mountainous terrain of the Himalayas due to the very low IMD rain gauge density⁵⁶. The sparse station density in the base dataset hinders the confident comparison of other datasets.

Methods

Interval-based performance measures

The performance of precipitation datasets is assessed to reproduce time-matched seven characteristic rainfall events using Interval-based Performance Measures (IBPMs). Base dataset (IMD) rainfall time series is binned into seven classes (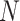) utilizing the IMD⁵⁷ prescribed thresholds 2.5, 7.5, 36, 65, 125, and 245 mm/day to demarcate the seven characteristic rainfall events. IBPM is computed for a bin if at least five data pairs are present to eliminate the bin classification dependency⁵⁸. IBPM utilizes two methods: (a) frequency-based performance measure (FBPM) and (b) composite performance measure (CPM) and its five variants⁵⁸.

FBPM is defined (in Eq. 1) as the weighted 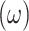sum of the frequency of ratios of the total number of data points in the base dataset 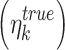to time index matched 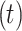rainfall observed rainfall in q^th dataset 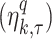, in each bin or class interval 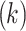⁵⁸. Chronological or time index matching denotes the collocated observation between the base and q^th datasets within each bin. Here, equal weight (1/7) is assigned to the bins conditioning 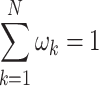. CPM is a variant of FBPM which incorporates the penalizing indices 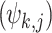and is defined in Eq. (2). Five 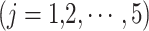penalising indices are used: variance index (VI), interquartile range index (IQRI), correlation index (CI), (d) bounded relative absolute error index (BRAEI) and Kolmogorov–Smirnov index (KSI), which are defined in Eqs. (S1.1)–(S1.5). Indices are normalized (between 0 and 1) by introducing the transformation function 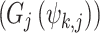to make the indices readily compare. For details on the five CPM indices refer supplementary text S1.

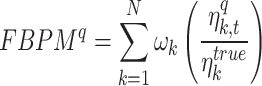1

2

where and represent the total number of rainfall data points observed in the base and dataset within bin; 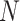is the total number of bins; 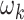denotes the weight assigned in k^th bin, 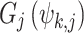is the transformation function in the k^th bin for 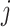CPM index.

Rank score and ranking of datasets

To find the optimal performing dataset, the rank score of each dataset is devised based on the six continuous metrics, two categorical metrics, and the absolute difference of mean and standard deviation, evaluated with respect to IMD. Six continuous performance measures considered are: systematic root mean square (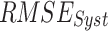), random RMSE (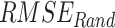) (obtained by decomposing the total RMSE⁵⁹), normalized RMSE (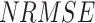), percentage bias (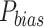), degree of agreement (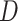) and Kendal’s correlation coefficient (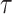). Critical success index (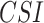) and false alarm ratio (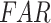) are the two categorical measures that are considered to characterize the rainfall detection capability of the examined datasets.

Data pairs with rainy (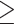 2.5 mm/day^16,25) days are used in the computation of continuous metrics instead of utilizing the entire daily monsoonal time series (of length 122 (number of summer monsoon days in a year) times 32 (temporal extend chosen) years) of each grid. 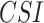, 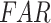and first two moment difference computation considers total time series. Continuous metrics are penalized with their respective rainfall detectability to isolate the performance of the examined datasets only during the true rainfall events. Additionally, this approach enables to reduce the sensitivity of metrics towards the abundant low (or zero) values^58,60.

The rank score is defined as the weighted mean of the absolute normalized metric values (Eq. (3)). The Eq. (3) is comprised of ten variables, whereby each represents one performance metric (defined in Eqs. (S1.6) to (S1.13) of supplementary text S2), and coefficients are the weights assigned by the user. To compare the multiple error metrics, absolute values or magnitudes of each metric are taken, given that the metric takes a negative value⁶¹. For this purpose, absolute values of 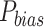, , 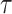mean and standard deviation difference are considered. Additionally, all used measures are normalized with corresponding maximum (absolute) value observed across datasets^62,63. Considering a grid, for instance, seven percentage bias values corresponding to each dataset are observed. Then, the absolute values of seven biases are normalized with the maximum of the seven absolute biases.

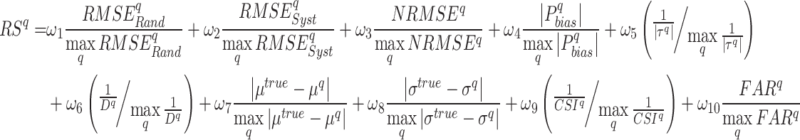3

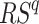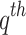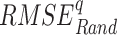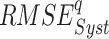
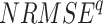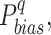
where represents the rank score of dataset. Similarly, , , , , 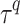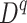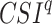and 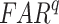are random RMSE, systematic RMSE, normalized RMSE, percentage bias, correlation coefficient, degree of agreement, critical success index, and false alarm ratio of qth dataset, respectively. 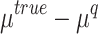and 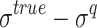are the mean and standard deviation differences of the 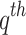dataset with respect to the base dataset (IMD; designated as ‘truth’), respectively. 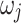is weight 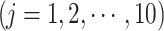, i.e., 0.1 to ensure .

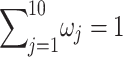In the present study, the ranking of examined datasets is performed based on their departure from reference data and ability to preserve the statistical moments of reference data and rainfall detectability as in reference data, indicating significant improvement in suitability assessment compared to the past studies^64,65. The rank score is devised so that the lowest score corresponding to a dataset represents the optimal values of ten variables. Consequently, the respective data product is considered most suitable (i.e., rank one is assigned). The range and optimal value of the rank score are 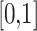and 0, respectively. The lower magnitude of all the metrics used to compute the rank score representing the better suitability, except 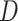, 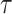and 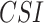. Thus, the inverse is used to align the direction of these three measures.

Bootstrap sampling procedure

A grid-wise bootstrap sampling is performed to quantify the sensitivity of the devised rank score. Corresponding to each grid point, 1000 samples are drawn randomly, in which sample length is 70% (2733 observations) of the total data available for each grid spanning over a summer monsoon period (122 days of June to September) of 32 years 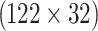. First, sampling on a series of integer values with length 3904 is done to draw the indices of random samples in each grid. Drawn index values are considered to sample rainfall values from IMD and seven examined datasets. Following this procedure, 1000 such bootstrap samples are picked for each grid point with replacement.

Each bootstrap sample rainfall is utilized to compute the rank score (based on the procedure elucidated in section "Rank score and ranking of datasets"), which has resulted in the 1000 rank score values for each grid. The 95^th percentile of the 1000 rank scores (now considered as the equivalent to population) are computed to define the 95% confidence limit of rank score corresponding to a grid cell ^66,67. The rank score obtained utilizing the entire time series of 32 years is indicated to be consistent if found to be within a 95% confidence interval (if not, then indicated by stripling) ^66,67. This procedure is repeated for all the observed grid points in the study area. To indicate the stripling in the ranks of each grid, the first seven rank score values corresponding to the seven datasets are sorted in ascending order to define ranks one to seven, respectively, and then ranks corresponding to the not-accepted rank scores are stripped.

Equality of proportions test

The fraction or proportion of grids corresponding to Rank 1, 2, and 3 (within a hydroclimatic unit) is calculated as the ratio of the total number of grid points (within a hydroclimatic unit) corresponding to ranks 1, 2, and 3 observed in all seven evaluating datasets to the total number of grid points within the entire region. The highest proportion (concerned with a rank and a region) observed in the dataset is assigned as the best product corresponding to the specified rank and region. That particular proportion is considered as the true ratio (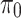). Other six ratios obtained with respect to the six other datasets 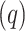of the same rank and region are considered as the 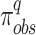. Each 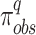are evaluated with respect to 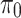to check the statistical similarity. For this purpose, another dataset is equally suitable if corresponding 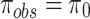(null hypothesis), alternatively not equally likely i.e., 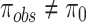. 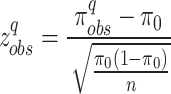is the test-statistic to evaluate the aforementioned statistical hypothesis⁶⁸. 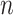is total number grid points observed. We find enough evidence to reject the null hypothesis p-value 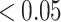in a 95% confidence interval.

Results and Analysis

Performance of data products in rainfall event characterization

The present study categorizes ISMR time series into seven intervals or bins based on their characteristic rainfall regimes (section "Interval-based performance measures"). Identified seven classes (listed in order of increasing rainfall intensity) are: (1) no-rain or drizzle (< 2.5 mm/day), (2) light rain (2.5–7.5 mm/day), (3) moderate rain (7.5–36 mm/day), (4) rather heavy rain (36–65 mm/day), (5) heavy rain (65–125 mm/day), (6) very heavy rain (125–245 mm/day), (7) exceptionally heavy rain (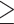 245 mm/day)^16,25,57. The spatial distribution of the seven-rainfall event’s frequency during JJAS is shown in Fig. S2.

Detectability of these rainfall events occurred in examined datasets in the vicinity of the time stamp observed in IMD is assessed by deploying the IBPMs⁵⁸. This analysis is performed at each grid level, and the spatial variation of each IBPM corresponding to rainfall events is presented in Figs. S3–S9. No rain, little rain, and moderate rain events are the highest frequency events observed over the thirty-two years of temporal extent (Fig. S2). No-rain condition is found to be the dominant (65% areas) event over the space, which is found to occur at the highest frequency (> 70% events) in the arid and semi-arid regions of northwestern and peninsular India. It depicts a non-rainy inflated distribution.

Rather heavy and heavy rain events are observed for < 5% frequency and mostly confined along the west coast and northeast, the two heaviest rainfall-receiving regions of India. Very heavy rain and exceptionally heavy rain events are even rarer and found to occur in these two regions as well. Distinctively, it is observed that exceptionally high rain (> 245 mm/day) is not even captured in other datasets, and poor performance in identifying the very heavy rainfall (125–245 mm/day) (Figs. S8 and S9).

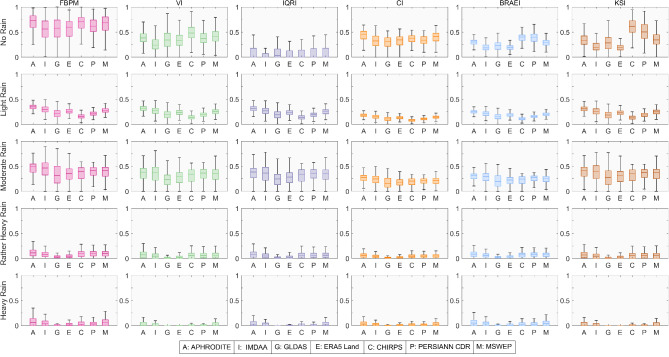
The spatial variability of the six IBPMs (FBPM and five variants of CPM) concerning the seven datasets for the first five rainfall events are summarized in Fig. 2. From Fig. 2 and the maps of IBPMs, it is visually identifiable that the performance of the datasets drops for the higher rainfall intensity classes (which restricted to enlist first five classes in Fig. 2). Across the datasets, (a) observation, satellite, and hybrid datasets and (b) reanalysis datasets form two data products’ clusters, in which datasets of each cluster depict distinctive and similar degree of performance. The varying performance of a particular dataset across six IBPMs is also noticed.

Fig. 2.

Spatial variability of six interval-based performance measures (IBPMs) (columns from left to right: frequency-based performance measure (FBPM), variance index (VI), interquartile range index (IQRI), correlation index (CI), bounded relative absolute error index (BRAEI) and Kolmogorov–Smirnov index (KSI)) implemented to detect five rainfall events (rows from top to bottom: no-rain or drizzle (< 2.5 mm/day), light rain (2.5–7.5 mm/day), moderate rain (7.5–36 mm/day), rather heavy rain (36–65 mm/day), heavy rain (65-125mm/day)).

Seven examined datasets have shown the best performance in detecting the no-rain or drizzle event (< 2.5 mm/day) (first row in Fig. 2). Specifically, over the semi-arid regions, all seven datasets have shown high (> 0.7) frequency-based performance measure (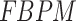), while over the windward side of the Western Ghats and northeastern India, a poor performance (< 0.4) is noted (Fig. S3). A similar explanation also holds for the variability index (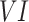), correlation index (CI), bounded relative absolute error index (BRAEI), and Kolmogorov–Smirnov index (KSI). Over space, seven datasets have produced the spatial median of FBPM between 0.5 and 0.7 for no-rain class (Fig. 2). Specifically, APHRODITE, CHIRPS, PERSIANN-CDR, and MSWEP perform far better in the IBPMs than reanalysis datasets. Later three datasets have higher KSI values compared to other datasets, which implies the higher distributional similarity of no-rain condition with respect to IMD compared to the other four examined datasets. It is also evidently observed in VI and BRAEI. ERA5-Land and GLDAS perform distinctively better than IMDAA, which is primarily attributed to the wet bias of IMDAA.

APHRODITE, IMDAA, MSWEP, and ERA-Land better detect light rain events (2.5–7.5 mm/day) than the other three datasets (Fig. S4). Additionally, these four datasets have consistently produced higher spatial median and low variability across six considered IBPMs compared to other datasets (Fig. 2). However, it is noticed that seven datasets have a better ability to quantify the moderate intensity (7.5–36 mm/day) rainfall events, particularly over the central India, northeast and along the west coastal plain, which are important geographical location concerning the ISMR characteristics. APHRODITE and IMDAA perform better than other datasets in detecting moderate-intensity events, and the other five datasets show a similar degree of performance in all six IBPMs.

Values of IBPMs have considerably decreased (< 0.2) in capturing the rather heavy rain and heavy rain in all seven datasets. Specifically, GLDAS, followed by ERA5-Land, has the lowest performance, and APHRODITE has shown the best performance for these two rainfall events across all IBPMs. Compared to the seven gridded datasets, APHRODITE and MSWEP have the best performance in capturing rain events with intensity > 40 mm/day, reflected across the IBPMs (Figs. S6–S7). However, seven datasets fail to perform satisfactorily (< 0.15) for the rainfall events with > 60 mm/day threshold (Fig. 2).

Performance of data products in event detection and magnitude reproduction

In this section, to assess the ability of the examined data products to detect the individual rainfall events (delineated based on the event magnitude exceeding 2.5 mm/day) and associated event magnitudes, we deploy two categorical metrics (Critical Success Index (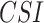), False Alarm Ratio (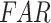)) and six continuous metrics (random root mean square error (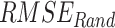), systematic RMSE (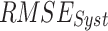), normalized RMSE (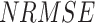), percentage bias (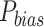), degree of agreement (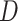), and Kendall’s correlation coefficient (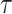)), respectively (Fig. S10). It is noted in the previous section that all data products perform well in capturing the no-rain or drizzle events, and the ability to capture rain events decreases with the increasing rain event intensity (although the very high intensity is a rarity). Hence, we examine the departure and agreement of event magnitude during the rainy days, which allows us to penalize the additional performance of the datasets arising from non-rainy day observations.

APHRODITE, IMDAA, MSWEP, and ERA5-Land demonstrate the high true (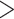 0.6 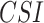) and low false ( 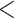0.2 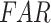) rainfall event detection ability, respectively, along the west coast, northeastern India, and monsoon core zone, which are important regions for understanding ISMR characteristics. PERSIANN-CDR and CHIRPS have shown poor performance in detecting the events (0.35 <  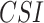< 0.45) over these regions. Except APHRODITE and MSWEP, other datasets (specifically the reanalysis data products) have shown significantly high false rainfall event detection (> 0.6 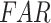) over the semi-arid and sub-humid regions.

The highest agreement with IMD data is observed in MSWEP (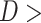 0.45 and 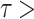0.25), followed by APHRODITE ( 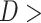0.55 and 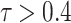), especially over the high rain-bearing side of the Western Ghats and northeastern India. The lowest agreement (0.3 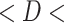0.4 and 0.05 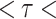0.15) is observed in GLDAS and ERA5-Land. IMDAA, CHIRPS, and PERSIANN-CDR have a similar degree of agreement, while these datasets show low agreement over the drier regions.

The reanalysis datasets (i.e., IMDAA, GLDAS, and ERA5-Land) have consistently high systematic departure (> 15 mm/day) over central India, and a similar order of high departure is observed along the west coast and Himalayan foothill regions in the satellite datasets (CHIRPS and PERSIANN-CDR). APHRODITE produces a relatively low degree of 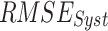in comparison to the six other datasets (Fig. S10). However, high 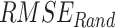(> 28 mm/day) is observed in the windward side of the Western Ghats, over central India, and the foothills of the Himalayas across all seven datasets. On the leeward side of the Western Ghats, both 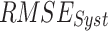(5–9 mm/day) and 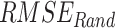(< 16 mm/day) is low. Over the entire India (except the northwestern Himalayan terrain, where IMD has high uncertainty due to low gauging density^30,69,70), APHRODITE shows low 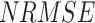(0.9–1.1), whereas the other six datasets show almost double .

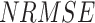Although having good performance in terms of 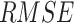, APHRODITE depicts strong negative bias (< 40 mm/day over the arid and semi-arid regions and 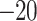to 30 mm/day in other areas) and relatively drier conditions than observed over the entire Indian sub-continent, which is also noted in past studies^26,71. The satellite and hybrid datasets show low negative bias (0 to − 20 mm/day) over the monsoon core zone. Positive bias (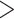 15 mm/day) is noted in the northeastern section of the country in all datasets, whereas IMDAA produces consistent overestimation (wetter state than usual) over the entire Himalayan foothill tracts. High differences in mean and uncertainty of different datasets are predominantly observed over the high-intensity rainfall regions.

Rank score and ranking data products

Results elucidated in the last section have indicated the varied responses of a single dataset in different performance measures. APHRODITE, for instance, has demonstrated the highest bias among seven examined datasets; on the other hand, it is the only dataset that has reported the highest 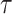, 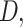and 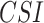. It indicates that APHRODITE outperforms other datasets in rightly detecting rainfall events (primarily attributed to gauge-based development); however, it underestimates the event magnitude. Further, GLDAS and ERA5-Land have reported less departure in reproducing rainfall magnitude but indicate a low degree of agreement compared to other examined datasets.

We summarize and generalize the performance of datasets observed across the metrics into an aggregate index or measure. We hypothesize that a dataset producing the lowest departure, highest agreement, and better detectability has to be considered as the most suitable among the examined data. Based on this rationale, an aggregate function is developed (see methods) as a linear combination of the considered metrics (inverse of metrics if high value is optimal). It is designated as the rank score. The lowest rank score of a dataset, consequently, indicates better suitability of the dataset among the examined datasets.

The spatial distribution of rank score is shown in Fig. 3. Lowest rank score is observed in APHRODITE, MSWEP, and CHIRPS (in descending order) among the seven datasets. Both APHRODITE and MSWEP have shown low-rank scores over the Western Ghats regions and most parts of the northeast, which indicates the reliability of these two datasets in analyzing the heavy rainfall events over these two regions. IMDAA and ERA5-Land have also produced a low-rank score over the Western Ghats region.

Fig. 3.

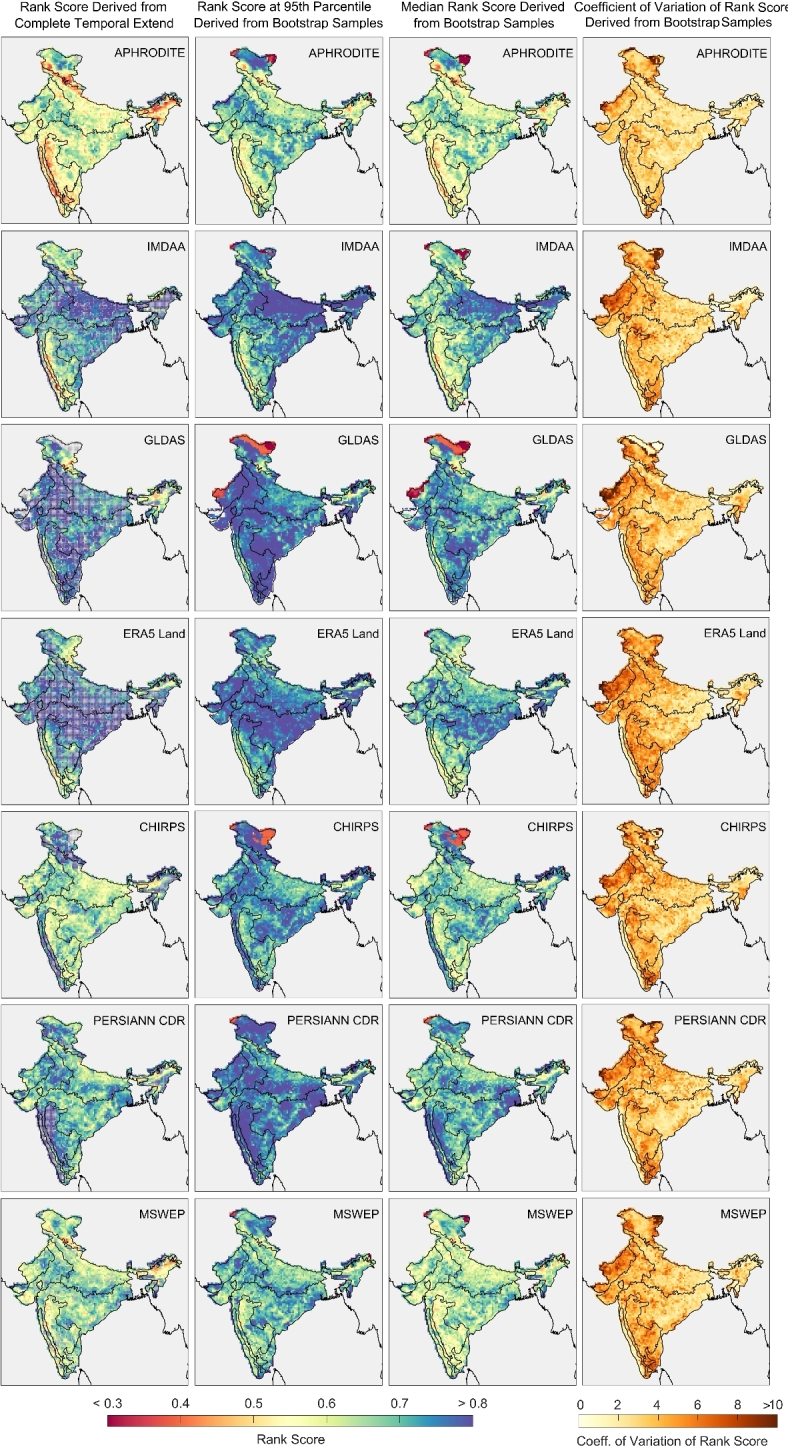
Spatial distribution of rank score derived from the data corresponding to complete temporal extent (32 years) (first column), 95th percentile (second column), median (third column), and coefficient of variation (fourth column) rank scores derived from 1000 bootstrap samples. The grid locations (first column) are stripped where the rank score (first column) calculated from the entire temporal extent is insignificant within a 95% confidence interval (second column).

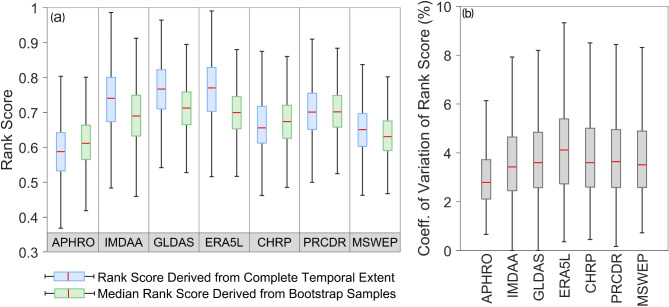
To examine the amount of variability that could arise due to the changing temporal extent of the dataset (reproducibility) and the sensitivity of the rank score of the rank scores in datasets, we performed 1000 bootstrap sampling (constitute the theoretical population) with replacement (see methods). It is noted that CHIRPS and PERSIANN-CDR produce high-rank scores, which are not statistically significant (in a 95% confidence interval). Consistent with the performance of reanalysis datasets highlighted in the previous sections, these datasets have produced considerably high rank scores, which is majorly not significant. Additionally, rank scores of 40–50% pixels in reanalysis datasets are significant, while rank scores of more than 80% pixels in observational, hybrid, and satellite datasets are found to be significant (Fig. S11).

The median rank scores derived from the bootstrap samples (third column of Fig. 3) produce a spatially coherent distribution with respect to the rank score derived for the temporal extent of 32 years (first column in Fig. 3). This indicates the robustness of the rank score. APHRODITE, MSWEP, CHIRPS, and PERSIANN-CDR have produced higher rank scores (typically > 0.6) over central (Gangetic basin) and peninsular India. Additionally, APHRODITE, MSWEP, and CHIRPS have produced the lowest spatial rank score median and indicate the highest order of suitability (Fig. 4a). In the seven considered datasets, the variability is found to be high (8%) over the arid western region and semi-arid southern peninsular region (fourth column in Fig. 3). Moreover, the low variance is observed in the central and east Indian region and along the west coast. The lowest and highest spatial variability are produced by APHRODITE and ERA5-Land, respectively (Fig. 4b). However, the spatial range of rank score variability, by and large, is of similar order in all seven datasets.

Fig. 4.

Comparison of rank score produced using the rainfall time series of entire temporal extent (32 years; indicated in blue) and median rank score derived from bootstrap samples (indicated in green) (a), and coefficient of variation of rank scores (b). Wilcoxon rank sum test confirms that six datasets except PERSIANN-CDR show different median rank score. Additionally, the Kruskal–Wallis test results show that the distribution of the coefficient of variation of rank score is significantly different in all seven datasets. Both tests are evaluated in 95% confidence interval.

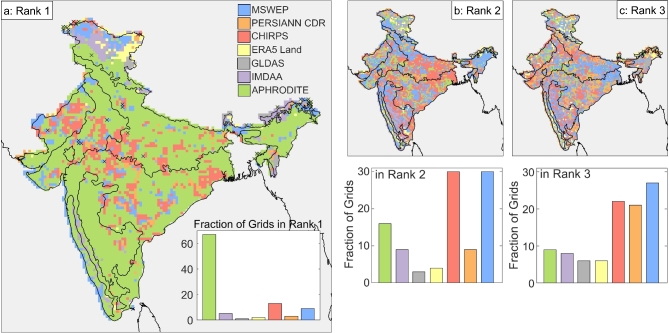
The seven examined datasets are ranked based on the corresponding dataset’s rank score, and the spatial distribution of ranks is presented in Fig. 5 (rank 1–3) and Fig. S12 (rank 4–7). The APHRODITE data is ranked foremost (i.e., one) due to its consistently lower rank score over a majority of regions (~70% of total grids) compared to other datasets (Fig. 5a). However, CHIRPS is found to be the most suitable dataset over central India (encompassing ~15% of total grids). CHIRPS (MSWEP) is the second-best dataset over the eastern (central, western, northern plain) region (Fig. 5b). These two datasets share 60% of the total number of grids, and APHRODITE occupies 15% in rank 2. CHIRPS, and MSWEP, along with APHRODITE (prevalently over the entire India) together share 75% pixels. Over the Gangetic basin, MSWEP has become the ranked three datasets (Fig. 5c) and share ~28% grids over India. PERSIANN-CDR and CHIRPS are the next best set of third-choice datasets in the mix over central and peninsular India (encompasses ~40% areas over India). MSWEP, PERSIANN-CDR, and CHIRPS appear to be the third best choice for ~ 70% of the total pixels. PERSIANN-CDR shows the desired rank four dataset over a majority of the pixels (Fig. S12a). The distribution of datasets from rank five to seven is not significant as the corresponding rank score in the dataset is not accepted (Fig. S12b–d).

Fig. 5.

Spatial distribution of the datasets obtained the rank 1 (a), 2 (b), and 3 (c). The stripped grids indicate the not-significant rank score and subsequently derived rank. The bottom insets indicate the percentage of grids corresponding to a particular rank in seven datasets (ratio of number of grids for a rank in a dataset to the total number of grids).

Regional suitability of rainfall data products

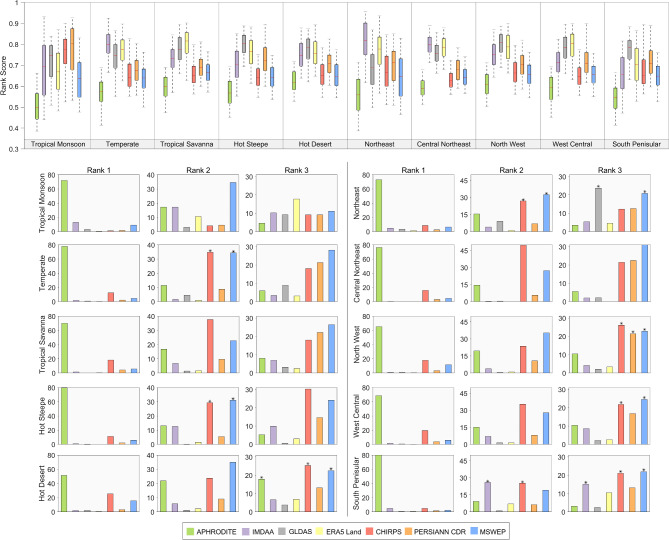
In the previous section, it is noted that rank (degree of suitability) of the datasets are spatially clustered. Hence, the regional suitability of the datasets is generalized using five Koppen-Gieger climatic zones and five homogenous rainfall regions. Figure 6 summarizes the ten considered region-specific variability of rank score (first row), and subsequently first three ranks.

Fig. 6.

Variability of rank score of seven datasets over the homogenous hydroclimatic regions (first row). Percentage fraction of grids in rank one, two, and three in seven datasets are shown in subsequent rows. The star above the bars indicates a statistically significant (in 95% confidence interval) equal proportion of grid points in the respective datasets.

Over the high rainfall receiving tropical monsoon region (Am), APHRODITE and MSWEP have the lowest spatial median of rank score and subsequently turned out to be the most suitable dataset over this region. Additionally, APHRODITE is found to be the best dataset (rank one) over ten regions, and no other dataset shares statistically significant (equality of proportion test; see method) equivalent suitability, which is consistent with the rank score distribution. Mostly, APHRODITE shares at least 60% (often 80%) rank one grid to the total number of grids observed within a region. APHRODITE, MSWEP, and CHIPRS constitute the set of the best suitable datasets concerned to the lowest spatial median and variability (indicated by interquartile range or box height) of the rank score and consequently, these three datasets have highest proportion of grid point share in the first three ranks. MSWEP, CHIRPS, and PERSIANN CDR (in descending order) indicate the higher grid share proportions, mostly in ranks two and three.

IMDAA, GLDAS, and ERA5-Land consistently show high rank scores in the ten regions. However, IMDAA has performed considerably better over Peninsular India than the other two reanalysis datasets. The suitability of reanalysis datasets is low over tropical monsoon regions because of the high spatial median and variability of rank scores. Interestingly, it is noticed that ERA5-Land has a considerably lower median and variation of rank score compared to the two other reanalysis datasets and shares a similar degree of suitability with MSWEP. This indicates that ERA5-Land could be a potential data product for studying rainfall variability over a longer temporal extent in the tropical monsoon region. Additionally, it is found that IMDAA shares an equivalent number of grid points as in MSWEP and CHIRPS over the peninsular India.

Markedly, GLDAS produces a similar degree of performance (also shares a statistically significant equal number of grids) as in the MSWEP and CHIRPS in the northeast homogenous rainfall region. GLADAS and MSWEP are equally suitable (significant) rank three datasets in the northeastern homogenous region. MSWEP and CHIRPS generally share almost equal amounts of grid fractions in ranks two and three, except in tropical monsoon regions where MSWEP highly dominates in rank two, and mixed response is noted for rank three.

A high-rank score is observed in the reanalysis datasets over hot desert, hot steppe, northwest, and west central regions. Particularly, over the tropical savannah, hot steppe, temperate, west-central, south peninsular, north-central, northwest, and hot desert regions, PERSIANN-CDR appears consistently the third highest grid point sharing dataset both in rank two and three distribution.

Discussion

This study evaluated the overall suitability of seven rainfall datasets in detecting the rainfall event occurrence and associated event magnitude and in the reproduction ability of chronologically matched specific events. Reasonably good performance is observed in seven datasets in detecting the no-rain or drizzle events (< 2.5 mm/day). The datasets report a decrease in their performance with the increasing event magnitude, especially for the very intense extreme rainfall events that are infrequent and primarily confined in the western slope faces of the Western Ghats and Meghalaya Plateau region.

APHRODITE and MSWEP better detect time-matched rainfall events and their corresponding magnitude as in IMD. Additionally, satellite datasets are observed to reproduce rainfall events better than reanalysis-based datasets. Specifically, APHRODITE, MSWEP, and CHIRPS are the best datasets that generate the highest rainfall agreement with the IMD data during the true rainfall events (i.e., during the rainfall intensity 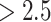mm/day). However, APHRODITE produces a strong negative bias (underestimation, also indicated by past study⁷²), and reanalysis-based datasets yield a strong positive bias. MSWEP shows the lowest degree of departure or rainfall magnitude mismatch, which also agrees with previous findings³⁷.

Although APHRODITE suffers from a strong negative bias, it has been found to outperform its counterpart datasets in other performance metrics. APHRODITE, consequently, produces the lowest rank score and is found to be the most suitable dataset. The proposed rank score metric shows total performance and allows one to holistically comment on the overall suitability and to readily compare a data product with the other datasets. Additionally, previous studies indicated that the better performance of the APHRODITE makes it reliable for forcing data in large-scale hydrological and climatic models⁷³. The long-term data availability allows using the APHRODITE as the potential data source to conduct the long-term hydrometeorological trend analysis (e.g., assessment of the changing nature of droughts and extreme precipitation under the changing climate).

MSWEP and CHRIPS are found to be the second and third most suitable data products. Nonetheless, pronounced spatial variability of rank scores is seen in ranks two and three. Particularly, APHRODITE, MSWEP, and CHRIPS have better performance over the Western Ghats, Meghalaya Plateau, foothills of Himalaya, and monsoon core (central Indian) region, which are particularly important regions in characterizing the ISMR. Higher suitability and fine spatial resolution of MSWEP would allow to investigate the sub-grid scale processes. It is also noted that PERSIANN CDR and IMDAA have reasonably performance, which leverages the potential applicability of these fine spatiotemporal resolution datasets.

Furthermore, the latest modification on the PERSIANN-CDR has yielded reliable finer spatial (~ 4 km) and temporal (3-hourly) resolution data. This could open the avenue for implementing fine spatial–temporal real-time satellite retrieved rainfall data and providing associated services to society, e.g., urban flood management. This study has additionally offered the regional (over five Koppen-Gieger and five homogenous rainfall zones) suitability assessment of the datasets for regional hydroclimatic studies. Consistent with the spatial variability of data products’ suitability, we find that satellite and hybrid datasets outperform the reanalysis datasets over ten regions. Hence, APHRODITE, MSWEP, CHIRPS, and PERSIAAN CDR constitute the best data product set over these homogenous hydroclimatic regions.

It is noted that rainfall data products demonstrate the spatial variability of performance measure and their consequent suitability. Hence, while selecting a rainfall data product for hydroclimatic analysis (e.g., rainfall-runoff modelling, watershed management, extreme event monitoring), it is imperative to account for research application, the trade-offs between performance measures pertinent to the study, the dataset’s optimized performance for the geographic region of interest, the requisite spatial and temporal resolution, and the extent of available data. The discerned results from this study can be used in future studies to appropriately choose the application and site-specific dataset, which is required for data-scarce regions like India. Additionally, it portrays the relative importance of the presence of various data sources and their uses, along with the informed limitations offered by this study. The findings of this study have also demonstrated the potential applicability of various data products at the regional level if biases and systematic errors are addressed or rectified prior to application in any particular analysis.

A multitude of evidence on the performance of the rainfall data products is shown in the present study, which is primarily derived from the IMD gridded data. However, in future research, the evaluation of the IMD rainfall gridded datasets independently with respect to quality-controlled gauge observed rainfall records and consequently reporting its variation of suitability over space would enhance the applicability of the discerned results from this study. The scarcity of reliable gauge observation inhabits such analysis in the present study.

Author contributions

S.P., P.J.S., R.S.V.T.: Conceptualization; S.P., P.J.S.: Methodology; S.P.: Data curation, Formal analysis, Validation, Visualization; S.P., P.J.S.: Investigation; P.J.S., R.S.V.T.: Supervision; S.P.: Writing—original draft; S.P., P.J.S., R.S.V.T.: Writing—review & editing.

Data availability

The data analyzed in this study are sourced from various open-source and publicly available domains. The IMD gridded rainfall data can be accessed from the following link: < https://www.imdpune.gov.in/cmpg/Griddata/Rainfall_25_NetCDF.html > . APHRODITE data is accessible to registered users (free registration) at < http://aphrodite.st.hirosaki-u.ac.jp/download/ > . IMDAA and ERA5-Land reanalysis data can be obtained using the CDS at < https://rds.ncmrwf.gov.in/dashboard/download > and < https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land?tab = form > , respectively. GLDAS-Noah precipitation data is accessible from < https://giovanni.gsfc.nasa.gov/giovanni/ > over the required spatial domain. CHIRPS data can be readily downloaded from < https://data.chc.ucsb.edu/products/CHIRPS-2.0/global_daily/netcdf/p25/ > . PERSIANN-CDR data is available for download at < https://chrsdata.eng.uci.edu/ > over the desired domain. MSWEP data can be obtained at < https://www.gloh2o.org/mswep/ > upon free registration. All datasets are available in netCDF format.

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-75320-5.