Large-scale-integration and collective oscillations of 2D artificial cells

Abstract

The on-chip large-scale-integration of genetically programmed artificial cells capable of exhibiting collective expression patterns is important for fundamental research and biotechnology. Here, we report a 3D biochip with a 2D layout of 1024 DNA compartments as artificial cells on a 5 × 5 mm² area. Homeostatic cell-free protein synthesis reactions driven by genetic circuits occur inside the compartments. We create a reaction-diffusion system with a 30 × 30 square lattice of artificial cells interconnected by thin capillaries for diffusion of products. We program the connected lattice with a synthetic genetic oscillator and observe collective oscillations. The microscopic dimensions of the unit cell and capillaries set the effective diffusion and coupling strength in the lattice, which in turn affects the macroscopic synchronization dynamics. Strongly coupled oscillators exhibit fast and continuous 2D fronts emanating from the boundaries, which generate smooth and large-scale correlated spatial variations of the oscillator phases. This opens a class of 2D genetically programmed nonequilibrium synthetic multicellular systems, where chemical energy dissipated in protein synthesis leads to large-scale spatiotemporal patterns.

Large-scale-integration of artificial cells on a chip can reveal emergent multicellular phenomena. Here, authors report 2D coupled lattices of artificial cells programmed by genetic oscillators, exhibiting synchrony and front propagation with microscopic dimensions affecting collective behaviour.

Introduction

In the 1970s, miniaturization and fabrication of monolithic 2D layers on silicon chips enabled large-scale integration (LSI) of thousands of individual interacting components onto an area of less than 5 × 5 mm², leading to the development of integrated circuits and the microprocessor. Similarly, in the early 2000s, microfluidic LSI technology was made possible by fabricating a layer of soft monolithic actuated microvalves to control thousands of fluid chambers in a multiplexed and addressable manner¹. By analogy, on-chip LSI of artificial cells programmed by cell-free protein synthesis holds the potential to create synthetic biological devices capable of autonomous collective behavior and biological computation across scales much larger than a cell. The development of cell-free transcription-translation (TXTL) genetic circuits^2–5 has pushed forward the assembly of minimal cell models in embodiments such as liposomes, emulsions, coacervates, and solid-state compartments^6–13, with work toward cell-cell communication showing examples of light activation, signaling, front propagation and synchronization^14–20. In addition, front propagation, and synchrony of Belousov-Zhabotinsky chemical oscillators were investigated in a reaction-diffusion array of microfluidic compartments and in planar networks of droplets^21,22.

We previously developed the solid-state compartments as a step toward “artificial cells” on a chip¹³. A series of miniaturized structures carved on a chip and DNA-driven reactions, with materials diffusing into and between the compartments, recreated steady-state and oscillating protein expression patterns. So far, however, the design has been topologically limited to 1D chains of communicating artificial cells^15,19.

Here, we transitioned from 1D to 2D on-chip artificial cells by carving feeding wells that traverse the chip from side to side, creating a perforated membrane-like structure. Using the third dimension to connect every cell with the outside environment for the exchange of nutrients solves the topology problem. This enables 2D layouts of interconnected artificial cells that exhibit tissue-like gene expression patterns, and here we study the case of coupled oscillators. We observe synchrony and front propagation in 2D, investigating the effect of coupling on the front shape, smoothness, and propagation velocity, which are markedly different from 1D networks of coupled oscillators.

Results and discussion

A 3D architecture for LSI of on-chip monolithic artificial cells in 2D

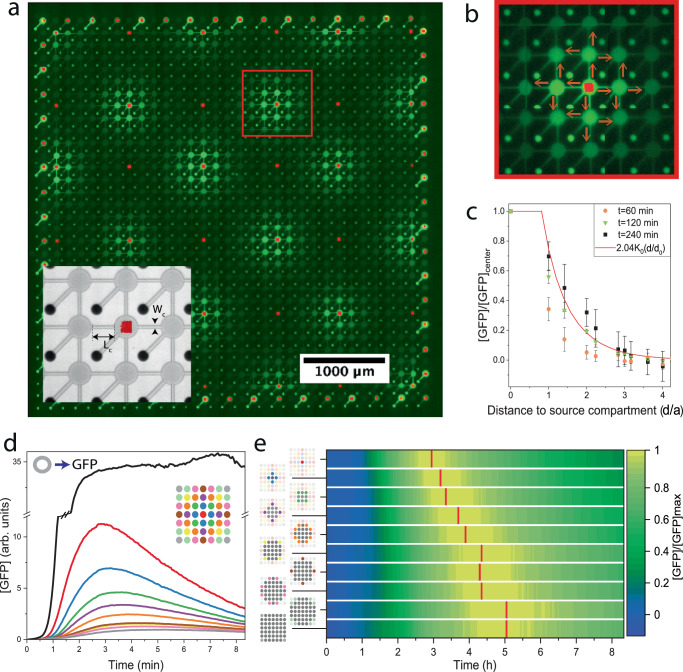
We fabricated a square lattice of 32 × 32 independent artificial cells (unit length a = 150 μm) on a silicon wafer with protein synthesis compartments at the front side and feeding channels at the back (Fig. 1). The compartments are shaped as thin pancakes (radius R = 30 μm; thickness h = 3 μm), with narrow capillaries (width w = 10 μm; length L = 80 μm) connected to perpendicular wells traversing the chip from side to side (radius R_W = 20 μm; length H = 200 μm). The back side includes 32 parallel microfluidic channels, each aligned with a row of wells (Supplementary Fig. 1). Linear double-stranded DNA (dsDNA) brushes (20 × 20 μm²) are immobilized on the surface of every compartment, each addressable and programmable by a different set of gene constructs (Supplementary Fig. 2). Each DNA brush co-localizes TXTL machinery and products, creating favorable conditions for gene regulation and multi-component interactions^23,24. With up to $1000\mathrm{dsDNA}/\mathrm{\mu }{\mathrm{m}}^2$, the brush enables control of gene composition, and copy number down to the single gene level where expression is stochastic²⁵. Protein synthesis occurs when an E.coli cell-free TXTL system^26,27 flowing in the feeding channel diffuses through the well to initiate protein synthesis at the DNA brush source. In turn, newly made proteins diffuse out of the compartment along the capillary and the well, where they are transported out by the flow at the backside. The entire design is monolithic, with no moving or actuated parts.

Fig. 1. Large-scale integration of artificial cells on a chip.

a Scheme of chips. Frontside: A 2D lattice of artificial cells, each comprising of a disk-shaped compartment carved h = 3 μm deep, with an immobilized DNA brush, and a thin capillary connecting the compartment to the backside through a well. Backside: microfluidic channels transport E.coli TXTL system diffusing through the well into the compartment to initiate and sustain protein synthesis. In turn, newly made proteins diffusing out of the well are flown away to create a source-sink and, hence, steady-state gene expression. b Spatial distribution of the gene mixtures in the compartments according to the spotted DNA solutions. Red: P70-gfp; green: P70-σ28, P28-gfp; magenta: oscillator reported by P70-gfp; blue: oscillator reported by P28-gfp; orange: PT7-gfp. The oscillator is a set of five genes described in the SI. c Fluorescent overlayed images of DNA brush (red, Alexa 647) and cell-free expressed GFP (green). Scale bar 100 μm d Fluorescent image of GFP expression according to map in (b) at t = 3.35 h. The chip contained 900 identical compartments on a square lattice. Scale bar 1000 μm e Expression profiles according to (b). The error bars represent the standard deviation within the chip (over 180 compartments). f Bright field image of a chip of compartments with different lifetimes (5–19 min), scale bar 150 μm g Expression of the genetic oscillator in corresponding compartments. h Scanning electron microscope image of a single compartment, scale bar 20 μm. i The period of the oscillator as a function of the compartment lifetime. The error bars represent the standard deviation within the chip (over 15 compartments).

The scenario of a localized protein source at the DNA brush and a sink at the bottom of the well implies that a steady state is attained when the rate of synthesis balances the rate of dilution out by diffusion. The solution of the diffusion equation in the capillary is a piece-wise linear concentration gradient, dropping from the source along the capillary, and then along the well to the exit point sink, where the concentration vanishes due to the flow (Supplementary Information; Supplementary Fig. 3). Theoretically, the system reaches steady-state within an effective lifetime that is set by geometry, $\tau \approx {\tau }_0\left(1+\mathrm{\Delta }L/L\right),$ where ${\tau }_0=\pi R^{2}L/D_{0}w=20\min$ is the compartment lifetime without the well, and $D_0\approx 40\mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ is the typical diffusion constant of newly made proteins. The contribution of the well is to effectively elongate the capillary by a relative factor $\mathrm{\Delta }L/L=whH/\pi R_w^{2}L$, which is only about 12%, because the capillary has a comparable length to the well, $H\approx L$, but a smaller cross-section $wh\ll \pi R_w^2$ (Supplementary Fig. S3b). This implies that protein concentration in steady-state scales with ${\tau }_0$ (Supplementary Fig. 4abd).

To test the source-sink model, we measured protein expression dynamics in artificial cells using several different DNA constructs in parallel with GFP as a reporter: an unregulated strong promoter, a transcriptional cascade, and a nonlinear oscillator constructed by an activator-repressor feedback circuit^13,19 (Fig. 1d, e and Supplementary Fig. S3). The data showed an increase in protein synthesis for about an hour, followed by a transition to a steady concentration for the unregulated and cascade, and to oscillations for the activator-repressor feedback circuit. The spatial concentration profile dropped linearly along the capillary from the DNA brush to the center of the well, extrapolating to zero at a point located only $\mathrm{\Delta }L/L\approx 18\%$ down the well, implying that the sink is not altered much by the presence of the well (Supplementary Fig. 3). We then varied the capillary length and compartment radius and observed that steady-state concentrations, oscillator amplitude and period scale with ${\tau }_0$, thereby validating the source-sink model (Fig. 1f, g, i and Supplementary Fig. 4).

Programmable reaction-diffusion on a square lattice of artificial cells

To transition from isolated artificial cells to a coupled system, we fabricated a device containing a square lattice of cells interconnected by thin capillaries of width $w_c=10\mathrm{\mu }\mathrm{m}$, and length $L_c=\mathrm{a}-2\mathrm{R}=80\mathrm{\mu }\mathrm{m}$. Proteins synthesized at a given source diffuse out of the well as well as into the four neighboring cells, where they recurrently dilute out through the respective additional wells (Supplementary Movie 1). By the same source-sink scenario, the concentration profile diffusing out of the source decreases linearly at every step on the lattice. We describe the coupled system of sources on the lattice by a discretized 2D reaction-diffusion equation for the concentration of proteins $P_{i,j}$ at coordinates (i,j) (Supplementary Information):

$${\partial }_t{P}_{i,j}=-\frac{P_{i,j}}{{\tau }_0}+D_{eff}\mathrm{\Delta }{P}_{i,j}+f\left(P_{i,j}\right)$$ 1

The first term is the dilution due to compartment lifetime, the second is the diffusion of gene expression products in the lattice, and the third is the source function $f\left(P_{i,j}\right)$, representing the DNA program in each compartment. Here, $\mathrm{\Delta }{P}_{i,j}$ is the discrete Laplacian with an effective coefficient diffusion on the lattice, $D_{eff}=\frac{a^2}{{\tau }_0}\beta$. The coupling strength, $\beta ={\tau }_0/{\tau }_c=L{w}_c/L_{c}w$, is the ratio between compartment lifetime and lifetime to dilute out into neighboring cells, ${\tau }_c=\pi R^2{L}_c/D_0{w}_c$. The concentration profile of a constant source in the lattice decays on a length scale of $\lambda ~a\sqrt{\beta }$ (SI). When $\beta \ll 1$, products diffuse out of the well more than to neighbors hence, the compartments are weakly coupled and conversely for $\beta \gg 1$. In this discrete cellular system, transcription activators and repressors regulate gene expression only on the DNA brush and carry no function when diffusing between compartments.

We next measured the expression and diffusion profiles from localized sources surrounded by empty compartments in a lattice of $\beta =1$. We used isolated constant sources of proteins expressed under a strong promoter, as well as oscillator sources and, as a reference, we also used uncoupled sources on the periphery of the lattice (Fig. 2). The expression dynamics of sources in the sparse lattice did not attain steady-state during eight hours of expression, and were unstable in time because of the recurrent dilution out to the neighboring cells and wells, in contrast to the stable profiles of uncoupled sources (Fig. 2d) or sources in a fully occupied lattice (Supplementary Fig. 5e). The spatial profile of an isolated source dropped linearly along the capillaries at every step and decayed to background levels three cells away. The profile was essentially symmetric in all directions, except for a minor drift of 6% along the direction of the underlying flow channel at the bottom layer (Supplementary Fig. 5c). From the space-time profiles, we extracted an effective diffusion constant of ${\mathrm{D}}_{\mathrm{eff}}=27\pm 2\mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$. We also measured the expression and diffusion profile of single oscillator sources and estimated a similar diffusion constant and a short delay between the oscillating peaks in neighboring cells of $\mathrm{\Delta }\mathrm{t}\approx 5\min$ (Supplementary Fig. 5d). These data establish the expression and diffusion terms of sources in a lattice.

Fig. 2. Diffusion from a single source in a coupled lattice of compartments.

a A chip of 30 × 30 connected compartments surrounded by isolated ones along the boundaries. Inset: bright field image and fluorescent image of DNA. Connecting capillaries length $L_c=80\mathrm{\mu }\mathrm{m}$, and width $w_c=10\mathrm{\mu }\mathrm{m}$, and coupling strength β = 1. Fluorescent image of GFP expression from a dilute lattice of single sources (P70-GFP; square DNA brushes labeled in red; P70-gfp, 16 bright regions; oscillator circuit, 18 dim regions (reported in Supplementary Fig. 5)). Scale bar 1000 μm. (Supplementary Movie 1) b Close-up of one source expressing GFP and diffusing into neighboring compartments. c The spatial profile at t = 60 min (orange disk),  t = 120 min (green triangle), and t = 240 min (black square) as a function of the Euclidean distance d of neighbors. The solid red line is the analytical solution $\left[\mathrm{GFP}\right]=\mathrm{\lambda }{\mathrm{K}}_0\left(\frac{d}{d_0}\right)$, with ${\mathrm{d}}_0=a\sqrt{\beta }=a$. The error bars represent the standard deviation within the chip. d The temporal expression profile of the source (red) and profiles of diffused GFP into neighbors (distance designated by color) with a reference to an uncoupled compartment (black). The 1st neighboring compartments are averaged and reported by the blue line. Green, purple, orange, yellow, brown, pink, light green, and gray, report on the nth neighboring compartments, respectively. (Supplementary Fig. 5a) e Plot of expression profile as a function of time and cumulated compartment area from source, with maximal GFP concentrations designated in red. A linear fit to the maxima yields an effective diffusion constant of ${\mathrm{D}}_{\mathrm{eff}}=27\pm 2\mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$.

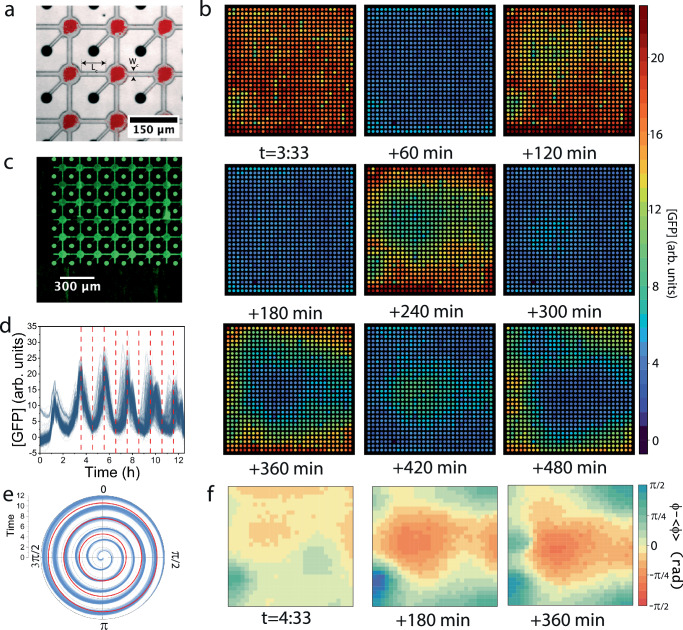
Dynamics of coupled oscillators in a 2D lattice

We then measured the dynamics of the lattice with 30 × 30 coupled oscillators (Fig. 3a–d). The oscillations were roughly in unison for about 3 cycles, before slightly drifting apart in time. The mean period, $\mathrm{T}=119\pm 3\%\min$, had a dispersity smaller than 10–15% for uncoupled identical oscillators, which indicated significant synchrony. This gradual dephasing of the initially synchronized oscillations occurred concomitantly with the appearance of 2D fronts propagating inward from the boundaries, which created smooth large-scale spatial variations from perfect synchrony (Fig. 3b and Supplementary Movie 2). A polar plot of the instantaneous phase, $\mathrm{\varphi }\left(\mathrm{t}\right)$, of the oscillators indeed shows that its spread increased in time (Fig. 3e), consistent with the slow loss of perfect synchrony (“Methods”). The spatial map of the phase in the lattice evolved into a stable and smooth function that varied slowly across the lattice (Fig. 3f).

Fig. 3. Amplitude and phase in a 30 × 30 coupled lattice of genetic oscillators.

a Overlay of brightfield and fluorescence image of DNA brushes of genetic oscillator circuit (red squares) in a 30 × 30 coupled lattice with $L_c=80\mathrm{\mu }\mathrm{m},w_c=10\mathrm{\mu }\mathrm{m}$, and coupling β = 1. Scale bar 150 μm b 2D rendering of GFP expression map in the lattice at nine-time points, as denoted and in C (red lines). c Image of GFP expression in the compartments, diffusing along the capillaries and down the wells (bright dots). Scale bar $300\mathrm{\mu }\mathrm{m}$. d GFP signal in time for all 900 oscillators. e Polar plot of the phase function for all 900 oscillators relative to the mean. Time points are marked in red. f 2D rendering of the phase of the oscillators relative to the spatial mean at three-time points, as denoted.

Oscillators within a region of a few cells close to the edges were in advance relative to those in the center of the lattice, which is consistent with the observation that the period of the oscillators was slightly shorter at the boundaries (Supplementary Figs. 6–8). In addition, the mean coupled oscillator period was longer by 10% than for identical uncoupled oscillators. These data suggest that oscillators at the lattice edges and corners, with 3 or 2 neighbors, respectively, have a shorter period compared to an oscillator inside the lattice with 4 neighbors. To test this, we simulated the dynamics of the negative feedback loop of the genetic oscillator in a cell coupled to up to 4 neighboring cells and confirmed that the period of the oscillator increases with coordination number, provided we introduce a delay^28,29 due to diffusion of the activator and repressor between the cells, as measured (Supplementary Fig. S9). Taken together, the dynamics of coupled oscillators are synchronized despite being affected by the lattice boundaries as a natural source of variation.

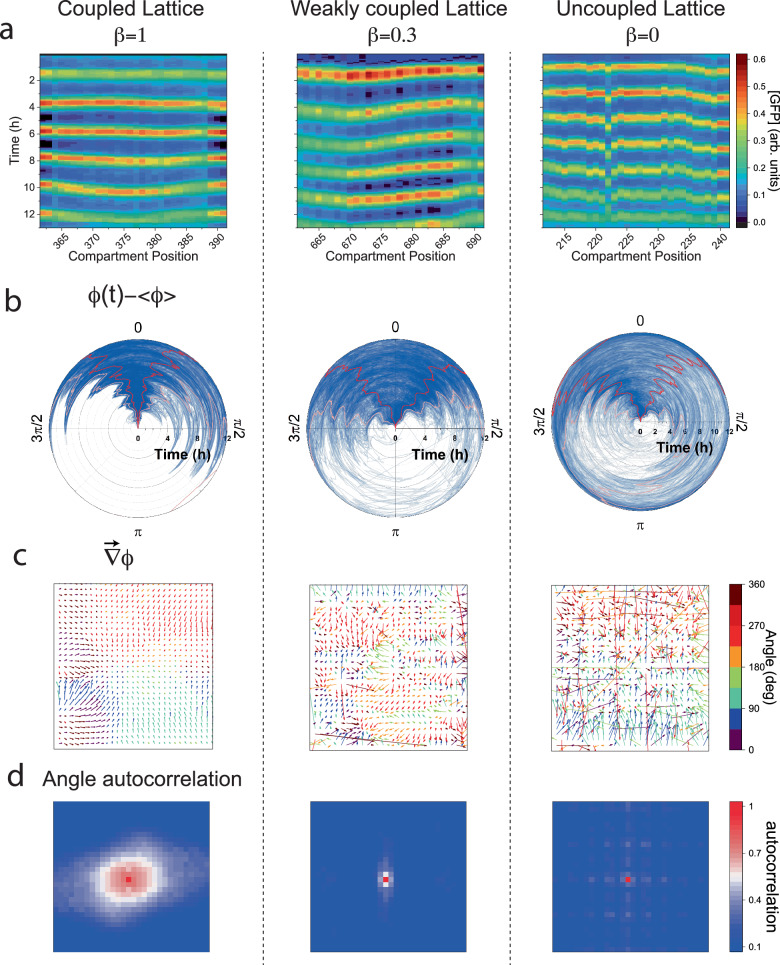
Long-range correlations of the oscillator phase gradient in a coupled lattice

We next investigated the effect of coupling strength on the dynamics by comparing the oscillations in the β = 1 lattice with a weakly coupled one, β = 0.3, and a disconnected one, β = 0, across replica devices (Fig. 4, Supplementary Figs. 6–8 and Supplementary Movie 3–5). As in Fig. 2, from the space-time profile of a source in a β = 0.3 lattice, we obtained a short decay length of just one cell and reduced effective diffusion, $D_{eff}=10\mathrm{\mu }{\mathrm{m}}^2/s$ (Supplementary Fig. 10), as predicted by our model. Generally, we find that replicas of lattices of the same coupling exhibited similar oscillations, front propagation, and spatial patterns. Yet, each lattice had distinct features due to inherent inhomogeneities, which created intrinsic variability between replicas. Fronts did not always emanate from the edges as defects in the lattice were also a source of fronts, for example, a wetting inhomogeneity that resulted in delayed filling and initiation of protein expression (Supplementary Figs. S6–8).

Fig. 4. Synchrony and dephasing in coupled and uncoupled 2D lattices.

a Space-time kymographs for one line of 30 oscillators, with a coupled ($\beta =1$), weakly coupled ($\beta =0.3$), and uncoupled lattice for reference ($\beta =0$). b The phases of all 900 oscillators relative to the mean, denoting 5 and 95% quantiles (pink line), and 25% and 75% quantiles (red lines). c Phase gradient fields for the respective lattices around the 4^th oscillation. Timepoints for these gradients are t = 9:30, 8:00, and 9:30 (h:min), respectively. Color code indicates the orientation of the gradient field, showing the local direction of the fronts in the lattice. d Angle autocorrelation of the respective phase gradient field.

Uncoupled lattices $\left(\beta =0\right)$ also exhibited dynamics of apparent synchrony because the oscillators were patterned identically, their expression was initiated together, and inherent inhomogeneities could result in front-like patterns. However, without the nonlinear feedback induced by coupling, no signature of collective dynamics could be observed. To show this, we measured: (i) space-time kymographs along vertical or horizontal lines across the lattice (Fig. 4a), (ii) phase dispersion in time (Fig. 4b), and (iii) phase gradients and angular auto-correlations (Fig. 4c, d). For coupled lattices, the kymographs were continuous and nearly straight lines across the lattice for $\beta =1$, whereas for $\beta =0.3$ they were continuous but bent, a sign of entrainment and local synchrony. The effect of lattice boundaries as a source of fronts was diminished for $\beta =0.3$ compared to $\beta =1$, implying that weakly coupled systems are more responsive to inner defects. By contrast, the kymograph for the uncoupled lattice was straight on average but locally discontinuous. Consistent with local synchrony, polar plots of all 900 oscillator phase differences²¹, indicated slow dephasing in time, with a narrow angular spread for $\beta =1$ than for $\beta =0.3$, and broadly distributed for $\beta =0$.

We next studied the phase gradient vector field in the lattice, which reports on the continuity and variations of the phase function in space (Methods). The phase gradient of the $\beta =1$ lattice showed a smooth, slowly varying vector field with correlated domains of size 10–15 cells. The mean angles of these domains were coaligned with the direction of the fronts, whereas the magnitude was inversely proportional to their velocity³⁰. We normalized the phase gradient by its local magnitude to account for the angular dependence and computed the angular autocorrelation, which revealed the long-range orientational order of the oscillator phase variations in the lattice. By comparison, the phase gradient for the $\beta =0.3$ lattice was continuous but less smooth, having smaller correlated domains about 3–5 cells in size, whereas the uncoupled lattice was discontinuous, erratic, without any angular correlations (Fig. 4d and Supplementary Fig. 11).

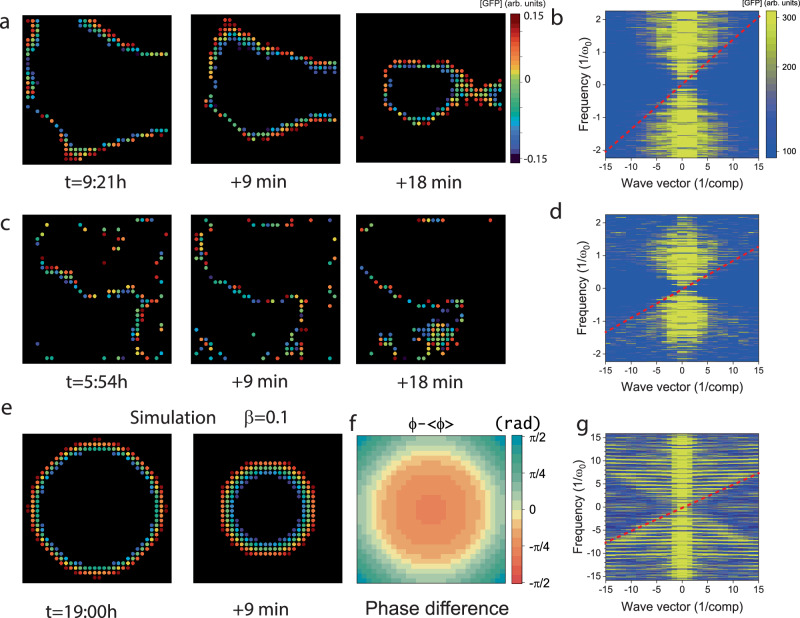
Front propagation in 2D coupled oscillator lattices

With feedback circuits such as the genetic oscillator, the nonlinear reaction-diffusion equation above supports propagating front solutions^31,32, with a lower bound on the velocity determined by diffusion and characteristic time scale: $v_0=\sqrt{\frac{D_{eff}}{{\tau }_0}}=\frac{a}{{\tau }_0}\sqrt{\beta }$, implying that strongly coupled lattices carry faster fronts than weakly coupled ones³³. We identified and tracked the fronts, observing continuous, rigid, and smooth 2D contours propagating inward for $\beta =1$ but disjoint, noisy, free-form contours for $\beta =0.3$. We then computed the Fourier transform in terms of frequency and wavevector and observed a conic, hourglass shape with a cutoff minimal velocity of $v_0=45\mathrm{\mu }\mathrm{m}/\min$ (0.31 compartments/period) and $v_0=28\mathrm{\mu }\mathrm{m}/\min$, (0.18 compartments/period) respectively, thereby confirming that front velocity increases with coupling strength (Fig. 5a–d). For $\beta =0$, the front analysis and the Fourier transform did not indicate a clear signature of a minimal velocity, and apparent front-like dynamics, or phase waves, might stem from any spatial inhomogeneities in oscillator periods, as in a moving digital text, unrelated to local entrainment and synchrony. We experimentally demonstrated that coupling is necessary to smooth the front and determine a lower bound for the wave velocity. Finally, we simulated the gene expression dynamics of coupled oscillators on a square lattice over more cycles than we could track experimentally (Supplementary Movie 6). The simulations reproduced all the observed phenomenology of coupled oscillations, namely, synchrony, diffusion in the lattice, and front propagation from the boundaries, as well as an hourglass-shaped Fourier transform with a minimal velocity similar to the measurements (Fig. 5e, f).

Fig. 5. Front propagation in 2D coupled lattices.

a Fronts in the coupled lattice ($\beta =1$) at time points separated by 9 min. b Fourier transform of data in a, as a function of the wave-vector k (x-axis, plotted in units of 1/compartment) and the frequency ω (y-axis, in units of the mean frequency of the oscillators ${\omega }_0$). The oblique shell corresponds to the front as the minimal velocity scale (red line) of $\mathrm{v}=45\mathrm{\mu }\mathrm{m}/\min$. c, d Same as in (a, b) but for a weakly coupled lattice ($\beta =0.3$), with a respective front velocity of $\mathrm{v}=28\mathrm{\mu }\mathrm{m}/\min$. e Simulation of the front propagation in a 30 × 30 coupled lattice (30 cycles). Oscillators at the boundaries are given a slightly reduced period to trigger the fronts. t = 19:00 h f 2D rendering of the phase difference for the corresponding simulation at the time t = 19:00 h g Corresponding Fourier transform projection reveals a front propagation at a speed of ${\mathrm{v}}_{\mathrm{sim}}=24\mathrm{\mu }\mathrm{m}/\min$.

Conclusion

In summary, we presented the LSI of 1024 disconnected artificial cells on an area of 5 × 5 mm² and established their working principles for steady-state gene expression. The artificial cells were programmed by immobilized DNA brushes. We then transitioned to an interconnected square lattice, validating a discrete reaction-diffusion system. We programmed the connected lattice by a genetic circuit of a nonlinear oscillator and observed collective oscillations and front propagation. The dynamics of the system, including effective protein lifetime and diffusion constant, the strength of intercellular coupling, and propagation speed, are determined by the dimensions of the cells and the lattice, as well as by the expression of the genes in the cell-free system. We find that strong coupling between oscillators leads to faster fronts as well as smooth, continuous, and long-range correlations of the oscillator phase gradient. These results highlight the effect of boundaries as natural defects in a finite 2D lattice, which are inherently different than a 1D lattice due to connectivity and coordination number. Discrete cell signaling relays can exhibit diffusive wave dynamics that depend on the effective dimensionality³⁴, and further work is required to explore various scenarios. LSI and collective oscillations is a case study of a nonequilibrium, programmable, synthetic multicellular system, where chemical energy dissipated in protein synthesis leads to spatiotemporal gene expression patterns.

Methods

Silicon chip fabrication

The silicon chip is fabricated in a three-step photolithography process. The silicon wafer (Double side polished, 4”, 0.3 mm thickness, test grade, p-type, University wafer) is patterned using standard photolithography techniques (Photoresists S18XX series and AZ 4562, Microchem) and is etched by an ICP-RIE (Surface Technology Systems). The front side is 3 μm deep and is composed of a lattice of 30 × 30 connected or disconnected compartments (20–30 μm radius), and communication capillaries (6–12 μm wide). The second step consists of etching the backside of the wafer to a depth of 100 μm. The photoresist is exposed after backside alignment, developed, and etched by a Bosch process (200 cycles). A third step is added to carve the well. After frontside alignment, the wafer is aligned and then patterned by laser lithography, as well as trenches delimiting the chip. They  are then etched all the way through the wafer by the Bosch process (700 loops). The device is then coated on the front side with a SiO₂ layer of 45 nm using PECVD (Plasma-Therm).

Creating a photoactivable biochip

Chips coated with SiO₂ are then incubated with a biocompatible photoactivable polymer which self-assembles at the surface^13,35. The biopolymer is composed of a PEG backbone, a trialkosyloxane function at one end (reacts with SiO₂ deposited at the surface of the chip), and a Nvoc-protected amine at the other end. Chips are incubated at 0.2 mg/mL of the polymer in toluene for 40 min and then rinsed in toluene.

Patterning the biochip with UV light

The polymer-coated chip is aligned and exposed with a 400 nm LASER (Microwriter - Durham Magneto Optics Ltd). The monolayer of the photoactivable reactive amine group is exposed to a dose of 1000 mJ/cm² spatially patterned. Square surfaces are activated inside the compartments to designate the area of DNA brushes.

Biotinylation of the surface

The chip is then dipped in a biotin-NHS (NHS: N-hydroxysuccinimide) solution in Borate buffer for 15 min. The biotin-NHS molecule reacts with the photoactivated amine group leaving the surface covered with patterned biotin.

DNA preparation

DNA-streptavidin (SA) linear conjugated fragments are prepared by Polymerase Chain Reaction (PCR) in KAPA Readymix (Roche). Biotin and Atto 647 N are attached to the DNA fragment by using correspondent primers (IDT). PCR products are then cleaned (Promega Wizard PCR cleaning kit) and then conjugated to SA in PBS. The final DNA concentration is 150–300 nM. Sequences are reported in supplementary materials.

DNA deposition

Dense brushes of dsDNA are formed by the deposition of nanoliter droplets on the artificial cell compartment. Droplets of DNA-SA in PBS (5% glycerol) are spotted individually (GIX Microplotter, Sonoplot, and SciFLEXARRAYER S3 Scienion), and incubated for 2 h. The chips are finally rinsed in PBS and then water.

Sealing of the device

The chip is sealed at the backside by a PDMS (Sylgard) slab (thickness 7 mm). The inlet and outlet are pierced through the slab and are aligned with the silicon chip. On the frontside, a glass coverslip covered with a 100 μm thick layer of hard PDMS (Gelest) seals the device. Both the PDMS slab and the coverslip are gently pressed on the silicon chip to ensure sealing and held in place using a custom-made holder.

Imaging

The device is then placed in a temperature chamber at 30 °C and is connected to a syringe pump (Harvard apparatus) and a cell-free extract container. The latter is kept at 2 °C by a Peltier cell throughout the duration of the experiment while the cell-free extract flows in by gentle suction. The device is then imaged by an inverted microscope (Axiovert Zeiss) equipped with an automated stage and a sensitive wide-view camera (Andor Ixon Ultra 897).

Cell-free transcription-translation

Cell-free gene expression was carried out using an E. coli TXTL system described previously. Briefly, E. coli cells were grown in a 2xYT medium supplemented with phosphates²⁷. Cells were pelleted, washed, and lysed with a cell press. After centrifugation, the supernatant was recovered and preincubated at 37 °C for 80 min. After a second centrifugation step, the supernatant was dialyzed for 3 h at 4 °C. After a final spin-down, the supernatant was aliquoted and stored at − 80 °C. The TXTL reactions comprised the cell lysate, the energy and amino acid mixtures, maltodextrin (30 mM) and ribose (30 mM), magnesium (2–5 mM) and potassium (50–100 mM), PEG8000 (3-4%) and water. Linear DNA was either stabilized by adding Lambda GamS (5 μM) in the TXTL mixture, or by using TXTL reactions from a modified strain which is Δ-recBCD.

Methods of analysis

Phase

For each compartment, we extract the signal inside ($s_{inside}$) of the compartment and the signal outside ($s_{outside}$)

$$s\left(x,y,t\right)=s_{inside}-s_{outside}$$ 2

This signal s is a periodic signal, and to analyze it we extract the phase through the Hilbert transform of $\mathcal{H}\left(s-<s{>}_{\mathrm{t}}\right)$. The phase is therefore defined as:

$$\varphi \left(x,y,t\right)=\arg \left(\mathcal{H}\left(s\left(x,y,t\right)-<s\left(x,y\right){>}_{\mathrm{t}}\right)\right)$$ 3

The phase function continuously increases as the signal oscillates, reaching values of $2n\pi$ when the function is at a maximum, and $\left(2n+1\right)\pi$ when the signal is at a minimum, with n being the number of the oscillation.

Fronts

We detect the propagating fronts by selecting the signals only when the phase is around $\left(n+\frac{1}{2}\right)\pi$. The normalized signal (the maxima and minima are set to − 1 and 1 by normalizing the signal with the modulus of its Hilbert transform) is therefore, recomposed to keep only the propagating fronts. this means we keep the signal, which is comprised in [− 0.15; 0.15] and the rest of the signal is set to zero. We then proceed to the discrete Fourier transform in three dimensions and represent it function of the wave vector modulus k (x-axis) and ω (y-axis).

Phase gradient

For every t, we can also define the gradient of the phase $\overrightarrow{\nabla }\varphi \left(x,y,t\right)$. The gradient is composed of two fields ($\overrightarrow{\nabla }\varphi .\overrightarrow{e_x}$ and $\overrightarrow{\nabla }\varphi .\overrightarrow{e_y}$).

Let’s call Ψ the normalized gradient $\overrightarrow{\mathrm{\psi }}\left(x,y,t\right)=\frac{\overrightarrow{\nabla }\varphi }{\mid \mid \overrightarrow{\nabla }\varphi \mid \mid }$

Front velocity

The relationship between the front velocity and the phase gradient is the following³⁰:

$$v=-\frac{2\pi }{T}\frac{1}{\mid \mid \overrightarrow{\nabla }\varphi \mid \mid }$$ 4

Angular Autocorrelation Function from the normalized phase gradient

Then we perform the autocorrelation function $C\left({\overrightarrow{r}}_0,t\right)$ of the normalized matrix $\overrightarrow{\mathrm{\psi }}$.

$$C\left({\overrightarrow{r}}_0,t\right)=<\overrightarrow{\mathrm{\psi }}\left(\overrightarrow{r},t\right).\overrightarrow{\mathrm{\psi }}\left(\overrightarrow{r}+{\overrightarrow{r}}_0,t\right){>}_{\overrightarrow{\mathrm{r}}}$$ 5

$<.{>}_{\overrightarrow{\mathrm{r}}}$ is the sum over all possible $\overrightarrow{r}$ (overlapping matrices)

The radial autocorrelation function is defined as

$$C\left(r_0\right)=\frac{1}{2\pi }{\int }_0^{2\pi }<\psi \left(\overrightarrow{r}+{\overrightarrow{r}}_0\left(\rho ,\theta \right)\right)\cdot \psi \left(\overrightarrow{r}\right){>}_{\overrightarrow{r}}d\theta$$ 6

is displayed in Supplementary Fig. 7.

Statistics and reproducibility

Every experiment was reproduced independently at least three times (examples of reproductions are given in the supplementary materials, Supplementary Figs. 6–8).

No statistical method was used to predetermine sample size. No data were excluded from the analyses. The experiments were not randomized. The Investigators were not blinded to allocation during experiments and outcome assessment.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

J.R., A.T., E.K., S.S.D., and R.B.Z. designed the project. V.N. and A.K. produced the cell-free expression system. J.R., P.M., and O.S. fabricated the chips, designed and performed the experiments. O.V. and S.S.D. supported the biological and experimental setup. J.R. performed the analysis. J.R. and R.B.Z. discussed and wrote the paper.

Peer review

Peer review information

Nature Communications thanks Henrike Niederholtmeyer, and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data generated in this study have been deposited in the Zenodo database (10.5281/zenodo.10805243). Other relevant data are available within the paper as Source Data and Supplementary Information. Source data are provided in this paper.

Code availability

MATLAB (MathWorks) functions were used for the analysis and are described in the Methods section.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-54098-0.