LIMO-GCN: a linear model-integrated graph convolutional network for predicting Alzheimer disease genes

Abstract

Alzheimer’s disease (AD) is a complex disease with its genetic etiology not fully understood. Gene network-based methods have been proven promising in predicting AD genes. However, existing approaches are limited in their ability to model the nonlinear relationship between networks and disease genes, because (i) any data can be theoretically decomposed into the sum of a linear part and a nonlinear part, (ii) the linear part can be best modeled by a linear model since a nonlinear model is biased and can be easily overfit, and (iii) existing methods do not separate the linear part from the nonlinear part when building the disease gene prediction model. To address the limitation, we propose linear model-integrated graph convolutional network (LIMO-GCN), a generic disease gene prediction method that models the data linearity and nonlinearity by integrating a linear model with GCN. The reason to use GCN is that it is by design naturally suitable to dealing with network data, and the reason to integrate a linear model is that the linearity in the data can be best modeled by a linear model. The weighted sum of the prediction of the two components is used as the final prediction of LIMO-GCN. Then, we apply LIMO-GCN to the prediction of AD genes. LIMO-GCN outperforms the state-of-the-art approaches including GCN, network-wide association studies, and random walk. Furthermore, we show that the top-ranked genes are significantly associated with AD based on molecular evidence from heterogeneous genomic data. Our results indicate that LIMO-GCN provides a novel method for prioritizing AD genes.

Introduction

Alzheimer’s disease (AD) is a complex neurodegenerative disorder. AD is highly genetic, with estimated heritability ranging between 60 and 80% [1]. However, its genetic etiology remains not fully understood. Predicting novel AD risk genes plays an essential role in advancing our understanding of AD mechanisms. Genome-wide association studies (GWAS) represent a major approach for identifying risk variants or genes. So far, a number of AD risk genes have been identified, including ABCA7, BIN1, TREM2, and CR1. For example, Jansen et al. performed a GWAS meta-analysis and identified 29 risk loci involving potential causative genes, such as ADAMTS4, CLNK, KAT8 [2]. The identified genes are found to be strongly expressed in immune-related cell types such as microglia and are enriched in pathways including lipid processing and degradation of amyloid precursor proteins. Very recently, Bellenguez et al. developed a two-stage GWAS with diagnosed or proxy AD cases and matched controls. A total of 49 new risk loci such as SORT1 and ANK3 are identified [1].

GWAS aim at identifying genetic variation associated with diseases, without considering the information of other types of genomic data such as transcriptomic and proteomic data. Functional Gene Networks (FGNs), which can integrate heterogeneous genomic data, were utilized to predict disease genes [3–8]. For example, Krishnan et al. proposed a machine learning approach that utilized a brain-specific FGN to predict the associated genes of autism spectrum disorder (ASD) [6]. In this approach, they first constructed a brain-specific FGN that models the interaction among genes and then used a linear support vector machine to learn the relationship between networks and disease genes from a training set of ASD risk genes. To capture the nonlinear relationship between FGNs and disease genes, a tree-based model was used to build disease gene prediction model in our previous work(Lin et al., 2022). As a nonlinear method that can also utilize the structural information of networks, graph convolutional network (GCN) can be used for disease gene prediction and was proven to be competitive [9–12].

The way to model the data nonlinearity plays a key role in the performance of disease gene prediction models. We reason that the above methods still have limitations in their ability to model the nonlinear relationship between FGN and disease genes, because (i) any data can be theoretically decomposed into the sum of a linear part and a nonlinear part, (ii) the linear part can be best modeled by a linear model because a nonlinear model is biased and can be easily overfit, and (iii) the above methods simply use a nonlinear algorithm to build a model without separating the linear part from the nonlinear part. To address the limitation, we propose linear model-integrated GCN (LIMO-GCN), which combines a GCN and a linear neural network to separately model the nonlinear and the linear part in real-world data. The motivation of this method is 2-fold. First, GCN is by design a nonlinear method and is naturally suitable to exploit the nonlinear graph structure of gene networks. Second, the linear neural network is used to best handle the linearity.

In this work, we first describe the algorithm of LIMO-GCN. Second, we apply LIMO-GCN to build a model for predicting AD genes. We benchmark our method with the state-of-the-art approaches used for predicting AD risk genes. The experiments show that our method performs better through cross-validation. Third, to prioritize novel AD genes, the developed model is used to score all other genes that are not in the training set. We show that the top-ranked genes are significantly associated with AD based on various molecular evidence, including GWAS, known AD pathways, and biological processes. Taking together, our results show that the proposed method could be valuable for prioritizing AD genes.

Materials and methods

Data collection and preprocessing

AD risk genes

In this work, we use a curated set of AD risk genes obtained from our previous study [7]. Briefly, these genes are hand-curated high risk AD genes, which are from multiple disease gene databases, including OMIM [13], GWAS Catalogue [14], AlzGene [15], AlzBase [16], and DisGeNet [17]. The dataset contains 147 positive (AD-associated) genes. The genes are publicly available from https://github.com/genemine/ADBrainNexus.

Genes not associated with AD

After removing all possible AD-associated genes from disease gene databases(OMIM, GWAS Catalogue, AlzGene, AlzBase, DisGeNET, and OpenTarget [18]), we collected 3866 genes as negative (non-AD associated) reservoir.

In previous papers, some opted to model the same number of negative samples (random genes or genes not associated with AD) with that of positive samples (AD risk genes) [19, 20], while others considered using all irrelevant genes as negative samples [21, 22]. However, there is no conclusion on which approach is superior.

In this paper, we test the different ratios of positive and negative samples at 1:1,1:5,1:10,1:20, and also consider all 3866 irrelevant genes as negative samples. We select the optimal negative sample number by comparing the counts of positive samples among the top K (100, 200, 500, 1000) genes.

Adjacency matrix and feature matrix

The feature matrix of the genes includes protein–protein interaction networks from STRING database [23], AD-specific FGN (ADFGN) [7], and molecular signatures [24] like chemical and genetic perturbations and molecular function from the Human Molecular Signatures Database (MSigDB) [24]. Pathways with size smaller than 5000 are considered to build the feature matrix. For the PPI data from STRING database, we obtained the interaction strength score (which is not a binary value but a continuous value), and used this score in the feature matrix construction. The molecular signatures in the MSigDB database are digitalized into a matrix of 0 or 1, with 1 meaning that the gene is annotated to the corresponding signature and 0 not. There are 15505, 15485, and 5237 features generated from STRING, ADFGN, and MSigDB, respectively.

GCN requires as input an adjacency matrix. In this work, the adjacency matrix is obtained from the ADFGN constructed in our previous network[7]. After removing those genes with all edge weights lower than 0.05, there are totally 15 485 genes in the ADFGN. We use ADFGN as the adjacency matrix.

Methods

The architecture of LIMO-GCN is designed to contain two components: a linear model that learns the data linearity and a GCN that learns the data nonlinearity. The motivation of LIMO-GCN is 2-fold. First, the real-world data can be thought of as the sum of a linear part and a nonlinear part. Second, we assume that the linear part could be better modeled by a linear model rather than a nonlinear model. So, we use a linear layer to learn a linear model and a GCN to learn a nonlinear model. The outputs of these two models are combined as the final output of LIMO-GCN. The corresponding framework of LIMO-GCN is shown in Fig. 1.

Figure 1.

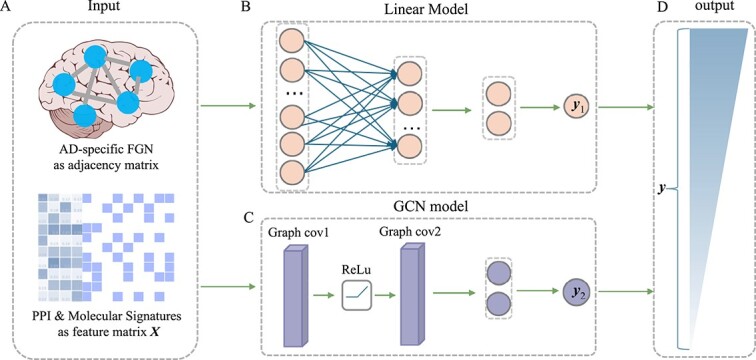
Framework of LIMO-GCN. (A) The input of LIMO-GCN. It contains an adjacency matrix generated from AD-specific FGN and a feature matrix X, which is comprised of PPI from STRING database and molecular signatures from MSigDB. (B) The linear model of LIMO-GCN. (C) The GCN model of LIMO-GCN. (D) The output of vector y is taken as predicted score. Gene with a darker color indicates a higher association score with AD.

The inputs of LIMO-GCN are described as below. LIMO-GCN requires a network as input in addition with a feature matrix. Given a gene network, let A and D denote the adjacent matrix and degree matrix, respectively. Let Xdenote an 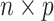feature matrix of n genes in rows and p features in columns. Let y denote a 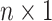vector of prediction scores, where higher scores for genes suggest a stronger association with AD. The algorithm of LIMO-GCN is described in detail in the following.

Modeling data linearity using a linear model

A linear neural network is introduced to learn the linear relationship between X and y. The input layer contains p neurons. The network transforms the input data to a lower dimensional latent space and outputs a probabilistic value 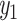. The larger the value is, the more likely the input gene is associated with AD.

Modeling data nonlinearity using a GCN

FGNs are graph structured data, with nodes representing genes and edges representing co-functional probability between two genes. GCN is designed to model graph data and has been proven powerful in the field of classification tasks such as image classification [25], text classification [26], disease classification [27]. Therefore, we choose GCN to model the data nonlinearity.

GCN takes a network represented by the adjacency matrix A and a feature matrix X as input. Given these two inputs, GCN is applied to learn low-dimensional embedding of each gene. In a GCN layer, the input feature vector of a given gene is computed as the sum of the weighted combination of its neighbors defined in A, thus achieving the effects of utilizing neighbor information. Mathematically, this process can be expressed as follows:

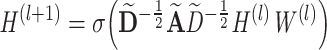(1)

where 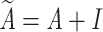, which is the adjacency matrix of graph, I is an identity matrix, D is a diagonal matrix, 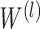is the trainable weight matrix of the lth layer, and 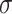is the activation function. 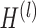is the matrix of activations of the lth layer, when l = 0, 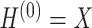. Based on the above formula, it can be found that using a single GCN layer contains the first-order neighbor information, and using two GCN layers will incorporate the information of second-order neighbors, and so far. As graph convolution is essentially a smoothing process, too many layers may result in over-smoothing, i.e. loss of sample-specific information. In this work, we choose to use two GCN layers, which is a common practice in this field.

The GCN layer is followed by a fully-connected (FC) layer for classification. For each gene, the FC layer finally outputs probabilistic value 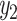, measuring the likelihood that the input gene is associated with AD.

Integration of linear model and GCN

LIMO-GCN computes the final output, denoted by y, as the weighted sum of 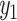from the linear model and 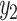from GCN as following:

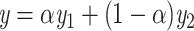(2)

where 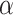is a weight parameter in the range of [0, 1], which needs to be specified by the user. 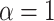indicates using linear model, 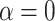indicates using only GCN model, and 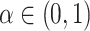means the combination of a linear model and a GCN. In LIMO-GCN, we choose the cross entropy with L1 loss as the loss function for training the model. The loss function can be expressed as follows:

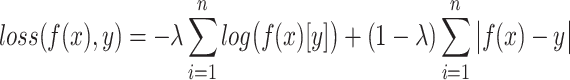(3)

We implemented LIMO-GCN using the pyTorch framework [28]. The LIMO-GCN is developed with GCNs in PyTorch [29] by combining the module of linear neural network. The source codes are publicly available on GitHub (https://github.com/CuixiangLin/LIMO-GCN).

Benchmark methods

We compare LIMO-GCN with state-of-the-art methods for predicting AD genes. These methods include random walk with restart on multiplex-heterogeneous graphs (RWR-MH) [30], GenePlexus [31], ADFGN modeled by ridge regression (ADFGN-RR) [7], GCN-GENE [11], Gene set integration (GSI) [19], DISHyper [32] methods are described below.

RWR-MH extended the RWR algorithm from single network to multiplex and heterogeneous networks [30]. GenePlexus [31] is a web server for disease gene prediction based on network-based machine learning method. It provides researchers options of networks including BioGRID, STRING, STRING-EXP, and GIANT-TN. The corresponding tool PyGenePlexus was then developed for users to train model on their need [33]. ADFGN-RR constructs an AD brain-specific functional gene network (ADFGN) by integrating AD brain omics data and uses ridge regression to score the association between genes and disease [7]. GCN-GENE [11] was proposed to predict disease-related genes by utilizing GCN. Gene set integration (GSI) utilizes biological data like pathways and annotated gene set to predict brain disease genes [19]. DISHyper integrates annotated gene sets to predict disease genes based on hypergraph [32].

Evaluation metrics

We employ 5-fold cross-validation to obtain the prediction results. To ensure a fair comparison with state-of-the-art methods, we maintain consistency in the training and test sets across these methods. The prediction results for unknown genes are derived from the average of the results from the 5-fold cross-validation. For labeled genes, we model the training set, predict scores for the test set, and then aggregate the predicted results from the five test sets.

We first use AUROC (area under receiver operating characteristic curve) and area under precision recall curve (AUPRC) to evaluate the effectiveness of different prediction methods. The ROC curve is drawn with true positive rate (TPR) as the y-axis and false positive rate (FPR) as the x-axis. The PR curve is drawn with precision as the y-axis and recall as the x-axis. The definitions of TPR, FPR, precision, and recall are as follows:

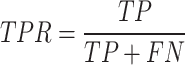(4)

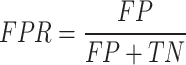(5)

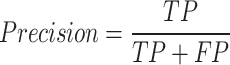(6)

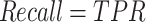(7)

where TP is true positive, FP is false positive, TN is true negative, and FN is false negative.

Second, we compare their performance through precision@K, which is defined as below.

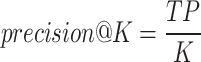(8)

In addition, we test the top K genes for enrichment in AD risk genes using the binomial test. The P-value of Fisher’s exact test is shown below.

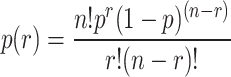(9)

• . n: the sample size (e.g. all genes in the genome or all genes tested in the experiment).

• . p: the expected proportion (p=).

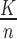• . r: the number of AD risk genes ranked in top K.

The evaluation metrics above are aimed at containing known AD risk genes in the whole prediction. We also evaluate the association with AD of top-ranked genes after excluding known AD risk genes. The assessment methods encompass various types of evidence, including novel genes (not included in training datasets) from DisGeNET, novel genes from GWAS, associated SNPs with AD, literature evidence, differential expression, differential methylation, alterations in cognitive function, and clinical severity.

Results

Comparison of LIMO-GCN with the state-of-the-art methods

We test our model using different proportions of 1:1, 1:5, 1:10, 1:20, and all negative samples.

For each proportion, we select 20 sets of negative samples randomly from 3866 negative samples, and take the average of the number of AD risk gene predicted in the corresponding topK. We compare the results according to numbers of AD risk genes in the top K (100, 200, 500, 1000) ranked genes. The results imply that considering all negative samples into our model is superior among all tests(Fig. 2). Besides, we also test the state-of-the-art methods using the different ratios (Supplementary Fig. 1). Take in top-500 genes for example, GSI and GenePlexus achieve the best performance when the ratio is 1:10. For ADBN-RR, it is 1:20. For DISHyper and GCN-GENE, they achieve the best performance when the ratio is 1:1. Among methods and all ratios, the best performance is achieved by LIMO-GCN at the ratio of 1: all.

Figure 2.

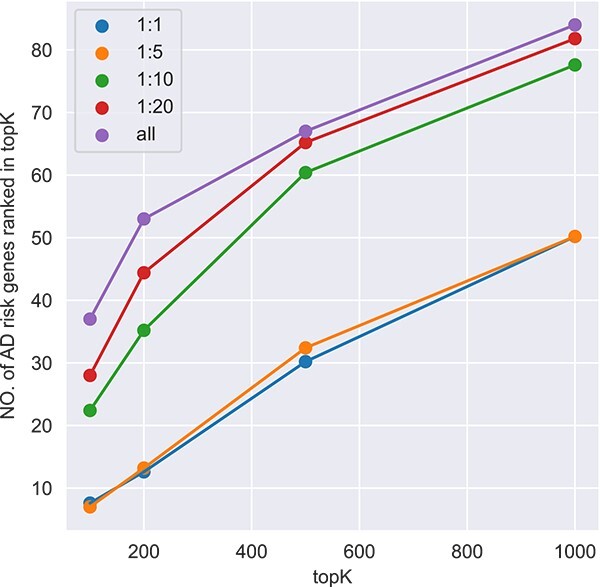
The performance of different proportions of negative samples in model.

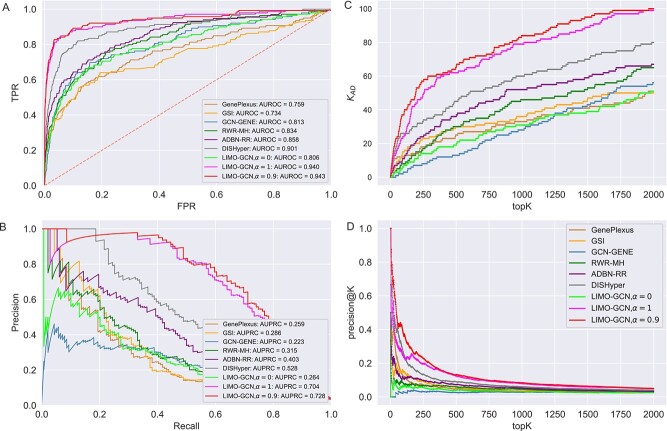
We compare LIMO-GCN with the state-of-the-art methods in predicting AD genes. First, we compare the prediction performance of the proposed method with benchmarking methods including RWR-MH, GenePlexus, ADFGN-RR, GSI, GCN-GENE, and DISHyper using AUROC and AUPRC. The AUROC and AUPRC of LIMO-GCN are 0.943 and 0.728, respectively. We also compare the model performance of LIMO-GCN under the parameters of 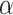=0, 0.9, 1 and 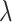=0.4. The results of LIMO-GCN (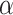=0.9, AUROC= 0.943, AUPRC= 0.728) outperform when the model only contains GCN module only (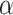=0, AUROC= 0.806, AUPRC= 0.264) and linear module only (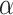=1, AUROC= 0.940, AUPRC= 0.704). Besides, the results also indicate that LIMO-GCN has better performance than GCN-GENE, GSI, ADFGN-RR, DISHyper, RWR-MH, and GenePlexus (Fig. 3A and B).

Figure 3.

Comparison of LIMO-GCN (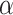=0, 0.9, 1 with 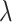=0.4) with the state-of-the-art methods. (A) The area under the ROC curves of LIMO-GCN and other methods. (B) The AUPRC of LIMO-GCN and other methods. Comparison from No. of AD risk genes in topK and Precision@K. (C) Comparison of No. of AD risk genes in topK ( 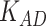stands for the number of AD risk genes in top K ranked genes.). (D) Comparison of Precision@K of LIMO-GCN and other methods.

The results in Fig. 3A and B can be used to illustrate the advantage of separating linear and nonlinear part of the data. First, taking GCN-GENE (a nonlinear method) and GSI (a linear method) as examples, their performance is not as good as LIMO-GCN which models the linear and nonlinear part in the data separately. Furthermore, specifically for LIMO-GCN, we also provide the results of both the linear model (i.e. LIMO-GCN with 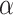=1) and the fully nonlinear model (i.e. LIMO-GCN with 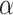=0) (Fig. 3A and B); it can be found that neither the model with 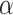=0 nor the model with 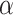=1 performs better than LIMO-GCN. This result shows that separating the linear part and the nonlinear part is useful for improving disease gene prediction.

Second, we evaluate their performance using No. of AD risk genes in topK and precision@K. No. of AD risk genes in top 100 for LIMO-GCN, DISHyper, RWR-MH, GenePlexus, ADFGN-RR, GSI, and GCN-GENE is 37, 26, 8, 12, 11, 15, and 9, respectively. The results of No. of AD risk genes in topK and precision@K show that LIMO-GCN outperforms the other methods (Fig. 3C and D).

Third, we evaluate their performance through enrichment analysis of top-ranked genes in AD risk genes. The enrichment analysis of top-ranked genes indicates that the top-ranked genes predicted by LIMO-GCN are more significantly enriched in the AD risk genes compared to the results predicted by the other methods (Table 1). We first check the numbers of AD risk genes in top 50, top 100, top 200, and top 1000 genes in the predicted results (It should be noted that the scores of labeled genes are derived from the prediction of the test set. Supplementary Table 1). We observe that there are 24 genes labeled AD risk genes in top 50. Among these genes, APOE, APP, PSEN1, CLU, and BIN1 rank in the top five. We set 0.01 as the expected proportion according to the given condition(147 AD risk genes versus 15 485 genes). We then conducted binomial tests for these four types of top K. Their corresponding results are shown in Table 1.

Table 1.

The enrichment analysis of predicted AD risk genes in top-ranked genes

	LIMO-GCN		DISHyper		GCN-GENE		GSI		ADBN-RR		GenePlexus		RWR-MH
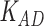
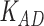
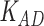
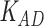
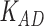
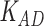
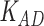
topK		P-value		P-value		P-value		P-value		P-value		P-value		P-value
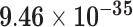
50	24		20	3.54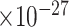	4	1.60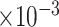	9	1.73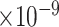	7	6.85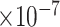	12	8.54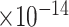	5	1.46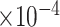
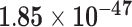
100	37		26	3.42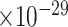	9	8.39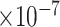	15	1.14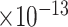	11	6.26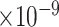	12	4.65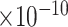	8	8.22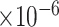
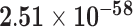
200	53		30	7.85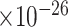	20	2.89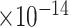	20	2.89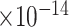	22	2.04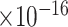	14	2.08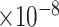	15	2.58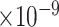
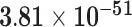
500	66		45	3.54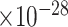	29	9.61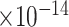	30	1.51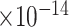	36	1.16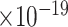	25	1.08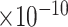	30	1.51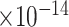
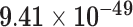
1000	84		60	1.84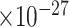	38	7.88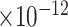	36	1.19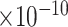	52	2.86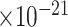	33	5.67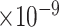	46	5.47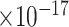

Note: 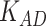stands for the number of AD risk genes in top K ranked genes.

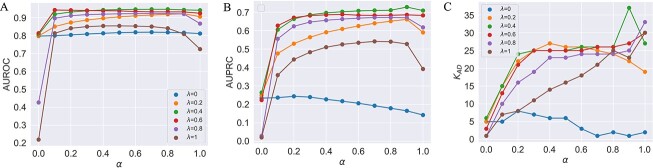
Influence of parameters on LIMO-GCN performance

We first test the influence of the parameters of LIMO-GCN in predicting AD-associated genes by using all negative samples (Fig. 4). LIMO-GCN has two important parameters 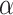and 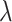. 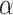is the weight to combine the linear module and the GCN module. 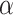is in the range of [0, 1]. 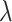is a parameter to balance cross entropy and L1 loss in our loss function. In our study, we conducted experiments by varying the parameter 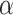in steps of 0.1 and 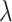in steps of 0.2 (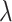, 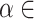[0,1]). We perform the experiments at default setting of learning rate, weight decay, number of hidden units, and drop out at 0.0001, 0.0001, 128, and 0.8, respectively.

Figure 4.

(A) AUROCs of LIMO-GCN in different parameters (the results are generated by using all negative samples). Comparison of different parameters influencing on LIMO-GCN performance. We systematically varied these parameters to understand their impact and identify the optimal settings for our disease gene prediction task. 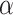indicates the weight of GCN modules in the model. 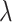is to balance the loss function by combining L1 loss and cross-entropy loss. (B) AUPRCs of LIMO-GCN in different parameters. (C) No. of AD risk genes (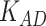) in training data among top 100 ranked genes under different parameters.

Different values of 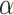and 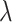are tested and the results of all experiments are shown in Fig. 4A–C. First, we fix the value of 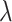to observe the performance of models with the change of 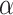from 0 to 1. Taking 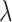= 0.2 for example, the AUROC increases when 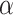is from 0 to 0.9 and then drops. When 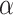= 0 (the model takes the module of GCN only), its AUPRC score is 0.223. When 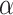= 1(the model only contains fully linear layers), its AUPRC score is 0.589. Second, we fix the value of 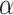to observe the change of performance in different 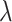. We observe that there is poor performance when both 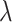is 0 and 1. And when the value of 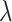approximates into the range of 0.4 and 0.6, the model performs better than 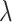in the other values. For the evaluation metric of AUROC, AUPRC, and 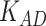(K = 100), the model performs best when 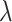= 0.4 and 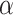= 0.9, the AUROC and AUPRC are 0.943 and 0.728, respectively.

Then, the performance of different ratios (1:1, 1:5, 1:10, 1:20) between positive and negative is also tested (Supplementary Fig. 2). Based on these results, we find that the best results are most often achieved at the above used optimal 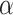and 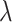values (i.e. 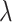= 0.4 and 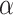=0.9) are close to the optimal values.

By systematically varying parameters, we can observe how different values affect the results and identify the optimal value that yields the best performance. This approach helps us to understand the sensitivity of our method to the parameters and provides insights into its influence on disease gene prediction. Through these experiments, we aim to gain a comprehensive understanding of the relationship between parameters and prediction performance, enabling us to make informed decisions about the parameter selection in our method.

LIMO-GCN predicts AD risk genes more accurately based on four independently collected AD-associated gene sets.

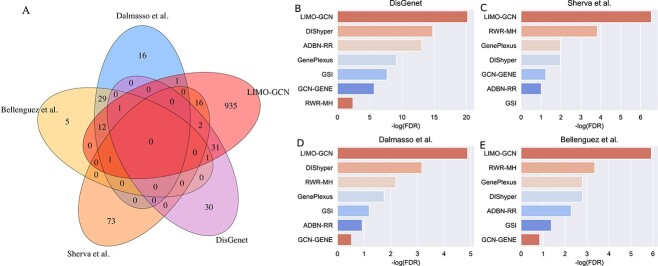
We collect four AD-associated gene sets as validation data that do not contain any of the AD risk genes (liked those used earlier in Figs 2 and 3) used to build the prediction modeling. There are 123 genes (score >0.3) associated with AD from DisGeNet. In addition, 190, 115, and 95 AD-associated genes were reported in three recent GWAS studies [1, 34, 35]. After removing those that are already in the training data, 65 (DisGenet), 92 (Sherva et al.), 60 (Dalmasso et al.), and 49 (Bellenguez et al.) novel risk genes are finally obtained, respectively. These novel genes can be used as independent data for validating the predictions of LIMO-GCN. We can observe that they share very few novel genes between genes from DisGenet and genes from GWAS studies (Fig. 5A). Besides, we find that Sherva et al.’s GWAS [34] focused on the rate of cognitive decline in AD, whereas the other two studies focused on AD diagnosis [1, 35]. This might be the reason of Sherva et al.’s GWAS sharing few genes with the other two studies. Novel genes from the study by Sherval et al. [34] only share ADAM17 and ADAMTS1 with genes from DisGenet. MAF is the only gene shared together by novel genes from these three GWAS studies. We observe that there are 65 genes overlapped with these four independently collected AD-associated gene sets together (Fig. 5A).

Figure 5.

Top-ranked genes predicted by LIMO-GCN are more accurate based on four independent AD-associated gene sets. (A) The Venn diagram shows the overlap among four independent AD-associated gene sets. (B) Enrichment analysis on top ranked genes obtained by different prediction methods in novel genes from DisGenet. (D) Enrichment analysis on top ranked genes obtained by different prediction methods in 92 novel GWAS genes identified by Sherva et al.. (E) Enrichment analysis on top ranked genes obtained by different prediction methods in 60 novel GWAS genes identified by Dalmasso et al.. (F) Enrichment analysis on top ranked genes obtained by different prediction methods in 49 novel GWAS genes identified by Bellenguez et al.

We then evaluate the association of the top-ranked genes with AD using the decile enrichment test [4], which is based on binomial test, to validate the association of the top-ranked genes with AD. The result reveals that the top-ranked genes (top 1000 genes after eliminating labeled genes) are significantly enriched in the independent validation sets of novel genes (P-value = 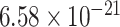,Fig. 5B; P-value = 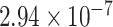, Fig. 5C; P-value = 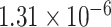, Fig. 5D; P-value =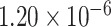, Fig. 5E). Besides, we also compare with the results obtained by the other methods. It shows that the top-ranked genes obtained by LIMO-GCN are more significantly enriched in the novel genes than the other methods (Fig. 5). In detail, we provide detail information of some genes in the top-ranked GWAS genes by our method (Table 2).

Table 2.

The genes supported by independent GWAS

Gene	Score	SNP	P-value
EGFR	0.9971	rs76928645
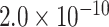
LDLR	0.9934	rs2569540
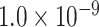
GRB2	0.9894	rs55994995
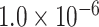
SORT1	0.9886	rs141749679
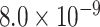
TLR4	0.9792	rs1927914
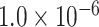
HLA-DQA1	0.9718	rs6605556
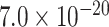
SCN2A	0.9709	rs111535588
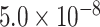
CTSB	0.9556	rs1065712
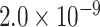
GRN	0.9488	rs5848
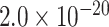
ADAM17	0.9446	rs72777026
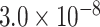
MME	0.9381	rs61762319
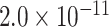
MAF	0.9267	rs450674
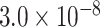
SPI1	0.9212	rs10437655
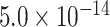
ABCB1	0.9177	rs28381924
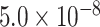
MSR1	0.9139	rs6985143
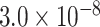
BLNK	0.9035	rs6584063
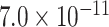
LILRB2	0.9004	rs587709

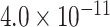
Note: These genes are not included in training data.

We investigate the predictive power of LIMO-GCN on independent genes from GWAS studies and DisGeNet in the perspective of AUROC and AUPRC. First, we select the GWAS summary statistics of the Bellenguez C GWAS study [1] as a GWAS predicted method for comparison (the GWAS summary statistics of the other two GWAS studies are not available). For the other two GWAS studies [34, 35], the significant associations are used to generate an independent dataset of AD-associated genes (with any gene that is in the training data removed). In this way, we collect 151 genes with suggestive association evidence with AD and randomly select 151 genes (not in training set) as negative samples. After repeating the selection of negatives for 100 times, we calculate AUROCs and AUPRCs for all these methods (Supplementary Fig. 3A and B). Among these methods, LIMO-GCN achieves the best performance. Second, we also compare the predictive power of the methods in predicting another set of 65 AD-associated genes collected from DisGeNet as positives, and we randomly select 65 genes as negatives for 100 times (Supplementary Fig. 3C and D). The result indicates that LIMO-GCN performs better in predicting AD-associated genes from DisGeNet too.

The predicted genes by LIMO-GCN show significant association with AD-associated biological processes and AD traits

To gain the biological function, we perform GO enrichment analysis of the top-ranked genes by PANTHER [36]. The genes in the top-ranked list are enriched in AD-associated biological processes [7, 37] (Supplementary Table 2). The most significant enriched AD-associated biological processes [37] include immune response-regulating signaling pathway (GO:0002764, FDR = 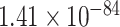), modulation of chemical synaptic transmission (GO:0050804, FDR = 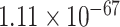), regulation of trans-synaptic signaling (GO:0099177, FDR = 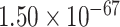), cognition (GO:0050890, FDR = 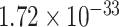), learning or memory (GO:0007611, FDR = 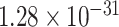), response to amyloid-beta(GO:1904645, FDR = 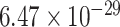), etc (Supplementary Table 2).

In addition, we evaluate the association of the set of top-ranked genes with AD traits including CERAD, Braak Stage score, and CDR (clinical dementia rating scale) using an eigengene-based approach, which is to evaluate how a set of genes are associated with diseases/traits [7, 38]. The results show that the top ranked genes are significantly associated with the three AD traits: the CERAD, Braak Stage score, and CDR score (Supplementary Fig. 4).

Functional module analysis

Motivated by the observation that disease-associated genes often form modules [39], we investigate the functional module for top-ranked genes using a previously established approach [6]. First, we extract a subnetwork from ADFGN by including only the curated AD risk genes and the first decile ranked genes. Second, we identify network modules by applying the GLay community detection algorithm using Cytoscape. In this work, we consider those modules with more than 25 genes. In this way, we obtain five major modules, called M1, M2, M3, M4, and M5 (Fig. 6), which contain 616, 140, 191, 184, and 35 genes (Supplementary Table 3), respectively.

Figure 6.

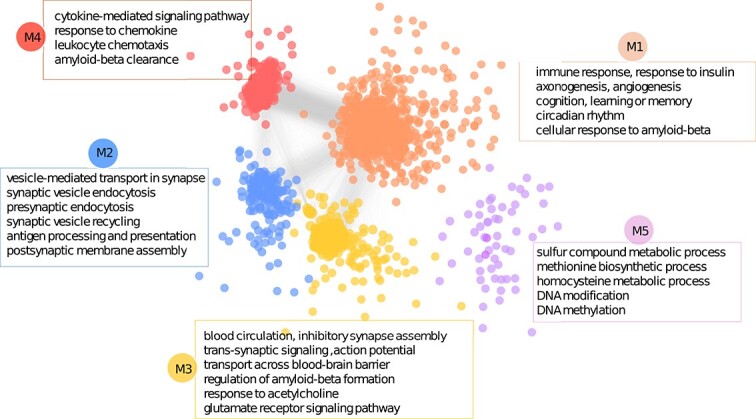
The functional modules enriched in the top-ranked genes. First, a subnetwork is extracted from ADFGN by including only the curated AD risk genes and the top-ranked genes. Second, the functional modules are obtained by applying the GLay community detection algorithm using Cytoscape. The five major modules are labeled with M1, M2, M3, M4, and M5, respectively. Some of the most significant enriched functions for each module are listed.

The genes in M1 are significantly enriched in familiar AD-associated pathways, which include immune response, cellular response to amyloid-beta, cognition, learning or memory, MAPK cascade, circadian rhythm, response to insulin, angiogenesis, and axonogenesis. The immune response plays a significant role in the pathogenesis and progression of AD [40]. In response to amyloid-beta plaques, microglia become chronically activated [41]. Understanding the complex interplay between the immune response and AD is crucial for developing effective therapeutic strategies aimed at modulating neuroinflammation and protecting neurons from immune-mediated damage. The second module (M2) is about vesicle-mediated transport in synapse and synaptic vesicle recycling. Synaptic vesicle recycling is essential for maintaining synaptic transmission and plasticity, and its dysfunction has been implicated in AD [42]. Researchers observed that synaptic activity influences amyloid-beta levels in the brain interstitial fluid, suggesting a link between synaptic vesicle recycling and amyloid-beta metabolism [42].The M3 module shows significant enrichment in transport across blood-brain barrier (BBB), regulation of amyloid-beta formation, response to acetylcholine, glutamate receptor signaling pathway, and blood circulation. AD is associated with increased BBB permeability, which can allow potentially harmful substances to enter the brain and contribute to neuroinflammation and neuronal damage [43]. BBB dysfunction can lead to impaired clearance and increased influx of amyloid-beta, contributing to its accumulation in the brain. Understanding these mechanisms provides valuable insights for developing therapeutic strategies to protect BBB integrity and enhance amyloid-beta clearance in AD [44]. Acetylcholine is a neurotransmitter that plays a crucial role in various brain functions, including learning, memory, and attention. AD patients tend to have low levels of acetylcholine [45]. Module 4 (M4) is significantly enriched in cytokine-mediated signaling pathway, response to chemokine, and amyloid-beta clearance. Cytokines are involved in the neuroinflammatory response and can influence the clearance of amyloid-beta plaques, which are a hallmark of the diseaseAlterations in chemokine receptor expression have been observed in the brains of AD patients, indicating a dysregulation of chemokine signaling in the disease [46]. The pathways enriched in M5 include sulfur compound metabolic process, DNA modification, DNA methylation, methionine biosynthetic process, and homocysteine metabolic process. Sulfur-containing compounds have been studied for their potential effects on AD. Researchers focus on the therapeutic potential of sulfur compounds, including their antioxidant and metal-chelating properties in the treatment of AD [47]. Sulfur compounds have been shown to influence DNA modification and DNA methylation. Studies show that both methionine and homocysteine are risk factors of AD [48, 49]. These findings indicate that the genes in each module are associated with AD. Further research and investigation are needed to fully understand the implications of these enriched biological processes in AD.

Case studies on top-ranked genes

In this section, we conduct case studies on top-ranked genes, including those with AD genetic variation records from GWAS and without such association.

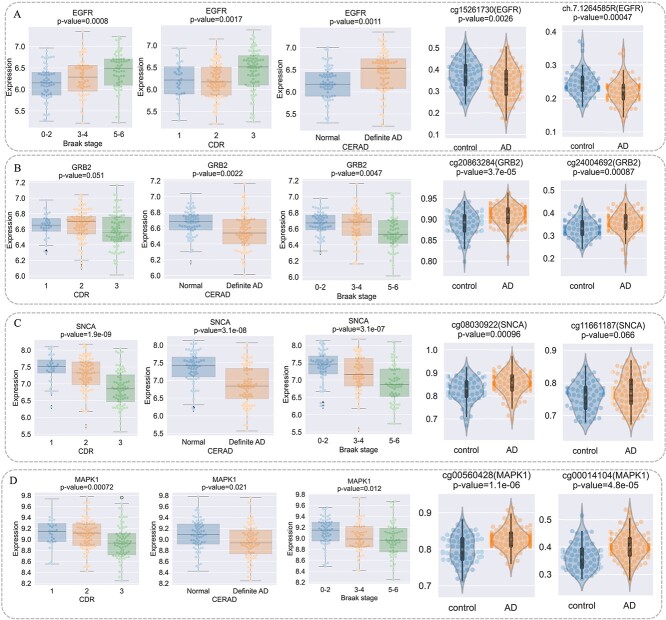
We first investigate the AD-relevance of the top-ranked genes with AD genetic variation through transcriptomic analysis. These genes are EGFR [1], GRB2 [34], TLR4 [50], and MAPK1. To reveal their association with AD, we perform transcriptomic analysis by utilizing independent data from the Mount Sinai Brain Bank (MSBB) study [51]. First, we conduct significant test of correlation between gene expression and phenotypes including Braak stage score, CDR, and CERAD. Next, we perform t-test of methylation level of corresponding CpG sites of genes between control and AD patients from MSBB study. The results show that these three genes have significant correlation with neuropathological and clinical traits (Fig. 7). For example, EGFR shows higher expression in AD patients and its corresponding methylation CpG sites including cg15261730 and ch.7.1264585R appear in lower level in AD patients (Fig. 7A). In addition, GRB2, TLR4, and MAPK1 are also significantly associated with AD phenotypes and their corresponding CpG sites show significant higher or lower levels (Fig. 7B–D).

Figure 7.

The association analysis of EGFR2, GRB2, and TLR4 with AD from neuropathological traits and methylation perspectives. (A) Significant test of correlation between EGFR gene expression and Braak Stage score, CDR, CERAD, and differential methylation of cg15261730 and ch.7.1264585R, which are EGFR CpG sites. (B) Significant test of correlation between GRB2 gene expression and Braak Stage score, CDR, CERAD, and differential methylation of cg20863284 and cg24004692, which are CpG sites of GRB2. (C) Significant test of correlation between TLR4 gene expression and Braak Stage score, CDR, CERAD, and differential methylation of cg02515422 and cg08902905, which are TLR4 CpG sites. (D) Significant test of correlation between MAPK1 gene expression and Braak Stage score, CDR, CERAD, and differential methylation of cg00014104 and cg00560428, which are MAPK1 CpG sites.

For genes with high rankings and no AD genetic variation records from the GWAS database, we selected the top 10 candidates (TNF, ALB, MMP9, AKT1, JUN, STAT1, CD4, FYN, INS, TNFAIP3) for AD neuropathological analysis and literature validation (Supplementary Table 4). We first analyze these genes for association with AD from neuropathological traits of MSBB. We observe TNF, ALB, and INS are not in the gene list of MSBB and the other seven genes show their relevance with AD at least one neuropathological trait (Supplementary Figs 5, 6 and 7). Then we conducted literature validation analysis on these genes of their association with AD (Supplementary Table 4). For example, TNF has been implicated in the pathogenetic processes of AD [52–54] and elevated levels of TNF have been detected in the serum and cerebrospinal fluid (CSF) of AD patients [55]. Besides, TNF inhibitors may slow cognitive decline and enhance daily activities in patients with AD [56].

Discussion

We develop a GCN-based method, namely LIMO-GCN. The feature of this method is that it is able to simultaneously learn the linearity and nonlinearity of the data. The motivation is the linearity in a data could be better modeled by a linear model rather than a nonlinear model because a nonlinear model is theoretically biased from linear model. Using this approach, we train a model to predict AD risk genes. Using a curated dataset of AD risk genes, we show that LIMO-GCN outperforms conventional GCN and other state-of-the-art approaches in predicting AD genes based on 5-fold cross-validation. We focus on the top-ranked genes after excluding any gene in the training data. The predicted genes are found to be more significantly enriched in AD-associated pathways. Besides, these genes are significantly enriched in risk genes identified in recent GWAS. The comparison with other methods indicates that our prediction is more convincing. Furthermore, we also provide functional module analysis showing that the predicted genes are functionally clustered and associated with AD biological processes.

Despite the performance, LIMO-GCN has the potential to be improved. First, the feature data we currently considered include the ADFGN network and biological processes. More feature data can be included to better characterize genes. Second, regarding the method to integrate the knowledge in gene sets, we encode each gene set simply into a binary vector without considering the relationship between gene sets, such as GO terms and biological pathways. In the future, more advanced methods such as biological knowledge graph-based methods [57–59] can be considered to make better use of gene sets. Third, the weight parameter of the linear layer needs to be optimized by users. Designing a method that can automatically select an optimal weight would be interesting.

Although we focus on the prediction of risk genes, LIMO-GCN can be directly extended to make more fine-grained prediction, such as risk single nucleotide polymorphisms (SNPs). Public domains have accumulated an abundant data for obtaining SNP networks and SNP features, making it currently feasible to study the prediction of risk SNPs. As SNP-level predictions complement gene-level predictions, we anticipate that simultaneous prediction at both SNP-level and gene-level may be interesting and may enhance the performance of each other. We plan to study this question in the future.

Although LIMO-GCN is applied to AD in this work, it can be readily applied to other complex diseases like Parkinson disease and obesity as well, given the availability of disease risk genes and related biological networks and the nonlinear relationship between the biological network and risk genes. For example, GWAS have identified a number of risk genes for ASD and schizophrenia, making our proposed method readily applicable to these diseases. We envision that LIMO-GCN could become a valuable approach for understanding disease genetics and will be gain more and more applications in the future.

Key Points

• We propose LIMO-CGN, which models both data linearity and nonlinearity by integrating a linear model with GCN, and it outperforms state-of-the-art methods.

• Multiomics datasets including PPI networks and molecular signatures improve the performance.

• LIMO-GCN predicted novel candidate genes for AD accurately. The association of top-ranked genes with AD was validated using genetic, transcriptomic, and proteomic data from multiple external datasets.

Author contributions

JXW and HDL conceived the whole project. CXL programmed the code, wrote the manuscript, and analyzed the results. JXW and HDL reviewed the manuscript.

Conflict of interest: none.

Funding

This work was supported by STI2030-Major Projects (No. 2022ZD0213700) and National Natural Science Foundation of China (No. 62302426, No. U22A2041).The results published here are in part based on data obtained from the AMP-AD Knowledge Portal (https://adknowledgeportal.synapse.org/). The Mayo RNA-seq data were provided by the following sources: The Mayo Clinic Alzheimer’s Disease Genetic Studies, led by Dr Nilufer Ertekin-Taner and Dr Steven G. Younkin, Mayo Clinic, Jacksonville, FL using samples from the Mayo Clinic Study of Aging, the Mayo Clinic Alzheimer’s Disease Research Center and the Mayo Clinic Brain Bank. Data collection was supported through funding by NIA grants P50 AG016574, R01 AG032990, U01 AG046139, R01 AG018023, U01 AG006576, U01 AG006786, R01 AG025711, R01 AG017216, R01 AG003949, NINDS grant R01 NS080820, CurePSP Foundation, and support from Mayo Foundation. Study data include samples collected through the Sun Health Research Institute Brain and Body Donation Program of Sun City, Arizona. The Brain and Body Donation Program is supported by the National Institute of Neurological Disorders and Stroke (U24 NS072026 National Brain and Tissue Resource for Parkinson’s Disease and Related Disorders); the National Institute on Aging (P30 AG19610 Arizona Alzheimer’s Disease Core Center); the Arizona Department of Health Services (contract 211002, Arizona Alzheimer’s Research Center); the Arizona Biomedical Research Commission (contracts 4001, 0011, 05-901 and 1001 to the Arizona Parkinson’s Disease Consortium) and the Michael J. Fox Foundation for Parkinson’s Research. The MSBB data were generated from postmortem brain tissue collected through the Mount Sinai VA Medical Center Brain Bank and were provided by Dr. Eric Schadt from Mount Sinai School of Medicine. This work was supported in part by the High Performance Computing Platform of Xiangtan University.

Data availability

The data used in this work are from public domains and their sources are provided in the main text.