Skip to main content
NCBI home page
The Journal of Physiology logoLink to The Journal of Physiology
. 1997 Oct 15;504(Pt 2):401–424. doi: 10.1111/j.1469-7793.1997.401be.x

Functional identification of the input-output transforms of motoneurones in the rat and cat.

A V Poliakov 1, R K Powers 1, M D Binder 1
PMCID: PMC1159920  PMID: 9365914

Abstract

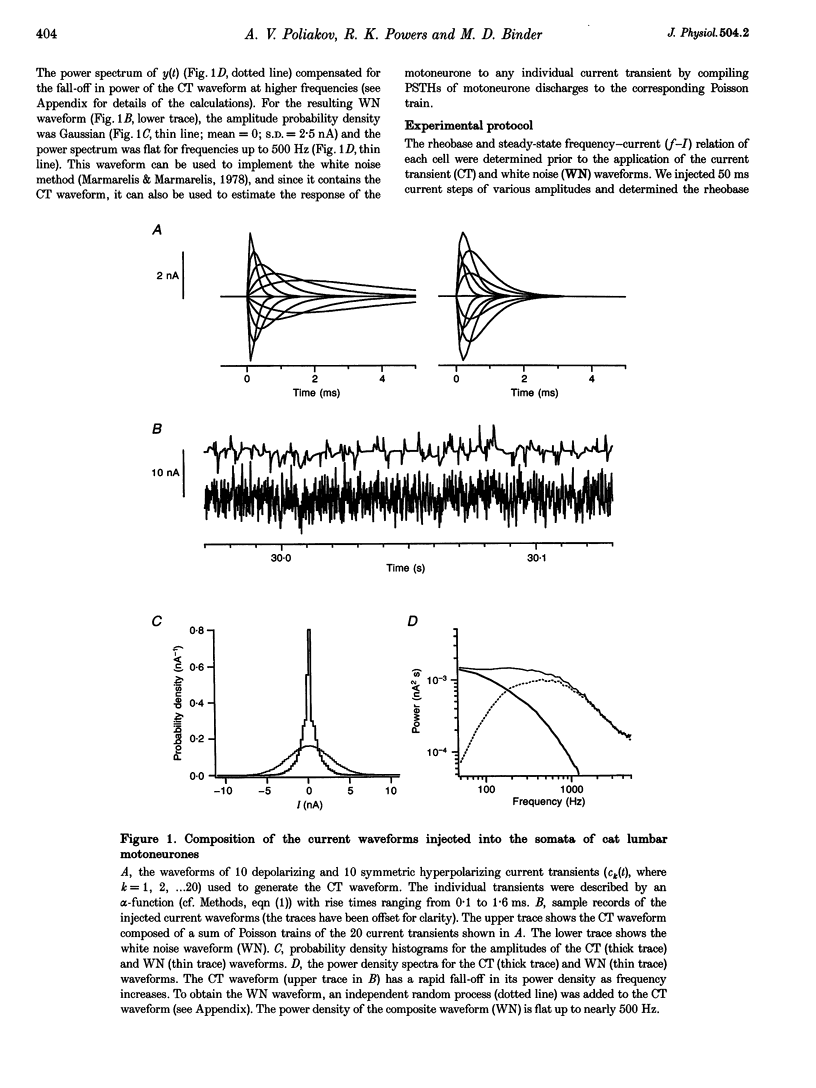
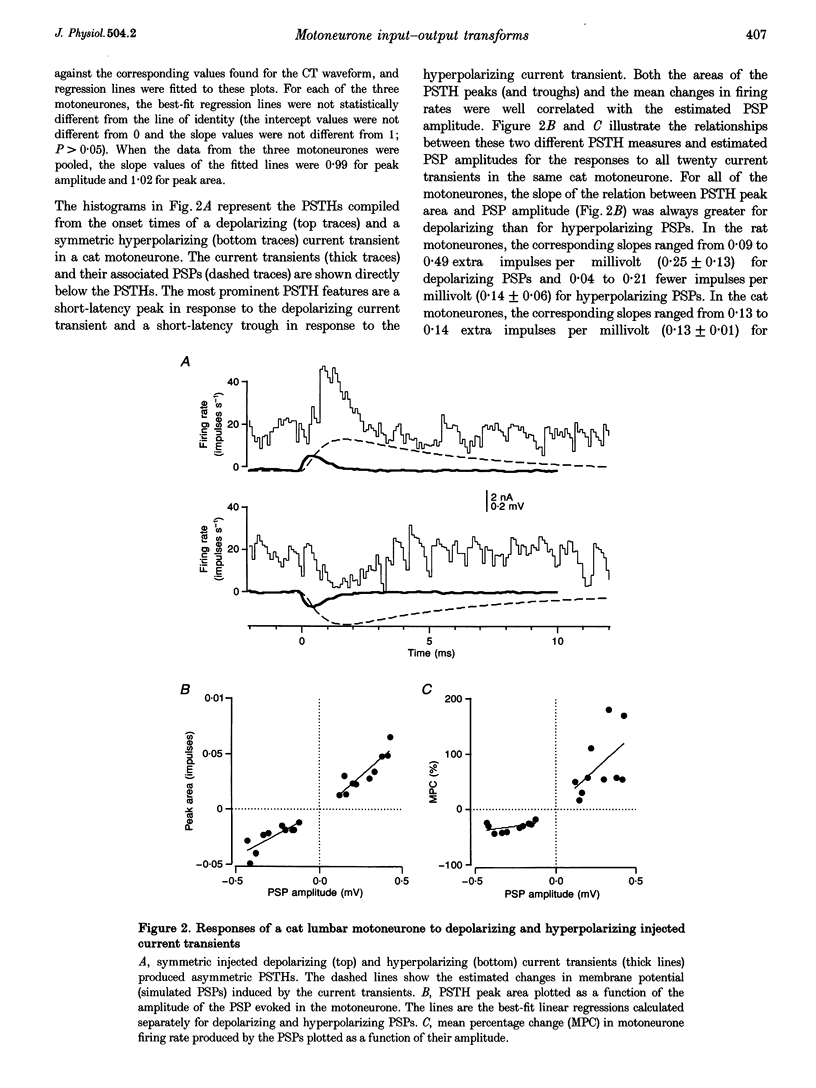
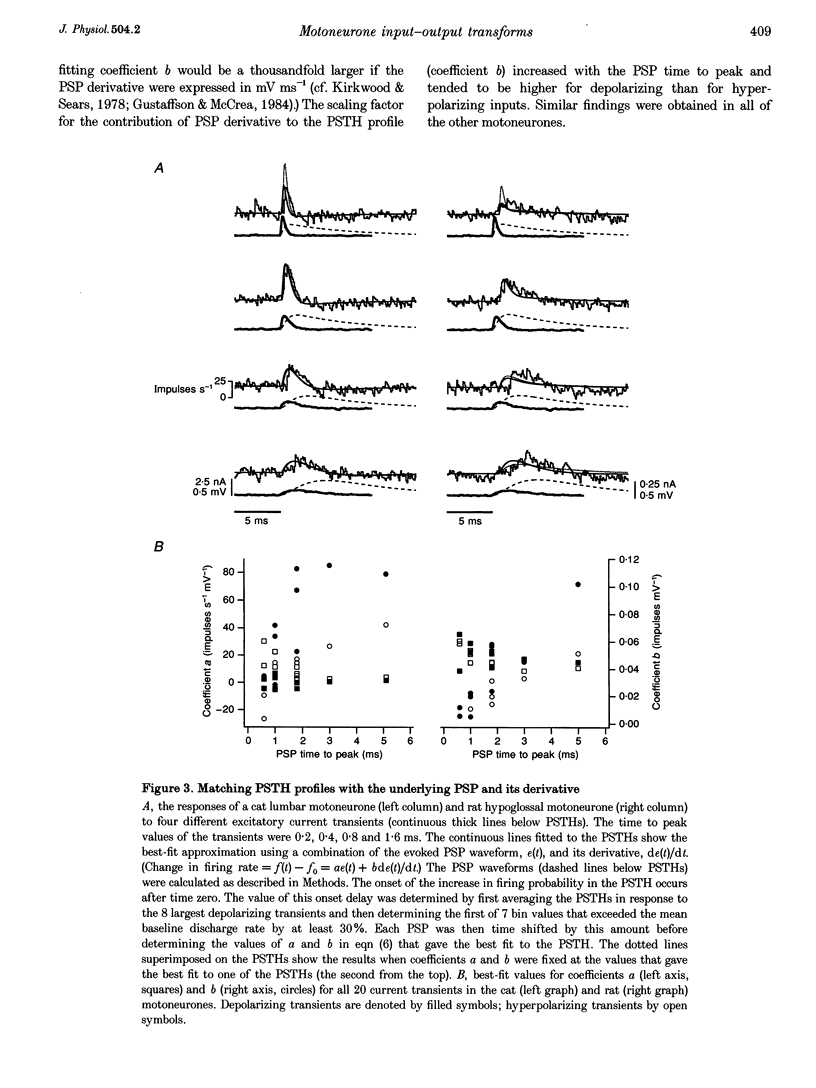
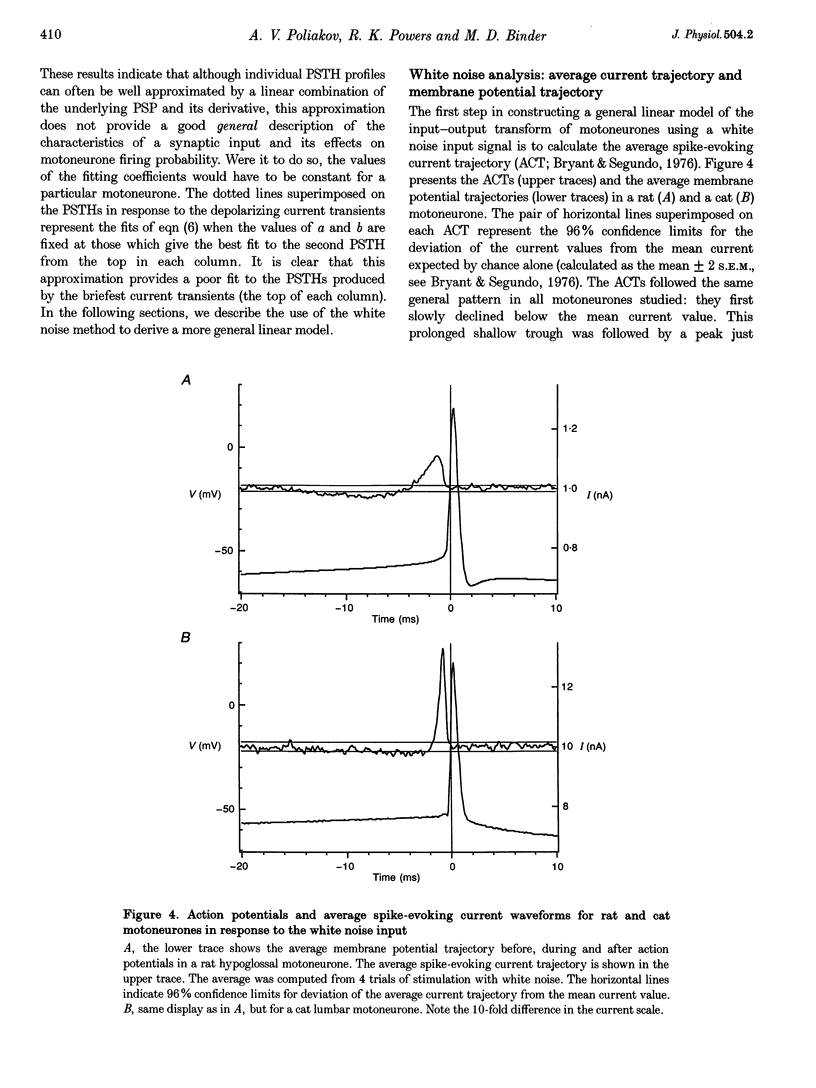
1. We studied the responses of rat hypoglossal and cat lumbar motoneurones to a variety of excitatory and inhibitory injected current transients during repetitive discharge. The amplitudes and time courses of the transients were comparable to those of the synaptic currents underlying unitary and small compound postsynaptic potentials (PSPs) recorded in these cells. Poisson trains of ten of these excitatory and ten inhibitory current transients were combined with an additional independent, high-frequency random waveform to approximate band limited white noise. The white noise waveform was then superimposed on long duration (39 s) suprathreshold current steps. 2. We measured the effects of each of the current transients on motoneurone discharge by compiling peristimulus time histograms (PSTHs) between the times of occurrence of individual current transients and motoneurone discharges. We estimated the changes in membrane potential associated with each current transient by approximating the passive response of the motoneurone with a simple resistance-capacitance circuit. The relations between the features of these simulated PSPs and those of the PSTHs were similar to those reported previously for real PSPs: the short-latency PSTH peak (or trough) was generally longer than the initial phase of the PSP derivative, but shorter than the time course of the PSP itself. Linear models of the PSP to PSTH transform based on the PSP time course, the time derivative of the PSP, or a linear combination of the two parameters could not reproduce the full range of PSTH profiles observed. 3. We also used the responses of the motoneurones to the white noise stimulus to derive zero-, first- and second-order Wiener kernels, which provide a quantitative description of the relation between injected current and discharge probability. The convolution integral computed for an injected current waveform and the first-order Wiener kernel should provide the best linear prediction of the associated PSTH. This linear model provided good matches to the PSTHs associated with a wide range of current transients. However, for the largest amplitude current transients, a significant improvement in the PSTH match was often achieved by expanding the model to include the convolution of the second-order Wiener kernel with the input. 4. The overall transformation of current inputs into firing rate could be approximated by a second-order Wiener model, i.e. a cascade of a dynamic, linear filter followed by a static non-linearity. At a given mean firing rate, the non-linear component of the response of the motoneurone could be described by the square of the linear component multiplied by a constant coefficient. The amplitude of the response of the linear component increased with the average firing rate, whereas the value of the multiplicative coefficient in the non-linear component decreased. As a result, the overall transform could be predicted from the mean firing rate and the linear impulse response, yielding a relatively simple, general description of the motoneurone input-output function.

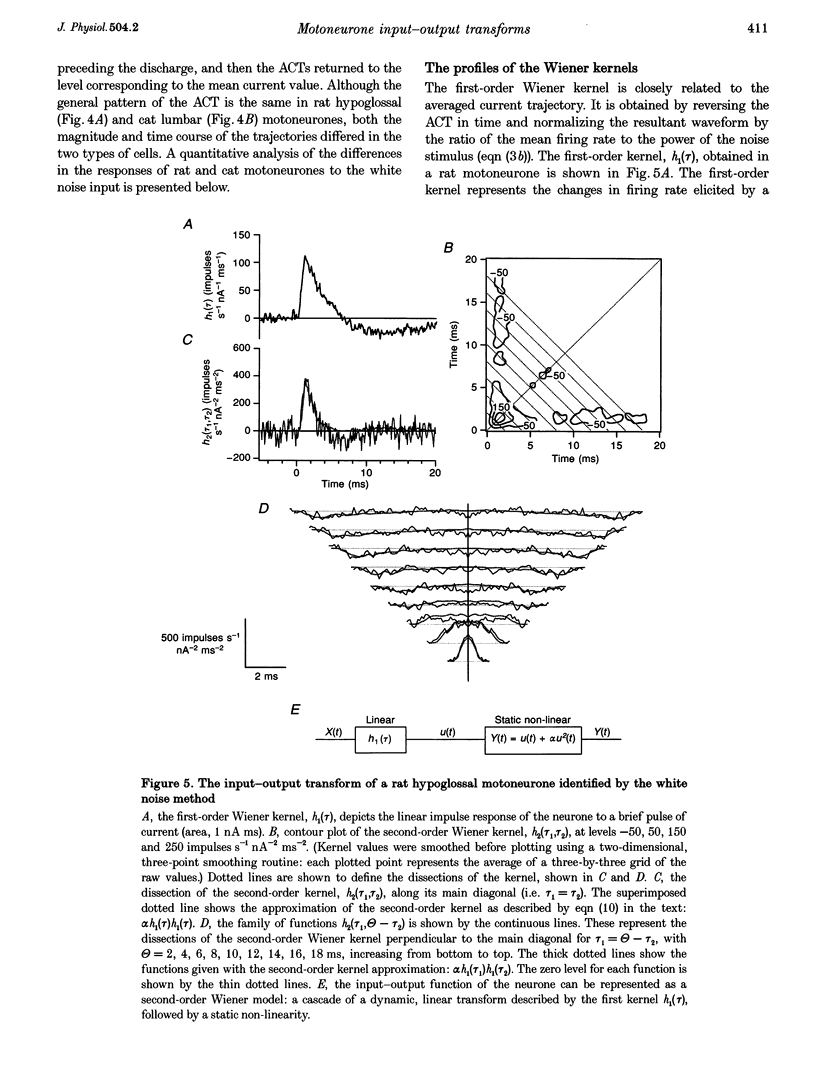
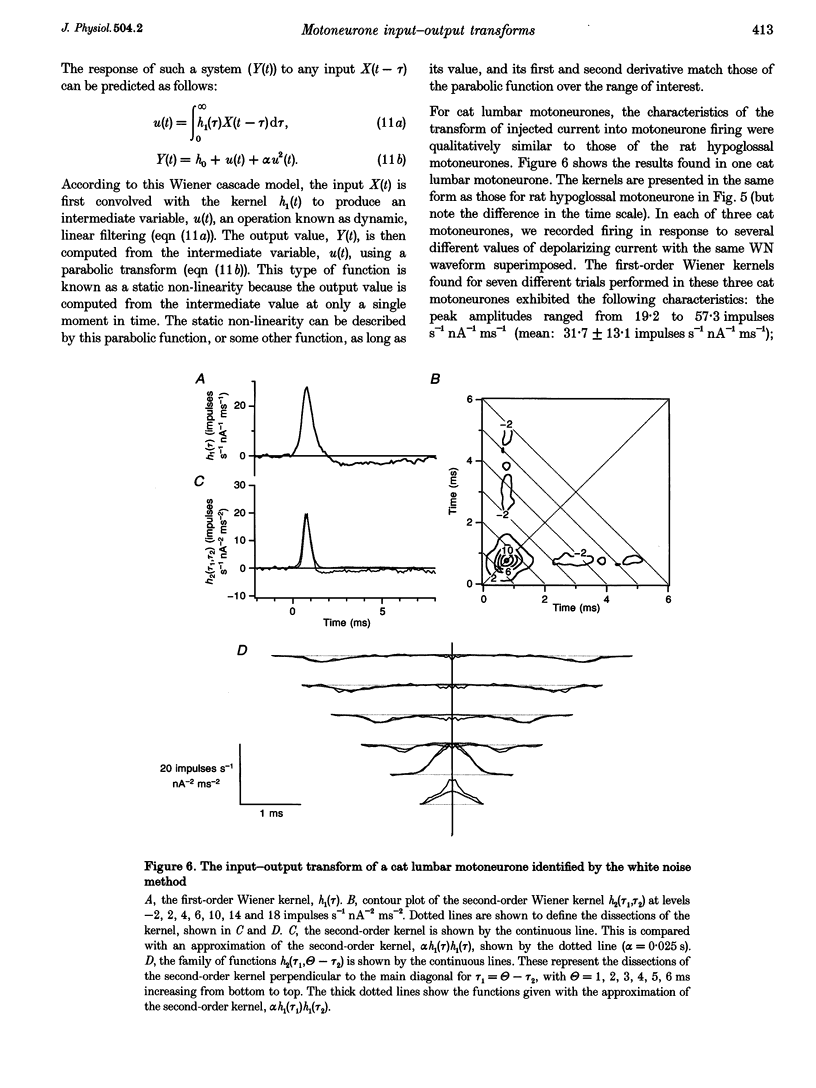
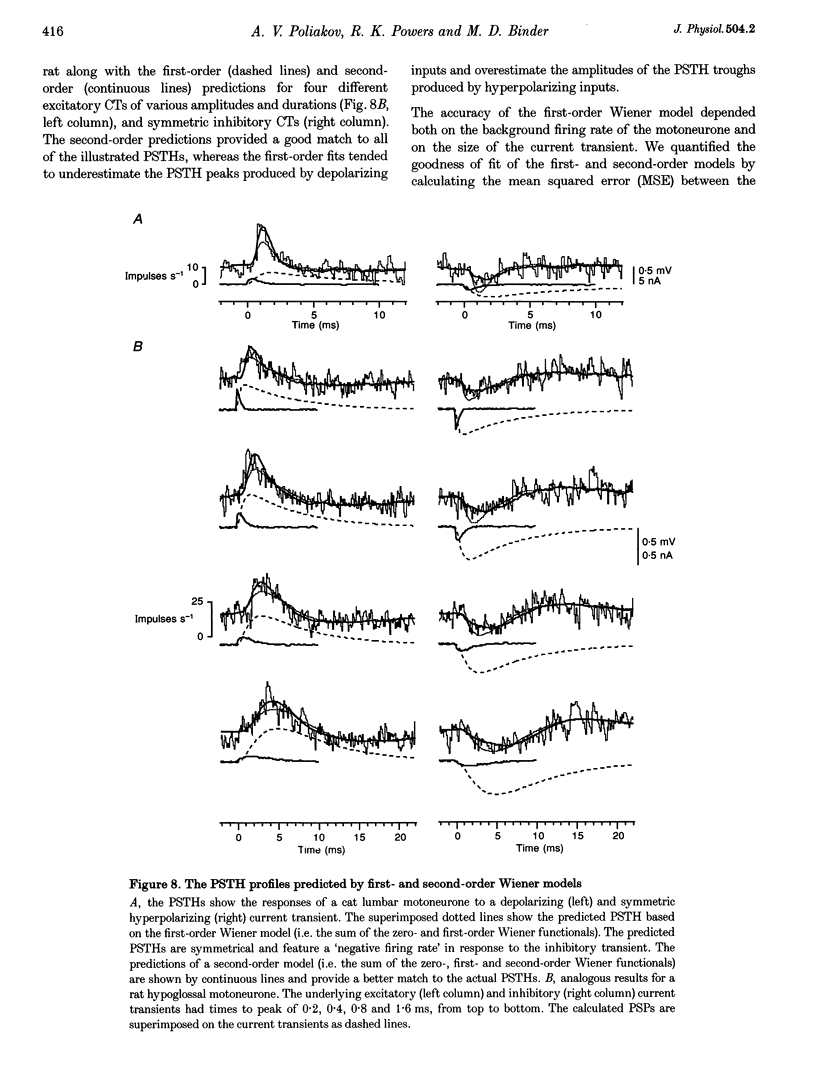
Full text

PDF
401

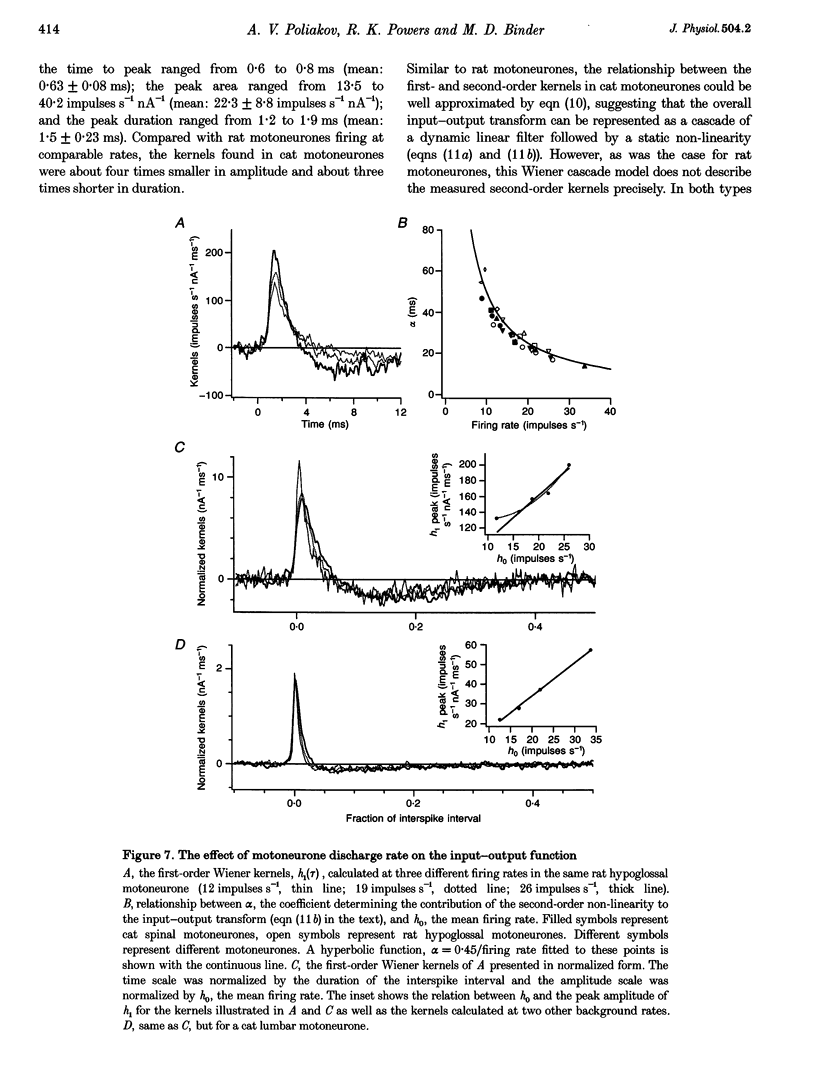
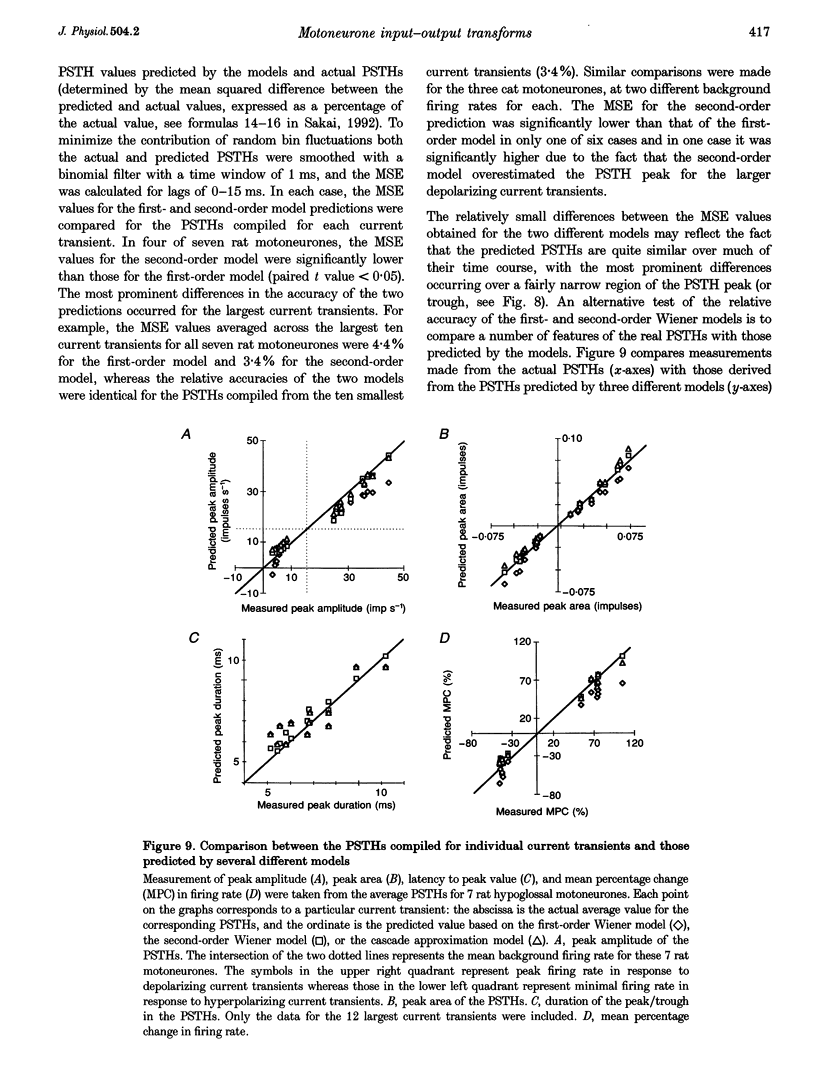
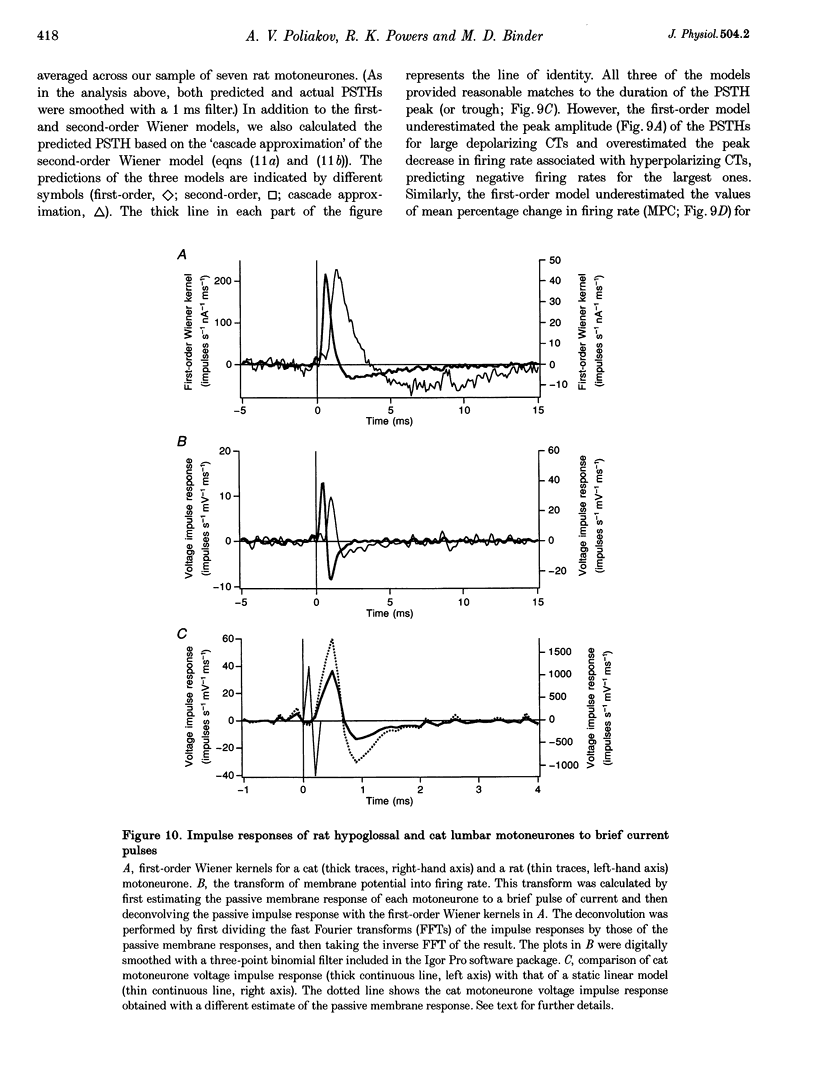
Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Boskov D., Jocic M., Jovanovic K., Ljubisavljevic M., Anastasijevic R. Spike discharges of skeletomotor neurons during random noise modulated transmembrane current stimulation and muscle stretch. Biol Cybern. 1994;71(4):341–348. doi: 10.1007/BF00239621. [DOI] [PubMed] [Google Scholar]
  2. Bryant H. L., Segundo J. P. Spike initiation by transmembrane current: a white-noise analysis. J Physiol. 1976 Sep;260(2):279–314. doi: 10.1113/jphysiol.1976.sp011516. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Calvin W. H. Three modes of repetitive firing and the role of threshold time course between spikes. Brain Res. 1974 Apr 5;69(2):341–346. doi: 10.1016/0006-8993(74)90012-2. [DOI] [PubMed] [Google Scholar]
  4. Conway B. A., Halliday D. M., Rosenberg J. R. Detection of weak synaptic interactions between single Ia afferent and motor-unit spike trains in the decerebrate cat. J Physiol. 1993 Nov;471:379–409. doi: 10.1113/jphysiol.1993.sp019906. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cope T. C., Fetz E. E., Matsumura M. Cross-correlation assessment of synaptic strength of single Ia fibre connections with triceps surae motoneurones in cats. J Physiol. 1987 Sep;390:161–188. doi: 10.1113/jphysiol.1987.sp016692. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ellaway P. H. Cumulative sum technique and its application to the analysis of peristimulus time histograms. Electroencephalogr Clin Neurophysiol. 1978 Aug;45(2):302–304. doi: 10.1016/0013-4694(78)90017-2. [DOI] [PubMed] [Google Scholar]
  7. Fetz E. E., Cheney P. D., Mewes K., Palmer S. Control of forelimb muscle activity by populations of corticomotoneuronal and rubromotoneuronal cells. Prog Brain Res. 1989;80:437–430. doi: 10.1016/s0079-6123(08)62241-4. [DOI] [PubMed] [Google Scholar]
  8. Fetz E. E., Gustafsson B. Relation between shapes of post-synaptic potentials and changes in firing probability of cat motoneurones. J Physiol. 1983 Aug;341:387–410. doi: 10.1113/jphysiol.1983.sp014812. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. French A. S., Korenberg M. J. A nonlinear cascade model for action potential encoding in an insect sensory neuron. Biophys J. 1989 Apr;55(4):655–661. doi: 10.1016/S0006-3495(89)82863-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gustafsson B., McCrea D. Influence of stretch-evoked synaptic potentials on firing probability of cat spinal motoneurones. J Physiol. 1984 Feb;347:431–451. doi: 10.1113/jphysiol.1984.sp015074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. HODGKIN A. L., HUXLEY A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952 Aug;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Haddad G. G., Donnelly D. F., Getting P. A. Biophysical properties of hypoglossal neurons in vitro: intracellular studies in adult and neonatal rats. J Appl Physiol (1985) 1990 Oct;69(4):1509–1517. doi: 10.1152/jappl.1990.69.4.1509. [DOI] [PubMed] [Google Scholar]
  13. Hunter I. W., Korenberg M. J. The identification of nonlinear biological systems: Wiener and Hammerstein cascade models. Biol Cybern. 1986;55(2-3):135–144. doi: 10.1007/BF00341929. [DOI] [PubMed] [Google Scholar]
  14. Kirkwood P. A. On the use and interpretation of cross-correlations measurements in the mammalian central nervous system. J Neurosci Methods. 1979 Aug;1(2):107–132. doi: 10.1016/0165-0270(79)90009-8. [DOI] [PubMed] [Google Scholar]
  15. Kirkwood P. A., Sears T. A. The synaptic connexions to intercostal motoneurones as revealed by the average common excitation potential. J Physiol. 1978 Feb;275:103–134. doi: 10.1113/jphysiol.1978.sp012180. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Knox C. K. Cross-correlation functions for a neuronal model. Biophys J. 1974 Aug;14(8):567–582. doi: 10.1016/S0006-3495(74)85936-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Knox C. K., Poppele R. E. Correlation analysis of stimulus-evoked changes in excitability of spontaneously firing neurons. J Neurophysiol. 1977 May;40(3):616–625. doi: 10.1152/jn.1977.40.3.616. [DOI] [PubMed] [Google Scholar]
  18. Korenberg M. J., French A. S., Voo S. K. White-noise analysis of nonlinear behavior in an insect sensory neuron: kernel and cascade approaches. Biol Cybern. 1988;58(5):313–320. doi: 10.1007/BF00363940. [DOI] [PubMed] [Google Scholar]
  19. Korenberg M. J., Sakai H. M., Naka K. Dissection of the neuron network in the catfish inner retina. III. Interpretation of spike kernels. J Neurophysiol. 1989 Jun;61(6):1110–1120. doi: 10.1152/jn.1989.61.6.1110. [DOI] [PubMed] [Google Scholar]
  20. Matthews P. B. Relationship of firing intervals of human motor units to the trajectory of post-spike after-hyperpolarization and synaptic noise. J Physiol. 1996 Apr 15;492(Pt 2):597–628. doi: 10.1113/jphysiol.1996.sp021332. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Moore G. P., Auriemma R. A. Prediction of muscle stretch receptor behavior using Wiener kernels. Brain Res. 1985 Apr 1;331(1):185–189. doi: 10.1016/0006-8993(85)90733-4. [DOI] [PubMed] [Google Scholar]
  22. Moore G. P., Perkel D. H., Segundo J. P. Statistical analysis and functional interpretation of neuronal spike data. Annu Rev Physiol. 1966;28:493–522. doi: 10.1146/annurev.ph.28.030166.002425. [DOI] [PubMed] [Google Scholar]
  23. Moore G. P., Segundo J. P., Perkel D. H., Levitan H. Statistical signs of synaptic interaction in neurons. Biophys J. 1970 Sep;10(9):876–900. doi: 10.1016/S0006-3495(70)86341-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Person R. S., Kudina L. P. Discharge frequency and discharge pattern of human motor units during voluntary contraction of muscle. Electroencephalogr Clin Neurophysiol. 1972 May;32(5):471–483. doi: 10.1016/0013-4694(72)90058-2. [DOI] [PubMed] [Google Scholar]
  25. Poliakov A. V., Powers R. K., Sawczuk A., Binder M. D. Effects of background noise on the response of rat and cat motoneurones to excitatory current transients. J Physiol. 1996 Aug 15;495(Pt 1):143–157. doi: 10.1113/jphysiol.1996.sp021580. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Powers R. K. A variable-threshold motoneuron model that incorporates time- and voltage-dependent potassium and calcium conductances. J Neurophysiol. 1993 Jul;70(1):246–262. doi: 10.1152/jn.1993.70.1.246. [DOI] [PubMed] [Google Scholar]
  27. Powers R. K., Binder M. D. Experimental evaluation of input-output models of motoneuron discharge. J Neurophysiol. 1996 Jan;75(1):367–379. doi: 10.1152/jn.1996.75.1.367. [DOI] [PubMed] [Google Scholar]
  28. Rall W. Distinguishing theoretical synaptic potentials computed for different soma-dendritic distributions of synaptic input. J Neurophysiol. 1967 Sep;30(5):1138–1168. doi: 10.1152/jn.1967.30.5.1138. [DOI] [PubMed] [Google Scholar]
  29. Rall W. Time constants and electrotonic length of membrane cylinders and neurons. Biophys J. 1969 Dec;9(12):1483–1508. doi: 10.1016/S0006-3495(69)86467-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Reyes A. D., Fetz E. E. Effects of transient depolarizing potentials on the firing rate of cat neocortical neurons. J Neurophysiol. 1993 May;69(5):1673–1683. doi: 10.1152/jn.1993.69.5.1673. [DOI] [PubMed] [Google Scholar]
  31. Sakai H. M. White-noise analysis in neurophysiology. Physiol Rev. 1992 Apr;72(2):491–505. doi: 10.1152/physrev.1992.72.2.491. [DOI] [PubMed] [Google Scholar]
  32. Sawczuk A., Powers R. K., Binder M. D. Spike frequency adaptation studied in hypoglossal motoneurons of the rat. J Neurophysiol. 1995 May;73(5):1799–1810. doi: 10.1152/jn.1995.73.5.1799. [DOI] [PubMed] [Google Scholar]
  33. Stuart G. J., Redman S. J. Voltage dependence of Ia reciprocal inhibitory currents in cat spinal motoneurones. J Physiol. 1990 Jan;420:111–125. doi: 10.1113/jphysiol.1990.sp017903. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Viana F., Bayliss D. A., Berger A. J. Postnatal changes in rat hypoglossal motoneuron membrane properties. Neuroscience. 1994 Mar;59(1):131–148. doi: 10.1016/0306-4522(94)90105-8. [DOI] [PubMed] [Google Scholar]
  35. Viana F., Bayliss D. A., Berger A. J. Repetitive firing properties of developing rat brainstem motoneurones. J Physiol. 1995 Aug 1;486(Pt 3):745–761. doi: 10.1113/jphysiol.1995.sp020850. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES