Molecular-scale insights into the electrical double layer at oxide-electrolyte interfaces

Abstract

The electrical double layer (EDL) at metal oxide-electrolyte interfaces critically affects fundamental processes in water splitting, batteries, and corrosion. However, limitations in the microscopic-level understanding of the EDL have been a major bottleneck in controlling these interfacial processes. Herein, we use ab initio-based machine learning potential simulations incorporating long-range electrostatics to unravel the molecular-scale picture of the EDL at the prototypical anatase TiO₂-electrolyte interface under various pH conditions. Our large-scale simulations, capable of capturing interfacial water dissociation/recombination reactions and electrolytic proton transport, provide unprecedented insights into the detailed structure of the EDL. Moreover, the larger capacitance of the EDL under basic relative to acidic conditions, originating from the higher affinity of the cations for the oxide surface, is found to give rise to distinct charging mechanisms on negative and positive surfaces. Our results are validated by the agreement between the computed EDL capacitance and experimental data.

Microscopic understanding of the electrical double layer (EDL) is key to optimizing interfacial processes in water splitting and batteries. Here, the authors report the insight of EDL at oxide-electrolyte interfaces with ab initio machine learning simulations that agrees with available experiments.

Introduction

When a metal oxide is interfaced with an aqueous electrolyte with a pH different from its pH point of zero proton charge (pH_PZC), a net charge forms on the surface^1–3: at pH <pH_PZC, the surface adsorbs protons from the electrolyte and becomes positively charged, while at pH > pH_PZC it adsorbs hydroxide ions and becomes negatively charged. Electrolyte ions of opposite charges are then drawn closer to the interface to balance the surface charge. This electrostatic attraction, competing with thermal fluctuations and (de)solvation thermochemistry, leads to inhomogeneous ion distributions near the interface. Additionally, adjacent water molecules reorient in response to the surface and ionic charges. The combination of the charged surface, adjacent ions, and neighboring water molecules constitutes what is known as the electrical double layer (EDL)^1–3. The EDL governs the chemical reactivity and physical properties of the interface and is crucial in diverse environmental, biological, colloidal, and electrochemical processes^4–7.

The EDL has often been described based on the Gouy-Chapman-Stern (GCS) model, which assumes a uniformly charged, laterally homogeneous surface and treats water as a homogeneous dielectric continuum^3,8. However, as the understanding of solid-electrolyte interfaces has advanced through theory and experiment, it has become apparent that the properties of the first few interfacial water layers depend on the surface structure and deviate considerably from those of bulk water⁹, a clear indication of the limitations of the GCS mean-field description^3–5. To overcome these limitations, GCS has been combined with surface complexation models that account for discrete active surface sites^10–13. These approaches have been useful for the interpretation of several experimental data but could not explicitly deal with key features such as the water ions originating from the pH of the solution. Moreover, growing experimental evidence underscores the inadequacy of classical mean-field descriptions in the presence of dynamic events such as proton/electron transfer and chemical reactions^3,4,6,14. There is thus an urgent need for a microscopic understanding of the EDL that goes beyond mean-field theory and semi-empirical descriptions.

Investigations of the EDL at oxide-electrolyte interfaces are notoriously challenging. Experimentally, although surface-sensitive techniques are becoming increasingly available to investigate the structure and dynamics of solid-liquid interfaces^3,15,16, the EDL’s microscopic properties are still difficult to probe. Theoretically, force field simulations and multiscale modeling have been widely used and provided important insights^8,15,17,18, but are generally not accurate enough for describing reactive processes such as water dissociation and proton transfer at aqueous interfaces^19–21. In contrast, density functional theory (DFT)-based ab initio molecular dynamics (AIMD) can in principle provide more accurate information on both atomistic details of the EDL and on macroscopic observables^19–22. However, the computational cost of AIMD simulations makes them practical only for system sizes (hundreds of atoms) and simulation times (tens of picoseconds) that are often insufficient to characterize the EDL and pH-dependent surface chemistry^21–23. For example, AIMD provided estimates of Helmholtz capacitances at oxide-electrolyte interfaces^19,24,25, but could not predict equilibrium ion distributions in the EDL, for which longer simulation times and larger cells would be needed.

In the past few years, machine-learned potentials (MLPs)^26–30 have emerged as a viable approach to enable large-scale ab initio-level simulations of bulk systems, interfaces and reactive processes^{21,23,31–34}. Of such MLP methods, the Deep Potential (DP) scheme^27,28 has been successfully applied to model bulk aqueous electrolytes³¹ and water-oxide interfaces^{21,23,32–34}. Moreover, this scheme has recently been extended to include long-range electrostatic interactions³⁵, a component missing in standard MLPs but found to be important for simulating the acid-base chemistry in water³⁶.

In this work, we use the deep potential long-range (DPLR) method³⁵ to conduct large-scale molecular dynamics simulations of the anatase TiO₂ (101) surface in contact with electrolyte solutions at various pHs. TiO₂ is a typical functional oxide and one of the most widely used materials in (photo-)electrochemistry^37–39. Our simulations provide a comprehensive molecular-scale picture of the EDL at TiO₂ interfaces including the occurrence of distinct microscopic surface charging mechanisms at low and high pHs. We also developed a method to calculate the electrostatic potential profile with ab initio DFT accuracy that enabled us to evaluate the interfacial capacitance due to the adsorption of protons or hydroxide ions and the corresponding counterions, a macroscopic property measurable from experiments that is highly reflective of the EDL’s nature^19,24,25,40. The computed capacitances agree with experimental results⁴⁰, underscoring the reliability of our ab initio-based, machine-learned description of the EDL.

Results and discussion

Structure of the EDL

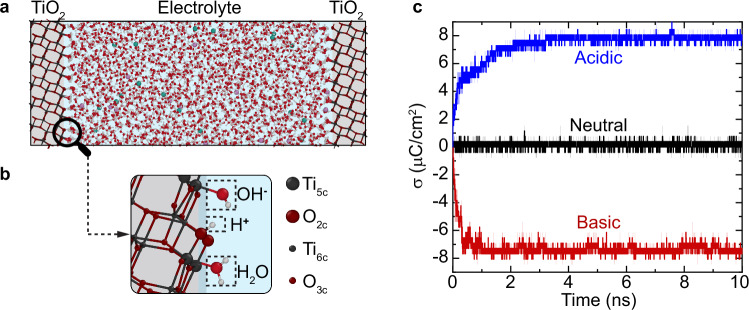
To characterize the EDL, we performed DPLR molecular dynamics simulations on periodically repeated systems consisting of a five-layer anatase (101) slab with a ($30.7\mathrm{\AA }\times 33.9\mathrm{\AA }$) surface cell in contact with a 67 Å thick aqueous electrolyte (Fig. 1a). In the following discussion we focus on three experimentally relevant solutions⁴⁰, namely neutral 0.4 M NaCl (NaCl_(aq), composed of 2376 H₂O molecules and 18 NaCl), acidic 0.4 M NaCl + 0.2 M HCl (with 10 HCl added to the neutral solution), and basic 0.4 M NaCl + 0.2 M NaOH (with 10 NaOH added to the neutral solution). In the electrolyte, NaCl serves as a background salt, and adding 0.2 M NaOH or HCl changes the pH of the initial configuration from a nominal value of 7 to 13.3 or 0.7. Additional results for TiO₂ interfaces with electrolytes containing higher concentrations of NaOH and HCl are reported in Supplementary Section 10 and Fig. 3c. The magnified view of the interface (Fig. 1b) shows that the TiO₂ surface exposes five-fold coordinated titanium (Ti_5c) and two-fold coordinated oxygen (O_2c) atoms (108 Ti_5c and 108 O_2c sites in total, considering the two surfaces of the slab). The undercoordinated Ti_5c atoms act as (Lewis) acid sites for the adsorption of water or OH⁻ ions, while the O_2c atoms act as Brønsted bases which can accept a hydrogen bond or a H⁺ from water. Water dissociation thus results in protons on O_2c sites (bridging hydroxyls) and OH⁻ groups on Ti_5c sites (terminal hydroxyls), as depicted in Fig. 1b.

Fig. 1. Surface charging.

a Supercell of the anatase (101)-electrolyte interface employed in the DPLR simulations. The TiO₂ regions are shaded in gray, while the electrolyte region is shaded in blue. b Magnified view of the interface showing surface undercoordinated Ti_5c and O_2c sites and adsorbed H₂O, H⁺ and OH⁻ at these sites. For visual clarity, only relevant atoms are shown. c Surface charge density $\sigma =e\left({\mathrm{N}}_{\mathrm{H}+}-{\mathrm{N}}_{\mathrm{OH}-}\right)/S$, where S is the surface area, as a function of simulation time for anatase (101) in contact with three different types of electrolytes. All results and error bars (shaded areas) were derived from simulations using two independent DPLR models. Source data are provided as a Source Data file.

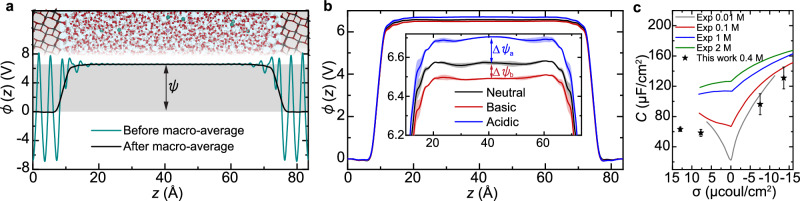
Fig. 3. Potential drop at interfaces.

a Representative snapshot from our DPLR simulation of the anatase TiO₂-NaCl solution interface (top) and plane-averaged electrostatic potential $\varphi$ along the $z$-direction, before and after macroscopic (macro-) average (bottom). The potential drop $\psi$ is determined from the macro-averaged potential difference between the bulk solid and bulk liquid regions. b Macro-averaged electrostatic potential at the TiO₂ interfaces with three different types of electrolytes. All curves are aligned to zero $z=0$. The magnified view in the inset shows the potential drop differences between the negatively (positively) charged surface and the neutral surface, denoted as $\mathrm{\Delta }{\psi }_b$ ($\mathrm{\Delta }{\psi }_a$), which is obtained by further averaging the macro-averaged electrostatic potentials over 31.8 $\ddot{\mathrm{A}}$ < z < 51.8 $\ddot{\mathrm{A}}$. All results and error bars were derived from simulations using two independent DPLR models. c Comparison between our computed interfacial capacitance (star symbols) and experiments for rutile TiO₂-aqueous NaNO₃ interfaces (solid lines)^40[,51. Different colors of the experimental curves represent different concentrations of the background NaNO₃ salt. Source data are provided as a Source Data file.

For the TiO₂-NaCl_(aq) interface, the simulations show an equal number of adsorbed H⁺ (${\mathrm{N}}_{\mathrm{H}+}$) and OH^– (${\mathrm{N}}_{\mathrm{OH}-}$) species, originating from the dissociation of adsorbed water molecules. Consequently, the surface charge density (black line in Fig. 1c) is close to zero. This suggests that the pH of the neutral NaCl_(aq) is approximately equal to the pH_PZC of anatase, a result consistent with the experimental pH_PZC of anatase being around 6 ( ± 1)^13,41,42. To support this inference, we performed enhanced sampling DPLR simulations to explicitly evaluate the pH_PZC of the anatase (101)-neat water interface (Supplementary Section 4). We focused on neat water in this simulation because pH_pzc is defined to reflect only the protonation reactions⁴³, unaffected by the presence of salt ions. We obtained a pH_PZC of 7.0$\pm 0.1$, a value within the experimental range.

Interfaces of TiO₂ with acidic and basic solutions were generated starting from an equilibrated configuration of TiO₂-NaCl_(aq), and subsequently adding 0.2 M HCl or NaOH at random positions within the electrolyte solution. All additional H⁺ (or OH⁻) ions were gradually adsorbed on the surface within 3 ns, leading to a positively (or negatively) charged surface (Fig. 1c). Averaging over 3-10 ns, we obtained surface charge densities ${{\sigma }_a=7.69\pm 0.04\mu C/cm}^2$ and${{\sigma }_b=-7.54\pm 0.13\mu C/cm}^2$ at the interfaces with the acidic and basic electrolyte, respectively. In experiments¹³, such values of ${\sigma }_a$ and ${\sigma }_b$ equilibrate with bulk solutions that have pHs of ≈ 4.4 and 7.4, respectively. For our simulation cell size (2376 water molecules), a pH value of 4.4 (or 7.4) corresponds to a negligible amount of ~$2\times {10}^{-3}$ H⁺ (or $1\times {10}^{-5}$ OH⁻) ions in the electrolyte solution. This is consistent with the fact that there are no H⁺ or OH⁻ ions left in the bulk region of our electrolyte solution.

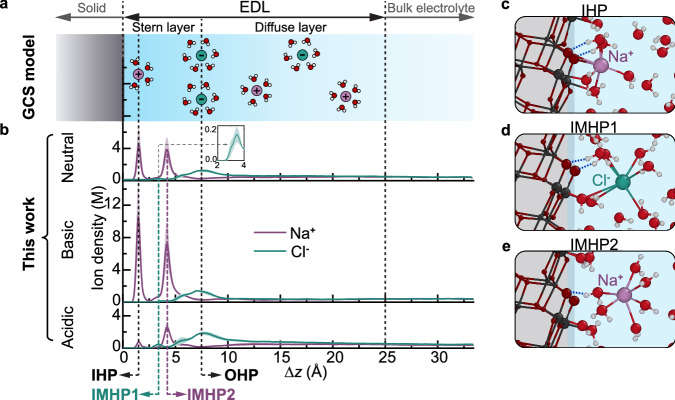
Upon surface charging, an EDL forms to compensate for the surface charge^1–3. In the GCS model, the electrolyte ions form discrete (Helmholtz) planes, with the outer Helmholtz plane (OHP) separating the Stern layer from a diffuse layer where the ions follow the Poisson-Boltzmann distribution (Fig. 2a). The counter-ion and co-ion densities converge to an equal value in the EDL’s tail, indicating that the electrolyte recovers its bulk-like behavior. Within the Stern layer, the inner Helmholtz plane (IHP) is formed by ions that are specifically adsorbed at the surface and lack a complete hydration shell (Fig. 2a).

Fig. 2. Ion distribution.

a Schematic of the Gouy-Chapman-Stern (GCS) model of the electric double layer (EDL): the outer Helmholtz plane (OHP) separates the EDL into Stern and diffuse layers. Within the Stern layer, the inner Helmholtz plane (IHP) is defined by the distance at which ions specifically adsorb. b Ion density distributions as functions of distance $\mathrm{\Delta }z=z-z_{\mathrm{surface}}$ from the solid surface, obtained from DPLR simulations of anatase (101) in contact with different electrolytes; the position of the solid surface, $z_{\mathrm{surface}}$, corresponds to the average position of the O_2c sites. Besides the IHP predicted by the GCS model, these simulations reveal two additional ionic density peaks within the Stern layer, which we define as the intermediate Helmholtz planes (IMHPs). The inset in b amplifies the small IMHP1 peak in the neutral system. The computed ion densities are averaged over the two interfaces in the supercell. All results and error bars were derived from simulations using two independent DPLR models. c–e Illustrative snapshots of the microscopic structures of IHP, IMHP1, and IMHP2. Color code: purple (Na⁺), green (Cl^-), white (H), light red (O in water or water ions), dark red (O in TiO₂), and gray (Ti). Lines between ions and neighboring oxygens indicate distances smaller than the ionic hydration shell radius. Dashed blue lines indicate hydrogen bonds between water and surface O_2c. For visualization purposes, only the most relevant atoms are shown. Source data are provided as a Source Data file.

The electrolyte ion distributions obtained from our simulations are shown in Fig. 2b. The structure of the diffuse layer agrees with that given by the GCS model, i.e., the Cl⁻/Na⁺ density decreases/increases with increasing distance from the OHP until the two densities become identical within the error bars of the simulation. However, the ion distribution within the Stern layer is more complex than suggested by the GCS model and by previous force field simulations^15,18. Specifically, within the Stern layer, we identify not just a single ionic peak, but three distinct peaks: a first Na⁺ peak at 1.5 Å from the surface, followed by a Cl⁻ peak at 3.4 Å of low intensity due to the repulsion between the Cl⁻ and the electronegative O_2c atoms, and another Na⁺ peak at 4.2 Å. The Na⁺ ions forming the first peak are, on average, coordinated to two surface O_2C atoms (Fig. 2c), consistent with previous DFT results¹³. The distance, $r_{\mathrm{Na}-\mathrm{O}2\mathrm{c}}$, between Na⁺ and O_2C fluctuates around 2.3 Å (Supplementary Fig. 17), a value similar to the distance between Na⁺ ions and water molecules in their first hydration shell in bulk solution. With the O_2C atoms substituting hydration water molecules, these Na⁺ ions exhibit incomplete hydration shells (Fig. 2c) and can thus be identified as inner-sphere surface complexes^15,18 and the corresponding peak as the IHP. Instead, the Cl⁻ ions forming the second peak (Fig. 2 d) and the Na⁺ ions contributing to the third peak (Fig. 2e) exhibit complete hydration shells. While this characteristic is consistent with the definition of outer-sphere surface complexes⁴⁴, these ions do not satisfy the OHP criterion that their interactions with the surface involve only long-range electrostatic forces⁴⁵. As shown in Fig. 2d and Fig. 2e, some water molecules in the hydration shell of these ions are either adsorbed on Ti_5c atoms or form strong hydrogen bonds with surface O_2c atoms. Since these surface water molecules have a diffusion coefficient 1~2 orders of magnitude smaller than that of bulk water⁴⁶, these ions can be considered as semi-adsorbed on the surface via surface water molecules. Consequently, these two ionic peaks cannot be classified as either IHP or OHP. In this work, we designate the corresponding layers as intermediate Helmholtz planes (IMHPs), since their peaks fall between the IHP and the OHP. We also find that the ions within the Stern layer are not fixed but can exchange with other ions of the same type in the electrolyte. Specifically, Na⁺ ions in the IHP have a residence time on the order of nanoseconds, while ions in IMHPs have a residence time of tens to hundreds of picoseconds (Supplementary Information Section 5).

In contrast to the GCS prediction that the EDL only forms when a net (electronic or protonic) surface charge is present, our results show that the charge-neutral TiO₂-NaCl_(aq) interface also exhibits an EDL (Fig. 2b). This occurs because, even when the overall surface charge is zero, local charges remain imbalanced. Specifically, the outermost oxide surface layer is composed of electronegative O_2c atoms, which favor the adsorption of Na⁺ ions and, in combination with the water molecules adsorbed or hydrogen bonded to the surface, determine the ionic peak positions (Fig. 2c-e). Therefore, altering the surface charge density modifies the peak intensities of the ion distribution but does not appreciably change their relative positions (Fig. 2b). In particular, regardless of the surface charge, anions dominate at the OHP and in the diffuse layer to compensate the Na⁺ ions in the IMHP2 − another important feature missed by the GCS model.

The water molecules within the EDL exhibit distribution and orientation patterns which, as the ion distributions, are mostly determined by the surface structure. Our DPLR simulations show that the water distribution and orientation undergo subtle changes in response to both the surface charge and the adjacent ions (Supplementary Section 6).

Differential capacitance

The microscopic structure of the EDL determines the differential capacitance C of the interface, which is composed of contributions from the capacitance of the Stern layer ($C_H$, also called Helmholtz capacitance) and the diffuse layer ($C_D$)⁴⁷, with $\frac{1}{C}=\frac{1}{C_H}+\frac{1}{C_D}$. While $C_H$ has been studied previously by AIMD simulations^19,24,25, the calculation of C with ab initio accuracy has been a long-standing challenge due to the long simulation times and large simulation cells needed to equilibrate the EDL. Interestingly, experiments found that, at equivalent magnitudes of charge densities, negatively charged oxide interfaces have a higher capacitance than their positively charged counterparts for metal oxides such as anatase⁴⁰, rutile⁴⁰, and zinc oxide⁴⁸. This is in contrast to the symmetric capacitance predicted by the GCS model, suggesting that the EDL at these oxide surfaces can screen negative surface charges more effectively than positive ones. However, the underlying reason for this phenomenon remains a topic of active debate. Some studies attributed the larger capacitance under basic conditions to the high affinity of cations to the oxide^12,40. In contrast, recent AIMD studies proposed that the difference is due to the distinct properties of water under basic and acidic conditions^24,25,49. For example, Ref ²⁴. attributed it to the larger interfacial water fluctuations under basic conditions, Ref ²⁵. explained it in terms of the orientation of chemisorbed water, and Ref ⁴⁹. attributed it to the water adsorption energy.

To obtain insight into the observed asymmetry of C, we calculated this quantity with ab initio accuracy using our DPLR method. Specifically, starting from the definition of C as the first-order derivative of the surface charge density σ with respect to the electrostatic potential drop ψ, $C=\frac{\mathrm{d}\sigma }{\mathrm{d}\psi }$, we used the finite difference expression $C\approx \frac{\mathrm{\Delta }\sigma }{\mathrm{\Delta }\psi }$, where ∆ represents the deviation of a charged interface from a neutral reference interface. While σ is readily available in simulations (Fig. 1c), ψ depends not only on the distribution of the ions but also on that of valence electrons, which is generally not available in simulations based on force fields. In our DPLR approach³⁵, however, ψ can be explicitly calculated (see “Methods” for details). The average potential profile calculated in this way for the TiO₂-NaCl_(aq) interface is displayed by the green line in Fig. 3a. Within the TiO₂ region, the potential exhibits pronounced oscillations, while the homogeneous and isotropic nature of the liquid electrolyte results in a more uniform profile. Macroscopic averaging⁵⁰ of $\varphi \left(z\right)$ yields the black line in Fig. 3a, from which the potential drop ψ, defined as the potential difference between solid and liquid phases, is extracted. At this point, the capacitance can be calculated. Taking the neutral TiO₂-NaCl_(aq) interface as the reference and using the results in Fig. 1c, we have $\mathrm{\Delta }{\sigma }_b={-7.54\pm 0.13\mu C/cm}^2$ for the TiO₂-NaCl+NaOH basic solution interface, and $\mathrm{\Delta }{{\sigma }_a=7.69\pm 0.04\mu C/cm}^2$ for the TiO₂-NaCl+HCl acidic solution interface. By comparing the macroscopically averaged⁵⁰ electrostatic potential at the acidic and basic solution interfaces with the neutral reference (Fig. 3b), we determine the potential drop differences $\mathrm{\Delta }{\psi }_a=131.6\pm 10.6mV$ and $\mathrm{\Delta }{\psi }_b=-78.3\pm 11.2mV,$ respectively. Consequently, the differential capacitances are $C_a=58.4\pm 4.7\mu F/{cm}^2$ and $C_b=96.2\pm 13.8\mu F/{cm}^2$ under acidic and basic conditions, respectively. As shown in Fig. 3c, our results (which include the computed capacitances at higher HCl and NaOH concentrations reported in Supplementary Section 10) reproduce the experimental trends^40,51 quite satisfactorily. In particular, our calculated ratio of $C_b/C_a=1.6\pm 0.3$ agrees well with previous DFT^19,24 and experimental⁴⁰ results showing $C_b/C_a\approx 1.5$ at similar oxide/electrolyte interfaces.

Based on our simulations, the larger capacitance observed under basic conditions in comparison to acidic ones can be understood as follows. For the negative (positive) surface, the positive Na⁺ (negative Cl⁻) ions are drawn towards the surface to screen the surface charge. However, the abilities of Na⁺ and Cl⁻ to screen the surface charge differ. Figure 2b shows that Na⁺ can approach the surface more closely than Cl⁻ ions because the outermost layer of TiO₂ surface is composed of electronegative O_2c atoms. This allows Na⁺ to screen the surface charge more effectively than Cl^–. In more detail, when the system is negatively charged under basic conditions, the affinity of Na⁺ ions to the electronegative surface O_2c atoms draws them close to the surface, effectively screening the surface OH⁻ ions. This effect is evidenced by Fig. 2b, which shows a significant amplification of the Na⁺ peak intensity when transitioning from a neutral to a basic system. In contrast, when the system is positively charged under acidic conditions, a substantial proportion of O_2c atoms (82% in our acidic system) do not bind H⁺ ions (Fig. 2d). These electronegative O_2c atoms repel Cl^- ions, preventing them from moving close to the surface to screen the surface H⁺ ions. Consequently, the transition from a neutral to an acidic system induces a modest increase in the Cl⁻ peak intensity as shown in Fig. 2b. This leads to a smaller absolute value of $\mathrm{\Delta }{\psi }_b$ than $\mathrm{\Delta }{\psi }_a$, and consequently a larger $C_b$ than $C_a$. Compared to the significant changes of ion distributions at different pHs, the water distribution and orientation undergo smaller changes (Supplementary Section 6). Therefore, our simulations agree with the suggestion that the larger capacitance under basic conditions is primarily due to the higher affinity of cations to the oxide. Differences between our findings and previous AIMD simulations^19,24 are likely related to the higher ion concentrations used in the latter, their short equilibration times, and their focus on the Helmholtz part only of the differential capacitance.

Microscopic surface charging mechanism

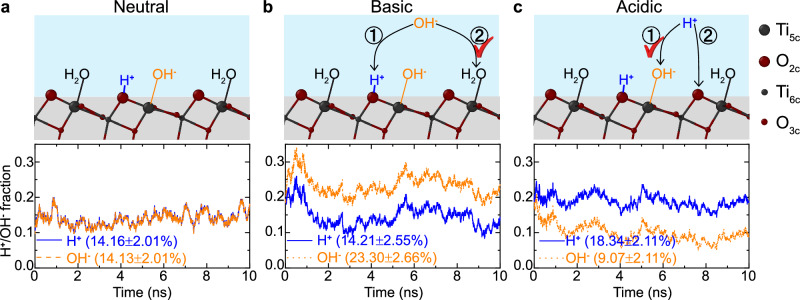
The distinct interfacial capacitances resulting from the higher affinity of cations to the oxide surface, compared to anions, are found to give rise to distinct microscopic charging mechanisms on negative and positive surfaces. As shown in Fig. 4a, for the charge-neutral TiO₂-NaCl_(aq) interface, $14\pm 2\%$ water molecules adsorbed at Ti_5c sites are dissociated into adsorbed H⁺ at O_2c and OH⁻ at Ti_5c, with zero net surface charge. Starting with an equilibrated TiO₂-NaCl_(aq) configuration, when we add bases or acids into the electrolyte, the OH⁻ or H₃O⁺ ions have two potential pathways to be adsorbed at the surface. For an electrolyte OH^– (Fig. 4b), one pathway is to recombine with a surface H⁺ ion at the O_2c site to form a water molecule in the liquid, which decreases the surface’s H⁺ population. Another pathway is to recombine with an H⁺ from an adsorbed H₂O, which results in an additional OH⁻ ion adsorbed at the surface Ti_5c site. Similarly, an electrolyte H⁺ can either recombine with a surface terminal OH⁻ into a water molecule or occupy an empty O_2c site (Fig. 4c). Although both pathways result in the same net surface charge σ, the total number of surface charges, N_SC = N_H⁺ + N_OH⁻, is different. The first pathway reduces N_SC, whereas the second increases it.

Fig. 4. Surface charging mechanisms.

Time evolution of the surface H⁺ and OH⁻ coverage on TiO₂ interfaces with (a) neutral, (b) basic, and (c) acidic solutions. The legends list the surface ion coverages averaged between 3-10 ns. Schematics in (a) show molecularly absorbed H₂O at Ti_5C sites and an H₂O dissociated into adsorbed H⁺ at O_2c and OH⁻ at Ti_5C sites. Schematics in (b and c) illustrate two potential pathways an additional water ion might take upon adsorption to the surface. Specifically, in b, a solvated OH⁻ can either recombine with an adsorbed H⁺ to form an H₂O molecule (pathway 1) or replace an adsorbed H₂O molecule (pathway 2). Similarly, in (c) a solvated H⁺ can either recombine with an adsorbed OH⁻ to form an H₂O molecule (pathway 1) or get adsorbed at a O_2c site (pathway 2). Pathway 2 is preferred in (b) while pathway 1 is preferred in (c) as discussed in the text. Source data are provided as a Source Data file.

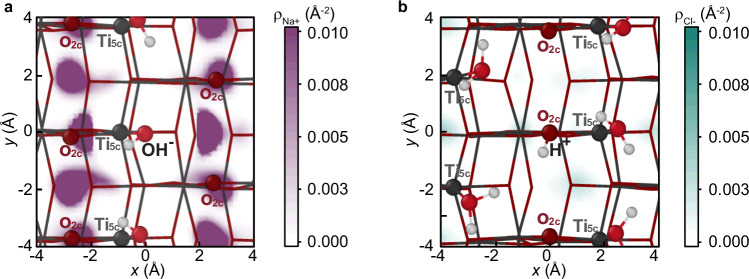
The averaged ion coverages in Fig. 4 suggest that OH^– ions prefer the second pathway (increasing N_SC), whereas protons slightly prefer the first (decreasing N_SC). As a result, if we define the water dissociation fraction as the smaller value between the fraction of surface H⁺ ions and the fraction of surface OH⁻ ions, the average water dissociation fraction decreases significantly (to ~9%) with the acidic electrolyte whereas it remains approximately the same as that of the neutral interface under basic conditions, consistent with the increase of water dissociation fraction with the pH reported in a previous AIMD study²⁵. These trends can be related to the different capacitances under basic and acidic conditions. The large capacitance under basic conditions indicates a strong ability of the EDL to screen the OH⁻ surface charge. This is evidenced by the high number density of Na⁺ ions surrounding an OH⁻ surface ion, as shown in Fig. 5a. Consequently, the surface can accommodate more OH⁻ ions in-plane, making the second pathway favorable under basic condition. In contrast, the small capacitance under acidic conditions reflects a weak ability of the EDL to screen the H⁺ surface charge. This is demonstrated by the low probability of Cl^- ions surrounding an H⁺ surface ion, as shown in Fig. 5b. As a result, the surface cannot accommodate more H⁺ ions in-plane, making the first pathway favorable under acidic conditions. The fact that negatively charged surfaces allow a larger density of surface hydroxyl groups is important in photocatalysis because these groups can trap photo-generated holes and form hydroxyl radicals^38,52, which are key intermediates of many photo-oxidation reactions. The photooxidation of water is indeed known to be faster at high pH⁵³.

Fig. 5. In-plane ion distribution.

Top view of the anatase TiO₂ surface, with x and y corresponding to the [$\overline{1}01$] and [010] directions, respectively. The contours represent the 2D projected number densities of (a) the IHP Na⁺ ion around a surface OH⁻ ion for the TiO₂-NaCl_(aq)+NaOH_(aq) interface, and (b) the IMHP1 Cl^- ion around a surface H⁺ ion for the TiO₂-NaCl_(aq)+HCl_(aq) interface. Source data are provided as a Source Data file.

The ab initio-level molecular-scale picture of the EDL at the TiO₂-electrolyte interface provided by our simulations exhibits Stern layer features that are not included in the GCS model, particularly intermediate Helmholtz planes associated with outer-sphere complexes of electrolyte ions. The shorter adsorption distance of positive vs. negative ions results in a larger capacitance at high pH, in good agreement with experiment. The different capacitances at low and high pHs are associated with distinct microscopic surface charging mechanisms, a feature that can help optimize photo(electro)catalytic processes. These results underscore the utility of machine learning-enabled, ab initio-quality simulations to characterize the specific chemistry and inhomogeneity of (photo)electrochemical interfaces and pave the way to further studies including the presence of external fields.

Methods

DFT calculations

Static DFT calculations were conducted using the strongly constrained and appropriately normed (SCAN)⁵⁴ exchange-correlation functional as implemented in the Quantum ESPRESSO⁵⁵ package. The SCAN functional⁵⁴ has been found to well describe TiO₂ interfaces⁵⁶ and electrolyte solutions^31,57,58 in previous studies. Valence electron-ion interactions were described by Optimized Norm-Conserving Vanderbilt (ONCV)⁵⁹ pseudopotentials. Electron wavefunctions were expanded in plane waves using a cutoff energy of 150 Ry. A total energy convergence threshold of 1 × 10 Ry was adopted. Because of the large size of our supercells, the Brillouin zone sampling was restricted to the Gamma point. Following each self-consistent calculation, maximally localized Wannier functions (MLWFs)⁶⁰ were determined using the Wannier90 code⁶¹. Each MLWF was associated with its closest Ti, O, Na, or Cl atom, resulting in each of these atoms carrying four doubly occupied MLWFs. From the MLWFs, the coordinates of the Wannier Centroids (WCs) relative to their corresponding atoms were obtained by computing the average position of the Wannier centers associated with each given atom³⁵.

Deep neural network (DNN) models

The training dataset for the DNN models was collected through an active machine-learning approach²⁸. This dataset comprehensively spans the configurational space of bulk anatase TiO₂, water, and various aqueous electrolyte solutions (NaCl, NaOH, HCl, NaCl + NaOH, and NaCl +  HCl solutions), as well as anatase (101) interfaces with each of these liquids (see Supplementary Table 1). The exploration spanned temperatures of 200−800 K (systems 1–11) or 300−400 K (systems 12-15), under conditions of either a pressure of 1 bar or a constant volume corresponding to experimental densities. The final dataset comprises 30,103 configurations in total. The DPLR and Deep Wannier (DW)⁶² DNN models were trained on this training dataset using the DeePMD-kit package⁶³. For both DPLR and DW, two independent models were generated using different initial random parameters. The two models were used to run independent simulations from which average properties and corresponding error bars were derived.

To evaluate the performance of our DNN models, we generated a testing dataset of configurations not included in the training. This was achieved by conducting deep potential long-range (DPLR) molecular dynamics (MD) simulations on the following four representative systems.

• The anatase (101)-liquid water interface, comprising 60 TiO₂ units and 82 H₂O molecules.

• The anatase (101)-NaCl_(aq) solution interface, comprising 60 TiO₂ units, 82 H₂O molecules, and 1 NaCl ion pair.

• The anatase (101) -NaCl_(aq)+NaOH_(aq) solution interface, comprising 60 TiO₂ units, 80 H₂O molecules, 1 NaCl ion pair, and 1 NaOH ion pair.

• The anatase (101)-NaCl_(aq)+ HCl_(aq) solution interface, comprising 60 TiO₂ units, 81 H₂O, 1 NaCl ion pair, and 1 HCl ion pair.

In the above, the 60 TiO₂ units correspond to a five-layer (1 × 3) anatase (101) slab. For each system, we conducted 5 ns DPLR MD simulations within the canonical ensemble at 330 K. The initial 1 ns of each simulation was discarded for equilibration purposes. From the subsequent 4 ns, 50 configurations were uniformly extracted from each trajectory, resulting in a total of 200 configurations for the testing dataset.

DPLR method

The DPLR method³⁵ assumes that the potential energy surface has short- and long-range contributions. The short-range contribution is represented as in the standard deep potential model⁶⁴, while the long-range contribution is approximated by the electrostatic energy of a system of spherical Gaussian charges associated with the ions (nuclei + core electrons) and the valence electrons. We calculate the electrostatic energy of the Gaussians via the particle-particle-particle-mesh method⁶⁵ for evaluating Ewald sums. The location, charge magnitude, and spatial spread of the Gaussians are determined as follows.

• Location: Ionic Gaussians are centered at the atomic sites, and electronic Gaussians are centered at the maximally localized Wannier centers⁶⁶. For computational simplicity, Wannier centers associated with the same atom are combined into a single Wannier Centroid (WC)³⁵, located at the instantaneous average position of these Wannier centers. The locations of WCs are predicted by the DW DNN model⁶².

• Charge magnitude: The magnitudes of the ionic charges are ${+Z}_{V}e$, with $Z_V$ being the number of their valence electrons. The pseudopotential applied in this work treats the 3 s²3p⁶ 3d²4s² electrons of Ti, 1 s electron of H, 2 s²2p⁴ electrons of O, 2 s²2p⁶ 3 s¹ electrons of Na, and 3s²3p⁵ electrons of Cl as valence electrons explicitly. Consequently, $Z_V$ equals 12, 1, 6, 9, and 7 for Ti, H, O, Na, and Cl, respectively. For electrons, each Wannier center carries a charge of $-2e$. Given that each Ti, O, Na, and Cl ion has four Wannier centers, their WCs carry a charge of $-8e$. The DFT calculations show that the average distance of Ti’s WCs from the Ti ions is significantly smaller (0.002 Å, averaged over $x$, $y$, and $z$ directions) compared to that of O’s WCs from O ions (0.026 Å, averaged over $x$, $y$, and $z$ directions). This suggests a negligible contribution of the polarization of Ti’s WCs to the overall electrostatic energy. Therefore, for computational efficiency, our DPLR model further simplifies the representation of Ti ions: instead of accounting for a $+12e$ charge on the Ti ion counterbalanced by a $-8e$ charge from its WCs, we simplify our DPLR model by omitting the WCs of Ti and treating each Ti ion as a $+4e$ charge. The WCs of O, Na⁺, and Cl^- are all treated explicitly.

• Spatial spread: The long-range electrostatic contribution up to dipole terms is independent of the spread parameter, which can then be chosen to ensure charge neutrality in the bulk of the solution as well as good numerical representability by a DNN of the short-range contribution. In our DPLR, the spatial spread of the Gaussians for both ions and electrons is (2${\beta \left)\right)}^{-1},$ where $\beta$ is an adjustable parameter. In the limit of $\beta \to 0$, the Gaussian width is infinite and the DPLR model reduces to the standard short-range DP (hereafter denoted as DPSR) model. Conversely, as $\beta \to \infty$, the Gaussian charges become point-like, leading to singular potentials incompatible with DNN representations³⁵. To determine an optimal $\beta$ for our system, we conducted systematic training of DPLR models across a range of $\beta$ values: 0.0, 0.1, 0.2, 0.3, and 0.4 ${\mathrm{\AA }}^{-1}$. The performance analysis, depicted in Supplementary Fig. 1, reveals that, for both the training and testing datasets, $\beta =0.1{\mathrm{\AA }}^{-1}$ minimizes the root mean square error (RMSE) in the prediction of energies and forces in comparison to the DFT calculations. We thus adopted $\beta =0.1{\mathrm{\AA }}^{-1}$ for our DPLR simulations.

Supplementary Fig. 1 also shows that the RMSE for the testing dataset is lower than that for the training dataset. This is because the training dataset includes higher temperature (up to 800 K) configurations compared to the 330 K temperature used for the testing dataset. At higher temperatures, the magnitudes of forces and energies are larger, resulting in larger absolute errors. Given that the production runs of our work were conducted at 330 K, the errors at 330 K are more representative and indicative of the model’s performance under our specific conditions of interest.

DPSR fails to properly describe oxide-electrolyte interfaces, because, in the absence of long-range interactions, charge accumulation at the interface due to surface charging and/or EDL formation may result in charge neutrality violation in the bulk of an electrolytic solution. DPLR remedies this deficiency because the electrostatic energy penalizes bulk charging (Supplementary Section 3). In the absence of dissolved ions, as in the case of the anatase (101) interface with neat water, DPLR gives results that agree with DPSR (Supplementary Section 2).

DPLR MD simulations

The large-scale DPLR MD simulations presented in the main manuscript were conducted on model systems consisting of a five-layer ($3\times 9$) anatase (101) slab (540 TiO₂ units) in contact with a 67 $\mathrm{\AA }$ thick layer of aqueous electrolyte within a periodically repeated supercell of size $30.7\mathrm{\AA }\times 33.9\mathrm{\AA }\times 83.4\mathrm{\AA }$ along the three orthogonal directions $\left[\overline{1}01\right],\left[010\right]\mathrm{and}\left[101\right]$ of the anatase crystal lattice. All simulations were conducted in the canonical ensemble for 10 ns with a temperature of 330 K. The 30 K elevation is to partially compensate for the overestimation of the melting temperature of ice by the SCAN functional and describe a liquid with diffusivity close to that of water at standard conditions⁶⁷. The TiO₂ interfaces with the acidic and basic solutions were initially simulated at 400 K for 0.9 ns to accelerate equilibration and subsequently cooled to the target temperature of 330 K. In all simulations, hydrogen was replaced by deuterium to allow the use of a larger simulation time step of 0.5 fs. The ion and water densities presented in this work were averaged over the period from 3 to 10 ns. To check the convergence of ion and water densities with respect to simulation time, we plotted the ion and water density averaged over the periods from 3 to 6.5 ns and from 6.5 to 10 ns, respectively, in Supplementary Figs. 2 and 3. The results averaged over 3 to 6.5 ns agree well with those averaged over 6.5 to 10 ns, indicating the 10 ns simulation is well converged.

Electrostatic potential calculation

The electrostatic potential drop, $\psi$, is an average property that requires knowledge of the plane-averaged density profile of the electrons along $z$, which can be estimated accurately from the positions of the Wannier centroids, provided by the DW³¹ neural network model, and from the average spread of the associated electron distributions, provided by DFT calculations on smaller systems. The density profile of the total charge (ions + valence electrons) is obtained by adding the plane-averaged ion density profile to the valence electron density profile. Then, $\varphi \left(z\right)$, the electrostatic potential profile, is calculated by solving a one-dimensional Poisson’s equation. As shown in Supplementary Section 7, this procedure is remarkably accurate when compared to DFT calculations on reference systems.

Author contributions

A.S. and R.C. designed the project. C.Z. and M.F.C.A. carried out the simulations and performed the analysis. C.Z., A.S., and R.C. wrote the manuscript. M.F.C.A. and Z.K.G. reviewed the manuscript. A.S.R., Y.L., P.M.P., and X.W. contributed fruitful discussions.

Peer review

Peer review information

Nature Communications thanks Chao Zhang, Jun Cheng, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The complete DFT training datasets and the deep potential models generated in this study have been deposited in the Figshare database (https://figshare.com/s/3c4e7eb02ee64fd8b3bf)⁶⁸. Source data are provided as a Source Data file. Source data are provided with this paper.

Code availability

Deep potential long-range molecular dynamics simulations were conducted using the DeePMD-kit package (https://github.com/deepmodeling/deepmd-kit) in conjunction with LAMMPS. The code used to generate the plots shown in the main text is available from the corresponding author upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-54631-1.