Application of non-dominated sorting genetic algorithm (NSGA-III) and radial basis function (RBF) interpolation for mitigating node displacement in smart contact lenses

Abstract

With the rapid development of wearable technology, smart contact lenses (SCL) are gradually gaining attention as a breakthrough innovation. The emergence of these products suggests that smart glasses, which incorporate electronic components and visual aids, are expected to become the mainstream of human-computer interaction in the future. However, realizing this vision requires not only advanced electronics but also highly sophisticated manufacturing processes. Therefore, this paper provides an in-depth discussion on the process of manufacturing smart contact lenses using in-mold electronic decoration technology and focuses on the multi-objective problem of optimizing injection parameters such as melt temperature and holding pressure to achieve on micro-molecular displacements as well as residual stresses. First, the background and technical requirements of smart contact lenses are described in detail, emphasizing the prospect of SCL for a wide range of applications in augmented reality, healthcare, and smart assistance. Subsequently, the key role of IME technology in SCL manufacturing is discussed. Focusing on the optimization of melting temperature, holding pressure and holding time, the effects of these three key parameters on eyewear were systematically analyzed with the goal of improving the overall performance and biocompatibility of SCL. The multi-objective optimization of melting temperature and holding pressure was achieved by NSGA-III. Radial basis function interpolation was used as an auxiliary method to provide finer optimization results for NSGA-III. During the multi-objective optimization process, efforts were made to achieve uniform flow of melt temperature and optimal adjustment of holding pressure to maximize the transparency, stability and comfort of SCL. The final results obtained achieved an optimization rate of 95.60% and 93.47% for nodal displacement and residual stress, respectively, compared with the initially recommended process parameters.

Introduction

The manufacture of complex, customized products such as smart contact lenses (SCL) highlights the importance of polymer machining in modern engineering. Unlike metal machining, polymer machining offers greater precision and allows complex geometries to be manufactured with high accuracy. This precision is critical to the production of smart contact lenses, as small variations can have a significant impact on functionality and wearer comfort. In short, polymer machining, with its unrivaled precision, material versatility, scalability and cost-effectiveness, makes it an indispensable tool in modern engineering. As the demand for personalized and technologically advanced medical solutions continues to grow, polymer processing will play an increasingly critical role in meeting these evolving needs.

Contact lenses have always been designed to correct vision; however, as technology continues to advance, smart glasses, a type of augmented reality (AR) device, offer users a more immersive and seamless digital experience. The introduction of smart contact lenses has taken the use of contact lenses to a new level. The technology not only provides vision correction, but also integrates digital information into the user’s field of vision, enabling a true augmented reality experience.

SCL enhance the everyday experience by enabling users to see overlaid digital information in the real world. Some of the application areas of SCL are shown in Fig. 1. This includes features such as digital navigation, real-time translation, and virtual screens that allow users to more easily access information about their surroundings. Integrating voice recognition and display technology, SCL can act as mobile assistants, performing tasks such as sending messages and making phone calls, while maintaining the user’s connection to the real environment. In medical, military, and industrial fields, SCL can provide real-time visualization information for navigation, training, surgery, and other specialized applications to improve efficiency and accuracy.

Fig. 1.

SCL application field.

SCL, an advanced smart contact lens, consists of the following key components: Display, which is built into the contact lens and is used to present digital information, allowing the user to see virtual content superimposed on the real world. Motion sensors, including gyroscopes, accelerometers, etc., which are used to track the user’s head and body movements, enabling the device’s localization and orientation perception in 3D space. Image sensors (cameras), which are used to capture the user’s surroundings and the scene that the user is gazing at, to realize environment sensing, object recognition, and real-time scene information acquisition. Power supply: Provides adequate power support, usually by means of small batteries or other power supply devices. Of course, this is only the main component of SCL, the rest also includes, for example, transparent display technology allows users to realize through translucent reflective lenses or transparent display technology.

It is envisioned that printed circuits and IME (In-mold electronics) technology will be used to realize circuit components for AR contact lenses. This paper propose the use of flexible printed circuit technology, which allows circuit components (e.g., sensors, wires) to be printed directly onto soft materials, resulting in thinner, lighter, and more pliable circuit designs. IME technology offers the possibility of embedding circuits by integrating electronic components into plastic parts during the injection molding process. When manufacturing frames or transparent materials for SCL, it is possible to consider integrating the circuitry components with the structure of the lenses, thereby reducing volume and weight and improving overall performance.

Injection molding is a key process method in the manufacture of SCL, aiming to create contact lenses that look good and perform well. First, the shape and internal structure of the eyewear is determined through precise design and mold preparation. The selection of materials suitable for injection molding is critical, ensuring that they possess properties such as transparency, flexibility and biocompatibility. The injection molding process involves heating the plastic to a molten state, injecting it into a mold, and cooling it to form a solid eyewear. Meanwhile, IME technology allows electronic components to be embedded into the structure of the eyewear during the injection molding process, enabling thinner and more integrated designs. Finally, the eyewear’s electronics and overall performance are verified through quality control and testing to ensure compliance with design specifications. This integrated manufacturing approach provides an effective and viable way to produce AR glasses for high-performance, digitally augmented reality experiences.

In the manufacturing of SCL, the issue of micromolecular displacement and residual stress is a critical challenge with potential and serious impacts on eyewear performance.

First of all, micro-molecular displacements may lead to changes in the electrical properties of electronic components, causing signal interference, resistance changes or even functional failures. In SCL, this could mean inaccurate transmission of virtual information, affecting user experience and operational accuracy. Second, micro-molecular displacements may affect the transparency and optical properties of the material, leading to a decrease in the optical transparency of the glasses, reducing the clarity and display quality of the virtual information. Finally, micro-molecular displacements may cause ongoing quality issues over the lifetime of the eyewear, affecting the reliability and durability of the eyewear. This is extremely detrimental to a device that needs to maintain consistent performance in a variety of environments and usage conditions.

Residual stress is an internal stress created during the manufacturing process of smart contact lenses that may have a significant impact on the performance and stability of smart contact lenses. Firstly, residual stress may cause the optical properties of smart contact lenses to be affected, such as causing optical aberrations, astigmatism and other problems. Secondly it may affect the mechanical properties of smart contact lenses, including aspects such as strength, toughness and wear resistance. Finally, the SCL is integrated with sensors or microelectronic components, and the residual stress may have an impact on the performance of these devices, such as affecting the stability and accuracy of the signal transmission, thus affecting the function and performance of the smart contact lens.

Therefore, practical measures must be taken during the design and production process to minimize the effects of micro-molecular displacements and residual stresses. This may include careful selection of materials, optimization of parameter combinations, and selection. Only if the problems of micro-molecular displacements and residual stresses are effectively addressed can SCL ensure long-term stable performance.

Finally, the connection between wire diameter and current frequency is explored in depth by extrapolating the relationship between the two and considering the potential impact of wire diameter changes on current. By optimizing the node displacement, the accuracy of signal transmission is determined by assessing whether the electrical nodes in the circuit will vary beyond the allowable range of the current. This analysis contributes to a better understanding of the impact of wire diameter variations on circuit performance and how parameters can be optimized to ensure stability and reliability when designing smart contact lens circuits.

This thesis is organized as follows: the second chapter is a literature review of background information, aiming to summarize and analyze previous studies related to smart contact lenses (SCL) and their manufacturing processes, highlighting the innovation and necessity of this study. The third section details the principles of the material selection and methodology, explaining the material properties employed in SCL manufacturing and their impact on the final product performance, as well as the methodological basis used. Section IV describes the design of the simulation experiments, highlighting how the injection molding process can be optimized through simulation experiments simulation and parameter tuning to ensure the reliability and validity of the simulation results. Section V demonstrates the results obtained through the optimization method and provides an in-depth discussion of the relationship between junction displacement and wire diameter, revealing the influence of key parameters on SCL performance. Finally, Section VI summarizes the full paper, outlining the main findings and contributions of this study and suggesting possible future research directions and applications.

Literature review

With the rapid development of science and technology, smart contact lenses have aroused extensive research interest as a compelling technology. Numerous scholars have conducted in-depth research on the composition and use of smart contact lenses, with a view to making significant progress in enhancing user experience and solving practical problems.

In 2014, Giovanni A. Salvatore et al.¹ presented a wafer-scale process scheme to realize ultra-flexible, lightweight and transparent electronics on 1 mm thick poly(parylene) films, which are released from a carrier substrate after the polyvinyl alcohol layer is dissolved in water. Meanwhile, the use of amorphous oxide semiconductors and high-k dielectrics enables analog amplifiers operating at 12v and above 1mhz. Electrons can be transported across any object, surface and biological tissue, such as human skin and plant leaves.

In 2017, Joohee Kim et al.² developed a multifunctional contact lens sensor, which was also designed to monitor glucose in tears, as well as monitor intraocular pressure using the resistance and capacitance of electronic devices. In addition, the developed contact lens sensor can measure both glucose levels in tears and intraocular pressure, but independently based on different electrical responses.

In 2017, Sangkyu Lee et al.³ proposed that graphene can protect the eyes from electromagnetic waves that can cause eye diseases such as cataracts. A highly conductive contact lens platform based on graphene that reduces exposure to electromagnetic waves and dehydration is reported. The sheet resistance of graphene on contact lenses was as low as 593 Ω/sq (± 9.3%), which was maintained in humid environments.

In 2018, Jihun Park et al.⁴ presented an unconventional approach to fabricating soft smart contact lenses in which glucose sensors, wireless power transmission circuits, and display pixels are fully integrated together using transparent and stretchable nanostructures to display sensing signals in real time. Such soft, smart contact lenses can be transparent, providing a clear view by matching the refractive index of their locally patterned areas. The resulting soft, smart contact lenses provide real-time, wireless operation and have in vivo tests to monitor glucose concentration in tears (suitable for determining fasting glucose levels in tears of diabetic patients) while providing sensing results via the contact lens display.

In 2020, Do Hee Keum et al.⁵ investigated smart contact lenses for continuous glucose monitoring and diabetic retinopathy treatment. The smart contact lens device is made of a biocompatible polymer and contains ultrathin flexible circuitry and a microcontroller chip for real-time electrochemical biosensing, on-demand controlled drug delivery, wireless power management and data communication.

In 2022, Cheng Yang et al.⁶ proposed an integrated wireless therapeutic contact lens for in-situ electrical sensing of intraocular pressure and on-demand anti-glaucoma drug delivery. The wireless IOP sensing modality can detect IOP fluctuations ultra-sensitively due to the unique cantilever structure design of the capacitive sensing circuit. The drug delivery modality employs a highly efficient wireless power transmission circuit to trigger the entry of anti-glaucoma drugs into the aqueous chamber via iontophoresis.

Studies have shown that the composition of smart contact lenses not only includes core components such as miniature displays, sensors and communication chips, but also involves advanced material science and manufacturing technology. The design of these glasses pursues features such as non-interference, free interaction, and real-time information presentation, aiming to provide users with a more convenient and realistic mixed reality experience. By optimizing the use of smart contact lenses, researchers are committed to expanding their application areas, including healthcare, augmented reality, real-time navigation, and many other aspects, laying a solid foundation for the future development of smart glasses.

In 2023, Hanjui Chang et al.⁷ adopted the in-mold electronic decoration technology to achieve the purpose of damage detection by using the node displacement change after the surface film is damaged. Through wavelet analysis, the singularity of the wavelet function can be found and the damaged part can be determined. The Lipschitz index can be used to judge the singularity of the wavelet function, so as to detect the local damage of the armor surface.

In 2018, Jiao-Hong Yi et al.⁸ introduced an adaptive mutation operator aimed at improving the performance of the standard NSGA-III algorithm. The proposed adaptive mutation operator strategy is evaluated on three crossover operators, namely, Simulated Binary Crossover (SBX), Uniform Crossover (UC), and Single-Intersection (SI) of NSGA-III. Subsequently, three enhanced NSGA-III algorithms (NSGA-III SBXAM, NSGA-III SIAM and NSGA-III UCAM) were developed.

In 2019, Zhihua Cui et al.⁹ designed a new selection elimination operator to balance convergence and diversity. Firstly, a reference point with the least number of ecological niches is identified using the selection operator, and then an individual with the shortest intersection distance of the boundaries based on the penalty is selected; secondly, a reference point with the largest number of ecological niches is identified, and an individual with the longest intersection distance of the boundaries based on the penalty is removed by the elimination operator, and the simulation results show that the improved strategy can obtain better performance.

In 2019, Xiaolong Xu et al.¹⁰ proposed a computational offloading method called COM for supporting cloud edge computing for IoT. In addition, NSGA-III (non-dominant sorting genetic algorithm III) algorithm is used to solve the multi-objective optimization problem of task offloading in cloud edge computing. Finally, experiments and comprehensive simulations of the system are carried out to verify the effectiveness of the proposed approach.

In 2020, Jiao-Hong Yi et al.¹¹ benchmarked the performance of three crossover operators of the NSGA-III algorithm using a large-scale optimization problem based on human electroencephalography (EEG) signal processing. In addition, an enhanced version of the NSGA-III algorithm is proposed by introducing the Stud concept and designing improved crossover operators for SBX, UC and SI. The performance of the proposed NSGA-III variant is verified on six large-scale optimization problems. Experimental results show that the NSGA-III method combining UC and UC-stud (UCS) outperforms other developed variants.

In 2020, Zi-Min Gu et al.¹² introduced an information feedback model to improve the ability of NSGA-III to solve large-scale optimization problems. Six individual selection models are proposed. Each of these six models is embedded into NSGA-III to generate six improved NSGA-III algorithms (these six algorithms are collectively referred to as IFM-NSGAIII). These six algorithms were compared with the original NSGA-III on 9 benchmark problems to search for the best information feedback model and the best IFM-NSGAIII algorithm.

In 2022, Imen Khettabi et al.¹³ developed improved versions of the Non-dominated Sorting Genetic Algorithm (NSGA) method, i.e., new dynamic NSGA-ii (NewDNSGA-II) and new NSGA-iii. The results of the proposed method are presented and analyzed by means of three metrics (Inverse Generation Distance (IGD), Diversity Measure (DM), and Mixed Pareto Frontier Basis (CMPF)), rich experimental results are presented and analyzed to demonstrate the effectiveness of the proposed method.

In 2023, Hanjui Chang et al.¹⁴ investigated the manufacturing parameters of Fresnel lenses during injection molding. The objective was to reduce the nodal displacement of the Fresnel lens surface and improve the transmission performance. To achieve this goal, a Kriging model was developed to map the design parameters and optimization objectives by linking the process parameters to the optimization objectives. Based on the Kriging model, the NSGA-II algorithm is combined with the prediction model to obtain the Pareto optimal solution.

In 2023, Hanjui Chang et al.¹⁵ used the population-based optimization algorithm NSGA-III to simulate the injection molding process of lenses made of LSR materials using analytical software, focusing on the relationship between the elongation of the tie rod and the optimized process parameters. During the study, key process parameters, including melt temperature, holding pressure and holding time, were intentionally varied to analyze their effects on residual stresses in the final product.

Compared to other optimization algorithms, such as NSGA-II and Undominated Whale Optimization, NSGA-III has significant advantages in multi-objective optimization problems. By introducing the concepts of non-dominated ordering and multi-level Pareto optimization frontiers, NSGA-III is able to capture and maintain the diversity of the problem more efficiently, as well as find a more comprehensive balance between multiple objectives. The application of the algorithm is designed to comprehensively consider the multiple objectives of molding quality, productivity and energy consumption in smart contact lens manufacturing, providing a reliable tool for achieving an optimized configuration of injection molding parameters. This choice is based on NSGA-III’s excellent adaptability to multi-objective optimization problems and the remarkable results achieved in practice, providing strong support for improving the efficiency of the injection molding process and optimizing eyewear performance. Therefore, in this study, this paper chose the Non-dominated Sorting Genetic Algorithm III (NSGA-III) as a tool for the optimization of injection molding parameters for smart contact lenses.

In 2021, O. Nikan et al.¹⁶ presented an efficient numerical method for solving the approximate solution of the fourth-order reaction-diffusion equation of fractional order of time in the sense of the Riemann-Liouville derivatives, i.e., the localized radial basis function generated by finite difference (LRBF-FD). The time fractional order derivatives are approximated using exact formulas with second order accuracy and the spatial terms are discretized using the LRBF-FD method. The advantage of the local configuration method is that it approximates the differential operator by deriving an RBF expansion that weights and sums the values of the function over a local set of nodes (local support).

In 2021, O. Nikan et al.¹⁷ proposed an efficient local meshless configuration algorithm to approximate a time-fractional order evolution model and applied it to the modeling of heat flow in materials with memory. The model is based on the Riemann-Liouville fractional integral. This localization approach, based on dividing the original domain into several subdomains by kernel approximation on each local domain, reduces the computational cost while significantly sparsifying the algebraic system with a small condition number.

In 2022, Yaru Liu et al.¹⁸ explored an effective identification method for time-varying and spatially variable distributed dynamic loads based on finite acceleration response. In terms of spatial distribution reconstruction, a radial basis function (RBF) interpolation strategy is adopted to determine the hyperparameters through a hierarchical clustering algorithm to approximate the DDL and convert the continuous function to finite dimension. In the time domain, the RBF coefficients at each discrete moment are obtained by the least squares solution of the modal forces based on the inverse Newmark iteration. For the multi-source uncertainty that lacks an exact probability distribution, a multi-dimensional interval model that uniformly quantifies the convex and fuzzy parameters is established. On this basis, the chebyhev interval agent model with different orders is constructed, and the fuzzy interval boundaries of ddl are obtained.

Smart contact lenses can be mass-produced by an injection molding process, thereby reducing costs. An injection molding method for microdevice production was proposed by Siegel et al. To manufacture contact lenses using injection molding technology, a mold should be designed for injecting the contact lens material^19,20. This paper focus on the use of injection molding for the production of smart contact lenses.

The fabrication of IOP monitoring sensors as thin as 150 μm in wearable contact lens sensors using soft lithography was reported by Agagu et al. Soft lithography has been used in microcontact printing (µCP), replica molding (REM), and micro transfer molding (µTM) methods to make master molds in contact lens manufacturing²¹. Thus the printed circuit films in smart contact lenses can be designed using soft lithography, and then the printed circuit films can be placed inside the contact lenses by in-mold electron decoration (IME) technique.

Smart contact lenses are not only suitable for continuous, minimally invasive disease monitoring, but also play an important role in the treatment of eye diseases. With advances in microscale technology and biomaterials, contact lenses can now be engineered to have the ability to continuously release drugs²². The development of contact lenses capable of detecting multiple chemical components in real time will make contact lenses an even more powerful biomedical tool. In addition, the implementation of electronic sensors will greatly expand the capabilities of contact lenses to detect physical signals (i.e., temperature and pressure) and to record or modulate the electroretinogram of the eye or the electrical stimulation of visual neurons. Therefore, it is important to ensure that the line transmits the signals accurately. The main focus of this paper is to optimize the surface of smart contact lenses to minimize the micro-molecular bias.

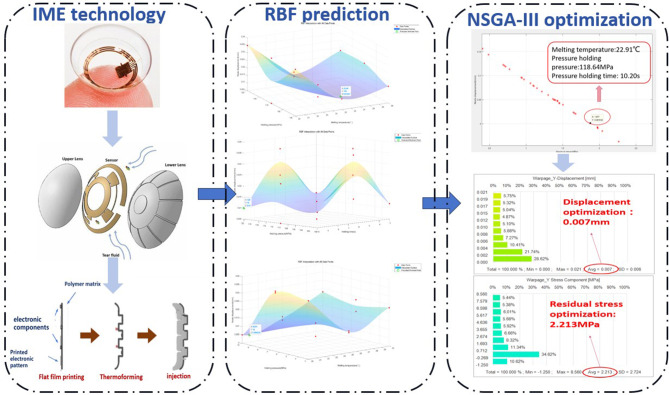
In this study, a multilevel optimization strategy using NSGA-III as the primary method, combined with radial basis function (RBF) as the secondary method, was used to comprehensively optimize the injection molding parameters of smart contact lenses, as shown in Fig. 2. NSGA-III, as a multi-objective genetic algorithm, is able to find the balance point between multiple objectives and efficiently search the parameter space to achieve multi-objective optimization NSGA-III as a multi-objective genetic algorithm can find the balance point among multiple objectives and search the parameter space efficiently to realize multi-objective optimization. The RBF, as a sub-method, models the complex relationships of injection molding parameters through interpolation techniques, thus providing more information and helping to predict the performance of parameter combinations more accurately.

Fig. 2.

Optimization concepts for SCL.

According to the above literature summary, the advantage of this combined application is that NSGA-III is able to comprehensively and efficiently search the parameter space for the Pareto-optimal solution set, while RBF provides a global approximation of the injection molding parameter space, helping the optimization algorithms to explore the critical regions in a more targeted manner. The combination of these two approaches provides a powerful tool for the optimization of smart contact lens injection molding parameters, aiming to improve manufacturing efficiency, optimize performance, and advance science and technology in the field. By drawing on the advantages of these two methods, the injection molding parameters during the manufacturing process of smart contact lenses can be optimized more comprehensively and accurately, laying the foundation for their excellent performance in practical applications.

Materials and methods

Common materials used in contact lens manufacturing include PMMA, PET, PHEMA and LSR, as shown in Table 1. The choice of contact lens materials lies in balancing properties such as transparency, gas permeability, biocompatibility, mechanical strength, and resistance to protein adsorption. Among the commonly used materials, PMMA and PET have high mechanical strength but low gas permeability; PHEMA exhibits excellent transparency and gas permeability, as well as excellent biocompatibility for prolonged wear; and PDMS excels in both transparency and gas permeability and possesses excellent biocompatibility and resistance to protein adsorption. Therefore, choosing the right material according to the needs of contact lens users is essential to provide optimal comfort and visualization. With its high transparency, good gas permeability and biocompatibility, PHEMA material is an ideal contact lens material, especially for users who need to wear it for a long time.

Table 1.

Properties of commonly used contact lens materials.

Material	Molecular formula	Procs/Cons	References
PMMA	(C5H8O2)n	Outstanding optical, properties, low oxygen permeability, high rigidity and toughness	23
PET	(C10H8O4)n	Low glass transition temperature, low rigidity, low surface energy, hydrophobic, excellent chemical resistance, and thermal stability	24
PHEMA	(C6H10O3)n	Tunable mechanical properties, relatively high water content, and good chemical and thermal stability	25
LSR	(C2H6OSi)n	Flexibility and high oxygen permeability	26

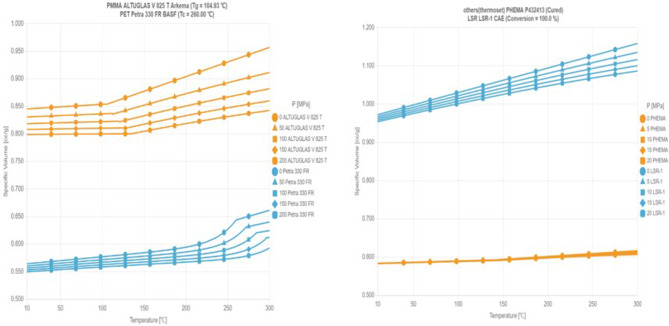
As shown in Fig. 3, the volumetric behavior of the heat-shrinkable materials PMMA and PET can be observed by comparing their PVT plots (temperature-volume-pressure plots) under changes in temperature and pressure. PMMA and PET are both thermoplastic polymers, but due to the differences in their molecular structures, they exhibit some significant differences in their PVT plots. Comparing the PVT plots of LSR and pHEMA, LSR is usually a thermoset elastomer while pHEMA is a thermoplastic material. On the PVT plot, LSR exhibits significantly different properties from pHEMA, mainly in terms of its cross-linking and hardening at elevated temperatures, whereas pHEMA exhibits volume change characteristics typical of thermoplastic polymers.

Fig. 3.

PVT comparison diagram of four materials.

In summary, PHEMA (hydroxyethyl methacrylate) exhibits many advantages in contact lens materials, making it an ideal choice for contact lens manufacturing.

PHEMA exhibits excellent transparency and gas permeability, guaranteeing users a clear, comfortable visual experience while wearing contact lenses and reducing discomfort caused by oxygen deprivation. PHEMA has excellent biocompatibility and is compatible with the surface of the eye, reducing irritation of the eye tissue and the risk of allergy and inflammation. This makes PHEMA contact lenses suitable for extended wear. Despite its relatively low mechanical strength, PHEMA’s softness allows the contact lens to conform more closely to the surface of the eye, improving wearer comfort. PHEMA’s lower adsorption of proteins compared to other materials reduces protein deposits on the surface of the lens, prolonging its service life.

Using PHEMA as an injection molding material for contact lenses, the selection of the right film material is crucial when considering IME technology next. The film material should have good electrical conductivity, optical transparency and biocompatibility to ensure proper function and comfort of the smart contact lens.

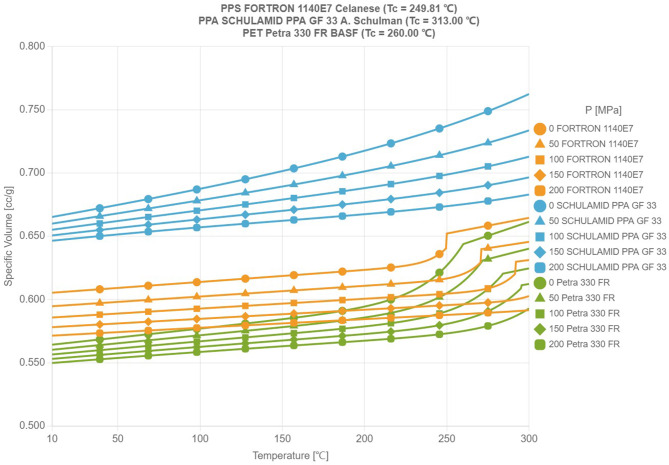
As in Fig. 4, by comparing the three common conductive polymer materials such as PET, PA and PPS, this paper found that PPS material has a superior performance in contact lens molding²⁷. First of all, PPS has high thermal and chemical stability, can maintain stability at high temperatures, and is not easy to deform or decompose, which makes PPS materials more suitable for injection molding and other high-temperature processing techniques. Secondly, PPS has high strength and hardness, which can maintain the shape stability after molding and is not easy to be deformed or broken, which is conducive to the production of contact lens products with precise shape and stable size. In addition, PPS material has good electrical conductivity, which can effectively transmit electrical signals and meet the requirement of electrical conductivity in contact lenses. Considering the above factors, PPS was finally chosen as the molding material for contact lenses to ensure the molding quality, stability and electrical conductivity of the product, as well as to improve the service life and performance of the contact lenses.

Fig. 4.

PVT comparison diagram of four materials.

Finally, this paper decided to choose PHEMA as the injection molding material for contact lenses and PPS as the IME membrane material. As a polymer material widely used in medical devices, PHEMA has good biocompatibility and hydration, which is compatible with the surface of the eyeball and provides a comfortable wearing experience. In addition, PHEMA has good optical transparency and processing performance, which can meet the requirements of contact lenses for transparency and shape precision, while PPS, as a kind of IME film material, has excellent chemical stability, thermal stability, and mechanical properties, which can provide stable support for the electronic components inside the contact lenses to realize effective transmission of electrical signals. Taking into account the performance characteristics of PHEMA and PPS, this combination of materials can provide a reliable foundation for contact lens production, ensuring good comfort, wear resistance and functionality.

Non-dominated sorting genetic algorithm (NSGA-III)

With the continuous development of technology, smart contact lenses have attracted much attention as an innovative augmented reality (AR) device. However, the optimization of its injection molding parameters is one of the important challenges to achieve high performance and comfort. Optimization of injection molding parameters needs to maximize productivity and energy savings while ensuring manufacturing quality. To solve this complex multi-objective problem, the use of efficient optimization algorithms is crucial.

Among many optimization algorithms, the Non-dominated Sorting Genetic Algorithm III (NSGA-III) has attracted much attention for its outstanding performance in multi-objective optimization problems. NSGA-III is an evolved version of the NSGA algorithm, which has strong global search capability and superior convergence. The basic idea behind it is to gradually evolve a Pareto-optimal frontier for the objective function by simulating natural selection and genetic inheritance mechanisms.

In smart contact lens manufacturing, the selection of injection parameters directly affects the molding quality, productivity and energy consumption of the glasses. The application of NSGA-III aims to find the Pareto optimal solution set through global search and non-dominated sorting mechanism to achieve multi-objective optimization.

1. Formalize the smart contact lens injection molding parameter optimization problem as a multi-objective optimization problem. The objective function can include multiple indicators such as molding quality, production efficiency and energy consumption.

2. Configure the parameters of NSGA-III, including population size, crossover probability, variance probability and so on. This needs to be adjusted appropriately according to the complexity of the problem and computational resources.

3. Explicitly define the objective functions of the injection molding parameters and the trade-offs between these objective functions. This is to ensure that NSGA-III is able to find a balance between multiple objectives and generate a Pareto-optimal solution set.

4. Sort the population using NSGA-III’s non-dominated sorting mechanism to classify individuals into different frontiers. By selection operation, solutions with high fitness are filtered out and genes of the next generation are retained.

5. Generate the next generation of individuals through crossover and mutation operations. The design of these operations needs to be adapted to the characteristics of the spectacle injection problem to ensure diversity and convergence of the search process.

6. Repeated iterations of NSGA-III are performed to progressively approach the Pareto optimization frontier. Each generation generates a set of solutions which constitute the set of optimized solutions for the injection parameters.

7. Conduct a detailed analysis of the optimization results of NSGA-III to verify whether these solutions meet the actual requirements of the injection molding parameters of smart contact lenses. The evaluation of Pareto’s optimal solution set can help manufacturers make informed decisions among multiple objectives.

Solving a multi-objective optimization problem can be mathematically modeled using two large matrices:

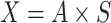The objective is to divide S into two matrices obeying S = S(1) + S(2), Let C be the Pearson correlation coefficient.

Here covar(·) is the covariance and σ(·) is the standard deviation.

Our main goal (f1) is to create C by using the largest diagonal and smallest off-diagonal elements. the next goal (f2) is to solve the problem of minimizing the distance between S and S(1). Therefore, the elements of S(1) are decision variables.

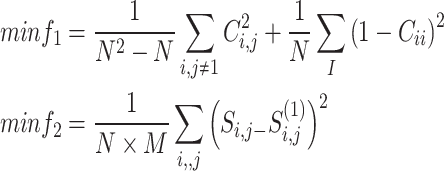Let T = A × S(1), 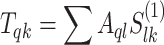. The statistical characterization of Tq can be given as the qth row of the matrix T

Next, the derivatives of 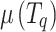and can be used as

接下来, 和的导数可以用

The covariance of and 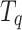can be given by

和的协方差可由

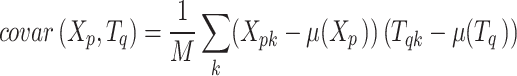Therefore, his derivative can be given by

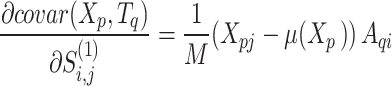If 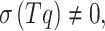we get the derivative of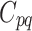

Thus, the sub gradients of the two objectives can be provided as follows.

Radial basis function interpolation (RBF)

Radial Basis Function Interpolation (RBF Interpolation) is an interpolation technique based on the kernel method for modeling the target value in the parameter space. The basic principle is to perform a nonlinear mapping from the parameter space to the target value by defining a radial basis function. A typical radial basis function is a Gaussian kernel function with the expression:

where r is the distance between the two points in the parameter space, and 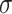is a parameter controlling the width of the function. RBF interpolation is used to model the target values at the points by expressing the target value at each point as a linear combination of radial basis functions to RBF interpolation fits the distribution of target values in the parameter space by representing the target values at each point as a linear combination of radial basis functions.

The performance of the RBF interpolation model is highly dependent on the selection of radial basis functions, determination of centroids and optimization of weights. In practice, the parameters of the model need to be adjusted by methods such as cross-validation. The selection of centroids can usually be sampling points or obtained through clustering methods. Optimization weights, on the other hand, are determined by minimizing the fitting error, i.e., the difference between the actual target value and the predicted value by RBF interpolation. Techniques such as regularization can also be used in this step to prevent overfitting.

In injection molding parameter optimization, RBF interpolation is used to construct a mapping model between the parameter space and the target values. By taking the known injection molding parameters and the corresponding target values as training samples, the target values under unknown parameters can be predicted using the RBF interpolation model. Combined with the non-dominated sorted whale optimization algorithm, the optimal solution can be searched efficiently in the parameter space. This combined use takes into account the nonlinear relationship between the parameters and searches for the optimal solution in the global range, which improves the robustness and global nature of the optimization. This makes RBF interpolation an effective tool in multi-parameter optimization problems.

In the problem definition and goal setting stage, the focus of this paper is to optimize the injection parameters of SCL, including melt temperature, holding pressure and holding time. These parameters will directly affect the molding quality and performance of the glass. Our final optimization goal is to achieve a balance between two key metrics: micro-molecular deformation and residual stress.

First, this paper focuses on node displacement on the surface, which is a key factor in preventing coil deflection inside smart contact lenses, thus ensuring the accuracy of the transmitted signal. Proper control of the micromolecules is critical to maintaining the stability of the internal structure of the glasses, which helps prevent signal drift or inaccuracies in the device during use.

Next, consider optimizing residual stress to ensure light transmission through the eyewear. Residual stress may cause deformation or distortion of optical components, which directly affects the transparency and visual quality of smart contact lenses. By rationally optimizing injection molding parameters, we aim to minimize residual stress to ensure the clarity and comfort of the glasses.

In order to explore the optimal combination of injection molding parameters more comprehensively and efficiently, this paper adopts an integrated optimization strategy with NSGA-III as the primary method and radial basis function (RBF) as the secondary method. The purpose of this integrated approach is to provide additional information through the interpolation technique of RBF under the multi-objective optimization framework of NSGA-III, so as to more accurately evaluate and guide the search process of injection molding parameters. The flowchart of the whole method is shown in Fig. 5.

Fig. 5.

Optimization method flow chart.

Case study

The study in this paper adopts a simulation modeling approach, and all experimental data and results are obtained through Moldex3D simulation software. As shown in Fig. 6, in designing the experimental process for SCL fabrication using IME technology, the first step is to carefully design the circuit based on the performance requirements. In order to achieve a high degree of integration of electronic components, planar thin-film printing technology was used. In this step, we were able to precisely print the circuits on a flexible substrate to ensure the compactness and reliability of the electronic components. Next, the thermoforming process is performed, a step that is critical to the overall shape and structure of the SCL. Through high-temperature thermoforming, the shape of the flexible substrate is molded to ensure that the electronic components fit the eye comfortably. Subsequently, the injection molding process becomes a critical step in SCL manufacturing. By placing pre-designed circuits and shape-optimized flexible substrates into injection molds, materials with excellent molding properties are injected using IME technology. During injection molding, the electronic components are embedded into the eyewear structure to ensure its robustness and integrity.

Fig. 6.

IME technology application process.

Temperatures during the thermoforming and injection molding phases, as well as other injection molding parameters, are key constraints in the implementation of smart contact lens (SCL) manufacturing processes. By optimizing melt temperature and holding pressure, this paper aims to achieve a multi-objective optimization goal to improve the overall performance, biocompatibility and manufacturing efficiency of smart contact lenses.

First, the focus was on optimizing the melt temperature. Melt temperature directly affects the flow, viscosity, and ability of the injection molded material to fill the mold. By precisely controlling the melt temperature, the goal of this paper is to achieve uniform material flow during the injection molding process, ensuring molding uniformity in the line in the sand and a tight fit of the internal electronic components. At the same time, proper melt temperature also helps avoid excessive material decomposition during the injection molding process, ensuring the stability of the eyewear component.

Next, the focus was on optimizing the holding pressure. The holding pressure directly affects the residence time of the eyewear material in the mold and the curing effect after molding. By adjusting the holding pressure, we sought to minimize deformation and residual stress during the manufacturing process while ensuring that the mold is fully filled. This helps to improve the clarity, shape stability, and comfort of SCLs while reducing the stress on electronic components caused by micro-molecular deformation.

Finally, the focus is on optimizing the holding time. A longer holding time ensures that the plastic fully fills the mold cavities and stays filled, thus reducing air bubbles and voids in the product. In addition, longer holding times help reduce residual stresses and improve the mechanical strength and durability of the product. However, excessively long holding times may result in longer production cycles. Therefore, a suitable holding pressure time can optimize the injection molding of smart contact lenses and ensure a balance between product quality and productivity.

In this section, injection molding of smart contact lenses is simulated. In this study, the use of IME technology (Injection Molding Engineering) and PHEMA materials was chosen with the aim of simulating contact lenses with excellent performance. The object of the simulation, i.e. the lens of the contact lens, was first defined. Through an in-depth study of the standards and user requirements in the contact lens market, I determined the dimensional parameters of a suitable contact lens for the simulation, with a diameter of 14 mm, a base arc radius of 8.6 mm, and a center thickness of 0.1 mm (Fig. 7).

Fig. 7.

SCL 3D model and specific dimensions.

PHEMA (polyhydroxyethyl methacrylate) is a biocompatible material commonly used in the manufacture of contact lenses. PHEMA was chosen as the base material for the simulation to mimic the material properties and biocompatibility of eyeglasses. In the material selection stage, the optical properties, transparency, and interaction with ocular tissues of PHEMA were considered in this paper. Before performing the simulation, we carefully set the parameters related to the IME technology and the PHEMA material, including injection temperature, injection pressure, and injection time. The proper setting of these parameters is essential to simulate contact lenses with excellent performance, while also taking into account the computational efficiency of the simulation process.

As shown in Fig. 8, the use of integrated molding electronics (IME) technology is enough to ensure that the material fully fills the mold and maintains the desired shape after injection by accurately controlling parameters such as temperature and pressure. The circuit system of the smart contact lens was also designed to ensure better reception and processing of feedback from the outside world. The electronic film consists of several key components, including a hybrid substrate, functional devices such as rectifiers, LEDs and sensors, and a transparent stretchable conductor. The synergy of these components enables the smart contact lens to collect, process and transmit data, allowing for real-time monitoring and feedback on the user’s eye condition.

Fig. 8.

SCL circuit design drawing.

An initial average nodal displacement of 0.159 mm and a residual stress of 24.057 MPa were obtained based on the initial conditions provided (initial holding pressure of 250 MPa, plastic temperature of 20 °C, and holding time of 3 s). These initial values provide baseline data that can be used to evaluate the effects of subsequent parameter changes on nodal displacement and residual stress. We found that larger average values of nodal displacement and residual stress, nodal displacement may lead to breakage of the wires on the IME membrane in the smart contact lenses, which may result in unstable signal transmission, while larger residual stress may lead to a decrease in transparency and penetration of the lenses. For the case of large nodal displacement and residual stress, the data are next predicted and analyzed using the radial basis function, while the data are iteratively optimized in combination with NSGA-III to find the optimal parameter combination through the combination of the two methods.

Results and discussion

Find the optimal parameter

By simulating 20 sets of data, this paper investigates the effects of melt temperature, holding pressure and holding time on nodal displacement and residual stress. During the simulation process, the values of these three parameters were adjusted separately and their effects on nodal displacement and residual stress were observed. The results show that an increase in melting temperature leads to an increase in nodal displacement, while the magnitude of residual stress is closely related to the holding pressure and holding time.

As shown in Table 2 and 20 groups of parameter combinations were obtained by screening parameters in the range of melt temperature of 20–30 °C, holding pressure of 100–120 MPa, and holding time of 3–10 s using orthogonal analysis. Then, we carried out simulation experiments for each group of parameter combinations to obtain the corresponding nodal displacement and residual stress data.

Table 2.

Node displacement and residual stress obtained under different parameter combinations.

Node	Melting temperature (°C)	Holding pressure (MPa)	Holding time (s)	Node displacement (mm)	Residual stress (MPa)
1	25	110	6.5	0.013	0.198
2	20	120	6.5	0.035	0.198
3	25	110	6.5	0.013	0.198
4	30	120	6.5	0.023	0.196
5	25	110	6.5	0.013	0.198
6	20	100	6.5	0.036	0.199
7	20	110	10	0.005	0.198
8	25	110	6.5	0.013	0.198
9	25	110	6.5	0.013	0.198
10	25	110	6.5	0.013	0.198
11	30	100	6.5	0.016	0.196
12	25	120	10	0.01	0.197
13	20	110	3	0.035	0.198
14	25	120	3	0.013	0.198
15	25	100	10	0.012	0.198
16	30	110	3	0.023	0.195
17	30	110	10	0.023	0.196
18	25	100	3	0.012	0.198
19	25	110	6.5	0.013	0.198
20	25	110	6.5	0.013	0.198

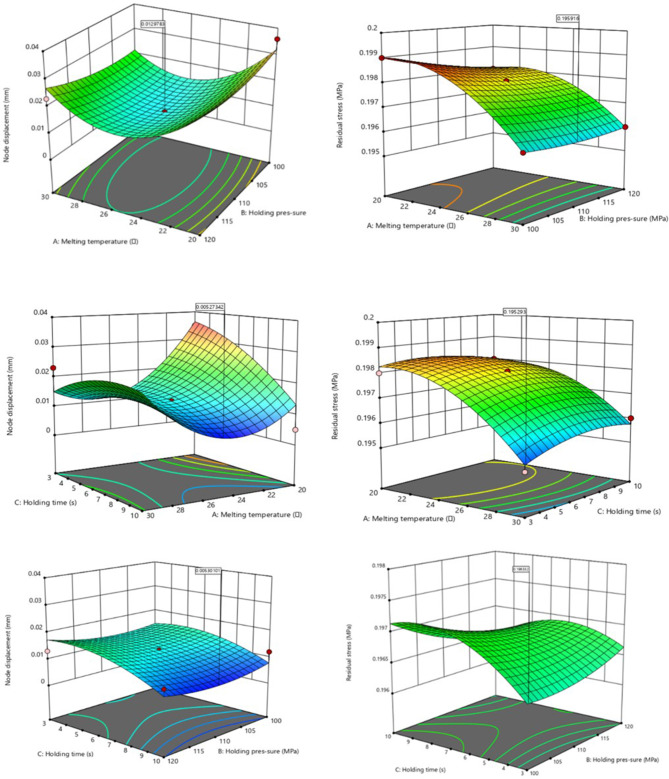
By plotting the response surface graphs, as shown in Fig. 9, the nodal displacements show a significant decreasing trend under the modulation of melting temperature, holding pressure and holding time, especially the melting temperature has the greatest effect on the nodal displacements. The residual stresses responded less to the changes of these three parameters, but the tuning of melt temperature and holding pressure time had a certain effect on them. It should be noted that for further study of residual stress, other parameters or more complex factors may need to be considered.

Fig. 9.

Response surface plots of the three injection moldin g parameters to the target values. (a) Shows the response surface of melt temperature and holding pressure to nodal displacement and residual stress, respectively; (b) shows the response surface of melt temperature and holding time to nodal displacement and residual stress, respectively; (c) shows the response surface of holding pressure and holding time to nodal displacement and residual stress, respectively.

According to the response surface analysis of the effects of melt temperature, holding pressure and holding time on nodal displacement and residual stress, it is found that the nodal displacement and residual stress show different trends under different combinations of parameters. Under the influence of melt temperature and holding pressure, the minimum value of nodal displacement is 0.013 mm, and the minimum value of residual stress is 0.196 MPa, while under the influence of melt temperature and holding time, the minimum value of nodal displacement is 0.005 mm, and the minimum value of residual stress is 0.195 MPa. Under the influence of holding pressure and holding time, the minimum value of nodal displacement is 0.005 mm, and the minimum value of residual stress is 0.196 MPa. Under the influence of holding pressure and holding time, the minimum value of nodal displacement is 0.005 mm and the minimum value of residual stress is 0.196 MPa. Considering the influence of various parameter combinations, we get the optimal solution of nodal displacement is 0.005 mm, and the optimal solution of residual stress is 0.195 MPa. In the next step, we will use the radial basis model to further predict and optimize the molding parameters in order to obtain more optimal values of nodal displacement and residual stress.

In order to predict the trends of nodal displacement and residual stress more accurately, radial basis functions will be used for analysis and prediction. The radial basis function, as a commonly used interpolation method, is capable of estimating values at other locations based on the eigenvalues of known data points. By fitting a radial basis function to the data, a function model is built to predict the changes in nodal displacement and residual stress for different parameter values.

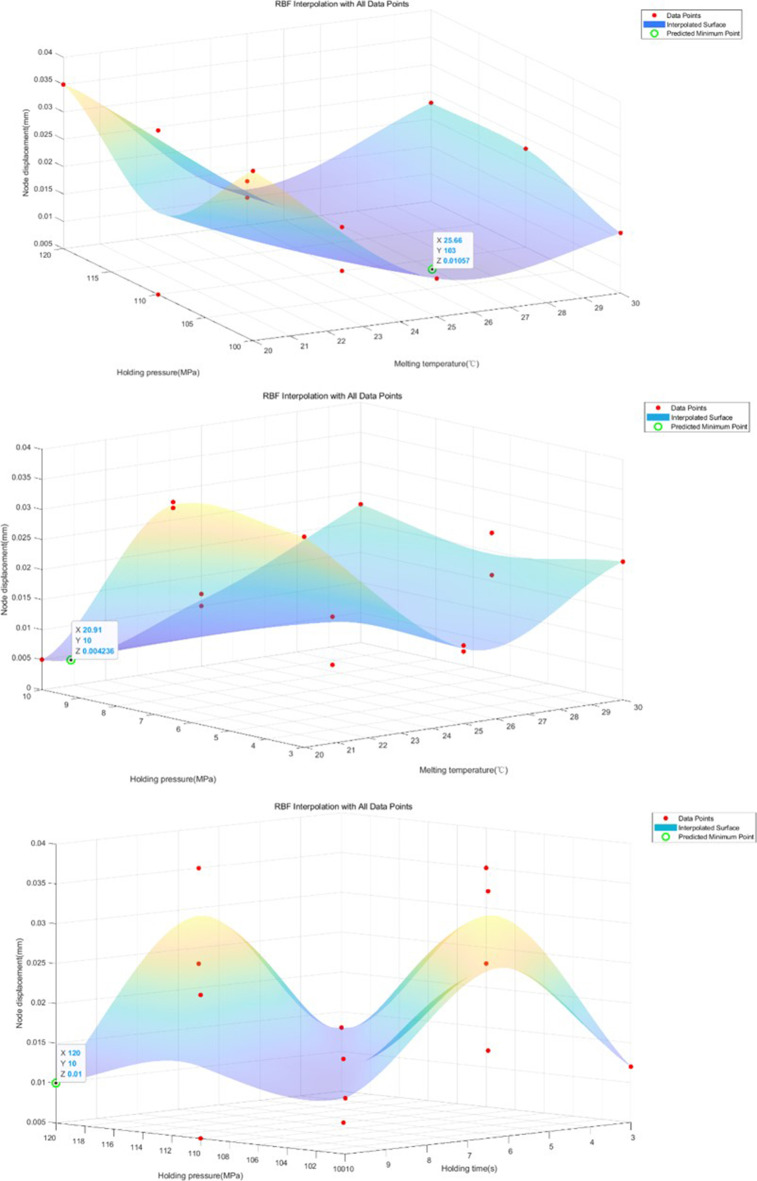
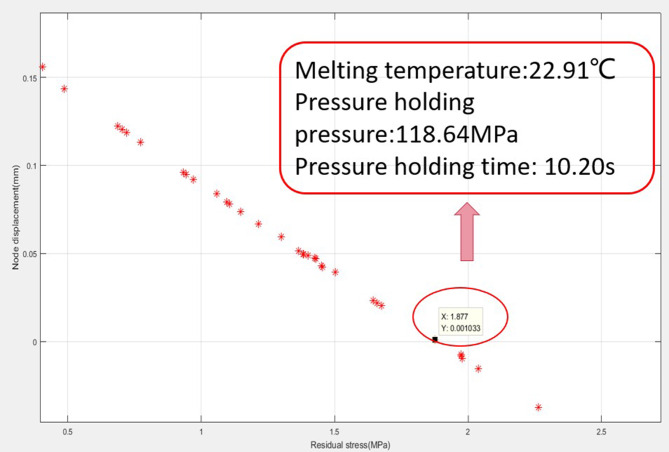
First, the three factors, melting temperature, holding pressure and holding time, were interpolated using a two-dimensional RBF radial basis function to predict the micromolecular displacements and residual stresses, respectively. Through this step, we obtained the resultant plots as shown in Fig. 10, which clearly present the trend of the effect of different parameters on the micromolecular displacement and residual stress (Table 3).

Fig. 10.

RBF prediction model. (a) Shows the prediction model of melt temperature and insulation pressure on node displacement; (b) shows the prediction model of melt temperature and holding time on node displacement. (c) shows the prediction model of holding pressure and holding time on node displacement.

Table 3.

Comparison of process optimization results for manufacturing.

	Melting temperature (°C)	Holding pressure (MPa)	Holding time (s)	Node displacement (mm)	Residual stress (MPa)
Pre-optimization	20.000	250.000	3.000	0.159	24.057
Post-optimization	22.910	118.640	10.200	0.007	2.213
Optimization rate (%)	–	–	–	95.600	90.80

Using this model, we can estimate the magnitude of the node displacement given the melting temperature, holding pressure and holding time. Figure 10 shows the prediction results of node displacement after fitting with radial basis function, which intuitively reflects the influence of parameter changes on node displacement. The prediction results using the radial basis function show that the predicted nodal displacement can be as small as 0.011 mm when the melt temperature is 25.66 °C and the holding pressure is 103 MPa; if the holding pressure is increased to 120 MPa and the holding time is 10 s, the predicted nodal displacement can be as small as 0.01 mm. And in the case of a melt temperature of 20.91 °C and a holding time of 10 s, the predicted nodal displacement can be as small as 0.004 mm.

As a result, we found that the nodal displacement can be minimized to 0.004 mm under specific conditions. Specifically, this result was observed when the melt temperature was 22.91 °C and the holding pressure time was 10 s. The results of the predicted models were shown in the following table. Further analysis reveals that in the first two sets of prediction models, the nodal displacement is smaller when the holding pressure is 120 MPa.

Considering the small variation of residual stresses, in this paper, we decided to further optimize three injection molding parameters, namely melt temperature, holding pressure and holding time, using NSGA-III algorithm. By weighing multiple optimization objectives, the aim is to further optimize the SCL node displacement and residual stress of the smart contact lens. Next, we use the NSGA-III multi-objective optimization algorithm to iteratively optimize the fitting functions of the three parameters, namely melt temperature, holding pressure, and holding time, using the node displacements and residual stresses as the multi-objective optimization to obtain the final Pareto front, as shown in Fig. 11. In order to ensure the minimum node displacement, the data were further screened, and it was found that in the optimized parameter combination, the minimum node displacement could be up to 0.001003 mm, and the corresponding residual stress value was 1.887 MPa.

Fig. 11.

Multi-objective Pareto frontier results.

It is clear that there exists no combination of process parameters that optimizes both objectives simultaneously. Therefore, it is necessary to select the most appropriate solution set based on different weights. Through the global optimization of NSGA-III, the optimal process parameters were determined: melt temperature 20.91 °C, curing pressure 118.64 MPa, and curing time 10.20 s. The parameter combinations obtained by the boundaries were then simulated to further validate the reliability of the multi-objective optimization, and the resultant plots as in Fig. 12 were obtained, where the average junction displacement could be up to 0.007 mm, and the average residual stress could be up to 2.213 MPa, which were therefore similar to the expected Pareto optimal solution values. 2.213 MPa, which are similar to the expected Pareto optimal solution values, thus also verifying the reliability of the optimization method. As shown in Table 4, the optimization rates of nodal displacement and residual stress reached 95.60% and 93.47%, respectively, compared to the initially recommended process parameters. This marks a significant enhancement in the optimization results.

Fig. 12.

Simulation verification results.

Table 4.

The relationship between wire diameter and current and temperature.

Temp rise (°C)	10			20			30
Copper	1/2 oz	1 oz	2 oz	1/2 oz	1 oz	2 oz	1/2 oz	1 oz	2 oz
Trace width (Inch)	Maximum current amps (A)
0.010	0.5	1	1.4	0.6	1.2	1.6	0.7	1.5	2.2
0.015	0.7	1.2	1.6	0.8	1.3	2.4	1	1.6	3
0.020	0.7	1.3	2.1	1	1.7	3	1.2	2.4	3.6
0.025	0.9	1.7	2.5	1.2	2.2	3.3	1.5	2.8	4
0.030	1.1	1.9	3	1.4	2.5	4	1.7	3.2	5
0.050	1.5	2.6	4	2	3.6	6	2.6	4.4	7.3
0.075	2	3.5	5.7	2.8	4.5	7.8	3.5	6	10
0.100	2.6	4.2	6.9	3.5	6	9.9	4.3	7.5	12.5
0.200	4.2	7	11.5	6	10	11	7.5	13	20.5

Research on the relationship between node displacement and line diameter

Obviously, the optimal parameter combinations were obtained by comparing the optimization results of the RBF radial basis function prediction and the NSGA-III multi-objective genetic algorithm for the node displacements and residual stresses. In order to ensure that the obtained node displacements do not affect the stability of signal transmission, the optimized node displacements were analyzed for current and frequency to determine whether they are within the variable range of current and frequency.

As integrated circuit processes have become smaller, precise control of copper lead line widths has become a serious challenge for micrographics and etching processes. Small variations in copper conductor line widths have become impossible to ignore, mainly because line width variations cause the thickness of the dielectric layer between the copper conductors to no longer remain constant, resulting in an uneven distribution of the electric field within the dielectric layer. This non-uniformity leads to localized areas around the copper conductor that are subjected to high electric fields, which in turn reduces the reliability of the dielectric layer.

According to IPC documents, as shown in Table 4, there is the following relationship between the temperature rise of the circuit board ΔT, the cross-sectional area of the wire (= copper foil thickness × line width) A and the current I: I = k∆T0.44A0.75 where the coefficient k is a curve, the PCB inner line and the outer line k value is very different (the outer layer is easier to heat). Because k is similar to a straight line, for simplicity, at room temperature (25 °C), the inner line k = 0.024, the outer line k = 0.048. Note that the cross-sectional area in the above formula is measured in square mil. The data provided by IPC-STD-275 is shown in the following table. The unit of line width is Inch (1 inch = 25.4 mm). 1 oz. Copper = 0.035 mm, 2oz.=0.07 mm.

Figure 13 shows the relationship between wire diameter, temperature and allowable through current. We find that an increase in wire diameter is positively correlated with the amount of current allowed to pass. In addition, as the temperature increases, the current allowed to pass also increases. In order to simulate the actual operation of a smart contact lens in an ocular environment, the temperature of the eye, which is usually around 10 °C, was chosen as a benchmark for the change in wire diameter current. In this case, a functional relationship between the current and the width of the wire is obtained. When the copper wire is 1/2oz, the functional expression is ; when the copper wire is 1oz, the functional expression is ; and when the copper wire is 2oz, the functional expression is . Since the previously obtained results showed an average change in node displacement of 0.007 mm, this change was converted to 0.0002756 inches. Therefore, this value was substituted into the functional expression to obtain the current change values shown in Table 5.

Table 5.

Current change caused by node displacement at 10℃

Copper (oz)	1/2	1	2
Function expression	Y = 0.44 + 19.55X	Y = 0.86 + 31.69X	Y = 1.18 + 53.53X
Maximum of current (Pre-optimization) (A)	0.5624	1.0584	1.5151
Maximum of current (Post-optimization) (A)	0.4454	0.8687	1.1947

Fig. 13.

Relation between diameter and current of copper wire.

As can be seen from Table 5, the current optimization increases gradually with the increase in the thickness of the copper wires (1/2oz to 2oz), which are 0.117 A, 0.1897 A and 0.3204 A. This indicates that a larger current optimization can be achieved by optimizing the process parameters with a larger thickness of the copper wires. In addition, since thicker copper wires usually have lower resistance, the amount of current optimization increases accordingly under the same process conditions. The reduced change in current after optimization can reduce the degree of signal distortion, ensure the accuracy of the signal during transmission, and thus improve the reliability of data transmission. Secondly, this optimization also saves energy and improves the energy efficiency of the circuit, which is especially important for mobile devices or wireless communication systems.

Finally, the optimized node displacement and current reduction indicate that our proposed process parameter optimization scheme is effective. The reduction of nodal displacement can improve the comfort and stability of contact lenses; meanwhile, the reduction of current helps to reduce the irritation of ocular tissues during use. In subsequent studies, other performance indicators of smart contact lenses, such as oxygen permeability and hydration, can be further tested to enhance the comfort and adaptability of contact lenses. Secondly, new materials and process technologies, such as the use of new biocompatible materials and the introduction of nanotechnology, can be explored to improve the performance and function of contact lenses.

Author contributions

Conceptualization, Hanjui Chang; Data curation, Daiyao Lin; Methodology, Shuzhou Lu; Project administration, Yue Sun; Writing—original draft, Hanjui Chang. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

Data availability

The authors declare that the data supporting the results of this study are available in the paper. If any raw data files in other formats are required, they can be obtained from the corresponding author upon reasonable request.

Declarations

Competing interests

The authors declare no competing interests.