Abstract
This Perspective explores the integration of machine learning potentials (MLPs) in the research of heterogeneous catalysis, focusing on their role in identifying in situ active sites and enhancing the understanding of catalytic processes. MLPs utilize extensive databases from high-throughput density functional theory (DFT) calculations to train models that predict atomic configurations, energies, and forces with near-DFT accuracy. These capabilities allow MLPs to handle significantly larger systems and extend simulation times beyond the limitations of traditional ab initio methods. Coupled with global optimization algorithms, MLPs enable systematic investigations across vast structural spaces, making substantial contributions to the modeling of catalyst surface structures under reactive conditions. The review aims to provide a broad introduction to recent advancements and practical guidance on employing MLPs and also showcases several exemplary cases of MLP-driven discoveries related to surface structure changes under reactive conditions and the nature of active sites in heterogeneous catalysis. The prevailing challenges faced by this approach are also discussed.
Keywords: heterogeneous catalysis, machine learning potential, global optimizations, active sites, structure prediction
1. Introduction
Heterogeneous catalysis plays a significant role in the modern chemical industry, serving as a critical facilitator for a wide range of chemical reactions essential for producing fuels, plastics, pharmaceuticals, and other chemicals.1,2 With the growing demand for renewable energy sources and carbon neutrality, there is an urgent need for novel heterogeneous catalysts that exhibit robust performance, stability, activity, and selectivity for various chemical processes. Advancements in catalyst development and research require a comprehensive understanding of active-sites, a challenge compounded by the dynamic nature of catalytic reaction systems and often disordered or amorphous catalyst surface structures.3
For heterogeneous catalysts, it is well-known that not the entire surface of the nanoparticle participates in catalytic reactions, but rather, certain active sites do.4 These active sites, as pointed out by Sabatier’s principle, should neither bind too strongly nor too weakly to adsorbates and must bind the transition state more tightly than the substrate. This delicate balance lies at the heart of catalysis at the active site. Given the extraordinary complexity of active sites in heterogeneous catalysis, theorists have to simplify these systems, make predictions based on these simplifications, and, where possible, validate them under experimental conditions. Quantum mechanical (QM) methods, such as Density Functional Theory (DFT), are frequently used for probing catalytic processes at the atomic scale, predicting material behavior, and guiding experimental efforts.5 Although DFT offers a favorable balance between computational efficiency and accuracy, its application is generally constrained by the computational demand, particularly for large systems or extensive simulation time.6 While theoretical surface science studies have significantly advanced our understanding of active sites, the necessary simplifications regarding time, temperature, pressure, and structural complexity fall short of capturing the full reality of catalytic processes and the nature of active sites.
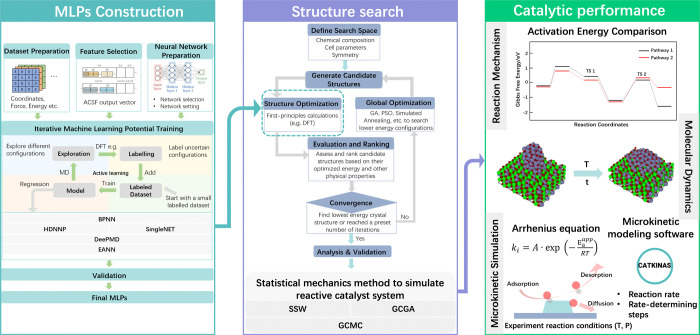
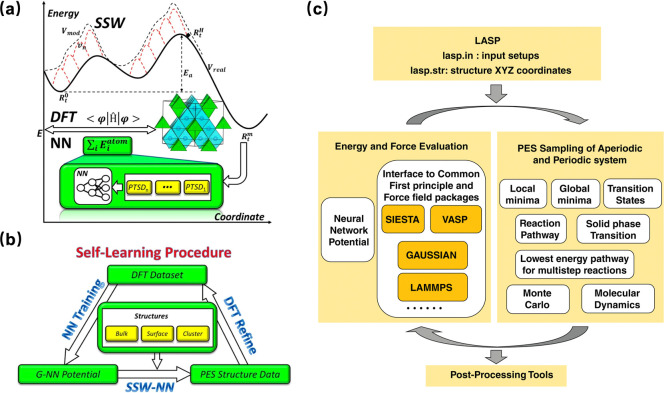
Recent advancements in machine learning-based atomic simulations6−13 offer promising enhancements to this challenge. One of the most promising applications of ML in heterogeneous catalyst research is the emergence of machine learning potentials (MLPs).14−20 This is attributed to the development of well-defined materials structure databases,21 the rapid innovations of machine learning models, and iterative learning algorithms. As shown in Figure 1, the construction of MLPs through algorithms that learn the relationship between atomic configurations and their potential energies based on QM calculations, thereby enabling the efficient and accurate prediction of energies and forces for new configurations.22,23 Various types of MLPs training models have been developed and widely applied. For example, the Behler-Parinello Neural Networks (BPNN) is one of the pioneering neural network approaches for potential energy surfaces.24 BPNN uses a high-dimensional neural network to represent the potential energy surface and employs symmetry functions to describe the local environment of the atoms. The deep learning potentials, including various architectures like Convolutional Neural Networks (CNNs), Graph Neural Networks (GNNs), and Recurrent Neural Networks (RNNs),25 can model complex potential energy surfaces. For instance, DeePMD utilizes deep learning techniques to predict atomic forces.26 There are also other types of MLPs, including Gaussian Approximation Potentials (GAP),27−30 which uses Gaussian process regression to interpolate between known atomic configurations; Spectral Neighbor Analysis Potential (SNAP),31 which uses bispectrum components of neighbor atoms to create a descriptor that is input into a linear or nonlinear model; and Many-Body Tensor Representation (MBTR), which uses many-body tensor representations to describe the local chemical environment of atoms etc.32−38
Figure 1.
Schematic representation of the construction of machine learning potentials and its application in catalytic research.
By using MLPs, it is now possible to perform global optimizations that reliably produce a putative global minimum structure at given conditions, providing a speed-up of 4 orders of magnitude compared to DFT calculations. This efficiency enables us to perform large-scale global optimization algorithms like Stochastic Surface Walking (SSW),39 Genetic Algorithms (GA),40 and Grand Canonical Monte Carlo (GCMC)41 across thousands of compositions, tracking the structural evolution of major low-energy surfaces, the structure search process flowchart is illustrated in Figure 1. The resulting surface structures, paired with DFT calculations, AIMD, and microkinetic modeling, enable the evaluation of catalytic performance and locate the in situ active sites, as shown in the catalytic performance block in Figure 1.
This review presents an overview of recent achievements using MLP-based methodologies for structural search and active site determination in heterogeneous catalysis. We start with an introduction to the underlying principles and training of MLPs, followed by a review of different global optimization algorithms for structural search. We also highlight several prominent case studies in which MLP-driven methodologies have discovered active sites in various heterogeneous catalysis reaction systems. Current challenges and future perspectives on the development of MLPs and their application to heterogeneous catalysis are also presented.
2. Machine Learning Potentials
The initial attempt to use ML methods to construct potential energy surface can be traced back to the early 1990s.42 Sumpter et al. pioneered the use of an artificial neural network model to predict anharmonic vibrational parameters for a polymer’s PES in 1992.43 Three years later, Doren and co-workers utilized a feed-forward neural network to model global properties of potential PES in low-dimensional systems depending on the positions of a few atoms.44 Their initial tests of the neural network method to construct the H2/Si(100)-2 × 1 potential achieved a mean absolute deviation (MAD) of 1.7 kcal/mol. This result indicates that the method is capable of making chemically accurate predictions of the potential energy for systems with multiple degrees of freedom. Although significant progress has been made in developing machine learning potentials during this period, the iteration and optimization of MLPs did not achieve rapid development as expected in the following ten years. This progress was hindered by bottlenecks in computing resources, insufficient training data sets, and limitations in neural networks and theoretical methods at that time. At the beginning of the 21st century, Hinton et al. proposed deep belief nets (DBNs) to overcome the traditional neural network’s limitation on the number of layers, marking the arrival of the deep learning era.45 The advent of continuously improved machine learning techniques, along with the advancement of GPUs and the emergence of distributed computing, has accelerated the prosperity of contemporary MLPs.46−50
2.1. Behler-Parrinello Framework-Based MLPs
The Behler-Parinello Neural Networks (BPNN) introduced by Jörg Behler and Michele Parrinello in 2007 utilized a feed-forward neural network architecture to fit a two-dimensional PES, employs symmetry functions to transform the raw atomic positions into a set of descriptors that are invariant to rotation, translation, and permutation of identical atoms.24 The structure of the BPNN neural network is shown in Figure 2a. This network contains an input layer to generalize system coordinates and an output layer to yield associated energy, and the atomic energies depend on the local chemical environment within a cutoff radius. Between the input and output layers, there are one or more hidden layers; the simple neural network denoted as Si has been used as a subnet. For high-dimensional potential energy surfaces, radial symmetry G1 function and angular symmetry function G2 are applied to construct the total energy E of the system as a sum of atomic energies Ei, and the expression is as follows:
| 1 |
| 2 |
| 3 |
Figure 2.
(a) The schematic of standard HDNNPs. (b) Radial distribution function (RDF) of a silicon melt at 3000 K was obtained using a cubic 64-atom cell from BPN, other neural network (NN) potentials, and density-functional theory (DFT) (Left). The difference between the energies predicted by the BPNN and the recalculated energies obtained from density-functional theory (DFT) for the initial and final structures in each step of a metadynamics simulation of bulk silicon (Right). Reproduced from ref (24). Copyright 2007 American Physical Society. (c) The schematic of SingleNet. Reproduced from ref (57). Copyright 2020 American Chemical Society. (d) Scheme for LASP implementation of the Behler-Parinello-type NN. Reproduced from ref (59). Copyright 2017 The Royal Society of Chemistry.
This model was used to perform molecular dynamics (MD) simulations on the radial distribution function (RDF) of a silicon melt at 3000 K. The performance of the BPNN model only has a small difference when compared with DFT results, while other empirical potentials show significant deviations, as illustrated in Figure 2b. The accuracy and broad applicability of this model have been validated through numerous subsequent applications across various systems.51,52 However, there are major limitations of BPNN schemes. First, BPNN needs to be enhanced in terms of dimensionality.53 The recent advancements in High-Dimensional Neural Network Potentials (HDNNPs) compared to BPNNs include more refined descriptors of the atomic environment and optimized network architectures.54,55 These advancements make use of many-body atom-centered symmetry functions (ACSFs) to describe the atomic environments and a set of atomic neural networks to connect the descriptor vectors to energies.56 This enables a better capture of the interactions between atoms, ultimately improving the accuracy of the model.14 Second, the BPNN symmetry functions are specific to each system, and the atomic energies of atoms from different elements are calculated by using different NNs. To address this limitation, SingleNet is proposed as a modified version of BPNN.57 SingleNet shares weights for the nonlinear layers among different elements. The weighted symmetry functions evolved from eqs 2-3. As shown in Figure 2c, its network is designed to facilitate the transfer of knowledge between atoms. This approach can notably accelerate the training process, decrease the necessary amount of training data, and still maintain moderate accuracy compensation. Liu et al. utilized a high-dimensional neural network (HDNN) in their stochastic surface walking (SSW) method to provide an efficient and predictive platform for large-scale computational material screening.58 The neural network architecture is shown in Figure 2d. They incorporated the stress tensor into the performance function during neural network training, allowing for the simultaneous fitting of energy, forces, and the stress tensor. This approach can help avoid overfitting, produce more accurate forces, and ultimately improve predictive ability.59 So far, BPNNs have undergone various optimizations to enhance their performance, accuracy, and applicability.60,61
2.2. Deep Learning Potentials
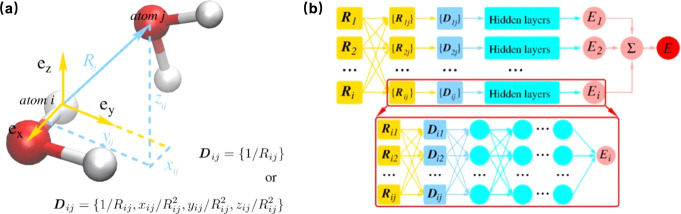
The Behler-Parinello neural networks were a significant advancement in utilizing machine learning for predicting the potential energy. However, they were built on relatively “shallow” neural networks instead of deep architectures. The first widely recognized potential of deep learning is arguably the Deep Potential (DP) model in the Deep Potential Molecular Dynamics (DeePMD) method, developed by Wang et al.62 Introduced around 2017, the DP model utilized deep neural networks to learn the potential energy and forces of atoms in a system directly from ab initio data. The deep learning architecture enables the model to capture complex, high-dimensional relationships in the data, making it a powerful tool for molecular dynamics simulations. DeePMD overcomes the limitations associated with auxiliary quantities such as symmetry functions or the Coulomb matrix. Instead of handcrafted symmetry functions, DeePMD uses a different approach to describe the local environment of atoms by employing a more flexible and general representation learned by the neural network itself.63 The descriptors in DeePMD are learned features that are automatically extracted from the raw coordinates of the atoms during the training process. This is achieved through the use of embedding networks that map the local atomic environments to a high-dimensional feature space. The learned descriptors are optimized to capture the relevant information for predicting energies and forces, which can enhance generalization and transferability.
As mentioned above, the DeePMD method is trained end-to-end, meaning that the input features (atomic positions) are directly mapped to the output quantities (energies and forces) without the need for handcrafted intermediate descriptors.26,64−66 DeePMD uses a local environment representation for each atom, which allows the model to capture the physics of interactions within the cutoff radius Rc. This locality ensures that the model scales well with system size. The potential energy of each atomic configuration is represented in eq 1, where Eiis determined by the local environment of atom i within a cutoff radius Rc. The local coordinate information Dij is represented as 1/Rij, and serves as input of a deep neural network, which return Ei in output, as illustrated in Figure 3a. The neural network as shown in Figure 3b is also designed to be invariant to translation, rotation, and permutation of identical atoms, which are fundamental symmetries in physics, as mentioned before. This invariance is crucial for the model to make physically consistent predictions. DeePMD represents a true deep learning approach, leveraging the advances in deep neural networks that have been successful in other domains such as image and speech recognition. It has set the stage for subsequent developments in deep learning potentials and has been applied to a variety of systems, from simple molecules to complex materials.
Figure 3.
(a) Schematic plot of the neural network input for the environment of atom i, taking water as an example. (b) Schematic plot of the DeePMD model. The frame in the box is the zoom-in of a DNN. Reproduced from ref (62). Copyright 2018 American Physical Society.
2.3. Embedded Atom Neural Network Potentials
An embedded atom neural network (EANN) was proposed by Zhang et al.67 The EANN utilizes a symmetry-invariant embedded density descriptor inspired by the empirical embedded atom method (EAM) model as the atomic representation. It employs a deep neural network as a regressor, which can implicitly contain the three-body information without requiring an explicit sum of the conventional costly angular descriptor, making it highly efficient. This model has been demonstrated to achieve better efficiency in accelerating MD and spectroscopic simulations at the ab initio level of accuracy.
In the EAM framework, the embedding energy can be approximated as a function of the scalar local electron density and an electrostatic interaction. Therefore, the total energy of an N system can be expressed as
| 4 |
where Fi is the embedding function, Øij represent the electrostatic interaction between atoms. In EANN, to improve the representation of the embedded density and the function F, the distance r between the central atom and its neighbor can be described by the same type of Gaussian-type functions (GTOs) as
| 5 |
where α and r are parameters that determine radial distribution while lx + ly + lz = L captures the angular distribution similar to atomic orbitals. The complete atomic representation denoted as embedded atomic density is calculated by taking the square of the linear combination of ϕ from neighbor atoms as
| 6 |
where cj is equivalently an element-dependent coefficient. This representation only requires α, rs, and L as hyperparameters, as a cosine type cutoff function is applied to each orbitals making the interaction decay to zero and approaching rc smoothly. Replacing the F with an atomic NN, eq 1 can be rewritten as
| 7 |
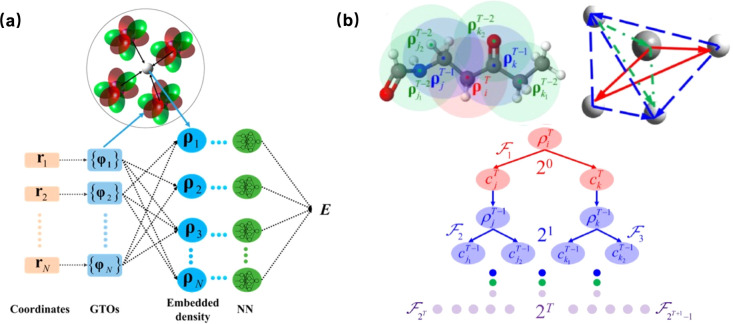
where ρi represents a set of local atomic density descriptors. The density-like descriptors rely solely on Cartesian coordinates, eliminating the need to classify two-body and three-body terms, which makes it efficient for programming. The architecture of the EANN is illustrated in Figure 4a.
Figure 4.
(a) Schematic plot of the EANN neural network input for the environment of atom i, taking water as an example. Reproduced from ref (130). Copyright 2019 American Chemical Society. (b) Schematic plot of the REANN model. The frame in the box is the zoom-in of a DNN. Reproduced from ref (68). Copyright 2021 American Physical Society.
In order to incorporate complete many-body correlations in the EANN model, Zhang et al. proposed a Recursively Embedded Atom Neural Networks (REANN) that integrates the message-passing concept into a well-defined three-body descriptor to incorporate some nonlocal interactions beyond the cutoff radius without explicitly computing high-order terms.68,69 Take CH4 as example, Figure 4a shows how the density descriptor is recursively embedded. The orbital expansion coefficient cj should vary with the molecular configuration, to cast this physical concept into the descriptor one way is to make cj itself a function of the jth atom’s neighbor environment. The orbital coefficient is recursively embedded as
| 8 |
where ct – 1j and rt – 1j are the collections of orbital coefficients and atomic positions in the neighborhood of the central atom j in the (t-1)th iteration. As orbital coefficients are expanded, the number of three-body functions doubles in each iteration until the last environment-independent ones, as illustrated in Figure 4b. Then, the higher-order correlations are incorporated in this recursion by implementing cij into the embedded density descriptor. It is worth noting that REANN can be easily adapted to enhance other complex many-body descriptors without changing their basic structures. For instance, this can be achieved by adjusting the atomic weights of the weighted atom-centered symmetry functions based on their local environment or by incorporating learnable coefficients into the DeepMD descriptors.70
3. Active Learning in MLPs Training
In this section, we introduce the popular training protocols of MLP, active learning. Active learning, a machine learning strategy in the realm of supervised learning, is designed to automatically sample, select and label new data with the goal of efficiently generating a diverse and relevant data set to train a more robust ML model.71 The core idea of active learning is that the model can actively identify and request the labels of the data points that are most helpful for improving its performance. Thus, active learning is particularly suitable for situations where the training data set is difficult and expensive to obtain. In materials science and molecular simulation. MLPs typically perform poorly in extrapolation due to a limited data distribution. If the training data do not cover all areas of the PES of interest, the MLP will struggle to make predictions in regions not represented in the training set because the model has not learned the characteristics and patterns of those areas. When applying MLP to optimize an extrapolative configuration, it could result in structures and energies that are not physically realistic.72 One solution to address this issue is to iteratively update the MLP during the structure search in an on-the-fly manner by continuously incorporating extrapolative configurations into the training set. This approach not only accelerates the structure search but also helps in the construction of a highly accurate and transferable MLP.
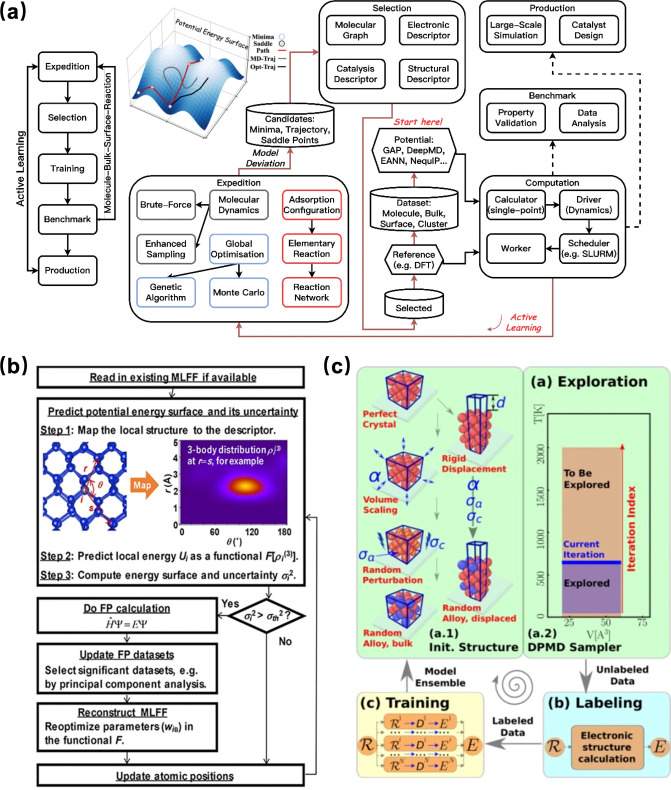
So far, active learning is widely applied to efficiently generate training data, avoiding the need for large, expensive first-principle calculations to obtain high-performance MLPs.73−77 Xu developed an efficient active learning pipeline named Generating Deep Potential with Python (GDPy), which aims to automate the structure exploration and the model training for MLPs.78 The workflow is shown in Figure 5a. The iterative active learning procedure is embedded with various exploration algorithms, model uncertainty estimation, and descriptor-based selection procedures to construct an efficient active learning pipeline. Jinnouchi et al. summarized the on-the-fly generation of interatomic potentials for large-scale atomistic simulations using active learning schemes. As illustrated in Figure 5b, a MLP is generated on the fly during an MD simulation.79 The core of this workflow is to utilize the current MLP for predicting energy, forces, stress tensor components, and uncertainty. The predicted uncertainty is estimated to determine whether to perform a first-principles calculation or not. If the model decides not to carry out the first-principles calculation, the predicted energy, forces, and stress tensor components are used to update the atomic positions and velocities. Otherwise, the first-principal calculation is carried out, and the resulting structural data set is added to the reference data sets. DeepMD also has a built-in active learning framework known as Deep Potential Generator (DP-GEN)63,80 to automate the creation of training data sets for molecular dynamics simulations. Illustrated in Figure 5c, it initiated with a basic model of the MLP, DP-GEN performs molecular dynamics simulations to explore atomic configurations, identifying areas where the model’s predictions are uncertain due to insufficient learning. These configurations are then subject to DFT calculations to generate accurate data labels for retraining the model, with iterating this process to enhance model accuracy and transferability.
Figure 5.
(a) Schematic of the workflow of GDPy. Reproduced from ref (126). (b) Schematic of machine-learning force field generation by active learning on the fly during an MD simulation. Reproduced from ref (79). Copyright 2020 American Chemical Society. (c) Schematic plot of one iteration of the DP-GEN scheme, taking the Al–Mg system as an example. Iterative steps of exploration with DPMD, labeling, and training are also illustrated. Reproduced from ref (80). Copyright 2019 American Physical Society.
4. Algorithm and Method in Catalyst Structure Prediction
In heterogeneous catalysis, the composition, size, and morphology of the catalyst surface may change during reaction conditions, leading to the emergence of various electronic and geometric structures that determine the intrinsic activity and selectivity of catalysts.81−84 For example, catalysts with different crystal phases have varying symmetries and could expose very different facets with distinct electronic and geometrical properties.85−87 These differences can significantly influence the activity, selectivity of the active sites, and the site density.88 Experimental techniques and molecular modeling methods using electronic structure methods can model the equilibrium structures of catalysts with acceptable accuracy.89 However, it remains a significant challenge to determine structures directly under extreme conditions.90 Therefore, in designing new catalysts, research on catalytic mechanisms and catalyst screening under reaction conditions utilizing crystal structure prediction (CSP) methods has been extensively explored.91−97
4.1. Stochastic Surface Walking Method
The emergence of software packages like LASP (Large-scale Atomistic Simulation with neural network potentials) is driven by the increasing overlap between ML and computational chemistry.98 The LASP software project initiated by Liu et al. in early 2018 aims to develop a single package for improved usability by merging two major simulation tools: the global PES exploration-based stochastic surface walking (SSW) method and the fast PES evaluation using global neural network (G-NN) potential developed by their group.59
The SSW method was designed as a promising solution to explore the complex potential energy surface (PES) of materials for the automatic prediction of unknown material structures without relying on any experimental knowledge. The SSW method is based on the concept of bias-potential-driven dynamics99 and Metropolis Monte Carlo targeting for rapid exploration of the PES. The bias-potential-driven dynamics originate from the bias-potential-driven constrained Broyden dimer (BP-CBD) method used for TS searching in complex catalytic systems by applying a bias potential in a constrained manner.100 The SSW algorithm utilized a small step-size in structure displacement to explore both minima and saddle points on the PES in an unbiased manner. The climbing mechanism incorporates bias potentials as shown in eqs 9 and 10 to overcome the barrier between minima, enabling the smooth structural configuration to move on PES from a local minimum to a high-energy configuration along one random mode direction and drive the system toward saddle points, as illustrated in Figure 6a.101 The Metropolis Monte Carlo scheme in the structure selection module is used to accept or reject the new minimum at the end of each SSW step.
| 9 |
| 10 |
Figure 6.
(a) Scheme of the SSW-NN. (b) Self-learning procedure of the global NN potential. Reproduced from ref (101). Copyright 2019 AIP Publishing. (c) Architecture and modular map of LASP code. Reproduced from ref (98). Copyright 2019 Wiley Periodicals, Inc.
Another key simulation tool in LASP software is the SSW-NN method, which generates G-NN potentials for performing DFT-level accuracy calculations. In essence, the G-NN potentials are trained by learning from the first-principles data set of the global PES generated from SSW global optimization. A self-learning procedure is established for obtaining G-NN potentials, as shown in Figure 6b. It begins by training a neural network potential from a small collection of training data sets obtained by short-time SSW sampling for small systems based on DFT calculations, followed by recalculation with a high-accuracy DFT setup. Next, neural network potential is trained to carry out extensive SSW global optimization for a variety of complex systems. Then, a small data set with diverse structures on PES from previous SSW optimization was screened out, and high-accuracy setup DFT was used to recalculate the data set, and then it was added to the training data set for a new iteration of NN potential update. Hundreds of iterations are needed to obtain a transferable G-NN potential with acceptable accuracy, in terms of energy and forces.
The combination of the SSW with G-NN potential has solved many challenging problems, ranging from structure determination to reaction pathway prediction, due to its strengths in sampling unbiasedly and globally in multidimensional PES for complex materials.102,103 Although the SSW-NN method has proven to be a key feature that distinguishes LASP from other packages, LASP is now evolving toward a platform-based software to provide solutions for an even wider range of simulation purposes. The overview of LASP architecture is shown in Figure 6c. A large set of powerful simulation techniques has been integrated into the LASP platform. For the energy and force evaluation, interfaces for first-principles and force field packages are incorporated in addition to the G-NN potential. In terms of the PES exploration, LASP has implemented various local/global geometry optimization and transition state search methods as well as incorporated molecular dynamics (MD) functionalities.
4.2. Genetic Algorithm
The Global Optimization (GO) algorithm is a crucial component of the structure prediction workflow.104 It is utilized to explore a vast number of energy minima on a high-dimensional energy surface, aiming to find potential crystal structures with the lowest global energy under given chemical compositions and external conditions. The number of potential energy minima increases exponentially with the system size. Therefore, structure prediction involves finding the global minimum in a vast search space. So far, many optimization methods, such as random sampling,105 basin-hopping,106 minima hopping,107 simulated annealing,108 metadynamics,109 and evolutionary algorithms,110 have been applied. Among them, genetic algorithms (GAs) are metaheuristic optimization algorithms inspired by biological evolution, such as natural selection, mutation, and reproduction.40,111−116 The basic steps of a GA begin by initializing a population. A set of crystal structures is randomly generated or seeded with specific structures. Symmetry constraints can be added to ensure diversity. The energy of each crystal structure is evaluated using first-principles calculations or other accurate computational methods, and this energy serves as the fitness of the structure. Then, select the structures with higher fitness to be the parents for the next generation, which allows the genetic information on the fittest structures to be passed on to future generations. New crystal structures are generated by simulating the crossover and mutation processes of biological genetics. Crossover involves combining features of two “parent” structures to create “offspring” structures, while mutation involves randomly altering certain features within a structure, as illustrated in Figure 7. The newly generated structures, along with the selected parent structures, form the new generation. The above process was iterated to perform an extensive local search until it reached the convergence criterion. This process can be highly parallelized because the energy calculation for each crystal structure is independent. The application of genetic algorithms in crystal structure prediction has proven to be very effective, especially in cases where the structures are highly complex or the potential structure space is vast.
Figure 7.
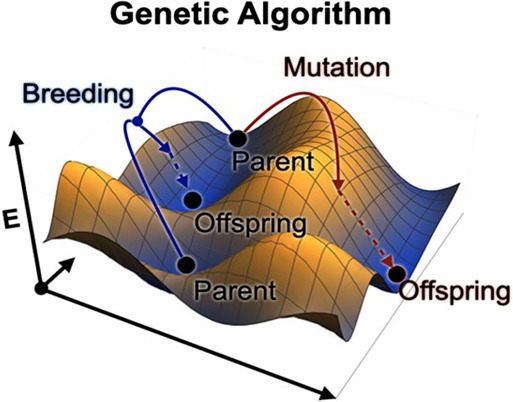
Schematic illustration of genetic algorithm crystal structure prediction method in a 2D PES. Reproduced from ref (110). Copyright 2020 American Chemical Society.
In the past decades, many GAs have been released that can be used for crystal structure prediction. The Universal Structure Predictor: Evolutionary Xtallography (USPEX) is probably the most widely applied method, gaining widespread recognition and application in the field of materials science and catalyst research.117 The USPEX code enables the prediction of crystal structures under arbitrary pressure–temperature conditions based solely on the chemical composition of the material.118 It can also identify stable chemical compositions and their crystal structures by using only the element names. Beyond predicting stable structures, USPEX can find a wide range of metastable structures and perform simulations with different levels of prior knowledge, making it useful for discovering low-energy metastable phases and surface reconstructions for catalytic systems. Therefore, USPEX has proven to be a powerful tool for predicting crystal structures in cases where experimental data may be lacking or for conditions that are difficult to achieve experimentally.119
4.3. Grand Canonical Based Method
Grand Canonical Genetic Algorithm
The Grand Canonical Genetic Algorithm (GCGA) is an extension of the traditional genetic algorithm specifically designed to handle variable-composition problems. Unlike traditional GAs that work with a fixed number of atoms, GCGA can dynamically add or remove particles during the optimization process. This flexibility enables GCGA to explore a wider range of crystal structure compositions. That is achieved through the grand canonical ensemble, which is a statistical ensemble that governs the exchange of particles with a reservoir. This enables the algorithm to simulate realistic conditions where the system can experience gains or losses of particles, and where volume and temperature can vary under specific conditions, leading to the identification of stable structures.120 In addition, GCGA is designed to optimize the free energy of a system, which is a more general thermodynamic potential than a potential energy. This is particularly important for systems in which the number of particles can change, such as in chemical reactions or phase transitions.
GCGA consists of several components, some of which are similar to conventional GA as described in the above section, while others are modified for the current grand canonical (GC) approaches. For example, the mutation operation in GA is typically carried out using various methods to alter the positions of the atoms. These methods include random displacement and reflection with a mirror symmetry. Two additional operations are introduced in the current GCGA method. They add and remove adsorbates to the system. Taking the hydrogen-covered Pt cluster system as an example, the “adding” operation is completed by inserting an additional hydrogen atom in the vicinity of a randomly selected Pt atom while ensuring it does not overlap with other atoms within specified parameters.121 The “removing” operation is carried out by randomly deleting a hydrogen atom from the system.
GCGA can be utilized to predict the stable and metastable surface structures of catalysts under various environmental conditions, such as varying temperatures and pressures, which are common in catalytic processes.122 By allowing the number of atoms to vary, GCGA can help to determine the optimal composition of a catalyst that maximizes its activity, selectivity, or stability. The GCGA provides a versatile and powerful computational tool for designing and optimizing heterogeneous catalysts. It offers insights that can guide experimental research and accelerate the development of more efficient catalytic systems.
Grand Canonical Monte Carlo
Grand Canonical Monte Carlo (GCMC) simulation is one of the methods with reasonable computational cost for conducting large-scale simulations. It allows the exploration of a variety of configurations of catalyst surfaces to gain insights into surface changes under real conditions.123,124 The off-lattice GCMC has no constraints on the surface lattice, enabling consideration of interactions between adsorbates and the surface lattice. This is essential for studying amorphous surface systems through simulation methods. The grand canonical ensemble is a statistical mechanics framework used to describe the behavior of a system that is in thermal and chemical equilibrium with a much larger system, known as a reservoir.120 This ensemble is particularly useful for describing systems that can exchange both energy and particles with the reservoir. Therefore, the GCMC allows the number of particles in the system to exchange with the environment during the simulation, making it particularly suitable for studying catalytic activities such as adsorption, desorption, and phase equilibria. This ensemble is characterized by three fixed parameters: temperature (T), volume (V), and chemical potential (μ). In each step of a GCMC simulation, the system interacts with an external reservoir through two actions: the move action and the exchange action. The probability of accepting an attempted “move” step is
| 11 |
The exchange step can be further divided into insertion and deletion. The probability of acceptance for “insertion” and “deletion” are
| 12 |
| 13 |
The conventional GCMC simulation can be time-consuming due to a large number of attempts that generate high-energy configurations with extremely low acceptance probabilities.125 Therefore, realistic modeling requires comprehensive exploration of the PES at DFT-level accuracy. To address the complexity among all of these distinct systems, MLPs are promising methods due to their near-DFT accuracy and low computational cost. Recent studies have highlighted the successful application of MLPs in conducting large-scale grand-canonical Monte Carlo (GCMC) simulations. Examples include the EANN potential accelerated GCMC using the open-source package GDPy126 and the GCMC/SSW-NN simulation conducted by Li et al.41,127
5. Applications of MLPs for Heterogeneous Catalysis
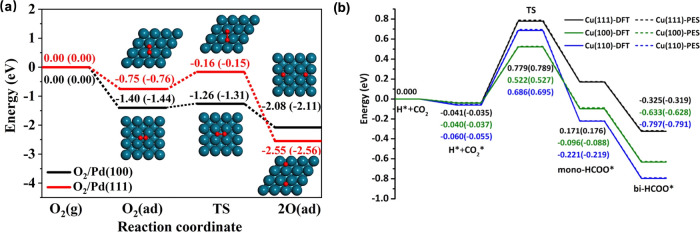
The recent advancements in combining MLPs with crystal structure prediction methods have been extensively applied for high-throughput screening of catalytically active phases and sites.128 Taking the theoretical study of the Eley–Rideal recombination of hydrogen atoms on the Cu(111) catalyst surface as an example, the reaction between incident H/D atoms and precovered D/H atoms on Cu(111) is the research focus of this catalytic system.129 The detailed experimental data of the final state-resolved for this reaction have long been accessible. However, theoretical simulation has been hindered by the high cost of computational resources required to conduct extensive AIMD and the limitations of the theoretical models. The highly efficient EANN is utilized to train MLP that consider all molecular and surface degrees of freedom.130 It enables a comprehensive analysis of the reaction dynamics through extensive quasiclassical molecular dynamics simulations, incorporating the excitation of low-lying electron–hole pairs (EHPs). The results demonstrate a good agreement with experimental data. This level of detail extends beyond what was previously possible with other theoretical approaches, enabling quantitative comparisons with the experimental data. In addition, the EANN MLP was used to study the equilibration dynamics of hot oxygen atoms following the dissociation of O2 on Pd(100) and Pd(111) surfaces, as reported by Lin et al.131 The EANN provides a comprehensive and scalable description that can simulate the interactions between O2 and O within different Pd supercells more efficiently. It allows MD simulations to be as accurate as AIMD but orders of magnitude faster, providing detailed insight for understanding experimental findings and equilibration dynamics at a microscopic level. The results indicate that the previously recognized ballistic movement of hot O atoms on Pd(100) was an accidental outcome of an ideal initial molecular orientation and surface configuration. This study has also shown that the MLP can accurately describe a variety of supercell sizes with first-principles accuracy, making it suitable for future studies of dynamic processes on different surfaces and under various initial conditions. The comparison of minimum energy paths for O2 dissociation on Pd(100) and Pd(111) obtained by EANN PES and DFT is shown in Figure 8a. This work represents a significant advancement in modeling the dynamics of surface reactions using MLPs, providing a more comprehensive insight into the equilibration process of reactive species on metal surfaces to enhance theory-experiment agreement. Similarly, the investigation of the postdecomposition dynamics of formate (HCO2) on catalyst surfaces of Cu demonstrated the application of EANN MLP in classical trajectory calculations.132 The simulation results agree with available experimental measurements, revealing the key role of the transition state in the energy disposal of the products in this surface reaction. The accuracy of MLP is comparable to DFT within 10 meV, the minimum energy paths of HCO2 decomposition are shown in Figure 8b. This research contributed to a fundamental understanding of the mechanisms of catalytic reactions catalyzed by copper and highlights the importance of considering the structural aspects of catalyst surfaces in the design and optimization of catalytic processes.
Figure 8.
(a) Minimum energy paths of O2 dissociation on Pd(100) and Pd(111) obtained from the EANN MLP and DFT. Reproduced from ref (131). Copyright 2023 American Chemical Society. (b) Minimum energy paths of HCO2 decomposition on relaxed Cu(111), Cu(100), and Cu(110) surfaces optimized with DFT and EANN MLP. Reproduced from ref (132). Copyright 2023 American Chemical Society.
Furthermore, the scheme of MLPs accelerated structure search using optimization algorithms such as genetic algorithms (GA), followed by DFT validation, has emerged as an effective method for screening thermodynamically favored catalyst surface structures under reaction conditions.72 For example, Han et al. utilized EANN MLPs paired with an active learning procedure in an iterative process to accelerate GA-based global optimization. This was done to identify the most stable surface configurations of ZnO with various concentrations of oxygen vacancies (OVs).133 Observed from the simulation results, the surface structure transitions from the wurtzite to body-centered-tetragonal phases in the presence of OVs. It was found that the ZnO(101̅0) surface with 0.33 ML monolayer (ML) OVs is the most stable phase with a formation energy of −0.30 eV under the experimental conditions. The results show that the catalytic activity of intrinsic sites is almost constant, while the activity of the OV sites is strongly dependent on the concentration of OVs. This comprehensive study provides new insights into the role of oxygen vacancies in the catalytic processes of ZnO surfaces and demonstrates the potential of combining ML techniques with first-principles simulations to accelerate the discovery and optimization of catalytic materials.
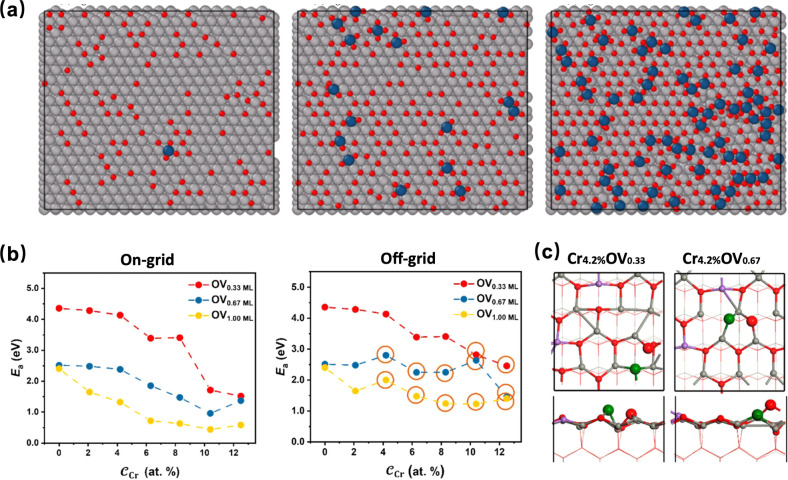
Further advancement was made by Xu et al.; his work focused on the oxidation of large-scale flat and stepped PtOx surfaces during the catalysis process in real conditions. The EANN MLP is utilized to conduct GCMC simulations because off-lattice GCMC has no limits on the surface lattice and is more suitable for investigating the oxidation process. The surface structure of oxidized Pd catalyst is shown in Figure 9a. This approach is typically not feasible with expensive traditional ab initio calculations and is hindered by technical limitations in experiments, as most experimental studies have examined the surface oxidation under ultrahigh vacuum conditions, which may differ significantly from real conditions.78 The observations in this work not only consist of existing experimental observations and DFT calculations on several key PdOx intermediates, such as Pt2O6 strips and PtO4 square planar, but also reveal the formation mechanism of surface oxide formation on Pt without the need to manually construct a surface model. It provides insight into oxidation on other metal surfaces and demonstrates the capabilities of MLPs in large-scale simulations, making it a powerful tool to investigate realistic structures and the formation mechanisms of complex systems. This methodology has also been applied to search for ZnO and Cr-doped ZnO catalytic systems under reactive conditions.134 The complexity of their structures poses significant challenges for traditional approaches, both experimental and theoretical. This study successfully investigates Cr-doped ZnO (101̅0) under different ratios of Cr and oxygen vacancies. The overall performance reached a Root Mean Square Error (RMSE) in the energy of 0.02 eV/atom. The activation energy for CO is calculated using DFT on different Cr-doped ZnO (101̅0) surfaces to investigate the influence of metal dopants and oxygen vacancies on syngas conversion over metal oxides. The results in Figure 9b, c show that the CO activation energy decreases significantly with an increasing number of oxygen vacancies, which can be attributed to the geometry of the reaction site. This study demonstrates the effectiveness of the state-of-the-art method and provides deeper insights into the concentration and distribution of oxygen vacancies for syngas conversion.
Figure 9.
(a) Pt catalyst surface structure studied utilize Large-Scale machine learning potential-based GCMC. Reproduced from ref (78). Copyright 2022 American Chemical Society. (b) Changes of Ea on the structure with increasing CCr and COV based on the on-grid (left) and off-grid (right) strategy. (c) The optimized TSs of C–O bond dissociation on the ZnO surface with Cr4.2%OV0.33 and Cr4.2%OV0.67. Reproduced from ref (134). Copyright 2023 American Chemical Society.
Similar to the GCMC, the GCGA method also operates within the grand canonical ensemble framework. However, GCMC is a sampling method aimed at calculating the equilibrium properties of a system, whereas GCGA is an optimization technique focused on finding the most stable configurations. Sun et al. innovatively applied GCGA combined with DFT calculations to explore the ensemble of low free energy structures of hydrogenated Pt8 clusters on two surfaces: α-Al2O3(0001) and γ-Al2O3(100), under different hydrogen chemical potentials.121 Determination of the structure of the PtnHx cluster under specific conditions is challenging because the hydrogen coverage of the small Pt cluster varies strongly with temperature and hydrogen pressure. The standard approach, which explores each coverage independently and then evaluates the phase diagram based on the optimal geometry at different compositions, has limitations. The limitations may lead to phases that are far from realistic and may require simulations to use significant computational resources. Therefore, the various reconstructions of Pt8Hx on each support have been simulated using the GCGA method. The results show that the different supports do not significantly change the optimal hydrogen coverage on the cluster but induce different morphological transitions. This provides insights into the origin and strength of alumina support-Pt cluster interactions and their impact on the structure and coverage of small Pt clusters under hydrogen pressure. This method has also been applied to study the hydrogen-induced restructuring of Cu(100) and Cu(111) under electrocatalytic reduction conditions and achieved excellent performance.135
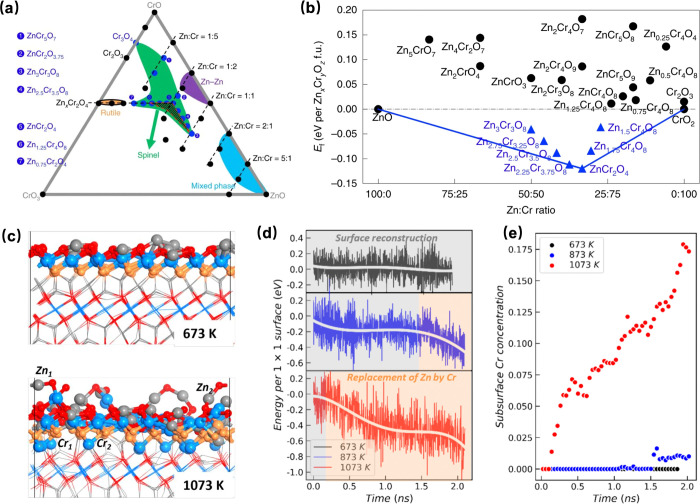
The SSW-NN method, as implemented in the LASP code, has been successfully applied in numerous heterogeneous catalysis systems to investigate the surface status of catalysts under reaction conditions, in situ active site searching, and reaction rate studies since it was first proposed in 2018. The zinc–chromium oxide (ZnCrO) catalyst for the conversion of syngas has been extensively studied using the MLPs-based method.136 Previous studies have shown that even small changes in the composition of Zn:Cr in ZnxCryOz can lead to dramatically different catalytic properties.137 To investigate the mechanism of catalytic syngas conversion over ternary ZnCrO catalysts at different Zn:Cr ratios, Ma et al. employed the SSW-NN approach to resolve complex ZnCrO structures, including bulk, layer, and cluster compositions. They then calculated the bulk phase diagram, the Ov phase diagram, and the formation energy of thermodynamically allowed ZnCrO phases, as shown in Figure 10a,b.138 A planar [CrO4] site available at Zn:Cr in a ratio above 1:2 is identified as the active center for methanol production. This finding also provides a deeper understanding of metal oxide alloy catalysts for hydrogenation reactions by revealing the atomic structures, which were previously unknown, even though its high catalyst activity has been experimentally verified. The study conducted by Ma et al. utilized state-of-the-art GNN potential and SSW algorithm to perform long-time MD simulations investigating the deactivation of zinc–chromium oxide (ZnCryOz) catalysts. Their findings indicate that deactivation is caused by the formation of subsurface Ov and migration of neighboring Zn/Cr cations. This process leads to the disappearance of the [CrO4] active site for methanol synthesis, resulting in a decrease in reaction activity, the structure and MD results are shown in Figures 10c, d, and e.139
Figure 10.
(a) Ternary phase diagram of Zn–Cr–O. The spinel ZnCrO phases in the red dashed triangle are thermodynamically allowed. (b) Formation energy of ZnCrO phases in the red dashed area of (a). Reproduced from ref (138). Copyright 2019 Springer Nature Limited. (c) Structure after 2 ns MD simulation at 673 and 1073 K. (d) The energy variations against the MD simulation time at different temperature for O-defective Zn3Cr3O8 (0001) surface with the initial OV concentrations of 0.25 ML. (e) Variations of the surface Cr concentration. Reproduced from ref (139). Copyright 2023 Elsevier Inc.
Another example is the study of Fischer–Tropsch Synthesis (FTS) on a FeCx catalyst system. Liu et al. utilized the SSW-NN global structure search method to identify the composition and structure of thermodynamically favorable reconstructed FeCx surfaces under different C coverages.140 They also studied the mechanism of FTS, considering the reaction-induced surface reconstruction powered by the machine-learning-based transition state exploration (ML-TS) they developed to efficiently expedite the exploration of the extensive FT hydrocarbon reaction network on a series of FeCx surfaces. Similar applications of SSW-NN methods have also been reported in studies conducted on PdAg and Au/ZnO catalyst systems.141,142
Moreover, to further enhance the efficiency, accuracy, and scalability of MLPs in heterogeneous catalysis research, more efforts have been made to combine the application of MLPs with various optimization algorithms. A microkinetic-guided machine learning pathway search (MMLPs) approach is developed based on the G-NN SSW reaction sampling method to resolve complex catalytic networks with many likely intermediates at different surface coverages in an automated way. A showcase of this method is the study of the hydrogenation of the CO2/CO mixture on a Cu–Zn catalyst surface. Their findings agree with previous isotope experiments, indicating that the CO2 hydrogenation dominates methanol synthesis instead of CO hydrogenation. CO plays a role in helping to form the CuZn surface alloy, which occurs preferentially at the step-edge site on Cu(211). On Cu(111), CO can reduce the cationic Zn to form [−Zn–OH–Zn−], exposing metal sites for methanol synthesis. The thermodynamically favorable active phase of CuZn alloy and the kinetically favorable pathway for CO2 hydrogenation are also determined.143 A recent study by Chen et al. aimed to clarify the active site of Ag-catalyzed ethene epoxidation, which has remained unknown due to the lack of tools to probe this under high-temperature and high-pressure conditions.144 They demonstrated a machine learning-based automated search for the Optimal Surface Phases (ASOP) method, which is a grand canonical global optimization approach. The ASOP method is implemented based on stochastic surface walking global optimization using a global neural network potential. This method can help identify the surface phase on Ag surfaces under industrial reaction conditions. They found that a unique O5 surface oxide phase grown on Ag (100) stands out from more than three million structural candidates as the only phase selectively producing ethylene oxide (EO). The O5 phase contains a square-pyramidal subsurface oxygen and strongly adsorbed ethene, which can selectively convert ethene to EO, thereby offering high catalytic activity and selectivity.
The deep potential (DP) along with its accompanying software suite, the DeePMD-kit, is predominantly utilized for conducting molecular dynamics simulations and exploring the properties of materials.145,146 In the realm of heterogeneous catalysis research, the DP potential serves as a machine-learning-driven alternative to conventional AIMD simulations, offering a powerful tool for the precise and efficient investigation of catalytic processes at the atomic level. Liu et al. conducted deep potential molecular dynamics using DeePMD-kit interfaced with LAMMPS to capture the atomic-scale dynamics of the metal-oxide interface of the Au/CeO2 and Au/SiO2 catalysts.147 This study was conducted because Au nanoparticles (NPs) on oxides were found to play an important role in improving the catalytic performance for CO oxidation. In this work, the researchers compared the interaction behavior of Au nanoparticles with CeO2 and SiO2. The results indicate that the metal affinity of active and inert supports is the key descriptor relevant to the sintering and deactivation of heterogeneous catalysts. This is consistent with the experimental observations and the Sabatier principle of the metal–support interaction for the design of sintering-resistant metal nanocatalysts established recently. In the study of CO oxidation on Pd(111), the DeePMD-kit is used to train a neural network (NN) potential for the global optimization of a genetic algorithm.148 They developed a self-adaptive simulation workflow driven by first-principles microkinetic modeling and genetic-algorithm-based global structural search accelerated by MLPs. This workflow allows the identification of the Pd(111) active phases at the kinetically steady state in CO/O2 reaction mixtures, uncovering the structural and compositional evolution of Pd(111) under reaction conditions, which is a classic open problem. Their results demonstrate a more realistic catalytic CO oxidation process that initiates with the Pd(111) metal catalyst and concludes with a dynamically stable PdO0.44 surface oxide. This oxide exhibits higher catalytic activity for CO oxidation compared to Pd(111) and overoxidized PdO catalysts. This work provides atomic-scale insight into the transformation of catalysts and how their activity can be altered accordingly.
6. Summary and Perspectives
In summary, this review provides an introduction to the basic principles of MLPs, including theory, training protocols, implementation, and their application in structure prediction with a focus of recent research progress to search for the in situ active sites in heterogeneous catalysis. MLPs, offering nearly 4 orders of magnitude faster computations than DFT, while maintaining comparable accuracy, significantly broaden the scope of systems that can be effectively analyzed. Coupled with global optimization algorithms, MLPs enable systematic exploration of realistic systems across vast structural spaces, accommodating thousands of atoms. This review briefly touches on recent research advancements, which by no means represents an exhaustive list of all possible examples. The application of MLPs has markedly advanced our understanding of catalyst surface structure changes under reactive conditions, and the nature of active sites and elementary reaction steps.
However, several challenges remain. MLPs are highly dependent on extensive, high-quality data sets for effective training, which can be challenging to obtain, especially for complex or less-studied systems. While crystal structure databases like the Materials Project can provide initial structures for MLP training, extensive sampling is still necessary to build a robust training set. More recently, specialized databases such as OC20/22 have emerged, tailored to facilitate the development of machine learning models capable of predicting catalyst properties.149−151 Additionally, many MLPs, particularly those based on deep learning, operate as “black boxes,″ which makes it challenging to comprehend the physical principles they capture, leading to a lack of interpretability Hence, there is advocacy for developing physics-informed models, like SISSO, which initiate from fundamental physical quantities.152 Furthermore, MLPs often struggle with transferability, limiting their ability to generalize beyond the chemical space covered by their training data, which restricts their applicability to new systems or conditions. To address this issue, strategies such as transfer learning and delta learning are employed to enhance the generalizability of MLPs.153 Additionally, more effective sampling methods, such as SSW, which are discussed in this paper, are utilized to achieve better coverage of the chemical space for better robustness. Moreover, while MLPs are generally much faster than ab initio methods, the training phase can be computationally intensive, and the efficiency of the models can vary. Therefore, it is predictable that these existing challenges will stimulate further development of methodology, training, and implantation to expand the capabilities of MLPs, and pave the way for even more accurate and broadly applicable models.
Looking ahead, the future of MLPs in heterogeneous catalysis is poised for significant growth and innovation. From a broader perspective, currently, two distinct integration pathways exist for machine learning in catalysis: one involves training entirely on experimental data, while the other relies on calculated data. Each pathway presents unique challenges: experimental data are often costly and biased toward successful trials, whereas calculated data, though more abundant and covering a broader chemical space, can be overwhelming in volume and often involves too much simplification. With the rapid development of new models, databases, and training strategies, it is expected to yield more accurate and efficient simulations of catalytic processes under realistic conditions, effectively bridging the gap between microscopic understanding and experimental observations. Thus, we can envision a hybrid farmwork wherein MLPs are used as pretrained models, subsequently fine-tuned with experimental data to accelerated discovery of novel catalysts with optimized activity and selectivity, foreseeing a new era of catalyst design driven by advanced computational insights.
Acknowledgments
We are grateful to the NKRDPC (2021YFA1500700) and NSFC (92045303). X.C. is grateful for financial support from ShanghaiTech University.
The authors declare no competing financial interest.
References
- Bonati L.; Polino D.; Pizzolitto C.; Biasi P.; Eckert R.; Reitmeier S.; Schlögl R.; Parrinello M. The Role of Dynamics in Heterogeneous Catalysis: Surface Diffusivity and N 2 Decomposition on Fe(111). Proc. Natl. Acad. Sci. U. S. A. 2023, 120 (50), e2313023120. 10.1073/pnas.2313023120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mai H.; Le T. C.; Chen D.; Winkler D. A.; Caruso R. A. Machine Learning for Electrocatalyst and Photocatalyst Design and Discovery. Chem. Rev. 2022, 122 (16), 13478–13515. 10.1021/acs.chemrev.2c00061. [DOI] [PubMed] [Google Scholar]
- Vogt C.; Weckhuysen B. M. The Concept of Active Site in Heterogeneous Catalysis. Nat. Rev. Chem. 2022, 6 (2), 89–111. 10.1038/s41570-021-00340-y. [DOI] [PubMed] [Google Scholar]
- Wang C.; Wang Z.; Mao S.; Chen Z.; Wang Y. Coordination Environment of Active Sites and Their Effect on Catalytic Performance of Heterogeneous Catalysts. Chin. J. Catal. 2022, 43 (4), 928–955. 10.1016/S1872-2067(21)63924-4. [DOI] [Google Scholar]
- Baseden K. A.; Tye J. W. Introduction to Density Functional Theory: Calculations by Hand on the Helium Atom. J. Chem. Educ. 2014, 91 (12), 2116–2123. 10.1021/ed5004788. [DOI] [Google Scholar]
- Xu J.; Cao X.-M.; Hu P. Perspective on Computational Reaction Prediction Using Machine Learning Methods in Heterogeneous Catalysis. Phys. Chem. Chem. Phys. 2021, 23 (19), 11155–11179. 10.1039/D1CP01349A. [DOI] [PubMed] [Google Scholar]
- Schaaf L. L.; Fako E.; De S.; Schäfer A.; Csányi G. Accurate Energy Barriers for Catalytic Reaction Pathways: An Automatic Training Protocol for Machine Learning Force Fields. Npj Comput. Mater. 2023, 9 (1), 180. 10.1038/s41524-023-01124-2. [DOI] [Google Scholar]
- Friederich P.; Häse F.; Proppe J.; Aspuru-Guzik A. Machine-Learned Potentials for next-Generation Matter Simulations. Nat. Mater. 2021, 20 (6), 750–761. 10.1038/s41563-020-0777-6. [DOI] [PubMed] [Google Scholar]
- Goldsmith B. R.; Esterhuizen J.; Liu J.; Bartel C. J.; Sutton C. Machine Learning for Heterogeneous Catalyst Design and Discovery. AIChE J. 2018, 64 (7), 2311–2323. 10.1002/aic.16198. [DOI] [Google Scholar]
- Filippov V. G.; Mikhailov Ya. A.; Elyshev A. V. Machine Learning and Big Data Analysis in the Field of Catalysis (A Review). Kinet. Catal. 2023, 64 (2), 122–134. 10.1134/S0023158423020027. [DOI] [Google Scholar]
- Margraf J. T. Science-Driven Atomistic Machine Learning. Angew. Chem., Int. Ed. 2023, 62 (26), e202219170. 10.1002/anie.202219170. [DOI] [PubMed] [Google Scholar]
- Papadimitriou I.; Gialampoukidis I.; Vrochidis S.; Kompatsiaris I. AI Methods in Materials Design, Discovery and Manufacturing: A Review. Comput. Mater. Sci. 2024, 235, 112793. 10.1016/j.commatsci.2024.112793. [DOI] [Google Scholar]
- Khorshidi A.; Peterson A. A. Amp: A Modular Approach to Machine Learning in Atomistic Simulations. Comput. Phys. Commun. 2016, 207, 310–324. 10.1016/j.cpc.2016.05.010. [DOI] [Google Scholar]
- Gerrits N. Accurate Simulations of the Reaction of H 2 on a Curved Pt Crystal through Machine Learning. J. Phys. Chem. Lett. 2021, 12 (51), 12157–12164. 10.1021/acs.jpclett.1c03395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishin Y. Machine-Learning Interatomic Potentials for Materials Science. Acta Mater. 2021, 214, 116980. 10.1016/j.actamat.2021.116980. [DOI] [Google Scholar]
- Xin H. Catalyst Design with Machine Learning. Nat. Energy 2022, 7 (9), 790–791. 10.1038/s41560-022-01112-8. [DOI] [Google Scholar]
- Kitchin J. R. Machine Learning in Catalysis. Nat. Catal. 2018, 1 (4), 230–232. 10.1038/s41929-018-0056-y. [DOI] [Google Scholar]
- Mou T.; Pillai H. S.; Wang S.; Wan M.; Han X.; Schweitzer N. M.; Che F.; Xin H. Bridging the Complexity Gap in Computational Heterogeneous Catalysis with Machine Learning. Nat. Catal. 2023, 6 (2), 122–136. 10.1038/s41929-023-00911-w. [DOI] [Google Scholar]
- Mueller T.; Hernandez A.; Wang C. Machine Learning for Interatomic Potential Models. J. Chem. Phys. 2020, 152 (5), 050902. 10.1063/1.5126336. [DOI] [PubMed] [Google Scholar]
- Behler J. First Principles Neural Network Potentials for Reactive Simulations of Large Molecular and Condensed Systems. Angew. Chem., Int. Ed. 2017, 56 (42), 12828–12840. 10.1002/anie.201703114. [DOI] [PubMed] [Google Scholar]
- Yang W.; Fidelis T. T.; Sun W.-H. Machine Learning in Catalysis, From Proposal to Practicing. ACS Omega 2020, 5 (1), 83–88. 10.1021/acsomega.9b03673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faber F. A.; Hutchison L.; Huang B.; Gilmer J.; Schoenholz S. S.; Dahl G. E.; Vinyals O.; Kearnes S.; Riley P. F.; von Lilienfeld O. A. Machine Learning Prediction Errors Better than DFT Accuracy. J. Chem. Theory Comput. 2017, 13 (11), 5255–5264. 10.1021/acs.jctc.7b00577. [DOI] [PubMed] [Google Scholar]
- Wan K.; He J.; Shi X. Construction of High Accuracy Machine Learning Interatomic Potential for Surface/Interface of Nanomaterials—A Review. Adv. Mater. 2024, 36, 2305758. 10.1002/adma.202305758. [DOI] [PubMed] [Google Scholar]
- Behler J.; Parrinello M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98 (14), 146401. 10.1103/PhysRevLett.98.146401. [DOI] [PubMed] [Google Scholar]
- Kocer E.; Ko T. W.; Behler J. Neural Network Potentials: A Concise Overview of Methods. Annu. Rev. Phys. Chem 2022, 73, 163. 10.1146/annurev-physchem-082720-034254. [DOI] [PubMed] [Google Scholar]
- Wang H.; Zhang L.; Han J.; E W. DeePMD-Kit: A Deep Learning Package for Many-Body Potential Energy Representation and Molecular Dynamics. Comput. Phys. Commun. 2018, 228, 178–184. 10.1016/j.cpc.2018.03.016. [DOI] [Google Scholar]
- Stocker S.; Jung H.; Csányi G.; Goldsmith C. F.; Reuter K.; Margraf J. T. Estimating Free Energy Barriers for Heterogeneous Catalytic Reactions with Machine Learning Potentials and Umbrella Integration. J. Chem. Theory Comput. 2023, 19 (19), 6796–6804. 10.1021/acs.jctc.3c00541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deringer V. L.; Bartók A. P.; Bernstein N.; Wilkins D. M.; Ceriotti M.; Csányi G. Gaussian Process Regression for Materials and Molecules. Chem. Rev. 2021, 121 (16), 10073–10141. 10.1021/acs.chemrev.1c00022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartók A. P.; Payne M. C.; Kondor R.; Csányi G. Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons. Phys. Rev. Lett. 2010, 104 (13), 136403. 10.1103/PhysRevLett.104.136403. [DOI] [PubMed] [Google Scholar]
- Klawohn S.; Darby J. P.; Kermode J. R.; Csányi G.; Caro M. A.; Bartók A. P. Gaussian Approximation Potentials: Theory, Software Implementation and Application Examples. J. Chem. Phys. 2023, 159 (17), 174108. 10.1063/5.0160898. [DOI] [PubMed] [Google Scholar]
- Wood M. A.; Thompson A. P. Extending the Accuracy of the SNAP Interatomic Potential Form. J. Chem. Phys. 2018, 148 (24), 241721. 10.1063/1.5017641. [DOI] [PubMed] [Google Scholar]
- Novikov I. S.; Gubaev K.; Podryabinkin E. V.; Shapeev A. V. The MLIP Package: Moment Tensor Potentials with MPI and Active Learning. Mach. Learn. Sci. Technol. 2021, 2 (2), 025002. 10.1088/2632-2153/abc9fe. [DOI] [Google Scholar]
- Shapeev A. V. Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials. Multiscale Model. Simul. 2016, 14 (3), 1153–1173. 10.1137/15M1054183. [DOI] [Google Scholar]
- Takamoto S.; Izumi S.; Li J. TeaNet: Universal Neural Network Interatomic Potential Inspired by Iterative Electronic Relaxations. Comput. Mater. Sci. 2022, 207, 111280. 10.1016/j.commatsci.2022.111280. [DOI] [Google Scholar]
- Unke O. T.; Chmiela S.; Gastegger M.; Schütt K. T.; Sauceda H. E.; Müller K.-R. SpookyNet: Learning Force Fields with Electronic Degrees of Freedom and Nonlocal Effects. Nat. Commun. 2021, 12 (1), 7273. 10.1038/s41467-021-27504-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schütt K. T.; Hessmann S. S. P.; Gebauer N. W. A.; Lederer J.; Gastegger M. SchNetPack 2.0: A Neural Network Toolbox for Atomistic Machine Learning. J. Chem. Phys. 2023, 158 (14), 144801. 10.1063/5.0138367. [DOI] [PubMed] [Google Scholar]
- Schütt K. T.; Arbabzadah F.; Chmiela S.; Müller K. R.; Tkatchenko A. Quantum-Chemical Insights from Deep Tensor Neural Networks. Nat. Commun. 2017, 8 (1), 13890. 10.1038/ncomms13890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schütt K. T.; Kindermans P.-J.; Sauceda H. E.; Chmiela S.; Tkatchenko A.; Müller K.-R. SchNet: A Continuous-Filter Convolutional Neural Network for Modeling Quantum Interactions. arXiv 2017, 08566. 10.48550/arXiv.1706.08566. [DOI] [Google Scholar]
- Ma S.; Liu Z.-P. Machine Learning for Atomic Simulation and Activity Prediction in Heterogeneous Catalysis: Current Status and Future. ACS Catal. 2020, 10 (22), 13213–13226. 10.1021/acscatal.0c03472. [DOI] [Google Scholar]
- Katoch S.; Chauhan S. S.; Kumar V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 2021, 80 (5), 8091–8126. 10.1007/s11042-020-10139-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X.; El Khatib M.; Lindgren P.; Willard A.; Medford A. J.; Peterson A. A. Atomistic Learning in the Electronically Grand-Canonical Ensemble. Npj Comput. Mater. 2023, 9 (1), 73. 10.1038/s41524-023-01007-6. [DOI] [Google Scholar]
- Brenner D. W. Empirical Potential for Hydrocarbons for Use in Simulating the Chemical Vapor Deposition of Diamond Films. Phys. Rev. B 1990, 42 (15), 9458–9471. 10.1103/PhysRevB.42.9458. [DOI] [PubMed] [Google Scholar]
- Sumpter B. G.; Noid D. W. Potential Energy Surfaces for Macromolecules. A Neural Network Technique. Chem. Phys. Lett. 1992, 192 (5–6), 455–462. 10.1016/0009-2614(92)85498-Y. [DOI] [Google Scholar]
- Blank T. B.; Brown S. D.; Calhoun A. W.; Doren D. J. Neural Network Models of Potential Energy Surfaces. J. Chem. Phys. 1995, 103 (10), 4129–4137. 10.1063/1.469597. [DOI] [Google Scholar]
- Hinton G. E.; Osindero S.; Teh Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18 (7), 1527–1554. 10.1162/neco.2006.18.7.1527. [DOI] [PubMed] [Google Scholar]
- Dolgirev P. E.; Kruglov I. A.; Oganov A. R. Machine Learning Scheme for Fast Extraction of Chemically Interpretable Interatomic Potentials. AIP Adv. 2016, 6 (8), 085318. 10.1063/1.4961886. [DOI] [Google Scholar]
- Deng B.; Zhong P.; Jun K.; Riebesell J.; Han K.; Bartel C. J.; Ceder G. CHGNet: Pretrained Universal Neural Network Potential for Charge-Informed Atomistic Modeling. arXiv 2023, 5, 1031. 10.1038/s42256-023-00716-3. [DOI] [Google Scholar]
- Ghasemi S. A.; Hofstetter A.; Saha S.; Goedecker S. Interatomic Potentials for Ionic Systems with Density Functional Accuracy Based on Charge Densities Obtained by a Neural Network. Phys. Rev. B 2015, 92 (4), 045131. 10.1103/PhysRevB.92.045131. [DOI] [Google Scholar]
- Zhang D.; Bi H.; Dai F.-Z.; Jiang W.; Liu X.; Zhang L.; Wang H. DPA-1: Pretraining of Attention-Based Deep Potential Model for Molecular Simulation. npj Comput Mater 2024, 10, 7. 10.1038/s41524-024-01278-7. [DOI] [Google Scholar]
- Zubatyuk R.; Smith J. S.; Leszczynski J.; Isayev O. Accurate and Transferable Multitask Prediction of Chemical Properties with an Atoms-in-Molecules Neural Network. Sci. Adv. 2019, 5 (8), eaav6490. 10.1126/sciadv.aav6490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Artrith N.; Kolpak A. M. Grand Canonical Molecular Dynamics Simulations of Cu–Au Nanoalloys in Thermal Equilibrium Using Reactive ANN Potentials. Comput. Mater. Sci. 2015, 110, 20–28. 10.1016/j.commatsci.2015.07.046. [DOI] [Google Scholar]
- Natarajan S. K.; Behler J. Neural Network Molecular Dynamics Simulations of Solid–Liquid Interfaces: Water at Low-Index Copper Surfaces. Phys. Chem. Chem. Phys. 2016, 18 (41), 28704–28725. 10.1039/C6CP05711J. [DOI] [PubMed] [Google Scholar]
- Behler J.; Martoňák R.; Donadio D.; Parrinello M. Pressure-induced Phase Transitions in Silicon Studied by Neural Network-based Metadynamics Simulations. Phys. Status Solidi B 2008, 245 (12), 2618–2629. 10.1002/pssb.200844219. [DOI] [Google Scholar]
- Gubler M.; Finkler J. A.; Schäfer M. R.; Behler J.; Goedecker S. Accelerating Fourth-Generation Machine Learning Potentials by Quasi-Linear Scaling Particle Mesh Charge Equilibration. arXiv 2024, 4c00334. 10.1021/acs.jctc.4c00334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ko T. W.; Finkler J. A.; Goedecker S.; Behler J. A Fourth-Generation High-Dimensional Neural Network Potential with Accurate Electrostatics Including Non-Local Charge Transfer. Nat. Commun. 2021, 12 (1), 398. 10.1038/s41467-020-20427-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behler J. Atom-Centered Symmetry Functions for Constructing High-Dimensional Neural Network Potentials. J. Chem. Phys. 2011, 134 (7), 074106. 10.1063/1.3553717. [DOI] [PubMed] [Google Scholar]
- Liu M.; Kitchin J. R. SingleNN: Modified Behler–Parrinello Neural Network with Shared Weights for Atomistic Simulations with Transferability. J. Phys. Chem. C 2020, 124 (32), 17811–17818. 10.1021/acs.jpcc.0c04225. [DOI] [Google Scholar]
- Huang S.-D.; Shang C.; Kang P.-L.; Liu Z.-P. Atomic Structure of Boron Resolved Using Machine Learning and Global Sampling. Chem. Sci. 2018, 9 (46), 8644–8655. 10.1039/C8SC03427C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S.-D.; Shang C.; Zhang X.-J.; Liu Z.-P. Material Discovery by Combining Stochastic Surface Walking Global Optimization with a Neural Network. Chem. Sci. 2017, 8 (9), 6327–6337. 10.1039/C7SC01459G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Artrith N.; Urban A. An Implementation of Artificial Neural-Network Potentials for Atomistic Materials Simulations: Performance for TiO2. Comput. Mater. Sci. 2016, 114, 135–150. 10.1016/j.commatsci.2015.11.047. [DOI] [Google Scholar]
- Miksch A. M.; Morawietz T.; Kästner J.; Urban A.; Artrith N. Strategies for the Construction of Machine-Learning Potentials for Accurate and Efficient Atomic-Scale Simulations. Mach. Learn. Sci. Technol. 2021, 2 (3), 031001. 10.1088/2632-2153/abfd96. [DOI] [Google Scholar]
- Zhang L.; Han J.; Wang H.; Car R.; E W. Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics. Phys. Rev. Lett. 2018, 120 (14), 143001. 10.1103/PhysRevLett.120.143001. [DOI] [PubMed] [Google Scholar]
- Zhang L.; Han J.; Wang H.; Saidi W. A.; Car R.; E W. End-to-End Symmetry Preserving Inter-Atomic Potential Energy Model for Finite and Extended Systems. arXiv 2018, 2, 09003. 10.48550/arXiv.1805.09003. [DOI] [Google Scholar]
- Mou L.; Han T.; Smith P. E. S.; Sharman E.; Jiang J. Machine Learning Descriptors for Data-Driven Catalysis Study. Adv. Sci. 2023, 10 (22), 2301020. 10.1002/advs.202301020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L.; Wang H.; Muniz M. C.; Panagiotopoulos A. Z.; Car R.; E W. A Deep Potential Model with Long-Range Electrostatic Interactions. J. Chem. Phys. 2022, 156 (12), 124107. 10.1063/5.0083669. [DOI] [PubMed] [Google Scholar]
- Zeng J.; Zhang D.; Lu D.; Mo P.; Li Z.; Chen Y.; Rynik M.; Huang L.; Li Z.; Shi S.; Wang Y.; Ye H.; Tuo P.; Yang J.; Ding Y.; Li Y.; Tisi D.; Zeng Q.; Bao H.; Xia Y.; Huang J.; Muraoka K.; Wang Y.; Chang J.; Yuan F.; Bore S. L.; Cai C.; Lin Y.; Wang B.; Xu J.; Zhu J.-X.; Luo C.; Zhang Y.; Goodall R. E. A.; Liang W.; Singh A. K.; Yao S.; Zhang J.; Wentzcovitch R.; Han J.; Liu J.; Jia W.; York D. M.; E W.; Car R.; Zhang L.; Wang H. DeePMD-Kit v2: A Software Package for Deep Potential Models. J. Chem. Phys. 2023, 159 (5), 054801. 10.1063/5.0155600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y.; Jiang B. Universal Machine Learning for the Response of Atomistic Systems to External Fields. Nat. Commun. 2023, 14 (1), 6424. 10.1038/s41467-023-42148-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y.; Xia J.; Jiang B. Physically Motivated Recursively Embedded Atom Neural Networks: Incorporating Local Completeness and Nonlocality. Phys. Rev. Lett. 2021, 127 (15), 156002. 10.1103/PhysRevLett.127.156002. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Xia J.; Jiang B. REANN: A PyTorch-Based End-to-End Multi-Functional Deep Neural Network Package for Molecular, Reactive, and Periodic Systems. J. Chem. Phys. 2022, 156 (11), 114801. 10.1063/5.0080766. [DOI] [PubMed] [Google Scholar]
- Gastegger M.; Schwiedrzik L.; Bittermann M.; Berzsenyi F.; Marquetand P. WACSF - Weighted Atom-Centered Symmetry Functions as Descriptors in Machine Learning Potentials. J. Chem. Phys. 2018, 148 (24), 241709. 10.1063/1.5019667. [DOI] [PubMed] [Google Scholar]
- Cohn D.; Atlas L.; Ladner R. Improving Generalization with Active Learning. Mach. Learn. 1994, 15 (2), 201–221. 10.1007/BF00993277. [DOI] [Google Scholar]
- Tong Q.; Gao P.; Liu H.; Xie Y.; Lv J.; Wang Y.; Zhao J. Combining Machine Learning Potential and Structure Prediction for Accelerated Materials Design and Discovery. J. Phys. Chem. Lett. 2020, 11 (20), 8710–8720. 10.1021/acs.jpclett.0c02357. [DOI] [PubMed] [Google Scholar]
- Sivaraman G.; Krishnamoorthy A. N.; Baur M.; Holm C.; Stan M.; Csányi G.; Benmore C.; Vázquez-Mayagoitia Á. Machine-Learned Interatomic Potentials by Active Learning: Amorphous and Liquid Hafnium Dioxide. Npj Comput. Mater. 2020, 6 (1), 104. 10.1038/s41524-020-00367-7. [DOI] [Google Scholar]
- Vandermause J.; Xie Y.; Lim J. S.; Owen C. J.; Kozinsky B. Active Learning of Reactive Bayesian Force Fields Applied to Heterogeneous Catalysis Dynamics of H/Pt. Nat. Commun. 2022, 13 (1), 5183. 10.1038/s41467-022-32294-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X.; Bhowmik A.; Vegge T.; Hansen H. A. Neural Network Potentials for Accelerated Metadynamics of Oxygen Reduction Kinetics at Au–Water Interfaces. Chem. Sci. 2023, 14 (14), 3913–3922. 10.1039/D2SC06696C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Podryabinkin E. V.; Shapeev A. V. Active Learning of Linearly Parametrized Interatomic Potentials. Comput. Mater. Sci. 2017, 140, 171–180. 10.1016/j.commatsci.2017.08.031. [DOI] [Google Scholar]
- Vandermause J.; Torrisi S. B.; Batzner S.; Xie Y.; Sun L.; Kolpak A. M.; Kozinsky B. On-the-Fly Active Learning of Interpretable Bayesian Force Fields for Atomistic Rare Events. Npj Comput. Mater. 2020, 6 (1), 20. 10.1038/s41524-020-0283-z. [DOI] [Google Scholar]
- Xu J.; Xie W.; Han Y.; Hu P. Atomistic Insights into the Oxidation of Flat and Stepped Platinum Surfaces Using Large-Scale Machine Learning Potential-Based Grand-Canonical Monte Carlo. ACS Catal. 2022, 12 (24), 14812–14824. 10.1021/acscatal.2c03976. [DOI] [Google Scholar]
- Jinnouchi R.; Miwa K.; Karsai F.; Kresse G.; Asahi R. On-the-Fly Active Learning of Interatomic Potentials for Large-Scale Atomistic Simulations. J. Phys. Chem. Lett. 2020, 11 (17), 6946–6955. 10.1021/acs.jpclett.0c01061. [DOI] [PubMed] [Google Scholar]
- Zhang L.; Lin D.-Y.; Wang H.; Car R.; E W. Active Learning of Uniformly Accurate Interatomic Potentials for Materials Simulation. Phys. Rev. Mater. 2019, 3 (2), 023804. 10.1103/PhysRevMaterials.3.023804. [DOI] [Google Scholar]
- Bunting R. J.; Cheng X.; Thompson J.; Hu P. Amorphous Surface PdO X and Its Activity toward Methane Combustion. ACS Catal. 2019, 9 (11), 10317–10323. 10.1021/acscatal.9b01942. [DOI] [Google Scholar]
- Sumaria V.; Nguyen L.; Tao F. F.; Sautet P. Atomic-Scale Mechanism of Platinum Catalyst Restructuring under a Pressure of Reactant Gas. J. Am. Chem. Soc. 2023, 145 (1), 392–401. 10.1021/jacs.2c10179. [DOI] [PubMed] [Google Scholar]
- Artrith N.; Kolpak A. M. Understanding the Composition and Activity of Electrocatalytic Nanoalloys in Aqueous Solvents: A Combination of DFT and Accurate Neural Network Potentials. Nano Lett. 2014, 14 (5), 2670–2676. 10.1021/nl5005674. [DOI] [PubMed] [Google Scholar]
- Li H.; Jiao Y.; Davey K.; Qiao S. Data-Driven Machine Learning for Understanding Surface Structures of Heterogeneous Catalysts. Angew. Chem. 2023, 135 (9), e202216383. 10.1002/ange.202216383. [DOI] [PubMed] [Google Scholar]
- Sumaria V.; Sautet P. CO Organization at Ambient Pressure on Stepped Pt Surfaces: First Principles Modeling Accelerated by Neural Networks. Chem. Sci. 2021, 12 (47), 15543–15555. 10.1039/D1SC03827C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng X.; Wang Z.; Mao Y.; Hu P. Evidence of the O–Pd–O and Pd–O 4 Structure Units as Oxide Seeds and Their Origin on Pd(211): Revealing the Mechanism of Surface Oxide Formation. Phys. Chem. Chem. Phys. 2019, 21 (12), 6499–6505. 10.1039/C8CP06224B. [DOI] [PubMed] [Google Scholar]
- Owen C. J.; Xie Y.; Johansson A.; Sun L.; Kozinsky B. Stability, Mechanisms and Kinetics of Emergence of Au Surface Reconstructions Using Bayesian Force Fields. arXiv 2023, 07311. 10.48550/arXiv.2308.07311. [DOI] [Google Scholar]
- Xie W.; Xu J.; Chen J.; Wang H.; Hu P. Achieving Theory–Experiment Parity for Activity and Selectivity in Heterogeneous Catalysis Using Microkinetic Modeling. Acc. Chem. Res. 2022, 55 (9), 1237–1248. 10.1021/acs.accounts.2c00058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S.; Sun J.; Chen W.; Ren Y.; Wang J.; Yang Y. Molecular Dynamics Simulation of In Situ Polymerization: Chain Conformation Transition. Macromolecules 2024, 57, 3c02577. 10.1021/acs.macromol.3c02577. [DOI] [Google Scholar]
- Shi X.; Lin X.; Luo R.; Wu S.; Li L.; Zhao Z.-J.; Gong J. Dynamics of Heterogeneous Catalytic Processes at Operando Conditions. JACS Au 2021, 1 (12), 2100–2120. 10.1021/jacsau.1c00355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng G.; Gong X.-G.; Yin W.-J. Crystal Structure Prediction by Combining Graph Network and Optimization Algorithm. Nat. Commun. 2022, 13 (1), 1492. 10.1038/s41467-022-29241-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S.; Noh J.; Gu G. H.; Aspuru-Guzik A.; Jung Y. Generative Adversarial Networks for Crystal Structure Prediction. ACS Cent. Sci. 2020, 6 (8), 1412–1420. 10.1021/acscentsci.0c00426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oganov A. R.; Pickard C. J.; Zhu Q.; Needs R. J. Structure Prediction Drives Materials Discovery. Nat. Rev. Mater. 2019, 4 (5), 331–348. 10.1038/s41578-019-0101-8. [DOI] [Google Scholar]
- Wei L.; Li Q.; Omee S. S.; Hu J. Towards Quantitative Evaluation of Crystal Structure Prediction Performance. Comput. Mater. Sci. 2024, 235, 112802. 10.1016/j.commatsci.2024.112802. [DOI] [Google Scholar]
- Woodley S. M.; Catlow R. Crystal Structure Prediction from First Principles. Nat. Mater. 2008, 7 (12), 937–946. 10.1038/nmat2321. [DOI] [PubMed] [Google Scholar]
- Yang F.; Cheng G.; Yin W.-J. Comparative Study of Crystal Structure Prediction Approaches Based on a Graph Network and an Optimization Algorithm. Sci. China Mater. 2024, 67 (4), 1273–1281. 10.1007/s40843-024-2868-x. [DOI] [Google Scholar]
- Musa E.; Doherty F.; Goldsmith B. R. Accelerating the Structure Search of Catalysts with Machine Learning. Curr. Opin. Chem. Eng. 2022, 35, 100771. 10.1016/j.coche.2021.100771. [DOI] [Google Scholar]
- Huang S.; Shang C.; Kang P.; Zhang X.; Liu Z. LASP: Fast Global Potential Energy Surface Exploration. WIREs Comput. Mol. Sci. 2019, 9 (6), e1415. 10.1002/wcms.1415. [DOI] [Google Scholar]
- Shang C.; Liu Z.-P. Stochastic Surface Walking Method for Structure Prediction and Pathway Searching. J. Chem. Theory Comput. 2013, 9 (3), 1838–1845. 10.1021/ct301010b. [DOI] [PubMed] [Google Scholar]
- Shang C.; Liu Z.-P. Constrained Broyden Dimer Method with Bias Potential for Exploring Potential Energy Surface of Multistep Reaction Process. J. Chem. Theory Comput. 2012, 8 (7), 2215–2222. 10.1021/ct300250h. [DOI] [PubMed] [Google Scholar]
- Ma S.; Shang C.; Liu Z.-P. Heterogeneous Catalysis from Structure to Activity via SSW-NN Method. J. Chem. Phys. 2019, 151 (5), 050901. 10.1063/1.5113673. [DOI] [Google Scholar]
- Kang P.-L.; Shi Y.-F.; Shang C.; Liu Z.-P. Artificial Intelligence Pathway Search to Resolve Catalytic Glycerol Hydrogenolysis Selectivity. Chem. Sci. 2022, 13 (27), 8148–8160. 10.1039/D2SC02107B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X.-J.; Shang C.; Liu Z.-P. From Atoms to Fullerene: Stochastic Surface Walking Solution for Automated Structure Prediction of Complex Material. J. Chem. Theory Comput. 2013, 9 (7), 3252–3260. 10.1021/ct400238j. [DOI] [PubMed] [Google Scholar]
- Kolsbjerg E. L.; Peterson A. A.; Hammer B. Neural-Network-Enhanced Evolutionary Algorithm Applied to Supported Metal Nanoparticles. Phys. Rev. B 2018, 97 (19), 195424. 10.1103/PhysRevB.97.195424. [DOI] [Google Scholar]
- Wang Y.; Lv J.; Gao P.; Ma Y. Crystal Structure Prediction via Efficient Sampling of the Potential Energy Surface. Acc. Chem. Res. 2022, 55 (15), 2068–2076. 10.1021/acs.accounts.2c00243. [DOI] [PubMed] [Google Scholar]
- Ouyang R.; Xie Y.; Jiang D. Global Minimization of Gold Clusters by Combining Neural Network Potentials and the Basin-Hopping Method. Nanoscale 2015, 7 (36), 14817–14821. 10.1039/C5NR03903G. [DOI] [PubMed] [Google Scholar]
- Amsler M.; Goedecker S. Crystal Structure Prediction Using the Minima Hopping Method. J. Chem. Phys. 2010, 133 (22), 224104. 10.1063/1.3512900. [DOI] [PubMed] [Google Scholar]
- Doll K.; Schön J. C.; Jansen M. Structure Prediction Based on Ab Initio Simulated Annealing for Boron Nitride. Phys. Rev. B 2008, 78 (14), 144110. 10.1103/PhysRevB.78.144110. [DOI] [Google Scholar]
- Martoňák R.; Oganov A. R.; Glass C. W. Crystal Structure Prediction and Simulations of Structural Transformations: Metadynamics and Evolutionary Algorithms. Phase Transit. 2007, 80 (4–5), 277–298. 10.1080/01411590701228398. [DOI] [Google Scholar]
- Falls Z.; Avery P.; Wang X.; Hilleke K. P.; Zurek E. The XtalOpt Evolutionary Algorithm for Crystal Structure Prediction. J. Phys. Chem. C 2021, 125 (3), 1601–1620. 10.1021/acs.jpcc.0c09531. [DOI] [Google Scholar]
- Alhijawi B.; Awajan A. Genetic Algorithms: Theory, Genetic Operators, Solutions, and Applications. Evol. Intell. 2024, 17, 1245. 10.1007/s12065-023-00822-6. [DOI] [Google Scholar]
- Chen S. Y.; Zheng F.; Wu S. Q.; Zhu Z. Z. An Improved Genetic Algorithm for Crystal Structure Prediction. Curr. Appl. Phys. 2017, 17 (4), 454–460. 10.1016/j.cap.2017.01.010. [DOI] [Google Scholar]
- Jennings P. C.; Lysgaard S.; Hummelshøj J. S.; Vegge T.; Bligaard T. Genetic Algorithms for Computational Materials Discovery Accelerated by Machine Learning. Npj Comput. Mater. 2019, 5 (1), 46. 10.1038/s41524-019-0181-4. [DOI] [Google Scholar]
- Lazauskas T.; Sokol A. A.; Woodley S. M. An Efficient Genetic Algorithm for Structure Prediction at the Nanoscale. Nanoscale 2017, 9 (11), 3850–3864. 10.1039/C6NR09072A. [DOI] [PubMed] [Google Scholar]
- Wu S. Q.; Ji M.; Wang C. Z.; Nguyen M. C.; Zhao X.; Umemoto K.; Wentzcovitch R. M.; Ho K. M. An Adaptive Genetic Algorithm for Crystal Structure Prediction. J. Phys.: Condens. Matter 2014, 26 (3), 035402. 10.1088/0953-8984/26/3/035402. [DOI] [PubMed] [Google Scholar]
- Vilhelmsen L. B.; Hammer B. A Genetic Algorithm for First Principles Global Structure Optimization of Supported Nano Structures. J. Chem. Phys. 2014, 141 (4), 044711. 10.1063/1.4886337. [DOI] [PubMed] [Google Scholar]
- Glass C. W.; Oganov A. R.; Hansen N. USPEX—Evolutionary Crystal Structure Prediction. Comput. Phys. Commun. 2006, 175 (11–12), 713–720. 10.1016/j.cpc.2006.07.020. [DOI] [Google Scholar]
- Oganov A. R.; Glass C. W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124 (24), 244704. 10.1063/1.2210932. [DOI] [PubMed] [Google Scholar]
- Lyakhov A. O.; Oganov A. R.; Stokes H. T.; Zhu Q. New Developments in Evolutionary Structure Prediction Algorithm USPEX. Comput. Phys. Commun. 2013, 184 (4), 1172–1182. 10.1016/j.cpc.2012.12.009. [DOI] [Google Scholar]
- Melander M. M. Grand Canonical Ensemble Approach to Electrochemical Thermodynamics, Kinetics, and Model Hamiltonians. Curr. Opin. Electrochem. 2021, 29, 100749. 10.1016/j.coelec.2021.100749. [DOI] [Google Scholar]
- Sun G.; Alexandrova A. N.; Sautet P. Pt8 Cluster on Alumina under a Pressure of Hydrogen: Support-Dependent Reconstruction from First-Principles Global Optimization. J. Chem. Phys. 2019, 151 (19), 194703. 10.1063/1.5129296. [DOI] [PubMed] [Google Scholar]
- Tipton W. W.; Hennig R. G. A Grand Canonical Genetic Algorithm for the Prediction of Multi-Component Phase Diagrams and Testing of Empirical Potentials. J. Phys.: Condens. Matter 2013, 25 (49), 495401. 10.1088/0953-8984/25/49/495401. [DOI] [PubMed] [Google Scholar]
- Senftle T. P.; Van Duin A. C. T.; Janik M. J. Methane Activation at the Pd/CeO 2 Interface. ACS Catal. 2017, 7 (1), 327–332. 10.1021/acscatal.6b02447. [DOI] [Google Scholar]
- Liu S.; Dupuis R.; Fan D.; Benzaria S.; Bonneau M.; Bhatt P.; Eddaoudi M.; Maurin G. Machine Learning Potential for Modelling H 2 Adsorption/Diffusion in MOFs with Open Metal Sites. Chem. Sci. 2024, 15 (14), 5294–5302. 10.1039/D3SC05612K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ekberg V.; Samways M. L.; Misini Ignjatović M.; Essex J. W.; Ryde U. Comparison of Grand Canonical and Conventional Molecular Dynamics Simulation Methods for Protein-Bound Water Networks. ACS Phys. Chem. Au 2022, 2 (3), 247–259. 10.1021/acsphyschemau.1c00052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Towards real dynamics in heterogeneous catalysis using machine learning interatomic potential simulations queens university belfast (Author). Jul 2023. [Google Scholar]
- Li J.-L.; Li Y.-F.; Liu Z.-P. In Situ Structure of a Mo-Doped Pt–Ni Catalyst during Electrochemical Oxygen Reduction Resolved from Machine Learning-Based Grand Canonical Global Optimization. JACS Au 2023, 3 (4), 1162–1175. 10.1021/jacsau.3c00038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan Y.; Chaffart D.; Liu G.; Tan Z.; Zhang D.; Wang Y.; Li J.; Ricardez-Sandoval L. Machine Learning in Solid Heterogeneous Catalysis: Recent Developments, Challenges and Perspectives. Chem. Eng. Sci. 2022, 248, 117224. 10.1016/j.ces.2021.117224. [DOI] [Google Scholar]
- Zhu L.; Hu C.; Chen J.; Jiang B. Investigating the Eley–Rideal Recombination of Hydrogen Atoms on Cu (111) via a High-Dimensional Neural Network Potential Energy Surface. Phys. Chem. Chem. Phys. 2023, 25 (7), 5479–5488. 10.1039/D2CP05479E. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Hu C.; Jiang B. Embedded Atom Neural Network Potentials: Efficient and Accurate Machine Learning with a Physically Inspired Representation. J. Phys. Chem. Lett. 2019, 10 (17), 4962–4967. 10.1021/acs.jpclett.9b02037. [DOI] [PubMed] [Google Scholar]
- Lin Q.; Jiang B. Modeling Equilibration Dynamics of Hyperthermal Products of Surface Reactions Using Scalable Neural Network Potential with First-Principles Accuracy. J. Phys. Chem. Lett. 2023, 14 (33), 7513–7518. 10.1021/acs.jpclett.3c01708. [DOI] [PubMed] [Google Scholar]
- Yin R.; Xia J.; Jiang B.; Guo H. Theoretical Insights into Structure Sensitivity in Formate Decomposition Dynamics on Cu Surfaces. ACS Catal. 2023, 13 (21), 14103–14111. 10.1021/acscatal.3c03655. [DOI] [Google Scholar]
- Han Y.; Xu J.; Xie W.; Wang Z.; Hu P. Comprehensive Study of Oxygen Vacancies on the Catalytic Performance of ZnO for CO/H 2 Activation Using Machine Learning-Accelerated First-Principles Simulations. ACS Catal. 2023, 13 (8), 5104–5113. 10.1021/acscatal.3c00658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han Y.; Xu J.; Xie W.; Wang Z.; Hu P. Unravelling the Impact of Metal Dopants and Oxygen Vacancies on Syngas Conversion over Oxides: A Machine Learning-Accelerated Study of CO Activation on Cr-Doped ZnO Surfaces. ACS Catal. 2023, 13 (22), 15074–15086. 10.1021/acscatal.3c03648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng D.; Wei Z.; Zhang Z.; Broekmann P.; Alexandrova A. N.; Sautet P. Restructuring and Activation of Cu(111) under Electrocatalytic Reduction Conditions. Angew. Chem., Int. Ed. 2023, 62 (20), e202218575. 10.1002/anie.202218575. [DOI] [PubMed] [Google Scholar]
- Guan S.-H.; Li Y.-F.; Liu Z.-P. Structural Origin for the Enhanced Photocatalysis of Zr – Ti Oxide Composites from Machine Learning. J. Phys. Chem. C 2023, 127 (46), 22537–22547. 10.1021/acs.jpcc.3c04177. [DOI] [Google Scholar]
- Guo S.; Fan S.; Wang H.; Wang S.; Qin Z.; Dong M.; Fan W.; Wang J. Selective Conversion of CO 2 to Trimethylbenzene and Ethene by Hydrogenation over a Bifunctional ZnCrO x /H-ZSM-5 Composite Catalyst. ACS Catal. 2024, 14 (1), 271–282. 10.1021/acscatal.3c03689. [DOI] [Google Scholar]
- Ma S.; Huang S.-D.; Liu Z.-P. Dynamic Coordination of Cations and Catalytic Selectivity on Zinc–Chromium Oxide Alloys during Syngas Conversion. Nat. Catal. 2019, 2 (8), 671–677. 10.1038/s41929-019-0293-8. [DOI] [Google Scholar]
- Ma S.; Shang C.; Liu Z.-P. Destruction and Preservation of Nonstoichiometric ZnCr Oxide Catalyst from Machine-Learning Simulation. J. Catal. 2023, 426, 294–300. 10.1016/j.jcat.2023.07.024. [DOI] [Google Scholar]
- Liu Q.-Y.; Chen D.; Shang C.; Liu Z.-P. An Optimal Fe–C Coordination Ensemble for Hydrocarbon Chain Growth: A Full Fischer–Tropsch Synthesis Mechanism from Machine Learning. Chem. Sci. 2023, 14 (35), 9461–9475. 10.1039/D3SC02054A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao Y.; Peng Y.; Cheng D.; Chen L.; Wang M.; Shang C.; Zheng L.; Ma D.; Liu Z.-P.; He L. Room-Temperature CO Oxidative Coupling for Oxamide Production over Interfacial Au/ZnO Catalysts. ACS Catal. 2023, 13 (1), 735–743. 10.1021/acscatal.2c05358. [DOI] [Google Scholar]
- Li X.-T.; Chen L.; Shang C.; Liu Z.-P. In Situ Surface Structures of PdAg Catalyst and Their Influence on Acetylene Semihydrogenation Revealed by Machine Learning and Experiment. J. Am. Chem. Soc. 2021, 143 (16), 6281–6292. 10.1021/jacs.1c02471. [DOI] [PubMed] [Google Scholar]
- Shi Y.-F.; Kang P.-L.; Shang C.; Liu Z.-P. Methanol Synthesis from CO 2 /CO Mixture on Cu–Zn Catalysts from Microkinetics-Guided Machine Learning Pathway Search. J. Am. Chem. Soc. 2022, 144 (29), 13401–13414. 10.1021/jacs.2c06044. [DOI] [PubMed] [Google Scholar]
- Chen D.; Chen L.; Zhao Q.-C.; Yang Z.-X.; Shang C.; Liu Z.-P. Square-Pyramidal Subsurface Oxygen [Ag4OAg] Drives Selective Ethene Epoxidation on Silver. Nat. Catal. 2024, 7, 536. 10.1038/s41929-024-01135-2. [DOI] [Google Scholar]
- Mo P.; Li C.; Zhao D.; Zhang Y.; Shi M.; Li J.; Liu J. Accurate and Efficient Molecular Dynamics Based on Machine Learning and Non von Neumann Architecture. Npj Comput. Mater. 2022, 8 (1), 107. 10.1038/s41524-022-00773-z. [DOI] [Google Scholar]
- Zhang C.; Tang L.; Sun Y.; Ho K.-M.; Wentzcovitch R. M.; Wang C.-Z. Deep Machine Learning Potential for Atomistic Simulation of Fe-Si-O Systems under Earth’s Outer Core Conditions. Phys. Rev. Mater. 2022, 6 (6), 063802. 10.1103/PhysRevMaterials.6.063802. [DOI] [Google Scholar]
- Liu J.-C.; Luo L.; Xiao H.; Zhu J.; He Y.; Li J. Metal Affinity of Support Dictates Sintering of Gold Catalysts. J. Am. Chem. Soc. 2022, 144 (45), 20601–20609. 10.1021/jacs.2c06785. [DOI] [PubMed] [Google Scholar]
- Wu J.; Chen D.; Chen J.; Wang H. Structural and Composition Evolution of Palladium Catalyst for CO Oxidation under Steady-State Reaction Conditions. J. Phys. Chem. C 2023, 127 (13), 6262–6270. 10.1021/acs.jpcc.2c07877. [DOI] [Google Scholar]
- Jain A.; Ong S. P.; Hautier G.; Chen W.; Richards W. D.; Dacek S.; Cholia S.; Gunter D.; Skinner D.; Ceder G.; Persson K. A. Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater. 2013, 1 (1), 011002. 10.1063/1.4812323. [DOI] [Google Scholar]
- Chanussot L.; Das A.; Goyal S.; Lavril T.; Shuaibi M.; Riviere M.; Tran K.; Heras-Domingo J.; Ho C.; Hu W.; Palizhati A.; Sriram A.; Wood B.; Yoon J.; Parikh D.; Zitnick C. L.; Ulissi Z. Open Catalyst 2020 (OC20) Dataset and Community Challenges. ACS Catal. 2021, 11 (10), 6059–6072. 10.1021/acscatal.0c04525. [DOI] [Google Scholar]
- Tran R.; Lan J.; Shuaibi M.; Wood B. M.; Goyal S.; Das A.; Heras-Domingo J.; Kolluru A.; Rizvi A.; Shoghi N.; Sriram A.; Therrien F.; Abed J.; Voznyy O.; Sargent E. H.; Ulissi Z.; Zitnick C. L. The Open Catalyst 2022 (OC22) Dataset and Challenges for Oxide Electrocatalysts. ACS Catal. 2023, 13 (5), 3066–3084. 10.1021/acscatal.2c05426. [DOI] [Google Scholar]
- Ouyang R.; Curtarolo S.; Ahmetcik E.; Scheffler M.; Ghiringhelli L. M. SISSO: A Compressed-Sensing Method for Identifying the Best Low-Dimensional Descriptor in an Immensity of Offered Candidates. Phys. Rev. Mater. 2018, 2 (8), 083802. 10.1103/PhysRevMaterials.2.083802. [DOI] [Google Scholar]
- Bogojeski M.; Vogt-Maranto L.; Tuckerman M. E.; Müller K.-R.; Burke K. Quantum Chemical Accuracy from Density Functional Approximations via Machine Learning. Nat. Commun. 2020, 11 (1), 5223. 10.1038/s41467-020-19093-1. [DOI] [PMC free article] [PubMed] [Google Scholar]