Abstract
Phylodynamics is central to understanding infectious disease dynamics through the integration of genomic and epidemiological data. Despite advancements, including the application of deep learning to overcome computational limitations, significant challenges persist due to data inadequacies and statistical unidentifiability of key parameters. These issues are particularly pronounced in poorly resolved phylogenies, commonly observed in outbreaks such as SARS-CoV-2. In this study, we conducted a thorough evaluation of PhyloDeep, a deep learning inference tool for phylodynamics, assessing its performance on poorly resolved phylogenies. Our findings reveal the limited predictive accuracy of PhyloDeep (and other state-of-the-art approaches) in these scenarios. However, models trained on poorly resolved, realistically simulated trees demonstrate improved predictive power, despite not being infallible, especially in scenarios with superspreading dynamics, whose parameters are challenging to capture accurately. Notably, we observe markedly improved performance through the integration of minimal contact tracing data, which refines poorly resolved trees. Applying this approach to a sample of SARS-CoV-2 sequences partially matched to contact tracing from Hong Kong yields informative estimates of superspreading potential, extending beyond the scope of contact tracing data alone. Our findings demonstrate the potential for enhancing phylodynamic analysis through complementary data integration, ultimately increasing the precision of epidemiological predictions crucial for public health decision-making and outbreak control.
Keywords: phylodynamics, deep learning, contact tracing, superspreading
Introduction
Phylogenetic analysis of genomic sequence data offers a powerful toolkit for understanding the emergence, spread, and evolution of infectious diseases. As an interdisciplinary field, phylodynamics aims to integrate genomic and epidemiological data in a unified framework to extract detailed insights into epidemic history (Drummond et al. 2005; Volz et al. 2009; Stadler et al. 2013), population dynamics (Volz et al. 2009; Stadler and Bonhoeffer 2013), and disease emergence (Worobey et al. 2014; Pekar et al. 2022). Its key advantage lies in providing independent information regarding epidemic history, complementing traditional epidemiological surveillance data (Voznica et al. 2022; Vaughan et al. 2024). This makes it invaluable for validating and substantiating findings from epidemiological modeling, particularly in contexts where conventional surveillance data are scarce and genomic sampling is randomized.
However, many conventional phylodynamic models based on likelihood approaches (e.g. maximum likelihood [ML] estimation and Bayesian approaches) are computationally intensive and can become practically unfeasible as the number of taxa increases (Hohna and Drummond 2012). Addressing this issue sometimes involves likelihood-free methods such as approximate Bayesian computation (Saulnier et al. 2017), which sidestep the need for direct likelihood calculations. More recently, deep learning methods such as PhyloDeep (Voznica et al. 2022) have emerged as another potential solution, enabling rapid estimation of epidemiological parameters from large phylogenetic trees in a matter of seconds. To achieve this, PhyloDeep utilizes deep neural network models trained against phylogenies simulated under well-established birth–death models: the basic birth–death model (BD) (Stadler et al. 2012; Leventhal et al. 2014), the birth–death model with exposed and infectious classes (BDEI) (Stadler et al. 2013; Kuhnert et al. 2016), and the birth–death model with superspreading (BDSS) (Stadler et al. 2013). PhyloDeep has also been validated for diversification analyses (Lambert et al. 2023) and viral phylogeography (Thompson et al. 2024).
Despite these methodological advancements, critical challenges remain concerning the adequacy of data sets and the statistical identifiability of the parameters of interest from sequence data. This issue is particularly pronounced for viral sequences arising from epidemics and outbreaks, which frequently yield many identical sequences, resulting in poorly resolved phylogenies with numerous polytomies. Examples include SARS-CoV-2, Mpox (monkeypox) virus (Paredes et al. 2024), and respiratory syncytial virus (Eden et al. 2022). These poorly resolved trees typically do not align with the “idealistic,” well-resolved trees posited by phylodynamic models like birth–death models, where branching events are assumed to correspond to transmission events. Such misalignment could introduce biases, compromising the accuracy and reliability of inference methods and potentially leading to incorrect interpretations of epidemic dynamics and disease transmission.
To address these concerns, this study utilizes the PhyloDeep framework to assess the impact of potential biases introduced by poorly resolved phylogenies, using the SARS-CoV-2 as an example of a virus outbreak characterized by the BDSS model, which splits population into normal and superspreaders while tracking superspreading potential (Fig. 1). Our analysis reveals that neural network models in PhyloDeep (and other state-of-the-art approaches) struggle to precisely predict epidemiological parameters when applied to poorly resolved phylogenetic trees, but performance does improve when models are trained on poorly resolved, realistically simulated phylogenies rather than on “idealistic” trees from birth–death models, as previously done in PhyloDeep. However, capturing superspreading dynamics remains a challenge. Notably, integrating contact tracing data substantially enhances predictive accuracy by constraining tree space and aligning them more closely with “idealistic” trees. Additionally, this integration also proves beneficial in the Bayesian inference framework implemented in BEAST2 (Bouckaert et al. 2014). We illustrate these findings using real SARS-CoV-2 data collected during the third and fourth waves of the epidemic in Hong Kong.
Fig. 1.
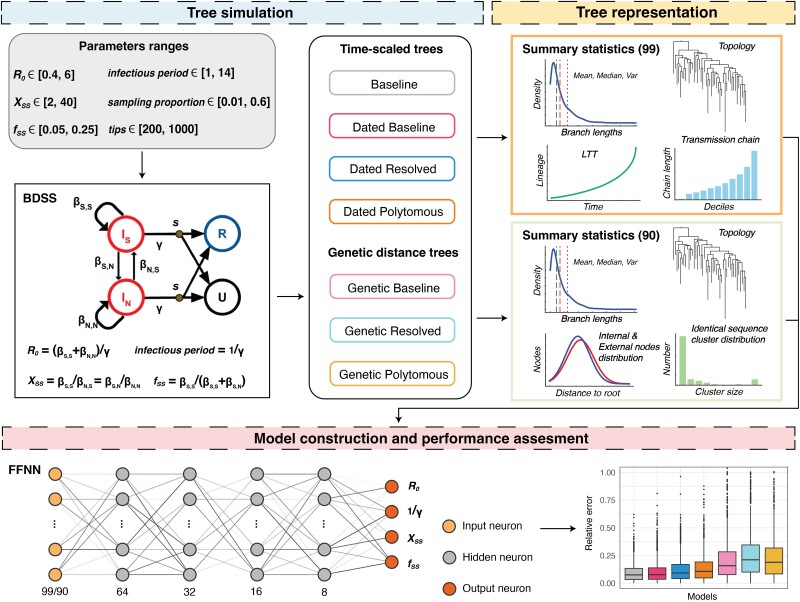
An overview of training neural network models based on simulated phylogenetic trees. The BDSS model categorizes individuals as superspreaders (S) or normal spreaders (N), extending the traditional birth–death model parameters R0 (basic reproductive number) and 1/γ (infectious period). fss indicates the fraction of superspreaders in the population, while Xss represents the ratio of the transmission rate of superspreaders to that of normal spreaders. The BDSS model illustration adapted from PhyloDeep. Seven types of trees, Baseline, Dated Baseline, Dated Resolved, Dated Polytomous, Genetic Baseline, Genetic Resolved, Genetic Polytomous, are detailed in Fig. 2.
Results
Building on the PhyloDeep approach, we simulated phylogenetic trees (idealistic) using the BDSS model, covering a broad range of epidemiological parameter values associated with the SARS-CoV-2 virus (Fig. 1). These simulated trees were transformed into six additional forms, ranging from idealized simulations to those reflecting the complexities of real-world sequences and trees (Figs. 1 and 2). Neural networks trained with summary statistics (SSs) were applied to each tree type to perform regression tasks, estimating epidemiological parameters and evaluating the performance of these models comprehensively.
Fig. 2.
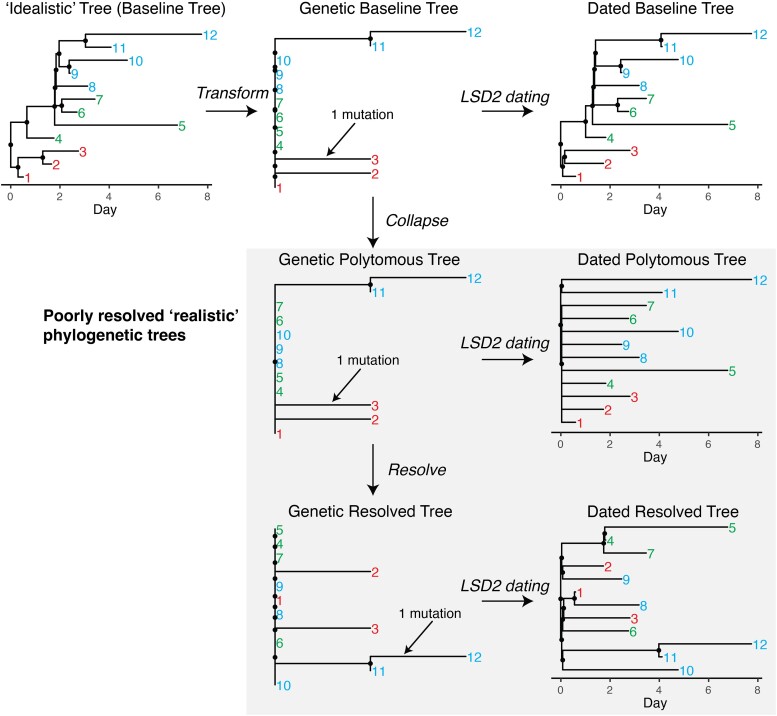
Examples of seven types of phylogenetic trees used in simulations. Internal nodes are marked as black dots, while tips are denoted by numerical labels. Among these, four trees represent poorly resolved, realistic phylogenetic structures that can be derived from sequence data and are highlighted with a gray background. To effectively highlight the differences between poorly resolved trees, which can be constructed from sequence data, and fully resolved idealistic trees, which cannot, tips have been color-coded into three distinct clusters. Each type of simulated tree used in this study has tip counts ranging from 200 to 1,000 (supplementary table S1, Supplementary Material online).
Simulations of Phylogenetic Trees
Initially, we simulated 200,000 time-scaled trees using the BDSS model (Fig. 2, baseline tree). These trees serve as our reference “idealistic” trees and capture transmission events at internal nodes consistent with the PhyloDeep framework. To emulate SARS-CoV-2 phylogenetic trees, all baseline trees were transformed into genetic distance trees (Fig. 2, genetic baseline tree).This transformation relied on a binomial distribution of mutation counts given a mean substitution rate of 8 × 10−4 per site per year, resulting in approximately 24 mutations observed annually for a sequence length of 29,903 bases (see Materials and Methods for details). Branches with lengths representing zero mutation were collapsed, resulting in trees with polytomies (Fig. 2, genetic polytomous tree), which were then randomly resolved using a coalescent approach, yielding binary trees (Fig. 2, genetic resolved tree). The number and size of polytomies in our simulated trees varied from 1 to 170 and 3 to 934, respectively, with a total tip range of 200 to 1,000, encompassing those observed in SARS-CoV-2 trees in Hong Kong (supplementary fig. S1, Supplementary Material online). Lastly, each of the three transformed genetic distance trees was dated using LSD2 (To et al. 2016) (Fig. 2, dated baseline tree, dated polytomous tree, and dated resolved tree). Genetic Polytomous Trees, Genetic Resolved Trees, Dated Polytomous Trees, and Dated Resolved Trees represent entirely altered topologies and are deemed poorly resolved, realistic trees. They are analogous to trees inferred from sequencing data using established software such as RAxML-NG (Kozlov et al. 2019), IQ-TREE (Nguyen et al. 2015), PhyML (Guindon et al. 2010), FastTree (Price et al. 2010), or TreeTime (Sagulenko et al. 2018). In contrast, the remaining three types, namely Baseline Trees, Genetic Baseline Trees, and Dated Baseline Trees, retain a known correct topology that cannot be derived from sequence data alone (Fig. 2).
Performance Comparison of Neural Network Models for Each Type of Phylogenetic Tree
We utilized a data set totaling 199,000 trees to train the neural network models, reserving 1,000 trees for validation purposes. Ensuring consistency across the models, we utilized the same 99 SS representations and feed-forward neural network architectures for each tree type, as used in PhyloDeep (Fig. 1). Specifically, for the three types of genetic distance trees, namely Genetic Baseline Trees, Genetic Polytomous Trees, and Genetic Resolved Trees, we adapted the 99 SSs designed for time-scaled trees to 90 SSs for genetic distance trees (refer to the Materials and Methods section). Consequently, we trained seven neural network models: Baseline-Model, Dated Baseline-Model, Dated Resolved-Model, Dated Polytomous-Model, Genetic Baseline-Model, Genetic Resolved-Model, and Genetic Polytomous-Model.
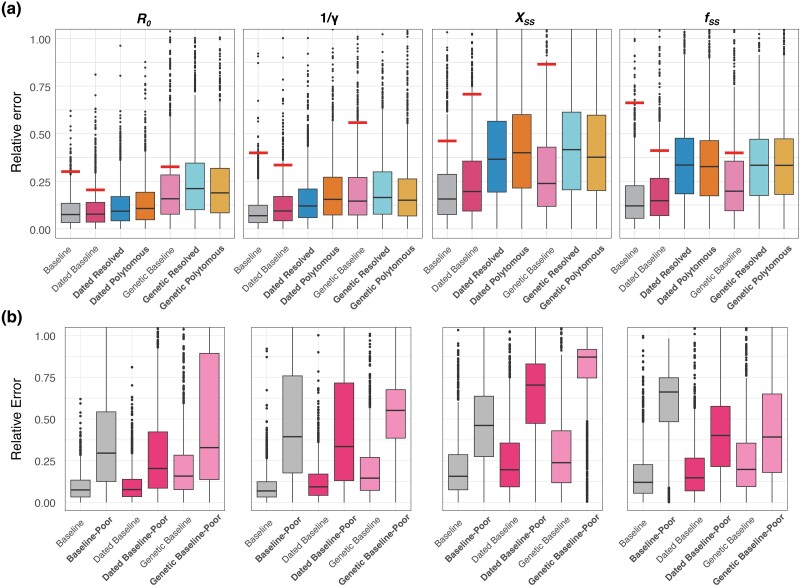
Our results show that models trained and tested on trees with unchanged topologies (i.e. Baseline-Model, Dated Baseline-Model, and Genetic Baseline-Model) did well in predicting all parameters. Estimates for R0 and 1/γ tended to exhibit greater accuracy compared to superspreading parameters (Xss and fss) (Fig. 3a and supplementary table S2, Supplementary Material online), which is consistent with the findings from PhyloDeep (Voznica et al. 2022). As expected, the Baseline-Model exhibited the best performance, achieving mean relative errors (MREs) of 0.095 for R0, 0.092 in 1/γ, 0.215 for Xss, and 0.167 for fss. Conversely, models trained and tested on trees with altered topologies (Dated Resolved-Model, Dated Polytomous-Model, Genetic Polytomous-Model, and Genetic Resolved-Model) encountered challenges in accurately predicting superspreading parameters. This suggests that phylogenetic trees with polytomies lack sufficient phylogenetic resolution to accurately recover parameters related to superspreading. Models trained and tested on dated trees generally outperformed those trained and tested on the equivalent genetic distance trees in most scenarios, demonstrating the value of tip dates for informing model learning and estimating parameters.
Fig. 3.
Performance comparison of models. a) Performance comparison of models trained on seven types of phylogenetic trees. Each bar depicts the relative error observed when testing trees of the same type as those used in training. The horizontal lines above the boxes denote the median relative error when testing the Baseline-Model and Dated Baseline-Model with Dated Resolved Trees, as well as the Genetic Baseline-Model with Genetic Resolved Trees. Models trained using poorly resolved phylogenetic trees (i.e. Dated Resolved, Dated Polytomous, Genetic Resolved, and Genetic Polytomous) are highlighted in bold. b) Performance comparison of models tested using poorly resolved phylogenetic trees. “Baseline-Poor” represents the evaluation of the Baseline-Model tested using Dated Resolved Trees. “Dated Baseline-Poor” indicates the assessment of the Dated Baseline-Model with Dated Resolved Trees, while “Genetic Baseline-Poor” reflects the performance of the Genetic Baseline-Model when testing with Genetic Resolved Trees.
Impact of Poorly Resolved Phylogenetic Trees on Models Trained with “Idealistic” Trees
To evaluate the impact of using poorly resolved realistic phylogenetic trees as input on neural network models trained with “idealistic” trees, we tested the Baseline-Model and Dated Baseline-Model with 1,000 Dated Resolved Trees and the Genetic Baseline-Model with 1,000 Genetic Resolved Trees (Fig. 3 and supplementary table S2, Supplementary Material online). The results revealed that the relative error for each parameter was approximately twice as high or more compared to when using “idealistic” test trees (Fig. 3b). Notably, the relative errors for the superspreading parameters (Xss and fss) were around or exceeded 0.5 (50%). This demonstrates that models trained on “idealistic” trees struggled to predict accurately epidemiological parameters from poorly resolved, realistic phylogenetic trees. Conversely, models trained on poorly resolved trees (such as Genetic Polytomous, Genetic Resolved, Dated Polytomous, and Dated Resolved) performed better, underscoring the importance of training on data that mirror real-world complexity (Fig. 3a). However, despite improvements, the higher predictive errors specific to superspreading parameters relative to other epidemiological parameters seemed to persist (Fig. 3), highlighting the inherent challenge in estimating superspreading potential from such poorly resolved trees. Additionally, despite repeatedly generating different Genetic Resolved and Dated Resolved trees from the polytomous trees as input, the predicted parameters tended to converge toward similar estimates, which differed substantially from the actual parameters originally input, thus indicating a form of bias in the estimations.
Improving Predictions by Integrating Contact Tracing Data
To improve model accuracy, a reasonable approach involves correcting the observed topology of input trees so that they closely resemble the equivalent “idealistic” trees. In this context, we investigated the potential of leveraging contact tracing data (including cluster information and infection times) to aid in refining the topology of Genetic Polytomous Trees, for example, to match Baseline or Dated Baseline trees to varying extents (supplementary fig. S2, Supplementary Material online). We derived contact tracing information from the simulated Baseline trees, treating all descendants of each internal node as a cluster, with the dates of internal nodes considered as infection times of each cluster's index case (supplementary fig. S3, Supplementary Material online). With this addition of cluster information and assuming perfect observation, the topology of Genetic Polytomous Trees can be fully corrected (matching the Genetic Baseline Trees), with external nodes subsequently dated to produce Dated Baseline trees (supplementary fig. S2, Supplementary Material online). Furthermore, if the infection times of clusters are known, time constraints can also be applied to internal nodes, effectively recovering equivalent Baseline trees from the Genetic Polytomous Trees. In real-world scenarios, however, the extent of case observation is often limited and imperfect, and the accuracy of any available contact tracing data is uncertain and subject to additional biases.
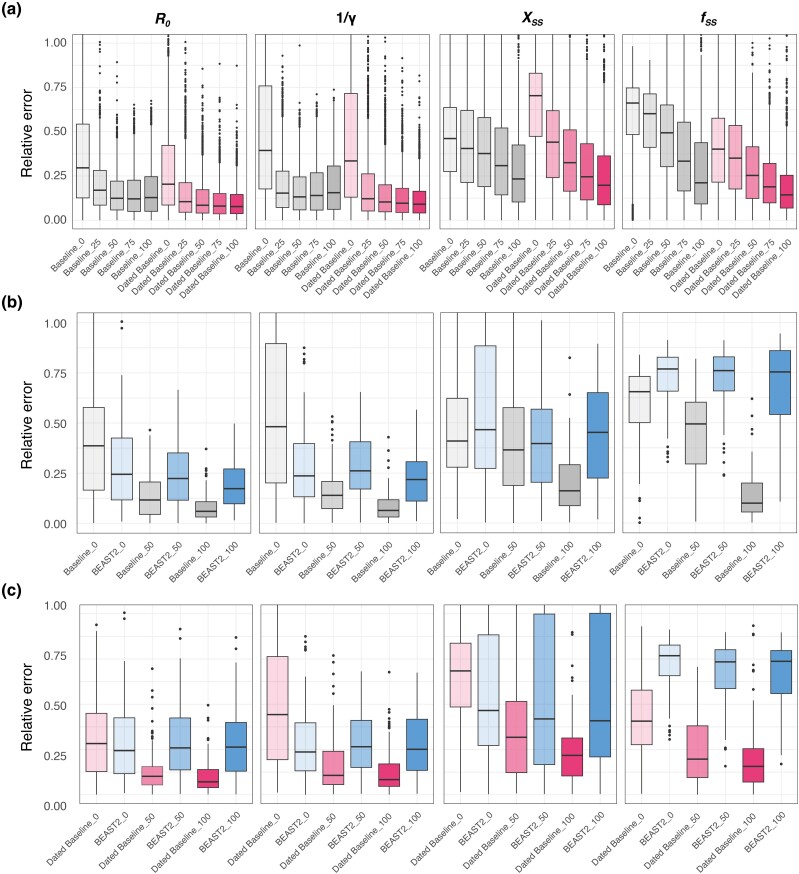
Therefore, to assess how the quantity of contact tracing data influences our predictions within the context of phylogenetic trees, we simulated scenarios where 0%, 25%, 50%, 75%, and 100% of internal nodes were randomly selected to provide cluster information and infection times. We then evaluated the performance of the Baseline-Model and Dated Baseline-Model (Fig. 4a and supplementary table S3, Supplementary Material online). The former requires cluster information to resolve polytomies and infection times, with a time constraint margin of 1 d, to estimate the lengths of newly created internal branches from Genetic Polytomous Trees (supplementary fig. S2g, Supplementary Material online), while the latter relies solely on cluster information (supplementary fig. S2f, Supplementary Material online). For any remaining nodes lacking contact tracing data, we resolved them randomly as before. Our results indicated that even with just 25% of contact tracing data incorporated, the MREs for R0 and 1/γ could be reduced to below 0.2, representing an improvement of 48% to 66% (supplementary table S3, Supplementary Material online). As the availability of contact tracing data increased, model performance consistently improved, particularly in predicting superspreading parameters as could be expected. Incorporating 50% or more of contact tracing data yielded estimates of superspreading parameters, with MREs around or below 30%, achieving an improvement of at least 22% (supplementary table S3, Supplementary Material online). Notably, the Dated Baseline-Model generally outperformed the Baseline-Model except when contact tracing was 100% complete and a harsh time constraint margin of 0.1 d (supplementary table S3, Supplementary Material online). Furthermore, the Dated Baseline-Model only required cluster information to refine the input trees, suggesting its greater relevance to real-world scenarios.
Fig. 4.
Performance comparison by incorporating varying levels of contact tracing data based on Baseline-Model, Dated Baseline-Model, and BEAST2. a) Comparison between the Baseline-Model and Dated Baseline-Model with varying levels of contact tracing data based on 1,000 simulated trees. The models are represented by Baseline-Model and Dated Baseline-Model, with the color intensity within each bar signaling the degree of contact tracing data integrated into the input trees. Darker shades denote a higher percentage of data incorporation. The term “Baseline_50” refers to the performance of the Baseline-Model with Genetic Polytomous Trees refined using 50% contact tracing data, encompassing cluster information and infection times. “Dated Baseline_50” indicates the performance of the Dated Baseline-Model with Genetic Polytomous Trees refined using 50% contact tracing data, including only cluster information. It is notable that the input trees are refined by infection time, with a 1-day time constraint margin using LSD2 (To et al. 2016), and an additional refinement with a stricter margin of 0.1 day, as shown in supplementary table S3, Supplementary Material online. b) Comparison between the Baseline-Model and BEAST2 (blue bar) with varying levels of contact tracing data (cluster information and infection times) based on 100 simulated trees. c) Comparison between Dated Baseline-Model and BEAST2 (blue bar) with varying levels of contact tracing data (cluster information only) based on 100 simulated trees. “BEAST2_50” indicates the performance of BEAST2 with Genetic Polytomous Trees refined using 50% contact tracing data, incorporating both cluster information and infection times in b), and only cluster information in c).
We compared the Dated Baseline-Model and Baseline-Model to the gold standard likelihood-based Bayesian tool BEAST2 (Bouckaert et al. 2014) across varying levels of contact tracing data. BEAST2's performance improved with increased proportions of contact tracing data, which includes cluster information and infection times (Fig. 4b and supplementary table S4, Supplementary Material online). However, BEAST2 consistently underperformed compared to our Baseline-Model, except when no contact tracing data were incorporated. Even in this scenario, it still performed worse than models trained on poorly resolved phylogenies (Fig. 3a and supplementary tables S2 and S4, Supplementary Material online). Additionally, BEAST2 struggled to accurately infer superspreading parameters, even with 100% contact tracing data, which aligns with the findings of PhyloDeep (Voznica et al. 2022). Further, providing only cluster information, which modifies the tree topology without correcting the time of internal nodes, did not substantially enhance BEAST2's performance (Fig. 4c and supplementary table S4, Supplementary Material online), likely due to the loss of this crucial temporal information.
Case Study of SARS-CoV-2 Waves in Hong Kong
By 2022, Hong Kong had effectively controlled the local spread of SARS-CoV-2, experiencing four significant waves during which extensive sequence sampling and epidemiological surveillance were conducted, as detailed in our previous study (Gu et al. 2022). To demonstrate our method of integrating contact tracing data to improve model prediction, we used real-world SARS-CoV-2 data from the third and fourth waves in Hong Kong, analyzed from 2020 May 13 to August 1 (460 sequences and 1,930 local cases) and from 2020 September 30 to December 8 (243 sequences and 1,577 local cases). Utilizing all available SARS-CoV-2 sequences from these periods along with partial contact tracing data (only cluster information available), covering 16.56% for the third wave and 9.50% for the fourth wave (see Materials and Methods), we evaluate the differences in prediction outcomes when using the Dated Baseline-Model, with input trees refined by contact tracing data (Dated Resolved-Cluster) and without it (Dated Resolved, random resolution of polytomies).
Initially, we verified the suitability of the input trees generated by RAxML-NG (Kozlov et al. 2019) using the GTR +G4 + FO substitution model with random resolution of polytomies, through principal component analysis (PCA) and by comparing the range of each simulated SS to ensure the models and scenarios were predictive. All trees from Hong Kong passed this PCA check, but seven SSs related to transmission chain features for the Dated Resolved tree of wave 4 were outside the [min, max] range of the simulated values (supplementary fig. S4 and table S5, Supplementary Material online). After integrating the available contact tracing data (9.50%, as detailed in the Materials and Methods), only one SS remained outside the simulated range, albeit very close to the lower boundary (supplementary table S5, Supplementary Material online).
The prediction results indicated a notable change when contact tracing data were used to refine tree topology, especially for wave 4 (Table 1). With the Dated Resolved-Cluster tree, we estimated an R0 of 1.59 and 1.52, infection-to-sampling periods (infectious periods, 1/γ) of 4.6 and 8.6 d, Xss of 8.1 and 16.4, and fss of 0.091 and 0.078 for waves 3 and 4, respectively. Given Xss and fss, we can calculate the dispersion value k (see Materials and Methods), which is commonly used as a measure of superspreading potential. For waves 3 and 4, we calculated k = 0.47 and 0.25, respectively, where lower values of k represent increasing superspreading potential. Conversely, using the Dated Resolved tree, we estimated an R0 of 1.70 and 2.06, infection-to-sampling periods of 5.7 and 20.1 d, Xss of 7.6 and 7.2, fss of 0.090 and 0.076, and k of 0.49 and 0.66 for waves 3 and 4, respectively. The unusually long infection-to-sampling periods of 20.1 d observed in wave 4 may be attributed to the seven SSs that exceeded the expected range, which likely influenced these skewed predictions (supplementary fig. S4 and table S5, Supplementary Material online). Further, based solely on epidemiological records, we estimated an R0 of 1.69 and 1.93, and k of 0.45 and 0.26 for waves 3 and 4, separately (Table 1). The observed discrepancies highlight the critical need for integrating diverse data sources and analytical methods in estimating epidemiological parameters, thereby enabling a more comprehensive and systematic understanding of epidemic dynamics.
Table 1.
Comparison of inference of epidemiological parameters based on waves 3 and 4 of SARS-CoV-2 in Hong Kong
| Waves | Input tree | R 0 | Infection-to-sampling period (d) | X ss | f ss | Dispersion k |
|---|---|---|---|---|---|---|
| 3 | Dated Resolved | 1.699 ± 0.096 (1.460, 2.172) |
5.720 ± 1.018 (4.427, 10.804) |
7.608 ± 1.496 (4.141, 18.696) |
0.090 ± 0.022 (0.057, 0.163) |
0.488 (0.441, 0.543) |
| Dated Resolved-Cluster | 1.588 ± 0.077 (1.330, 1.993) |
4.636 ± 0.635 (3.373, 8.238) |
8.078 ± 1.709 (3.911, 17.733) |
0.091 ± 0.021 (0.054, 0.167) |
0.467 (0.418, 0.517) |
|
| Epidemiological inferencea | 1.693 (1.649, 1.738) |
NA | NA | NA | 0.451 (0.421, 0.481) |
|
| 4 | Dated Resolved | 2.062 ± 0.072 (1.628, 3.220) |
20.071 ± 1.663 (14.235, 32.668) |
7.232 ± 1.423 (2.197, 23.198) |
0.076 ± 0.009 (0.050, 0.154) |
0.658 (0.596, 0.737) |
| Dated Resolved-Cluster | 1.518 ± 0.091 (1.284, 2.055) |
8.629 ± 0.881 (6.548, 14.929) |
16.388 ± 2.692 (5.895, 33.409) |
0.078 ± 0.007 (0.050, 0.161) |
0.250 (0.227, 0.278) |
|
| Epidemiological inferencea | 1.933 (1.858, 2.012) |
NA | NA | NA | 0.264 (0.248, 0.279) |
Values predicted by neural network models are expressed as mean ± standard deviation generated by randomly resolving polytomies n = 200 times. Values in parentheses are the 95% CI. In the BDSS model, the term “infectious period” refers to the interval from the time of infection to the sampling date. To prevent confusion in epidemiological contexts, we have opted to use “infection-to-sampling period” in place of “infectious period.”
aEpidemiological inference uses a combination of line-listed incidence data to estimate R0 and contact tracing data to estimate k.
Additionally, we conducted 200 random resolutions of polytomies for these SARS-CoV-2 trees to measure the robustness of the predictions. The resulting standard deviations were notably small (Table 1), indicating that the predictions were not significantly affected by the random resolution of polytomies, suggesting our models could efficiently extract essential cluster information and guide robust predictions. The 95% confidence intervals (CIs) were generated by parametric bootstrap as per the methodology of PhyloDeep. The substantial width of CIs for superspreading parameters again highlights the inherent difficulty in predicting these metrics.
Discussion
In this study, we assessed the performance of established neural network models (PhyloDeep) in predicting epidemiological parameters and the applicability of these models to real-world scenarios using SARS-CoV-2 as a case study for both simulation and empirical analyses. Our findings demonstrate the relative performance limitations of utilizing neural network models trained on simulated phylogenetic trees (“idealistic” trees) when predicting parameters from poorly resolved trees (“realistic” trees) and show that models alternatively trained on simulated trees of similar resolution can improve the accuracy of predictions. Beyond upstream improvements to model training, we show that by using contact tracing data to partially resolve the topology and node dates of input trees downstream, additional performance enhancements can be achieved. We apply this approach to SARS-CoV-2 genome sequences from Hong Kong matched to minimal contact tracing data, producing new phylodynamic estimates of both R0 (basic reproductive number) and k (dispersion measure of superspreading potential).
Without the incorporation of contact tracing data, we found that our improved models trained on simulated poorly resolved trees still struggled to accurately estimate parameters related to superspreading, even when attempting to overfit neural network models on smaller subsets of trees (supplementary table S6, Supplementary Material online). This issue is particularly pronounced when sequences are nearly identical, like for SARS-CoV-2, which results in potentially biased estimations likely to misinform public health decision-makers. Traditional phylodynamic inference methods (e.g. ML estimation and Bayesian approaches) with models that assume ideal binary trees and not representing sequence evolution also struggle in parameter estimation under these conditions (supplementary table S4, Supplementary Material online) (Lewis et al. 2005; Morel et al. 2021). Together this emphasizes the importance of incorporating even minimal contact tracing data as we have done in our study, but also utilizing more comprehensive SSs focused on clusters and polytomies that can effectively capture the complexity of the underlying transmission dynamic. One previous study (Tran-Kiem and Bedford 2024) has demonstrated a connection between the size distribution of identical sequence clusters and transmission dynamics; however, our attempts to incorporate similar information into our neural network models, trained on genetic distance trees, yielded limited improvements. As an ongoing area of research interest, future studies could evaluate the relative predictive performance of models that expand the potential range of SSs related to clusters and polytomies, and experiment with alternate architectures such as Graph Neural Networks and Convolutional Neural Networks incorporating a more complete representation of trees, such as Compact Bijective Ladderized Vectors (Voznica et al. 2022).
Besides superspreading, the incubation period is another significant aspect of pathogen transmission dynamics. For example, estimates of the SARS-CoV-2 incubation period were used to justify the World Health Organization's (WHO) recommendation of a 14-d quarantine period for contacts of infected cases (Wells et al. 2021). In our approach, we utilized a BDSS model, which does not account for the incubation period, but defines the infectious period as the interval from infection time to sampling date otherwise known as the delay interval. Employing the Dated Baseline-Model with the Dated Resolved-Cluster tree, we determined the infectious period/delay interval of waves 3 and 4 to be approximately 1 week; however, the delay for wave 4 was longer than that for wave 3, suggesting case detection speed was somewhat challenged. The longer delay in wave 4 could be explained by the sudden rise in cases associated with the largest single SARS-CoV-2 superspreading event detected in Hong Kong prior to widespread vaccination, which also triggered the start of wave 4 (Adam et al. 2022; Gu et al. 2022).
Remarkably, the estimation of R0 exhibited robust performance across our neural network models, with models trained on dated trees outperforming those based on genetic distance trees. This underscores the value of tip dates for R0 estimation, particularly as sequence variability decreases. This is in line with recent studies that highlight the increasing importance of sampling dates for phylodynamic inference when sequence variability is low (Featherstone et al. 2023). When poorly resolved trees were used as input, models like the Dated Resolved-Model and Dated Polytomous-Model showed excellent performance, suggesting their potential for effective and accurate R0 and 1/γ predictions from sequence data. This offers a promising avenue for tracking epidemic dynamics using sequence data, which, when compared with epidemiological records, can provide deeper insights and mitigate potential sampling biases. Future investigations are needed to ascertain the extent to which sequence data can facilitate robust predictions and to evaluate the effects of progressively incorporating new sequence samples.
Our study acknowledges certain limitations. Notably, the BDSS model does not account for the incubation period of the disease, introducing a significant source of uncertainty. The omission of the incubation period from our transmission models necessitates further exploration in future studies to mitigate these uncertainties. For example, an alternative approach could use a Susceptible-Exposed-Infected-Recovered model with a superspreading compartment, grounded in structured coalescent theory (Volz and Siveroni 2018), which has been used to study superspreading and nonlinear incidence in SARS-CoV-2 studies (Miller et al. 2020; Moreno et al. 2020; Geidelberg et al. 2021; Ragonnet-Cronin et al. 2021). Additionally, real-world contact tracing data may contain inherent biases and inaccuracies. In applying our model to the SARS-CoV-2 data set from Hong Kong, we presumed the accuracy of the contact tracing data. This assumption allowed us to collapse all associated children (see Materials and Methods), including those are not recorded within the cluster, potentially leading to an inaccurate refinement of the tree topology and biased predictions. Our primary epidemiological inference of R0 assumed a comparable SIR model of transmission and an exponentially distributed generation time like BDSS, though tended to be slightly higher than the mean R0 estimated from PhyloDeep (Table 1). This method, which links the initial growth rate of an epidemic to R0 (Wallinga and Lipsitch 2007) is however known to exhibit a slight upward bias for smaller R0 values (R0 < 2) (Obadia et al. 2012). Further sensitivity analyses assuming gamma-distributed generation times, unlike BDSS, resulted in even higher values R0, partially validating the results from our Dated Baseline-Model with Dated Resolved-Cluster tree (supplementary table S8, Supplementary Material online).
Importantly, making trees poorly resolved during training hinges on the specific sequence length and evolution rate of SARS-CoV-2, rendering the neural networks trained in this study inapplicable to other viruses. To extend their use to other pathogens, modifications are required to accommodate variations in sequence length and evolution rate, training pathogen-specific neural networks as we show for SARS-CoV-2. This contrasts with PhyloDeep, which was designed for studying a diverse array of pathogens. Correspondingly, the choice of a specific birth–death model emerges as another crucial factor that must be carefully considered.
Overall, this study highlights the challenges of relying solely on viral phylogenetic trees generated from sequences for estimating superspreading events. The integration of even minimal contact tracing data can significantly enhance model predictions, emphasizing the importance of such data in surveillance efforts for emerging infectious diseases, particularly when viral sequences lack variability. We hope our comprehensive evaluation will not only enhance deep learning applications but also extend beyond, enriching established methodologies within phylogenetics and phylodynamics.
Materials and Methods
Simulations
In this study, SARS-CoV-2 served as the reference pathogen for evaluating the performance of the existing deep learning model PhyloDeep. Given the marked overdispersion in SARS-CoV-2 transmission dynamics, characterized by superspreading (Adam et al. 2020; Du et al. 2022; Guo et al. 2022), we used treesimulator (v0.1.7; Zhukova and Gascuel 2024) to generate time-scaled phylogenetic trees (detailed in supplementary table S1, Supplementary Material online). These trees were generated with a BDSS model, distinguishing cases into superspreaders (S) and normal spreaders (N), in addition to the conventional parameterization of the birth–death model, i.e. R0 and 1/γ. Superspreaders constitute a small fraction of the total simulated population [denoted by ] but can transmit the virus at rates significantly higher than normal spreaders, where the superspreading transmission ratio is denoted as . Upon reviewing the 98 SSs (see details in the Feature Representation and Neural Network Models section), it was noted that certain metrics associated with branch lengths and superspreading events based on the SARS-CoV-2 data set from Hong Kong fell outside the [min, max] range of simulated values in PhyloDeep, characterized by a lower median/mean SS and increased variance SS (detailed in supplementary table S7, Supplementary Material online). Consequently, to better capture the complexities of SARS-CoV-2 transmission dynamics, we expanded the range of epidemiological parameters for tree simulation in PhyloDeep, summarized in supplementary table S1, Supplementary Material online.
Simulated time-scaled trees are transformed into Genetic Baseline Trees, with branch lengths determined by a binomial process, B (n = sequence length, p = evolutionary rate × branch length of time-scaled trees). For SARS-CoV-2, the sequence length is 29,903, and the evolutionary rate has a mean of 8 × 10−4 and a standard deviation of 4 × 10−4 substitutions per site per year, with a lognormal distribution (Hadfield et al. 2018; Jolly and Scaria 2021). In Genetic Baseline Trees, branches representing zero mutation are collapsed to form Genetic Polytomous Trees. Within these trees, polytomies are resolved by randomly coalescing two offspring until binary trees, termed Genetic Resolved Trees, are obtained. These genetic distances are then redated using LSD2 (To et al. 2016), assigning dates to the tips by adding the lengths from the tips to the root within the time-scaled trees to a dummy date designated as the root date. Additionally, a temporal constraint for the root is established by setting a range (dummy date − 1 d, dummy date + 1 d), ensuring the root’s time is not excessively early. The clock rate used is the same as mentioned above, with a mean of 8 × 10−4 and a standard deviation of 4 × 10−4 substitutions per site per year.
Additional 100,000 trees were simulated, and the PhyloDeep methodology was applied to establish the 95% CIs.
Feature Representation and Neural Network Models
We represent time-scaled phylogenetic trees using sampling probability and 98 SSs, as employed in PhyloDeep (Saulnier et al. 2017; Voznica et al. 2022). However, for genetic distance trees, certain concepts like transmission chains (14 SSs) associated with superspreading and lineage through time (49 SSs) are not directly applicable. To address this, we designed 62 SSs to capture the distribution of nodes in the phylogenetic tree: 31 SSs for internal nodes (nonleaf nodes within the tree structure, corresponding to transmission events) and 31 SSs for external nodes (leaves of the tree, corresponding to sampling events), by counting the nodes that are n (0 to 30) mutations away from the tree root. Additionally, we included 10 SSs related to the size distribution of clusters of identical sequences. These counts capture the number of clusters for each size from 1 to 9, with a combined count for clusters larger than 9, reflecting the underlying transmission dynamics and heterogeneity (Tran-Kiem and Bedford 2024). Consequently, 90 SSs are utilized to characterize the genetic distance tree. While time-scaled trees are rescaled so the average branch length equals 1 prior to representation (Voznica et al. 2022), genetic distance trees do not require this adjustment.
Following the PhyloDeep methodology, we implemented our neural network model using Python 3.6, with the Tensorflow 1.5.0, Keras 2.2.4, and scikit-learn 0.19.1 libraries. We partitioned 200,000 simulated phylogenetic trees into 190,000 for training, 9,000 for validation, and 1,000 for testing. The network architecture includes an input layer with either 99 or 90 nodes, followed by four sequential hidden layers arranged in a funnel shape with 64, 32, 16, and 8 neurons, respectively, and an output layer that predicts the four parameters of the BDSS model (R0, 1/γ, Xss, and fss). We experimented with adding or removing hidden layers in the Baseline-Model, which did not improve accuracy. The neurons in the last hidden layer utilize linear activation, whereas the others employ exponential linear (ELU) activation. The model employs the Adam optimization algorithm and uses mean absolute percentage error (MAPE) as the loss function, with a batch size of 200 and a maximum of 1,000 epochs. Early stopping, with a patience value of 50, was used to prevent overfitting based on MAPE performance on the validation set. A dropout rate of 0.5 was applied in the hidden layers, and variations in dropout rates between 0.3 and 0.7 did not enhance the Baseline-Model's accuracy. The performance of our neural network models is assessed as the MRE of the estimator:
where n is the number of simulated trees used in the test set.
To draw a parallel with epidemiological inference, Xss and fss can be transformed into the dispersion k. Utilizing the multitype birth–death model process (Stadler and Bonhoeffer 2013), it becomes possible to estimate the probability of an individual infecting “n” others over its lifespan, aligning with a geometric distribution. By synthesizing the probability with the cumulative number of infections, the offspring distribution was ascertained. The approach outlined in the Estimating R0 and k from Epidemiological Data Only section was employed to derive k from this offspring distribution.
Integration of Contact Tracing Data into Phylogenetic Trees
In our simulations, we utilize time-scaled trees to derive contact tracing data, treating all descendants of each internal node as a single cluster, with the node’s age representing the infection time (supplementary fig. S3, Supplementary Material online). Using such contact tracing data, we refine the phylogenetic trees by identifying the most recent common ancestor (MRCA) for each cluster. We then iterate through children of the MRCA and coalesce all associated children, encompassing both leaves and children of internal nodes within the cluster. This process enables us to resolve polytomies in Genetic Polytomous Trees, facilitating their transformation back into Genetic Baseline Trees (supplementary fig. S2, Supplementary Material online).
Additionally, by applying the infection times as time constraints on the internal nodes, we can revert Genetic Baseline Trees to their Baseline counterparts using LSD2 (To et al. 2016). We achieve this by setting a specific time range for the internal nodes, using a margin of (infection time − 1 d, infection time + 1 d). Narrowing this margin to 0.1 d brings the converted trees even closer to the Baseline trees, thereby yielding performance on the Baseline-Model that is nearly identical to that obtained when directly using Baseline trees for testing, as detailed in supplementary tables S2 and S3, Supplementary Material online.
SARS-CoV-2 Data Set in Hong Kong
We used sequences and epidemiological data from the third and fourth waves of SARS-CoV-2 in Hong Kong, as detailed in our prior study (Gu et al. 2022). These waves were characterized by single introduction events that sparked local transmissions, and they were notable for their relatively consistent sequence sampling and comprehensive surveillance data. In this study, we focused on the exponential stages of waves 3 and 4, which spanned from 2020 May 13 to August 1, with 460 sequences and 1,930 local cases, and from 2020 September 30 to December 8, with 243 sequences and 1,577 local cases, respectively. The sampling rates for waves 3 and 4 were 23.8% and 15.4%, respectively. During wave 3, 84.35% (388 out of 460) of sequences were linked to cluster information involving 191 clusters, among which 76 clusters comprised more than one sequence. This indicates that 16.56% (76 out of 459) of the data were supported by contact tracing. In wave 4, 90.53% (220 out of 243) of sequences were associated with 35 clusters, with 23 clusters containing multiple sequences, amounting to 9.50% (23 out of 242) contact tracing data availability.
For waves 3 and 4, we reconstructed ML phylogenies using RAxML-NG (Kozlov et al. 2019) with the GTR + G4 +FO substitution model. We maintained consistency with simulated trees in terms of collapsing internal nodes and the random resolution of polytomies. Our findings revealed that the distribution of the number of offspring from collapsed internal nodes falls within the range observed in our simulations (supplementary fig. S1, Supplementary Material online). Subsequently, these trees were dated using LSD2 (To et al. 2016), following a strict molecular clock assumption of 8 × 10−4 substitutions per site per year (Hadfield et al. 2018; Jolly and Scaria 2021), and applying time constraints for the root as inferred by Gu et al. (2022).
Estimating R0 and k from Epidemiological Data Only
We compared the results for R0 and k estimated using our deep learning models to those estimated from line-list data on SARS-CoV-2 available during the exponential periods of waves 3 and 4 in Hong Kong. Comparable estimates of R0 were estimated as per methods described in Wallinga and Lipsitch (2007) and implemented in the R package R0 (Obadia et al. 2012) that assumes an SIR model of transmission like BDSS. We used line-listed incidence data of SARS-CoV-2 symptom onset dates and an exponential generation time distribution also like BDSS (mean = 5.7, SD = 1.8; Hu et al. 2021) with results listed in Table 1. Additional sensitivity analyses were conducted assuming alternative parameterizations of the generation time (mean = 7.27, SD = 3.81; Chen et al. 2022), and/or a gamma-distributed generation time are summarized in supplementary table S8, Supplementary Material online.
Epidemiological estimates of k were generated by constructing empirical offspring distributions from contact tracing data on SARS-CoV-2 available from previous studies in Hong Kong (Adam et al. 2022). These distributions were generated from infector–infectee pairs, where the number of secondary cases is counted for each unique infector and includes chain-terminating infectees as zero. We subsetted the empirical offspring distributions to the same exponential periods for wave 3 and wave 4 as before, given the estimated infection date of each paired case as a deconvolution of the generation time, incubation period, and delay distributions given the onset date or report dates if asymptomatic between infector–infectee pairs. Importantly, offspring counts were not artificially right censored, meaning the observed count of each infector case was included even if the estimated infection date of paired infectee(s) fell outside the exponential periods of each wave. Following the approach of Lloyd-Smith et al. (2005), k is estimated directly from the finalized offspring distributions by ML estimation, assuming a negative binomial model jointly parameterized by the mean and dispersion parameter k, with 95% intervals generated by nonparametric bootstrap estimation sampling 1,000 replicates with replacement.
Parameter Inference Comparison with BEAST2
We assessed the predictive performance of the Dated Baseline-Model and Baseline-Model against the well-established Bayesian structured birth–death model, implemented via the bdmm package (Scire et al. 2022) in BEAST2 (Bouckaert et al. 2014) (version 2.6.2). We applied the same priors as used in PhyloDeep (Voznica et al. 2022), maintaining the equality and fixing the sampling proportion and tree topology during parameter estimation. Markov chain Monte Carlo analysis was run for 10 million steps, sampling every 1,000 steps with a 10% as burn-in, and effective sample size values were assessed using Tracer (Rambaut et al. 2018). The analysis was conducted on 100 simulated Genetic Polytomous Trees incorporating varying levels of contact tracing data (0%, 50%, and 100%) to facilitate transforming the input trees back into Baseline and Dated Baseline Trees, the latter using only cluster information. Additionally, we conducted the BEAST2 analysis on the Hong Kong data sets, which produced different estimations (supplementary table S9, Supplementary Material online). However, the poor performance in our simulation analysis without contact tracing data, or when only incorporating cluster information, along with the limited cluster data available in the Hong Kong data sets, was insufficient to meaningfully improve predictions.
Supplementary Material
Acknowledgments
We acknowledge the technical support provided by colleagues from the Centre for PanorOmic Sciences of the University of Hong Kong. We also acknowledge the Centre for Health Protection of the Department of Health for providing epidemiological data for the study. The computations were performed using research computing facilities offered by Information Technology Services, the University of Hong Kong. The funding bodies had no role in the design of the study and collection, analysis, and interpretation of data and writing of the manuscript. The work described in this paper was substantially supported by a fellowship award from the Research Grants Council of the Hong Kong Special Administrative Region, China (Project No. HKU PDFS2425-7S01).
Contributor Information
Ruopeng Xie, School of Public Health, LKS Faculty of Medicine, The University of Hong Kong, Hong Kong S.A.R., China; HKU-Pasteur Research Pole, School of Public Health, LKS Faculty of Medicine, The University of Hong Kong, Hong Kong S.A.R., China.
Dillon C Adam, School of Public Health, LKS Faculty of Medicine, The University of Hong Kong, Hong Kong S.A.R., China.
Shu Hu, School of Public Health, LKS Faculty of Medicine, The University of Hong Kong, Hong Kong S.A.R., China; HKU-Pasteur Research Pole, School of Public Health, LKS Faculty of Medicine, The University of Hong Kong, Hong Kong S.A.R., China.
Benjamin J Cowling, School of Public Health, LKS Faculty of Medicine, The University of Hong Kong, Hong Kong S.A.R., China; Laboratory of Data Discovery for Health, Hong Kong Science and Technology Park, New Territories, Hong Kong S.A.R., China.
Olivier Gascuel, Biologie intégrative des populations, Evolution moléculaire (BIPEM), Institut de Systématique, Evolution, Biodiversité (ISYEB, UMR 7205—CNRS, MNHN, SU, EPHE, UA), Muséum National d’Histoire Naturelle, Paris 75005 France.
Anna Zhukova, Bioinformatics and Biostatistics Hub, Institut Pasteur, Université de Paris, Paris 75015, France; G5 Evolutionary Dynamics of Infectious Diseases, Institut Pasteur, Université de Paris, Paris 75015, France.
Vijaykrishna Dhanasekaran, School of Public Health, LKS Faculty of Medicine, The University of Hong Kong, Hong Kong S.A.R., China; HKU-Pasteur Research Pole, School of Public Health, LKS Faculty of Medicine, The University of Hong Kong, Hong Kong S.A.R., China.
Supplementary Material
Supplementary material is available at Molecular Biology and Evolution online.
Funding
National Institutes of Health contract number 75N93021C00016 (V.D.). Research Grants Council of the Hong Kong Special Administrative Region, China (Project No. T11-705/21-N) (V.D.). The Collaborative Research Scheme (Project No. C7123-20G) of the Research Grants Council of the Hong Kong Special Administrative Region, China (B.J.C., D.C.A.). Health and Medical Research Fund Seed Grant Scheme (Project No. 22211192) of the Hong Kong Special Administrative Region, China (D.C.A.). HKU-Pasteur Research Pole Fellowship 2023 (S-AC23005-01) (R.X.). Research Grants Council of the Hong Kong Special Administrative Region, China (Project No. HKU PDFS2425-7S01) (R.X.). PaRis AI Research InstitutE (PRAIRIE; ANR-19-P3IA-0001) (O.G.).
Data Availability
All anonymized data, code, and analysis files are available in the GitHub repository (https://github.com/vjlab/dl-phylodynamics-ct).
References
- Adam D, Gostic K, Tsang T, Wu P, Lim WW, Yeung A, Chen D, et al. Time-varying transmission heterogeneity of SARS and COVID-19 in Hong Kong. Res Sq. 10.21203/rs.3.rs-1407962/v1, 2022, preprint: not peer reviewed. [DOI] [Google Scholar]
- Adam DC, Wu P, Wong JY, Lau EHY, Tsang TK, Cauchemez S, Leung GM, Cowling BJ. Clustering and superspreading potential of SARS-CoV-2 infections in Hong Kong. Nat Med. 2020:26(11):1714–1719. 10.1038/s41591-020-1092-0. [DOI] [PubMed] [Google Scholar]
- Bouckaert R, Heled J, Kühnert D, Vaughan T, Wu C-H, Xie D, Suchard MA, Rambaut A, Drummond AJ. BEAST 2: a software platform for Bayesian evolutionary analysis. PLoS Comput Biol. 2014:10(4):e1003537. 10.1371/journal.pcbi.1003537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen D, Lau Y-C, Xu X-K, Wang L, Du Z, Tsang TK, Wu P, Lau EHY, Wallinga J, Cowling BJ, et al. Inferring time-varying generation time, serial interval, and incubation period distributions for COVID-19. Nat Commun. 2022:13(1):7727. 10.1038/s41467-022-35496-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond AJ, Rambaut A, Shapiro B, Pybus OG. Bayesian coalescent inference of past population dynamics from molecular sequences. Mol Biol Evol. 2005:22(5):1185–1192. 10.1093/molbev/msi103. [DOI] [PubMed] [Google Scholar]
- Du Z, Wang C, Liu C, Bai Y, Pei S, Adam DC, Wang L, Wu P, Lau EHY, Cowling BJ. Systematic review and meta-analyses of superspreading of SARS-CoV-2 infections. Transbound Emerg Dis. 2022:69(5):e3007–e3014. 10.1111/tbed.14655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eden J-S, Sikazwe C, Xie R, Deng Y-M, Sullivan SG, Michie A, Levy A, Cutmore E, Blyth CC, Britton PN, et al. Off-season RSV epidemics in Australia after easing of COVID-19 restrictions. Nat Commun. 2022:13(1):2884. 10.1038/s41467-022-30485-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Featherstone LA, Duchene S, Vaughan TG. Decoding the fundamental drivers of phylodynamic inference. Mol Biol Evol. 2023:40(6). 10.1093/molbev/msad132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geidelberg L, Boyd O, Jorgensen D, Siveroni I, Nascimento FF, Johnson R, Ragonnet-Cronin M, Fu H, Wang H, Xi X, et al. Genomic epidemiology of a densely sampled COVID-19 outbreak in China. Virus Evol. 2021:7(1):veaa102. 10.1093/ve/veaa102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu H, Xie R, Adam DC, Tsui JL-H, Chu DK, Chang LDJ, Cheuk SSY, Gurung S, Krishnan P, Ng DYM, et al. Genomic epidemiology of SARS-CoV-2 under an elimination strategy in Hong Kong. Nat Commun. 2022:13(1):736. 10.1038/s41467-022-28420-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guindon S, Dufayard J-F, Lefort V, Anisimova M, Hordijk W, Gascuel O. New algorithms and methods to estimate maximum-likelihood phylogenies: assessing the performance of PhyML 3.0. Syst Biol. 2010:59(3):307–321. 10.1093/sysbio/syq010. [DOI] [PubMed] [Google Scholar]
- Guo Z, Zhao S, Lee SS, Mok CKP, Wong NS, Wang J, Jia KM, Wang MH, Yam CHK, Chow TY, et al. Superspreading potential of COVID-19 outbreak seeded by Omicron variants of SARS-CoV-2 in Hong Kong. J Travel Med. 2022:29:taac049. 10.1093/jtm/taac049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hadfield J, Megill C, Bell SM, Huddleston J, Potter B, Callender C, Sagulenko P, Bedford T, Neher RA. Nextstrain: real-time tracking of pathogen evolution. Bioinformatics. 2018:34(23):4121–4123. 10.1093/bioinformatics/bty407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hohna S, Drummond AJ. Guided tree topology proposals for Bayesian phylogenetic inference. Syst Biol. 2012:61(1)(1):1–11. 10.1093/sysbio/syr074. [DOI] [PubMed] [Google Scholar]
- Hu S, Wang W, Wang Y, Litvinova M, Luo K, Ren L, Sun Q, Chen X, Zeng G, Li J, et al. Infectivity, susceptibility, and risk factors associated with SARS-CoV-2 transmission under intensive contact tracing in Hunan, China. Nat Commun. 2021:12(1):1533. 10.1038/s41467-021-21710-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jolly B, Scaria V. Computational analysis and phylogenetic clustering of SARS-CoV-2 genomes. Bio Protoc. 2021:11(8):e3999. 10.21769/BioProtoc.3999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozlov AM, Darriba D, Flouri T, Morel B, Stamatakis A. RAxML-NG: a fast, scalable and user-friendly tool for maximum likelihood phylogenetic inference. Bioinformatics. 2019:35(21):4453–4455. 10.1093/bioinformatics/btz305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhnert D, Stadler T, Vaughan TG, Drummond AJ. Phylodynamics with migration: a computational framework to quantify population structure from genomic data. Mol Biol Evol. 2016:33(8):2102–2116. 10.1093/molbev/msw064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambert S, Voznica J, Morlon H. Deep learning from phylogenies for diversification analyses. Syst Biol. 2023:72(6):1262–1279. 10.1093/sysbio/syad044. [DOI] [PubMed] [Google Scholar]
- Leventhal GE, Gunthard HF, Bonhoeffer S, Stadler T. Using an epidemiological model for phylogenetic inference reveals density dependence in HIV transmission. Mol Biol Evol. 2014:31(1):6–17. 10.1093/molbev/mst172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis PO, Holder MT, Holsinger KE. Polytomies and Bayesian phylogenetic inference. Syst Biol. 2005:54(2):241–253. 10.1080/10635150590924208. [DOI] [PubMed] [Google Scholar]
- Lloyd-Smith JO, Schreiber SJ, Kopp PE, Getz WM. Superspreading and the effect of individual variation on disease emergence. Nature. 2005:438(7066):355–359. 10.1038/nature04153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller D, Martin MA, Harel N, Tirosh O, Kustin T, Meir M, Sorek N, Gefen-Halevi S, Amit S, Vorontsov O, et al. Full genome viral sequences inform patterns of SARS-CoV-2 spread into and within Israel. Nat Commun. 2020:11(1):5518. 10.1038/s41467-020-19248-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morel B, Barbera P, Czech L, Bettisworth B, Hübner L, Lutteropp S, Serdari D, Kostaki E-G, Mamais I, Kozlov AM, et al. Phylogenetic analysis of SARS-CoV-2 data is difficult. Mol Biol Evol. 2021:38(5):1777–1791. 10.1093/molbev/msaa314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno GK, Braun KM, Riemersma KK, Martin MA, Halfmann PJ, Crooks CM, Prall T, Baker D, Baczenas JJ, Heffron AS, et al. Revealing fine-scale spatiotemporal differences in SARS-CoV-2 introduction and spread. Nat Commun. 2020:11(1):5558. 10.1038/s41467-020-19346-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen LT, Schmidt HA, von Haeseler A, Minh BQ. IQ-TREE: a fast and effective stochastic algorithm for estimating maximum-likelihood phylogenies. Mol Biol Evol. 2015:32(1):268–274. 10.1093/molbev/msu300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Obadia T, Haneef R, Boelle PY. The R0 package: a toolbox to estimate reproduction numbers for epidemic outbreaks. BMC Med Inform Decis Mak. 2012:12(1):147. 10.1186/1472-6947-12-147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paredes MI, Ahmed N, Figgins M, Colizza V, Lemey P, McCrone JT, Müller N, Tran-Kiem C, Bedford T. Underdetected dispersal and extensive local transmission drove the 2022 mpox epidemic. Cell. 2024:187(6):1374–1386.e13. 10.1016/j.cell.2024.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pekar JE, Magee A, Parker E, Moshiri N, Izhikevich K, Havens JL, Gangavarapu K, Malpica Serrano LM, Crits-Christoph A, Matteson NL, et al. The molecular epidemiology of multiple zoonotic origins of SARS-CoV-2. Science. 2022:377(6609):960–966. 10.1126/science.abp8337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price MN, Dehal PS, Arkin AP. FastTree 2—approximately maximum-likelihood trees for large alignments. PLoS One. 2010:5(3):e9490. 10.1371/journal.pone.0009490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragonnet-Cronin M, Boyd O, Geidelberg L, Jorgensen D, Nascimento FF, Siveroni I, Johnson RA, Baguelin M, Cucunubá ZM, Jauneikaite E, et al. Genetic evidence for the association between COVID-19 epidemic severity and timing of non-pharmaceutical interventions. Nat Commun. 2021:12(1):2188. 10.1038/s41467-021-22366-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rambaut A, Drummond AJ, Xie D, Baele G, Suchard MA. Posterior summarization in Bayesian phylogenetics using Tracer 1.7. Syst Biol. 2018:67(5):901–904. 10.1093/sysbio/syy032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sagulenko P, Puller V, Neher RA. TreeTime: maximum-likelihood phylodynamic analysis. Virus Evol. 2018:4(1):vex042. 10.1093/ve/vex042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saulnier E, Gascuel O, Alizon S. Inferring epidemiological parameters from phylogenies using regression-ABC: a comparative study. PLoS Comput Biol. 2017:13(3):e1005416. 10.1371/journal.pcbi.1005416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scire J, Barido-Sottani J, Kühnert D, Vaughan TG, Stadler T. Robust phylodynamic analysis of genetic sequencing data from structured populations. Viruses. 2022:14(8):1648. 10.3390/v14081648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadler T, Bonhoeffer S. Uncovering epidemiological dynamics in heterogeneous host populations using phylogenetic methods. Philos Trans R Soc Lond B Biol Sci. 2013:368(1614):20120198. 10.1098/rstb.2012.0198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadler T, Kouyos R, von Wyl V, Yerly S, Böni J, Bürgisser P, Klimkait T, Joos B, Rieder P, Xie D, et al. Estimating the basic reproductive number from viral sequence data. Mol Biol Evol. 2012:29(1):347–357. 10.1093/molbev/msr217. [DOI] [PubMed] [Google Scholar]
- Stadler T, Kuhnert D, Bonhoeffer S, Drummond AJ. Birth-death skyline plot reveals temporal changes of epidemic spread in HIV and hepatitis C virus (HCV). Proc Natl Acad Sci U S A. 2013:110(1):228–233. 10.1073/pnas.1207965110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson A, Liebeskind B, Scully EJ, Landis M. Deep learning and likelihood approaches for viral phylogeography converge on the same answers whether the inference model is right or wrong. Syst Biol. 2024:73(1):183–206. 10.1093/sysbio/syad074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- To TH, Jung M, Lycett S, Gascuel O. Fast dating using least-squares criteria and algorithms. Syst Biol. 2016:65(1):82–97. 10.1093/sysbio/syv068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tran-Kiem C, Bedford T. Estimating the reproduction number and transmission heterogeneity from the size distribution of clusters of identical pathogen sequences. Proc Natl Acad Sci U S A. 2024:121(15):e2305299121. 10.1073/pnas.2305299121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughan TG, Scire J, Nadeau SA, Stadler T. Estimates of early outbreak-specific SARS-CoV-2 epidemiological parameters from genomic data. Proc Natl Acad Sci U S A. 2024:121(2):e2308125121. 10.1073/pnas.2308125121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volz EM, Kosakovsky Pond SL, Ward MJ, Leigh Brown AJ, Frost SD. Phylodynamics of infectious disease epidemics. Genetics. 2009:183(4):1421–1430. 10.1534/genetics.109.106021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volz EM, Siveroni I. Bayesian phylodynamic inference with complex models. PLoS Comput Biol. 2018:14(11):e1006546. 10.1371/journal.pcbi.1006546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voznica J, Zhukova A, Boskova V, Saulnier E, Lemoine F, Moslonka-Lefebvre M, Gascuel O. Deep learning from phylogenies to uncover the epidemiological dynamics of outbreaks. Nat Commun. 2022:13(1):3896. 10.1038/s41467-022-31511-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallinga J, Lipsitch M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proc Biol Sci. 2007:274(1609):599–604. 10.1098/rspb.2006.3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells CR, Townsend JP, Pandey A, Moghadas SM, Krieger G, Singer B, McDonald RH, Fitzpatrick MC, Galvani AP. Optimal COVID-19 quarantine and testing strategies. Nat Commun. 2021:12(1):356. 10.1038/s41467-020-20742-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worobey M, Han GZ, Rambaut A. Genesis and pathogenesis of the 1918 pandemic H1N1 influenza A virus. Proc Natl Acad Sci U S A. 2014:111(22):8107–8112. 10.1073/pnas.1324197111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhukova A, Gascuel O. Accounting for partner notification in epidemiological birth-death-models. medRxiv, 2024.2009.2009.24313296. 10.1101/2024.09.09.24313296, 2024, preprint: not peer reviewed. [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All anonymized data, code, and analysis files are available in the GitHub repository (https://github.com/vjlab/dl-phylodynamics-ct).