The FoldX web server: an online force field

Abstract

FoldX is an empirical force field that was developed for the rapid evaluation of the effect of mutations on the stability, folding and dynamics of proteins and nucleic acids. The core functionality of FoldX, namely the calculation of the free energy of a macromolecule based on its high-resolution 3D structure, is now publicly available through a web server at http://foldx.embl.de/. The current release allows the calculation of the stability of a protein, calculation of the positions of the protons and the prediction of water bridges, prediction of metal binding sites and the analysis of the free energy of complex formation. Alanine scanning, the systematic truncation of side chains to alanine, is also included. In addition, some reporting functions have been added, and it is now possible to print both the atomic interaction networks that constitute the protein, print the structural and energetic details of the interactions per atom or per residue, as well as generate a general quality report of the pdb structure. This core functionality will be further extended as more FoldX applications are developed.

INTRODUCTION

A wide range of strategies for estimating protein energetics exists, ranging from methods based on the statistical analysis of known protein structures at one extreme, to more physically based methods, at the other. These are designated by Lazaridis and Karplus (1) as statistical (SEEF) and physical (PEEF) effective energy functions, respectively. A third class of methods, based mainly on empirical data derived from experimental work on proteins, called EEEF, for empirical effective energy functions, are also widely used (2). The FoldX force field (FOLDEF) belongs to this group and was developed for the fast and accurate estimation of mutational free energy changes on the stability of a protein, or a protein complex (3). It was also successfully applied to the prediction of protein folding pathways in a Gō-like approach (4–6). FoldX aims to describe the energetic contributions to protein stability in simple empirical terms that allow easy interpretation by non-specialists. It is thus geared at high-throughput structural biocomputing tasks, such as screening the effect of SNPs on protein stability (7) or in silico drug lead screening. Here we present the FoldX web server, which provides free access to a selection of FoldX-based structural analysis tools.

MATERIALS AND METHODS

The FoldX web server is hosted on IBM X35 server, with 2 Xeon 2.4 GHz processors and 2 GB RAM. The operating system is Redhat Linux 9.0, the web server is Tomcat 5.0.25 and the database engine is postgreSQL 7.4.1.

The ScienceHost framework for hosting scientific prediction algorithms on the World Wide Web is a database driven application composed of three layers. (i) The prediction algorithm is installed on the same machine as the web server or on a more powerful calculation cluster. (ii) On the same computer as the first layer, a calculation server application is installed that can accept commands from the web server and control the algorithm accordingly. The only requirement is that the scientific software needs to be command line controllable. (iii) On the web server a Java-servlet based application is installed that reads information about commands, options and users from an SQL database and displays them in HTML to the user. In this way, a general framework is created that can rapidly be configured to host different applications.

THE FoldX FORCE FIELD

The details of the FoldX calculation fall outside the scope of this manuscript. However, we present a brief overview that should allow the user to interpret the results obtained from the web server. The following linear combination of empirical terms is used to calculate free energy (in kcal mol⁻¹) by FoldX.

$$\begin{array}{c}\Delta G=a\cdot \Delta G_{\text{vdw}}+b\cdot \Delta G_{\text{solvH}}+c\cdot \Delta G_{\text{solvP}}+d\cdot \Delta G_{\text{wb}}\\ +e\cdot \Delta G_{\text{hbond}}+f\cdot \Delta G_{\text{el}}+g\cdot \Delta G_{\text{kon}}+h\cdot \text{T}\Delta {\text{S}}_{\text{mc}}\\ +k\cdot \text{T}\Delta {\text{S}}_{\text{sc}}+l\cdot \Delta G_{\text{clash}}.\end{array}$$

In this expression (a…l) are relative weights of the different energy terms used for the free energy calculation. The interaction with the solvent is treated in two steps: first, the bulk solvent is treated as a desolvation term that is continuously scaled with the burial of an atom and separated into contributions from hydrophobic (ΔG_solvH) and polar (ΔG_solvP)groups. These solvation parameters have been derived from experiments in which amino acids are transferred from water to an organic solvent, this is assumed to mimic the transition that is experienced by an amino acid during folding from solvent exposure in the unfolded state to burial in a hydrophobic environment in the native state. In addition, those water molecules that have a persistent interaction with groups of the protein, i.e. make more than two hydrogen bonds with the protein, are calculated explicitly in the ΔG_wb term (8,9). The combination of a continuous solvation scale with an explicit consideration of the essential water molecules allows fast calculations while providing essential details. The Van der Waals terms, ΔG_vdw, is calculated in a similar fashion to the desolvation, but now taking into account experimental transfer energies from water to vapour. Hydrogen bonds are calculated on the basis of simple geometric considerations and their energy, ΔG_hbond, is inferred from protein engineering double mutant cycles. The electrostatic contribution to the free energy, ΔG_el, is calculated from a simple implementation of Coulomb's law, in which the dielectric constant is scaled with the burial of the bond under consideration. Hypothetical atoms are included in the calculations of the Coulombic interactions in order to capture some specific aspects of protein stability: (i) charged atoms are placed at the N- and C-terminal of each α-helix, to obtain some measure of the helix dipole interaction and (ii) aromatic rings carry positive charges on the edges and negative charges above the centre of the ring. For protein complexes, an additional electrostatic contribution is calculated between atoms of different polypeptide chains, ΔG_kon, based on the empirical equation of Schreiber et al. (10), which was shown to give a good estimation of the association rate (k_on) of complex formation. An important difference between FoldX and other force fields is the crude entropy estimation that is used to obtain a measure of the free energy. Entropy calculations usually involve large simulations of the conformational freedom of the side chains and the backbone of the protein. In FoldX the entropic penalty for fixing the backbone in a given conformation, ΔS_mc, is derived from a statistical analysis of the phi–psi distribution of a given amino acid as observed in a set of non-redundant high-resolution crystal structures. This entropy is scaled by (i) the accessibility of the main chain atoms and (ii) energetics of hydrogen bond interactions made by the corresponding residue or its direct neighbours. The entropy cost of fixing a side chain in a particular conformation, ΔS_sc, is obtained by scaling a set entropy parameters calculated by Abagayan and co-workers (11) to the burial of the side chain. Finally, the ΔG_clash term provides a measure of the steric overlaps between atoms in the structure. There are two methods of incorporating the resulting repulsive energy into the FoldX calculation: (i) when analysing point mutations it is recommended to use a soft penalization of the Van der Waals clashes; however, (ii) when doing protein design full penalizations should be applied.

STRENGTHS AND LIMITATIONS

The highest accuracy in the FoldX predictions is achieved when the energy difference can be calculated between two well-defined structures, such as between the wild type and a mutant, or between the bound and unbound forms of a protein complex (to determine the binding free energy). The difference in the calculated free energies (ΔΔG) between the final state (the mutant) and the reference state (the wild-type protein) correlates well with the experimentally observed change in stability. On the other hand, the free energy of folding is calculated from the difference in Gibbs free energy between the detailed 3D structure found in the PDB file and a hypothetical unfolded reference state of which no structural detail is available. The main assumption in this approach is the absence of persistent structure in the denatured state, which in a range of proteins was experimentally shown to be only partly correct. Therefore, although the free energy for folding predicted by the FoldX force field for most small protein domains yields a number between −5.0 and −15 kcal mol⁻¹, this value should not be considered as absolute since it could have large error. Nevertheless, positive energies are normally indicative of problems with the structure under scrutiny and as such, one should bear in mind when using FoldX that the best results are obtained when comparing known structures. Indeed, FoldX was calibrated using experimental mutational free energy changes from a collection of more than 1000 point mutants, covering XX proteins (9), and in its current release yields a correlation of 0.81 with a SD of 0.46 kcal mol⁻¹ between calculated and experimental ΔΔGs.

THE FoldX WEB SERVER

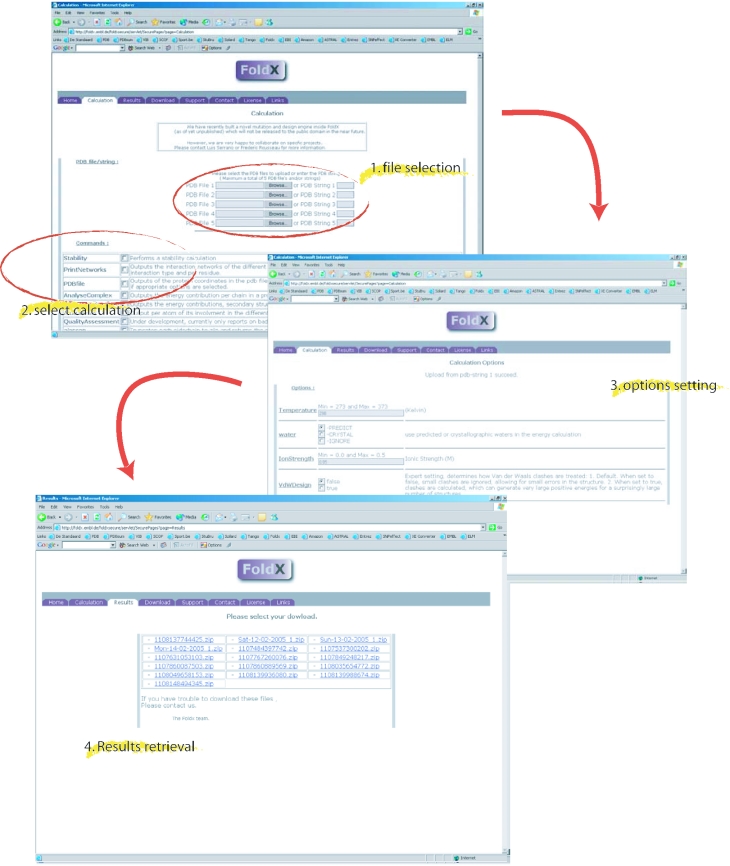
The FoldX web server is located at http://foldx.embl.de/ and requires a password and a login to connect, either as a guest or as a registered user (registration is free). The web engine behind FoldX web server is a general framework for hosting scientific software on the World Wide Web called ScienceHost^© (see Materials and Methods) that also drives the TANGO (12) website (http://TANGO.embl.de/). Besides the web interface, it is also possible to download the executable, allowing analysis on a large scale locally (Figure 1), as well as the manual and the related publications.

Figure 1.

How to set up a calculation in the FoldX web server. After selecting the pdb files by browsing the local pc or by entering the pdb identifier for download from the database, the user selects the calculations through tick boxes. After setting some optional parameters, the web server displays the results for download.

Initiation of a calculation job on the FoldX web server starts with uploading a maximum of five protein structures (pdb files) for simultaneous analysis (Figure 1), either by uploading the pdb files directly from a local computer or by retrieving them from the Brookhaven Protein Data Bank (13) using the four-letter pdb identifier. Protein structures that are selected simultaneously are analysed using identical settings. To apply different settings or analyses, the user needs to initiate several calculations. The different FoldX calculations and analyses to be applied to the uploaded structures can be selected through tick-boxes. The user is then directed to the ‘Options’ tab, where parameters can be set to provide extra control over the calculations (see below and Figure 1). Upon finishing the requested job the FoldX server sends an email notification to the address specified by the user. The email contains a direct link to the results tab, where the user can pick up the output bundled in a single zip-compressed archive (Figure 1). This file will always include at least three text files: error.txt, logfile.txt and a file named yourlogin∼∼youremail∼∼jobnumber∼∼∼runlog.txt. The file error.txt will encompass any error that occurred during the analysis and logfile.txt will contain information about obvious problems in the structure such as Van der Waals clashes and unfavourable dihedral and torsion angles.

OPTIONS

Temperature. The default temperature setting in FoldX is 298 K. Although the parameter can be changed, it should be kept in mind that deviation of >10 K from the default value will not generate relevant results since many of the parameters in FoldX were derived from experiments carried out around this temperature; these include the transfer energies from water to vapour and organic solvents among others. Although some scaling is possible mathematically, one should repeat the basic experiments under different conditions to extend the predictive range of FoldX.

Water. As discussed above, FoldX uses explicit representation of those water molecules that specifically interact with the protein through two or more hydrogen bonds. These water molecules are essential to correctly predict mutational free energy changes near the surface of the protein or in protein–protein or protein–DNA complexes. As the prediction of water bridges slows down the FoldX calculation and the water bridges are not essential to the analysis of amino acid residues in the core of the protein, the Water option allows three settings. (i) With the PREDICT setting, FoldX will predict the water bridges (J.W.H. Schymkowitz, F. Rousseau, I.C. Martins, J. Ferkinghoff-Borg, F. Stricher and L. Serrano, manuscript in preparation). (ii) With the CRYSTAL setting, FoldX reads the positions of the water molecules that are present in the pdb file that make at least two hydrogen bonds with the protein. (iii) With the IGNORE setting, FoldX is instructed not to include explicit consideration of water molecules.

Ionic strength. The ionic strength of the ‘buffer’ surrounding the protein, by default set to 0.05 M, is used in the calculation of the electrostatic interactions. A higher ionic strength will tend to lower the electrostatics on the surface of the protein owing to shielding effects.

VdW design. The steric overlaps between atoms are called Van der Waals clashes. The VdW design option allows two methods for handling these overlaps. (i) When set to false, FoldX will ascribe small overlaps to experimental uncertainties and hence ignore them. For most structures this setting yields reasonable energies. (ii) When set to true, FoldX assigns strong repulsive energies to the overlaps. Although the latter setting is a more accurate representation of the quality of a structure, it should only be applied to structures of the highest quality or for the evaluation of protein design models.

PDB FILES

When selecting pdb files to be used in FoldX calculations, a few considerations should be made: (i) FoldX reads the old style pdb format and currently cannot process files in the mmCIF format. (ii) In general FoldX assigns better free energies and detects less problems in high-resolution crystal structures (resolutions of ∼2.6 Å or better) compared with lower resolution cyrstal structures and most nuclear magnetic resonance (NMR) structures. Although the discrepancy with NMR structures could arguably be due to the overtraining of FoldX parameters on crystallographic structures, our data suggest otherwise as NMR structures that are refined using additional experimental data, such as dipolar couplings, approximate the free energy observed for their crystallographic counterparts (data not shown). (iii) The pdb format is not as standardized as could be expected and FoldX does not correctly read all files due to the variety of deviations that are present in a relatively large amount of structures. Although the pdb-reader in FoldX is continually extended to handle more exceptions, standardizing the format of anomalous files most often solves the problem—this can easily be achieved by opening and saving the file using Swiss PDB viewer (14) or WHATIF (15).

CALCULATIONS AND ANALYSES

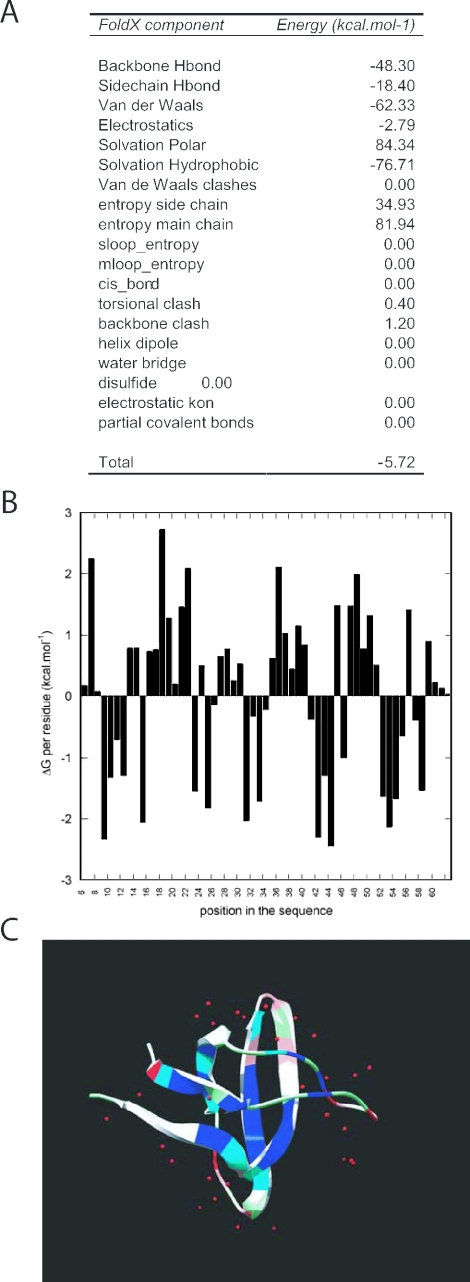
Stability. The most basic analysis performs a free energy calculation and outputs the Gibbs free energy of folding (in kcal mol⁻¹) decomposed in the different energy terms used by FoldX. Apart from the components discussed in Introduction, the following energy terms can be found in the output: Backbone Hbond represents the contribution of hydrogen-bond formation between backbone atoms, all other hydrogen bonds involving at least one side chain atom are summed up in Sidechain Hbond. Van der Waals clashes represent the penalties applied to the overall energy when atoms interpenetrate, i.e. when the distance between two atoms is less than the sum of their Van der Waals radii, resulting in a strong repulsive interaction. These clashes are divided in torsional clash, which arises when a side chain adopts a conformation that causes an overlap between its own atoms or its backbone and Van der Waals clashes, which are the clashes between atoms from different residues. Helix dipole is the electrostatic contribution due to the inclusion of the helix dipole (see above). Disulfide represents the stabilizing energy given by the formation of disulfide bridges, calculated as entropy restrictions in the unfolded state by the logN rule of Creighton (16,17). Partial covalent represents specific bonds between a metal ion and polar or charged atoms in the protein are calculated separately as partial covalent interactions. Entropy complex is a specific entropy cost that arises when the rotational and translational freedom of two protein molecules is restricted in respect to each other due to their binding. The additional entropy cost of complex formation caused by the conformational restriction of backbone or side chains is included in the standard entropy components of FoldX (see above) (Figure 2).

Figure 2.

A typical result of the FoldX web server: a stability analysis of an SH3 domain (1shg). (A) The free energy of folding (the stability) of the protein broken down into the energy components used by FoldX is shown. (B) The contribution of each residue to the stability of the protein and (C) a pdb file colour coded according to the data in (B)—blue indicates highly stable regions and red indicates instable regions.

PrintNetworks. In order to achieve a free energy calculation, FoldX computes per energy component discussed in Introduction an interaction network between all the atoms in the protein. The PrintNetworks command generates seven files, in which all the pairwise interactions in the different networks are listed, grouped by residue and by atom. charge_bonds.txt contains the network of electrostatic interactions, including the energy (in kcal mol⁻¹) assigned to each pairwise electrostatic interaction. contact_bonds.txt describes all the Van der Waals clashes. The penalty applied for each clash is given, either as torsion or as sc_clash, depending if the clash is between atoms of the same residue or between atoms of different residues, respectively. disulfide_bonds.txt is the list of the cysteines involved in disulfide bridges. H_bonds.txt contains the list of hydrogen bonds that are stabilizing the protein; for each bond the acceptor or donor atoms are specified. partcov_bonds.txt contains the list of interactions between metal ions and protein atoms. volumetric_bonds.txt in FoldX, interaction energies are scaled with the solvent accessibility of the atoms involved in the interaction. The solvent accessibility is estimated using the atomic occupancy method (Occ) (18–20) which sums the volumes of the atoms j surrounding a given atom i. The occupancy of an atom i, Occ(i), is calculated using an envelope function (21) with a distance cut-off of 6 Å (9). The numbers produced by this equation approximate closely the results of a surface accessible area calculation, which is traditionally performed by rolling a water molecule over the surface of the protein, but its execution is significantly faster. The list of volumetric bonds contains for each pair of atoms the volume of atom i that is occupied by atom j and vice versa (the occupancy function is not symmetric). In case the PREDICT water options is selected, the list of all existing water bridges is output in water_bonds.txt; this specifies the position of the water molecules as well as the protein atoms by which they are coordinated.

PDBfile. This command prints a pdb-style file with the coordinates of each atom of the protein. FoldX computes the position of all protons associated with the atoms of the protein using a set of canonical coordinates for each type of amino acid. The protons of methyl groups are not included in this computation, since FoldX does not represent them explicitly. As described in Guerois et al. (9) and Schymkowitz et al. (manuscript in preparation), FoldX represents the essential waters in a protein, i.e. the waters making at least two hydrogen bonds with the protein. These so-called water-bridges are computed using a collection of canonical waters for each polar atom of each residue, extracted from positional clustering of water molecules in high resolution crystal structures. If the appropriate options are selected, PDB file also prints the calculated protons and/or the predicted waters.

AnalyseComplex. The interaction between two molecules is driven by the free energy of binding, (ΔG_binding), that is directly related to the thermodynamic dissociation constant (K_d) by the following equation: ΔG_binding = −RT ln(K_d), where R is the gas constant (1.9859 cal mol⁻¹ K⁻¹) and T is the temperature in kelvin. In order to calculate the free energy of binding of a complex AB, FoldX computes the Gibbs energies of the complex (ΔG_AB) and of the two molecules A and B alone. The interaction energy is then given by: ΔG_binding = ΔG_AB − (ΔG_A + ΔG_B). The output contains the ΔG_binding for each pair of polypeptide chains in the pdb file, decomposed into the different energy terms used by FoldX (see above) plus an additional term that reflects the intrachain clashes of residues forming part of the interface. This term needs to be considered since a residue that makes a good interaction with another polypeptide chain could go unnoticed in the analysis above when it adopts a strained conformation: the large clash penalty assigned to the unfavourable conformation would more than compensate for the beneficial interaction energy between the polypeptide chains.

SequenceDetail. For each residue this command generates a detailed list of features, such as contribution to the total free energy computed by FoldX, decomposed in the different energy terms. Furthermore, the burial of the residue is given, divided in main chain and side chain burial. FoldX also outputs the occupancy of the residue, i.e. the volume occupied by protein atoms around the atoms of the side chain or the main chain. Finally, the backbone dihedral angles are given as well as the secondary structure assignment, this is done according to the dssp algorithm (22) that is based on the hydrogen bond pattern, extended with consideration of the dihedral angles. The different secondary structure elements indicated are: E for extended, b for parallel beta-strand, B for anti-parallel beta-strand, a for α-helix, 3 for 3–10 helix and T for turn. In addition, helix capping elements are indicated with c for C-cap and n for N-cap.

AtomDetail. For each atom this command details a list of different characteristics. Among them, the occupancy (ContRat) and the burial (Facc) of each atom are given, as well as some energy terms: the electrostatic interaction (Electro), the clashes this atom have with atoms belonging to the same (torsion) or another residue (VdWClash), the hydrogen bonding energy assigned to this atom if engaged in one (or more) H-bond (Hbond), the energy assigned if the atom is involved in a disulfide bridge (disulfide) and if the atom is at the interface of a complex, the electrostatic contribution of complex formation (energy_kon). Finally, should the atom coordinate a metal ion, the energy assigned to the partially covalent bond (partcov) and the number of such bonds (partcovbonds) are output.

QualityAssessment. A report is generated that lists the most obvious problems detected in the structure, including residues with impossible omega dihedral angles or highly unfavourable backbone dihedral angles or improbable side chain dihedral angles for prolines (χ₁ and χ₂), presence of strong overlaps (Van der Waals clashes) between atoms, as well as missing atoms and gaps in the backbone.

Alascan. The command performs a virtual alanine scanning of the protein and evaluates the direct effect each single point mutation has on the overall stability of the protein. Each position (except glycine and alanine) of the given protein is truncated to Alanine and the position of the neighboring side chains is optimized. The result given is the difference in energy (ΔΔG, in kcal mol⁻¹) between the ‘mutant’ and the ‘wild-type’ structure, decomposed into the FoldX energy terms.

Complex_alascan. This command performs a virtual alanine scanning of the binding surface between two proteins or peptides. The side chains in the interface between the polypeptide chains are systematically mutated to alanine, the rest of the structure is relaxed and the effect of the truncation on the binding energy between the chains is calculated, decomposed into the FoldX energy terms.

FoldX AND OTHER ONLINE RESOURCES

TANGO (11). FoldX is developed for free energy calculations of biological macromolecules based on the full structural detail of their all atom crystal structures. For protein aggregation no such detail is available, although recently the first ever crystal structure of an amyloid fibre was released (23). The crystal structure confirms the widespread observation in the field that protein aggregates are generally rich in cross-beta structure (24), which allows a low-resolution structural approach to predict protein aggregation. The statistical mechanics algorithm TANGO, publicly available at http://TANGO.embl.de/, provides such a predictive model. When calculating the tendency of an amino acid sequence to form β-sheet aggregates, TANGO considers a phase space that encompasses several local structural motifs, as well as the native state. The latter state needs to be included since aggregation may be increased quite dramatically by a mutation that does not alter intrinsic aggregation parameters, such as hydrophobicity or charge, but that alternatively destabilizes the native state of protein. Hence, as one of the input parameters to TANGO, the stability of the native state can be specified. We obtained good results using the changes in protein stability predicted by FoldX as an input for the TANGO algorithm in order to obtain a prediction of aggregation with increased accuracy. In this fashion, TANGO predicts correctly both the disease causing and protective mutations in a wide range of proteins including Alzheimers' Aβ peptide, lysozyme and transthyretin (12).

SNPEffect (7). The base unit of the variability of a genome is the single nucleotide polymorphism (SNP), the change of 1 bp. SNPs hold promise to better our understanding of the differences between individuals in a population, such as responses to medical therapy or allergic reactions. A subset of SNPs cause a non-synonymous codon change in a protein-coding region. A mutation engine has been developed for FoldX, but it is not currently released to the public domain and is awaiting publication. However, the SNPEffect server, located at http://snpeffect.vib.be/, contains the FoldX analysis of the structural effect of human SNPs and disease related point mutations available in the Ensembl database for which a wild-type crystal structure could be retrieved. The repertoire of mutations is continually being extended.