REPPER—repeats and their periodicities in fibrous proteins

Abstract

REPPER (REPeats and their PERiodicities) is an integrated server that detects and analyzes regions with short gapless repeats in protein sequences or alignments. It finds periodicities by Fourier Transform (FTwin) and internal similarity analysis (REPwin). FTwin assigns numerical values to amino acids that reflect certain properties, for instance hydrophobicity, and gives information on corresponding periodicities. REPwin uses self-alignments and displays repeats that reveal significant internal similarities. Both programs use a sliding window to ensure that different periodic regions within the same protein are detected independently. FTwin and REPwin are complemented by secondary structure prediction (PSIPRED) and coiled coil prediction (COILS), making the server a versatile analysis tool for sequences of fibrous proteins. REPPER is available at http://protevo.eb.tuebingen.mpg.de/repper.

INTRODUCTION

Many proteins display repeat patterns in their sequences. The size of these repeats may range from entire domains, such as the IG and FN domains in titin, over subdomain-sized supersecondary structures, such as the α–α hairpins in TPR proteins or the β-meanders in β-propellers, to the short elements making up fibrous proteins, such as coiled coils, collagens and β-helices.

Most currently available repeat detection tools are homology-based and built to identify divergent, gapped repeats of variable length and spacing in the size range of 20 residues and above (i.e. supersecondary structures and domains). For example, SMART (1), Pfam (2), and REP (3) detect repeats by reference to a database of repeat profiles, while REPRO (4) and RADAR (5) detect repeats by aligning the query sequence with itself. None of these methods is suited to detect repeats shorter than ∼20 residues. The profile-based methods do not contain templates for such short elements, while in REPRO short ungapped repeats obtain low scores by virtue of the program using pairwise comparisons to determine significance, and in RADAR such repeats are even explicitly masked out to reduce complexity. Thus, these programs are not useful for analyzing one of the largest classes of repetitive proteins, the fibrous proteins, in which the repeat size is typically <15 residues.

For fibrous proteins the most commonly used tool for analysis is Fourier Transform (FT) (6–11). Indeed, the FORTRAN implementation of this method by McLachlan may have represented the first bioinformatic program for sequence analysis (6). This tool has been widely used, particularly in the analysis of coiled coils, and has proven crucial for deducing properties of the tertiary structure, for example, supercoil handedness (12).

With FT, a string of numerical values representing a protein sequence can be approximated by a linear combination of trigonometric functions with different periodicities. If the function has a certain periodic pattern, the contribution of the trigonometric function with this particular periodicity is greater than the contribution of trigonometric functions with other periodicities. The FT gives the quantities of the contributions as a function of the periodicity. FT is useful in detecting repeats of any size and nature, provided that the analysis is made over a window sufficiently large to include many copies of the repeating unit and that the window contains only repeating units of one type.

In conjunction with programs that predict secondary structure and the occurrence of coiled coils, FT can be very powerful in the analysis of fibrous proteins. In addition, these methods can be usefully complemented by a sequence comparison tool (REPwin), which is conceptually similar to the ones named above, but tailored to detect short consecutive repeats by aligning a sequence to itself, shifted by multiples of a variable offset. We have therefore built a server that implements new versions of FT (FTwin) and sequence self-comparison (REPwin) and combines their output with that of secondary structure prediction (PSIPRED) (13) and coiled coil prediction (COILS) (14–16) into an integrated and detailed overview. The programs are implemented using a sliding window, so as to show the boundaries of periodic regions and allow the detection of multiple regions with different periodicities in the same protein.

COMPONENT PROGRAMS

FTwin

FTwin is a Fourier Transform analysis tool that employs a sliding window of user-defined size (default value 100). A protein sequence is represented by a discrete function of real numbers. Two scales for the analysis of hydrophobic periodicity are provided by the program, one derived from the Kyte–Doolittle hydrophobicity scale (17) and the other reflecting a binary weighting of aliphatic residues. In addition, other scales can be set by the user.

For each periodicity p the corresponding intensity can be calculated as

$$I_p=\frac{1}{W^2}\left[{({\displaystyle \sum _{j=0}^{W-1}}{a}_{j}cos\frac{2\pi j}{p})}^2+{({\displaystyle \sum _{j=0}^{W-1}}{a}_{j}sin\frac{2\pi j}{p})}^2\right],$$ 1

with window size W. For a given sequence (or alignment of sequences) the program returns a graph with the significant periodicities as a function of the position in the sequence. Periodicities are significant if they are above a certain threshold that is defined as μ_i + tσ_i, where μ_i is the average intensity 〈I_p〉 in the window with starting position i, t is the FTwin threshold parameter and σ_i is the standard deviation (SD) of the intensities in window i. The threshold parameter t as well as values for the window size and the periodicity range can be changed via the user interface.

REPwin

Repeat patterns can also be found by sequence self-comparison. REPwin compares a protein sequence with itself, using the Gonnet similarity matrix (18) and a sliding window of user-defined size. It returns a graph (19) which shows regions of significant self-similarities with their corresponding periodicities (Figure 1b). A similarity in the self-alignment is indicative of a region with a periodicity equal to the offset.

Figure 1.

REPPER analysis of YadA. (a) FTwin output showing periodicities along the sequence; level of significance color-coded from yellow to blue. When clicking on a colored bar, a Fourier spectrum is calculated for this part of the sequence (see spectra for the head and stalk domain). (b) REPwin output displaying periodicities along the sequence. The head domain with periodicity 14 and the stalk domain with periodicity 15 are clearly distinguished. (c) PSIPRED output; α-helices are displayed in red, β-sheets in green. (d) COILS output with intermediate probabilities for the stalk domain (window sizes: red, 28; blue, 21; green, 14).

For each position i and periodicity p REPwin calculates

$$\text{Score}(i,p)={\displaystyle \sum _k}{\displaystyle \sum _j}S(x_j,x_{j+kp}).$$ 2

S(x_j, x_j+kp) is the Gonnet substitution matrix element for residues x_j and x_j+kp. The sum runs over all k and j such that j and j + kp are inside the window (i,…,i + W − 1). Score (i, p) is normalized by dividing through the SD for nonperiodic sequences. The final score value for each residue i and periodicity p is the maximum over all windows containing residue i. The size of the sliding window is the same as for FTwin. The threshold may also be changed.

COILS

COILS (14–16) is a program that compares a sequence to a sequence profile derived from a database of known parallel two-stranded coiled coils and calculates a similarity score for each sliding window position (window sizes for COILS are 14, 21 and 28). By comparing this score with the distribution of scores in globular and coiled-coil proteins, the program then calculates the probability that the sequence will adopt a coiled-coil conformation.

PSIPRED

PSIPRED is a program developed by David Jones (13), which predicts protein secondary structure using the position specific scoring matrices generated by PSI-BLAST (20). It helps to interpret the predicted periodicities.

EXAMPLE ANALYSIS

As an example for the application of this server we will briefly discuss its output for the non-fimbrial adhesin YadA from Yersinia enterocolitica (gi 401465) (11). This protein is responsible for the adhesion of the pathogen to human tissue and appears in electron micrographs as a lollipop with a small head perched on a long stalk. The head is a left-handed β-helix (PDB: 1P9H) with a degenerate periodicity close to 14 and the stalk is a coiled coil with an unusual periodicity of 15 residues. The protein is anchored in the outer membrane by a porin-like domain consisting of four transmembrane β-strands. Since it contains two domains with different periodicities and secondary structures, YadA makes an ideal example to demonstrate the impact of a sliding window on the analysis.

As can be seen in Figure 1a and b, FTwin and REPwin clearly identify the two regions with their correct periodicities. The 15-residue periodicity of the coiled coil differs markedly from the canonical 7-residue repeat and COILS therefore only returns intermediate probabilities (Figure 1d). In fact, a 15-residue periodicity yields a helical structure with 3.75 residues per turn; it has a right-handed supercoil twist, which is of the same magnitude but opposite handedness to that of canonical coiled coils. This fact was predicted from theoretical considerations (11,12) and was proven by the crystal structure of a 15-residue periodic protein (PDB: 1USE). PSIPRED also has problems with this region, since its beginning and end are conserved in many adhesins that lack the coiled coil. Because PSIPRED uses a PSI-BLAST derived profile for prediction, the corruption of the profile by locally dissimilar sequences leads to a misprediction in this area. Note, however, that the beginning and end of the coiled coil, which are conserved, are correctly predicted as α-helices. PSIPRED is also accurate in assigning an α-helix to the signal sequence and β-strands to the head and anchor regions. Overall the juxtaposition of the four sequence analysis methods provides a clear view of the nature, location and extent of the two periodic regions in YadA (Figure 1).

USING PROFILES

In REPPER (REPeats and their PERiodicities), the programs FTwin and COILS allow the user to take a multiple sequence alignment as input, and there is also the option to calculate a profile for a given single input sequence using PSI-BLAST with two iterations and an E-value cutoff of 0.001.

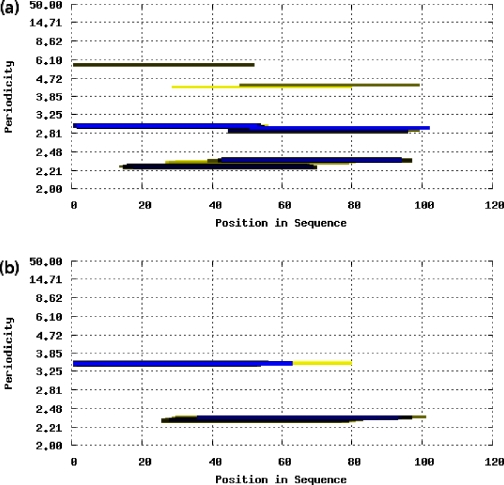
This can improve the accuracy of FTwin (Figure 2). The single sequence of the long coiled coil cortexillin does not display the typical periodicity of 3.5, although this coiled coil is regular. If an alignment is used as input, a periodicity of exactly 3.5 is revealed. As many coiled coils have exceptions to the hydrophobic-polar repeat pattern, the FT results get blurred, but as soon as other similar sequences are aligned the pattern becomes more pronounced and therefore more significant in the results.

Figure 2.

FTwin periodicities in multiple-sequence mode differ from those in single-sequence mode (window size 50, threshold parameter 3). (a) FTwin output for the cortexillin single sequence (PDB: 1D7M). The characteristic periodicity of 7/2 = 3.5 is not detected. (b) FTwin output for a cortexillin multiple sequence alignment (based on Blast hits with E-value cutoff 10⁻⁴ over the NCBI nonredundant protein database). It reveals the dominant periodicity of 3.5 over a substantial part of the protein and a periodicity of 7/3 = 2.3. The exact periodicities are shown when clicking on the colored bars.

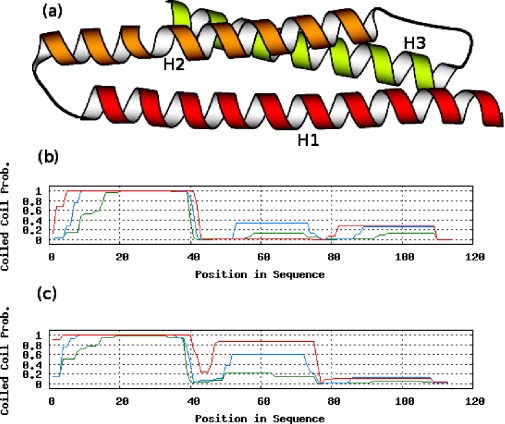
Profiles may also lead to an improvement of COILS. For example, the Bag domain (PDB: 1HX1) is a three-helix bundle with features typical for coiled coils (Figure 3). In a single-sequence analysis, only the first helix (H1) obtains high coiled-coil probabilities. H2 contains a slight deformation of the helix, which substantially lowers its score. When using a multiple sequence alignment as input, this discontinuity is averaged with many regular sequences, thereby markedly improving the scores for H2 and yielding a better match to the structure.

Figure 3.

Comparison between COILS in single-sequence mode and in multiple-sequence mode (window sizes: red, 28; blue, 21; green, 14). (a) Structure of the Bag domain (PDB: 1HX1) showing the three coiled-coil-like helices H1–H3 (21). (b) COILS output for the Bag domain single sequence. (c) COILS output for a multiple sequence alignment (based on Blast hits of the Bag domain sequence with E-value cutoff 10⁻⁴ over the NCBI nonredundant protein database filtered to 70% sequence identity with no low-complexity regions).

One should note from the previous example of the YadA coiled coil that, when produced automatically with PSI-BLAST, profiles may get corrupted, in which case a single-sequence prediction is clearly more accurate. For this reason the default setting of the server is in the single-sequence mode. Users are encouraged to take advantage of the multiple-sequence mode by using their own curated alignments.

CONCLUSION

FTwin and REPwin are two new programs for the prediction of periodic patterns in protein sequences. Although they are aimed primarily at the analysis of fibrous proteins, they can be used for any kind of repetitive sequence provided the following criteria are met: Repeats of the same nature must be consecutive in the sequence, must be of approximately the same size (no major insertions or deletions) and must occur in sufficient number to be detectable by FT. This number is a function of the sequence similarity between the repeats; whereas nearly identical repeats can even be detected in occurrences of 2–5, more degenerate repeats typically require at least 10 occurrences (the size of the scanning window in REPPER must be set to reflect this). FTwin and REPwin are complementary, since REPwin searches for repeats in a general way, using a global amino acid replacement matrix, wheras FTwin searches for periodicities of particular, user-defined types (hydrophobic, polar, positively charged, etc.). Their combination with secondary structure and coiled-coil prediction into a single integrated server provides a powerful new tool for the analysis of protein sequences.