Abstract
Accurate Alzheimer’s Disease (AD) progression prediction is essential for early intervention. The TADPOLE challenge, involving 92 algorithms, used multimodal biomarkers to predict future clinical diagnosis, cognition, and ventricular volume. The winning algorithm, FROG, utilized a Longitudinal-to-Cross-sectional (L2C) transformation to convert variable longitudinal histories into fixed-length feature vectors, which contrasted with most existing approaches that fitted models to entire longitudinal histories, e.g., AD Course Map (AD-Map) and minimal recurrent neural networks (MinimalRNN). The TADPOLE challenge only utilized the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset. To evaluate FROG’s generalizability, we trained it on the ADNI dataset and tested it on three external datasets covering 2,312 participants and 13,200 timepoints. We also introduced two FROG variants. One variant, L2C feedforward neural network (L2C-FNN), unified all XGBoost models used by the original FROG with an FNN. Across external datasets, L2C-FNN and AD-Map were the best for predicting cognition and ventricular volume. For clinical diagnosis prediction, L2C-FNN was the best, while AD-Map was the worst. L2C-FNN compared favorably with other approaches regardless of the number of observed timepoints, and when predicting from 0 to 6 years into the future, underscoring its potential for long-term dementia progression prediction. Pretrained ADNI models are publicly available: GITHUB_LINK.
Keywords: Alzheimer’s disease, longitudinal progression modelling, domain generalization, recurrent neural networks, XGBoost, feature engineering
1. Introduction
Alzheimer’s disease (AD) is a devastating neurodegenerative disorder (Jack et al., 2018; Hampel et al., 2021), which transitions slowly from a preclinical phase to a fully manifested clinical syndrome (Villemagne et al., 2013). There is no cure for AD, although medications exist to slow down cognitive decline in early AD (Van Dyck et al., 2023). The growing consensus is that early intervention is critical for slowing or stopping disease progression (Dubois et al., 2016; Scheltens et al., 2016, 2021). Therefore, predicting AD progression is an important clinical task (Zhang et al., 2017; Venkatraghavan et al., 2019) that can enable early treatment and caregiver planning (de Vugt & Verhey, 2013; Rasmussen & Langerman, 2019), decrease clinical trial costs by enriching enrollment (Burns et al., 2021; Oxtoby et al., 2022), and decrease costs by prioritizing expensive drugs for patients most at risk for dementia (Cummings et al., 2019).
Most disease progression prediction studies focus on a “static” setup, using cross-sectional (baseline) data to predict outcomes at a single future timepoint (Qiu et al., 2020; Hebling Vieira et al., 2022), such as whether individuals with mild cognitive impairment will develop dementia within 3 years (Basaia et al., 2019; El-Sappagh et al., 2021). However, real-world data often involves a variable number of observed timepoints, reflecting irregular clinical observations. Therefore, in The Alzheimer’s Disease Prediction Of Longitudinal Evolution (TADPOLE) challenge (Marinescu et al., 2019, 2021), multimodal AD biomarkers at one or more timepoints are used to predict cognition, ventricular volume and clinical diagnosis of each individual every month into the future. This setup presents three challenges: (1) variable number of observed timepoints per participant, (2) predicting indefinitely into the future1, and (3) significant missing data since not all biomarkers are available at every timepoint.
To tackle the TADPOLE challenge, dynamical state models, such as linear state space models and recurrent neural networks (RNNs), have been proposed (Ghazi et al., 2019; Nguyen et al., 2020; Jung et al., 2021; Xu et al., 2022). In these models, an individual’s latent state is represented by a vector, thus providing a rich encoding of an individual’s “disease state” beyond a single integer (as in the case of discrete state hidden Markov models). At each timepoint, observations are used to update the latent state of the individual at that timepoint. The latent state is in turn used to predict observations at the next time point. If some (or even all) observations are missing at the next time point, the model predictions can be used to fill in the missing data. Therefore, predicting missing data and future disease progression are unified into a single prediction task. One early algorithm in this category was the MinimalRNN model, which achieved second place on the TADPOLE leaderboard at the time of publication, behind the FROG algorithm (Nguyen et al., 2020).
Second, inspired by theoretical models of a sigmoidal evolution of AD biomarkers (Jack et al., 2010; Villemagne et al., 2013; Selkoe & Hardy, 2016), approaches have emerged to fit parametric sigmoid-like functions to longitudinal biomarkers. Mixed-effects models capture group-level trends as fixed effects and individual variations as random effects (Iddi et al., 2019; Li, Iddi, et al., 2019; Oxtoby, 2023). Jedynak and colleagues used dynamic time-warping to align individual biomarker data to a group template represented by sigmoid curves (Jedynak et al., 2012). A Bayesian extension incorporated individual-specific latent time shifts (Bilgel et al., 2019). This line of research was extended to fit a constrained generalized sigmoidal function (Ghazi et al., 2021). A disease course mapping framework integrating Riemannian geometry and mixed-effects modeling with time reparameterization, known as AD course map (AD-Map), has demonstrated great promise (Koval et al., 2021), outperforming MinimalRNN for predicting cognition (Maheux et al., 2023).
By contrast, the TADPOLE winner FROG utilized a longitudinal-to-cross-sectional (L2C) transformation technique (Nanopoulos et al., 2001; Deng et al., 2013; Barandas et al., 2020) to convert participants’ variable visit histories into a cross-sectional format, thus reducing the TADPOLE problem into a traditional “static” prediction problem with fixed length input features. XGBoost (eXtreme Gradient Boost; Chen & Guestrin, 2016) was then used to predict disease progression with the L2C features, training separate models for different forecast windows and target variables. FROG was the best for predicting clinical diagnosis and the overall TADPOLE winner. However, FROG has only been tested in the ADNI dataset, so it remains unclear how well it generalizes to new datasets. Furthermore, as far as we know, the L2C approach is relatively unique in the medical imaging community, with most approaches falling into either parametric model fitting (e.g., AD-Map) or dynamic state modeling (e.g., MinimalRNN).
Therefore, in the current study, we evaluated the FROG algorithm by training it on the ADNI dataset and evaluating its cross-dataset performance in three external datasets comprising 2312 participants with 13200 timepoints from the United States, Australia and Singapore. In addition, we considered two additional FROG variants. One FROG variant unified all XGBoost models with a single feedforward neural network (FNN) model, which we refer to as L2C-FNN. We also compared the FROG variants with a representative parametric approach (AD-Map) and a representative dynamic state modeling approach (MinimalRNN).
2. Methods
2.1. Problem overview
The problem setup followed the TADPOLE challenge (Marinescu et al., 2019, 2021). Given multimodal biomarkers and diagnostic history (Table 1) at one or more timepoints of an individual, we aimed to predict the cognitive state, ventricle volume normalized by intracranial volume (ICV), and clinical diagnosis of the individual for every subsequent month beyond the last observed timepoint up to 120 months into the future. Cognitive state was measured with the Alzheimer’s Disease Assessment Scale Cognitive Subdomain (ADAS-Cog13) in the original TADPOLE challenge. However, not all the external datasets had ADAS-Cog13, so we switched to predicting mini mental state examination (MMSE) in this study.
Table 1.
Features used in the current study. MMSE: mini mental state examination.
| Baseline features | Sex (male, female), Genetics (number of APOE-ε4 allele), Marital status (married, not married), Education level (number of years of education) | |
| Recurring features | MRI features | Hippocampus, Fusiform, Middle Temporal, Ventricle, Whole Brain, ICV |
| Cognitive features | MMSE (0–30), CDR GLOBAL (0, 0.5, 1, 2, 3) | |
| Diagnostic features | Clinical diagnosis (CN, MCI, DEM) | |
| Demographics | Age | |
CDR: Clinical Dementia Rating scale. CN: cognitively normal. MCI: mild cognitive impairment. DEM:Dementia with various etiologies. Note that FROG variants use all features. AD-Map was not developed to handle categorical variables or covariates, so do not utilize any of the baseline features or clinical diagnosis (see Section 2.5 for more details). MinimalRNN was not developed to handle covariates, so do not utilize any baseline features and age (see Section 2.4 for more details).
We used four datasets: the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset, the Australian Imaging Biomarkers and Lifestyle Study of Ageing (AIBL) dataset, the Memory, Ageing and Cognition Centre (MACC) Harmonization Cohort, and the Open Access Series of Imaging Studies (OASIS) dataset. These datasets consisted of longitudinal multimodal data, such as T1-weighted structural MRI data, cognitive measurements and clinical diagnosis, as well as baseline demographics. The diagnostic categories corresponded to cognitively normal (CN), mild cognitive impairment (MCI), as well as dementia with various etiologies (DEM). Data collection was approved by the Institutional Review Board (IRB) at each corresponding institution. The analysis in the current study is approved by the National University of Singapore IRB.
2.2. Datasets, preprocessing and participant selection
2.2.1. Datasets
The ADNI dataset (Jack et al., 2008; Petersen et al., 2010) is a comprehensive multicenter research initiative in the United States with three phases: ADNI1 (2004–2009), ADNI-GO/2 (2010–2016), and ADNI3 (2017–2023), with a primary focus on advancing the understanding of Alzheimer’s disease dementia. Each phase incorporates newly enrolled participants and individuals transitioning from earlier phases. Notably, there are variations in MRI scanner models and protocols across the phases, with ADNI1 primarily employing 1.5T scanners and subsequent phases adopting 3T scanners (see Table S1 for details). T1 images were downloaded from the USC Laboratory of Neuro Imaging’s Image and Data Archive (IDA). The ADNIMERGE spreadsheet (the ADNI team, 2023) containing various phenotypic data (e.g., demographics, clinical diagnoses, cognitive measurements) was also downloaded.
The AIBL study (Fowler et al., 2021) is an Australian flagship initiative that shares a similar goal and technical infrastructure with ADNI. MRI scans were acquired using both 1.5T and 3T (Avanto, Tim Trio and Verio) scanners (see Table S2 for details). MRI scans and phenotypic data were obtained from the USC Laboratory of Neuro Imaging’s Image and Data Archive (IDA).
The MACC Harmonization dataset (Hilal et al., 2020) focuses on a memory clinic population in Singapore. T1 images in this dataset were acquired exclusively using 3T (Tim Trio and Prisma) scanners (see Table S3 for details). Note that this dataset contained participants with vascular dementia and/or Alzheimer’s Disease dementia, which we have grouped together as Vascular/Alzheimer’s disease dementia (DEM). The mixed pathology allowed us to evaluate the generalizability of these models beyond AD dementia. However, for completeness, we will also report results for only AD dementia.
The OASIS dataset (LaMontagne et al., 2019) serves as a multimodal resource for studying normal aging and cognitive decline. It consists of four releases: OASIS-1 (cross-sectional) and OASIS-2 (longitudinal) as smaller-scale studies, OASIS-3 as the primary large dataset that includes OASIS-1 and OASIS-2 subjects, and OASIS-4, which encompasses a separate clinical cohort. For this study, we utilized OASIS-3 data. Note that this dataset included both AD and non-AD dementia, which we have grouped together as DEM (similar to MACC). However, for completeness, we will also report results for only AD dementia. The imaging data in OASIS were acquired using both 1.5T and 3T scanners (see Table S4 for details). MRI scans and phenotypic data were downloaded from the XNAT Central (Herrick et al., 2016).
2.2.2. Preprocessing
All T1 images were de-obliqued and reoriented to the RPI orientation. Subsequently, we used the FreeSurfer 6.0 recon-all pipeline (Fischl et al., 2002; Desikan et al., 2006) to derive the volumes of various regions of interest (ROIs). Following the FROG algorithm, we derived five brain ROI volumetric features associated with AD-dementia, namely Hippocampal volume, Fusiform volume, Middle Temporal (MidTemp) volume, Ventricle volume, and Whole Brain volume (see Table S5 for details). We also incorporated intracranial volume (ICV) as an additional feature and standardized the five brain ROI features with respect to ICV (Table 1).
The generated brain ROI features were then merged with downloaded phenotypic data (e.g., demographics, clinical diagnoses, cognitive measurements). Notably, non-MRI phenotypes (e.g., clinical diagnoses and cognitive measurements) and MRI scans might not have been performed on the same day. Following the ADNIMERGE convention, if the non-MRI and MRI dates were within 6 months of each other, then the non-MRI and MRI phenotypes were merged into one timepoint corresponding to the non-MRI date.
We systematically eliminated empty or duplicate entries, along with those displaying outliers or errors. Certain datasets used inconsistent coding for missing values, such as NaN or special integers (e.g., −1, −4, 999). To ensure consistency, we replaced all special integers with NaN. Consequently, we obtained a clean longitudinal data table where each row represents one timepoint of a participant, containing MRI features and/or cognitive features and/or diagnostic features (Table 1).
2.2.3. Participant selection and characteristics
Our objective was to predict the longitudinal progression of dementia, so across all four datasets, we only included participants with recurring features (Table 1) at two or more timepoints. We note that under this criterion, the recurring features did not need to all occur in the same timepoints. For example, a participant with only MRI features in timepoint 1 and only cognitive features in timepoint 2 was considered acceptable.
With the above selection criterion, the final ADNI dataset comprised 2111 participants with a total of 15791 timepoints, including 9668 timepoints with MRI features. In the case of AIBL, the final dataset comprised 402 participants with a total of 1220 timepoints, including 940 timepoints with MRI features. In the case of MACC, the final dataset comprised 650 participants with a total of 3067 timepoints, including 1453 timepoints with MRI features. In the case of OASIS, the final dataset comprised 1260 participants with a total of 8913 timepoints, including 2519 timepoints with MRI scans.
The demographics, disease severity and number of timepoints vary significantly between ADNI and the three external datasets (Table 2). Actual distributions are plotted in Figures S1 and S2. Compared with ADNI, the AIBL participants were younger and had higher MMSE scores. There were also proportionally more female and CN participants in the AIBL dataset than the ADNI dataset. Compared with ADNI, the MACC participants had lower MMSE scores. Furthermore, there were proportionally more female and participants with DEM diagnosis in MACC than ADNI. Finally, compared with ADNI, the OASIS participants were younger and had higher MMSE scores. There were also proportionally more female and CN participants in the OASIS dataset than the ADNI dataset.
Table 2.
Participant characteristics in the four datasets.
| ADNI (N = 2111) | |||||||
|---|---|---|---|---|---|---|---|
| mean ± std | p | p | p | ||||
| Baseline age (y) | 73.3 ± 7.2 | 2.9e-2 | 7.8e-2 | 1.0e-4 | |||
| Baseline MMSE | 27.4 ± 2.6 | 1.0e-4 | 1.0e-4 | 1.0e-4 | |||
| Sex (M/F) | 1135 / 976 (54% / 46%) | 2.9e-2 | 1.6e-5 | 2.0e-7 | |||
| Baseline diagnosis (CN/MCI/DEM) | 745 / 995 / 371(35%/47%/18%) | 8.4e-60 | 2.7e-29 | 7.6e-138 | |||
| Baseline DEM (AD/Other dementias) | - | - | - | - | |||
| Cognitively Normal (CN) | |||||||
| Baseline Age (y) | 73.0 ± 6.2 | 2.5e-2 | 1.0e-4 | 1.0e-4 | |||
| Sex (M/F) | 333 / 412 (45% / 55%) | 8.1e-1 | 1.0 | 5.6e-1 | |||
| Mild Cognitive Impairment (MCI) | |||||||
| Baseline age (y) | 73.0 ± 7.5 | 4.2e-2 | 9.2e-1 | 4.3e-1 | |||
| Sex (M/F) | 592 / 403 (59% / 41%) | 9.8e-1 | 7.1e-4 | 8.3e-1 | |||
| Dementia (DEM) | |||||||
| Baseline age (y) | 74.6 ± 7.8 | 5.2e-2 | 8.4e-1 | 6.1e-1 | |||
| Sex (M/F) | 210 / 161 (57% / 43%) | 2.2e-1 | 5.3e-5 | 2.8e-1 | |||
| Number of visits | 7.5 ± 4.5 | 1.0e-4 | 1.0e-4 | 1.7e-2 | |||
| Follow-up duration (y) | 4.5 ± 3.4 | 1.0e-4 | 1.0e-4 | 1.0e-4 | |||
| Percentage of timepoints with missing data for recurring features | |||||||
| CDR Global | 28.6% | 2.7e-101 | 5.8e-224 | 0.0 | |||
| MMSE | 30.1% | 1.4e-109 | 7.6e-240 | 2.3e-122 | |||
| MRI features | 38.8% | 5.9e-28 | 4.6e-46 | 0.0 | |||
| Diagnosis | 30.2% | 5.8e-110 | 1.7e-249 | 5.3e-80 | |||
Statistical tests were performed to compare ADNI and each external dataset. For continuous variables (e.g., age and MMSE), a permutation test was used. For discrete variables (e.g., sex and diagnosis), the chi square test was used. Bolded p values indicate statistical significance after correcting for multiple comparisons with false discovery rate (FDR) q < 0.05. Note that not all OASIS participants have clinical diagnosis at baseline, so the percentages of participants with baseline diagnosis do not add up to 100%.
Furthermore, both the AIBL and MACC datasets typically have fewer than 7 timepoints collected within a span of 7 years. In contrast, some participants in the ADNI and OASIS datasets have up to 20 to 30 timepoints, covering a tracking period of over 15 years. The percentage of timepoints with missing data was also highly different across the datasets (Table 2).
2.3. Training, validation and test procedure
We compared five different models: MinimalRNN, AD-Map, original FROG (L2C-XGBw), FROG variant 1 (L2C-XGBnw) and FROG variant 2 (L2C-FNN). We trained different models using ADNI and evaluated their performance within the ADNI dataset (within-dataset evaluation) and in AIBL, MACC and OASIS datasets (cross-dataset evaluation). More specifically, we randomly divided the ADNI participants into 20 groups. As all participants contributed data collected at multiple timepoints, care was taken to ensure that all timepoints for any given participant were exclusively assigned to a single group, precluding any division across multiple groups.
To train a given model, 18 groups were used for training, while 1 group was used as a validation set to tune the hyperparameters. The remaining group was used as test set to evaluate the within-cohort performance of the model. To ensure stability of results (Kong et al., 2019; Li, Kong, et al., 2019; Varoquaux, 2018), this procedure was repeated 20 times with a different group being the test set (e.g., group 5) and the group next to it being the validation set (e.g., group 6). Therefore, we ended up with 20 sets of trained models together with 20 sets of within-cohort evaluation results. The 20 sets of trained models were applied to all participants in AIBL, MACC, and OASIS for cross-cohort evaluation (Figure 1).
Figure 1. Training and testing procedure.
All models were trained on the ADNI dataset and subsequently applied to three unseen test datasets to assess generalizability. ADNI participants were randomly divided into training, validation, and test sets (ratio of 18:1:1) for hyperparameter tuning and within-cohort evaluation. This procedure was repeated 20 times to ensure result stability. Care was taken to ensure non-overlapping test sets, covering the entirety of the ADNI dataset across the 20 data splits. Trained models were then evaluated on participants from the three unseen test datasets (AIBL, MACC, and OASIS) for cross-cohort evaluation.
Following TADPOLE convention, for participants in the ADNI validation and test sets, as well as all participants in AIBL, MACC, and OASIS, the first half of each participant’s timepoints were used to predict the second half of the same participant’s timepoints. For example, if a participant had 10 timepoints, then the first 5 timepoints were used as input (observed) timepoints, and we sought to predict the second 5 timepoints (unobserved). On the other hand, the entire longitudinal time series of training participants were used during training to increase data efficiency.
The Optuna library (Akiba et al., 2019) was utilized to find the best hyperparameters by maximizing model performance on the validation set. We note that this optimization was performed independently for each training/validation/test split of the dataset. The hyperparameter search spaces for each algorithm are described in their respective method sections.
2.4. MinimalRNN
MinimalRNN is a recurrent neural network (RNN) with less parameters than LSTM (Long short-term memory) to mitigate overfitting. In our previous study (Nguyen et al., 2020), we found that MinimalRNN performed better than the more complex LSTM, as well as a simpler linear state space model in the TADPOLE challenge. As such, the MinimalRNN struck the perfect complexity balance, yielding the best prediction performance among the RNN models we tested.
In RNNs, the same computational unit is repeated at each time step, where the output at the current step becomes the input at the next step. Therefore, the longitudinal data of a participant is analyzed sequentially, where the input features at a particular timepoint is used to update the internal “disease” state of the participant. This internal state is then used to predict the input features at the next time point.
For our experiments, we utilized the publicly available code from https://github.com/ThomasYeoLab/CBIG/tree/master/stable_projects/predict_phenotypes/Nguyen2020_RNNAD. However, we replaced the HORD hyperparameter search algorithm (Eriksson et al., 2019; Ilievski et al., 2017) employed in our previous study (Nguyen et al., 2020) with Optuna (Akiba et al., 2019) because of its ease of use.
Table 3 summarizes the hyperparameters optimized by Optuna and their corresponding search range. Consistent with the original study (Nguyen et al., 2020), MinimalRNN only utilized the recurring MRI features, cognitive features and clinical diagnosis (Table 1), but not any baseline features (sex, education, marital status and number of APOE-ε4) and age. Our previous experiments (not shown) found that these additional information did not improve prediction performance.
Table 3.
Hyper-parameters and corresponding search ranges for MinimalRNN estimated from the validation sets using Optuna.
| Hyper-parameter | Range |
|---|---|
| Input dropout rate | 0–0.5 |
| Recurrent dropout rate | 0–0.5 |
| L2 weight regularization | 10−7–10−5 |
| Learning rate | 10−5–10−2 |
| # hidden layers | 1–3 |
| Size of hidden state | 128–512 |
2.5. AD Course Map (AD-Map)
AD-Map is a parametric Bayesian non-linear mixed-effects model designed to predict cognition and brain atrophy. It was shown to outperform MinimalRNN (Maheux et al., 2023). AD-Map assumes that each biomarker follows a logistic curve, with different biomarkers exhibiting distinct progression rates and ages at inflexion point. The model adjusts these curves for each individual by learning individual-specific shifts in disease onset, progression rates, and the timing/ordering of biomarker progression. As a result, the model predicts an individual-specific set of logistic curves, which show the value of each biomarker at any age of the participant.
For our experiments, we used the Leaspy software (https://gitlab.com/icm-institute/aramislab/leaspy) and optimized hyperparameters (Table 4) via Optuna (Akiba et al., 2019). We note that intracranial volume (ICV) was not included as a feature since AD-Map requires time-dependent features, and ICV shows minimal change with time (Courchesne et al., 2000; Jenkins et al., 2000). However, we remind the reader that the other MRI volumetric features were normalized with respect to ICV, consistent with other algorithms.
Table 4.
Hyper-parameters and corresponding search ranges for AD-Map estimated from the validation sets using Optuna.
| Hyper-parameter | Range |
|---|---|
| Source dimension | 1–5 |
| # iterations | (1–10) * 500 |
Consistent with the original study (Maheux et al., 2023), we did not include clinical diagnosis as a biomarker. Instead, to predict clinical diagnosis, we converted the predicted CDR score into probabilities for CN, MCI, and DEM using standard cut-off points (O’Bryant et al., 2010; Tariot et al., 2024): CDR 0 was mapped to CN, CDR 0.5 was mapped to MCI, and CDR 1, 2, and 3 were mapped to DEM. For predicted CDR scores between 0 and 0.5, we used linear interpolation, so for instance, a CDR score of 0.1 resulted in 80% probability for CN, and 20% probability for MCI, and 0% probability for DEM. For scores between 0.5 and 1, we again used linear interpolation, so for instance, a CDR score of 0.6 resulted in 0% probability for CN, and 80% probability for MCI, and 20% probability for DEM. CDR scores of 1 or higher are fully assigned to DEM.
We also explored including clinical diagnosis directly into AD-Map by treating it as a score (CN = 0, MCI = 1, DEM = 2). This approach improved clinical diagnosis prediction, but led to very poor MMSE and ventricular volume prediction. Therefore, consistent with the original study (Maheux et al., 2023), we did not include clinical diagnosis as a feature in the AD-Map algorithm. Furthermore, the AD-Map package does not take in any baseline features (sex, education, marital status and number of APOE-ε4), so in summary, the AD-Map only used recurring MRI features (excluding ICV), cognitive features and age.
2.6. Original FROG: Longitudinal-to-Cross-sectional XGBoost with Windows (L2C-XGBw)
2.6.1. Longitudinal-to-Cross-sectional (L2C) transformation
The TADPOLE problem set up is challenging for standard machine learning algorithms (e.g., support vector machine) because of the variable length of observed timepoints. The winner of the TADPOLE challenge FROG used a feature engineering technique (Nanopoulos et al., 2001; Deng et al., 2013; Barandas et al., 2020) that transformed the longitudinal visit history of participants into a cross-sectional format, which we will refer to L2C (Longitudinal-to-Cross-sectional) transformation.
More specifically, suppose for a given participant, we observed data at m timepoints t1, t2, t3, t4, …, tm, and we would like to predict clinical diagnosis (or MMSE or ventricular volume) at a future timepoint tf. Note that these timepoints might not be equally spaced in time. To convert the variable length input features, FROG proposed the following L2C transformation, in which each continuous input modality (i.e., MMSE, CDR_GLOBAL, six anatomical ROI volumes) is converted into seven features (Table 5) and clinical diagnosis is converted into eight features (Table 6), resulting in 8 × 7 + 8 = 64 features. These 64 features were augmented by age at future timepoint tf, baseline sex, baseline education level, baseline marital status, APOE status and number of months between future timepoint tf and the first (baseline) visit. In total, there were 64 + 6 = 70 features. Please refer to Supplementary Table S6 for the complete set of L2C features used by FROG.
Table 5.
L2C feature names and their corresponding meaning for continuous input modalities.
| L2C feature names | Meaning |
|---|---|
| mr_fname | most recent measurement for feature |
| time_since_mr_fname | time since the most recent measurement |
| mr_change_fname | most recent change rate |
| low_fname | lowest historical measurement |
| time_since_low_fname | time since lowest historical measurement |
| high_fname | highest historical measurement |
| time_since_high_fname | time since highest historical measurement |
Table 6.
L2C feature names and their corresponding meaning for clinical diagnosis.
| L2C feature names | Meaning |
|---|---|
| mr_dx | most recent non-missing diagnosis |
| time_since_mr_dx | time since the most recent non-missing diagnosis |
| best_dx | best historical diagnosis |
| time_since_best_dx | time since best historical diagnosis |
| worst_dx | worst historical diagnosis |
| time_since_worst_dx | time since worst historical diagnosis |
| milder | 1 if a milder diagnosis occurred in history |
| time_since_milder | time since the milder diagnosis and 999 if no milder diagnosis |
2.6.2. Data augmentation
In addition to the L2C transformation, FROG proposed the following data augmentation strategy during training. Suppose we observed data at m timepoints t1, t2, t3, t4, …, tm for a particular training participant. FROG then generated m−1 training samples by using t1 to predict t2, or t3 or t4 or t5 etc. FROG also generated another m−2 training samples by using t1 and t2 to predict t3 or t4 or t5 etc. In total, given m timepoints, FROG generated m * (m−1)/2 training samples.
2.6.3. L2C eXtreme Gradient Boost with separate windows (L2C-XGBw)
The L2C transformation converted variable length input features into fixed length input features (Section 2.6.1), while the data augmentation procedure generated more training samples (Section 2.6.2). The original FROG team used eXtreme Gradient Boost (XGBoost; Chen & Guestrin, 2016) to predict the target variables from the L2C features. Gradient boosting is a model ensemble of individual decision trees that are trained sequentially such that a new tree improves the error of the previous tree ensemble. XGBoost is an optimized distributed gradient boosting library. The original FROG submission used the XGBoost R library, while we reimplemented the FROG algorithm in python. We performed 5 repetitions of train/validation/test split in the ADNI dataset to ensure our python implementation yields numerically the same results as the R code.
Furthermore, consistent with the original FROG submission to the TADPOLE challenge, we trained separate XGBoost models for each target variable (clinical diagnosis, MMSE, ventricle volume). Following the original FROG submission, we also trained separate models based on specific forecast interval ranges, with the assumption that certain models may excel in short-term predictions while others in long-term forecasts. The forecast interval ranges (i.e., forecast windows) for each target variable (measured in months) adhere to the FROG team’s settings (Table 7). Hence, we referred to this algorithm as L2C eXtreme Gradient Boost with separate windows (L2C-XGBw).
Table 7.
L2C-XGBw (FROG) trained a separate XGBoost model for each forecast window and each target variable.
| Target variables | Forecast Windows (months) |
|---|---|
| MMSE | 0–9, 9–15, 15–27, 27–39, >54 |
| Clinical diagnosis | 0–8, 8–15, 15–27, 27–39, 39–60, >60 |
| Ventricle volume | 0–9, 9–15, 15–30, >30 |
Three important hyperparameters were tuned in the ADNI validation sets using Optuna (Akiba et al., 2019). The three hyperparameters and search ranges are detailed in Table 8. We note that there is no extra feature normalization or missing data imputation since the XGBoost package handles such issues internally.
Table 8.
Hyper-parameters and corresponding search ranges for L2C-XGBw estimated from the validation sets using Optuna.
| Hyper-parameter | Range |
|---|---|
| Max depth | 3–8 |
| Subsample rate | 0.4–1 |
| Learning rate (η) | 0.01–0.2 |
2.7. FROG variant 1: L2C eXtreme Gradient Boost with no window (L2C-XGBnw)
L2C-XGBw (FROG) involved training a separate XGBoost model for each forecast window. This is not ideal because the forecast windows are themselves hyperparameters, which might be hard to pick for new target variables. We hypothesized that the multiple forecast windows might not be necessary because L2C features like “time since baseline” and “time since most recent measurement” already encode the necessary temporal information for the model. Therefore, we considered a variant of FROG, where a single XGBoost model was trained for all future timepoints, as opposed to a separate model for each time window. We refer to this baseline as L2C eXtreme Gradient Boost with no window (L2C-XGBnw). All other implementation details remain consistent with those of L2C-XGBw.
2.8. FROG variant 2: L2C Fully-Connected Feedward Neural Network (L2C-FNN)
L2C-XGBnw trained a separate XGBoost model for each target variable. Previous studies have suggested that predicting multiple target variables can potentially improve prediction performance. By learning shared representations to capture common patterns among related tasks, these shared representations might enhance data efficiency, accelerate learning, and mitigate overfitting issues (Rahim et al., 2017; Crawshaw, 2020).
A natural choice to incorporate multi-task learning is to replace XGBoost with a fully connected feedforward neural network (FNN) model, with the output layer predicting all target variables jointly. Adding new target variables only increases the dimension of the output layer, which eliminates the need for separate models and simplifies the coding and hyperparameter tuning. Similar to L2C-XGBnw, we will train a single FNN model to predict all future timepoints, instead of the original FROG implementation which trained a separate XGBoost model for each forecast window. We will refer to this model as the L2C Fully-Connected Feedward Neural Network (L2C-FNN).
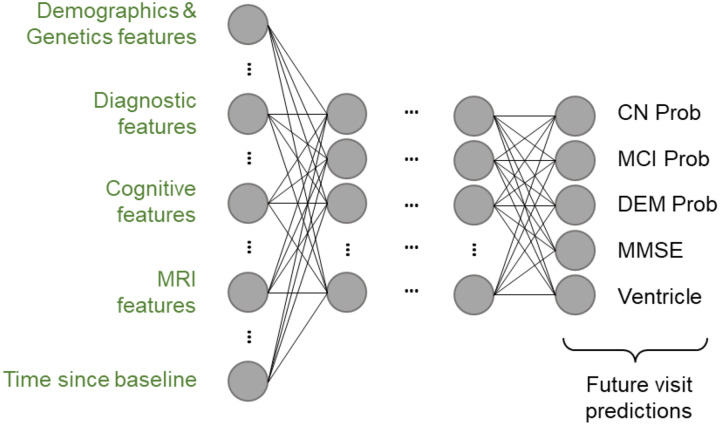
Figure 2 illustrates the L2C-FNN architecture. LeakyReLU (Maas, 2013) was chosen as the activation function, and dropout (Srivastava et al., 2014) was applied after each activation function to enhance model generalizability. The FNN output is a 5-dimensional vector: the first three elements represent the individual’s probabilities of being diagnosed as CN, MCI, or DEM at a future timepoint, computed using a SoftMax function, while the fourth and fifth elements correspond to MMSE and ventricle volume predictions.
Figure 2. Architecture of the L2C Fully Connected Feedforward Neural Network (L2C-FNN).
FNN incorporates leaky rectified linear units (LeakyReLU) between layers. The input layer comprises multimodal L2C features, among which “time since baseline” denotes the duration from the baseline visit to the timepoint we want to predict, aiding in longitudinal prediction. The final layer simultaneously outputs clinical diagnosis probabilities (calculated with a soft-max function), MMSE score, and ventricle volume for multi-task learning.
Input features are similar to L2C-XGBw (FROG), with additional preprocessing steps. Due to FNN sensitivity to input scale and missing data compared to tree-based models such as XGBoost, we performed Gauss Rank normalization, a special form of quantile normalization (Zhao et al., 2020), with a Gaussian reference distribution. The transformation was performed using the Scikit-learn quantile transform function (Pedregosa et al., 2011). Discrete features, such as APOE, sex, and most recent diagnosis (mr_dx) were encoded using one-hot encoding. To handle missing data, an “unknown” class was introduced for all discrete features, and missing values were assigned to this class. Numeric feature imputation involved replacing missing values with the median of the training set before Gauss Rank transformation. During inference, the learned Gauss Rank transformations and statistics from the training set were used to impute and transform validation and test data. Notably, the “time since milder clinical diagnosis” feature was removed due to its high proportion of NaN values (91.57%) which primarily stems from two causes: either because there is no milder clinical diagnosis in the patient’s history or the clinical diagnosis data is missing. Overall, this yields a 101-dimensional input vector for L2C-FNN (see Supplementary Table S7 for details).
The loss function is computed by comparing the predictions with the ground truth. Similar to MinimalRNN, cross-entropy loss was used for clinical diagnosis prediction, while mean absolute error (MAE) loss was employed for MMSE and ventricle volume prediction (based on the Gauss Rank values). Because MAE was based on Gauss Rank values, the three losses were of similar magnitude, and so the three losses were added together with equal weighting. Changing the relative weights of the three terms could potentially influence the model performance. However, this would increase the number of hyperparameters, so we did not experiment with different weights in this study.
Finally, stochastic gradient descent (SGD) with momentum (Qian, 1999; Sutskever et al., 2013) was chosen as the optimizer, with Optuna utilized to search for optimal hyperparameters. Table 9 shows all the hyperparameters considered and their corresponding search range. The ExponentialLR scheduler was employed to regulate learning rate behavior.
Table 9.
Hyper-parameters and corresponding search ranges for L2C-FNN estimated from the validation sets using Optuna.
| Hyper-parameter | Range |
|---|---|
| Dropout rate | 0–0.5 |
| LeakyReLU slope | 0.01–0.1 |
| L2 weight regularization | 10−7–10−4 |
| SGD momentum | 0–0.9 |
| Learning rate | 10−5–10−1 |
| ExponentialLR gamma | 0.1–0.9 |
| Num of hidden layers | 2–5 |
| Size of hidden state | 128–512 |
2.9. Further analyses
We performed two additional analyses to study the effectiveness of all five models (MinimalRNN, AD-Map and the three FROG variants).
2.9.1. Impact of the number of observed timepoints on cross-cohort prediction accuracy
For a disease progression model to be effective in early detection of AD-dementia risk, it should ideally perform well with a small number of input timepoints. We evaluated the performance of all four models on external test datasets using only 1, 2, 3, or 4 input timepoints. This contrasts with the main benchmarking analysis (Section 3.4), where half the total number of timepoints (for each participant) were used to predict the remaining timepoints.
For the OASIS dataset, test subjects with fewer than 4 input timepoints were discarded so that the same test subjects were evaluated across the four conditions (i.e., 1, 2, 3, or 4 input timepoints). In contrast, the maximum number of input timepoints for each subject is less than 4 in the AIBL and MACC datasets (2 for AIBL and 3 for MACC). Consequently, we discarded test subjects with fewer than 2 input timepoints for AIBL and fewer than 3 input timepoints for MACC. Because we excluded some test subjects, the results of this analysis are not directly comparable to those of the main benchmarking analysis (Section 3.4).
2.9.2. Breakdown of cross-cohort prediction in yearly intervals
We extended our investigation of cross-cohort prediction performance by breaking down the prediction results into yearly intervals up to 6 years into the future. Each participant’s future timepoints were categorized into yearly intervals based on the duration between the last input timepoint and the target future timepoint for prediction. For instance, considering a participant with 10 timepoints, if the last input timepoint (5th timepoint) was at month 60 and the 6th timepoint was at month 70, the prediction at the 6th timepoint would be classified as 1 year into the future due to the 10-month duration.
We anticipated that all tested algorithms would experience a decline in performance as the prediction horizon extended further into the future. Nevertheless, for effective early detection of AD-dementia, a robust algorithm was expected to maintain relatively high performance even in later years, ensuring clinical utility.
2.10. Deep neural network implementation
MinimalRNN and L2C-FNN were implemented using PyTorch (Paszke et al., 2019) and computed on NVIDIA RTX 3090 GPUs with CUDA 11.0.
2.11. Performance evaluation and statistical tests
In the preceding sections, we utilized a 20-fold cross-validation procedure to train the five models (MinimalRNN. AD-Map and three FROG variants) on data from ADNI, predicting clinical diagnosis, MMSE score, and ventricle volume. Our evaluation aims to assess the performance of these algorithms within the ADNI dataset (within-dataset evaluation) and across external test datasets (cross-dataset evaluation), with a specific focus on evaluating their generalizability. This section provides a detailed description of the statistical evaluation procedure.
Diagnosis classification accuracy was evaluated using the multiclass area under the operating curve (mAUC; Hand & Till, 2001) following the TADPOLE challenge. The mAUC was computed as the average of three two-class AUC (DEM vs not DEM, MCI vs. not MCI, and CN vs not CN). For mAUC, higher values indicate better performance. The mAUC is a group-level metric whereby the predictions were first pooled over all test participants across their entire forecast horizon into a vector of length # total future timepoints, before calculating the mAUC, resulting one value per test set.
MMSE and ventricles prediction accuracy was evaluated using mean absolute error (MAE). Lower MAE indicates better performance. The MAE were averaged across all forecast timepoints within each participant, resulting in a vector of length #test_participant values per test set.
For within-cohort evaluation, because of the 20-fold cross-validation, there were 20 mAUC values, 20 MAE values for MMSE and 20 MAE values for ventricle volumes. Although the test sets do not overlap, the participants used for training do overlap across the test sets. Therefore, the prediction metrics were not independent across the 20 test sets. To account for the non-independence, we utilized the corrected resampled t-test (Bouckaert & Frank, 2004) to assess performance differences between algorithms. Separate tests were performed for mAUC, MMSE and ventricle volume.
For cross-cohort evaluation, the final performance was computed by averaging the performance metrics across 20 trained models of each algorithm. To assess performance differences between algorithms, since each participant in the external datasets were independent, we performed paired sample t-test (Cohen, 1988) for MMSE MAE and ventricle volume MAE, as well as a permutation test (Good, 2000) for group-level metrics (mAUC). Supplementary Figures S3 and S4 illustrate the t-test and permutation test respectively.
Multiple comparisons were corrected with a false discovery rate (FDR) of q < 0.05 (Benjamini & Hochberg, 1995) for both within and cross-cohort evaluations.
3. Results
3.1. FROG variants perform the best for within-cohort clinical diagnosis prediction
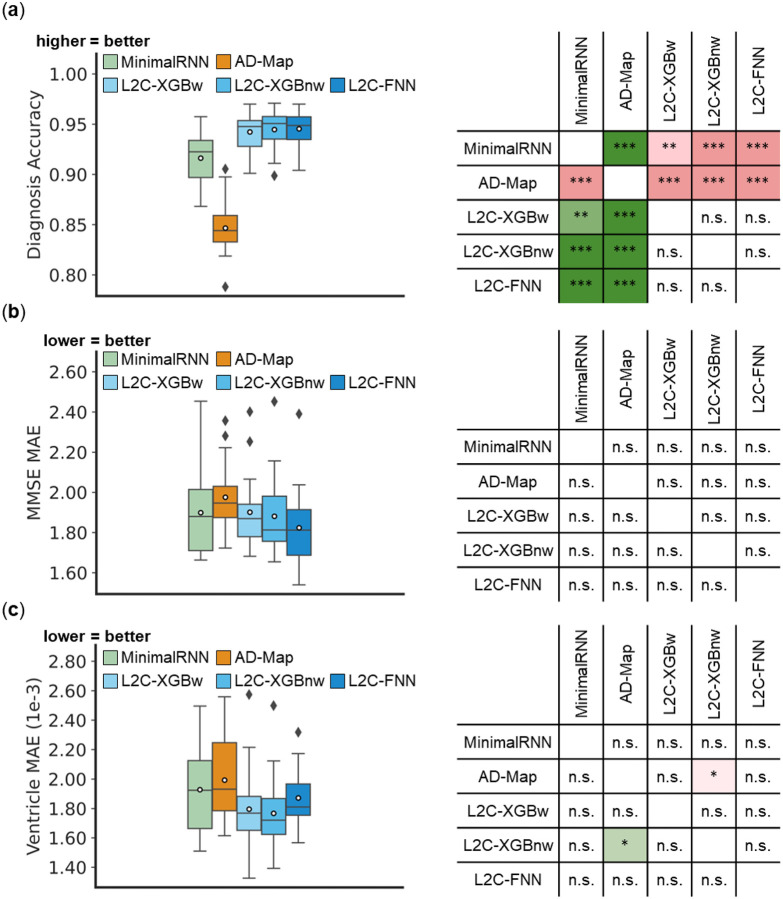
Figure 3 illustrates the performance of MinimalRNN, AD-Map and three FROG variants (L2C-XGBw, L2C-XGBnw and L2C-FNN) for within-cohort (ADNI) clinical diagnosis, MMSE and ventricle volume prediction. All models exhibited similar performance for predicting MMSE and ventricle volume. However, for predicting future clinical diagnosis, the three FROG variants were better than MinimalRNN, which was in turn better than AD-Map.
Figure 3. Within-cohort (ADNI) prediction performance.
(a) Left: Boxplots represent variability across 20 test sets for clinical diagnosis prediction measured using mAUC. Right: Statistical difference between all models. “***” indicates p < 0.00001 and statistical significance after multiple comparison correction (FDR q < 0.05). “**” indicates p < 0.001 and statistical significance after multiple comparison correction (FDR q < 0.05). “n.s.” indicates no statistical significance (p ≥ 0.05) or did not survive FDR correction. (b) Same as (a) but for MMSE prediction error (MAE). (c) Same as (a) but for ventricle volume prediction error (MAE).
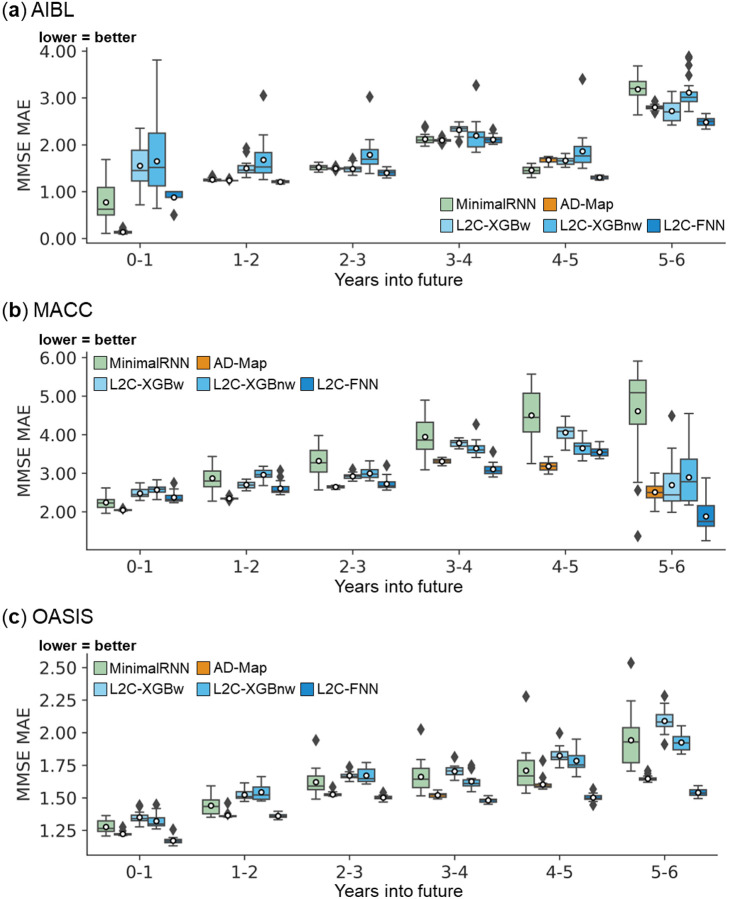
3.2. AD-Map and L2C-FNN performed the best for cross-cohort MMSE prediction
Figure 4 illustrates the prediction error of MinimalRNN, AD-Map and three FROG variants (L2C-XGBw, L2C-XGBnw and L2C-FNN) for cross-cohort MMSE prediction in three external datasets (AIBL, MACC, and OASIS). In the AIBL dataset, L2C-FNN was the best, followed by AD-Map and MinimalRNN. In the MACC dataset, AD-Map was the best followed by L2C-FNN. In the OASIS dataset, L2C-FNN was the best, followed closely by AD-Map. Overall, in this analysis, L2C-FNN and AD-Map were the best. Similar conclusions were obtained if we only considered AD dementia, with non-AD dementia set to NaN (Figure S5).
Figure 4. Cross-cohort MMSE prediction error (MAE) on three external test datasets.
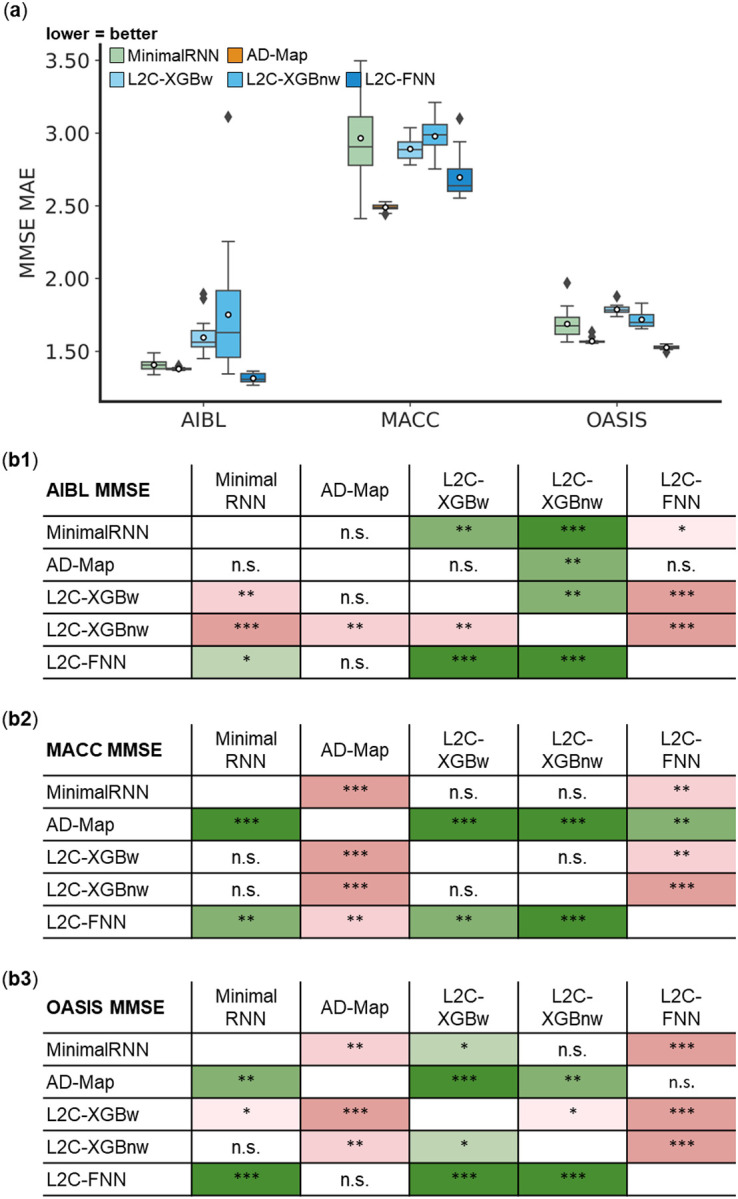
(a) Boxplots display the variability across 20 trained models (from ADNI) for MMSE prediction assessed using MAE. The x-axis denotes the test dataset used for evaluation. (b) Statistical significance in the prediction error between all models. Each row shows the statistical difference between a model and all other models. For example, the first row of each 5 × 5 table corresponds to the statistical difference between MinimalRNN and the other models – green indicates that MinimalRNN performs better, while red indicates that MinimalRNN performs worse. Therefore, the colors are always flipped between red and green across the diagonal. “*” indicates p < 0.05 and statistical significance after multiple comparisons correction (FDR q < 0.05). “**” indicates p < 0.001 and statistical significance after multiple comparisons correction (FDR q < 0.05). “***” indicates p < 0.00001 and statistical significance after multiple comparisons correction (FDR q < 0.05). “n.s.” indicates no statistical significance (p ≥ 0.05) or did not survive FDR correction.
3.3. L2C-FNN, L2C-XGBnw & AD-Map performed the best for cross-cohort ventricle volume prediction
Figure 5 illustrates the prediction error of MinimalRNN, AD-Map and three FROG variants (L2C-XGBw, L2C-XGBnw and L2C-FNN) for cross-cohort ventricle volume prediction in three external datasets (AIBL, MACC, and OASIS). In the AIBL dataset, all approaches had similar performance, although L2C-XGBnw was the best, followed closely by L2C-FNN. In the MACC dataset, L2C-FNN was the best, followed by AD-Map. In the OASIS dataset, AD-Map performed the best, followed by L2C-XGBnw. Overall, in this analysis, L2C-FNN, L2C-XGBnw and AD-Map performed the best. The original FROG algorithm (L2C-XGBw) and MinimalRNN performed the worst. Similar conclusions were obtained if we only considered AD dementia, with non-AD dementia set to NaN (Figure S6).
Figure 5. Cross-cohort ventricle volume prediction error (MAE) on three external test datasets.
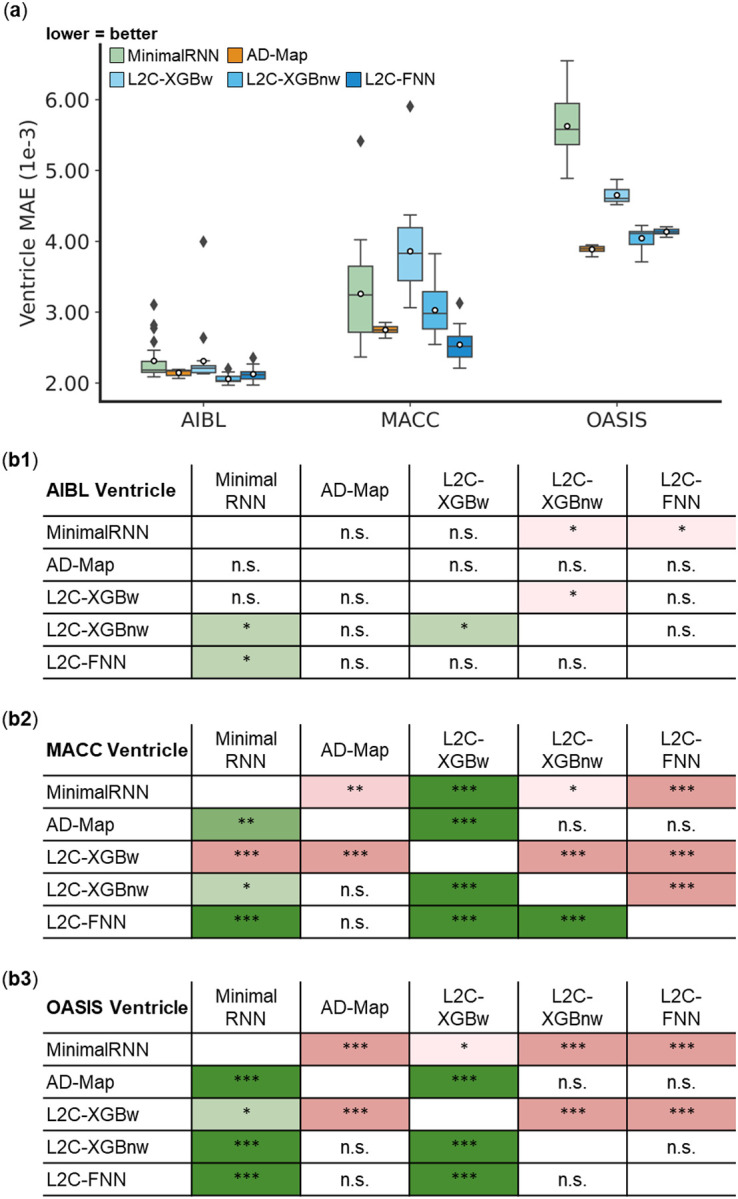
(a) Boxplots display the variability across 20 trained models (from ADNI) for ventricle volume prediction assessed using MAE. The x-axis denotes the test dataset used for evaluation. (b) Statistical significance in the prediction error between all models. Each row shows the statistical difference between a model and all other models. For example, the first row of each 5 × 5 table corresponds to the statistical difference between MinimalRNN and other models – green indicates that MinimalRNN performs better, while red indicates that MinimalRNN performs worse. Therefore, the colors are always flipped between red and green across the diagonal. “*” indicates p < 0.05 and statistical significance after multiple comparisons correction (FDR q < 0.05). “**” indicates p < 0.001 and statistical significance after multiple comparisons correction (FDR q < 0.05). “***” indicates p < 0.00001 and statistical significance after multiple comparisons correction (FDR q < 0.05). “n.s.” indicates no statistical significance (p ≥ 0.05) or did not survive FDR correction.
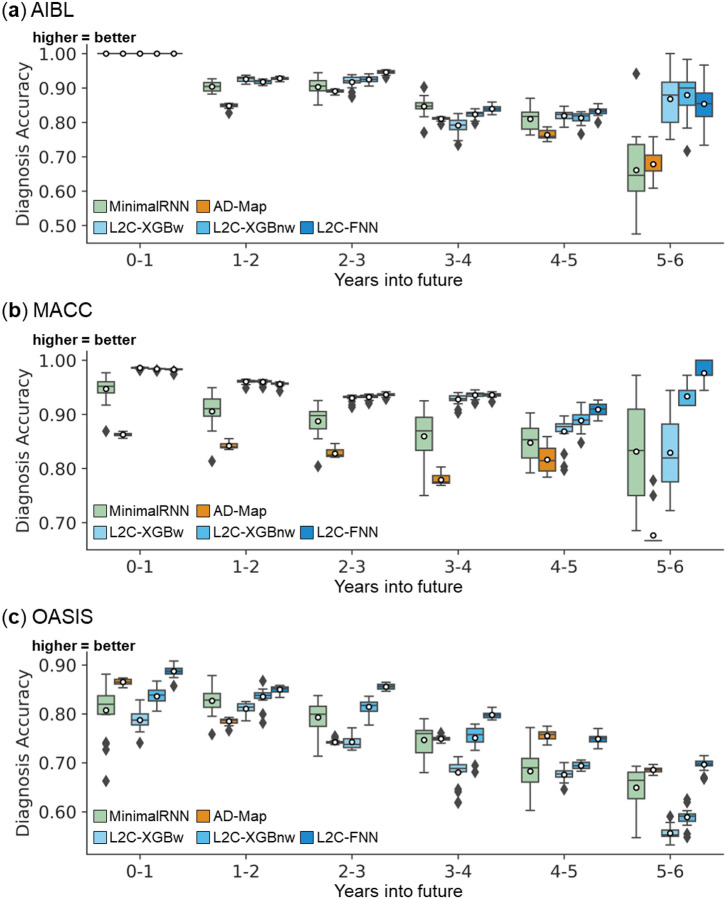
3.4. L2C-FNN outperformed other models for cross-cohort diagnosis prediction
Figure 6 illustrates the prediction accuracy of MinimalRNN, AD-Map and three FROG variants (L2C-XGBw, L2C-XGBnw and L2C-FNN) for cross-cohort clinical diagnosis prediction in three external datasets (AIBL, MACC, and OASIS). In the AIBL dataset, L2C-FNN was numerically the best, but there was no statistical difference among the FROG variants and MinimalRNN. However, AD-Map was statistically worse than the three FROG variants. In the MACC dataset, the three FROG variants performed similarly well and were all statistically better than MinimalRNN, which was in turn better than AD-Map. Finally, in the OASIS dataset, L2C-FNN was the best, while the original FROG algorithm (L2C-XGBw) was the worst. Overall, in this analysis, L2C-FNN performed the best. Similar conclusions were obtained if we only considered AD dementia, with non-AD dementia set to NaN (Figure S7).
Figure 6. Cross-cohort clinical diagnosis prediction accuracy (mAUC) on three external test datasets.
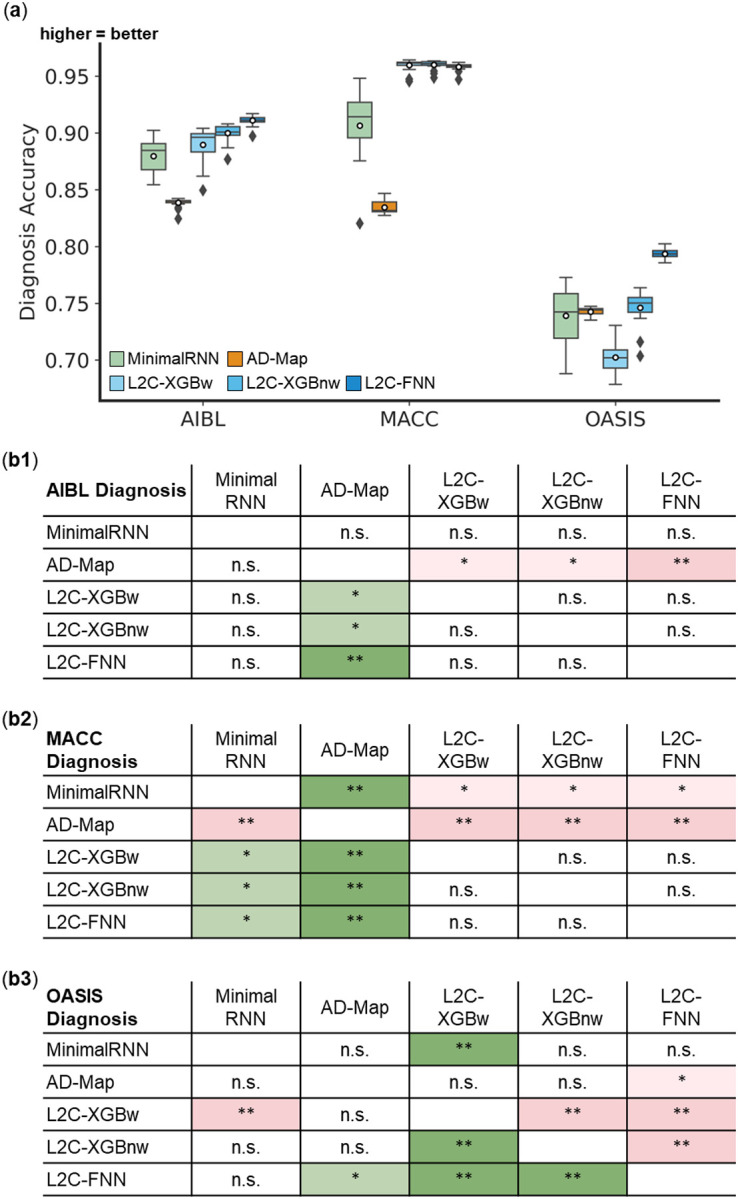
(a) Boxplots display the variability across 20 trained models (from ADNI) for clinical diagnosis prediction assessed using mAUC. The x-axis denotes the test dataset used for evaluation. (b) Statistical significance in the prediction error between all models. Each row shows the statistical difference between a model and all other models. For example, the first row of each 5 × 5 table corresponds to the statistical difference between MinimalRNN and other models – green indicates that MinimalRNN performs better, while red indicates that MinimalRNN performs worse. Therefore, the colors are always flipped between red and green across the diagonal. “*” indicates p < 0.05 and statistical significance after multiple comparisons correction (FDR q < 0.05). “**” indicates p < 0.001 and statistical significance after multiple comparisons correction (FDR q < 0.05). “***” indicates p < 0.00001 and statistical significance after multiple comparisons correction (FDR q < 0.05). “n.s.” indicates no statistical significance (p ≥ 0.05) or did not survive FDR correction.
3.5. Further analyses
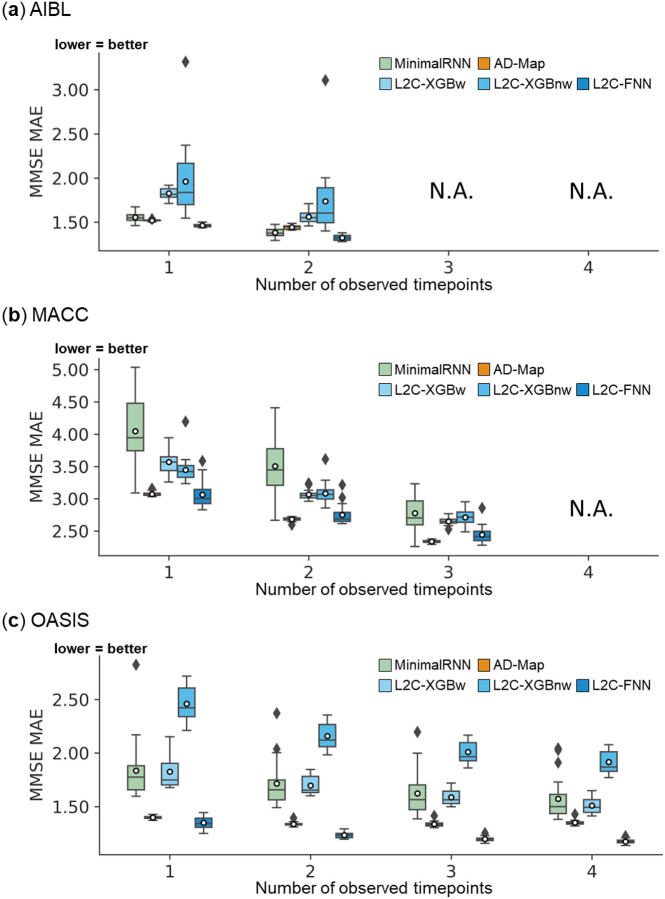
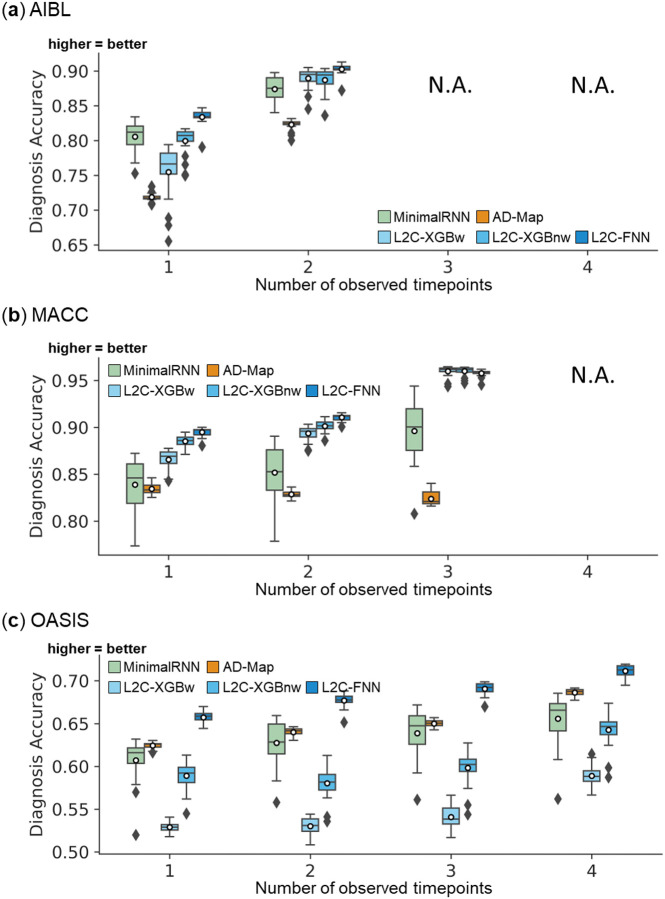
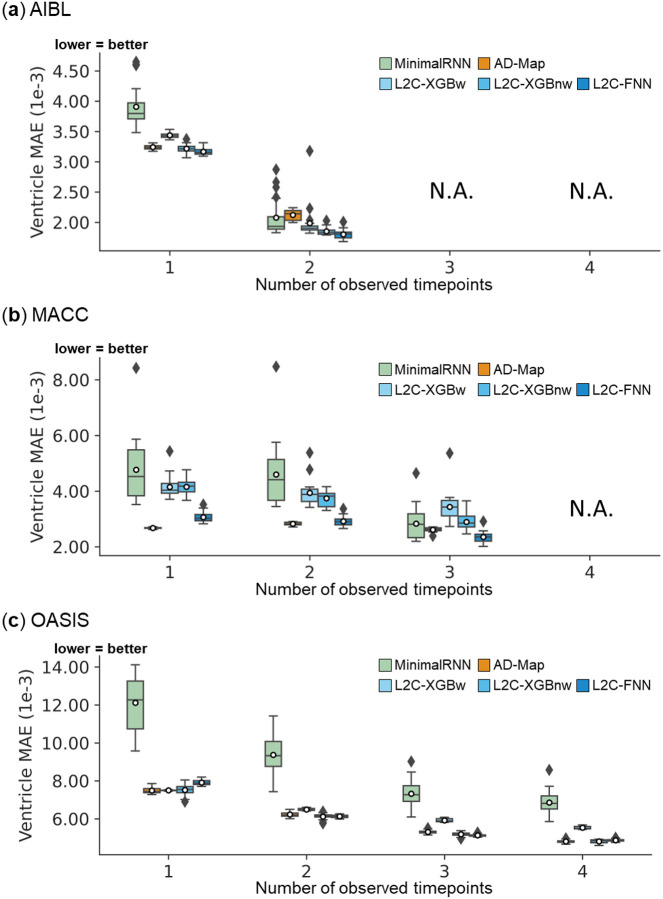
3.5.1. L2C-FNN compared favorably to other models across varying input timepoints
Figures 7 to 9 show the cross-dataset prediction performance of MinimalRNN, AD-Map and three FROG variants (L2C-XGBw, L2C-XGBnw and L2C-FNN) with varying number of input time points. Due to the constraints of the datasets, the maximum number of input timepoints for each participant is only 2 for AIBL and 3 for MACC. Therefore, results for AIBL with 3 and 4 timepoints and for MACC with 4 timepoints are marked as “N.A.”
Figure 7. Cross-cohort MMSE prediction performance using different numbers of input timepoints (after training with all timepoints in ADNI).
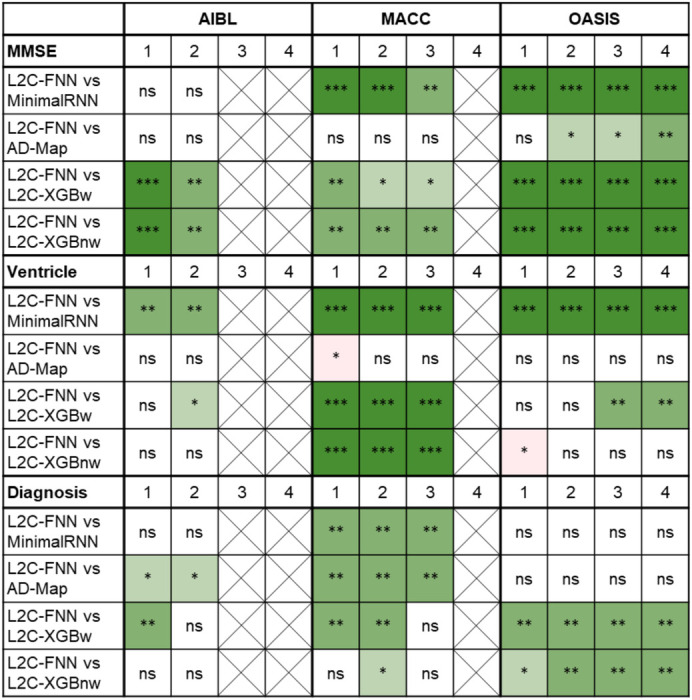
L2C-FNN compared favorably with respect to other approaches across three external test datasets. Results of statistical tests between L2C-FNN and other approaches are reported in Table 10.
Figure 9. Cross-cohort clinical diagnosis prediction performance using different numbers of input timepoints (after training with all timepoints in ADNI):
L2C-FNN significantly outperformed almost all other approaches across three external test datasets using different number of input timepoints. Results of statistical tests between L2C-FNN and other approaches are reported in Table 10.
Table 10 shows the results of statistical tests comparing L2C-FNN and other approaches. Overall, L2C-FNN consistently matched or outperformed other approaches across all datasets and different number of observed timepoints, with only two exceptions (Table 10). The first exception was that AD-Map was statistically better than L2C-FNN when predicting ventricle volume with 1 input timepoint in the MACC dataset (Table 10). The second exception was that L2C-XGBnw was statistically better than L2C-FNN when predicting ventricle volume with 1 input timepoint in the OASIS dataset (Table 10).
Table 10.
Statistical significance between L2C-FNN and other approaches for cross-cohort MMSE, ventricle volume, and clinical diagnosis prediction performance, using different numbers of input timepoints (after training with all timepoints in ADNI).
|
“*” indicates p < 0.05 and significance after multiple comparisons correction (FDR q < 0.05). “**” indicates p < 0.001 and significance after multiple comparisons correction (FDR q < 0.05). “***” indicates p < 0.00001 and significance after multiple comparisons correction (FDR q < 0.05). “ns” indicates no significance (p ≥ 0.05) or did not survive FDR correction. “Cross” indicates data was not available for evaluation. Green indicates that L2C-FNN was statistically better than other approaches compared, while red indicates that it was statistically worse.
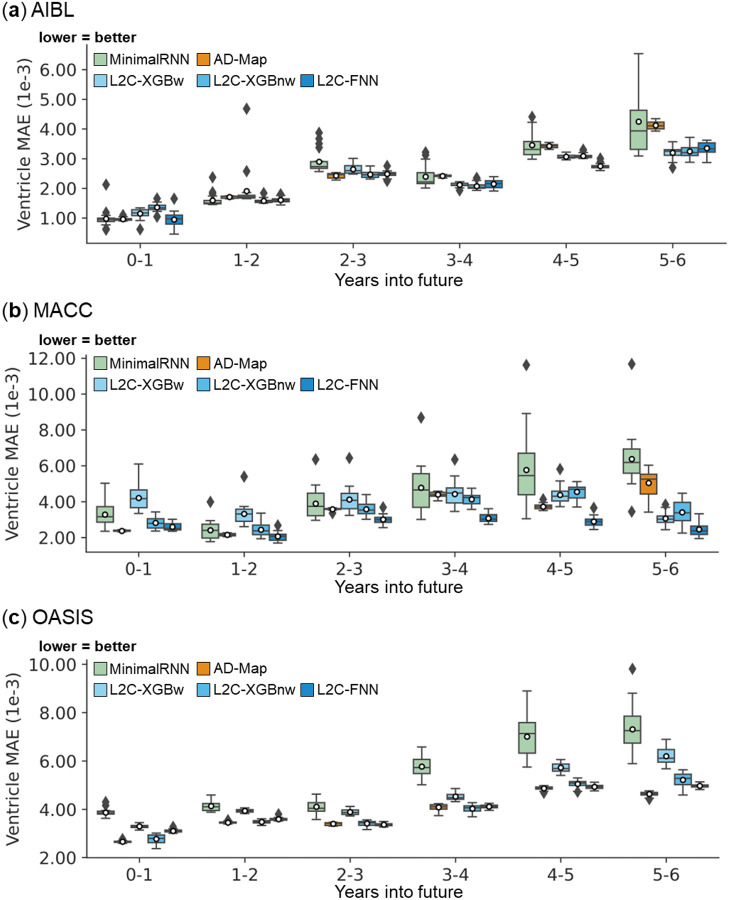
3.5.2. L2C-FNN compared favorably with other methods for all yearly intervals
Figures 10 to 12 show the yearly breakdown in prediction performance from Figures 4 to 6, extending up to 6 years into the future. As anticipated, the prediction accuracy for all algorithms declines as the prediction horizon increases. Table 11 shows the results of statistical tests comparing L2C-FNN with other approaches. L2C-FNN consistently matched or outperformed other methods from year 1 to year 6 across all datasets with two exceptions (Table 11). The exception was that AD-Map was statistically better than L2C-FNN when predicting MMSE in year 0–1 and year 1–2 in the MACC dataset.
Figure 10. Cross-cohort MMSE prediction performance (Figure 4) broken down into yearly intervals up to 6 years into the future.
Note that the last observed time point is at month 0, so year 0–1 means that the prediction was for a future observation at 0 < month ≤ 12, year 1–2 means that the prediction was for a future observation at 12 < month ≤ 24, etc. All algorithms became worse further into the future. L2C-FNN was comparable to or better than all models across all years in three external test datasets except AD-Map in MACC for years 0–1 and 1–2.
Figure 12. Cross-cohort clinical diagnosis prediction performance (Figure 6) broken down into yearly intervals up to 6 years into the future.
Note that the last observed time point is at month 0, so year 0–1 means that the prediction was for a future observation at 0 < month ≤ 12, year 1–2 means that the prediction was for a future observation at 12 < month ≤ 24, etc. All algorithms became worse further into the future. L2C-FNN was comparable to or better than all models across all years in three external test datasets.
Table 11.
Statistical significance between L2C-FNN and other approaches for cross-cohort MMSE, ventricle volume, and clinical diagnosis prediction performance (Figure 4–6) broken down into yearly intervals up to 6 years into the future.
| AIBL | MACC | OASIS | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MMSE | 0–1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | 0–1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | 0–1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 |
| L2C-FNN vs MinimalRNN | ns | ns | ns | ns | ns | ns | ns | ** | *** | ** | ns | ns | ** | * | ** | ** | ** | *** |
| L2C-FNN vs AD-Map | ns | ns | ns | ns | * | ns | *** | ** | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns |
| L2C-FNN vs L2C-XGBw | * | *** | ns | ns | * | ns | ns | ns | ns | ** | ns | ns | *** | *** | ** | *** | *** | *** |
| L2C-FNN vs L2C-XGBnw | ns | *** | * | ns | ** | ns | * | *** | * | ** | ns | ns | *** | ** | ** | * | ** | *** |
| Ventricle | 0–1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | 0–1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | 0–1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 |
| L2C-FNN vs MinimalRNN | ns | ns | * | ns | *** | ns | ** | ** | ** | ** | * | ns | * | ns | ns | * | ns | ** |
| L2C-FNN vs AD-Map | ns | ns | ns | ns | * | ns | ns | ns | ns | * | ns | ns | ns | ns | ns | ns | ns | ns |
| L2C-FNN vs L2C-XGBw | ns | ** | ns | ns | ns | ns | *** | *** | *** | *** | * | ns | ns | ns | * | ns | ns | ** |
| L2C-FNN vs L2C-XGBnw | * | ns | ns | ns | ns | ns | ns | *** | ** | *** | * | ns | ns | ns | ns | ns | ns | ns |
| Diagnosis | 0–1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | 0–1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | 0–1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 |
| L2C-FNN vs MinimalRNN | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns |
| L2C-FNN vs AD-Map | ns | ** | ns | ns | ns | ns | ** | ** | ** | ** | ns | ns | ns | ns | ** | ns | ns | ns |
| L2C-FNN vs L2C-XGBw | ns | ns | ** | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | * | ** | ns | ** |
| L2C-FNN vs L2C-XGBnw | ns | ns | * | ns | ns | ns | ns | ns | ns | ns | ns | ns | ** | ns | ns | ns | ns | * |
indicates p < 0.05 and significance after multiple comparisons correction (FDR q < 0.05).
indicates p < 0.001 and significance after multiple comparisons correction (FDR q < 0.05).
indicates p < 0.00001 and significance after multiple comparisons correction (FDR q < 0.05).
“ns” indicates no significance (p ≥ 0.05) or did not survive FDR correction. Green indicates L2C-FNN was statistically better than other approaches compared, while red indicated that it was statistically worse.
4. Discussion
In this study, we evaluated the winning algorithm of the TADPOLE challenge FROG, two FROG variants, MinimalRNN and AD-Map in the ADNI dataset, as well as three external datasets. In the ADNI dataset, all three FROG variants performed similarly well and outperformed MinimalRNN and AD-Map for clinical diagnosis. The excellent performance of FROG in clinical diagnosis was consistent with the outcome of the TADPOLE challenge, where FROG was ranked 1st in clinical diagnosis prediction (Marinescu et al., 2021). In the three external datasets, the FROG variant L2C-FNN compared favorably with the other two FROG variants, MinimalRNN and AD-map.
An inherent challenge in the TADPOLE problem set up is the pervasive missing data in each participant. Missing data occurs when participants fail to show up or fail to complete certain tests or scans during visits. In most longitudinal datasets, not all data is collected at all timepoints by design. For example, one visit might only involve MRI scans, while another visit might only involve detailed neuropsychological exams. Therefore, the implication is that in every participant, there is missing data at almost every observed time point.
State-based models, such as MinimalRNN, require specialized techniques to handle the missing data. By contrast, the L2C feature transformation significantly reduces the ratio of missing data. As a result, the input to models, comprising L2C features, contains substantially fewer missing data. This advantage of L2C transformation might explain the advantage of FROG variants over MinimalRNN. Another theoretical disadvantage of MinimalRNN is that each future prediction is based on previous predictions, which might lead to error accumulation (Fan et al., 2019). This error accumulation becomes particularly pronounced in longer-term predictions. This might be another reason why FROG variants outperformed MinimalRNN.
The original FROG algorithm (L2C-XGBw) constructs separate XGBoost models for each target variable and different forecast windows, resulting in a total of 15 models. However, the optimal window ranges might vary significantly between datasets. Furthermore, dividing training samples into different bins based on the forecast interval range reduces the available training samples in each bin. We hypothesized that eliminating forecast window stratification and enabling the model to implicitly leverage temporal information within L2C features (e.g., time since baseline, time since most recent measurements) could enhance model generalizability. To test this hypothesis, we trained a single FNN for all training samples with varying forecast intervals. Experimentally, L2C-FNN outperformed L2C-XGBw in nearly every prediction task (i.e., clinical diagnosis, MMSE, ventricle volume) across all external datasets.
Another feature of L2C-FNN is the use of multi-task learning, such that a single FNN is used to predict all three target variables (ventricle volume, cognition, clinical diagnosis) simultaneously. Multi-task learning leverages shared representations to capture common patterns among related tasks, which might enhance data efficiency, accelerate learning, and mitigate overfitting (Crawshaw, 2020). The FROG variant (L2C-XGBnw) helped to dissociate the effects of multi-task learning and the elimination of forecast window stratification by training a separate XGBoost model for each target variable. L2C-FNN again outperformed L2C-XGBnw in nearly every prediction task (i.e., clinical diagnosis, MMSE, ventricle volume) across all external datasets. Therefore, these results suggest the potential advantage of multi-task learning.
In our evaluation, AD-Map was highly competitive in terms of predicting MMSE and ventricle volume, but performed poorly for clinical diagnosis. Because AD-Map utilized a sigmoid-like parameterization, it might predict continuous variables (e.g., MMSE and ventricle volume) better than categorical variables (e.g., clinical diagnosis). Consistent with the original study (Maheux et al., 2023), we did not directly model clinical diagnosis in the AD-Map algorithm. We have also experimented with including clinical diagnosis in the AD-Map model, which improved clinical diagnosis prediction, but resulted in much worse MMSE and ventricle prediction (not shown).
A limitation of the current study is that the models are trained from a single dataset (ADNI). We expect that models trained from multiple datasets might lead to better generalization to new populations and scanners (Dou et al., 2019; Liu et al., 2020; Chen et al., 2024). Therefore, a potential future work is to collate multiple datasets and train a single L2C-FNN model for future usage. Another limitation is that the current study only considered biomarkers that existed in all four datasets, so blood and PET biomarkers were excluded. Blood and PET biomarkers have been shown to be important markers of AD dementia (Nordberg et al., 2010; Mattsson et al., 2017; Chételat et al., 2020; Chong et al., 2021), therefore future studies could likely benefit from the incorporation of these additional biomarkers.
5. Conclusion
In this study, we evaluated three FROG variants, MinimalRNN and AD-Map in predicting future dementia progression in the ADNI dataset and three external datasets. We found that a FROG variant (L2C-FNN) performed the best in the three external datasets. L2C-FNN maintained better prediction performance regardless of the number of observed timepoints in a participant. L2C-FNN also consistently matched or outperformed other approaches from year 1 to year 6 across all external datasets, underscoring its potential for reliable long-term prediction in dementia progression.
Supplementary Material
Figure 8. Cross-cohort ventricle volume prediction performance using different numbers of input timepoints (after training with all timepoints in ADNI):
L2C-FNN compared favorably with respect to other approaches across three external test datasets, except L2C-XGBnw on OASIS using 1 input timepoint. Results of statistical tests between L2C-FNN and other approaches are reported in Table 10.
Figure 11. Cross-cohort ventricle volume prediction performance (Figure 5) broken down into yearly intervals up to 6 years into the future.
Note that the last observed time point is at month 0, so year 0–1 means that the prediction was for a future observation at 0 < month ≤ 12, year 1–2 means that the prediction was for a future observation at 12 < month ≤ 24, etc. All algorithms became worse further into the future. L2C-FNN was comparable to or better than all models across all years in three external test datasets.
Acknowledgment
We would like to thank Christina Rabe, and Paul Manser from Team FROG for sharing their code with us, which significantly facilitated the current study. This research is supported by the NUS Yong Loo Lin School of Medicine (NUHSRO/2020/124/TMR/LOA), the Singapore National Medical Research Council (NMRC) LCG (OFLCG19May-0035), NMRC CTG-IIT (CTGIIT23jan-0001), NMRC STaR (STaR20nov-0003), NMRC OF-IRG (OFIRG24jan-0030), Singapore Ministry of Health (MOH) Centre Grant (CG21APR1009), the Temasek Foundation (TF2223-IMH-01), and the United States National Institutes of Health (R01MH120080 & R01MH133334). Our computational work was partially performed on resources of the National Supercomputing Centre, Singapore (https://www.nscc.sg). Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not reflect the views of the Singapore NMRC, MOH, Temasek Foundation or USA NIH.
Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.
Data were provided in part by OASIS-3: Longitudinal Multimodal Neuroimaging: Principal Investigators: T. Benzinger, D. Marcus, J. Morris; NIH P30 AG066444, P50 AG00561, P30 NS09857781, P01 AG026276, P01 AG003991, R01 AG043434, UL1 TR000448, R01 EB009352. AV-45 doses were provided by Avid Radiopharmaceuticals, a wholly owned subsidiary of Eli Lilly.
Footnotes
Code availability statement
Code for all five models can be found here (GITHUB_LINK). Two co-authors (L.A. and N.W.) reviewed the code before merging it into the GitHub repository to reduce the chance of coding errors.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Although the goal is to predict indefinitely into the future, evaluation can only rely on the available timepoints in the test set.
Data availability statement
The ADNI and the AIBL datasets can be accessed via the Image & Data Archive (https://ida.loni.usc.edu/). The MACC dataset can be obtained via a data-transfer agreement with the MACC (http://www.macc.sg/). The OASIS dataset can be requested from (https://www.oasis-brains.org/).
References
- Akiba T., Sano S., Yanase T., Ohta T., & Koyama M. (2019). Optuna: A Next-generation Hyperparameter Optimization Framework. Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2623–2631. 10.1145/3292500.3330701 [DOI] [Google Scholar]
- Altman D. G., Vergouwe Y., Royston P., & Moons K. G. M. (2009). Prognosis and prognostic research: Validating a prognostic model. BMJ, 338, b605. 10.1136/bmj.b605 [DOI] [PubMed] [Google Scholar]
- Barandas M., Folgado D., Fernandes L., Santos S., Abreu M., Bota P., Liu H., Schultz T., & Gamboa H. (2020). TSFEL: Time Series Feature Extraction Library. SoftwareX, 11, 100456. 10.1016/j.softx.2020.100456 [DOI] [Google Scholar]
- Basaia S., Agosta F., Wagner L., Canu E., Magnani G., Santangelo R., & Filippi M. (2019). Automated classification of Alzheimer’s disease and mild cognitive impairment using a single MRI and deep neural networks. NeuroImage: Clinical, 21, 101645. 10.1016/j.nicl.2018.101645 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y., & Hochberg Y. (1995). Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society: Series B (Methodological), 57(1), 289–300. 10.1111/j.2517-6161.1995.tb02031.x [DOI] [Google Scholar]
- Bilgel M., Jedynak B. M., & Initiative A. D. N. (2019). Predicting time to dementia using a quantitative template of disease progression. Alzheimer’s & Dementia: Diagnosis,Assessment & Disease Monitoring, 11(1), 205–215. 10.1016/j.dadm.2019.01.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouckaert R. R., & Frank E. (2004). Evaluating the Replicability of Significance Tests for Comparing Learning Algorithms (Dai H., Srikant R., & Zhang C., Eds.; Vol. 3056, pp. 3–12). Springer Berlin; Heidelberg. 10.1007/978-3-540-24775-3_3 [DOI] [Google Scholar]
- Burns D. K., Alexander R. C., Welsh-Bohmer K. A., Culp M., Chiang C., O’Neil J., Evans R. M., Harrigan P., Plassman B. L., Burke J. R., Wu J., Lutz M. W., Haneline S., Schwarz A. J., Schneider L. S., Yaffe K., Saunders A. M., Ratti E., Aarsland D., … Zimmerman C. (2021). Safety and efficacy of pioglitazone for the delay of cognitive impairment in people at risk of Alzheimer’s disease (TOMMORROW): A prognostic biomarker study and a phase 3, randomised, double-blind, placebo-controlled trial. The Lancet Neurology, 20(7), 537–547. 10.1016/S1474-4422(21)00043-0 [DOI] [PubMed] [Google Scholar]
- Chekroud A. M., Hawrilenko M., Loho H., Bondar J., Gueorguieva R., Hasan A., Kambeitz J., Corlett P. R., Koutsouleris N., Krumholz H. M., Krystal J. H., & Paulus M. (2024). Illusory generalizability of clinical prediction models. Science, 383(6679), 164–167. 10.1126/science.adg8538 [DOI] [PubMed] [Google Scholar]
- Chen P., An L., Wulan N., Zhang C., Zhang S., Ooi L. Q. R., Kong R., Chen J., Wu J., Chopra S., Bzdok D., Eickhoff S. B., Holmes A. J., & Yeo B. T. T. (2024). Multilayer meta-matching: Translating phenotypic prediction models from multiple datasets to small data. Imaging Neuroscience, 2, 1–22. 10.1162/imag_a_00233 [DOI] [Google Scholar]
- Chen T., & Guestrin C. (2016). XGBoost: A Scalable Tree Boosting System. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 785–794. 10.1145/2939672.2939785 [DOI] [Google Scholar]
- Chételat G., Arbizu J., Barthel H., Garibotto V., Law I., Morbelli S., Giessen E. van de, Agosta F., Barkhof F., Brooks D. J., Carrillo M. C., Dubois B., Fjell A. M., Frisoni G. B., Hansson O., Herholz K., Hutton B. F., Jack C. R., Lammertsma A. A., … Drzezga A. (2020). Amyloid-PET and 18F-FDG-PET in the diagnostic investigation of Alzheimer’s disease and other dementias. The Lancet Neurology, 19(11), 951–962. 10.1016/S1474-4422(20)30314-8 [DOI] [PubMed] [Google Scholar]
- Chong J. R., Ashton N. J., Karikari T. K., Tanaka T., Saridin F. N., Reilhac A., Robins E. G., Nai Y.-H., Vrooman H., Hilal S., Zetterberg H., Blennow K., Lai M. K. P., & Chen C. P. (2021). Plasma P-tau181 to Aβ42 ratio is associated with brain amyloid burden and hippocampal atrophy in an Asian cohort of Alzheimer’s disease patients with concomitant cerebrovascular disease. Alzheimer’s & Dementia, 17(10), 1649–1662. 10.1002/alz.12332 [DOI] [PubMed] [Google Scholar]
- Cohen J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.). Routledge. 10.4324/9780203771587 [DOI] [Google Scholar]
- Courchesne E., Chisum H. J., Townsend J., Cowles A., Covington J., Egaas B., Harwood M., Hinds S., & Press G. A. (2000). Normal Brain Development and Aging: Quantitative Analysis at in Vivo MR Imaging in Healthy Volunteers. Radiology, 216(3), 672–682. 10.1148/radiology.216.3.r00au37672 [DOI] [PubMed] [Google Scholar]
- Crawshaw M. (2020). Multi-Task Learning with Deep Neural Networks: A Survey. ArXiv. https://www.semanticscholar.org/paper/Multi-Task-Learning-with-Deep-Neural-Networks%3A-A-Crawshaw/74f23063ca77f5b1caa3770a5957ae5fc565843e [Google Scholar]
- Cummings J., Feldman H. H., & Scheltens P. (2019). The “rights” of precision drug development for Alzheimer’s disease. Alzheimer’s Research & Therapy, 11(1), 76. 10.1186/s13195-019-0529-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Vugt M. E., & Verhey F. R. J. (2013). The impact of early dementia diagnosis and intervention on informal caregivers. Progress in Neurobiology, 110, 54–62. 10.1016/j.pneurobio.2013.04.005 [DOI] [PubMed] [Google Scholar]
- Deng H., Runger G., Tuv E., & Vladimir M. (2013). A time series forest for classification and feature extraction. Information Sciences, 239, 142–153. 10.1016/j.ins.2013.02.030 [DOI] [Google Scholar]
- Desikan R. S., Ségonne F., Fischl B., Quinn B. T., Dickerson B. C., Blacker D., Buckner R. L., Dale A. M., Maguire R. P., Hyman B. T., Albert M. S., & Killiany R. J. (2006). An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage, 31(3), 968–980. 10.1016/j.neuroimage.2006.01.021 [DOI] [PubMed] [Google Scholar]
- Dou Q., Castro D. C., Kamnitsas K., & Glocker B. (2019). Domain generalization via model-agnostic learning of semantic features. In Proceedings of the 33rd International Conference on Neural Information Processing Systems (pp. 6450–6461). Curran Associates Inc. [Google Scholar]
- Dubois B., Hampel H., Feldman H. H., Scheltens P., Aisen P., Andrieu S., Bakardjian H., Benali H., Bertram L., Blennow K., Broich K., Cavedo E., Crutch S., Dartigues J.-F., Duyckaerts C., Epelbaum S., Frisoni G. B., Gauthier S., Genthon R., … Jack C. R. (2016). Preclinical Alzheimer’s disease: Definition, natural history, and diagnostic criteria. Alzheimer’s & Dementia : The Journal of the Alzheimer’s Association, 12(3), 292–323. 10.1016/j.jalz.2016.02.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- El-Sappagh S., Alonso J. M., Islam S. M. R., Sultan A. M., & Kwak K. S. (2021). A multilayer multimodal detection and prediction model based on explainable artificial intelligence for Alzheimer’s disease. Scientific Reports, 11(1), 2660. 10.1038/s41598-021-82098-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksson D., Bindel D., & Shoemaker C. A. (2019). pySOT and POAP: An event-driven asynchronous framework for surrogate optimization (arXiv:1908.00420). arXiv. 10.48550/arXiv.1908.00420 [DOI] [Google Scholar]
- Fan C., Wang J., Gang W., & Li S. (2019). Assessment of deep recurrent neural network-based strategies for short-term building energy predictions. Applied Energy, 236, 700–710. 10.1016/j.apenergy.2018.12.004 [DOI] [Google Scholar]
- Fischl B., Salat D. H., Busa E., Albert M., Dieterich M., Haselgrove C., van der Kouwe A., Killiany R., Kennedy D., Klaveness S., Montillo A., Makris N., Rosen B., & Dale A. M. (2002). Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron, 33(3), 341–355. 10.1016/s0896-6273(02)00569-x [DOI] [PubMed] [Google Scholar]
- Fowler C., Rainey-Smith S. R., Bird S., Bomke J., Bourgeat P., Brown B. M., Burnham S. C., Bush A. I., Chadunow C., Collins S., Doecke J., Doré V., Ellis K. A., Evered L., Fazlollahi A., Fripp J., Gardener S. L., Gibson S., Grenfell R., … the AIBL investigators. (2021). Fifteen Years of the Australian Imaging, Biomarkers and Lifestyle (AIBL) Study: Progress and Observations from 2,359 Older Adults Spanning the Spectrum from Cognitive Normality to Alzheimer’s Disease. Journal of Alzheimer’s Disease Reports, 5(1), 443–468. 10.3233/ADR-210005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghazi M., Nielsen M., Pai A., Cardoso M. J., Modat M., Ourselin S., & Sørensen L. (2019). Training recurrent neural networks robust to incomplete data: Application to Alzheimer’s disease progression modeling. Medical Image Analysis, 53, 39–46. 10.1016/j.media.2019.01.004 [DOI] [PubMed] [Google Scholar]
- Ghazi M., Nielsen M., Pai A., Modat M., Jorge Cardoso M., Ourselin S., & Sørensen L. (2021). Robust parametric modeling of Alzheimer’s disease progression. NeuroImage, 225, 117460. 10.1016/j.neuroimage.2020.117460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good P. (2000). Testing Hypotheses. In Good P. (Ed.), Permutation Tests: A Practical Guide to Resampling Methods for Testing Hypotheses (pp. 31–53). Springer. 10.1007/978-1-4757-3235-1_3 [DOI] [Google Scholar]
- Hampel H., Hardy J., Blennow K., Chen C., Perry G., Kim S. H., Villemagne V. L., Aisen P., Vendruscolo M., Iwatsubo T., Masters C. L., Cho M., Lannfelt L., Cummings J. L., & Vergallo A. (2021). The Amyloid-β Pathway in Alzheimer’s Disease. Molecular Psychiatry, 26(10), 5481–5503. 10.1038/s41380-021-01249-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hand D. J., & Till R. J. (2001). A Simple Generalisation of the Area Under the ROC Curve for Multiple Class Classification Problems. Machine Learning, 45(2), 171–186. 10.1023/A:1010920819831 [DOI] [Google Scholar]
- Hebling Vieira B., Liem F., Dadi K., Engemann D. A., Gramfort A., Bellec P., Craddock R. C., Damoiseaux J. S., Steele C. J., Yarkoni T., Langer N., Margulies D. S., & Varoquaux G. (2022). Predicting future cognitive decline from non-brain and multimodal brain imaging data in healthy and pathological aging. Neurobiology of Aging, 118, 55–65. 10.1016/j.neurobiolaging.2022.06.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrick R., Horton W., Olsen T., McKay M., Archie K. A., & Marcus D. S. (2016). XNAT Central: Open Sourcing Imaging Research Data. NeuroImage, 124(Pt B), 1093–1096. 10.1016/j.neuroimage.2015.06.076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilal S., Tan C. S., van Veluw S. J., Xu X., Vrooman H., Tan B. Y., Venketasubramanian N., Biessels G. J., & Chen C. (2020). Cortical cerebral microinfarcts predict cognitive decline in memory clinic patients. Journal of Cerebral Blood Flow and Metabolism: Official Journal of the International Society of Cerebral Blood Flow and Metabolism, 40(1), 44–53. 10.1177/0271678X19835565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iddi S., Li D., Aisen P. S., Rafii M. S., Thompson W. K., Donohue M. C., & for the Alzheimer’s Disease Neuroimaging Initiative. (2019). Predicting the course of Alzheimer’s progression. Brain Informatics, 6(1), 6. 10.1186/s40708-019-0099-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ilievski I., Akhtar T., Feng J., & Shoemaker C. (2017). Efficient Hyperparameter Optimization for Deep Learning Algorithms Using Deterministic RBF Surrogates. Proceedings of the AAAI Conference on Artificial Intelligence, 31(1), Article 1. 10.1609/aaai.v31i1.10647 [DOI] [Google Scholar]
- Jack C. R., Bennett D. A., Blennow K., Carrillo M. C., Dunn B., Haeberlein S. B., Holtzman D. M., Jagust W., Jessen F., Karlawish J., Liu E., Molinuevo J. L., Montine T., Phelps C., Rankin K. P., Rowe C. C., Scheltens P., Siemers E., Snyder H. M., … Contributors. (2018). NIA-AA Research Framework: Toward a biological definition of Alzheimer’s disease. Alzheimer’s & Dementia: The Journal of the Alzheimer’s Association, 14(4), 535–562. 10.1016/j.jalz.2018.02.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack C. R., Bernstein M. A., Fox N. C., Thompson P., Alexander G., Harvey D., Borowski B., Britson P. J., L Whitwell J., Ward C., Dale A. M., Felmlee J. P., Gunter J. L., Hill D. L. G., Killiany R., Schuff N., Fox-Bosetti S., Lin C., Studholme C., … Weiner M. W. (2008). The Alzheimer’s Disease Neuroimaging Initiative (ADNI): MRI methods. Journal of Magnetic Resonance Imaging: JMRI, 27(4), 685–691. 10.1002/jmri.21049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack C. R., Knopman D. S., Jagust W. J., Shaw L. M., Aisen P. S., Weiner M. W., Petersen R. C., & Trojanowski J. Q. (2010). Hypothetical model of dynamic biomarkers of the Alzheimer’s pathological cascade. The Lancet Neurology, 9(1), 119–128. 10.1016/S1474-4422(09)70299-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jedynak B. M., Lang A., Liu B., Katz E., Zhang Y., Wyman B. T., Raunig D., Jedynak C. P., Caffo B., & Prince J. L. (2012). A computational neurodegenerative disease progression score: Method and results with the Alzheimer’s disease neuroimaging initiative cohort. NeuroImage, 63(3), 1478–1486. 10.1016/j.neuroimage.2012.07.059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins R., Fox N. C., Rossor A. M., Harvey R. J., & Rossor M. N. (2000). Intracranial volume and Alzheimer disease: Evidence against the cerebral reserve hypothesis. Archives of Neurology, 57(2), 220–224. 10.1001/archneur.57.2.220 [DOI] [PubMed] [Google Scholar]
- Jung W., Jun E., & Suk H.-I. (2021). Deep recurrent model for individualized prediction of Alzheimer’s disease progression. NeuroImage, 237, 118143. 10.1016/j.neuroimage.2021.118143 [DOI] [PubMed] [Google Scholar]
- Kong R., Li J., Orban C., Sabuncu M. R., Liu H., Schaefer A., Sun N., Zuo X.-N., Holmes A. J., Eickhoff S. B., & Yeo B. T. T. (2019). Spatial Topography of Individual-Specific Cortical Networks Predicts Human Cognition, Personality, and Emotion. Cerebral Cortex (New York, N.Y.: 1991), 29(6), 2533–2551. 10.1093/cercor/bhy123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koval I., Bône A., Louis M., Lartigue T., Bottani S., Marcoux A., Samper-González J., Burgos N., Charlier B., Bertrand A., Epelbaum S., Colliot O., Allassonnière S., & Durrleman S. (2021). AD Course Map charts Alzheimer’s disease progression. Scientific Reports, 11(1), Article 1. 10.1038/s41598-021-87434-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- LaMontagne, Benzinger Tammie LS., Morris John C., Keefe Sarah, Hornbeck Russ, Xiong Chengjie, Grant Elizabeth, Hassenstab Jason, Moulder Krista, Vlassenko Andrei G., Raichle Marcus E., Cruchaga Carlos, & Marcus Daniel. (2019). OASIS-3: Longitudinal Neuroimaging, Clinical, and Cognitive Dataset for Normal Aging and Alzheimer Disease. medRxiv, 2019.12.13.19014902. 10.1101/2019.12.13.19014902 [DOI] [Google Scholar]
- Li D., Iddi S., Thompson W. K., Donohue M. C., & Alzheimer’s Disease Neuroimaging Initiative. (2019). Bayesian latent time joint mixed effect models for multicohort longitudinal data. Statistical Methods in Medical Research, 28(3), 835–845. 10.1177/0962280217737566 [DOI] [PubMed] [Google Scholar]
- Li J., Kong R., Liégeois R., Orban C., Tan Y., Sun N., Holmes A. J., Sabuncu M. R., Ge T., & Yeo B. T. T. (2019). Global signal regression strengthens association between resting-state functional connectivity and behavior. NeuroImage, 196, 126–141. 10.1016/j.neuroimage.2019.04.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Q., Dou Q., Yu L., & Heng P. A. (2020). MS-Net: Multi-Site Network for Improving Prostate Segmentation With Heterogeneous MRI Data. IEEE Transactions on Medical Imaging, 39(9), 2713–2724. 10.1109/TMI.2020.2974574 [DOI] [PubMed] [Google Scholar]
- Maas A. L. (2013). Rectifier Nonlinearities Improve Neural Network Acoustic Models. https://www.semanticscholar.org/paper/Rectifier-Nonlinearities-Improve-Neural-Network-Maas/367f2c63a6f6a10b3b64b8729d601e69337ee3cc
- Maheux E., Koval I., Ortholand J., Birkenbihl C., Archetti D., Bouteloup V., Epelbaum S., Dufouil C., Hofmann-Apitius M., & Durrleman S. (2023). Forecasting individual progression trajectories in Alzheimer’s disease. Nature Communications, 14(1), 761. 10.1038/s41467-022-35712-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marinescu R. V., Oxtoby N. P., Young A. L., Bron E. E., Toga A. W., Weiner M. W., Barkhof F., Fox N. C., Eshaghi A., Toni T., Salaterski M., Lunina V., Ansart M., Durrleman S., Lu P., Iddi S., Li D., Thompson W. K., Donohue M. C., … The Alzheimer’s Disease Neuroimaging Initiative. (2021). The Alzheimer’s Disease Prediction Of Longitudinal Evolution (TADPOLE) Challenge: Results after 1 Year Follow-up. Machine Learning for Biomedical Imaging, 1(December 2021 issue), 1–60. 10.59275/j.melba.2021-2dcc [DOI] [Google Scholar]
- Marinescu R. V., Oxtoby N. P., Young A. L., Bron E. E., Toga A. W., Weiner M. W., Barkhof F., Fox N. C., Golland P., Klein S., & Alexander D. C. (2019). TADPOLE Challenge: Accurate Alzheimer’s disease prediction through crowdsourced forecasting of future data. PRedictive Intelligence in MEdicine. PRIME (Workshop), 11843, 1–10. 10.1007/978-3-030-32281-6_1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattsson N., Andreasson U., Zetterberg H., Blennow K., & for the Alzheimer’s Disease Neuroimaging Initiative. (2017). Association of Plasma Neurofilament Light With Neurodegeneration in Patients With Alzheimer Disease. JAMA Neurology, 74(5), 557–566. 10.1001/jamaneurol.2016.6117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nanopoulos A., Alcock R., & Manolopoulos Y. (2001). Feature-based classification of time-series data. In Information processing and technology (pp. 49–61). Nova Science Publishers, Inc. [Google Scholar]
- Nguyen M., He T., An L., Alexander D. C., Feng J., & Yeo B. T. T. (2020). Predicting Alzheimer’s disease progression using deep recurrent neural networks. NeuroImage, 222, 117203. 10.1016/j.neuroimage.2020.117203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordberg A., Rinne J. O., Kadir A., & Långström B. (2010). The use of PET in Alzheimer disease. Nature Reviews Neurology, 6(2), 78–87. 10.1038/nrneurol.2009.217 [DOI] [PubMed] [Google Scholar]
- O’Bryant S. E., Lacritz L. H., Hall J., Waring S. C., Chan W., Khodr Z. G., Massman P. J., Hobson V., & Cullum C. M. (2010). Validation of the New Interpretive Guidelines for the Clinical Dementia Rating Scale Sum of Boxes Score in the National Alzheimer’s Coordinating Center Database. Archives of Neurology, 67(6), 746–749. 10.1001/archneurol.2010.115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxtoby N. P. (2023). Data-Driven Disease Progression Modeling. In Colliot O. (Ed.), Machine Learning for Brain Disorders. Humana. http://www.ncbi.nlm.nih.gov/books/NBK597485/ [PubMed] [Google Scholar]
- Oxtoby N. P., Shand C., Cash D. M., Alexander D. C., & Barkhof F. (2022). Targeted Screening for Alzheimer’s Disease Clinical Trials Using Data-Driven Disease Progression Models. Frontiers in Artificial Intelligence, 5, 660581. 10.3389/frai.2022.660581 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paszke A., Gross S., Massa F., Lerer A., Bradbury J., Chanan G., Killeen T., Lin Z., Gimelshein N., Antiga L., Desmaison A., Kopf A., Yang E., DeVito Z., Raison M., Tejani A., Chilamkurthy S., Steiner B., Fang L., … Chintala S. (2019). PyTorch: An Imperative Style, High-Performance Deep Learning Library. Advances in Neural Information Processing Systems, 32. https://papers.nips.cc/paper_files/paper/2019/hash/bdbca288fee7f92f2bfa9f7012727740-Abstract.html [Google Scholar]
- Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V., Vanderplas J., Passos A., Cournapeau D., Brucher M., Perrot M., & Duchesnay É. (2011). Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research, 12(85), 2825–2830. [Google Scholar]
- Petersen R. C., Aisen P. S., Beckett L. A., Donohue M. C., Gamst A. C., Harvey D. J., Jack C. R., Jagust W. J., Shaw L. M., Toga A. W., Trojanowski J. Q., & Weiner M. W. (2010). Alzheimer’s Disease Neuroimaging Initiative (ADNI): Clinical characterization. Neurology, 74(3), 201–209. 10.1212/WNL.0b013e3181cb3e25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian N. (1999). On the momentum term in gradient descent learning algorithms. Neural Networks, 12(1), 145–151. 10.1016/S0893-6080(98)00116-6 [DOI] [PubMed] [Google Scholar]
- Qiu S., Joshi P. S., Miller M. I., Xue C., Zhou X., Karjadi C., Chang G. H., Joshi A. S., Dwyer B., Zhu S., Kaku M., Zhou Y., Alderazi Y. J., Swaminathan A., Kedar S., Saint-Hilaire M.-H., Auerbach S. H., Yuan J., Sartor E. A., … Kolachalama V. B. (2020). Development and validation of an interpretable deep learning framework for Alzheimer’s disease classification. Brain, 143(6), 1920–1933. 10.1093/brain/awaa137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahim M., Thirion B., Bzdok D., Buvat I., & Varoquaux G. (2017). Joint prediction of multiple scores captures better individual traits from brain images. NeuroImage, 158, 145–154. 10.1016/j.neuroimage.2017.06.072 [DOI] [PubMed] [Google Scholar]
- Rasmussen J., & Langerman H. (2019). Alzheimer’s Disease—Why We Need Early Diagnosis. Degenerative Neurological and Neuromuscular Disease, 9, 123–130. 10.2147/DNND.S228939 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheltens P., Blennow K., Breteler M. M. B., Strooper B. de, Frisoni G. B., Salloway S., & Flier W. M. V. der. (2016). Alzheimer’s disease. The Lancet, 388(10043), 505–517. 10.1016/S0140-6736(15)01124-1 [DOI] [PubMed] [Google Scholar]
- Scheltens P., De Strooper B., Kivipelto M., Holstege H., Chételat G., Teunissen C. E., Cummings J., & van der Flier W. M. (2021). Alzheimer’s disease. Lancet (London, England), 397(10284), 1577–1590. 10.1016/S0140-6736(20)32205-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selkoe D. J., & Hardy J. (2016). The amyloid hypothesis of Alzheimer’s disease at 25 years. EMBO Molecular Medicine, 8(6), 595–608. 10.15252/emmm.201606210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava N., Hinton G., Krizhevsky A., Sutskever I., & Salakhutdinov R. (2014). Dropout: A Simple Way to Prevent Neural Networks from Overfitting. Journal of Machine Learning Research, 15(56), 1929–1958. [Google Scholar]
- Steyerberg E. W. (2019). Validation of Prediction Models. In Steyerberg E. W.(Ed.), Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating (pp. 329–344). Springer International Publishing. 10.1007/978-3-030-16399-0_17 [DOI] [Google Scholar]
- Sutskever I., Martens J., Dahl G., & Hinton G. (2013). On the importance of initialization and momentum in deep learning. Proceedings of the 30th International Conference on Machine Learning, 1139–1147. https://proceedings.mlr.press/v28/sutskever13.html [Google Scholar]
- Tariot P. N., Boada M., Lanctôt K. L., Hahn-Pedersen J., Dabbous F., Udayachalerm S., Raket L. L., Halchenko Y., Michalak W., Weidner W., & Cummings J. (2024). Relationships of change in Clinical Dementia Rating (CDR) on patient outcomes and probability of progression: Observational analysis. Alzheimer’s Research & Therapy, 16(1), 36. 10.1186/s13195-024-01399-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- the ADNI team. (2023). ADNIMERGE: Alzheimer’s Disease Neuroimaging Initiative (0.0.1) [R package]. https://adni.bitbucket.io/index.html
- Van Dyck C. H., Swanson C. J., Aisen P., Bateman R. J., Chen C., Gee M., Kanekiyo M., Li D., Reyderman L., Cohen S., Froelich L., Katayama S., Sabbagh M., Vellas B., Watson D., Dhadda S., Irizarry M., Kramer L. D., & Iwatsubo T. (2023). Lecanemab in Early Alzheimer’s Disease. The New England Journal of Medicine, 388(1), 9–21. 10.1056/NEJMoa2212948 [DOI] [PubMed] [Google Scholar]
- Varoquaux G. (2018). Cross-validation failure: Small sample sizes lead to large error bars. NeuroImage, 180, 68–77. 10.1016/j.neuroimage.2017.06.061 [DOI] [PubMed] [Google Scholar]
- Venkatraghavan V., Bron E. E., Niessen W. J., & Klein S. (2019). Disease progression timeline estimation for Alzheimer’s disease using discriminative event based modeling. NeuroImage, 186, 518–532. 10.1016/j.neuroimage.2018.11.024 [DOI] [PubMed] [Google Scholar]
- Villemagne V. L., Burnham S., Bourgeat P., Brown B., Ellis K. A., Salvado O., Szoeke C., Macaulay S. L., Martins R., Maruff P., Ames D., Rowe C. C., Masters C. L., & Australian Imaging Biomarkers and Lifestyle (AIBL) Research Group. (2013). Amyloid β deposition, neurodegeneration, and cognitive decline in sporadic Alzheimer’s disease: A prospective cohort study. The Lancet. Neurology, 12(4), 357–367. 10.1016/S1474-4422(13)70044-9 [DOI] [PubMed] [Google Scholar]
- Wang C., Li Y., Tsuboshita Y., Sakurai T., Goto T., Yamaguchi H., Yamashita Y., Sekiguchi A., & Tachimori H. (2022). A high-generalizability machine learning framework for predicting the progression of Alzheimer’s disease using limited data. Npj Digital Medicine, 5(1), Article 1. 10.1038/s41746-022-00577-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu L., Wu H., He C., Wang J., Zhang C., Nie F., & Chen L. (2022). Multi-modal sequence learning for Alzheimer’s disease progression prediction with incomplete variable-length longitudinal data. Medical Image Analysis, 82, 102643. 10.1016/j.media.2022.102643 [DOI] [PubMed] [Google Scholar]
- Zhang R., Simon G., & Yu F. (2017). Advancing Alzheimer’s Research: A Review of Big Data Promises. International Journal of Medical Informatics, 106, 48–56. 10.1016/j.ijmedinf.2017.07.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y., Wong L., & Goh W. W. B. (2020). How to do quantile normalization correctly for gene expression data analyses. Scientific Reports, 10(1), Article 1. 10.1038/s41598-020-72664-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou K., Liu Z., Qiao Y., Xiang T., & Loy C. C. (2022). Domain Generalization: A Survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1–20. 10.1109/TPAMI.2022.3195549 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The ADNI and the AIBL datasets can be accessed via the Image & Data Archive (https://ida.loni.usc.edu/). The MACC dataset can be obtained via a data-transfer agreement with the MACC (http://www.macc.sg/). The OASIS dataset can be requested from (https://www.oasis-brains.org/).