Stitchprofiles.uio.no: analysis of partly melted DNA conformations using stitch profiles

Abstract

In this study, we describe a web server that performs computations on DNA melting, thus predicting the localized separation of the two strands for sequences provided by the users. The output types are stitch profiles, melting curves, probability profiles, etc. Stitch profile diagrams visualize the ensemble of alternative conformations that DNA can adopt with different probabilities. For example, a stitch profile shows the possible loop openings in terms of their locations, sizes, probabilities and fluctuations at a given temperature. Sequences with lengths up to several tens or hundreds of kilobase pairs can be analysed. The tools are freely available at http://stitchprofiles.uio.no.

INTRODUCTION

Many software and web tools exist for computing various aspects of melting of double-stranded DNA (1–7). The repertoire of output that they provide is limited to a few categories. For example, in category comprises the plots of some quantity along the chain describing the base-pair stabilities or states. We report a web server that adds to the repertoire a recently developed type of diagram called stitch profiles. A DNA stitch profile indicates the multitude of possible conformations that a partly melted DNA may adopt, and it shows what regions can be base-paired or melted more specifically than the traditional plots. The web server provides a new type of information that may be useful in genomics (8,9), in studying the relationship between the structure and the biological functions of DNA, in comparison with the single-molecule techniques, and as a part of the experimental techniques that utilize the melting and the hybridization properties of DNA (3,5).

INPUT

When using the web server, a user must specify a DNA sequence by either (i) uploading a text file with the sequence, or (ii) retrieving the sequence from the NCBI GenBank using its GI number, or (iii) typing the sequence (or copy/paste) into a text box. In addition, the user has the option of specifying a start position and a stop position in the sequence, which allows for an analysis of the specified fragment only. In order to reduce the load on the server, certain restrictions on the sequence length are imposed, which is explained on the website.

The following sections describe the four presently available types of calculation on the server and their required input besides the sequence. In addition to stitch profile calculations, the three ‘usual’ types of melting profile can be performed: melting curves, probability profiles and temperature profiles. (They are sometimes known under different terms, such as melting maps, melting profiles, stability maps and denaturation maps.)

Stitch profiles

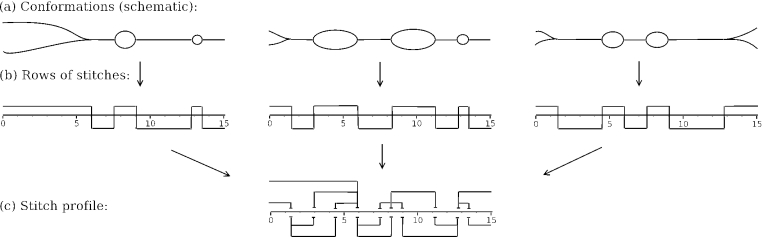
Stitch profile diagrams were introduced by Tøstesen et al. (10) and a complete description of the methodology is given by E. Tøstesen (submitted for publication). A stitch profile is a set of ‘stitches’, where each stitch spans a region of the sequence and characterizes a possible conformation of that region. Figure 1 shows an example of how a stitch profile diagram can represent three alternative DNA conformations. Each conformation corresponds to a row of stitches that are divided into the upper and lower sides, where the upper-side stitches indicate single-stranded (melted) regions and the lower-side stitches indicate double-stranded (not melted) regions. The three rows of stitches are then merged into the same stitch profile. The regions spanned by the stitches can overlap each other, indicating alternative conformations of a region. The horizontal direction in a stitch profile diagram corresponds to sequence position, while the vertical direction is being used for separating the overlapping stitches and for dividing the stitches into the upper and lower sides. The upper-side stitches are further distinguished as either ‘tails’ or ‘loops’, according to whether they reach the end of the molecule or not, respectively. For each stitch, the probability p_v of that region of the molecule being in that state is calculated (loop, tail or helical) while leaving the rest of the molecule unspecified. These probabilities can be shown in the diagram by labelling or colouring the stitches.

Figure 1.

(a) Three possible conformations of a 15 kb DNA. (b) Each conformation corresponds to a row of stitches. (c) The three rows of stitches are merged in a single stitch profile diagram.

In order to calculate a stitch profile, three parameters are required as input: the temperature T, a maximum depth D_max and a probability cut-off p_c. Instead of the temperature, however, a helicity θ can be specified, whereupon the corresponding temperature is calculated. The probability cut-off determines how many stitches are included in the profile, as stitches having probabilities below p_c are excluded. The maximum depth D_max determines the level of uncertainty in locating the positions of each stitch. This uncertainty is indicated in the diagram by horizontal ‘fluctuation bars’ at both ends of each stitch. A more detailed introduction to the concepts and the methods of stitch profiles is given by E. Tøstesen (submitted for publication).

Melting curves

A ‘melting curve’ is a plot of the helicity θ as a function of T. The helicity is the average total fraction of closed base pairs, and it decreases from 1 to 0 over the melting range of temperatures. For intermediate length sequences (10³–10⁴ bp), the curve declines in a stepwise manner reflecting the domain subtransitions (2,11). Experimentally, melting curves can be measured using ultraviolet (UV) spectroscopy where the absorption is related to the helicity. Plots of the derivative −dθ/dT as a function of T are also referred to as melting curves, and they usually show a series of peaks located at the temperatures where the different domains melt. A melting curve can be calculated as a first step in a sequence analysis to find the range of temperatures where interesting melting events take place. The server calculates θ as the average of the base-pairing probabilities, $\theta ={\sum }_i{p}_{\text{bp}}\left(i\right)/N,$ and plots it versus T. The user must specify either a temperature interval (on the x-axis) or the corresponding helicity interval (on the y-axis). The temperature step size can be chosen specifically (default 1°C) or it can be determined automatically to limit the computation time.

Probability profiles

A ‘probability profile’ depends on the temperature and is a plot of the base-pairing probability p_bp(i) versus sequence position i. Plots of 1 − p_bp(i) are also called probability profiles. A probability profile indicates on average the regions that are base-paired and the regions that are melted at a specific temperature T. This information can be used for identifying the structural changes behind each peak in a melting curve. The server can plot several probability profiles p_bp(i) at different temperatures in the same diagram, which can provide an overview of the melting process. The required input is either (i) a list of one or more temperatures, or (ii) a list of helicities, from which the corresponding temperatures are calculated.

Temperature profiles

For a given value p between 0 and 1, the corresponding ‘temperature profile’ is a plot of the temperature T_p(i) at which the i-th base-pairing probability p_bp(i) equals p versus sequence position i. As a special case, a ‘T_m profile’ is a temperature profile with p = 0.5, i.e. a plot of the base-pair melting temperatures T_m(i) versus i. Usually, a temperature profile has plateaus for regions of the sequence that melt cooperatively. A T_m profile provides the different melting temperatures of these domains. Whereas a probability profile describes the molecule at a single temperature only, a T_m profile summarizes the behaviour over a range of temperatures. The server can plot a temperature profile T_p(i) of the sequence at any p-value chosen by the user (0.5 is default). The T_p(i)-values are calculated by interpolation between a set of probability profiles.

OUTPUT

The result of each of the four kinds of calculation is shown on a results page as a PNG picture produced by using Gnuplot. For those plots having sequence position on the horizontal axis, the width of the picture increases with increasing sequence length N, so as to keep a constant scale (pixels per kb). A link leads the user to a text file with the numerical data behind the graphics. From the results page of a stitch profile, it is possible to submit a new p_c-value that is greater than the original value, which produces a new diagram containing fewer stitches.

This paper should be cited when using the results and the data from the server. Refs [(10) and E. Tøstesen, submitted for publication] can also be cited as appropriate.

ALGORITHMS

All the results are based on the Poland–Scheraga model of DNA melting (12) that considers two possible states of each base pair. However, instead of Poland's 1974 algorithm (13), we use our more recent DNA melting algorithm (10). The algorithm builds on the partition function approach of Yeramian et al. (14), to which we added two main characteristics: all types of probabilities are calculated by multiplying left-hand side and right-hand side partition functions, which is faster (10); and instead of using an approximation that was originally introduced by Gotoh and Tagashira (15), we implement an exact scheme for adding the nearest neighbour quantities (10). The DNA melting algorithm calculates base-pairing probabilities and certain block probabilities. The base-pairing probabilities are used for obtaining the usual melting profiles using standard methods. The block probabilities are used in a second algorithm that calculates stitch profiles: it is a probability peak finding algorithm (E. Tøstesen, submitted for publication), which basically finds and groups the conformations that give rise to the same probability peak, and distinguishes those conformations that belong to different probability peaks. The peak finding algorithm is demanding for long sequences: the computation time depends on both the sequence length N and the temperature, and is believed to be O(N²), but this has not been confirmed. However, typical examples of stitch profile calculations on the server are 10 s for 3000 bp, 1 min for 10 kb and 17 min for 48 kb.

Under the heading ‘Advanced options’, the user can change some thermodynamic and algorithmic settings. Several sets of empirical thermodynamic parameters can be used (11,15–18). Currently, the recommended default is Blake and Delcourt's parameters (16) with Blossey and Carlon's modified loop entropy (11). For some parameter sets, it is possible to choose the salt concentration (11,16,18). For the usual melting profiles, two versions of the DNA melting algorithm (10) can be chosen: a slower version using the exact loop entropy factor and a faster version using instead a multiexponential approximation. For stitch profile calculations, only the faster version is implemented.

THE MULTIEXPONENTIAL APPROXIMATION

It is established how a multiexponential approximation of the loop entropy factor can reduce the computation time of melting algorithms (14,17). The exact loop entropy factor (11,12) has a power law dependence on loop size: Ω(x) ∝ x^−α. In the approximation, x^−α is substituted by a sum of I exponential functions:

$$x^{-\alpha }\approx \text{const }\times {\displaystyle \sum _{n=1}^I}{A}_{n}exp(-B_{n}x).$$ 1

It is a curve-fitting problem to find the parameters A_n, B_n and I and the obtained accuracy depends on the method (19). We have devised a simple method in which the A_n, B_n and I depend on the sequence length N and the exponent α through the following formulas: I ≥ 2 + ln 2N, B_n = e^n−I and

$$A_n={\text{e}}^{1-\alpha (I-n)}-{\displaystyle \sum _{m=1}^{n-1}}{A}_{m}exp(1-{\text{e}}^{m-n}).$$ 2

Using this approximation, the computation time of a probability profile on the server is of the order O(I × N). Note that this is not strictly ‘linear’, as has previously been stated (10), but rather of the order O(Nlog N) because the number I grows logarithmically with N.

FUTURE DEVELOPMENTS

The web server has been launched recently and the future developments are expected. For example, a user will be able to provide an email address in order to be notified automatically when the results are ready. This will make computations on longer sequences possible. Another development could be plots that highlight the difference between the melting behaviours of two different sequences or at different temperatures, which would be useful in analysing mutations and other perturbations. All the developments will be documented on a ‘News’ page on the website.