Derivations of the Total Radiation Belt Electron Content

Abstract

We present multiple derivations of the Total Radiation Belt Electron Content (TRBEC), an indicator of the global number of electrons that instantaneously occupy the radiation belts. Derived from electron flux measurements, the TRBEC reduces the spatial information into a scalar quantity that concisely describes global aspects of the system. This index provides a simple, global, and long‐term assessment of the radiation belts that enables systematic analysis. In this work, we examine the TRBEC using the adiabatic invariants of $\left(\mu ,K,L^{\ast }\right)$ which has been used in previous articles as this coordinate system removes reversible adiabatic effects. We then introduce a new expression to compute the TRBEC using the non‐adiabatic coordinates of $\left(E,{\alpha }_{eq},L^{\ast }\right)$, relevant in the contexts of energetic electron precipitation, chorus, and hiss scattering where adiabatic invariant quantities are no longer conserved. From both expressions of the TRBEC we demonstrate that an erroneous factor of ${(2\pi )}^3$ that appeared in previous works using the adiabatic derivation led to an overestimate of the reported electron populations. In addition, we quantify electron loss in the outer radiation belt $\left(3.5<L^{\ast }<5\right)$ via a case study using the Van Allen Probes data over a 20‐day period from March 2013 specifying particle populations both in terms of the aforementioned adiabatic and non‐adiabatic variables. The total number of electrons in the outer radiation belt reached upwards of $10^{28}$ electrons at the peak of the storm, a rest mass of roughly 10 g.

Key Points

• We provide full derivations for Total Radiation Belt Electron Content (TRBEC) using both adiabatic and non‐adiabatic coordinates

• The TRBEC provides a simple, global, and long‐term assessment of the radiation belts that enables systematic analysis

• In comparison to past results that describe the TRBEC using adiabatic invariants, we conclude the radiation belt content has been overestimated by a factor of (${2\pi )}^3$

1. Introduction

In‐situ measurements of particle fluxes have been, and will continue to be, a crucial method to observe particles in the radiation belts. The deployment of Geiger‐Müller tubes on board the Sputnik 2 and Explorer 1 satellites marked the first observations of particles in the near‐Earth environment and led to the discovery of the Van Allen radiation belts (Van Allen, 1959). Continual advancements in instrumentation have allowed for increased particle energy and pitch angle resolutions, giving insight into the mechanisms that affect particle populations and dynamics. Trapped populations in the inner radiation belt are relatively stable; however, in the outer belt particle fluxes fluctuate more readily due to the competition between the acceleration and loss depending on solar activity, geomagnetic conditions, and other factors (e.g., Millan & Baker, 2012). For instance, the relative level of particle fluxes following geomagnetic storms in this region is difficult to predict as electron fluxes have been observed to rise, fall, or remain in a similar proportion (Reeves et al., 2003; Turner et al., 2015), although recent results using integrated adiabatic measures reveal more repeatable patterns (Murphy et al., 2018). Many processes contribute to the acceleration and loss of particles in the radiation belts, leading to questions about how the source and loss processes affect the total number of particles (Ripoll et al., 2020). The Total Radiation Belt Electron Content (TRBEC) provides a means to explore this and related questions through a quantitative accounting of the overall number of particles in a given volume of phase space.

By name, the Radiation Belt Content (RBC) was first presented by Baker et al. (2004), itself an extension of earlier work completed by Baker et al. (2001). The RBC was developed in these studies to investigate the variability of highly energetic electrons using a single parameter computed from data gathered by the low Earth orbiting Solar Anomalous and Magnetospheric Particle Explorer (SAMPEX) spacecraft (Baker et al., 1993). The number of electrons, $N$, was approximated as $N=\eta V$ where the average density of electrons, $\eta$, was determined using omnidirectional flux measurements and $V$ is the volume contained by the radiation belts (Baker et al., 2004). Since many of the trapped orbits are not observable from Low Earth Orbit (LEO), accurately quantifying the radiation belts in their entirety is challenging with LEO satellites (Pierrard, Botek, et al., 2021; Pierrard, Ripoll, et al., 2021). The RBC was then termed the Total Radiation Belt Electron Content by Selesnick (2006) and subsequent work by Selesnick and Kanekal (2009), who focused on storm time source and loss rates, expanded on the previous methodology to account for adiabatic effects. Their end product was presented as the number of electrons per unit of energy and is the first account in which the TRBEC was determined by integrating a measured electron phase space density (Selesnick & Kanekal, 2009). Separately, Zhang et al. (2017) computed the total electron content to estimate electron loss during precipitation events using data from the Van Allen Probes Magnetic Electron Ion Spectrometer (MagEIS) (Blake et al., 2013; Spence et al., 2013) instruments. This case study complemented their work on reporting characteristics of radiation belts particles from other satellite and balloon observations (Zhang et al., 2017). The methodology stemmed from proton ring current studies by Williams et al. (1976) and subsequent refinements by Zhao et al. (2015) that derived an equation for the total kinetic energy within a flux tube. Zhang et al. (2017) utilized this flux tube expression to compute the total electron content of a fixed energy range by summing over all of the flux tubes within a given $L$‐shell range in $0.1R_E$ increments.

An alternative TRBEC expression was presented in the work of Forsyth et al. (2016) that used MagEIS data to study the effects of substorms on the electron content within the radiation belts. The TRBEC expression provided in Forsyth et al. (2016) used the adiabatic invariants $\mu$, $K$ and $L^{\ast }$ so that the number of electrons computed would be unaffected by slow adiabatic changes. This adiabatic description of the TRBEC was also utilized by Murphy et al. (2018) and Duderstadt et al. (2021) to complete statistical studies using Van Allen Probes data and to quantify the amount of depletion during select intervals.

In this work, we combine the formalism used to derive the adiabatic TRBEC with the coordinate system of the earlier works to derive and provide a new expression for the TRBEC that is a function of electron kinetic energies, equatorial pitch angles, and drift shells. We also complete a separate derivation for the TRBEC in adiabatic coordinates which is absent from the primary source material where it is presented or used (Duderstadt et al., 2021; Forsyth et al., 2016; Murphy et al., 2018). Moreover, from our derivations and auxiliary comparisons, we demonstrate that the published results using adiabatic invariants overestimate the TRBEC by a factor of ${(2\pi )}^3\approx 248$. The previous studies mainly focus on relative changes of the TRBEC, and their results are essentially unaffected by this correction. However, the correct normalization becomes increasingly important for studies that rely on reporting the TRBEC directly. From the TRBEC equations, in both coordinate frames, we present considerations for computing the TRBEC numerically and, then, apply these methods to a case study utilizing Van Allen Probes data for a quiet geomagnetic interval in early March of 2013.

2. Definitions and Derivations

2.1. First Principles Approach in Position‐Momentum Phase Space

We begin by defining the Phase Space Density (PSD), $f$, as

$$f=\frac{j}{p^2}$$ (1)

where $j$ represents the differential particle flux and $p$ is the relativistic momentum (Roederer & Zhang, 2014). As a function of the kinetic energy, $E$, the momentum is

$$p=\frac{\sqrt{E^2+2E{m}_0{c}^2}}{c}$$ (2)

where $m_0$ is the electron rest mass and $c$ is the speed of light in a vacuum. The PSD is then rewritten as

$$f=\frac{1}{2.99792458\times 10^{10}}\frac{j}{E^2+2E{m}_0{c}^2}\left[{\left(\frac{\mathrm{c}}{\text{MeV}\cdot \text{cm}}\right)}^3\right].$$ (3)

Given $j$ is provided in units of $\#/\left({\text{cm}}^2\mathrm{s}\text{MeV}\text{sr}\right)$, along with $E$ and $m_0$ in units of MeV and MeV/$c^2$ respectively, then the resulting units for the PSD are given in the brackets. Taylor et al. (2004) discuss the preferred units for the PSD and provide conversions between alternative units.

The Total Radiation Belt Electron Content (TRBEC) is defined as the total number of particles in a given volume of phase space. Denoting a generalized coordinate and momentum conjugate pair, $(\mathbf{q},\mathbf{p})=\left(q_1,q_2,q_3,p_1,p_2,p_3\right)$, the TRBEC in position‐momentum phase space is

$$N={\iiint }_{\mathbf{q}}{\iiint }_{\mathbf{p}}f(\mathbf{q},\mathbf{p})d^3\mathbf{q}{d}^3\mathbf{p}$$ (4)

where the integration limits are used to determine the region of phase space and, hence, a particular particle population and region within the radiation belts. In principle, the TRBEC $N$ can be calculated over any well‐defined phase space volume by using Equation 4. Practically, a direct estimate for the six‐dimensional integral would require a prohibitively large number of measurements, so the TRBEC concept becomes more useful if we can apply some assumptions to reduce its dimensionality.

Under the restrictive assumption of a dipole magnetic field, we could represent momentum space in terms of $E$, ${\alpha }_{eq}$, and ${\varphi }_p$ (kinetic energy, equatorial pitch angle, and gyro phase angle) and position space in terms of $L$, $s$, and ${\varphi }_q$ (distance from the geomagnetic center to the equatorial crossing of the field line, distance along the field line, and azimuthal angle). We could then integrate analytically over ${\varphi }_p,{\varphi }_q$ and $s$ to reduce the initially six‐dimensional integral to an integral over $\left(E,{\alpha }_{eq},L\right)$, which could then be estimated with a practical number of measurements.

Under less restrictive assumptions in a non‐dipole model field, integrating over $s$ and ${\varphi }_q$ would be numerically cumbersome. Rather than performing that calculation, we instead imagine adiabatically “turning off” the non‐dipole contributions to the real field, and then evaluate $N$ in the resulting dipole field. The adiabatic transformation takes a particle phase space density observed at $\left(E_{\mathit{sat}},{\alpha }_{\mathit{sat}},\vec{x}\right)$ and maps it to a phase space position in the dipole field $\left(E,{\alpha }_{eq},L^{\ast }\right)$, where $L^{\ast }$ is described by Roederer (1970) (Roederer & Lejosne, 2018; Roederer & Zhang, 2014) and ${\alpha }_{eq}$ and $E$ can be calculated using conservation of the first and second adiabatic invariants (Schulz & Lanzerotti, 1974). The total number of particles $N$ is the same in the transformed dipole field as in the original non‐dipole field, making for a well‐defined and useful simplification, although we note that boundaries in $L^{\ast }$ are not strictly spatial boundaries in the real (non‐dipolar) space.

The goal is now to derive an expression for the TRBEC explicitly in terms of $E$, ${\alpha }_{eq}$, and $L^{\ast }$ by integrating in a dipole field. We initially opt to parameterize the six‐dimensional integral of Equation 4 using position coordinates of $L$, $s$, and ${\varphi }_q$, and momentum coordinates of the electron total linear momentum, $p$, pitch angle, $\alpha$, and gyro phase angle, ${\varphi }_p$. The coordinates of the canonical momentum form a spherical coordinate system resulting in a volume element of

$$\begin{array}{ll}\hfill d^3\mathbf{p}& \hfill =(dp)\left(pd{\varphi }_p\right)\left(p\sin (\alpha )d\alpha \right)\\ \hfill & \hfill =p^2\sin (\alpha )dpd{\varphi }_{p}d\alpha .\end{array}$$ (5)

whereas the corresponding volume element of the generalized coordinates is

$$\begin{array}{ll}\hfill d^3\mathbf{q}& \hfill =\frac{A(s)}{A_{eq}}\left(ds\right)\left(R_{E}d{L}^{\ast }\right)\left(R_E{L}^{\ast }d{\varphi }_q\right)\\ \hfill & \hfill =\frac{A(s)}{A_{eq}}{\left(R_E\right)}^2{L}^{\ast }dsd{L}^{\ast }d{\varphi }_q.\end{array}$$ (6)

In Equation 6, $A(s)/A_{eq}$ is the ratio between the cross‐section area of a flux tube at a position $s$ compared to the area at the equator, where the path length is zero $(s=0)$, and is required to account for the shape of flux tubes in a dipole magnetic field. Provided magnetic flux is conserved along field lines,

$$\frac{A(s)}{A_{eq}}=\frac{B_{eq}}{B(s)}$$ (7)

so Equation 6 is rewritten as

$$d^3\mathbf{q}=\frac{B_{eq}}{B(s)}{\left(R_E\right)}^2{L}^{\ast }dsd{L}^{\ast }d{\varphi }_q.$$ (8)

Substituting Equations 5 and 8 into the TRBEC from Equation 4 and integrating both ${\varphi }_p$ and ${\varphi }_q$ from 0 to $2\pi$ gives

$$N=4{\pi }^2{\left(R_E\right)}^2{\int }_s{\int }_p{\int }_{\alpha }{\int }_{L^{\ast }}f\left(s,p,\alpha ,L^{\ast }\right)\frac{B_{eq}}{B(s)}{p}^2\sin (\alpha )L^{\ast }dsdpd\alpha d{L}^{\ast }.$$ (9)

For now the integration bounds will be left undefined, but will later be restricted so that only trapped particles in the radiation belts are accounted for.

The remaining steps in this TRBEC derivation are to change coordinates to the desired variables. This is completed by converting the momentum to an equivalent energy, the local to equatorial pitch angle, ${\alpha }_{eq}$, and the parameterization for the distance along a field line from $s$ to the geomagnetic latitude. By Liouville's theorem, the density of particles in phase space is constant so the PSD at any position along a field to the PSD at a point on the equatorial plane is related via

$$f\left(s,p,\alpha ,L^{\ast }\right)=f\left(s=0,p,{\alpha }_{eq},L^{\ast }\right).$$ (10)

Differentiating the relation between a particle's momentum and its equivalent energy from Equation 2 the relation between $dp$ and $dE$ is

$$pdp=\gamma m_{0}dE$$ (11)

where

$$\gamma =\frac{E}{m_0{c}^2}+1$$ (12)

is the Lorentz factor. By the conservation of the first adiabatic invariant,

$$\mu =\frac{\left(E^2+2E{m}_0{c}^2\right){\sin }^2(\alpha )}{2m_0{c}^{2}B},$$ (13)

where B is the local magnetic field, it can be shown that for an electron with a set energy

$$\sin (\alpha )=\sin \left({\alpha }_{eq}\right)\sqrt{\frac{B(s)}{B_{eq}}}.$$ (14)

Differentiating Equation 14 above yields the following relation between $d\alpha$ and $d{\alpha }_{eq}$.

$$\cos (\alpha )\frac{d\alpha }{d{\alpha }_{eq}}=\cos \left({\alpha }_{eq}\right)\sqrt{\frac{B(s)}{B_{eq}}}$$ (15)

Substituting the PSD relation from Equation 10 and the coordinate changes from Equations 11 and 15 into the TRBEC from Equation 9 gives

$$\begin{array}{l}\hfill N=4{\pi }^2{\left(R_E\right)}^2{m}_0{\int }_s{\int }_E{\int }_{{\alpha }_{eq}}{\int }_{L^{\ast }}f\left(E,{\alpha }_{eq},L^{\ast }\right)\gamma p\sqrt{\frac{B_{eq}}{B(s)}}\frac{\sin (\alpha )\cos \left({\alpha }_{eq}\right)}{\cos (\alpha )}{L}^{\ast }dsdEd{\alpha }_{eq}d{L}^{\ast }\\ \hfill =4{\pi }^2{\left(R_E\right)}^2{m}_0{\int }_s{\int }_E{\int }_{{\alpha }_{eq}}{\int }_{L^{\ast }}f\left(E,{\alpha }_{eq},L^{\ast }\right)\gamma p\frac{\sin \left({\alpha }_{eq}\right)\cos \left({\alpha }_{eq}\right)}{\sqrt{1-{\sin }^2\left({\alpha }_{eq}\right)\frac{B(s)}{B_{eq}}}}{L}^{\ast }dsdEd{\alpha }_{eq}d{L}^{\ast }\end{array}$$ (16)

where the second equality first expands $\cos (\alpha )$ using the Pythagorean identity and then substitutes $\sin (\alpha )$ from Equation 14.

The integration bounds over the field line path $s$ and equatorial pitch angle ${\alpha }_{eq}$ are now specified to limit the integration to trapped electrons in the radiation belts. The endpoints for $s$ occur at the mirror points in the northern and southern hemispheres, $+s_m$ and $-s_m$, which in turn depend on ${\alpha }_{eq}$. The domain for ${\alpha }_{eq}$ includes all angles outside the loss cone, from $+{\alpha }_{eq,LC}$ to $-{\alpha }_{eq,LC}$, where the loss cone edge is calculated at 100 km. With these changes Equation 16 becomes

$$\begin{array}{l}\hfill N=4{\pi }^2{\left(R_E\right)}^2{m}_0{\int }_E{\int }_{{\alpha }_{eq}=-{\alpha }_{eq,LC}}^{+{\alpha }_{eq,LC}}{\int }_{s=-s_m}^{+s_m}{\int }_{L^{\ast }}f\left(E,{\alpha }_{eq},L^{\ast }\right)\gamma p\frac{\sin \left({\alpha }_{eq}\right)\cos \left({\alpha }_{eq}\right)}{\sqrt{1-{\sin }^2\left({\alpha }_{eq}\right)\frac{B(s)}{B_{eq}}}}{L}^{\ast }dsdEd{\alpha }_{eq}d{L}^{\ast }\end{array}$$ (17)

due to the symmetry about the equatorial plane.

For the final variable change for this derivation, the path described by the line element will be replaced with the geomagnetic latitude, $\lambda$. The distance element of a dipole field is related to the geomagnetic latitude by

$$ds=R_E{L}^{\ast }\sqrt{1+3{\sin }^2(\lambda )}\cos (\lambda )d\lambda$$ (18)

and in addition,

$$\frac{B(\lambda )}{B_{eq}}=\frac{\sqrt{1+3{\sin }^2(\lambda )}}{{\cos }^6(\lambda )}$$ (19)

shows the ratio between the local magnetic field strength parameterized in terms of $\lambda$ and on the equatorial plane (Schulz & Lanzerotti, 1974; Walt, 1994). Substituting Equations 18 and 19 into Equation 17 gives

$$\begin{array}{l}\hfill N=16{\pi }^2{\left(R_E\right)}^3{m}_0{\int }_E{\int }_{{\alpha }_{eq}={\alpha }_{eq,LC}}^{\pi /2}{\int }_{\lambda =0}^{{\lambda }_m}{\int }_{L^{\ast }}f\left(E,{\alpha }_{eq},L^{\ast }\right)\gamma p{\left(L^{\ast }\right)}^2\\ \hfill \frac{\sin \left({\alpha }_{eq}\right)\cos \left({\alpha }_{eq}\right)}{\sqrt{1-{\sin }^2\left({\alpha }_{eq}\right)\frac{\sqrt{1+3{\sin }^2(\lambda )}}{{\cos }^6(\lambda )}}}\sqrt{1+3{\sin }^2(\lambda )}\cos (\lambda )dEd{\alpha }_{eq}d\lambda d{L}^{\ast }.\end{array}$$ (20)

For notational convenience, the latitude and equatorial pitch angle dependencies of Equation 20 are condensed into a single function that we denote as $W\left({\alpha }_{eq}\right)$.

$$W\left({\alpha }_{eq}\right)=\sin \left({\alpha }_{eq}\right)\cos \left({\alpha }_{eq}\right){\int }_0^{{\lambda }_m}\frac{\sqrt{1+3{\sin }^2(\lambda )}\cos (\lambda )}{\sqrt{1-{\sin }^2\left({\alpha }_{eq}\right)\frac{\sqrt{1+3{\sin }^2(\lambda )}}{{\cos }^6(\lambda )}}}d\lambda$$ (21)

The upper integration bound of the latitude at a mirror point can be computed using the following relation to the equatorial pitch angle in a dipole magnetic field.

$$\frac{1}{{\sin }^2\left({\alpha }_{eq}\right)}=\frac{\sqrt{1+3{\sin }^2\left({\lambda }_m\right)}}{{\cos }^6\left({\lambda }_m\right)}$$ (22)

The latitude‐dependent terms of $W\left({\alpha }_{eq}\right)$ are denoted as $T\left(y=\sin \left({\alpha }_{eq}\right)\right)$ in Schulz and Lanzerotti (1974), accompanied by a numerical approximation for the function. The significance of $T(y)$ is that it describes the full helical trajectory of the bounce path and is therefore proportional to the bounce period (Schulz & Lanzerotti, 1974). Referring to $W\left({\alpha }_{eq}\right)$, a special case is when it is precisely zero, occurring at ${\alpha }_{eq}=0$ and $\pi /2$ corresponding to when either the volume in momentum phase space and position phase space is zero. Although there is no closed‐form solution to the $W\left({\alpha }_{eq}\right)$ or $T\left({\alpha }_{eq}\right)$ integrals (Schulz & Lanzerotti, 1974; Walt, 1994), an interesting finding is that the numeric result of $W\left({\alpha }_{eq}\right)$ integrated between ${\lambda }_m=0$ to $\pi /2$ is approximately 0.4571. Within error, this corresponds to the ratio between the volume contained within a magnetic dipole shell and its enclosing sphere, exactly $16/35$ as shown in Appendix A.

Returning to the TRBEC derivation, using $W\left({\alpha }_{eq}\right)$ from Equation 21 simplifies Equation 20 to

$$N=16{\pi }^2{\left(R_E\right)}^2{m}_0{\int }_{E_{\text{min}}}^{E_{\text{max}}}{\int }_{{\alpha }_{eq}={\alpha }_{eq,LC}}^{\pi /2}{\int }_{L_{\text{min}}^{\ast }}^{L_{\text{max}}^{\ast }}f\left(E,{\alpha }_{eq},L^{\ast }\right)\gamma p{\left(L^{\ast }\right)}^{2}W\left({\alpha }_{eq}\right)dEd{\alpha }_{eq}d{L}^{\ast }$$ (23)

which is our final expression of the TRBEC in $\left(E,{\alpha }_{eq},L^{\ast }\right)$ coordinates. We note again that both $\gamma$ and $p$ are functions of $E$ through Equations 2 and 12. The integration bounds over ${\alpha }_{eq}$ ensure all trapped particles are counted and the maximum and minimum bounds of energy and $L$‐shell can be chosen to select a given particle population.

2.2. Coordinate Transformation to Adiabatic Invariants

Adiabatic invariants, such as $\left(\mu ,K,L^{\ast }\right)$, are desirable coordinates to specify a particle population for the TRBEC as the boundaries are unaffected by adiabatic changes. However, integrating the PSD over a constant range of adiabatic invariants is not simple using the TRBEC defined in terms of the generalized coordinates as shown in Equation 4. This would define an irregular shape in the $(\mathbf{q},\mathbf{p})$ phase space so it is advantageous to derive a separate expression of the TRBEC that specifies a region in phase space comprised of adiabatic invariants.

To define the TRBEC using adiabatic invariants we begin by performing a volume‐preserving transformation in phase space from $(\mathbf{q},\mathbf{p})$ to a new set of canonical variables. Using the action‐angle variables of $(\mathit{\omega },\mathbf{J})$ as the target frame the frequencies and constants of the motion are determined without knowledge of individual particle paths. The action variables $J_i$ are the adiabatic invariants of the system where $J_1$, $J_2$, and $J_3$ are associated with the gyro, bounce, and drift motions respectively. They are approximated from the generalized Poincaré invariants, ${\mathcal{J}}_i$, that are defined as the following integrals over one complete period of $q_i$ (Northrop, 1963).

$$J_i\approx {\mathcal{J}}_i=\oint p_{i}d{q}_i$$ (24)

The function that generates the canonical transformation from $(\mathbf{q},\mathbf{p})$ to $(\mathit{\omega },\mathbf{J})$ is Hamilton's characteristic function, $W=W(\mathbf{q},\mathbf{J})$, and, from this, the transformation equations are

$$p_i=\frac{\partial W(\mathbf{q},\mathbf{J})}{\partial q_i}$$ (25)

and

$${\omega }_i=\frac{\partial W(\mathbf{q},\mathbf{J})}{\partial J_i}$$ (26)

with the latter being the definition of the angle variable (e.g., Goldstein et al., 2008). From the definition of the action variables, shown in Equation 24, and the transformation equations, Equations 25 and 26, it follows that over a single period of a given motion, the change in the angle variable of that motion is by unity (e.g., Chow, 2013; Dittrich & Reuter, 2017).

$$\oint d{\omega }_i\left(q_j\right)=\oint \frac{\partial {\omega }_i}{\partial q_j}d{q}_j=\oint \frac{{\partial }^{2}W(\mathbf{q},\mathbf{J})}{\partial q_j\partial J_i}d{q}_j=\frac{\partial }{\partial J_i}\oint \frac{\partial W(\mathbf{q},\mathbf{J})}{\partial q_j}d{q}_j=\frac{\partial }{\partial J_i}\oint p_{j}d{q}_j={\delta }_{ij}$$

$$\Rightarrow \oint d{\omega }_i\left(q_i\right)=1$$ (27)

From the definition of the TRBEC, the corresponding expression for the TRBEC using the action‐angle variables $(\mathit{\omega },\mathbf{J})$ is

$$\begin{array}{ll}\hfill N& =\oint \oint {\oint }_{\mathit{\omega }}{\iiint }_{\mathbf{J}}f(\mathbf{J})d^3\mathit{\omega }{d}^3\mathbf{J}\hfill \\ \hfill & ={\iiint }_{\mathbf{J}}f(\mathbf{J})d^3\mathbf{J}\hfill \end{array}$$ (28)

by Equation 27 as it is assumed that the PSD is only dependent on the action variables, $f=f(\mathbf{J})$.

The choice to use $J_i$, as defined in Equation 24, follows the action‐angle variable notation presented by many authors (e.g., Baumjohann & Treumann, 1997; Chow, 2013; Dittrich & Reuter, 2017; Fitzpatrick, 2015; Greiner, 2004; Hazeltine & Waelbroeck, 2004; Kivelson & Russell, 1995; Northrop, 1963; Roederer & Zhang, 2014; Spiegel & Proykova, 1980; Walt, 1994). Other authors opt to define the action variable as $I_i=J_i/(2\pi )$ (e.g., Arnold, 1997; Landau & Lifshits, 1976; Woodhouse, 2009). Some texts discuss both of these definitions (e.g., Cline, 2018; Goldstein et al., 2008; Schulz & Lanzerotti, 1974). The choice of the action variable does matter as different definitions affect the normalization of the associated angle variable. For example, the conjugate angle variable to $I_i$, ${\phi }_i$, is incremented by $2\pi$ (e.g., Arnold, 1997) over a complete motion cycle instead of 1 as is the case with ${\omega }_i$ shown in Equation 27. However, consistently defined action‐angle variables do not affect the outcome of the TRBEC as a change in the definition of the action variables is offset by the subsequent change of the closed loop integral over the associated angle variable. For example, using the $(\mathit{\phi },\mathbf{I})$ pair gives

$$\begin{array}{ll}\hfill N& \hfill =\oint \oint {\oint }_{\mathit{\phi }}{\iiint }_{\mathbf{I}}f(\mathbf{I})d^3\mathit{\phi }{d}^3\mathbf{I}\\ \hfill & \hfill =8{\pi }^3{\iiint }_{\mathbf{I}}f(\mathbf{I})d^3\mathbf{I}\end{array}$$ (29)

as an alternative expression of the TRBEC which is consistent with Equation 28.

At this stage, a final transformation is required to write the TRBEC using other preferred invariant quantities instead of the action variables $J_1$, $J_2$, and $J_3$ (e.g., Schulz & Lanzerotti, 1974; Walt, 1994). Specifically, we use $\mu$ as the first adiabatic invariant and $K$ (defined below) and $L^{\ast }$ as the second and third respectively. To transform to the $\left(\mu ,K,L^{\ast }\right)$ frame we perform a change of variables on Equation 28 using the Jacobian determinant, a matrix with entries of ${\mathbf{J}}_{ij}=\partial f_i/\partial x_j$ that describes the transforms between variables $x_i$ and $y_i$ that are related by a set of equations of the form $y_i=f_i(\mathbf{x})$. The equations that relate the $\left(J_1,J_2,J_3\right)$ frame in terms of the $\left(\mu ,K,L^{\ast }\right)$ are computed by evaluating the integrals of the three Poincaré invariants (Schulz & Lanzerotti, 1974). The associated action variables for the gyro and bounce motions can be evaluated as

$$J_1=\frac{2\pi m_0}{q}\mu ,$$ (30)

and

$$J_2=\sqrt{8m_0\mu }K,$$ (31)

where

$$K={\int }_{s=-s_m}^{+s_m}\sqrt{B_m-B(s)}ds$$ (32)

parameterizes the bounce path using the path length variable $s$. The location of the two distinct mirror points are denoted by $-s_m$ and $+s_m$ in Equation 32 where $B(s)$ and $B_m$ represent the magnetic field strength at an arbitrary position along the bounce path and a mirror point. The associated adiabatic invariant of the drift motion is

$$J_3=\frac{2\pi q{\mu }_E}{R_E{L}^{\ast }}$$ (33)

where $L^{\ast }$ is the drift shell parameter and

$${\mu }_E=B_E{R}_E^3$$ (34)

is a constant representing the magnetic moment of the Earth where $B_E$ is the magnetic field strength on the surface at the equator ($\approx 0.311653$G) and $R_E$ is the radius of Earth ($\approx 6371$km) (Schulz & Lanzerotti, 1974).

The Jacobian of the mapping between these two sets of coordinates is then

$$\mathbf{J}\left(\mu ,K,L^{\ast }\right)=\frac{-8\sqrt{2}{\pi }^2{\mu }_E{m}_0^{3/2}}{R_E}\frac{\sqrt{\mu }}{{\left(L^{\ast }\right)}^2}$$ (35)

using Equations (30), (31) and 33 as the transformation equations. Completing the change of variables to the TRBEC expression from Equation 28 using the Jacobian above gives

$$\begin{array}{ll}\hfill N& \hfill ={\int }_{\mu }{\int }_K{\int }_{L^{\ast }}f\left(\mu ,K,L^{\ast }\right)\left|\mathbf{J}\left(J_1,J_2,J_3;\mu ,K,L^{\ast }\right)\right|d\mu dKd{L}^{\ast }\\ \hfill & \hfill =\frac{8\sqrt{2}{\pi }^2{m}_0^{3/2}{\mu }_E}{R_E}{\int }_{{\mu }_{\text{min}}}^{{\mu }_{\text{max}}}{\int }_{K=0}^{K_{LC}}{\int }_{L_{\text{min}}^{\ast }}^{L_{\text{max}}^{\ast }}\frac{f\left(\mu ,K,L^{\ast }\right)\sqrt{\mu }}{{\left(L^{\ast }\right)}^2}d\mu dKd{L}^{\ast }\end{array}$$ (36)

which completes the abridged derivation in adiabatic coordinates. The intermediate steps of the mathematical derivation are available in Loridan (2018) and Pitzel (2022). In Equation 36, the range of $\mu$ and $L^{\ast }$ can be chosen freely to specify an electron population although to consider all trapped particle trajectories the integration bounds of $K$ in Equation 36 must encompass particles whose mirror points lie between the equatorial plane $(K=0)$ and the loss cone boundary $\left(K=K_{LC}\right)$.

2.3. Normalization Verification

To verify the TRBEC expressed in Equation 36 we perform another change of variables from the adiabatic variables to the energy and equatorial pitch angle frame to retrieve Equation 23 with consistent normalization. As before, for the transformation we require each $J_i$ to be expressed in terms of $E$, ${\alpha }_{eq}$, and $L^{\ast }$. Substituting Equation 13 into Equation 30

$$J_1=\frac{\pi \left(E^2+2E{E}_0\right){\sin }^2\left({\alpha }_{eq}\right){\left(L^{\ast }\right)}^3}{q{c}^2{B}_E}.$$ (37)

In a similar manner, Equation 31 becomes

$$J_2=4R_E{L}^{\ast }\frac{\sqrt{E^2+2E{E}_0}}{c}{\int }_0^{\lambda m}\sqrt{1-{\sin }^2\left({\alpha }_{eq}\right)\frac{\sqrt{1+3{\sin }^2(\lambda )}}{{\cos }^6(\lambda )}}\sqrt{1+3{\sin }^2(\lambda )}\cos (\lambda )d\lambda$$ (38)

from expanding $K$ from Equation 32 using the magnetic latitude to parameterize the bounce path assuming a dipole magnetic field. Equations 37 and 38 combined with Equation 33 then define the coordinate transformation between $\left(J_1,J_2,J_3\right)$ and $\left(E,{\alpha }_{eq},L^{\ast }\right)$. The associated Jacobian is

$$\mathbf{J}\left(E,{\alpha }_{eq},L^{\ast }\right)=16{\pi }^2{\left(R_E\right)}^3{\left(L^{\ast }\right)}^2{m}_0\gamma pW\left({\alpha }_{eq}\right)$$ (39)

where both $\gamma$ and $p$ are functions of energy as previously defined.

The expression for the TRBEC in the $\left(E,{\alpha }_{eq},L^{\ast }\right)$ coordinate frame is then

$$\begin{array}{ll}\hfill N\hfill & \hfill ={\int }_E{\int }_{{\alpha }_{eq}}{\int }_{L^{\ast }}f\left(E,{\alpha }_{eq},L^{\ast }\right)\left|\mathbf{J}\left(J_1,J_2,J_3;E,{\alpha }_{eq},L^{\ast }\right)\right|dEd{\alpha }_{eq}d{L}^{\ast }\\ \hfill & \hfill =16{\pi }^2{\left(R_E\right)}^3{m}_0{\int }_{E_{\text{min}}}^{E_{\text{max}}}{\int }_{{\alpha }_{eq}={\alpha }_{eq,LC}}^{\pi /2}{\int }_{L_{\text{min}}^{\ast }}^{L_{\text{max}}^{\ast }}f\left(E,{\alpha }_{eq},L^{\ast }\right)\gamma pW\left({\alpha }_{eq}\right){\left(L^{\ast }\right)}^{2}dEd{\alpha }_{eq}d{L}^{\ast }\end{array}$$ (40)

which is identical to Equation 23. The intermediate steps are completed in full in Pitzel (2022). Similar to Equation 36, chosen ranges of $E$ and $L^{\ast }$ in Equation 40 define a particle population for study while the stated range over the equatorial pitch angle limits the integration to all trapped particle paths. In this instance the latter restriction follows from the Jacobean transformations being one‐to‐one so the $K=0$ to $K_{LC}$ integral bounds directly corresponds to ${\alpha }_{eq}={\alpha }_{eq,LC}$ to $\pi /2$ without further manipulation.

2.4. Normalization Comparisons

In regards to the TRBEC in non‐adiabatic coordinates, our Equation 23 is consistent with previous TRBEC works by Selesnick and Kanekal (2009) and Zhang et al. (2017). Detailed comparisons with these works are given in Appendix B. Conversely, our TRBEC derivation in adiabatic coordinates, Equation 36, differs from the recent literature relying on the adiabatic formulation; with all else equal, a factor of ${(2\pi )}^3$ appears in the equations presented in Forsyth et al. (2016) and Murphy et al. (2018), and used by Duderstadt et al. (2021), that is absent from non‐adiabatic TRBEC in Equation 23.

Since our adiabatic TRBEC result is not entirely consistent with the literature, we present an additional verification test in this section. To verify our normalization of the TRBEC equations in the previous sections, we compute the Phase Space Volume (PSV), the domain of integration, as it can readily be computed using Equation 23 and also independently.

2.4.1. Expected Phase Space Volume

Geometrically, the expected six‐dimensional PSV is the product of the two three‐dimensional phase spaces. Using the canonical momentum and generalized position, the PSV can be expressed as

$$V_{PS}={\iiint }_{\mathbf{q}}{\iiint }_{\mathbf{p}}{d}^3\mathbf{q}{d}^3\mathbf{p}=V_{\mathbf{q}}{V}_{\mathbf{p}}$$ (41)

where $V_{\mathbf{q}}$ and $V_{\mathbf{p}}$ are the volumes contained in the $\mathbf{q}$ and $\mathbf{p}$ phase spaces respectively.

2.4.2. PSV Derived From the TRBEC

To derive the PSV from TRBEC the PSD is set to a unitless constant of one. For example, using the TRBEC expression in $(\mathbf{q},\mathbf{p})$ from Equation 4 with $f=1$ leads directly to the result of Equation 41 above. Given that the normalization between Equations 23 and 36 is consistent from Section 2.3 we only need to compute the PSV from one of them. We opt to use Equation 23 as the final result is simpler to interpret in physical space compared to adiabatic space.

From Equation 23, with $f=1$, we carry out the integration over $E$ and $L^{\ast }$ between finite minimum and maximum bounds. In ${\alpha }_{eq}$, the integration is completed between 0 and $\pi /2$ which is necessary to account for the phase space of all particles.

$$V_{PS}=16{\pi }^2{\left(R_E\right)}^3{m}_0{\int }_{E_{\text{min}}}^{E_{\text{max}}}{\int }_{{\alpha }_{eq}=0}^{\pi /2}{\int }_{L_{\text{min}}^{\ast }}^{L_{\text{max}}^{\ast }}{\left(L^{\ast }\right)}^2\gamma pW\left({\alpha }_{eq}\right)dEd{\alpha }_{eq}d{L}^{\ast }$$ (42)

With the PSD set as a constant, Equation 42 is separable and can be evaluated further.

$$V_{PS}=16{\pi }^2{\left(R_E\right)}^3{\int }_{E_{\text{min}}}^{E_{\text{max}}}\gamma m_{0}pdE{\int }_{{\alpha }_{eq}=0}^{\pi /2}W\left({\alpha }_{eq}\right)d{\alpha }_{eq}{\int }_{L_{\text{min}}^{\ast }}^{L_{\text{max}}^{\ast }}{\left(L^{\ast }\right)}^{2}d{L}^{\ast }$$ (43)

To obtain a result for the PSV in the desired momentum‐position space the integral in energy in Equation 43 is converted to an equivalent one in momentum by Equation 11. The function $W\left({\alpha }_{eq}\right)$, Equation 21, integrated numerically from ${\alpha }_{eq}=0$ to $\pi /2$ is approximately 0.4571. Evaluating the remaining integrals, the PSV reduces as

$$\begin{array}{ll}\hfill V_{PS}& \hfill =16{\pi }^2{\left(R_E\right)}^{3}0.4571{\int }_{p_{\text{min}}}^{p_{\text{max}}}{p}^{2}dp{\int }_{L_{\text{min}}^{\ast }}^{L_{\text{max}}^{\ast }}{\left(L^{\ast }\right)}^{2}d{L}^{\ast }\\ \hfill & \hfill =16{\pi }^2{\left(R_E\right)}^{3}0.4571{\left.\left(\frac{1}{3}{p}^3\right)\right|}_{p_{\text{min}}}^{p_{\text{max}}}{\left.\left(\frac{1}{3}{\left(L^{\ast }\right)}^3\right)\right|}_{L_{\text{min}}^{\ast }}^{L_{\text{max}}^{\ast }}\\ \hfill & \hfill =\left(\frac{4}{3}\pi \left({\left(p_{\text{max}}\right)}^3-{\left(p_{\text{min}}\right)}^3\right)\right)\left(0.4571\frac{4}{3}\pi {\left(R_E\right)}^3\left({(L_{\text{max}}^{\ast })}^3-{(L_{\text{min}}^{\ast })}^3\right)\right).\end{array}$$ (44)

Equation 44 is equivalent to the expected result from Equation 41. The left term of the final equality of Equation 44 shows the volume in momentum space is the volume between two concentric spheres determined by the minimum and maximum integration bounds. Similarly, the right terms correspond to the volume in position space which is the volume between two concentric dipole shells determined by the integration limits over $L^{\ast }$. The factor of 0.4571 accounts for the difference between the volume contained within a dipole compared to that of an enclosing sphere which is an approximation of the exact ratio of $\frac{16}{35}$ (cf. Appendix A).

The equivalence of the PSV computed with the TRBEC in non‐adiabatic coordinate with $f=1$, in comparison to the expected result, Equation 41, confirms that the proper normalization of the TRBEC is as it appears in Equation 23. Furthermore, given that Equations 23 and 36 are consistent with one another it follows that Equation 36 does not require a correction of ${(2\pi )}^3$ as used in the aforementioned literature.

3. Estimating the TRBEC From Van Allen Probes Observations

We now briefly outline important considerations for the numeric computation of the TRBEC and then demonstrate these methods using data from the Van Allen Probes Magnetic Electron Ion Spectrometer (MagEIS) instrument (Blake et al., 2013) in the Energetic particle, Composition, and Thermal plasma (ECT) instrument suite (Spence et al., 2013). The identical satellites, in operation from 2012 to 2019, were placed on similar highly elliptical and low inclination orbits (1.1 by $5.8R_E$ at $10°$) (Mauk et al., 2013) which situated MagEIS to measure the bulk of both seed and relativistic electrons, between 20 keV and 4.8 MeV (Blake et al., 2013). To estimate the TRBEC, we converted the measured electron flux to a PSD in the desired coordinate frame, followed by estimating the unmeasured populations (noted below), and then computed the TRBEC integral itself for each 4.5 hr half orbit (i.e., apogee to perigee or perigee to apogee) of the Van Allen Probes. We used $L^{\ast }$ and $K$ values computed using the Tsyganenko and Sitnov (2005) magnetic field model. The MagEIS data used in this work is presented as a pitch angle resolved background corrected flux (Claudepierre et al., 2019). In this coordinate frame, it is not computationally intensive to compute the PSD for the non‐adiabatic TRBEC since the corresponding PSD is kept in the same reference frame. Conversely, obtaining the PSD in adiabatic coordinates is not as straightforward (Boyd, 2016; Hartley & Denton, 2014) as a conversion from $j\left(E,\alpha ,L^{\ast }\right)$ to $j\left(\mu ,K,L^{\ast }\right)$ is required before invoking Equation 1.

3.1. Unmeasured Particle Populations

The Van Allen Probes orbits coupled with MagEIS's instrument capabilities allowed for measurements over a wide range of the electron pitch angle distribution, but a small fraction of electron populations that pertain to the TRBEC are left unobserved. We must estimate three particle populations, at the boundaries of the TRBEC integration bounds, to complete the numerical integration of either Equation 23 or Equation 36. The following electron populations must be estimated: (a) equatorially mirroring electrons, (b) electrons with small pitch angles that mirror at the loss cone boundary, and (c) electrons with relatively large $\mu$ and $K$ (i.e., ultra‐relativistic electrons). We note that all of these computations are completed for a comparably small portion of the TRBEC, as the first two populations listed represent a relatively small portion of phase space and the third has a negligible phase space density.

The Van Allen Probes primarily operate slightly off the equatorial plane, and electrons that mirror at lower inclinations cannot be observed. We approximate this unmeasured population by assuming that the PSD at the equator is constant in pitch angle between $90°$ (equatorially mirroring) and ${\alpha }_{\mathit{loc}}$, the equatorial pitch angle of a particle that mirrors at the satellite location. Since ${\alpha }_{\mathit{loc}}$ is close to $90°$ for the Van Allen Probes orbit, the unmeasured volume of phase space is relatively small and the possible error introduced by this approximation is limited for reasonable particle distributions. If we instead assume zero PSD for the unmeasured population, it typically reduces the TRBEC values by a few percent.

The second unmeasured population that we must estimate are electrons inside and near the loss cone, since the pitch angle channels of MagEIS are not always sufficient to resolve the loss cone. When the loss cone is smaller than the smallest pitch angle bin of MagEIS we assume that the PSD is constant out to the loss cone. This will slightly overestimate the population, however, determining the size of the loss cone is vital to the TRBEC computation and we stress that this region in phase space is relatively small. In the $\left(E,{\alpha }_{eq},L^{\ast }\right)$ and $\left(\mu ,K,L^{\ast }\right)$ coordinate frames respectively, the loss cones size is dependent on the drift shell as

$${\alpha }_{eq,LC}\approx {\sin }^{-1}\left(\frac{1+\frac{3}{2}\frac{h}{R_E}}{{\left(L^{\ast }\right)}^{3/2}{\left(4-\frac{3}{L^{\ast }}\left(1+\frac{h}{R_E}\right)\right)}^{1/4}}\right),$$ (45)

where the altitude $h$ is taken as 100 km, and

$$K_{LC}\approx 2.110L^{\ast }-2.267.$$ (46)

For the second adiabatic invariant, the relationship with $L^{\ast }$ is linear and so we have opted for a numerical approximation by directly integrating Equation 32 rather than an equivalent analytical expression (Pitzel, 2022).

The final population we consider are electrons with relatively large $\mu$ and $K$ values. This particle population is encompassed by the TRBEC using linear adiabatic bounds. However, due to the mapping of the PSD between $E$ and ${\alpha }_{eq}$ to $\mu$ and $K$ this region in $(\mu ,K)$ phase space is entirely unobserved. Given that the flux distribution falls off with energy, we assume the PSD is zero $(f=0)$ for electrons corresponding to $\mu =2000$ MeV/G and $K=K_{LC}$ (Equation 46).

3.2. March 2013 Case Study

Figure 1 shows the geomagnetic conditions (Dst and Ap geomagnetic indices) and the TRBEC in adiabatic invariants (Equation 36) in early March 2013. Four chosen sets of integration bounds for each panel account for all trapped particles between a fixed $L^{\ast }$ range of 3.5–5 with given ranges of $\mu$ between 50 and 2,000 MeV/G. The similarity of the TRBEC computed from the MagEIS observations between Van Allen Probe A and B illustrates the excellent cross‐calibration between instruments during this interval.

Figure 1.

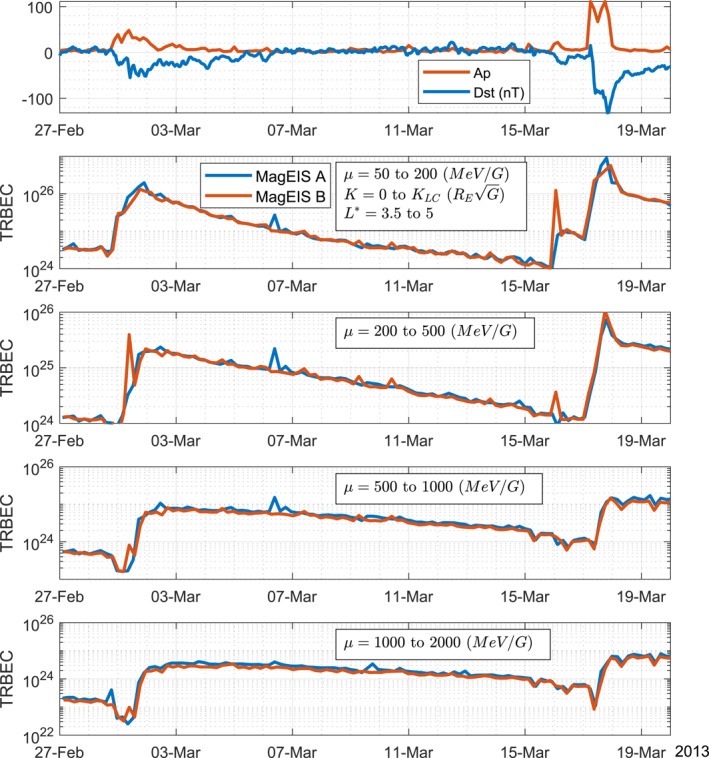
The TRBEC of electron populations determined by the listed integration bounds in the adiabatic coordinates of $\left(\mu ,K,L^{\ast }\right)$. The Dst and Ap indices during the case study interval are included in the top plot.

At the beginning of the period of interest on 1 March 2013, there is a storm indicated by increased activity in the geomagnetic indices, followed by another on 17 March. During these two events, there is an immediate increase in the number of particles across all the studied $\mu$ ranges. In the quiet period between the storms (4 March–15 March) the TRBEC steadily decreases. The decay is exponential for particles with $\mu >200$ MeV/G with a rate that decreases for increasing particle energy, showing that in the quiet phase between storms higher energy particles have more stable trajectories. The exponential decay implies a loss rate proportional to the number of available electrons in the radiation belts.

In the $\mu$ ranges of 200–500 MeV/G (500–1,000 MeV/G), there is a $95\%$ $(90\%)$ reduction in the TRBEC plots from the peak following the initial storm to the end of the decay period. Respectively, both these observations reproduce the results presented in Duderstadt et al. (2021) and Forsyth et al. (2016) from their TRBEC computations over comparable integration bounds. While the relative change is consistent between our work and the cited works, in both cases the absolute number of electrons in Figure 1 is a factor of $\approx 250$ less than the previous results. This is accounted for by the factor of ${(2\pi )}^3$ difference in the equations used to compute the TRBEC.

The TRBEC computed in non‐adiabatic coordinates is shown in Figure 2 over the same period. The selected region in phase space mainly represents the TRBEC for relativistic particles in the slot region and outer radiation belt from top to bottom in Figure 2. Similarly to the adiabatic TRBEC, there is an increase in the number of particles after the storms on 1 March and 17 March across all energies. However, at $L^{\ast }>4$ there are multiple injections of lower energy particles, less than 100 keV, on 9 March that decay relatively quickly compared with the loss rates prior to it. This is consistent with simulations during this period that show the main driver of loss in the slot is due to whistler mode hiss waves which are most efficient in this energy range (Ripoll et al., 2017, 2019). This increase is not observed in Figure 1 due to the higher energy of the selected boundaries. A minimum of $\mu =50$ MeV/G in Figure 1 is equivalent to a 244 keV equatorially mirroring particle at L = 4.

Figure 2.

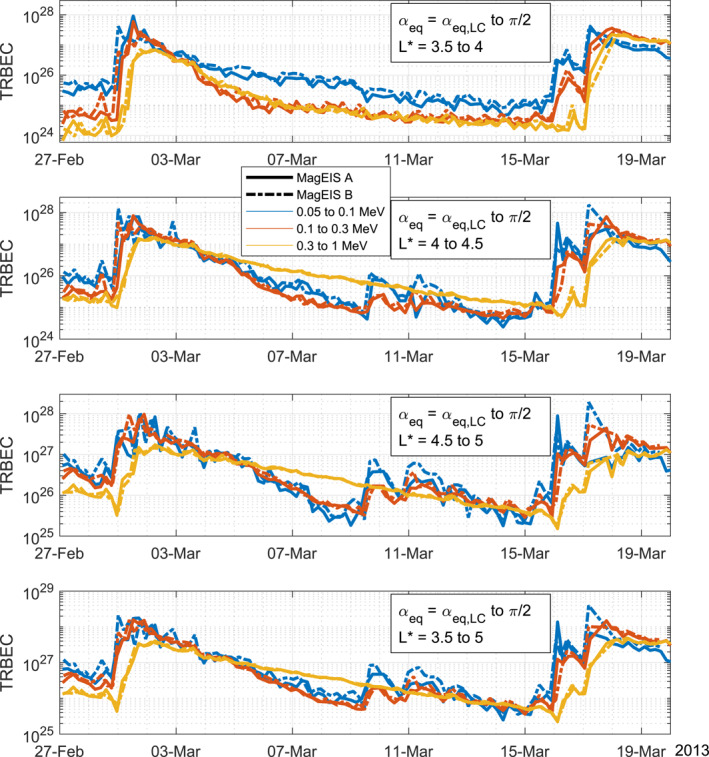
The TRBEC of electron populations determined by the listed integration bounds in the non‐adiabatic coordinates of $\left(E,{\alpha }_{eq},L^{\ast }\right)$.

In the slot region ($L^{\ast }=3.5$ to 4, Figure 2 top panel) the electron populations decay quickly before converging to a stable value due to the noise floor of the MagEIS instrument. Outside of the slot region, the electron decay is largely exponential. For lower energies ($<$300 keV), the exponential decay is interrupted by the injection on 9 March, whereas for 300–1,000 keV electrons the exponential decay is sustained until the 17 March storm. The higher‐energy particles are more stable over this period, as shown by the decreased decay rate, and before 9 March represent the bulk of the electrons in the outer belt.

These results show the strength of examining the TRBEC both in physical space $\left(E,{\alpha }_{eq},L^{\ast }\right)$ and in adiabatic space $\left(\mu ,K,L^{\ast }\right)$. Higher‐energy particles show a slow exponential loss during quiet times that is particularly smooth in adiabatic space. Lower‐energy particles show injections and loss features due to non‐adiabatic processes where mapping to invariant space is less applicable.

4. Summary

We presented further developments and refinements to the Total Radiation Belt Electron Content (TRBEC) from its origins in Baker et al. (2001) for its continued use as a homogeneous long‐term radiation belt and space weather index. From an information perspective, it is clear that TRBEC significantly reduces the amount of spectral, spatial, and temporal information from measured fluxes, but its functionality comes by way of the ability to simplify a complex system into a scalar quantity. It provides a simple, global, and long‐term assessment of the radiation belt that enables systematic analysis. This relationship between the electron flux and the TRBEC parallels geomagnetic indices such as the Ap and Dst in that global disturbances to the magnetic field are computed and reduced by combining many magnetometer measurements. Furthermore, in the absence of acceleration or loss, the total number of particles is conserved which is a property not held by particle fluxes.

We first presented a derivation of the TRBEC by specifying an electron population for a given range in the non‐adiabatic coordinates of energy, equatorial pitch angle, and $L^{\ast }$. Then, using the Hamiltonian formalism, we derived the TRBEC using action‐angle variables to present the TRBEC in terms of adiabatic invariant quantities, namely $\mu$, $K$, and $L^{\ast }$. We followed these derivations by showing consistency in the normalization of these expressions and compared both derivations to previous results. We showed agreement with Selesnick and Kanekal (2009) and Zhang et al. (2017) with our non‐adiabatic derivation of the TRBEC, however, we also conclude that the adiabatic form of the TRBEC presented in Forsyth et al. (2016), Murphy et al. (2018) and used by Duderstadt et al. (2021) overstates the TRBEC by a factor of ${(2\pi )}^3$ $(\approx 248)$. The impact of the latter discrepancy on the listed papers is limited, since they focus on relative differences in electron populations rather than on absolute number.

We showed numerically how we computed the TRBEC over a 20‐day period in 2013, finding similar trends as Forsyth et al. (2016) and Duderstadt et al. (2021) using the adiabatic formulation of the TRBEC. The TRBEC in physical space $\left(E,{\alpha }_{eq},L^{\ast }\right)$ is newly derived here, and may be better adapted to describe dynamic radiation belts evolving in ways that do not conserve the two first adiabatic invariants. Beyond showing that particles undergo exponential decay, a future application of the TRBEC would be to use its ability to quantify electron loss from the radiation belts to estimate global precipitation rates during geomagnetic quiet intervals.

Overall, the total number of electrons in the radiation belts is immense, reaching upwards of $10^{28}$ electrons at the peak of the storm studied. The total kinetic energy of those electrons is also very large, on the order of $10^{14}$ J. However, if these electrons could be collected then the combined rest mass would be on a more human scale: about 10 g.

Appendix A. Volume Contained by a Dipole Shell

Here we show that the exact ratio between the volume contained within a magnetic dipole shell and the volume of its enclosing sphere is $\frac{16}{35}$. Using the polar coordinates $(r,\lambda )$,

$$r=R_E{L}^{\ast }{\cos }^2(\lambda )$$ (A1)

describes the radial distance of magnetic dipole field lines to the origin (e.g., Schulz & Lanzerotti, 1974). In polar coordinates, the volume of a solid generated by the revolution of the area bounded by a curve, given by $r(\lambda )$, is

$$V=\frac{2}{3}\pi {\int }_{{\lambda }_1}^{{\lambda }_2}{\left(r(\lambda )\right)}^3\cos (\lambda )d\lambda$$ (A2)

where ${\lambda }_1$ and ${\lambda }_2$ are the bounding radii vectors of the curve (e.g., Phúc, 2020). The specific form of Equation A2 sweeps the curve around the geomagnetic pole axis $(\lambda =\pi /2)$. Implementing the dipole field from Equation A1 with Equation A2 and evaluating the expression gives the volume contained within a dipole field line, $V_{\text{dipole}}$, in terms of the fractional volume of a sphere with a radius corresponding to the equatorial crossing distance of the dipole field lines.

$$\begin{array}{ll}\hfill V_{\text{dipole}}& \hfill =\frac{2}{3}\pi {\int }_{-\pi /2}^{\pi /2}{\left(R_E{L}^{\ast }{\cos }^2(\lambda )\right)}^3\cos (\lambda )d\lambda \\ \hfill & \hfill =\frac{2}{3}\pi {\left(R_E{L}^{\ast }\right)}^3{\int }_{-\pi /2}^{\pi /2}{\cos }^7(\lambda )d\lambda \\ \hfill & \hfill =\left(\frac{4}{3}\pi {\left(R_E{L}^{\ast }\right)}^3\right){\int }_0^{\pi /2}{\cos }^7(\lambda )d\lambda \\ \hfill & \hfill =V_{\text{sphere}}{\left.\left(\frac{1225\sin (\lambda )+245\sin (3\lambda )+49\sin (5\lambda )+5\sin (7\lambda )}{2240}\right)\right|}_0^{\pi /2}\\ \hfill & \hfill =\frac{16}{35}{V}_{\text{sphere}}\end{array}$$ (A3)

Appendix B. Comparisons to Previous Results

In this Appendix, we show consistency between the TRBEC derived here and previous work by Selesnick and Kanekal (2009) (henceforth abbreviated as SK09) and Zhang et al. (2017) (henceforth abbreviated as Z17).

Selesnick and Kanekal (2009) assume a differential flux (electron intensity) $j$

$$j=p^{2}f=g{\sin }^{2n}\alpha .$$ (B1)

For the case $n=0$ (i.e., an isotropic distribution function) in a dipole, and using $N_{\mathit{SK09}}$ to denote the SK09 solution, the resulting TRBEC is given by their Equation 21:

$$\frac{d{N}_{\mathit{SK09}}}{dE}=\frac{256{\pi }^2{a}^{3}E}{35p{c}^2}{\int }_{L_1}^{L_2}{L}^{2}g(L)dL$$ (B2)

We reconcile nomenclatures by setting $a=R_E$ and noting that $n=0$ implies $g=f{p}^2$:

$$\frac{d{N}_{\mathit{SK09}}}{dE}=\frac{256{\pi }^2{\left(R_E\right)}^{3}Ep}{35c^2}{\int }_{L_1}^{L_2}{L}^{2}f(L)dL$$ (B3)

For our solution, we start with Equation 23 and note that the integral of $W(\alpha )$ over the range $\alpha =0$ to $\pi /2$ is 16/35. Differentiating with respect to energy, setting $L=L^{\ast }$ (i.e., using the same dipolar assumption as in SK09 Equation 21), and dropping any dependence of $f$ on $\alpha$,

$$\begin{array}{ll}\hfill \frac{dN}{dE}& \hfill =16{\pi }^2{\left(R_E\right)}^2{m}_0\frac{16}{35}{\int }_{L_1}^{L_2}f(L)L^2\gamma pdL\\ \hfill & \hfill =\frac{256{\pi }^2{\left(R_E\right)}^2{m}_0\gamma p}{35}{\int }_{L_1}^{L_2}{L}^{2}f(L)dL\end{array}$$ (B4)

Using $E=\gamma m_0{c}^2$ gives

$$\frac{dN}{dE}=\frac{256{\pi }^2{\left(R_E\right)}^{2}Ep}{35c^2}{\int }_{L_1}^{L_2}{L}^{2}f(L)dL$$ (B5)

which is consistent with Equation B3.

For Zhang et al. (2017), we start with their Equation 6, giving the total content in a flux tube. Denoting their solution for the flux tube content with $N_{FT}$:

$$N_{FT}=8\pi A_0{r}_0{\int }_{v_1}^{v_2}{v}^{2}dv{\int }_0^{\pi /2}{f}_v\left({\alpha }_0\right)\sin {\alpha }_0\cos {\alpha }_0\left(1.30-0.56\sin {\alpha }_0\right)d{\alpha }_0$$ (B6)

where $A_0$ is the flux tube area at the equator and $r_0=L{R}_E$ is the distance to the flux tube considered.

Z17 uses a non‐relativistic formulation throughout, and their phase space density (denoted $f_v$ above and $f$ in Z17) is in units of ${(\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\times \mathrm{v}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y})}^{-3}$, related to the differential flux $j$ as $f_v=\frac{m}{v^2}j$ (Z17, below Equation 6). The phase space density $f$ in this work is in units of ${(\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\times \mathrm{m}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{u}\mathrm{m})}^{-3}$, defined as $f=j/p^2$. In the non‐relativistic limit, $p=mv$ and so $f_v=m^{3}f$. Converting $f_v$ and using $r_0=L{R}_E$:

$$N_{FT}=8\pi A_{0}L{R}_E{m}^3{\int }_{v_1}^{v_2}{v}^{2}dv{\int }_0^{\pi /2}f\left({\alpha }_0\right)\sin {\alpha }_0\cos {\alpha }_0\left(1.30-0.56\sin {\alpha }_0\right)d{\alpha }_0$$ (B7)

According to the paragraph preceding Z17 Equation 6, the term $\sin {\alpha }_0\cos {\alpha }_0\left(1.30-0.56\sin {\alpha }_0\right)$ is equivalent to $W\left({\alpha }_0\right)$ in this work (and is indeed a good approximation).

$$N_{FT}=8\pi A_{0}L{R}_E{m}^3{\int }_{v_1}^{v_2}{v}^{2}dv{\int }_0^{\pi /2}f\left({\alpha }_0\right)W\left({\alpha }_0\right)d{\alpha }_0$$ (B8)

Replacing the flux tube area $A_0$ with a differential area element $R_{E}LdLd\theta$ and integrating gives a quantity that is directly comparable to our TRBEC $N$ and which we will denote $N_{\mathit{Z17}}$:

$$N_{\mathit{Z17}}=8\pi m^3{\int }_0^{2\pi }d\theta {\int }_{L_1}^{L_2}{L}^2{R}_E^{2}dL{\int }_{v_1}^{v_2}{v}^{2}dv{\int }_0^{\pi /2}f\left({\alpha }_0\right)W\left({\alpha }_0\right)d{\alpha }_0$$ (B9)

performing the integral in $\theta$ gives

$$N_{\mathit{Z17}}=16{\pi }^2{R}_E^2{m}^3{\int }_{L_1}^{L_2}{L}^{2}dL{\int }_{v_1}^{v_2}{v}^{2}dv{\int }_0^{\pi /2}f\left({\alpha }_0\right)W\left({\alpha }_0\right)d{\alpha }_0$$ (B10)

Using the non‐relativistic relation $E=1/2m{v}^2$ gives $dv=dE/(mv)$, and so

$$N_{\mathit{Z17}}=16{\pi }^2{R}_E^2{m}^3{\int }_{L_1}^{L_2}{L}^{2}dL{\int }_{E_1}^{E_2}\frac{v}{m}dE{\int }_0^{\pi /2}f\left({\alpha }_0\right)W\left({\alpha }_0\right)d{\alpha }_0$$ (B11)

Or, with $p=mv$:

$$N_{\mathit{Z17}}=16{\pi }^2{R}_E^{2}m{\int }_{L_1}^{L_2}{L}^{2}dL{\int }_{E_1}^{E_2}pdE{\int }_0^{\pi /2}f\left({\alpha }_0\right)W\left({\alpha }_0\right)d{\alpha }_0$$ (B12)

which is equivalent to our Equation 23 in the non‐relativistic limit $(\gamma =1)$.

Pitzel, J. C. , Cully, C. M. , Ripoll, J.‐F. , Loridan, V. , Huang, C.‐L. , Spence, H. E. , et al. (2024). Derivations of the total radiation belt electron content. Journal of Geophysical Research: Space Physics, 129, e2024JA032940. 10.1029/2024JA032940

Data Availability Statement

The Van Allen Probes flux data is available through the Coordinated Data Analysis Web (CDAWeb), or directly from the Los Alamos National Laboratory (LANL), at https://cdaweb.gsfc.nasa.gov/ and https://rbsp‐ect.newmexicoconsortium.org/data_pub/ respectively. The PSD data is available from the Van Allen Probes Science Gateway at https://rbspgway.jhuapl.edu/. We thank the MagEIS and Van Allen Probes Science Gateway teams for providing these data sets. The MATLAB code used to compute the TRBEC in both the energy and adiabatic invariant coordinate frames, plus data files of the computed TRBEC are archived in an open‐access repository (Pitzel, 2024) and maintained at https://github.com/JPitzel/Total_Radiation_Belt_Electron_Content/.