H++: a server for estimating pK_as and adding missing hydrogens to macromolecules

Abstract

The structure and function of macromolecules depend critically on the ionization (protonation) states of their acidic and basic groups. A number of existing practical methods predict protonation equilibrium pK constants of macromolecules based upon their atomic resolution Protein Data Bank (PDB) structures; the calculations are often performed within the framework of the continuum electrostatics model. Unfortunately, these methodologies are complex, involve multiple steps and require considerable investment of effort. Our web server http://biophysics.cs.vt.edu/H++ provides access to a tool that automates this process, allowing both experts and novices to quickly obtain estimates of pKs as well as other related characteristics of biomolecules such as isoelectric points, titration curves and energies of protonation microstates. Protons are added to the input structure according to the calculated ionization states of its titratable groups at the user-specified pH; the output is in the PQR (PDB + charges + radii) format. In addition, corresponding coordinate and topology files are generated in the format supported by the molecular modeling package AMBER. The server is intended for a broad community of biochemists, molecular modelers, structural biologists and drug designers; it can also be used as an educational tool in biochemistry courses.

INTRODUCTION

Electrostatic interactions are often a key factor determining the properties of biomolecules (1–5), including their biological function such as catalytic activity (6,7), ligand binding (8), complex formation (9) and proton transport (10), as well as their structure and stability (11,12).

The electrostatic properties of a molecule can change dramatically depending on the ionization (protonation) states of its titratable groups. The latter depend on the groups' type, location within the macromolecule, ionization state of other titratable sites and the pH and ionic strength of the surrounding solvent.

On one hand, experimental determination, usually by NMR, of protonation equilibria is expensive and often cannot be performed for every group of interest; on the other hand, individual protons are usually not resolved by ‘standard’ X-ray crystallography, and so most of the structures from the Protein Data Bank (PDB) are incomplete, in that they are missing hydrogen atoms. Coordinates of most of the missing protons, e.g. those on CH₃ groups, are relatively easy to reconstruct based on a set of straightforward chemical rules; however, predicting the protonation states of titratable groups such as Asp, Glu, Arg, Lys, Tyr, His or Cys is not trivial. A complete, all-atom structural model is usually required as input for many common molecular modeling techniques such as molecular dynamics (MD) simulations.

A number of theoretical methods exist that predict pK_a and protonation states of ionizable groups; see e.g. (13–27). Most of these methods are based on the ‘implicit solvent’ model, in which individual water molecules and mobile solvent ions are replaced by a continuous medium with the average properties of the solvent. Some approaches go beyond this and explicitly take into account the solvent's degrees of freedom (19,21,27), albeit at a significantly larger computational expense. Since electrostatic interactions are the key factor determining the protonation equilibria, considerable effort has been spent to improve the accuracy of their estimation. Apart from the very early approaches (13,28) that represented a molecule as a low dielectric sphere and that made mostly qualitative predictions, all modern methods use atom-detail information from high-resolution PDB structures. Generally, higher resolution data yield more accurate predictions. Although these methods vary in the details of the underlying physical models, they share one common feature—computational and algorithmic complexity. The latter stems, in general, from the sensitivity of the computed electrostatic interactions to the approximations involved and the details of the input structure. Hence, the computational process usually involves multiple non-trivial steps. There is often an additional complication arising from irregularities within the input PDB structures, such as naming inconsistencies and missing or duplicate atom records. Significant ‘pre-processing’ of structures is therefore required. As a result, modern methods that predict protonation equilibria and add missing hydrogens to PDB structures are frequently associated with a rather steep learning curve, often precluding novices from using them. Even for experts, the manual set-up of such calculations is often time consuming, and potentially useful variations of the input parameters and/or structural models remain unexplored.

This paper describes the freely available web server http://biophysics.cs.vt.edu/H++, which is designed to automate prediction of pK_a and protonation states of ionizable residues in macromolecules, using atomic resolution structures as input. The output structure contains missing hydrogens added according to calculated protonation states and is available in several formats used by a number of popular molecular modeling packages. The calculations are based on the standard continuum solvent methodology (15), within the frameworks of either the generalized Born (GB) or the Poisson–Boltzmann (PB) models (user-specified). All steps of the computational process are fully automated. Commonly used input parameters are accessible via a simple interface that provides reasonable defaults. The server is intended for both experts and non-experts.

MATERIALS AND METHODS

Pre-processing of submitted structures

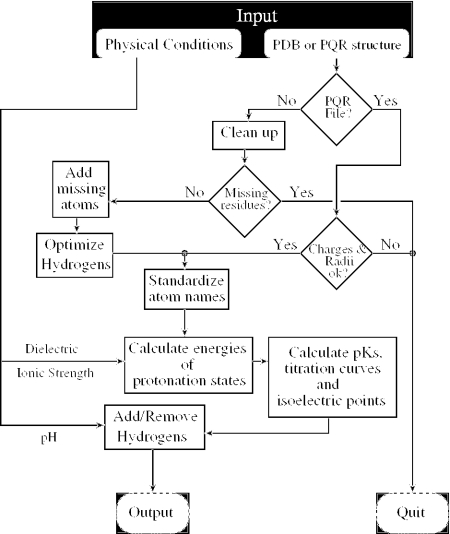
Structures are pre-processed differently depending upon their input format (see the flowchart in Figure 1). Two input formats are supported by the H++ website, PDB and PQR. These files differ in that PQR files already have charges and radii assigned to each atom whereas PDB files do not.

Figure 1.

Flowchart of computations performed by the H++ server described here. The input is a structure file in either PDB or PQR (PDB + charges + radii) format. The output includes computed pK_1/2 values for all titratable groups, as well as titration curves, isoelectric point and the original structure, in which the protonation states of all ionization groups have been made consistent with the calculated pKs. The generated structure is available in several formats used by popular molecular modeling packages.

If the input file is in PQR format, H++ makes minimal changes because it is assumed that the format is already suitable for electrostatic calculations. Changes made are as follows: atom names of all titratable amino acids are brought into accordance with the format adopted by the AMBER (29) package and consistency checks are performed. These checks ensure that the total charge of the system is an integer (within a ±0.05 unit charge tolerance per amino acid) and the atomic radii are between 0.5 and 3 Å. If any of the above checks fail, the sequence of residues is discontinuous or the atom names are different from the PDB standard and cannot be recognized, execution terminates.

For a structure submitted in the conventional PDB format, H++ deletes all HETATM records; that is, only those atoms that belong to amino acids or nucleotides are kept. This is the ‘clean-up’ step in Figure 1. Removal of explicit water molecules and mobile counterions is generally consistent with the implicit solvent framework in which solvation effects are accounted for in the mean-field manner. If necessary, removed ligands can be included in the calculations by submitting the complete structure in the PQR format, avoiding the ‘clean-up’ step. Sequence continuity is verified and all atom names are brought into accordance with the format adopted by the AMBER package. Deuterium atoms are replaced with equivalent hydrogens.

Addition of missing atoms and optimization of hydrogens

This section applies only to input structures in PDB format. Missing heavy atoms and protons (assuming standard protonation states of titratable groups) are added, and atomic partial charges and radii (Bondi) are assigned using the PROTONATE and LEAP modules of AMBER. This is followed by an MD-based optimization of the positions of the added hydrogens. The protocol was tested earlier (10) in a similar context; it consists of three consecutive stages during which only hydrogens are allowed to move: first, 100 steps of conjugate gradient minimization; second, 500 steps of MD at 300 K, with all torsional potentials involving hydrogens set to zero; and third, 100 steps of conjugate gradient minimization with the torsional potential returned to normal values. The AMBER parm99 force-field is used, where the integration time-step is 1 fs and the charge–charge interactions are computed in a uniform ‘vacuum’ of dielectric ɛ_out = 4.

Electrostatic calculations

The continuum electrostatics methodology widely used to calculate the energetics of proton transfer is described elsewhere (15,30); the model is available in the free software package MEAD (31). The H++ calculations rely upon the single-conformer version of MEAD; conformational variability is partially accounted for by the ‘smeared charge’ representation of titratable groups (see below) and the simulated annealing of protons described above. Although it is not the most systematic or exhaustive way of incorporating conformational variability, we believe, based on previous experiences (10,22,30), that this particular model is a reasonable balance between speed and accuracy, and is therefore a good choice for web-based calculations. In this model, the molecule is treated as a low dielectric medium ɛ_in, and the surrounding solvent is assigned a high dielectric constant ɛ_out. The electrostatic screening effects of (monovalent) salt enter via the Debye–Huckel screening parameter $\kappa \left[{\AA }^{-1}\right]\approx 0.316\sqrt{\left[\text{salt}\right][\text{mol}/\text{l}]}$. The salt concentration, ɛ_in and ɛ_out are accessible to the user, and reasonable defaults are provided. The difference between the pK_a of a sidechain and the pK_a of the corresponding model compound in free solution is determined by the combined effect of two distinct contributions to the total electrostatic (free) energy change. The first is the ‘Born term’ or desolvation penalty, which always penalizes burial of a charge inside a low dielectric medium. The second is the background term, which represents the electrostatic interactions of the group in question with all other fixed charges in the molecule not belonging to any titratable groups. These energy terms, as well as the matrix of site–site interactions, are estimated through a sequence of calculations in which sites in the protein and their corresponding model compounds have their charge distributions set to those of the protonated or deprotonated form, and suitable energy differences are taken. For the protonated states of Asp and Glu, in which the correct location of the proton is not known a priori, a ‘smeared charge’ representation is employed, in which the neutralizing positive charge is symmetrically distributed: 0.45 on each carbonyl oxygen atom, and 0.1 on the carbon atom. The electrostatic calculations are based either on a GB or a PB model, as requested by the user. The particular GB model we are using was found earlier (32) to work reasonably well in pK calculations on proteins; here its improved version (33) is used. The set-up and finite-difference solution of the PB problems or analytical GB calculations are carried out using the MEAD program package. In the finite-difference lattices, two levels of focusing are used. In the coarsest level the bounding box is set to twice the molecule's maximum extent and the grid points are spaced 2 Å apart. The finest lattice is focused on the region of interest, and the grid points are 0.5 Å apart. The probe radius for defining the molecular surface, which is used as the boundary between the interior and exterior dielectric regions, is set to 1.4 Å.

Calculating titration curves, pK_1/2 and protonation states

The electrostatic calculations outlined above provide (free) energies of each of the 2^N protonation microstates (10) in the system, where N is the number of ionizable sites. To make the subsequent calculation of the partition functions (and pK_1/2) manageable, a fast variant of a clustering approach is used (34). The approach subdivides the interacting sites into independent clusters based upon the strength of electrostatic site–site interactions between them. All electrostatic interactions for each ionizable site are sorted from highest to lowest; the top C_max sites are then selected to contribute to the calculation, and all others are ignored. The partition function for the site is then factored into computationally manageable components of maximum size C_max. Here, C_max = 17 is used: in tests on 600 representative proteins (35), we found (J. Myers, G. Grothaus and A. Onufriev, manuscript submitted) that C_max = 17 resulted in average errors of 0.2 pK units, compared with a standard treatment based upon a Monte Carlo approach (16).

The probability of protonation is computed for every site over a range of pH values equally spaced by 0.1 pH units apart. Individual curves can be displayed for user-selected residues, and the total protonation curve is generated, showing the computed isoelectric point of the molecule. A diagram showing the 10 lowest protonation states and their relative free energies is also generated. These diagrams were found useful (10) for analysis of proton transfer events in biomolecular systems.

Generating the PDB structure in its predicted protonation state

The computed titration curves provide an estimate of the probability of protonation of each titratable site at the (user-specified) pH of the solvent. A simple scheme is used for assignment of protonation states: if the estimated probability is <0.5, the site is considered deprotonated; otherwise, the site is protonated. We follow AMBER conventions in placement of new hydrogen atoms and selection of hydrogen atoms to be removed. Deprotonated (neutral) states of Arg and Tyr, not available in the AMBER databases, are obtained from the protonated forms by removal of the HH22 and HH protons, respectively; their partial charges are brought into accordance with the appropriate model compound values supplied by the MEAD package. The structures submitted in PQR format do not undergo re-assignment of protonation states, allowing greater flexibility for this input format.

CONCLUSION

The H++ web server described here automates the process of calculating pK_a, protonation states and titration curves of ionizable groups in macromolecules, given an atomic resolution structure as input. In addition, the server generates the properly protonated structures for use in other popular molecular modeling applications, such as MD. The calculations are based on the established continuum electrostatics methodology, which has been successfully used for this purpose over more than a decade. We expect H++ to become a useful tool for the broad biochemical, structural and computational biology community, as well as drug designers. It can also be a useful educational resource.