Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Nov 13;18(47):32508–32516. doi: 10.1021/acsnano.4c08382

Enhanced Control of Single-Molecule Emission Frequency and Spectral Diffusion

Rocco Duquennoy †,⊥,∥, Simon Landrieux ‡,⊥, Daniele De Bernardis †,⊥, Juergen Mony †, Maja Colautti †,⊥, Lin Jin §,#, Wolfram HP Pernice §,#, Costanza Toninelli †,⊥,*
PMCID: PMC11603773  PMID: 39537346

Abstract

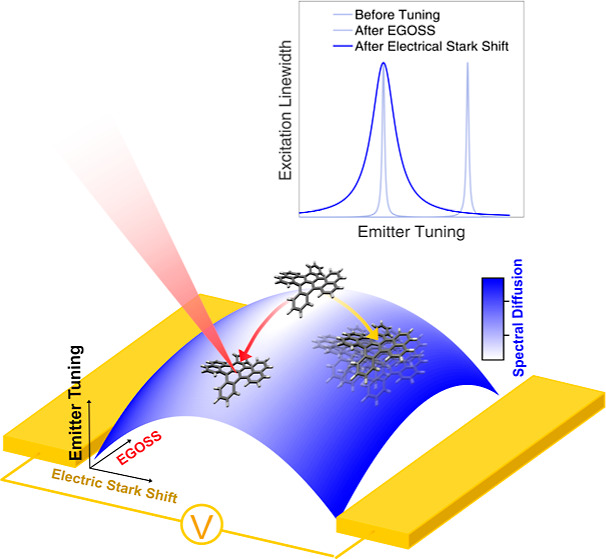
graphic file with name nn4c08382_0007.jpg

The Stark effect provides a powerful method to shift the spectra of molecules, atoms, and electronic transitions in general, becoming one of the simplest and most straightforward ways to tune the frequency of quantum emitters by means of a static electric field. At the same time, in order to reduce the emitter sensitivity to charge noise, inversion symmetric systems are typically designed, providing a stable emission frequency with a quadratic-only dependence on the applied field. However, such nonlinear behavior might be reflected in correlations between the tuning ability and unwanted spectral fluctuations. Here, we provide experimental evidence of this trend using molecular quantum emitters in the solid state cooled down to liquid helium temperatures. We finally combine the electric field generated by electrodes, which is parallel to the molecule’s induced dipole, with optically excite long-lived charge states acting in the perpendicular direction. Based on the anisotropy of the molecule’s polarizability, our two-dimensional control of the local electric field allows us not only to tune the emitter’s frequency but also to sensibly suppress the spectral instabilities associated with field fluctuations.

Keywords: quantum emitters, spectral-diffusion control, Stark shift, single molecule, quantum technologies

Introduction

Photons have a central role in quantum technology as flying qubits in quantum communication implementations,1,2 as well as in quantum sensing and quantum metrology experiments.3,4 Besides the recent advances in integrated platforms for the implementation of linear optical quantum computing and quantum simulations,5,6 quantum advantage has been demonstrated with photons in boson sampling experiments.7,8 Most of these applications rely on two-particle interference, resulting in an effective interaction between photons, ideally requiring indistinguishable photons on demand.9

Several methods can be used to produce single photons from solid-state platforms, such as spontaneous parametric down conversion (SPDC)10 or the radiative decay of triggered quantum emitters, like organic molecules,11 quantum dots,12 or color centers in diamond.13 Exploiting quantum emitters is desirable to overcome the hurdles of probabilistic generation processes. Nevertheless, residual spectral diffusion (SD) critically prevents scaling up the number of photons by using independent sources. Besides a tuning method able to compensate for the inhomogeneous broadening of the ensemble, this case requires indeed a high level of absolute frequency stability, as the emitters should remain resonant over the time scale of the entire experiment (typically for minutes).

The Stark effect provides a basic tuning mechanism that is available in most systems. This consists in imposing a controlled static electric field that shifts by different amounts the energy levels involved in the transition.14 However, it was demonstrated, for instance, with color centers in diamond and quantum dots, that the Stark effect increases the sensitivity of the emitter to the external electric field variations.15−18 This results in random fluctuations of the emitter’s line over multiple time scales, corresponding to the phenomenon known as SD.19

High single-photon purity, photostability, and Fourier-limited line widths are regularly measured in the emission from polyaromatic hydrocarbon molecules in host matrices,20−22 making them well-established systems for photonic quantum technologies. Using an optically induced Stark shift (OSS) on dibenzoterrylene molecules in anthracene nanocrystals (DBT:Ac NCs),23 quantum interference was observed in the emission from distinct molecules. In this experiment, the limited visibility was ascribed to residual frequency fluctuations.24−26 It is thus a prominent challenge in photonic quantum technologies to tune quantum emitters, and among them single molecules, without backfiring on their frequency stability.

In this paper, we address this problem and demonstrate a viable path, by combining the aforementioned OSS technique with the more standard Stark tuning approach, due to an electrode-induced electric field. As a first result, we bring insight into the unknown microscopic nature of the molecular-transition optical shift by exploiting the externally applied electric field. Then, a combination of optical pumping and electrode-generated electric field is implemented (electrically guided optical Stark shift: EGOSS), yielding a high degree of control on the local applied field with high spatial resolution and out-of-plane orientation. This allows for a reduction of spectral fluctuation (by a factor of 12) for a given frequency shift, with respect to the case of an in-plane-only electric field manipulation. In this way, the emission frequencies of single molecules can be tuned without degrading their spectral stability. This paper hence suggests a new understanding and crucial control tools for this widely common effect in solid-state quantum emitters.

The article is organized as follows. In the first section, we introduce the motivations and the main ideas behind the performed experiments. In the second one, “Results and Discussion”, we expose the experimental results divided into three subsections. First, the Stark shift is presented for the zero-phonon line (ZPL) of DBT molecules due to the application of an external in-plane static electric field along the direction of the DBT principal axis, highlighting its impact on molecule SD. In the following discussion, the Stark effect from the externally applied electric field is combined with the OSS and the phenomenology of the EGOSS approach is characterized. Finally, we demonstrate that EGOSS can be used to control the local electric field on the molecule allowing tuning of its ZPL while minimizing SD. All setup and experimental details are reported in the “Experimental Methods” section. Further details regarding the theory and fitting procedure are reported in the “Supporting Information”.

Motivations and Basic Ideas

Organic molecules are generally characterized by a single-photon electronic transition with a large dipole moment,11 which is dubbed 0–0 zero-phonon line (ZPL), as it does not couple to molecular vibrations. In particular, this transition is selected for the generation of indistinguishable photons, being lifetime-limited at a cryogenic temperature. As with any purely electronic transition, the frequency of the ZPL can be modified by the presence of a static electric field based on the well-known Stark effect acting on the involved energy levels. The induced Stark shift can be expressed as follows

graphic file with name nn4c08382_m001.jpg 1

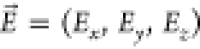Here, Inline graphic is the static external electric field, d⃗ and α are the differences in the static dipole moment and in the polarizability tensor between the ground and the excited state of the ZPL transition, respectively. For centrosymmetric molecules, d⃗ is expected to be zero, and the Stark effect is completely dominated by the polarizability tensor difference α, giving a quadratic shift in the electric field strength. The polarizability tensor can be calculated by means of perturbation theory, as discussed in the Supporting Information.

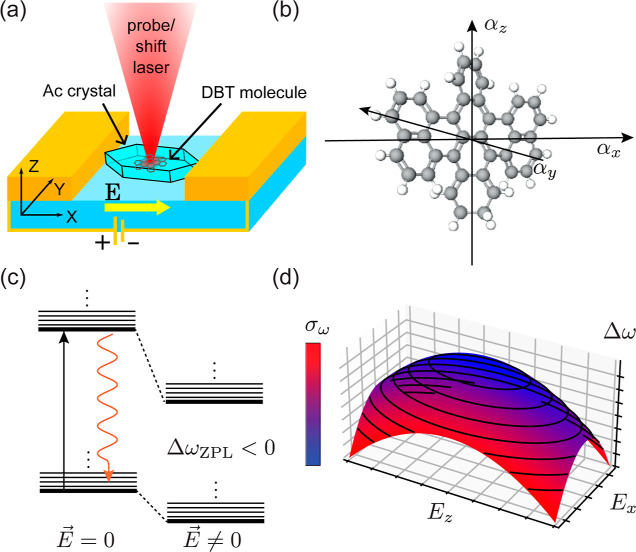
In this work, the molecular quantum emitter consists of DBT molecules inserted as impurities into Ac nanocrystals. The crystals are dispersed on glass between interdigitated electrodes, which are used to apply a controlled electric field (see Figure 1a for a sketch). The ZPL of the quantum emitter is given by the transition between the singlet excited state |e⟩ and ground state |g⟩ with a characteristic frequency of ωZPL/(2π) ≈ 381 THz. It is characterized by a high quantum yield (QY) > 50%27 and Debye–Waller factor (DW) ≃ 70%.28 At cryogenic temperatures (T ≈ 2.7 K), the line width narrows down close to the Fourier-limit of 40 MHz.25

Figure 1.

Figure 1

Open in a new tab

(a) Sketch of the studied sample. DBT-doped nanocrystals are dispersed on a glass substrate, nanostructured with 4 μm gap interdigitated gold electrodes. The applied voltage can be scanned in a [−100:+100] V range, producing an electric field along the x direction. Optical access is available along the z axis and is used in excitation for optical shift and fluorescence collection. (b) Cartoon picture of the DBT molecule, indicating the three symmetry axes corresponding to the diagonal components of the polarizability tensor. (c) Level structure of the ZPL before and after the application of a local electric field. The measurements are performed by resonantly exciting the ZPL and then detecting the Stokes-shifted emitted light due to relaxation through a phononic sideband. (d) Illustrative example of the ZPL frequency shift as a function of the local electric field. The resulting surface is a squeezed paraboloid, narrower along the axis defined by αxx and broader along the axis defined by αzz. The color scale represents the SD experienced by the emitter increasing linearly with the value of the local electric field (Ex, Ez). The contour lines represent the isofrequency curves. From this representation it is clear that it is possible to change SD by moving on an isofrequency line.

Considering the geometry of the DBT molecule, mostly preserved after the insertion in the host matrix, we identify the three symmetry axes that diagonalize α, labeled as x, y, and z and reported in Figure 1b. In this reference frame, the shift can be written as

graphic file with name nn4c08382_m003.jpg 2

Here we have neglected the y-component of the polarizability, αyy, which is expected to be much smaller than the other two, given the planar geometry of the molecule.

As a distinct feature of the DBT molecule, its polarizability tensor difference is always positive along the x and z directions, leading to a red-shift quadratic in the field,29 as schematically represented in Figure 1c. As a consequence, the Stark shift can be represented as a two-dimensional concave paraboloid as a function of the applied electric field, as depicted in Figure 1d. (Individual molecules can in general deviate from centrosymmetric geometry because of external factors like localized charge impurities and geometrical defects in the neighboring crystal sites.30,31 Even though those phenomena could induce d⃗ different from zero, the discussion can be formally mapped to the following one, by inserting a nonzero value of the local field 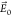Inline graphic in the absence of the external one.) With this powerful technique, shifts as large as 400 GHz32 have been reported, allowing for the observation of cooperative effects among pairs of resonant molecules.33,34

Notably, the sensitivity of the ZPL emission frequency to the local electric field is expected to have consequences in terms of the stability of the source’s emission, becoming detrimental for experiments and applications based on multiple resonant emitters. In particular, at large fields, the molecule will be more affected by fluctuations in the external electric field or electric field noise due to fluctuating charges,19,35,36 leading to enhanced SD, (color scale Figure 1d). Indeed, considering the electric field only along the x direction and assuming that this is Gaussianly distributed around the value Ex with variance σE, the shift probability will also be a Gaussian p(δω, ΔωZPL, σω) centered in ℏΔωZPL = -αxxE2x with variance ℏσω = 2αxxExσE, (see Supporting Information for major details). Interestingly, these relations can be used to link together the Stark shift to the SD as follows

graphic file with name nn4c08382_m005.jpg 3

explicitly showing the characteristic square-root dependence of the Gaussian line-broadening component with the frequency shift and the polarizability tensor component. (In a more realistic description, independent contribution to spectral fluctuations that can arise from electric field noise in different directions or from other physical processes would add up quadratically.)

In this work, we have taken further this description, experimentally testing the idea that one can apply electric fields along different directions and obtain the same frequency shift. Having the SD mainly dominated by charge noise, an eventual anisotropy in the polarizability tensor will result in independent control of SD. Indeed, given the different values of the absolute Stark shift gradient along the molecule’s isofrequency lines represented in Figure 1d, one could apply the tuning electric field in the direction where the polarizability tensor is minimum, attaining the same frequency shift while minimizing the electric-field sensitivity. The impact of the presented findings goes beyond the field of molecular single photon sources, putting forward a possible strategy for performing quantum optics experiments with indistinguishable photons from multiple distinct emitters.

Results and Discussion

In this section, we describe the obtained experimental results, which confirm the intuitive picture presented in the previous section. The basic technique used in this work is excitation spectroscopy: scanning a tunable laser over the ZPL and collecting the Stokes-shifted fluorescence after spectral filtering, we measure the molecule excitation spectrum (color-coded traces in Figure 2a). For the purpose of this work, it will be sufficient to observe isolated lines to ascribe them to independent emitters. Due to the fluctuating electric environment, these spectra diffuse in time, as can be observed in the repeated set of measurements shown in Figure 2a. By integrating such measurements over time, a profile such as the one reported on the top panel is obtained. This type of data yields information about SD, by fitting a Voigt profile and extracting its Gaussian component (for more details, see the Supporting Information). In the case of Figure 2a, for example, we estimate σω/(2π) = 64 ± 6 MHz. Here, each line corresponds to a laser scan at 0.5 GHz/s scanning speed, and a 2 min interval is to be considered among subsequent scans, resulting in an overall measurement time over 12 min. For a single trace, we obtain a characteristic profile like that reported in Figure 2b. It is worth noticing that in this case also, the measured line is well fitted by a Voigt profile resulting from the convolution of a Lorentzian line with fwhm γ/(2π) = 70 ± 7 MHz and a Gaussian distribution p(δω) with σω/(2π) = 40 ± 3 MHz. In fact, the observation time required to perform a single laser scan, typically around 3 s, provides an intrinsic integration time for our measurements during which SD cannot be completely neglected. Comparing the two profiles in Figure 2, it is clear that the width of the Gaussian component in the spectrum (which is associated with SD) critically depends on the observation time.

Figure 2.

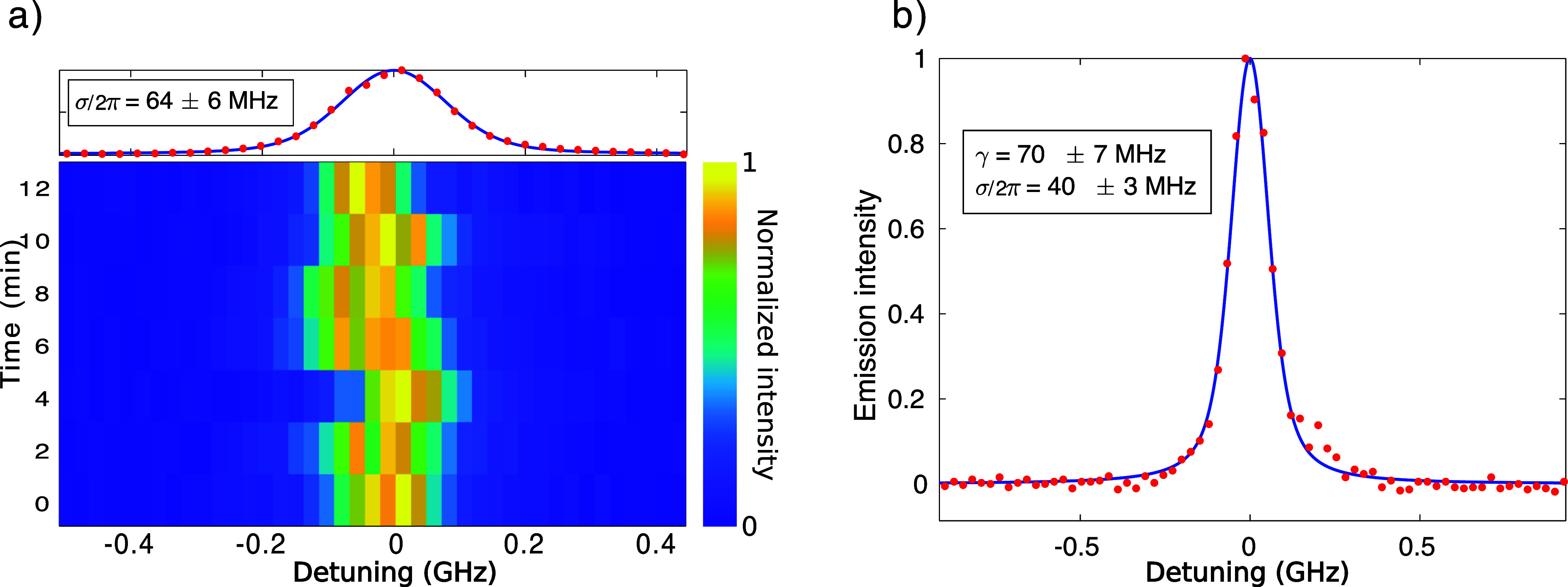
Figure 2

Open in a new tab

Excitation spectroscopy and SD. The excitation spectrum from a DBT emitter, obtained by recording the red-shifted fluorescence signal (red dots) as a function of the excitation laser frequency, is fitted by a Voigt profile (blue solid lines). The homogeneous (γ) and the inhomogeneous (σ) broadening components can be extracted from the fits. Here, each overall swipe is obtained at a scan speed of 0.5 GHz/s. (a) Each line corresponds to an excitation spectrum plotted in color scale. The total measurement time for the repeated swipes amounts to 12 min. The integrated signal is plotted in the top panel. (b) A single snapshot is shown where the lower σ component confirms that the SD depends on the observation time.

Using this methodology, we now investigate how the molecular emission properties are modified under the influence of an applied electric field.

Principal-Axis Electric Stark Shift and Related Spectral Diffusion

The Stark shift is measured here by applying a finite voltage between the interdigitated electrodes shown in Figure 1a, thus generating an in-plane electric field 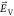Inline graphic along the x direction, as reported in Figure 3a. For each value of the electric field, an excitation spectrum is collected, and the fluorescence intensity is reported on a color scale in Figure 3b.

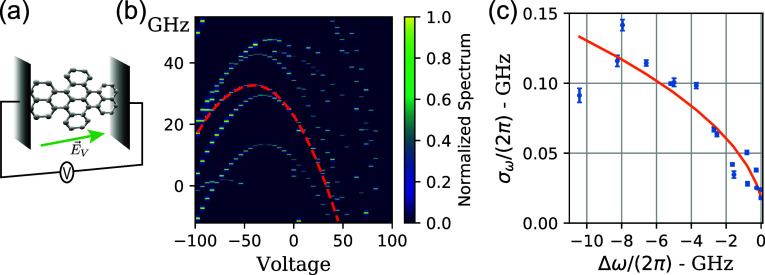
Figure 3.

Figure 3

Open in a new tab

Stark shift and SD (a) cartoon picture of the specific configuration. We perform the spectral measurements on a DBT molecule embedded between two electrodes at fixed voltage difference generating a tunable in-plane electric field in the direction of the principal polarization axis defined by αxx. (b) Typical measurement of the excitation spectra (color coded along the y axis of the figure) as a function of the applied voltage on the electrodes. Each parabola can be associated with a different molecule. The measurements are obtained with a scan speed of 0.5 GHz/s. At this scanning speed the observed line is broadened by the fast components of SD. (c) Measured SD as a function of the frequency shift extracted from the data highlighted by the red dashed line in (b); the values of σω are extracted by fitting each fixed voltage spectrum with a Voigt profile. The orange line corresponds to the best fit of the square-root dependence of SD against the shift predicted in eq 3.

As several DBT molecules are embedded in the same nanocrystal addressed in confocal microscopy, multiple lines appear in the figure columns, corresponding to the ZPL frequencies of the different emitters. As expected (see eq 2), their frequency position shifts following a parabolic behavior as a function of the applied voltage. It is worth noticing that molecules do not shift all by the same amount due to the applied electric field. This can be ascribed to a small disorder in the alignment with respect to the b axis.37 Moreover, the local electric field difference giving rise to the inhomogeneous broadening might also determine an effectively different response to the externally applied field. For molecules whose dipole transition is perpendicular to the direction of the external electric field, we do not detect any shift. This observation justifies the approximation αyy = 0 used in eq 2 and is coherent with the planar nature of the DBT molecule, for which charge mobility is strongly suppressed in the direction orthogonal of the molecular plane. Indeed, as represented in Figure 1a, the DBT molecule trapped in the anthracene crystal is expected to have the secondary axis in the z direction, perpendicular to our substrate plane.29 For these reasons, we expect that all of the Stark effect observed due to the electrodes is given by the αxx polarizability. The coefficient of the quadratic term of each parabola yields, hence, the x-polarizability difference of the molecule in the direction of the applied field. Since in our setup the electric field applied on the molecule through the electrodes can be as large as Ex ≈ ± 200 kV/cm (see Experimental Methods), the polarizability along the x direction can be estimated by fitting the parabolas in Figure 3b as αxx/ℏ ≈ 2π × 1.82 ± 0.11 MHz/(kV/cm)2, in agreement with previous results.29 As discussed in the Supporting Information, this value is also reasonably close to the theoretical estimates for DBT,38 where a range of values is reported, αxx/ℏ ≈ 2π × 0.2–2 MHz/(kV/cm)2.

In the following, we discuss the procedure to test the square root dependence of the SD with the frequency shift. Each excitation spectrum is fitted with a Voigt profile, whose fwhm is given by39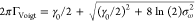Inline graphic. The Lorentzian component is fixed to γ0/(2π) = 80 MHz, obtained as the line width of a Lorentzian fit to the narrowest measured line. From the Voigt profile, we hence extract the parameter σω, associated solely to SD. The dependence of σω on the measured Stark shift ΔωZPL is found to be correctly expressed by eq 3 where an offset σ0 is added quadratically, so as to take into account the charge noise in the z direction. The results are shown in Figure 3c, where only measurements between −100 and −15 V are considered in order to avoid the region where the lines from two molecules were overlapping. From the fit to the data in Figure 3c with eq 3, the product of the electric field variance with the polarizability difference can be estimated, yielding a value αxxσ2E/ℏ = 2π × 0.410 ± 0.001 MHz. Using the previously estimated value for the polarizability difference, the local electric field variance can be obtained, amounting to a value of σE = 0.47 ± 0.20 kV/cm. These electric field fluctuations can be probably ascribed to the presence of moving charges in the matrix environment where the molecule is hosted. Regardless of the specific physical origin, it is interesting to compare this variance with the one of fluctuating fields in other material platforms. In this case, the quantum emitter is used as a probe to test the noise level of the electric environment where it is hosted. For instance, this value is significantly smaller than the one recently measured in SnV centers15 and colloidal quantum dots,16 whereas it is 3 orders of magnitude larger with respect to field fluctuations in charge-engineered semiconductor quantum dots.40−42 This observation puts the molecular platform in an excellent position for quantum optics experiments, as very high visibility of two-photon interference has been observed also without charge engineering.43

When the frequency shift is small, ΔωZPL → 0, and the molecule is approaching the summit of its Stark-parabola, we observe that the SD decreases, approaching zero for certain molecules, such as the one shown in Figure S1 of the Supporting Information. The measurement time scale here is the same as that used for the data in Figure 2b, corresponding to a scan speed of 0.5 GHz/s.

Two-Dimensional Electric Field Control: OSS and EGOSS

The laser-induced frequency shift of DBT emission has been discovered in recent years23 and is now an established tool in current quantum optics studies based on such molecular setups.25,44 The OSS technique is implemented by focusing an intense light beam on the emitter at cryogenic temperatures, for periods of time on the order of minutes (1 to 16 min for the experiments reported here). The ZPLs of the embedded molecules shift to the red side of the spectrum and remain there even after the external laser has been switched off. With respect to the more standard shifting approach using external electrodes, it has the advantage of being fabrication free and having a much higher spatial resolution, limited only by the diffraction limit of the shifting laser beam. Its reversibility is bounded by a typical relaxation time that is specific for every sample and can typically take even a few hours.23 These features come at the cost of being less reproducible.

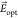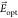The laser-induced shift has been interpreted as a Stark shift induced by long-lived charge-separated states arising from the ionization cascade induced by the laser illumination.23 These charges generate a local electric field, denoted here Inline graphic, which shifts the molecule frequency via the Stark effect. However, the spatial distribution of these charges remains unknown, and previous studies do not provide any indication of the Inline graphic direction.

In the following, we test this hypothesis and study the interplay of the optically induced effect with the electrode-induced Stark shift, identifying a combined tuning method, i.e., the electrically guided OSS, hereafter named EGOSS.

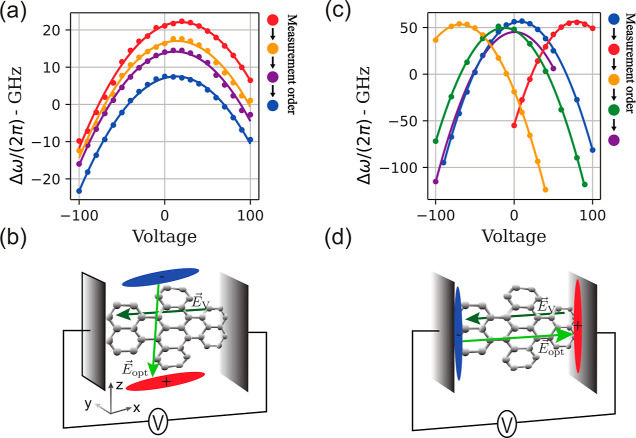
At first, several runs of OSS are applied, each corresponding to a laser pulse with a 10 kW/cm2 intensity and exposure times reported in the legend of Figure 4a. After each one, the excitation spectrum is measured for different applied voltages along the x axis, and a characteristic parabola is reconstructed by plotting the corresponding central frequency of the Voigt profile. The effect of the OSS on the charge distribution can be appreciated by observing the different colored parabolas in Figure 4a, as they progressively down-shift toward lower emission frequencies. This rigid translation indicates that the laser-generated charges have produced a field in a direction orthogonal to the one probed by the electrodes geometry. In this picture, one can look at the red-shifting parabolas as different slices of the paraboloid in Figure 1c, corresponding to various values of the field along the z axis. Indeed, as discussed in the previous sections, due to the thin geometry of the DBT molecule along the y direction, we expect it to have negligible polarizability on that axis, αyy ∼ 0. This implies that the measured Stark effect can be attributed to the Inline graphic electric field having a finite amplitude along the z direction. Although we do not have direct access to the spatial distribution of charges displaced by the optical pump, this observation suggests that a significant portion of this charge accumulation occurs along the z direction, as schematically illustrated in Figure 4b. Once this process is complete, the charges are trapped and their configuration remains stationary over the typical time scales of the experiment.

Figure 4.

Figure 4

Open in a new tab

OSS and EGOSS. (a) Measured ZPL frequency shift ΔωZPL/(2π) after subsequent OSS runs are plotted as colored dots. Solid lines represent the best fit to the data with parabolic functions. The experimental configuration is sketched in panel (b). Applying the optical shift results in an accumulation of charges along the z axis that gives rise to an electric field along the secondary polarizability axis of the DBT molecule; as a second step, an in-plane electric field along the x axis is applied through the electrodes, varying the voltage V. (c) Measured ZPL frequency shift ΔωZPL/(2π) after subsequent EGOSS runs are plotted as colored dots. Solid lines represent the best fit to the data with parabolic functions. The experimental configuration is sketched in panel (d). In this case, fixed bias voltages impose a preferential direction for the excited charges to move, accumulating them in the direction of the electrodes-applied field. This results in an effective screening of the in-plane electric field between the electrodes and hence in an electric field offset in the Stark-parabola. All OSS and EGOSS cycles have been performed with 100 μW pump power. Applied voltages and exposure times are reported in the legends next to the plots.

Now, the idea can be put forward to use an external electric field to better control such generated charges in the OSS scheme and combine the benefits of the two methods in an electrically guided OSS (EGOSS). Indeed, we immediately notice that the OSS is strongly influenced by the contextual application of an external electric field. When a bias voltage is maintained on the electrodes during the OSS run, a subsequent voltage sweep on the electrodes produces a result markedly different from that previously described. In this case, the parabolas also shift in the horizontal direction, indicating that the OSS generates an offset electric field in the same direction as the one generated by the electrodes. The final result is a displacement of the vertex of the parabola toward the applied bias voltage, as shown in Figure 4c. The application of the EGOSS sequence at +100 V between the blue and the red parabolas shows that, with an exposure time of 120 s, there is an almost complete screening of the external field at the emitter’s position. Subsequent EGOSS sequences confirm this behavior and show that the screening can also be saturated with longer exposure times, as can be appreciated considering the last OSS sequence between the green and purple parabola that lasted for 300 s. This behavior can be explained by considering that when optical pumping is performed while an external electric field is present, the charges move in the direction of the field to compensate for it (see Figure 4d). We interpret the saturation behavior of the screening as a consequence of the fact that the lower the local field, the harder it is to free charges from the defects of the crystal, making the effect progressively less efficient. We note in passing that this shielding effect associated with EGOSS is effective also when the applied voltage is zero. Indeed, the green parabola is shifted toward zero voltage with respect to the yellow one, as a result of a simple OSS procedure (see Figure 4 caption). This effect is less visible in panel (a), as the local field for the pristine crystal is already quite close to zero. It is worth noticing that this technique is reversible, as the parabolas can move in both directions, with only a minor residual vertical component of the shift. Notably, the reported observations represent experimental evidence of the OSS phenomenon’s electrical nature and provide an excellent knob to tackle the problem of Stark-shift-induced SD.

EGOSS for the Reduction of Spectral Diffusion

As a major outcome of this work, in this section, we demonstrate that the EGOSS-assisted tuning method allows for much smaller SD with respect to the case of tuning by the traditional in-plane electric field while keeping control of the operating voltage. Indeed, as αzz < αxx, following eq 3, we expect that for equal values of the frequency shift, the optical shift acting along the z axes should determine a lower SD. Moreover, thanks to the presence of the external electric field, the experiment can be performed at arbitrary values of the applied voltage. This instance can be crucial when multiple emitters must be brought in resonance.

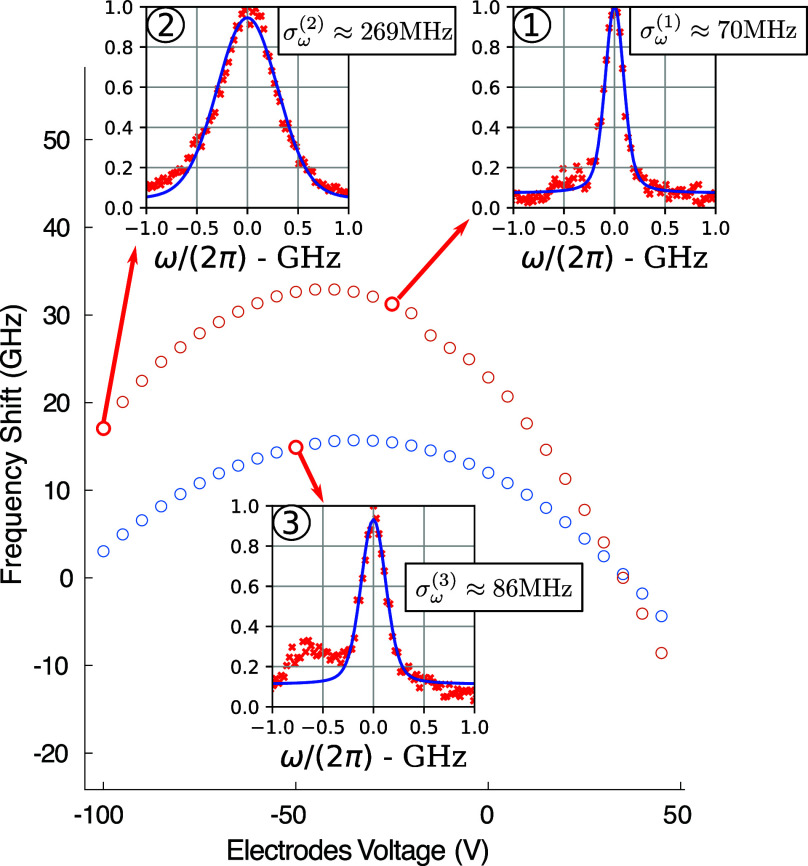
We here consider, for instance, the case of a molecule that is intrinsically biased, hence exhibiting a parabola vertex at finite voltages (see, e.g., orange dots in Figure 5). In order to compare the molecule SD at different emission frequencies, while operating the setup at similar values of the applied field, an EGOSS sequence at −25 V is applied. The following response to the in-plane electric field is shown as blue dots in Figure 5. SD is then measured in correspondence to the three highlighted dots, averaging 30 excitation spectra (scan speed 0.5 GHz/s) over a time span of about 12 min (red dots in Figure 5 insets). More details on the time traces are provided in Supporting Information. Close to the vertex of the orange parabola, obtained before EGOSS, σ(1)ω amounts to a value of 70 ± 2 MHz. A 13 GHz shift obtained by applying an electrode-induced field results in an increased SD characterized by σ(2)ω = 269 ± 3 MHz. This significant stability degradation can be partially avoided by exploiting the results presented in the previous section. The implementation of the EGOSS method leads to a frequency shift by a very similar amount (14 GHz) but with a much smaller increase of SD (σ(3)ω = 86 ± 5 MHz). Moreover, the tuning obtained with this combination is as persistent as the bare optical shift on the time scales of our experiments (hours). While the ratio of the postshift SDs, σ(2)ω/σ(3)ω = 3.1, already proves the effectiveness of the method, the relative increase with respect to the starting SD (σ(2)ω–σ(1)ω)/(σ(3)ω–σ(1)ω) = 12 underlines how effective a higher degree of control on the fields can be in order to control SD. The relation αxx > αzz is expected from simple considerations of the size of the molecule in the x and z directions and is in line with the observed reduction of SD. However, such a big improvement also suggests that the field fluctuations σE could be smaller in the vertical direction. Further measurements would be required in order to test this hypothesis.

Figure 5.

Figure 5

Open in a new tab

Effect of electric field control on SD. The parabolas are obtained by monitoring the frequency of emission of a molecule during a scan over the electrode voltage. The orange dots are measured before any optical shift while the blue ones after a combined shift that allowed for the creation of a local field in the z direction. In correspondence to the red highlighted points, we measured SD by repeating excitation spectroscopy measurements. The integrated signal is presented in the insets. A Voigt profile fit on each of the integrated signals allowed for the isolation of the Gaussian component of the broadening associated with SD.

Conclusions

In this work, we experimentally demonstrate 2-D control over the local electric field around a single DBT molecule, exploiting a combination of an electrode-induced field and optically generated charge-separated states. These experiments enhance our understanding of the microscopic mechanisms behind the optically induced frequency shift (OSS) in molecules and allow for efficient control of molecular emissions while remaining almost fabrication-free.

By combining optical shifts with the electrode-induced field, we have developed a versatile method for shifting the ZPL, which is dubbed EGOSS. This dual approach allows us to achieve significant shifts in the emission frequency, with minimal impact on the final frequency stability as opposed to ordinary approaches. The demonstrated improvement amounts to a factor of 12, yielding a promising result for the advancement of organic molecules as single photon sources in quantum technologies. The methodologies used in this paper could also be exploited in future works to measure local charge noise in the environment of quantum emitters.

Experimental Methods

The sample used for these experiments consists of a glass substrate covered with 150 nm thick gold interdigitated electrodes with 4 μm wide gaps that enable the application of an electric field. A COMSOL simulation of the geometry of the electrodes indicates electric field magnitudes in the range [80, 160] kV/cm for an applied voltage of +100 V, depending on the distance from the metal.

The DBT:Ac nanocrystal growth procedure consists of injecting 100 μL of a 1:25,000 mixture of 1 mM DBT-toluene solution and 5 mM Ac-acetone solution into 1 mL of sonicating water. During the 30 min long sonication, solvents dissolve in water and DBT:Ac crystals are formed. The suspension is drop-casted onto the interdigitated electrodes and the water evaporated in a vacuum. Solvents and Ac were purchased from Sigma-Aldrich, water was deionized by a Milli-Q Advantage A10 system (18.2 mΩ cm at 25 °C), and DBT was purchased from Mercachem.

The DBT-doped nanocrystals are dispersed on the electrodes and then covered with a 100 nm layer of polyvinyl alcohol (PVA, dissolved in water at 5% concentration, molecular weight = 13,000–23,000 purchased from Sigma-Aldrich) via spin-coating (5000 rounds per minute for 120 s), in order to avoid sublimation of the Ac matrix during the cooldown of our cryostat. Figure 1a shows a sketch of the sample as well as the reference frame used throughout this discussion. The x axis is the direction of the applied electric field, while the z axis corresponds to the vertical direction and coincides with the optical path of the confocal microscope.

A scheme of the optical system used in the experiments is shown in Figure 6. The sample is glued on the coldfinger of our closed-cycle cryostat (Montana Cryostation) by means of thermally conductive silver paste (RS PRO 123-9911). In order to achieve the desired thermal contact between the sample and the coldfinger, we let the silver paste fully dry before the vacuum pumping of the cold chamber; this procedure avoids the formation of bubbles underneath the sample that would reduce the thermal contact and thus increase the temperature at the molecule position. The DBT molecules, kept at 2.7 K, are excited on their ZPLs using a continuous wave DFB laser (Toptica LD-0785-0080-DFB-1) that can be reproducibly tuned in the range between 783 and 786 nm. A high numerical aperture objective (NA = 0.67, SigmaKoki PAL-50-NIR-HR-LC07) is used to both focus the excitation beam on the emitter of interest and collect the emission from it. A half-wave plate at the back entrance of the objective allows for the selection of polarization of the excitation light. The laser beam is separated from the detection path using a 90/10 unbalanced beam splitter followed by a long-pass filter (Semrock Razoredge-785RS-25), rejecting the scattered laser light. The Stokes-shifted fluorescence emitted by the molecule is transmitted by the filter and its total intensity, directly proportional to the population of the excited state of the ZPL transition, is then focused on a single photon avalanche photodiode (APD, Excelitas SPCM 800 14 FC). The power of the excitation laser is kept lower than the saturation intensity of the single emitters and the laser frequency is scanned over the ZPL; the collected signal reproduces the shape of the emission line and provides a measurement of the absolute frequency of each DBT molecule. This procedure is what has been dubbed excitation spectroscopy.

Figure 6.

Figure 6

Open in a new tab

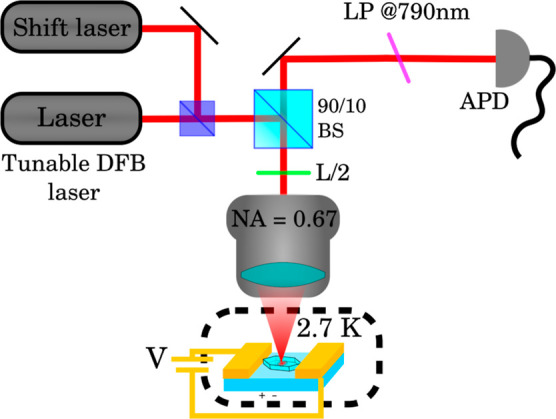
Optical setup. Molecules are excited and observed in a confocal microscope setup whose main elements are schematically shown here. BS stands for beam splitter, L/2 for half-wave plate, LP for long-pass filter, and APD for avalanche photodiode.

The laser-induced shift is implemented by using a continuous wave laser at 767 nm (Toptica DXL 110) focused on the emitter of interest. Using power in a range between 100 μW and 1 mW we detect a ZPL shift. The magnitude of the shift is small when compared to previously published results because in this case the observed nanocrystals do not lie on a mirror that would have increased the power density at the confocal spot. Since the optical shift is semipermanent and persists for hours after switching off the shifting laser, it is possible to follow the shift of the line using excitation spectroscopy between different shift rounds.

Acknowledgments

This work has been cofunded by the European Union - NextGeneration EU, ”Integrated infrastructure initiative in Photonic and Quantum Sciences” - I-PHOQS [IR0000016, ID D2B8D520, CUP B53C22001750006]. The research has been cofunded by the EC under the FET-OPEN- RIA project STORMYTUNE (G.A. 899587). It is also cofunded by the European Union (ERC, QUINTESSEnCE, 101088394). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. The authors wish to acknowledge Pietro Lombardi for advice on sample fabrication.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.4c08382.

  • Theoretical estimate of the polarizability difference tensor based on simulations of the energy level structure of DBT; clarification on the shape of the profile measured via excitation spectroscopy; experimental measurements of the square root dependence of SD on frequency shift at faster scan speed; and time traces whose integrated versions are in the insets of Figure 5 (PDF)

The authors declare no competing financial interest.

Notes

The article is also available on the ArXiv platform as Rocco Duquennoy, Simon Landrieux, Daniele De Bernardis, Juergen Mony, Maja Colautti, Lin Jin, Wolfram H.P. Pernice, Costanza Toninelli. “Enhanced control of single-molecule emission frequency and SP”. 2024, 2409.01840. ArXiv. URL: https://arxiv.org/abs/2409.01840 (accessed Sep 3, 2024).

Supplementary Material

nn4c08382_si_001.pdf (808.9KB, pdf)

References

  1. Zapatero V.; van Leent T.; Arnon-Friedman R.; Liu W.-Z.; Zhang Q.; Weinfurter H.; Curty M. Advances in device-independent quantum key distribution. Npj Quantum Inf. 2023, 9, 10–11. 10.1038/s41534-023-00684-x. [DOI] [Google Scholar]
  2. Hu X.-M.; Guo Y.; Liu B.-H.; Li C.-F.; Guo G.-C. Progress in quantum teleportation. Nat. Rev. Phys. 2023, 5, 339–353. 10.1038/s42254-023-00588-x. [DOI] [Google Scholar]
  3. Polino E.; Valeri M.; Spagnolo N.; Sciarrino F. Photonic quantum metrology. AVS Quantum Sci. 2020, 2, 024703. 10.1116/5.0007577. [DOI] [Google Scholar]
  4. Pirandola S.; Bardhan B. R.; Gehring T.; Weedbrook C.; Lloyd S. Advances in photonic quantum sensing. Nat. Photonics 2018, 12, 724–733. 10.1038/s41566-018-0301-6. [DOI] [Google Scholar]
  5. Kok P.; Munro W. J.; Nemoto K.; Ralph T. C.; Dowling J. P.; Milburn G. J. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 2007, 79, 135–174. 10.1103/RevModPhys.79.135. [DOI] [Google Scholar]
  6. Maring N.; Fyrillas A.; Pont M.; Ivanov E.; Stepanov P.; Margaria N.; Hease W.; Pishchagin A.; Lemaître A.; Sagnes I.; et al. A versatile single-photon-based quantum computing platform. Nat. Photonics 2024, 18, 603–609. 10.1038/s41566-024-01403-4. [DOI] [Google Scholar]
  7. Zhong H.-S.; Wang H.; Deng Y. H.; Chen M. C.; Peng L. C.; Luo Y. H.; Qin J.; Wu D.; Ding X.; Hu Y.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. 10.1126/science.abe8770. [DOI] [PubMed] [Google Scholar]
  8. Madsen L. S.; Laudenbach F.; Askarani M. F.; Rortais F.; Vincent T.; Bulmer J. F. F.; Miatto F. M.; Neuhaus L.; Helt L. G.; Collins M. J.; et al. Quantum computational advantage with a programmable photonic processor. Nature 2022, 606, 75–81. 10.1038/s41586-022-04725-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bouchard F.; Sit A.; Zhang Y.; Fickler R.; Miatto F. M.; Yao Y.; Sciarrino F.; Karimi E. Two-photon interference: the Hong-Ou-Mandel effect. Rep. Prog. Phys. 2021, 84, 012402. 10.1088/1361-6633/abcd7a. [DOI] [PubMed] [Google Scholar]
  10. Jin B.; Mishra D.; Argyropoulos C. Efficient single-photon pair generation by spontaneous parametric down-conversion in nonlinear plasmonic metasurfaces. Nanoscale 2021, 13, 19903–19914. 10.1039/D1NR05379E. [DOI] [PubMed] [Google Scholar]
  11. Toninelli C.; Gerhardt I.; Clark A. S.; Reserbat-Plantey A.; Götzinger S.; Ristanović Z.; Colautti M.; Lombardi P.; Major K. D.; Deperasińska I.; et al. Single organic molecules for photonic quantum technologies. Nat. Mater. 2021, 20, 1615–1628. 10.1038/s41563-021-00987-4. [DOI] [PubMed] [Google Scholar]
  12. Senellart P.; Solomon G.; White A. High-performance semiconductor quantum-dot single-photon sources. Nat. Nanotechnol. 2017, 12, 1026–1039. 10.1038/nnano.2017.218. [DOI] [PubMed] [Google Scholar]
  13. Sipahigil A.; Lukin M. D.. Current Trends in Atomic Physics; Oxford University Press, 2019; pp 1–28. [Google Scholar]
  14. Wild U. P.; Guttler F.; Pirotta M.; Renn A. Single molecule spectroscopy: Stark effect of pentacene in p-terphenyl. Chem. Phys. Lett. 1992, 193, 451–455. 10.1016/0009-2614(92)85830-4. [DOI] [Google Scholar]
  15. De Santis L.; Trusheim M. E.; Chen K. C.; Englund D. R. Investigation of the Stark Effect on a Centrosymmetric Quantum Emitter in Diamond. Phys. Rev. Lett. 2021, 127, 147402. 10.1103/PhysRevLett.127.147402. [DOI] [PubMed] [Google Scholar]
  16. Conradt F.; Bezold V.; Wiechert V.; Huber S.; Mecking S.; Leitenstorfer A.; Tenne R. Electric-Field Fluctuations as the Cause of Spectral Instabilities in Colloidal Quantum Dots. Nano Lett. 2023, 23, 9753–9759. 10.1021/acs.nanolett.3c02318. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Zuber J.; Li A. M.; Puigibert M.; Happacher J.; Reiser P.; Shields B. J.; Maletinsky P. Shallow Silicon Vacancy Centers with Lifetime-Limited Optical Linewidths in Diamond Nanostructures. ACS Nano Letters 2023, 23, 10901–10907. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gorlitz J.; Herrmann D.; Fuchs P.; Iwasaki T.; Taniguchi T.; Rogalla D.; Hardeman D.; Colard P.; Markham M.; Hatano M.; Becher C. Coherence of a charge stabilised tin-vacancy spin in diamond. Npj Quantum Inf. 2022, 8, 45. 10.1038/s41534-022-00552-0. [DOI] [Google Scholar]
  19. Kubo A.; Pontius N.; Petek H.. Stochastic Processes in Chemical Physics. A Stochastic Theory of Line Shape; Interscience Publisher, 1969; Vol. 15, pp 101–127. [Google Scholar]
  20. Pazzagli S.; Lombardi P.; Martella D.; Colautti M.; Tiribilli B.; Cataliotti F. S.; Toninelli C. Self-Assembled Nanocrystals of Polycyclic Aromatic Hydrocarbons Show Photostable Single-Photon Emission. ACS Nano 2018, 12, 4295–4303. 10.1021/acsnano.7b08810. [DOI] [PubMed] [Google Scholar]
  21. Rezai M.; Wrachtrup J.; Gerhardt I. Polarization-entangled photon pairs from a single molecule. Optica 2019, 6, 34–40. 10.1364/OPTICA.6.000034. [DOI] [Google Scholar]
  22. Rezai M.; Wrachtrup J.; Gerhardt I. Coherence Properties of Molecular Single Photons for Quantum Networks. Phys. Rev. X 2018, 8, 031026. 10.1103/PhysRevX.8.031026. [DOI] [Google Scholar]
  23. Colautti M.; Piccioli F. S.; Ristanović Z.; Lombardi P.; Moradi A.; Adhikari S.; Deperasinska I.; Kozankiewicz B.; Orrit M.; Toninelli C. Laser-Induced Frequency Tuning of Fourier-Limited Single-Molecule Emitters. ACS Nano 2020, 14, 13584–13592. 10.1021/acsnano.0c05620. [DOI] [PubMed] [Google Scholar]
  24. Lettow R.; Rezus Y. L. A.; Renn A.; Zumofen G.; Ikonen E.; Götzinger S.; Sandoghdar V. Quantum Interference of Tunably Indistinguishable Photons from Remote Organic Molecules. Phys. Rev. Lett. 2010, 104, 123605. 10.1103/physrevlett.104.123605. [DOI] [PubMed] [Google Scholar]
  25. Duquennoy R.; Colautti M.; Emadi R.; Majumder P.; Lombardi P.; Toninelli C. Real-time two-photon interference from distinct molecules on the same chip. Optica 2022, 9, 731. 10.1364/OPTICA.452317. [DOI] [Google Scholar]
  26. Duquennoy R.; Colautti M.; Lombardi P.; Berardi V.; Gianani I.; Toninelli C.; Barbieri M. Singular spectrum analysis of two-photon interference from distinct quantum emitters. Phys. Rev. Res. 2023, 5, 023191. 10.1103/PhysRevResearch.5.023191. [DOI] [Google Scholar]
  27. Ren P.; Wei S.; Zhang P.; Chen X.-W. Probing fluorescence quantum efficiency of single molecules in an organic matrix by monitoring lifetime change during sublimation. Optica 2022, 20, 073602. 10.3788/COL202220.073602. [DOI] [Google Scholar]
  28. Clear C.; Schofield R. C.; Major K. D.; Iles-Smith J.; Clark A. S.; McCutcheon D. P. S. Phonon-Induced Optical Dephasing in Single Organic Molecules. Phys. Rev. Lett. 2020, 124, 153602. 10.1103/PhysRevLett.124.153602. [DOI] [PubMed] [Google Scholar]
  29. Nicolet A. A.; Bordat P.; Hofmann C.; Kol’chenko M. A.; Kozankiewicz B.; Brown R.; Orrit M. Single dibenzoterrylene molecules in an anthracene crystal: Main insertion sites. ChemPhysChem 2007, 8, 1929–1936. 10.1002/cphc.200700340. [DOI] [PubMed] [Google Scholar]
  30. Moradi A.; Ristanovic Z.; Orrit M.; Deperasinska I.; Kozankiewicz B. Cover Feature: Matrix-induced Linear Stark Effect of Single Dibenzoterrylene Molecules in 2,3-Dibromonaphthalene Crystal (ChemPhysChem 1/2019). ChemPhysChem 2019, 20, 2. 10.1002/cphc.201801157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Smit R.; Ristanovic Z.; Deperasinska I.; Kozankiewicz B.; Orrit M. Probingthe in-plane dipolemoment vector between ground and excited state of single molecules by the Stark effect. ChemPhysChem 2024, 25, e202300881 10.1002/cphc.202300881. [DOI] [PubMed] [Google Scholar]
  32. Schädler K. G.; Ciancico C.; Pazzagli S.; Lombardi P.; Bachtold A.; Toninelli C.; Reserbat-Plantey A.; Koppens F. H. L. Electrical Control of Lifetime-Limited Quantum Emitters Using 2D Materials. Nano Lett. 2019, 19, 3789–3795. 10.1021/acs.nanolett.9b00916. [DOI] [PubMed] [Google Scholar]
  33. Trebbia J.-B.; Deplano Q.; Tamarat P.; Lounis B. Tailoring the superradiant and subradiant nature of two coherently coupled quantum emitters. Nat. Commun. 2022, 13, 2962. 10.1038/s41467-022-30672-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hettich C.; Schmitt C.; Zitzmann J.; Kühn S.; Gerhardt I.; Sandoghdar V. Nanometer resolution and coherent optical dipole coupling of two individual molecules. Science 2002, 298, 385–389. 10.1126/science.1075606. [DOI] [PubMed] [Google Scholar]
  35. Kambs B.; Becher C. Limitations on the indistinguishability of photons from remote solid state sources. New J. Phys. 2018, 20, 115003. 10.1088/1367-2630/aaea99. [DOI] [Google Scholar]
  36. Shkarin A.; Rattenbacher D.; Renger J.; Honl S.; Utikal T.; Seidler P.; Gotzinger S.; Sandoghdar V. Nanoscopic Charge Fluctuations in a Gallium Phosphide Waveguide Measured by Single Molecules. Phys. Rev. Lett. 2021, 126, 133602. 10.1103/PhysRevLett.126.133602. [DOI] [PubMed] [Google Scholar]
  37. Musavinezhad M.; Renger J.; Zirkelbach J.; Utikal T.; Hail C. U.; Basche T.; Poulikakos D.; Gotzinger S.; Sandoghdar V. High-Resolution Cryogenic Spectroscopy of Single Molecules in Nanoprinted Crystals. ACS Nano 2024, 18, 21886–21893. 10.1021/acsnano.4c02003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Sadeq Z. S.; Muniz R. A.; Sipe J. E. One- and two-photon absorption spectra of dibenzoterrylene. Phys. Rev. Materials 2018, 2, 075202. 10.1103/PhysRevMaterials.2.075202. [DOI] [Google Scholar]
  39. Whiting E. E. An empirical approximation to the Voigt profile. J. Quant. Spectrosc. Radiat. Transf. 1968, 8, 1379–1384. 10.1016/0022-4073(68)90081-2. [DOI] [Google Scholar]
  40. Kuhlmann A. V.; Houel J.; Ludwig A.; Greuter L.; Reuter D.; Wieck A. D.; Poggio M.; Warburton R. J. Charge noise and spin noise in a semiconductor quantum device. Nat. Phys. 2013, 9, 570–575. 10.1038/nphys2688. [DOI] [Google Scholar]
  41. Zhai L.; Lobl M. C.; Nguyen G. N.; Ritzmann J.; Javadi A.; Spinnler C.; Wieck A. D.; Ludwig A.; Warburton R. J. Low-noise GaAs quantum dots for quantum photonics. Nat. Comm 2020, 11, 4745. 10.1038/s41467-020-18625-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Zhai L.; Nguyen G. N.; Spinnler C.; Ritzmann J.; Lobl M. C.; Wieck A. D.; Ludwig A.; Javadi A.; Warburton R. J. Quantum interference of identical photons from remote GaAs quantum dots. Nat. Nano 2022, 17, 829–833. 10.1038/s41565-022-01131-2. [DOI] [PubMed] [Google Scholar]
  43. Lombardi P.; Colautti M.; Duquennoy R.; Murtaza G.; Majumder P.; Toninelli C. Triggered emission of indistinguishable photons from an organic dye molecule. Appl. Phys. Lett. 2021, 118, 204002. 10.1063/5.0048567. [DOI] [Google Scholar]
  44. Lange C. M.; Daggett E.; Walther V.; Huang L.; Hood J. D. Superradiant and subradiant states in lifetime-limited organic molecules through laser-induced tuning. Nat. Phys. 2024, 20, 836–842. 10.1038/s41567-024-02404-4. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn4c08382_si_001.pdf (808.9KB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES