Quantitative analyses of how optimally heterogeneous neural codes maximize neural information in jittery transmission environments

Abstract

Various spike patterns from sensory/motor neurons provide information about the dynamic sensory stimuli. Based on the information theory, neuroscientists have revealed the influence of spike variables on information transmission. Among diverse spike variables, inter-trial heterogeneity, known as jitter, has been observed in physiological neuron activity and responses to artificial stimuli, and it is recognized to contribute to information transmission. However, the relationship between inter-trial heterogeneity and information remains unexplored. Therefore, understanding how jitter impacts the heterogeneity of spiking activities and information encoding is crucial, as it offers insights into stimulus conditions and the efficiency of neural systems. Here, we systematically explored how neural information is altered by number of neurons as well as by each of three fundamental spiking characteristics: mean firing rate (MFR), duration, and cross-correlation (spike time tiling coefficient; STTC). First, we generated groups of spike trains to have specific average values for those characteristics. Second, we quantified the transmitted information rate as a function of each parameter. As population size, MFR, and duration increased, the information rate was enhanced but gradually saturated with further increments in number of cells and MFR. Regarding the cross-correlation level, homogeneous and heterogeneous spike trains (STTC_AVG = 0.9 and 0.1) showed the lowest and highest information transmission, respectively. Interestingly however, when jitters were added to mimic physiological noisy environment, the information was reduced by ~ 46% for the spike trains with STTC_AVG = 0.1 but rather substantially increased by ~ 63% for the spike trains with STTC_AVG = 0.9. Our study suggests that optimizing various spiking characteristics may enhance the robustness and amount of neural information transmitted.

Introduction

Information theory serves as a crucial tool for quantifying the information encoded by cells regarding stimuli¹ and elucidating the intricate relationships among spike variables². Neuroscience researchers have focused on both efficient ‘reading’ and accurate ‘decoding’ of complex neural signals to understand how the brain deciphers information. In addition to these endeavors, neuroscientists have attempted to control neural activities using various stimulation modalities such as electric, magnetic, ultrasound, and optogenetic approaches^3–7. These efforts include neural prosthetic research aimed at ‘encoding’ sensory information and ‘writing’ artificial neural activities.

The early generation of prosthetic systems has paved the way for upcoming new generations of neural prostheses, which may cure various psychiatric diseases and/or restore sensory/motor functions. However, the best performance of state-of-the-art neural prostheses still falls short of completely overcoming diseases and enabling daily activities⁸. For sophisticated physiological functions, various aspects of spiking activities need to be considered for the development of advanced neural prosthetic systems that facilitate elaborate modulation of neural activities. Developing these advanced systems requires understanding under what conditions different spiking patterns compress an enormous amount of information and communicate with downstream neurons in the brain⁹. Thus, for successful neuromodulation implementation, it seems critical to examine the relationship between the amount of neural information and population spiking response patterns.

Many neuroscientists have suggested various neural coding schemes that describe what aspects of sensory/motor features are encoded by neurons and how neurons precisely encode these features via spike trains¹. Representative examples of encoding schemes include rate coding¹, temporal coding¹⁰, population coding¹¹, and correlation coding^12,13. Although these encoding schemes examined the effect of four major resource constraints on information transmission: number of cells, mean firing rates, spiking duration, and cross-correlation level, it has not been well quantified to what extent these four resources affect information transmission. In particular, the intrinsic diversity (cell-to-cell variation/heterogeneity) of neurons is a system developed for efficient information transmission, stemming from differences in morphological features or distributions of ion channels^14–16. For instance, heterogeneous cell groups can transmit twice as much information as homogeneous ones¹⁴, exhibiting robust properties against noise and contributing to a role in reducing redundancy among populations of neurons¹⁴.

While some studies in the past decades have shown the relationship between cell-to-cell heterogeneity and information transfer^14,17–20, the variability between trials has remained largely unexplored. This inter-trial variance is known as jitter and represents the spike timing precision and reliability. The occurrence of jitter arises from the multi-layered architecture of the brain and sensory organs²¹. Noteworthy is the observation of jitter not only in physiological neuron activities but also in responses to artificial stimuli^22,23. For example, jitters of several milliseconds have been observed in diverse neuromodulation approaches which have stimulated cortical neurons²⁴, motor neurons²⁵, and retinal neurons^26,27; those jitters are known to be influenced by disease conditions²⁸. It is suggested that jitters in spiking activities also affect information about stimulus conditions²⁹, and low-jitter spiking activities boost information transmission^30,31. Therefore, it is essential to systematically understand how jitter affects the information encoded in the population neural code.

In this paper, we separately quantified the influence of basic spike variables such as the number of cells, mean firing rate, spiking duration, and intracellular spiking correlation on the amount of information. The primary goal of our study was to offer a comprehensive view of how neural information transmission is altered by the aforementioned variables. To systematically explore the dependency of information on each parameter, we generated spike trains in a controlled manner for populational spiking activities to have desired characteristics, and then we calculated how much information may be transmitted by the corresponding spike trains to the downstream neurons. Since it is difficult to collect all spiking neurons that satisfy various specific conditions, it is more efficient to use an artificial neuron model which is highly reproducible and allows more focus on analysis³². Specifically, we employed the ‘Brian2’ model in this study, which has been well-established to computationally represent biologically realistic spiking neuron activity^33–35. This model is widely recognized for its ability to capture the intricacies of neural activity with high biological fidelity, allowing researchers to mimic realistic neuronal dynamics in a controlled environment. Additionally, it provides the computational efficiency needed to analyze large-scale networks or explore complex neural processes with varying conditions. Furthermore, we also added jitters to those sets of the generated spiking activities to maximize the heterogeneity and examined the transition of information amount as a function of noise levels. Our present work suggests that optimizing neural responses to maximize the amount of information transmitted in response to stimuli could ultimately enhance the performance of neural prostheses, as more effective information allows the patients to better interact with the prosthesis, leading to more natural and functional outcomes.

Methods

Generating spike trains in a controlled manner

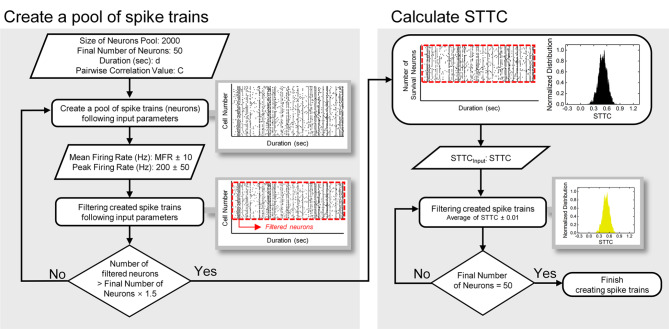
We created spike trains using a modified version of ‘Brian 2’³⁶, a Python open-source library for simulation of spiking neural networks. Input parameters for generating a pool of spike trains (neurons or cells) were (1) size of neurons for initial pool, (2) final number of neurons, (3) spiking duration (d), (4) average pairwise correlation value (C), (5) mean firing rate (MFR), and (6) peak firing rate (PFR) (Fig. 1). First, we generated 5 different groups of correlated 2,000 spike trains that have 0.2, 0.4, 0.6, 0.8, and 1-sec-long spiking duration, respectively. Subsequently, the generated spike trains were filtered according to the target spiking magnitudes (20, 40, 60, 80, and 100 ± 10 Hz for MFR; 200 ± 50 Hz for PFR), which were in the range of physiological spiking magnitudes of retinal ganglion cells^37–40. The firing rates were calculated for every 20-msec-long bin with a step size of 5 msec. This step was terminated if the number of surviving spike trains became above 1.5 times of the desired final number of neurons for each condition. Then, from the surviving spike trains, our customized MATLAB code randomly chose 50 spike trains until the average correlations between those spike trains reached within the range of specific values (i.e., 0.1, 0.3, 0.5, 0.7, and 0.9 ± 0.01). The neuron size of the initial pool of 2,000 and the final number of neurons of 50 were selected to maximize computational efficiency while obtaining reliable results within a range that allows for reduced computation time and memory use based on our trials and errors.

Fig. 1.

Model schematic for generating spiking trains under the controlled manners. First, a pool of spike trains was created based on modified version of ‘Brian2’, open-source Python code with input parameters such as size of neurons pool, final number of neurons, duration (d = 0.2, 0.4, 0.6, 0.8, and 1 s), pairwise correlation value (C = 0.1, 0.3, 0.5, 0.7, and 0.9). Second, the generated artificial neurons were filtered by mean firing rate (20, 40, 60, 80 and 100 ± 10 Hz), and peak firing rate (200 ± 50 Hz). Third, the surviving (filtered) spike trains were transmitted to customized MATLAB codes to find 50 population combination which satisfy target spike time tiling coefficient (STTC) values (0.1, 0.3, 0.5, 0.7, and 0.9 ± 0.01).

To quantify the correlation level across the generated spike trains, we computed the spike time tiling coefficient (STTC) which is defined as the equation shown below⁴¹:

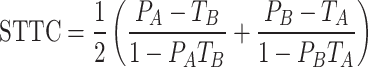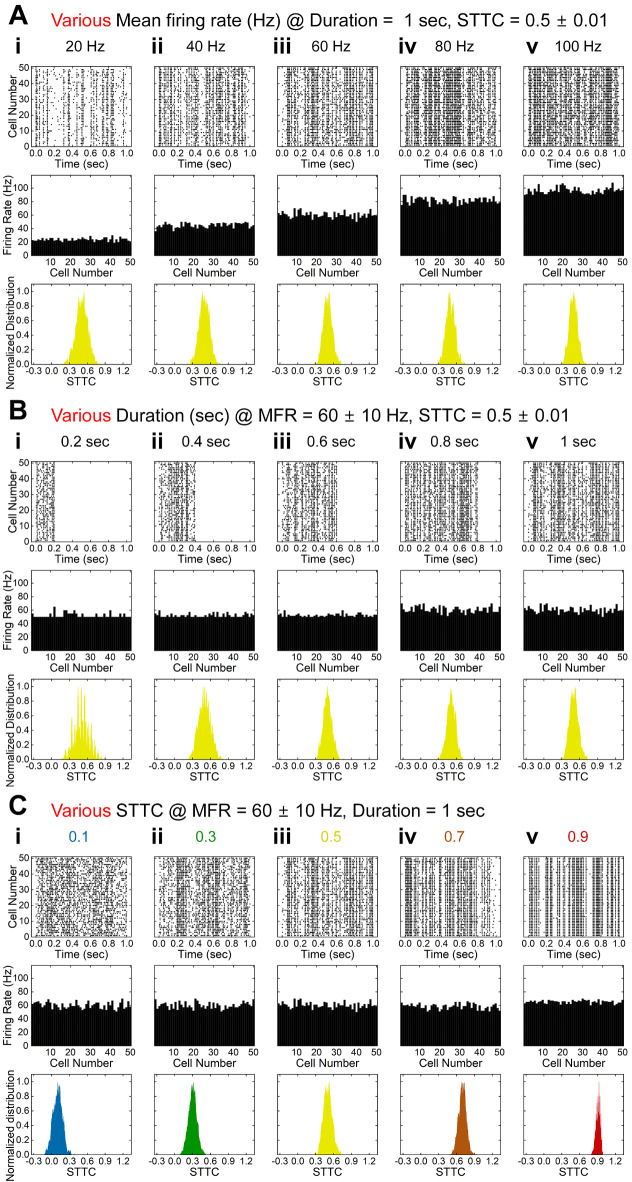
where P_A (or P_B) is defined as the proportion of spikes in spike trains A (or B) which lie within the time window (±Δt) of each spike in spike trains B (or A). T_A (or T_B) is defined as the proportion of ± Δt for each spike in spike train A (or B) of total recording time. STTC determines whether one spike train co-occurs with a higher or lower proportion within a given time window (±Δt) of another spike train⁴². In the present study, we computed all STTCs between every pair of the 50 selected spike trains in each group using Δt of 4 msec to compare with the results of previous work⁴³. The characteristics of the selected spike trains were represented in forms of raster plots, bar graphs of MFR, and distribution histograms of STTC values (Fig. 2). In raster plots, each dot indicates a single action potential (the first rows of Fig. 2A, 2B, and 2C). Also, in bar graphs, each bar indicates the MFR of a selected cell (the second rows of Fig. 2A, 2B, and 2C). Rolling histograms of STTCs visualize how STTC values distribute (the third rows of Fig. 2A, 2B, and 2C); the number of STTCs in every 0.01 bin with a moving step of 0.002. The average STTC (STTC_AVG) was used to represent the populational cross-correlation levels of the given set of spike trains.

Fig. 2.

(A) Result of generated spike trains with different mean firing rates (20, 40, 60, 80, and 100 ± 10 Hz while duration and spike time tiling coefficient (STTC) were maintained 1 s and 0.5 ± 0.01, respectively. First, second, and third rows show raster plot, firing rate, and histogram of STTC values of each cell, respectively. (B) Same as A but for different spiking durations (0.2, 0.4, 0.6, 0.8, and 1 s) while MFR and STTC were maintained 60 ± 10 Hz and 0.5 ± 0.01, respectively. (C) Same as A but for different STTC values while MFR and duration were maintained 60 ± 10 Hz and 1 s, respectively. STTC histograms are shown in different colors depending on their average STTCs (STTC_AVG), i.e., blue, green, yellow, orange, and red for 0.1, 0.3, 0.5, 0.7, and 0.9, respectively.

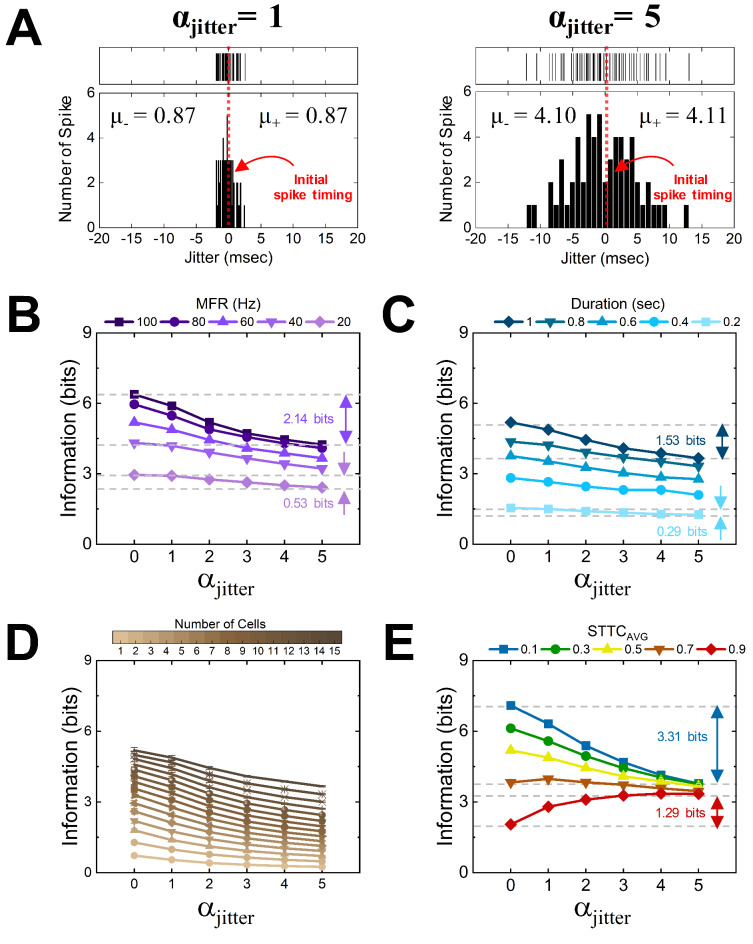
Assuming that the 50 spike trains were created from different 50 cells, “ten trials” were generated by adding jitters to initial spike trains (i.e., trial-to-trial variability). In detail, the original spike timings of individual spikes were altered based on the standard normal distribution (see red vertical dotted line and black vertical solid lines at top of Fig. 4A for original spike timing and changed spike timing, respectively). The mean and standard deviation of Gaussian distribution were fixed 0 and 1, respectively (see histogram of jitter distribution at bottom of Fig. 4A). In other words, the red vertical dotted line which means original spike timing can be moved to one of black vertical solid lines (i.e., changed spike timing; at top of Fig. 4A) based on the possibility which was shown in the histogram at bottom of Fig. 4A. Next, the level of distribution was also varied by multiplying α_jitter ranging from 1 to 5 (compare left and right of Fig. 4A for α_jitter = 1 and 5, respectively). At positive jitter side, the calculated average values of jitter were 0.87 and 4.11 msec with α_jitter of 1 and 5, respectively. As a result, when there is no jitter (α_jitter = 0), variability was not observed across all trials, however, after adding jitter (α_jitter = 5) the spike timing in all trials changed (compare upper and lower raster plots of Fig. 5B).

Fig. 4.

Inter-trial variability (jitter) reduces the amount of information in somewhat heterogeneous population but not in homogenous population. (A) (top) Exemplar distributions of spike timings after adding jitters for α_jitter = 1 and 5 (left and right, respectively). Red vertical dotted line drawn at 0 msec represents the original spike timing without any jitter. Depending on the α_jitter value, the initial spike timings were moved by the possibility density of Gaussian distribution (see METHODS). Each black vertical solid line indicates a single spike; 60 spikes in total are shown drawn at their jitter level. (bottom) Histograms of jitter distributions display the number of spikes for each jitter range; jitter bin sizes varied depending on α_jitter but the total number of bins was fixed to be 30 for the whole range of jitters. The average values for negative and positive jitters (µ₋ and µ₊, respectively) were shown in each plot. (B-E) Information rates were plotted as a function of α_jitter for different (B) MFRs, (C) spiking durations, (D) numbers of cells, and (E) STTCs_AVG. For panels A-C, population responses with the STTC_AVG of 0.5 were used (15 cells for panels A and B). For panel D, 15-cell population responses with the spiking duration of 1.0 s and the MFR of 60 Hz were used. Two pairs of gray horizontal dashed lines show the difference in the information rates for α_jitter of 0 and 5 for STTCs_AVG of 0.1 and 0.9 (3.31 and 1.29 bits with blue and red arrows, respectively).

Fig. 5.

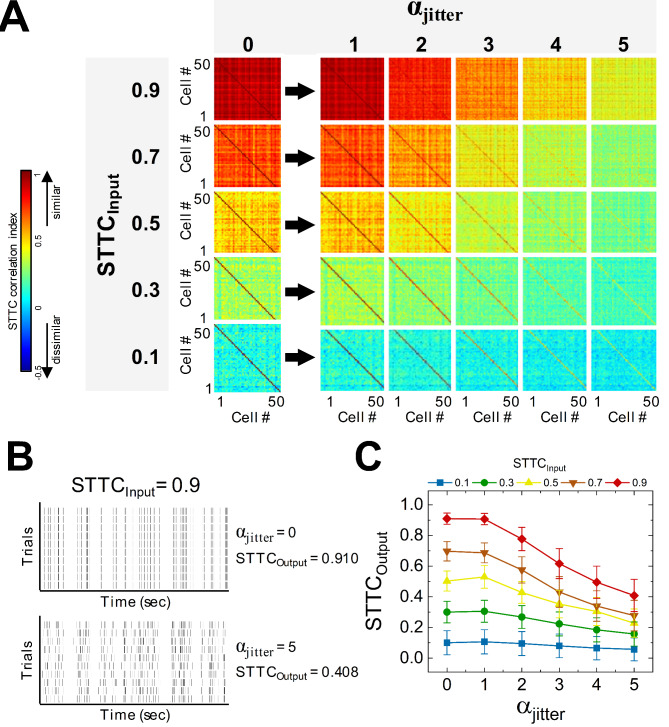
Heterogeneous spike trains are less affected by additional jitters than homogenous spike trains. (A) Color-coded matrices of spike time tiling coefficients (STTCs) visualize the level of pair-wise cross-correlation of spiking trains of 50 cells. STTC matrices were drawn before (α_jitter = 0) and after adding jitters for α_jitter ranging from 1 to 5. (B) Raster plots of spike trains representing ten trials without and with (upper and lower, respectively) jitters created by α_jitter of 5 to original spike trains with STTC_Input of 0.9. With no jitter, STTC_Output was 0.910 but STTC_Output became 0.408 by additional jitters. (C) Final STTC values (STTCs_Output) were plotted as a function of α_jitter ranging from 0 to 5 for several input STTC values (STTC_Input). Homogeneous spikes trains are more sensitive to the additional jitters in terms of final correlation levels.

Computation of the amount of neural information

To quantify the average information transmitted by certain groups of spikes trains, we used the direct method which computes information by the difference between total entropy and noise entropy^1,43–45, which is more generally known as mutual information^1,2,46. For the entropy calculation, each spike train was first changed into a binary code array^43–45,47: spikes were allocated into 4-msec-long time bins⁴³. Then, if one or more spikes exist in a given time bin, 1 was assigned; while if there is no spike, 0 was assigned. Second, we initially generated 50 cells by randomly selecting them from a pool of 2000 spike trains, created based on pre-determined populational spiking conditions such as duration, MFR, and STTC_AVG (Fig. 1). Then, to investigate how much information is transmitted by a subset of cells, we randomly selected n cells from the 50 generated cells and made 50 combinations of these n cells. For each combination of n cells, there were 10 trials for each cell. From these trials, we randomly selected one trial per cell and created 2,000 different combinations of trials across all combinations of cells. Both the total entropy and noise entropy were calculated over these 2,000 combinations for each of the 50 combinations of cells. Total entropy was calculated by the equation shown below:

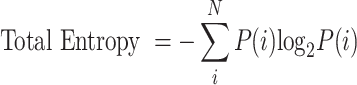where P(i) represents the probability of a particular “word” in one of 50 combinations for the entire time period of 1 s. Here, when binary code of each spike train is in sequence, the “word” i refers to a column vector of 0s and 1s and N indicates to the total number of possible words (i.e., 2ⁿ). Similarly, noise entropy can be calculated using the equation below:

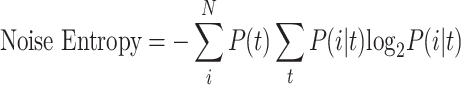where P(i|t) represents the conditional probability of a particular word i at a specific time, t. Finally, average information transmitted by n cells is obtained by averaging the value obtained by subtracting the noise entropy from the total entropy for 50 combinations.

Results

Controlled generation of spike trains

To more systematically investigate neural information changes as a function of the MFR, spiking duration, and STTC, we generated various groups of 50 spike trains that have different average values for each parameter while fixing other parameters (see METHODS). First, we created five groups of 1-sec-long spike trains which have different MFRs (Fig. 2A). As the MFR increased (20, 40, 60, 80, and 100 ± 10 Hz from Fig. 2Ai to Fig. 2Av), the raster plots became denser (the first row of Fig. 2A) and the heights of MFR bar graphs increased (the second row of Fig. 2A). The STTCs_AVG of all five groups were well controlled to be 0.5 ± 0.01, respectively (the third row of Fig. 2A).

Second, we generated the other five groups of spike trains which had durations of 0.2, 0.4, 0.6, 0.8, and 1.0 s, respectively; but, the MFR and the STTC_AVG were fixed at 60 ± 10 Hz and 0.5 ± 0.01, respectively (Fig. 2B). As designed, the raster plots (the first row of Fig. 2B) show longer spiking durations while the density of spikes was maintained, resulting in similar heights across the MFR bar graphs (the second row of Fig. 2B). As shown in the STTC histograms (the last row of Fig. 2B), the pairwise cell-to-cell spiking heterogeneities were similar to have the average STTC around 0.5 for all groups.

Lastly, we also created the last five groups of spike trains for different STTC_AVG values (i.e., 0.1, 0.3, 0.5, 0.7, and 0.9 ± 0.01) but the same MFR (60 ± 10 Hz) and spiking duration (1 s) (Fig. 2C). The raster plots became systematically more homogeneous spiking activities as the STTC_AVG increased (the first row of Fig. 2C). Accordingly, the peak of STTC distribution plots gradually shifted from the left to the right (the last row of Fig. 2C). Taken all together, the abovementioned results indicate our spike generation methods created diverse sets of 50 spike trains in controlled manners.

Information rates increase with all control variables but STTC

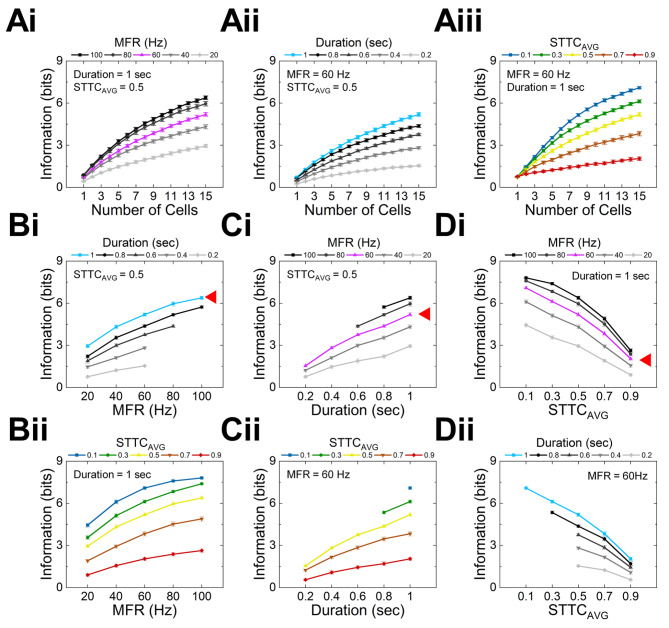
From the spike trains we generated in the earlier section, we next examined how the neural information transmission is altered by each of spiking parameters. First, we plotted the amount of information as a function of the number of cell (n) ranging from 1 to 15 when only one of the three parameters (i.e., MFR, duration, and STTC_AVG) was varied (Fig. 3Ai-3Aiii which are corresponding to Fig. 2A-2C). It is well-known that multiple cells conveyed more information than a single (Fig. 3Ai-3Aiii). Interestingly however, when the values of each parameter were changed (i.e., MFR, duration, and STTC_AVG), the increasing rate of information was greater with the large population (n = 15) than the small population (n = 1). For example, a single cell and a group of 15 cells transmitted 0.46 and 3.43 bits more of information when the MFR increased from 20 to 100 Hz, respectively (Fig. 3Ai). Similar to MFR, both spiking duration and STTC_AVG also showed the smallest and largest information changes at a single cell and 15 cells, respectively (Fig. 3Aii and 3Aiii).

Fig. 3.

Amount of transmitted information rises with increasing mean firing rate (MFR), spiking duration, but not with average spike time tiling coefficient (STTC_AVG). (A) Information rate as a function of number of cells for different (Ai) MFRs, (Aii) durations and (Aiii) STTCs_AVG. (B) Information rate as a function of MFR for different (Bi) durations and (Bii) STTCs_AVG. (C) Information rate as a function of duration for different (Ci) MFRs and (Cii) STTCs_AVG. (D) Information rate as a function of STTCs_AVG for different (Di) MFRs, and (Dii) durations. Color-coded line marked with red arrowheads in Bi-Di indicate basic conditions which are shown in Fig. 2A–2C, respectively. All pairs of neighboring data points in Bi-Di showed statistical significance (p < 0.05) in one-way ANOVA tests.

It is noteworthy that the information rate enhanced as more cells were involved in the transmission; however, the increasing speed appeared to be getting slower. For example, when the MFR was 60 Hz, as the number of cells tripled from 3 to 9, the amount of information increased by 2.14 times (a purple curve in Fig. 3Ai). However, when the number of cells increased 5 times from 3 to 15, information increased by only 2.88 times. Since the transmission of neural information is not done by only one single neuron, but by large populations of neurons, it must be important to find ways to allow large populations of neurons to efficiently transmit information²¹. Regarding this matter, it is intriguing that the absolute amount of information seems smaller but the speed of information saturation appears slower for higher than lower STTC_AVG (i.e., homogeneous vs. heterogeneous responses across cells; the bottom red and the top blue curves in Fig. 3Aiii, respectively).

Because neural information is modulated by various elements (i.e., MFR, duration, and STTC_AVG), it is also important to examine how the information rates change when two parameters are altered together (Fig. 3B, 3C, and 3D). For the fixed number of cells (n = 15; the largest population size we tested), we plotted the amount of information as a function of one single parameter while the other parameter is altered. For example, the information was plotted as a function of MFR for several spiking durations or STTC_AVG (Fig. 3Bi or 3Bii). Note that purple and sky blue curves marked with red arrowheads of Fig. 3Bi-3Bii, 3Ci-3Cii, and 3Di-3Dii were from two different identical sets of population responses.

We first estimated the amounts of neural information as a function of MFR for the group of spike trains that all have 1-sec-long spike trains and STTC_AVG of 0.5 (the sky blue curve marked with the red arrow in Fig. 3Bi). As the MFR increased from 20 to 100 Hz, the neural information also increased from 2.95 ± 0.11 to 6.38 ± 0.13 bits (mean ± stdev). This trend is consistent with previous studies^48–50, which confirmed that more information was transferred as the MFR increased. However, it is worth to note the slopes were different between information changes at low and high MFRs. For example, as shown in Fig. 3Bi, when the duration was 1.0 s, the information change between 80 and 100 Hz (from 5.96 ± 0.16 to 6.38 ± 0.13 bits; ~7% increment) was not as steep as that between 20 and 40 Hz (from 2.95 ± 0.11 to 4.32 ± 0.15 bits; ~46% increment). This slow-down of information enrichment indicates that an additional MFR increase may not be effective for further information enhancement above a certain MFR level. It might be tempting to think that the amount of neural information would be almost tripled if MFRs of a given set of spike trains were tripled when the other parameters were unchanged. However, our results indicate that the neural information is increased much less than being tripled when MFR was increased from 20 to 60 Hz. Also, given the fact that pump consumes 9 × 106 molecules of adenosine triphosphate (ATP) per spike⁵¹, neural information transmission with much higher MFR seems less energy-efficient as the rate is expected to be saturated at some point. When the MFR increased from 20 to 100 Hz, the information increments were 3.36 and 1.73 bits for the two groups of spike trains with the STTCs_AVG of 0.1 and 0.9, respectively (Fig. 3Bii). It appears that, when the change of MFR was the same, the amount of information more increased at heterogeneous spike trains.

Second, we also observed the increase in the amount of neural information as the duration increased (Fig. 3C). This is quite straightforward because more information would be conveyed the longer the spiking activities occur. However, since it is hard to create heterogeneous responses within a limited spiking period, the spike trains which have STTC values of 0.1 and 0.3 were not generated (i.e., one and two data points were shown for blue and green curves in Fig. 3Cii). This result also indicates that if the spiking duration is short, then the cells are unable to respond heterogeneously.

Lastly, we plotted the neural information vs. STTC_AVG (Fig. 3D). For spike trains with the MFR of 60 Hz (see a purple curve marked with a red arrowhead in Fig. 3Di), information was transmitted at the highest rate of 7.09 ± 0.08 bits when the STTC_AVG was 0.1. On the other hand, when the STTC_AVG was 0.9, information was tremendously reduced to 2.05 ± 0.12 bits. This contrast indicates that remarkably dissimilar spiking patterns across cells showed the biggest transmission rate compared to similar spiking patterns across cells. Although earlier studies suggested that heterogeneous populational responses convey more information than homogeneous ones^14,43,52 it has not been well quantified how the levels of population heterogeneity alter the amount of neural information. In our simulation, the increment of STTC_AVG from 0.1 to 0.9 (i.e., the decreased heterogeneity across spiking activities) resulted in ~ 71% loss of the information transmitted by 15 cells which lasted their spiking for 1 s in 60 Hz of MFR.

The effects of MFR and spiking duration were more prominent in heterogeneous spike trains than homogeneous ones (Fig. 3D). For example, when the MFR decreased from 60 to 20 Hz for 1-sec-long spike trains, the information decreased by 2.65 and 1.16 bits with the STTCs_AVG value of 0.1 and 0.9, respectively (Fig. 3Di). Also, when the spiking duration increased from 0.2 to 1.0 s, the cells transmitted 3.65 and 1.49 bits of more information with the STTCs_AVG value of 0.5 and 0.9, respectively (Fig. 3Dii).

Jitters reduce the neural information in heterogeneous but not in homogeneous population responses

When an identical stimulus is given to neurons for multiple times, they often elicit slightly different spiking patterns across those repeats due to the stochastic nature of spiking activities⁵³ as well as internal/external noises⁵⁴, resulting in trial-to-trial variabilities (i.e., jitters)^10,47. Accordingly, we also studied the changes in neural information rates when random jitters were added to spike trains (see METHODS). We altered each original spike timing (see red dotted line at 0 msec of Fig. 4A) based on the Gaussian distribution. The changed spike timing (i.e., jitters; black vertical lines at top of Fig. 4A) was most likely located close to the initial spike timing (see histogram of jitters at the bottom of Fig. 4A), but the distribution of jitters changed depending on the value of α_jitter ranging from 1 to 5 (compare left and right of Fig. 4A for α_jitter = 1 and 5, respectively). For all MFRs, durations, and the number of cells, the amount of transmitted information decreased as jitters were added to various sets of spike trains that had the STTC_AVG of 0.5 (Fig. 4B–4D). In detail, the spike trains of 100 Hz in the MFR transferred 2.14 bits (~ 33.5%) less information as the α_jitter increased from 0 to 5 (top curve of Fig. 4B) while the other spike trains of 20 Hz showed an information reduction of 0.53 bits (~ 18.0%) for the same jitter increment (bottom curve of Fig. 4B). Koch et al.⁵⁰ earlier demonstrated that, among brisk-transient, brisk-sustained, and local-edge cells, brisk-transient cells transferred the most information due to the highest firing rates and the lowest jitter. Taken together, our results suggest that even though the cells with higher MFRs transmit a larger amount of information, the information decreases rapidly as more jitters are added.

We also examined how the neural information changed as jitters were added when we varied the spiking duration and the number of cells (Fig. 4C and 4D). For those, we fixed the STTC_AVG to be at 0.5 and the MFR to be at 60 Hz. When the duration of spike trains was 1.0 s, the information was diminished by 1.53 bits as the α_jitter increased from 0 to 5 (Fig. 4C). For the same α_jitter change, the information was reduced by 0.29 bits when the duration was 0.2 s (Fig. 4C). For the all numbers of cells we tested, the information was consistently reduced as the jitter increased (Fig. 4D). These results are no surprise because additional jitters increase noise (or noise entropy). However, it is worth to note that the jitter was more critical to the population responses which carry higher amount of information than lower amount.

Interestingly, however, the jitters transformed the neural information quite differently depending on the STTC_AVG of spike trains (Fig. 4E). There was a remarkable contrast that cells with high vs. low heterogeneity transmitted less vs. more information as the jitters were added to their spike trains (blue and red curves in Fig. 4E, respectively). In more detail, the spike trains with the STTC_AVG of 0.1 or 0.9 transmitted 3.31 bits less or 1.29 bits more when the α_jitter was altered from 0 to 5, respectively (as marked with blue and red arrows in Fig. 4E, respectively). In the case of the STTC_AVG of 0.7, the information rate stayed pretty similar across various levels of jitters (an orange curve of Fig. 4E). All in all, the amount of information transmission decreased as the jitter increased for every parameter space (i.e., MFR, duration, and the number of cells) only when spike trains were somewhat heterogeneous (note that Fig. 4B–4D were plotted for the STTC_AVG of 0.5). On the other hand, the information rather increased from homogeneous sets of spike trains (e.g., when the STTC_AVG was 0.9).

Higher jitters transmute homogeneous population responses into heterogeneous ones to convey more information

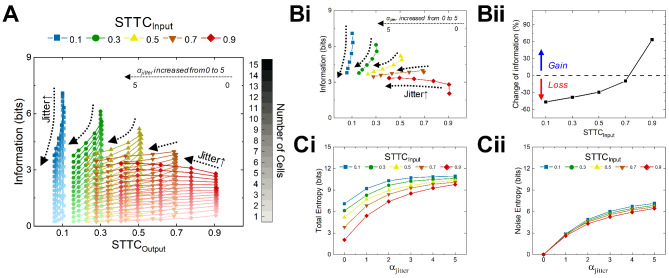
As intuitively expected, the additional jitters did neither substantially change MFR nor response durations. Therefore, the unique feature of neural information regarding the heterogeneity (i.e., STTC_AVG) of population responses (Fig. 4E) is likely because the STTC_AVG was considerably altered due to jitters. Hereafter, to clearly distinguish the two types of STTC_AVG before and after adding jitter, we referred to the target STTC_AVG value used for generating original spike trains as STTC_Input, and the changed STTC_AVG with added jitters as STTC_Output. The heat matrices of STTCs_Output clearly show that the influence of jitters on STTCs varied depending on the value of STTC_Input (Fig. 5A). Particularly, for homogeneous spike trains, the STTCs_Output were strongly influenced by the level of jitter (dramatic color changes are shown in the first row of heat matrices in Fig. 5A). In detail, we displayed the raster plots of STTC_Input of 0.9 without/with α_jitter of 5 (upper and lower raster plots of Fig. 5B), respectively. In addition to irregular spiking timings across trials (the lower raster of Fig. 5B), the STTC_Output was also substantially decreased (top red curve of Fig. 5C). In sharp contrast, however, for heterogeneous spike trains, the level of inter-cellular spiking variance (i.e., STTC) was minimally altered by all the levels of jitter we tested (i.e., 1–5 of α_jitter). For example, with the STTC_Input of 0.1, the STTCs_Output were 0.106 and 0.058 for the α_jitter of 1 and 5, respectively (bottom row of Fig. 5A and bottom blue curve of Fig. 5C). As a whole, the discrepancies across STTCs_Output were considerably reduced when the α_jitter of 5 were introduced to original spike trains with no jitters (compare left-most and right-most data points of each curve in Fig. 5C), resulting in much smaller gaps in the amount of information (Fig. 4E).

It is remarkably intriguing that the cells with the most heterogeneous responses were least affected by the jitter in terms of STTC_AVG, but their information was tremendously reduced (compare blue curves of Fig. 5C vs. 4E). On the other hand, the cells with the most homogeneous responses were significantly affected by the jitter in terms of STTC_AVG, but their information was somewhat enhanced (compare red curves of Fig. 5C vs. 4E). To further explore these disparities, we also plotted how the neural information rates changed as a function of the STTC_Output for different α_jitter as well as various network sizes (Fig. 6A). Indeed, for the low STTC_Input values such as 0.1 and 0.3, the jitters showed moderate STTC_AVG changes for every network size but considerable drops in information transmission (blue and green curves in Fig. 6A). To more clearly visualize how the inter-trial jitters alter the information rate, we remained the population responses for n = 15 in the information vs. STTC_Output plot (Fig. 6Bi), and plotted information change ratio between α_jitter of 5 vs. no jitter (α_jitter of 0) cases (Fig. 6Bii). For example, the STTC_Output was changed only between 0.100 and 0.058 for the STTC_Input of 0.1, but the information change was ~ 46% at most (n = 15; blue curve in Fig. 6Bi). It was because the noise entropy increased more rapidly (from 0.00 to 7.14 bits) than the total noise (7.09 to 10.92 bits) as jitters were added (from 0 to 5 of α_jitter) to the spike trains when the STTC_Input was 0.1 (see top blue curves in Fig. 6Ci and 6Cii). However, for the high STTC_Input value indicating homogeneous spike trains, the jitters produced a positive effect of increasing the information rate. In other words, a higher jitter transforms homogeneous spike trains into more heterogeneous ones, thereby lowering the STTC_Output and increasing information. For example, the additional jitters demonstrated a wide range of STTCs_Output (from 0.910 to 0.408) for the STTC_Input of 0.9, but the information rather increased by 2.05 to 3.34 bits (~ 63%) for the network size of 15 (red curve of Fig. 6Bi). It was because the total entropy increased more rapidly (from 2.05 to 9.77 bits) for higher STTCs_Input with the addition of jitters (from 0 to 5 of α_jitter) while the noise entropy was increased relatively slowly (from 0.00 to 6.43 bits) compared to other STTCs_Input (see bottom red curves in Fig. 6Ci and 6Cii).

Fig. 6.

Jitter increases both total and noise entropy and results positive impact to increase information rate at relatively homogenous neurons in the analysis population. (A) Population information as a function of STTC_Output with different jitter with α_jitter ranging from 0 to 5 for STTCs_Input of 0.1, 0.3, 0.5, 0.7, and 0.9 (shown at top with different colors). For each plot in the same color, different tint levels indicate various network sizes; the darkest and the lightest (i.e., top and bottom) curves are for n = 15 and n = 1, respectively. (Bi) Same as A but for n = 15 only. (Bii) Change of information after introducing α_jitter of 5: 1-[(information rate with jitters)/(information rate without jitters)] was plotted for STTCs_Input. Data points above/below the dashed horizontal line indicate gain/loss in information by the added jitter. (Ci) Total and (Cii) noise entropy as a function of α_jitter ranging from 0 to 5 for STTCs_Input of 0.1, 0.3, 0.5, 0.7, and 0.9.

To understand neural information more deeply, it is necessary to examine the relationship between intercellular spiking heterogeneity (i.e., STTC) and intertrial spiking jitter (i.e., noise). We examined above how the information changed as the noise (i.e., jitter) was added to the spike trains. The higher heterogeneity, the more information was transmitted when other factors were fixed and the noise was small. However, in practice, it is difficult for the cells to respond with no trial-to-trial variability. In other words, due to the stochastic nature of spiking, the neural code cannot be completely identical across repeats of external stimuli. It can be clearly seen that the neural information was lost by additional jitters until STTC_Input was 0.7, but the transmitted information increased when STTC_Input was 0.9 (below and above the dashed horizontal line in Fig. 6Bii). Taken all together, our results show moderate STTCs_AVG make neuronal information transmission most robust to internal/external noises. Therefore, our results indicate existence of optimal heterogeneity of spiking activities.

Discussion

Implication of our study in neural prosthetic application

Our results imply that, in neural prosthetic applications, it is highly likely to be important to convey optimal amount of information (i.e., similar amount of information that would arise during normal/healthy states) by figuring out how much information each cell can transmit in response to electric stimulation (or other forms of artificial stimulation). To elaborate on this point further, an artificial retina device can be considered as an illustrative example. Although promising clinical outcomes have been reported for these retinal prostheses which electrically stimulate the remaining inner retinal neurons^55–61, the retinal prostheses still have not yet formed artificial visual percepts that allow patients to carry out daily activities^55–61. Numerous previous retinal prosthetic studies have focused on novel methods to enhance the ability to drive individual retinal ganglion cells (RGCs) in a scalable manner to more faithfully mimic various aspects of retinal neural activities that arise during the natural viewing: (1) high-spatial resolution stimulation^62–65, (2) cell type-specific stimulation^{26,27,66–68}, or (3) faithful duplication of physiological-like (i.e., natural) spiking activities^39,69.

It is important to note that, compared to natural viewing, electrically-evoked population responses seem to have considerably different characteristics in terms of neural information. For example, in previous publication, interesting result was reported that OFF types of retinal ganglion cells (RGCs) transmit more information than ON types in both brisk transient (BT) and brisk sustained (BS) pathways in responses to light stimulation⁴³. Intriguingly, however, in the case of electric stimulation, the OFF cells transfer significantly less amount of information than the ON cells regardless of their subtypes (e.g., BT or BS) because the population responses of OFF cells became too homogeneous⁴³. Also, a recent sight restoration study reported better animal behavioral responses when their retinal ganglion cells evoked more heterogeneous spiking³⁷. Likewise, it may be necessary to manipulate jitter or other relevant parameters (e.g., duration, MFR, correlation levels) to ensure whether artificially-evoked responses can convey as much information as naturally-evoked responses for efficient neuromodulation, not only in retinal prosthetic applications but also in other neural prosthetic applications⁷⁰. Stimulus-induced (or stimulus-locked) spiking events are thought to be a better encoding method because of its high temporal precision⁷¹. In a given spike train, spike-timing precision seems to enhance information transmission²¹. However, our results indicate that, if a population of neurons is activated by an identical series of pulses, their collective spiking activities would be highly homogeneous (i.e., high STTC), resulting in less amount of information than more heterogeneous spike trains (see the leftmost data points of red vs. blue colors in Fig. 4E). Moreover, collective information of both the homogeneous and the heterogeneous spike trains were all altered by additionally introduced jitters (see the rightmost data points of red vs. blue colors in Fig. 4E). Therefore, for optimal information transmission using neural prostheses in a jittery environment, it seems crucial to use stimuli that induce a moderate level of correlation across spiking activities arising in different neurons. Rather than having too high or too low correlation, maintaining an optimal level of correlation allows the neural network to optimize the capacity to convey information by effectively balancing precision and variability. Such fine-tuning could help neural prostheses better encode and replicate natural neuronal behaviors, ultimately leading to improved functional outcomes for prosthetic users by offering more information to be deciphered. Thus, the present work offers a new aspect to be considered as a guideline for future research, suggesting that adjusting stimulation parameters for optimal information transmission can ultimately enhance the overall performance quality of prosthetics.

Variability can be a potential source for heterogeneous neural codes which are robust to noise

Both cell-to-cell heterogeneity and trial-to-trial variability in neurons have been reported in the earlier studies^20,29,72. Also, it has been also well known that diverse morphologies/ion channels of nerve cells create remarkably heterogeneous spiking activities^14–16,50. Because of these diversities, it appears that each neuron could maximize the amount of transmitted information by encoding different characteristics of the stimulus⁷³. However, other studies found that some level of redundancy is also essential to encode information efficiently since redundancy makes the cell more tolerant to noise and danger, which in turn reduces error^20,74,75. Therefore, it can be inferred that cells with the moderate levels in terms of both variability and redundancy would transmit information maximally. Throughout this study, we also confirmed that the tendency of information transmission differed depending on the correlation levels of population responses even with the same changes in jitter (Fig. 6). Also, as argued in recent literature⁷⁰, the present study has shown that the biological/physiological jitter can differentially affect the total amount of transmitted neural information depending on the level of populational heterogeneity. To be specific, heterogeneous population responses transmitted less information as jitters were added while homogenous population responses conveyed more information as the identical jitter was added since jitter greatly increased the total entropy (Fig. 6C). However, it is worth to note that, with no jitters, the homogeneous responses have lower information than the heterogeneous ones (Fig. 6B). In addition to normal physiological conditions, neural degeneration diseases such as retinal degeneration can significantly increase jitter in neural responses, reducing spiking reliability. As reported by Yoon et al.²⁸, retinal degeneration reduces the consistency of spiking responses arising in retinal ganglion cells, which can lead to lower information transmission in heterogeneous spike trains. These findings indicate that optimal response heterogeneity may be necessary to compensate for physiological and/or biological noise, allowing for maximal neural information transmission in both normal and degenerate retinas.

As observed in our results, the information transmission for highly heterogeneous spike trains appears to approach a plateau as the number of cells increases, though it is unlikely to fully plateau. Figure 3Aiii shows the information without jitter for the most heterogenous spike trains we tested (STTC_AVG = 0.1) is likely to approach a plateau at some point, possibly around several tens of cells; however, it is unlikely to be completely plateaued.

Future studies

In this study, we used spiking patterns in-silico rather than using actual neurophysiology data. For instance, we created and analyzed subsets of spike trains which have the same spiking duration, it appears that durations of both physiological and electrically-evoked spiking activities vary significantly even in an identical neuron type^39,76. Also, it should be noted that we assumed the situation of a population coding for a single modality stimulation, considering that we fixed certain MFRs and filtered out spike trains beyond the criteria of a target range of correlation (STTC). Under this assumption, the putative network configuration would be a set of either recurrent layer neurons or feedforward layer neurons projected from common or correlated input pathway, which is likely to be different from most neural networks.

However, it is highly likely that, in real in-vivo cases, other factors could affect the transmission and/or interpretation of neural information. For example, it has been known that psychological attention such as alertness and spatial attention decreases spiking variability⁷⁷, thus probably reducing the cell-to-cell heterogeneity. Subsequently, the attention is likely to decrease the neural information. Other examples are cortico-thalamic feedback in the downstream visual pathway^78–80 and dynamic viewing conditions which have much shorter spiking duration^74,81. Therefore, to gain insights into how population spiking responses should be shaped in practice to convey maximal/optimal neural information, it is crucial to massively record natural spiking activities in-/ex-vivo in responses to various stimulus types and apply the neural information analysis. Also, in the case of in-silico approaches, novel algorithms and computational modeling can be helpful to mimic the spiking patterns observed in the real neurophysiological recordings. Implementing more sophisticated models with accurate cellular diversities in terms of types or densities of various ion channels/receptors would enable more realistic investigation which may lead to the development of high-quality neuromodulation systems.

Author contributions

M.I. and H.-M.L. formulated the problem, H.R. and S.K. carried out the simulation and wrote the original draft. H.R., S.K., and M.I. analyzed the data and created the plots. H.-M.L. reviewed the manuscript and M.I. revised it.

Data availability

All data are presented in the manuscript and figures.

Declarations

Competing interests

The authors declare no competing interests.