Abstract
Background
Precise lower limb measurements are crucial for assessing musculoskeletal health; fully automated solutions have the potential to enhance standardization and reproducibility of these measurements. This study compared the measurements performed by BoneMetrics (Gleamer, Paris, France), a commercial artificial intelligence (AI)-based software, to expert manual measurements on anteroposterior full-leg standing radiographs.
Methods
A retrospective analysis was conducted on a dataset comprising consecutive anteroposterior full-leg standing radiographs obtained from four imaging institutions. Key anatomical landmarks to define the hip–knee–ankle angle, pelvic obliquity, leg length, femoral length, and tibial length were annotated independently by two expert musculoskeletal radiologists and served as the ground truth. The performance of the AI was compared against these reference measurements using the mean absolute error, Bland–Altman analyses, and intraclass correlation coefficients.
Results
A total of 175 anteroposterior full–leg standing radiographs from 167 patients were included in the final dataset (mean age = 49.9 ± 23.6 years old; 103 women and 64 men). Mean absolute error values were 0.30° (95% confidence interval [CI] [0.28, 0.32]) for the hip–knee–ankle angle, 0.75 mm (95% CI [0.60, 0.88]) for pelvic obliquity, 1.03 mm (95% CI [0.91,1.14]) for leg length from the top of the femoral head, 1.45 mm (95% CI [1.33, 1.60]) for leg length from the center of the femoral head, 0.95 mm (95% CI [0.85, 1.04]) for femoral length from the top of the femoral head, 1.23 mm (95% CI [1.12, 1.32]) for femoral length from the center of the femoral head, and 1.38 mm (95% CI [1.21, 1.52]) for tibial length. The Bland–Altman analyses revealed no systematic bias across all measurements. Additionally, the software exhibited excellent agreement with the gold-standard measurements with intraclass correlation coefficient (ICC) values above 0.97 for all parameters.
Conclusions
Automated measurements on anteroposterior full-leg standing radiographs offer a reliable alternative to manual assessments. The use of AI in musculoskeletal radiology has the potential to support physicians in their daily practice without compromising patient care standards.
Keywords: Leg measurements, Artificial intelligence, Radiography
Background
Evaluation of the alignment, joint orientation, and lengths of the lower limbs on anteroposterior full-leg standing radiographs plays a pivotal role in understanding musculoskeletal health. For example, varus and valgus deformities are recognized as a major risk factor for knee osteoarthritis [1–3]. Moreover, leg length discrepancy is often associated with vestibular dysfunction and spinal alterations [4]. Accurate radiographic assessment of lower limb alignment not only is critical for mitigating these risks but also forms a cornerstone of effective surgical planning in high tibial osteotomy or knee arthroplasty [5–7].
Numerous parameters of the lower extremities can be measured on anteroposterior full-leg standing radiographs to diagnose varus and valgus knees or leg length discrepancy [8, 9]. These include the hip–knee–ankle (HKA) angle, pelvic obliquity, leg lengths, femoral lengths, and tibial lengths. In clinical practice, they are often performed manually or with interactive software applications [10]. Despite their widespread use, these approaches have been criticized for their time-consuming and labor-intensive nature [10], and for occasionally lacking consistency and accuracy. The variability in results is compounded by the absence of a universal consensus on the placement of landmark points [11, 12]. Moreover, manual radiographic measurements have been shown to be affected by the experience of the reader [13].
Fully automated solutions could minimize the challenges posed by more traditional measurement methodologies by providing standardized analysis and reproducible measurements of radiographic images. The Data Science Institute of the American College of Radiology highlights the importance of automating lower limb measurements. They list leg length discrepancy as one of the use case scenarios for which artificial intelligence (AI) holds the potential to improve medical care [14]. The latter exemplifies the increased interest in AI in the realm of musculoskeletal imaging [15–17]. AI-based solutions have been shown to aid in the detection of fractures [18–20], to increase the precision of bone age assessment [21, 22], or to predict the progression of osteoarthritis [23, 24]. The automation of skeletal measurements has garnered increased attention, and software have been developed for the spine [25, 26], the hip [27, 28], the foot [29, 30], and the leg [31–33]. Worthy of note, both conventional radiography and advanced imaging modalities such as EOS imaging can be used for such measurements [34].
This study aimed to compare the performance of a European Conformity (CE)-certified commercially available AI solution (BoneMetrics, Gleamer, Paris, France) to the manual measurements of expert musculoskeletal radiologists on anteroposterior full-leg standing radiographs. The assessment focused on estimating a comprehensive array of lower limb angles and lengths from conventional radiography and EOS imaging. Secondary objectives were to compare AI performance across these modalities and evaluate differences on the basis of the use of distinct landmark points. It was hypothesized that BoneMetrics would achieve accuracies comparable to the reference standard.
Methods
The study received institutional review board approval for the retrospective collection of patient data from four institutions (ethics approval number CRM-2209-306). Each institution informed patients about the use of their anonymized data for research purposes, and provided instructions on how to opt out of the study.
Dataset
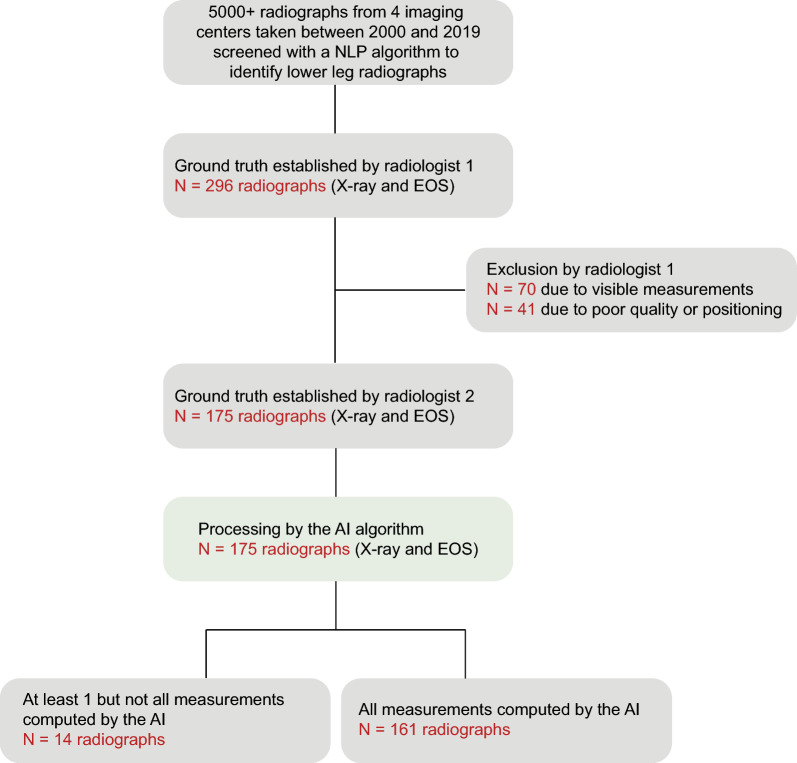
Radiographs were selected from a database aggregating data from four radiology private practices in France, spanning a period from January 2015 to October 2019. Radiologists’ reports were queried in the database to identify radiographs that had been acquired for leg measurements using a natural language processing (NLP) algorithm. The latter method involved using regular expressions (“pangonogram,” “goniometry,” “measurement(s),” “angle(s),” and “degree(s)”) to identify phrases related to lower limb measurements from text. Data on participant sex were extracted from the Digital Imaging and Communication in Medicine (DICOM) tags. Inclusion criteria were anteroposterior full-leg standing radiographs, acquired with conventional radiography or EOS imaging, from patients over 3 years old. Radiographs with orthopedic implant were deemed eligible. A sample of 296 radiographs met the inclusion criteria. An expert musculoskeletal radiologist (N.R.) with 13 years of experience reviewed the dataset and excluded radiographs for one of the following reasons: visible measurements on the image, poor image quality (e.g., blurry, under-exposed, or containing a grid), incorrect patient positioning obscuring key anatomical details, rotational issues, or non-weight-bearing X-rays.
Measurement definitions
This study focused on a comprehensive set of leg and hip measurements including the hip–knee–ankle (HKA) angle, pelvic obliquity, leg lengths, femoral lengths, and tibial length. Each measurement was performed separately on the left and right legs, with the exception of pelvic obliquity. In total, there were seven measurements of interest. The HKA angle was defined as the angle between the line drawn from the center of the femoral head to the center of the femoral intercondylar notch and the line drawn from the center of the tibial spines to the center of the distal tibia [8, 9]. Pelvic obliquity was computed as the distance between the horizontal line passing through the top of the right femoral head and the horizontal line passing through the top of the left femoral head and a vertical line [35]. Pelvic obliquity can only be measured on radiographs for which both right and left legs are analyzable. Two distinct leg lengths were defined according to the position of the landmark point on the femoral head. The “top leg length” and “center leg length” were computed as the axes running from the top of the femoral head to the center of the distal tibia and from the center of the femoral head to the center of the distal tibia [36]. Similarly, two distinct femoral lengths were defined as a function of the position of the landmark point on the femoral head. The “top femoral length” and the “center femoral length” were defined as the axes extending from the top of the femoral head to the center of the femoral intercondylar notch and from the center of the femoral head to the center of the femoral intercondylar notch [36]. Finally, tibial length was outlined as the distance from the center of the tibial spines to the center of the distal tibia [36].
Manual ground truth measurements
Two expert musculoskeletal radiologists with 13 and 12 years of experience carried out manual measurements independently (N.R. and L.L.). Radiographs were presented on a dedicated web-based data annotation platform (Kili) equipped with an array of labeling tools such as zoom, pan, contrast adjustment, and a circle drawer. Annotators placed 10 landmarks on each image: the top of the left and right femoral heads, the center of the left and right femoral heads, the center of the left and right femoral intercondylar notches, the center of the left and right tibial spines, and the center of the left and right distal tibiae. In cases where hip or knee implants were present, the radiologists placed the landmarks on the basis of identifiable prosthesis features, such as the top or the center of the prosthetic femoral head and the well-defined midpoint of the femoral and tibial components of the knee implant. These landmarks allowed the measurements to be computed for each leg. The ground truth was defined as the mean of the measurements provided by both radiologists. To evaluate intra-reader reliability, one of the two expert musculoskeletal radiologists (N.R.) re-annotated a random sample of 28 anteroposterior full-leg standing radiographs from the dataset after a 1-month washout period.
Automated AI measurements
This study tested the BoneMetrics AI-based software (version 2.3.1, Gleamer, Paris, France). BoneMetrics is a CE-marked image processing tool that automates musculoskeletal measurements on conventional radiographs and EOS images. The software consists of multiple convolutional neural networks that allow for the detection and localization of landmark points and the subsequent computation of measurements. The algorithm predicts landmark points with a confidence score from 0 to 100, and only points with scores exceeding the predefined threshold of 50 are used to calculate the set of measurements. BoneMetrics relies on varied architectures including a top-down model implemented with detectron2, a lightweight HRNet (litehrnet), and a bottom-up approach. Such diversity strengthens the flexibility and robustness of the AI across a wide array of radiographic images.
The algorithm was trained on a dataset comprising more than 5000 images from 20+ European imaging centers, and included patients with and without implants. The radiographs were labeled by 10 radiographers and radiologists who had received prior training. All annotations were reviewed by an expert musculoskeletal radiologist with 14 years of experience to ensure optimal quality of the training dataset. No radiograph or patient included in the present study was used for the development of the AI.
Statistical analysis
The sample sizes for this study were based on calculations from a previous similar study [32]. They computed the sample sizes necessary to compare AI measurements with ground truth values for various parameters of interest, including the HKA angle, leg length, femur length, tibial length, and pelvic obliquity. Their computations were guided by a method for Bland–Altman analysis, which requires the clinically meaningful maximum difference allowed [37]. At an alpha of 0.05 and a power of 0.8, they found the required sample sizes to be 16 legs for the HKA, 10 legs for leg length, 8 legs for femur length, 22 legs for tibial length, and 60 legs for pelvic obliquity.
Summary statistics were computed for patient characteristics (sex and age) and for image characteristics (modality and center of origin). Analyses were conducted independently for each leg except for pelvic obliquity, which was computed at the patient level. Performance of the AI algorithm was evaluated using the root mean square error (RMSE) and mean absolute error (MAE), with 95% confidence intervals (CI) calculated using 1000 bootstrap resamples. To address data dependencies from multiple radiographs per patient and multiple measurements per radiograph (left and right), patient resampling was used for all parameters but pelvic obliquity. The MAE was also computed for radiographs of pediatric versus adult patients and patients with and without hip or knee implant and for conventional radiography versus EOS imaging. Additionally, the MAE for the HKA was compared between patients with and without lower limb malalignment, genu varum and genu valgum being characterized by an HKA angle differing by 3° or more from neutral alignment [38, 39]. Differences between these groups were assessed using the Mann–Whitney U test for pelvic obliquity and linear mixed models for all other measurements with patient as a random effect to account for dependencies within the dataset. Statistical significance was set at p = 0.007 (= 0.05/7 measurements) for the children versus adults, knee implant versus no implant, and conventional radiography versus EOS analyses and at p = 0.008 (= 0.05/6 measurements) for the hip implant versus no implant after adjusting for multiple comparisons using the Bonferroni method.
Agreement between the AI software and the ground truth was assessed using Bland–Altman analyses. For pelvic obliquity, the traditional Bland–Altman method was applied. For all other parameters, a mixed-effects approach to the Bland–Altman analysis was used, with the patient as a random effect and both radiograph and laterality as fixed effects. In addition, intraclass correlation coefficients (ICC) were calculated to assess AI and ground truth agreement and intra-reader variability, on the basis of two-way mixed-effects models with absolute agreement, as well as inter-reader variability, on the basis of a two-way random-effects model with absolute agreement. ICC values were classified as poor (ICC < 0.5), moderate (0.5 ≤ ICC < 0.75), good (0.75 ≤ ICC < 0.9), or excellent (ICC ≥ 0.9), according to Koo et al. (2016) [40]. All statistical computations were performed using R (v4.3.2) in RStudio (v2023.09.1 + 494) with the “irr” and “blandr” packages.
Results
Dataset characteristics
The reviewing phase by the expert musculoskeletal radiologist led to the exclusion of 111 images: 41 due to poor quality and 70 due to measurements being visible on the radiograph (Fig. 1). The final dataset included in the study comprised 175 anteroposterior full-leg standing radiographs from 167 patients, including 129 conventional radiographs (73.7%) and 46 EOS images (26.3%). Eight patients had two radiographs taken at different time points. The distribution of radiographs across center was as follows: 17 images from Center 1 (9.7%), 22 images from Center 2 (12.6%), 106 images from Center 3 (60.6%), and 30 images from Center 4 (17.1%). There were 107 radiographs from 103 female patients (61.1%) and 68 radiographs from 64 male patients (38.9%). The mean age of patients was 50 years (standard deviation = 24), and ages ranged from 3 to 89 years (Table 1). Among the 26 pediatric patients included in the study, 10 patients still had open growth plates.
Fig. 1.
Flowchart describing dataset selection, data processing, and final available measurements
Table 1.
Characteristics of patients included in the dataset
| Patients | Radiographs | |
|---|---|---|
| Sample size (n) | 167 | 175 |
| Age | ||
| Mean ± SD (years) | 49.9 ± 23.6 | |
| Range (years) | [3.1–89.0] | |
| Number of children | 26 | |
| Sex | ||
| Women (%) | 103 (61.7%) | 107 (61.1%) |
| Men (%) | 64 (38.3%) | 68 (38.9%) |
| Imaging modality | ||
| Conventional radiography (%) | 121 (72.5%) | 129 (73.7%) |
| EOS (%) | 46 (27.5%) | 46 (26.3%) |
| Orthopedic implant | ||
| Hip prosthesis (%) | 22 (13.2%) | 24 (13.7%) |
| Knee prosthesis (%) | 38 (22.8%) | 38 (21.7%) |
| Malalignment | ||
| Unilateral genu varum (%) | 45 (26.9%) | 48 (27.4%) |
| Bilateral genu varum (%) | 38 (22.8%) | 39 (22.3%) |
| Unilateral genu valgum (%) | 16 (9.6%) | 17 (9.7%) |
| Bilateral genu valgum (%) | 4 (2.4%) | 4 (2.3%) |
| Leg length discrepancy (%) | 22 (13.2%) | 22 (12.6%) |
Within the dataset, there were 57 patients with an orthopedic implant (34.1%) including 19 patients with a hip prosthesis (11.4%), 35 with a knee prosthesis (21.0%), and 3 with both (1.8%). Regarding malalignment, unilateral genu varum (HKA angle > 3°) was identified in 45 patients (26.9%), while bilateral genu varum was observed in 38 patients (22.8%). Unilateral genu valgum (HKA angle < −3°) was present in 16 patients (9.6%) and bilateral genu valgum in 4 patients (2.4%). Finally, leg length discrepancy, defined as a difference greater than 10 mm between the left and right legs, was noted in 22 patients (13.2%; Table 1). Among these, six patients had orthopedic implants (27.3%).
AI performance and agreement with ground truth
In total, 350 legs were available from 175 radiographs. Figure 2 provides illustrations of how the radiologists who established the ground truth placed the landmark points. There were 163 missing measurements from 28 radiographs; the missing measurements were thus excluded from subsequent analyses (Table 2). Pelvic obliquity measurements were missing in the presence of a hip prosthesis, as the AI software does not yield any output in such instances. Most of the other missing parameters were also observed in patients with a hip prosthesis due to low AI confidence scores (< 50%).
Fig. 2.
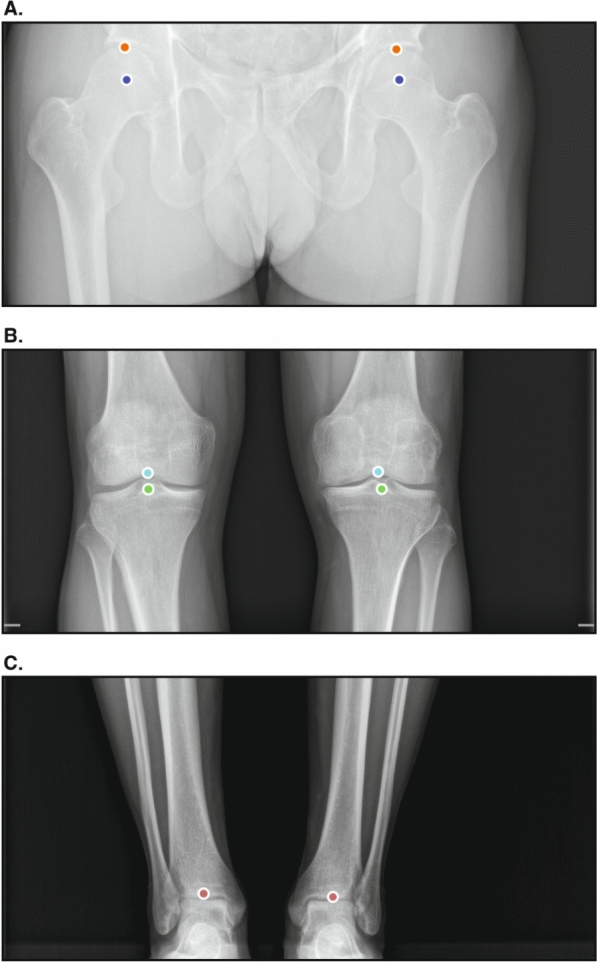
Illustrations of the landmark points placed by the annotators who established the ground truth on a dedicated web-based platform. There were five unique landmarks for each leg. A The orange point corresponds to the top of the femoral head and the purple point to the center of the femoral head. B The light blue point corresponds to the femoral intercondylar notch and the green point to the center of the tibial spine. C The red point corresponds to the center of the distal tibia
Table 2.
Number of legs for which a measurement was not computed by the AI
| Lengths and angles | Legs without measurement/total (%) |
|---|---|
| HKA | 19/350 (5.4%) |
| Pelvic obliquity | 25/175 (7.1%) |
| Top leg length | 41/350 (11.7%) |
| Center leg length | 18/350 (5.1%) |
| Top femoral length | 38/350 (10.9%) |
| Center femoral length | 16/350 (4.6%) |
| Tibial length | 6/350 (1.7%) |
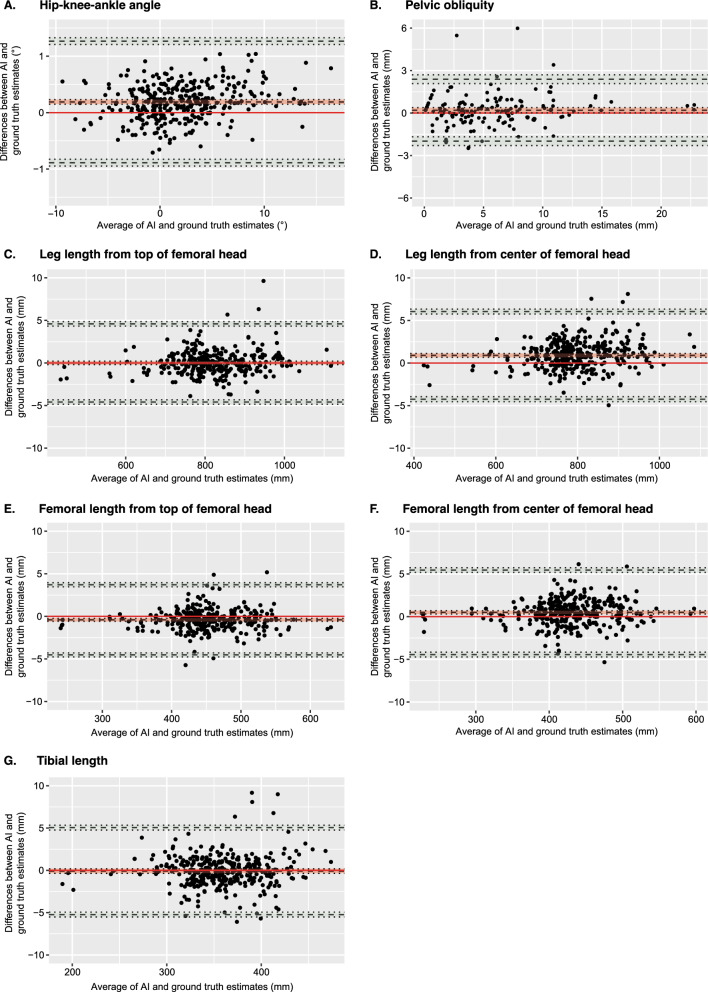
RMSE and MAE for each measurement are displayed in Table 3, and results of the Bland–Altman analyses are shown in Table 4 and Fig. 3. RMSE was smallest for the HKA angle (0.37°, 95% CI [0.34, 0.39]) and pelvic obliquity (1.13 mm, 95% CI [0.87, 1.30] and largest for the tibial length (2.02 mm, 95% CI [1.60, 2.29]). MAE was also smallest for the HKA angle (0.30°, 95% CI [0.28, 0.32]) and pelvic obliquity (0.75 mm, 95% CI [0.64, 0.86]), but it was largest for the center leg length (1.46 mm, 95% CI [1.34, 1.57]). Regarding Bland–Altman analyses, the HKA angle and pelvic obliquity demonstrated small biases of 0.19° (95% CI [0.15, 0.23]) and 0.20 mm (95% CI [0.019, 0.38]), respectively, with narrow limits of agreement. Top leg length and tibial length exhibited near-zero biases of 0.004 mm (95% CI [−0.19, 0.20]) and −0.087 mm (95% CI [−0.36, 0.18]), respectively. In contrast, center leg length, top femoral length, and center femoral length displayed higher biases, with the center leg length showing the highest bias at 0.90 mm (95% CI [0.68, 1.11]). Notably, all leg measurements were associated with wider limits of agreement (Table 4).
Table 3.
Performance of the AI algorithm for each measurement
| Lengths and angles | Sample size (N) | RMSE [95% CI] | MAE [95% CI] |
|---|---|---|---|
| HKA (°) | 331 | 0.37 [0.34, 0.39] | 0.30 [0.28, 0.32] |
| Pelvic obliquity (mm) | 150 | 1.13 [0.87, 1.30] | 0.75 [0.64, 0.86] |
| Top leg length (mm) | 309 | 1.45 [1.19, 1.61] | 1.03 [0.92,1.13] |
| Center leg length (mm) | 331 | 1.89 [1.68, 2.04] | 1.46 [1.34, 1.57] |
| Top femoral length (mm) | 312 | 1.29 [1.14, 1.42] | 0.95 [0.86, 1.04] |
| Center femoral length (mm) | 334 | 1.57 [1.44, 1.69] | 1.23 [1.13, 1.32] |
| Tibial length (mm) | 344 | 2.02 [1.60, 2.29] | 1.38 [1.21, 1.53] |
Performance was assessed by root mean square error (RMSE) and mean absolute error (MAE). In addition, 95% confidence intervals were computed using bootstrapping with patient resampling to account for data dependencies. Sample size (N) is also displayed
Table 4.
Results of the Bland–Altman analyses for each measurement of interest
| Lengths and angles | Sample size (N) | Bias [95% CI] | Lower LOA [95% CI] | Upper LOA [95% CI] |
|---|---|---|---|---|
| HKA (°) | 331 | 0.19 [0.15, 0.23] | −0.89 [−0.95, −0.83] | 1.27 [1.21, 1.33] |
| Pelvic obliquity (mm) | 150 | 0.20 [0.019, 0.38] | −1.99 [−2.30, −1.68] | 2.39 [2.08, 2.69] |
| Top leg length (mm) | 309 | 0.004 [−0.19, 0.20] | −4.59 [−4.85, −4.33] | 4.60 [4.33, 4.86] |
| Center leg length (mm) | 331 | 0.90 [0.68, 1.11] | −4.25 [−4.53, −3.97] | 6.04 [5.76, 6.32] |
| Top femoral length (mm) | 312 | −0.41 [−0.57, −0.25] | −4.53 [−4.76, −4.29] | 3.71 [3.47, 3.94] |
| Center femoral length (mm) | 334 | 0.50 [0.32, 0.69] | −4.45 [−4.72, −4.17] | 5.45 [5.18, 5.72] |
| Tibial length (mm) | 344 | −0.087 [−0.36, 0.18] | −5.23 [−5.51, −4.95] | 5.06 [4.78, 5.33] |
For all measurements but pelvic obliquity, a mixed-effects approach was applied to account for data dependencies. Patient was modeled as a random effect, while radiograph and laterality of the measurement were treated as fixed effects. Sample size (N), bias, lower limit of agreement (LOA), upper LOA and their 95% confidence intervals (CI) are displayed
Fig. 3.
Bland–Altman plots showing the differences between AI and ground truth predictions against their means. Plots are displayed for hip–knee–ankle angle (A), pelvic obliquity (B), leg length measured from the top of the femoral head (C), leg length from the center of the femoral head (D), femoral length measured from the top of the femoral head (E), femoral length measured from the center of the femoral head (F), and tibial length (G). The red line depicts the scenario in which AI estimates would perfectly align with the ground truth, indicating no differences between the two. The light red interval around the black dotted line corresponds to the 95% confidence interval for the mean difference. The black dotted lines at the extremities of the plot represent the upper and lower limits of agreement with their respective 95% confidence intervals in light green. For all measurements but pelvic obliquity, a mixed effects Bland–Altman analysis was used to account for dependencies within the dataset
The ICC between AI predictions and the ground truth was excellent (≥ 0.97) for all seven measurements (Table 5). Top leg length and top femoral length had the lowest RMSE (1.13 mm, 95% CI [0.87, 1.30]; 1.29 mm, 95% CI [1.14, 1.42]) and MAE (1.03 mm, 95% CI [0.92, 1.13]; 0.95 mm, 95% CI [0.86, 1.04]), suggesting that these parameters deviated less from the ground truth. In contrast, center leg length and center femoral length showed slightly higher RMSE (1.89 mm, 95% CI [1.68, 2.04]; 1.57 mm, 95% CI [1.44, 1.69]) and MAE (1.46 mm, 95% CI [1.34, 1.57]; 1.23 mm, 95% CI [1.13, 1.32]), underlining greater deviation from the ground truth.
Table 5.
Results of the agreement analyses
| Lengths and angles | Sample size (N) | ICC between AI and GT [95% CI] | Intra-reader reliability [95% CI] | ICC between radiologists [95% CI] |
|---|---|---|---|---|
| HKA | 331 | > 0.99 [> 0.99, 1] | > 0.99 [> 0.99, 1] | > 0.99 [0.99, 1] |
| Pelvic obliquity | 150 | 0.97 [0.96, 0.98] | 0.98 [0.95, 0.99] | 0.99 [0.98, 0.99] |
| Top leg length | 309 | > 0.99 [> 0.99, 1] | > 0.99 [> 0.99, 1] | > 0.99 [0.95, 1] |
| Center leg length | 331 | > 0.99 [> 0.99, 1] | > 0.99 [> 0.99, 1] | > 0.99 [> 0.99, 1] |
| Top femoral length | 312 | > 0.99 [> 0.99, 1] | > 0.99 [> 0.99, 1] | > 0.99 [> 0.99, 1] |
| Center femoral length | 334 | > 0.99 [> 0.99, 1] | > 0.99 [> 0.99, 1] | > 0.99 [> 0.99, 1] |
| Tibial length | 344 | > 0.99 [> 0.99, 1] | > 0.99 [> 0.99, 1] | > 0.99 [> 0.99, 1] |
Agreement between AI and the ground truth (GT) was assessed with intraclass correlation coefficients (ICC) from a two-way mixed-effects model with absolute agreement for multiple raters. The intra-reader reliability was assessed with ICC from a two-way mixed-effects model with absolute agreement for a single rater. Agreement between the two radiologists who established the ground truth was evaluated with ICC from a two-way random-effects model with absolute agreement for multiple raters. Sample size (N) is also displayed
The performance of the AI was compared between pediatric and adult patients, and no statistically significant differences were noted for any parameter (Table 6). To evaluate the influence of hip and knee implants on the accuracy of AI measurements, separate analyses were conducted for radiographs of patients with and without implants (Table 6). Statistically significant differences were found between patients with and without hip implants for the algorithm’s estimation of the center leg length (p = 0.006) and center femoral length (p < 0.001). Patients with hip implants (1.25 mm, 95% CI [0.97, 1.49]) had lower MAE values than those without for the center leg length (1.46 mm, 95% CI [1.30, 1.60]). In contrast, patients with hip implants (1.43 mm, 95% CI [1.17, 1.66]) had higher MAE values than those without for the center femoral length (1.18 mm, 95% CI [1.07, 1.29]). Significant differences were also noted in the accuracy of tibial length estimates (p < 0.001), with a MAE of 1.82 mm (95% CI [1.44, 2.16]) in the presence of a knee implant compared with 1.15 mm (95% CI [1.01, 1.28]) without implant. The HKA angle was the only parameter for which the accuracy of AI measurements was significantly affected by imaging modality (p < 0.001; Table 6). Measurements on conventional radiographs had a MAE of 0.32° (95% CI [0.30, 0.24]), while those on EOS images had a significantly smaller MAE of 0.25° (95% CI [0.22, 0.28], p < 0.001). To assess the impact of malalignment on the HKA angle, measurements for patients with genu varum or genu valgum were compared with those of patients with neutral alignment (Table 6). The MAE for patients with genu varum was significantly higher than that for patients without (p < 0.001), with respective values of 0.35° (95% CI [0.32, 0.39]) and 0.30° (95% CI [0.28, 0.32]). No significant differences were found in the estimation of the HKA angle between patients with and without genu valgum (p = 0.28).
Table 6.
Comparison of the performance of the AI algorithm across different groups
| Lengths and angles | MAE [95% CI] | Statistical test | |
|---|---|---|---|
| Children (N = 26) | Adults (N = 141) | ||
| HKA (°) | 0.27 [0.22, 0.31] | 0.31 [0.28, 0.33] | F(1, 162) = 6.00, p = 0.02 |
| Pelvic obliquity (mm) | 0.58 [0.43, 0.72] | 0.79 [0.66, 0.91] | W = 1365, p = 0.15 |
| Top leg length (mm) | 0.87 [0.75, 0.99] | 1.07 [0.94, 1.17] | F(1, 155) = 1.51, p = 0.22 |
| Center leg length (mm) | 1.13 [0.96, 1.30] | 1.53 [1.38, 1.65] | F(1, 162) = 1.31, p = 0.25 |
| Top femoral length (mm) | 0.73 [0.62, 0.83] | 1.00 [0.89, 1.09] | F(1, 156) = 0.01, p = 0.92 |
| Center femoral length (mm) | 0.90 [0.74, 1.04] | 1.29 [1.19, 1.39] | F(1, 163) = 0.00, p = 0.99 |
| Tibial length (mm) | 1.22 [0.96, 1.47] | 1.41 [1.20, 1.58] | F (1, 164) = 3.81, p = 0.05 |
| Hip implant (N = 19) | No implant (N = 110) | ||
|---|---|---|---|
| HKA (°) | 0.26 [0.21, 0.30] | 0.30 [0.27, 0.32] | F(1, 127) = 4.50, p = 0.04 |
| Pelvic obliquity (mm) | NA | NA | NA |
| Top leg length (mm) | 0.74 [0.56, 0.93] | 1.01 [0.88, 1.12] | F(1, 120) = 0.014, p = 0.91 |
| Center leg length (mm) | 1.25 [0.97, 1.49] | 1.46 [1.30, 1.60] | F(1, 127) = 7.82, p = 0.006* |
| Top femoral length (mm) | 0.83 [0.43, 1.16] | 0.89 [0.80, 0.98] | F(1, 121) = 0.034, p = 0.85 |
| Center femoral length (mm) | 1.43 [1.17, 1.66] | 1.18 [1.07, 1.29] | F(1, 128) = 11.49, p < 0.001* |
| Tibial length (mm) | 1.84 [1.04, 2.50] | 1.15 [1.02, 1.29] | F(1, 129) = 1.60, p = 0.21 |
| Knee implant (N = 35) | No implant (N = 110) | ||
|---|---|---|---|
| HKA (°) | 0.33 [0.29, 0.36] | 0.30 [0.27, 0.32] | F(1, 142) = 0.098, p = 0.75 |
| Pelvic obliquity (mm) | 1.04 [0.69, 1.33] | 0.66 [0.57, 0.75] | W = 2173, p = 0.48 |
| Top leg length (mm) | 1.16 [0.99, 1.34] | 1.01 [0.88, 1.12] | F(1, 142) = 0.030, p = 0.86 |
| Center leg length (mm) | 1.57 [1.36, 1.78] | 1.46 [1.30, 1.60] | F(1, 142) = 0.12, p = 0.72 |
| Top femoral length (mm) | 1.16 [0.94, 1.36] | 0.89 [0.80, 0.98] | F(1, 143) = 0.68, p = 0.41 |
| Center femoral length (mm) | 1.28 [1.10, 1.45] | 1.18 [1.07, 1.29] | F(1, 143) = 0.049, p = 0.83 |
| Tibial length (mm) | 1.80 [1.48, 2.07] | 1.15 [1.02, 1.29] | F(1, 142) = 34.30, p < 0.001* |
| Conventional radiographs (N = 121) | EOS images (N = 46) | ||
|---|---|---|---|
| HKA (°) | 0.32 [0.30, 0.34] | 0.25 [0.22, 0.28] | F(1, 162) = 25.22, p < 0.001* |
| Pelvic obliquity (mm) | 0.80 [0.65, 0.93] | 0.58 [0.45, 0.72] | W = 1788, p = 0.32 |
| Top leg length (mm) | 1.04 [0.91, 1.16] | 1.01 [0.86, 1.15] | F(1, 155) = 5.40, p = 0.02 |
| Center leg length (mm) | 1.54 [1.40, 1.68] | 1.26 [1.10, 1.41] | F(1,162) = 2.43, p = 0.12 |
| Top femoral length (mm) | 0.97 [0.87, 1.08] | 0.89 [0.72, 1.04] | F(1, 156) = 2.55, p = 0.11 |
| Center femoral length (mm) | 1.24 [1.14, 1.35] | 1.19 [1.05, 1.33] | F(1, 163) = 1.05, p = 0.31 |
| Tibial length (mm) | 1.44 [1.22, 1.63] | 1.22 [1.06, 1.38] | F(1, 164) = 0.67, p = 0.41 |
| Genu varum (N = 83) | All (N = 167) | ||
|---|---|---|---|
| HKA (°) | 0.33 [0.30, 0.36] | 0.30 [0.28, 0.32] | F(1, 162) = 14.79, p < 0.001* |
| Genu valgum (N = 20) | All (N = 167) | ||
|---|---|---|---|
| HKA (°) | 0.28° [0.22, 0.34] | 0.30 [0.28, 0.32] | F(1, 162) = 1.18, p = 0.28 |
Performance of the AI algorithm on pediatric and adult patients, on images with and without implant (knee and hip prosthesis), on conventional radiographs versus EOS images, and on images with and without malalignment for the HKA angle, as assessed by the mean absolute error (MAE). Mann–Whitney U tests were computed to evaluate how implant and imaging modality influenced differences between AI-based and ground truth measurements of pelvic obliquity. Linear mixed models with patient as a random effect were employed to assess the influence of implant and imaging modality on all measurements but pelvic obliquity. Additional linear mixed models with patient as a random effect were computed to examine the influence of genu varum and genu valgum on differences between AI and ground truth measurements. Counts represent the number of patients rather than the number of images.
*Statistically significant result
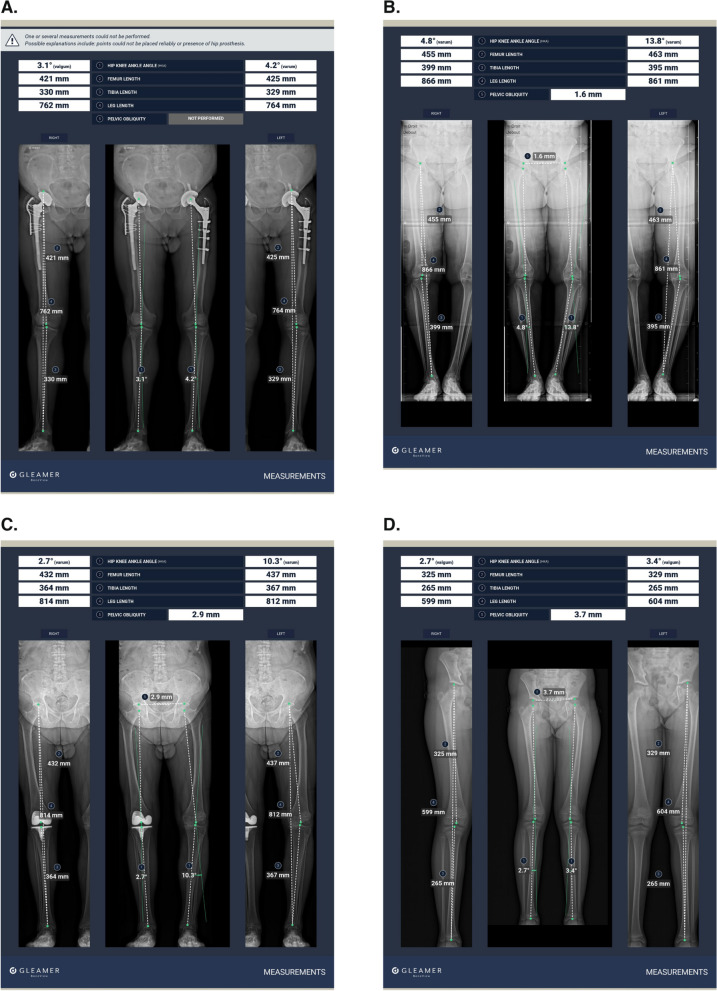
Figure 4 illustrates BoneMetrics outcomes in a patient with a hip prosthesis, a patient with genu varum, a patient with a knee prosthesis, and a pediatric patient with genu valgum.
Fig. 4.
Examples of radiographs processed by the AI algorithm. A A 60-year-old male patient with bilateral hip prostheses. Note that pelvic obliquity is not processed by the AI algorithm if the patient has a hip prosthesis. B A 73-year-old female patient with bilateral genu varum deformity. C A 78-year-old male patient with a right knee prosthesis and severe left genu varum deformity. D An 8-year-old girl with genu valgum deformity
Inter-reader and intra-reader agreement
ICC estimates between the two expert radiologists who established the ground truth showed excellent agreement across all measurements, with ICCs ≥ 0.99. The intra-reader reliability also exhibited excellent agreement, with ICCs ≥ 0.98 (Table 5).
Discussion
Our study investigated the performance of BoneMetrics for automated leg measurements on anteroposterior full-leg standing radiographs. It revealed excellent agreement between the AI algorithm and the gold standard for all parameters (ICC ≥ 0.97). Results demonstrated the high accuracy of the AI algorithm with a MAE equal to 0.3° for the HKA angle and less than 1.5 mm for the pelvic obliquity, top leg length, center leg length, top femoral length, center femoral length, and tibial length. Clinically meaningful differences in most previous reports have been defined as deviations greater than 2° for angle measurements and superior to 5 mm for length measurements [31, 41–43]. In this study, discrepancies between automated measurements and ground truth manual measurements were far below these thresholds. Additionally, Bland–Altman plots highlighted the absence of strong bias associated with the automated measurements.
The MAE values between AI and ground truth measurements of the HKA angle range from 0.20° to 0.58° in the literature and are comparable to the value of 0.30° found in this study [31, 32, 42, 44]. For leg length measurements, our MAE values spanned from 0.95 mm to 1.46 mm. Reported differences between AI and manual measurements vary rather widely, with values from 0.10 mm [32] up to 5 mm [31]. Interestingly, lengths measured from the top of the femoral head deviated less from the ground truth (MAE = 0.95–1.03 mm) than lengths measured from the center of the femoral head (MAE = 1.23–1.46 mm). The latter findings may be explained by the poorer reproducibility in determining the center compared with the top of the femoral head, and they suggest that full-leg and femoral length measurements with this AI algorithm are more accurate using the top of the femoral head.
The AI algorithm provided reliable measurements across a very diverse patient population. The AI demonstrated equal accuracy in both pediatric and adult patients. This finding is particularly significant as undiagnosed lower limb malalignment in children can result in abnormal motor development and gait [45]. On radiographs of patients with hip implants, measurements were comparable to those of patients without implants for five out of seven parameters. Interestingly, in patients with hip implants, the AI made larger errors in measuring the center femoral length but smaller errors in measuring the center leg length. This discrepancy could be due to the higher likelihood of these patients also having knee osteoarthritis. Research has shown that knee osteoarthritis is associated with intercondylar notch stenosis, which could complicate the accurate placement of the center of the femoral intercondylar notch, a necessary landmark in measuring femoral length [46, 47]. Regarding patients with knee implants, the AI algorithm made larger errors in measuring tibial length on radiographs with knee implants than on those without. This finding suggests that positioning a landmark at the center of the knee constitutes a less reproducible task in patients with a knee prosthesis. Interestingly, EOS imaging enhanced the accuracy of HKA angle measurements in comparison with conventional radiography and did not have a significant impact on the other parameters, suggesting that AI measurements are robust to imaging modality. These findings are particularly relevant given that EOS imaging offers multiple advantages over conventional radiography, including the absence of stitching artifacts and reduced radiation exposure [48].
Our study has several strengths. First, this study is the first, to the best of our knowledge, to examine the performance of an AI algorithm on total leg and femoral length measurements from two distinct landmark points, as most studies to date have focused predominantly on angle measurements [33, 41, 42, 44, 49–51]. Our results confirm the feasibility of automated measurements not only for angles but also for a comprehensive set of leg length measurements.
Additionally, the AI software exhibited highly reliable measurements of the HKA angle, even in patients with malalignment including genu varum and genu valgum. Although the MAE was significantly different between patients with genu varum (0.33°) and those without (0.30°), it remained well below clinically meaningful thresholds. A key strength of this study also pertains to the generalizability of findings, as data were collected consecutively across various centers, manufacturers, and imaging modalities. Future investigations should further expand patient diversity to test the performance of the AI on images with skeletal abnormalities or different implant configurations. Finally, it is important to highlight that the issue of data dependencies was alleviated by employing a mixed-effects approach to the Bland–Altman analysis.
There are limitations to our study. First, the retrospective design means that the performance of the AI algorithm in a clinical setting and its impact on physicians’ workflow and patient care could not be evaluated. Moreover, the small dataset may not have fully captured the diversity of patient demographics and radiographic conditions, thus restricting the AI’s generalizability. The study did not examine key leg alignment parameters, such as the medial proximal tibial angle, lateral distal femoral angle, and joint line convergence angle, which play an essential role in clinical decision-making and surgical planning. Future studies should evaluate the performance of the AI on these specific measurements. Another limitation is that some landmark points were positioned with low confidence levels (< 50%) by the AI algorithm for reasons that are difficult to disentangle. Finally, the dataset exhibited a bias toward radiographs of patients with malalignment, resulting in an under-representation of healthy lower limbs.
In conclusion, our study underscores the reliability of a commercially available AI-based software in automating measurements on anteroposterior full-leg standing radiographs. The AI algorithm exhibited good accuracy in computing critical lower limb parameters including the HKA angle, pelvic obliquity, total leg length (measured from two distinct landmark points), femoral leg length (measured from two distinct landmark points), and tibial length. The results closely align with findings reported in similar previous studies. Future work should focus on whether the integration of such an AI tool into clinical workflows could alleviate physicians’ workload by facilitating laborious and time-consuming tasks. It should also evaluate the clinical implications of automated measurements, particularly for preventive medicine, surgical planning, and postoperative monitoring.
Acknowledgements
Not applicable.
Abbreviations
- AI
Artificial intelligence
- Center femoral length
Femoral length from the center of the femoral head
- Center leg length
Leg length from the center of the femoral head
- HKA
Hip–knee–ankle
- ICC
Intraclass correlation coefficient
- MAE
Mean absolute error
- RMSE
Root mean square error
- Top femoral length
Femoral length from the top of the femoral head
- Top leg length
Leg length from the top of the femoral head
Author contributions
Project supervision: L.L., N.E.R., A.D., J.D.L., and A.G. Funding acquisition: N.E.R. and A.D. Conception and design: All authors. AI development and training: Z.Z. and N.N. Data curation: J.V., V.M., and L.C. Analysis and interpretation of data: L.L., N.E.R., and J.D.L. Statistical analyses: M.D. and J.V. Original manuscript draft: M.D. and J.V. Visualization: M.D. and J.V. Review and edition: All authors. Final read and approval: All authors.
Funding
The work was funded by Gleamer (Paris, France).
Availability of data and materials
The datasets used and analyzed for the current study are available from the corresponding author upon reasonable request. The dataset used for developing the AI model, as well as the AI model itself, are components of proprietary software and are therefore not publicly available.
Declarations
Ethics approval and consent to participate
The study was performed in accordance with the ethical standards in the 1964 Declaration of Helsinki. The ethics committee of the Collège des Enseignants en Radiologie de France (CERF), the Centre d’Éthique de la Recherche en Imagerie Médicale (CERIM), approved the study (Institutional Review Board approval number CRM-2209-306).
Consent for publication
Consent forms were not required for patients, as the images used in this study were completely unidentifiable and there were no specific details on individuals reported within the manuscript. Furthermore, all patients had been informed about the use of their anonymized data for research purposes, which included clear instructions on how to opt out if they chose to do so.
Competing interests
L.L., M.D., J.V., V.M., L.C., Z.Z., N.N., and J.D.L. are employees of Gleamer; N.E.R. is a co-founder and chief medical officer of Gleamer. A.D. is a co-founder and chief technical officer of Gleamer. A.G. is a shareholder of BICL, LLC, and consultant to Pfizer, Novartis, TrialSpark, Coval, ICM, Medipost, and TissueGene.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Felson DT, Niu J, Gross KD, Englund M, Sharma L, Cooke TDV, Guermazi A, Roemer FW, Segal N, Goggins JM, Lewis CE, Eaton C, Nevitt MC (2013) Valgus malalignment is a risk factor for lateral knee osteoarthritis incidence and progression: findings from MOST and the osteoarthritis initiative. Arthritis Rheum 65(2):355–362 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sharma L, Song J, Dunlop D, Felson D, Lewis CE, Segal N, Torner J, Cooke TDV, Hietpas J, Lynch J, Nevitt M (2010) Varus and valgus alignment and incident and progressive knee osteoarthritis. Ann Rheum Dis 69(11):1940–1945 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sharma L, Chmiel JS, Almagor O, Felson D, Guermazi A, Roemer F, Lewis CE, Segal N, Torner J, Cooke TDV, Hietpas J, Lynch J, Nevitt M (2013) The role of varus and valgus alignment in the initial development of knee cartilage damage by MRI: the MOST study. Ann Rheum Dis 72(2):235–240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Applebaum A, Nessim A, Cho W (2021) Overview and spinal implications of leg length discrepancy: narrative review. Clin Orthop Surg 13(2):127–134 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kumar N, Yadav C, Raj R, Anand S (2014) How to interpret postoperative X-rays after total knee arthroplasty. Orthop Surg 6(3):179–186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.van de Pol GJ, Verdonschot N, van Kampen A (2012) The value of the intra-operative clinical mechanical axis measurement in open-wedge valgus high tibial osteotomies. Knee 19(6):933–938 [DOI] [PubMed] [Google Scholar]
- 7.Kim SH, Park Y-B, Song M-K, Lim J-W, Lee H-J (2018) Reliability and validity of the femorotibial mechanical axis angle in primary total knee arthroplasty: navigation versus weight bearing or supine whole leg radiographs. Knee Surg Relat Res 30(4):326–333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lin Y-H, Chang F-S, Chen K-H, Huang K-C, Su K-C (2018) Mismatch between femur and tibia coronal alignment in the knee joint: classification of five lower limb types according to femoral and tibial mechanical alignment. BMC Musculoskelet Disord 19(1):411 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sheehy L, Felson D, Zhang Y, Niu J, Lam Y-M, Segal N, Lynch J, Cooke TDV (2011) Does measurement of the anatomic axis consistently predict hip-knee-ankle angle (HKA) for knee alignment studies in osteoarthritis? Analysis of long limb radiographs from the multicenter osteoarthritis (MOST) study. Osteoarthritis Cartilage 19(1):58–64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Khalifa AA, Mullaji AB, Mostafa AM, Farouk OA (2021) A protocol to systematic radiographic assessment of primary total knee arthroplasty. Orthop Res Rev 13:95–106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tipton SC, Sutherland JK, Schwarzkopf R (2016) The assessment of limb length discrepancy before total hip arthroplasty. J Arthroplasty 31(4):888–892 [DOI] [PubMed] [Google Scholar]
- 12.Heaver C, St Mart J-P, Nightingale P, Sinha A, Davis ET (2013) Measuring limb length discrepancy using pelvic radiographs: the most reproducible method. HIP Int 23(4):391–394 [DOI] [PubMed] [Google Scholar]
- 13.Vaishya R, Vijay V, Birla VP, Agarwal AK (2016) Inter-observer variability and its correlation to experience in measurement of lower limb mechanical axis on long leg radiographs. J Clin Orthop Trauma 7(4):260–264 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Define-AI Use Case Directory. https://www.acrdsi.org/DSI-Services/Define-AI. Accessed 30 Jan 2024.
- 15.Chen K, Stotter C, Klestil T, Nehrer S (2022) Artificial intelligence in orthopedic radiography analysis: a narrative review. Diagnostics 12(9):2235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kijowski R, Liu F, Caliva F, Pedoia V (2020) Deep learning for lesion detection, progression, and prediction of musculoskeletal disease. J Magn Reson Imaging 52(6):1607–1619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gyftopoulos S, Lin D, Knoll F, Doshi AM, Rodrigues TC, Recht MP (2019) Artificial intelligence in musculoskeletal imaging: current status and future directions. Am J Roentgenol 213(3):506–513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Regnard N-E, Lanseur B, Ventre J, Ducarouge A, Clovis L, Lassalle L, Lacave E, Grandjean A, Lambert A, Dallaudière B, Feydy A (2022) Assessment of performances of a deep learning algorithm for the detection of limbs and pelvic fractures, dislocations, focal bone lesions, and elbow effusions on trauma X-rays. Eur J Radiol 154:110447 [DOI] [PubMed] [Google Scholar]
- 19.Guermazi A, Tannoury C, Kompel AJ, Murakami AM, Ducarouge A, Gillibert A, Li X, Tournier A, Lahoud Y, Jarraya M, Lacave E, Rahimi H, Pourchot A, Parisien RL, Merritt AC, Comeau D, Regnard N-E, Hayashi D (2022) Improving radiographic fracture recognition performance and efficiency using artificial intelligence. Radiology 302(3):627–636 [DOI] [PubMed] [Google Scholar]
- 20.Canoni-Meynet L, Verdot P, Danner A, Calame P, Aubry S (2022) Added value of an artificial intelligence solution for fracture detection in the radiologist’s daily trauma emergencies workflow. Diagn Interv Imaging 103(12):594–600 [DOI] [PubMed] [Google Scholar]
- 21.Dallora AL, Anderberg P, Kvist O, Mendes E, Diaz Ruiz S, Sanmartin Berglund J (2019) Bone age assessment with various machine learning techniques: a systematic literature review and meta-analysis. PLoS ONE 14(7):e0220242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nguyen T, Hermann A-L, Ventre J, Ducarouge A, Pourchot A, Marty V, Regnard N-E, Guermazi A (2023) High performance for bone age estimation with an artificial intelligence solution. Diagn Interv Imaging 104(7):330–336 [DOI] [PubMed] [Google Scholar]
- 23.Lee LS, Chan PK, Wen C, Fung WC, Cheung A, Chan VWK, Cheung MH, Fu H, Yan CH, Chiu KY (2022) Artificial intelligence in diagnosis of knee osteoarthritis and prediction of arthroplasty outcomes: a review. Arthroplasty 4(1):16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ahmed SM, Mstafa RJ (2022) A comprehensive survey on bone segmentation techniques in knee osteoarthritis research: from conventional methods to deep learning. Diagnostics 12(3):611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pan Y, Chen Q, Chen T, Wang H, Zhu X, Fang Z, Lu Y (2019) Evaluation of a computer-aided method for measuring the Cobb angle on chest X-rays. Eur Spine J 28(12):3035–3043 [DOI] [PubMed] [Google Scholar]
- 26.Korez R, Putzier M, Vrtovec T (2020) A deep learning tool for fully automated measurements of sagittal spinopelvic balance from X-ray images: performance evaluation. Eur Spine J 29(9):2295–2305 [DOI] [PubMed] [Google Scholar]
- 27.Jensen J, Graumann O, Overgaard S, Gerke O, Lundemann M, Haubro MH, Varnum C, Bak L, Rasmussen J, Olsen LB, Rasmussen BSB (2022) A deep learning algorithm for radiographic measurements of the hip in adults—a reliability and agreement study. Diagnostics 12(11):2597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schwarz GM, Simon S, Mitterer JA, Huber S, Frank BJ, Aichmair A, Dominkus M, Hofstaetter JG (2023) Can an artificial intelligence powered software reliably assess pelvic radiographs? Int Orthop 47(4):945–953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Day J, De Cesar NC, Richter M, Mansur NS, Fernando C, Deland JT, Ellis SJ, Lintz F (2021) Evaluation of a Weightbearing CT artificial intelligence-based automatic measurement for the M1–M2 intermetatarsal angle in hallux valgus. Foot Ankle Int 42(11):1502–1509 [DOI] [PubMed] [Google Scholar]
- 30.Li T, Wang Y, Qu Y, Dong R, Kang M, Zhao J (2022) Feasibility study of hallux valgus measurement with a deep convolutional neural network based on landmark detection. Skeletal Radiol 51(6):1235–1247 [DOI] [PubMed] [Google Scholar]
- 31.Simon S, Schwarz GM, Aichmair A, Frank BJH, Hummer A, DiFranco MD, Dominkus M, Hofstaetter JG (2022) Fully automated deep learning for knee alignment assessment in lower extremity radiographs: a cross-sectional diagnostic study. Skeletal Radiol 51(6):1249–1259 [DOI] [PubMed] [Google Scholar]
- 32.Archer H, Reine S, Xia S, Vazquez LC, Ashikyan O, Pezeshk P, Kohli A, Xi Y, Wells JE, Hummer A, Difranco M, Chhabra A (2023) Deep learning generated lower extremity radiographic measurements are adequate for quick assessment of knee angular alignment and leg length determination. Skeletal Radiol 53:923–933 [DOI] [PubMed] [Google Scholar]
- 33.Stotter C, Klestil T, Chen K, Hummer A, Salzlechner C, Angele P, Nehrer S (2023) Artificial intelligence-based analyses of varus leg alignment and after high tibial osteotomy show high accuracy and reproducibility. Knee Surg Sports Traumatol Arthrosc 31:5885–5895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hau MYT, Menon DK, Chan RJN, Chung KY, Chau WW, Ho KW (2020) Two-dimensional/three-dimensional EOS™ imaging is reliable and comparable to traditional X-ray imaging assessment of knee osteoarthritis aiding surgical management. Knee 27(3):970–979 [DOI] [PubMed] [Google Scholar]
- 35.Simone Waldt KW (2013) Measurements and classifications in musculoskeletal radiology. Georg Thieme Verlag, Stuttgart [Google Scholar]
- 36.Birkenmaier C, Levrard L, Melcher C, Wegener B, Ricke J, Holzapfel BM, Baur-Melnyk A, Mehrens D (2024) Distances and angles in standing long-leg radiographs: comparing conventional radiography, digital radiography, and EOS. Skeletal Radiol 53(8):1517–1528 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lu M-J, Zhong W-H, Liu Y-X, Miao H-Z, Li Y-C, Ji M-H (2016) Sample size for assessing agreement between two methods of measurement by bland−altman method. Int J Biostat 12(2):1–8 [DOI] [PubMed] [Google Scholar]
- 38.Ramazanian T, Yan S, Rouzrokh P, Wyles CC, O’Byrne TJ, Taunton MJ, Maradit Kremers H (2022) Distribution and correlates of hip-knee-ankle angle in early osteoarthritis and preoperative total knee arthroplasty patients. J Arthroplasty 37(6):S170–S175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Thienpont E, Schwab PE, Cornu O, Bellemans J, Victor J (2017) Bone morphotypes of the varus and valgus knee. Arch Orthop Trauma Surg 137(3):393–400 [DOI] [PubMed] [Google Scholar]
- 40.Koo TK, Li MY (2016) A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J Chiropr Med 15(2):155–163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Pagano S, Müller K, Götz J, Reinhard J, Schindler M, Grifka J, Maderbacher G (2023) The role and efficiency of an AI-powered software in the evaluation of lower limb radiographs before and after total knee arthroplasty. J Clin Med 12(17):5498 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Schwarz GM, Simon S, Mitterer JA, Frank BJH, Aichmair A, Dominkus M, Hofstaetter JG (2022) Artificial intelligence enables reliable and standardized measurements of implant alignment in long leg radiographs with total knee arthroplasties. Knee Surg Sports Traumatol Arthrosc 30(8):2538–2547 [DOI] [PubMed] [Google Scholar]
- 43.Knutson GA (2005) Anatomic and functional leg-length inequality: a review and recommendation for clinical decision-making. Part I, anatomic leg-length inequality: prevalence, magnitude, effects and clinical significance. Chiropr Osteopat 13(1):11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mitterer JA, Huber S, Schwarz GM, Simon S, Pallamar M, Kissler F, Frank BJH, Hofstaetter JG (2023) Fully automated assessment of the knee alignment on long leg radiographs following corrective knee osteotomies in patients with valgus or varus deformities. Arch Orthop Trauma Surg 144(3):1029–1038 [DOI] [PubMed] [Google Scholar]
- 45.Rerucha CM, Dickison C, Baird DC (2017) Lower extremity abnormalities in children. Am Fam Physician 96(4):226–233 [PubMed] [Google Scholar]
- 46.León HO, Blanco CER, Guthrie TB, Martínez OJN (2005) Intercondylar notch stenosis in degenerative arthritis of the knee. Arthroscopy 21(3):294–302 [DOI] [PubMed] [Google Scholar]
- 47.Wada M, Tatsuo H, Baba H, Asamoto K, Nojyo Y (1999) Femoral intercondylar notch measurements in osteoarthritic knees. Rheumatology 38(6):554–558 [DOI] [PubMed] [Google Scholar]
- 48.Dubousset J, Charpak G, Dorion I, Skalli W, Lavaste F, Deguise J, Kalifa G, Ferey S (2005) A new 2D and 3D imaging approach to musculoskeletal physiology and pathology with low-dose radiation and the standing position: the EOS system. Bull Acad Natl Med 189(2):287–297 [PubMed] [Google Scholar]
- 49.Schock J, Truhn D, Abrar DB, Merhof D, Conrad S, Post M, Mittelstrass F, Kuhl C, Nebelung S (2020) Automated analysis of alignment in long-leg radiographs by using a fully automated support system based on artificial intelligence. Radiol Artif Intell 3(2):e200198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Erne F, Grover P, Dreischarf M, Reumann MK, Saul D, Histing T, Nüssler AK, Springer F, Scholl C (2022) Automated artificial intelligence-based assessment of lower limb alignment validated on weight-bearing pre- and postoperative full-leg radiographs. Diagnostics 12(11):2679 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kim SE, Nam JW, Kim JI, Kim J-K, Ro DH (2024) Enhanced deep learning model enables accurate alignment measurement across diverse institutional imaging protocols. Knee Surg Relat Res 36(1):4 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and analyzed for the current study are available from the corresponding author upon reasonable request. The dataset used for developing the AI model, as well as the AI model itself, are components of proprietary software and are therefore not publicly available.