Abstract
The exploration of chemical space holds promise for developing influential chemical entities. Molecular representations, which reflect features of molecular structure in silico, assist in navigating chemical space appropriately. Unlike atom-level molecular representations, such as SMILES and atom graph, which can sometimes lead to confusing interpretations about chemical substructures, substructure-level molecular representations encode important substructures into molecular features; they not only provide more information for predicting molecular properties and drug‒drug interactions but also help to interpret the correlations between molecular properties and substructures. However, it remains challenging to represent the entire molecular structure both intactly and simply with substructure-level molecular representations. In this study, we developed a novel substructure-level molecular representation and named it a group graph. The group graph offers three advantages: (a) the substructure of the group graph reflects the diversity and consistency of different molecular datasets; (b) the group graph retains molecular structural features with minimal information loss because the graph isomorphism network (GIN) of the group graph performs well in molecular properties and drug‒drug interactions prediction, showing higher accuracy and efficiency than the model of other molecular graphs, even without any pretraining; and (c) the molecular property may change when the substructure is substituted with another of differing importance in group graph, facilitating the detection of activity cliffs. In addition, we successfully predicted structural modifications to improve blood‒brain barrier permeability (BBBP) via the GIN of group graph. Therefore, the group graph takes advantages for simultaneously representing molecular local characteristics and global features.
Scientific contribution The group graph, as a substructure-level molecular representation, has the ability to retain molecular structural features with minimal information loss. As a result, it shows superior performance in predicting molecular properties and drug‒drug interactions with enhanced efficiency and interpretability. 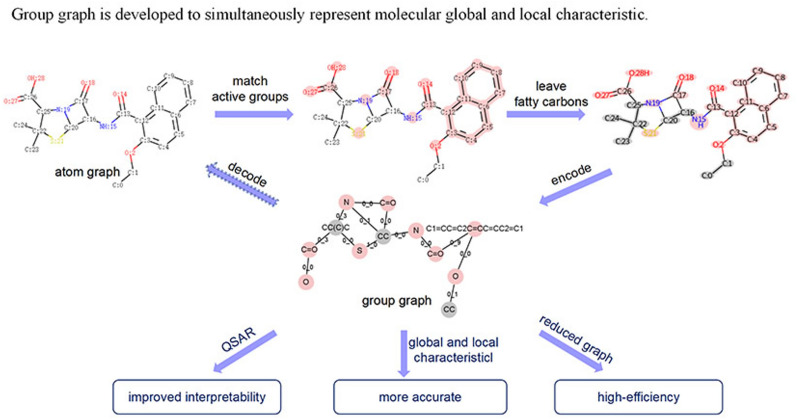
Supplementary Information
The online version contains supplementary material available at 10.1186/s13321-024-00933-x.
Introduction
Artificial intelligence (AI) plays a crucial role in various aspects of preclinical stages of small-molecule drug development, including virtual screening, molecular property prediction, structure‒activity relationship analysis and lead optimization [1, 2]. Molecular representations, which reflects the features of molecules in silico, serve as inputs for AI models and significantly affect the performance and application of related algorithms [3–6].
Atom-level molecular representations such as simplified molecular input line entry system (SMILES), atom graph, and structural coordinate, which directly illustrating molecular structural features, have superior performance in forecasting molecular properties, drug‒drug interactions and molecular generation [7–9]. However, atom-level molecular representations overlook the important effects of molecular substructures such as functional groups or pharmacophores, often failing to capture atoms within important substructures in the interpretation of quantitative structure‒activity relationships (QSAR) or quantitative structure‒property relationships (QSPR) [10, 11], which is confusing in term of chemistry. Meanwhile, SMILES-based representations would not reflect the learned parameters of explainable artificial intelligence, making them unreliable in interpretability [12]. Substructure-level chemical fingerprints such as extended connectivity fingerprints (ECFP) and molecular access system (MACCS), bridging molecular substructure characteristics with molecular global features [13], are usually used for QSAR, QSPR and similarity searches. However, they do not consider the connections between substructures. Rataj et al. developed a matrix of occurrences and connections between substructures as a chemical fingerprint (SCFP) and demonstrated that the performance of molecular activity prediction can be enhanced by adding substructural connections to molecular fingerprints [14]. Cai et al. reported that the FP-GNN, which combines a graph neural network of atom graph (GNN) with a fully connected neural network of mixed chemical fingerprints (FPN), performed the best in the prediction of molecular properties, whereas the pure FPN performed the worst [15]. The results revealed that substructure-level chemical fingerprints lost some molecular structural information that was retained in the atom graph.
Molecular formulas depict how atoms and bonds build molecules, akin to how graphs use nodes and edges to map networks. In the atom graph, atoms are the nodes, with bonds as edges. Compared to the confusion caused by different SMILES representations of the same molecular structure, molecular graphs offer greater interpretability, as they represent molecular structures in a unique and unambiguous way [12]. Molecular substructure graphs go a step further by treating substructures as nodes and links between substructures as edges, enabling a more detailed exploration of both molecular substructure characteristics and global features [16]. Molecule fragmenting algorithms, such as the breaking of retrosynthetically interesting chemical substructures (BRICS), the retrosynthetic combinatorial analysis procedure (RECAP) or CCQ (www.chemaxon.com), are provided to obtain substructures in molBLOCKS [17]. Methods such as eMolFrag retain the connections between substructures that fragmented by the BRICS and build substructure graphs [18, 19]. However, owing to the lack of bonds that can be fragmented by BRICS, many molecules fail to form substructure graphs via BRICS; to address this, there are certain methods for identifying more breakable bonds for molecular fragmentation.
The substructures obtained by BRICS are further decomposed by cutting the self-defined cleavable bonds in the MGSSL [20]. The sixteen types of cleavable bonds in BRICS are extended to 49 in MacFrag [21]. pBRICS further decomposes molecules into smaller substructures by extracting the Bemis‒Murcko framework and matching fragments from a comprehensive library of fragments after BRICS [22]. However, BRICS cannot fragment molecules into common substructures such as functional groups, usually resulting in a large substructure vocabulary. Even in advanced BRICS, the size of the vocabulary may be 1–10 times the size of the dataset, which possibly results in a high-dimensional chemical space [20].
Self-defined molecule fragmentation overcomes the limitations of BRICS. JTVAE uses self-defined rules to transform a molecule into a substructure junction tree [23–25], and the size of the substructure vocabulary is one tenth that of MGSSL. HierVAE decomposes a molecule into substructures by cutting all the bridge bonds, producing a substructure vocabulary that holds 1%-10% of the size of the dataset; however, HierVAE uses a tertiary structure to represent the molecular structure, resulting in low efficiency [26]. Pharmacophore graph regard common pharmacophores as substructures [27], and functional groups (FGS) graph extract molecular functional groups that affect chemical properties as substructures [28]. Once combined with an atom graph, a substructure junction tree, a pharmacophore graph and a FGS graph could enhance the performance of molecular property prediction by providing supplementary information about local molecular structures. Nevertheless, the single substructure junction tree, pharmacophore graph and FGS graph perform worse than the atom graph in molecular property prediction, indicating the loss of essential molecular structural information in the substructure junction tree, FGS graph and pharmacophore graph [29, 30].
Graph neural networks (GNNs) are designed to embed graph features through neighborhood aggregation or message passing. The graph isomorphism network (GIN) is considered capable of closely approximating the theoretical upper bound of GNNs expressiveness because it is as powerful as the Weisfeiler–Lehman (WL) test for distinguishing nonisomorphic graphs [31]. The good performance of the GIN has also been confirmed by many studies [32]. In this study, we developed a molecular substructure graph by self-defined molecule fragmentation and called it a group graph. The GIN of the group graph was applied in the prediction of downstream tasks to evaluate the performance of the group graph as an effective molecular representation. The group graph shows the potential in several fields as follows:
The substructures in the group graph reflect the diversity and consistency of different molecular datasets, providing a tool for analyzing molecular datasets.
All substructures had no overlapping atoms and were linked by single bonds, indicating the potential of the group graph for molecular generation.
A group graph can also be encoded as a node table and adjacent matrix, such as an atom graph, making it simple to adapt to other graph models.
The GIN of the group graph outperformed that of the atom graph and other substructure graph in the prediction of molecular properties and drug‒drug interactions without any pretraining. Moreover, the runtime of the GIN of the group graph decreased by approximately 30% compared with that of the atom graph, suggesting that the group graph is a reduced molecular graph with minimal molecular structural information loss.
The GIN of the group graph captured the substructure to interpret the change in molecular properties. The results revealed that the importance of different substructures changed in 80% of the molecule pairs containing activity cliffs. In addition, structural modifications aimed at improving blood‒brain barrier permeability (BBBP) were successfully predicted by QSPR based on group graph. Therefore, a group graph can be used for QSPR, QSAR and lead optimization.
Materials and methods
Active groups
To facilitate identification in molecules, traditional functional groups were broken into charged atoms, halogens and small groups containing only double or triple bonds. For example, the ester group in this study was decomposed into two active groups, carbonyl and oxygen. Unlike MACCS keys, which view all rings as independent substructures, only aromatic rings are considered independent substructures in our study because of their distinctive effects on molecular properties [33]. Other rings would be fragmented if they were matched by a broken functional group pattern. Details of traditional functional groups and broken functional groups pattern are shown in Figs. S1–S2. The broken functional groups and aromatic rings are two parts of the active groups.
Construction of the group graph
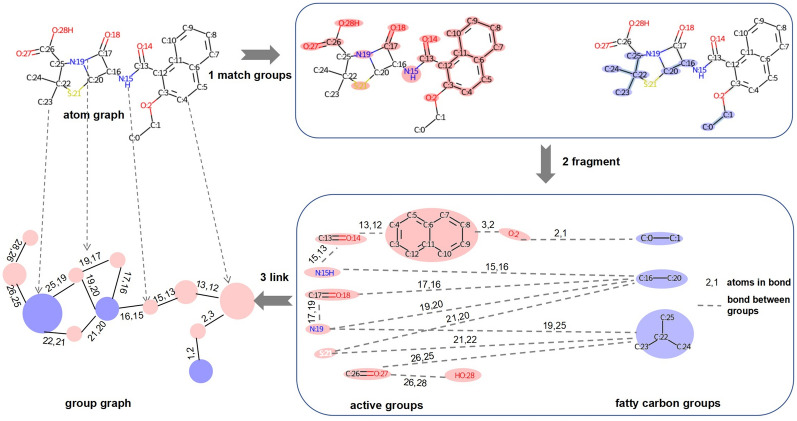
As shown in Fig. 1, there are 3 steps for constructing a molecular group graph.
Group matching. First, all aromatic atoms are found in a molecule via the open-source package RDKit 2020.9 (https://www.rdkit.org/); then, aromatic atoms that are bonded to each other are grouped together as aromatic rings. Second, the atom IDs of broken functional groups in a molecule are obtained via pattern matching. These data provide all the atom IDs of the active groups in the molecule. Third, bonded atoms from the remaining nonactive groups can be grouped together as fatty carbon groups.
Substructure extraction. Active groups such as N, O, C=O, S, and C1=CC=C2C=CC=CC2=C1 (SMILES of groups) and fatty carbon groups such as C, CC, and CC(C)C are extracted from PubChem id 23568 according to their atom IDs and then put into the substructure vocabulary. Two substructures have links if they are bonded in the original atom graph. Bonded atom pairs between substructures are viewed as attachment atom pairs. For example, substructure C:17=O:18 is bonded with N:19 by atom 17 and atom 19, so (17, 19) is the attachment atom pair between C:17=O:18 and N:19.
Substructure linking. A group graph is obtained by viewing substructures as nodes, links between substructures as edges, and features of attachment atom pairs as features of edges.
Fig. 1.
Construction of the group graph of PubChem id 23568 (SMILES: CCOc1ccc2ccccc2c1C(=O)NC1C(=O)N2C1SC(C)(C)C2C(=O)O)
Datasets in substructure vocabulary analysis
The GDB-17 dataset contains molecules with C, N, O and F following simple chemical stability and synthetic feasibility rules (https://gdb.unibe.ch/downloads/) [34]. We separated molecules with 9, 10, 11, 13, and 17 atoms from the original GDB-17 dataset to create datasets GDB9, GDB10, GDB11, GDB13 and GDB17. Furthermore, five substructure vocabulary are given and analyzed from selected 100,000 molecules of these five datasets.
Natural products are well-known for their diverse substructures, so a natural product dataset (https://www.npatlas.org/) was selected to obtain a substructure vocabulary for analysis of the features of substructures in the group graph [35].
Datasets for the prediction of molecular properties and drug‒drug interactions and performance evaluation metrics
Nine datasets from MoleculeNet were used for the prediction of molecular properties (Table 1) [36]. There were six regression datasets, including two quantum chemical datasets, namely, QM7 and QM8, and three physicochemical datasets, namely, ESOL, FreeSolv and Lipo. The performance of the ESOL, FreeSolv and Lipo was evaluated via the root mean square error (RMSE), and the performance of QM7 and QM8 was evaluated via the mean absolute error (MAE). There were four classification datasets, including two bioactivity and biophysics datasets, HIV and BACE, and two physiology and toxicity datasets, BBBP and ClinTox. The performance of classification tasks was evaluated by the area under the receiver operating characteristic curve (ROC-AUC). These nine datasets were split into training/testing datasets via fivefold cross validation (5-CV). To make a rigorous comparison, the same split was used for different models. In this study, optimization of models to the GIN of the atom graph in nine tasks was used to evaluate their performance in the prediction of molecular properties, and the optimization is described in Eq. 1:
| 1 |
Table 1.
Datasets for the prediction of molecular properties (MPs) and drug‒drug interactions (DDI)
| Regression tasks for MP prediction | Class tasks for MP prediction | Class tasks for DDI prediction | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Task name | ESOL | FreeSolv | Lipo | QM7 | QM8 | BACE | BBBP | ClinTox | HIV | BIOSNAP | DrugBankDDI |
| Task num | 1 | 1 | 1 | 1 | 12 | 1 | 1 | 1 | 1 | 1 | 1 |
| Sample | 1127 | 642 | 4200 | 6830 | 21,786 | 1513 | 2037 | 1478 | 41,127 | 42,040 | 443,046 |
| Vocab | 190 | 98 | 470 | 202 | 563 | 162 | 459 | 478 | 2879 | 1487 | 576 |
| Metrics | RMSE | RMSE | RMSE | MAE | MAE | ROC_AUC | ROC_AUC | ROC_AUC | ROC_AUC | ROC_AUC | ROC_AUC |
In each classification task and regression task, Oc and Or represent the optimization of the models to the GIN of the atom graph; Pca and Pra represent the performance of the GIN of the atom graph; Pc and Pr represent the performance of the models; and the average optimization is the average of the optimization of the models in nine tasks.
Two binary classification tasks, BIOSNAP [37] and DrugBankDDI [38], were used for drug‒drug interaction prediction. The datasets were split into training/testing sets at a ratio of 4:1, and 12.5% of the training data were selected as the validation set. To conduct a precise comparison, the data split of the GIN of the group graph was consistent with that of ReLMole.
Baseline models of the molecular graph and chemical fingerprint
To compare the performance of the group graph with that of other molecular representations in the prediction of molecular properties and drug‒drug interactions, several molecular graph models and random forest models based on extended-connectivity fingerprint with ratio 4 (ECFP4) were used. The detailed model information is as follows:
DMPNN: Messages associated with bonds instead of atoms were used in a directed message passing neural network (MPNN) for the prediction of molecular properties [39]. The codes of the DMPNN also provided a random forest model based on ECFP4 as a benchmark model.
Random forest: The codes of random forest (RF) based on ECFP4 came from the DMPNN. Default hyperparameters, such as 500 trees, were selected in the RF model for the prediction of molecular properties.
GIN (motif-pretraining): Known as MGSSL, it builds a substructure graph called the motif tree and then employs atom embeddings that learned by the GIN of the atom graph to generate the motif tree, so the GIN of the atom graph was pretrained via this self-supervised generation, and the pretrained GIN of the atom graph was applied for the prediction of molecular properties [20].
GIN (atom graph): Without pretraining, the MGSSL only retains the GIN of the atom graph. The raw GIN of the atom graph from the MGSSL was also applied for the prediction of molecular properties.
GIN (group graph): A similar GIN model with the MGSSL was applied to the group graph without pretraining for the prediction of molecular properties and drug‒drug interactions.
GIN (FGS graph): This model fragments the molecule into traditional functional groups to obtain a functional groups (FGS) graph, and the GIN of the FGS graph is used for the prediction of molecular properties [28].
GIN (FGS-pretraining): The GIN of the FGS graph was pretrained through contrastive learning (CL) between the molecular embedding obtained by the GIN of the FGS graph and the molecular chemical fingerprint. The GIN of the FGS-pretraining was applied for the prediction of molecular properties and drug‒drug interactions.
SimNN: Some features related to drug‒drug similarities were input into the neural network for the prediction of drug‒drug interactions [40].
DeepDDI: A deep neural network based on task-specific structural similarity profiles of each drug‒drug pair was proposed for the prediction of drug‒drug interactions [41].
CASTER: The latent vectors of drug‒drug pairs were embedded in features of the substring distribution obtained via an encoder‒decoder framework, and then the latent vectors of drug‒drug pairs were input into a neural network for the prediction of drug‒drug interactions [42].
PertrainGNN: The atom context was predicted to pretrain a GNN of the atom graph, and then the pretrained GNN of the atom graph was applied for the prediction of drug‒drug interactions [43].
Graph isomorphism network (GIN) of the atom graph, FGS graph and group graph
An atom graph was characterized by atom features and bond features as the codes of the MGSSL. A FGS graph was characterized by group embedding and link features as the codes of ReLMole. A group graph was characterized by chemical fingerprints including molecular descriptors, ECFP4 or MACCS of group, and link features. The detailed information is described in the supporting information.
The GIN model was selected to obtain node embeddings in the atom graph, FGS graph and group graph. For a graph, node u is the neighbor of node v; in the kth layer, the representation of node v is hv(k); hv(k) is updated by aggregating all neighbors’ representations to itself, and the process is described in Eq. 2 [30]:
| 2 |
Pooling of hv(k) of all nodes results in the acquisition of the molecular features (Readout). The final prediction is obtained by putting the molecular features into a 2-layer fully connected layer (MLP) (Fig. 2).
Fig. 2.
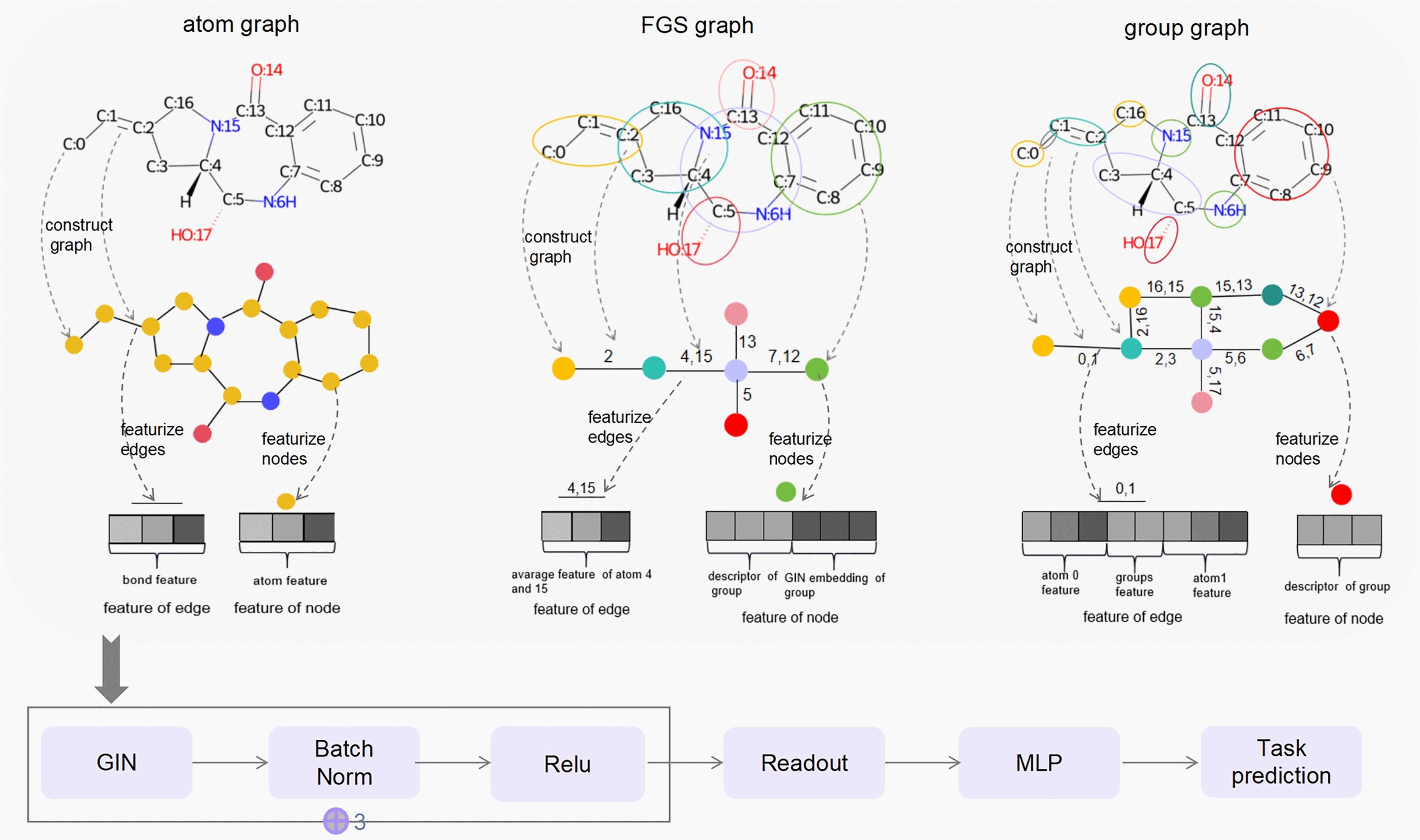
Architecture of the GIN of the atom graph, functional groups (FGS) graph and group graph
Search for matched molecular pairs with only one pair of different groups
Matched molecular pairs (MMPs) are defined as pairs of molecules with only small differences in local structure [44]. In this study, a MMP was searched out once the group graph of two molecules had the same group number and only one pair of different groups. Moreover, the similarity of two molecules must be greater than 0.8, which is defined as the maximum Levenshtein distance and MCS Tanimoto similarity between two molecules.
Explanation of the GIN of the group graph by comparison of the node importance of a matched molecular pair
The group importance of the group graph was measured by the gradient class activation map (Grad-CAM), which has been used for the evaluation of atom importance in graph convolutional neural networks [45]. Graph g = (X, A), where X represents the node features and A represents the adjacency matrix, which contains N nodes. For node n, the kth feature at the lth layer is denoted by Fk,nl, the final score y for class c is calculated as yc, the Grad-CAM average class-specific weights αkl,c are calculated by back-propagated gradients of yc (Eq. 3), and the Grad-CAM class-specific node importance LGrad-CAMc[n] is the average LGrad-CAMc[l,n] at all layers (Eqs. 4, 5):
| 3 |
| 4 |
| 5 |
A MMP contains molecule A with class CA and molecule B with CB. The group graphs of molecules A and B have N nodes and only differ in groups m and n. The node importance values LGrad-CAMc [m] and LGrad-CAMc[n] are ranked as x, y in ascending order within the molecule. The change of group importance x and y (E) were evaluated via the following equation (Eqs. 6, 7):
| 6 |
| 7 |
Equations (6) and (7) guarantee that a positive E signifies increased group importance, whereas a negative E signifies decreased group importance. Taking error into account, the group importance decreased if E was less than -0.3; group importance was changeless if E was less than 0.3 and greater than -0.3; and group importance increased if E was greater than 0.3.
Contributions of nodes in the group graph and the atom graph to BBBP
After being trained via BBBP, the models of the GIN of the group graph and atom graph were saved, the readout layer was removed from the trained GIN, and the output of the MLP layer was used to compute the contributions of nodes in the group graph and atom graph to BBBP.
Results and discussion
Data formats of group graphs in silico
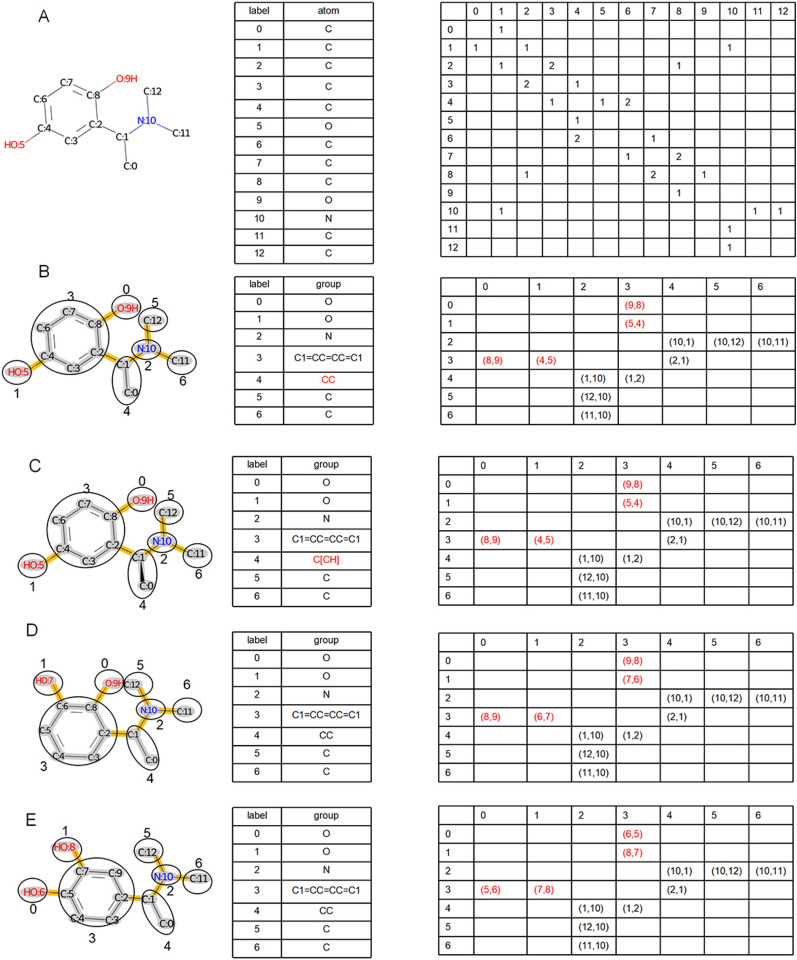
Like an atom graph, a group graph can also be encoded as a nodes table and adjacent matrix. These data can be stored via open graph representation tools such as PyTorch Geometric [46] and Deep Graph Library [47], enabling the easy transfer of group graphs to different graph models.
The node table and adjacent matrix of the atom graph and group graph of molecule A are shown in Fig. 3A and B. Atoms and groups are labeled by the unique node ID in the node tables of the atom graph and group graph. Both the horizontal axis and the vertical axis represent node IDs in the adjacent matrix, and 1, 2, and 3 in the adjacent matrix of the atom graph indicate single bonds, double bonds or triple bonds between two atoms, respectively, whereas (ID 1, ID 2) in the adjacent matrix of the group graph represents two atom IDs of the attachment atom pair between two groups. The atom of ID 1 comes from the group with a horizontal node ID, and the atom of ID 2 comes from the group with a vertical node ID. In total, there are 13 nodes and 24 edges in the atom graph and 7 nodes and 12 edges in the group graph of molecule A. In summary, a decrease in the number of nodes and edges in the group graph indicates the ability of the group graph to simplify the molecular graph.
Fig. 3.
Graph containing the node table and adjacent matrix of the geometric isomer. A Atom graph of molecule A (SMILES: CC(c1cc(O)ccc1O)N(C)C); B Group graph of molecule A; C Group graph of molecule B (SMILES: C[C@@H](c1cc(O)ccc1O)N(C)C; D Group graph of molecule C (SMILES: CC(c1cccc(O)c1O)N(C)C); E Group graph of molecule D (SMILES: CC(c1ccc(O)c(O)c1)N(C)C)
Three group graphs of molecules B, C and D, the geometric isomers of molecule A, are shown in Fig. 3C–E. Molecule B is the chiral isomer of molecule A, and the chiral mark of atom 1 [C@@H] is transferred to [CH]C in the group graph (Fig. 3C). [CH] loses an atom-chiral type but remains atom-chiral location, so the group graph remains partial stereochemistry. However, it has similar performance with isomeric group graph that remains whole stereochemistry in molecular property prediction (Fig. S3, Table S2-S3), so the group graph with partial stereochemistry is used in this study. In the adjacent matrix, attachment atom pairs (1,2) (4,5) (8,9) of molecule A (Fig. 3B), attachment atom pairs (1,2) (6,7) (8,9) of molecule B (Fig. 3D), and attachment atom pairs (1,2) (5,6) (7,8) of molecule C (Fig. 3E) capture the isomeric ortho-para-position, ortho-meta-position, and meta-para-position between C1=CC=CC=C1 and two O. By displaying geometric isomers differently, a group graph effectively differentiates similar molecular structures.
Comparison of the substructures in the group graph and other substructure graphs
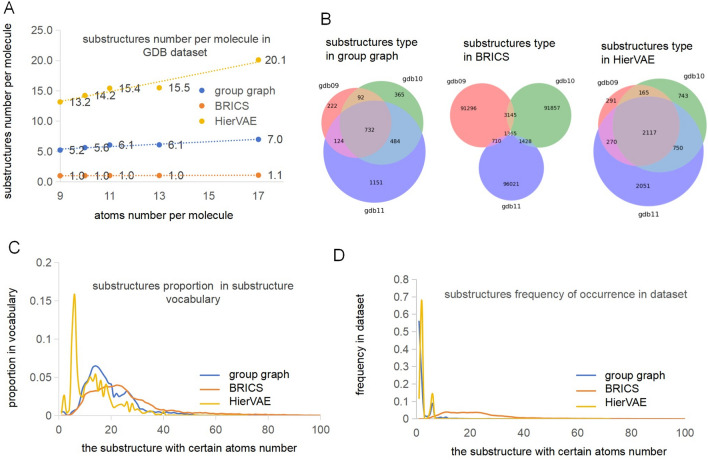
Substructures in substructure graphs should have a limited size, or the dimension of the molecular representation would be too large, resulting in a complex and inefficient model. Therefore, the substructures of the group graph were compared with the substructures of the substructure graph built by BRICS [19] and HierVAE [26].
We counted the substructures number per molecule in the dataset by dividing the total number of substructures by the size of the dataset. Figure 4A shows that the substructures number per molecule became increasingly larger, in the group graph and the substructure graph of HierVAE, as the atoms number per molecule increased, suggesting that the group graph and the substructure graph of HierVAE can reflect the molecular complexity of the dataset. However, in the substructure graph of BRICS, the substructures number per molecule is close to one, demonstrating that most molecules could not be broken by BRICS. The substructures number per molecule is greater than the atoms number per molecule in the substructure graph of HierVAE, indicating that the substructure graph of HierVAE is more complex than an atom graph is; however, the substructures number per molecule in the group graph was approximately half of the atoms number per molecule in all GDB datasets, indicating that a group graph can fragment different datasets and simplify a molecular graph.
Fig. 4.
Characteristics of substructures from different datasets and in three types of substructure groups. A The substructures number per molecule in the group graph, the substructure graph of BRICS and HierVAE, from GDB9, GDB10, GDB11, GDB13 and GDB17; B The substructure types in the group graph, the substructure graph of BRICS and HierVAE, from GDB9, GDB10 and GDB11; C The proportion of the substructure with same atoms number to size of the substructure vocabulary from natural products dataset, in the group graph, the substructure graph of BRICS and HierVAE; D The frequency of occurrence of substructures with same atoms number in the natural products dataset, in the group graph, the substructure graph of BRICS and HierVAE [33]. The proportion of the substructure with same atoms number in the substructure vocabulary and the frequency of occurrence of substructures with same atoms number in the dataset are explained in the supporting information
The substructure types in the group graph and substructure graphs of BRICS and HierVAE, from GDB9, GDB10 and GDB11, were compared and shown in Fig. 4B. The group graph has the least number of substructure types, so substructures in the group graph are the most common, thus leading to the simplest molecular representation. The same substructures from three datasets account for less than 3% in the substructure graph of BRICS, but account for more than 50% in the substructure graph of HierVAE and the group graph, which demonstrates that similar substructures are obtained in HierVAE and the group graph from similar datasets.
Moreover, in the group graph, substructure graph of BRICS and HierVAE, the proportion of substructures with same atoms number in substructure vocabulary were compared and are shown in Fig. 4C. The substructures with the atoms number greater than 20 holds 50% in the substructure graph of BRICS; in the substructure graph of HierVAE, the substructure type with the atoms number less than 10 holds 50% and that near 6 holds 20%, showing that BRICS tends to generate large substructures whereas HierVAE tends to generate small substructures, particularly with the atoms number near 6. The proportion of the substructure in the group graph initially increases and then decreases as the atoms number in the substructure increases, because the substructure has increased variety and a decreased occurrence probability with increasing number of atoms. In Fig. 4D, the frequency of occurrence of substructures with same atoms number in natural product dataset is no more than 5% in the substructure graph of BRICS, which means that these substructures rarely occur between different molecules. Substructures within 10 atoms occur frequently in the substructure graph of HierVAE and the group graph, which means that the substructure graph of HierVAE and the group graph can reflect the common substructures.
In conclusion, a group graph can reflect the features of a molecular dataset.
Representation of the group graph for molecular properties
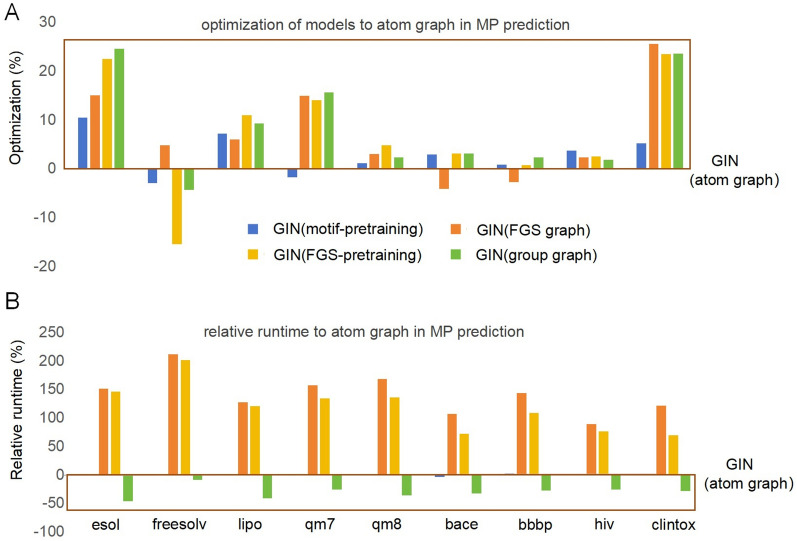
The representation of the group graph for the molecular properties was confirmed by predicting the molecular properties and drug‒drug interactions in the GIN. The GIN of the group graph was compared with other models, such as the GIN of the atom graph, DMPNN, GIN of motif-pretraining, GIN of FGS graph, GIN of FGS-pretraining, and the random forest (RF) model based on ECFP4 under the same 5-CV, and their runtime was computed via the same hardware. The performance of the models on nine tasks of molecular property prediction is shown in Table 2, and the optimization of the models for the GIN of the atom graph in each dataset is shown in Fig. 5A and is computed via Eq. 1, and the average optimization was used to evaluate the overall performance of the models. Compared with the GIN of the atom graph, the DMPNN, MGSSL, FGS graph, and group graph each excelled in various tasks, whereas the random forest based on ECFP4 performed the worst, with the average optimization decreasing by 27.9%. The DMPNN and GIN of FGS graph showed medium performance, and the GIN of the group graph performed the best, with the average optimization increasing by 7.7%. In addition, other substructure graph including the junction tree and pharmacophore graph exhibited inferior performance in predicting molecular properties compared to the atom graph [28], our results testified that group graph outperformed atom graph, FGS graph, junction tree, and pharmacophore graph when predicting molecular properties (Table S4).
Table 2.
The performance of predicting molecular properties via the GIN of the group graph and other baseline models
| Tasks | ESOL | FreeSolv | Lipo | QM7 | QM8 | BACE | BBBP | HIV | ClinTox | Aver.Opti |
|---|---|---|---|---|---|---|---|---|---|---|
| Metrics | RMSE ↓ | MAE ↓ | AUC_ROC ↑ | % ↑ | ||||||
| GIN (atom graph) |
0.881 ±0.062 |
1.31 ±0.16 |
0.720 ±0.048 |
66.9 ±3.0 |
0.012 ±0.0002 |
0.871 ±0.018 |
0.917 ±0.011 |
0.807 ±0.016 |
0.732 ±0.051 |
0 |
| RF (morgan) |
1.183 ±0.035 |
2.15 ±0.35 |
0.828 ±0.027 |
125.2 ±2.3 |
0.014 ±0.0002 |
0.826 ±0.020 |
0.792 ±0.034 |
0.657 ±0.009 |
0.526 ±0.030 |
− 27.9 |
| DMPNN |
0.698 ±0.032 |
1.19 ±0.18 |
0.637 ±0.037 |
72.3 ±3.0 |
0.012 ±0.0002 |
0.851 ±0.020 |
0.906 ±0.014 |
0.823 ±0.022 |
0.882 ±0.020 |
5.4 |
| GIN (motif-pretraining) |
0.790 ±0.094 |
1.35 ±0.11 |
0.669 ±0.051 |
68.1 ±2.6 |
0.012 ±0.0003 |
0.895 ±0.014 |
0.924 ±0.016 |
0.838 ±0.014 |
0.769 ±0.076 |
2.6 |
| GIN (FGS graph) |
0.750 ±0.064 |
1.25 ±0.15 |
0.679 ±0.022 |
57.0 ±2.8 |
0.012 ±0.0002 |
0.832 ±0.004 |
0.891 ±0.016 |
0.825 ±0.008 |
0.919 ±0.016 |
6.4 |
| GIN (FGS-pretraining) |
0.685 ±0.045 |
1.51 ±0.14 |
0.642 ±0.023 |
57.6 ±2.9 |
0.011 ±0.0003 |
0.897 ±0.015 |
0.923 ±0.013 |
0.827 ±0.011 |
0.903 ±0.026 |
6.6 |
| GIN (group graph) |
0.666 ±0.060 |
1.37 ±0.28 |
0.654 ±0.013 |
56.5 ±3.4 |
0.012 ±0.0002 |
0.886 ±0.015 |
0.931 ±0.006 |
0.821 ±0.016 |
0.904 ±0.031 |
7.7 |
The average values and 95% confidence intervals from 5-CV are reported. Aver. Opti is the average optimization of models relative to the GIN of the atom graph (Eq. 1)
Fig. 5.
Performance and efficiency of the models relative to the GIN of the atom graph in molecular property (MP) prediction. A Optimization of the GIN of motif-pretraining, FGS graph, FGS-pretraining and group graph to the GIN of the atom graph (Eq. 1); higher optimization means better performance than GIN of the atom graph. B Relative runtime of the GIN of motif-pretraining, FGS graph, FGS-pretraining and group graph to the GIN of the atom graph. A negative relative runtime means a shorter runtime than the GIN of the atom graph
Furthermore, compared with the GIN of the atom graph, the runtime of the GIN of FGS graph increased by 140%, and the extra time consumption reached approximately 3 days and 1 day in motif pretraining and FGS pretraining, respectively, whereas the group graph decreased the runtime by 30% (Fig. 5B, Table S5). The GIN of motif pretraining embeds local molecular characteristics into an atom graph via motif generation. The GIN of FGS-pretraining embeds molecular local characteristics via contrastive learning, and the GIN of the group graph can directly embed molecular local characteristics without pretraining because the molecular descriptors of the group are used as node features of the group graph. In conclusion, a group graph has a better and simpler representation of molecular global properties.
Two drugs were embedded in two GINs of the group graph, and the embeddings of the two drugs were subsequently concatenated and fed into a two-layer MLP for drug‒drug interaction prediction. The results of SimNN, DeepDDI, CASTER, PretrainGNN, and the GIN of FGS-pretraining were taken from a published paper [28]. The results of the GIN of the group graph were obtained under the same data split with the GIN of FGS-pretraining. The performance of the GIN of the group graph with no pretraining and the 3-layer raw GIN was slightly better than the GIN of FGS-pretraining in the two binary tasks of drug‒drug interaction prediction (Table 3). As shown in Fig. 2, FGS graph extracts functional groups as substructures to embed local molecular characteristics. However, common atoms would be contained in different substructures because atoms might be matched by different functional group patterns (Fig. S1), resulting in substructures in FGS graph being embedded by related features, which may be a disadvantage for model performance. Unlike FGS graph, the group graph extracted the most common substructures such as broken functional groups and aromatic rings as substructures, helping to highlight molecular differences and consistency.
Table 3.
Performance of predicting drug‒drug interactions via the GIN of the group graph and other baseline models
| Tasks | BIOSNAP | DrugBankDDI | ||||
|---|---|---|---|---|---|---|
| Metric | AUC_ROC↑ | PRC_AUC↑ | F1↑ | AUC_ROC↑ | AUC_PRC↑ | F1↑ |
| SimNN |
0.8530 ±0.0010 |
0.8480 ±0.0010 |
0.7140 ±0.0010 |
0.7860 ±0.0030 |
0.7530 ±0.0030 |
0.7090 ±0.0040 |
| DeepDDI |
0.8860 ±0.0010 |
0.8710 ±0.0070 |
0.8170 ±0.0070 |
0.8440 ±0.0030 |
0.8280 ±0.0020 |
0.7720 ±0.0060 |
| CASTER |
0.9100 ±0.0050 |
0.8870 ±0.0012 |
0.8430 ±0.0050 |
0.8610 ±0.0050 |
0.8290 ±0.0030 |
0.7960 ±0.0070 |
| PretrainGNN |
0.9948 ±0.0002 |
0.9939 ±0.0001 |
0.9607 ±0.0022 |
0.9716 ±0.0003 |
0.9668 ±0.0004 |
0.9172 ±0.0007 |
| GIN(FGS-pretraining) |
0.9957 ±0.0005 |
0.9940 ±0.0008 |
0.9795 ±0.0010 |
0.9792 ±0.0002 |
0.9755 ±0.0006 |
0.9343 ±0.0010 |
| GIN(group graph) |
0.9962 ±0.0002 |
0.9950 ±0.0003 |
0.9793 ±0.0015 |
0.9865 ±0.0004 |
0.9842 ±0.0007 |
0.9498 ±0.0011 |
The average values and 95% confidence intervals from three independent runs are reported
The good performance of the group graph for the prediction of molecular properties and drug‒drug interactions means that the group graph can retain molecular structural features with minimal information loss.
Matched molecular pair analysis based on group graph
Matched molecular pair analysis (MMPA) is a common tool for determining the structure–activity relationship, structure–property relationship and lead optimization, in which the changes in molecular activities or properties were attributed to the different local structures of the MMP. Substructure-level chemical fingerprints such as ECFP4 and MACCS bridge molecular substructure characteristics with molecular activities or properties, so they are usually used for MMPA [44]. However, machine learning models based on substructure-level chemical fingerprints seem to be inferior to the GNNs of molecular graphs in molecular property prediction [48]. The group graph excels in predicting molecular properties and representing local structures, providing a distinct advantage in the MMPA.
The Matched molecular pairs (MMPs) that were identified from BBBP, BACE and HIV are shown in Table 4. The prediction accuracy of the MMP is similar to the accuracy of the whole, and a limited number of MMPs with different molecular activities means that the change in one group makes it difficult to alter the molecular properties. The group importance for the molecular property is computed via Eqs. 3–5, and the change of group importance are evaluated via Eqs. 6–7.
Table 4.
Total number, true prediction number and label type of the MMPs from BBBP, BACE and HIV
| MMP Num | True prediction | Label by 0,0 | Label by 1,1 | Label by 0,1 | |
|---|---|---|---|---|---|
| BBBP | 278 | 276 | 25 | 227 | 24 |
| BACE | 718 | 574 | 316 | 226 | 32 |
| HIV | 9246 | 8528 | 8508 | 19 | 1 |
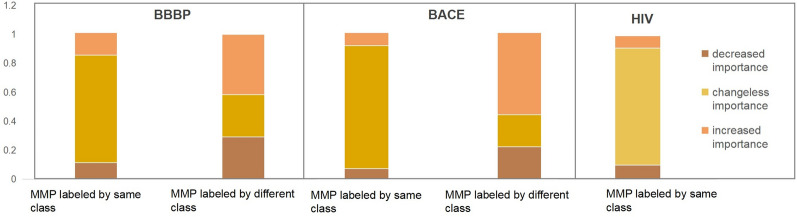
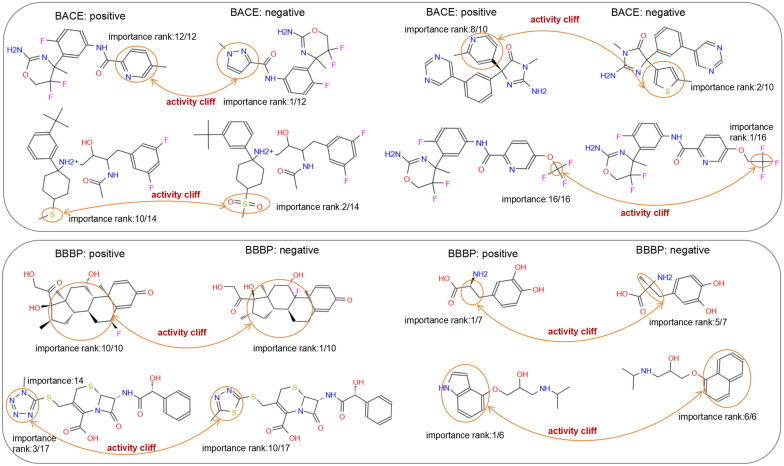
The changes in certain substructures that result in significant shifts in activity are referred to as activity cliffs, which are crucial for virtual screening [49] and cannot be accurately detected via atom-level molecular representations. As shown in Figs. 6 and 7, the group graph takes advantage of finding activity cliffs within the MMP. As shown in Fig. 6, MMPs, which have different groups with changeless importance and the same activity, account for 74%, 88% and 81% of BBBP, BACE and HIV, respectively, demonstrating that molecular activity does not change if the group is replaced by a group with changeless importance. MMPs, which have different groups with changed importance and different activities, are identified as containing activity cliffs, accounting for 71% and 89% of BACE and BBBP, respectively, which means that molecular activity might change if one group is replaced by another with changed importance. Some examples of MMP-containing activity cliffs in BBBP and BACE are shown in Fig. 7, and four types of activity cliffs are identified, including aromatic nuclei, R-groups, chirality, and functional group replacement.
Fig. 6.
The relationships between the change of the group importance and the change of molecular class label, in the matched molecular pair containing the only two different groups and same group number, from BACE and BBBP and HIV respectively
Fig. 7.
The change of group importance in eight matched molecular pairs (MMPs) with different activity (activity cliffs), MMP containing the only two different groups and same group number, from BBBP and BACE respectively
Quantitative structure‒property relationship analysis by group graph and atom graph
Central nervous system (CNS) disease is the second leading cause of death, and its treatment is still challenging due to selective permeability of the blood‒brain barrier. To address this issue, structural modification of blood‒brain barrier permeability (BBBP) should be a key consideration when designing CNS leads [50].
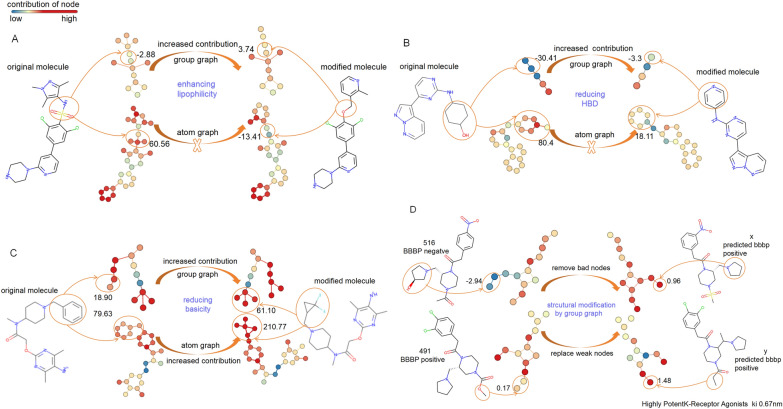
The detailed contributions of groups and atoms to BBBP are computed by the trained GIN of the group graph and atom graph (Fig. 8, Fig. S4). The modified substructures contribute larger to BBBP than the original substructure according to chemical explanations [51]. As shown in Fig. 8A, Replacing NS(=O)(=O) (SMILES of original substructure) with CO (SMILES of modified substructure) could enhance molecular lipophilicity and thus improve BBBP, indicating that CO contributes more to BBBP than NS(=O)(=O). The rule is followed by the GIN of the group graph but is objected to by the GIN of the atom graph. Similarly, replacing C1CCCCC1O with C1=CC=CC=N1 could reduce the number of hydrogen bond donors (HBDs), thus enhancing BBBP. The fact that C1=CC=CC=N1 makes a larger contribution (− 3.3) in BBBP than C1CCCCC1O (− 30.41) also follows this rule in the GIN of the group graph, but the GIN of the atom graph does not (Fig. 8B). Substituting (F)(F)C1CC1C with CC1=CC=CC=C1 could reduce basicity, which improves BBBP, and the fact that (F)(F)C1CC1C makes a larger contribution than CC1=CC=CC=C1 also follows this rule in both the GIN of the group graph and the atom graph (Fig. 8C).
Fig. 8.
Contribution of original substructures and modified substructures to BBBP, which was measured by the GIN of the atom graph and group graph separately. A Modified substructures enhance lipophilicity; B Modified substructures reduce HBD; C Modified substructures reduce basicity; D Structural modification for improving BBBP, which is predicted by the GIN of the group graph
As shown in Fig. 8D and Fig. S4D, we found out molecule 516, with negative BBBP, and molecule 491, with positive BBBP, and then computed their group contribution. The hydroxyl group in molecule 516 is predicted to have a negative contribution (− 0.96) to BBBP. Additionally, its neighboring substructure, N1CCCC1, is also affected, and its contribution to BBBP is − 1.98. In contrast, N1CCCC1 has a positive contribution (1.03) in a similar context to that of molecule 491, except that it lacks a hydroxyl group (Fig. S4D). These results suggest that the hydroxyl group in molecule 516 is a bad group for BBBP. By removing the bad hydroxyl group, the modified molecule was identified in PubChem (https://pubchem.ncbi.nlm.nih.gov/) and predicted to be positive for BBBP by the GIN of the group graph, although its property has not be experimentally confirmed yet. Moreover, replacing the weak contribution of the O (0.05) in the COC(=O) in molecule 491 with C, the modified molecule has been experimentally confirmed as a highly potent k-receptor agonist with a ki of 0.67 nM [52], aligning with the prediction of the GIN of the group graph (Fig. 8D).
Overall, with the combined consideration of context information and important substructures, the GIN of the group graph determines the contribution of each substructure to BBBP, providing instructions for local structural modification in quantitative structure‒property relationship analysis (QSPA).
Conclusions
A group graph is a substructure-level molecular representation that captures both local molecular characteristics and global structures. The substructures in the group graph come from two origins: one is 72 predefined broken functional groups, and the other is the aromatic rings and fatty carbon groups that are automatically extracted by an algorithm, enabling the group graph to adapt to unknown chemical structures. Furthermore, the substructures in the group graph have the smallest size, which is approximately one tenth or one percent of the substructure graph of BRICS, allowing for a group graph to cover a vast chemical space with reduced dimensionality. The GIN of a group graph has better performance in predicting molecular properties and drug‒drug interactions, with a shorter runtime than other molecular graphs do, which means that a group graph efficiently and accurately represents molecular global structures.
Unlike some black-box machine learning models, the GIN of a group graph is interpretable. The effect of group transformation on molecular properties is measured by the MMPA of group graph, and activity cliffs are subsequently identified. Since molecular optimization often involves altering groups to improve key properties such as bioavailability, solubility, or target specificity, the contributions of groups predicted by the GIN of a group graph can guide molecular optimization.
Supplementary Information
Acknowledgements
The authors acknowledge open-source tools used in this work. The numerical calculations in this paper have been done on Hefei advanced computing center.
Author contributions
Piao-Yang Cao developed the idea, methodology and the framework of the manuscript. Yang He helped to improve the idea and code. Ming-Yang Cui edited the manuscript. Xiao-Min Zhang prepared data and coded. Qingye Zhang reviewed and edited the manuscript. Hong-Yu Zhang supervised the study and provided funding. All authors contributed to the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant 31870837, Grant 32471294), and the Fundamental Research Funds for the Central Universities (Grant 2662024SZ006).
Availability of data and materials
The code, foundational model, trained models, and associated datasets can be accessed at our GitHub repository: https://github.com/piaoyang1992/group-graph.git.
Declarations
Ethics, consent to participate, and consent to publish declarations
Not applicable.
Competing interests
The author declares no competing interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Schuhmacher A, Gatto A, Hinder M, Kuss M, Gassmann O (2020) The upside of being a digital pharma player. Drug Discov Today 25:1569–1574 [DOI] [PubMed] [Google Scholar]
- 2.Chen W, Liu X, Zhang S, Chen S (2023) Artificial intelligence for drug discovery: resources, methods, and applications. Mol Ther Nucleic Acids 31:691–702 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Medina-Franco JL, Chávez-Hernández AL, López-López E, Saldívar-González FI (2022) Chemical multiverse: an expanded view of chemical space. Mol Inform 41:e2200116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jiang D, Wu Z, Hsieh CY, Chen G, Liao B, Wang Z, Shen C, Cao D, Wu J, Hou T (2021) Could graph neural networks learn better molecular representation for drug discovery? A comparison study of descriptor-based and graph-based models. J Cheminform 13:12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Flam-Shepherd D, Zhu K, Aspuru-Guzik A (2022) Language models can learn complex molecular distributions. Nat Commun 13:3293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wigh DS, Goodman JM, Lapkin AA (2022) A review of molecular representation in the age of machine learning. Wires Comput Mol Sci 12:e1603 [Google Scholar]
- 7.Li Z, Jiang M, Wang S, Zhang S (2022) Deep learning methods for molecular representation and property prediction. Drug Discov Today 27:103373 [DOI] [PubMed] [Google Scholar]
- 8.Meyers J, Fabian B, Brown N (2021) De novo molecular design and generative models. Drug Discov Today 26:2707–2715 [DOI] [PubMed] [Google Scholar]
- 9.Wang NN, Zhu B, Li XL, Liu S, Shi JY, Cao DS (2024) Comprehensive review of drug-drug interaction prediction based on machine learning: current status, challenges, and opportunities. J Chem Inf Model 64:96–109 [DOI] [PubMed] [Google Scholar]
- 10.Danishuddin KAU (2016) Descriptors and their selection methods in QSAR analysis: paradigm for drug design. Drug Discov Today 21:1291–1302 [DOI] [PubMed] [Google Scholar]
- 11.Karpov P, Godin G, Tetko IV (2020) Transformer-CNN: Swiss knife for QSAR modeling and interpretation. J Cheminform 12:17 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hartog PBR, Krüger F, Genheden S, Tetko IV (2024) Using test-time augmentation to investigate explainable AI: inconsistencies between method, model and human intuition. J Cheminform 16:39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yang J, Cai Y, Zhao K, Xie H, Chen X (2022) Concepts and applications of chemical fingerprint for hit and lead screening. Drug Discov Today 27:103356 [DOI] [PubMed] [Google Scholar]
- 14.Rataj K, Czarnecki W, Podlewska S, Pocha A, Bojarski AJ (2018) Substructural connectivity fingerprint and extreme entropy machines-a new method of compound representation and analysis. Molecules 23:1242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cai H, Zhang H, Zhao D, Wu J, Wang L (2022) FP-GNN: a versatile deep learning architecture for enhanced molecular property prediction. Brief Bioinform 23:bbac408 [DOI] [PubMed] [Google Scholar]
- 16.Jinsong S, Qifeng J, Xing C, Hao Y, Wang L (2024) Molecular fragmentation as a crucial step in the AI-based drug development pathway. Commun Chem 7:20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ghersi D, Singh M (2014) molBLOCKS: decomposing small molecule sets and uncovering enriched fragments. Bioinformatics 30:2081–2083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu T, Naderi M, Alvin C, Mukhopadhyay S, Brylinski M (2017) Break down in order to build up: decomposing small molecules for fragment-based drug design with eMolFrag. J Chem Inf Model 57:627–631 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Marco P, Davide B, Alessio M (2020) A deep generative model for fragment-based molecule generation. PMLR 108:2240–2250 [Google Scholar]
- 20.Zhang Z, Liu Q, Wang H, Lu C, Lee CK (2021) Motif-based graph self-supervised learning for molecular property prediction. NeurIPS 34:15870–15882 [Google Scholar]
- 21.Diao Y, Hu F, Shen Z, Li H (2023) MacFrag: segmenting large-scale molecules to obtain diverse fragments with high qualities. Bioinformatics 39:btad012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vangala SR, Krishnan SR, Bung N, Srinivasan R, Roy A (2023) pBRICS: a novel fragmentation method for explainable property prediction of drug-like small molecules. J Chem Inf Model 63:5066–5076 [DOI] [PubMed] [Google Scholar]
- 23.Jin W, Barzilay R, Jaakkola T (2018) Junction tree variational autoencoder for molecular graph generation. In: ICML, pp 2323–2332
- 24.Jin W, Yang K, Barzilay R, Jaakkola T (2019) Learning multimodal graph-to-graph translation for molecular optimization. arXiv:1812.01070
- 25.Chen Z, Min MR, Parthasarathy S, Ning X (2021) A deep generative model for molecule optimization via one fragment modification. Nat Mach Intell 3:1040–1049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jin W, Barzilay R, Jaakkola T (2020) Hierarchical generation of molecular graphs using structural motifs. arXiv:2002.03230
- 27.Stiefl N, Watson IA, Baumann K, Zaliani A (2006) ErG: 2D pharmacophore descriptions for scaffold hopping. J Chem Inf Model 46:208–220 [DOI] [PubMed] [Google Scholar]
- 28.Ji Z, Shi R, Lu J, Li F, Yang Y (2022) ReLMole: molecular representation learning based on two-level graph similarities. J Chem Inf Model 62:5361–5372 [DOI] [PubMed] [Google Scholar]
- 29.Kengkanna A, Ohue M (2024) Enhancing property and activity prediction and interpretation using multiple molecular graph representations with MMGX. Commun Chem 7:74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jiang Y, Jin S, Jin X, Xiao X, Wu W, Liu X, Zhang Q, Zeng X, Yang G, Niu Z (2023) Pharmacophoric-constrained heterogeneous graph transformer model for molecular property prediction. Commun Chem 6:60 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Keyulu X, Weihua H, J Leskovec, Stefanie J (2019) How powerful are graph neural networks? arXiv:1810.00826
- 32.Wieder O, Kohlbacher S, Kuenemann M, Garon A, Ducrot P, Seidel T, Langer T (2020) A compact review of molecular property prediction with graph neural networks. Drug Discov Today Technol 37:1–12 [DOI] [PubMed] [Google Scholar]
- 33.Xiao Z, Morris-Natschke SL, Lee KH (2016) Strategies for the optimization of natural leads to anticancer drugs or drug candidates. Med Res Rev 36:32–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ruddigkeit L, van Deursen R, Blum LC, Reymond JL (2012) Enumeration of 166 billion organic small molecules in the chemical universe database GDB-17. J Chem Inf Model 52:2864–2875 [DOI] [PubMed] [Google Scholar]
- 35.van Santen JA, Jacob G, Singh AL, Aniebok V, Balunas MJ, Bunsko D, Neto FC, Castaño-Espriu L, Chang C, Clark TN, Cleary Little JL, Delgadillo DA, Dorrestein PC, Duncan KR, Egan JM, Galey MM, Haeckl FPJ, Hua A, Hughes AH, Iskakova D, Khadilkar A, Lee JH, Lee S, LeGrow N, Liu DY, Macho JM, McCaughey CS, Medema MH, Neupane RP, O’Donnell TJ, Paula JS, Sanchez LM, Shaikh AF, Soldatou S, Terlouw BR, Tran TA, Valentine M, van der Hooft JJJ, Vo DA, Wang M, Wilson D, Zink KE, Linington RG (2019) The natural products atlas: an open access knowledge base for microbial natural products discovery. ACS Cent Sci 5:1824–1833 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wu Z, Ramsundar B, Feinberg EN, Gomes J, Geniesse C, Pappu AS, Leswing K, Pande V (2017) MoleculeNet: a benchmark for molecular machine learning. Chem Sci 9:513–530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Marinka Z, Sosic, Rok S, Sagar M, Jure L (2018) BioSNAP datasets: Stanford biomedical network dataset collection. http://snap.stanford.edu/biodata
- 38.Wishart DS, Knox C, Guo AC, Cheng D, Shrivastava S, Tzur D, Gautam B, Hassanali M (2008) DrugBank: a knowledgebase for drugs, drug actions and drug targets. Nucleic Acids Res 36:D901–D906 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yang K, Swanson K, Jin W, Coley C, Eiden P, Gao H, Guzman-Perez A, Hopper T, Kelley B, Mathea M, Palmer A, Settels V, Jaakkola T, Jense K, Barzilay R (2019) Analyzing learned molecular representations for property prediction. J Chem Inf Model 59:3370–3388 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Vilar S, Uriarte E, Santana L, Lorberbaum T, Hripcsak G, Friedman C, Tatonetti NP (2014) Similarity-based modeling in large-scale prediction of drug-drug interactions. Nat Protoc 9:2147–2163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang Y, Min Y, Chen X, Wu J (2021) Multi-view graph contrastive representation learning for drug-drug interaction prediction. In: WWW’21, pp 2921–2933
- 42.Huang K, Xiao C, Hoang T, Glass L, Sun JC (2020) CASTER: predicting drug interactions with chemical substructure representation. Proc AAAI Conf Artif Intell 34:702–709 [Google Scholar]
- 43.Hu W, Liu B, Gomes J, Zitnik M, Liang P, Pande V, Leskovec L (2020) Strategies for pre-training graph neural networks. arXiv:1905.12265
- 44.Yang Z, Shi S, Fu L, Lu A, Hou T, Cao D (2023) Matched molecular pair analysis in drug discovery: methods and recent applications. J Med Chem 66:4361–4377 [DOI] [PubMed] [Google Scholar]
- 45.Pope PE, Kolouri S, Rostami M, Martin CE, Hoffmann H (2019) Explainability methods for graph convolutional neural networks. In: CVPR, pp 10772–10781
- 46.Matthias F, Jan EL (2019) Fast graph representation learning with pytorch geometric. arXiv:1903.02428
- 47.Wang M, Zheng D, Ye Z, Gan Q, Li M, Song X, Zhou J, Ma C, Yu L, Gai Y (2019) Deep graph library: a graph-centric, highly-performant package for graph neural networks. arXiv:1909.01315
- 48.Ren GP, Wu KJ, He Y (2023) Enhancing molecular representations via graph transformation layers. J Chem Inf Model 63:2679–2688 [DOI] [PubMed] [Google Scholar]
- 49.van Tilborg D, Alenicheva A, Grisoni F (2022) Exposing the limitations of molecular machine learning with activity cliffs. J Chem Inf Model 62:5938–5951 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Patel MM, Patel BM (2017) Crossing the blood-brain barrier: recent advances in drug delivery to the brain. CNS Drugs 31:109–133 [DOI] [PubMed] [Google Scholar]
- 51.Xiong B, Wang Y, Chen Y, Xing S, Liao Q, Chen Y, Li Q, Li W, Sun H (2021) Strategies for structural modification of small molecules to improve blood-brain barrier penetration: a recent perspective. J Med Chem 64:13152–13173 [DOI] [PubMed] [Google Scholar]
- 52.Zhang WY, Maycock AL, Marella MA, Kumar V, Gaul F, Guo DQ (2001) Kappa agonist compounds, pharmaceutical formulations and method of prevention and treatment of pruritus therewith. US Patent 20,010,803,957
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The code, foundational model, trained models, and associated datasets can be accessed at our GitHub repository: https://github.com/piaoyang1992/group-graph.git.