How to handle high subgenome sequence similarity in allopolyploid Fragaria x ananassa: linkage disequilibrium based variant filtering

Abstract

Background

The allo-octoploid Fragaria x ananassa follows disomic inheritance, yet the high sequence similarity among its subgenomes can lead to misalignment of short sequencing reads (150 bp). This misalignment results in an increased number of erroneous variants during variant calling. To accurately associate traits with the appropriate subgenome, it is essential to filter out these erroneous variants. By classifying variants into correct (type 1) and erroneous types (homoeologous variants—type 2, and multi-locus variants—type 3), we can improve the reliability of downstream analyses.

Results

Our analysis reveals that while erroneous variant types often display skewed average allele balances (AAB) for heterozygous calls, this measure alone is insufficient. To mitigate the erroneous variants further, we employed a Linkage Disequilibrium (LD) based filtering method that correlates highly (99%) with an approach that utilizes a genetic map from a biparental population. This combined filtering strategy—using both LD-based and average allele balance methods—resulted in the lowest switch error rate (0.037). Notably, our best filtering approach decreased phasing switch error rates by 44% and preserved 72% of the original dataset.

Conclusions

The results indicate that identifying erroneous variants due to subgenome similarity can be effectively achieved without extensive genotyping of mapping populations. By implementing the LD-based filtering method, the phasing accuracy improved which improves the tracability of important alleles in the germplasm, paving the way for better understanding of trait associations in F. x ananassa.

Supplementary Information

The online version contains supplementary material available at 10.1186/s12864-024-10987-8.

Background

In the current era, molecular tools have become an important part of commercial breeding. Using genomic selection for making breeding decisions can accelerate breeding success and therefore can give competitive advantages to breeding companies [1]. As every breeding program has its unique germplasm, it is important to utilize genotyping techniques that can identify the whole genetic diversity of the germplasm. Fortunately, Whole Genome Sequencing (WGS) can do this, and as technology improves and patents expire, it is becoming affordable for individual breeding programs. For many crops (like vegetable or staple crops) molecular breeding and WGS are already utilized, however, less economically important crops and crops with more complicated genetic structures are now also moving towards WGS-based molecular breeding.

One of these crops is the garden strawberry: Fragaria × ananassa Duchesne ex Rozier (2n = 8x = 56) [2]. Because of its polyploid nature, advancements in molecular breeding for F. x ananassa have consistently lagged behind those for diploid organisms. F. x ananassa consistently follows a disomic inheritance in linkage mapping studies which makes many bioinformatic tools developed for diploid crops compatible with F. x ananassa [3]. Although the adoption of molecular tools was initially rather slow in F. x ananassa, it is now rapidly increasing: for example, Single Nucleotide Polymorphism (SNP) arrays were the first high-throughput genotyping platforms (since 2015) available for F. x ananassa [4–6]. Its first genome was sequenced and assembled in 2019 and multiple other genomes have been sequenced and assembled since then, making WGS a viable genotyping strategy for F. x ananassa [7–10].

A typical WGS bioinformatic pipeline consists of alignments of the sequencing reads to a reference genome followed by a variant calling step. However, the allopolyploid nature of F. x ananassa makes the alignment of sequencing reads (WGS data) more challenging due to the high similarity of its subgenomes. This can result in partial misalignment of sequencing reads, which can give problems when calling variants (variant discovery). As a result, erroneous variants can be discovered, e.g., variants that may be wrongly attributed to a homoeologous subgenome (i.e., all sequencing reads from subgenome A align on subgenome B), or variants that seem to be polymorphic (because reads from two or more subgenomes are aligning on the same subgenome). In summary, we can classify variants that result from a diploid WGS variant calling pipeline in F. x ananassa into three main types:

1. Accurate variants on the biologically correct chromosome and subgenome: reads align on the same chromosome and subgenome as they originate from (correct variants).

2. Erroneous variants from another subgenome: reads align on a different subgenome than they originate from (homoeologous variants).

3. Erroneous variants: resulting from reads with multiple origins with varying read numbers (multi-locus variants).

Genome-wide association studies (GWAS) are often used to find associations between traits and genetic variants, also in F. x ananassa [11, 12]. The resulting Manhattan plots are illustrative for different variant types, where in a regular diploid situation only a single peak is expected for a single Quantitative Trait Locus (QTL). However, in allopolyploid F. x ananassa, a single QTL typically results in multiple other significant SNPs on homoeologous subgenomes. These may caused by type 2 variants, that are wrongly assigned on homoeologous chromosomes which subsequently can be misidentified as significant SNPs for separate (or homoeo-) QTLs while they are in high linkage disequilibrium (LD) with the SNPs in the main peak on another subgenome and as such only represent a single QTL. An example of this can be found in Saiga et al. [11], where the Manhattan plot of a WGS-based GWAS on the everbearing locus in F. x ananassa shows significant associations for SNPs on multiple homoeologous chromosomes. Here, the authors correctly did not identify the other peaks as true QTLs on different Fvb4 homoeologes, as the main QTL on Fvb4-4 contained 5640 candidate SNPs compared to 59–82 candidate SNPs on the other homoeologs [11]. Another method to filter out these false QTL signals is by fitting the main QTL as a fixed effect in the GWAS model because false QTL signals will not explain additional variation in the trait [13]. Both methods are a way to identify true QTL signals, but other additional filtering criteria are required to mitigate these issues in other genomic analyses. For instance, these erroneous variants could potentially be a major problem in allele phasing resulting in wrong haplotypes and subsequently lower imputation accuracies because wrong haplotypes are imputed [14].

Erroneous variants can be partially identified by genotyping mapping populations and subsequently verifying the variant’s segregation [15]. For example, a linkage map based on sequencing reads of the mapping population Holiday × Korona was constructed for all chromosomes except chromosome 7C, and type 2 variants were identified [16]. As such, this could give a valid indication of the number of erroneous type 2 variants expected. However, in a breeding setting such an approach will not be practical nor cost-effective and an alternative method needs to be developed that could be validated using the linkage map approach.

A possible alternative route for identifying these erroneous variants could be investigating the Allele Balance (AB) of heterozygous variants. The Allele Balance (AB) of heterozygous variants is calculated as the ratio of reference reads to the total number of reads at a specific variant site [17]. A general estimate of AB for a single variant can be obtained by averaging its AB values across all individuals, resulting in an Average Allele Balance (AAB) value for each variant. However, this may involve a variable number of contributing individuals per variant as the frequency of heterozygous individuals differs per variant. Yet it can provide a useful indication of the chances that a variant is erroneous. Variants in regions that are highly similar to regions in other subgenomes may show a skewed allele balance, as reads can potentially align to multiple subgenomes. This may lead to reads originating from multiple homoeologous subgenomes aligning to a single subgenome. The final AAB depends then on how similar the reads are to each part of the different subgenomes, the reference genome quality, and its similarity to the aligned genotype.

In addition, Linkage Disequilibrium (LD) among the variants in a diversity panel is also able to position markers on a genome by utilizing markers that are anchored on the genome [18]. A similar rationale can be followed for identifying erroneous variants in allopolyploid strawberry. Strawberry shows disomic inheritance which means for most cases that variants on different subgenomes are expected to have low LD values with each other. On the other hand, variants that originate from the same haplotype are physically linked and are expected to show high LD values and a consistent decay with increasing genetic distance. This means that correct variants (type 1) are expected to show high LD values being variants from the same subgenome. On the other hand, variants from different subgenomes are expected to show low LD values and can be identified as erroneous. Identification of the two erroneous variant types is possible because type 2 variants (homoeologous variants) will have higher LD values with variants on another homoeologous subgenome and type 3 variants (multi-locus variants) will have lower LD values and fewer variants that are in LD with them. Type 3 variants will be the hardest to detect because of the many different possibilities.

This study explored how many erroneous SNPs occurred in allopolyploid F. x ananassa by investigating average allelic balance and LD-based filtering methods in a mapping population and a diversity panel. Specific filtering methods were proposed for identifying these variants so these could be filtered out for downstream analyses. In addition, it was investigated whether some regions or subgenomes were more likely to have a higher density of erroneous variants than others. The filtering methods were subsequently validated by phasing the (filtered) SNP datasets and calculating the switch error rate.

Methods

Genotypic data

A diversity panel (n = 136) from the Fresh Forward B.V. breeding population and a biparental mapping population (Holiday × Korona, n = 46) were resequenced (Illumina Paired-End 150 bp). DNA was isolated using a modified CTAB procedure, then multiplexed and sequenced by BGI Genomics (Shenzen, China). The individuals in the diversity panel had an average depth of 22x, where 124 had a mean depth > 15x, 5 individuals had a mean depth between 10x and 15x, and 7 individuals had a mean depth below 5x. The H × K population had an average depth of 27x (ranging from 8x to 56x). Variant Call Format (VCF) files were obtained by aligning the 150 bp paired-end Illumina resequencing reads to the reference genome farr1 (Royal Royce) by using minimap2 (v2.24) with the -ax sr preset (the short reads option). Then sambamba (v1.0.0) was used to convert the SAM output from minimap2 into BAM format, while simultaneously filtering out unmapped reads using the filter -F “(not unmapped)”, the reads were then sorted by using samtools sort (v1.9). Bcftools (v1.9) mpileup (using -B option) and call (using the multiallelic caller: -mv ) were used for variant calling to obtain the final VCF files [8, 19, 20]. In the variant calling step, also 321 other individuals were included (for which sequencing data was available from different breeding programs, all external material) to increase the variant detection accuracy. Then, biallelic SNPs were extracted from these VCF files and filtered on strict quality criteria: INFO/QUAL > 998, INFO/MAPQ > 55, INFO/DP > 7000, INFO/DP < 18,000, and MAF > 0.05. The 321 extra individuals for variant calling and quality filtering were removed for downstream analyses due to their genetic distance or overrepresented genetic variation to the selected diversity panel (e.g., external material, mapping populations, or wild material) resulting in the 136 individuals. Both, the variant and individual filtering were done using bcftools (v1.16). The genetic diversity of the diversity panel was assessed by using a principal components analysis (using PCA from the sklearn package in python) on 140,000 variants (5000 randomly selected SNPs per chromosome, 136 individuals), missing variant calls were imputed by the mean of all variant calls to limit their influence on the analysis.

Exploring problematic SNPs in a biparental mapping population

A valid question is how many variants are erroneous when using resequencing data and a standard diploid variant calling pipeline. This was explored by investigating the segregation patterns in a mapping population. To compare the validity of our approach we used an already available genetic map for the Holiday × Korona (H × K) population (chromosome 7 C is lacking). This genetic map consisted of marker bins, where co-segregating markers were put in the same bin, and bins with ≥ 40 markers were retained [16].

Then, we extracted all SNPs where at least Holiday or Korona was heterozygous to obtain all segregating SNPs for this population. Allele balance was computed per heterozygous call for these SNPs and subsequently, the average allele balance (AAB) of heterozygous calls was calculated per SNP. Linkage Disequilibrium (LD) within the H × K population was estimated as squared Pearson correlation coefficients (r²) between each of the remaining SNPs (5.5 M) and all marker bins (6478) from the genetic map [16]. For each SNP, the marker bin with the highest LD was kept and only SNPs where retained that had an LD value > 0.5 with a marker bin.

Filtering method 1: average allele balance (diversity panel)

Segregation patterns in mapping populations can provide useful information on erroneous variants but the translation to diversity panels is crucial to assert all variants (i.e., the variants that are homozygous in / not segregating in selected mapping populations) for downstream genomic analyses in breeding practices. Therefore, the average allele balance (AAB) was computed for the diversity panel. For each heterozygous call, the allele balance was calculated as reference allele count divided by the total allele count by a custom bash script (Supplementary Information, Script1_AAB.sh). Then, these allele balances were averaged per variant over all individuals in the population to obtain a single average allele balance value per variant. Due to the varying MAF of each variant, the average allele balance for each SNP is based on a varying number of heterozygous calls.

The high sequence similarity between subgenomes in strawberry can cause misalignment of reads, where reads originating from multiple homoeologous subgenomes align to a single subgenome. This misalignment may lead to deviations in the average allelic balance from the expected 0.5 ratio (1:1, AB, 50% reference reads and 50% alternative reads). Depending on the sequence similarity among homoeologous chromosomes, various skewed allelic balance (AAB) values can be expected, such as 0.875 (7:1, AAAAAAAB), 0.833 (5:1, AAAAAB), 0.75 (3:1, AAAB), and 0.667 (4:2, AAAABB).

Filtering method 2: LD-based subgenome prediction and position estimation (diversity panel)

For computing LD values and estimating the best sub-chromosome for each SNP, we developed a custom Python pipeline (Supplementary Figure S1). It uses two datasets as input: an “anchor” set of SNPs and a dataset with all SNPs that need checking (target set). A naive approach is to compute pairwise LD estimates for all SNPs available. However, to reduce the computational complexity of this problem we defined an anchor set. The SNPs in the anchor set are used to predict the chromosome and position of all SNPs in the target set. Therefore, these need to be carefully selected or the number of SNPs needs to be large enough so that the correct SNPs limit the impact of erroneous SNPs on chromosome and position predictions. In this study, we chose the latter option, so we randomly selected 5000 SNPs per chromosome as the anchor set, which resulted in a total of 140,000 SNPs over the 28 chromosomes. Variant calls were extracted for both the anchor set and the target set for all 28 chromosomes.

Before computing the LD values, the SNPs were filtered on minor allele frequency (MAF > 0.05, corresponding to minor allele count (MAC) > 13) because rare SNPs do not provide enough information for accurate LD estimation. LD values were then computed for each SNP with all SNPs in the anchor set and subsequently filtered on LD < 0.3. The LD values were then squared to mitigate the effect of large numbers of SNPs with low LD. The squared LD values were summed per chromosome to estimate the correct chromosome, e.g., the chromosome with the highest sum of squared LD values (SSLD). For type 1 (correct variants) and type 2 variants (homoeologous variants), the correct chromosome is expected to have a much higher SSLD than the other chromosomes because it should have high LD values for many SNPs. Hence, the predicted chromosome for each SNP is the chromosome with the highest SSLD. However, type 3 variants are expected to have lower LD values in general but could also have LD values > 0.3 with SNPs on different homoeologous chromosomes or perhaps even completely different chromosomes due to the overrepresentation of heterozygous variant calls. So, type 3 variants are not only expected to not have a single chromosome with a much higher SSLD than other chromosomes but also to have lower SSLD values in general. To distinguish between type 1 and type 2 versus type 3 variants, the ratio of the SSLD for the best chromosome to the total SSLD of all chromosomes was computed. SNPs that have this ratio (> 0.8) were retained for downstream analyses, which means that the SSLD of the best chromosome is at least 4 times higher than the SSLD of all other chromosomes combined. Most of the time variants will be predicted on the same or a different subgenome, but sometimes another chromosome will have the highest SSLD ratio. Therefore, we preferred the term “predicted chromosome” in this paper, which most of the time will be a predicted subgenome.

Effect of filtering methods on phasing the diversity panel

Filtering type 2 (homoeologous variants) and type 3 (multi-locus) variants out of the set of used variants is crucial for downstream analyses. One way to assess the effectiveness of different filtering options for type 2 and 3 variants could be assessed by phasing the variants and subsequently computing the phasing accuracy. Four different datasets were obtained from the > 9.2 M SNPs (after quality filtering) from the diversity panel by the following filtering combinations: no filtering (Standard), filtering on average allele balance (AAB), LD-based filtering (LD), and a combination of both methods (AAB + LD) (Table 1). These were then phased with SHAPEIT5 (phase_common) in default settings, except for MAF (filter-maf), to exclude rare variants with MAF < 0.05, and effective population size (hmm-ne) which was set to 50 [21].

Table 1.

Overview of the filtering methods that were used on SNPs before phasing with SHAPEIT5

Filtering method	Description
Standard	No filtering
AAB	AAB > 0.35, AAB < 0.65
LD	Ratio of SSLD > 0.8, highest SSLD on the same chromosome
AAB + LD	AAB > 0.35, AAB < 0.65, ratio of SSLD > 0.8, highest SSLD on the same chromosome

In the context of phasing, the switch error rate (SER) is often used as a measure of phasing accuracy [14]. Therefore, filtering methods that successfully filter for type 2 and 3 variants are expected to show a lower SER compared to when no filtering is applied. Vice versa, if filtering methods are not successful in filtering for these variant types, a similar SER to the scenario with no filtering is expected. A total of 36 duos and trios were present in the diversity set (n = 136) and were used to assess phasing accuracy by calculating the switch error rate of heterozygous variants by employing the SHAPEIT5_switch command. Before phasing, parents of the duos and trios were excluded from the dataset so that the offspring were phased regardless of their parental genomes. Consequently, 14 duos and trios were removed because some offsprings of these duos and trios were parents of others, resulting in 22 duos and trios for which the switch error rate was computed.

LD decay patterns of different variant types

LD decay patterns can give insight into what type of variants the SNPs are. LD values are generally expected to gradually decrease the further away linked variants are located from the investigated variant (type 1 variants), with the speed of this decay depending on linkage decay. A set of four representative variants was chosen based on LD-based prediction in both the mapping population (highest r² with best marker bin) and the diversity panel (highest SSLD and minimum of 0.8 for the ratio SSLD to the total SSLD). Four other variants were chosen to showcase type 2 and 3 variants. The LD decay was then computed using LD values of the SNPs with all SNPs in the anchor set.

Results

Mapping population

Type 2 and 3 variants in a mapping population

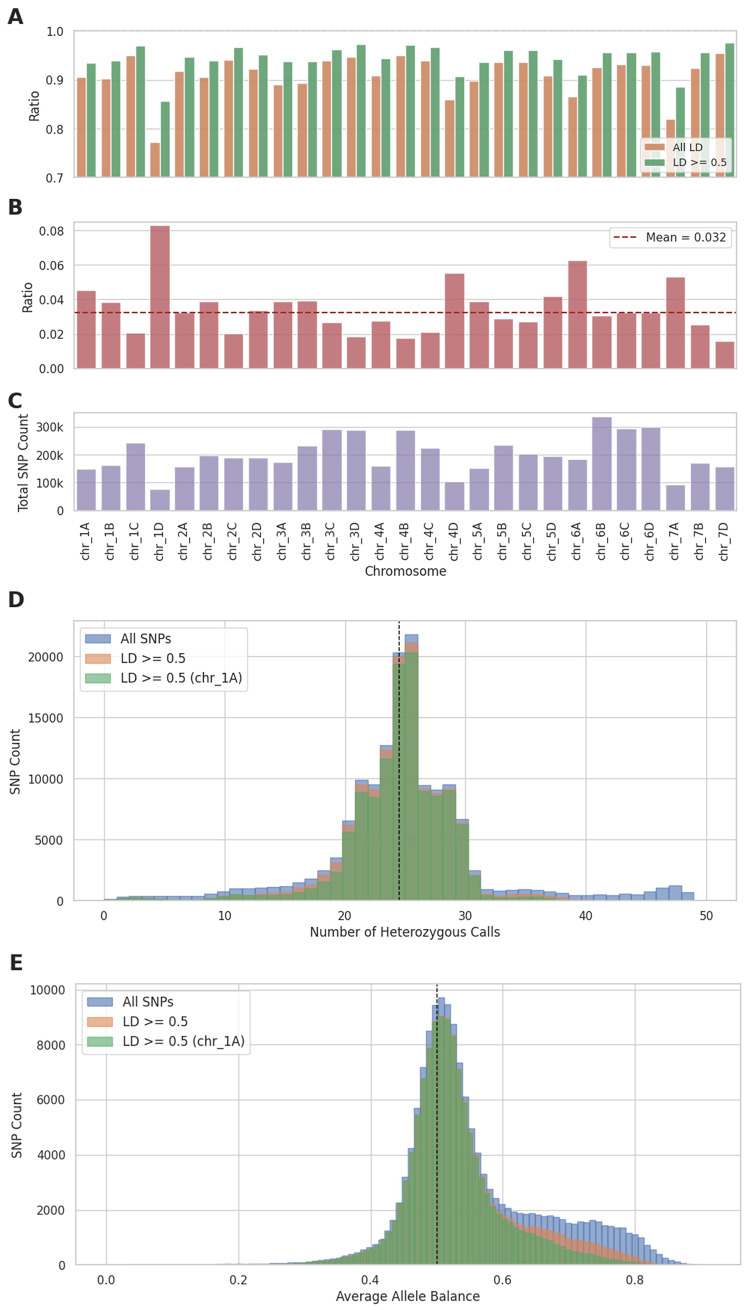
To investigate type 2 and 3 variants in a mapping population, all SNPs that segregated in the H × K population and that complied with the quality filtering criteria were selected. LD values were computed for all SNPs with representative SNPs of all the marker bins from the genetic map on all chromosomes except chr_7C [16]. The LD could not be calculated for 10.1% of the variants which are erroneous and could be type 3 variants, due to lack of variation (e.g., all offspring genotypes are heterozygous but also one of the parents is heterozygous which means the SNP was marked as segregating SNP). Of the remaining SNPs, 92% had the highest LD with a marker bin on the same chromosome, where it was originally discovered (type 1 variants). There were no chromosomes that deviated much from this percentage, except for chr_1D or chr_7A (Fig. 3A) where the percentage of SNPs with the highest LD with a marker bin on the same chromosome was somewhat lower (around 80%). When the SNPs were filtered more stringently on a minimum of 0.5 LD, the percentage of SNPs that had the highest LD with a marker bin on the same chromosome increased to 95.1% whereas the percentage of SNPs without a predicted marker bin increased to 18.6%.

Fig. 3.

Figures regarding the Holiday × Korona mapping population. (A) The ratio between all SNPs and the number of SNPs that have the highest LD with a marker bin on the same chromosome (All LD), and the ratio of SNPs that have an LD value ≥ 0.5 with the best marker bin on the same chromosome (LD ≥ 0.5). (B) The ratio of the number of SNPs that have the highest r² (≥ 0.5) with a marker bin on a homoeologous chromosome to the total number of SNPs per chromosome. The dashed brown line represents the mean of this ratio over all chromosomes. (C) The total number of segregating SNPs in the H × K population per chromosome. D, E) Histograms of the number of SNPs that are heterozygous in at least Holiday (P1) or Korona (P2) plotted against the number of heterozygous calls per SNP (figure D) and their Average Allele Balance (figure E). All SNPs assessed without selection are in blue (no filter), from these, all SNPs that have r² > 0.5 with a marker bin (on any chromosome) are in orange. From these SNPs in orange, the SNPs that have r² > 0.5 with a marker bin on chr_1A are depicted in green

The ratio of SNPs with the highest LD with a marker bin on a homoeologous chromosome was computed to investigate how many SNPs were type 2 variants and therefore were assigned to a different (sub) chromosome. The mean of this ratio (over all chromosomes) was 0.032. This means that we could classify 3.2% of all the SNPs that had an LD value ≥ 0.5 with a marker bin on a homoeologous chromosome as type 2 variants (Fig. 3B). Chr_1D, chr_4D, and chr_7A stood out because of their high ratio but these had relatively low SNP numbers which were due to stretches of homozygosity in the H × K population [22]. Additionally, chr_6A also showed an elevated ratio of type 2 variants and compared to the other subgenomes of chromosome 6, it also had a lower total SNP number.

Positions of variants that belong on homoeologous chromosomes

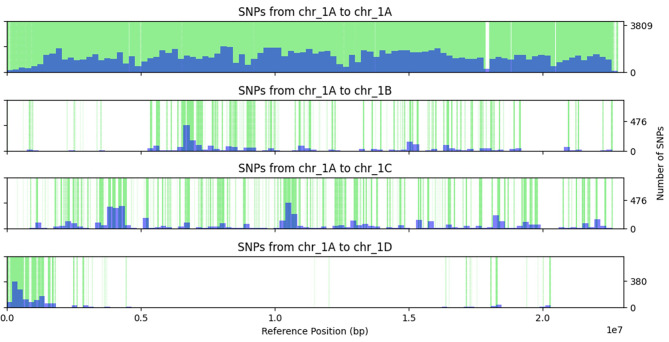
To get an idea of whether some regions showed a higher density of variants that belonged on other homoeologous chromosomes, the LD values for each SNP that had the highest LD value with a marker bin located on a homoeologous chromosome were plotted against the position where the variant was originally discovered. Figure 1 shows the distribution of chromosome 1 A variants over the homoeologous chromosomes based on the LD-based predictions, e.g., at the top of chr_1A many variants had the highest LD values with a marker bin on chr_1D whereas the rest of the chromosome did not have many variants that seemed to belong on chr_1D. In general, it seemed that type 2 variants clustered together in regions, although large regions were observed where no SNPs were predicted to homoeologous chromosomes.

Fig. 1.

Occurrence of SNPs that are originally discovered on chr_1A and, based on the mapping population, have the highest r² (r² ≥ 0.5) to a marker bin on chr_1A or a homoeologous chromosome (green vertical lines). Density is plotted as histogram in blue

Heterozygous calls and average allele balance

The segregation ratios in the mapping population may provide insights into the quality of the variants. The expected segregation ratios of unique SNPs in a diploid mapping population are either 1:1 (0 × 1, 1 × 0, 1 × 2, and 2 × 1 SNPs) or 1:2:1 (1 × 1 SNPs), which means that in both scenarios the heterozygous group should encompass approximately 50% of the individuals. As can be seen in Fig. 3D, the average number of heterozygous calls fluctuated around the expected number of 24 (half of the total population size). However, a small enrichment of SNPs with > 46 heterozygous calls is visible, which means that almost all individuals had a heterozygous call for these SNPs. The rest did not seem to deviate much from the expected Gaussian distribution (Fig. 3D, All SNPs).

Another measure that could give insights in potential erroneous variants is the Average Allele Balance. Therefore, these were also computed for all segregating SNPs (heterozygous in at least one parent) in this mapping population to investigate how this relates to the number of heterozygous individuals per segregating SNP (Fig. 3E, All SNPs). An average allele balance of around 0.5 is expected for SNPs did not result from reads across different (highly similar) regions (e.g., from homoeologous subgenomes). An enrichment was visible between 0.6 and 0.9, which means these SNPs have on average 1.5 to 9 times as many reference reads than alternative reads for heterozygous calls.

The SNPs that deviate from expected segregation patterns might also have skewed Average Allele Balance values. Squared Pearson’s correlation coefficient (r²) based filtering on the marker bins was applied to investigate the influence of the average allele balance filtering on SNPs that segregated in the H × K population (149,270). From these, 118,489 SNPs remained (79.4%) after filtering for average allele balance (0.35 < AAB < 0.65). When the SNPs were filtered on r² > = 0.5 (LD_filt, TABLE) 129,406 SNPs (86.7%) remained and 112,868 of these also had an average allele balance between 0.35 and 0.65. If on top of the r² filtering, the SNPs also are filtered on having the highest r² with a marker bin on the same chromosome (chr_1A), 120,873 SNPs (80.1%) are left, of which 111,181 also had an average allele balance between 0.35 and 0.65.

The same plot was made but now only for the SNPs with an allele balance > 0.35 and < 0.65 to investigate the effect of allele balance on the number of heterozygous individuals (Supplementary Figure S2). It showed a slight decrease in SNPs where the number of heterozygous individuals deviated from the expected number (half of the population, 24).

Diversity panel

To confirm if we can identify type 2 and type 3 variants in a diversity panel as well, SNPs were extracted for 136 genotypes, and biallelic SNPs were filtered resulting in > 9.2 M SNPs. From these, 5000 SNPs were randomly selected per chromosome and included in the anchor set, resulting in a mostly homogeneously distributed dataset across the genome (Supplementary Figure S3). A few gaps existed, for example, a gap between 22 and 23 Mb on subgenome 1B, which could be accounted for by a possible assembly error as no high-quality SNPs were discovered in that region and other reference genomes (Camarosa v1, FaFB2) either miss this part of the genome or have a largely different sequence at that region [7, 10]. In the principal components analysis, no obvious outliers could be distinguished. The first axis likely reflects the chilling requirement across the different individuals (Supplementary Figure S4).

Homoeologous SNPs in the diversity panel

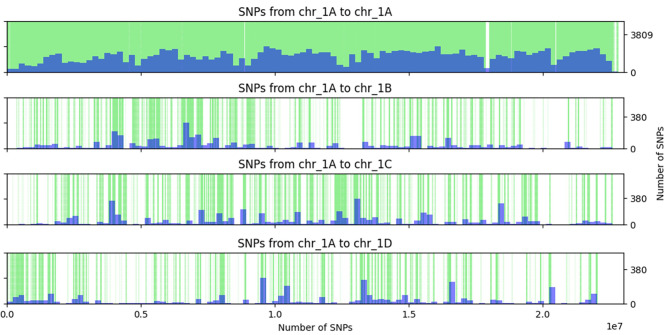
Type 2 variants (homoeologous SNPs) were found in the mapping population and to investigate whether similar patterns can be found with LD analysis in the diversity panel, SNPs that were originally discovered on chr_1A and predicted to chr_1A or on a homoeologous chromosome were plotted (Fig. 2). Similarly to results in the mapping population, small continuous regions were found where various SNPs were predicted on a homoeologous chromosome, although in this diversity panel, these regions seemed to be smaller and more fragmented. Interestingly, many SNPs at the start of chr_1A were predicted on chr_1D, just as in the mapping population. Therefore, it seemed that erroneous variants in the mapping population were also marked as erroneous in the diversity panel.

Fig. 2.

Occurrence of SNPs that are originally found on chr_1A and, based on the diversity panel, have the highest SSLD on chr_1A or a homoeologous chromosome with ratio of SSLD > 0.8 (green vertical lines). Density is plotted as histogram in blue

Erroneous SNPs identification: mapping population vs. diversity panel

The LD-based subgenome prediction method in the diversity panel was evaluated to determine whether it correctly identified SNPs that were also flagged as erroneous in the mapping population. The SNPs from chr_1A that occurred in both populations were extracted, all SNPs predicted to the same chromosome in both methods and those predicted to different chromosomes were counted (Table 2). This resulted in 122,510 SNPs predicted in both the mapping population and the diversity panel. To further increase prediction accuracy by both the mapping population and the diversity panel, SNPs in the mapping population were filtered on r² with a marker bin > 0.5 and SNPs from the diversity panel were filtered on the ratio of SSLD > 0.8. This resulted in 117,736 and 114,420 remaining SNPs, respectively. In total, 110,459 SNPs remained when both filtering methods were applied. After these filters, 99.2% of all SNPs had similar predictions in the mapping population and the diversity panel (Table 2).

Table 2.

Matching chromosome predictions for SNPs by predicted marker bin in the mapping population and LD-based prediction in a diversity panel (only including SNPs predicted by both methods)

Chromosome 1 A	No filtering	Mapping population prediction: marker bin r2 > 0.5	Diversity panel prediction: ratio SSLD > 0.8	Combination of mapping population and diversity panel prediction
Total Predicted SNPs	122510 (100%)	117736 (100%)	114420 (100%)	110459 (100%)
Total mismatching predicted SNPs	2896 (2.4%)	2147 (1.8%)	1262 (1.1%)	850 (0.8%)
Total matching predicted SNPs	119609 (97.6%)	115589 (98.2%)	113158 (98.9%)	109609 (99.2%)
SNPs predicted on 1A (match)	112433 (91.8%)	110781 (94.1%)	107115 (93.6%)	105531 (95.5%)
SNPs predicted on same homoeologous chromosome (match)	5338 (4.4%)	3976 (3.4%)	4515 (3.9%)	3397 (3.1%)
SNPs predicted on same nonhomoeologous chromosome (match)	1838 (1.5%)	832 (0.7%)	1528 (1.3%)	681 (0.6%)
Not Predicted (in both)*	4371	6170	6380	8987
Not Predicted (in one of the two)*	22389	25364	28470	29824

* The last two rows include the number of SNPs that were not predicted in both the mapping population and the diversity panel (Not Predicted (in both)) or not predicted in one of the two: the mapping population or the diversity panel (Not Predicted (in one of the two))

Some SNPs could only be predicted in one of the two populations (Not Predicted (in both)). This number of SNPs increased with 7435 SNPs when the corresponding quality filtering method was used for each of the two populations (mapping population: marker bin r² > 0.5 & diversity panel: ratio SSLD > 0.8).

Erroneous SNPs identification: average allele balance after LD-based filtering

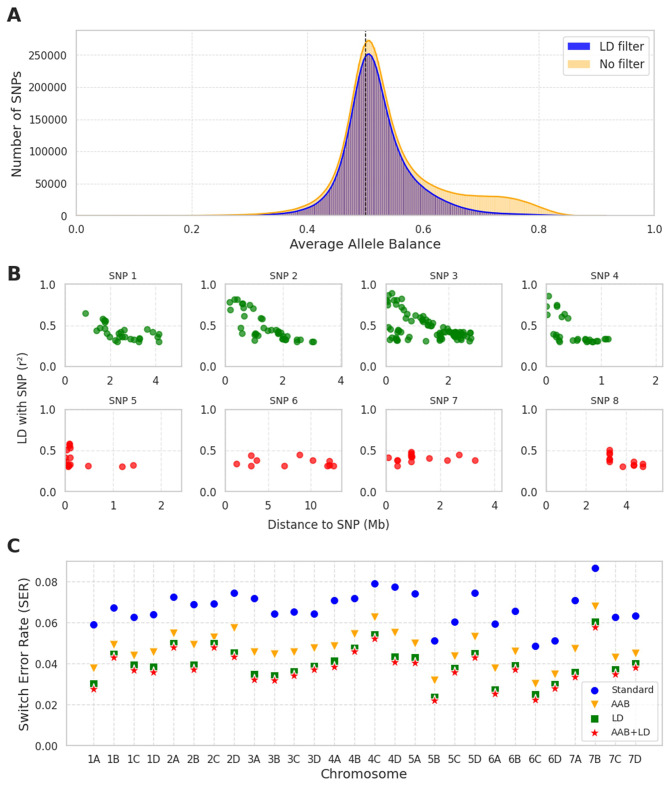
To investigate the agreement between LD-based and Average Allele Balance (AAB) based filtering, the Average Allele Balance was computed for 9.0 M SNPs (MAF > 0.05) in the diversity panel (Fig. 4A). The LD-based filtering method did not only filter out many SNPs that have a skewed AAB (> 0.65 or < 0.35) but also SNPs closer to an average allele balance of 0.5, resulting in 6.6 M SNPs that were predicted to be of type 1 (correct).

Fig. 4.

(A) Histogram of the Average Allele Balance (AAB) of all SNPs (with MAF > 0.05) from the diversity panel (n = 136) (orange) and of the SNPs that remained after the LD-based filtering (blue) was applied. (B) Linkage Disequilibrium Decay in the diversity panel for 8 SNPs originally discovered on chr_1A. The top row (SNP1, SNP2, SNP3 and SNP4) were predicted on chr_1A by the LD-based method (ratio of total SSLD > 0.8) and also by r² analysis in the mapping population (r² > 0.5). Bottom row (SNP5, SNP6, SNP7, SNP8) were predicted on a different chromosome than chr_1A by LD-based filtering in the diversity panel and also in the mapping population analysis. (C) Switch Error Rate (SER) per chromosome, computed on 23 duos/trios. Four different filtering methods were used prior to phasing: Standard, AAB, LD, and AAB + LD

Validation by phasing switch error rate

To validate the efficiency of filtering out erroneous SNPs of all four filtering methods, the SNPs were phased and SER was computed by using 22 duos and trios for each chromosome (Fig. 4C). Each filtering method improved the SER for all chromosomes compared to the Standard (no filtering), starting at an average SER of 0.066 for the Standard, improving to 0.047 for AAB, 0.040 for LD, and 0.037 if both filtering methods were used (AAB + LD). The switch error rate varied per subgenome and showed the same pattern regardless of the filtering method. For instance, chromosome 7B had the highest SER in all filtering methods. Chromosomes 5B and 6 C were the chromosomes with the lowest SER in all methods.

The optimal filtering method should maximize accuracy while retaining as many SNPs as possible. Although both methods combined (AAB + LD) resulted in the lowest switch error rate, they also resulted in the lowest number of retained SNPs. In total, the standard filtering contains 9.2 M SNPs. After AAB filtering, 7.9 M SNPs were left (86%). After LD filtering, 6.9 M SNPs remained (75%). If both filtering methods were applied, only 6.6 M SNPs remained (72%) (Supplementary Figure S6).

To exclude the possibility that the switch error rate improvement was only due to the lower number of remaining SNPs, the dataset was down sampled to 6.2 M random SNPs. These were then phased and the computed switch error rate was on average 0.072 over all chromosomes. Interestingly, the switch error rate for this randomly down sampled dataset is consistently higher than the standard (no extra filtering) method, for each chromosome.

Linkage disequilibrium decay patterns of different variant types

The LD-based filtering gave the best phasing results when applied as the only filtering method. To understand why certain SNPs were flagged as erroneous by the LD-based filtering method, LD decay patterns were investigated for various SNPs. The LD decay patterns differed for different variant types. Type 1 (correct) variants showed gradually decreasing LD decay patterns (SNP1, SNP2, SNP3, and SNP4 in Fig. 4B). Erroneous variants (type 2 and 3 variants: SNP5, SNP6, SNP7, and SNP8 in Fig. 4B) did not show gradually decreasing LD decay patterns. These two types were difficult to distinguish from each other, but it was expected that type 2 variants have high LD values with other SNPs in the same homoeologous region because homoeologous SNPs seemed to group in regions (e.g., SNP5 and SNP8). In addition, they were also broken up by smaller regions where no homoeologous SNPs were present. Consequently, it was expected that type 2 variants would have higher LD values with multiple SNPs but these were concentrated in several (or one) small region(s). On the contrary, type 3 variants were expected to have lower LD values in general (e.g., SNP6 and SNP7).

Discussion

Allo-octoploid strawberry can be treated as a diploid in most genetic analyses due to its disomic inheritance. However, allopolyploidy causes issues in genomics due to the high sequence similarities across its subgenomes. The partial misalignment of sequencing reads could result in erroneous variants (type 2: homoeologous variants; and type 3: multi-locus variants) which are not filtered out by common filtering criteria such as read depth or mapping quality. These erroneous variants cause problems in downstream analyses such as difficult interpretation of GWAS results and lower phasing accuracy [11, 14]. Therefore, it is crucial to develop filtering strategies that can tag these erroneous variant types.

Mapping population illustrates the need for filtering

From the segregating SNPs in the biparental mapping population for which Pearson’s correlation coefficient could be computed with marker bins (r² > 0.5), most SNPs were assigned to the correct (same) chromosome, but a small number was assigned to a different chromosome. The percentage of SNPs going to a homoeologous chromosome (3.2%) after filtering on r² was like what has been found in another study (5%) for the same population, which assigned SNPs to subgenomes based on the consensus chromosome and position of the marker bin [16]. One major difference was that this study used an older reference genome (Camarosa v1) while in our study a reference genome of better quality (FaRR1) has been used [7, 8]. Although these percentages could not be directly compared due to the different filtering methods, SNPs that belong to other homoeologous chromosomes were prevalent in both studies, and most likely due to similarities in DNA sequence between subgenomes. An improved reference genome might improve this issue in case of misassemblies, deletions, and missing parts of the assembly. The use of pangenomes could further mitigate these issues because there is more diversity in the pangenome than a single reference genome which means that chances are higher that the correct subgenome (of any reference genome in the pangenome) is more similar to the read than homoeologous subgenomes. However, a pangenome alone will never completely solve these issues because it is still limited to the reference genomes represented in the pangenome. An alternative could be longer reads (> 150 bp) which are more likely to align uniquely in a single subgenome.

The above analysis only considers SNPs that have an r² > 0.5, so those that are wrongly assigned are mainly erroneous SNPs that are of type 2 (homoeologous SNPs). Most SNPs of type 3 (erroneous SNPs due to reads originating from several chromosomes) would have been excluded already in the filtering step. These type 3 SNPs fall in the category “Not Predicted” (Table 2), i.e., the SNPs for which either no Pearson’s correlation coefficient could be computed (due to too little variation) or the SNPs that are filtered out by r² > 0.5. There are more SNPs in this “Not Predicted” category than the type 2 SNPs. The “Not Predicted” category reaches 18.6% of the total number of SNPs if r² filtering (> 0.5) is applied. However, this category does not only consist of type 3 variants because also sequencing errors will dedicate SNPs to this category, especially because of errors in a relatively small mapping population. Therefore, the real percentage of type 3 variants will be lower than 18.6%. Nonetheless, this is a large proportion of the total number of SNPs, larger than the type 2 erroneous variants (4.5%). This emphasizes the importance of adequate filtering methods in allo-octopoid strawberry even more.

Average allele balance only partly tags type 2 and 3 variants

Mapping populations are useful in many genetic studies due to the simple inheritance patterns, the H × K population gave us insight into the type 2 and 3 variants and the effectiveness of subsequent filtering strategies. We found a Gaussian distribution of heterozygous individuals per SNP around 50% of the population size (which in our study is 24) but we also found a small enrichment of SNPs that deviated from 50% heterozygosity with almost 100% heterozygosity (Fig. 3D). The best filtering method in this mapping population is by comparing the SNPs with the “ground truth”: the marker bins of the genetic map. Sufficient r² (> 0.5) with one of these marker bins shows that these SNPs are either type 1 or type 2 because their segregation pattern is similar to a segregating marker bin. If this marker bin is located on the same chromosome (chr_1A), the SNP can be considered as a type 1 variant, otherwise it is a type 2 variant. These type 2 variants are mainly composed of variants that have high r² with marker bins on homoeologous chromosomes (4.5%, Fig. 3B). The remaining SNPs (13.3%) do not have a segregation pattern that is expected so these can be considered as type 3 variants or as variants with too many errors. The average allele balance (Fig. 3E) seems to have skewed values that might be attributed to reference bias. The average allele balance of the different variant types does seem to have different values, type 1 variants, in green, mainly have an AAB of around 0.5 but have tails extending to 0.2 and 0.8. Type 2 variants, in orange, mainly have AAB values between 0.6 and 0.8 just as the variants in blue which are either type 3 variants or just variants with too many errors. This means that false variants tend to have inflated AAB values which explain most of the skewed AAB values (shoulder pattern). On top of this, filtering only on average allele balance (e.g., 0.35 < AAB < 0.65) is not sufficient as it filters out some type 1 variants (Fig. 3E).

Interestingly, some variants had r² < 0.5 with a marker bin and did have average allele balances around 0.5. Possible causes are e.g., misassembly of the reference genome or an inaccurate AAB due to a limited number of heterozygous calls. These variants cannot be filtered out by filtering on average allele balance. In addition, when 0.35 < AAB < 0.65 is used as filtering criteria, the enrichment of SNPs with almost 100% heterozygosity did not decrease much (Supplementary Figure S2A). This indicates that these SNPs do not have an obvious skewed AAB, which could be caused by two reasons. First, the segregating SNPs are selected based on the parental variant calls. So if one of the parents is scored as heterozygote whereas biologically it is homozygous, there is no segregation in the offspring. Second, if these variants are subgenome-specific variants, where reads from a homoeologous chromosome align then a variant is almost always scored as heterozygous, i.e., half of the aligned reads originate from the original chromosome but the other half of the aligned reads (including a different nucleotide: a subgenome specific SNP) comes from a homoeologous chromosome. These SNPs will not segregate in a mapping population and are expected to show an average allele balance of approximately 0.5.

Diversity panel LD-based predictions match mapping population predictions

To investigate whether similar results can be achieved in a diversity panel without the use of marker bins from a genetic map, an LD-based approach for the diversity panel was investigated. If the specific quality filtering criteria are applied for each population (r² with marker bin > 0.5 and ratio SSLD > 0.8) and only predicted SNPs are considered, 99.2% accuracy is achieved on chr_1A for 110,459 SNPs in total (Table 2). This means that the LD-based filtering in a diversity panel is a good solution to find type 1 and 2 variants, therefore avoiding the need for setting up and genotyping many mapping populations.

On the other hand, type 3 variants are difficult to compare between the two populations. In the mapping population, the group of SNPs that were of type 3 or that had too many errors was 13.3% of the total number of SNPs. In the diversity panel, the “Not Predicted” group, i.e., the group of SNPs that do not fulfill the filtering criteria, is composed of type 3 SNPs, SNPs with too many errors but also SNPs with MAF < 0.05 (MAC < 13). However, similar numbers of SNPs (8987 in total) were not predicted with LD-based (r²) analysis in both the mapping population and the diversity panel. This indicates that these SNPs are probably type 3 variants because they have neither a clear linkage with marker bins in the mapping population nor with SNPs in the LD anchor set from the diversity panel.

As shown in Table 2, the majority of the predicted SNPs were predicted on the same subgenome in both populations. A smaller proportion of SNPs was not predicted in one of the two methods which is mainly caused by the MAF < 0.05 filtering in the diversity panel and by the SNPs for which no Pearsons correlation coefficient could be computed. However, when the SNPs were filtered in both populations (marker bin r² > 0.5 & ratio SSLD > 0.8,) the number of SNPs in the “Not Predicted (in one of the two)” group increased with 7435 SNPs, which means that these were filtered out on the quality filtering criteria. This means that the subgenomes of these SNPs could be predicted in one population (classified as type 1 or 2 variants) but not in the other (classified as type 3 variants). A reason why some variants could be considered as type 1 or 2 in one population but as type 3 in another population could be that the accuracy of a variant classification is not consistent for all individuals. It could be that reads from certain genotypes align to a wrong subgenome, but reads from the same location but from different genotypes align to the correct subgenome. As a result, these variants can behave as type 1 (correct) variants in one genetic background but as type 2 or 3 variants in other genetic backgrounds. In the LD analysis in the diversity panel, this could give consistent segregation patterns for multiple variants if this phenomenon occurs for a larger region.

In comparison with the method for placing unpositioned variants introduced by Yadav et al. [18], we followed a similar rationale but because of the different purpose we needed a different method. Their method predicts the position of target variants if the top 2 variants with the highest LD are anchored on the same chromosome. This is disadvantageous for identifying erroneous variants in strawberry because erroneous variants (type 2 and 3) could have 2 variants with the highest LD on the same subgenome but are still erroneous. This is because the alignment of reads to the wrong subgenome may extend to small regions as has been shown in the results for chromosome 1. In addition, one of the variants with the highest LD could be a homoeologous variants (type 2) causing disconcordance between the subgenomes of the two anchored variants with the highest LD. As a result, some correct type 1 variants could remain unpredicted. This could be mitigated by extending the number of variants in the anchor set. In addition, the accuracy of both the method from Yadav et al. [18] and our LD-based identification of erroneous variants will improve by extending the diversity panel with extra genotypes, thereby increasing allele counts and distinctiveness of variant segregation patterns.

Colocalization of type 2 variants

In the mapping population regions with type 2 variants of varying lengths could be identified (Fig. 1). In general, these regions were fragmented. The same graph was made based on chromosome predictions of the LD-based filtering in the diversity panel and similar patterns could be observed, only the fragmentation increased (Fig. 2). This means that indeed SNPs are colocalizing, but the regions with these type 2 variants were small and fragmented. This is also what could be seen in LD decay plots, where SNPs that were predicted on a homoeologous chromosome were in LD with SNPs on the original chromosome, but these SNPs clustered together in a small region (SNP5 and SNP8 in Fig. 4B). Interestingly, in the mapping population, there was a tendency for SNPs at the top of chromosome 1 A to have high LD values with marker bins on chr_1D (Fig. 1) and in the diversity panel, this 1 A region also has SNPs predicted on chr_1D (Fig. 2). This was expected due to the high percentage of overlapping predictions by the mapping population and the diversity panel.

LD-based SNP filtering in a diversity panel successfully filters out erroneous variants

The effect of the filtering methods was tested on downstream phasing by computing switch error rates (SER) after phasing the different filtered SNP datasets. The assumption was that if more erroneous SNPs are present in the dataset the switch error rate will increase. From the results, LD-based SNP filtering in a diversity panel proved to result in better results than filtering on average allele balance. However, if average allele balance filtering was added on top of the LD-based filtering, the switch error rate improved slightly. This indicated that most but not all erroneous variant types (types 2 and 3) were already filtered out by LD-based filtering alone, leaving room for slight improvement. To further improve the phasing accuracy, for example, the ratio of SSLD filter could be set more stringent, or the anchor set could be extended or improved.

Interestingly, the switch error rate varied across the different chromosomes, e.g., chr_7B had a higher SER after filtering than chr_5B, chr_6C, or chr_6D had before filtering. However, this was probably due to phasing characteristics and not by different filtering success across chromosomes because the switch error rate pattern seemed to be consistent among different filtering methods. For example, this could be due to runs of homozygosity, then only erroneous type 2 and 3 variants are used for SER estimation in these regions resulting in higher SER. Regions of selection could also influence the SER per chromosome, suggesting that selective pressure results in higher allele counts for variants linked to this allele, thereby decreasing allele counts of variants linked to other alleles at that location. These rare variants complicate phasing efforts [21]. This could be the case for chr_7B because a major gene for resistance to Phytophtora cactorum (FaRPc-2) is located on this chromosome [23]. To mitigate this, a larger diversity panel could be utilized, focusing on adding rare genetic variation instead of genetic variation already represented well in the original panel, for example by constructing a breeding core collection [24].

LD decay plots illustrate why LD-based filtering works

The LD decay analysis gave insight into why LD-based SNP filtering works in a diversity panel. The plots in Fig. 4B showed typical LD patterns of SNPs that were predicted to be type 1 (SNP1, SNP2, SNP3, SNP4). These patterns differed from the SNPs that were predicted to be located on another chromosome (type 2) or SNPs that had a low ratio of SSLD (SNP5, SNP6, SNP7, SNP8). The LD decay of the latter types was not as that of the type 1 SNPs because it was either fragmented (SNP5, SNP8) or not systematically declining with physical distance (SNP6, SNP7). Fragmentation could be expected because several small regions of homoeologous chromosomes will interfere, but not all, resulting in fragmented LD patterns. A systematic decline is not expected for SNPs that are type 3 variants, where reads from multiple origins combine into a single SNP resulting in a specific variant calls pattern with many heterozygous variant calls. Therefore, the SNP has a low chance of being in high LD with SNPs from the anchor set but there will be several SNPs that also have many heterozygous variant calls resulting in moderate LD values with SNPs scattered throughout the genome (SNP6, SNP7).

Genetic structure in populations

When using the LD-based SNP filtering in other populations one should be aware of the genetic structure of the population because it could influence the outcome of LD-based SNP filtering. The assumption for using the LD-based filtering method is the following: for any true variant multiple other variants show a similar segregation pattern on the same subgenome. If, for any reason, this assumption is violated in a certain population or for certain variants, this method should be used with caution. For example, for recent mutations in the genome which are rare but true variants, there are not many other similar variants. Second, true variants that are in high LD but on different chromosomes cannot be distinguished from false variants and will subsequently be filtered out by this analysis. This can occur if there has been strong selection pressure in the population for multiple alleles at the same time.

Conclusions

In conclusion, this paper shows that LD-based filtering can tag erroneous variants that are the result of high sequence similarity among subgenomes in allopolyploid strawberry. Type 2 and 3 variants can be identified and filtered out which improves downstream genomic analyses, in this case, it decreased the phasing error by 44%. It is important to know which subgenome is important for a desired phenotypic value of a particular trait and filtering out these erroneous variants decreases the chance that a wrong subgenome is associated with such a trait. In addition, it improves phasing accuracy which ensures that important alleles are easier to trace through the germplasm.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

Investigation, visualization, and writing of the original draft were contributed by T.K., programming scripts was perfomed by T.K., D.H. and J.H.W., methodology and manuscript improvement were contributed by T.K., J.H.W., P.A., R.G.F.V. and C.M. All authors read and approved the final manuscript.

Funding

This project was supported by Fresh Forward Breeding B.V. and the TKI project ‘LWV20.112 Application of sequence-based multi-allelic markers in genetics and breeding of polyploids’ (BO-68–001-042-WPR).

Data availability

Script for computing average allele balances from variant call format (VCF) is available in the supplementary material (Script1_AAB.sh). Python pipeline for LD-based chromosome and position prediction is available on GitHub (https://github.com/FreshForward/LD_SNP_Assigner_releaser). The datasets generated and/or analysed during the current study are not publicly available because they are owned by private company Fresh Forward Breeding B.V. but are available from the corresponding author on reasonable request.

Declarations

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.