Abstract
In general multiple medical devices orthogonal frequency-division multiplexing (OFDM) communication systems, all the interfering medical users are legitimate but will cause disturbance to the desired user. In this work, we evaluate three deep learning (DL) algorithms: fully connected deep neural networks, convolutional neural networks, and long short-term memory neural networks for signal processing and detection in uncoded multiple medical devices OFDM communications systems. The bit error rates (BER) of these DL methods are compared with the conventional linear minimum mean squared error (LMMSE) detector. Additionally, the relationships between the BER and signal-to-interference ratio, signal-to-noise ratio, the number of interferences, and modulation type are investigated. Numerical results show that DL methods outperform LMMSE under different multiple medical device interference situations and are robust when the wireless channel has high variability. Also, DL methods are proven to have strong anti-interference ability and are useful in multiple medical devices OFDM systems.
Subject terms: Electrical and electronic engineering, Information theory and computation
Introduction
In recent years, to combat multipath fading in wireless channels, orthogonal frequency-division multiplexing (OFDM) has become a widely used modulation scheme in various wireless communications systems1. To gain the channel state information (CSI) and recover the transmitted symbols in OFDM systems, many works have been conducted for channel estimation and signal detection2. There are several classical estimation methods for wireless channels, such as least squares (LS), minimum mean squared error (MMSE), and linear MMSE (LMMSE). Generally, the performance of LS is worse than MMSE and LMMSE, which use more channel statistics3.
Since deep learning (DL) algorithms are widely used in various fields4, many researchers have focused on applying DL to wireless communications. Especially, deep learning-based approaches estimate CSI implicitly and recover the transmitted symbols directly5. In6,7, DL methods were used to improve the performance of the MMSE estimator. In8, a fully convolutional beamforming model named FC-BFNet, and a convolutional blind denoising network, were developed for channel estimation of millimeter-wave massive multiple-input multiple-output (MIMO) systems. In9, a fully convolutional beamforming model named FC-BFNet is studied. In addition, recently, deep learning has been applied to OFDM communication systems. In10, a residual learning-based OFDM channel estimation method was presented. In11, a DL-based estimator was proposed to adapt to the scenarios of high mobility in the MIMO-OFDM system, showing high robustness. In12, a generative adversarial network was developed for channel super-resolution to gain more details of the CSI with performance close to that of LMMSE. In5, a fully connected neural network (FCDNN) was used for signal detection. It was shown that, when the cyclic prefix was omitted and the number of pilots was small, the DL-based detector was more robust than LS and MMSE detectors. In13, a DL-based channel estimator with a joint pilot design was presented. In the scheme, the inherent correlations in MIMO-OFDM were utilized to improve the performance of estimation. In14, a channel estimation network and a channel-conditioned recovery network were proposed for channel estimation and signal detection to make them robust to the variation of parameters. However, all these works have considered only a single user.
On the other hand, how to improve the accuracy of signal processing in multiuser conditions has received a lot of attention. In15, a convolutional neural networks (CNNs) approach to restoring the desired signal impaired by the multiple-input multiple-output (MIMO) channel. In16, the design of non-orthogonal multiple access (NOMA) beamforming is investigated in a spatial division multiple access (SDMA) legacy system. In17, dynamic partially connected (DPC) CNN was used in the hybrid precoding with multi-user optimization. The proposed detector gave higher accuracy than the conventional MMSE detection scheme. In18, an RIS-assisted multiuser multiple-input single-output orthogonal frequency division multiplexing (MU-MISO-OFDM) system, and propose a practical transmission protocol with non-uniformly spaced comb-type pilots for compressed channel estimation and data transmission. In19, a deep learning (DL) aided receiver was proposed for NOMA joint signal detection.
The works mentioned above are all for a specific multiuser scenario, such as multiuser SDMA16, NOMA19, MIMO15 or MISO18. Different from them, in this work, we will study DL-based signal processing and detection for an uncoded multiuser OFDM system. In this system, there are one or more legitimate interfering users, and multiuser interference will be added directly at the OFDM receiver. For the receiver, it is difficult to distinguish and recover the transmitted symbols from the desired user. The performances of different DL methods in such a tough system will be evaluated. FCDNN has been proved suitable for OFDM signal detection in5. CNNs are popular in image processing. It is worth trying to extract the features of reshaped wireless signals as a 2D image. Furthermore, transmitted symbols can be regarded as sequence data. To address the non-trivial problem of estimating channel fading states and signals simultaneously, two deep learning (DL)-aided minimum mean square error (MMSE) estimation schemes are proposed7. Therefore, these three DL methods are chosen. To evaluate their anti-interference ability in multiuser situations, we compare the bit error rates (BERs) of offline-trained FCDNN, CNN, and LSTM neural networks. The BERs for different signal-to-interference ratios (SIRs), signal-to-noise ratios (SNRs), numbers of interfering users (NoI), and modulation types of interfering users will be investigated to evaluate the performance.
Results
In this section, we compare the performances of the different methods. The FCDNN, CNN, and LSTM models were trained offline and subsequently deployed for online testing. To evaluate their effectiveness, we used bit error rate (BER) as the primary performance metric. It is important to note that all signal-to-interference ratio (SIR) values discussed in this section represent the transmitting SIRs.
In signal processing systems, successive interference cancellation schemes are often employed. However, these methods frequently encounter challenges such as decoding and estimation errors. Among traditional statistical estimation methods, including least squares (LS), minimum mean squared error (MMSE), and linear MMSE (LMMSE), LMMSE offers a favorable balance between computational complexity and estimation accuracy. Therefore, we use the BER of the LMMSE method as a benchmark for comparison with the deep learning models.
For the desired user, we utilize 4-ary quadrature amplitude modulation (4-QAM) signaling. The modulation types of interfering users and signal-to-interference ratios (SIRs) vary across different experiments. The OFDM channel is modeled as a Rayleigh frequency-selective fading channel, with a 1D random fade variance of 0.5. The Rayleigh fading models are commonly employed to simulate multipath environments, where signals reflect off various objects before reaching the receiver. This results in the signal arriving with different delays and strengths, leading to interference and signal fading. Since OFDM is designed to address the challenges posed by multipath fading, the use of a Rayleigh model is a natural choice for testing the robustness of OFDM systems under realistic conditions.
To determine the optimal number of epochs, the training loss curve with 4-QAM interference when SNR = 15 dB and SIR = 0 dB is illustrated in Fig. 1. A batch size of 1000 is chosen for training. In Fig. 1, the loss function decreases significantly before the 25th epoch. After the 25th epoch, it declines slowly and continuously. Similarly, the BER curves show a sharp decreasing trend before the 25th epoch. When the epoch exceeds 100, the BER no longer changes. All the methods reach their error floor in this situation. However, after the 150th epoch, overfitting occurs, leading to noticeable fluctuations in the BER. Consequently, we select 150 epochs as the optimal training duration.
Fig. 1.
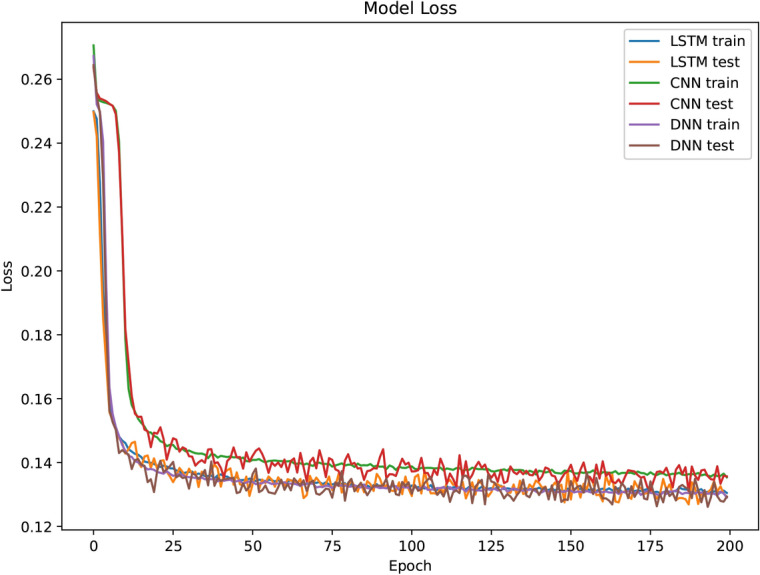
Training loss when SNR = 15 dB and SIR = 0 dB.
Comparison of methods
To validate the performance of the deep learning (DL) models in OFDM detection, Fig. 2 presents the BER results for the DL models in an OFDM system without interference. All three models demonstrate reliable performance. Specifically, when the SNR exceeds > 5 dB, the BER remains 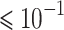 , and when SNR > 15 dB, the BER
, and when SNR > 15 dB, the BER 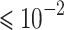 . Notably, the lowest BER achieved by both the LSTM and CNN models is
. Notably, the lowest BER achieved by both the LSTM and CNN models is 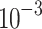 .
.
Fig. 2.
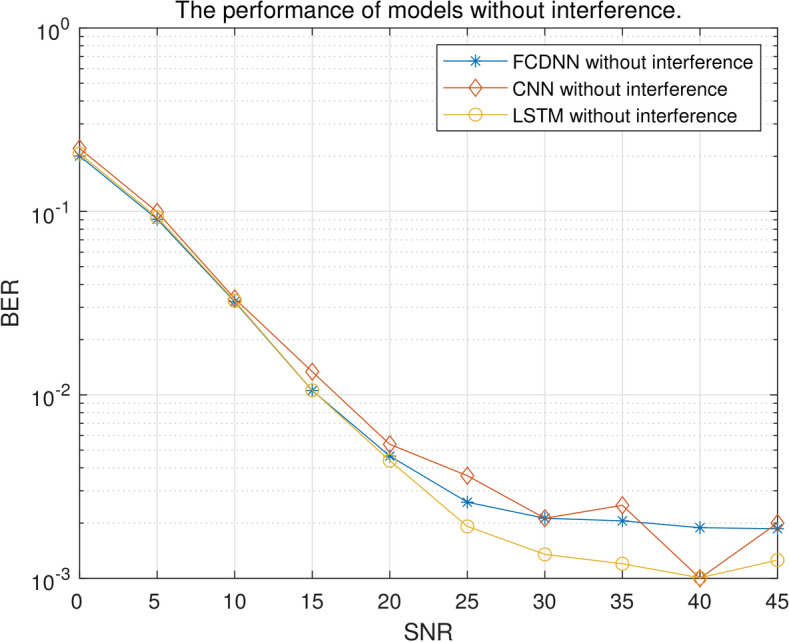
BERs of DL models without interference.
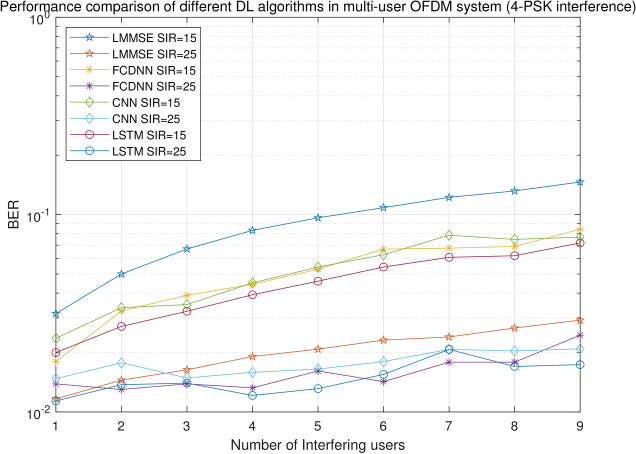
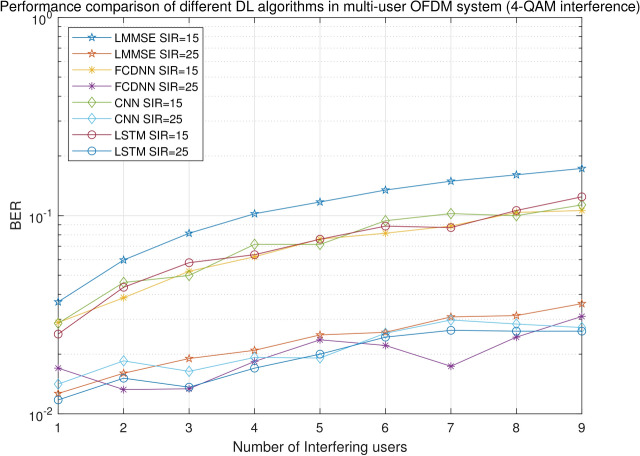
Figures 3 and 4 give the performance comparison of different DL algorithms and LMMSE detector when 4-ary phase shift keying (4-PSK) and 4-QAM are used by interfering users and SNR = 15 dB. In both figures, the BERs of DL and LMMSE increase with increasing NoI. When interfering users are 4-PSK modulated, at SIR = 15 dB, the BERs of FCDNN, CNN, and LSTM are 0.04, 0.039, 0.047 smaller than LMMSE in average, respectively. When SIR is increased to 25 dB, the gap between LMMSE and DL methods are smaller. The BERs of FCDNN, CNN, and LSTM are 0.005, 0.003, and 0.006 smaller than LMMSE. When 4-QAM, the same modulation type as the desired user, is used by the interfering users, all methods exhibit higher BERs compared to 4-PSK. Nevertheless, the DL algorithms continue to outperform LMMSE at both 15 dB and 25 dB SIR levels. Overall, while the BER differences between FCDNN and LSTM remain small, CNN performs slightly worse in the presence of 4-PSK interference. As the SIR increases, the DL models outperform the conventional LMMSE method, particularly under severe interference conditions.
Fig. 3.
BERs of different methods with 4-PSK interference.
Fig. 4.
BERs of different methods with 4-QAM interference.
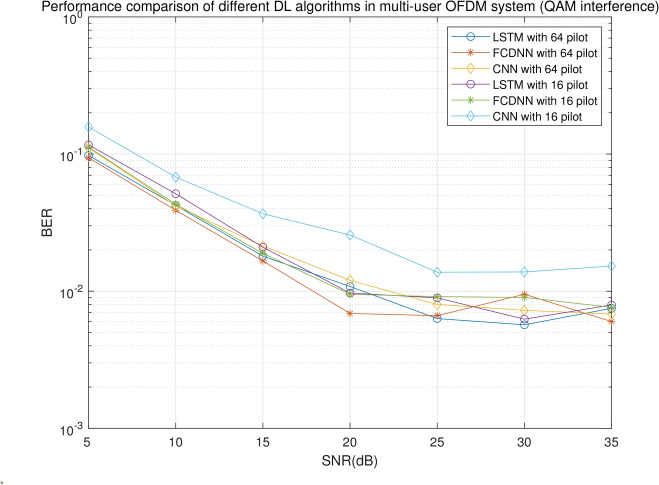
To evaluate the robustness of the methods, we compare their performance with different numbers of pilots. Figure 5 shows the BERs of the methods when 16 pilots and 64 pilots are used in a frame of 128 symbols. For the CNN model, the BER with 16 pilots is between 0.006 and 0.0466 higher than the BER with 64 pilots for different numbers of interfering users (NoI). In contrast, the BER increase for FCDNN and LSTM is smaller, with the difference being no more than 0.019 between the two pilot configurations. This indicates that the decrease from 64 to 16 pilots has a less significant effect on the performance of FCDNN and LSTM compared to CNN.
Fig. 5.
BERs with different number of pilots.
Overall, LSTM and FCDNN demonstrate better and more robust performance against interference compared to CNN. When compared with the conventional LMMSE detector, the deep learning (DL) models show significantly lower BERs in scenarios with weaker interference. This advantage is attributed to the ability of neural networks to learn and adapt to signal and channel features through extensive training over multiple epochs.
NoI and SNR
The received signal is affected by both AWGN and interference. To better understand the impact of these disturbances, we examine the BER for various SNR values and NoI. In this analysis, the SIR is fixed at 20 dB.
Figure 6 illustrates the performance of three DL algorithms for different SNRs with NoI values of 1, 5, and 9. As NoI increases, interference becomes more significant. The BER differences between DL methods at the same SNR and NoI are very small too. However, the BER of CNN at lower SNR is higher than FCDNN and LSTM, which means that CNN model is less robust in lower SNR regions. For LSTM, when SNR > 25 dB, each curve flattens out and reaches the error floor of SIR = 20 dB. When SNR 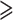 20 and NoI = 1, all of the DL methods can reach BER of
20 and NoI = 1, all of the DL methods can reach BER of 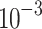 .
.
Fig. 6.
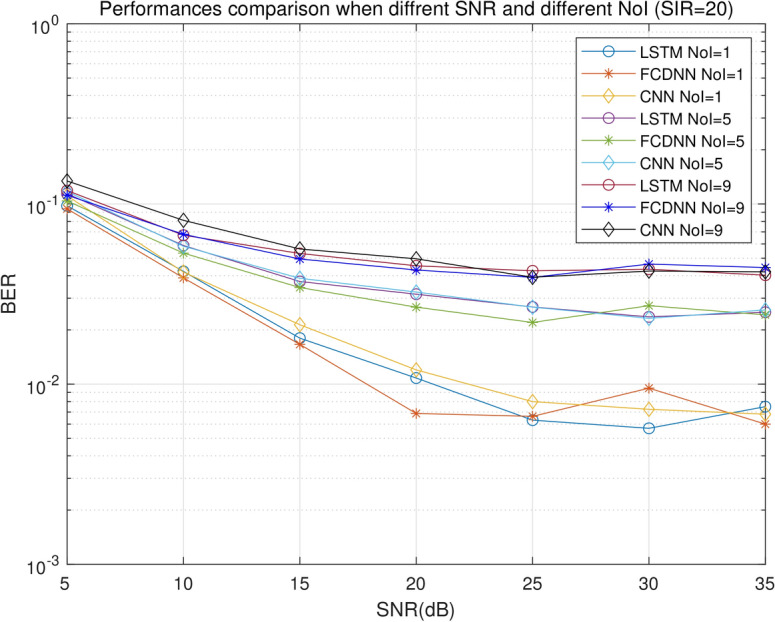
BERs when different SNR and different NoI.
Interference modulation types
Different modulation types result in varying signal complexities, which can influence the detection accuracy of deep learning (DL) algorithms in the presence of interference signals.
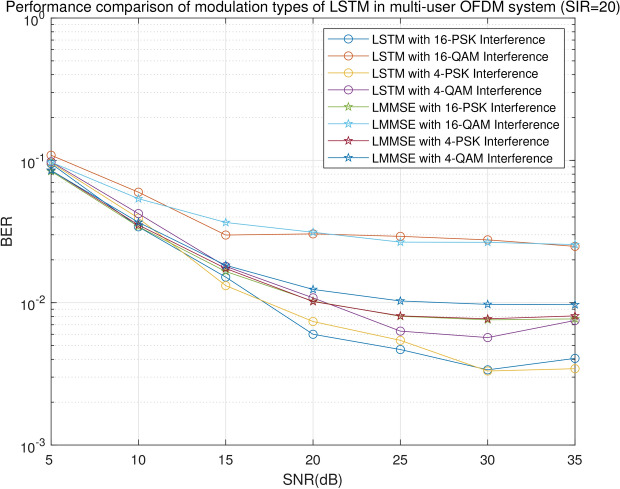
To investigate the impact of interference signaling, Fig. 7 illustrates BERs of LSTM and LMMSE for five different types of modulation when SIR = 20 dB and SNR = 15 dB. In the order from smallest to largest by BER of LSTM, are 4-PSK, 16-PSK, 4-QAM, and 16-QAM. LSTM method outperforms LMMSE in all cases, but the gap between LSTM and LMMSE is very small in 16-QAM modulation. For LSTM, the BERs of QAM interference are higher than those of PSK interference. The BER of 16-QAM interference is noticeably higher than the that of 4-QAM. On the contrary, there is only a small gap between BERs of 4-PSK and 16-PSK curves. For QAM modulation, higher constellation size leads to higher BER, this is because the Euclidean distance of interfering signal decreases with constellation size. In summary, QAM interference has a greater impact than PSK interference due to the differences in both phase and amplitude in QAM signaling, while PSK symbols only differ in phase. Additionally, the impact of constellation size is more significant in QAM than in PSK. Similar tests were conducted for the FCDNN network, and the BER of FCDNN is comparable to that of LSTM.
Fig. 7.
BERs of LSTM and LMMSE with different interference.
Methods
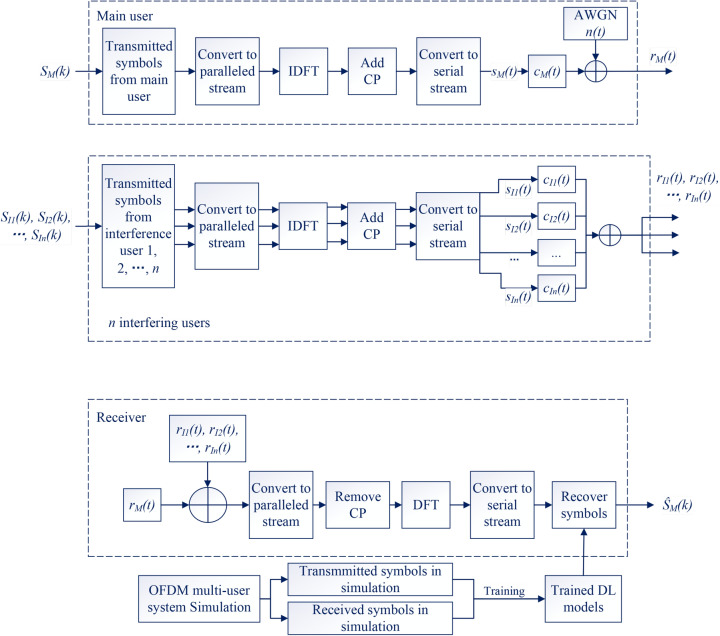
System structure
The structure of the proposed deep learning-based OFDM communication system is illustrated in Fig. 8. The transmitted symbols 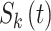 with pilots are converted from serial to parallel stream. The signal is then transformed into the time domain using the inverse discrete Fourier transform (IDFT). After inserting a cyclic prefix (CP) into the symbols, the signal is converted back into a serial stream and transmitted over the wireless channel. The signal at the receiver is
with pilots are converted from serial to parallel stream. The signal is then transformed into the time domain using the inverse discrete Fourier transform (IDFT). After inserting a cyclic prefix (CP) into the symbols, the signal is converted back into a serial stream and transmitted over the wireless channel. The signal at the receiver is
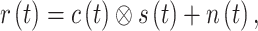 |
1 |
where 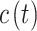 is the wireless channel,
is the wireless channel, 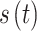 is the transmitted signal after IDFT and
is the transmitted signal after IDFT and 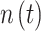 is the additive white Gaussian noise (AWGN). In this work, similar to5, the WINNER II channel model is used as the OFDM channel for both the desired user and all interfering users, with a maximum delay of 16 sampling periods. The carrier frequency is set to 2.6 GHz, and the number of paths is 24. For the desired user, whose signal we aim to receive, we denote the transmitted signal, received signal, and wireless channel as
is the additive white Gaussian noise (AWGN). In this work, similar to5, the WINNER II channel model is used as the OFDM channel for both the desired user and all interfering users, with a maximum delay of 16 sampling periods. The carrier frequency is set to 2.6 GHz, and the number of paths is 24. For the desired user, whose signal we aim to receive, we denote the transmitted signal, received signal, and wireless channel as 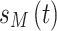 ,
, 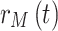 , and
, and 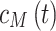 respectively. The NoI is
respectively. The NoI is 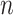 . For the
. For the 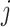 th interfering user, the transmitted signal, received signal, and wireless channel are denoted as
th interfering user, the transmitted signal, received signal, and wireless channel are denoted as 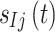 ,
, 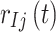 , and
, and 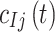 respectively. At the receiver, the desired signal
respectively. At the receiver, the desired signal 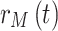 is interfered by
is interfered by 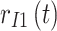 ,
, 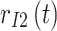 , ...,
, ..., 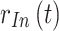 . After parallel-to-serial conversion, removal of CP, discrete Fourier transform (DFT), and serial-to-parallel conversion,
. After parallel-to-serial conversion, removal of CP, discrete Fourier transform (DFT), and serial-to-parallel conversion, 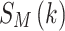 is recovered using DL without CSI. The CSI is unknown at the receiver. The recovered symbols are denoted as
is recovered using DL without CSI. The CSI is unknown at the receiver. The recovered symbols are denoted as 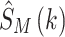 . In the system, DL is trained offline. At the deployment stage when DL is online, the weight of the network has been fixed and there is no training at this stage. To learn the characteristics of the channel, the DL model is trained using a large dataset of
. In the system, DL is trained offline. At the deployment stage when DL is online, the weight of the network has been fixed and there is no training at this stage. To learn the characteristics of the channel, the DL model is trained using a large dataset of 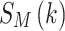 and unrecovered symbols at the receiver, accommodating a dynamic OFDM channel in various scenarios. All the OFDM channels in the simulation are multipath fading channels and change randomly.
and unrecovered symbols at the receiver, accommodating a dynamic OFDM channel in various scenarios. All the OFDM channels in the simulation are multipath fading channels and change randomly.
Fig. 8.
System structure.
The network does not need to be re-generated or re-trained for different NoI, SNR or SIR. Similar to5, to enhance performance, each frame of 128 symbols is used as input across 8 parallel networks, with each network detecting 16 symbols. For transmitted signals, the pilot symbols are the same in the training and testing stages, while the data symbols are generated randomly in each simulation. The output layer will give a result of 8 16 symbols.
16 symbols.
Deep learning networks
As previously mentioned, this work utilizes FCDNN, CNN, and LSTM to recognize transmitted symbols. In the physical layer of communications, the transmitted symbols are binary, represented as 0 or 1. Thus, the detection process can be viewed as a straightforward binary classification problem. To accommodate the different networks, the data will be reshaped into various sizes.
In the CNN input layer, the complex channel parameters and transmitted signals will be transformed into a 2D array using their real and imaginary parts. In contrast, the LSTM network will process the input data as a sequence.The mean squared error function is chosen to calculate the loss. The loss function 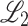 can be described as
can be described as
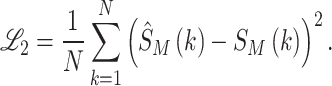 |
2 |
All the numbers of neurons and layers below are determined after testing in different values.
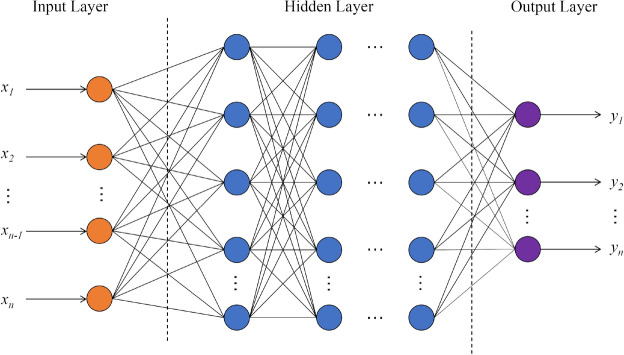
As the structure in Fig. 9 shows, an FCDNN is an advanced version of an artificial neural network that is composed of several layers, each of which contains multiple neurons. Each neuron in each layer is connected to all neurons in the upper and lower layers. The FCDNN structure includes an input layer, several hidden layers, and an output layer. For the FCDNN network, the detector can be represented as follows
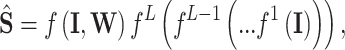 |
3 |
where 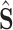 represents the recovered transmitted symbols, which is the output of the neural network,
represents the recovered transmitted symbols, which is the output of the neural network, 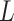 denotes the number of layers,
denotes the number of layers, 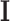 is the input data, and
is the input data, and 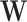 refers to the network weights that need to be optimized during the training process. In5, the FCDNN has been proved as a effective method for OFDM signal detection. In this work, after testing, the number of neurons was adjusted to suit the multiuser scenario. The architecture of the network is shown in Table 1.
refers to the network weights that need to be optimized during the training process. In5, the FCDNN has been proved as a effective method for OFDM signal detection. In this work, after testing, the number of neurons was adjusted to suit the multiuser scenario. The architecture of the network is shown in Table 1.
Fig. 9.
Structure of an FCDNN.
Table 1.
Architecture of FCDNN network.
| Layer name | Parameters | Activation |
|---|---|---|
| Input size | 256 1 1 |
|
| Dense | 512 neurons | Relu |
| Dense | 512 neurons | Relu |
| Dense | 128 neurons | Relu |
| Output size | 16 8 8 |
Sigmoid |
Essentially, a CNN is a neural network constructed by forward propagation and trained by back propagation. The structure of a CNN is similar to that of an FCDNN; it consists of multiple layers, including an input layer, several hidden layers, and an output layer. However, in contrast to an FCDNN, a CNN has particular hidden layers known as convolution layers. These are the core layers of a CNN, and they generate most of its computation. Convolution is widely used in image processing. For example, a discrete 2D filter, which is also called a convolution kernel, is used to perform convolution operations on 2D images. This 2D filter (Conv2D) slides to all positions on the 2D image and calculates the inner product with the central pixel point and the areas neighbouring that point. For CNN, the output of two Conv2D layers can be written as
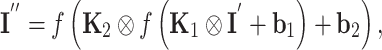 |
4 |
where 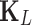 represents the
represents the  th convolutional kernel,
th convolutional kernel, 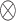 denotes the convolution operation, and
denotes the convolution operation, and 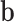 represents the bias. As mentioned before, because CNN has its own advantage on 2D image feature extraction, the received signal is transformed to a 2D matrix like an image. The architecture of the CNN network used in this work is shown in Table 2. We use 1*2 and 2*1 filters to match the 64*2*2 input data. The pooling layer is omitted due to the small size of the input data.
represents the bias. As mentioned before, because CNN has its own advantage on 2D image feature extraction, the received signal is transformed to a 2D matrix like an image. The architecture of the CNN network used in this work is shown in Table 2. We use 1*2 and 2*1 filters to match the 64*2*2 input data. The pooling layer is omitted due to the small size of the input data.
Table 2.
Architecture of CNN network.
| Layer name | Parameters | Activation |
|---|---|---|
| Input size | 2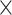 2 2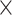 64 64 |
|
| Conv2D | 1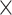 2 filter 2 filter |
Relu |
| Conv2D | 2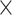 1 filter 1 filter |
Relu |
| Dense | 128 neurons | Relu |
| Output size | 16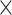 8 8 |
Sigmoid |
The LSTM network is a development from a recurrent neural network (RNN). In an RNN, the hidden state of node 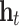 can be represented as
can be represented as
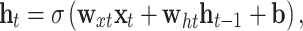 |
5 |
where 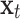 represents the
represents the 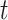 -th observation, and
-th observation, and 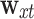 and
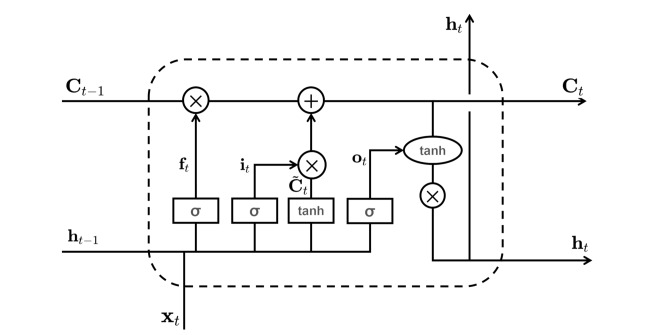
and 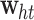 are the network weights. However, with an RNN, long-term series data will lead to long-term dependence problems; this means that earlier information recorded in the memory unit will be diluted with the passage of time steps. As a result, it will be difficult to establish the dependency relationships between parameters and the information in earlier time steps. The LSTM network solves the long-term dependence problem by incorporating a ‘gate’ into each memory unit to control the flow and loss of features.
are the network weights. However, with an RNN, long-term series data will lead to long-term dependence problems; this means that earlier information recorded in the memory unit will be diluted with the passage of time steps. As a result, it will be difficult to establish the dependency relationships between parameters and the information in earlier time steps. The LSTM network solves the long-term dependence problem by incorporating a ‘gate’ into each memory unit to control the flow and loss of features.
The structure of the memory block of an LSTM network is illustrated in Fig. 10. It consists of one memory cell with input gate, forget gate and output gate. The input gate reads data from input 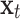 , while the output gate writes output to
, while the output gate writes output to 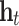 . The forget gate can help the cell reset the stored input data
. The forget gate can help the cell reset the stored input data 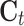 . Their function is
. Their function is
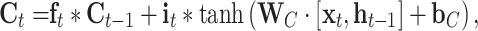 |
6 |
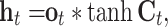 |
7 |
where 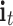 ,
, 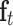 and
and 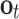 denote the output of the input gate, forget gate and output gate, respectively.
denote the output of the input gate, forget gate and output gate, respectively. 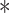 stands for element-wise multiplication,
stands for element-wise multiplication, 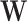 and
and 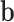 are the weight and the bias term, respectively. The network architecture is shown in Table 3.
are the weight and the bias term, respectively. The network architecture is shown in Table 3.
Fig. 10.
Structure of an LSTM block, where 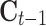 and
and 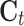 are respectively the cell states at the
are respectively the cell states at the 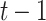 -th and
-th and 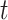 -th observations,
-th observations, 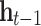 and
and 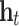 are respectively the hidden states of the
are respectively the hidden states of the 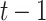 -th and
-th and 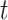 -th nodes,
-th nodes, 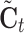 is the cell state update value,
is the cell state update value, 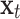 is the input data,
is the input data, 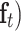 ,
, 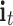 , and
, and 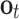 are the states of forget gate, input gate, and output gate, respectively.
are the states of forget gate, input gate, and output gate, respectively.
Table 3.
Architecture of LSTM network.
| Layer name | Parameters | Activation |
|---|---|---|
| Input size | 256*1 sequence | |
| LSTM | 128 neurons | |
| LSTM | 128 neurons | |
| Dense | 64 neurons | Relu |
| Output size | 16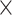 8 8 |
Sigmoid |
At the training stage, to learn the features of OFDM channels, sets of transmitted symbols and their corresponding unrecovered received signals through various OFDM channels, with an SNR of 15 dB, are generated for training and validation. In this work, 1000 training samples are generated for each epoch. Then, the sets of symbols in OFDM situations at transmitter and receiver are generated to test the anti-multiuser interference performance of deep learning (DL) models. The transmitted bits are either 0 or 1. Therefore, the BER is used to represent the detection accuracy as
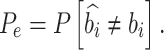 |
8 |
Computational complexity analysis
For the fully connected layer, the number of parameters is calculated as 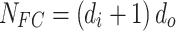 , where
, where 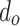 and
and 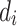 denote the number of input units and output units of the layer, respectively. For the convolutional layer, the number of parameter relates to the filter size, it is calculated as
denote the number of input units and output units of the layer, respectively. For the convolutional layer, the number of parameter relates to the filter size, it is calculated as 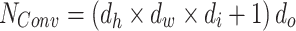 , where
, where 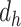 and
and 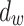 denote the height and width of the filter, respectively. A LSTM layer contains 4 non-linear transformation, which leads to 4 non-linear mapping layers. Thus the number of parameters for the LSTM layer is
denote the height and width of the filter, respectively. A LSTM layer contains 4 non-linear transformation, which leads to 4 non-linear mapping layers. Thus the number of parameters for the LSTM layer is 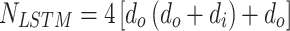 , In the training, the computational complexity for each time step and parameter of these methods is
, In the training, the computational complexity for each time step and parameter of these methods is 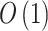 . Therefore, the complexities for the models are
. Therefore, the complexities for the models are 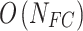 ,
, 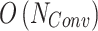 , and
, and 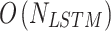 . To illustrate the complexities of the DL networks, the numbers of parameters are listed in Table 4.
. To illustrate the complexities of the DL networks, the numbers of parameters are listed in Table 4.
Table 4.
The number of parameters for DL networks.
 layer layer |
Deep learning network | ||
|---|---|---|---|
| FCDNN | CNN | LSTM | |
| 1 | 131584 | 66048 | 197120 |
| 2 | 262656 | 262400 | 131584 |
| 3 | 65664 | 32896 | 8256 |
| Total | 459904 | 361344 | 336960 |
Discussion
In this work, we explored the effectiveness of deep learning (DL) algorithms for signal processing and detection in uncoded OFDM communication systems. Specifically, we evaluated the performance of offline-trained FCDNN, CNN, and LSTM models in detecting transmitted symbols and compared them to the conventional LMMSE method. Our simulation results demonstrate that the DL-based methods consistently achieve lower bit error rates (BER) than LMMSE across various conditions. We conducted extensive experiments, varying key parameters such as SIR, SNR, number of interfering users (NoI), and modulation types. Among the tested DL models, LSTM and FCDNN consistently outperformed CNN, though all models encountered performance limits, manifesting as error floors under specific scenarios. Additionally, the models were trained across a variety of wireless channel simulations and subsequently tested on different parameter sets. This demonstrated the robustness of the DL models, particularly in handling high channel variability. Notably, our findings reveal that QAM interference has a greater impact on detection accuracy compared to PSK, a result consistent across the DL methods.
Acknowledgements
This work is supported by the Science and Technology Innovation 2025 Major Project of Ningbo (No.2023Z236, No. 2024Z148, No. 2024Z234).
Author contributions
Y.Z. and H.W. conceived the experiment(s), K.W. , W.Z. and Y.Y. conducted the experiment(s), Y.Y., X.L. and Y.Y. analysed the results. All authors reviewed the manuscript.
Data availibility
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
Declarations
Competing interests
The authors declare that they have no competing financial interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Kun Wei, Email: 303896041@qq.com.
Youjie Ye, Email: yyj0127@vip.qq.com.
Yulin Zhou, Email: zhou.yulin@zju.edu.cn.
References
- 1.Yuan, M., Wang, H., Yin, H. & He, D. Alternating optimization based hybrid transceiver designs for wideband millimeter-wave massive multiuser mimo-ofdm systems. IEEE Trans. Wirel. Commun.22, 9201–9217. 10.1109/TWC.2023.3269056 (2023). [Google Scholar]
- 2.Peng, Q., Li, J. & Shi, H. Deep learning based channel estimation for OFDM systems with doubly selective channel. IEEE Commun. Lett.26, 2067–2071. 10.1109/LCOMM.2022.3187161 (2022). [Google Scholar]
- 3.Wang, X., Shen, X., Hua, F. & Jiang, Z. On low-complexity MMSE channel estimation for OCDM systems. IEEE Wirel. Commun. Lett.10, 1697–1701. 10.1109/LWC.2021.3077641 (2021). [Google Scholar]
- 4.Li, Z., Liu, F., Yang, W., Peng, S. & Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst.33, 6999–7019. 10.1109/TNNLS.2021.3084827 (2022). [DOI] [PubMed] [Google Scholar]
- 5.Ye, H., Li, G. Y. & Juang, B.-H. Power of deep learning for channel estimation and signal detection in OFDM systems. IEEE Wirel. Commun. Lett.7, 114–117. 10.1109/LWC.2017.2757490 (2018). [Google Scholar]
- 6.Ahmed, I., Alam, M. S., Hossain, M. J. & Kaddoum, G. Deep learning for MMSE estimation of a gaussian source in the presence of bursty impulsive noise. IEEE Commun. Lett.25, 1211–1215. 10.1109/LCOMM.2020.3045665 (2021). [Google Scholar]
- 7.Haider, M. et al. Deep learning aided minimum mean square error estimation of gaussian source in industrial internet-of-things networks. IEEE Trans. Indus. Cyber-Phys. Syst.2, 185–195. 10.1109/TICPS.2024.3420823 (2024). [Google Scholar]
- 8.Jin, Y., Zhang, J., Ai, B. & Zhang, X. Channel estimation for MMWAVE massive MIMO with convolutional blind denoising network. IEEE Commun. Lett.24, 95–98. 10.1109/LCOMM.2019.2952845 (2020). [Google Scholar]
- 9.Liu, J., Zhang, H. & Peng, J. Flexible beamforming of dynamic MIMO networks through fully convolutional model. IEEE Signal Process. Lett.29, 717–721. 10.1109/LSP.2022.3143771 (2022). [Google Scholar]
- 10.Li, L., Chen, H., Chang, H.-H. & Liu, L. Deep residual learning meets OFDM channel estimation. IEEE Wirel. Commun. Lett.9, 615–618. 10.1109/LWC.2019.2962796 (2020). [Google Scholar]
- 11.Liao, Y., Hua, Y. & Cai, Y. Deep learning based channel estimation algorithm for fast time-varying MIMO-OFDM systems. IEEE Commun. Lett.24, 572–576. 10.1109/LCOMM.2019.2960242 (2020). [Google Scholar]
- 12.Zhao, S., Fang, Y. & Qiu, L. Deep learning-based channel estimation with srgan in ofdm systems. In 2021 IEEE Wireless Communications and Networking Conference (WCNC), 1–6, 10.1109/WCNC49053.2021.9417242 (2021).
- 13.Mashhadi, M. B. & Gündüz, D. Pruning the pilots: Deep learning-based pilot design and channel estimation for MIMO-OFDM systems. IEEE Trans. Wirel. Commun.20, 6315–6328. 10.1109/TWC.2021.3073309 (2021). [Google Scholar]
- 14.Yi, X. & Zhong, C. Deep learning for joint channel estimation and signal detection in OFDM systems. IEEE Commun. Lett.24, 2780–2784. 10.1109/LCOMM.2020.3014382 (2020). [Google Scholar]
- 15.Chuan, L., Qing, C. & Xianxu, L. Uplink noma signal transmission with convolutional neural networks approach. Journal of Systems Engineering and Electronics 31, 890–898, 10.23919/JSEE.2020.000068 (2020) [DOI]
- 16.Ding, Z. Noma beamforming in SDMA networks: Riding on existing beams or forming new ones?. IEEE Commun. Lett.26, 868–871. 10.1109/LCOMM.2022.3146583 (2022). [Google Scholar]
- 17.Liu, F. et al. DPC-CNN algorithm for multiuser hybrid precoding with dynamic structure. IEEE Trans. Green Commun. Netw.[SPACE]10.1109/TGCN.2024.3376571 (2024). [Google Scholar]
- 18.Jiang, R. et al. Bivariate pilot optimization for compressed channel estimation in RIS-assisted multiuser MISO-OFDM systems. IEEE Trans. Veh. Technol.72, 9115–9130. 10.1109/TVT.2023.3250252 (2023). [Google Scholar]
- 19.Xie, Y., Teh, K. C. & Kot, A. C. Deep learning-based joint detection for OFDM-NOMA scheme. IEEE Commun. Lett.25, 2609–2613. 10.1109/LCOMM.2021.3077878 (2021). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.