Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2024 Nov 29;14:29728. doi: 10.1038/s41598-024-81075-w

A multi-level thresholding image segmentation algorithm based on equilibrium optimizer

Pei Hu 1, Yibo Han 1, Zheng Zhang 1, Shu-Chuan Chu 2, Jeng-Shyang Pan 2,3,✉
PMCID: PMC11607085  PMID: 39613878

Abstract

Multi-level thresholding for image segmentation is one of the key techniques in image processing. Although numerous methods have been introduced, it remains challenging to achieve stable and satisfactory thresholds when segmenting images with various unknown properties. This paper proposes an equilibrium optimizer algorithm to find the optimal multi-level thresholds for grayscale images. The proposed algorithm AEO (advanced equilibrium optimizer) uses two sub-populations to balance exploration and exploitation during the multi-level threshold search process. Two mutation schemes are proposed for the sub-populations to prevent them from being trapped in local optima. AEO offers a repair function to avoid generating duplicate thresholds. The performance of AEO is evaluated on multiple benchmark images. Experimental results demonstrate that AEO has an outstanding ability for multi-level threshold image segmentation in terms of cross-entropy, signal-to-noise ratio (PSNR), structural similarity index measure (SSIM), and feature similarity index (FSIM).

Keywords: Multi-level thresholding, Image segmentation, Equilibrium optimizer

Subject terms: Computer science, Machine learning

Introduction

Image segmentation is an essential technology in computer vision that partitions an image into related, uniform, and non-overlapping regions1–3. These regions consist of image pixels with similar feature values. Its purpose is to simplify and structure complex image information, and it establishes the foundation for subsequent image analysis, feature extraction, and object recognition4,5. The efficiency and accuracy of image processing can be improved by using image segmentation to extract objects and regions of interest6,7.

Image segmentation is widely utilized in various fields8–10. In medical image processing, segmenting organs and lesions can aid doctors in diagnosing and planning treatment11,12. In autonomous driving, segmenting roads, pedestrians, and vehicles enhances environmental perception and supports decision-making13. In remote sensing image analysis, segmenting land cover types supports environmental monitoring and resource management14,15. Other applications include security monitoring, robot vision, industrial inspection, and more. Image segmentation provides refined and intelligent solutions for these fields16–18.

Classic image segmentation methods include: (1) Boundary detection, including edge detection, boundary tracking, etc. These methods detect edges by utilizing the discontinuity in pixel intensity values. (2) Region segmentation, including threshold segmentation, region growth, and region merging. Image thresholding is a common and simple way to analyze images, and there are two main types of techniques: bi-level and multi-level thresholding19,20. Bi-level thresholding produces a binary image where one region corresponds to objects, and the complementary region represents the background. In contrast, multi-level thresholding divides an image into more than two regions21,22.

For decades, it has been a challenge to choose the optimal multi-level thresholds, which is an NP-hard problem23,24. Generally, thresholding can be further divided into parametric and non-parametric methods by optimizing a criterion function defined from image histograms25,26. Parametric methods assume that the grayscale distribution of images follows a given statistical model, and thresholds are determined by estimating the parameters of this distribution. However, these approaches usually result in nonlinear estimation difficulties and demand considerable computational resources. Non-parametric methods, on the other hand, find the optimal threshold based on certain discriminant selection criteria such as inter-class variance, Bayesian error, and entropy. Non-parametric methods are flexible and they have been shown to be more robust and accurate. The computational burden of classical exhaustive searches increases significantly as the threshold increases.

Meta-heuristic algorithms provide an efficient approach to generate near-optimal solutions at a small computational cost when solving complex optimization problems27–29. Consequently, the selection of optimal thresholds is regarded as a single-objective optimization problem. In recent years, meta-heuristic algorithms have been brought to solve multi-level threshold problems, such as particle swarm optimization (PSO)30, artificial bee colony algorithm (ABC)31, and differential evolution (DE)32.

Motivation

Although the aforementioned algorithms provide a good solution, they generally lack global search capability and tend to produce duplicate thresholds in low-dimensional environments. This paper presents a multi-threshold image segmentation model based on equilibrium optimizer (EO). EO is a meta-heuristic algorithm inspired by the concepts of equilibrium and dynamic balance in physics. It simulates the interactions among particles in a system to find optimal solutions by adjusting their positions. EO has been applied in various research fields and applications, including feature selection33, optimization tasks34, job shop scheduling35, and image registration36. The original EO is easy to falling into local traps, so we bring a multi-population to balance exploration and exploitation. The initial population is divided into two sub-populations: one for exploration and the other for exploitation. The sub-populations exchange information regularly and combine their search results to share and integrate optimal solutions. Each solution consists of a set of values representing the thresholds. In order to evaluate the quality of these solutions, cross-entropy is used as the objective function, and the best solution has the smallest value. Duplication may happen because the threshold for image segmentation is limited to the range of 1 to 255. Based on this, we propose a repair method for solutions. The followings are the main contributions:

  1. Establish a multi-population approach to balance global search and local optimization for multi-level thresholds.

  2. Provide two mutation methods to enable the algorithm to thoroughly search thresholds.

  3. Develop a repair strategy to prevent duplicate thresholds within a solution.

The structure of this paper is as follows: “Related works” reviews the latest research progress in image segmentation. “Multi-level threshold image segmentation” details the multi-level image thresholding method based on EO. “Experimental results and analysis” tests the performance of the proposed algorithm using multiple images and algorithms. “Conclusions” summarizes the work and discusses future prospects.

Related works

Generally, image segmentation is defined as the process of grouping homogeneous pixels of an image into a class, and there are many techniques available to accomplish this task. Image segmentation is considered one of the most important steps in computer vision and image processing, and it has been applied to different fields, such as medical imaging, remote sensing, crack detection, and security monitoring. Table 1 shows a summary of some image segmentation techniques proposed in the literature.

Table 1.

Summary of image segmentation methods.

Reference Field Summary
37 General Hybrid firefly and PSO algorithm for six benchmark images
38 General A quantum-behaved PSO for six benchmark images
39 General Parallel multi-verse optimizer (MVO) for eight benchmark images
40 General EO for seven benchmark images
41 General Hybrid arithmetic optimization algorithm (AOA) and harris hawks optimization (HHO)
42 Medical Snake optimizer (SO) for color image segmentation in agricultural diseases
43 Medical PSO for 2D MRI images
44 Medical PSO for brain tumor images
45 Medical Sailfish optimizer algorithm (SOA) for abdominal, lung, and brain images
46 Remote sensing Ant colony optimization (ACO), PSO, and genetic algorithm (GA) for long-term detection
47 Remote sensing DE for air pollution
48 Remote sensing Cuckoo search (CS) based on Renyi entropy
49 Remote sensing African vultures optimization algorithm (AVOA) for Geological images
50 Crack detection Invasive weed optimization algorithm (IWOA) for bi-level thresholding
3 Crack detection PSO based on the minimum arithmetic-geometric divergence
51 Security monitoring A hybrid algorithm for finding spoiled food
52 Security monitoring PSO for PCB defect detection
Open in a new tab

AOA is very strong in exploration, and HHO is also quite powerful in exploitation during the early stages. Consequently, Qiao et al. utilized the characteristics of these algorithms for local and global searches throughout the entire search space to find the optimal solution41. Otsu and Kapur’s thresholding methods are two well-known methods that maximize the inter-class variance and entropy in grayscale image histograms, respectively. Both methods are designed for bi-level thresholding, but a lot of computation is required to adapt them for multi-level image thresholding. Rahkar et al. utilized a hybrid algorithm of firefly and PSO to determine the optimal threshold for multi-level image thresholding37. Yang and Wu proposed a quantum-behaved PSO (NrQPSO) algorithm to find the optimal multi-level threshold for grayscale images38. A non-revisiting scheme is used to avoid re-evaluating the candidate solutions that have already been evaluated. To reduce unnecessary computational costs, NrQPSO provides an automatic stopping mechanism that measures the exploration progress and stops the algorithm in a natural way. Wang et al. proposed a parallel MVO (PMVO)39. The initial solutions are arranged in random groups, and the information from each group is shared after each fixed iteration. This significantly improves the collaborative nature of the MVO algorithm and reduces the drawbacks of premature convergence, search stagnation, and easily falling into the local optimal search space. PMVO demonstrates exceptional performance in image segmentation.

Image segmentation is a challenging task in magnetic resonance imaging (MRI) due to various tumor types, sizes, locations, and shapes. Gtifa et al. presented an effective method for segmenting brain tumors in 3D that utilizes an enhanced PSO43. This algorithm converts 2D images into the topological relationships of slices of 3D MRI images. Some brain tumors may exhibit complex ’bottleneck’ shapes, which are essentially circular with long, tapered, and blurry tails. This leads to difficulties in image segmentation, particularly around the extended tail regions or the ’bottleneck’ areas. Zhang et al. improved a random position search method with a PSO algorithm to segment brain tumor images in an attempt to solve this problem44. Shajin et al. proposed a multi-level threshold SOA based on Levy flight, chaos, and opposition for precise medical image segmentation45. The optimal multi-level thresholds are utilized to segment abdominal, lung, and brain images using Otsu entropy and Kapur entropy.

Remote sensing images carry a vast amount of critical information, and image segmentation helps analyze remote sensing data. Sheoran et al. introduced the application of ACO, PSO, and GA to optimize remote sensing image processes46. The detection of long-term changes over time can be achieved by segmenting remote sensing images into different sub-regions. Ramadas et al. applied a divergent DE algorithm to segment the collected remote sensing images47. The proposed algorithm effectively detects air quality and significantly reduces computation time. Pare et al. combined CS with Renyi entropy to determine the optimal threshold48. They modify the Levy flight step size to enhance convergence speed, and this algorithm achieves precise segmentation with low time complexity.

Gharehchopogh et al. used an improved AVOA49, and employed Kapur entropy, Tsallis entropy, and Otsu entropy as evaluation criteria. The quantum rotation gate mechanism increases population diversity during the optimization phase and improves the performance by escaping local traps. The association strategy method is used to obtain and search for the optimal solution quickly. These two mechanisms increase the diversity of solutions produced at all optimization stages, as AVOA mainly focuses on the exploration phase during the early iterations.

Some grayscale histograms of reinforced concrete bridge crack images are unimodal, but more often they are multimodal. Solving the multimodal search space is a complex and exhaustive task. Abdelkader et al. brought a detection method based on adaptive multi-objective optimization50. The proposed method combines the flexibility of information theory functions with the invasive weed optimization algorithm (IWOA) for bi-level thresholding. This approach improves the performance of image segmentation for reinforced concrete bridge crack images. Nie et al. proposed an enhanced PSO algorithm with local random perturbations3. For crack detection, they utilize a threshold criterion based on the minimum arithmetic-geometric divergence, which adaptively determines the threshold according to the distribution of pixel values in images. The enhanced PSO algorithm increases the diversity of candidate solutions and improves global convergence performance.

Goel et al. developed an algorithm based on visual data to assess food quality and deployed it in food storage facilities to detect early signs of spoilage51. They introduce various segmentation techniques to identify spoiled food effectively. Additionally, they create a hybrid algorithm of moth flame optimization (MFO), gravitational search algorithm (GSA), and PSO to enhance K-means clustering and multi-level thresholding. In view of the problems of low accuracy, complex equipment, and high costs in the automatic detection of printed circuit board (PCB) defects, Chang et al. proposed a method for accurately locating these defects52. They employ PSO to enhance the efficiency of image segmentation. Additionally, they integrate the strengths of the fast library for approximate nearest neighbors (FLANN) algorithm and the speeded-up robust features (SURF) method. This combination enhances the performance of feature matching and reduces registration errors in images.

As a new meta-heuristic algorithm, Abdel-Basset et al. applied EO to image segmentation40. Experiments show that EO is superior to whale optimization algorithm (WOA), bat algorithm (BA), sine-cosine algorithm (SCA), salp swarm algorithm (SSA), HHO, crow search algorithm (CSA), PSO on the Berkeley dataset in terms of peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and maximum absolute error.

In the algorithms mentioned above, such as HHO and ChOA, etc., when they are searching for the optimal threshold, these algorithms may fall into the local optima and encounter duplicate thresholds. The advanced EO algorithm (AEO) specifically designs mutation and duplicate solution repair mechanism to address multi-threshold image segmentation.

Multi-level threshold image segmentation

Image segmentation divides an image into a set of non-overlapping regions, each with different features, so that some interesting objects are highlighted. This paper concentrates on pixel-based image segmentation, accomplished by analyzing image features and pixel distances. Figure 1 illustrates the specific image segmentation process.

Figure 1.

Figure 1

Open in a new tab

The image segmentation process.

Objective function

Cross-entropy is a mathematically sound and theoretically justified objective function used in multi-threshold image classification that is directly aimed at reducing classification errors. Compared to other criteria, cross-entropy effectively manages probability distributions and adapts thresholds according to local and global environments. By minimizing the difference between predicted and actual class distributions, cross-entropy ensures that the algorithm learns to classify pixels more accurately, so it is particularly well-suited for complex classification tasks such as multi-threshold image processing.

We utilize the minimization of cross-entropy as the segmentation criterion and introduce the concept of selecting multiple thresholds in grayscale images. Since image histograms can contain valleys and wide peaks with different heights, the cross-entropy method addresses these issues by measuring the uniformity of histogram information between the original and segmented images.

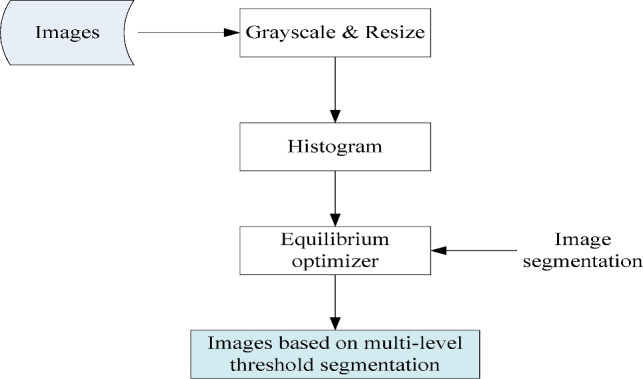
A lower cross-entropy value indicates lower uncertainty and higher uniformity between the original and thresholded images. Let I be the original image and h(i), i = 1, 2, ..., L be the corresponding histogram. The threshold (th) is used to construct the thresholded image (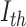Inline graphic) as follows:

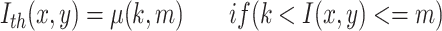graphic file with name M2.gif 1
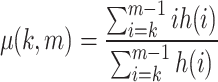graphic file with name M3.gif 2

where I(x, y) is the gray level of the pixel at coordinates (x, y), and k and m are threshold values.

53,54 suggested a more efficient recursive programming approach to find the cross-entropy for gray images, as depicted in Equation (3).

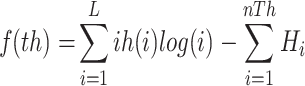graphic file with name M4.gif 3
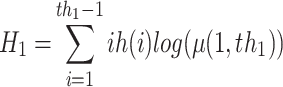graphic file with name M5.gif 4
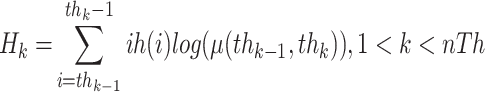graphic file with name M6.gif 5
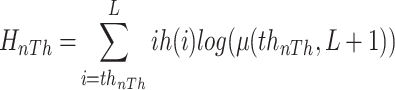graphic file with name M7.gif 6

where th = [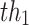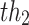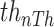Inline graphic, Inline graphic, ..., Inline graphic], nTh is the number of thresholds, and L represents the gray levels of an image.

Advanced equilibrium optimizer

Meta-heuristic algorithms are required to balance exploration and exploitation in multi-level threshold segmentation of images. Exploitation results in the algorithms failing to fully cover the search space and reduces population diversity. On the other hand, exploration causes a slow convergence of them and impedes the ability to find the optimal solution in potential threshold areas. We employ a multi-population EO algorithm to segment images with multi-thresholds. The population is split into two sub-populations: one for exploration and the other for exploitation. This method increases the search space coverage and prevents the algorithm from prematurely converging to a local optimum. The sub-populations regularly share information and combine their findings, thereby improving the global search capability and search efficiency. This multi-population strategy increases the probability of finding the global optimal threshold, and Algorithm 1 describes the pseudo code of AEO.

Algorithm 1.

Algorithm 1

Open in a new tab

AEO

Equilibrium optimizer

In the original EO, position updates are performed using the equilibrium pool and Equation (7)55.

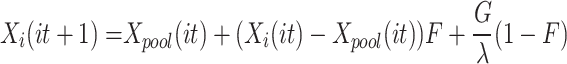graphic file with name M11.gif 7
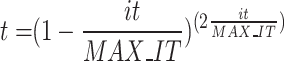graphic file with name M12.gif 8
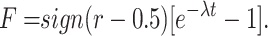graphic file with name M13.gif 9
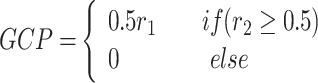graphic file with name M14.gif 10
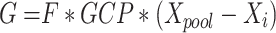graphic file with name M15.gif 11

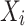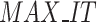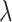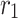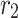where Inline graphic implies the position of individual i, and it represents the current iteration. Inline graphic represents the maximum iteration. Sign is the signum function of Matlab. Inline graphic, r, Inline graphic, and Inline graphic are random values between [0,1]. The equilibrium pool consists of four optimal solutions and their average position (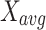Inline graphic), and 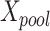Inline graphic is selected randomly from the pool.

  1. Exploration In Equation (7), if the generated random number r2 is less than 0.5, G won’t be involved in the position update, thus reducing population diversity. Sub-population P1 is responsible for exploration, and we optimize its equation to:
    graphic file with name M23.gif 12
    Equation (12) ensures that P1 maintains diversity and enhances exploration capability.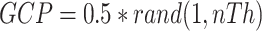
  2. Exploitation 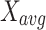Inline graphic in the equilibrium pool increases the random possibility of the population, but it slows down convergence. Sub-population P2 cancels this position and Equation (7) is modified to: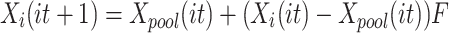
    graphic file with name M25.gif 13

Equation (13) guarantees that P2 converges quickly to the four optimal solutions and enhances its exploitation capability.

Mutation

Mutation is instrumental in EO. It increases population diversity by introducing random changes and prevents EO from converging to local optimal solutions too early. A larger step size aids in exploring new areas of the search space and enhancing global search ability, while a smaller step size helps in refining the search and improving the accuracy of local exploitation. If the four optimal solutions remain unchanged after 10 iterations, P1 has not yet discovered the potential optimal solution area. It needs to be forced P1 to change the search area through mutation. P2 must fine-tune its search direction to find the optimal solution when it is not updated in 10 iterations. P2 follows the mutation process described in Algorithm 2, while P1 mutates in the manner shown in Algorithm 3:

Algorithm 2.

Algorithm 2

Open in a new tab

Mutation1

Algorithm 3.

Algorithm 3

Open in a new tab

Mutation2

In37, PSO focuses more on local search exploitation, while FA excels in global exploration. The hybrid algorithm is not always dynamically adjustable, and in some cases, it can result in premature convergence or inefficient exploration. AEO’s two mutations provide a consistent balance and robustness in finding high-quality solutions, especially for complex problems such as image segmentation, where local fine-tuning and global exploration are necessary. The mutation operation perturbs certain parts of the existing solutions, so that AEO explores new areas in the search space for improving global search capability and solution quality. The algorithm continuously discovers and optimizes solutions during the iteration process. For ease of understanding, Figure 2 shows examples of two mutations.

Figure 2.

Figure 2

Open in a new tab

The examples of the proposed mutations.

Repairing solutions

In the process of multi-threshold image segmentation, the presence of the same threshold will lead to loss of detail information and unstable segmentation. Segmentation algorithms cannot accurately distinguish between different regions and often ignore important features. However, duplication may occur since the threshold for image segmentation is constrained to the range of 1 to 255. To address this issue, we propose a method for repairing the solutions, as shown in Algorithm 4 and Figure 3.

Algorithm 4.

Algorithm 4

Open in a new tab

Repairing operation

Figure 3.

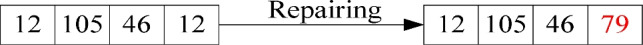
Figure 3

Open in a new tab

The examples of the proposed repairing method.

Computational complexity

The AEO algorithm mainly includes position update and objective function calculation, so its time complexity for each iteration is O(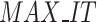Inline graphic*N*dim) and O(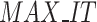Inline graphic*N*g), respectively. g represents the execution time of the objective function, while N is the population size. The maximum time complexity of AEO is O(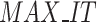Inline graphic*N*dim+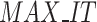Inline graphic*N*g).

Experimental results and analysis

Chimp optimization algorithm (ChOA)56, EO40, HHO53, SSA57 are state-of-the-art image segmentation algorithms used to evaluate the performance of the proposed algorithm AEO. The population size of these algorithms is set to 30, with a maximum of 100 iterations. Table 2 exhibits the basic parameter settings of the algorithms to ensure fairness in the experiments.

Table 2.

The key parameters of the compared algorithms.

Algorithm Key parameters
EO & AEO a1=2; a2=1; GP=0.5;
HHO E1=2; 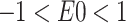Inline graphic;
ChOA C1G1=C1G2=1.95; C1G3=C1G4=2.5; C2G1=G2G2=C2G3=C2G4=2.5;
SSA c1 = 2 * exp (-(4*it/Inline graphic)Inline graphic)
Open in a new tab

Experimental analysis on benchmark images

Our experiments use nine test images from Berkeley University Dataset58 for testing the performance of our algorithm, namely Airplane, Barbara, Cameraman, Chelsea, Coffee, Livingroom, Mandrill, Monarch, and Peppers, and it has been widely used to benchmark segmentation algorithms in the literature37–40.

High-level thresholds are usually employed to evaluate the quality of image segmentation algorithms. According to the reports by53,56, the numbers of thresholds (nTh) selected are 2, 3, 4, and 5. Before segmenting, we first transform color images into 8-bit grayscale images of 256*256 pixels. The data presented in this paper are derived from 20 runs of all the algorithms.

From the results in Table 3, it is evident that AEO achieves the optimal solutions on 7, 5, 6, and 6 images when nTh=2, 3, 4, and 5, respectively. AEO significantly outperforms the comparison algorithms in cross-entropy. EO performs better than HHO and SSA, while ChOA exhibits the poorest performance. We further utilize the Friedmanran rank test, a nonparametric statistical method, to compare the differences of multiple related results. The average ranks of AEO, EO, HHO, ChOA, and SSA are 1.53, 2.81, 2.81, 5, and 2.86, respectively. The superior results of AEO can be attributed to the introduction of two cooperative sub-populations, which allow the solution space to be more thoroughly utilized. AEO demonstrates more effective search capabilities to achieve better results. The algorithms perform closest to the theoretical optimal solution in Barbara, while their performance is the worst in Coffee. AEO excels in correctly distinguishing target regions from background areas. AEO accurately segmented images by measuring the difference between predicted and actual probability distributions.

Table 3.

The fitness values of the algorithms on the benchmark images.

Level Image AEO EO HHO ChOA SSA
2 Airplane 0.2298 0.2299 0.2299 0.2727 0.2299
Barbara 0.0252 0.0277 0.0325 0.0707 0.0285
Cameraman 0.4196 0.4184 0.4194 0.4741 0.4191
Chelsea 0.2930 0.2935 0.2931 0.3782 0.2932
Coffee 0.7046 0.7054 0.7049 0.7969 0.7049
Livingroom 0.5071 0.5076 0.5072 0.6008 0.5073
Mandrill 0.2958 0.2964 0.2967 0.3601 0.2965
Monarch 0.3592 0.3580 0.3563 0.4362 0.3561
Peppers 0.5083 0.5085 0.5087 0.5668 0.5085
3 Airplane 0.2298 0.2301 0.2299 0.2770 0.2299
Barbara 0.0276 0.0252 0.0286 0.0715 0.0282
Cameraman 0.4192 0.4185 0.4193 0.4903 0.4190
Chelsea 0.2930 0.2934 0.2933 0.3508 0.2932
Coffee 0.7046 0.7051 0.7049 0.7859 0.7049
Livingroom 0.5071 0.5077 0.5071 0.5638 0.5072
Mandrill 0.2958 0.2963 0.2961 0.3868 0.2961
Monarch 0.3592 0.3566 0.3648 0.4199 0.3602
Peppers 0.5083 0.5084 0.5083 0.5684 0.5083
4 Airplane 0.2298 0.2301 0.2344 0.2703 0.2314
Barbara 0.0309 0.0297 0.0358 0.0669 0.0321
Cameraman 0.4191 0.4194 0.4187 0.4606 0.4192
Chelsea 0.2930 0.2935 0.2931 0.3962 0.2932
Coffee 0.7046 0.7051 0.7049 0.8135 0.7049
Livingroom 0.5071 0.5076 0.5072 0.5569 0.5072
Mandrill 0.2958 0.2962 0.3009 0.3860 0.2976
Monarch 0.3592 0.3595 0.3577 0.4167 0.3576
Peppers 0.5083 0.5086 0.5113 0.5796 0.5094
5 Airplane 0.2298 0.2300 0.2301 0.4224 0.2301
Barbara 0.0270 0.0262 0.0316 0.0607 0.0283
Cameraman 0.4196 0.4192 0.4190 0.4591 0.4197
Chelsea 0.2930 0.2939 0.2945 0.3761 0.2941
Coffee 0.7046 0.7052 0.7052 0.7661 0.7052
Livingroom 0.5071 0.5075 0.5071 0.5963 0.5072
Mandrill 0.2958 0.2963 0.2961 0.4242 0.2961
Monarch 0.3577 0.3579 0.3572 0.4378 0.3571
Peppers 0.5083 0.5085 0.5129 0.6182 0.5099
Open in a new tab

Significant values are in bold.

We also examine the average CPU time required for each algorithm to complete 100 iterations, as shown in Table 4 (in seconds). It can be concluded that EO has fast computation because its running time is shorter than ChOA, AEO, HHO, and SSA. The computation time for AEO is longer due to the additional mechanisms to prevent local traps, as well as the position correction and sub-population communication. We also found that the running time difference between AEO and HHO is less than 0.01 seconds. However, the solution quality of AEO is superior to HHO. Nonetheless, its computation time remains manageable. In all cases where AEO is not the fastest algorithm, the average CPU time required by AEO is less than 18% compared to the fastest algorithm. In short, AEO’s performance is still acceptable for multi-level thresholding image segmentation.

Table 4.

The average running time of the algorithms on the benchmark images.

Level Image AEO EO HHO ChOA SSA
2 Airplane 0.3387 0.2881 0.3483 0.3182 0.3250
Barbara 0.3771 0.3028 0.3619 0.3263 0.3354
Cameraman 0.3408 0.2896 0.3645 0.3164 0.3156
Chelsea 0.3456 0.2892 0.3499 0.3201 0.3183
Coffee 0.3380 0.2878 0.3468 0.3178 0.3242
Livingroom 0.3380 0.2888 0.3462 0.3187 0.3243
Mandrill 0.3496 0.2914 0.3507 0.3227 0.3306
Monarch 0.3381 0.2875 0.3468 0.3195 0.3241
Peppers 0.3364 0.2898 0.3504 0.3187 0.3255
3 Airplane 0.3418 0.2894 0.3509 0.3194 0.3274
Barbara 0.3880 0.3024 0.3591 0.3290 0.3398
Cameraman 0.3408 0.2864 0.3517 0.3175 0.3149
Chelsea 0.3456 0.2910 0.3546 0.3199 0.3188
Coffee 0.3454 0.2849 0.3470 0.3171 0.3258
Livingroom 0.3361 0.2875 0.3451 0.3180 0.3229
Mandrill 0.3478 0.2878 0.3506 0.3210 0.3287
Monarch 0.3425 0.2877 0.3495 0.3174 0.3266
Peppers 0.3371 0.2893 0.3468 0.3196 0.3244
4 Airplane 0.3395 0.2861 0.3467 0.3182 0.3241
Barbara 0.3836 0.3038 0.3606 0.3271 0.3382
Cameraman 0.3403 0.2870 0.3495 0.3212 0.3162
Chelsea 0.3514 0.2905 0.3518 0.3194 0.3204
Coffee 0.3388 0.2859 0.3443 0.3200 0.3230
Livingroom 0.3425 0.2848 0.3481 0.3183 0.3251
Mandrill 0.3460 0.2892 0.3498 0.3214 0.3283
Monarch 0.3374 0.2867 0.3493 0.3205 0.3245
Peppers 0.3418 0.2906 0.3464 0.3169 0.3263
5 Airplane 0.3410 0.2908 0.3472 0.3195 0.3263
Barbara 0.3818 0.3000 0.3590 0.3268 0.3362
Cameraman 0.3413 0.2872 0.3441 0.3200 0.3162
Chelsea 0.3516 0.2888 0.3565 0.3207 0.3204
Coffee 0.3369 0.2846 0.3448 0.3205 0.3140
Livingroom 0.3367 0.2857 0.3473 0.3180 0.3232
Mandrill 0.3483 0.2916 0.3513 0.3206 0.3304
Monarch 0.3400 0.2905 0.3469 0.3175 0.3258
Peppers 0.3463 0.2862 0.3451 0.3162 0.3259
Open in a new tab

Significant values are in bold.

To further evaluate the performance of these algorithms, we use PSNR, SSIM, and feature similarity index (FSIM) to check the quality of output images.

PSNR is a metric used to evaluate the quality of a reconstructed image compared to its original version. It is particularly useful in image compression, segmentation, and other image processing applications. PSNR is expressed in decibels (dB) and can be calculated using the following equations:

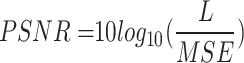graphic file with name M33.gif 14
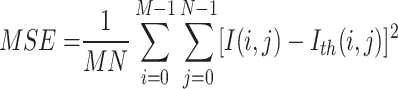graphic file with name M34.gif 15

where M and N represent the length and width pixels of an image.

SSIM is used to measure the similarity of two images.

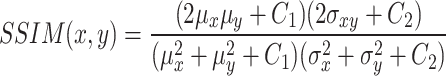graphic file with name M35.gif 16

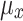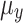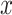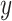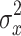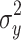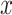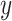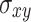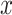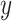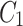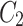where Inline graphic and Inline graphic are the averages of Inline graphic and Inline graphic, respectively. Inline graphic and Inline graphic are the variances of Inline graphic and Inline graphic, respectively. Inline graphic is the covariance of Inline graphic and Inline graphic. Inline graphic and Inline graphic are small constants to stabilize the division with a weak denominator. 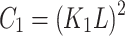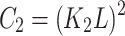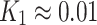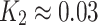Typically, Inline graphic and Inline graphic, with Inline graphic and Inline graphic.

FSIM combines phase congruency (PC) and gradient magnitude to evaluate the similarity between two images.

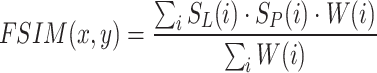graphic file with name M53.gif 17

where 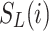Inline graphic is the similarity measure based on luminance, 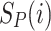Inline graphic is the similarity measure based on phase congruency, and 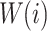Inline graphic is the weight assigned to each pixel based on its significance.

Table 5 lists the average PSNR values of the algorithms. From the results given in the table, it can be noted that for threshold levels of 2, 3, 4, and 5, AEO achieves the best PSNR in 4, 3, 2, and 2 test images, respectively. For nTh=4 and 5, EO outperforms AEO in 4 and 3 images. The Friedmanran test reveals that the average ranks of AEO, EO, HHO, ChOA, and SSA are 2.42, 2.47, 2.44, 4.89, and 2.78, respectively. AEO demonstrates greater stability than EO, with less fluctuation in PSNR values. Even though AEO is inferior to EO when nTh=4 and 5, it can still be concluded that the proposed AEO generally produces segmented images with higher quality compared to other algorithms. The algorithms perform best in Barbara.

Table 5.

The PSNR of the algorithms on the benchmark images.

Level Image AEO EO HHO ChOA SSA
2 Airplane 22.7977 22.7469 22.7824 22.4995 22.7801
Barbara 36.0394 35.2534 35.1534 29.9533 35.4912
Cameraman 22.5898 22.8931 22.6339 22.4283 22.5247
Chelsea 24.4050 24.3953 24.4047 23.1315 24.3965
Coffee 20.8108 20.8181 20.8086 20.6459 20.7034
Livingroom 22.3471 22.3370 22.3446 21.6939 22.3449
Mandrill 22.9328 22.9570 22.9558 21.7140 22.9163
Monarch 19.3626 19.4360 19.5186 18.3581 19.4391
Peppers 22.0450 22.0443 22.0473 21.7446 22.0478
3 Airplane 22.7932 22.7328 22.7616 22.0086 22.7425
Barbara 35.3271 35.7405 36.1063 29.8758 35.7246
Cameraman 22.6926 22.8282 22.6697 21.8937 22.6741
Chelsea 24.4072 24.3952 24.3946 23.4987 34.3949
Coffee 20.8086 20.8023 20.7979 20.7101 20.8032
Livingroom 22.3454 22.3321 22.3471 21.8897 22.3415
Mandrill 22.9246 22.9335 22.9521 21.3973 22.9312
Monarch 19.3540 19.5094 19.3897 18.8436 19.3276
Peppers 22.0438 22.0450 22.0564 21.5978 22.0425
4 Airplane 22.8015 22.7725 22.7148 22.0777 22.7834
Barbara 34.5485 35.3140 34.9118 30.8472 33.8273
Cameraman 22.6905 22.7079 22.7852 22.5535 22.6800
Chelsea 24.4072 24.3935 24.4035 22.9627 24.4057
Coffee 20.8142 20.7775 20.8166 20.5471 20.8187
Livingroom 22.3445 22.3391 22.3495 22.0458 22.3381
Mandrill 22.9316 22.9682 22.9316 21.6042 22.9317
Monarch 19.3617 19.4014 19.4542 18.4922 19.3863
Peppers 22.0468 22.0579 22.0142 21.6335 22.0396
5 Airplane 22.8015 22.7706 22.7613 19.6120 22.7869
Barbara 35.7486 35.8347 35.1857 31.1585 35.5897
Cameraman 22.5993 22.7433 22.7375 22.5143 22.6934
Chelsea 24.4081 24.3862 24.3748 23.1257 24.3974
Coffee 20.8060 20.7972 20.8364 20.8430 20.8025
Livingroom 22.3454 22.3518 22.3455 21.6994 22.3442
Mandrill 22.9331 22.9486 22.9598 19.2814 22.9636
Monarch 19.4204 19.4603 19.5192 18.4894 19.4663
Peppers 22.0498 22.0629 21.9937 21.2420 22.0291
Open in a new tab

Significant values are in bold.

SSIM evaluates the performance of image segmentation algorithms in preserving image structure, brightness, and contrast. By comparing local regions between segmented images and original images, it quantifies the similarity in texture, edges, and detail retention. High SSIM values indicate that segmentation algorithms effectively retain the original features of images. According to the SSIM results in Table 6, it can be observed that AEO outperforms other algorithms at threshold levels 2, 4, and 5, and it has the best SSIM in 2, 3, 2, and 4 out of 9 cases, respectively, which accounts for about 31%. EO and HHO exhibit similar results. Although EO achieves the same number of optimal solutions as AEO, its average rank value is 2.39, higher than AEO’s 2.36. This indicates that AEO’s stability in SSIM is superior to EO. From threshold levels 2 to 5, the proposed AEO provides higher SSIM values and high-quality segmented images based on the obtained thresholds.

Table 6.

The SSIM of the algorithms on the benchmark images.

Level Image AEO EO HHO ChOA SSA
2 Airplane 0.8272 0.8255 0.8267 0.8430 0.8265
Barbara 0.9080 0.8911 0.8791 0.7319 0.8954
Cameraman 0.7157 0.7224 0.7162 0.7248 0.7156
Chelsea 0.8222 0.8215 0.8224 0.7866 0.8220
Coffee 0.6741 0.6739 0.6737 0.6630 0.6737
Livingroom 0.7968 0.7973 0.7968 0.7771 0.7967
Mandrill 0.8499 0.8502 0.8503 0.8227 0.8503
Monarch 0.7838 0.7864 0.7893 0.7464 0.7861
Peppers 0.7687 0.7688 0.7686 0.7589 0.7687
3 Airplane 0.8271 0.8254 0.8260 0.8193 0.8255
Barbara 0.8912 0.9035 0.9043 0.7265 0.8906
Cameraman 0.7181 0.7211 0.7172 0.7167 0.7175
Chelsea 0.8226 0.8214 0.8219 0.7964 0.8220
Coffee 0.6742 0.6739 0.6741 0.6609 0.6741
Livingroom 0.7967 0.7974 0.7968 0.7824 0.7967
Mandrill 0.8497 0.8497 0.8502 0.8148 0.8497
Monarch 0.7836 0.7884 0.7859 0.7631 0.7826
Peppers 0.7688 0.7688 0.7689 0.7565 0.7688
4 Airplane 0.8274 0.8267 0.8278 0.8259 0.8273
Barbara 0.8726 0.8906 0.8714 0.7578 0.8712
Cameraman 0.7182 0.7178 0.7196 0.7216 0.7181
Chelsea 0.8226 0.8219 0.8224 0.7834 0.8223
Coffee 0.6740 0.6745 0.6737 0.6581 0.6739
Livingroom 0.7967 0.7971 0.7970 0.7874 0.7969
Mandrill 0.8499 0.8504 0.8498 0.8175 0.8498
Monarch 0.7838 0.7853 0.7873 0.7508 0.7855
Peppers 0.7688 0.7688 0.7673 0.7566 0.7683
5 Airplane 0.8274 0.8264 0.8260 0.7237 0.8262
Barbara 0.9001 0.9045 0.8821 0.7765 0.8956
Cameraman 0.7155 0.7183 0.7186 0.7238 0.7185
Chelsea 0.8227 0.8215 0.8216 0.7847 0.8219
Coffee 0.6743 0.6741 0.6735 0.6654 0.6740
Livingroom 0.7967 0.7971 0.7968 0.7778 0.7966
Mandrill 0.8499 0.8501 0.8504 0.7177 0.8496
Monarch 0.7859 0.7871 0.7895 0.7585 0.7853
Peppers 0.7688 0.7687 0.7676 0.7489 0.7687
Open in a new tab

Significant values are in bold.

FSIM assesses the performance of image segmentation algorithms in retaining image details and edge information by comparing the phase congruency and gradient magnitude between the original and segmented images. High FSIM values indicate excellent performance in these aspects. Table 7 illustrates the comparison results of AEO with other algorithms in terms of FSIM. At threshold levels 2, 3, 4, and 5, AEO outperforms the comparison algorithms. Especially at threshold levels 2, 3 and 5, AEO has a significant advantage. Moreover, it’s worth mentioning that AEO has the lowest average rank value out of all threshold levels, followed by EO, HHO, SSA, and ChOA. EO and HHO have similar performance at threshold level 5.

Table 7.

The FSIM of the algorithms on the benchmark images.

Level Image AEO EO HHO ChOA SSA
2 Airplane 0.8624 0.8613 0.8621 0.8588 0.8622
Barbara 0.9136 0.9064 0.9050 0.8610 0.9083
Cameraman 0.8610 0.8678 0.8618 0.8591 0.8615
Chelsea 0.8457 0.8451 0.8457 0.8131 0.8455
Coffee 0.8143 0.8140 0.8142 0.8084 0.8142
Livingroom 0.8429 0.8428 0.8429 0.8286 0.8429
Mandrill 0.8863 0.8869 0.8872 0.8689 0.8868
Monarch 0.8501 0.8489 0.8482 0.8680 0.8491
Peppers 0.8243 0.8243 0.8242 0.8166 0.8242
3 Airplane 0.8623 0.8612 0.8616 0.8459 0.8617
Barbara 0.9063 0.9122 0.9171 0.8586 0.9081
Cameraman 0.8634 0.8664 0.8627 0.8495 0.8631
Chelsea 0.8458 0.8449 0.8454 0.8230 0.8454
Coffee 0.8143 0.8140 0.8140 0.8085 0.8141
Livingroom 0.8429 0.8426 0.8429 0.8341 0.8428
Mandrill 0.8861 0.8862 0.8869 0.8642 0.8859
Monarch 0.8500 0.8478 0.8497 0.8595 0.8492
Peppers 0.8243 0.8243 0.8243 0.8141 0.8243
4 Airplane 0.8624 0.8618 0.8610 0.8510 0.8617
Barbara 0.8990 0.9094 0.9047 0.8709 0.9044
Cameraman 0.8633 0.8633 0.8653 0.8584 0.8640
Chelsea 0.8458 0.8454 0.8458 0.8101 0.8457
Coffee 0.8144 0.8136 0.8143 0.8034 0.8141
Livingroom 0.8429 0.8428 0.8429 0.8349 0.8431
Mandrill 0.8863 0.8872 0.8869 0.8664 0.8868
Monarch 0.8501 0.8500 0.8484 0.8685 0.8495
Peppers 0.8243 0.8244 0.8231 0.8127 0.8238
5 Airplane 0.8624 0.8620 0.8617 0.8128 0.8620
Barbara 0.9111 0.9137 0.9063 0.8727 0.9271
Cameraman 0.8609 0.8640 0.8642 0.8590 0.8630
Chelsea 0.8459 0.8450 0.8449 0.8121 0.8449
Coffee 0.8143 0.8138 0.8145 0.8097 0.8142
Livingroom 0.8429 0.8429 0.8429 0.8279 0.8429
Mandrill 0.8863 0.8866 0.8871 0.8126 0.8862
Monarch 0.8491 0.8491 0.8480 0.8665 0.8487
Peppers 0.8243 0.8243 0.8226 0.8063 0.8237
Open in a new tab

Significant values are in bold.

Experimental analysis on deep crack images

The second set of images is used to determine the performance of the algorithms in crack detection, and it consists of 500 images obtained from the Deep Crack Database59. Tables 8, 9, 10, 11 and 12 provide a comprehensive overview of the comparison results based on various metrics, including objective function values, running time, PSNR, SSIM, and FSIM. The results clearly indicate that the AEO algorithm excels across these performance indicators.

Table 8.

The fitness values of the algorithms on the deep crack images.

Level AEO EO HHO ChOA SSA
2 0.1866 0.1875 0.1902 0.2350 0.1996
3 0.1900 0.1909 0.1926 0.2390 0.1984
4 0.1964 0.1972 0.1988 0.2448 0.1985
5 0.1907 0.1915 0.1933 0.2387 0.1987
Open in a new tab

Significant values are in bold.

Table 9.

The average running time of the algorithms on the deep crack images.

Level AEO EO HHO ChOA SSA
2 172.7738 145.7688 175.6381 160.3513 159.6313
3 173.0267 145.9586 175.7741 160.4077 159.7977
4 172.9613 146.0909 175.8209 160.5211 159.8578
5 172.6752 145.9023 175.9485 160.5550 159.7108
Open in a new tab

Significant values are in bold.

Table 10.

The PSNR of the algorithms on the deep crack images.

Level AEO EO HHO ChOA SSA
2 22.5741 22.5124 22.4377 21.3755 22.1540
3 22.5883 22.5204 22.4585 21.3653 22.1580
4 22.4684 22.4141 22.3532 21.3466 22.0764
5 22.5871 22.5308 22.4640 21.4487 22.1889
Open in a new tab

Significant values are in bold.

Table 11.

The SSIM of the algorithms on the deep crack images.

Level AEO EO HHO ChOA SSA
2 0.7437 0.7415 0.7389 0.7072 0.7308
3 0.7420 0.7396 0.7374 0.7046 0.7287
4 0.7404 0.7385 0.7363 0.7055 0.7281
5 0.7423 0.7403 0.7378 0.7065 0.7297
Open in a new tab

Significant values are in bold.

Table 12.

The FSIM of the algorithms on the deep crack images.

Level AEO EO HHO ChOA SSA
2 0.7787 0.7771 0.7762 0.7475 0.7678
3 0.7748 0.7733 0.7728 0.7467 0.7649
4 0.7760 0.7745 0.7738 0.7468 0.7658
5 0.7735 0.7721 0.7716 0.7447 0.7634
Open in a new tab

Significant values are in bold.

Specifically, AEO achieves the lowest objective function value at a threshold of 2, indicating a highly efficient segmentation at this setting, while it reaches the highest value at a threshold of 3. When ranking the algorithms based on their objective function values, AEO outperforms all others, followed by EO, HHO, SSA, and ChOA. Notably, EO demonstrates the fastest execution speed among the algorithms. AEO, although slightly slower, still exhibits reasonable efficiency, and outperforms HHO. The execution times across different thresholds do not vary significantly, and the algorithms maintain consistent performance regardless of the threshold values.

In terms of PSNR, AEO demonstrates superior performance at thresholds of 3 and 5 compared to 2 and 4, and it has ability to maintain high image quality in segmentation. Conversely, the other algorithms generally yield their best performance at a threshold of 5. When evaluating SSIM and FSIM, AEO consistently delivers better results than the comparison algorithms, it achieves optimal SSIM and FSIM values at a threshold of 2. These metrics are crucial as they indicate not just the accuracy of the segmentation, but also how well the segmented images preserve structural information relative to the original images.

In conclusion, the findings strongly suggest that AEO stands out as the most effective algorithm among the five metrics. This superior performance is attributed to its ability to effectively integrate global exploration with local search, and it balances exploration and exploitation better than other algorithms.

Conclusions

Complex algorithms can offer higher accuracy, but they often require more computational resources. It is important to consider the application’s constraints when balancing these factors. High-quality segmentation without excessive computational overhead can be achieved with the help of optimization techniques and hybrid models. This study introduces an advanced EO method for image segmentation. The proposed approach uses two sub-populations to search the threshold space and exchange information. We conduct a series of experiments to evaluate its performance and compare it with HHO, EO, ChOA, and SSA. The experimental results confirm the high quality of segmented images based on PSNR, FSIM, SSIM, and fitness values. The selection of control parameters significantly impacts the performance of AEO. Incorrect parameter tuning can lead to premature convergence (overfitting) or excessively long computational times. AEO can overfit when it focuses too much on specific training data features, particularly in tasks involving high-dimensional or noisy datasets. The algorithm’s performance on training data is excellent but performs poorly on unseen test data due to its failure to generalize. AEO acquires better feature extraction, object recognition, and image enhancement through parameter tuning. The population size is a key parameter for balancing exploration and exploitation. While larger populations improve exploration and diversity, they also increase computational costs. The optimal population size is usually set at 30 to 100 individuals. Iterations are crucial to the success of an algorithm in reaching the global optimal solution. More iterations generally improve performance but at the expense of increased computational time. The optimal number of iterations depends on the complexity of the problem, and it is typically in the range of 50 to 200 iterations. In our experiments, we adopt the settings commonly used in most image segmentation problems, precisely a population size of 30 and an iteration number of 100. The primary drawback of AEO is the incorporation of mutation mechanisms, which results in a longer running time compared to the original EO. Parallelization is a promising solution for addressing these challenges by reducing the running time of the AEO algorithm without compromising its accuracy. By parallelizing AEO, it could utilize modern multi-core processors, GPUs, or distributed systems to speed up execution by processing multiple tasks simultaneously. AEO’s performance could be further optimized by parallelizing fitness evaluations and population updates and using distributed systems.

In the future, AEO may be used in a variety of fields, including image editing, computer vision, and dam safety warnings, demonstrating its versatility and efficiency. For example, in geological exploration, AEO can play a crucial role in analyzing satellite or aerial imagery to identify geological features, such as mineral deposits, fault lines, and vegetation cover.

Acknowledgements

This work is supported by the Research on the Key Technology of Damage Identification Method of Dam Concrete Structure based on Transformer Image Processing (242102521031), the Research on Situational Awareness and Behavior Anomaly Prediction of Social Media Based on Multimodal Time Series Graph (232102520004), and Key Scientific Research Project of Higher Education Institutions in Henan Province (25B520019).

Author contributions

Conceptualization, P. Hu; Investigation, S.C. Chu; Methodology, P. Hu, Y. Han and J.S. Pan; Project administration, J.S. Pan; Resources, S.C. Chu; Software, P. Hu and Z. Zhang; Supervision, Y. Han, J.S. Pan and S.C. Chu; Validation, Y. Han; Writing - original draft, P. Hu; Writing - review & editing, Z. Zhang.

Data availability

Data is available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.

Footnotes

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

References

  • 1.Huang, T., Yin, H. & Huang, X. Improved genetic algorithm for multi-threshold optimization in digital pathology image segmentation. Sci. Rep.14, 22454 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Hossain, S., Mukhopadhyay, S., Ray, B., Ghosal, S. K. & Sarkar, R. A secured image steganography method based on ballot transform and genetic algorithm. Multimed. Tools Appl.81, 38429–38458 (2022). [Google Scholar]
  • 3.Nie, F., Liu, M. & Zhang, P. Multilevel thresholding with divergence measure and improved particle swarm optimization algorithm for crack image segmentation. Sci. Rep.14, 7642 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Sun, G., Zhang, A., Yao, Y. & Wang, Z. A novel hybrid algorithm of gravitational search algorithm with genetic algorithm for multi-level thresholding. Appl. Soft Comput.46, 703–730. 10.1016/j.asoc.2016.01.054 (2016). [Google Scholar]
  • 5.Mukhopadhyay, S., Hossain, S., Ghosal, S. K. & Sarkar, R. Secured image steganography based on Catalan transform. Multimed. Tools Appl.80, 14495–14520 (2021). [Google Scholar]
  • 6.Wang, Z. et al. Improved Latin hypercube sampling initialization-based whale optimization algorithm for covid-19 x-ray multi-threshold image segmentation. Sci. Rep.14, 13239 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Ray, B., Mukhopadhyay, S., Hossain, S., Ghosal, S. K. & Sarkar, R. Image steganography using deep learning based edge detection. Multimed. Tools Appl.80, 33475–33503 (2021). [Google Scholar]
  • 8.Rodríguez-Esparza, E. et al. Optimizing road traffic surveillance: A robust hyper-heuristic approach for vehicle segmentation. IEEE Access12, 29503–29524 (2024).
  • 9.Pramanik, P., Mukhopadhyay, S., Kaplun, D. & Sarkar, R. A deep feature selection method for tumor classification in breast ultrasound images. In International Conference on Mathematics and Its Applications in New Computer Systems. 241–252 (Springer, 2021).
  • 10.Ghosal, S. K., Mukhopadhyay, S., Hossain, S. & Sarkar, R. Application of Lah transform for security and privacy of data through information hiding in telecommunication. Trans. Emerg. Telecommun. Technol.32, e3984 (2021). [Google Scholar]
  • 11.Pan, H. et al. A complete scheme for multi-character classification using EEG signals from speech imagery. IEEE Trans. Biomed. Eng.71, 2454–2462 (2024). [DOI] [PubMed] [Google Scholar]
  • 12.Zhou, G. & Liu, X. Orthorectification model for extra-length linear array imagery. IEEE Trans. Geosci. Remote Sens.60, 1–10 (2022). [Google Scholar]
  • 13.Li, S., Chen, J., Peng, W., Shi, X. & Bu, W. A vehicle detection method based on disparity segmentation. Multimed. Tools Appl.82, 19643–19655 (2023). [Google Scholar]
  • 14.Zhou, G. et al. Orthorectification of fisheye image under equidistant projection model. Remote Sens.14, 4175 (2022). [Google Scholar]
  • 15.Cheng, D., Chen, L., Lv, C., Guo, L. & Kou, Q. Light-guided and cross-fusion u-net for anti-illumination image super-resolution. IEEE Trans. Circuits Syst. Video Technol.32, 8436–8449 (2022). [Google Scholar]
  • 16.Mukhopadhyay, S., Hossain, S., Malakar, S., Cuevas, E. & Sarkar, R. Image contrast improvement through a metaheuristic scheme. Soft Comput.27, 13657–13676 (2023). [Google Scholar]
  • 17.Pramanik, P., Mukhopadhyay, S., Mirjalili, S. & Sarkar, R. Deep feature selection using local search embedded social ski-driver optimization algorithm for breast cancer detection in mammograms. Neural Comput. Appl.35, 5479–5499 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Ghosal, S. K., Mukhopadhyay, S., Hossain, S. & Sarkar, R. Exploiting Laguerre transform in image steganography. Comput. Electr. Eng.89, 106964 (2021). [Google Scholar]
  • 19.Liu, Q., Li, N., Jia, H., Qi, Q. & Abualigah, L. Modified remora optimization algorithm for global optimization and multilevel thresholding image segmentation. Mathematics10 (2022).
  • 20.Jiang, Y., Zhang, D., Zhu, W. & Wang, L. Multi-level thresholding image segmentation based on improved slime mould algorithm and symmetric cross-entropy. Entropy25 (2023). [DOI] [PMC free article] [PubMed]
  • 21.Liu, Q., Li, N., Jia, H., Qi, Q. & Abualigah, L. A chimp-inspired remora optimization algorithm for multilevel thresholding image segmentation using cross entropy. Artif. Intell. Rev.56, 159–216 (2023). [Google Scholar]
  • 22.Xu, H., Li, Q. & Chen, J. Highlight removal from a single grayscale image using attentive GAN. Appl. Artif. Intell.36, 1988441 (2022). [Google Scholar]
  • 23.Yao, F., Zhang, H. & Gong, Y. Difsg2-ccl: Image reconstruction based on special optical properties of water body. IEEE Photon. Technol. Lett.36, 1417–1420 (2024). [Google Scholar]
  • 24.Zhou, G. et al. Shadow detection on high-resolution digital orthophoto map (DOM) using semantic matching. IEEE Trans. Geosci. Remote Sens.61, 1–20 (2023). [Google Scholar]
  • 25.Yin, W. et al. Physics-informed deep learning for fringe pattern analysis. Opto-Electron. Adv.7, 230034 (2024). [Google Scholar]
  • 26.Cai, G., Zheng, X., Guo, J. & Gao, W. Real-time identification of borehole rescue environment situation in underground disaster areas based on multi-source heterogeneous data fusion. Saf. Sci.181, 106690 (2025). [Google Scholar]
  • 27.Jia, H., Rao, H., Wen, C. & Mirjalili, S. Crayfish optimization algorithm. Artif. Intell. Rev.56, 1919–1979 (2023). [Google Scholar]
  • 28.Jia, H., Peng, X. & Lang, C. Remora optimization algorithm. Expert Syst. Appl.185, 115665 (2021). [Google Scholar]
  • 29.Hu, P., Pan, J.-S., Chu, S.-C. & Sun, C. Multi-surrogate assisted binary particle swarm optimization algorithm and its application for feature selection. Appl. Soft Comput.121, 108736 (2022). [Google Scholar]
  • 30.Xiaoqiong, W. & Zhang, Y. E. Image segmentation algorithm based on dynamic particle swarm optimization and k-means clustering. Int. J. Comput. Appl.42, 649–654 (2020). [Google Scholar]
  • 31.Gupta, S. & Deep, K. Hybrid sine cosine artificial bee colony algorithm for global optimization and image segmentation. Neural Comput. Appl.32, 9521–9543 (2020). [Google Scholar]
  • 32.Ren, L. et al. Multi-level thresholding segmentation for pathological images: Optimal performance design of a new modified differential evolution. Comput. Biol. Med.148, 105910 (2022). [DOI] [PubMed] [Google Scholar]
  • 33.Ahmed, S., Ghosh, K. K., Mirjalili, S. & Sarkar, R. Aieou: Automata-based improved equilibrium optimizer with u-shaped transfer function for feature selection. Knowl.-Based Syst.228, 107283 (2021). [Google Scholar]
  • 34.Pan, J.-S., Hu, P., Pan, T.-S. & Chu, S.-C. Improved equilibrium optimizer for short-term traffic flow prediction. J. Database Manag. (JDM)34, 1–20 (2023). [Google Scholar]
  • 35.Sun, Y., Pan, J.-S., Hu, P. & Chu, S.-C. Enhanced equilibrium optimizer algorithm applied in job shop scheduling problem. J. Intell. Manuf.34, 1639–1665 (2023). [Google Scholar]
  • 36.Gui, P., He, F., Ling, B.W.-K. & Zhang, D. United equilibrium optimizer for solving multimodal image registration. Knowl. -Based Syst.233, 107552 (2021). [Google Scholar]
  • 37.RahkarFarshi, T. & K. Ardabili, A. A hybrid firefly and particle swarm optimization algorithm applied to multilevel image thresholding. Multimed. Syst.27, 125–142. (2021)
  • 38.Yang, Z. & Wu, A. A non-revisiting quantum-behaved particle swarm optimization based multilevel thresholding for image segmentation. Neural Comput. Appl.32, 12011–12031 (2020). [Google Scholar]
  • 39.Wang, X., Pan, J.-S. & Chu, S.-C. A parallel multi-verse optimizer for application in multilevel image segmentation. IEEE Access8, 32018–32030 (2020). [Google Scholar]
  • 40.Abdel-Basset, M., Chang, V. & Mohamed, R. A novel equilibrium optimization algorithm for multi-thresholding image segmentation problems. Neural Comput. Appl.33, 10685–10718 (2021). [Google Scholar]
  • 41.Qiao, L., Liu, K., Xue, Y., Tang, W. & Salehnia, T. A multi-level thresholding image segmentation method using hybrid arithmetic optimization and Harris Hawks optimizer algorithms. Expert Syst. Appl.241, 122316 (2024). [Google Scholar]
  • 42.Song, H., Wang, J., Bei, J. & Wang, M. Modified snake optimizer based multi-level thresholding for color image segmentation of agricultural diseases. Expert Syst. Appl.255, 124624 (2024). [Google Scholar]
  • 43.Gtifa, W., Hamdaoui, F. & Sakly, A. 3D brain tumor segmentation in MRI images based on a modified PSO technique. Int. J. Imaging Syst. Technol.29, 501–509 (2019). [Google Scholar]
  • 44.Zhang, T., Zhang, J., Xue, T. & Rashid, M. H. A brain tumor image segmentation method based on quantum entanglement and wormhole behaved particle swarm optimization. Front. Med.9, 794126 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Shajin, F. H., Aruna Devi, B., Prakash, N., Sreekanth, G. & Rajesh, P. Sailfish optimizer with levy flight, chaotic and opposition-based multi-level thresholding for medical image segmentation. Soft Comput.27, 12457–12482 (2023). [Google Scholar]
  • 46.Sheoran, S., Mittal, N. & Gelbukh, A. Improved change detection in remote sensed images by artificial intelligence techniques. J. Indian Soc. Remote Sens.49, 2079–2092 (2021). [Google Scholar]
  • 47.Ramadas, M. & Abraham, A. Segmentation on remote sensing imagery for atmospheric air pollution using divergent differential evolution algorithm. Neural Comput. Appl.35, 3977–3990 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Pare, S. et al. Remote sensing imagery segmentation: A hybrid approach. Remote Sens.13, 4604 (2021). [Google Scholar]
  • 49.Gharehchopogh, F. S. & Ibrikci, T. An improved African vultures optimization algorithm using different fitness functions for multi-level thresholding image segmentation. Multimed. Tools Appl.83, 16929–16975 (2024). [Google Scholar]
  • 50.Abdelkader, E. M. et al. A multi-objective invasive weed optimization method for segmentation of distress images. Intell. Autom. Soft Comput.26, 643–661 (2020). [Google Scholar]
  • 51.Goel, L. et al. Hybrid computational intelligence algorithms and their applications to detect food quality. Artif. Intell. Rev.53, 1415–1440 (2020). [Google Scholar]
  • 52.Chang, Y. et al. PCB defect detection based on PSO-optimized threshold segmentation and surf features. Signal Image Video Process.18, 4327–4336 (2024). [Google Scholar]
  • 53.Rodríguez-Esparza, E. et al. An efficient Harris Hawks-inspired image segmentation method. Expert Syst. Appl.155, 113428 (2020). [Google Scholar]
  • 54.Yin, P.-Y. Multilevel minimum cross entropy threshold selection based on particle swarm optimization. Appl. Math. Comput.184, 503–513 (2007). [Google Scholar]
  • 55.Faramarzi, A., Heidarinejad, M., Stephens, B. & Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl. -Based Syst.191, 105190 (2020). [Google Scholar]
  • 56.Eisham, Z. K. et al. Chimp optimization algorithm in multilevel image thresholding and image clustering. Evolv. Syst.14, 605–648 (2023). [Google Scholar]
  • 57.Alwerfali, H. S. N. et al. A multilevel image thresholding based on hybrid salp swarm algorithm and fuzzy entropy. IEEE Access7, 181405–181422 (2019). [Google Scholar]
  • 58.Berkeley segmentation dataset. https://www2.eecs.berkeley.edu/research/projects/cs/vision/grouping/resources.html. Accessed Nov 2024 [online].
  • 59.Xu, H. et al. Automatic bridge crack detection using a convolutional neural network. Appl. Sci.9, 2867 (2019). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

Data is available from the corresponding author on reasonable request.

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES