Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2024 Dec 2;14:29974. doi: 10.1038/s41598-024-80501-3

Extensive Q-factor tuning for leaky modes with minimal frequency variation in asymmetric slab grating structures

Hyeon Sang Bark 1,#, Seong-Han Kim 1,#, Young Bin Ji 1, Jae Gwang Kwon 1, Chul Kang 1, In Hyung Baek 2, Kitae Lee 2, Seung Jae Oh 3, Tae-In Jeon 4, Chul-Sik Kee 1,✉
PMCID: PMC11612294  PMID: 39622877

Abstract

We investigated an asymmetric slab grating structure to achieve significant tuning of the quality (Q) factor for a leaky mode while minimizing frequency variation. This structure comprises two identical gratings placed on the top and bottom of a slab waveguide, with one grating laterally shifted to introduce asymmetry. Simulations demonstrate that lateral shifting of one grating induces extensive changes in the Q-factor with minimal frequency variation, particularly near the band-flip filling fraction because the band-flip filling fraction remains unaffected by the shifting. The independence of the band-flip filling fraction from lateral shifting is attributed to the superposition property of Bragg scattering processes in the asymmetric grating structure. Experimental verification in the terahertz range confirms significant control over the Q-factor of the leaky mode of the structure. The proposed asymmetric slab grating structure offers possibilities for mechanically controllable optical devices, which are applicable to tunable filters and sensors. This study advances our understanding and application of leaky modes in asymmetric grating structures, revealing a previously unexplored aspect of asymmetric optical lattice.

Subject terms: Terahertz optics, Micro-optics

Introduction

A structure that strongly confines the energy of electromagnetic waves is crucial for studying the interactions between electro-magnetic waves and matter1–3. A typical example is a resonator composed of mirrors. The quality (Q) factor of the resonator indicates how effectively it stores electromagnetic energy. Resonators with high Q-factors are valuable for applications such as efficient lasers, high-resolution filters, and sensitive sensors4–9. The coupling between the leaky modes of the resonator and the free space modes in the air is a critical factor in releasing electromagnetic energy from the resonator into the surrounding air.

Recently, it has been demonstrated that simple optical lattices, distinct from conventional resonator structures, can exhibit a mode that does not couple with free-space modes in air—a nonleaky mode10–12. Because the electromagnetic energy of the nonleaky mode does not dissipate into the air, it possesses an infinite Q-factor. This nonleaky mode is termed a bound state in the continuum (BIC), drawing an analogy with bound states in quantum systems13,14.

A slab waveguide with a one-dimensional grating structure is a common example of a simple optical lattice. Extensive research has been conducted on the fundamental properties and applications of BIC modes within the slab grating structure15. However, achieving a BIC mode with an infinite Q-factor may not be practically feasible. The key challenge lies in tuning a BIC mode into a leaky mode with a high Q-factor to induce a sharp guided mode resonance (GMR) for effective applications16.

To address this challenge, materials with inherent loss, such as graphene, or an asymmetric structure have been incorporated into the slab grating structure17–23. This approach facilitates the transformation of a BIC mode into a leaky mode with a high Q-factor suitable for practical applications. In the former case, the Q-factor of a leaky mode can be tuned without significant frequency changes because the lossy material does not affect the structural properties of the slab grating structure17,18. However, in the latter case, the frequency of a leaky mode varies considerably, while its Q-factor can be adjusted19–21. As a result, asymmetric slab grating structures exhibit weaknesses and limitations in their applications. The characteristics of leaky modes of asymmetric grating structures have received less attention and remain relatively unexplored.

In this study, an asymmetric slab grating structure with a disrupted up-down mirror symmetry is proposed to achieve broad tuning of the Q-factor for a leaky mode while maintaining minimal frequency variation. The up-down asymmetric grating comprises two identical gratings positioned on the top and bottom of the waveguide. The asymmetry is introduced by laterally shifting the position of one of the two gratings. Theoretical analysis indicates that the Q-factor of a leaky mode in the up-down asymmetric grating structure can be extensively tuned by shifting one grating, with the frequency of the leaky mode experiencing minimal change, particularly near the band-flip filling fraction. Experimental observations of Q-factor tuning for the leaky mode in the up-down asymmetric grating structure, achieved by shifting one grating, were conducted in the terahertz range. The proposed structure holds potential for applications in mechanically reconfigurable optical grating devices.

Results

The up-down asymmetric grating structure comprises two identical gratings and a slab waveguide, as depicted in Fig. 1. The up-down asymmetric grating is formed by displacing one of the gratings, resulting in a broken up-down mirror symmetry. For convenience, it is referred to as a d/Λ-shifted asymmetric grating, where d denotes the longitudinal distance between the centers of the top and bottom gratings and Λ is the period of the grating. For instance, when d = Λ/2, the structure is termed a 0.5-shifted asymmetric grating. The heights of the top and bottom gratings are denoted as t1 and t3, respectively, while t2 represents the width of the slab waveguide. The filling fraction is represented by F. Dispersion relations (photonic bands) and spectral properties of guiding modes for the shifted asymmetric grating were calculated using finite-element-method (FEM) simulation.

Fig. 1.

Fig. 1

Open in a new tab

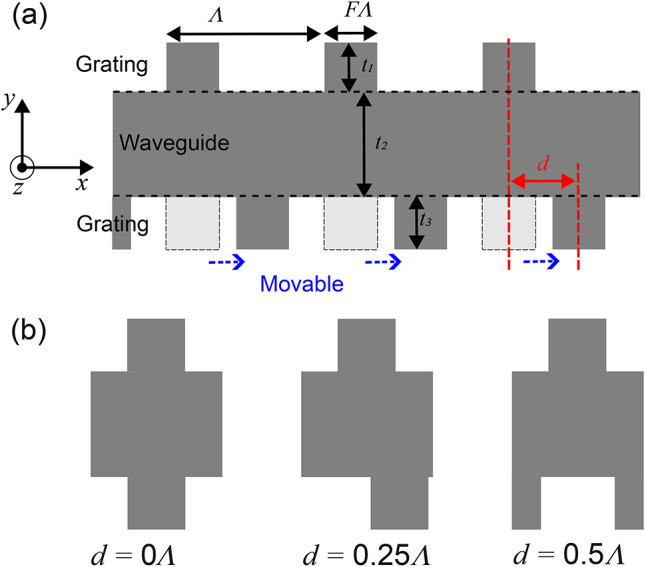
(a) Schematic of an asymmetric grating structure with a broken up-down mirror symmetry. The up-down asymmetric grating is formed by displacing one of the gratings. d denotes the longitudinal distance between the centers of the top and bottom gratings and Λ is the period of the grating. The heights of the top and bottom gratings are denoted as t1 and t3, respectively, while t2 represents the width of the slab waveguide. The filling fraction is represented by F. (b) Unit cell structures for d/Λ = 0, 0.25, and 0.5.

For typical symmetric grating structures, the properties of the BIC mode and the leaky mode, responsible for generating the GMR, have been extensively explored in the second and third bands around the Γ point15,24. Their placement is influenced by the filling fraction and the dielectric modulation of the grating. Consequently, there exists a band-flip filling fraction where their positions interchange25. At the band-flip filling fraction, the frequencies of the BIC and leaky modes become very close, resulting in a practically zero band gap.

It is reasonable to anticipate that the shifted asymmetric grating lacks a symmetry-protected BIC mode and exhibits a leaky mode with considerable radiation loss. If the band-flip filling fraction remains unaffected by the shifting, the manipulation of radiation loss in the leaky mode can be achieved through a shifting parameter while keeping the frequency of the leaky mode constant at the band-flip filling fraction. Therefore, exploring the dependence of the band-flip filling fraction on the shifting parameter is valuable for examining the conjecture.

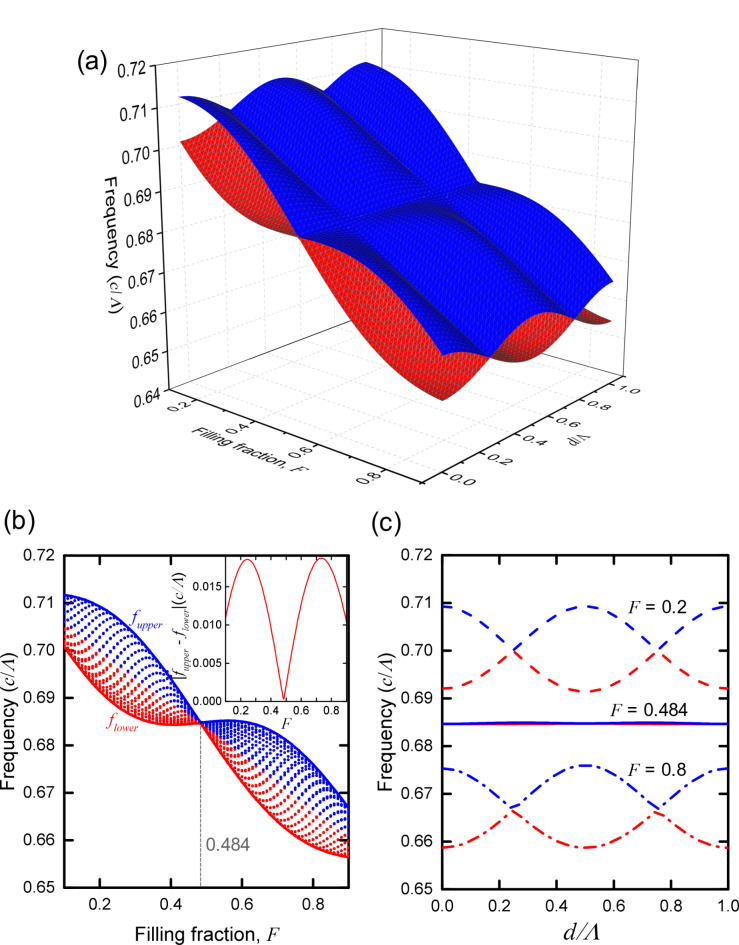
Figure 2a represents the dependence of the frequencies of the second and third bands at Γ point, the edge frequencies, on the filling fraction F and the shifting parameter d/Λ when t1 = t3 = 0.1Λ, t2 = 0.324Λ, and refractive index of a material is 1.75. The frequency is normalized to c/Λ, with the upper (lower) edge frequency denoted by blue (red) color. c is the speed of light. Figure 2b projects the dependence of the edge frequencies on the filling fraction along the d/Λ axis, revealing that the band-flip fraction remains fixed at 0.484 for all d/Λ. In Fig. 2c, the dependence of the edge frequencies on d/Λ is shown for three filling fraction values of 0.2, 0.484, and 0.8. The results demonstrate that the band-flip filling fraction of the shifted asymmetric grating structure remains nearly constant.

Fig. 2.

Fig. 2

Open in a new tab

(a) Dependence of the frequencies of the second and third bands at Γ point, the edge frequencies, on the filling fraction F and d/Λ when t1 = t3 = 0.1Λ, t2 = 0.324Λ, and refractive index of a material is 1.75. The frequency is normalized to c/Λ, with the upper (lower) edge frequency fupper (flower) denoted by blue (red) color. (b) Dependence of the edge frequencies on F projected along the d/Λ axis. It reveals that the band-flip fraction remains fixed at 0.484 for all d/Λ. The inset shows the difference between fupper and flower as a function of F. (c) Dependence of the edge frequencies on d/Λ for F = 0.2, 0.484, and 0.8.

Previous studies have reported that the band flip is induced by the superposition of Bragg processes denoted by BRq, n, where q indicates the Bragg order and n denotes the Fourier harmonic of the dielectric modulation25,26. The band flip filling fraction of the second and third bands is determined when the interplay of BR2,1 and BR1,2 transitions from a negative to positive value, or vice versa. The shifting-independent band-flip filling fraction implies that shifting one grating, without varying the dielectric constant modulation, does not affect the transition-filling fraction.

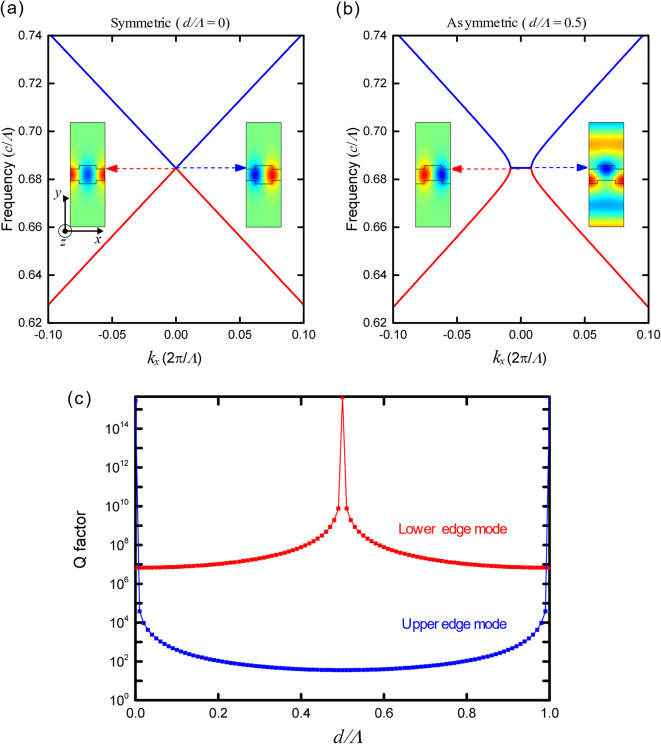
Figure 3a, b depict the second and third bands around Γ point for the symmetric and shifted asymmetric grating, respectively, at the band-flip filling fraction when t1 = t3 = 0.1Λ, t2 = 0.324Λ, and refractive index of a material is 1.75. The insets represent the xy-plane spatial distributions of electric fields of the edge modes at Γ point. The direction of a wave vector is x-direction. The polarization of the electric field is z-direction. The electric field distributions of the symmetric (0.5-shifted asymmetric) grating reveal that the upper band edge mode is the symmetry-protected BIC (leaky) mode, and the lower band edge mode is the leaky (BIC) mode. The 0.5-shifted asymmetric grating supports the BIC mode due to its 180° rotational symmetry around the y-axis27. However, the 0.5-shifted asymmetric grating exhibits a flattened band and an exceptional point, leading to significant radiation loss around Γ point26. The field distribution of the leaky mode effectively explains this characteristic.

Fig. 3.

Fig. 3

Open in a new tab

The second and third bands around Γ point for the symmetric (a) and 0.5-shifted asymmetric grating (b) at the band-flip filling fraction when t1 = t3 = 0.1Λ, t2 = 0.324Λ, and refractive index of a material is 1.75. The insets represent the xy-plane spatial distributions of electric fields of the edge modes at Γ point. The direction of a wave vector is x-direction. The polarization of the electric field is z-direction. (c) Dependence of Q-factors of the edge modes on d/Λ.

The dependence of the Q-factor of the leaky mode on d/Λ informs about how the radiation loss of the mode varies with d/Λ, as the Q-factor is inversely proportional to the radiation loss. Figure 3c illustrates the dependence of Q-factors of the edge modes on d/Λ. The results indicate that the shifted asymmetric grating exhibits two leaky modes, except for the case of d/Λ = 0.5 as expected. The shifting significantly alters the Q-factor of the leaky mode in the shifted asymmetric grating (depicted in blue) because the BIC mode of the symmetric grating transitions to the lossy leaky mode of the shifted asymmetric grating. Consequently, at the band-flip filling fraction, it becomes possible to exert substantial control over the Q-factor (or radiation loss) of one leaky mode through shifting, without a variation in the frequency of the leaky mode. This newly discovered property holds potential applications in the development of mechanically controllable optical devices.

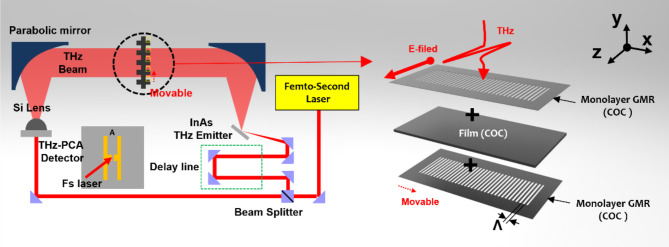
An experiment was conducted to measure the frequencies and Q-factors of the leaky modes of the shifted asymmetric grating in the terahertz (THz) range using a standard THz-time domain spectroscopy (TDS) system28,29. In our home-made THz-TDS setup, as illuminated in Fig. 4, we used a femtosecond laser with a pulse width of 150 femtoseconds and a central frequency of 780 nm to generate terahertz pulses. The laser beam was split by a beam splitter (BS) into two parts in an 80:20 ratio. One path was used for generating THz pulses, while the other was for detection. THz pulses were generated by focusing a 0.8 W laser pulse at the Brewster angle onto a p-type Indium Arsenide (InAs) wafer. These broadband terahertz pulses were then converted into a 2-inch plane wave using a silicon lens and two 90° off-axis parabolic mirrors with a 2-inch focal length. To detect the terahertz pulses, we irradiated the split laser beam onto a photoconductive antenna (PCA) with a power of 12mW. The amplified PCA current, resulting from the terahertz pulses, was measured using a pump-probe method with the split femtosecond laser. The antenna, made of low-temperature-grown Gallium Arsenide (LT-GaAs), had a line width of 10 μm and a spacing of 5 μm, with a 5 μm dipole gap suitable for measuring broadband THz waves. The asymmetric slab grating structures were positioned between two parabolic mirrors for transmission measurement30.

Fig. 4.

Fig. 4

Open in a new tab

Schematics of our home-made THz-TDS setup and the asymmetric grating formed by displacing the bottom COC grating film.

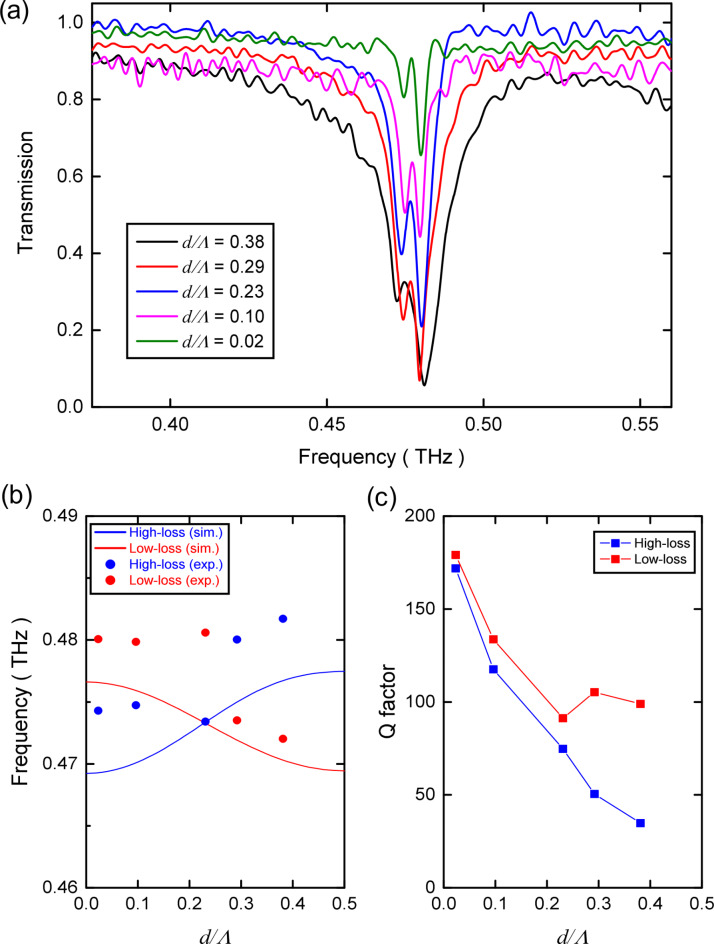
Figure 5a displays the microscopy image of the asymmetric grating formed by displacing the bottom COC grating film. d = 190 μm and Λ = 500 μm. The focal plane of the microscope is adjusted to the upper COC grating film, making it clearly visible, while the bottom COC grating film appears blurred. Heights of ridges, t1 and t3 = 0.25Λ, thickness of the slab waveguide, t2 = 0.2Λ, and F = 0.5. COC (Cyclic Olefin Copolymer) is a polymer material chemically produced by combining cyclic olefins with other monomers. It is known for its excellent optical, mechanical, and chemical properties, especially among plastic materials. It also possesses low refractive index and low absorption in the terahertz range30–35. The real and imaginary parts of the refractive index of the COC film are 1.52 and 9.9 × 10− 4, respectively. These values are nearly invariant under 9.0 THz36. It is essential to note that the femtosecond laser machining fabrication processes for the COC grating film do not guarantee an exact band-flip fraction due to potential inaccuracies. However, the transmission spectrum near the band-flip filling fraction clearly distinguishes the two GMR resonance dips corresponding to the two leaky modes of the shifted asymmetric grating. Figure 5b represents the experimental time-domain transmitted THz signals of d/Λ = 0.38 and air (reference), measured with a step size of 40 μm, resulting in 2000 data points. The numerous oscillations in the transmitted THz signal of d = 0.38Λ effectively represent the characteristics of GMR resonances. The small signal appearing near 160ps is the reflection signal from the measurement photoconductive antenna, induced by the interaction of the main pulse with the measurement setup37.

Fig. 5.

Fig. 5

Open in a new tab

(a) The microscopy image of the asymmetric grating formed by displacing the bottom COC grating film. The focal plane of the microscope is adjusted to the upper COC grating film, making it clearly visible, while the bottom COC grating film appears blurred. (b) Measured time-domain transmitted THz signals of d = 0.38Λ and air. The numerous oscillations in the transmitted THz signal of d = 0.38Λ effectively represent the characteristics of GMR resonances.

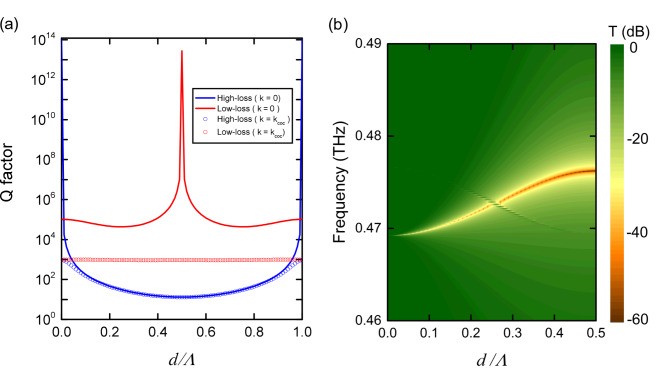
Figure 6 presents the simulated Q-factor of the two leaky modes (a) and transmission spectra (b) as a function of d/Λ when t1 = t3 = 0.25Λ, t2 = 0.2Λ, and F = 0.5. The real and imaginary parts of the refractive index of the COC film are 1.52 and 9.9 × 10− 4, respectively The lines in Fig. 6a represent the simulated Q-factors of the two leaky modes without the imaginary refractive index to account for the material loss. The Q-factor of the low-loss leaky mode (red circles) undergoes a significant decrease due to material loss, stabilizing at an almost constant value of approximately 103. 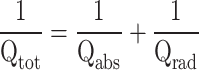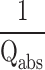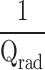A simple formula for determining the total Q factor of a system is written by Inline graphic, where Inline graphic and Inline graphic account for the loss due to material absorption and radiation, respectively. For COC film, 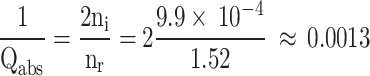Inline graphic and for low-loss band, 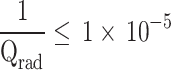Inline graphic. Therefore, the total Q factor, 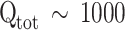Inline graphic, for the low-loss band in the system in simulation. In contrast, the Q-factor of the high-loss leaky mode (blue circles) is minimally affected by material loss, particularly when the shifting parameter exceeds 0.1. These characteristics of the Q-factors are also evident in the transmission spectra in Fig. 6b. The transmission spectra reveal that the frequency of the low-loss leaky mode decreases from around 0.48–0.47 THz, while that of the high-loss leaky mode increases from approximately 0.47–0.48 THz.

Fig. 6.

Fig. 6

Open in a new tab

The simulated Q-factors of the two leaky modes (a) and transmission spectra (b) as a function of d/Λ when Λ = 500 μm, t1 = t3 = 0.25Λ, t2 = 0.2Λ, and F = 0.5. The real and imaginary parts of the refractive index of the COC film are 1.52 and 9.9 × 10− 4, respectively The lines represent the simulated Q-factors of the two leaky modes without the imaginary refractive index to account for the material loss.

Figure 7a depicts the transmission spectra obtained from the measured time-domain transmitted THz signals for five shifting parameters. The two dips corresponding to the GMR resonances from the two leaky modes are clearly observed. The frequencies and Q-factors of the two GMR resonances were obtained by Lorentzian fitting. The observed two GMR resonance frequencies (dots) and the simulated two leaky mode frequencies (lines) are illustrated in Fig. 7b. Red (Bule) color denotes the frequency of the low(high)-loss leaky mode. Overall, the measured dependency trend of the GMR resonance frequencies on the shifting parameter corresponds to the theoretical trend of the leaky mode frequencies, even though the GMR frequencies deviate from the trend near a shifting parameter of 0.23. The overall discrepancy between the observed and the simulated frequencies is likely due to the finite width of the sample. The dependence of measured Q-factors from the transmission spectra at the two GMR resonance frequencies (dots) are represented in Fig. 7c. The Q-factor of the high-loss leaky mode significantly decreases from 170 to 40 by the shifting. The measured Q-factor characteristic for the high-loss leaky mode closely matches the simulated dependency trend of the Q-factor on the shifting parameter, as depicted in Fig. 6a. However, the Q-factor behavior for the low-loss leaky mode deviates from the simulation.

Fig. 7.

Fig. 7

Open in a new tab

(a) The transmission spectra obtained from the measured time-domain transmitted THz signals for five shifting parameters. The two dips corresponding to the GMR resonances from the two leaky modes are clearly observed. (b) The observed two GMR resonance frequencies (dots) and the simulated two leaky mode frequencies (lines). Red (Bule) color denotes the frequency of the low(high)-loss leaky mode. (c) The dependence of measured Q-factors from the transmission spectra at the two GMR resonance frequencies (dots).

There are some issues in the experiment. The COC film is not rigid, so it partially expands or contracts during shifting, leading to a non-uniform grating period. The three layers of COC films composing the sample are strongly held together by electrostatic forces. So, the distance between the films is believed to be negligible compared to the THz wavelength. The discrepancy between the measured and simulated characteristics of leaky modes may be attributed to the non-uniform grating period and the distance being non-negligible compared to the wavelength. Therefore, for practical applications of the proposed asymmetric grating structure, a suitable material should be rigid, maintaining a constant grating period during shifting. Additionally, when layered, the gaps between the layers should be negligible compared to the wavelength of the desired light.

Discussion and conclusions

In conclusion, we proposed and explored an asymmetric slab grating structure with broken up-down mirror symmetry to achieve broad tuning of the Q-factor for a leaky mode while minimizing frequency variation. The up-down asymmetric grating demonstrated the potential for extensive Q-factor tuning by laterally shifting one of the identical gratings, maintaining minimal frequency change, particularly near the band-flip filling fraction. Experimental verification in the terahertz range confirmed significant control over the Q-factors of leaky modes in the proposed structure. The asymmetric slab grating structure introduces possibilities for mechanically controllable optical devices, with potential applications in tunable filters and sensors. The study contributes to the understanding and utilization of leaky modes in asymmetric grating structures, shedding light on an unexplored aspect of asymmetric optical lattices.

Method

Sample fabrication

Our approach to achieving precise ridges with hundreds of micrometers periodicity on COC films involved the application of femtosecond laser machining technology. Femtosecond lasers, characterized by their extremely short pulse duration in the femtosecond range (10–15 s), offer a distinct advantage: their pulse duration is shorter than the thermal diffusion time of the material, thus preventing thermal damage or structural changes. This capability enables precise machining across various materials, including metals, dielectrics, and ceramics, leveraging the principle of multiphoton absorption. Furthermore, there are minimal limitations on the type of material that can be processed. The femtosecond laser utilized in our process featured specific parameters: a wavelength of 1030 nm, pulse width of 230 fs, repetition rate of 30 kHz, beam diameter of 10 μm, and power output of 1 W. Operating under these precise conditions, we successfully produced the desired structures on the COC films.

Acknowledgements

This research was funded by the Technology Innovation Program (20026766, The development of customized sensor technology for installation of safety diagnostic equipment for facilities/food) funded By the Ministry of Trade, Industry and Energy (MOTIE, Korea), An internal R&D programme at KAERI funded by the Ministry of Science and ICT (MIST) of the Republic of Korea (524570-24).

Author contributions

H.S.B. and S.-H.K. conceived and designed the study. C.K., Y.B.J. and J.G.K. performed the simulations and theoretical analysis. Y.B.J. and J.G.K. conducted the experiments and collected the data. I.H.B. and S.J.O. analyzed the experimental data and contributed to the interpretation of the results. K. L., T.-I.J. and C.-S.K. supervised the project and provided critical feedback. H.S.B., S.-H.K. and C.-S.K. wrote the main manuscript text and prepared Figs. 1, 2, 3, 4, 5, 6 and 7. All authors reviewed and approved the final manuscript.

Data availability

The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.

Footnotes

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

These authors contributed equally to this work.

References

  • 1.Chenhao, L. et al. Metafiber transforming arbitrarily structured light. Nat. Commun.14, 7222 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Ishizaki, K. & Noda, S. Manipulation of photons at the surface of three-dimensional photonic crystals. Nature460, 367–370 (2009). [DOI] [PubMed] [Google Scholar]
  • 3.Seo, M. A. et al. Terahertz field enhancement by a metallic nano slit operating beyond the skin-depth limit. Nat. Photonics. 3, 152–156 (2009). [Google Scholar]
  • 4.Matsubara, H. et al. GaN photonic-crystal surface-emitting laser at blue-violet wavelengths. Science319, 445–447 (2008). [DOI] [PubMed] [Google Scholar]
  • 5.Hirose, K. et al. Watt-Class high-power, high-beam-quality photonic-crystal lasers. Nat. Photonics. 8, 406–411 (2014). [Google Scholar]
  • 6.Yanik, A. A. et al. Seeing protein monolayers with naked eye through plasmonic Fano resonances. Proc. Natl. Acad. Sci.108, 11784–11789 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Zhen, B. et al. Enabling enhanced emission and low-threshold lasing of organic molecules using special Fano resonances of macroscopic photonic crystals. Proc. Natl. Acad. Sci.110, 13711–13716 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Foley, J. M., Young, S. M. & Phillips, J. D. Symmetry-protected mode coupling near normal incidence for narrow-band transmission filtering in a dielectric grating. Phys. Rev. B. 89, 165111 (2014). [Google Scholar]
  • 9.Liu, W., Li, Y., Jiang, H., Lai, Z. & Chen, H. Controlling the spectral width in compound waveguide grating structures. Opt. Lett.38, 163–165 (2013). [DOI] [PubMed] [Google Scholar]
  • 10.Kazarinov, R. & Henry, C. Second-order distributed feedback lasers with mode selection provided by first-order radiation losses. IEEE J. Quantum Electron.21, 144–150 (1985). [Google Scholar]
  • 11.Ding, Y. & Magnusson, R. Band gaps and leaky-wave effects in resonant photonic-crystal waveguides. Opt. Express. 15, 680–694 (2007). [DOI] [PubMed] [Google Scholar]
  • 12.Dong, Z. et al. Nanoscale mapping of optically inaccessible bound-states-in-the-continuum. Light-Sci Appl.11, 20 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Marinica, D. C., Borisov, A. G. & Shabanov, S. V. Bound States in the Continuum in Photonics. Phys. Rev. Lett.100, 183902 (2008). [DOI] [PubMed] [Google Scholar]
  • 14.Hsu, C. W., Zhen, B., Stone, A. D., Joannopoulos, J. D. & Soljačić, M. Bound states in the continuum. Nat. Rev. Mater.1, 1–13 (2016). [Google Scholar]
  • 15.Kang, M., Liu, T., Chan, C. T. & Xiao, M. Applications of bound states in the continuum in photonics. Nat. Rev. Phys.5, 659–678 (2023). [Google Scholar]
  • 16.Joseph, S., Pandey, S., Sarkar, S. & Joseph, J. Bound states in the continuum in resonant nanostructures: an overview of engineered materials for tailored applications. Nanophotonics10, 4175–4207 (2021). [Google Scholar]
  • 17.Kim, M., Kee, C-S. & Kim, S. Graphene-based fine tuning of Fano resonance transmission of quasi-bound states in the continuum. Opt. Express. 30, 30666–30671 (2022). [DOI] [PubMed] [Google Scholar]
  • 18.Kim, M., Kim, S. H., Kang, C., Kim, S. & Kee, C. S. Highly efficient graphene terahertz modulator with tunable electromagnetically induced transparency-like transmission. Sci. Rep.13, 6680 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Koshelev, K., Lepeshov, S., Liu, M., Bogdanov, A. & Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett.121, 193903 (2018). [DOI] [PubMed] [Google Scholar]
  • 20.Głowadzka, W., Wasiak, M. & Czyszanowski, T. True- and quasi-bound states in the continuum in one-dimensional gratings with broken up-down mirror symmetry. Nanophotonics10, 3979–3993 (2021). [Google Scholar]
  • 21.Park, G. C. & Park, K. Quasi-bound states in the continuum in asymmetric hetero-bilayer metasurfaces. Opt. Laser Technol.170, 110191 (2024). [Google Scholar]
  • 22.Avrutsky, I. A., Svakhin, A. S. & Sychugov, V. A. Interference phenomena in Waveguides with two corrugated boundaries. J. Mod. Opt.36, 1303–1320 (1989). [Google Scholar]
  • 23.Hemmati, H. & Magnusson, R. Resonant dual-grating metamembranes supporting spectrally narrow bound States in the Continuum. Adv. Opt. Mater.7, 1900754 (2019). [Google Scholar]
  • 24.Ding, Y. & Magnusson, R. Resonant leaky-mode spectral-band engineering and device applications. Opt. Express. 12, 5661–5674 (2004). [DOI] [PubMed] [Google Scholar]
  • 25.Lee, S. G. & Magnusson, R. Band flips and bound-state transitions in leaky-mode photonic lattices. Phys. Rev. B. 99, 045304 (2019). [Google Scholar]
  • 26.Razmjooei, N. & Magnusson, R. Experimental band flip and band closure in guided-mode resonant optical lattices. Opt. Lett.47, 3363–3366 (2022). [DOI] [PubMed] [Google Scholar]
  • 27.Li, L., Li, Y., Zhu, Y. & Yin, H. Rotational symmetry of photonic bound states in the continuum. Sci. Rep.10, 18243 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Neu, J., Schmuttenmaer, C. A. & Tutorial An introduction to terahertz time domain spectroscopy (THz-TDS). J. Appl. Phys.124, 231101 (2018). [Google Scholar]
  • 29.Bark, H. S. et al. Terahertz Spectral properties of PEO-based anti-adhesion films cross-linked by electron beam irradiation. Polymers14, 2008 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Bark, H. S. et al. Broadband terahertz guided-mode resonance filter using cyclic olefin copolymer. Opt. Express. 30, 7976–7986 (2022). [DOI] [PubMed] [Google Scholar]
  • 31.Hack, E., Shorubalko, I., Graf, J., Zolliker, P. & Mavrona, E. Fabrication of freestanding photonic devices combining polymer films with microfabrication techniques and 3D printing. Opt. Express. 31, 29968–29974 (2023). [DOI] [PubMed] [Google Scholar]
  • 32.Cai, L., Jiang, Z. H., Wu, J. B., Chen, H. & Hong, W. Low-loss and flexible terahertz bandpass frequency selective surface based on cyclic olefin copolymer substrate via solvent-free synthesis. Opt. Express. 31, 21706–21720 (2023). [DOI] [PubMed] [Google Scholar]
  • 33.Bark, H. S. & Jeon, T. I. Dielectric film sensing with TE mode of terahertz guided-mode resonance. Opt. Express. 26, 34547–34556 (2018). [DOI] [PubMed] [Google Scholar]
  • 34.Lee, S. B., Bark, H. S. & Jeon, T. I. Enhancement of THz resonance using a multilayer slab waveguide for a guided-mode resonance filter. Opt. Express. 27, 29357–29366 (2019). [DOI] [PubMed] [Google Scholar]
  • 35.Bark, H. S., Jang, K. H., Lee, K. & Jeong, Y. U. THz guided-mode resonance notch filter with variable filtering strength. Sci. Rep.11, 1307 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Cunningham, P. D. et al. Broadband terahertz characterization of the refractive index and absorption of some important polymeric and organic electro-optic materials. J. Appl. Phys.109, 043505 (2011). [Google Scholar]
  • 37.Grischkowsky, D., Keiding, S., Van Exter, M. & Fattinger, C. Far-infrared time-domain spectroscopy with terahertz beams of dielectrics and semiconductors. JOSA B. 7, 2006–2015 (1990). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES