Abstract
Recent laboratory tests and large-scale observations have revealed the complex interplays between aseismic and seismic deformation, as well as the progressive localization of the rock failure process. To investigate these processes, we conducted triaxial tests that combined distributed strain sensing (DSS) with acoustic emission (AE) sensors. Progressive strain localization was detected by DSS at 80% of the peak stress but did not produce measurable AEs. Closer to the peak stress, regions exhibiting strain localizations began to show clusters of AEs. This reveals that DSS measurements are more informative during the preparatory stage of brittle rock failure. The frequency-magnitude distribution of the AEs showed an inverse correlation with the volumetric deformation rate a few seconds preceding catastrophic failure. Our results are consistent with recent large-scale observations and offer crucial insights into progressive failure assessment.
Subject terms: Geology, Seismology
Introduction
Large-scale distributed deformations constrained geodetically have revealed significant aseismic deformation in the preparation zones near the hypocentre of impending earthquakes1–3. These zones, with large aseismic deformation, have been associated with increases in seismic activity prior to the mainshock (e.g.,3–5). For example, in the preseismic phase of the Iquique earthquake of moment magnitude 8.2, localized aseismic deformation close to the eventual hypocentre was accompanied with low magnitude seismicity and the 6.7 foreshock4. There is ongoing debate as to whether aseismic deformation is the cause or consequence of precursory seismicity4,5. While Kato et al.4 could not discard either option for the 8.2 Iquique earthquake, Wang et al.5 proposed a model in which a transient aseismic deformation drove the last hour of the foreshock sequence and eventually triggered the Yangbi 6.1 mainshock. The assessment of theoretical models using large-scale observations has presented several obstacles that are difficult to reconcile6. Studying the spatial-temporal relationship between precursory seismic activity and deformation in a controlled environment has the potential to improve our understanding of earthquake preparation and nucleation.
At laboratory scale the stick-slip tests on saw-cut samples are commonly used to study fault zones7–9. In this end-member test, regions of preparatory aseismic slip can accumulate along the thin frictionally controlled planar discontinuity, increasing in both spatial extent and slip magnitude prior to the dynamic slip10,11. While laboratory-scale earthquake nucleation on saw-cut samples is to some extent well understood, the up-scaling to real faults remains a challenge6. Off-fault rock damage has been inferred from seismicity around the eventual rupture zones preceding large earthquakes6,12. These observations encouraged the development of the “progressive localization” earthquake model12. This model describes progressive damage localization from distributed damage in a rock volume to more localized deformation. Once the damage is localized in a thin region, a large dynamic fracture nucleates6. Volumetric deformation is especially important in complex crustal fault systems, but is also relevant for subduction zones and major continental plate boundary fault, where the systems are not dominated by an existing weak fault with little strength recovery13.
Triaxial laboratory tests on intact rock samples constitute the other experimental end-member, commonly used to investigate catastrophic failure in confined conditions14. These tests may represent localized volumetric damage processes around the eventual macrofracture15. Developing more insights into the preparatory processes that lead to failure at laboratory scales may provide further insights into the progressive localization and integrated models6,12,13. In addition, triaxial tests on intact samples constrain important mechanisms of fault reactivation and rock body failure that occur in natural and man-made environments (e.g., injection-induced earthquakes16,17 and mining).
During triaxial testing, micro-fracturing of the rock can generate elastodynamic stress waves referred to as acoustic emissions (AEs, 18). AEs generated in laboratory experiments posses spectral properties similar to seismicity observed in nature19. Both AE and seismicity in nature have been observed to follow the Gutenberg-Richter (GR) frequency-magnitude distribution20–22. An important parameter in the GR law (where N is the number of events equal to or above magnitude , and a and b are constants) is the b-value, which indicates the relative proportion of small to large earthquakes in a given region23. AE catalogues have shown a decrease in the b-value as failure is approached, which correlates with increasing differential stress21,24,25. However, fluctuations in the b-value are not always correlated with differential stress18,26. This raises the question of whether other parameters can be correlated with b-value fluctuations to assess rock failure.
Spatial-temporal analyses of AEs in triaxial tests have shown complex localization and delocalization prior to failure27, which can be quantified using the fractal pattern in the spatial distribution of AE hypocenters (D-value, 28). Randomly distributed events are characterized by a higher D-value, while spatially localized events show a decrease in the D-value. In crystalline rock, localizations of AEs have been observed to begin near the peak strength of the sample, and are attributed to the formation of the macrofracture18,29. The macrofracture nucleates in a region that exhibited only background level of AE activity, and is therefore believed to occur in a zone without significant preparatory damage29, even if the nucleation occurs at the sample periphery30. However, the recent implementation of distributed deformation measurements has allowed Cartwright et al.31 to observe the early nucleation of localized preparatory damage that is undetectable by the AE sensors. They used the dynamic X-ray computed tomography (XR-CT) in combination with two AE sensors to measure the seismic and aseismic deformation within sandstone samples in low confinement triaxial tests. This implementation also allowed for the observation of a transition to a dilation-dominated strain as a precursor to a sudden increase in the AE rate31. In uniaxial tests conducted on granite samples using digital image correlation (DIC) and AE sensors, clusters of AEs were observed to nucleate in zones of accelerated localized strain32,33. The utilization of distributed measurements may provide insight into the early stages of damage mechanisms experienced by deep rock masses, which, as have been shown25,34,35, may differ from those observed in unconfined environments. Moreover, the integration of distributed measurements with an array of AE sensors, required for a quantitative understanding, enables the study of the spatial-temporal correlation between aseismic and seismic deformations leading up to catastrophic failure.
Another methodology used to better constrain the aseismic deformation field on the surface of the sample is distributed strain sensing (DSS) based on the use of optical fibres36,37. Compared to XR-CT, this method offers reduced spatial resolution but increased temporal resolution; it can be used on larger sample sizes and is compatible with high confinement pressures. In this study, we extended the DSS method by coupling it with an array of fully calibrated AE sensors. This integrated setup allowed for the simultaneous measurement of distributed deformation and the study of AE locations throughout the failure process in confined conditions. We implemented this method in a confined compression test to failure on an intact granite sample. Following the test, we employed XR-CT to visualize the fracture network produced during the failure test. The combined analysis of DSS and AE data provides a framework for developing a quantitative understanding of seismic and aseismic damage mechanisms leading to catastrophic failure in rocks. We report the results from the best instrumented experiment, when confining pressure (10 MPa) was applied to a dry intact sample of Rotondo granite (101.6-mm height, 49.5-mm diameter), and the sample was axially loaded (strain rate of 4.9 /s, constant until the beginning of dilatancy). However, these results are representative and several preparatory experiments were conducted38,39.
Results
Slow to accelerated deformation leading to failure
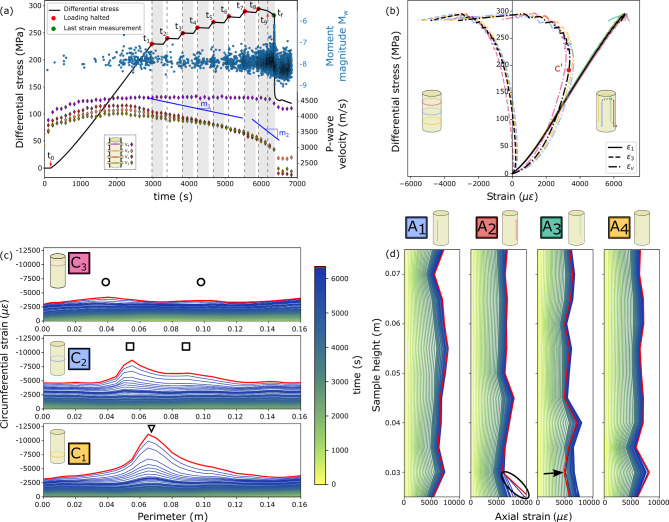
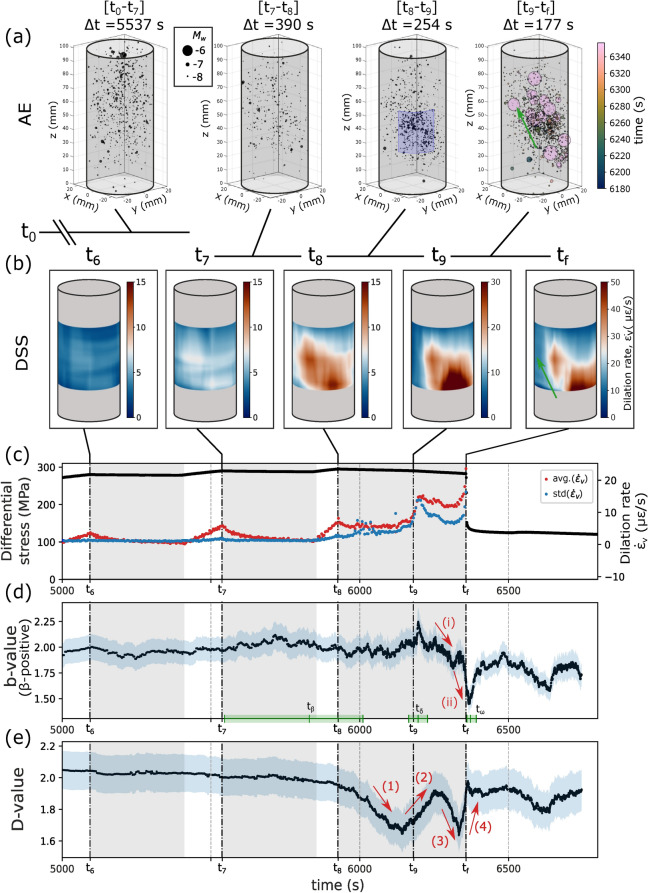
Figure 1a shows the macroscopic stress response of the sample following the experimental protocol described in Section Experimental protocol. The intervals colored in light gray indicate the time periods during which the displacement of the loading piston was stopped (holding phases) in order to slow the failure process (see Section Experimental protocol). Red dots indicate the beginning of the holding phases ( to ), while the red arrow indicates an accelerated drop in the differential stress rate (). Catastrophic failure occurred at , when a dynamic stress drop of approximately 160 MPa was observed. The average axial () and circumferential () strains measured in each segment on the sample’s periphery are shown in Fig. 1b. The average volumetric strain () was calculated for each circumferential segment (indicated by colored dash-dot line) and for the entire sample (indicated by the dash-dot black line). We calculated the Young’s modulus to be E = 50.7 GPa and the Poission’s ratio to be = 0.26, which both fall within the limits reported in the literature (see Section 1 of the Supplementary Material).
Fig. 1.
(a) Observed differential stress response, temporal evolution of AE magnitudes (blue circles) and P-wave velocity during the test. Isolated P-wave velocity plot is provided in the Section 6 of Supplementary Material, and a zoom of the final relaxation phase is provided in Section 2 of the Supplementary Material. (b) Average of the implemented four axial and three circumferential DSS segments and the volumetric strain. Colour code is given in the small sample scheme and in the squares in panels (c) and (d). (c) Distributed circumferential strain at the three implemented segments: lower (yellow, ), middle (blue, ) and upper (purple, ) (see Fig. 8). Regions of localized strain are marked with triangles, squares, and circles in the lower, middle, and upper segments, respectively. (d) Distributed axial strain at the four implemented segments: first (, blue), second (, red), third (, green) and fourth (, yellow). The colormap indicates the time, with the last measurement in red.
The results of the active surveys at the four heights of the AE array (Fig. 8 in Section Instrumentation) are also shown in Fig. 1a. The P-wave velocity at each height was calculated from the pair of sensor that transect the eventual macro-fracture horizontally, determined from the XR-CT (Fig. 5 in Section Additional insight into progressive failure in brittle rock). Across all heights, the P-wave velocity shows an initial increase during the first 1500 s, reaching 4600 m/s in the upper height (purple diamonds). At about 2500 s, the velocity was observed to decrease at a constant rate () in the three lower heights (orange, red and green diamonds). An increased rate of velocity reduction () was observed at different times throughout the sample. This transition between and occurs approximately at in the second height, and at in the first and third heights. After the initial velocity increase (first 1500 s), an approximately constant velocity was observed in the fourth height (purple diamonds), remaining approximately constant until just before .
Fig. 8.
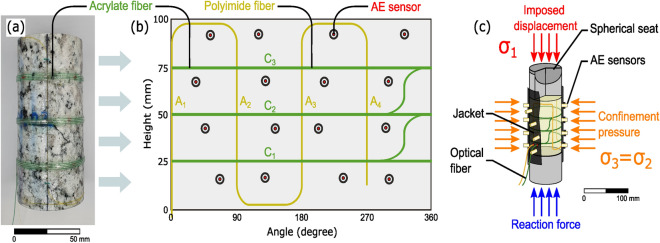
Rotondo granite sample instrumentation. (a) Sample implemented with both types of optical fibres before jacketing. (b) Unwrapped surface of the sample with the location of the implemented AE and DSS sensors. Polyimide-coated fibre (yellow) overlapped by the acrylate-coated fibre (green). (c) Schematics of the triaxial setup with AE sensors and the optical fibres used for DSS. A picture of the sample mounted in the triaxial device is given in Section 7 of the Supplementary Material.
Fig. 5.
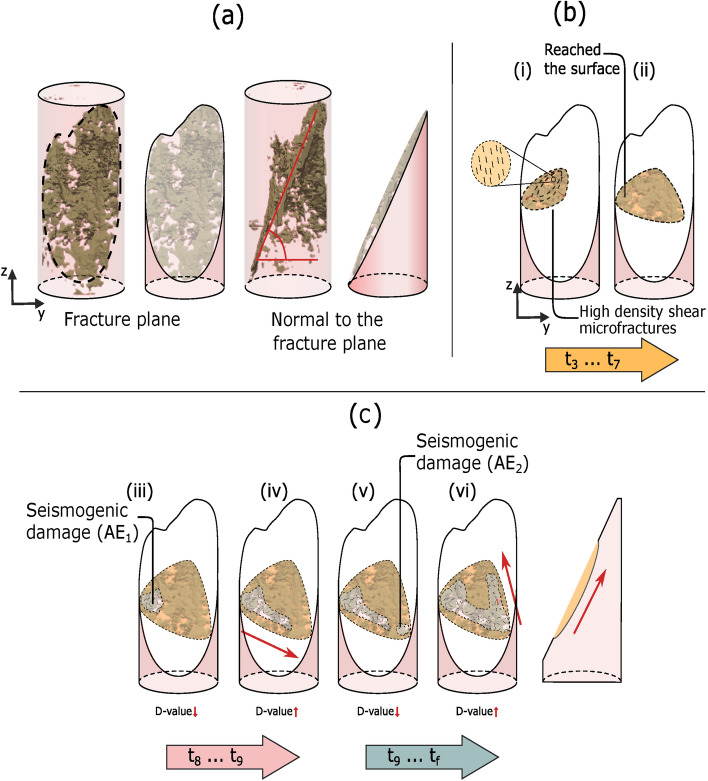
Schematic of the hypothetical damage initiation and subsequent fracture propagation. Cross-sections represent a plane parallel to the macro-fracture that caused the failure. (a) Two XR-CT cross sections obtained post-test: parallel and perpendicular to the macro-fracture plane. The evolution of the localized preparatory damage shown in this figure was also reflected in the spatial-temporal variations of the P-wave velocity (Fig. 1a). (b) The nucleation of a zone hosting a large numbers of shear microfractures (preparatory damage) is represented by the light orange zone. (c) Seismogenic damage is indicated by the zones showing the macro-fracture, which originated near the boundary of the sample and propagated to the opposite side. Dynamic rupture occurred when the length of the preparatory damage exceeded a certain threshold, which may have resulted in an energy balance that produced unstable fracture growth (e.g., 53).
The distributed circumferential and axial strain evolution are shown in Fig. 1c and d, respectively. At the lower level (), the localization of the strain in the circumferential direction developed at approximately 0.065 m on the perimeter (marked with a triangle in Fig. 1c). In the middle segment (), the localization of the strain was observed in two regions, which are marked with squares located at 0.05 m and 0.09 m on the perimeter of the sample.
A relatively uniform strain distribution across the sample was observed in the axial direction, as shown in Fig. 1d. However, small regions of localization were observed in the lower portions of the sample in the second segment (; indicated by the black ellipse). The increased weakening rate, observed as a faster decrease in differential stress at , was reflected as a sudden and local, relative reduction in axial strain (see the last measurement in red in Fig. 1c and d). The black arrow in indicates the largest decrease in compressive axial strain.
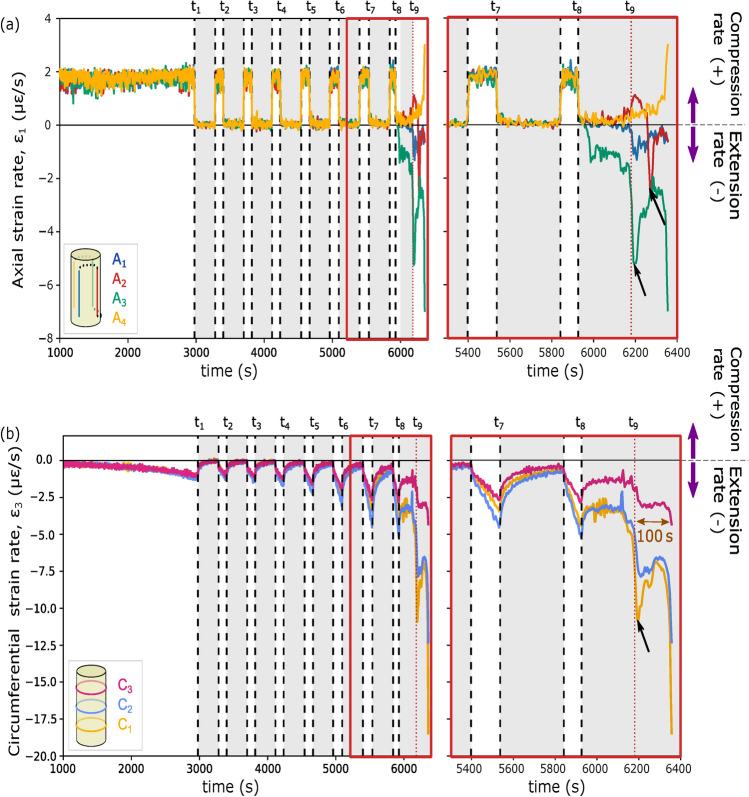
Figure 2a and b show the average strain rate for the axial and circumferential segments of the optical fibre, respectively. The strain rate of the axial segments (Fig. 2a) displays a sharp compression response to the holding and also the reloading. Following the holding (constant displacement) phase , we observed an increasing extension strain rate in line . After , a sharper increase in axial extension rate was observed in and (indicated by the black arrows). At this moment, all axial lines, except , showed an extension rate, rather than an expected compression rate. Few seconds before failure, a sudden increase was observed in both the extension rate in line and the compression rate in line .
Fig. 2.
Mean (or average) strain rates of (a) the four axial segments and, (b) the three circumferential segments. The time interval marked by the light red box (5300 s – 6400 s) is zoomed on the right panel. The colour code is given in the small schematics of the sample. Intervals colored in light gray indicate the holding phases.
Figure 2b shows the circumferential strain rate averaged for each loop. Whenever the loading was resumed (white intervals), the sample exhibited a small sudden acceleration in the circumferential extension rate followed by a gradual increase. Loading produced a progressive increase in the extension rate with each successive loading cycle. During the holding phases (grey intervals), relaxation in the sample caused a gradual decrease in the extension rate, which decayed toward zero over time. Different magnitudes of extension rate were observed in the circumferential segments, with the difference becoming more pronounced after .
At the beginning of the last holding phase (), the extension rate in the upper segment () is half the magnitude measured in the other segments ( and ). An increase in the extension rate was observed in all circumferential segments that initiated prior to . The largest extension rate increase was observed in the lower segment (indicated by the black arrow). After this increase, local accelerations and decelerations were observed, followed (∼ 40 s before failure) by a rapid increase in the extension rate, starting in the lower segment (), followed by the middle () and upper () segments.
Seismogenic response
A total of 6,034 events were located in our test, of which 3271 events occurred before the dynamic stress drop. Analysis of the source type of the AEs showed that 97% of the catalogue were deviatoric or “shear” events (see Section 3 of the Supplementary Material). Figure 3a shows the spatial-temporal distribution of the AEs sorted into four time interval to illustrate the process of AEs localization and delocalization.
Fig. 3.
(a) Spatial distribution of the seismic catalogue located prior to failure. The sizes of the markers are proportional to the of the AE events. The events in the moments before failure ( to ) are colored by their timing. A larger version of this sub-figure can be found in Section 4 of the Supplementary Material. (b) Virtual reproduction of the volumetric strain rate, which was linearly interpolated and superimposed on the surface following Salazar Vásquez et. al.37. (c) Comparison of average volumetric strain rate (red dots), standard deviation of the distributed volumetric strain rate (blue dots), and the differential stress (black line) leading up to failure. Volumetric strain rate (=+2) was calculated from the average of the axial and circumferential strain rates shown in Fig. 2. (d) Fluctuations of the b-value during the experiment. Light blue region represent the standard error calculated using Eq. 5. We have selected three sub-catalogues (, , and ) to illustrate their duration, which are represented by the green bars. (e) Spatial clustering of the AEs using the D-value. The localization and delocalization of AEs are indicated by red arrows. The b- and D-values were calculated using a running sub-catalogue of 480 events (see Section AE data processing).
During -, the AEs occurred homogeneously throughout the sample. Towards the end of the test (-), the events were localized in the lower left region of the sample (blue square in Fig. 3a). The events responsible for the increase in the AE rate observed seconds before the dynamic stress drop (Fig. 2a) registered a significant increase in their moment magnitude, ranging from to . This cluster of large events originated in the lower part of the sample and propagated upward (green arrow in Fig. 3a).
Figure 3b shows snapshots of the dilation rate superimposed on the virtual samples. Localization of the dilation strain rate was first observed in the middle and lower regions of the sample ( and ). This localization developed further during in the region close to where the clusters of AEs later nucleated (blue square at - in Fig. 3a). We observed a preferential orientation in the dilative strain rate on the sample surface at , which correlated qualitatively with the orientation of the AEs observed during -. The spatial-temporal correlation between AEs and the localization of strain is examined in detail in Section Spatial-temporal evolution of seismic and aseismic deformation.
Temporal variations in b- and D-value
Figure 3c shows the differential stress (black line) in the later stages of the experiment. Average axial and circumferential strain rates were used to calculate the volumetric strain rate (red dots) over all segments shown in Fig. 1c and d. We noticed an increase in the dilatation rate at , which continued to decrease slightly prior to a second rapid increase in the volumetric strain rate that preceded the dynamic stress drop.
Fluctuations in the b-value leading up to failure are shown in Fig. 3d. An initial increase in the b-value was observed from 5540 s to 5800 s, increasing from 1.9 to 2.0. After this period, the b-value remained approximately constant until , where it increased to its global maximum of 2.18. Two distinct decreases in the b-value were observed during the failure sequence: (i) from 6200 s to 6300 s, the b-value decreased from 2.18 to 1.8; and (ii) from 6340 s to 6360 s, the b-value decreased from 2.0 to 1.48. 1.48 was the lowest b-value recorded, and corresponded to the dynamic stress drop. A small recovery in b-value was recorded within the failure sequence and following the dynamic stress drop.
Figure 3e shows the changes in the spatial-temporal distributions of earthquakes using the D-value. The D-value showed two distinct behaviours: (i) localization characterized by a decrease in the D-value; and (ii) delocalization characterized by a relative increase in the D-value40. We observed fluctuations between these two behaviours leading up to failure: (1) from to 6,160 s, the D-value decreased from 2.2 to 1.8 (localization); (2) from 6160 s to 6280 s, the D-value increased to 2.06; (3) from 6280 s to 6315 s, the D-value decreased to 1.9 (re-localization); and (4) from 6315 s to 6363 s, the D-value increased to 2.17 (re-delocalization).
Spatial-temporal evolution of seismic and aseismic deformation
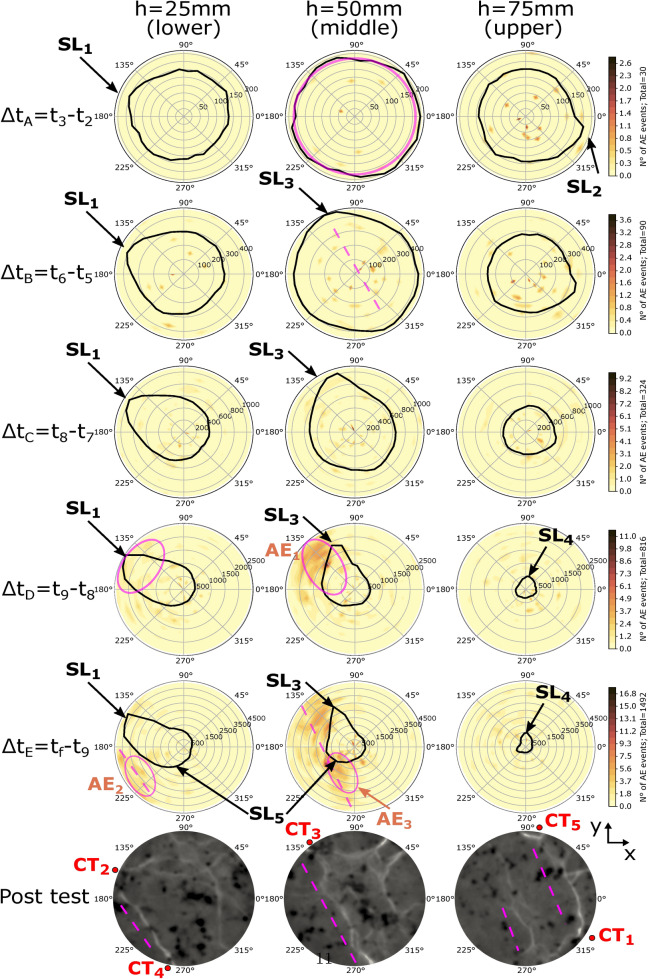
Figure 4 combines the results from the DSS, AE and XR-CT. Polar plots show the distributed circumferential strain changes on the periphery in the bottom (left column), middle (central column), and upper (right column) loops of the sample. The colour map within the polar plots shows a 2D histogram binned location of seismic events within various sub-divisions of the sample. Details on how these polar plots were constructed are outlined in Section 5 of the Supplementary Material. Each row in Fig. 4 represents snapshots of the strain and AEs between a given subset of the indicated times. Cross-sections using the XR-CT measurements taken at the same heights as the circumferential fibres are shown in the last row. The observations between DSS and AEs over each time frame are described below.
Fig. 4.
Polar plots of the circumferential strain distribution and spatial distribution of the AEs. Details of the plot construction are given in Section 5 of the Supplementary Material. The rows show different time intervals, while the columns are the three heights where the optical fibre was installed (Fig. 8). The scale of strain varies between each snapshot time (). Progressive strain localizations () and clusters of AE ( ) are indicated by red arrows. Clusters of AE nucleated in zones of large strain localization, which correlates with the position of the macrofracture on the sample surface (). The last rows show slices of the XR-CT at the same heights where the optical fibre was installed (columns).
) are indicated by red arrows. Clusters of AE nucleated in zones of large strain localization, which correlates with the position of the macrofracture on the sample surface (). The last rows show slices of the XR-CT at the same heights where the optical fibre was installed (columns).
An elastic homogeneous material would be expected to be represented by a circular shape in a polar representation of deformation. This is illustrated by the pink circle shown in the middle level. During this phase of the test, the middle section of the sample exhibited homogeneous deformation. However, we observed two regions where strain localized (denoted  ) during this time interval. This deviation from a homogeneous response occurred at (i) approximately in the lower level () and (ii) in the upper level (). At this stage, the magnitude of the localizations was slightly above the sample average ( and ). The strain localization in the lower level () increased from to , whereas no increase was observed in the upper level () over the same time intervals. The positions where strain was localized correlate with the location of the macro-fracture that emerged on the sample surface at their respective heights, as observed in the post-test cross sections ( and ).
) during this time interval. This deviation from a homogeneous response occurred at (i) approximately in the lower level () and (ii) in the upper level (). At this stage, the magnitude of the localizations was slightly above the sample average ( and ). The strain localization in the lower level () increased from to , whereas no increase was observed in the upper level () over the same time intervals. The positions where strain was localized correlate with the location of the macro-fracture that emerged on the sample surface at their respective heights, as observed in the post-test cross sections ( and ).
An elliptical strain profile starts to emerge in the middle of the sample with the major axis oriented in the 110°–305° direction (pink dashed line).
Compared to the opposite side of the cross-section (at 330°), more pronounced localization emerged towards 110°, which disrupted the symmetry of the elliptical strain response noted previously. During this time period, further localization of strain was observed in and . The upper level did not show pronounced localized strain lobes.
An increase in the rate and clustering of AEs was observed. Clustering was predominantly in the middle level of the sample, and events were localized adjacent to the regions and . Within this time interval, the emergence of strain localizing at 90° in the upper level () was observed. However, the magnitude of the localization in was significantly lower compared to and at the lower levels. The AE clusters ( and ) and localization of strain ( and ) correlated with the position where the macro-fracture appeared at the surface (, , and in the post-test sections).
AEs clustered in the lower () and middle () levels, ascending through the sample (see also the Supplementary Video 1 and 3). The AE clusters and the localization of strain showed similar orientation to the macro-fracture at these levels (marked with pink dashed lines on the XR-CT cross-sections).
Discussion
Additional insight into progressive failure in brittle rock
In general, two groups of models have been proposed to explain the mechanism of the macrofracture nucleation precluding brittle failure in intact rock29,41. Group 1 suggests that faulting occurs as a result of rupture nucleation due to the interaction of multiple microfractures, that form prior to faulting, and coalesce when their density reaches a critical value15,35,42–44. Group 2 views faulting as a process zone at the rupture tip (front) resulting from the interaction of two microfractures29,45,46. The absence of AE activity above background levels prior to the origination of faulting in granite samples (e.g.,18,24) has supported the mechanisms proposed by Group 2, under the assumption that AE sensors are capable of detecting all or most of the damage generated in the sample. However, our results suggest that this assumption may not always hold true, as damage can accumulate in an aseismic manner. Even though it is established that the energy radiated as AE represents a small fraction of the total energy dissipated during brittle failure40,47, understanding the temporal-spatial relationship between AE and strain localization provides new insights in the failure mechanism. This follows from recent inference into the damage mechanism of sandstone made using the XR-CT method in combination with two AE sensors, where the occurrence of preparatory damage may be missed if only seismicity is considered31.
Slow aseismic damage localization
Katz and Reches41 mapped the formation of tensile and shear microfractures using scanning electron microscope (SEM) micrographs of thin sections taken from samples of intact granite loaded to different stress levels. Tensile microfractures dominated the low stress-stage, while the relative density of the shear microfractures was found to increase with increasing stress, forming elongated zones41. Similar preparatory damage localization was observed in low porosity rock samples using the XR-CT method48,49. However, due to technical limitations, it is currently not possible to correlate their direct observation of damage in the sample with a spatio-temporal understanding of AE activity. We believe that the strain localization, first observed in the middle and lower parts of the sample, at approximately 80% of the maximum load (Fig. 4) was the expression of a zone hosting high number of microfractures, which were unable to produce detectable AE signals.
Although comparing laboratory and field data is notoriously difficult, laboratory tests have been effective in studying the underlying physical mechanisms that occur in natural systems30,40,47,50. Field observations suggest that the earthquake preparation and nucleation process can be described by the progressive localization12 and integrated models13 and begins with the formation of off-fault damage which progressively localizes to an eventual rupture zone12. Due to the progressive weakening of this localized pre-damage zone, clusters of foreshock sequences can nucleate, leading to the large rupture13. Consideration of rock volumes is especially important in systems that are not dominated by an existing weak fault with little strength recovery13. Our results show that damage can accumulate (or increase) aseismically, and this might occur in nature. Figure 5 conceptually illustrates the evolution of the preparatory damage in our sample, which showed a similar localization process (Fig. 5i–ii). The symmetry of the strain localizations observed at early stages of the test (dashed line at in Fig. 4), indicates that the zone hosting the preparatory damage was likely centred in the middle of the sample (light orange region in Fig. 5i). Symmetry began to break down at , as the pronounced lobe in Fig. 4 grows. We interpret this increasing prominence of the strain heterogeneity as the development and propagation of the damage zone from the middle towards the bottom of the sample (Fig. 5ii). In view of damage mechanics, this zone can be interpreted as an inclusion of a softer material, causing a stress redistribution that enhances its propagation. We believe that the localized damage zone in our sample (i.e., light orange zone Fig. 5ii) may be analogous to the fault zone described by the progressive localization model, which is preparing to generate clusters of precursor AEs. The presence of this zone of localized damage in our sample is also supported by the 30% decrease in the P-wave velocity measured in the middle and bottom regions of the sample (Fig. 1a). Similar levels of decreased P-wave velocities in natural fault zone structures have been reported. For example, a 25% - 40% decrease in the P-wave velocity has been observed in the Southern California fault zone51,52.
Accelerated seismogenic deformation
Loading and boundary conditions further promoted the formation of microfractures, increasing their number in the localized region, as observed by Katz and Reches41. We observed higher strain rates within the zones and at (Fig. 4) that precluded the onset of clustered and swarm-like AEs within this region. A rapid increase in AE activity beginning above 95% of the peak strength has been observed in granite samples24,27, similar to the cluster of AEs observed near failure in our test ( at in Fig. 4), causing the localization in D-value (red arrow (1) in Fig. 3e). This type of observation supports the Group 2 of macrofracture formation models29,41, but as described in the section Additional insight into progressive failure in brittle rock, we concluded that a pre-damaged region now hosts the bursts of AE activity. One hypothesis is that a critical microfracture number was reached in the pre-damaged region near the boundary, promoting seismogenic damage (Fig. 5iii). AEs propagated along the orientation of the zones with localized strain during (AE migration from to in Fig. 4), tracking the propagation of seismogenic damage along the zone hosting the pre-damaged that formed during - (Fig. 5iv).
Seismic and geodetic observations have shown a step-like increase (i.e., acceleration and deceleration) in deformation before some large earthquakes13. This step-like process can be due to the breakage of smaller patches on the eventual fault and foreshocks, making the surrounding more susceptible to rupture13. Ben-Zion and Zaliapin12 employed three complementary approaches to investigate the processes associated with earthquake preparation: (i) localization of background seismicity, (ii) fractional area of the localized seismicity, and (iii) clustering of earthquakes. They observed complex localization and delocalization processes. Prior to large seismic events in California and Turkey, localization patterns were associated with the formation of rock damage around the eventual rupture zones. In contrast, the delocalization observed prior to the 2004 6 Parkfield event was thought to be the result of a progressive stress build-up leading to failure over progressively wider regions12. A similar faulting process was observed in our test (Fig. 3a).
The step-like process differs from those usually observed in tests on saw-cut samples with homogeneous surfaces, where a smooth accelerated deformation is observed before failure13. However, partial stress drops prior to the onset of catastrophic failure, routinely observed in triaxial rock tests on intact and pre-existing rough fractures26,54,55, has been attributed to breakdown of larger asperities which can produce delocalization in the D-value as they breakdown40 and fluctuations in b-value56. In our test, the slow stress drop (Fig. 1a) and the delocalization, re-localization and de-relocalization ((2), (3) and (4) in Fig. 3e) may be explained by the seismogenic break down of asperities within the pre-damaged zone ((iii)–(iv) in Fig. 5). The seismogenic damage also corresponded to complex variations in the local strain rate response in both the axial and circumferential directions (Fig. 2). Similar localization and delocalization processes were observed in the microfracture locations in other rock materials, associated with the propagation of the fault zone49,57. Progressive degradation of strength barriers may be required before the fracture can grow to a critical length, depending on an energy balance and the strength of the material in the system53. Progressive unlocking of frictional interfaces has been observed in laboratory experiments on rock-rock interfaces58 and on analogs59,60. This behavior has been modeled using the balance of released elastic energy and dissipated local fracture energy along the thin discontinuity61. Whether similar models can be used to explain progressive breakdown observed from a volumetric perspective (rather than thin discontinuity) remains to be seen, but these models could benefit from the observations produced in this study.
Partitioning of seismic to aseismic energy
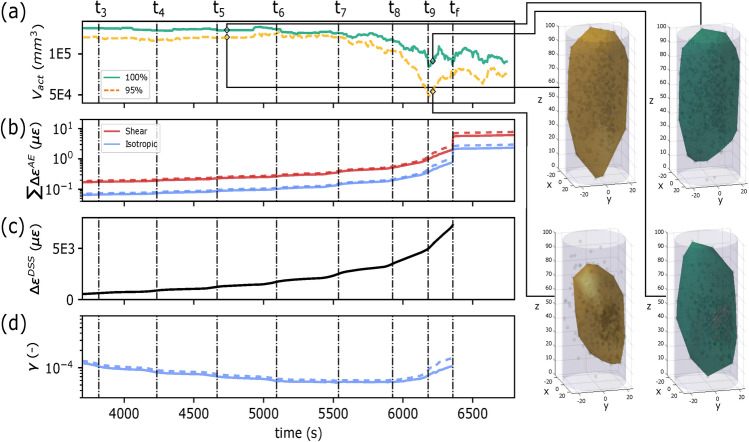
An emerging view has suggested that aseismic (slip) deformation may play a role in the preparation of large earthquakes. It is therefore critical for us to understand the conditions and relationships that lead to failure and may be produced by the interplay of seismic and aseismic deformation. Due to recent advances in geodetic and seismological observations, there is new evidence of a low seismic-to-aseismic deformation ratio is produced in the crust at various depth (e.g.,62). The quantitative comparison between the aseismic and seismic inelastic deformations is presented in Fig. 6. The seismic inelastic deformation () was calculated from the seismic moments of each AE event using two source models: a shear63 and isotropic20 source (Fig. 6b). We estimated the aseismic inelastic deformation () from the dilatancy measured by the DSS (Fig. 6c), minus the seismic component (see Section Aseismic and seismic inelastic volumetric deformation). A decrease in the inelastic seismic-to-asiesmic ratio () was observed (Fig. 6d), reaching a minimum around . At failure (), was computed to be = [0.01 to 0.02]%. This significant release of aseismic energy suggests monitoring the lower frequency bandwidth of deformation could potentially be more informative in preparatory damage detection.
Fig. 6.
Analysis of the inelastic cumulative seismic () to inelastic asiesmic deformation () leading up to failure. Details to the calculations are given in Section Aseismic and seismic inelastic volumetric deformation. (a) The activated volume determined by the cluster analysis. The inset images show the volume capturing 100th percentile (green, solid line) and 95th percentile (gold, dashed-line) for two random sub-catalog in time. (b) A shear (red lines, Eq. 9) and isotropic (blue lines, Eq. 10) models are used as end-member estimates for volumetric strain changes from the source. The dashed and solid lines represent the calculations made for the 95th and 100th percentile of activated volume. (c) The total inelastic strain () computed using the DSS measurements. (d) The inelastic seismic-to-aseismic ratio (, see Eq. 11) using only the isotropic source, since we are unable to measure the shear deformation using the implemented DSS configuration.
This low seismic-to-aseismic ratio was observed at smaller scales and under different loading conditions. At the laboratory scale, stick-slip experiments under confined conditions have shown between 2% and 0.1 % of the total energy released as seismic slip in saw-cut samples40,47. The failure mechanism of stick-slip events on rough faults involves the formation of a significantly wider damage zone, in comparison to saw-cut samples. This wider damage zone resembles the propagation of damage through intact rock64, seen in our experiment. Dresen et al.40 observed that the seismic-to-aseismic ratio decreased to ~ 0.01% for rough faults, similar to our observation (Fig. 6). In hydraulic shear experiments on decametre-scale faults in a crystalline setting, the seismic to total deformation ratio was observed to be [0.001 to 0.02]%65. Other underground rock laboratory experiments66,67 have also shown that aseismic slip contributes to a substantial portion of the total energy budget, although this phenomenon needs to be better understood to explain the production of seismicity through both fluid injection68 and tectonic stresses69.
Self-organized behaviour preceding failure
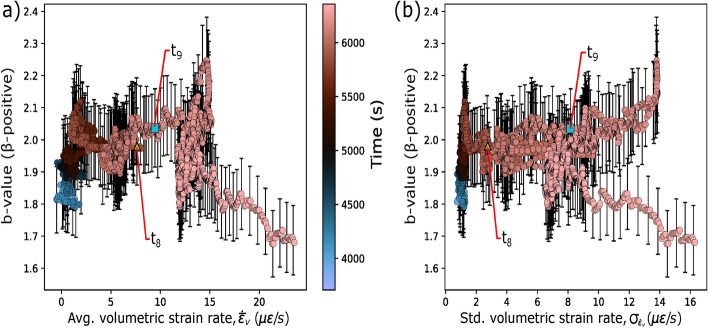
Laboratory experiments have shown a decrease in the b-value with increasing differential stress21,24. However, we observed significant variations in b-value at nearly constant differential stress (see Fig. 3c and d). This discrepancy can be attributed to the unconventional loading conditions used in our experiment, where the displacement of the loading piston was held rather than continuously increased. The differential stress reflects the energy stored in the sample, which was dissipated principally through inelastic processes that constitute some level of breakdown work70,71 that may occur in an aseismic and seismic fashion. An important question is whether these two forms of dissipated energy can reflect some self-organized behaviour. Figure 7 shows the fluctuations of the b-value with the average volumetric strain rate for our experiment. We observed an inverse correlation between the b-value and .
Fig. 7.
Fluctuation of b-value with volumetric strain rate ; colour indicates time during the test. The volumetric strain rate was linearly interpolated to the b-value time stamps. The yellow triangle marks the beginning of the second b-value decrease as observed in Fig. 3(b). An inverse correlation between the b-value and can be observed towards the end of the test.
This inverse correlation between the b-value and can be anticipated by stress corrosion models developed to explain fluctuations in b-value based on fracture mechanics28,72. In the case of a sample undergoing strain softening, the model anticipates two decreases in the b-value prior to failure, which correlates with our observation in Fig. 3b. This double b-value minimum has been observed in triaxial tests on intact, fluid-saturated sandstone samples73. This observation was associated with longer periods of strain softening and sub-critical cracking, which was probably achieved by the step loading protocol which produces relaxation loading conditions in our dry test. Main et al.28 extended the model to characterize the damage state in terms of a mean energy release rate. Their model anticipates an inverse correlation between the b-value and the mean energy release rate, which is consistent with the inverse correlation shown in Fig. 7. In our test, aseismic deformation dominated the mean energy release rate, as shown in Fig. 6.
Diverse models have been proposed to link the deformation rate to seismicity. Slower loading should allow contact junctions to heal74,75, thereby promoting larger foreshocks at slower loading rates. This was not the case in our test, where larger precursory AEs occurred at higher preseismic deformation rates (Fig. 3c and d). We need an alternative mechanism to explain this phenomenon, distinct from contact junction age and frictional healing. It has been observed that the b-value decreases with increasing loading rate76,77. Bolton et al.76 linked the AE energy with an increase in porosity due to dilation (more space allowing for particle motion upon failure), which in turn form larger force chains that bridge the shear zone that fails. Localized dilative behaviour was observed in our test using the DSS and was shown to precede the onset of seismogenic damage early in our experiment (see Figs. 3 and 4). Similar mechanisms may exist in the sections of the fault that hosted the majority of the localized preparatory damage (Fig. 5b and c). That potential dilation in the damage region allows for larger force chains to bridge the shear zone composed of the damaged material, leading to larger events during accelerated failure (Fig. 5b). Moreover, the dilation is only theoretically increased within the shear damage zone, not within the intact material for pressure-sensitive dilatant materials such as granite78. This later observation was supported by the DSS measurements (Figs. 3b and 4). The mechanism described in this paragraph may have been enhanced by the inhomogeneous nature of the Rotondo granite. Further investigation is needed to understand the influence of lithology on the decrease in b-values prior to failure, for example, in homogeneous materials where this mechanism may be inhibited.
Recent studies on field scales have observed promising correlations between the accelerated deformation and b-value. Gulia79 quantitatively related the volumetric strain rate, as measured by geodetic means, and the b-value by analysing the subsidence in the Groningen gas field. The study discovered an inverse correlation between the two parameters. On a large scale, increases in surface strain rate were observed in areas where a decrease in the b-value was measured, for example, near the epicentre of the 2015 Gorkha earthquake in the central Himalayas80. Many studies have highlighted the uptick in seismicity in regions experiencing accelerated precursory deformation (e.g., [1,4,81), some of which did not observe this decrease in b-value82. Our study was limited to volume preparatory processes (i.e., intact sample); however, the similarities between the inverse correlation of the accelerated deformation and b-value observed in our test (Fig. 7) and in some field cases suggest a correlation that could more accurately assess seismicity where geodetic strain and seismic data are available.
Conclusions
This work presents triaxial loading to failure of intact dry granite samples at a confining pressure of 10 MPa. Results of the best instrumented sample are presented in detail. The sample was implemented with a distributed strain method (DSS) to measure the deformation field on the sample’s surface combined with an array of calibrated acoustic emission (AE) sensors. This combination of monitoring techniques in triaxial conditions is unique and allows monitoring a broad bandwidth of deformation, from slow (DSS, 0.25 Hz) to fast (AE, 100 kHz to 1.5 MHz). Such conditions are currently inaccessible even to sophisticated X-ray computed tomography measurements31,48,49.
Previous triaxial tests on crystalline rock material, using only AE sensors, have shown the nucleation of a small number of AEs uniformly distributed over the sample during most of the test, and the later nucleation of clusters of AEs close to failure (approximately at 95% of the peak stress27,30). We have observed similar AE activity; however, in our study, the use of DSS has allowed the observation of early heterogeneities in the deformation field, which is related to quiescent damage generation during failure of the crystalline rock. These heterogeneities were observed as strain localizations that started at 80% of peak stress and continued to localize as the test progressed. The precursory AE clusters were generated inside the sample and in close proximity in regions that produced strain localization. This suggests that seismogenesis is generated within regions that reach a certain critical level of damage or zones with large strain gradient. Additionally, we observed the inverse correlation between the b-value (relative proportion of small to large seismic events) and volumetric strain rate prior to failure, which had been anticipated by stress corrosion models in rock fracture mechanics28,72.
Our results show that the distributed deformation is more informative than AE events in the early stages of our laboratory tests. The data collected by combining the DSS and AE methods could be used to validate theoretical and numerical models, which could provide further insights into the failure mechanisms of crystalline rock material. The observed inverse correlation may improve catastrophic failure assessment.
Extrapolating our small-scale results to large-scale natural applications is difficult, for example, due to the different bandwidth of the sensors. However, our laboratory results are qualitatively similar to recent field observations, suggesting that the failure mechanisms could be scalable. For instance, prior to the 2021 Yangbi earthquake, migrating foreshocks were driven by a slow deformation event5, and the inverse correlation between the b-value and volumetric strain rate has been observed in a natural gas field79. In addition, recently developed models of natural earthquakes proposed the formation of off-fault damage that progressively localizes to an eventual rupture zone12,13. Our data suggest a similar failure mechanism in laboratory settings. This similarity between the laboratory and field observations emphasises the importance of measuring the distributed deformations at both scales, and warrants the re-examination of the preparatory distributed deformations, when available, in case studies of large earthquakes.
Methods
Lithology and material properties
The test was performed on a sample of Rotondo granite that was collected from the Bedretto Underground Laboratory for Geosciences and Geoenergies (BULGG, Switzerland83). Rotondo granite belongs to the Gotthard massif, and two varieties have been identified within the tunnel: equigranular and porphyritic84,85. The sample was homogeneous, equigranular, and relatively fine-grained, light grey granite (aplitic granite) with variable biotite content85,86. The mineralogy observed in this type of Rotondo granite includes: quartz (25-35%); alkali feldspar (20-40%); plagioclase (10-25%); biotite (3-8%); and garnet, phengite, chlorite, epidote, apatite, muscovite, zircon and opaques as accessory minerals85,86. Based on the description in the literature, we estimated the average grain size of the Rotondo granite to be ~ 1 mm. This is comparable to the average grain size of the Westerly granite (0.75 mm87).
In general, Rotondo granite has a density of 2600 kg/m3, an elastic modulus of E = 50 GPa, and a Poisson’s ratio of = 0.3188. Under dry conditions, the experimental results showed an ultrasonic P-wave velocity () of 3500 m/s and an S-wave velocity () of 1800 m/s. More information on the properties of Rotondo granite can be found in Section 1 of the Supplementary Material.
Experimental facilities
We conducted the current test using a triaxial rock deformation apparatus (LabQuake) located in the Rock Physics and Mechanics Laboratory (RPMLab, https://rpml.ethz.ch/) at ETH Zurich. This apparatus was designed to induce shear fractures in an intact crystalline rock specimen under high confining pressures. The confining pressure was applied using temperature-resistant oil. The axial load was imposed with a servo-hydraulic actuator, which was used in displacement control in this test. At a confining pressure of 10 MPa, which was the confining pressure in our experiment, the triaxial cell had an axial stiffness of 470 kN/mm.
Distributed strain sensing (DSS) system
Two types of optical fibres were used in our test: acrylate- and polyimide-coated fibres. The fibre selection accounted for two problems inherent in the triaxial environment. A further description of the DSS sensor selection is provided in Section 7 of the Supplementary Material.
An optical backscatter reflectometer (OBR 4600, Luna Innovations) was used to interrogate the fibres. This optical interrogator can measure large strains using the incremental post-processing method described by Salazar Vásquez et al.37. In this study, the DSS system was configured to provide spatial resolution of 5 mm at a sampling rate of 0.25 Hz. The strain rate was calculated as the centred difference approximation of the average of each segment.
AE system
AE sensors were designed in-house and constructed to provide a flat frequency response from 70 kHz to 1.5 MHz, which decreased distortion in the physical interpretation of the wave field and allowed for the withstanding of high pressure and temperature conditions. Full details of the components and instrument responses of AE sensors with similar spectral responses were outlined in Selvadurai et al.89. Each individual AE sensor used in this study was calibrated on a transfer plate to provide a quantitative interpretation of the AEs produced as the sample was driven to failure. Further details on the AE sensor construction and calibration process are provided in Section 7 of the Supplementary Material.
During the experiment, each acoustic data channel was continuously sampled (at 10 MHz with 16-bit) using the TraNET EPC data acquisition module (Elsys Instruments AG). Signals were preconditioned using analogue preamplifiers with +40 dB gain (Elsys AE-AMP). Details of the data acquisition system and the high-voltage pulsing unit have been outlined by Selvadurai et al.89. Every 120 seconds, a loop of active pulses performed a tomographic survey. Each sensor was pulsed 10 times, and the multiplexer (Elsys HVP-MUX) would switch to the next sensor until all 16 sensors were used. This allowed us to construct a detailed understanding of the velocity model at various stages of the experiment.
Instrumentation
Figure 8a shows the cylindrical sample of Rotondo granite with a height of h = 101.6 mm and a diameter of d = 49.5 mm. It was first wrapped using two types of optical fibres, according to the layout shown in Fig. 8b. The polyimide-coated fibre was used to measure the distributed axial strain in four equidistant vertical lines (, , and ). Overlapping the axial fibre were three loops around the perimeter of the sample (, and ) that measured the distributed circumferential strain using the acrylate-coated optical fibre at three heights. This layout was adapted from Salazar Vásquez et al.37, who explain, in particular, specifics of coupling between the optical fibre and the rock sample. To mitigate light attenuation issues, the sample was wrapped sequentially, starting with the thin polyimide fibre followed by the thicker acrylate fibre. Each fibre was interrogated every 4 seconds using an optical switch. The measurements were processed with a spatial resolution of 5 mm. This resulted in 33 gauges per circumferential loop (total of 33 × 3 = 99) and 6 gauges per axial strand (total of 6 × 4 = 24).
AE sensors were strategically placed at various locations on the surface of the sample. These locations were carefully chosen to ensure that they did not overlap with any areas where the fibres were bonded; such overlap could potentially damage the fiber during confinement. Sixteen acoustic sensors were sealed in a nitrile rubber jacket that kept the confinement oil separate from the sample. Sensors were mounted in the portholes using two coats of two-part epoxy (Hysol EA 9455) applied at 8-hour intervals and oven-cured (T = 60 °C for 8 hours). The sample implemented with the optical fibres was carefully inserted into the jacket that already housed the AE sensors. The final position of the optical fibres and AE sensors are shown in Fig. 8b, which was confirmed with the XR-CT images.
Experimental protocol
Figure 8c shows a schematic view of the triaxial setup used in this experiment. Hydraulic oil was used to apply the radial stress () to the sides of the sample. The nitrile jacket acted as a barrier, isolating the oil from direct contact with the sample. Axial stress () was applied from the top of the sample, by moving the piston position (). Differential stress was defined as the difference between axial and radial stress (). The loading procedure (Fig. 2a) was designed to slow the later stages of failure when microfractures begin to coalesce into larger macro-fracture(s). This procedure served two purposes: to slow down the rate of AEs and to allow for more DSS measurements (see Section 5.2).
A constant confining pressure of = 10 MPa was applied to the intact and dry Rotondo sample. After the confinement phase, an external constant axial loading rate of m/s was imposed, which translate to 4.9 /s. Due to the cell stiffness, the strain rate measured with the LVDTs was 2.1 /s across the sample. Loading was paused when a nominal differential stress of = 230 MPa was reached and held for 5 minutes. During the holding phase, the sample was allowed to relax while the piston was held in position. Load-hold steps were resumed with 10 MPa steps in differential stress, with each step followed by 5 minutes of position hold. Eight of these load-hold steps ( through ) were implemented before the sample finally failed spontaneously at time . After the differential stress drop (), the piston was held in position for 2 minutes. Finally, the axial loading rate was resumed for 5 minutes to stress the macrofracture that had formed.
After the test, the fractured sample was retrieved and scanned using a high resolution X-ray at McGill University. The XR-CT scanning system uses a 420 kV tungsten X-ray source. To maintain the integrity of the fractured sample, it remained in the nitrile jacket. Images were collected horizontally across the sample diameter in 1 mm-thick slices at a resolution of 512 x 512 pixels. Numerical artifacts were removed from the images using Matlab. Further details of similar facilities and techniques can be found in Ketcham and Carlson90.
AE data processing
Parsing data
The AE catalogue was generated through analysis of the continuous recordings from the 16 calibrated AE sensors. The recordings were first analyzed using the short-time average/long-time average (STA/LTA) algorithm. This standard algorithm calculates the signal average on two moving windows: a short-time window (STA) and a long-time window (LTA). Picks determined were used as event classifiers. Events were considered when the STA/LTA found picks on a minimum of 12 detections within a time frame of 70 μs. This window corresponds to a predetermined maximum delay in P-wave travel time from any location within the sample.
Once an event was classified, a second picking phase detected the onset of the first arrival P-wave using the Akaike Information Criteria (AIC, 91). This was completed in a shorter time window (100 μ) around the STA/LTA pick and is a common technique used to detect first-break arrivals due to AEs in laboratory tests92.
We used a standard inversion of P-wave arrival times. P-wave onsets were taken from the AIC picks, using a minimum of eight sensors to compute the source locations. Out of the 6,034 events, 95% were located using up to 14 sensors. The source locations of the seismic events were determined using a homogeneous velocity model derived from the active surveys performed every 120 seconds. For more details on the AE methods, see Bianchi et al.93,94.
Focal mechanisms and moment tensor inversion
Aki and Richards95 defined seismic source representation using the generalized theory of elastic wave propagation as
| 1 |
where represent the convolution in time, is the spatial derivative of the Green’s function which describes the displacement in the k direction at point x and time t due to a unit impulsive force at location in the direction j at time , and is the moment tensor (MT96). This theory holds as long as the source-receiver distance is long enough.
Moment tensor representation has been successfully applied to AE sources generated in laboratory experiments on rock samples (e.g.,97–99). We adopted this approach by implementing the ‘focimt’ script within the Matlab-based software package98 hybridMT. For each AE source, the incident and take-off angles were P-wave ray paths travelling from the source to the receiver. A straight ray was assumed, and the incident angle to the sensitivity vector described the measurement direction of the AE sensors. We assumed that was oriented in the same direction as the computed instrument response. The low-frequency displacement plateau – commonly computed as the area under the first P-wave ground displacement pulse – is required for the MT inversion. Traditionally, this metric is difficult to quantify for AE sensors that measure ground motion in terms of the voltage generated by compression of the piezoelectric crystal. In our case, the sensors were calibrated independently, allowing us to compute the low-frequency displacement plateau directly using spectral deconvolution with the instrument response in the Fourier domain. was estimated as the mean value between 100 kHz 500 kHz of the corrected displacement spectra, as this band dominates the AE recordings99. This formalization allowed us to produce MT solutions with absolute estimates of the seismic magnitude.
The output of the hybridMT algorithm included all six components of the second order symmetric moment tensor as well as the error in the solution. The source moment magnitude 100 was used to characterize the intensity of the events, where (units Nm) was the scalar seismic moment101, defined as one-third of the trace of the moment tensor ().
Spatial and temporal analysis
Sub-catalogues consisting of = 480 events were used in a running window to study the temporal evolution of the spatial and frequency-magnitude distributions. Statistical parameters were computed for each sub-catalogue by adding and removing individual AEs in a “first in, last out” (FILO) methodology.
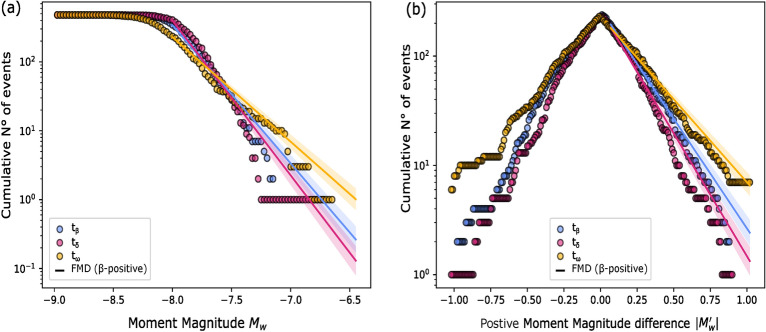
Earthquakes and AEs in the laboratory are often characterized by the well-known Gutemberg-Richter law21. This law can be rewritten as an exponential distribution of the magnitudes ,
| 2 |
where is a cutoff magnitude, referred to as the magnitude of completeness, and is the slope in the semi-logarithmic plane, indicating the relative proportion of small to large earthquakes in a given region. In Eq. 2, we have replaced the conventional b-value with 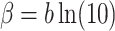 for mathematical convenience.
for mathematical convenience.
Traditionally, parameter 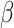 in the GR frequency-magnitude relation (Eq. 2) is computed by the least squares or maximum likelihood method on the magnitude sub-catalogues20,22. However, we adopted the -positive method to interpret the properties of the frequency-magnitude distribution102, as this method takes advantage of the exponential nature of the GR distribution. Van der Elst102 showed that the distribution of magnitude differences () between any two consecutive earthquakes follows the Laplace distribution, which is defined as
in the GR frequency-magnitude relation (Eq. 2) is computed by the least squares or maximum likelihood method on the magnitude sub-catalogues20,22. However, we adopted the -positive method to interpret the properties of the frequency-magnitude distribution102, as this method takes advantage of the exponential nature of the GR distribution. Van der Elst102 showed that the distribution of magnitude differences () between any two consecutive earthquakes follows the Laplace distribution, which is defined as
| 3 |
The laplace distribution slope in the positive semi-logarithmic space (-positive) is identical to the distribution of magnitudes (). We estimated the b-value as
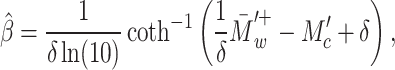 |
4 |
where is the positive magnitude differences of the sub-catalogue, is the bin size and is the cut-off magnitude of the positive magnitude difference distribution. A notable feature of this derivation is that the choice of does not greatly influences the estimate. This allowed us to compute (referred to as b-value in this article) within our potentially incomplete data set. We used and to calculate the b-value reported in this article. A quantitative justification of these parameters and a sensitivity analysis of and are presented in Section 9 of the Supplementary Material.
The standard error of the b-value () was estimated as103
| 5 |
where is the average of the magnitude in the sub-catalogue. Figure 9 illustrates the b-value estimates using three selected sub-catalogues. We compared the statistics of an early sub-catalogue () to the sub-catalogues with the maximum () and minimum () b-values. The timestamps of the selected sub-catalogues are shown in Fig. 3d. Figure 9a shows the magnitude distribution of the events, while Fig. 9b shows the magnitude difference distribution102. Estimates of the b-value obtained using Eq. 4 are depicted with solid lines.
Fig. 9.
Examples of three selected sub-catalogues that were statistically analyzed in our test. The timestamps of the three sub-catalogues are shown in Fig. 3d. (a) Magnitude distribution of the selected sub-catalogues. (b) Magnitude difference distribution and b-value (-positive) estimates102.
Spatial clustering of events was investigated quantitatively by applying a fractal analysis. To define the fractal dimension of the AE hypocenters that varied at different phases of the experiment, we used the Pair Correlation Function (PCF)
| 6 |
The PCF allowed us to quantify the variability in the separation distance, s, less than a certain value, r, between each pair of AEs, N104. For our catalogues, we found that the PCF in the Eq. 6 is approximately linear between r = 1 and 50 mm when fitted in a log-log space. This linear fit suggests a fractal pattern in the spatial distribution of AE hypocentres (e.g., 28). For this correlation (fractal) dimension, D is given as105
| 7 |
where is related to the number of events in the catalogue. For more details on this method and its robustness, see Goebel et al.106.
Aseismic and seismic inelastic volumetric deformation
The total inelastic deformation () was calculated as the difference between the measured volumetric strain and the projected linear-elastic behaviour (i.e., dilatancy[107). More details for this is found in Section 8 of the Supplementary Material. We can compute the aseismic component of inelastic strain () by subtracting the inelastic seismic component () from the total inelastic deformation, given by
| 8 |
Two models are used to estimate the inelastic seismic volume change due to AEs in our experiment95. Shear collapse occurring in a homogeneous isotropic body during an AE event is estimated as63
| 9 |
where is the second Lamé parameter and is the “activated” volume experiencing seismicity (Fig. 6a). A second estimate considers an AE event caused by a spherical volume undergoing a transformational expansion, where the inelastic seismic strain can be expressed as95
| 10 |
where is the first Lamé parameter.
The activated seismic volume is used rather than the total sample volume (). To estimate the activated seismic volume, a convex hull is drawn around the same sub-catalogs of AEs that are used to construct the b- and D-value analysis in Section 5.5. To understand the effect of the activated volume, we consider the 100th percentile (green region in Fig. 6a) and the 95th percentile (gold region in Fig. 6a) of the Mahalanobis distance108 of the AEs in each sub-catalog. Once the activated volumes are determined in time, these values are interpolated to the time stamps of each AE in the full catalog to study the cumulative inelastic seismic volume change due to AEs in our experiment.
We report the seismic-to-aseismic ratio as that of the cumulative inelastic seismic strain to the inelastic aseismic strain ,
| 11 |
Since we cannot discern between purely shear () or isotropic () source mechanisms, we evaluate both independently to determine the bounds for .
Supplementary Information
Acknowledgements
We would like to thank late Prof. Dr. Patrick Selvadurai and Pierre Dutilleul of McGill University for the providing the XR-CT scan of our sample and other technical support. We would like thank Thomas Mörgeli for his good disposition and technical support. Experiments were supported by the Swiss National Science Foundation (SNF) R‘Equip 206021-170766 - Physical constraints on natural and induced earthquakes using innovative lab-scale experiments: The LabQuake Machine. AFSV would like to thank the Innosuisse FLAGSHIP project “AEGIS-CH: Advanced geothermal systems to improve the resilience of the energy supply of Switzerland” (No. 2150009483) for the partial financial support during this investigation. Partial funding for A.F.S.V. and P.A.S. was provided from the European Research Council (ERC) project FEAR (grant 856559) under the European Community’s Horizon 2020 Framework Programme Funds. Founding for P.B. was provided from the Swiss National Science Foundation (SNSF No. 200021-192017). A.F.S.V. and P.A.S. would also like to thank Zihua Niu for initial data reduction efforts and discussions on the preliminary tests associated with this project. P.A.S. is indebted to Mehdi Nikkhoo for the fruitful discussion regarding Sections 3.2 and 5.6. L.N.G. was partially supported by the Utah FORGE project, U.S Department of Energy DEEE0007080 3-2514 and the CUSSP Energy Earthshot Research Center, U.S Department of Energy FWP 81834. He is grateful to Larry Murdoch, Scott DeWolf, and Dmitry Garagash for stimulating discussions. Authors are greatful to Alexis Cartwright-Taylor, Georg Dresen, and anonymous reviewers for useful comments that considerably improved the manuscript.
Author contributions
Conceptualization: A.F.S.V., P.A.S., P.B., C.M., L.N.G., A.M.P., S.W., C.R. DSS measurements and post-processing: A.F.S.V. AE measurements: P.B., P.A.S. AE post processing and statistical analysis: P.A.S., P.B., A.F.S.V. Funding acquisition: C.R., S.W., L.N.G. Methodology: A.F.S.V., P.A.S., P.B., C.M., L.N.G. Resources: C.M., C.R. The original draft was written by A.F.S.V., P.A.S., L.N.G., and all authors contributed to the reviewing and editing of this manuscript.
Data availability
DSS, XR-CT scan and the raw acoustic waveforms of the detected passive events and active shots are available at the ETH Zurich Data Collection (http://hdl.handle.net/20.500.11850/638141). The continuous passive AE recordings are stored on the Bedretto Underground Laboratory server and are available upon request due to their large size. .
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-75942-9.
References
- 1.Kato, A. et al. Propagation of slow slip leading up to the 2011 Mw 9.0 Tohoku-Oki Earthquake. Science335, 705–708 (2012). 10.1126/science.1215141. [DOI] [PubMed]
- 2.Obara, K. & Kato, A. Connecting slow earthquakes to huge earthquakes. Science353, 253–257 (2016). 10.1126/science.aaf1512. [DOI] [PubMed] [Google Scholar]
- 3.Durand, V. et al. Deciphering aseismic deformation along submarine fault branches below the eastern Sea of Marmara (Turkey): Insights from seismicity, strainmeter, and GNSS data. Earth Planet. Sci. Lett.594, 117702 (2022). https://www.sciencedirect.com/science/article/pii/S0012821X22003387.
- 4.Kato, A., Fukuda, J., Kumazawa, T. & Nakagawa, S. Accelerated nucleation of the 2014 Iquique, Chile Mw 8.2 Earthquake. Sci. Rep.6, 24792 (2016). 10.1038/srep24792. [DOI] [PMC free article] [PubMed]
- 5.Wang, H. & Zhou, Z. Advances of strain transfer analysis of optical fibre sensors. Pacific Sci. Rev.16, 8–18 (2014). https://www.sciencedirect.com/science/article/pii/S1229545014000035.
- 6.Martínez-Garzón, P. & Poli, P. Cascade and pre-slip models oversimplify the complexity of earthquake preparation in nature. Commun. Earth Environ.5, 120 (2024). 10.1038/s43247-024-01285-y. [Google Scholar]
- 7.Dieterich, J. H. Modeling of rock friction: 1. Experimental results and constitutive equations. J. Geophys. Res. Solid Earth84, 2161–2168 (1979). 10.1029/JB084iB05p02161.
- 8.Ohnaka, M. & Shen, L.-F. Scaling of the shear rupture process from nucleation to dynamic propagation: Implications of geometric irregularity of the rupturing surfaces. J. Geophys. Res. Solid Earth104, 817–844 (1999). 10.1029/1998JB900007. [Google Scholar]
- 9.Selvadurai, P. A. & Glaser, S. D. Laboratory-developed contact models controlling instability on frictional faults. J. Geophys. Res. Solid Earth120, 4208–4236 (2015). 10.1002/2014JB011690. [Google Scholar]
- 10.Dieterich, J. H. Preseismic fault slip and earthquake prediction. J. Geophys. Res. Solid Earth83, 3940–3948 (1978). 10.1029/JB083iB08p03940. [Google Scholar]
- 11.Rubin, A. M. & Ampuero, J.-P. Earthquake nucleation on (aging) rate and state faults. J. Geophys. Res. Solid Earth110 (2005). 10.1029/2005JB003686.
- 12.Ben-Zion, Y. & Zaliapin, I. Localization and coalescence of seismicity before large earthquakes. Geophys. J. Int.223, 561–583 (2020). 10.1093/gji/ggaa315. [Google Scholar]
- 13.Kato, A. & Ben-Zion, Y. The generation of large earthquakes. Nat. Rev. Earth Environ.2, 26–39 (2021). 10.1038/s43017-020-00108-w. [Google Scholar]
- 14.Brace, W. F., Paulding, B. W. Jr. & Scholz, C. Dilatancy in the fracture of crystalline rocks. J. Geophys. Res.1896–1977(71), 3939–3953 (1966). 10.1029/JZ071i016p03939. [Google Scholar]
- 15.Ashby, M. F. & Sammis, C. G. The damage mechanics of brittle solids in compression. Pure Appl. Geophys.133, 489–521 (1990). 10.1007/BF00878002.
- 16.Segall, P. Earthquakes triggered by fluid extraction. Geology17, 942–946 (1989). 10.1130/0091-7613(1989)017%3C0942:ETBFE%3E2.3.CO;2.
- 17.Garagash, D. I. & Germanovich, L. N. Nucleation and arrest of dynamic slip on a pressurized fault. J. Geophys. Res. Solid Earth117 (2012). 10.1029/2012JB009209.
- 18.Lockner, D. A. The role of acoustic emission in the study of rock fracture. Int. J. Rock Mech. Mini. Sci. Geomech. Abstracts30, 883–899 (1993). https://www.sciencedirect.com/science/article/pii/014890629390041B.
- 19.Selvadurai, P. A. Laboratory insight into seismic estimates of energy partitioning during dynamic rupture: An observable scaling breakdown. J. Geophys. Res. Solid Earth124, 11350–11379 (2019). 10.1029/2018JB017194. [Google Scholar]
-
20.Aki, K. Maximum likelihood estimate of
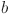 in the formula
in the formula 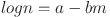 and its confidence limits. Bull. Earthquake Res. Inst. Tokyo Univ.43, 237–239 (1965). https://cir.nii.ac.jp/crid/1573387450038851840.
and its confidence limits. Bull. Earthquake Res. Inst. Tokyo Univ.43, 237–239 (1965). https://cir.nii.ac.jp/crid/1573387450038851840.
- 21.Scholz, C. H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am.58, 399–415 (1968). 10.1785/BSSA0580010399. [Google Scholar]
- 22.Wiemer, S. & Wyss, M. In Mapping spatial variability of the frequency-magnitude distribution of earthquakes (eds Dmowska, R. & Saltzman, B.) , Vol. 45 of Advances in Geophysics 259–V (Elsevier, 2002). https://www.sciencedirect.com/science/article/pii/S0065268702800073.
- 23.Gutenberg, B. & Richter, C. F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am.34, 185–188 (1944). [Google Scholar]
- 24.Lockner, D. A., Byerlee, J. D., Kuksenko, V., Ponomarev, A. & Sidorin, A. Quasi-static fault growth and shear fracture energy in granite. Nature350, 39–42 (1991). 10.1038/350039a0. [Google Scholar]
- 25.Amitrano, D. Brittle-ductile transition and associated seismicity: Experimental and numerical studies and relationship with the b value. J. Geophys. Res. Solid Earth108 (2003). 10.1029/2001JB000680.
- 26.Goebel, T. H., Schorlemmer, D., Becker, T. W., Dresen, G. & Sammis, C. G. Acoustic emissions document stress changes over many seismic cycles in stick-slip experiments. Geophys. Res. Lett.40, 2049–2054 (2013). 10.1002/grl.50507. [Google Scholar]
- 27.Lei, X. Typical phases of pre-failure damage in granitic rocks under differential compression. Geological Society, London, Special Publications261, 11–29 (2006). https://www.lyellcollection.org/doi/abs/10.1144/GSL.SP.2006.261.01.02.
- 28.Main, I. G., Meredith, P. G. & Sammonds, P. R. Temporal variations in seismic event rate and b-values from stress corrosion constitutive laws. Tectonophysics211, 233–246 (1992). https://www.sciencedirect.com/science/article/pii/004019519290061A.
- 29.Reches, Z. & Lockner, D. A. Nucleation and growth of faults in brittle rocks. J. Geophys. Res. Solid Earth99, 18159–18173 (1994). 10.1029/94JB00115. [Google Scholar]
- 30.Lockner, D. A., Byerlee, J., Kuksenko, V., Ponomarev, A. & Sidorin, A. in Chapter 1 Observations of Quasistatic Fault Growth from Acoustic Emissions , Vol. 51 of International Geophysics 3–31 (Academic Press, 1992). https://www.sciencedirect.com/science/article/pii/S0074614208628132.
- 31.Cartwright-Tylor, A. Mangriotis, MD., Main, I.G. et al. Seismic events miss important kinematically governed grain scale mechanisms during shear failure of porous rock. Nat. Commun.13, 6169 (2002). 10.1038/s41467-022-33855-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yu, Z., Zhu, Q., Zhang, E., Zhang, Y., Gu, L., Sui, L. & Yin, Y. Coupling study of deformation field evolution and acoustic emission response characteristics in rock failure and instability process. Sustainability14 (2022). https://www.mdpi.com/2071-1050/14/22/15037.
- 33.Pei, X., Cui, S., Zhu, L. et al. Quantitative investigation on localized deformation process of rocks by uniaxial test and digital image correlation. Environ. Earth Sci.82, 267 (2023). 10.1007/s12665-023-10939-7. [Google Scholar]
- 34.Tapponnier, P. & Brace, W. Development of stress-induced microcracks in Westerly Granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstracts13, 103–112 (1976). https://www.sciencedirect.com/science/article/pii/0148906276919379.
- 35.Germanovich, L. N., Salganik, R. L., Dyskin, A. V. & Lee, K. K. Mechanisms of brittle fracture of rock with pre-existing cracks in compression. Pure Appl. Geophys.143, 117–149 (1994). 10.1007/BF00874326.
- 36.Uchida, S., Levenberg, E. & Klar, A. On-specimen strain measurement with fiber optic distributed sensing. Measurement60, 104 – 113 (2015). http://www.sciencedirect.com/science/article/pii/S0263224114004345.
- 37.Salazar Vásquez, A. F., Rabaiotti, C., Germanovich, L. N. & Puzrin, A. M. Distributed fiber optics measurements of rock deformation and failure in triaxial tests. J. Geophys. Res. Solid Earth127, e2022JB023997 (2022). 10.1029/2022JB023997.
- 38.Niu, Z. Experimental study on the seismic and aseismic deformation during the failure of granitic rock. Master thesis, ETH Zurich, Zurich (2021). 10.3929/ethz-b-000516187.
- 39.Salazar Vásquez, A.F., Selvadurai, P.A., Niu, Z., Bianchi, P., Rabaiotti, C., Madonna, C., Wiemer, S. & Germanovich, L.N. Insights into Triaxial Testing Using Coupled Acoustic Emission and Distributed Optical Fiber Strain Measurements. Paper presented at the 56th Rock Mechanics/Geomechanics Symposium, Santa Fe, New Mexico (2022). 10.56952/ARMA-2022-0706.
- 40.Dresen, G., Kwiatek, G., Goebel, T. H. & Ben-Zion, Y. Seismic and aseismic preparatory processes before large stick-slip failure. Pure Appl. Geophys.177, 5741–5760 (2020). 10.1007/s00024-020-02605-x. [Google Scholar]
- 41.Katz, O. & Reches, Z. Microfracturing, damage, and failure of brittle granites. J. Geophys. Res. Solid Earth109 (2004). 10.1029/2002JB001961.
- 42.Peng, S. & Johnson, A. Crack growth and faulting in cylindrical specimens of chelmsford granite. Int. J. Rock Mech. Mini. Sci. Geomech. Abstracts9, 37–86 (1972). https://www.sciencedirect.com/science/article/pii/0148906272900502.
- 43.Horii, H. & Nemat-Nasser, S. Compression-induced microcrack growth in brittle solids: Axial splitting and shear failure. J. Geophys. Res. Solid Earth90, 3105–3125 (1985). 10.1029/JB090iB04p03105. [Google Scholar]
- 44.Ashby, M. & Hallam (Née Cooksley), S. The failure of brittle solids containing small cracks under compressive stress states. Acta Metallurgica34, 497–510 (1986). https://www.sciencedirect.com/science/article/pii/0001616086900866.
- 45.Cowie, P. A. & Scholz, C. H. Physical explanation for the displacement-length relationship of faults using a post-yield fracture mechanics model. J. Struct. Geol.14, 1133–1148 (1992). https://www.sciencedirect.com/science/article/pii/0191814192900655.
- 46.Dyskin, A.V. & Germanovich, L.N. A model of fault propagation in rocks under compression, Rock Mechanics, Proceedings of the 35th U.S. Symposium on Rock Mechanics, edited by Jaak J.K. Daemen and Richard A. Schultz, 956 Pages, CRC Press, pp. 731 - 738 (1995). ISB 9789054105527.
- 47.McLaskey, G. C. & Lockner, D. A. Preslip and cascade processes initiating laboratory stick slip. J. Geophys. Res. Solid Earth119, 6323–6336 (2014). 10.1002/2014JB011220. [Google Scholar]
- 48.Renard, F., Cordonnie, B., Kobchenko, M., Kandula, N., Weiss, J., & Zhu, W. Microscale characterization of rupture nucleation unravels precursors to faulting in rocks. Earth Planet. Sci. Lett.476, 69–78 (2017). https://www.sciencedirect.com/science/article/pii/S0012821X17304417.
- 49.Renard, F., McBeck, J., Kandula, N., Cordonnier, B., Meakin, P. & Ben-Zion, Y. Volumetric and shear processes in crystalline rock approaching faulting. Proc. Natl. Acad. Sci.116, 16234–16239 (2019). 10.1073/pnas.1902994116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Scholz, C. H. The Mechanics of Earthquakes and Faulting 3 edn (Cambridge University Press, 2019).
- 51.Allam, A. A. & Ben-Zion, Y. Seismic velocity structures in the southern California plate-boundary environment from double-difference tomography. Geophys. J. Int.190, 1181–1196 (2012). 10.1111/j.1365-246X.2012.05544.x. [Google Scholar]
- 52.Scott, J. S., Masters, T. G. & Vernon, F. L. 3-D velocity structure of the San Jacinto fault zone near Anza, California-I. P waves. Geophys. J. Int.119, 611–626 (1994). 10.1111/j.1365-246X.1994.tb00145.x.
- 53.Griffith, A. A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond.221, 163–198 (1921).
- 54.Thompson, B., Young, R. P. & Lockner, D. A. Premonitory acoustic emissions and stick-slip in natural and smooth-faulted westerly granite. J. Geophys. Res. Solid Earth114 (2009). 10.1029/2008JB005753.
- 55.Goebel, T.H.W., Becker, T.W., Schorlemmer, D., Stanchits, S., Sammis, C., Rybacki, E. & Dresen, G. Identifying fault heterogeneity through mapping spatial anomalies in acoustic emission statistics. J. Geophys. Res. Solid Earth117 (2012). 10.1029/2011JB008763.
- 56.Goebel, T. H.W., Becker, T. W., Sammis, C. G., Dresen, G. & Schorlemmer, D. Off-fault damage and acoustic emission distributions during the evolution of structurally complex faults over series of stick-slip events. Geophys. J. Int.197, 1705–1718 (2014). 10.1093/gji/ggu074. [Google Scholar]
- 57.Cartwright-Taylor, A., Main, I.G., Butler, I.B., Fusseis, F., Flynn, M. & King, A. Catastrophic Failure: How and When? Insights From 4-D In Situ X-ray Microtomography. J. Geophys. Res. Solid Earth125, e2020JB019642 (2020). 10.1029/2020JB019642.
- 58.Ke, C.-Y., McLaskey, G. C. & Kammer, D. S. Rupture termination in laboratory-generated earthquakes. Geophys. Res. Lett.45, 12784–12792 (2018). 10.1029/2018GL080492. [Google Scholar]
- 59.Rubinstein, S. M., Cohen, G. & Fineberg, J. Detachment fronts and the onset of dynamic friction. Nature430, 1005–1009 (2014). 10.1038/nature02830. [DOI] [PubMed] [Google Scholar]
- 60.Selvadurai, P. A., Glaser, S. D. & Parker, J. M. On factors controlling precursor slip fronts in the laboratory and their relation to slow slip events in nature. Geophys. Res. Lett.44, 2743–2754 (2017). 10.1002/2017GL072538. [Google Scholar]
- 61.Kammer, D. S. & McLaskey, G. C. Fracture energy estimates from large-scale laboratory earthquakes. Earth Planet. Sci. Lett.511, 36–43 (2019). https://www.sciencedirect.com/science/article/pii/S0012821X19300573.
- 62.Passarelli, L., Selvadurai, P. A., Rivalta, E. & Jónsson, S. The source scaling and seismic productivity of slow slip transients. Sci. Adv.7, eabg9718 (2021). 10.1126/sciadv.abg9718. [DOI] [PMC free article] [PubMed]
- 63.Kostrov, B. Seismic moment and energy of earthquakes, and seismic flow of rock. Izv. Earth Physics1, 23–40 (1974). [Google Scholar]
- 64.Zang, A., Wagner, F. C., Stanchits, S., Janssen, C. & Dresen, G. Fracture process zone in granite. J. Geophys. Res. Solid Earth105, 23651–23661 (2000). 10.1029/2000JB900239. [Google Scholar]
- 65.Villiger, L. et al. Influence of reservoir geology on seismic response during decameter-scale hydraulic stimulations in crystalline rock. Solid Earth11, 627–655 (2020). https://se.copernicus.org/articles/11/627/2020/.
- 66.Cappa, F., Scuderi, M. M., Collettini, C., Guglielmi, Y. & Avouac, J.-P. Stabilization of fault slip by fluid injection in the laboratory and in situ. Sci. Adv.5, eaau4065 (2019). 10.1126/sciadv.aau4065. [DOI] [PMC free article] [PubMed]
- 67.Duboeuf, L., De Barros, L., Cappa, F., Guglielmi, Y., Deschamps, A. & Seguy, S. Aseismic motions drive a sparse seismicity during fluid injections into a fractured zone in a carbonate reservoir. J. Geophys. Res. Solid Earth122, 8285–8304 (2017). 10.1002/2017JB014535. [Google Scholar]
- 68.De Barros, L., Guglielmi, Y., Rivet, D., Cappa, F. & Duboeuf, L. Seismicity and fault aseismic deformation caused by fluid injection in decametric in-situ experiments. Comptes Rendus Geoscience350, 464–475 (2018). https://www.sciencedirect.com/science/article/pii/S1631071318300920. Invited contributions by 2016-2017 geoscience laureates of the French Academy of Sciences.
- 69.Danré, P., De Barros, L., Cappa, F. & Ampuero, J.-P. Prevalence of aseismic slip linking fluid injection to natural and anthropogenic seismic swarms. J. Geophys. Res. Solid Earth127, e2022JB025571 (2022). 10.1029/2022JB025571. E2022JB025571 2022JB025571.
- 70.Ke, C.-Y., McLaskey, G. C. & Kammer, D. S. Earthquake breakdown energy scaling despite constant fracture energy. Nat. Commun.13, 1005 (2022). 10.1038/s41467-022-28647-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Kammer, D. S., McLaskey, G.C., Abecrombie, R.E. et al. Earthquake energy dissipation in a fracture mechanics framework. Nat. Commun15, 4736 (2024). 10.1038/s41467-024-47970-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Meredith, P. G., Main, I. G. & Jones, C. Temporal variations in seismicity during quasi-static and dynamic rock failure. Tectonophysics175, 249–268 (1990). https://www.sciencedirect.com/science/article/pii/004019519090141T. Earthquake Source Processes.
- 73.Sammonds, P. R., Meredith, P. G. & Main, I. G. Role of pore fluids in the generation of seismic precursors to shear fracture. Nature359, 228–230 (1992). 10.1038/359228a0. [Google Scholar]
- 74.Dieterich, J. H. & Kilgore, B. D. Direct observation of frictional contacts: New insights for state-dependent properties. Pure Appl. Geophys.143, 283–302 (1994). 10.1007/BF00874332.
- 75.Barbot, S. Modulation of fault strength during the seismic cycle by grain-size evolution around contact junctions. Tectonophysics765, 129–145 (2019). https://www.sciencedirect.com/science/article/pii/S0040195119301891.
- 76.Bolton, D. C., Shreedharan, S., Rivière, J. & Marone, C. Acoustic energy release during the laboratory seismic cycle: Insights on laboratory earthquake precursors and prediction. J. Geophys. Res. Solid Earth125, e2019JB018975 (2020). 10.1029/2019JB018975. [DOI] [PMC free article] [PubMed]
- 77.Ojala, I. O., Main, I. G. & Ngwenya, B. T. Strain rate and temperature dependence of omori law scaling constants of AE data: Implications for earthquake foreshock-aftershock sequences. Geophys. Res. Lett.31 (2004). 10.1029/2004GL020781.
- 78.Rudnicki, J. & Rice, J. Conditions for the localization of deformation in pressure-sensitive dilatant materials. J. Mech. Phys. Solids23, 371–394 (1975). https://www.sciencedirect.com/science/article/pii/0022509675900010.
- 79.Gulia, L. Time-Space Evolution of the Groningen Gas Field in Terms of b-Value: Insights and implications for seismic hazard. Seismological Research Letters 94 (4): 1807-1820 (2023). 10.1785/0220220396. [Google Scholar]
- 80.Sreejith, K. M., Sunil, P.S., Agrawal, R. et al. Audit of stored strain energy and extent of future earthquake rupture in central Himalaya. Sci. Rep.8, 16697 (2018). 10.1038/s41598-018-35025-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Ando, R. & Imanishi, K. Possibility of Mw 9.0 mainshock triggered by diffusional propagation of after-slip from Mw 7.3 foreshock. Earth Planets Space63, 767–771 (2011). 10.5047/eps.2011.05.016.
- 82.Stevens, V. L. & Avouac, J.-P. On the relationship between strain rate and seismicity in the India-Asia collision zone: Implications for probabilistic seismic hazard. Geophys. J. Int.226, 220–245 (2021). 10.1093/gji/ggab098. [Google Scholar]
- 83.Ma, X. et al. Multi-disciplinary characterizations of the BedrettoLab – a new underground geoscience research facility. Solid Earth13, 301–322 (2022). https://se.copernicus.org/articles/13/301/2022/.
- 84.Schneider, T. Basistunnel Furka - Geologische Aufnahme des Fensters Bedretto (Technical report, FurkaOberalp-Bahn AG, Brig, 1985).
- 85.Rast, M., Galli, A., Ruh, J. B., Guillong, M. & Madonna, C. Geology along the Bedretto tunnel: kinematic and geochronological constraints on the evolution of the Gotthard massif (central alps). Swiss J. Geosci.115, 8 (2022). 10.1186/s00015-022-00409-w. [Google Scholar]
- 86.Labhart, T. Geol. Atlas Schweiz 1:25000, Erläut. 68. Blatt 1251 Val Bedretto (2005).
- 87.Brace, W. F., Orange, A. S. & Madden, T. R. The effect of pressure on the electrical resistivity of water-saturated crystalline rocks. J. Geophys. Res.1896–1977(70), 5669–5678 (1965). 10.1029/JZ070i022p05669. [Google Scholar]
- 88.David, C., Nejati, M. & Geremia, D. On petrophysical and geomechanical properties of bedretto granite (Report, ETH Zurich, Zurich, 2020).
- 89.Selvadurai, P. A., Wu, R., Bianchi, P. et al. A methodology for reconstructing source properties of a conical piezoelectric actuator using array-based methods. J. Nondestr. Eval.41, 23 (2022). 10.1007/s10921-022-00853-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Ketcham, R. A. & Carlson, W. D. Acquisition, optimization and interpretation of X-ray computed tomographic imagery: applications to the geosciences. Comput. Geosci.27, 381–400 (2001). https://www.sciencedirect.com/science/article/pii/S0098300400001163. 3D reconstruction, modelling & visualization of geological materials.
- 91.Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control19, 716–723 (1974). [Google Scholar]
- 92.Kurz, J. H., Grosse, C. U. & Reinhardt, H.-W. Strategies for reliable automatic onset time picking of acoustic emissions and of ultrasound signals in concrete. Ultrasonics43, 538–546 (2005). https://www.sciencedirect.com/science/article/pii/S0041624X04003166. [DOI] [PubMed]
- 93.Bianchi, P., Selvadurai, P.A., Salazar Vásquez, A.F., Dal Zilio, L., Geyra, T., Madonna, C. & Wiemer, S. A study of progressive failure in porous rocks using numerical and experimental modeling. Paper presented at the 56th U.S. Rock Mechanics/Geomechanics Symposium, Santa Fe, New Mexico (2022). 10.56952/ARMA-2022-0621.
- 94.Bianchi, P., Selvadurai, P.A., Dal Zilio, L. et al. Pre-failure strain localization in siliclastic rocks: A comparative study of laboratory and numerical approaches. Rock Mech. Rock Eng.57, 5371–5395 (2024). 10.1007/s00603-024-04025-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Aki, K. & Richards, P. G. Quantitative Seismology 2 edn (University Science Books, 2002).
- 96.McLaskey, G. C. & Glaser, S. D. Acoustic emission sensor calibration for absolute source measurements. J. Nondestr. Eval.31, 157–168 (2012). 10.1007/s10921-012-0131-2. [Google Scholar]
- 97.Thompson, B., Young, R. P. & Lockner, D. A. Observations of premonitory acoustic emission and slip nucleation during a stick slip experiment in smooth faulted Westerly granite. Geophys. Res. Lett.32 (2005). 10.1029/2005GL022750.
- 98.Kwiatek, G., Martínez-Garzón, P. & Bohnhoff, M. HybridMT: A MATLAB/Shell environment package for seismic moment tensor inversion and refinement. Seismol. Res. Lett.87, 964–976 (2016). 10.1785/0220150251. [Google Scholar]
- 99.McLaskey, G. C. & Lockner, D. A. Shear failure of a granite pin traversing a sawcut fault. Int. J. Rock Mech. Min. Sci.110, 97–110 (2018). https://www.sciencedirect.com/science/article/pii/S1365160918302806.
- 100.Hanks, T. C. & Kanamori, H. A moment magnitude scale. J. Geophys. Res. Solid Earth84, 2348–2350 (1979). 10.1029/JB084iB05p02348. [Google Scholar]
- 101.Aki, K. Generation and propagation of G waves from the Niigata Earthquake of June 16, 1964.: Part 2. Estimation of earthquake moment, released energy, and stress-strain drop from the G wave spectrum. Bull. Earthq. Res. Inst.44, 73–88 (1966).
- 102.van der Elst, N. J. B-Positive: a robust estimator of aftershock magnitude distribution in transiently incomplete catalogs. J. Geophys. Res. Solid Earth126, e2020JB021027 (2021). 10.1029/2020JB021027.
- 103.Shi, Y. & Bolt, B. A. The standard error of the magnitude-frequency b value. Bull. Seismol. Soc. Am.72, 1677–1687 (1982). 10.1785/BSSA0720051677. [Google Scholar]
- 104.Kagan, Y. Y. & Knopoff, L. Spatial distribution of earthquakes: the two-point correlation function. Geophys. J. Int.62, 303–320 (1980). 10.1111/j.1365-246X.1980.tb04857.x. [Google Scholar]
- 105.Turcotte, D. L. Fractals, chaos, self-organized criticality and tectonics. Terra Nova4, 4–12 (1992). 10.1111/j.1365-3121.1992.tb00444.x. [Google Scholar]
- 106.Goebel, T. H., Kwiatek, G., Becker, T. W., Brodsky, E. E. & Dresen, G. What allows seismic events to grow big?: Insights from b-value and fault roughness analysis in laboratory stick-slip experiments. Geology45, 815–818 (2017). 10.1130/G39147.1. [Google Scholar]
- 107.Paterson, M. S. & Wong, T.-f. Experimental Rock Deformation: The Brittle Field Vol. 348 (Springer, 2005).
- 108.Anderson, T. W. An Introduction to Multivariate Statistical Analysis (Wiley, London, 1958). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
DSS, XR-CT scan and the raw acoustic waveforms of the detected passive events and active shots are available at the ETH Zurich Data Collection (http://hdl.handle.net/20.500.11850/638141). The continuous passive AE recordings are stored on the Bedretto Underground Laboratory server and are available upon request due to their large size. .