Abstract
To accommodate China’s electricity market reforms integrating medium and long-term (MLT) transactions and spot transactions, and to boost renewable energy consumption through the spot market, this paper proposes an optimized cross-provincial electricity trading strategy model based on a two-layer game framework. The proposed model incorporates an MLT green certificate contract decomposition method, enabling nested optimization of green certificate contracts and scheduling plans for cross-provincial power transactions. To encourage broader participation, a bilateral green certificate trading framework is established, which globally optimizes green certificate allocation to increase benefits for market participants. A Nash-Stackelberg game model is introduced to address complex game interactions among multiple participants under the green certificate mechanism and the limitation of assuming complete rationality. The game model combines supply and demand sides with an embedded demand-side evolutionary game. Additionally, an improved Aquila optimization algorithm (IAOA) is developed to accurately calculate electricity supply and demand. The algorithm integrates a Circle chaotic map, Sobol sequence, random walk strategy, and filtering technology to enhance optimization capabilities and manage complex constraints. The algorithm is then embedded with a distributed iterative approach to achieve equilibrium strategies. A real-world case study was conducted to validate the feasibility and effectiveness of the proposed model. The results demonstrate that the proposed approach effectively achieves equilibrium, optimizes trading strategies, and fosters win-win, coordinated development among participants in the cross-provincial electricity market.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-81133-3.
Keywords: MLT transactions, Tradable Green Certificate, Cross-provincial transaction, Nash-Stackelberg game, Evolutionary game, Aquila optimization algorithm
Subject terms: Renewable energy, Electrical and electronic engineering, Applied mathematics
Introduction
A new phase of power market reform in China was catalyzed by the issuance of the Implementation Opinions on Advancing Power Market Construction, issued by the National Development and Reform Commission and the National Energy Administration in November 20151.
This round of reform explicitly proposes that China’s power market construction should integrate both MLT contract transactions and spot market transactions2. The goal is to gradually establish a market system that manages risk through MLT contracts while optimizing the allocation of power resources through spot transactions, thereby uncovering true price signals3. Therefore, effectively establishing a spot market that considers MLT transactions has become the key to deepening the reform of the power system.
Numerous studies have been conducted on MLT transactions. In terms of trading strategies of market players, Reference4proposed a mixed integer programming model based on portfolio theory to describe the trading strategies of large power users in spot and MLT markets. Reference5described the negative correlation between wind power generation and electricity price through the time-varying copula model and proposed a research method for the transaction strategy of long-term wind power contracts. Reference6proposed a stochastic optimal scheduling model considering long-term power transactions in the wind power integrated energy system and introduced the power contract decomposition into the day-ahead optimal scheduling planning process. Reference7proposed an optimization model considering the monthly electricity imbalance and the uncertainty of competitors’ bidding strategies to deal with the problem of electricity imbalance in MLT transactions. In terms of the interaction effect between the MLT market and the spot market, Reference8provided a comprehensive analysis of both MLT and spot trading markets from a risk perspective, concluding that MLT transactions can avoid certain risks. Reference9proposed a transaction risk control model for power retailers, employing conditional risk return and value theory to assess the risk of MLT and spot transactions and to minimize such risk through market integration. Reference10proposed an equilibrium model based on the supply function and conducted an equilibrium analysis on the day-ahead market and the MLT trading market. The results showed that the price of the MLT contracts would follow the mathematical expectation of the day-ahead market price. Reference11presented a cobweb model, concluding that the introduction of MLT trading markets would be conducive to reducing the volatility of electricity prices, but other factors such as investment lag might lead to periodic fluctuations in electricity market prices. The above-mentioned studies have comprehensively analyzed and discussed the strategic behavior of market players in MLT and spot transactions, along with the effect of the two transaction markets. However, as power market reforms progress, the imperative to establish a unified national power market for the comprehensive coordination and optimal allocation of power resources has become increasingly evident12. The establishment of cross-provincial and cross-regional markets has become an important technology to improve the utilization rate of renewable energy, address the difficulties of renewable energy development, and achieve emission reduction goals. Therefore, research on MLT and spot transactions in the cross-provincial and cross-regional markets is crucial for China to construct a complete market system framework. The above-mentioned studies are all about the analysis and discussion of MLT transactions in a single area. Currently, there is a lack of analysis on the multi spatial scale power purchase and distribution of cross-provincial and cross-regional markets and intra provincial markets. Moreover, there is also a lack of cross provincial MLT transactions and joint research between cross provincial spot transactions. The influencing factors of MLT trading units and trading participants, such as the deviation of MLT contract completion of units and the daily load conditions of participating trading areas (trading participants in this paper) have been often overlooked in the relationship between MLT and spot transactions. Furthermore, the external monetary value of renewable energy power generation is ignored, and the actual national policies and mechanisms should be combined to promote the market to promote the consumption of renewable energy.
To further tap the potential of renewable energy consumption, researchers believe that a reasonable market mechanism can facilitate the development of a sustainable power market. The government introduced market mechanisms into resource allocation13, and transformed renewable energy subsidies from government behavior to market behavior, forming a trading system with Renewable Portfolio Standard (RPS) as the framework14, and Tradable Green Certificate (TGC) mechanism as the supporting mechanism15. Reference16proposed an inter-provincial hybrid energy dispatching model based on the TGC trading mechanism. Reference17established a comprehensive planning model consisting of a multiple regression model and a linear programming model to promote the optimization of renewable energy resource allocation through the inter-provincial distribution of renewable energy and the combination of RPS and TGC trading mechanism. Reference18discussed the role of the TGC trading mechanism in balancing the grid-connected price of photovoltaic power generation. Reference19proposed a mixed complementarity, multi-region partial equilibrium model that clears both electricity and green certificate markets, assuming Nash-Cournot competition. Reference20proposed a two-stage joint equilibrium model, based on the oligopoly competition equilibrium theory and the TGC trading mechanism, to provide insights for power market design. Reference21employed game theory to assess six potential TGC scenarios, enabling decision-makers to design and select the best TGC scenario to improve the effectiveness of interaction between the TGC system and the power market. Reference22compared the costs of two EU member countries under different policies and demonstrated that TGC transactions can ensure the cost-effectiveness of renewable energy power generation. Reference23proposed an equilibrium model for cross-regional TGC transactions to reduce part of the power generation costs. Reference24proposed a bi-level mathematical model to derive the optimal trading strategy for a strategic renewable energy aggregator in the joint auction-based electricity and green certificates market. Reference25proposed a simple linear programming mathematical framework to derive the optimal portfolio management and trading strategy for a renewable energy aggregator in the electricity, hydrogen, and green certificates markets. Currently, extensive research has been conducted on the TGC trading mechanism, providing a solid foundation for the implementation and theoretical exploration of RPS. However, China’s TGC transactions have shortcomings such as discontinuity and low trading volume, and the degree of marketization in China remains limited, with weak market awareness among all participants. A mandatory trading system is crucial for the effective implementation of market-oriented transactions and dynamic balancing of TGCs26. With the continuous development of the power grid form, the extensive access of large-scale new energy, and the continuous opening of the power market, the competition pattern of multiple market players has been accelerated27. Most of the above-mentioned research has examined the effect of TGC transactions, and some studies have investigated the equilibrium model and market design of TGC transactions. However, these studies have not considered the enthusiasm of participants in TGC transactions and the transaction environment (such as the transaction environment with limited rationality and limited information). Moreover, in the actual cross- provincial and cross-regional trading market, the interests of each subject are interactive and coupled. Scientific operation modes and reasonable planning methods need to be used to solve the complex relationship between participants and ensure the effective consumption of new energy and the stability and flexibility of the power supply. The model proposed in this paper considers the above factors, overcomes the defect of complete rationality of market participants in current research, and urges more market participants to participate in TGC transactions.
Game theory is an important theoretical tool to solve the above problems. It can effectively balance the conflicts of interest between different subjects. Different game models have significant differences in application scenarios and participant composition. To better illustrate the application areas and applicability of these models more clearly, Table 1compares some recent game models. Reference28established the Stackelberg game relationship between energy service providers and energy consumers to analyze the impact on the energy supply and consumption behavior of both parties and the economy of the system planning scheme. Reference29proposed a single-leader multi-follower Stackelberg game model that includes safety checks for the distribution system, considering the discrete characteristics of capacitor banks and substation transformer tap ratios. Reference30constructed a Nash-Stackelberg game model to analyze the bidding behavior of multiple distributed energy resource aggregators in the day-ahead electricity market. Reference31analyzed the relationship between revenue and cost of power generators and power purchasers based on cooperative game theory and proposed an improved Shapley allocation method for benefit distribution. Reference32analyzed the interest interaction between renewable energy power and thermal power generators in different regions based on cooperative game theory. The above-mentioned studies are based on the traditional non-cooperative/cooperative game, assuming that all participants are completely rational, and the information is completely symmetrical. However, there is a defect that the configuration scheme is too ideal. Evolutionary games do not require the assumption of complete rationality or perfect information symmetry among participants, enabling a more reasonable analysis of the decision-making behavior of participants in actual situations33,34. Currently, it has been applied in electricity market bidding strategy, generation side behavior analysis, electric vehicle charging infrastructure construction, and urban heating systems. Several studies have focused on the research of trading strategies between different areas. However, they are all modeled by completely rational individuals, without considering the individual selection under limited information and limited rationality. The existing research on cross-provincial and cross-regional electricity markets has not yet addressed the joint problem of supply-demand transactions and demand-side power purchase selection, failing to account for the interaction between the two in the actual cross-provincial and cross-regional transactions.
Table 1.
Comparison of different game models.
| Ref. | Game model | Participants | Application scenario |
|---|---|---|---|
| 28 | Stackelberg game | Energy service providers and energy consumers | Energy supply and consumption |
| 29,30 | Stackelberg /Nash-Stackelberg game | distributed energy resource aggregators, Independent System Operator and Distribution System Operator | Strategic bidding in electricity markets |
| 31 | Cooperative game | Power generators and power purchasers | Energy supply and consumption |
| 32 | Cooperative game | Renewable energy and thermal power producers | Energy supply |
| 35–38 | Evolutionary game | Various generation-side bidding entities | Generation-side power market bidding |
| 2,39 | Evolutionary game | Power producers | Analysis of power producers’ trading behavior |
| 40 | Evolutionary game | Electric vehicle station | Construction of electric vehicle charging infrastructure |
| 41 | Evolutionary game | Centralized heating companies and government | Urban heating system |
Furthermore, the problem of cross-provincial and cross-regional power market operation scheduling has historically hindered market development. Therefore, it is crucial to find an effective and powerful optimization algorithm to solve this problem. Reference42proposed a penalty function hybrid direct search method to solve the multi-region scheduling operation problem considering the large-scale integration of wind turbines. Reference43proposed an improved gradient-based Jaya algorithm to generate a feasible Pareto optimal solution set for the bi-objective cross-regional scheduling operation problem. Reference44proposed an evolutionary particle swarm optimization algorithm to optimize the scheduling operation strategy in multiple regions considering the unit valve point effect. Although the above-mentioned studies can effectively address the cross-regional operation dispatching problem, they are not directly applicable to modeling the complex game-theoretic interactions among multiple decision-making players in the power market, especially the two-layer game model. Reference45proposed a distributed iterative algorithm to solve the microgrid two-layer game power trading model. Reference46developed a two-layer game model for the electric vehicle charging and discharging scheduling strategy and the bidding strategy of multiple electric vehicle aggregators in the electricity market, employing a distributed iterative algorithm to solve the model. The direct use of the distributed iterative algorithm in the above-mentioned studies limits the speed and accuracy of solving the two-layer game model. To better solve the two-layer game model of cross-regional transactions, this paper first improves the Aquila optimization algorithm (AOA)47, which is used to calculate the supply and demand electricity on both supply and demand sides. The AOA is a relatively new natural heuristic optimization method that simulates the hunting process of the Skyhawk and has a good effect for optimization problems. To improve the optimization ability of the AOA, this paper introduces three strategies: Circle chaotic map, Sobol sequence and random walk. Fifteen test functions are used to compare the proposed improved AOA with four classical heuristic algorithms, validating its stability and accuracy. To further enhance the computational efficiency and accuracy of solving the two-layer game model for cross-regional transactions, the improved AOA is nested within the distributed iterative algorithm.
Based on the above analysis, this paper proposes an inter-provincial two-layer game power transaction optimization decision-making model considering the MLT trading plans. There are four specific contributions:
(1) To better balance the supply and demand of cross-provincial and cross-regional systems and minimize the costs and risks of purchasing electricity in the cross-provincial market, this paper proposes an optimization model that nests MLT contracts with the day-ahead scheduling plan. By decomposing MLT trading contracts and considering multiple factors including contract completion deviations of generating units and daily load conditions of participating regions, the model provides relatively efficient contract decomposition results, improving the enforceability of MLT trading plans and facilitating the connection between MLT and spot trading markets. Additionally, a two-layer game model is proposed to address the issues of multi-player decision-making under bounded rationality, the imbalance of interests between supply and demand sides in cross-regional transactions, the low enthusiasm of participants in TGC transactions, and the lack of dynamic balance in TGCs. The proposed model considers the double-layer coupling between the demand and supply sides during cross-regional transactions and jointly solves the demand-side selection evolutionary game and the supply-demand Nash-Stackelberg game in the electricity market. An evolutionary game model is constructed on the demand side, based on assumptions of “bounded rationality” and “limited information,” to depict the game behavior of demand-side users in actual decision-making scenarios, thus avoiding the idealization of game conclusions. This approach provides a scheduling scheme that balances the interests of participants across multiple markets, promoting more voluntary participation in TGC transactions.
(2) To achieve faster and more accurate computation of the optimal equilibrium result, an Improved Artificial Optimization Algorithm (IAOA) is proposed to calculate optimal electricity sales and purchases for both supply and demand sides. The proposed IAOA incorporates circle chaotic mapping, Sobol sequence, and random walk strategy, enhancing optimization capabilities and exhibiting significant improvements in stability and accuracy compared to other algorithms. Complex constraints are addressed through the application of filtering technology, and the IAOA is nested within a distributed iterative algorithm to obtain a trading equilibrium strategy.
(3) Using two provinces from western China and two from central China as case studies, this paper derives the trading behaviors of both supply and demand sides, exploring the impact of quota tasks, penalty coefficients, and the establishment of game relationships on the behavioral trends of multiple agents and system balance.
The remainder of this paper is structured as follows. Section "Operation mode of cross-provincial and cross-regional electricity market under the RPS" introduces the operation mode of the cross-provincial and cross-regional electricity market under the RPS. Section "Optimal decision-making model of cross-provincial power transaction considering the MLT transaction plan" presents an optimal decision-making model for cross-provincial power transactions that considers the MLT transaction plan. Section "The solution of the two-layer game model considering the MLT trading plan" provides a solution for the two-layer game model, which incorporates MLT trading plans. Simulation cases and comparative analyses are discussed in Sect. "Simulation of cases and comparative analysis". Lastly, Sect. "Conclusion" concludes the paper.
Operation mode of cross-provincial and cross-regional electricity market under the RPS
Operational framework
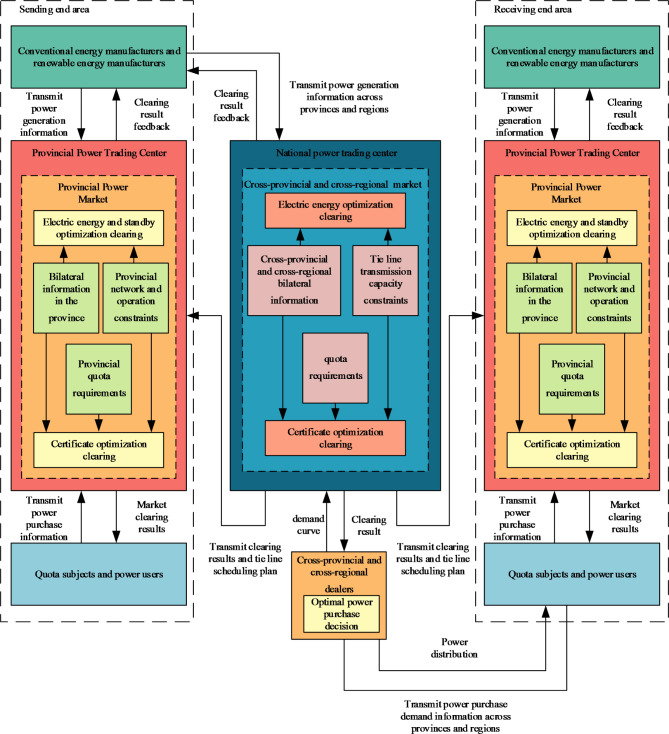
The two-level power market of “unified market, two-level operation” works together to ensure power supply and optimal allocation of resources through coordinated operation of cross-provincial and provincial power markets. The interprovincial electricity market, centered on interprovincial electricity trading, is strategically positioned to realize the national energy strategies, promote the consumption of clean energy, and optimize the allocation of large-scale resources. The provincial market is mainly positioned to realize the optimal allocation of resources in the province and ensure the balance of power supply and demand. Based on the actual situation of power transactions between and within provinces in China and the development direction of the future power market, this paper proposes an operation mode for a two-level power market under the RPS. The operation framework of the two-level power market is shown in Fig. 1.
Fig. 1.
Operation framework of two-level electricity market under RPS.
Before the opening of the spot market, market players can conduct bilateral contract transactions within a specific province or across different provinces and regions. After successful transactions, both parties are obligated to file the relevant details with the National Power Trading Center and the Provincial Trading Center.
After the opening of the spot market, the cross-provincial and cross-regional spot market shall be carried out first. The sending end of various units in the province shall report the power generation information to the cross-provincial and cross-regional dealers. The receiving end area of various power users and quota subjects in the province shall report the power load demand information to the cross-provincial and cross-regional dealers. The cross-provincial and cross-regional traders report the inter-provincial power purchase demands to the National Power Trading Center based on the generation bidding and load demand information, renewable energy output, and load demand forecast. The cross-provincial and cross-regional dealers make optimal decisions regarding electricity purchases by leveraging information on various units and load information. This ensures that new energy generation in the receiving end area accurately matches provincial electricity purchases.
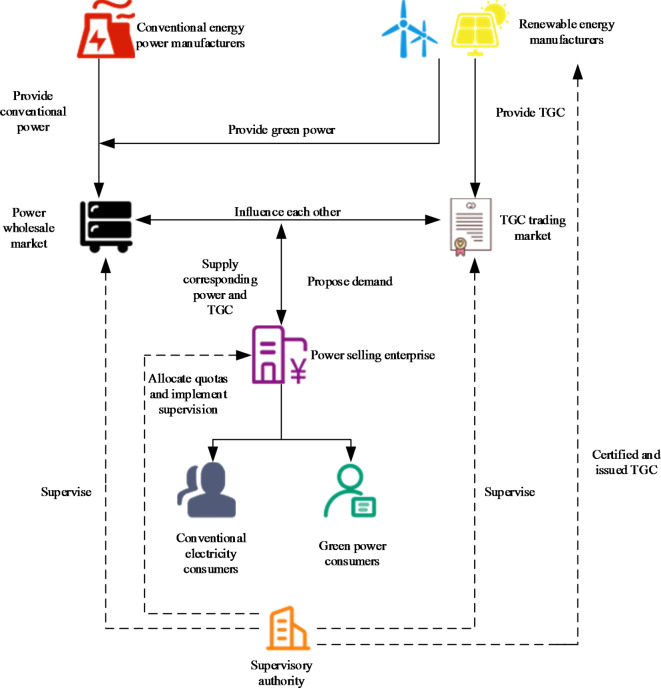
Once the cross-provincial and cross-regional spot transactions are cleared, the Provincial Power Trading Center organizes the intra-provincial spot transactions and receives the provincial bidding information from the market entities in the province. The Provincial Power Trading Center takes the results of the cross-provincial and cross-regional transactions and the inter-provincial tie line dispatching plan as the boundary conditions to clear the intra-provincial market and form the subsequent day’s intra-provincial dispatching plan. The specific supply relationship between entities in the province is shown in Fig. 2.
Fig. 2.
Supply relationship of market subjects in the province.
Optimal decision-making model of cross-provincial power transaction considering the MLT transaction plan
In this paper, the participants of the two-layer game in the electricity market include the sending end area (seller group) and the receiving end area (buyer group). The Stackelberg game model is established between the supply and demand sides in the two-layer game model of the cross-regional electricity market built in this paper. The sending end area and the receiving end area groups are the leaders and followers of the game, and the power interaction is realized through the tie lines. When there are two or more sending end areas, a Nash game is formed among the sending end areas.
At the same time, the evolutionary game model between the receiving end areas is established on the power demand side. The optimal power trading strategy is finally obtained by employing the two-layer game model to deal with the complex relationship between different market subjects. The two-layer game cycle enables the sending end area to provide a better electricity purchase price, which will help the evolution of the strategy of the evolutionary game. These two layers of the game are coordinated and evolving and will eventually develop to the equilibrium point. At this time, it becomes possible to simultaneously determine the optimal power distribution strategy in the sending end area, the optimal power purchase strategy in the receiving end area, and the optimal dispatching strategy within the sending end area and the receiving end area. This equilibrium point can effectively balance the economic benefits of multiple agents in both the sending and the receiving end areas, leading to mutually beneficial and win-win results.
Construction and analysis of the evolutionary game model of the power demand side
Evolutionary game theory is based on the assumption of “limited rationality”, which uses dynamic processes to study how participants adjust their behaviors to adapt to the environment or opponents in the evolution of the game and thus generates the evolution trend of group behavior48. “Limited rationality” means that the knowledge and information owned by the decision-making subject are incomplete, the computing and reasoning ability of the decision-making subject is limited, and the decision-making behavior is uncertain. Since the receiving end area is a bounded rational group in the power purchase process, an evolutionary game can more reasonably depict the game behavior of the receiving end area in the actual decision-making scenario. Therefore, the process of power purchase strategy in the receiving end area is modeled as an evolutionary game.
Basic elements of game
(1) Participants. The participants are the receiver regions, represented by RAn, and the set Np of participants is marked as 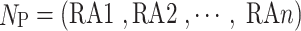 .
.
(2) Strategies. The strategy is the power purchase selection of each receiving area to the sending area. It is recorded as  , where i is the index of the receiving end area, with
, where i is the index of the receiving end area, with 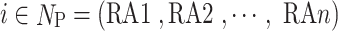
(3) Payments. The total payment vector of multiple receiving end areas for power purchase is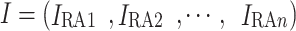 .
.
Description of the strategy set
In this paper, two types of power-selling regions, large and small, are formed due to the regional total renewable energy power generation and the gap between local load demand. The division standard is the regional saleable electricity capacity. The specific description of the set of evolutionary game strategies is shown in Table 2.
Table 2.
Description of the set of evolutionary game strategies.
| Game selection | Meaning |
|---|---|
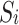 -Large area -Large area |
All electric power is purchased from large areas, and the probability of selecting large areas is 100%. |
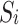 -Large area and small area -Large area and small area |
Purchase part of the electricity from large areas and small areas, and the selection probability is 100%. |
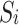 - small area - small area |
All electricity is purchased from small areas, and the probability of selecting large areas is 100%. |
Payment in the receiving end area
The payment of a single receiving end area is the difference between revenue and cost. The revenue includes the revenue from selling electricity to users 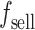 , the cost of generating electricity by conventional units
, the cost of generating electricity by conventional units 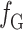 , the cost of generating electricity by renewable energy
, the cost of generating electricity by renewable energy 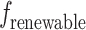 (photovoltaic power generation, wind power generation), the cost of purchasing renewable energy power
(photovoltaic power generation, wind power generation), the cost of purchasing renewable energy power 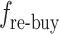 , the cost of purchasing TGCs
, the cost of purchasing TGCs 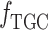 , and the penalty cost
, and the penalty cost 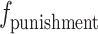 when the quota is not completed.
when the quota is not completed.
The specific expression is shown in the Eq. (1), where t is the index of each dispatching period in the typical daily total dispatching cycle, with 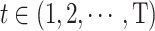 and T = 24 h;
and T = 24 h;
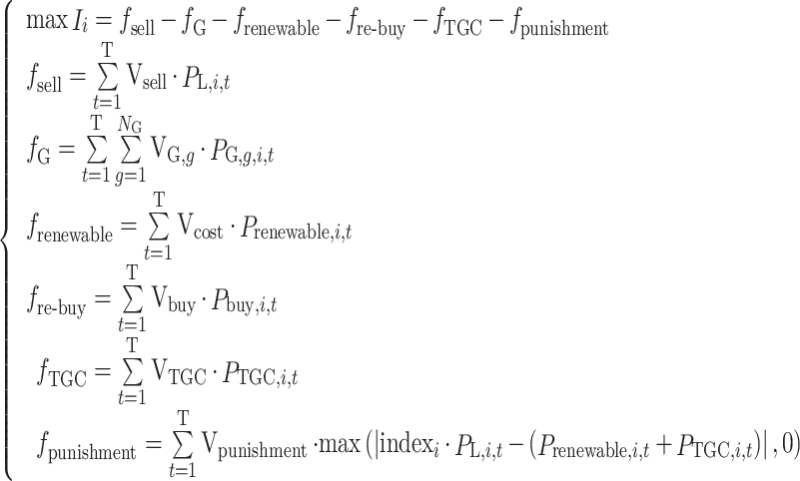 |
1 |
The receiving end area also has the following operational constraints:
(1) Power balance constraint. Power needs to be balanced in real time.
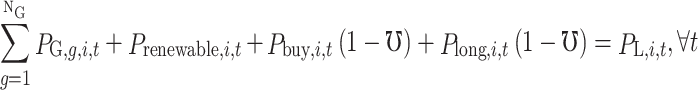 |
2 |
Where, 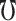 represents line loss rate.
represents line loss rate.
(2) Conventional unit constraints.
Constraint on output range of conventional units:
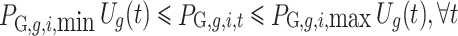 |
3 |
Unit climbing rate constraint:
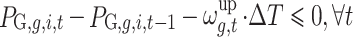 |
4 |
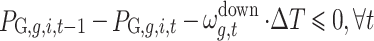 |
5 |
Minimum start-up and minimum shutdown hours constraints:
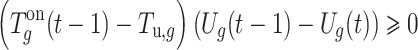 |
6 |
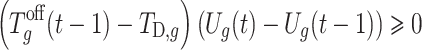 |
7 |
(3) Tie-line constraints.
Tie-line power direction constraint:
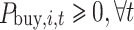 |
8 |
Upper and lower limit constraints of tie-line power:
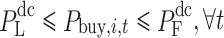 |
9 |
Tie-line power climbing rate constraints:
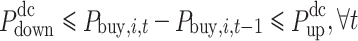 |
10 |
Tie-line power maintenance time constraint:
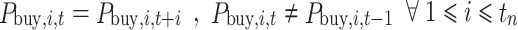 |
11 |
(4) Power purchase constraint.
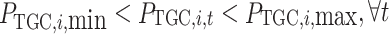 |
12 |
(5) security constraint.
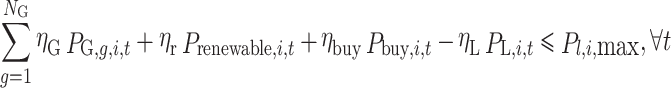 |
13 |
(6) Non-water quota requirements constraint.
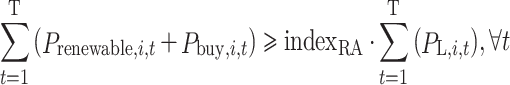 |
14 |
(7) Constraint on daily electricity quantity of MLT contracts.
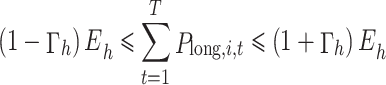 |
15 |
Where 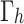 is determined according to the completion of the contract signed by the unit, and
is determined according to the completion of the contract signed by the unit, and 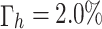 .
.
Construction of the evolutionary game model
It can be seen from Eq. (16) that the optimal electricity quantity purchased by buyer i from seller j in time period t is 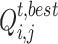 , (the payment function of buyer i reaches the maximum), which is:
, (the payment function of buyer i reaches the maximum), which is:
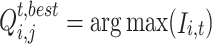 |
16 |
The probability that the buyer i purchases the required electricity from the seller j in time period t is 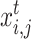 , meeting
, meeting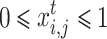 and
and 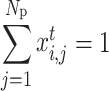 . Then the total electricity demand
. Then the total electricity demand 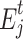 of the buyer group for the seller j in time period t is expressed as:
of the buyer group for the seller j in time period t is expressed as:
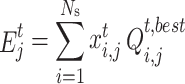 |
17 |
The optimal electricity 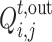 that seller j can sell in time period t is obtained by optimizing all resources in seller area j.
that seller j can sell in time period t is obtained by optimizing all resources in seller area j.
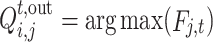 |
18 |
Where 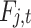 is the payment function of seller j in time period t.
is the payment function of seller j in time period t.
According to the optimal electricity demand and supply obtained by the buyer and the seller, respectively, the supply and demand ratio of the Seller j in time period t can be obtained as:
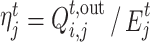 |
19 |
At this time, the actual electricity quantity that the buyer i can purchase from the seller j in time period t is as follows:
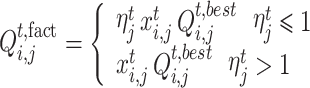 |
20 |
When 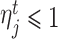 , it means that the electricity supply of seller j cannot meet the demand, and the sum of all the buyer’s actual purchased electricity
, it means that the electricity supply of seller j cannot meet the demand, and the sum of all the buyer’s actual purchased electricity 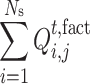 is equal to the seller j’s available electricity, as shown in the Eq. (21). When
is equal to the seller j’s available electricity, as shown in the Eq. (21). When  , it means that the electricity supply of seller j exceeds the demand, and seller j can meet the electricity demand of all buyers at this time.
, it means that the electricity supply of seller j exceeds the demand, and seller j can meet the electricity demand of all buyers at this time.
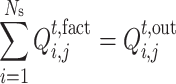 |
21 |
According to the electricity quantity purchased by the buyer, the income of buyer i in time period t is calculated as:
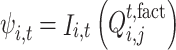 |
22 |
It is defined as the average income of all buyer groups in period t, and its calculation formula is:
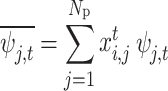 |
23 |
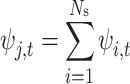 |
24 |
In this paper, the buyer group participates in the evolutionary game and takes the power purchase selection as the strategy set. Considering that the interaction between buyer groups is a repeated game characterized by limited rationality and information, the following replication dynamic equation is used to describe the evolution process49:
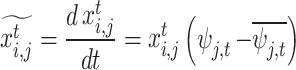 |
25 |
When the game reaches the evolutionary stable strategy (ESS), 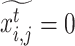 , the income of the buyer group is equal to the average income, and any buyer will not change the probability of selecting seller j.
, the income of the buyer group is equal to the average income, and any buyer will not change the probability of selecting seller j.
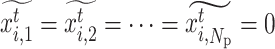 |
26 |
At this time, the evolutionary game equilibrium strategy is 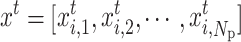 .
.
The discrete replication equation is used to approach the replication dynamic equation to obtain the dynamic evolution equation of the final buyer group:
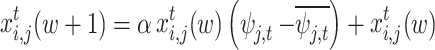 |
27 |
Where 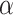 is the step adjustment coefficient and
is the step adjustment coefficient and 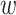 is the number of iterations. When
is the number of iterations. When 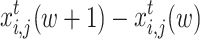 is infinitely close to 0, it indicates that the evolutionary game equilibrium is reached, and the iteration is terminated.
is infinitely close to 0, it indicates that the evolutionary game equilibrium is reached, and the iteration is terminated.
Construction and analysis of game model between power supply and demand
In this paper, the Stackelberg game theory is used to analyze the complex interest relationship between market players on both sides of supply and demand in cross-regional TGC bilateral transactions. The sending end area (seller group) is the leader of the game, and the receiving end area (buyer group) is the follower of the game. When there are two or more sending end areas, a Nash game is formed among the sending end areas.
Basic elements of Nash-Stackelberg game
According to the mechanism and methodology of the Stackelberg game in a competitive market environment50, the basic elements are as follows:
(1) Participants: The participants only include the sending and the receiving end areas represented by SAn and RAn, respectively. The set of participants is marked as 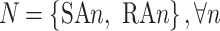 . The participants in the Nash game are the various sending-end regions.
. The participants in the Nash game are the various sending-end regions.
(2) Strategies: The strategy of the sending end area is the power selling price and TGC price of the receiving region in the TGC transaction, which are recorded as 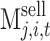 and
and 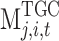 , respectively. The strategy of the receiving end area is the trading demand (i.e. trading volume) in the TGC transaction, which is recorded as
, respectively. The strategy of the receiving end area is the trading demand (i.e. trading volume) in the TGC transaction, which is recorded as 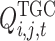 .
.
Both the sending and the receiving end areas have continuous policy space sets. The policy space set of each participant is marked as 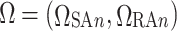 , which can be represented as
, which can be represented as 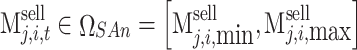 ,
,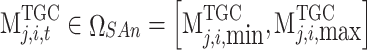 , and
, and 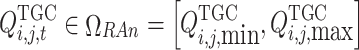 respectively. Where,
respectively. Where, 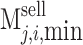 and
and 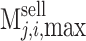 are the lower and the upper limits of the transaction price of purchasing renewable energy electricity, respectively,
are the lower and the upper limits of the transaction price of purchasing renewable energy electricity, respectively, 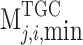 and
and 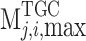 refer to the lower and the upper limits of TGC transaction price, respectively, and
refer to the lower and the upper limits of TGC transaction price, respectively, and 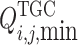 and
and 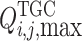 are the lower and the upper limits of the receiving end area’s demand for TGCs in TGC transactions, respectively.
are the lower and the upper limits of the receiving end area’s demand for TGCs in TGC transactions, respectively.
(3) Payments: The payment is defined as the profit (the difference between revenue and cost) of the participant in the overall scheduling cycle. Since the payment function of the receiving end area has been expressed in Sect. "Description of the strategy set", this section mainly describes the payment function of the sending end area. The total payment vector of the sending end area can be expressed as 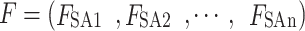 .
.
Payment in the sending end area
The revenue of a single sending end area includes revenue 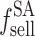 from selling electricity to users, income from the sale of renewable energy power
from selling electricity to users, income from the sale of renewable energy power 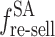 , proceeds from selling green certificates
, proceeds from selling green certificates 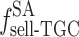 , generation cost
, generation cost 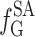 of conventional units and renewable energy power generation cost
of conventional units and renewable energy power generation cost 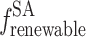 (photovoltaic power generation, wind power generation).
(photovoltaic power generation, wind power generation).
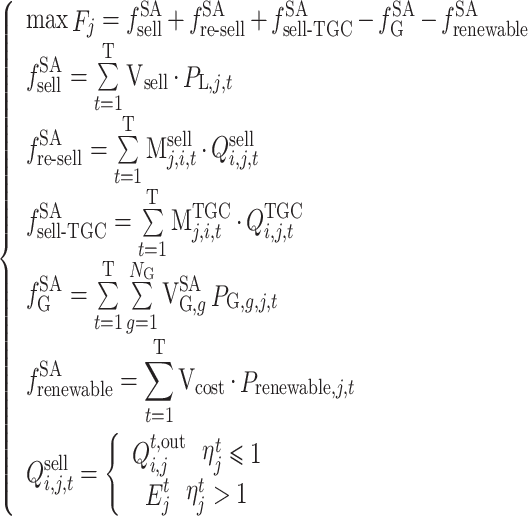 |
28 |
Since the conventional unit constraints (conventional unit output range constraint, unit climbing rate constraint, minimum start-up and minimum shutdown hours constraint) and tie-line constraints (tie-line power direction constraint, upper and lower limit constraint of tie-line power, tie-line power climbing rate constraint, tie-line power maintenance time constraint) are similar to those of the receiving end area, they will not be repeated here.
(1) Power balance constraint.
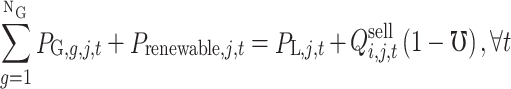 |
29 |
(2) Purchase price constraint.
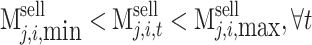 |
30 |
 |
31 |
(3) Security constraint.
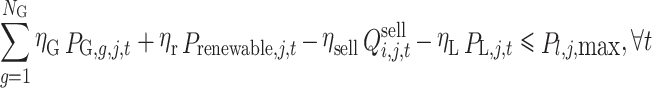 |
32 |
(4) Non-water quota requirements constraint.
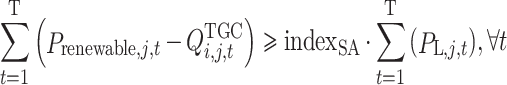 |
33 |
Equilibrium existence proofs for game models
Since the strategy space set of multi-participants 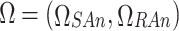 in bilateral transactions is a non-empty, compact, and convex subset of European space, the existence of Nash equilibrium can only be proved by assuming that the payment function of each participant is a continuous function or a continuous quasi-concave function in the corresponding strategy space.
in bilateral transactions is a non-empty, compact, and convex subset of European space, the existence of Nash equilibrium can only be proved by assuming that the payment function of each participant is a continuous function or a continuous quasi-concave function in the corresponding strategy space.
Theorem 1
For a strategic game 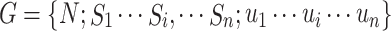 , if the strategy set
, if the strategy set 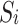 is a non-empty, compact, and convex subset of Euclid space and the payoff function
is a non-empty, compact, and convex subset of Euclid space and the payoff function 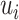 is continuous for the strategy combination S and quasi-concave for
is continuous for the strategy combination S and quasi-concave for 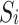 , then the game has a pure strategy Nash equilibrium.
, then the game has a pure strategy Nash equilibrium.
Theorem 2
For a strategic game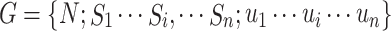 , if the strategy set
, if the strategy set 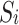 is a non-empty, compact, and convex subset of Euclid space and the payment function
is a non-empty, compact, and convex subset of Euclid space and the payment function 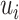 is continuous for the strategy combination S, there is a mixed strategy Nash equilibrium in the game.
is continuous for the strategy combination S, there is a mixed strategy Nash equilibrium in the game.
In the Nash game model, the existence of Nash equilibrium is established by proving the continuity or continuous quasi-concavity of the regional payment functions and supply-side strategies.
The payment 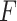 for the sending end area is divided into the linear term of the transaction price
for the sending end area is divided into the linear term of the transaction price 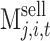 in the bilateral TGC transaction and is denoted as
in the bilateral TGC transaction and is denoted as 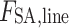 .
.
Where 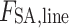 is a linear function of the transaction price
is a linear function of the transaction price 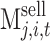 , including five parts, namely, the income from selling electricity to users, the income from selling renewable energy electricity, the income from selling TGCs, the cost of generating electricity from conventional units, and the cost of generating electricity from renewable energy. The following conversions can be made:
, including five parts, namely, the income from selling electricity to users, the income from selling renewable energy electricity, the income from selling TGCs, the cost of generating electricity from conventional units, and the cost of generating electricity from renewable energy. The following conversions can be made:
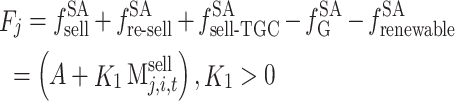 |
34 |
According to the definition of the concave function, a linear function is a concave function, and more rigorously, a quasi-concave function.
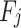 is continuous on the decision interval
is continuous on the decision interval 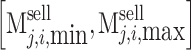 . Similarly,
. Similarly,  is continuous on
is continuous on 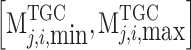 . Thus, the payment function
. Thus, the payment function 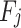 of the sending end area is a continuous function on the decision interval, and there is a strategic Nash equilibrium.
of the sending end area is a continuous function on the decision interval, and there is a strategic Nash equilibrium.
The Stackelberg game has an equilibrium if the following three conditions are met:
(1) The strategy set is non-empty, compact, and convex.
(2) Given the leader’s strategy, there exists a unique optimal solution for the follower.
(3) Given the follower’s strategy, there exists a unique optimal solution for the leader.
According to the above description of the Stackelberg game model, the strategies of the sending and receiving end areas satisfy their constraints. Thus, the strategy set for each participant is non-empty, compact, and convex. Hence, Condition 1 is met. When the upper-level price is given, the payment function of the receiving end area is a continuous function over the range of its decision variables, ensuring the existence of a unique optimal solution within the constraints. Similarly, when the lower-level transaction volume is given, the payment function of the sending end area is also a continuous function over the range of its decision variables, ensuring a unique optimal solution within the constraints. Hence, an equilibrium solution exists for this Stackelberg game.
The solution of the two-layer game model considering the MLT trading plan
A decomposition quadratic programming method for MLT contracted energy
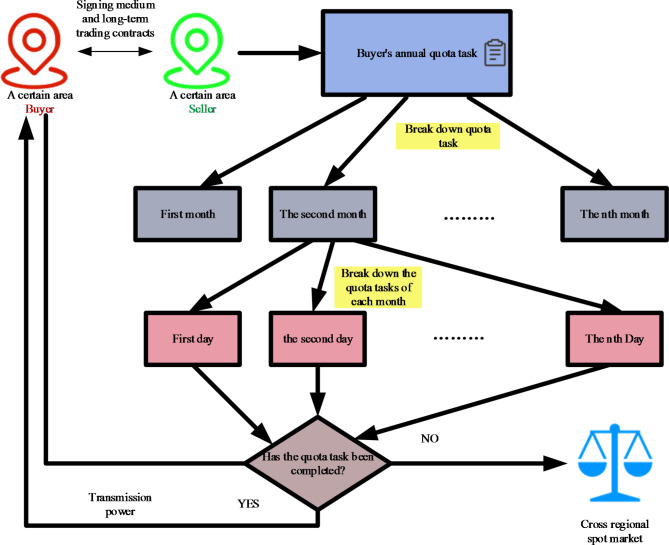
The MLT transaction of the MLT contract defines the responsibilities, and locks both demand and price, thereby mitigating risks effectively. This mechanism constitutes an excellent approach for implementing inter-provincial TGC transactions. Generally, the MLT transactions are divided into annual and monthly transactions according to time. Therefore, formulating and decomposing the MLT transaction plan and connecting with the short-term scheduling in an orderly manner are the key issues to be solved. The implementation process of MLT TGC transactions is shown in Fig. 3.
Fig. 3.
MLT trading framework and decomposition plan.
When making the daily dispatching plan, it is first necessary to decompose the MLT contract electricity into days and consider various factors including the contract completion schedule, load demand, and unit maintenance to ensure that the electricity completion schedule of each unit is consistent. The following optimization model is established to minimize the completion schedule deviation of contracted power between units:
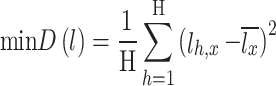 |
35 |
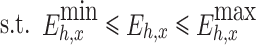 |
36 |
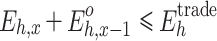 |
37 |
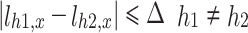 |
38 |
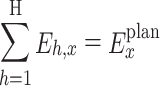 |
39 |
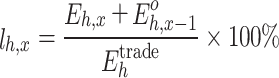 |
40 |
 |
41 |
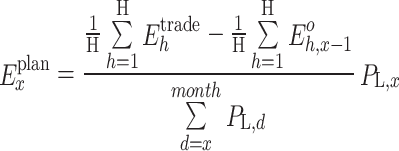 |
42 |
Equation (35) describes the difference in the completion progress of the contracted electricity between units using a variance. Equation (36) is the upper and lower limit constraint of the daily decomposition electricity of the unit. Equation (37) is the monthly contract energy constraint of the unit. Equation (38) refers to the constraint of completion schedule deviation of any two units’ contracted energy. Equation (39) refers to the constraint of the daily total generation capacity of units.
The MLT contract electricity quantity decomposition model is composed of a quadratic objective function and a series of linear constraints on the daily electricity quantity. Therefore, it is formulated as a standard quadratic programming model in this paper. This model calculates the daily executed electricity of each unit, which is subsequently introduced as a constraint condition into the constructed receiving end area model.
Two-layer game model solution
According to the game models established in Sect. "Construction and analysis of the evolutionary game model of the power demand side" and "Construction and analysis of game model between power supply and demand", the optimal electricity sale and purchase strategies in the sending and the receiving end areas, respectively, are both single-objective optimization problems. The above optimization problems contain a large number of decision variables and complex constraints. In this paper, the IAOA is used to solve the optimization problem.
The standard AOA
The AOA simulates the different hunting methods of the Skyhawk for different prey. The way Skyhawk hunts fast-moving prey reflects the global exploration ability of the algorithm, while the way it hunts slow-moving prey reflects the local development ability of the algorithm. Skyhawks mainly use four hunting methods, and most of them can flexibly and quickly change back and forth between different hunting methods according to different situations. Method 1 is vertical dive attack, Method 2 is contour flight and short gliding attack (the most commonly used method), Method 3 is low altitude flight and slow descent attack, and Method 4 is walking attack and capturing prey. In the AOA, the hunting behavior of the Skyhawk is equivalent to the process of predation in a given range to obtain the global optimal solution. The AOA ensures that the search area can be successfully created in both wide and narrow fields of vision during the optimization process. The four hunting methods used by Skyhawk are as follows:
(1) Expand exploration (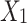 )
)
After identifying the prey and its area, Skyhawks select the best hunting area through vertical dive flight and high-altitude flight. This behavior is mathematically expressed by Eq. (43):
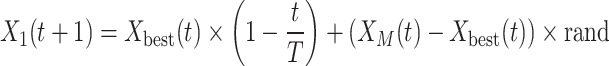 |
43 |
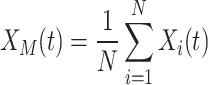 |
44 |
Where 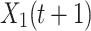 is the solution of the next iteration of the t-th iteration generated by the first search method,
is the solution of the next iteration of the t-th iteration generated by the first search method, 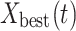 is the optimal solution of the t-th iteration,
is the optimal solution of the t-th iteration, 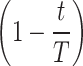 means exploration is controlled by the number of iterations,
means exploration is controlled by the number of iterations, 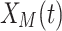 is the average value of the current solution at iteration t, rand is a random number between [0,1], t and T represent the current iteration number and the maximum iteration number, respectively, and N is the number of candidate solutions.
is the average value of the current solution at iteration t, rand is a random number between [0,1], t and T represent the current iteration number and the maximum iteration number, respectively, and N is the number of candidate solutions.
(2) Narrow the scope of exploration (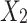 )
)
After finding the prey at a high altitude, Skyhawks will use contour flight and short gliding to approach the prey and launch attacks. This behavior is mathematically expressed by Eq. (45):
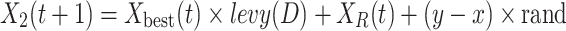 |
45 |
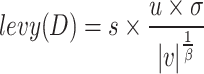 |
46 |
| 47 |
Where 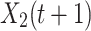 is the solution of the next iteration of the t-th iteration generated by the second search method, D is the dimensional space,
is the solution of the next iteration of the t-th iteration generated by the second search method, D is the dimensional space, 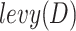 is the Levy flight distribution function,
is the Levy flight distribution function, 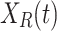 is the random solution with a value range of [1, N],
is the random solution with a value range of [1, N],  is a constant value fixed at 1.5, while
is a constant value fixed at 1.5, while 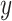 and
and 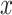 are in spiral form in search, and their calculation formulas are as follows:
are in spiral form in search, and their calculation formulas are as follows:
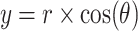 |
48 |
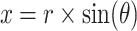 |
49 |
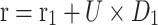 |
50 |
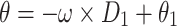 |
51 |
Where 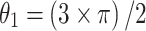 ,
, 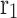 is the fixed periodic index between 1 and 20, the value of
is the fixed periodic index between 1 and 20, the value of 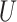 is 0.00565,
is 0.00565, 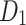 is an integer from 1 to the length of the search space and the value of
is an integer from 1 to the length of the search space and the value of 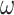 is 0.005.
is 0.005.
(3) Expand development (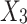 )
)
When the prey area is precisely targeted, Skyhawks will slowly reduce their flying height and take the preliminary attack to test the prey’s response. This behavior is mathematically expressed by Eq. (52):
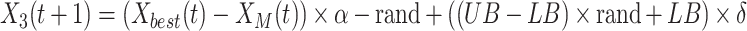 |
52 |
Where 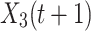 is the solution of the next iteration of the t-th iteration generated by the third search method,
is the solution of the next iteration of the t-th iteration generated by the third search method, 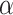 and
and 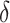 are mining adjustment parameters with small values within the range of (0,1), while LB and UB represent the upper and lower limits of the given problem, respectively.
are mining adjustment parameters with small values within the range of (0,1), while LB and UB represent the upper and lower limits of the given problem, respectively.
(4) Narrow the scope of development (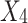 )
)
When Skyhawks approach the prey, they will walk on the land to attack the prey according to the random movement of the prey. This behavior is mathematically expressed by Eq. (53):
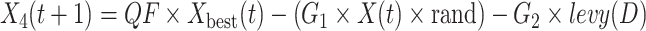 |
53 |
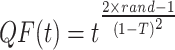 |
54 |
 |
55 |
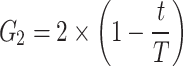 |
56 |
Where 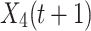 is the solution of the next iteration of the t-th iteration generated by the fourth search method, QF represents the quality function used to balance the search strategy,
is the solution of the next iteration of the t-th iteration generated by the fourth search method, QF represents the quality function used to balance the search strategy, 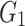 indicates the different methods taken by Skyhawk in tracking their prey,
indicates the different methods taken by Skyhawk in tracking their prey, 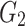 is the decreasing value from 2 to 0, representing the flying slope of the Skyhawk when tracking prey from the first position to the last position and
is the decreasing value from 2 to 0, representing the flying slope of the Skyhawk when tracking prey from the first position to the last position and 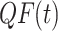 is the value of the mass function at iteration t.
is the value of the mass function at iteration t.
The IAOA
Although the AOA balances the exploration and development capabilities, it has room for further improvement in expanding exploration and narrowing exploration capabilities. Therefore, the following content improvements are made in the AOA.
(1) Chaotic sequence initialization.
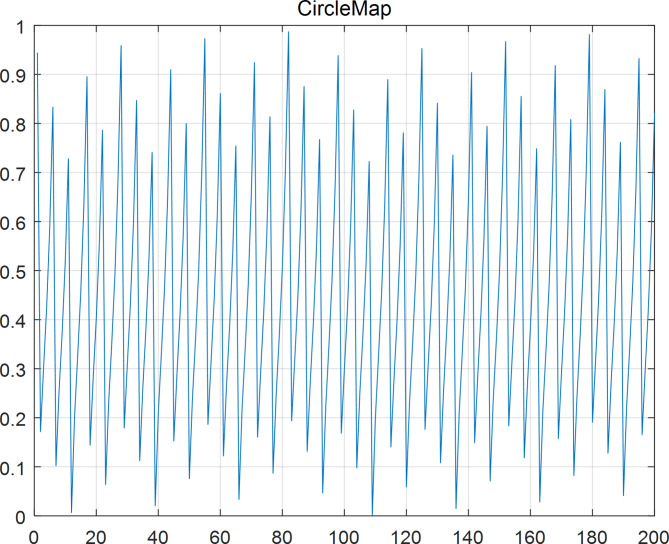
When the basic AOA is initialized, the population diversity becomes worse because it randomly initializes the population. Chaotic maps have the characteristics of good ergodicity, non-repetition, unpredictability, and aperiodicity, which can be used to improve the performance of the algorithm. The essential idea is to map variables into the value range of the chaotic variable space through the characteristics of chaos, and finally convert the solution linearly into the optimal variable space. Currently, different chaotic maps51 are available including the Iterative map, Tent map, Circle map, and Gauss map. This paper uses the Circle chaotic map to regenerate the initial population, which is defined as:
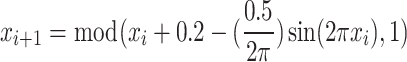 |
57 |
Where mod is the residue function.
The circle mapping distribution for 200 iterations is shown in Fig. 4.
Fig. 4.
Circle map distribution.
It can be seen from Fig. 4 that the distribution of the Circle map is between [0,1]. Compared with the population generated by random distribution, the population positions generated by the Circle map exhibit greater uniformity. This expands the search scope of the AOA algorithm and improves the optimization performance.
(2) Random walk strategy.
The random walk strategy52 is a statistical model proposed in 1905. The process involves the random selection of a neighboring point to the current solution. If the neighboring point is better than the current solution, it replaces the point as the new center. If no improvement is identified over N consecutive iterations, the current solution is considered the optimal value. The current step size is within the N-dimensional sphere of radius. At this time, if the step size is less than the threshold, the algorithm will terminate. Otherwise, the step length is halved and a new round of walking is started. In the iterative process, when certain conditions are reached, the convergence will be achieved, and a stable probability distribution will be obtained.
The process of the random walk can be mathematically expressed as:
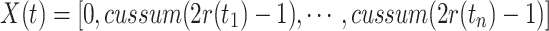 |
58 |
Where 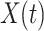 is the set of random walking steps. The statistics of the total steps of the random walk are expressed as
is the set of random walking steps. The statistics of the total steps of the random walk are expressed as 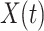 . The cumulative sum of steps taken is expressed in
. The cumulative sum of steps taken is expressed in 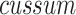 . The current number of walking steps is expressed in t. Taking a random function
. The current number of walking steps is expressed in t. Taking a random function 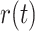 as shown in Eq. (59):
as shown in Eq. (59):
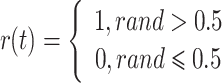 |
59 |
Where 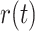 is a random number between [0,1].
is a random number between [0,1].
As the action track of the Skyhawk has a certain range, the position of the Skyhawk cannot be directly updated with the Eq. (58). To ensure that the Skyhawk walks within a certain range, it needs to be normalized, as shown in the Eq. (60):
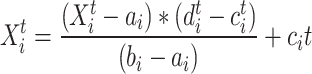 |
60 |
Where: 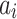 and
and 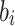 represent the minimum and maximum values of the i-dimension random walk variable, respectively, while
represent the minimum and maximum values of the i-dimension random walk variable, respectively, while 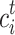 and
and 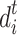 represent the minimum and maximum values of the i-dimension random walk variable in the t-th iteration, respectively.
represent the minimum and maximum values of the i-dimension random walk variable in the t-th iteration, respectively.
The improvement in this section is mainly carried out after the Skyhawk search, and the random walk strategy perturbs it, thereby enhancing its search performance. At the beginning of the iteration, the random walk range is large. After multiple iterations, the random walk range is reduced, which is conducive to improving the local search for the optimal location.
(3) Initializing population position based on Sobol sequence.
In this paper, a low-discrepancy sequence is used to replace a pseudo-random sequence with a deterministic low-discrepancy sequence, which is also called the Quasi-Monte Carlo (QMC) method. The QMC unifies the filled area as much as possible by selecting a reasonable sampling direction. Therefore, it has better ergodicity and uniformity in dealing with probability problems. In this paper, a low-discrepancy Sobol sequence is used to initialize the population. This deterministic quasi-random number sequence is used to replace the pseudo-random number sequence to achieve more uniform distribution within the multi-dimensional hypercube.
If the value range of the global solution is a random number of 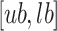 and
and 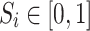 , the initial position of the population is defined in Eq. (61):
, the initial position of the population is defined in Eq. (61):
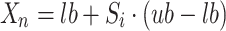 |
61 |
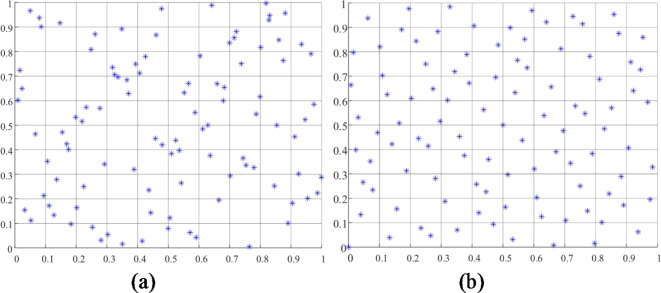
Assuming that the search space is two-dimensional, the upper and lower bounds are 1 and 0, respectively, and the population size is 100. Figure 5 compares the spatial distribution of the pseudorandom initialized population with that of the Sobol sequence initialized population. It can be seen from Fig. 5 that the initial population distribution generated by the Sobol sequence is more uniform and more ergodic.
Fig. 5.
Comparison of initial population distributions. (a) Initial distribution of the random population (b) Initial distribution of the Sobol sequence population.
Algorithm performance comparison
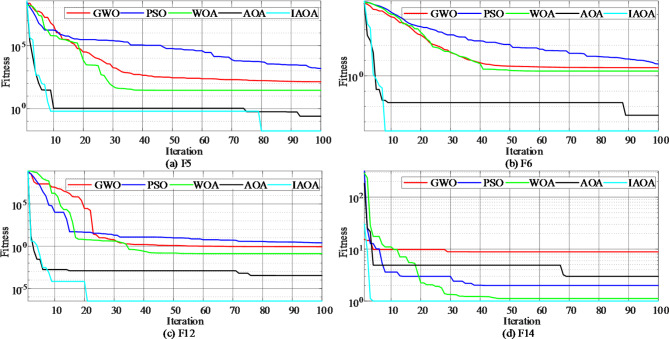
To evaluate the performance of the proposed IAOA, it was compared with the standard AOA, the Grey Wolf Optimization algorithm (GWO), the Whale Optimization algorithm (WOA), and the Particle Swarm Optimization (PSO), utilizing 15 classic test functions. To ensure the fairness and effectiveness of the experiment, the population size of all algorithms was set to 30, and the number of iterations was set to 100. The test functions and parameters are shown in Table A.1 in the appendix.
The above-mentioned five algorithms were independently run 20 times in 15 test functions. Table 3 compares the obtained average value and the standard deviation. It can be seen from the table that the IAOA has a good optimization effect in the test function, and the optimal value of the corresponding function can be directly searched.
Table 3.
Algorithm performance comparison.
| Fun | Metric | AOA | IAOA | GWO | PSO | WOA |
|---|---|---|---|---|---|---|
| F1 | mean | 2.1358E-26 | 6.1397E-31 | 1.2327E-02 | 4.0222E + 00 | 7.2064E-12 |
| std | 3.6992E-26 | 1.0536E-30 | 6.3953E-03 | 1.9826E + 00 | 1.0547E-11 | |
| F2 | mean | 2.8949E-16 | 3.7175E-17 | 1.7496E-02 | 9.1641E + 00 | 1.8271E-08 |
| std | 3.9320E-16 | 5.1639E-17 | 1.4192E-03 | 1.7183E-01 | 1.9721E-08 | |
| F3 | mean | 9.8205E-24 | 6.5068E-32 | 3.5188E + 02 | 8.6560E + 02 | 7.8766E + 04 |
| std | 1.3888E-23 | 9.1148E-32 | 1.6785E + 02 | 8.9442E + 01 | 2.1716E + 03 | |
| F4 | mean | 1.4002E-16 | 1.6860E-18 | 1.2019E + 00 | 5.1169E + 00 | 6.3832E + 01 |
| std | 1.9622E-16 | 1.6636E-18 | 5.2538E-02 | 1.9468E + 00 | 1.0905E + 01 | |
| F5 | mean | 1.8426E-01 | 1.8260E-02 | 3.0000E + 01 | 1.5800E + 03 | 2.8766E + 01 |
| std | 4.1825E-02 | 7.0675E-03 | 3.4804E-01 | 2.8242E + 02 | 2.9840E-02 | |
| F6 | mean | 2.8677E-03 | 1.6431E-04 | 2.4393E + 00 | 7.2263E + 00 | 1.8831E + 00 |
| std | 2.3632E-04 | 1.2661E-04 | 1.3397E + 00 | 1.8831E + 00 | 2.1588E-01 | |
| F7 | mean | 8.0655E-04 | 8.8142E-05 | 3.2970E-02 | 7.5480E + 00 | 1.8657E-02 |
| std | 4.5616E-04 | 1.9203E-05 | 1.2335E-02 | 3.0715E + 00 | 5.2969E-03 | |
| F8 | mean | −3.5249E + 03 | −3.7282E + 03 | −4.0552E + 03 | −2.8864E + 03 | −7.5734E + 03 |
| std | 1.0365E + 02 | 7.7337E + 01 | 1.7045E + 03 | 2.6475E + 02 | 1.3451E + 03 | |
| F9 | mean | 0.0000E + 00 | 0.0000E + 00 | 3.6812E + 01 | 2.0944E + 02 | 3.0411E-12 |
| std | 0.0000E + 00 | 0.0000E + 00 | 1.1423E + 01 | 1.7348E + 01 | 3.8185E-12 | |
| F10 | mean | 1.4557E-12 | 4.4409E-15 | 2.4330E-02 | 3.0610E + 00 | 3.8480E-07 |
| std | 2.0575E-12 | 5.0243E-15 | 1.3435E-03 | 7.0831E-01 | 3.9975E-07 | |
| F11 | mean | 0.0000E + 00 | 0.0000E + 00 | 1.0007E-01 | 1.9732E + 01 | 4.8755E-12 |
| std | 0.0000E + 00 | 0.0000E + 00 | 3.5171E-02 | 7.0276E + 00 | 6.6498E-12 | |
| F12 | mean | 1.7285E-04 | 2.2557E-07 | 6.9775E-01 | 1.3736E + 00 | 1.5048E-01 |
| std | 2.4104E-04 | 1.4064E-07 | 2.4924E-01 | 1.6342E + 00 | 2.5074E-02 | |
| F13 | mean | 1.0419E-04 | 5.0362E-05 | 1.5306E + 00 | 1.7448E + 00 | 8.3289E-01 |
| std | 9.9322E-05 | 3.0694E-05 | 2.5244E-02 | 8.8600E-01 | 1.7266E-01 | |
| F14 | mean | 1.4950E + 00 | 9.9815E-01 | 6.8727E + 00 | 1.5116E + 00 | 7.3658E + 00 |
| std | 7.0286E-01 | 2.0506E-04 | 5.5021E + 00 | 6.7946E-01 | 4.8047E + 00 | |
| F15 | mean | 1.0063E-03 | 5.5518E-04 | 6.9381E-04 | 8.8895E-04 | 1.4809E-03 |
| std | 1.9476E-04 | 9.5771E-05 | 3.9457E-05 | 2.7881E-04 | 1.0904E-03 |
Since there are many test functions, the convergence curves of four test functions are selected for separate analysis and are shown in Fig. 6. The advantages and disadvantages of the algorithm can be directly assessed through its convergence curve, which shows the convergence speed of the algorithm and the times of falling into local optimal values. It can be observed from Fig. 6 that the convergence speed of the proposed IAOA is faster than that of the other four algorithms in the entire iteration process, and the convergence accuracy is also the best among the five algorithms. The IAOA demonstrates superior global exploration ability than the other algorithms, while also exhibiting a reduced propensity to become trapped in local optima. The IAOA effectively balances the global exploration ability and local development ability. To verify the effectiveness of the improved strategy, the random initialization strategy was replaced with the chaos map initialization strategy and the Sobol sequence initialization strategy. Figure 6 shows that the IAOA is significantly faster than the standard AOA in terms of convergence speed. Moreover, the IAOA has rarely fallen into the local optimal value. Hence, the IAOA has a significant improvement in both the precision and speed of optimization compared with the standard AOA.
Fig. 6.
Comparison of different algorithms convergence curves.
Complex constraint processing method
In this paper, the filter technology is employed to deal with complex constraints. The filter technology forms a number pair (F, G) to express the filter element, in which the objective function F and the constraint violation degree G are expressed as:
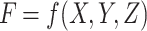 |
62 |
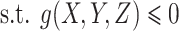 |
63 |
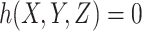 |
64 |
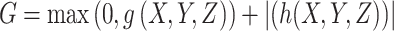 |
65 |
There are two definitions:
Definition 1
If 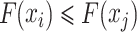 and
and 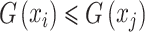 , filter
, filter 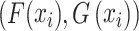 dominates
dominates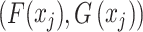 ;
;
Definition 2
Filters of filter subsets are independent of each other.
Game model solution
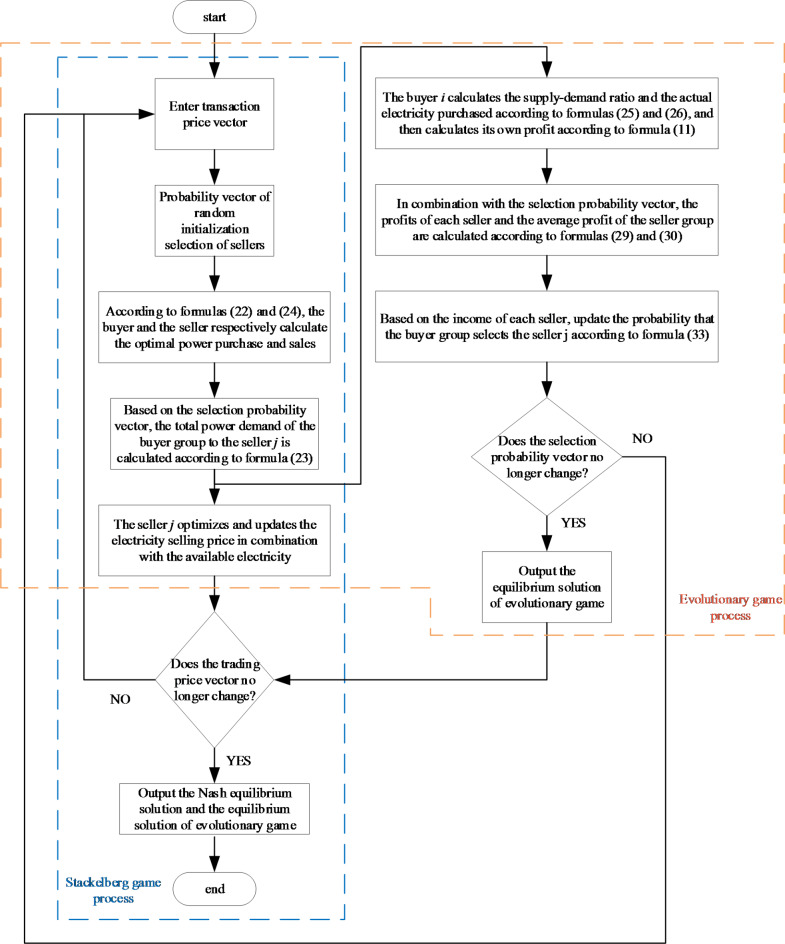
The solution of the two-layer game model proposed in this paper is divided into two parts: the solution of the evolutionary game on the demand side and the solution of the Nash-Stackelberg game on both sides of the supply and demand. The model-solving process is shown in Fig. 7.
Fig. 7.
Game model solving process.
In the Nash-Stackelberg game process, any seller j cannot obtain the quotation information of other sellers. Thus, the distributed iterative algorithm is used to update its electricity price until reaching the Nash-Stackelberg equilibrium. The iterative formula is:
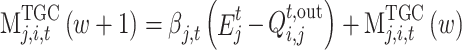 |
66 |
Where 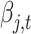 is the iteration speed parameter, and its value is set according to the specific situation. If the value of
is the iteration speed parameter, and its value is set according to the specific situation. If the value of 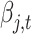 is too large, it will lead to excessive price oscillation. Therefore, it needs to be adjusted to a smaller value adaptively to ensure the normal progress of iteration. When
is too large, it will lead to excessive price oscillation. Therefore, it needs to be adjusted to a smaller value adaptively to ensure the normal progress of iteration. When 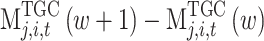 is infinitely close to 0, the iteration ends. At this time, the electricity supply and demand of seller j are equal, and the electricity price tends to a stable value, reaching Nash equilibrium.
is infinitely close to 0, the iteration ends. At this time, the electricity supply and demand of seller j are equal, and the electricity price tends to a stable value, reaching Nash equilibrium.
To enhance algorithm convergence, the step control method can be used to control the fluctuation of electricity price during iteration, thereby mitigating the adverse effects of excessive price volatility. The step control method is expressed as:
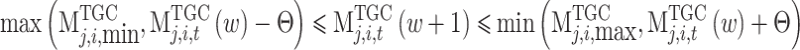 |
67 |
Where, 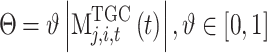 is the climbing rate and its specific value is dynamically adjusted according to the iteration situation and basic electricity price to ensure the iteration efficiency and convergence accuracy.
is the climbing rate and its specific value is dynamically adjusted according to the iteration situation and basic electricity price to ensure the iteration efficiency and convergence accuracy.
Simulation of cases and comparative analysis
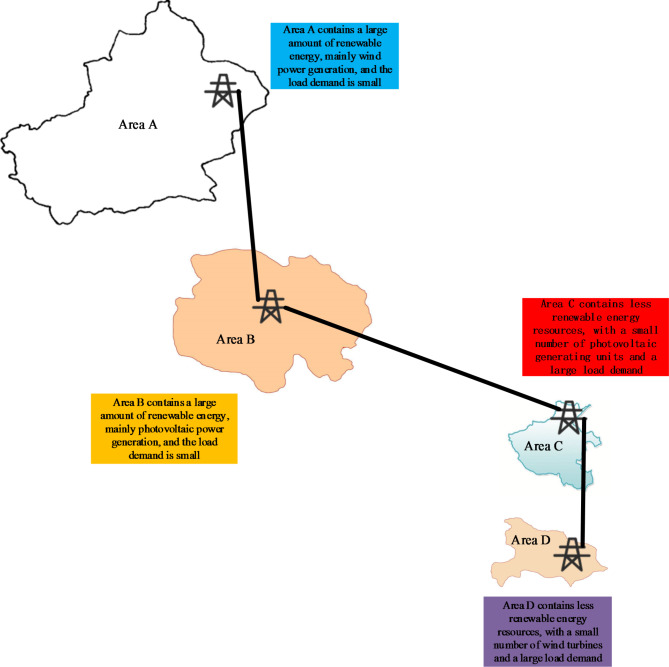
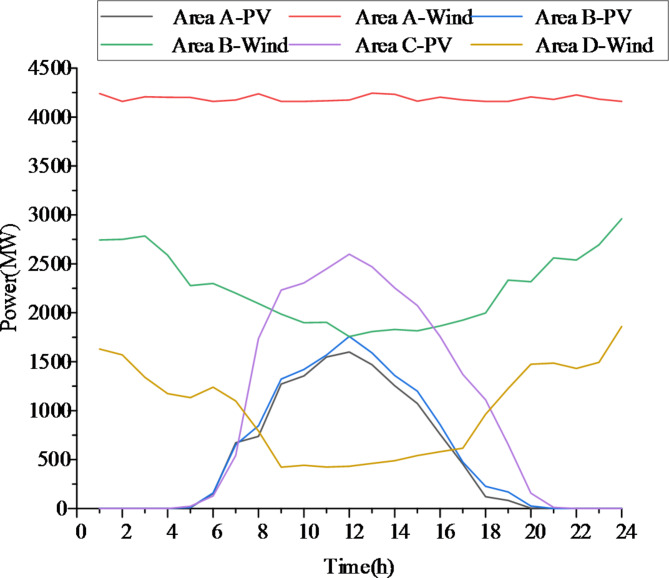
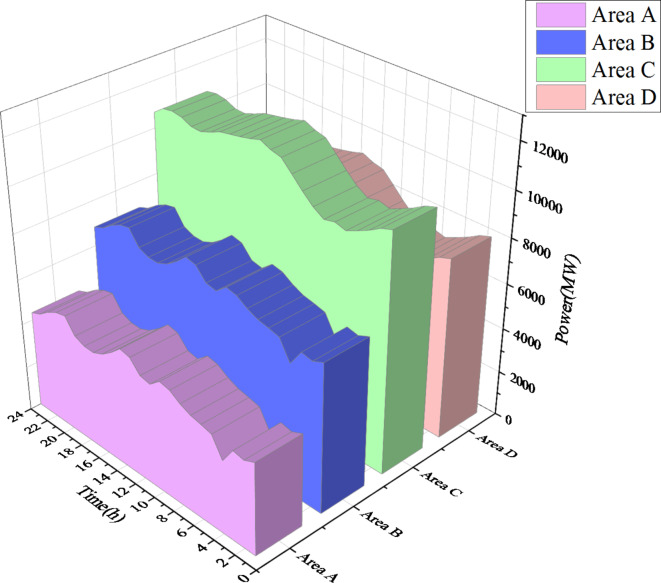
The case analysis was simulated using MATLAB R2018b (https://www.mathworks.com/products/matlab.html) on a Windows 11 PC (3.2 GHz, 16 GB RAM). This paper utilizes the actual data from provinces A and B in western China and provinces C and D in central China to verify and analyze the established cross-regional power transaction model. The inter-provincial interconnection grid structure is shown in Fig. 8. The total installed capacities of thermal power and photovoltaic units in sending end areas A and B were 9323 MW and 2150 MW, respectively. The installed capacities of wind turbines in sending end areas A and B were 5000 MW and 3100 MW, respectively. The total installed capacity of thermal power in receiving end areas C and D was 14,057 MW. The installed capacity of photovoltaic power in receiving end area C was 3150 MW. The installed capacity of wind power in receiving area D was 2000 MW. The transmission capacity of the tie-line was 3000 MW. See Appendix Table A.2-A.5 for the basic parameters of the generator set in the sending and receiving end areas. The power generation cost of renewable energy was set at 220 yuan/MWh53. To illustrate a typical wind power output scenario in the sending end area, Fig. 9 presents historical wind power and photovoltaic output data of the two provinces with a 1-hour resolution for the period from June 2 to July 2, 2018. The load data is shown in Fig. 10. After the above simulations, the model’s runtime was 15290.9961 s.
Fig. 8.
Cross-regional interconnected power grid structure.
Fig. 9.
Renewable energy output of each area.
Fig. 10.
Load demand of each area.
Decomposition results of MLT contracted energy
According to the contract completion progress and daily load, the quadratic programming method in Sect. 4.1 was adopted to determine the daily executive power of each MLT trading unit. Table 4 presents the decomposition results of MLT contracted energy in area C. Similarly, Table 5 shows the decomposition results in area D.
Table 4.
Decomposition results of MLT contract energy in area C.
| Renewable energy unit number |
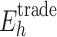
(105MW·h) |
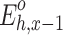
(105MW·h) |
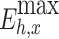
(MW·h) |
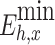
(MW·h) |
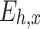
(103MW·h) |
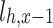
(%) |
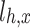
(%) |
|---|---|---|---|---|---|---|---|
| 1 | 1.2160 | 0.7310 | 2400 | 100 | 1.3577 | 60.12 | 61.23 |
| 2 | 1.2160 | 0.7156 | 2400 | 800 | 2.4000 | 58.85 | 60.83 |
| 3 | 1.2160 | 0.7248 | 2400 | 400 | 1.9144 | 59.61 | 61.18 |
| 4 | 3.0399 | 1.8209 | 6000 | 600 | 1.3245 | 59.90 | 60.33 |
| 5 | 1.2160 | 0.6869 | 2400 | 2000 | 2.0000 | 56.49 | 58.13 |
| 6 | 1.2160 | 0.6869 | 2400 | 2000 | 2.0000 | 56.49 | 58.13 |
| 7 | 2.4319 | 1.4466 | 4800 | 900 | 4.8000 | 59.49 | 61.46 |
| Variance | 2.10 | 1.80 |
Table 5.
Decomposition results of MLT contract energy in area D.
| Renewable energy unit number |

(105MW·h) |
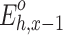
(105MW·h) |
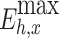
(MW·h) |
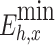
(MW·h) |
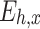
(103MW·h) |
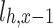
(%) |
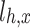
(%) |
|---|---|---|---|---|---|---|---|
| 1 | 0.9318 | 0.5601 | 2400 | 100 | 0.2763 | 60.12 | 60.41 |
| 2 | 0.9318 | 0.5484 | 2400 | 800 | 1.4276 | 58.85 | 60.38 |
| 3 | 0.9318 | 0.5554 | 2400 | 400 | 0.7207 | 59.61 | 60.38 |
| 4 | 2.3294 | 1.3953 | 6000 | 600 | 3.4203 | 59.90 | 61.37 |
| 5 | 0.9318 | 0.5263 | 2400 | 2000 | 2.0000 | 56.49 | 58.63 |
| 6 | 0.9318 | 0.5263 | 2400 | 2000 | 2.0000 | 56.49 | 58.63 |
| 7 | 1.8635 | 1.1085 | 4800 | 900 | 2.2595 | 59.49 | 60.70 |
| Variance | 2.10 | 0.93 |
It can be seen from the above tables that the planned daily power demand of area C is 38,505 MW·h, and the total executed power of all MLT trading units is 15,797 MW·h. The planned daily power demand of area D is 29,505 MW·h, and the total executed power of all MLT trading units is 12,104 MW·h. The variance of unit contract completion progress in areas C and D is reduced from 2.10 to 1.80 and 0.93, respectively, following decomposition. By introducing the constraint of contractual completion schedule deviation between any two units, the maximum completion schedule deviation between units in receiving areas C and D is constrained to 3.33% and 2.74%, respectively, remaining within 3.5%. This shows that the quadratic programming method of MLT contract energy decomposition adopted in this paper can provide a relatively friendly decomposition result, improve the fairness of MLT trading unit scheduling, and ensure the execution of the plan.
Analysis of evolutionary game results
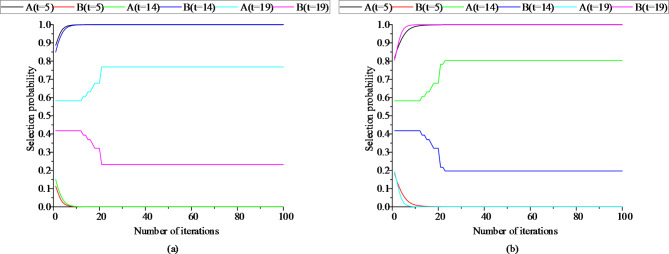
Given the complexity of the 24-hour evolution process, Fig. 11 shows selected time points, t = 5, t = 14, and t = 19 for presentation.
Fig. 11.
Convergence of evolutionary game.
It can be seen from Fig. 11 that the buyer group participates in the evolutionary game. As the income of the buyer group gradually approaches the average income, the buyer constantly updates the probability of selecting the seller until a stable value is achieved and finally reaches the equilibrium solution.
Since the decision-making process of the game is based on the constantly changing game environment, the size of the initial state is not proportional to the final stable state. It is determined by the game environment. Figure 11 (a) shows the evolution state curve of the buyer group’s selection probability for Seller A (sending end area A). It can be seen that when t = 14 and t = 5, the selection probability is very high, and finally the selection probability converges to 1, indicating that the buyer group only selects Seller A to purchase electricity at this time. The evolution state trends are different at different times, but the final convergence means that under the constantly changing game situation and environment, the selection strategy eventually becomes a stable strategy within the population. This stable strategy represents an evolutionarily stable strategy. Figure 11 (b) shows the evolution state curve of the buyer group’s selection probability for seller B (sending end area B). The stability strategy of the buyer group is shown in Fig. 12.
Fig. 12.
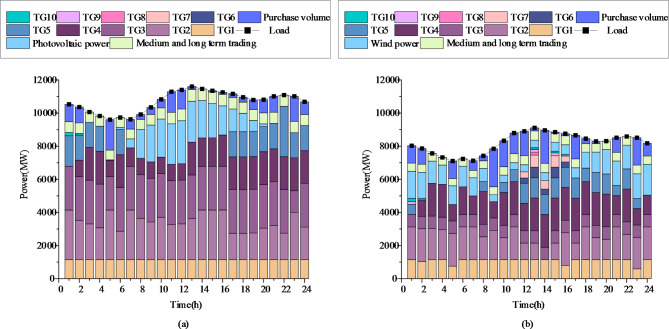
Strategy results of buyer group.
Figure 12 (a) and (b) show the internal strategy results of areas C and D, respectively. It can be seen that both areas can ensure the balance of power supply and demand. Moreover, since the overall load demand of area C is greater than that of area D, the thermal power output of area C is also relatively large. The overall power supply of the two areas is mainly from thermal power generation. Renewable energy is mainly used to complete quota tasks, and the thermal power output in peak hours will also be increased compared with other periods. It can also be seen in the figure that the power distribution size of MLT transactions in a dispatching cycle is decomposed according to the size proportion of the load, which further ensures the balance of power supply and demand. Furthermore, the power purchase is mainly concentrated in the time period with less renewable energy. Since photovoltaic power generation is mainly used in area C and photovoltaic power generation is mostly used in the noon and afternoon periods, morning and evening periods are the main power purchase periods. The wind power output of area D is mainly concentrated in the morning and evening. Thus, noon is the main power purchase period of area D.
Analysis of Nash-Stackelberg game results
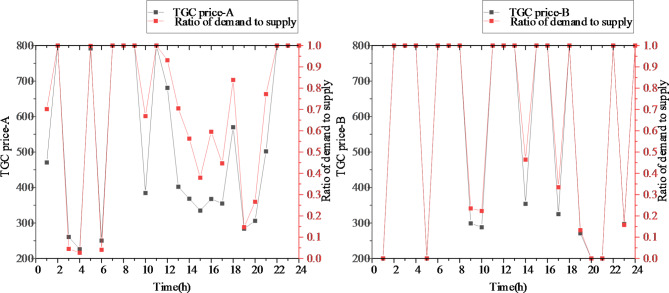
Figure 13 shows the TGC price per hour after the game. It can be seen from the figure that with the decrease in the ratio of demand to supply, the TGC price also decreases. During the game, the buyer’s area needs to purchase a large number of TGCs to complete the quota task and avoid huge penalty costs. However, the seller’s area prioritizes the completion of its regional quota tasks and the maximization of revenue generated from electricity sales. The seller’s area transmits the price signal to the buyer’s area, enabling the buyer to adjust its demand accordingly. When the ratio of demand to supply is large, it means that the TGC supply is smaller than the demand at this time, and the TGC price will increase to ensure the seller’s income, while the buyer will also reduce the demand because of the price increase. With the transmission of signals from both sides finally reaching a balanced state, the interests of both sides have also been balanced.
Fig. 13.
Results of trading price.
Sensitivity analysis of regional evolution behavior
The change in regional income is the source of driving the evolutionary behavior of each subject, which is usually accompanied by the change in the government’s new energy incentive policy and the area’s power generation capacity. The quota task and quota penalty coefficient are analyzed and discussed as follows.
Quota Tasks.
Three groups of different quota tasks were set for different regions. Case 1: The quota task coefficients of the seller’s area and the buyer’s area were set to 4% and 12%, respectively. Case 2: The quota task coefficients of the seller’s area and the buyer’s area were set to 7% and 15%, respectively. Case 3: The quota task coefficients of the seller’s area and the buyer’s area were set to 10% and 18%, respectively.
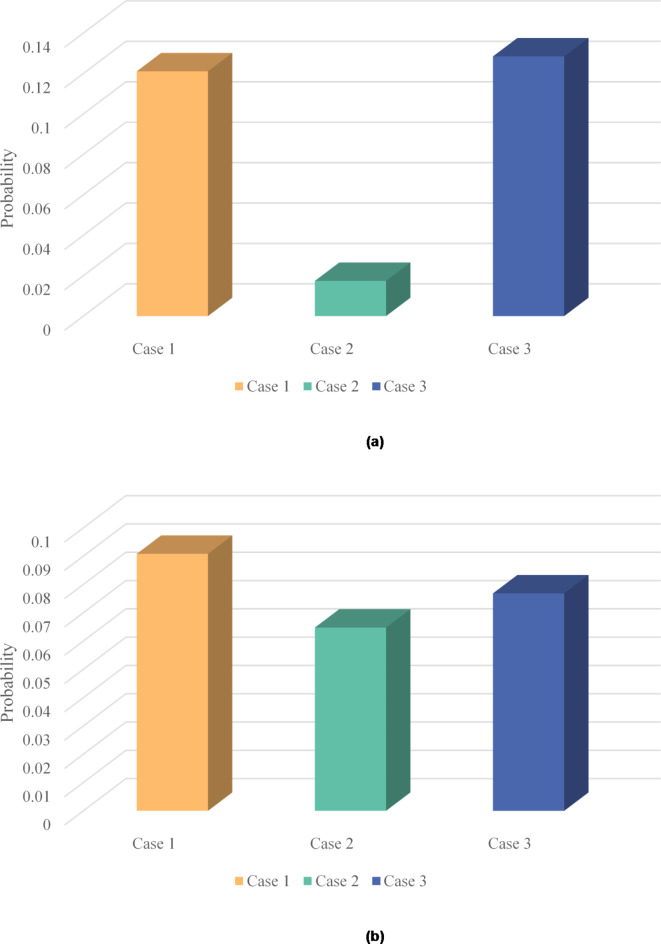
It can be seen from Fig. 14 (a) that the selection probability of Area C in Case 3 is higher because, under a high proportion of quota requirements, area C will be promoted to purchase more TGCs to complete quota tasks. At this time, the TGCs purchased only from Area A cannot meet the quota requirements of Area C. Thus, the selection probability of Area B will be increased. In Case 1, due to the low quota requirements, the supply of TGC in the market exceeds the demand, which will lead to a decrease in the price of TGC. Area C will buy some green electricity to replace thermal power generation. In Case 2, since the power supply of Area A is large, area A can meet the demand of Area C. Hence, the probability of selecting Area B is the smallest compared with the other two cases. It can be seen from Fig. 14 (b) that the selection probability of Area D in Case 1 is the highest because Area D chooses to purchase some green electricity to replace thermal power generation due to low quota requirements and to reduce its own power generation cost. In Case 3, it can be seen that the selection probability in Area D is smaller than that in Area C. Since the load in Area D is much smaller than that in Area C, the number of tasks in Area D quota is less under the same quota coefficient, which makes Area D purchase less from Area B. Hence, the selection probability in Area D is smaller.
Fig. 14.
Probability of areas C and D choosing B in different cases. (a) Purchase volume C-B. (b) Purchase volume D-B.
-
(2)
Quota penalty.
To investigate the impact of quota fines on the evolutionary game, the penalty coefficient was adjusted to values of 500, 900, and 1300, respectively, when quota tasks were not completed.
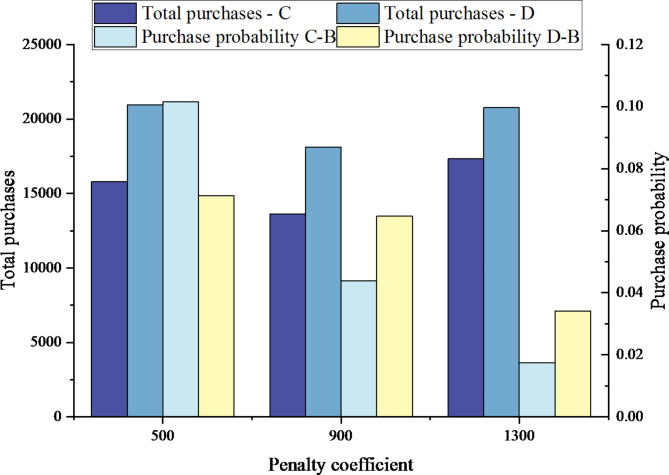
It can be seen from Fig. 15 that with the increase of the penalty coefficient, the purchase volume of Areas C and D decreases first and then increases. The selection probability of Areas C and D decreases gradually. When the penalty coefficient is small, the supply of TGC in the market will exceed the demand, which will reduce the price of TGC, and the selection probability of Area B is also the largest. Areas C and D will buy some green electricity to replace some thermal power generation. When the penalty coefficient increases, the market demand and price of TGC will increase. To ensure their economy, Areas C and D will not buy more green electricity, leading to a decrease in the selection probability for Area B. When the penalty coefficient further increases, Areas C and D will increase the purchase volume to ensure the completion of the quota task. This can lead to a situation where supply is less than demand, increasing the price of TGC. At this time, the selection probability of Area B is also the minimum.
Fig. 15.
Results of penalty coefficient variation.
Analysis of the game relationship between supply and demand
To study the advantages of the game relationship between supply and demand established in this paper, two scenarios were set for comparative simulation, as shown in Table 6. Scenario 1: There is no game relationship between supply and demand. Scenario 2: The supply and demand sides establish a game relationship.
Table 6.
Comparison of results of the game relationship.
| Area A | Area B | Area C | Area D | |
|---|---|---|---|---|
| Scenario 1 | 7.0576 × 107 | 4.8285 × 107 | 5.2609 × 107 | 3.5100 × 107 |
| Scenario 2 | 6.7491 × 107 | 4.7833 × 107 | 5.4359 × 107 | 3.6887 × 107 |
In Scenario 2, the income gap of the four areas is the smallest, and the results are the most satisfactory compared with other methods. In the game interaction between supply and demand, the interests of different market participants can be scientifically balanced. Scenario 2 leverages demand-side flexibility to mitigate the need for energy purchases from the supply-side area. By reasonably regulating and controlling the schedulable resources in the demand-side area, it can force the supply-side area to adjust the price curve, ultimately reducing the power purchase costs for the demand-side area. When the TGC price is high, the demand side area will reduce its purchase volume, and vice versa. Since the game relationship is added on both sides of supply and demand, the supply side area, as the leader, will send a TGC price signal to the demand side area. The demand side area will adjust the demand according to the price, and then feed back the demand to the supply side area. The supply side area will adjust the TGC price. The mutual information interaction will eventually reach a stable state, balancing the interests of both parties. The game interaction between the supply and demand sides in Scenario 2 can also better balance the interests of the market subjects of the buyer and seller.
Conclusion
This paper proposes an optimization model of a cross-provincial two-layer game power trading strategy considering MLT trading plans. The decomposition method of MLT contracts of TGCs is introduced into the cross-provincial power trading model to construct a bilateral trading framework of TGCs and optimize the global configuration of TGCs. Game theory is employed to solve the complex game interaction between multiple participants in the interprovincial electricity trading market under the TGC mechanism. This approach addresses the limitations inherent in the traditional game theory, which often assumes perfect rationality on the part of participants. Finally, the IAOA and iterative algorithm are used for the joint solution. Through case analysis, the following conclusions are obtained.
Case analysis reveals several key findings. First, the quadratic programming approach for decomposing medium- and long-term contracted energy successfully accounts for deviations in contract completion levels, achieving reductions in the variance of contract completion progress by 14.3% and 55.7% in Areas C and D, respectively. The maximum deviation in completion progress remains constrained within 3.5%, ensuring fairer scheduling for trading units and enhancing the feasibility of the plan’s execution. Second, the two-layer game model captures the dynamic interactions among various stakeholders on both the supply and demand sides, promoting balanced coordination of economic interests and promoting the development of the power market. Third, model sensitivity analysis indicates that adjusting quota ratios appropriately increases selection opportunities for smaller power-selling areas and helps balance benefits across different regions. Reducing penalties for specific units not only leads to a reduction in TGC prices but also stimulates demand-side purchase volumes, facilitating a more equitable selection of smaller power-supply areas. The establishment of a game-based framework between supply and demand sides simulates market dynamics, mitigates regional income disparities, and facilitates a scientifically balanced allocation of interests. Lastly, the proposed IAOA efficiently addresses the challenges posed by high-dimensional variables and complex constraints within the model. Its effectiveness was validated through testing on 15 benchmark and real-world power grid data, underscoring its significant performance advantages.
According to the conclusion of this study, some suggestions are made to the government.
The government should conduct a comprehensive assessment of the costs and benefits associated with both the power generation area and the development plan of the renewable energy industry. Based on this analysis, an effective quota ratio should be formulated to facilitate the implementation of renewable energy plans within the power generation sector. On the one hand, the government needs to scientifically set the quota penalty coefficient, and then strictly implement relevant measures. On the other hand, it is imperative to improve laws and regulations, management policies, and informal rules to facilitate effective supervision of each area, and compliance with RPS regulations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Abbreviations
- MLT
Medium and long term
- TGC
Tradable green certificate
- AOA
Aquila optimization algorithm
- IAOA
Improved Aquila optimization algorithm
- RPS
Renewable portfolio standard
List of symbols
- T
Scheduling cycle
Retail price of electricity
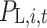
Load demand of receiving area i in time period t
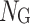
Number of conventional units in the receiving area
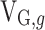
Generation cost coefficient of the g-th unit in the receiving area
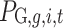
Generation power of the g-th unit in the receiving area i during time period t
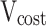
Cost coefficient of renewable energy units (photovoltaic, wind power)
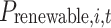
Generation power of renewable energy units in receiving area i during time period t
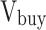
Power purchase price of renewable energy power
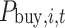
Renewable energy power purchase
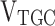
TGC price
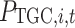
Number of TGCs purchased
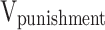
Penalty coefficient
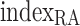
Quota coefficient of the receiving area
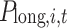
The MLT transaction volume of receiving area i at time period t
-
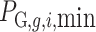 ,
,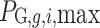
Lower and upper limits of conventional unit power in the receiving area i
-
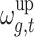 ,
,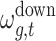
Power climbing rate of conventional unit g
-
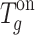 ,
,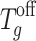
Continuous start-up and shutdown hours of conventional unit g
-
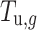 ,
,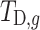
Minimum start-up and minimum shutdown hours of thermal power unit g
-
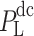 ,
,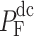
Lower and upper limits of tie-line power transmission
-
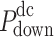 ,
, 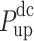
Climbing rate of transmission power of tie-line
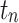
Minimum maintenance time of tie-line power
-
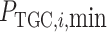 ,
,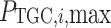
The upper and lower limits of TGC purchase
-
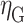 ,
,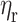 ,
,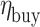 ,
,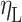
Transfer distribution factor of conventional units, renewable energy units, and renewable energy power purchase and load
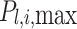
Line l transmission power limit
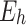
Daily executive power obtained by decomposition
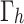
The tolerance of daily completed power deviation of MLT trading units is determined according to the completion of unit contracts
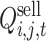
Sales volume from sending area i to receiving area j
-
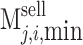 ,
,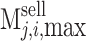
The upper and lower limits of the price for purchasing electricity
-
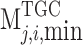 ,
,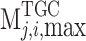
The upper and lower limits of the purchase price of TGC
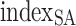
Quota coefficient of sending area
Number of units with an MLT electricity contract
Number of planned dates
Deviation of allowable power completion progress between units
-
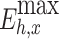 ,
,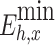
Upper and lower limits of daily decomposition energy of unit
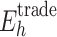
Monthly Contract Energy of Unit
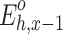
The unit has completed the contract power before the planned date
-
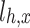 ,
,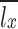
The completion progress of the unit as of day h of the contract power and the average completion progress of all units
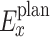
Total contract energy to be completed by each unit on the planned date
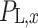
Planned daily electricity demand
Total number of days per month
Author contributions
Sizhe Yan: Methodology, Software, Data curation, Writing - original draft, Visualization, Revision and editing.Weiqing Wang: Conceptualization, Investigation. Xiaozhu Li: Conceptualization, Investigation. Hang He: Software, Methodology. Xin Zhao: Methodology, Revision and editing.
Funding
This work was supported by the National Natural Science Foundation of China (52267005), Xinjiang Uygur Autonomous Region Natural Science Foundation-Youth Fund (2024D01C249) and Graduate Innovation Project of Xinjiang Uygur Autonomous Region (XJ2023G053).
Data availability
All data generated or analyzed during this study are included in this published article and its Supplementary Information files.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Liu, W., Zhang, X., Wu, Y. & Feng, S. Economic Analysis of Renewable Energy in the Electricity Marketization Framework: a Case Study in Guangdong, China. Front. Energy Res.8, 98. 10.3389/fenrg.2020.00098 (2020). [Google Scholar]
- 2.Zhu, C., Fan, R. & Lin, J. The impact of renewable portfolio standard on retail electricity market: a system dynamics model of tripartite evolutionary game. Energy Policy. 136, 111072. 10.1016/j.enpol.2019.111072 (2020). [Google Scholar]
- 3.Liu, D. N. An interpretation of the Basic rules for mid-and long-term transactions in Electric Power (Provisional)---About protection of priority generation rights and renewable energy consumption. Energy Power Ind. China. 6, 4446 (2017). [Google Scholar]
- 4.Canelas, E., Pinto-Varela, T. & Sawik, B. Electricity Portfolio optimization for large consumers: Iberian Electricity Market Case Study. Energies13, 2249. 10.3390/en13092249 (2020). [Google Scholar]
- 5.Tranberg, B., Hansen, R. T. & Catania, L. Managing volumetric risk of long-term power purchase agreements. Energy Econ.85, 104567. 10.1016/j.eneco.2019.104567 (2020). [Google Scholar]
- 6.Chance-constrained optimal dispatch of integrated electricity. and natural gas systems considering medium and long-term electricity transactions. CSEE J Power Energy Syst (2019). 10.17775/CSEEJPES.2019.00320
- 7.Jiang, Y. et al. Optimal Bidding Strategy for a power producer under monthly pre-listing balancing mechanism in actual Sequential Energy Dual-Market in China. IEEE Access.7, 70986–70998. 10.1109/ACCESS.2019.2919347 (2019). [Google Scholar]
- 8.Sharifi, R., Anvari-Moghaddam, A., Fathi, S. H. & Vahidinasab, V. A bi-level model for strategic bidding of a price-maker retailer with flexible demands in day-ahead electricity market. Int. J. Electr. Power Energy Syst.121, 106065. 10.1016/j.ijepes.2020.106065 (2020). [Google Scholar]
- 9.Yu, X. & Sun, Y. Trading risk control model of electricity retailers in multi-level power market of China. Energy Sci. Eng.7, 2756–2767. 10.1002/ese3.457 (2019). [Google Scholar]
- 10.Banaei, M., Raouf-Sheybani, H., Oloomi-Buygi, M. & Boudjadar, J. Impacts of large-scale penetration of wind power on day-ahead electricity markets and forward contracts. Int. J. Electr. Power Energy Syst.125, 106450. 10.1016/j.ijepes.2020.106450 (2021). [Google Scholar]
- 11.Álvarez-Uribe, K. C., Arango-Aramburo, S. & Larsen, E. R. Forward contracts in electricity markets and capacity investment: a simulation study. Util. Policy. 54, 1–10. 10.1016/j.jup.2018.07.003 (2018). [Google Scholar]
- 12.Guo, H. et al. Power market reform in China: motivations, progress, and recommendations. Energy Policy. 145, 111717. 10.1016/j.enpol.2020.111717 (2020). [Google Scholar]
- 13.Tan, Q., Ding, Y., Zheng, J., Dai, M. & Zhang, Y. The effects of carbon emissions trading and renewable portfolio standards on the integrated wind–photovoltaic–thermal power-dispatching system: real case studies in China. Energy222, 119927. 10.1016/j.energy.2021.119927 (2021). [Google Scholar]
- 14.Xin-gang, Z. & Yu-qiao, Z. Analysis of the effectiveness of renewable portfolio standards: a perspective of shared mental model. J. Clean. Prod.278, 124276. 10.1016/j.jclepro.2020.124276 (2021). [Google Scholar]
- 15.Zhang, Q. et al. Substitution effect of renewable portfolio standards and renewable energy certificate trading for feed-in tariff. Appl. Energy. 227, 426–435. 10.1016/j.apenergy.2017.07.118 (2018). [Google Scholar]
- 16.Li, X. et al. Dynamic environmental economic dispatch of hybrid renewable energy systems based on tradable green certificates. Energy193, 116699. 10.1016/j.energy.2019.116699 (2020). [Google Scholar]
- 17.Fan, J-L., Wang, J-X., Hu, J-W., Wang, Y. & Zhang, X. Optimization of China’s provincial renewable energy installation plan for the 13th five-year plan based on renewable portfolio standards. Appl. Energy. 254, 113757. 10.1016/j.apenergy.2019.113757 (2019). [Google Scholar]
- 18.Tu, Q. et al. Achieving grid parity of solar PV power in China- the role of Tradable Green Certificate. Energy Policy. 144, 111681. 10.1016/j.enpol.2020.111681 (2020). [Google Scholar]
- 19.Helgesen, P. I. & Tomasgard, A. An equilibrium market power model for power markets and tradable green certificates, including Kirchhoff’s laws and Nash-Cournot competition. Energy Econ.70, 270–288. 10.1016/j.eneco.2018.01.013 (2018). [Google Scholar]
- 20.An, X., Zhang, S., Li, X. & Du, D. Two-stage joint equilibrium model of electricity market with tradable green certificates. Trans. Inst. Meas. Control. 41, 1615–1626. 10.1177/0142331217718619 (2019). [Google Scholar]
- 21.Ghaffari, M. & Hafezalkotob, A. Evaluating different scenarios for Tradable Green certificates by game theory approaches. J. Ind. Eng. Int.15, 513–527. 10.1007/s40092-018-0272-8 (2019). [Google Scholar]
- 22.Aune, F. R., Dalen, H. M. & Hagem, C. Implementing the EU renewable target through green certificate markets. Energy Econ.34, 992–1000. 10.1016/j.eneco.2011.07.006 (2012). [Google Scholar]
- 23.Zhang, Q., Wang, G., Li, H., Li, Y. & Chen, S. Study on the implementation pathways and key impacts of RPS Target in China using a dynamic game-theoretical Equilibrium Power Market Model. Energy Procedia. 105, 3844–3849. 10.1016/j.egypro.2017.03.784 (2017). [Google Scholar]
- 24.Dimitriadis, C. N., Tsimopoulos, E. G. & Georgiadis, M. C. Co-optimized trading strategy of a renewable energy aggregator in electricity and green certificates markets. Renew. Energy. 236, 121444. 10.1016/j.renene.2024.121444 (2024). [Google Scholar]
- 25.Voulkopoulos, X., Dimitriadis, C. N. & Georgiadis, M. C. Optimal scheduling of a RES – Electrolyzer aggregator in electricity, hydrogen and green certificates markets. Int. J. Hydrog Energy. 78, 1099–1107. 10.1016/j.ijhydene.2024.06.379 (2024). [Google Scholar]
- 26.Yu-zhuo, Z., Xin-gang, Z., Ling-zhi, R. & Yi, Z. The development of the renewable energy power industry under feed-in tariff and renewable portfolio standard: a case study of China’s wind power industry. J. Clean. Prod.168, 1262–1276. 10.1016/j.jclepro.2017.09.102 (2017). [DOI] [PubMed] [Google Scholar]
- 27.Haifeng, P. E. N. G., Jichun, L. I. U. & Junyong, L. I. U. Electricity purchasing and selling strategies for electricity retailers considering multiple types of retail packages in two level electricity market. Power Syst. Technol.46, 944–957 (2022). [Google Scholar]
- 28.Jiang, Q. et al. A Stackelberg Game-based planning approach for integrated community energy system considering multiple participants. Energy258, 124802. 10.1016/j.energy.2022.124802 (2022). [Google Scholar]
- 29.Lei, Z., Liu, M., Shen, Z., Lu, W. & Lu, Z. A data-driven Stackelberg game approach applied to analysis of strategic bidding for distributed energy resource aggregator in electricity markets. Renew. Energy. 215, 118959. 10.1016/j.renene.2023.118959 (2023). [Google Scholar]
- 30.Lei, Z., Liu, M., Shen, Z., Lu, J. & Lu, Z. A Nash–Stackelberg game approach to analyze strategic bidding for multiple DER aggregators in electricity markets. Sustain. Energy Grids Netw.35, 101111. 10.1016/j.segan.2023.101111 (2023). [Google Scholar]
- 31.Guo, H. W., Zhao, R., Lei, P. U., Jing, W. U. & Tan, Z. F. The Improved Shapley Model of Multi-Party Cooperation Profit Distribution in Trans-Provincial Power Transactions (Math Pract Theory, 2019). [Google Scholar]
- 32.He, Y., Song, D., Xia, T. & Liu, W. Mode of Generation Right Trade between Renewable Energy and Conventional Energy Based on Cooperative Game Theory. Power Syst. Technol.10.13335/j.1000-3673.pst.2016.2696 (2017). [Google Scholar]
- 33. Zheng, S. & Yu, L. The government’s subsidy strategy of carbon-sink fishery based on evolutionary game.Energy;254. (2022).
- 34. Jamali, M. B., Rastibarzoki, M., Khosroshahi, H. & Yan, J. An evolutionary game-theoretic approach to study the technological transformation of the industrial sector toward renewable electricity procurement: a case study of Iran.Appl. Energy (2022).
- 35.Cheng, L. et al. General Three-Population Multi-strategy Evolutionary games for Long-Term On-Grid Bidding of Generation-Side Electricity Market. IEEE Access.9, 5177–5198. 10.1109/ACCESS.2020.3046327 (2021). [Google Scholar]
- 36.Cheng, L. et al. Equilibrium analysis of general N-population multi-strategy games for generation-side long-term bidding: an evolutionary game perspective. J. Clean. Prod.276, 124123. 10.1016/j.jclepro.2020.124123 (2020). [Google Scholar]
- 37.Zaman, F., Elsayed, S. M., Ray, T. & Sarker, R. A. Co-evolutionary approach for strategic bidding in competitive electricity markets. Appl. Soft Comput.51, 1–22. 10.1016/j.asoc.2016.11.049 (2017). [Google Scholar]
- 38.Yang, H. & Mo, J. Research on the Bidding Behavior of Generation-Side enterprises based on stochastic Evolutionary games. IEEE Trans. Power Syst.37, 3693–3703. 10.1109/TPWRS.2021.3138400 (2022). [Google Scholar]
- 39.Xin-gang, Z., Ling-zhi, R., Yu-zhuo, Z. & Guan, W. Evolutionary game analysis on the behavior strategies of power producers in renewable portfolio standard. Energy162, 505–516. 10.1016/j.energy.2018.07.209 (2018). [Google Scholar]
- 40.Fang, Y. et al. Promoting electric vehicle charging infrastructure considering policy incentives and user preferences: an evolutionary game model in a small-world network. J. Clean. Prod.258, 120753. 10.1016/j.jclepro.2020.120753 (2020). [Google Scholar]
- 41.Fang, Y. et al. Coal or electricity? An evolutionary game approach to investigate fuel choices of urban heat supply systems. Energy181, 107–122. 10.1016/j.energy.2019.04.129 (2019). [Google Scholar]
- 42.Chen, C-L., Chen, Z-Y. & Lee, T-Y. Multi-area economic generation and reserve dispatch considering large-scale integration of wind power. Int. J. Electr. Power Energy Syst.55, 171–178. 10.1016/j.ijepes.2013.08.031 (2014). [Google Scholar]
- 43.Azizipanah-Abarghooee, R., Dehghanian, P. & Terzija, V. Practical multi‐area bi‐objective environmental economic dispatch equipped with a hybrid gradient search method and improved Jaya algorithm. IET Gener Transm Distrib.10, 3580–3596. 10.1049/iet-gtd.2016.0333 (2016). [Google Scholar]
- 44.Mohammadian, M., Lorestani, A. & Ardehali, M. M. Optimization of single and multi-areas economic dispatch problems based on evolutionary particle swarm optimization algorithm. Energy161, 710–724. 10.1016/j.energy.2018.07.167 (2018). [Google Scholar]
- 45.Buxiang, Z. H. O. U., Qiang, C. A. O., Tianlei, Z. A. N. G., Yue, Z. H. A. N. G. & Haoyu, P. E. N. G. Electricity trading optimization decision for microgrid based on blockchain and two-level game. Electr. Power Autom. Equip.42, 35–42 (2022). [Google Scholar]
- 46.Guowei, C. A. I., Yuqing, J. I. A. N. G., Nantian, H. U. A. N. G., Dazhi, Y. A. N. G. & Xiao, P. A. N. SHANG Wenying. Large-Scale Electric Vehicles Charging and discharging optimization scheduling based on Multi-agent two-level game under electricity demand response mechanism. Proc. CSEE. 10.13334/j.0258-8013.pcsee.212528 (2022). [Google Scholar]
- 47.Abualigah, L. et al. Aquila Optimizer: a novel meta-heuristic optimization algorithm. Comput. Ind. Eng.157, 107250. 10.1016/j.cie.2021.107250 (2021). [Google Scholar]
- 48.Yang, W., Yang, Y. & Chen, H. How to stimulate Chinese energy companies to comply with emission regulations? Evidence from four-party evolutionary game analysis. Energy258, 124867. 10.1016/j.energy.2022.124867 (2022). [Google Scholar]
- 49.Li, K. & Dong, F. Government strategy for banning gasoline vehicles: evidence from tripartite evolutionary game. Energy254, 124158. 10.1016/j.energy.2022.124158 (2022). [Google Scholar]
- 50.Dimitriadis, C. N., Tsimopoulos, E. G. & Georgiadis, M. C. A review on the Complementarity Modelling in competitive electricity markets. Energies14, 7133. 10.3390/en14217133 (2021). [Google Scholar]
- 51.Zhu, L. et al. A visually secure image encryption scheme using adaptive-thresholding sparsification compression sensing model and newly-designed memristive chaotic map. Inf. Sci.607, 1001–1022. 10.1016/j.ins.2022.06.011 (2022). [Google Scholar]
- 52.Xie, Y., Chang, S., Zhang, Z., Zhang, M. & Yang, L. Efficient sampling of complex network with modified random walk strategies. Phys. Stat. Mech. Its Appl.492, 57–64. 10.1016/j.physa.2017.09.032 (2018). [Google Scholar]
- 53.Lingzhi Ren. strategic behavior and contract design of tradable green certificates leased on common interest game. Doctoral Dissertation. North China Electric Power University, (2019).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data generated or analyzed during this study are included in this published article and its Supplementary Information files.