Application of machine learning in breast cancer survival prediction using a multimethod approach

Abstract

Breast cancer is one of the most prevalent cancers with an increasing trend in both incidence and mortality rates in Iran. Survival analysis is a pivotal measure in setting appropriate care plans.  To the best of our knowledge, this study is pioneering in Iran, introducing a multi-method approach using a Deep Neural Network (DNN) and 11 conventional machine learning (ML) methods to predict the 5 year survival of women with breast cancer. Supplying data from two centers comprising a total of 2644 records and incorporating external validation further distinguishes the study. Thirty-four features were selected based on a literature review and common variables in both datasets. Feature selection was also performed using a p value criterion (< 0.05) and a survey involving oncologists. A total of 108 models were trained. According to external validation, the DNN model trained with the Shiraz dataset, considering all features, exhibited the highest accuracy (85.56%). While the DNN model showed superior accuracy in external validation, it did not consistently achieve the highest performance across all evaluation metrics. Notably, models trained with the Shiraz dataset outperformed those trained with the Tehran dataset, possibly due to the lower number of missing values in the Shiraz dataset.

Introduction

Breast cancer remains a leading cause of mortality and morbidity in women globally, accounting for approximately 24.5% of all cancer diagnoses and 15.5% of cancer-related deaths^1,2. Notably, 2020 marked it as the most prevalent and lethal cancer for women in various countries^3–5. Despite an unwavering rise in incidence, mortality rates have fortunately stagnated or declined in recent years, potentially due to advancements in treatment modalities and the widespread adoption of mammography screening programs, particularly in developed nations^6–8. This paradoxical landscape of increasing incidence alongside stable or decreasing mortality underscores the critical need for accurate prognostic models, particularly those capable of predicting 5 year survival.

Despite a rising breast cancer incidence in Iran, underprivileged provinces experience slower increases, plausibly due to limited diagnostic infrastructure. Paradoxically, mortality rates currently remain lower in these regions. However, recent data suggest a potential trend reversal, foreshadowing a future rise in mortality within these communities^9,10. Furthermore, Iran exhibits a younger age of diagnosis compared to many developed nations by approximately a decade¹¹. Five-year and ten-year survival rates are estimated at 80% and 69%, respectively¹². These discrepancies in survival across regions likely stem from disparities in early detection initiatives and access to adequate healthcare facilities^13,14. This complex landscape underscores the need for tailored predictive models that account for such socio-economic and infrastructural variations.

Accurate 5 year survival prediction remains a critical, yet formidable, challenge for oncologists^15–19. This task lies at the heart of personalized medicine, informing crucial treatment decisions impacting medication selection and dosage regimens^20–22. Breast cancer prognosis remains a complex tapestry woven from diverse factors, encompassing patient demographics, tumor characteristics, biomarker profiles, and lifestyle habits^7,23,24.

Machine learning (ML) and its subfield, deep learning (DL), which involves algorithms that analyze data in a manner like human reasoning²⁵, have garnered substantial traction in oncology, particularly in the realm of diagnosis and detection using image processing^26–28, and survival prediction^29–32. These technologies offer compelling advantages, potentially aiding healthcare professionals at various treatment stages^33–36. Notably, they hold the promise of enhancing technical parameters (e.g., treatment quality and speed) while generating valuable clinical insights^37,38. Accurate survival models empower physicians to streamline decision-making, potentially minimizing false positives/negatives. For patients with lower predicted survival, this could inform the consideration of less invasive treatments with reduced side effects^39–41. To our knowledge, there have been limited studies addressing both conventional machine learning approaches and deep learning methods for predicting breast cancer survival using non-image data. Building upon existing research (Table 1), this study aimed to develop and compare the DL and ML models for predicting 5 year breast cancer survival.

Table 1.

Recent related studies.

Row	References	Method						Result
		ML methods	Tools	Dataset	Feature selection	Features (n)	Survival time
1	Nguyen et al.42	LR—LDA—LGBM—GBM—RF—AdaBoost—XgBoost—ANN—voting ensemble	MSSQL server—Python	6464 BC patients between 2008 and 2020 in 3 center	Literature Review	38	5 Years	AUC 0.95
2	Othman et al.43	CNN—LSTM, GRU		1980 BC patients in an online dataset (METABRIC)	mRMR	25	5 Years	Accuracy 98%
3	Lotfnezhad Afshar et al.44	C5.0—RIPPER	Excel—R	856 BC patients between 2006 and 2012		15		Accuracy 84.42%
4	Lou et al.45	DNN—KNN—SVM—NBC	Lifelines—Python	1178 BC patients between 2007 and 2010	Cox regression	24	10 Years	Accuracy 97.89%
5	Ganggayah et al.46	DT—RF—NN—SVM—XGBoost—LR	R—Python	8066 BC patients between 1993 and 2016	Physicians Survey—RF—VSURF	23		Accuracy 82.7%
6	Kalafi et al.47	MLP—SVM—RF- DT	Python	4092 BC patients between 1993 and 2017	Forests of trees	23	5 Years	Accuracy 88.2%
7	Tapak et al.48	NB—RF—Adaboost—SVM—LSSVM—Adabag—LR	R	550 BC patients between 1998 and 2013	RF	9		Accuracy Ranged from 80 to 93%
8	Zhao et al.49	XGBoost—RF—SVM—ANN—KNN	R	1874 BC patients between 2012 and 2016	KNN	27	5 Years	Accuracy Ranged from 69 to 73%
9	Montazeri et al.40	NB—TRF—1NN—Adaboost—SVM—RBFN—MLP	Weka software	900 BC patients between 1999 and 2007	1NN—TRF	8		Accuracy 96%

LR logistic regression, LDA linear discriminant analysis, LGBM light gradient boosting machine, GBM gradient boosting machine, RF random forest, AdaBoost boosting, XGBoost extreme gradient boosting, ANN artificial neural network, CNN convolutional neural network, LSTM long short-term memory, GRU gated recurrent unit, RIPPER repeated incremental pruning to produce error reduction, DNN deep neural network, KNN K-nearest neighbors, SVM support vector machine, NBC Naive Bayes classifier, DT decision tree, NN neural network, VSURF variable selection using random forests, MLP multilayer perceptron, NB Naive Bayes, LSSVM least squares support vector machine, TRF tree-based random forest, 1NN 1-nearest neighbor, RBFN radial basis function network, mRMR minimum redundancy maximum relevance, AUC Area under the curve

Materials and methods

This section represents the characteristics of leveraged datasets and outlines the step-by-step procedures employed, encompassing the entire process from dataset preparation to model development and evaluation.

Data source and dataset characteristics

The dataset in this study included the data of 2644 patients from two centers. One of these centers was the Breast Diseases Research Center of Shiraz University of Medical Sciences, which supplied data of 1465 patients from 2003 to 2013. Another center was the Cancer Research Center of Shahid Beheshti University of Medical Sciences, that provided data of 1179 patients from 2008 to 2018. The former and the later datasets consisted of 151 and 66 variables, respectively.

Data preparation

Following identifying common variables in the two datasets and a comprehensive review of relevant literature, 34 variables were selected, as outlined in Table 2. To augment patient data, the initial step involved gathering specific values from the Health Information Systems at Tajrish Hospital in Tehran and Shahid Motahari Clinic in Shiraz. In the second step, a total of 643 successful telephone calls were conducted to collect information on patients’ survival status and lifestyle. Simultaneously, the survival status of patients who did not respond was verified through the Iran Health Insurance System. Patients whose survival status could not be investigated through any of these measures were subsequently excluded from the study. In total, data from 1875 patients were utilized, comprising 741 individuals with less than a 5 year survival and 1134 individuals with a 5 year or greater survival. Finally, the datasets were normalized and the missing values were managed using K-Nearest Neighbors imputer.

Table 2.

Study variables. Quantified labels are indicated in parentheses before each variable state.

Row	Variables	Mean	Frequency
1	Age at diagnosis	49.44 years	–
2	Marital status	–	(1) Single: 117, (2) Married: 1169, (3) Widow: 135, (4) Divorced: 41
3	Child	–	(1) Yes: 1215, (0) No: 192, Unknown: 489
4	Number of children	3.1	–
5	ER	–	(1) Positive: 1211, (2) Weak positive: 14, (3) Negative: 461, Unknown: 190
6	PR	–	(1) Positive: 1084, (2) Weak positive: 10, (3) Negative: 579, Unknown: 203
7	HER2	–	(1) Negative: 553
			(2) 1 + : 353
			(3) 2 + : 254
			(4) 3 + : 369
			Unknown: 347
8	Tumor size	3.1 cm	–
9	Tumor grade	–	(1) 1: 211
			(2) 2: 811
			(3) 3: 454
			Unknown: 400
10	Tumor type	–	(1) IDC: 1573, (2) DCIS: 71, (3) LIC: 67, (4) LCIS: 2, (5) Other: 71, Unknown: 92
11	LVI	–	(1) Yes: 829, (0) No: 774, Unknown: 273
12	PNI	–	(1) Yes: 571, (0) No: 666, Unknown: 639
13	Chemotherapy	–	(1) Yes: 1482, (0) No: 385, Unknown: 9
14	Chemotherapy type	–	(1) Neoadjuvant: 271, (2) Adjuvant: 940, (3) Both: 127, Unknown: 144
15	Chemotherapy sessions	8.14	–
16	Radiotherapy	–	(1) Yes: 1394, (0) No: 471, Unknown: 11
17	Radiotherapy type	–	(1) EBRT: 1210, (2) IORT: 74, (3) Both: 106, Unknown: 4
18	Radiotherapy Sessions	26.25	–
19	Lymph node Management	–	(1) ALND: 830, (2) SLNB: 362, (3) Both: 169, Unknown: 515
20	Surgery type	–	(1) BCS: 973, (2) MRM: 683, (3) Both: 95, (0) No Surgery: 39, Unknown: 86
21	Physical activity	–	(1) Yes: 654, (0) No: 1091, Unknown: 131
22	Menopause status	–	(1) Yes: 805, (0) No: 392, Unknown: 679
23	Menopause age	47 years	–
24	Menstrual age	13.3 years	–
25	Metastasis	–	(1) Yes: 707, (0) No: 943, Unknown: 226
26	Recurrence	–	(1) Yes: 158, (0) No: 1482, Unknown: 236
27	Smoking	–	(1) Yes: 21, (0) No: 1728, Unknown: 127
28	Alcohol Consumption	–	(1) Yes: 16, (0) No: 1732, Unknown: 128
29	Breastfeeding	–	(1) Yes: 1176, (0) No: 223, Unknown: 477
30	Number of Breastfed Children	2.96	–
31	Breastfeeding Month	57.24 months	–
32	Laterality	–	(1) left: 943, (0) right: 830, (2) both: 28, Unknown: 75
34	Overall Survival	–	(1) at least 5 years: 1134, (0) less than 5 years: 741

The overall survival of patients was determined by calculating the time interval between the diagnosis and the time of death. Specifically, if this interval exceeded 5 years or if the patient was alive with more than 5 years having elapsed since the diagnosis of breast cancer, the label was assigned as 1; otherwise, it was labeled as 0.

Model development

DNN along with conventional machine learning models, such as LR, NB, KNN, DT, RF, Extra Trees, SVM, Adaboost, GBoost, XGB, and MLP were used in this study. A brief explanation of each algorithm is provided below:

DNN It is a type of artificial neural network with multiple hidden layers between the input and output layers. DNNs are designed to automatically learn and model complex patterns by passing data through layered architectures⁵⁰.

LR A statistical algorithm commonly applied to binary classification problems. It extends linear regression to model the likelihood of a dichotomous outcome (e.g., occurrence vs. non-occurrence of an event) by mapping predictions to probabilities⁵¹.

NB Bayes’ theorem is one of the fundamental principles in probability theory and mathematical statistics. In this algorithm, variables are assumed to be independent of each other⁵².

KNN A non-parametric classification algorithm that determines the class of a test sample based on the classes of its k nearest neighbors in the training data. The algorithm computes the distance between the test sample and all training samples to find these neighbors⁵³.

DT A predictive model that uses a tree-like structure to make decisions based on sequential tests of input data. Each node represents a decision rule, and each branch represents the outcome of that rule, they ultimately lead to prediction or classification⁵⁴.

RF A machine learning algorithm that combines multiple decision trees to improve the prediction accuracy and prevent overfitting. It operates by training each tree on a random subset of the data, with each tree providing a “vote” for the outcome, and the most common vote across all trees is selected as the final prediction⁵⁵.

Extra Trees An ensemble learning method used for classification and regression tasks, which improves performance by aggregating predictions from multiple decision trees. Unlike traditional decision trees, Extra Trees are built with more randomization in the tree creation process, notably by selecting random splits at each node, which helps to avoid overfitting and enhances model accuracy⁵⁶.

SVM A supervised machine learning algorithm works by finding the hyperplane that best separates different data classes in a high-dimensional space. SVM is particularly effective in handling complex, non-linear data by using kernel functions to transform data into higher dimensions, making it useful for accurate predictions⁵⁷.

AdaBoost an ensemble machine learning technique that focuses on improving the performance of weak classifiers by sequentially combining them into a stronger classifier⁵⁸.

GBoost A machine learning algorithm that iteratively builds a model by training a sequence of weak learners, typically decision trees, to correct the errors of previous ones⁵⁹.

XGBoost A highly efficient machine learning algorithm based on gradient boosting principles, known for its accuracy and speed in solving regression and classification problems. XGBoost also integrates several advanced features like regularization, handling missing values, and parallelization, making it suitable for large datasets⁶⁰.

MLP It is a type of artificial neural network composed of several layers of neurons, each of which processes data through nonlinear activation functions. This architecture enables MLPs to learn complex patterns in the data, making them suitable for classification and regression⁶¹.

The performance of these algorithms was thoroughly assessed and compared. Model development and evaluation were conducted using the Python programming language, leveraging scikit-learn^42,45,47, TensorFlow⁴², and Autokeras libraries within the Jupyter Notebook environment.

Feature selection was conducted through three distinct approaches^62,63. Initially, modeling was executed using all features, which were chosen based on a review of relevant articles while also taking into account dataset limitations. Subsequently, features were selected based on a two-tailed p value criterion (< 0.05) using scikit-learn. Lastly, features were chosen through a survey methodology. To identify essential variables, a questionnaire was formulated and completed by five oncology specialists, aiming to pinpoint essential features for the analysis.

As previously stated, the study involved modeling using a deep neural network and 11 conventional machine learning models. To train and fit the conventional machine learning models, the dataset was initially divided into two parts: the train set and the test set⁶⁴. The train set served for model development, hyperparameter tuning, and initial training. The train set was partitioned into five folds (k = 5), and the modeling process was iterated five times. In each iteration, one of the folds served as the validation set, while the remaining four were used as the train set. The model underwent training on the train set for each iteration and was subsequently validated on the designated validation set. Different hyperparameters were employed during each fold, determined through the Grid Search method. This method systematically explores a predefined range of hyperparameter values to identify an optimal set that maximizes performance measures such as accuracy. Five distinct evaluation points, or different accuracy values, were obtained for each iteration. The highest accuracy level signified the most optimal model within that algorithm. As an example, Fig. 1 shows the DT algorithm training process, with Shiraz datasets using k-fold and the accuracy score in each fold.

Fig. 1.

The DT algorithm training process and the accuracy score in each fold. Yellow boxes show the validation set in each iteration.

For training the deep neural network, the dataset was initially divided into two parts: the train set and the test set. Subsequently, the Neural Architecture Search method, a technique in deep learning for automatically exploring optimal neural network architectures, was applied. Hyperparameters were adjusted following this exploration. To determine the optimal architecture and set hyperparameters, the Autokeras library was utilized. Figure 2 illustrates the model development process employing both Deep Neural Network and conventional machine learning techniques. Sets of hyperparameters and also the best parameters in each trained model are attached as supplementary information.

Fig. 2.

Dataset preparation and modeling process.

Performance evaluation

At this stage, the trained models underwent evaluation on the test set to derive the ultimate estimate of their performance on previously unseen data. The evaluation process encompassed two distinct approaches, as illustrated in Fig. 1. Firstly, each model was assessed on a subset of the same dataset used for training, constituting a cross-validation. Secondly, the evaluation was repeated on the dataset from the other center, effectively constituting an external validation. These two evaluation methods provided a comprehensive understanding of the models’ performance across both internal and external datasets^65,66. It should be noted that the hyperparameter setting was exclusively performed on the training dataset. In this study, the following metrics were employed for evaluating the models.

1. Accuracy The percentage of people whose life status is correctly predicted.

   

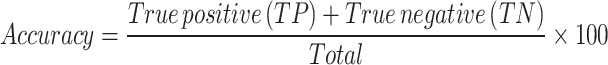
   True positive (TP) indicates those individuals who are alive and are correctly predicted as alive. True negative (TN) indicates those individuals who have died and are correctly considered dead.

2. Specificity The percentage of individuals who have died and are labeled 0 and are correctly considered dead.

   

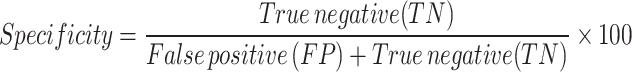
3. Sensitivity The percentage of individuals who are alive and have a label of 1 and are correctly predicted as alive.

   

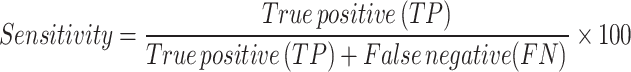
4. Area under the Curve Indicates how well the model can distinguish between class labels and correctly predicts the model for classes 0 and 1.

Results

In this study, modeling was conducted using conventional machine learning algorithms and Deep Neural Network in three distinct approaches. In the initial stage, modeling was executed using all available features extracted from related articles. Subsequently, in the second and third stages, modeling occurred alongside feature selection, taking into account p value and the opinions of 5 oncology experts, respectively. Given that each algorithm was trained with three datasets—Tehran, Shiraz, and a combination of the two—it can be stated that nine models were created for each algorithm. It is noteworthy that all models, except those trained using the combined dataset, underwent evaluation through both cross-validation and external evaluation methods. Based on the recorded evaluation metrics, the highest average accuracy in cross-validation was 94.29%, attributed to models trained with the Shiraz dataset and features selected by oncologists. Additionally, the highest average accuracy in external validation was 76.42%, observed in models trained with the Shiraz dataset and utilizing all features. The maximum average AUC in cross-validation, reaching 0.983, was associated with models trained using the Shiraz dataset and features selected based on the p-value. In external validation, this AUC value was 0.851, achieved by models trained with the Tehran dataset and features selected by oncologists. The subsequent section provides a detailed presentation of the evaluation results.

Evaluation and performance comparison of trained models with all features

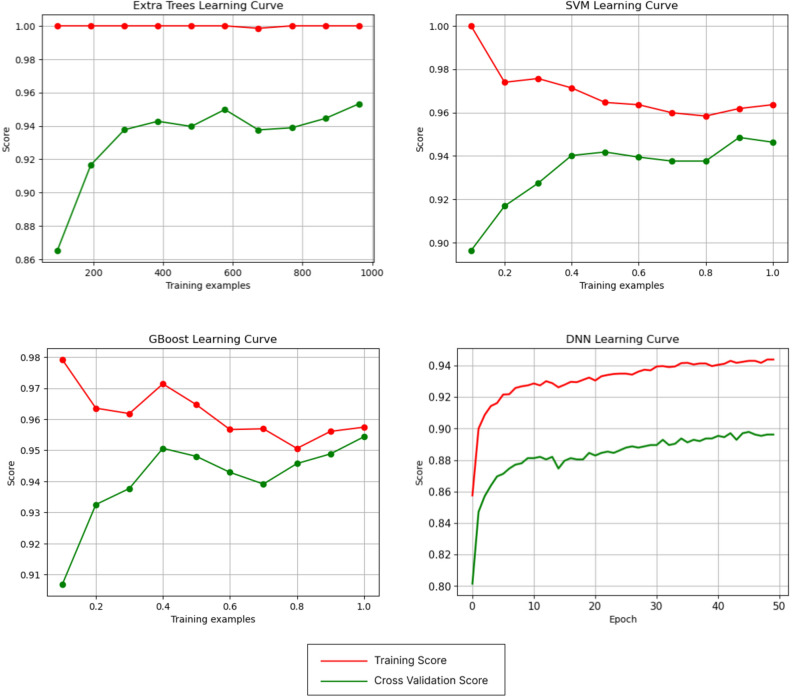
According to Table 3, the highest accuracy achieved on the test data in the cross-validation was 95.43%, which belongs to the GBoost and Extra Tree models, which were trained with the Shiraz dataset. Additionally, the highest accuracy level in external validation reached 85.56%, which was achieved using the DNN model. Figure 3 illustrates the architecture of this DNN model. Among the conventional models, the highest accuracy was 81.69%, obtained with the SVM model. Both models were trained with the Shiraz dataset and tested on the Tehran dataset. Figure 4 shows the learning curves of the models that recorded the highest cross or external validation accuracy. The pinnacle AUC levels in cross-validation were attained by XGB and Extra Trees with 0.994 and in external validation by Extra Trees with 0.960. Figure 5 illustrates the ROC curves of models that recorded the highest AUC in cross and external validation.

Table 3.

Evaluation results of trained models based on all features.

Models	Train dataset	Train accuracy	Test dataset	Test accuracy	AUC	Sensitivity	Specificity
KNN	Shiraz	94.49	Shiraz (cross)	93.77	0.986	93.8	93.75
			Tehran (external)	79.91	0.789	81.71	65.78
	Tehran	97.76	Tehran (cross)	87.4	0.767	100	10.52
			Shiraz (external)	45.22	0.921	100	0
	Combined	92.93	Combined (cross)	86.66	0.889	88.16	83.84
NB	Shiraz	92.41	Shiraz (cross)	93.36	0.966	90.26	96.09
			Tehran (external)	73.21	0.641	77.85	36.84
	Tehran	85.1	Tehran (cross)	75.55	0.708	84.48	21.05
			Shiraz (external)	49.12	0.770	94.42	12.48
	Combined	89.33	Combined (cross)	86.93	0.912	89.38	82.3
DT	Shiraz	95.94	Shiraz (cross)	94.6	0.966	92.03	96.87
			Tehran (external)	68.6	0.717	68.12	72.36
	Tehran	91.43	Tehran (cross)	86.67	0.673	97.41	21.05
			Shiraz (external)	46.05	0.499	99.25	3
	Combined	93.26	Combined (cross)	86.67	0.890	86.94	86.15
LR	Shiraz	94.9	Shiraz (cross)	93.36	0.984	92.03	94.53
			Tehran (external)	78.57	0.792	80.37	64.47
	Tehran	90.68	Tehran (cross)	85.18	0.765	98.27	5.26
			Shiraz (external)	46.79	0.954	99.25	4.36
	Combined	91.86	Combined (cross)	87.2	0.938	88.16	85.38
RF	Shiraz	96.05	Shiraz (cross)	95.02	0.991	92.03	97.65
			Tehran (external)	69.04	0.775	68.62	72.36
	Tehran	94..22	Tehran (cross)	86.66	0.784	100	5.26
			Shiraz (external)	44.72	0.935	100	0
	Combined	98.73	Combined (cross)	89.6	0.958	91.83	85.38
Extra Trees	Shiraz	99.89	Shiraz (cross)	95.43	0.994	92.92	97.65
			Tehran (external)	68.6	0.790	67.44	77.63
	Tehran	96.46	Tehran (cross)	87.4	0.810	100	10.52
			Shiraz (external)	44.72	0.960	100	0
	Combined	99.86	Combined (cross)	87.73	0.956	88.97	85.38
SVM	Shiraz	96.36	Shiraz (cross)	94.6	0.991	92.03	96.87
			Tehran (external)	81.69	0.805	83.89	64.47
	Tehran	94.59	Tehran (cross)	86.66	0.772	100	5.26
			Shiraz (external)	44.72	0.934	100	0
	Combined	96.26	Combined (cross)	87.73	0.937	88.97	85.38
AdaBoost	Shiraz	95.63	Shiraz (cross)	95.02	0.984	92.03	97.65
			Tehran (external)	69.34	0.753	68.95	72.36
	Tehran	99.44	Tehran (cross)	85.92	0.730	98.27	10.52
			Shiraz (external)	48.29	0.538	99.25	07.06
	Combined	92.06	Combined (cross)	86.93	0.948	87.34	86.15
GBoost	Shiraz	95.73	Shiraz (cross)	95.43	0.995	92.92	97.65
			Tehran (external)	69.34	0.751	68.95	72.36
	Tehran	93.48	Tehran (cross)	86.66	0.769	100	5.26
			Shiraz (external)	44.97	0.937	99.81	0.6
	Combined	93.66	Combined (cross)	87.46	0.949	87.75	86.92
XGB	Shiraz	99.89	Shiraz (cross)	95.85	0.994	95.57	96.09
			Tehran (external)	67.26	0.749	66.27	75
	Tehran	98.32	Tehran (cross)	90.37	0.854	100	31.57
			Shiraz (external)	46.63	0.908	99.25	04.06
	Combined	96.06	Combined (cross)	88.8	0.957	90.2	86.15
MLP	Shiraz	95.01	Shiraz (cross)	93.36	0.983	92.92	93.75
			Tehran (external)	78.86	0.806	80.7	64.47
	Tehran	91.06	Tehran (cross)	88.14	0.762	99.13	10.52
			Shiraz (external)	46.05	0.956	99.44	2.85
	Combined	91.93	Combined (cross)	87.46	0.944	88.57	85.38
DNN	Shiraz	94.38	Shiraz (cross)	89.62	0.958	88.49	90.62
			Tehran (external)	85.56	0.712	43.42	90.93
	Tehran	93.11	Tehran (cross)	85.92	0.738	96.55	21.05
			Shiraz (external)	44.72	0.540	99.62	0
	Combined	95.2	Combined (cross)	87.2	0.930	89.38	83.07

Fig. 3.

The Architecture of the DNN model that trained with the Shiraz dataset and showed the highest accuracy in external validation among all 108 trained models.

Fig. 4.

Learning curves for Extra Trees, SVM, GBoost, and DNN models trained on the Shiraz datasets with all features. The Extra Trees learning curve indicates that the training score does not improve with more training data, but the cross-validation score does. The SVM and GBoost learning curves show that while the training scores decrease with more training data, the cross-validation scores increase. Using all the training data makes the training and cross-validation scores more reasonable and realistic. The DNN learning curve indicates that both the training and cross-validation scores increase with more training data.

Fig. 5.

ROC curves for Extra Trees performance in cross and external validation and XGB in cross-validation.

Evaluation and performance comparison of trained models with selected features based on P value

In this part, feature selection was done based on two-tailed p value (< 0.05) before modeling. The selected features based on Shiraz, Tehran, and combined datasets are shown in Table 4.

Table 4.

Selected features in each dataset based on P value.

Dataset	Selected features and P values
Shiraz	Metastasis (0), Recurrence (0.021), Age at diagnosis (0.016), ER (0), PR (0), Chemotherapy (0), Chemotherapy type (0), Chemotherapy sessions (0), Tumor size (0), LVI (0), PNI (0), Lymph node management (0), Radiotherapy (0), Radiotherapy type (0), Radiotherapy sessions (0), Surgery Type (0), physical activity (0), Menopause status (0), Menopause age (0.013), Number of Children (0.003)
Tehran	Metastasis (0), Recurrence (0), ER (0), PR (0.018), Tumor size (0.031), LVI (0.001), Surgery Type (0.004), Smoking (0.013), Alcohol Consumption (0.014), Menopause status (0.030), Breastfeeding Month (0.029)
Combined	Metastasis (0), Age at diagnosis (0.006), ER (0), PR (0), HER2 (0.006), Chemotherapy (0), Chemotherapy type (0), Chemotherapy sessions (0), Tumor size (0), LVI (0), PNI (0), Lymph node management (0), Radiotherapy (0), Radiotherapy type (0), Radiotherapy sessions (0), Surgery Type (0), Physical Activity (0), Menopause age (0.024), Number of Children (0), Number of Breastfed Children (0), Breastfeeding Month (0.006)

According to Table 5, the highest accuracy achieved on the test data in cross-validation was 96.26%, which belongs to the DT model trained with the Shiraz dataset. Moreover, the highest level of accuracy in external validation was 82.89%, and it was obtained using the SVM model, which was trained with the Shiraz dataset and tested on the Tehran dataset. Figure 6 shows the learning curves of the models that recorded the highest cross or external validation accuracy. The highest level of AUC in cross and external validation was obtained using Extra Trees with 0.992 and MLP with 0.944, respectively. Figure 7 illustrates the ROC curves of models that recorded the highest AUC in cross and external validation.

Table 5.

Evaluation results of trained models based on selected features (P value).

Models	Train dataset	Train accuracy	Test dataset	Test accuracy	AUC	Sensitivity	Specificity
KNN	Shiraz	94.38	Shiraz (cross)	93.36	0.985	92.92	93.75
			Tehran (external)	82.74	0.763	85.91	57.89
	Tehran	100	Tehran (cross)	87.4	0.759	100	10.52
			Shiraz (external)	44.72	0.852	100	0
	Combined	92.13	Combined (cross)	86.66	0.936	87.34	85.38
NB	Shiraz	92.31	Shiraz (cross)	93.77	0.969	89.38	97.65
			Tehran (external)	68.45	0.712	68.46	68.42
	Tehran	85.28	Tehran (cross)	83.7	0.571	97.41	0
			Shiraz (external)	47.29	0.750	95.91	7.96
	Combined	88.6	Combined (cross)	85.33	0.903	90.2	76.15
DT	Shiraz	95.84	Shiraz (cross)	96.26	0.971	93.8	98.43
			Tehran (external)	65.62	0.738	63.76	80.26
	Tehran	90.5	Tehran (cross)	91.11	0.836	100	36.84
			Shiraz (external)	64.75	0.896	98.32	37.6
	Combined	91.87	Combined (cross)	85.6	0.920	85.3	86.15
LR	Shiraz	95.01	Shiraz (cross)	93.77	0.984	92.03	95.31
			Tehran (external)	81.99	0.781	85.07	57.89
	Tehran	91.24	Tehran (cross)	88.15	0.780	100	15.78
			Shiraz (external)	47.05	0.930	99.25	4.81
	Combined	91.13	Combined (cross)	88	0.935	91.42	81.53
RF	Shiraz	96.78	Shiraz (cross)	93.77	0.988	92.03	95.31
			Tehran (external)	69.64	0.767	69.46	71.05
	Tehran	91.99	Tehran (cross)	88.14	0.798	100	15.78
			Shiraz (external)	45.13	0.936	99.81	0.9
	Combined	99.26	Combined (cross)	90.13	0.944	93.46	83.84
Extra Trees	Shiraz	96.77	Shiraz (cross)	94.6	0.992	92.03	96.87
			Tehran (external)	77.08	0.775	78.69	64.47
	Tehran	100	Tehran (cross)	87.4	0.772	100	10.52
			Shiraz (external)	44.72	0.928	99.81	0
	Combined	100	Combined (cross)	88.53	0.948	91.02	83.84
SVM	Shiraz	96.57	Shiraz (cross)	93.36	0.987	92.03	94.53
			Tehran (external)	82.89	0.771	85.4	63.16
	Tehran	91.62	Tehran (cross)	88.14	0.798	99.13	21.05
			Shiraz (external)	46.96	0.884	99.62	4.36
	Combined	93.06	Combined (cross)	86.4	0.942	86.93	85.38
AdaBoost	Shiraz	95.74	Shiraz (cross)	94.6	0.981	92.03	96.87
			Tehran (external)	69.64	0.736	69.46	71.05
	Tehran	93.29	Tehran (cross)	85.92	0.584	100	0
			Shiraz (external)	45.71	0.427	99.81	1.95
	Combined	92.2	Combined (cross)	87.73	0.949	87.34	88.46
GBoost	Shiraz	95.74	Shiraz (cross)	94.6	0.987	92.03	96.87
			Tehran (external)	69.64	0.736	69.46	71.05
	Tehran	93.29	Tehran (cross)	88.14	0.819	99.13	21.05
			Shiraz (external)	47.21	0.882	99.44	4.96
	Combined	100	Combined (cross)	86.13	0.914	88.97	80.76
XGB	Shiraz	98.54	Shiraz (cross)	94.6	0.989	92.92	96.09
			Tehran (external)	67.71	0.732	66.44	77.63
	Tehran	94.04	Tehran (cross)	88.88	0.803	99.13	26.31
			Shiraz (external)	45.96	0.924	99.44	02.07
	Combined	99.53	Combined (cross)	88.26	0.946	89.79	85.38
MLP	Shiraz	94.91	Shiraz (cross)	93.77	0.984	92.03	95.31
			Tehran (external)	81.99	0.783	84.73	60.53
	Tehran	90.68	Tehran (cross)	87.4	0.780	98.27	21.05
			Shiraz (external)	50.37	0.944	98.69	11.27
	Combined	97	Combined (cross)	87.2	0.928	82.24	77.69
DNN	Shiraz	93.86	Shiraz (cross)	83.81	0.975	92.94	94.59
			Tehran (external)	75.59	0.646	79.02	48.68
	Tehran	91.24	Tehran (cross)	85.18	0.905	99.37	22.08
			Shiraz (external)	44.97	0.667	0.4	100
	Combined	91.73	Combined (cross)	82.93	0.894	95.91	58.46

Fig. 6.

Learning curves for DT and SVM models trained on the Shiraz datasets with features selected based on p values. The DT learning curve indicates that, despite fluctuations, both the training and cross-validation scores increase with more training data. The SVM learning curve shows that while the training scores decrease with more training data, the cross-validation scores increase, and using all the training data makes the training and cross-validation scores more reasonable and realistic.

Fig. 7.

ROC curves for MLP performance in external validation and Extra Trees in cross-validation.

Evaluation and performance comparison of trained models with features selected by oncologists

In this part, preceding the modeling process, feature selection was carried out based on a questionnaire completed by five oncology specialists. The questionnaire assigned importance and impact scores to each feature on the survival of breast cancer patients, ranging from 1 to 5 (1: unimportant, 5: very important). Features with an average score greater than or equal to 3 were selected for use in modeling. Figure 8 illustrates the selected features along with their respective average scores. It is noteworthy that the features selected in Shiraz and Tehran and the combined datasets were the same.

Fig. 8.

Selected features and their average scores determined by oncologists.

As per Table 6, the highest accuracy on the test data in cross-validation reached 95.85%, which is attributed to the GBoost model trained with the Shiraz dataset. Additionally, the highest accuracy in external validation was 81.54%, achieved by the DNN model. The highest accuracy of the conventional machine learning models was 77.82%, obtained with the LR model. Both the DNN and LR models were trained using the Shiraz dataset and tested on the Tehran dataset. Figure 9 shows the learning curves of the models that recorded the highest cross or external validation accuracy. The maximum AUC levels in cross-validation and external validation were attained by RF with 0.992 and LR with 0.972, respectively. Figure 10 illustrates the ROC curves of models that recorded the highest AUC in cross and external validation.

Table 6.

Evaluation results of trained models based on features selected by oncologists.

Models	Train dataset	Train accuracy	Test dataset	Test accuracy	AUC	Sensitivity	Specificity
KNN	Shiraz	94.28	Shiraz (cross)	93.77	0.985	92.03	95.31
			Tehran (external)	75	0.780	76.17	65.78
	Tehran	91.24	Tehran (cross)	88.14	0.660	100	15.78
			Shiraz (external)	45.71	0.904	99.81	1.95
	Combined	92.6	Combined (cross)	88.8	0.927	89.38	87.69
NB	Shiraz	92.2	Shiraz (cross)	93.77	0.960	90.26	96.87
			Tehran (external)	73.21	0.658	77.18	42.1
	Tehran	84.72	Tehran (cross)	77.03	0.697	83.62	36.84
			Shiraz (external)	54.03	0.819	98.69	17.89
	Combined	89.46	Combined (cross)	88.26	0.916	89.38	86.15
DT	Shiraz	95.11	Shiraz (cross)	95.43	0.976	92.92	97.65
			Tehran (external)	66.51	0.728	65.43	75
	Tehran	89.75	Tehran (cross)	84.44	0.636	96.55	10.52
			Shiraz (external)	52.95	0.815	99.07	15.63
	Combined	87.4	Combined (cross)	81.6	0.895	76.32	91.53
LR	Shiraz	95.01	Shiraz (cross)	93.77	0.984	92.03	95.31
			Tehran (external)	77.82	0.790	79.36	65.78
	Tehran	90.13	Tehran (cross)	88.14	0.775	100	15.78
			Shiraz (external)	54.94	0.972	99.81	18.64
	Combined	91.06	Combined (cross)	87.46	0.943	88.16	86.15
RF	Shiraz	99.37	Shiraz (cross)	95.02	0.992	92.03	97.65
			Tehran (external)	68.6	0.771	68.12	72.36
	Tehran	97.02	Tehran (cross)	88.14	0.744	100	15.78
			Shiraz (external)	49.62	0.829	98.88	9.77
	Combined	96.8	Combined (cross)	89.33	0.948	90.2	87.69
Extra Trees	Shiraz	95.94	Shiraz (cross)	95.02	0.991	92.03	97.65
			Tehran (external)	69.04	0.800	68.62	72.36
	Tehran	99.44	Tehran (cross)	88.14	0.765	100	15.78
			Shiraz (external)	44.88	0.959	99.81	0.4
	Combined	99.4	Combined (cross)	88.26	0.949	88.97	86.92
SVM	Shiraz	95.21	Shiraz (cross)	93.77	0.986	92.03	95.31
			Tehran (external)	77.23	0.807	78.02	71.05
	Tehran	91.99	Tehran (cross)	88.14	0.732	100	15.78
			Shiraz (external)	50.7	0.837	99.44	11.27
	Combined	95.13	Combined (cross)	87.46	0.942	88.57	85.38
AdaBoost	Shiraz	95.53	Shiraz (cross)	95.02	0.984	92.03	97.65
			Tehran (external)	69.04	0.755	68.62	72.36
	Tehran	89.75	Tehran (cross)	86.66	0.743	100	5.26
			Shiraz (external)	47.46	0.873	99.25	5.56
	Combined	95.33	Combined (cross)	88	0.931	89.79	84.61
GBoost	Shiraz	98.12	Shiraz (cross)	95.85	0.989	94.69	94.87
			Tehran (external)	68.45	0.766	67.78	73.68
	Tehran	91.06	Tehran (cross)	87.4	0.780	100	10.52
			Shiraz (external)	44.97	0.939	99.81	0
	Combined	99.53	Combined (cross)	88.26	0.945	88.97	86.92
XGB	Shiraz	98.23	Shiraz (cross)	95.02	0.990	93.8	96.09
			Tehran (external)	65.77	0.765	63.92	80.26
	Tehran	97.95	Tehran (cross)	88.88	0.790	100	21.05
			Shiraz (external)	46.3	0.938	99.62	3.15
	Combined	94.33	Combined (cross)	87.73	0.949	88.97	85.38
MLP	Shiraz	95.11	Shiraz (cross)	93.77	0.983	92.03	95.31
			Tehran (external)	74.25	0.804	74.32	73.68
	Tehran	90.68	Tehran (cross)	85.18	0.768	98.27	10.52
			Shiraz (external)	52.45	0.957	99.81	14.13
	Combined	91.6	Combined (cross)	87.46	0.943	87.34	86.92
DNN	Shiraz	94.59	Shiraz (cross)	91.28	0.967	92.94	95.9
			Tehran (external)	81.54	0.761	85.57	50
	Tehran	90.31	Tehran (cross)	85.92	0.873	100	8.77
			Shiraz (external)	52.72	0.376	100	0
	Combined	93.33	Combined (cross)	87.73	0.933	89.79	83.84

Fig. 9.

Learning curves for LR, GBoost, and DNN models trained on the Shiraz datasets with features selected by oncologists. The LR and DNN learning curves indicate that despite fluctuations, both the training and cross-validation scores increase with more training data. The GBoost learning curve shows that while the training score decreases with more training data, the cross-validation score increases, and using all the training data makes the training and cross-validation scores more reasonable and realistic.

Fig. 10.

ROC curves for LR performance in external validation and RF in cross-validation.

Discussion

In this study, the utilization of two datasets significantly mitigates the likelihood of bias associated with single-center studies, an issue often cited in similar research ⁴⁵. Moreover, each algorithm underwent training three times: once with all features, once with features selected based on p value, and once again with features selected by oncologists. This resulted in the development of a total of 108 models. Subsequently, the performance of conventional machine learning models and DNN was compared.

Certainly, one of the strengths of this study lies in the comprehensive consideration of various variables encompassing tumor characteristics, tumor markers, patient clinical information, patient characteristics, and lifestyle factors. As evident, an essential step before modeling is feature selection, a task accomplished through various methods such as RF, 1NN, KNN, and Cox regression. Beyond these techniques, another approach to feature selection involves consulting experts. Study ⁴² emphasizes the importance of specialist input in refining the feature set. Initially, their dataset contained 113 features, but after expert consultation, 89 features were discarded. As previously mentioned, in our study, feature selection was conducted not only based on p value but also through a survey involving oncologists. As a result of this expert input, 24 items were selected from the initial set of 32 features. In this study’s overall findings of feature selection methods, common features that emerged as significant include metastasis, recurrence, age at diagnosis, estrogen and progesterone hormone receptors, tumor size, lymph vascular invasion, and the type of surgery performed. It is noteworthy that tumor size, age at diagnosis, hormone receptors, and surgery have consistently been identified as important characteristics in many studies, aligning with the results observed in this investigation^46,47,49.

The results reveal that the Extra Trees and GBoost models, trained on all features, achieved the highest cross-validation accuracy at 95.43%. Moreover, the DNN model demonstrated the highest external validation accuracy at 85.56%. This finding is consistent with the results of study⁴⁵ that both cross and external validation were conducted. According to this study⁴⁵ the deep neural network model outperformed in all evaluation indicators. In contrast, among our models trained with all features, the XGB model demonstrated the highest AUC in cross-validation, whereas in study ⁴⁵ there was not a significant performance difference between XGB and other models.

For models trained on features selected based on p value, the DT model achieved the highest cross-validation accuracy at 96.26%. However, this contrasts with study⁴³, which reported negligible performance differences between DT, SVM, and RF models. In external validation, the SVM model’s accuracy of 82.89% supports findings from study⁴¹, which also recognized SVM’s strong performance after DNN. The highest amount of AUC among trained models with selected features based on P value in cross and external validations was related to Extra Trees and MLP, respectively. Meanwhile, based on the results of study⁴⁰, the AUC of the MLP model was not much different from other models.

Regarding models trained on features selected by oncologists, the highest accuracy of cross-validation was 95.85% and was related to the GBoost model. Besides, the highest accuracy of external validation was 81.59% and related to the DNN. This result is consistent with study⁴¹, which highlighted DNN’s superior performance in external validation. However, study⁴⁶, where feature selection was conducted with the assistance of expertise, the RF model demonstrated the highest level of performance accuracy. The highest AUCs for models trained with oncologist-selected features were achieved by RF in cross-validation and LR in external validation, contrasting with the findings of study⁴², where XGB recorded the highest AUC in cross-validation.

The findings of the current study are in line with study⁴¹, which reported the DNN as the best model. Overall, aside from DNN, other studies^36,38,43,45 indicated that models based on neural networks such as ANN and MLP, showed better performance. It is noteworthy to say that the mentioned contractions in studies^36,42,43,45 could be assigned to utilizing different datasets as well as feature selection approaches.

Study limitations and future considerations

This study encountered several limitations. Firstly, the inaccessibility of patients’ genetic data was a significant constraint. Combining genetic data with other available information could potentially enhance the efficiency of the models. Additionally, the absence of certain aspects of the patients’ medical history, such as blood pressure, blood sugar levels, and other cancers, could notably impact the performance and accuracy of both ML and DL models. Certainly, considering the drugs used in the treatment process would be a valuable addition, bringing the study results closer to the outcomes obtained in real-world scenarios. Future investigations could include using medical images in addition to other forms of data and training deep learning models like CNN. Moreover, developing and comparing metastasis and recurrence prediction models could provide a broader perspective in this field. Furthermore, incorporating online and accessible datasets for external validation could also be practical to enhance the applicability of our findings.

Conclusion

To the best of our knowledge, this study represents a pioneering effort in Iran, being the first to introduce a survival prediction model using deep learning. Leveraging data from two centers and incorporating external validation further distinguishes the study. The results indicate that, overall, the DNN model demonstrated superior prediction accuracy in external validation. This could be because DNN can capture non-linear relationships and interactions among features better than simpler models. However, DNN was not consistently at a higher level in other performance metrics. Moreover, among the conventional models, SVM showed the highest prediction accuracy in external validation. The reason behind this could be that SVM employs kernel functions to transform data into higher dimensions, allowing it to capture complex relationships between features. Notably, evaluation metrics were generally higher for models trained with the Shiraz dataset. This discrepancy might be attributed to the fewer missing values in the Shiraz dataset compared to the Tehran dataset, which was addressed using the KNN algorithm. With an increasing number of similar studies and positive outcomes, there is optimism that ongoing advancements in the field will lead to optimized medical decisions and improved disease prognosis through the utilization of deep learning algorithms to uncover hidden patterns in data.

Abbreviations

ANN

Artificial neural network

BC

Breast cancer

CNN

Convolutional neural network

DL

Deep learning

DNN

Deep neural network

DT

Decision tree

ER

Estrogen receptor

GBM

Gradient boosting machine

GBoost

Gradient boosting

GRU

Gated recurrent unit

HER2

Human epidermal growth factor receptor-2

KNN

K nearest neighbor

LDA

Linear discriminant analysis

LGBM

Light gradient boosting machine

LR

Logistic regression

LSTM

Long short-term memory

LVI

Lymphovascular invasion

ML

Machine learning

MLP

Multilayer perceptron

NB

Naive Bayes

PNI

Perineural invasion

PR

Progesterone receptor

RF

Random forest

RIPPER

Repeated incremental pruning to produce error reduction

ROC

Receiver operator characteristic

SVM

Support vector machine

XGB

Extreme gradient boosting

Author contributions

S.Z.H., R.R., H.E. and M.A. were responsible for the conceptualization and design of the study. S.Z.H and M.A. performed the development and evaluation of the ML and DL models. M.K., M.A, and V.Z. prepared the datasets and also facilitated the process of data gathering. S.Z.H. handled data gathering from the EHR and Iran Health Insurance System, as well as telephone interviews with patients and data cleansing. The initial draft was critically reviewed by R.R. and M.A. and ultimately all authors read and approved the final version of the manuscript.

Funding

Throughout this study, no financial resources or funding were received.

Data availability

The data that support the findings of this study are not openly available due to the policies and regulations of the data centers that provided data. The raw data could be made available from the corresponding authors upon reasonable request. The Python source code is available at https://doi.org/10.5281/zenodo.12805879.

Declarations

Conflict of interest

The authors declare no competing interests.

Ethical approval

All experimental protocols were approved by the Institutional Review Board of Shahid Beheshti University of Medical Sciences, with the approval code IR.SBMU.RETECH.REC.1401.823, and informed consent was obtained from all subjects and/or their legal guardians. In addition, all methods were performed in accordance with the relevant guidelines and regulations.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-81734-y.